Feasibility of Photovoltaic Module Single-Diode Model Fitting to the Current–Voltage Curves Measured in the Vicinity of the Maximum Power Point for Online Condition Monitoring Purposes
Abstract
Highlights
- Single-diode model fitting to partial I–U curves was systematically investigated.
- The I–U curves were measured in the vicinity of the MPP.
- The I–U curve region selected for fitting had a significant effect on the fit accuracy.
- Suitably constructed partial I–U curves can be used in online condition monitoring.
- PV module aging can be detected and quantified using partial I–U curves.
Abstract
1. Introduction
2. Methods and Data
2.1. Used Electrical Model and Fitting Procedure
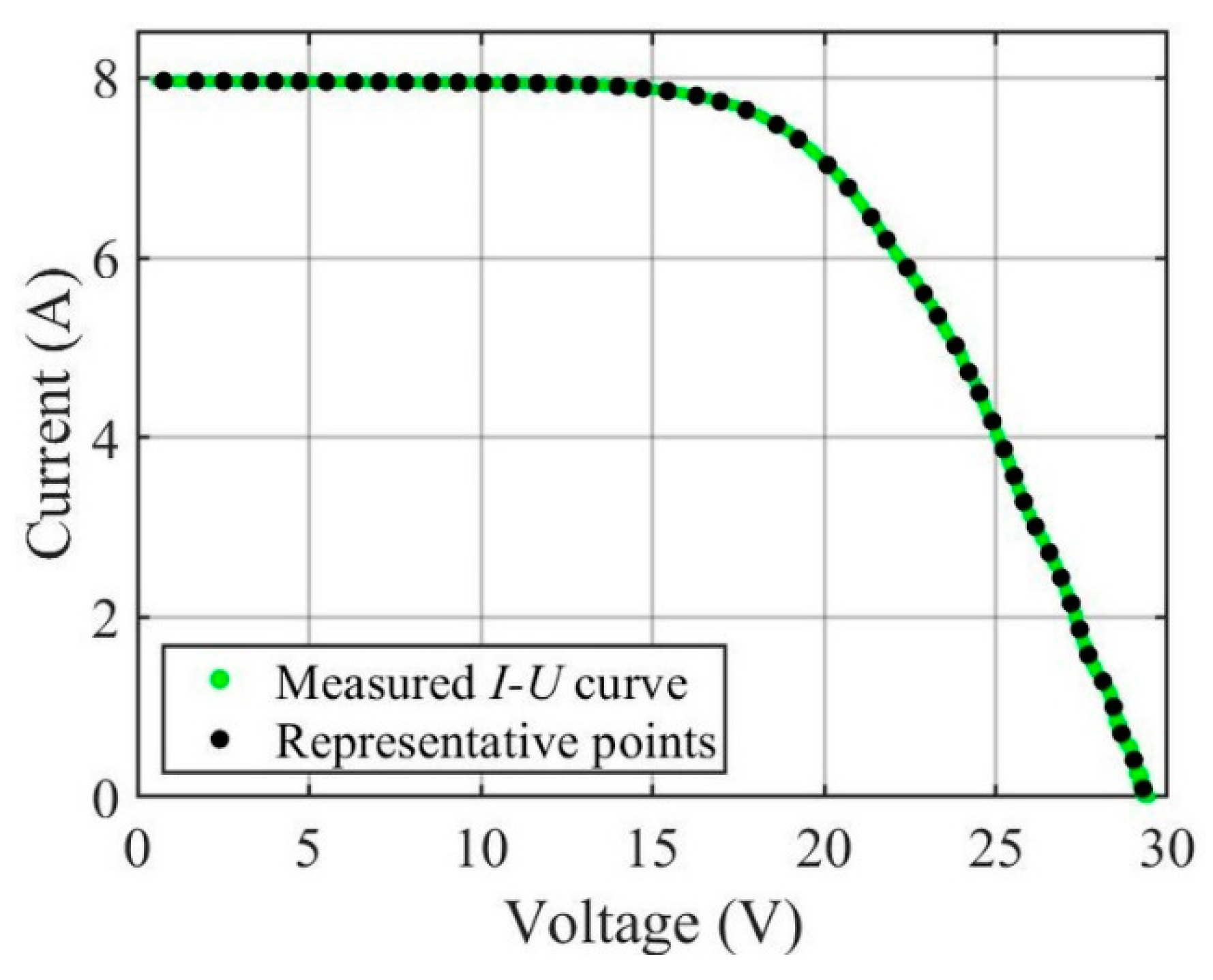
2.2. Used Measurement Data
2.3. Pre-Processing of Measurement Data
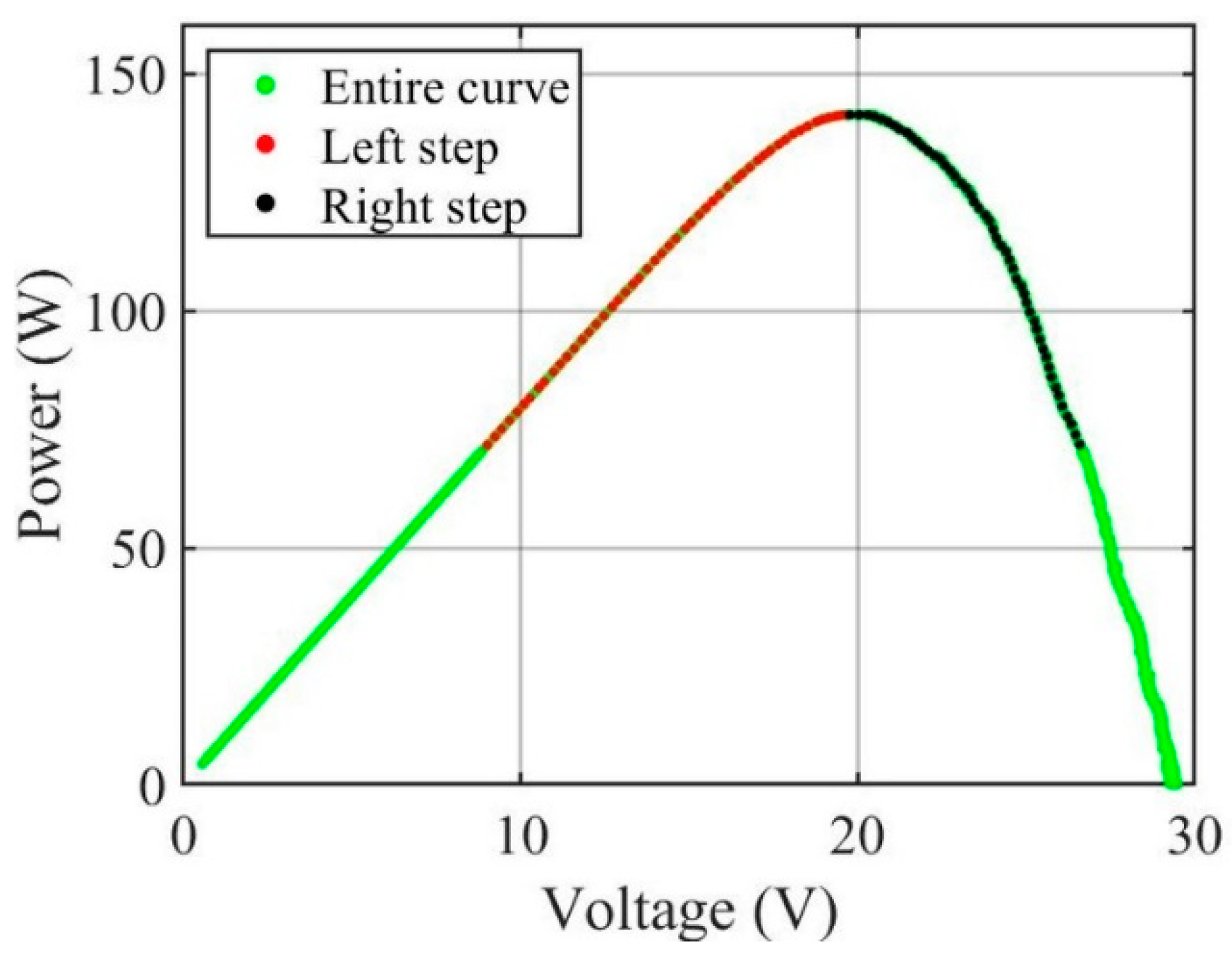
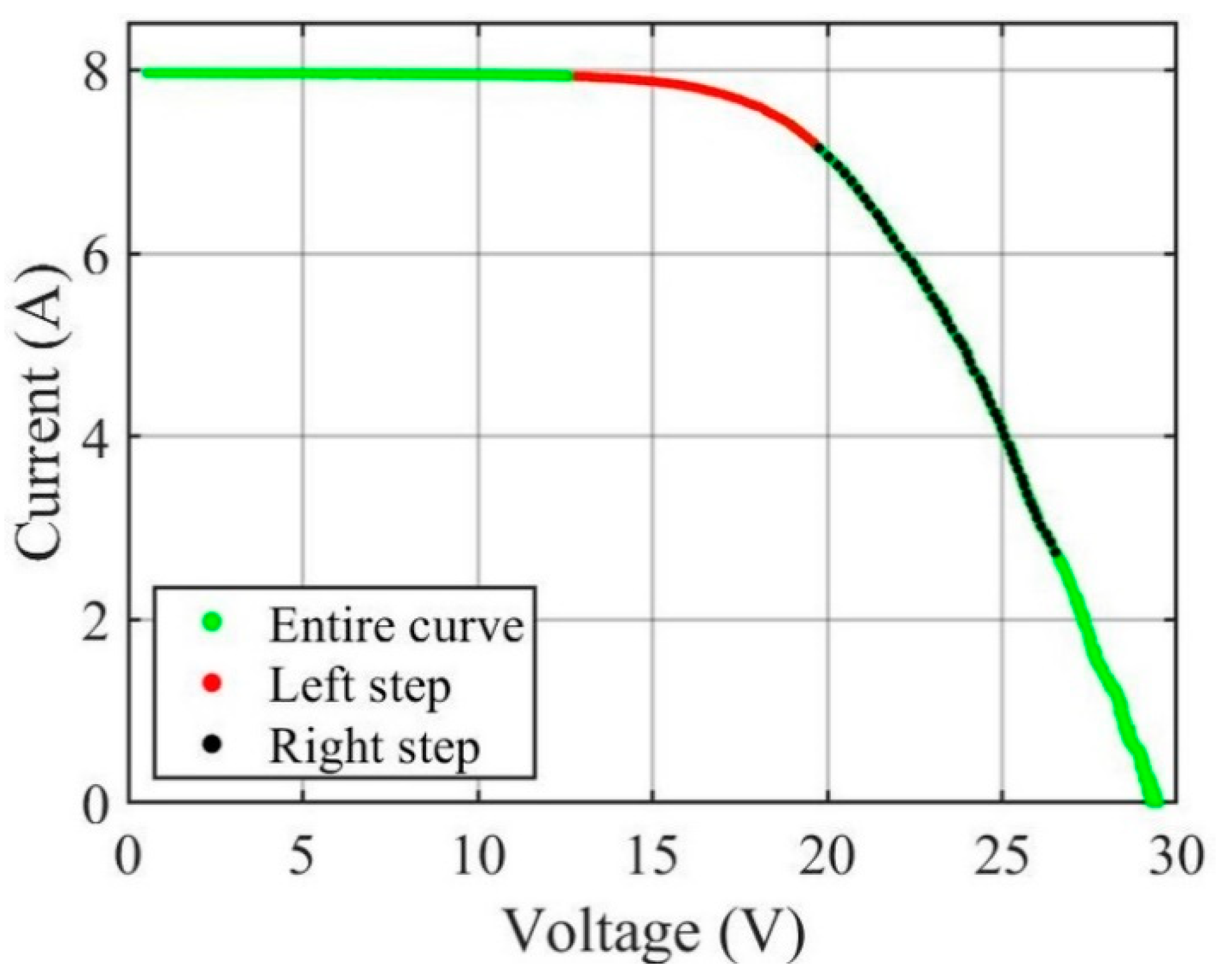
2.4. Fitting the Single-Diode Model to Partial I–U Curves
3. Results and Discussion
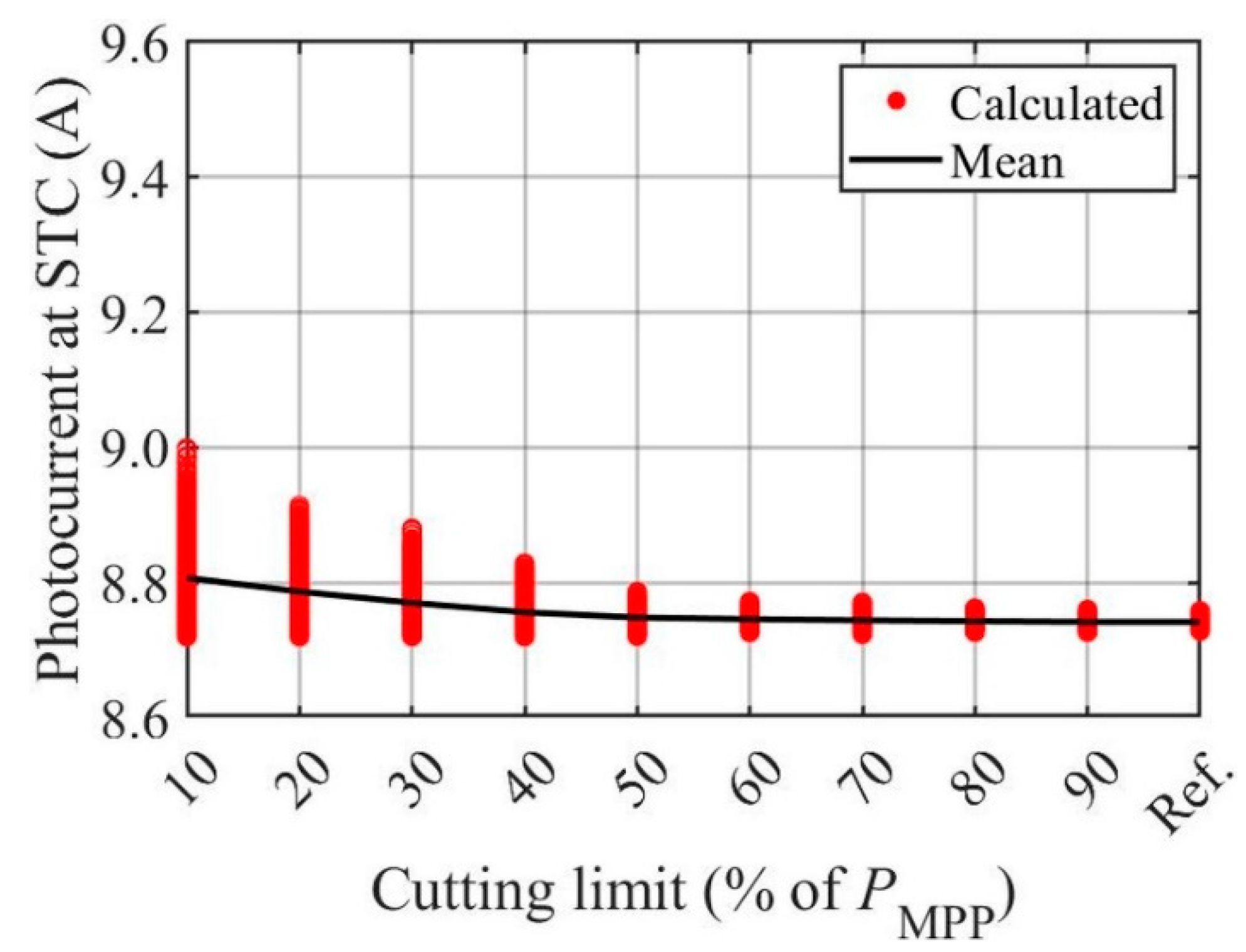
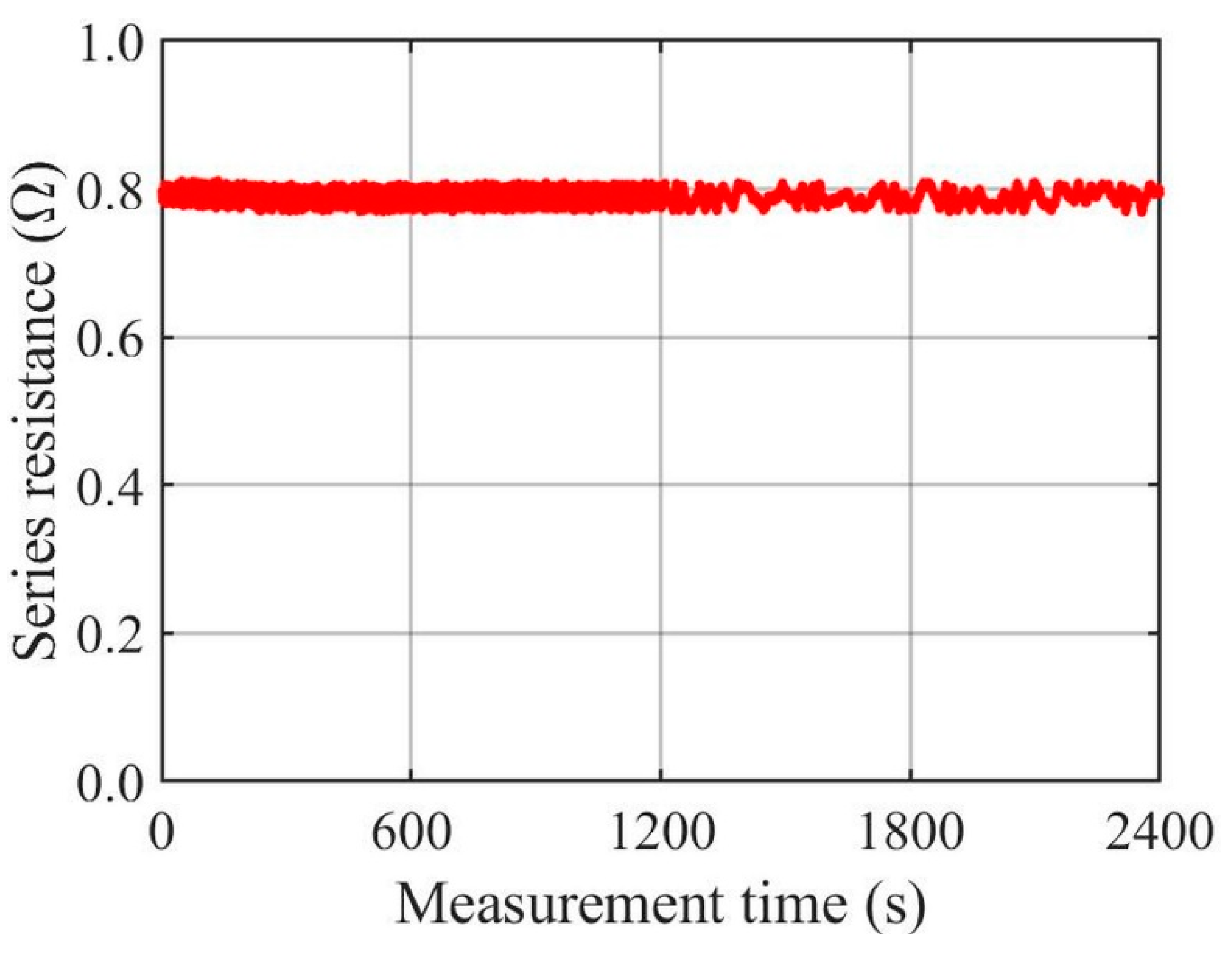
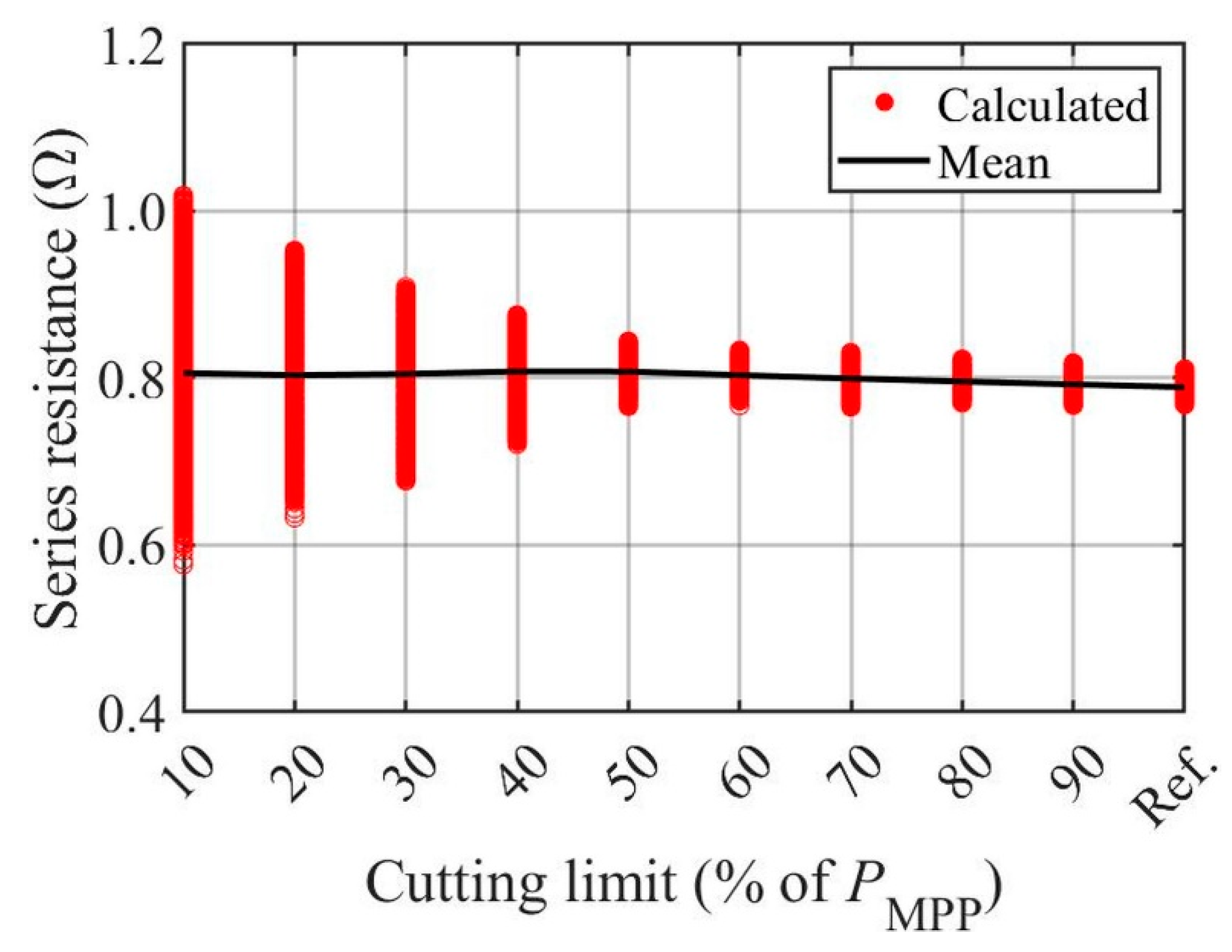
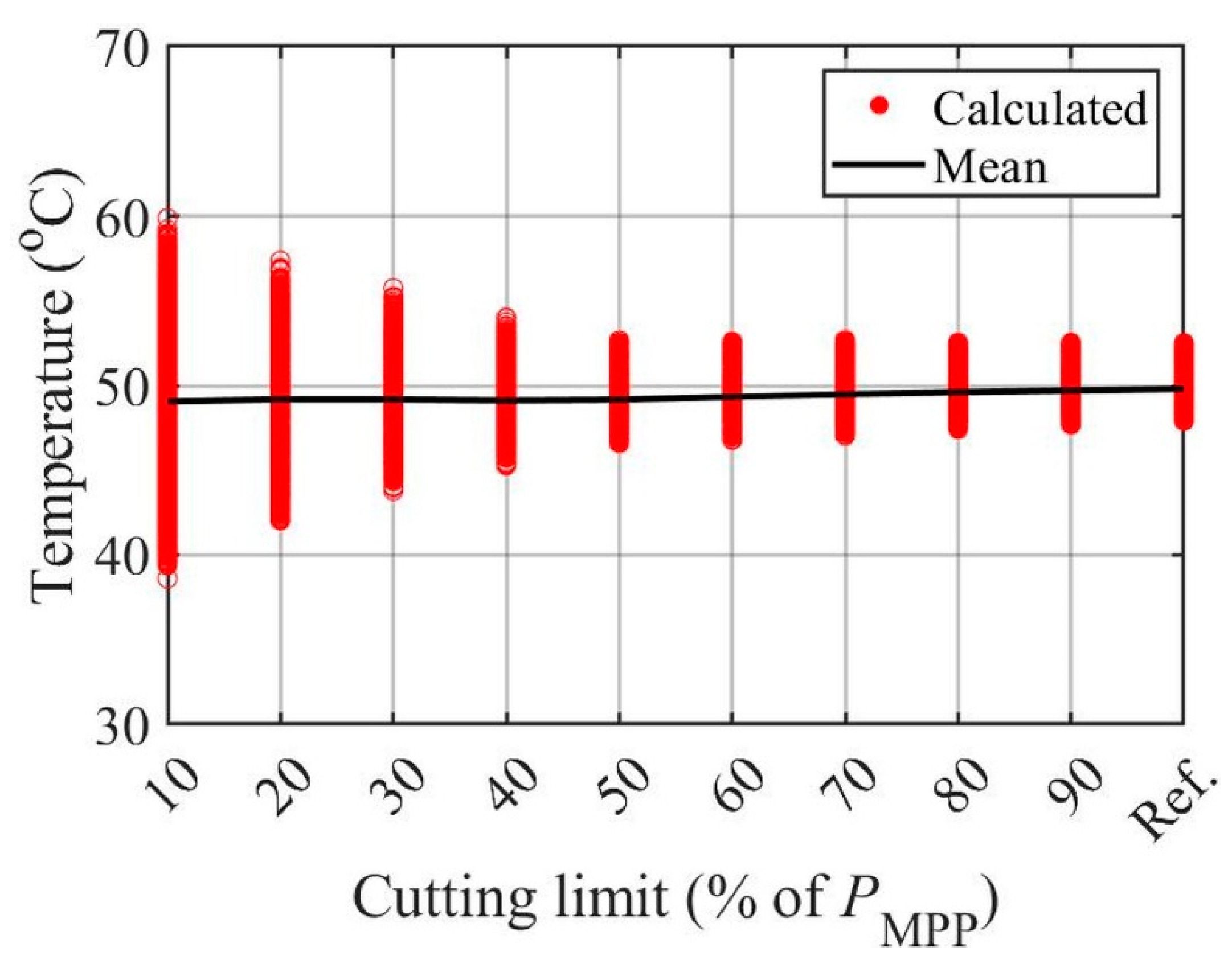
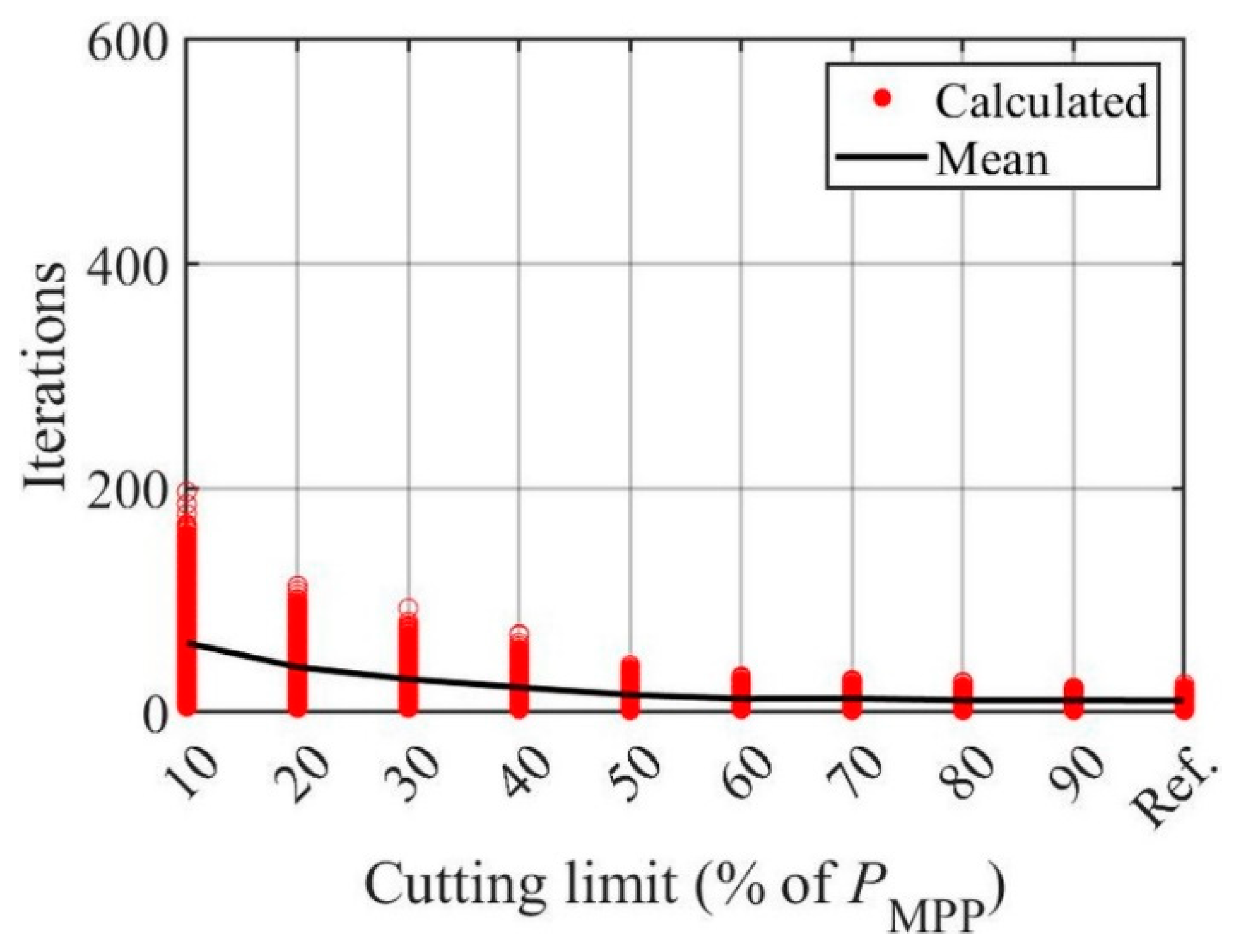
3.1. Symmetrical Cutting with Respect to MPP Power
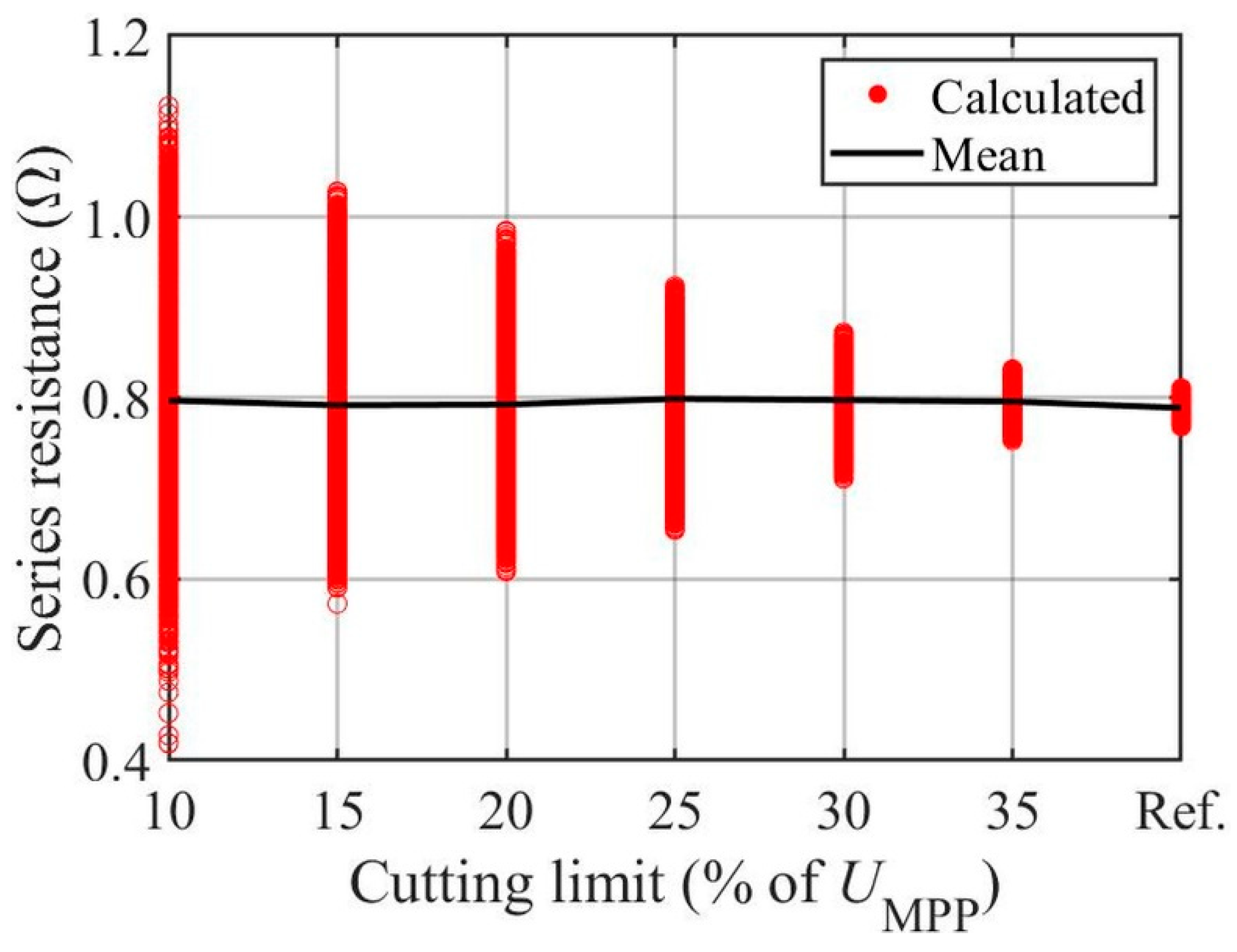
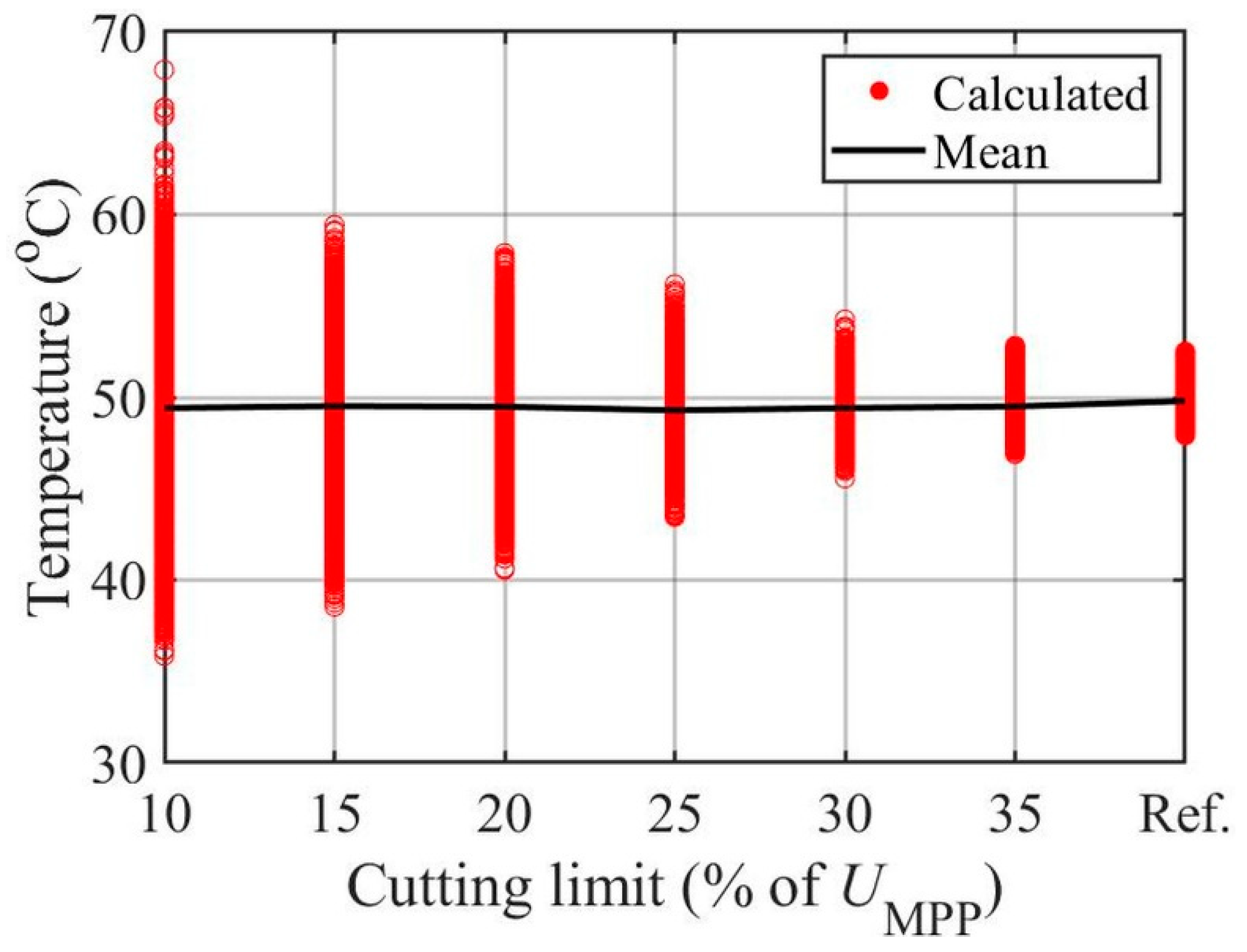
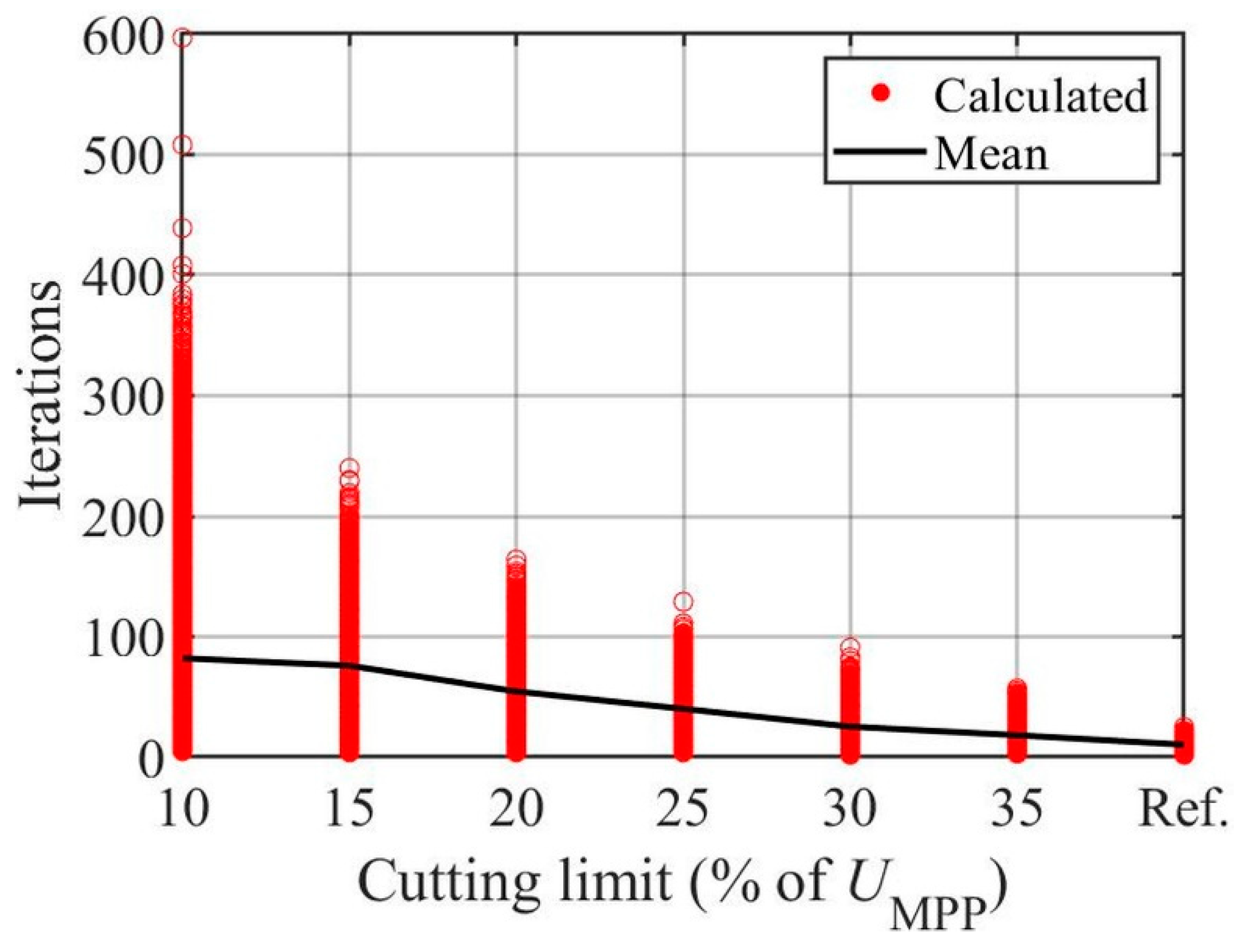
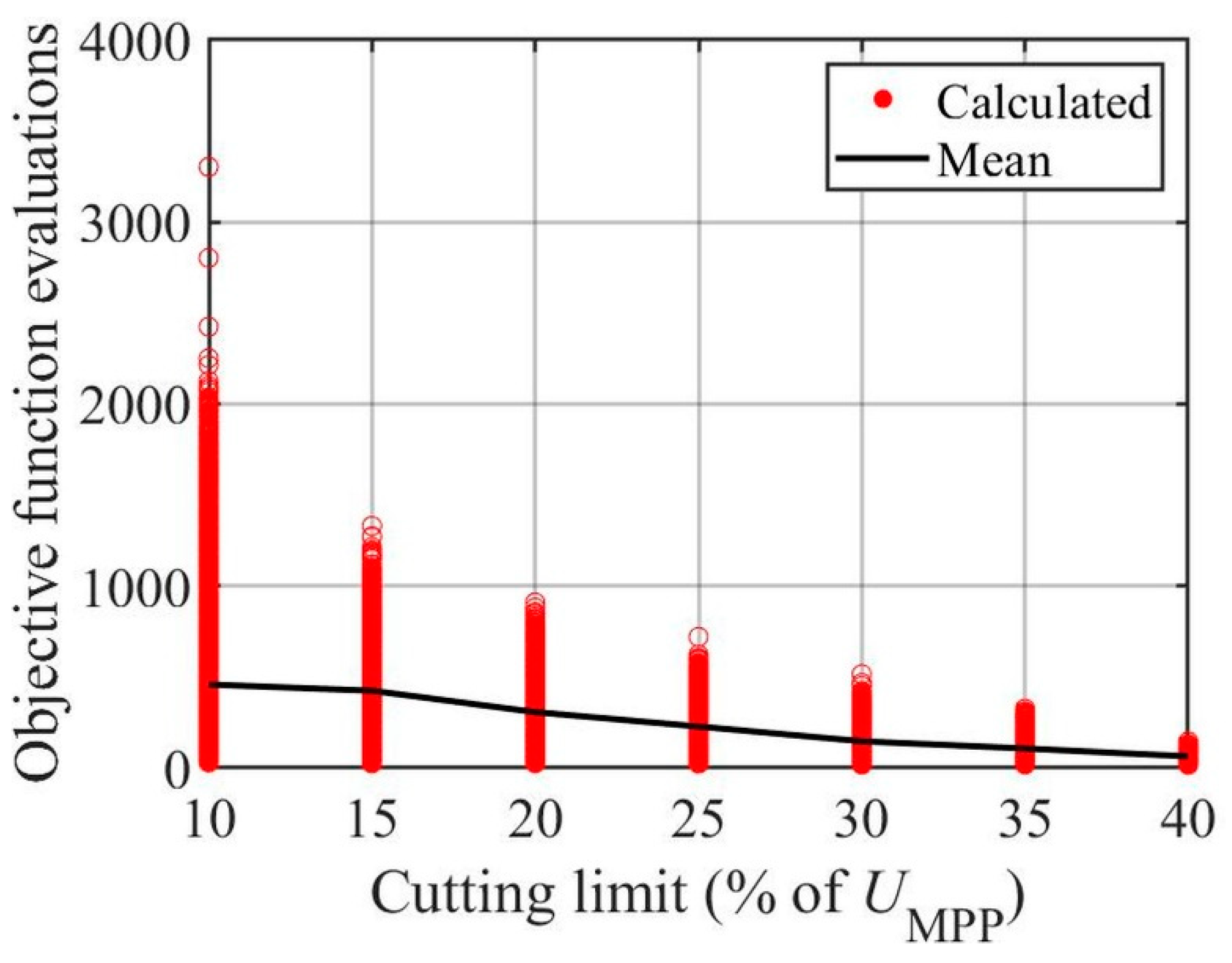
3.2. Symmetrical Cutting with Respect to MPP Voltage
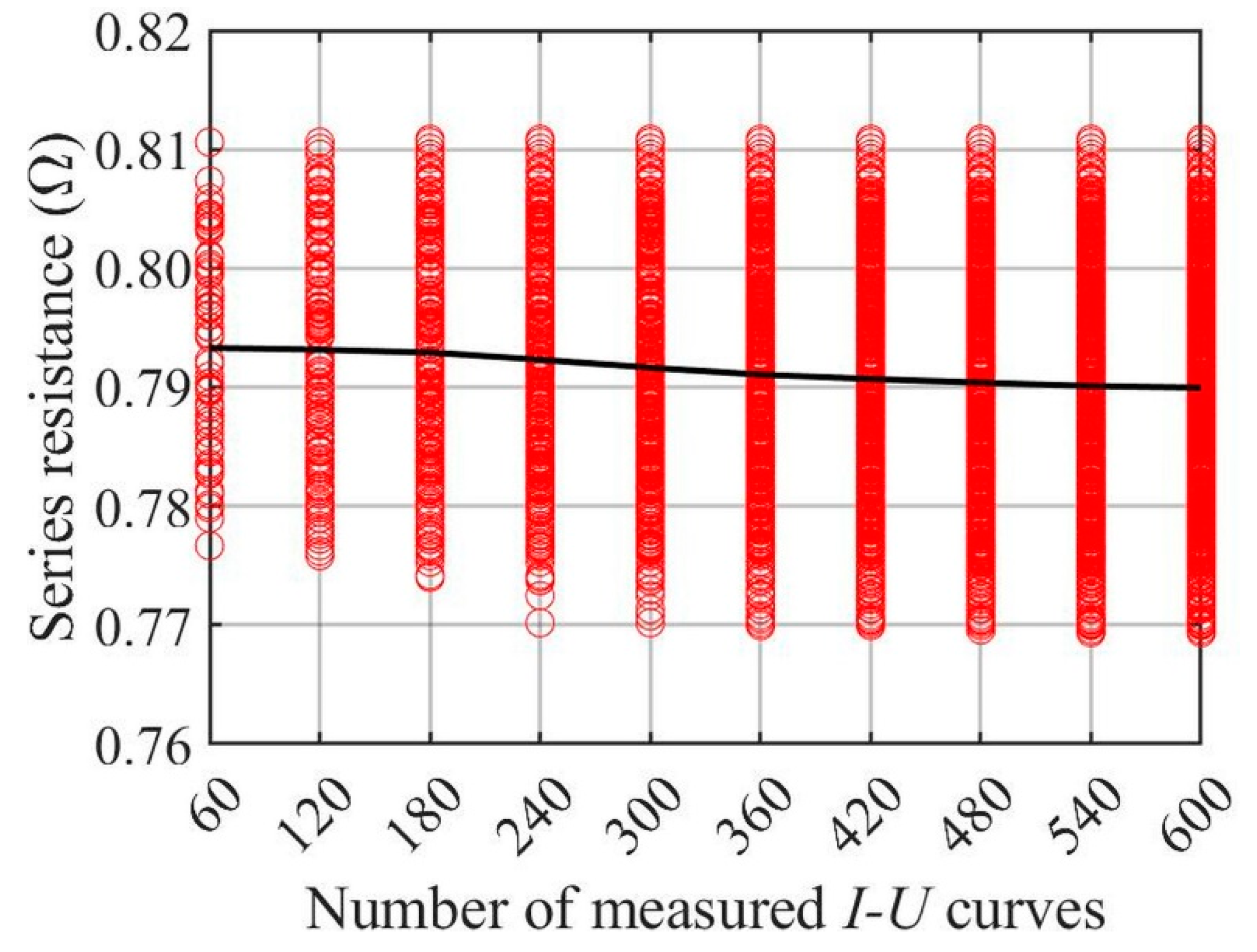
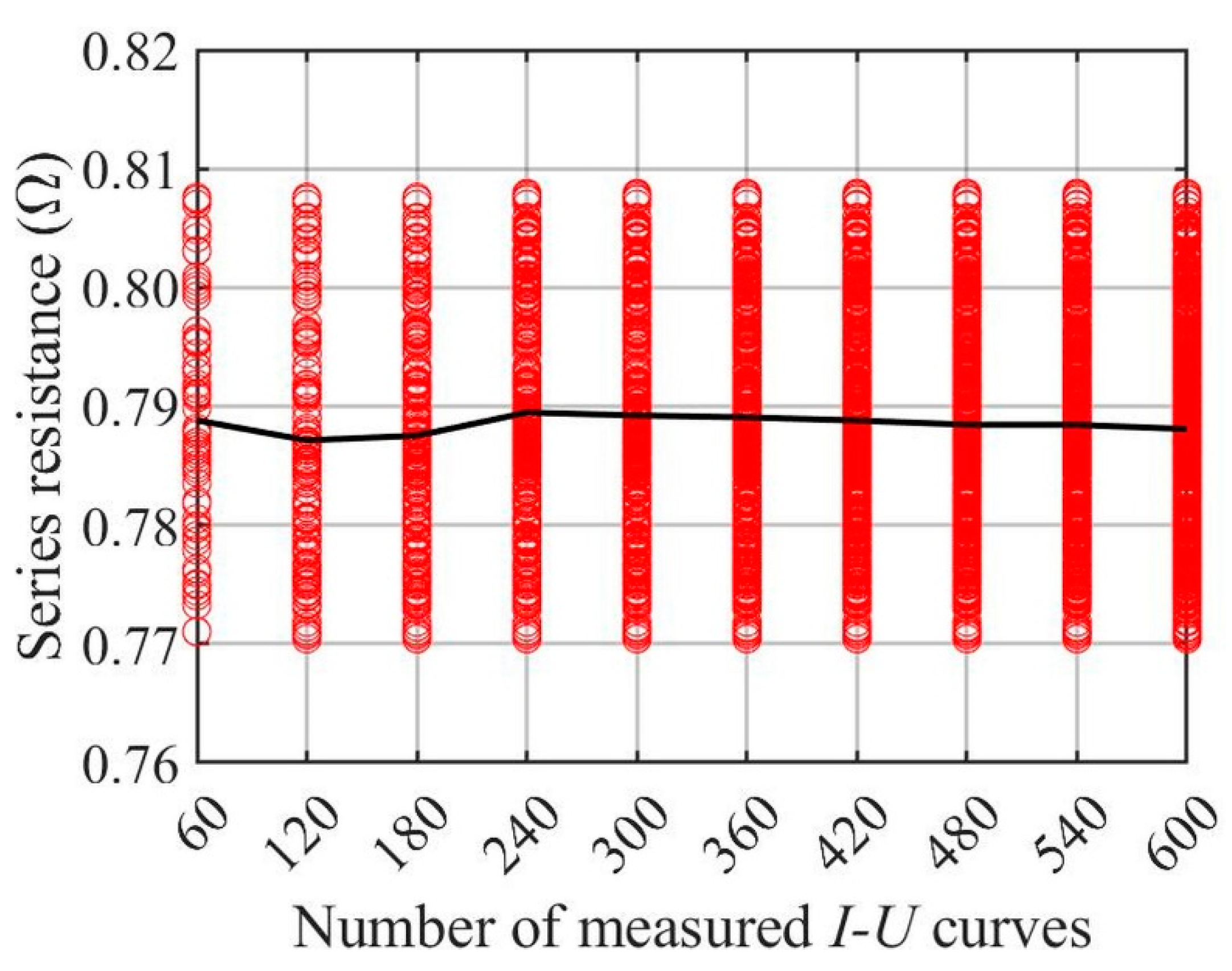
3.3. Required Number of I–U Curves for Reliable Series Resistance Analysis
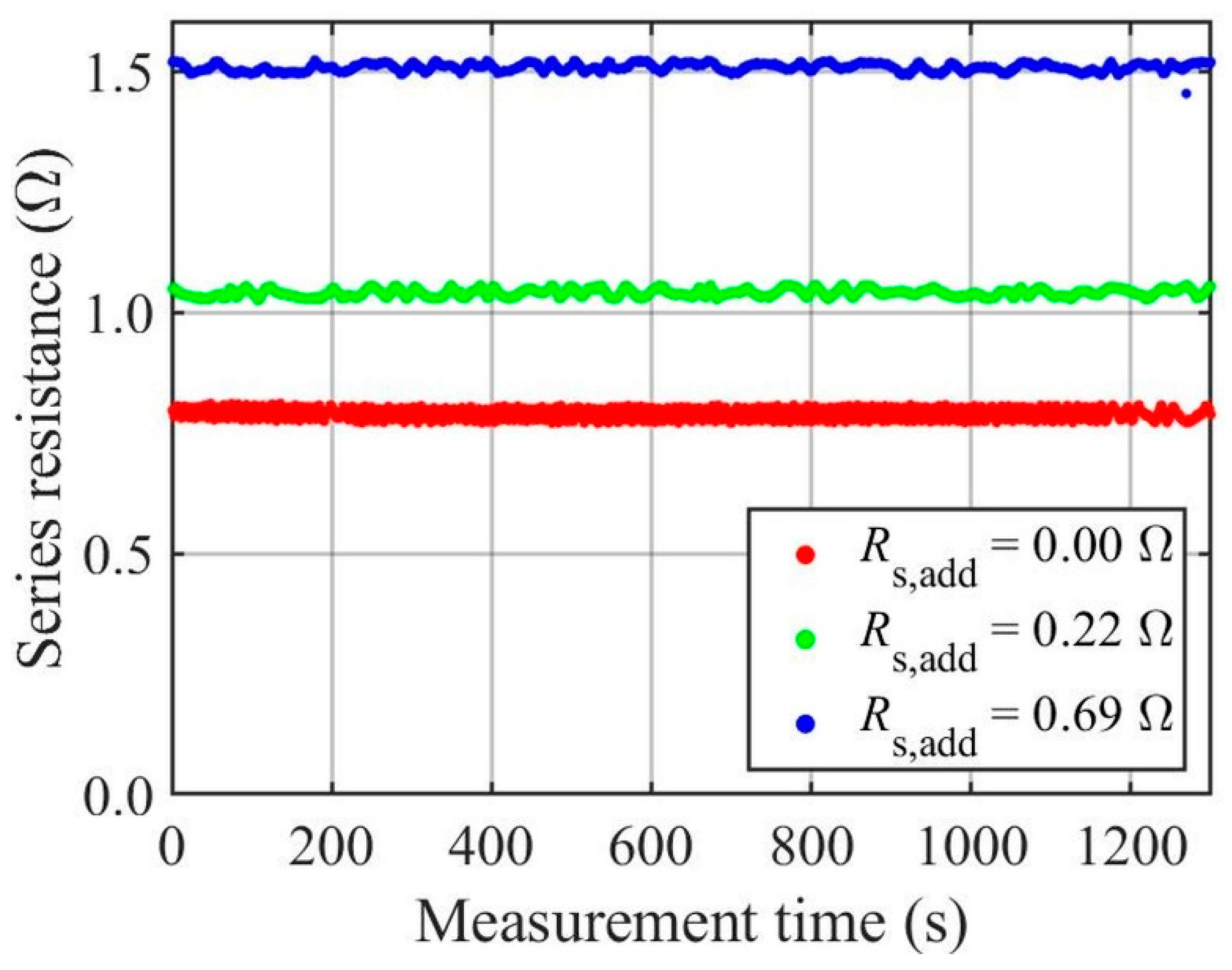
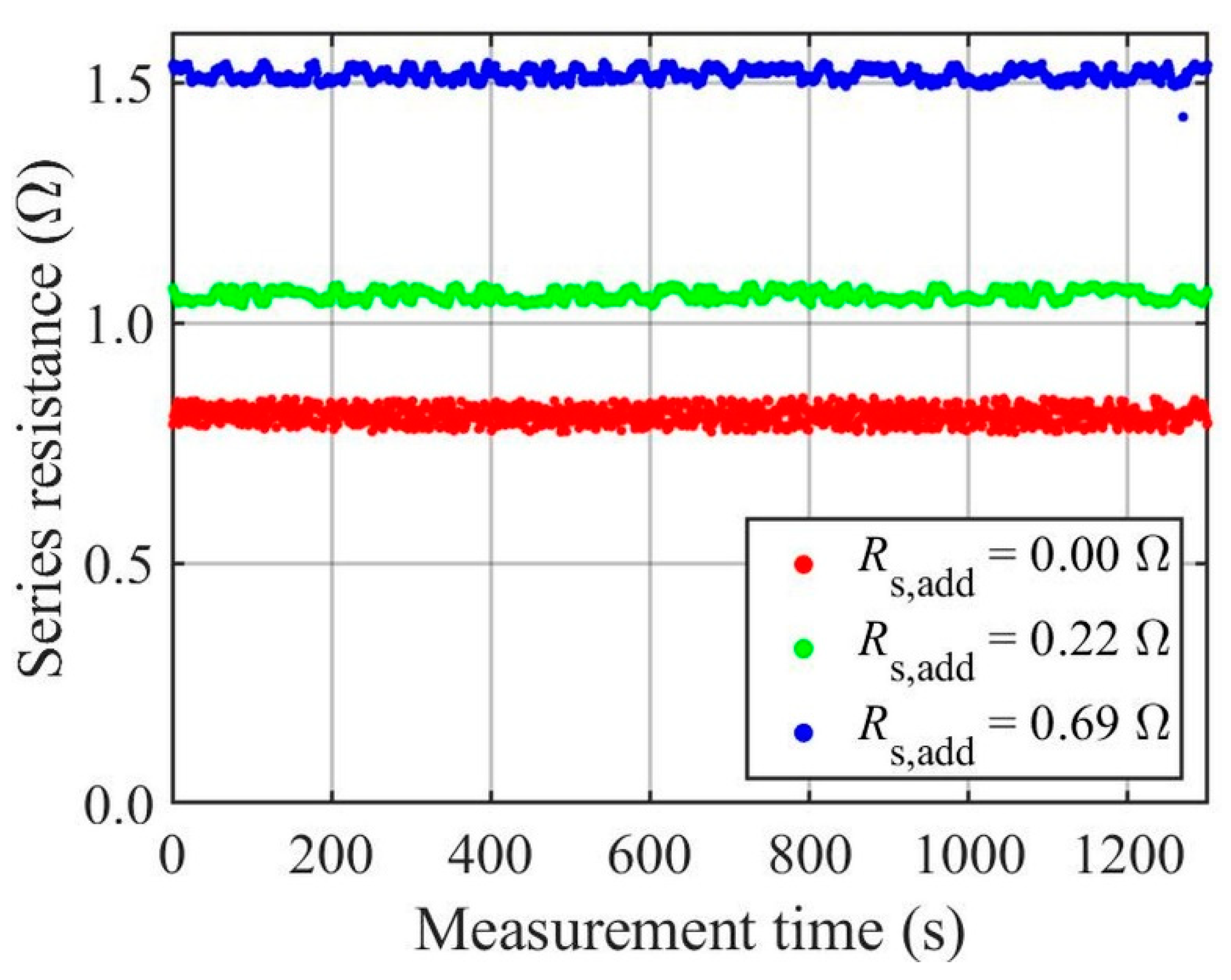
3.4. PV Module Aging Detection
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bastidas-Rodriguez, J.D.; Franco, E.; Petrone, G.; Ramos-Paja, C.A.; Spagnuolo, G. Quantification of photovoltaic module degradation using model based indicators. Math. Comput. Simul. 2017, 131, 101–113. [Google Scholar] [CrossRef]
- Sera, D.; Mathe, L.; Kerekes, T.; Teodorescu, R. A low-disturbance diagnostic function integrated in the PV array’s MPPT algorithm. IEEE Ind. Electron. Soc. 2011, 2456–2460. [Google Scholar] [CrossRef]
- Lappalainen, K.; Manganiello, P.; Piliougine, M.; Spagnuolo, G.; Valkealahti, S. Virtual Sensing of Photovoltaic Module Operating Parameters. IEEE J. Photovolt. 2020, 10, 852–862. [Google Scholar] [CrossRef]
- Hachana, O.; Hemsas, K.E.; Tina, G.M. Comparison of different metaheuristic algorithms for parameter identification of photovoltaic cell/module. J. Renew. Sust. Energy 2013, 5, 053122. [Google Scholar] [CrossRef]
- Cárdenas, A.A.; Carrasco, M.; Mancilla-David, F.; Street, A.; Cárdenas, R. Experimental Parameter Extraction in the Single-Diode Photovoltaic Model via a Reduced-Space Search. IEEE Trans. Ind. Electron. 2017, 64, 1468–1476. [Google Scholar] [CrossRef]
- Panchal, A.K. A per-unit-single-diode-model parameter extraction algorithm: A high-quality solution without reduced-dimensions search. Sol. Energy 2020, 207, 1070–1077. [Google Scholar] [CrossRef]
- Garrigós, A.; Blanes, J.M.; Carrasco, J.A.; Ejea, J.B. Real time estimation of photovoltaic modules characteristics and its application to maximum power point operation. Renew. Energy 2007, 32, 1059–1076. [Google Scholar] [CrossRef]
- Petrone, G.; Luna, M.; La Tona, G.; Di Piazza, M.C.; Spagnuolo, G. Online Identification of Photovoltaic Source Parameters by Using a Genetic Algorithm. Appl. Sci. 2018, 8, 9. [Google Scholar] [CrossRef]
- Blanes, J.M.; Toledo, F.J.; Montero, S.; Garrigós, A. In-Site Real-Time Photovoltaic I-V Curves and Maximum Power Point Estimator. IEEE Trans. Power Electron. 2012, 28, 1234–1240. [Google Scholar] [CrossRef]
- Toledo, F.J.; Blanes, J.M.; Garrigós, A.; Martinez, J.A. Analytical resolution of the electrical four-parameters model of a photovoltaic module using small perturbation around the operating point. Renew. Energy 2012, 43, 83–89. [Google Scholar] [CrossRef]
- Tay, S.; Lim, I.; Ye, Z.; Yang, D.; Garrigós, A. PV Parameter Identification using Reduced I-V Data. In Proceedings of the IECON 2017–43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 2653–2657. [Google Scholar] [CrossRef][Green Version]
- Toledo, F.J.; Blanes, J.M. Analytical and quasi-explicit four arbitrary point method for extraction of solar cell single-diode model parameters. Renew. Energy 2016, 92, 346–356. [Google Scholar] [CrossRef]
- Lappalainen, K.; Piliougine, M.; Spagnuolo, G. Experimental comparison between various fitting approaches based on RMSE minimization for photovoltaic module parametric identification. Energy Convers. Manag. 2022, 258, 115526. [Google Scholar] [CrossRef]
- Kalliojärvi-Viljakainen, H.; Lappalainen, K.; Valkealahti, S. Preprocessing of PV Panel Measured Current-Voltage Characteristics before Curve Fitting. In Proceedings of the 2020 47th IEEE Photovoltaic Specialists Conference (PVSC), Virtual, 15 June–21 August 2020; pp. 117–123. [Google Scholar] [CrossRef]
- Petrone, G.; Ramos-Paja, C.A.; Spagnuolo, G. Photovoltaic Sources Modeling; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Kalliojärvi-Viljakainen, H.; Lappalainen, K.; Valkealahti, S. A novel procedure for identifying the parameters of the single-diode model and the operating conditions of a photovoltaic module from measured current–voltage curves. Energy Rep. 2022, 8, 4633–4640. [Google Scholar] [CrossRef]
- Kratochvil, J.A.; Boyson, W.E.; King, D.L. Photovoltaic array performance model. Sandia Natl. Lab. 2004, 20, 2004–3535. [Google Scholar] [CrossRef]
- De Soto, W.; Klein, S.A.; Beckman, W.A. Improvement and validation of a model for photovoltaic array performance. Sol. Energy 2006, 80, 78–88. [Google Scholar] [CrossRef]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Comprehensive approach for modeling and simulation of photovoltaic arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Schroder, D.K. Semiconductor Material and Device Characterization; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Torres Lobera, D.; Mäki, A.; Huusari, J.; Lappalainen, K.; Suntio, T.; Valkealahti, S. Operation of TUT Solar PV Power Station Research Plant under Partial Shading Caused by Snow and Buildings. Int. J. Photoenergy 2013, 63, 837310. [Google Scholar] [CrossRef]
- Wolf, P.; Benda, V. Identification of PV solar cells and modules parameters by combining statistical and analytical methods. Sol. Energy 2013, 93, 153–157. [Google Scholar] [CrossRef]
- Moballegh, S.; Jiang, J. Modeling, prediction, and experimental validations of power peaks of PV arrays under partial shading conditions. IEEE Trans. Sust. Energy 2014, 5, 293–300. [Google Scholar] [CrossRef]
- Orozco-Gutierrez, M.L.; Spagnuolo, G.; Ramirez-Scarpetta, J.M.; Petrone, G.; Ramos-Paja, C.A. Optimized Configuration of Mismatched Photovoltaic Arrays. IEEE J. Photovolt. 2016, 6, 1210–1220. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| ISC, STC | 8.72 A |
| IMPP, STC | 7.94 A |
| UOC, STC | 32.8 V |
| UMPP, STC | 22.9 V |
| KU | –0.124 V/K |
| KI | 0.0047 A/K |
| Rs, STC | 0.768 Ω |
| Rh, STC | 354 Ω |
| A | 1.10 |
| Ns | 54 |
| Cutting Limit (% of PMPP) | Mean (Ω) | Standard Deviation (Ω) |
|---|---|---|
| Entire curve | 0.7892 | 0.0098 |
| 90 | 0.7925 | 0.0126 |
| 80 | 0.7960 | 0.0132 |
| 70 | 0.7995 | 0.0156 |
| 60 | 0.8036 | 0.0150 |
| 50 | 0.8079 | 0.0169 |
| 40 | 0.8081 | 0.0367 |
| 30 | 0.8050 | 0.0620 |
| 20 | 0.8035 | 0.0841 |
| 10 | 0.8060 | 0.1055 |
| Cutting Limit (% of UMPP) | Mean (Ω) | Standard Deviation (Ω) |
|---|---|---|
| Entire curve | 0.7892 | 0.0098 |
| 35 | 0.7962 | 0.0173 |
| 30 | 0.7979 | 0.0303 |
| 25 | 0.7992 | 0.0667 |
| 20 | 0.7929 | 0.0969 |
| 15 | 0.7922 | 0.1133 |
| 10 | 0.7973 | 0.1247 |
| 1–600 s | 1201–1800 s | |||
|---|---|---|---|---|
| Number of Curves | Mean (Ω) | Standard Deviation (Ω) | Mean (Ω) | Standard Deviation (Ω) |
| 60 | 0.7933 | 0.0085 | 0.7888 | 0.0102 |
| 120 | 0.7932 | 0.0093 | 0.7871 | 0.0105 |
| 180 | 0.7929 | 0.0095 | 0.7875 | 0.0100 |
| 240 | 0.7923 | 0.0096 | 0.7895 | 0.0101 |
| 300 | 0.7916 | 0.0097 | 0.7892 | 0.0099 |
| 360 | 0.7911 | 0.0098 | 0.7891 | 0.0096 |
| 420 | 0.7907 | 0.0099 | 0.7888 | 0.0094 |
| 480 | 0.7904 | 0.0098 | 0.7884 | 0.0091 |
| 540 | 0.7901 | 0.0099 | 0.7884 | 0.0091 |
| 600 | 0.7900 | 0.0100 | 0.7881 | 0.0091 |
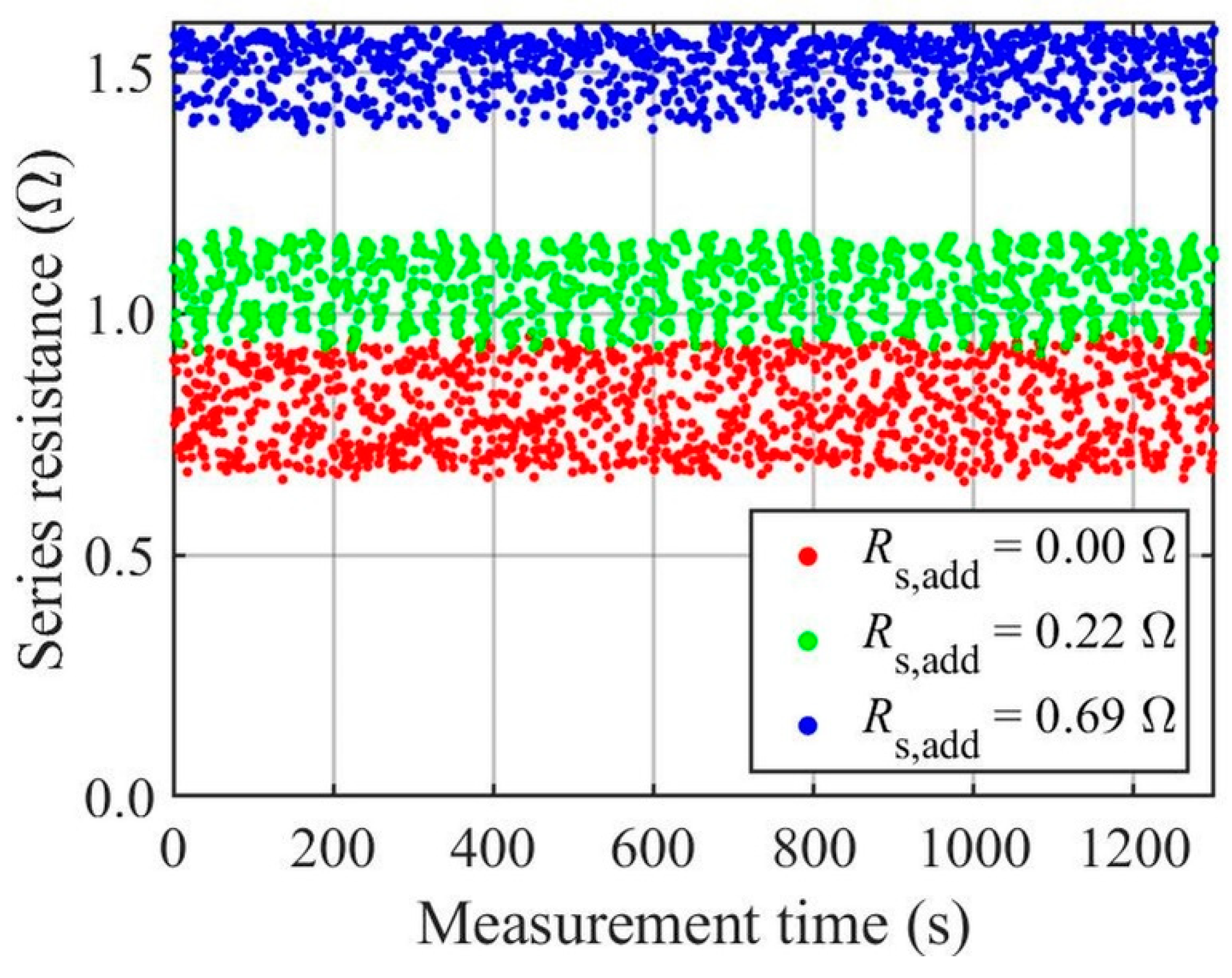
| Rs, add (Ω) | Cutting Limit (%) | Mean (Ω) | Standard Deviation (Ω) |
|---|---|---|---|
| 0.00 | 100 | 0.7894 | 0.0101 |
| 50 | 0.8075 | 0.0166 | |
| 20 | 0.8040 | 0.0841 | |
| 0.22 | 100 | 1.0401 | 0.0079 |
| 50 | 1.0568 | 0.0111 | |
| 20 | 1.0596 | 0.0690 | |
| 0.69 | 100 | 1.5077 | 0.0080 |
| 50 | 1.5158 | 0.0127 | |
| 20 | 1.5086 | 0.0580 |
| Rs, add (Ω) | Cutting Limit of 100% | Cutting Limit of 50% | Cutting Limit of 20% |
|---|---|---|---|
| 0.22 | 0.2507 | 0.2493 | 0.2556 |
| 0.69 | 0.7183 | 0.7083 | 0.7045 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalliojärvi, H.; Lappalainen, K.; Valkealahti, S. Feasibility of Photovoltaic Module Single-Diode Model Fitting to the Current–Voltage Curves Measured in the Vicinity of the Maximum Power Point for Online Condition Monitoring Purposes. Energies 2022, 15, 9079. https://doi.org/10.3390/en15239079
Kalliojärvi H, Lappalainen K, Valkealahti S. Feasibility of Photovoltaic Module Single-Diode Model Fitting to the Current–Voltage Curves Measured in the Vicinity of the Maximum Power Point for Online Condition Monitoring Purposes. Energies. 2022; 15(23):9079. https://doi.org/10.3390/en15239079
Chicago/Turabian StyleKalliojärvi, Heidi, Kari Lappalainen, and Seppo Valkealahti. 2022. "Feasibility of Photovoltaic Module Single-Diode Model Fitting to the Current–Voltage Curves Measured in the Vicinity of the Maximum Power Point for Online Condition Monitoring Purposes" Energies 15, no. 23: 9079. https://doi.org/10.3390/en15239079
APA StyleKalliojärvi, H., Lappalainen, K., & Valkealahti, S. (2022). Feasibility of Photovoltaic Module Single-Diode Model Fitting to the Current–Voltage Curves Measured in the Vicinity of the Maximum Power Point for Online Condition Monitoring Purposes. Energies, 15(23), 9079. https://doi.org/10.3390/en15239079










