Thermal Performance of Load-Bearing, Lightweight, Steel-Framed Partition Walls Using Thermal Break Strips: A Parametric Study
Abstract
:1. Introduction
2. Materials and Methods
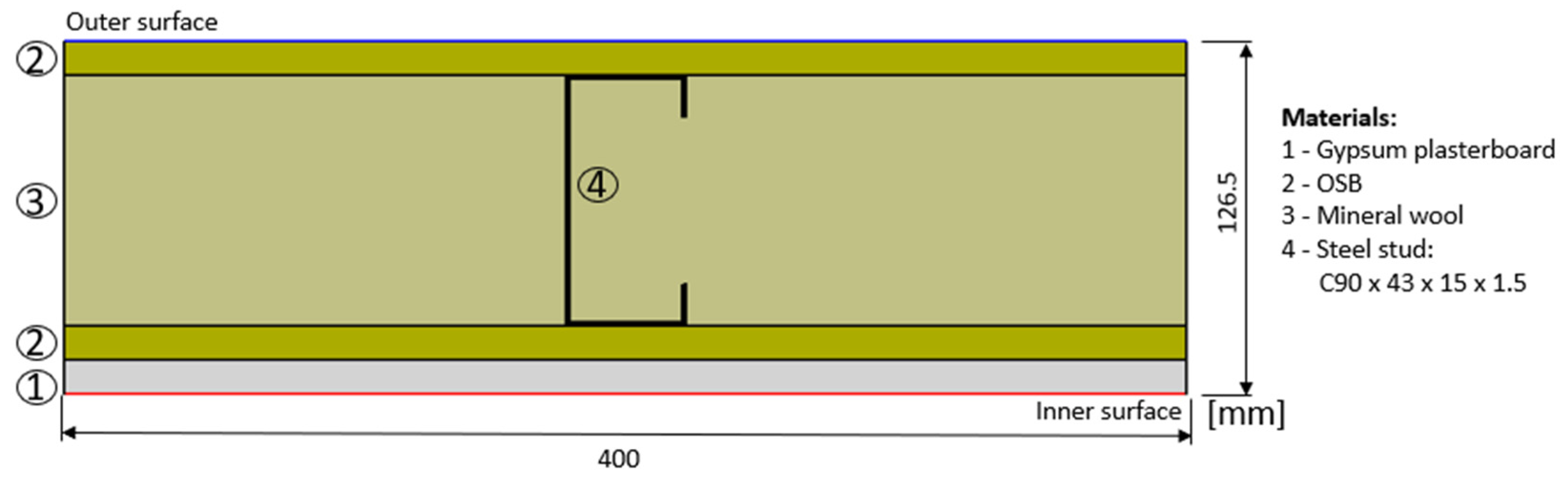
2.1. Reference Partition LSF Wall
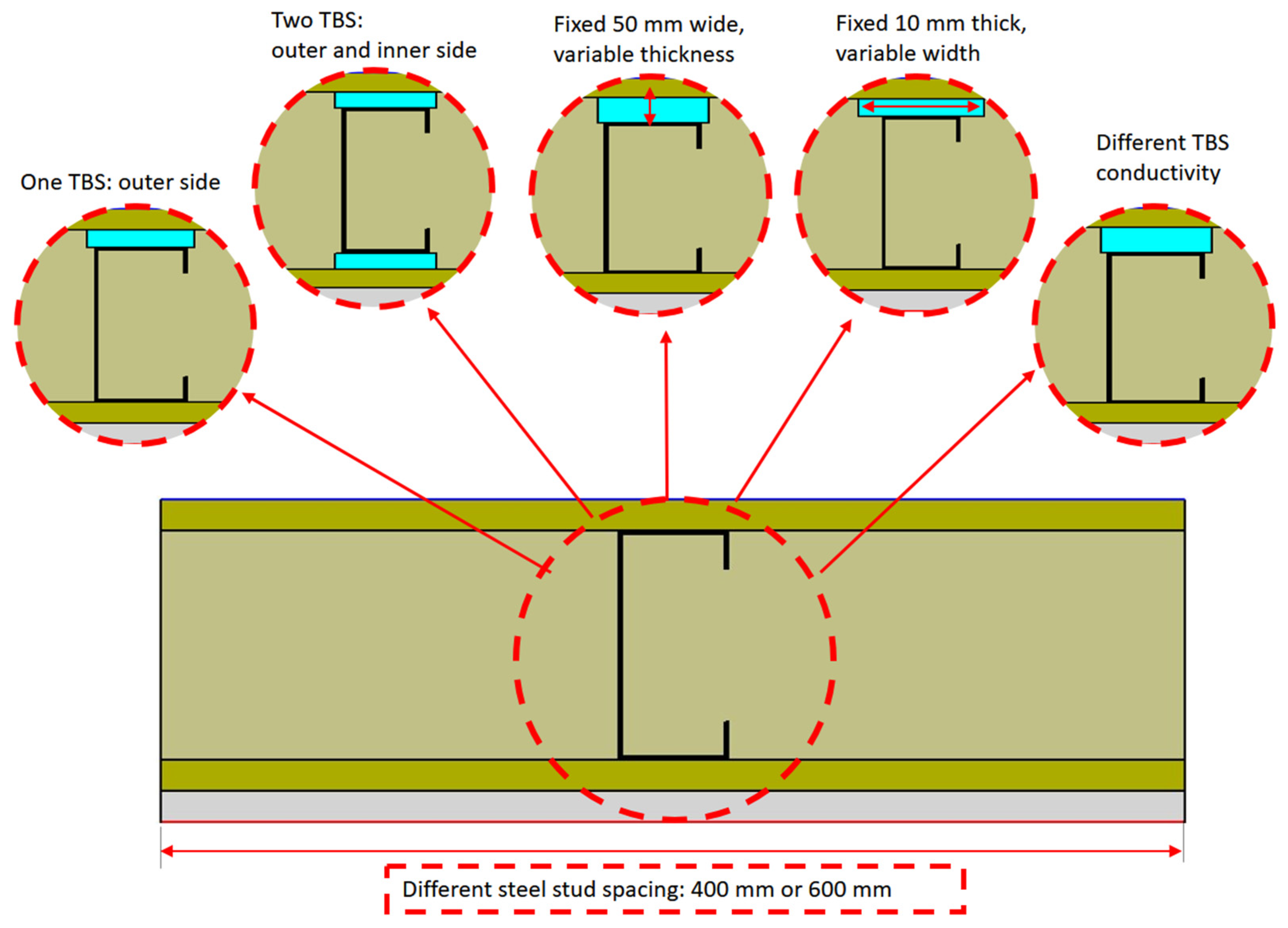
2.2. Evaluated Parameters and Values
- (1)
- their cross-section width was fixed (50 mm) and their thickness was changed within the interval of 5–15 mm, with an increment of 2.5 mm;
- (2)
- their thickness was fixed (10 mm) and their width ranged within the interval of 30–70 mm, with an increment of 10 mm;
- (3)
- for the two previous evaluated parameters, five different TBS thermal conductivities were studied (7.5, 15, 30, 60, and 120 mW/m/K);
- (4)
- the number of TBS was zero (without TBS), one TBS (outer flange side), and two TBS (both inner and outer flange side).
2.3. Characterization of Materials
2.4. Numerical Simulations
2.4.1. Discretization of the Models’ Domain
2.4.2. Boundary Conditions
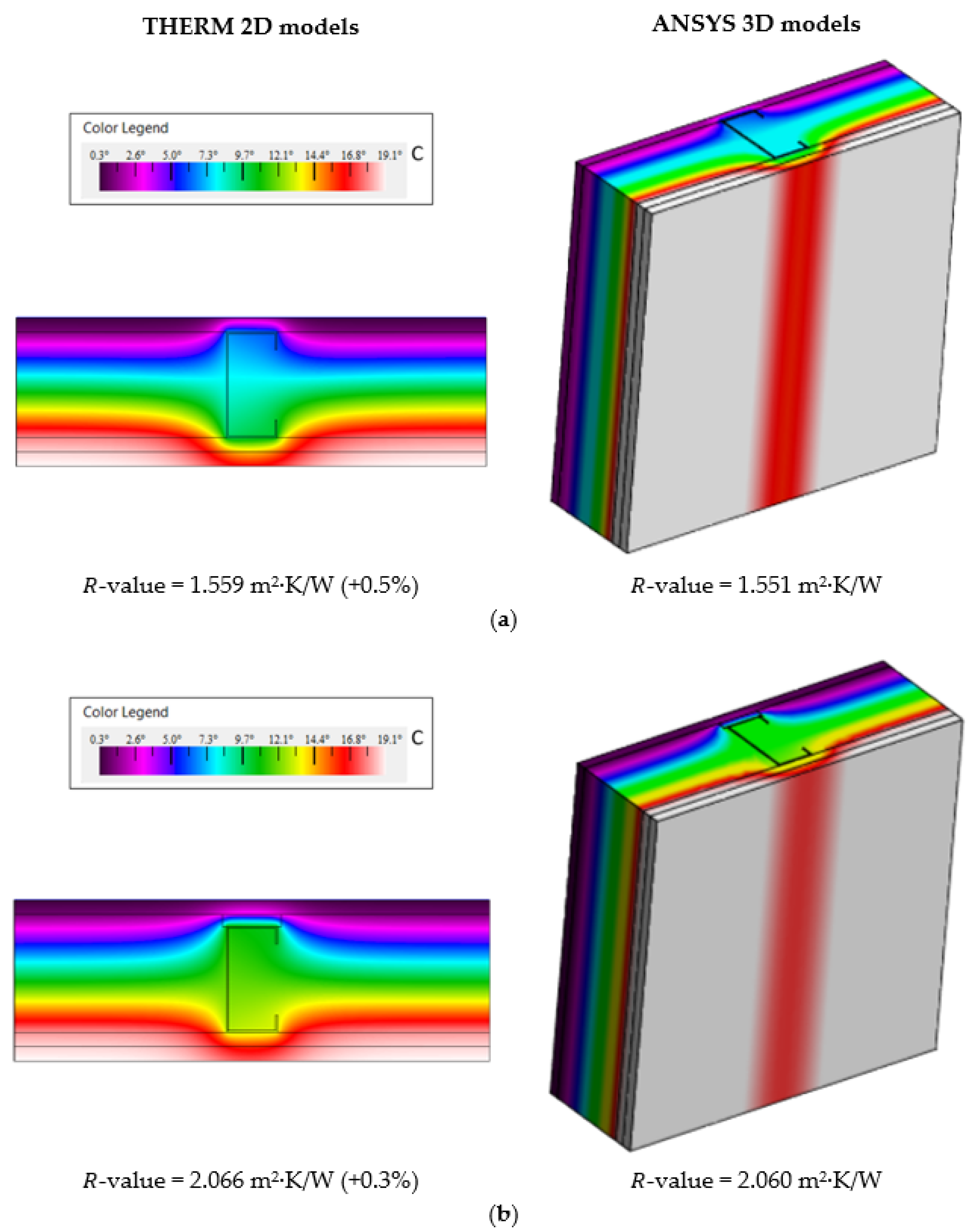
2.4.3. Verifications of Model Accuracy and Validation
- (1)
- ISO 10211 Test Cases Verification
- (2)
- ISO 6946 Analytical Approach Verification
- (3)
- 3D FEM Verification
- (4)
- Lab Measurement Validation
3. Results and Discussion
3.1. Reference Partition LSF Wall
3.2. One Thermal Break Strip
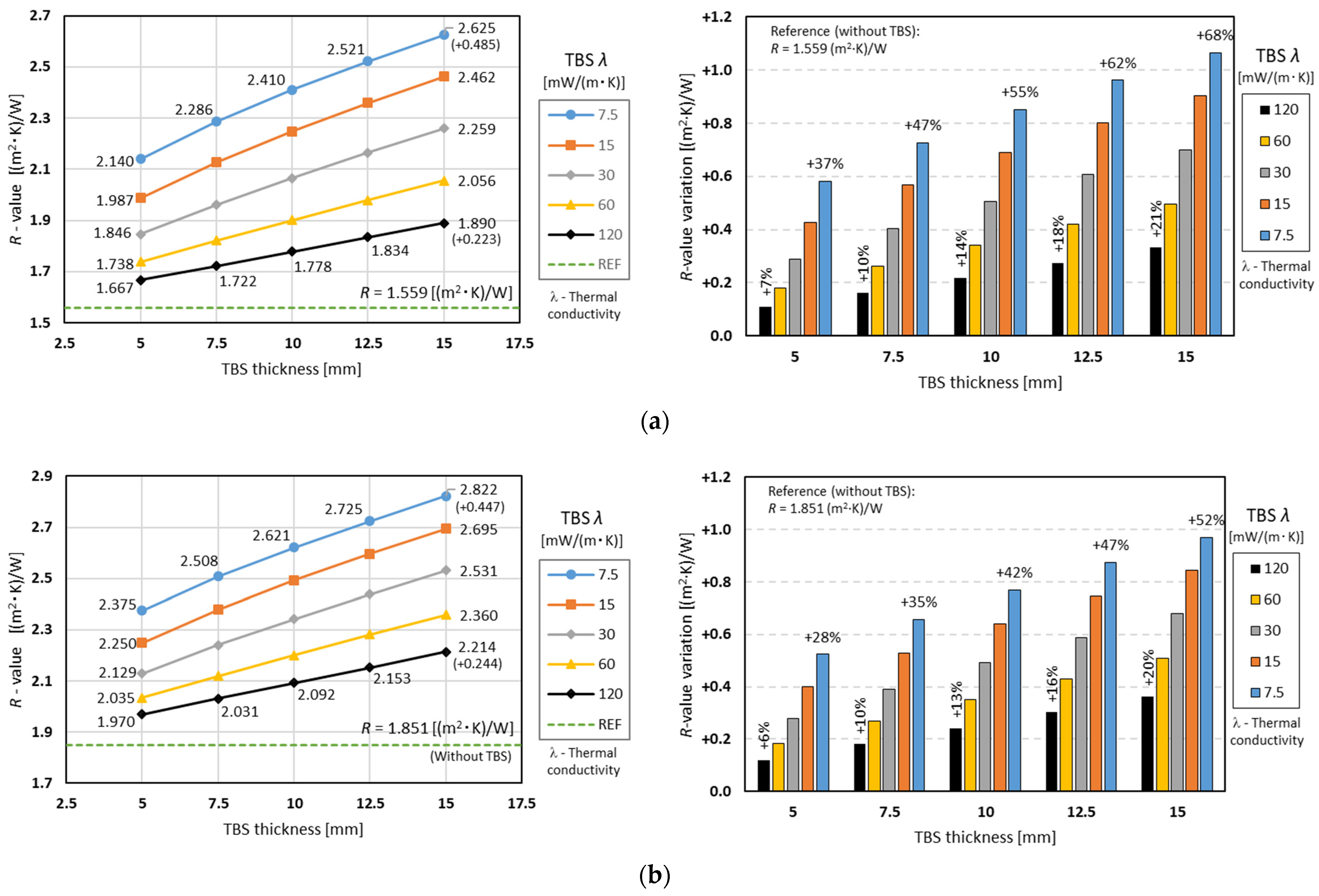
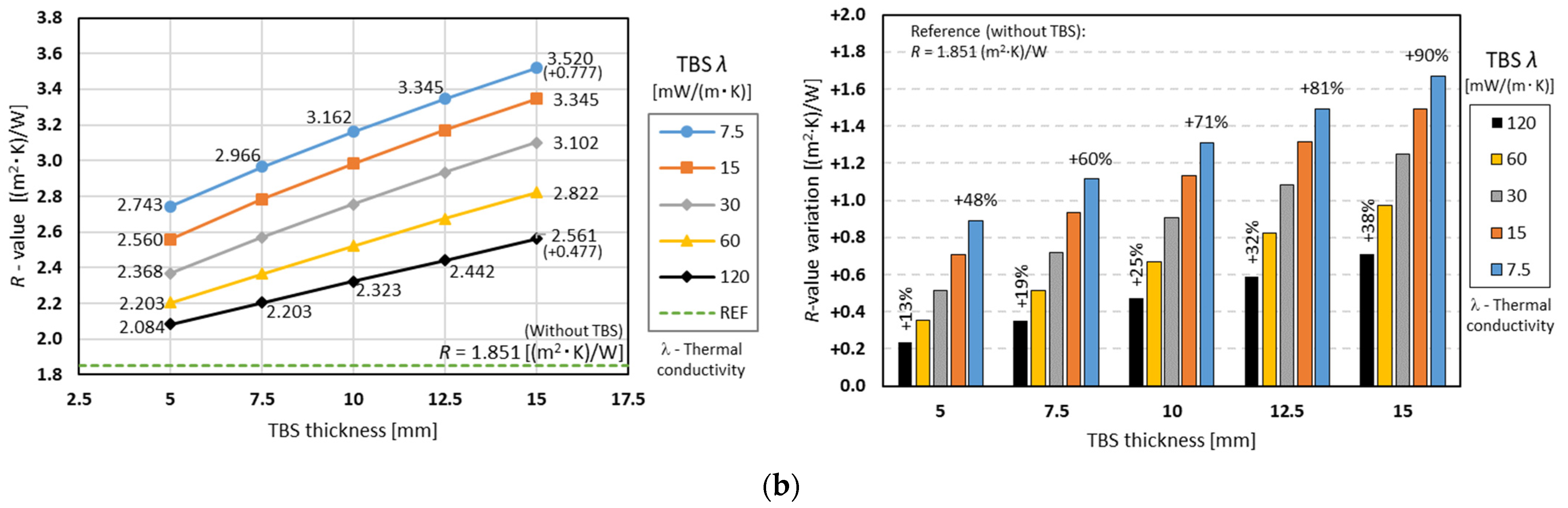
3.2.1. The Influence of TBS Thickness and Conductivity
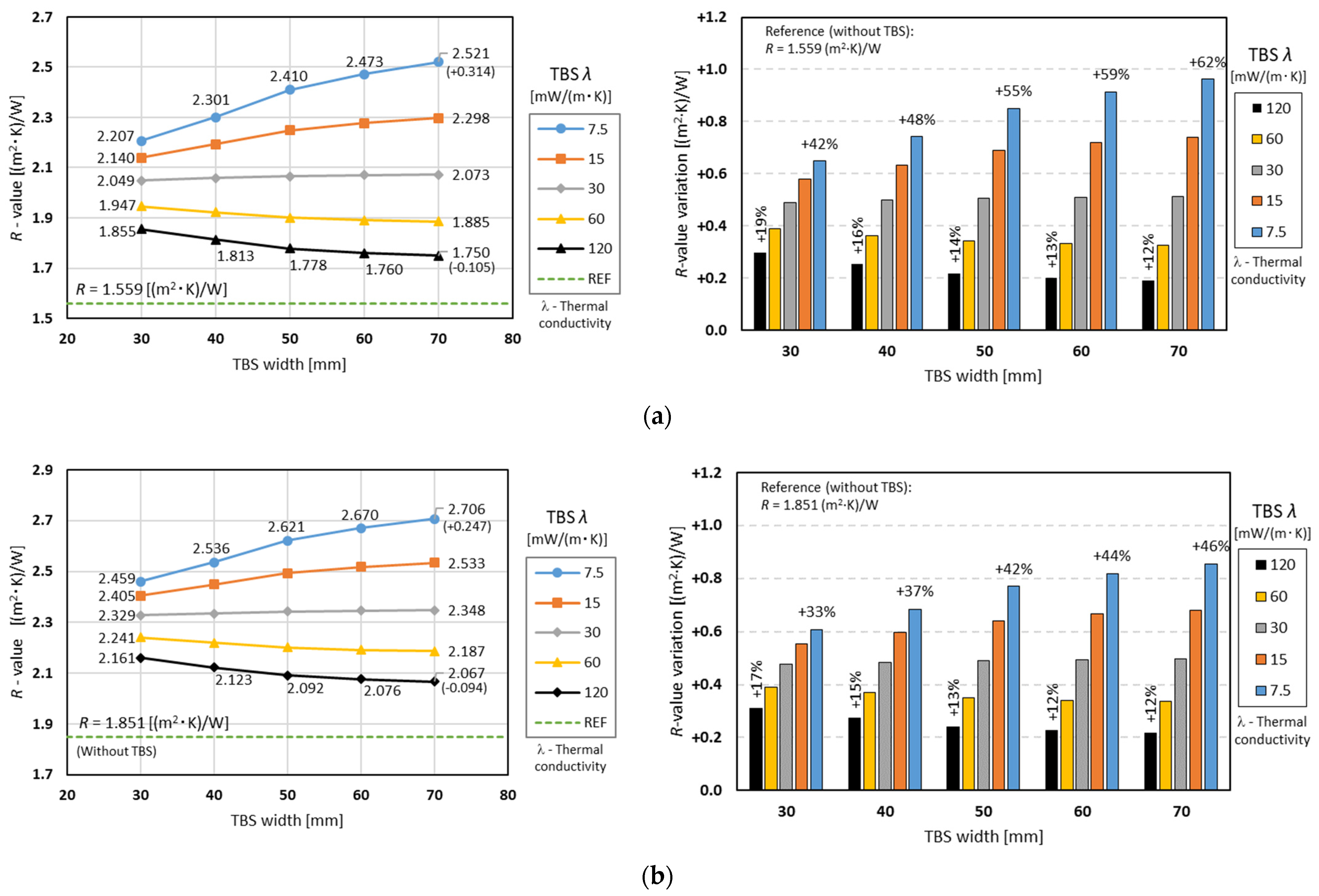
3.2.2. The Influence of TBS Width and Conductivity
3.3. Two Thermal Break Strips
3.3.1. The Influence of TBS Thickness and Conductivity
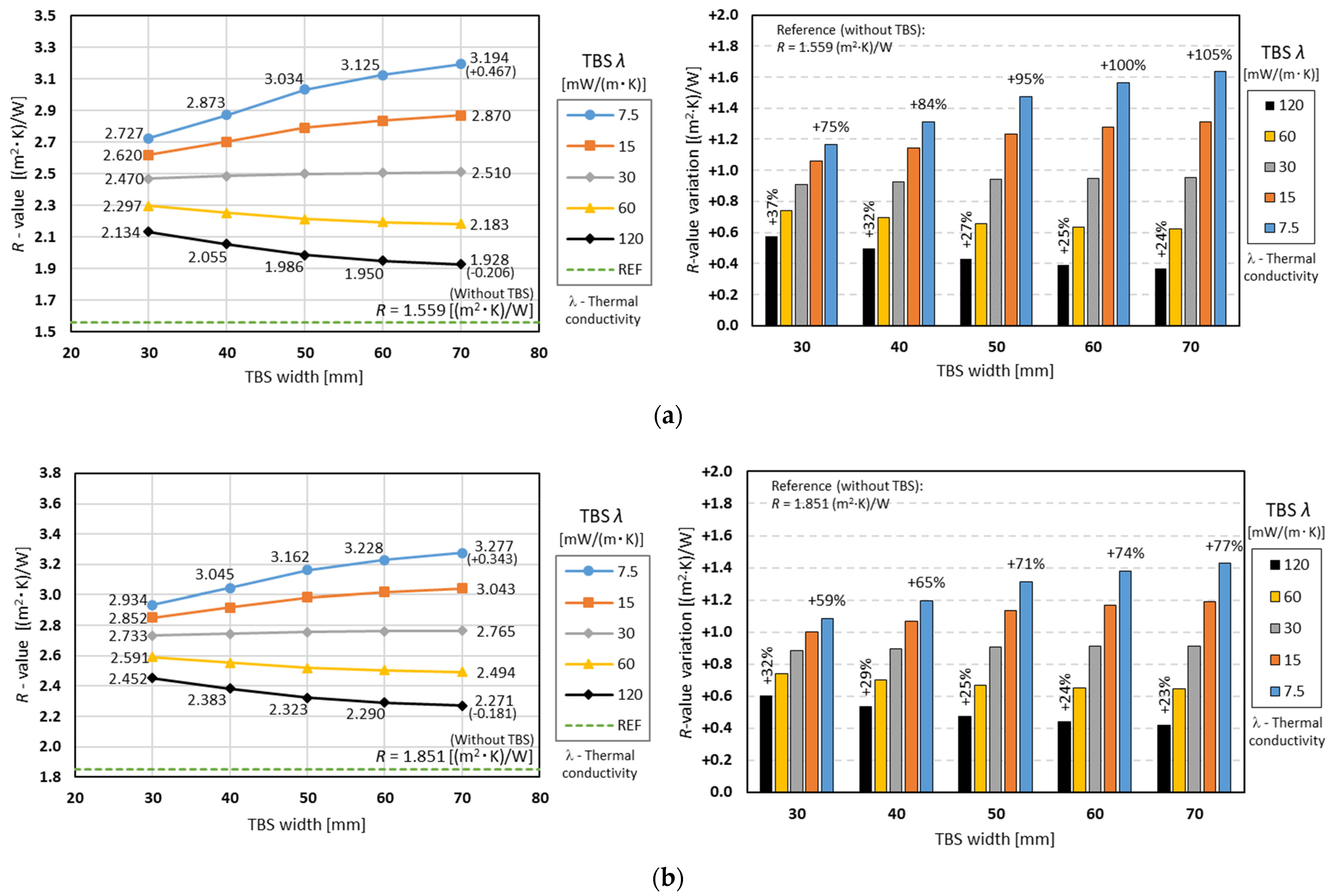
3.3.2. The Influence of TBS Width and Conductivity
4. Conclusions
- As expected, only by increasing the vertical steel stud spacing from 400 mm to 600 mm did we achieve a relevant thermal resistance improvement (+19%).
- Regardless of the TBS thermal conductivity, it is always worth increasing the thickness of the TBS due to the consequent increase in the wall cavity thickness and the resulting expansion of the batt insulation (in this study, mineral wool).
- Moreover, regardless of the evaluated TBS conductivities, the thermal resistances provided by the smaller assessed TBS width (30 mm) were always bigger than the ones provided by the smaller evaluated TBS thickness (5 mm).
- Surprisingly, the increase in the TBS width did not always lead to increased thermal resistance.
- In fact, for higher TBS conductivities, a thermal performance reduction occurred when increasing the width of the TBS.
- The previous happens whenever the thermal conductivity of the TBS is greater than the conductivity of the expansible batt insulation.
- Considering the preceding features, it was concluded that it is more effective to increase the TBS thickness rather than the width.
- The abovementioned features are more relevant for smaller stud spacing (400 mm instead of 600 mm) and when using two TBS instead of a single one.
Author Contributions
Funding

Acknowledgments
Conflicts of Interest
References
- Energy Efficiency in Buildings; European Commission, Department Energy: Brussels, Belgium, 2020.
- Global Alliance of Buildings and Construction. 2021 Global Status Report for Buildings and Construction; United Nations Environment Programme: Nairobi, Kenya, 2021. [Google Scholar]
- EU. Directive 8(EU) 2018/844 of the European Parliament and of the Council on the energy performance of buildings and on energy efficiency. Off. J. Eur. Union 2018, 2018, 75–91. [Google Scholar]
- EU. Directive (EU) 2018/2001 of the European Parliament and of the Council on the promotion of the use of energy from renewable sources. Off. J. Eur. Union 2018, 2018, 82–209. [Google Scholar]
- Zhan, Q.; Xiao, Y.; Musso, F.; Zhang, L. Assessing the hygrothermal performance of typical lightweight steel-framed wall assemblies in hot-humid climate regions by monitoring and numerical analysis. Build. Environ. 2020, 188, 107512. [Google Scholar] [CrossRef]
- Soares, N.; Santos, P.; Gervásio, H.; Costa, J.J.; da Silva, L.S. Energy efficiency and thermal performance of lightweight steel-framed (LSF) construction: A review. Renew. Sustain. Energy Rev. 2017, 78, 194–209. [Google Scholar] [CrossRef]
- Perera, D.; Upasiri, I.; Poologanathan, K.; Gatheeshgar, P.; Sherlock, P.; Hewavitharana, T.; Suntharalingam, T. Energy performance of fire rated LSF walls under UK climate conditions. J. Build. Eng. 2021, 44, 103293. [Google Scholar] [CrossRef]
- Kapoor, D.R.; Peterman, K.D. Quantification and prediction of the thermal performance of cold-formed steel wall assemblies. Structures 2021, 30, 305–315. [Google Scholar] [CrossRef]
- Kempton, L.; Kokogiannakis, G.; Green, A.; Cooper, P. Evaluation of thermal bridging mitigation techniques and impact of calculation methods for lightweight steel frame external wall systems. J. Build. Eng. 2021, 43, 102893. [Google Scholar] [CrossRef]
- Ge, H.; Baba, F. Dynamic effect of thermal bridges on the energy performance of a low-rise residential building. Energy Build. 2015, 105, 106–118. [Google Scholar] [CrossRef]
- Erhorn-Kluttig, H.; Erhorn, H. Impact of Thermal Bridges on the Energy Performance of Buildings; Buildings Platform; European Communities: Brussels, Belgium, 2009; pp. 1–8. [Google Scholar]
- Al-Sanea, S.A.; Zedan, M. Effect of thermal bridges on transmission loads and thermal resistance of building walls under dynamic conditions. Appl. Energy 2012, 98, 584–593. [Google Scholar] [CrossRef]
- Theodosiou, T.; Papadopoulos, A. The impact of thermal bridges on the energy demand of buildings with double brick wall constructions. Energy Build. 2008, 40, 2083–2089. [Google Scholar] [CrossRef]
- Jedidi, M.; Benjeddou, O. Effect of Thermal Bridges on the Heat Balance of Buildings. Int. J. Sci. Res. Civ. Eng. 2018, 2, 2456–6667. [Google Scholar]
- Santos, P.; Silva, L.; Ungureanu, V. Energy Efficiency of Lightweight Steel-Framed Buildings; Technical Committee 14-Sustainability & Eco-Efficiency of Steel Construction; European Convention for Constructional Steelwork (ECCS): Brussels, Belgium, 2012; ISBN 978-92-9147-105-8. [Google Scholar]
- Martins, C.; Santos, P.; Simoesdasilva, L. Lightweight steel-framed thermal bridges mitigation strategies: A parametric study. J. Build. Phys. 2015, 39, 342–372. [Google Scholar] [CrossRef]
- Santos, P.; Poologanathan, K. The importance of stud flanges size and shape on the thermal performance of lightweight steel framed walls. Sustainability 2021, 13, 3970. [Google Scholar] [CrossRef]
- Atsonios, I.A.; Mandilaras, I.D.; Kontogeorgos, D.A.; Founti, M.A. Two new methods for the in-situ measurement of the overall thermal transmittance of cold frame lightweight steel-framed walls. Energy Build. 2018, 170, 183–194. [Google Scholar] [CrossRef]
- François, A.; Ibos, L.; Feuillet, V.; Meulemans, J. In situ measurement method for the quantification of the thermal transmittance of a non-homogeneous wall or a thermal bridge using an inverse technique and active infrared thermography. Energy Build. 2021, 233, 110633. [Google Scholar] [CrossRef]
- Santos, P.; Lemes, G.; Mateus, D. Analytical Methods to Estimate the Thermal Transmittance of LSF Walls: Calculation Procedures Review and Accuracy Comparison. Energies 2020, 13, 840. [Google Scholar] [CrossRef] [Green Version]
- Santos, P.; Mateus, D. Experimental assessment of thermal break strips performance in load-bearing and non-load-bearing LSF walls. J. Build. Eng. 2020, 32, 101693. [Google Scholar] [CrossRef]
- Santos, P.; Abrantes, D.; Lopes, P.; Mateus, D. Experimental and Numerical Performance Evaluation of Bio-Based and Recycled Thermal Break Strips in LSF Partition Walls. Buildings 2022, 12, 1237. [Google Scholar] [CrossRef]
- Santos, P.; Mateus, D.; Ferrandez, D.; Verdu, A. Numerical Simulation and Experimental Validation of Thermal Break Strips’ Improvement in Facade LSF Walls. Energies 2022, 15, 8169. [Google Scholar] [CrossRef]
- Gomes, A.P.; de Souza, H.A.; Tribess, A. Impact of thermal bridging on the performance of buildings using Light Steel Framing in Brazil. Appl. Therm. Eng. 2012, 52, 84–89. [Google Scholar] [CrossRef] [Green Version]
- Kosny, J.; Christian, J.E. Thermal evaluation of several configurations of insulation and structural materials for some metal stud walls. Energy Build. 1995, 22, 157–163. [Google Scholar] [CrossRef]
- Santos, P.; Gonçalves, M.; Martins, C.; Soares, N.; Costa, J.J. Thermal transmittance of lightweight steel framed walls: Experimental versus numerical and analytical approaches. J. Build. Eng. 2019, 25, 100776. [Google Scholar] [CrossRef]
- Lupan, L.M.; Manea, D.L.; Moga, L.M. Improving Thermal Performance of the Wall Panels Using Slotted Steel Stud Framing. Procedia Technol. 2016, 22, 351–357. [Google Scholar] [CrossRef]
- Henriques, J.; Rosa, N.; Gervasio, H.; Santos, P.; da Silva, L.S. Structural performance of light steel framing panels using screw connections subjected to lateral loading. Thin Walled Struct. 2017, 121, 67–88. [Google Scholar] [CrossRef]
- Ibérica, G. Technical Sheet: Standard Gypsum Plasterboard. 2022. Available online: https://www.gyptec.eu/documentos/Ficha_Tecnica_Gyptec_A.pdf (accessed on 10 February 2022).
- Kronospan. Technical Sheet: Kronobuild Materials; Kronospan GmbH: Steinheim-Sandebeck, Germany, 2013. [Google Scholar]
- Volcalis. Technical Sheet: Alpha Mineral Wool. 2022. Available online: https://www.volcalis.pt/categoria_file_docs/fichatecnica_volcalis_alpharollo-386.pdf (accessed on 10 February 2022).
- Santos, C.; Matias, L. ITE50—Coeficientes de Transmissão Térmica de Elementos da Envolvente dos Edifícios (in Portuguese); LNEC—Laboratório Nacional de Engenharia Civil: Lisboa, Portugal, 2006. [Google Scholar]
- THERM. Software Version 7.6.1. Lawrence Berkeley National Laboratory, United States Department of Energy. 2017. Available online: https://windows.lbl.gov/software/therm (accessed on 14 February 2019).
- ISO 6946; Building Components and Building Elements—Thermal Resistance and Thermal Transmittance—Calculation Methods. ISO—International Organization for Standardization: Geneva, Switzerland, 2017.
- ISO 10211; Thermal Bridges in Building Construction-Heat Flows and Surface Temperatures-Detailed. ISO—International Organization for Standardization: Geneva, Switzerland, 2017.
- ANSYS Workbench Software, Version 19.1; ANSYS, Inc.: Canonsburg, PA, USA, 2018. Available online: http://www.ansys.com/products/(accessed on 8 June 2020).
- Roque, E.; Santos, P. The effectiveness of thermal insulation in lightweight steel-framedwalls with respect to its position. Buildings 2017, 7, 13. [Google Scholar] [CrossRef] [Green Version]
- Santos, P.; Lemes, G.; Mateus, D. Thermal transmittance of internal partition and external facade LSF walls: A parametric study. Energies 2019, 12, 2671. [Google Scholar] [CrossRef] [Green Version]
- Pico Technology. PicoLog 6 Software, Version 6.1.10. 2019. Available online: https://www.picotech.com/downloads (accessed on 1 September 2022).
- ISO 9869-1; Thermal Insulation–Building Elements—In-Situ Measurement of Thermal Resistance and Thermal Transmittance. Part 1: Heat Flow Meter Method. ISO—International Organization for Standardization: Geneva, Switzerland, 2014.
- Rasooli, A.; Itard, L. In-situ characterization of walls’ thermal resistance: An extension to the ISO 9869 standard method. Energy Build. 2018, 179, 374–383. [Google Scholar] [CrossRef]
- ASTM C1155-95; Standard Practice for Determining Thermal Resistance of Building Envelope Components from the In-Situ Data. ASTM—American Society for Testing and Materials: Philadelphia, PA, USA, 2013.


| Parameter | “Values” |
|---|---|
| Thermal break strips: | |
| 5, 7.5, 10 *, 12.5, 15 |
| 30, 40, 50 *, 60, 70 |
| 7.5, 15, 30, 60, 120 |
| Zero *, one 1, two 2 |
| Steel stud spacing [mm] | 400 *, 600 |
| Material | t [mm] | λ [W/(m·K)] | Ref. |
|---|---|---|---|
| Gypsum plasterboard | 12.5 | 0.175 | [29] |
| Oriented strand board | 12.0 | 0.100 | [30] |
| Mineral wool | 90.0 | 0.035 | [31] |
| Steel studs (C90 × 43 × 15 × 1.5) | 90.0 | 50.000 | [32] |
| LSF Wall Type | -Value [W/(m2·K)] | |
|---|---|---|
| Numerical (THERM) | Analytical (ISO 6946) | |
| Partition | 0.328 | 0.328 |
| Test N. | Sensors Position | -Value [m2·K/W] |
|---|---|---|
| 1 | Bottom | 1.607 |
| 2 | Middle | 1.576 |
| 3 | Top | 1.491 |
| Measurement Average | 1.558 | |
| Computed in THERM | 1.559 | |
| Percentage Deviation | +0.1% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, P.; Lopes, P.; Abrantes, D. Thermal Performance of Load-Bearing, Lightweight, Steel-Framed Partition Walls Using Thermal Break Strips: A Parametric Study. Energies 2022, 15, 9271. https://doi.org/10.3390/en15249271
Santos P, Lopes P, Abrantes D. Thermal Performance of Load-Bearing, Lightweight, Steel-Framed Partition Walls Using Thermal Break Strips: A Parametric Study. Energies. 2022; 15(24):9271. https://doi.org/10.3390/en15249271
Chicago/Turabian StyleSantos, Paulo, Paulo Lopes, and David Abrantes. 2022. "Thermal Performance of Load-Bearing, Lightweight, Steel-Framed Partition Walls Using Thermal Break Strips: A Parametric Study" Energies 15, no. 24: 9271. https://doi.org/10.3390/en15249271
APA StyleSantos, P., Lopes, P., & Abrantes, D. (2022). Thermal Performance of Load-Bearing, Lightweight, Steel-Framed Partition Walls Using Thermal Break Strips: A Parametric Study. Energies, 15(24), 9271. https://doi.org/10.3390/en15249271









