Wind Energy Harvesting and Conversion Systems: A Technical Review
Abstract
:1. Introduction
- What is the status in respect to wind capacity and what is the trajectory for wind energy in the near future?
- What are the advantages and limitations of wind energy as a proponent of an enhanced renewable energy infrastructure?
- What are the primary issues and technological considerations associated with effective wind energy harvesting?
- What configuration(s) are available for effective wind energy harvesting?
- What is the state of the art in respect to wind energy harvesting system optimization?
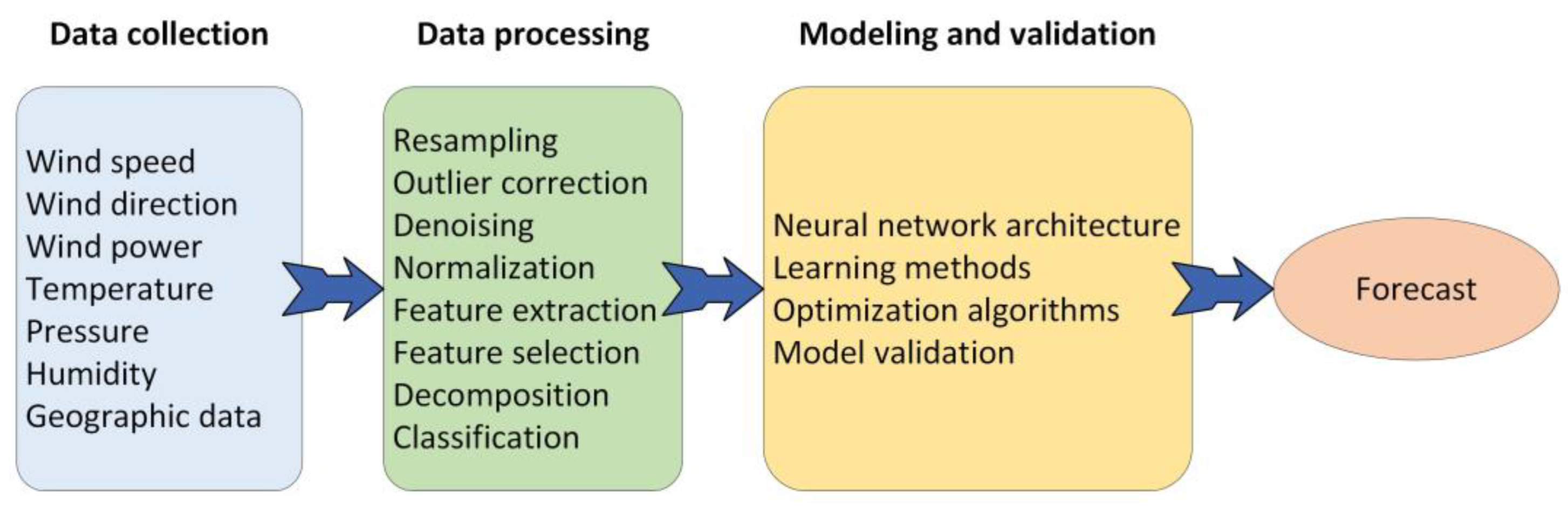
2. Wind Speed and Wind Power Forecasting
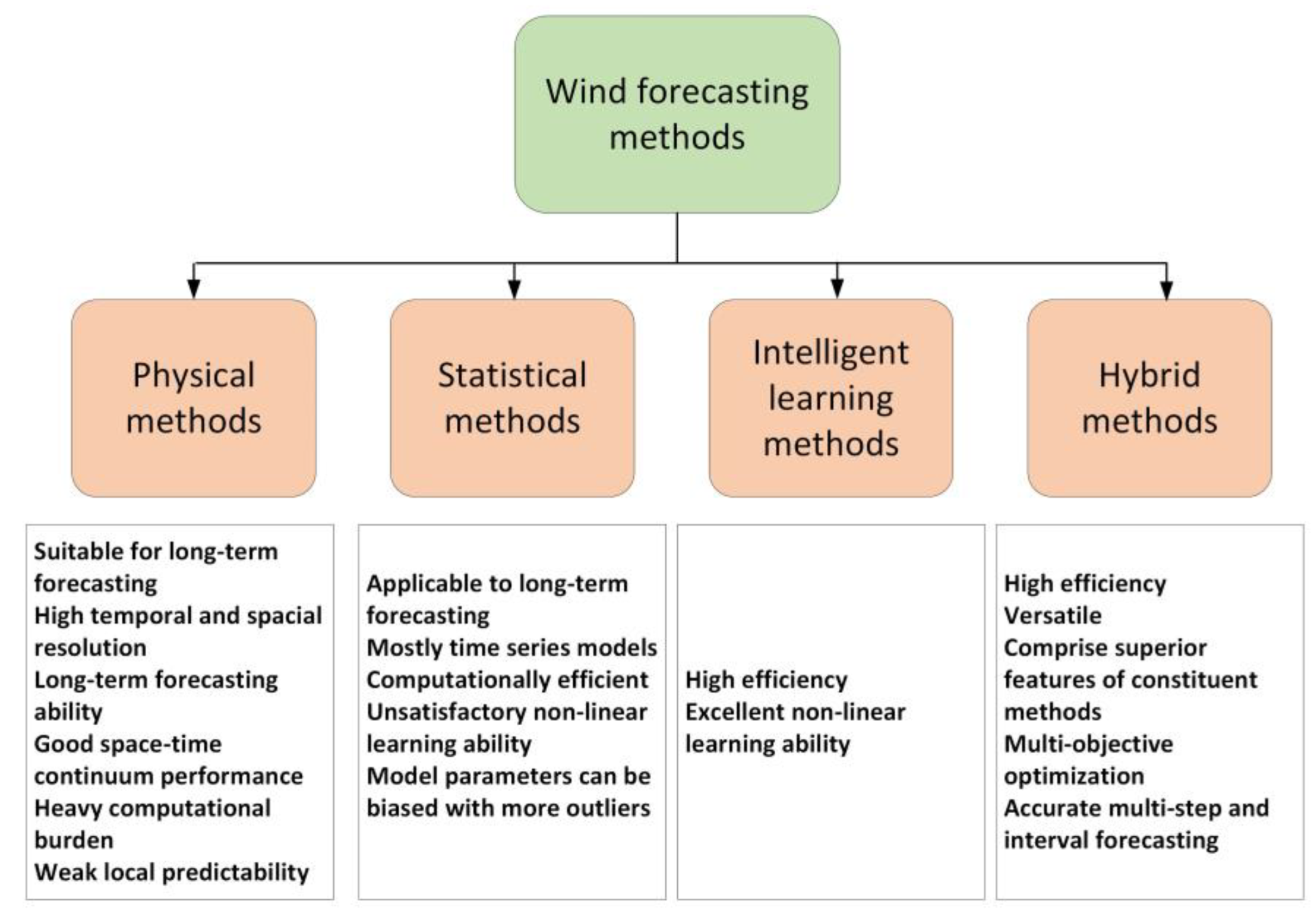
2.1. Statistical Methods
2.2. Physical Methods
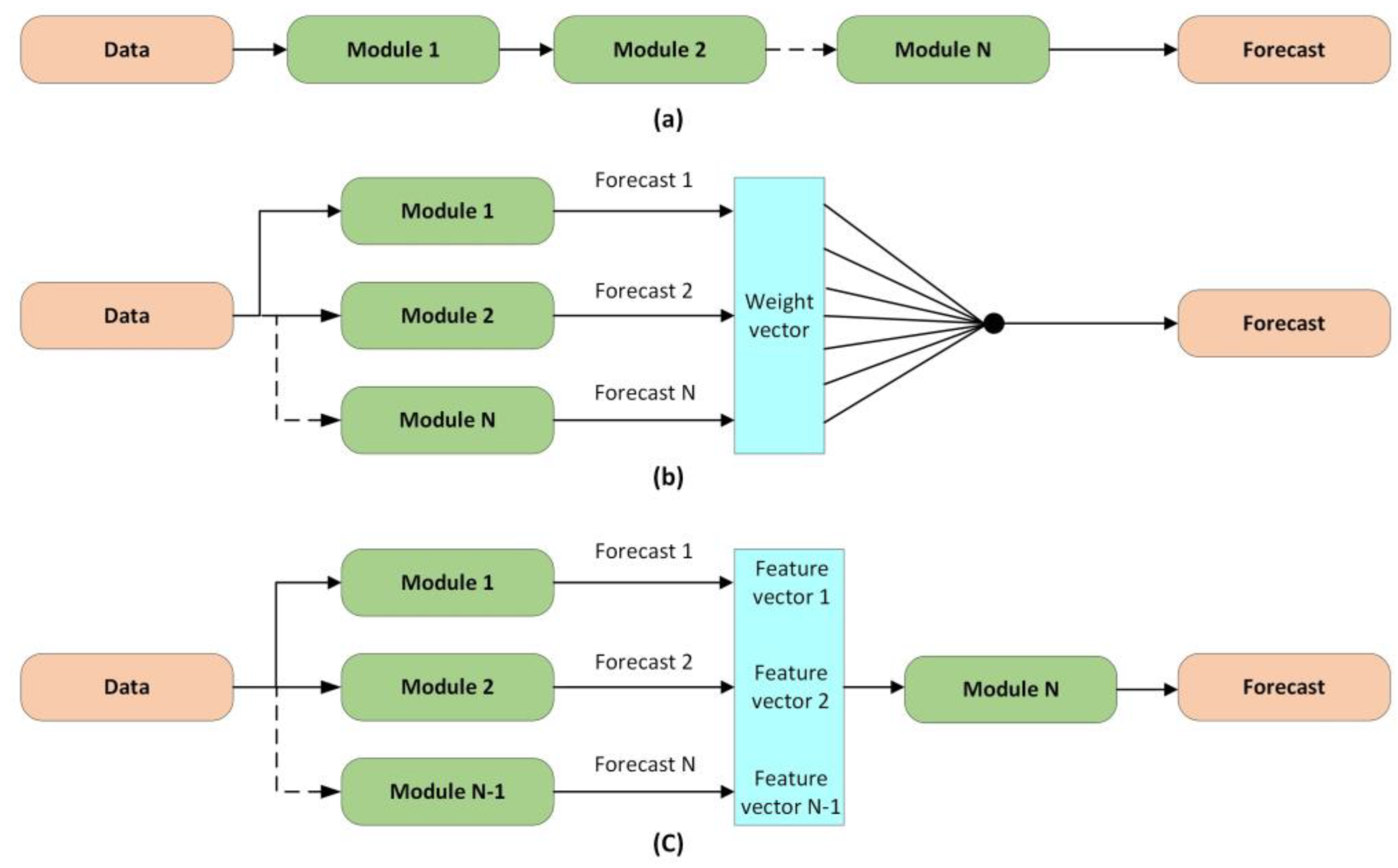
2.3. Intelligent Learning Methods and Hybrid Methods
2.3.1. Wind Speed Forecasting
2.3.2. Wind Power Forecasting
3. Technical Considerations
3.1. System Considerations
3.1.1. Off-Grid Systems
- Variety of loads: lighting, refrigeration, small appliances, etc.
- Peak consumption: when, how much power, and how often
- Average consumption: ongoing loads which are typically in use or on standby
- Minimum consumption: loads being run all the time and consistently
- AC or DC needs: (i.e., may require additional auxiliary components)
- Required availability: system as back-up or supplementary power supply.
3.1.2. Grid-Connected Systems
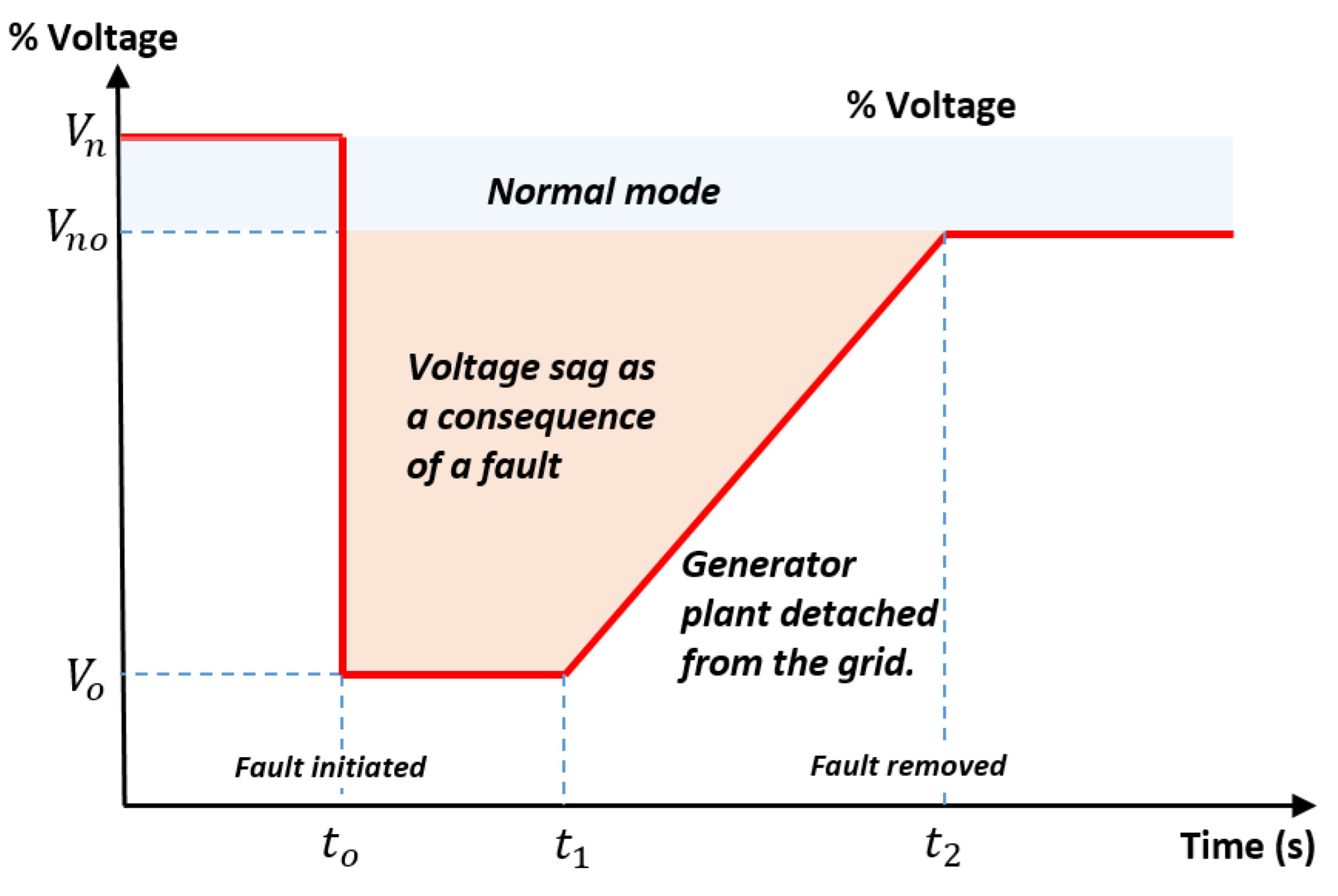
Fault Ride Through
Installation Requirements
- Type and capacity of the generator and the voltage level for connection to the grid (point of common coupling, PCC)
- Availability of power generated
- Variation of power generated with time and predictability of variation
- Reliability of the plant
- Technology and regulations for connection.
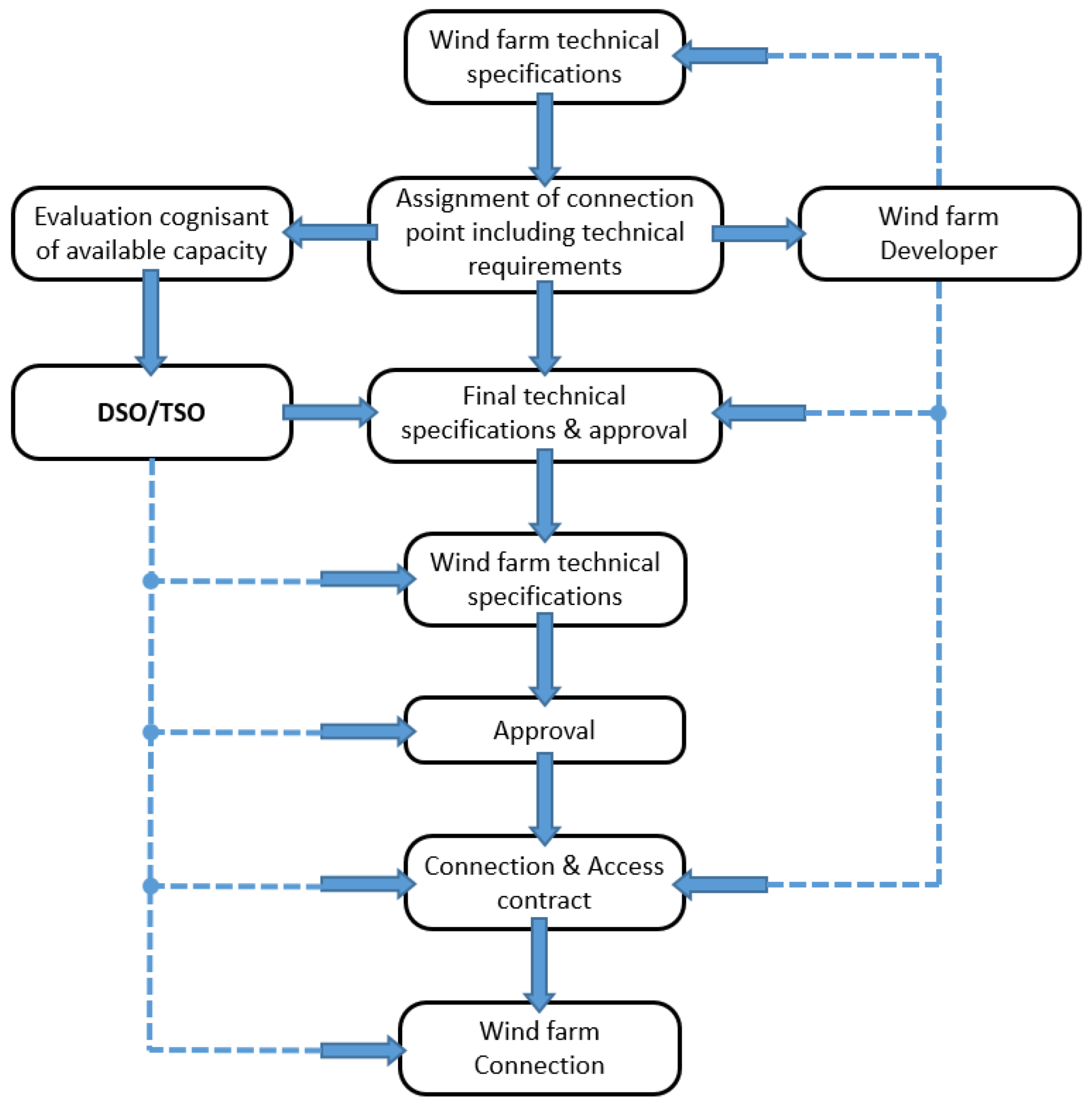
3.1.3. Grid Codes for Wind Turbine Connection
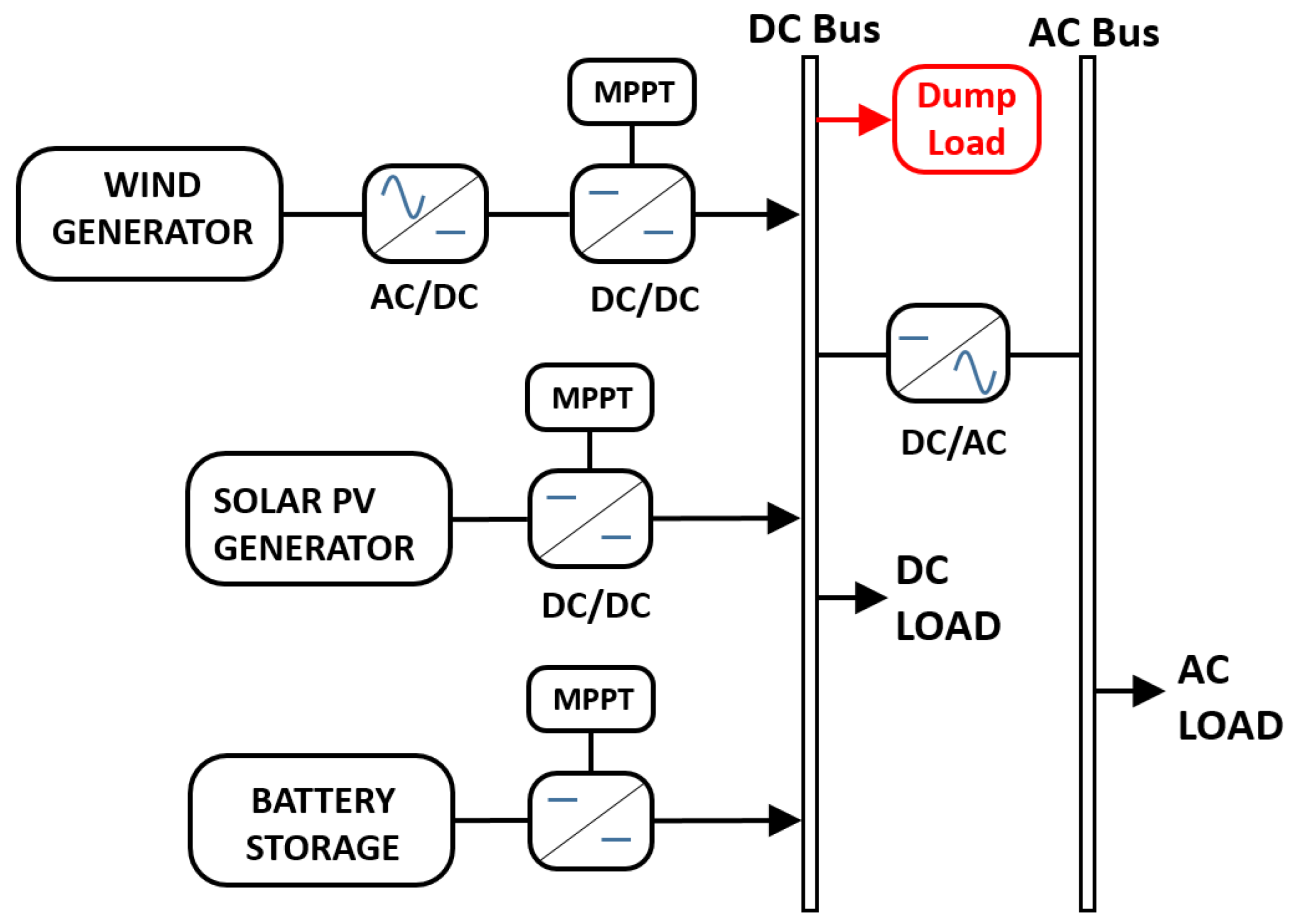
3.2. Hybrid Systems
4. Optimizing/Maximizing Potential
4.1. Wind Turbine Power Optimizing Technology
4.2. Optimization of Wind Turbine Design
4.3. Optimization and Enhanced Wind Energy Harvesting: A Hybrid Modality Consideration
4.4. Comparison of Optimization Techniques
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ang, T.-Z.; Salem, M.; Kamarol, M.; Das, H.S.; Nazari, M.A.; Prabaharan, N. A Comprehensive Study of Renewable Energy Sources: Classifications, Challenges and Suggestions. Energy Strategy Rev. 2022, 43, 100939. [Google Scholar] [CrossRef]
- Kardooni, R.; Yusoff, S.B.; Kari, F.B. Renewable Energy Technology Acceptance in Peninsular Malaysia. Energy Policy 2016, 88, 1–10. [Google Scholar] [CrossRef]
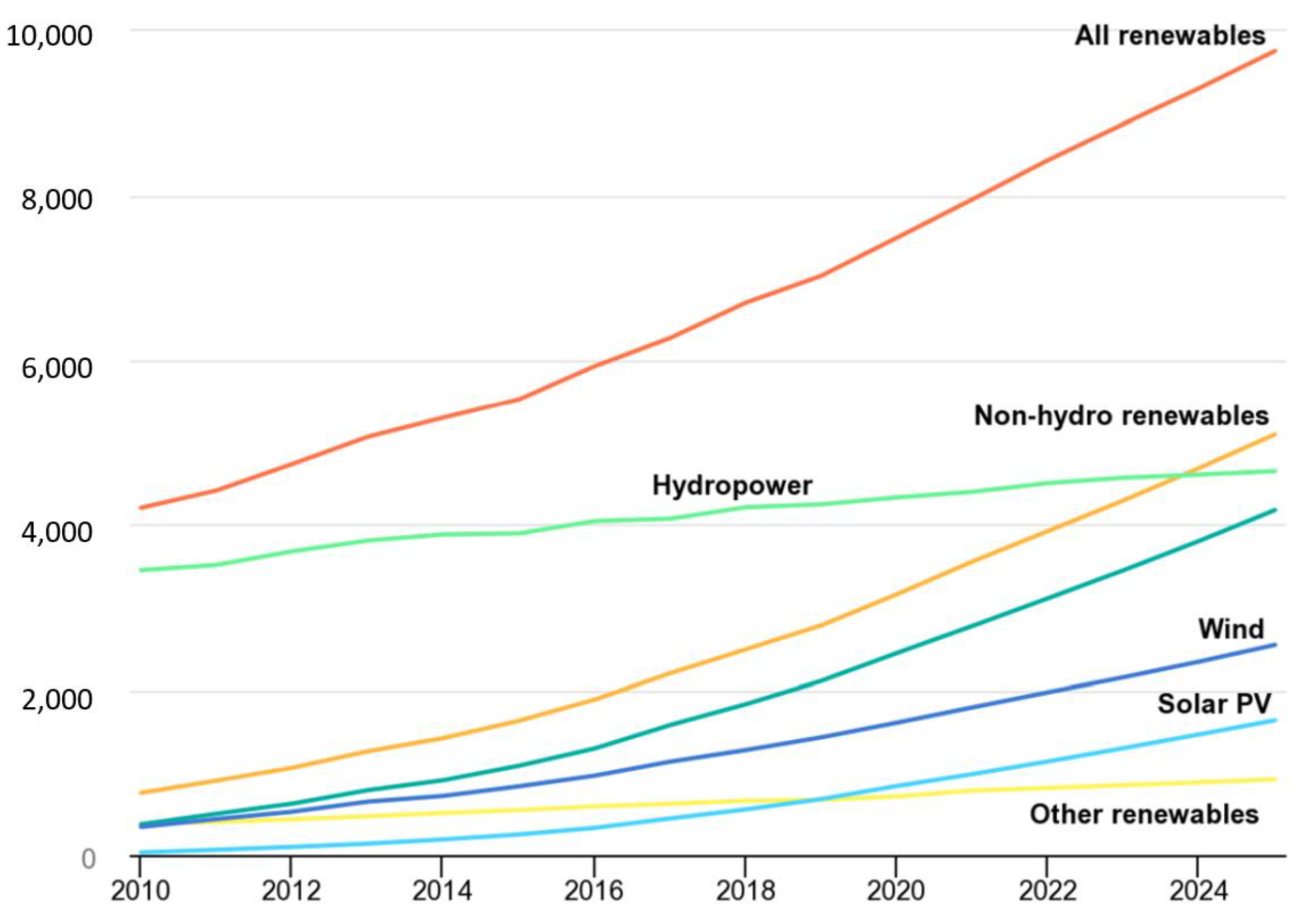
- IEA. Renewable Electricity Generation by Technology, 2010–2025. IEA: Paris, France. Available online: https://www.iea.org/data-and-statistics/charts/renewable-electricity-generation-by-technology-2010-2025 (accessed on 26 October 2022).
- International Energy Agency. Global Energy Review 2021—The Impacts of the COVID-19 Crisis on Global Energy Demand and CO2 Emissions; International Energy Agency: Paris, French, 2021.
- International Renewable Energy Agency (IRENA). Renewable Power Generation Costs in 2021; International Renewable Energy Agency (IRENA): Paris, French, 2021. [Google Scholar]
- Gönül, Ö.; Duman, A.C.; Deveci, K.; Güler, Ö. An Assessment of Wind Energy Status, Incentive Mechanisms and Market in Turkey. Eng. Sci. Technol. Int. J. 2021, 24, 1383–1395. [Google Scholar] [CrossRef]
- Dehghani-Sanij, A.R.; Al-Haq, A.; Bastian, J.; Luehr, G.; Nathwani, J.; Dusseault, M.B.; Leonenko, Y. Assessment of Current Developments and Future Prospects of Wind Energy in Canada. Sustain. Energy Technol. Assess. 2022, 50, 101819. [Google Scholar] [CrossRef]
- Wind Europe. Offshore Wind in Europe Key Trends and Statistics 2020; Wind Europe: Brussels, Belgium, 2021.
- Zou, R.; Song, M.; Wang, Y.; Wang, J.; Yang, K.; Affenzeller, M. Deep Non-Crossing Probabilistic Wind Speed Forecasting with Multi-Scale Features. Energy Convers. Manag. 2022, 257, 115433. [Google Scholar] [CrossRef]
- Xing, Q.; Wang, J.; Lu, H.; Wang, S. Research of a Novel Short-Term Wind Forecasting System Based on Multi-Objective Aquila Optimizer for Point and Interval Forecast. Energy Convers. Manag. 2022, 263, 115583. [Google Scholar] [CrossRef]
- Lee, J.; Zhao, F. GWEC Global Wind Report 2021; Global Wind Energy Council: Brussels, Belgium, 2021. [Google Scholar]
- Liu, M.; Cao, Z.; Zhang, J.; Wang, L.; Huang, C.; Luo, X. Short-Term Wind Speed Forecasting Based on the Jaya-SVM Model. Int. J. Electr. Power Energy Syst. 2020, 121, 106056. [Google Scholar] [CrossRef]
- Neshat, M.; Majidi Nezhad, M.; Mirjalili, S.; Piras, G.; Garcia, D.A. Quaternion Convolutional Long Short-Term Memory Neural Model with an Adaptive Decomposition Method for Wind Speed Forecasting: North Aegean Islands Case Studies. Energy Convers. Manag. 2022, 259, 115590. [Google Scholar] [CrossRef]
- Duan, J.; Wang, P.; Ma, W.; Fang, S.; Hou, Z. A Novel Hybrid Model Based on Nonlinear Weighted Combination for Short-Term Wind Power Forecasting. Int. J. Electr. Power Energy Syst. 2022, 134, 107452. [Google Scholar] [CrossRef]
- Tielens, P.; Henneaux, P.; Cole, S. Penetration of Renewables and Reduction of Synchronous Inertia in the European Power System—Analysis and Solutions; Université Libre de Bruxelles: Brussels, Belgium, 2020. [Google Scholar]
- Eggleston, J.; Halley, A.; Mancarella, P. System Non-Synchronous Penetration (SNSP) Metric and Potential Alternatives in Low-Carbon Grids. In Proceedings of the 11th Solar & Storage Power System Integration Workshop (SIW 2021), Berlin, Germany, 28 September 2021; Institution of Engineering and Technology: London, UK, 2021; pp. 30–34. [Google Scholar]
- Gao, Y.; Wang, J.; Yang, H. A Multi-Component Hybrid System Based on Predictability Recognition and Modified Multi-Objective Optimization for Ultra-Short-Term Onshore Wind Speed Forecasting. Renew. Energy 2022, 188, 384–401. [Google Scholar] [CrossRef]
- Tian, C.; Niu, T.; Wei, W. Developing a Wind Power Forecasting System Based on Deep Learning with Attention Mechanism. Energy 2022, 257, 124750. [Google Scholar] [CrossRef]
- Zhang, W.; Lin, Z.; Liu, X. Short-Term Offshore Wind Power Forecasting—A Hybrid Model Based on Discrete Wavelet Transform (DWT), Seasonal Autoregressive Integrated Moving Average (SARIMA), and Deep-Learning-Based Long Short-Term Memory (LSTM). Renew. Energy 2022, 185, 611–628. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, H.; Wang, D.; Wang, G.; Wu, J.; Bian, J.; Liu, J. A New Method for Wind Speed Forecasting Based on Copula Theory. Environ. Res. 2018, 160, 365–371. [Google Scholar] [CrossRef]
- Ding, M.; Zhou, H.; Xie, H.; Wu, M.; Liu, K.Z.; Nakanishi, Y.; Yokoyama, R. A Time Series Model Based on Hybrid-Kernel Least-Squares Support Vector Machine for Short-Term Wind Power Forecasting. ISA Trans. 2021, 108, 58–68. [Google Scholar] [CrossRef]
- Liu, H.; Chen, C.; Lv, X.; Wu, X.; Liu, M. Deterministic Wind Energy Forecasting: A Review of Intelligent Predictors and Auxiliary Methods. Energy Convers. Manag. 2019, 195, 328–345. [Google Scholar] [CrossRef]
- Liu, H.; Li, Y.; Duan, Z.; Chen, C. A Review on Multi-Objective Optimization Framework in Wind Energy Forecasting Techniques and Applications. Energy Convers. Manag. 2020, 224. [Google Scholar] [CrossRef]
- Qian, Z.; Pei, Y.; Zareipour, H.; Chen, N. A Review and Discussion of Decomposition-Based Hybrid Models for Wind Energy Forecasting Applications. Appl. Energy 2019, 235, 939–953. [Google Scholar] [CrossRef]
- Liu, H.; Chen, C. Data Processing Strategies in Wind Energy Forecasting Models and Applications: A Comprehensive Review. Appl. Energy 2019, 249, 392–408. [Google Scholar] [CrossRef]
- Okumus, I.; Dinler, A. Current Status of Wind Energy Forecasting and a Hybrid Method for Hourly Predictions. Energy Convers. Manag. 2016, 123, 362–371. [Google Scholar] [CrossRef]
- Wang, H.; Lei, Z.; Zhang, X.; Zhou, B.; Peng, J. A Review of Deep Learning for Renewable Energy Forecasting. Energy Convers. Manag. 2019, 198, 111799. [Google Scholar] [CrossRef]
- Paramasivan, S.K. Deep Learning Based Recurrent Neural Networks to Enhance the Performance of Wind Energy Forecasting: A Review. Rev. D’intell. Artif. 2021, 35, 1–10. [Google Scholar] [CrossRef]
- Tiwari, S.; Ling, J.M. A Review of Wind Energy Forecasting Techniques. In Proceedings of the ICT-PEP 2021—International Conference on Technology and Policy in Energy and Electric Power: Emerging Energy Sustainability, Smart Grid, and Microgrid Technologies for Future Power System, Yogyakarta, Indonesia, 29–30 September 2021; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2021; pp. 213–218. [Google Scholar]
- Navas Raja Mohamed, K.B.; Prakash, S. A Systematic Review on Wind Energy Resources Forecasting by Neural Network. In Proceedings of the 2020 5th IEEE International Conference on Recent Advances and Innovations in Engineering, Jaipur, India, 1–3 December 2020; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2020. [Google Scholar]
- Wang, J.; Song, Y.; Liu, F.; Hou, R. Analysis and Application of Forecasting Models in Wind Power Integration: A Review of Multi-Step-Ahead Wind Speed Forecasting Models. Renew. Sustain. Energy Rev. 2016, 60, 960–981. [Google Scholar] [CrossRef]
- Manero, J.; Béjar, J.; Cortés, U. Wind Energy Forecasting with Neural Networks: A Literature Review. Comput. Y Sist. 2018, 22, 1085–1098. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Luo, G.; Yang, Z.; Guo, Y.; Li, K.; Xue, Y. A Comprehensive Review on Deep Learning Approaches in Wind Forecasting Applications. CAAI Trans. Intell. Technol. 2022, 7, 129–143. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, S.; Liao, P.; Fu, T. Wind Speed Forecasting Based on Hybrid Model with Model Selection and Wind Energy Conversion. Renew. Energy 2022, 196, 763–781. [Google Scholar] [CrossRef]
- Venkata Rao, R. Jaya: A Simple and New Optimization Algorithm for Solving Constrained and Unconstrained Optimization Problems. Int. J. Ind. Eng. Comput. 2016, 7, 19–34. [Google Scholar] [CrossRef]
- Chen, G.; Tang, B.; Zeng, X.; Zhou, P.; Kang, P.; Long, H. Short-Term Wind Speed Forecasting Based on Long Short-Term Memory and Improved BP Neural Network. Int. J. Electr. Power Energy Syst. 2022, 134, 107365. [Google Scholar] [CrossRef]
- Wang, J.; Gao, D.; Zhuang, Z.; Wu, J. An Optimized Complementary Prediction Method Based on Data Feature Extraction for Wind Speed Forecasting. Sustain. Energy Technol. Assess. 2022, 52, 102068. [Google Scholar] [CrossRef]
- Wu, J.; Li, N.; Zhao, Y.; Wang, J. Usage of Correlation Analysis and Hypothesis Test in Optimizing the Gated Recurrent Unit Network for Wind Speed Forecasting. Energy 2022, 242, 122960. [Google Scholar] [CrossRef]
- Yildiz, C.; Acikgoz, H.; Korkmaz, D.; Budak, U. An Improved Residual-Based Convolutional Neural Network for Very Short-Term Wind Power Forecasting. Energy Convers. Manag. 2021, 228, 113731. [Google Scholar] [CrossRef]
- Al-qaness, M.A.A.; Ewees, A.A.; Fan, H.; Abualigah, L.; Elaziz, M.A. Boosted ANFIS Model Using Augmented Marine Predator Algorithm with Mutation Operators for Wind Power Forecasting. Appl. Energy 2022, 314, 118851. [Google Scholar] [CrossRef]
- Hu, J.; Luo, Q.; Tang, J.; Heng, J.; Deng, Y. Conformalized Temporal Convolutional Quantile Regression Networks for Wind Power Interval Forecasting. Energy 2022, 248, 123497. [Google Scholar] [CrossRef]
- Amaro Pinazo, M.; Romeral Martinez, J.L. Intermittent Power Control in Wind Turbines Integrated into a Hybrid Energy Storage System Based on a New State-of-Charge Management Algorithm. J. Energy Storage 2022, 54, 105223. [Google Scholar] [CrossRef]
- Baroudi, J.A.; Dinavahi, V.; Knight, A.M. A Review of Power Converter Topologies for Wind Generators. Renew. Energy 2007, 32, 2369–2385. [Google Scholar] [CrossRef]
- Ahshan, R.; Iqbal, M.T.; Mann, G.K.I. Controller for a Small Induction-Generator Based Wind-Turbine. Appl. Energy 2008, 85, 218–227. [Google Scholar] [CrossRef]
- Ibrahim, R.A.; Zakzouk, N.E. A PMSG Wind Energy System Featuring Low-Voltage Ride-through via Mode-Shift Control. Appl. Sci. 2022, 12, 964. [Google Scholar] [CrossRef]
- Putrus, G.; Bentley, E. Integration of Distributed Renewable Energy Systems into the Smart Grid. In Electric Renewable Energy Systems; 2016; pp. 487–518. Available online: https://www.researchgate.net/publication/303415890_Integration_of_distributed_renewable_energy_systems_into_the_smart_grid (accessed on 26 October 2022). [CrossRef]
- Twidell, J.T. Renewable Energy Resources, 4th ed.; Taylor & Francis Group: Oxford, UK, 2021. [Google Scholar]
- Distributed Wind Energy Association Off-Grid Distributed Wind. Available online: https://distributedwind.org/off-grid-distributed-wind-systems/ (accessed on 3 August 2022).
- Erturk, E. Sizing a Stand-Alone off-Grid Wind Turbine-Battery Power System for a Remote House in Catalca Istanbul Turkey. Int. J. Renew. Energy Res. 2018, 8, 1591–1603. [Google Scholar] [CrossRef]
- Belouda, M.; Jaafar, A.; Sareni, B.; Roboam, X.; Belhadj, J. Design Methodologies for Sizing a Battery Bank Devoted to a Stand-Alone and Electronically Passive Wind Turbine System. Renew. Sustain. Energy Rev. 2016, 60, 144–154. [Google Scholar] [CrossRef] [Green Version]
- United Nations. United Nations Sustainable Development Goal 7|Department of Economic and Social Affairs. Available online: https://sdgs.un.org/goals/goal7 (accessed on 12 August 2022).
- Khanna, R.A.; Li, Y.; Mhaisalkar, S.; Kumar, M.; Liang, L.J. Comprehensive Energy Poverty Index: Measuring Energy Poverty and Identifying Micro-Level Solutions in South and Southeast Asia. Energy Policy 2019, 132, 379–391. [Google Scholar] [CrossRef]
- Li, Q.S.; Shu, Z.R.; Chen, F.B. Performance Assessment of Tall Building-Integrated Wind Turbines for Power Generation. Appl. Energy 2016, 165, 777–788. [Google Scholar] [CrossRef]
- Tasneem, Z.; al Noman, A.; Das, S.K.; Saha, D.K.; Islam, R.; Ali, F.; Badal, F.R.; Ahamed, H.; Moyeen, S.I.; Alam, F. An Analytical Review on the Evaluation of Wind Resource and Wind Turbine for Urban Application: Prospect and Challenges. Dev. Built Environ. 2020, 4, 100033. [Google Scholar] [CrossRef]
- Wu, Y.-K.; Chang, S.-M.; Mandal, P. Grid-Connected Wind Power Plants: A Survey on the Integration Requirements in Modern Grid Codes. IEEE Trans. Ind. Appl. 2019, 55, 5584–5593. [Google Scholar] [CrossRef]
- Al-Shetwi, A.Q.; Hannan, M.A.; Jern, K.P.; Mansur, M.; Mahlia, T.M.I. Grid-Connected Renewable Energy Sources: Review of the Recent Integration Requirements and Control Methods. J. Clean. Prod. 2020, 253, 119831. [Google Scholar] [CrossRef]
- Ahmed, S.D.; Al-Ismail, F.S.M.; Shafiullah, M.; Al-Sulaiman, F.A.; El-Amin, I.M. Grid Integration Challenges of Wind Energy: A Review. IEEE Access 2020, 8, 10857–10878. [Google Scholar] [CrossRef]
- Chandra Vegunta, S.; François, C.; Watts, A.; Djokic, S.Z.; Milanović, J.V.; Higginson, M.J. Review of GB Electricity Distribution System’s Electricity Security of Supply, Reliability and Power Quality in Meeting UK Industrial Strategy Requirements. IET Gener. Transm. Distrib. 2019, 13, 3513–3523. [Google Scholar] [CrossRef]
- Dugan, R.C.; McGranaghan, M.F.; Santoso, S.; Beaty, H.W. Electrical Power Systems Quality, 3rd ed.; McGraw-Hill Professional: New York, NY, USA, 2012. [Google Scholar]
- Fooladi, M.; Akbari Foroud, A. Recognition and Assessment of Different Factors Which Affect Flicker in Wind Turbines. IET Renew. Power Gener. 2016, 10, 250–259. [Google Scholar] [CrossRef]
- Eroğlu, H.; Cuce, E.; Mert Cuce, P.; Gul, F.; Iskenderoğlu, A. Harmonic Problems in Renewable and Sustainable Energy Systems: A Comprehensive Review. Sustain. Energy Technol. Assess. 2021, 48, 101566. [Google Scholar] [CrossRef]
- Papathanassiou, S.A.; Papadopoulos, M.P. Harmonic Analysis in a Power System with Wind Generation. IEEE Trans. Power Deliv. 2006, 21, 2006–2016. [Google Scholar] [CrossRef]
- Tentzerakis, S.T.; Papathanassiou, S.A. An Investigation of the Harmonic Emissions of Wind Turbines. IEEE Trans. Energy Convers. 2007, 22, 150–158. [Google Scholar] [CrossRef]
- Schwanz, D.; Bollen, M.; Lennerhag, O.; Larsson, A. Harmonic Transfers for Quantifying Propagation of Harmonics in Wind Power Plants. Energies 2021, 14, 5798. [Google Scholar] [CrossRef]
- Meri, A.; Amara, Y.; Nichita, C. Impact of Fault Ride-Through on Wind Turbines Systems Design. In Proceedings of the 2018 7th International Conference on Renewable Energy Research and Applications (ICRERA), Piscataway, NJ, USA, 14–17 October 2018; pp. 567–575. [Google Scholar]
- Sharma, K.K.; Gupta, A.; Kaur, G.; Kumar, R.; Chohan, J.S.; Sharma, S.; Singh, J.; Khalilpoor, N.; Issakhov, A. Power Quality and Transient Analysis for a Utility-Tied Interfaced Distributed Hybrid Wind-Hydro Controls Renewable Energy Generation System Using Generic and Multiband Power System Stabilizers. Energy Rep. 2021, 7, 5034–5044. [Google Scholar] [CrossRef]
- Jin, K.-M.; Thinh, Q.N.; Kim, E.-H. DVR Control of DFIG for Compensating Fault Ride-through Based on Stationary and Synchronous Reference Frame. In Proceedings of the 7th International Power Electronics and Motion Control Conference, Harbin, China, 2–5 June 2012; ISBN 9781457720888. [Google Scholar]
- Buraimoh, E.; Davidson, I.E. Overview of Fault Ride-Through Requirements for Photovoltaic Grid Integration, Design and Grid Code Compliance. In Proceedings of the 2020 9th International Conference on Renewable Energy Research and Application (ICRERA), Glasgow, UK, 27–30 September 2020; ISBN 9781728173696. [Google Scholar]
- Buraimoh, E.; Davidson, I.E. Modeling and Assessment of the Fault Ride-Through Capabilities of Grid Supporting Inverter-Based Microgrids. In Proceedings of the 2020 Clemson University Power Systems Conference (PSC), Clemson, SC, USA, 10–13 March 2020. [Google Scholar]
- Popovic, D.; Wallace, I. International Review of Fault Ride Through for Conventional Generators; Eirgrid: London, UK, 2010. [Google Scholar]
- Beltran, H.; Gimeno, F.; Seguí-Chilet, S.; Torrelo, J.M. Review of the Islanding Phenomenon Problem for Connection of Renewable Energy Systems. Renew. Energy Power Qual. J. 2006, 1, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Yu, B.; Matsui, M.; Yu, G. A Review of Current Anti-Islanding Methods for Photovoltaic Power System. Sol. Energy 2010, 84, 745–754. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, Z.; Østergaard, J. Islanding Control Architecture in Future Smart Grid with Both Demand and Wind Turbine Control. Electr. Power Syst. Res. 2013, 95, 214–224. [Google Scholar] [CrossRef]
- Hossain, J.; Mahmud, A. (Eds.) Large Scale Renewable Power Generation; Springer: Singapore, 2014; ISBN 978-981-4585-29-3. [Google Scholar]
- Al Kez, D.; Foley, A.M.; McIlwaine, N.; Morrow, D.J.; Hayes, B.P.; Zehir, M.A.; Mehigan, L.; Papari, B.; Edrington, C.S.; Baran, M. A Critical Evaluation of Grid Stability and Codes, Energy Storage and Smart Loads in Power Systems with Wind Generation. Energy 2020, 205, 117671. [Google Scholar] [CrossRef]
- Wang, C.; Li, Y.; Fan, Y.; Chi, Y.; Qi, H.; Liu, H. Development of Wind-Energy Modeling Technology and Standards. Glob. Energy Interconnect. 2022, 5, 206–216. [Google Scholar] [CrossRef]
- Vrana, T.K.; Flynn, D.; Gomez-Lazaro, E.; Kiviluoma, J.; Marcel, D.; Cutululis, N.; Smith, J.C. Wind Power within European Grid Codes: Evolution, Status and Outlook. WIREs Energy Environ. 2018, 7, e285. [Google Scholar] [CrossRef] [Green Version]
- Rona, B.; Güler, Ö. Power System Integration of Wind Farms and Analysis of Grid Code Requirements. Renew. Sustain. Energy Rev. 2015, 49, 100–107. [Google Scholar] [CrossRef]
- Mohseni, M.; Islam, S.M. Review of International Grid Codes for Wind Power Integration: Diversity, Technology and a Case for Global Standard. Renew. Sustain. Energy Rev. 2012, 16, 3876–3890. [Google Scholar] [CrossRef]
- González, J.S.; Lacal-Arántegui, R. A Review of Regulatory Framework for Wind Energy in European Union Countries: Current State and Expected Developments. Renew. Sustain. Energy Rev. 2016, 56, 588–602. [Google Scholar] [CrossRef]
- European Wind Energy Association. Administrative and Grid Access Barriers to Wind Power; Wind Barriers Project; European Wind Energy Association: Brussels, Belgium, 2010.
- Nyholm, E.; Goop, J.; Odenberger, M.; Johnsson, F. Solar Photovoltaic-Battery Systems in Swedish Households—Self-Consumption and Self-Sufficiency. Appl. Energy 2016, 183, 148–159. [Google Scholar] [CrossRef] [Green Version]
- El-Sattar, H.A.; Sultan, H.M.; Kamel, S.; Khurshaid, T.; Rahmann, C. Optimal Design of Stand-Alone Hybrid PV/Wind/Biomass/Battery Energy Storage System in Abu-Monqar, Egypt. J. Energy Storage 2021, 44, 103336. [Google Scholar] [CrossRef]
- Khan, F.A.; Pal, N.; Saeed, S.H. Stand-Alone Hybrid System of Solar Photovoltaics/Wind Energy Resources: An Eco-Friendly Sustainable Approach. In Renewable Energy Systems; Elsevier: Amsterdam, The Netherlands, 2021; pp. 687–705. [Google Scholar]
- Niveditha, N.; Rajan Singaravel, M.M. Optimal Sizing of Hybrid PV–Wind–Battery Storage System for Net Zero Energy Buildings to Reduce Grid Burden. Appl. Energy 2022, 324, 119713. [Google Scholar] [CrossRef]
- Stroe, D.-I.; Zaharof, A.; Iov, F. Power and Energy Management with Battery Storage for a Hybrid Residential PV-Wind System—A Case Study for Denmark. Energy Procedia 2018, 155, 464–477. [Google Scholar] [CrossRef]
- Jadhav, R.S.; Patil, S.B. Design and Implementation of PV-Wind Battery Hybrid System for Off Grid and On Grid. In Proceedings of the 2020 Fourth International Conference on Inventive Systems and Control (ICISC), Coimbatore, India, 8–10 January 2020; pp. 612–618. [Google Scholar]
- Sharma, M.; Auther, C.; Kakran, S. An Energy Scheduling Algorithm for Commercial Loads Integrated with Wind Energy and Energy Storage System. In Proceedings of the 2021 IEEE 8th Uttar Pradesh Section International Conference on Electrical, Electronics and Computer Engineering (UPCON), Dehradun, India, 11–13 November 2021. [Google Scholar] [CrossRef]
- Sakthi, S.; Balaji, C.; Bharathi, K.; Sridevi, V.; Sasikumar, M. Effective Management of Small-Scale WECS with ESS for Power Control in RAP System. In Proceedings of the 2019 Fifth International Conference on Science Technology Engineering and Mathematics (ICONSTEM), Chennai India, 14–15 March 2019; pp. 354–361. [Google Scholar]
- Khezri, R.; Member, S.; Mahmoudi, A.; Member, S.; Haque, M.H.; Senior Member, L. Impact of Optimal Sizing of Wind Turbine and Battery Energy Storage for a Grid-Connected Household With/Without an Electric Vehicle. IEEE Trans. Industr. Inform. 2022, 18, 5838–5848. [Google Scholar] [CrossRef]
- Hemmati, R. Technical and Economic Analysis of Home Energy Management System Incorporating Small-Scale Wind Turbine and Battery Energy Storage System. J. Clean. Prod. 2017, 159, 106–118. [Google Scholar] [CrossRef]
- Haces-Fernandez, F.; Cruz-Mendoza, M.; Li, H. Onshore Wind Farm Development: Technologies and Layouts. Energies 2022, 15, 2381. [Google Scholar] [CrossRef]
- Narayana, M.; Putrus, G.A.; Jovanovic, M.; Leung, P.S.; McDonald, S. Generic Maximum Power Point Tracking Controller for Small-Scale Wind Turbines. Renew. Energy 2012, 44, 72–79. [Google Scholar] [CrossRef]
- Narayana, M.; Sunderland, K.; Putrus, G.; Conlon, M. Maximum Power Point Tracking: Adaptation Linear Prediction for Wind Energy Conversion Systems. In Proceedings of the 2018 53rd International Universities Power Engineering Conference (UPEC), Glasgow, UK, 4–7 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Abdullah, M.A.; Yatim, A.H.M.; Tan, C.W.; Saidur, R. A Review of Maximum Power Point Tracking Algorithms for Wind Energy Systems. Elsevier 2012, 16, 3220–3227. [Google Scholar] [CrossRef]
- Apata, O.; Oyedokun, D.T.O. An Overview of Control Techniques for Wind Turbine Systems. Sci. Afr. 2020, 10, e00566. [Google Scholar] [CrossRef]
- Ancuti, M.C.; Musuroi, S.; Sorandaru, C.; Dordescu, M.; Erdodi, G.M. Wind Turbines Optimal Operation at Time Variable Wind Speeds. Appl. Sci. 2020, 10, 4232. [Google Scholar] [CrossRef]
- Khoshrodi, M.N.; Jannati, M.; Sutikno, T. A Review of Wind Speed Estimation for Wind Turbine Systems Based on Kalman Filter Technique. Int. J. Electr. Comput. Eng. 2016, 6, 1406–1411. [Google Scholar] [CrossRef] [Green Version]
- Bian, F.; Meng, K.; Jia, Y.; Ma, J.; Hai, R. Application of Effective Wind Speed Estimation and New Sliding Mode Observer in Wind Energy Conversion System. Math. Probl. Eng. 2022, 2022, 1–11. [Google Scholar] [CrossRef]
- Kadri, A.; Marzougui, H.; Bacha, F. MPPT Control Methods in Wind Energy Conversion System Using DFIG. In Proceedings of the 2016 4th International Conference on Control Engineering & Information Technology (CEIT), Hammamet, Tunisia, 16–18 December 2016. [Google Scholar] [CrossRef]
- Nakamura, T.; Morimoto, S.; Sanada, M.; Takeda, Y. Optimum Control of IPMSG for Wind Generation System. In Proceedings of the Power Conversion Conference-Osaka 2002, Osaka, Japan, 2–5 April 2002; Volume 3, pp. 1435–1440. [Google Scholar]
- Morimoto, S.; Nakayama, H.; Sanada, M.; Takeda, Y. Sensorless Output Maximization Control for Variable-Speed Wind Generation System Using IPMSG. IEEE Trans. Ind. Appl. 2005, 41, 60–67. [Google Scholar] [CrossRef]
- Pucci, M.; Cirrincione, M. Neural MPPT Control of Wind Generators with Induction Machines without Speed Sensors. IEEE Trans. Ind. Electron. 2011, 58, 37–47. [Google Scholar] [CrossRef]
- Shirazi, M.; Viki, A.H.; Babayi, O. A Comparative Study of Maximum Power Extraction Strategies in PMSG Wind Turbine System. In Proceedings of the 2009 IEEE Electrical Power and Energy Conference, Montreal, QC, USA, 22–23 October 2009. [Google Scholar]
- Barakati, M.; Kazerani, M.; Aplevich, D. Maximum Power Tracking Control for a Wind Turbine System Including a Matrix Converter. IEEE Trans. Energy Convers. 2009, 24, 705–713. [Google Scholar] [CrossRef]
- Narayana, M.; Putrus, G. Optimal Control of Wind Turbine Using Neural Networks. In Proceedings of the Universities Power Engineering Conference, Cardiff, UK, 31 August–3 September 2010; pp. 1–5. [Google Scholar]
- Putrus, G.; Narayana, M.; Jovanovic, M.; Leung, P.S. Maximum Power Point Tracking for Variable-Speed Fixed-Pitch Small Wind Turbines. In CIRED 2009-20th International Conference and Exhibition on Electricity Distribution-Part 1; IET: London, UK, 2009. [Google Scholar]
- Habibi, H.; Howard, I.; Simani, S. Wind Turbine Pitch Actuator Regulation for Efficient and Reliable Energy Conversion: A Fault-Tolerant Constrained Control Solution. Actuators 2022, 11, 102. [Google Scholar] [CrossRef]
- Sitharthan, R.; Sundarabalan, C.K.; Devabalaji, K.R.; Yuvaraj, T.; Mohamed Imran, A. Automated Power Management Strategy for Wind Power Generation System Using Pitch Angle Controller. Meas. Control 2019, 52, 169–182. [Google Scholar] [CrossRef]
- Gao, R.; Gao, Z. Pitch Control for Wind Turbine Systems Using Optimization, Estimation and Compensation. Renew. Energy 2016, 91, 501–515. [Google Scholar] [CrossRef]
- Sierra-Garcia, J.E.; Santos, M. Deep Learning and Fuzzy Logic to Implement a Hybrid Wind Turbine Pitch Control. Neural Comput. Appl. 2021, 34, 10503–10517. [Google Scholar] [CrossRef]
- Thumthae, C.; Chitsomboon, T. Optimal Angle of Attack for Untwisted Blade Wind Turbine. Renew. Energy 2009, 34, 1279–1284. [Google Scholar] [CrossRef]
- Bagai, A.; Leishman, J.G. Rotor Free-Wake Modeling Using a Pseudoimplicit Relaxation Algorithm. J. Aircr. 1995, 32, 1276–1285. [Google Scholar] [CrossRef]
- Selig, M.S.; Coverstone-Carroll, V.L. Application of a Genetic Algorithm to Wind Turbine Design. J. Energy Resour. Technol. 1996, 118, 22–28. [Google Scholar] [CrossRef] [Green Version]
- Fuglsang, P.; Madsen, H.A. Optimization Method for Wind Turbine Rotors. J. Wind. Eng. Ind. Aerodyn. 1999, 80, 191–206. [Google Scholar] [CrossRef]
- Kenway, G.; Martins, J.R.R.A. Aerostructural Shape Optimization of Wind Turbine Blades Considering Site-Specific Winds. In Proceedings of the 12th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Victoria, BC, Canada, 10–12 September 2008; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2008. [Google Scholar]
- Wang, X.; Shen, W.Z.; Zhu, W.J.; Sørensen, J.N.; Jin, C. Shape Optimization of Wind Turbine Blades. Wind Energy 2009, 12, 781–803. [Google Scholar] [CrossRef]
- Narayana, M.; Putrus, G.A.; Leung, P.S.; Jovanovic, M.; McDonald, S. Development of a Model to Investigate the Yaw Behaviour of Small Horizontal Axis Wind Turbines. Proc. Inst. Mech. Eng. Part A J. Power Energy 2012, 226, 86–97. [Google Scholar] [CrossRef]
- Geleta, D.K.; Manshahia, M.S. Gravitational Search Algorithm-Based Optimization of Hybrid Wind and Solar Renewable Energy System. Comput. Intell. 2022, 38, 1106–1132. [Google Scholar] [CrossRef]
- Morshed, M.J.; Hmida, J.B.; Fekih, A. A Probabilistic Multi-Objective Approach for Power Flow Optimization in Hybrid Wind-PV-PEV Systems. Appl. Energy 2018, 211, 1136–1149. [Google Scholar] [CrossRef]
- Fulzele, J.B.; Daigavane, M.B. Design and Optimization of Hybrid PV-Wind Renewable Energy System. Mater. Today Proc. 2018, 5, 810–818. [Google Scholar] [CrossRef]
- Ghorbani, N.; Kasaeian, A.; Toopshekan, A.; Bahrami, L.; Maghami, A. Optimizing a Hybrid Wind-PV-Battery System Using GA-PSO and MOPSO for Reducing Cost and Increasing Reliability. Energy 2018, 154, 581–591. [Google Scholar] [CrossRef]
- UL HOMER Software. Available online: http://www.nrel.gov/homer (accessed on 14 August 2022).
- Nguyen, T.-T.; Boström, T. Multiobjective Optimization of a Hybrid Wind/Solar Battery Energy System in the Arctic. J. Renew. Energy 2021, 2021, 8829561. [Google Scholar] [CrossRef]
- Ekren, O.; Ekren, B.Y. Size Optimization of a PV/Wind Hybrid Energy Conversion System with Battery Storage Using Response Surface Methodology. Appl. Energy 2008, 85, 1086–1101. [Google Scholar] [CrossRef]
- Traoré, A.; Elgothamy, H.; Zohdy, M.A. Optimal Sizing of Solar/Wind Hybrid Off-Grid Microgrids Using an Enhanced Genetic Algorithm. J. Power Energy Eng. 2018, 06, 64–77. [Google Scholar] [CrossRef] [Green Version]
- Sawle, Y.; Gupta, S.C.; Bohre, A.K. Optimal Sizing of Standalone PV/Wind/Biomass Hybrid Energy System Using GA and PSO Optimization Technique. Energy Procedia 2017, 117, 690–698. [Google Scholar] [CrossRef]


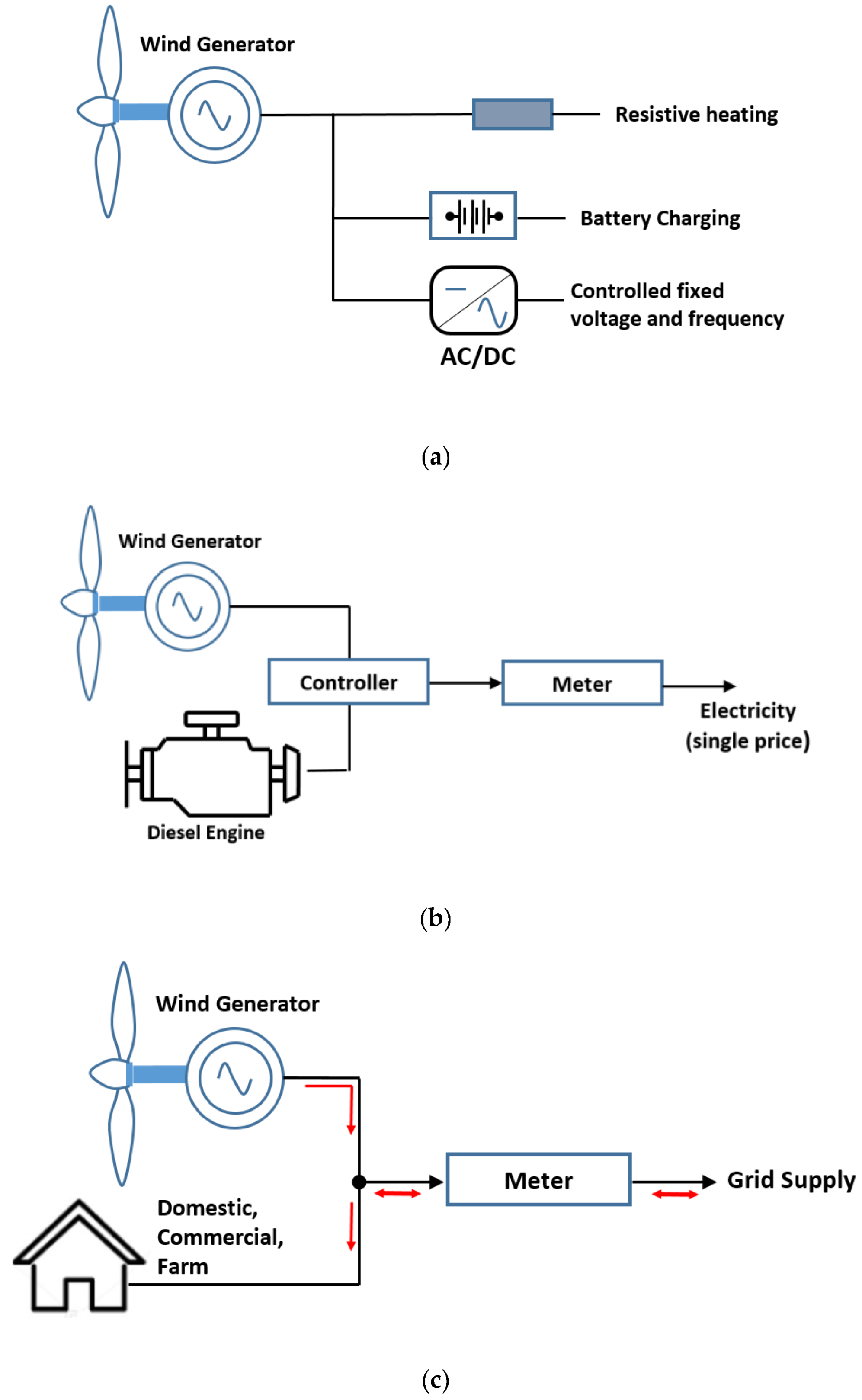


| Authors | Model Architecture | Application | Prediction Accuracy |
|---|---|---|---|
| Gao et al. [17] | Weighted hybrid kernel extreme learning machine with k-MoGE optimizer | Ultra-short-term onshore wind speed forecasting Single-step or multi-step (1–3 steps) | 0.0699 < RMSE < 0.1306 1.9236 < MAPE < 6.5364 |
| Liu et al. [12] | Support vector machine with Jaya optimization algorithm | Short-term onshore wind speed forecasting Single-step or multi-step (1–3 steps) | 0.6451 < MSE < 1.0154 0.5909 < MAE < 0.7633 11.87 < MAPE < 15.34 |
| Xing et al. [10] | Optimal benchmark model selection with multi-objective Aquila optimizer and fuzzy information granulation | Short-term onshore wind speed forecasting Single-step or multi-step (1–3 steps) | 0.4897 < RMSE < 2.4219 0.3821 < MAE < 1.7404 4.122 < MAPE < 33.725 |
| Chen et al. [36] | A hybrid model of the LSTM and BP neural networks with the sparrow search algorithm | Short-term onshore wind speed forecasting Single-step or multi-step (1–3 steps) | 0.039 < MAE < 0.135 0.051 < RMSE < 0.273 0.929 < MAPE < 2.478 0.003 < MSE < 0.062 |
| Zou et al. [9] | A hybrid probabilistic model of multilayer CNN and attention-based LSTM based on non-crossing quantile loss | Onshore Wind speed forecasting Single step | 0.6610 < MAE < 0.7075 1.0102 < RMSE < 1.0556 13.21 < MAPE < 14.15 |
| Neshat et al. [13] | A hybrid model based on QCNN and Bi-LSTM integrated with an adaptive decomposition technique.) | Long-term onshore wind speed forecasting. One-day ahead forecasting (single-step) | 0.0087 < MSE < 0.0138 0.0935 < RMSE < 0.1178 0.0510 < MAE < 0.0721 |
| Wang et al. [37] | An ensemble multi-feature complementary prediction model based on SVR and bidirectional LSTM. LWSM with CS algorithm is used to optimize of weight assignment | Onshore wind speed forecasting Single step | 0.063 < RMSE < 0.072 0.054 < MAE < 0.057 36.48 < MAPE < 57.35 |
| Wu et al. [38] | A deep learning gated recurrent unit (GRU) network | Long-term onshore wind speed forecasting. One-day ahead forecasting (single-step) | 22.29 < MAPE < 30.61 3.1754 < MSE < 8.1566 |
| Ding et al. [21] | Hybrid-kernel least-squares support vector machine with maximal wavelet decomposition and fuzzy C-means algorithm | Short-term wind power forecasting Multi-step (5–15 steps) | 8.78 < RMSE < 16.78 6.59 < MAE < 13.11 |
| Yildiz et al. [39] | An improved residual-based CNN with stochastic gradient descent optimization algorithm | Very short-term wind power forecasting Multi-step (1–3 steps) | 0.0248 < RMSE < 0.1362 0.0187 < MAE < 0.0827 |
| Jiandong et al. [14] | A hybrid model of the LSTM network and DBN network with particle swarm optimization | Short-term wind power forecasting Single step | MAE = 35.3776 RMSE = 42.9055 |
| Tian et al. [18] | A gated recurrent unit with a dual-stage self-attention mechanism | Single-step-ahead wind power forecasting | 80.6 < RMSE < 148.1 52.8 < MAE < 102.8 |
| Al-qaness et al. [40] | A hybrid technique of an augmented version of the marine predator algorithm using the mutation operators and adaptive neuro-fuzzy inference system | Short-term wind power forecasting Single step | 0.0056 < RMSE < 0.1757 0.0001 < MAE < 0.0050 |
| Hu et al. [41] | Temporal convolutional network combined with the conformalized quantile regression algorithm | Wind power forecasting Interval forecasting | 44.60 < MAE < 934.16 82.20 < RMSE < 1371.22 |
| Class/ | A | B | C |
|---|---|---|---|
| Summary | Figure 7a | Figure 7b | Figure 7c |
| : wind turbine capacity; : linked generation capacity | |||
| Example of PG Example of system | Battery Autonomous | Diesel generator Wind/diesel | Central power station Grid embedded |
| Common wind turbine generator type | Permanent Magnet | Induction | (a) doubly-fed induction (b) multi-pole with AC/ DC/AC interface |
| G98 | G99 | ||
|---|---|---|---|
| Generator power | Prated: 3.68 kW (1-ph) Prated: 11.04 kW (3-ph) | Type A | The registered capacity is >16 A/phase and above, but less than 1 MW |
| Type B–D | The connection point is below 110 kV (in practice in GB this is at 66 kV or below). | ||
| Voltage at point of common coupling (PCC) | Vrated = 400 V 3-p HVrated = 230 V 1-ph | Type A | Installations where the registered capacity is at or above 1 MW, |
| Type B | Generation connected at or above 110 kV (in practice in GB this is at 132 kV or above) | ||
| Method/Software | Model/Software Objectives/Capabilities | Ref. |
|---|---|---|
| Computational Fluid Dynamics (CFD) model and rotor free-wake modeling using a pseudo implicit relaxation algorithm | Flow simulation of wind turbines with the untwisted blade to determine the optimal angle of attack that produces the highest power output of wind turbines. | [112,113] |
| Genetic Algorithm with an inverse design method | To determine the optimum blade pitch and blade chord and twist distributions that maximize the annual energy production. | [114] |
| Numerical Multi-disciplinary Optimization Method | Minimum cost of energy (COE), cognizant of fatigue and extreme loads in the design stage for capital cost and the annual energy production for a given site condition. | [115] |
| Sequential Quadratic Programming (SQP) method | Optimizing for the COE to maximize the annual energy production (AEP) cognizant of the original baseline design. | [116] |
| Gradient-Based Optimization method | Optimization of three different wind turbine rotors with the objective of minimum COE. | [117] |
| Dynamic Analysis by MATLAB/SIMULINK | Effect of yaw behaviour for power generation in small wind turbines. | [118] |
| Gravitational Search Algorithm (GSA) | Optimisation in terms of total annual cost evaluation of wind and solar (hybrid) renewable energy systems to satisfy the predesigned demand. | [119] |
| Monte Carlo Simulation (MCS) combined with Antithetic Variates Method (AVM) | Determining the probability distribution function (PDF) of the power generated by the hybrid system. | [120] |
| iHOGA | Employing a genetic algorithm to determine the optimal sizing of the desired hybrid energy system. | [121] |
| HOMER | Micro power optimization tool, which consists of optimization and sensitivity algorithms. | [122,123] |
| Particle Swarm Optimization (PSO) | A multi-objective optimization approach to design an optimal design of hybrid wind turbine/PV/battery energy system by comprehensively investigating the effects of various factors on the cost-reliability relations. | [124] |
| Response Surface Methodology (RSM) | Employing design parameter relationships such as the PV size, wind turbine rotor swept area, etc., to determine the system cost of an autonomous (hybrid) PV/wind integrated hybrid energy system with battery storage. | [125] |
| Enhanced Genetic Algorithm (GA) | System design parameter optimisation for minimizing the total cost of the system, while incorporating the micro-grid system reliability based on the loss of power supply probability. | [126] |
| GA combined with PSO | Optimal planning/configuration of a PV-wind-biomass system with energy storage and a backup diesel generator, with minimized COE as an objective function. | [127] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perera, S.M.H.D.; Putrus, G.; Conlon, M.; Narayana, M.; Sunderland, K. Wind Energy Harvesting and Conversion Systems: A Technical Review. Energies 2022, 15, 9299. https://doi.org/10.3390/en15249299
Perera SMHD, Putrus G, Conlon M, Narayana M, Sunderland K. Wind Energy Harvesting and Conversion Systems: A Technical Review. Energies. 2022; 15(24):9299. https://doi.org/10.3390/en15249299
Chicago/Turabian StylePerera, Sinhara M. H. D., Ghanim Putrus, Michael Conlon, Mahinsasa Narayana, and Keith Sunderland. 2022. "Wind Energy Harvesting and Conversion Systems: A Technical Review" Energies 15, no. 24: 9299. https://doi.org/10.3390/en15249299






