Direct Contact Condensers: A Comprehensive Review of Experimental and Numerical Investigations on Direct-Contact Condensation

Abstract

Direct contact heat exchangers can be smaller, cheaper, and have simpler construction than the surface, shell, or tube heat exchangers of the same capacity and can operate in evaporation or condensation modes. For these reasons, they have many practical applications, such as water desalination, heat exchangers in power plants, or chemical engineering devices. This paper presents a comprehensive review of experimental and numerical activities focused on the research about direct condensation processes and testing direct contact condensers on the laboratory scale. Computational Fluid Dynamics (CFD) methods and CFD solvers are the most popular tools in the numerical analysis of direct contact condensers because of the phenomenon’s complexity as multiphase turbulent flow with heat transfer and phase change. The presented and developed numerical models must be carefully calibrated and physically validated by experimental results. Results of the experimental campaign in the laboratory scale with the test rig and properly designed measuring apparatus can give detailed qualitative and quantitative results about direct contact condensation processes. In this case, the combination of these two approaches, numerical and experimental investigation, is the comprehensive method to deeply understand the direct contact condensation process.

1. Introduction

Direct Contact Condensers (DCCs) have been used in industry since the beginning of the 20th century [1], covering a wide range of various applications in chemical engineering, water desalination, air conditioning, and energy conversion processes.

In this device, the cooling liquid is directly mixed with gas or vapour, which results in condensation and a significant decrease in device volume [2]. Involving a surface condenser of the same capacity direct condenser has several advantages. Due to direct contact with process fluids, its construction is simpler and more corrosion resistant [3], less expensive [4], easier to maintain, and simpler in operation [5].

Direct contact condensers are generally divided into spray-type, film-type, and bubbling type [6]. In the first solution, the sprayed liquid phase flows downwards and is in contact with flowing upwards gas. In the second case, both phases flow counter currently. In the latter solution, the bubbling gas phase passes through the liquid layer. Furthermore, spray condensers can exist with constant pressure or constant area jet ejectors [7]. Despite these apparatuses’ wide range of applications, plenty of studies summarize theoretical and practical aspects of their development. Aidoun et al. [8,9] presented results of experimental and numerical studies focusing on ejectors and their applications in refrigeration systems. Mil’man and Anan’ev [10] focused on the application of air-cooled condensing units in thermal power plants. Xu et al. [11] discussed recent advances in humidification-dehumidification desalination processes, including direct and indirect contact condensers. They are also commonly used as dehumidifiers in solar-driven humidification-dehumidification desalination [12,13] and seawater greenhouse [14] systems. The application of direct and indirect condensers in the pyrolysis of waste plastics was discussed by Kartik et al. [15], and in pyrolysis of biomass to bio-oil was presented in [16].

The wide range of possible and actual applications of these devices indicates the need to investigate more deeply the direct contact condensation process by using simulation and experimental studies devoted to developing direct contact condensers. This paper aims to present various analyses and their main outcomes to give the full view of the most important factors that must be considered during theoretical and experimental research.

2. Direct Contact Condensers

Direct Contact Heat Exchangers (DCHEs) play an important role in various technological processes, including humidifying air, cooling water, and removing excess heat from flue gases. The exchange processes in such apparatuses occur under contact with the liquid phase (e.g., water) and gas phase (e.g., air) at the interphase surface. In this case, heat and mass transfer are mainly determined by the geometric dimensions of the surface area for contact between the two phases. A specific value of this surface area (attributed, for instance, to the volume of the active zone of DCHE) depends on the method of interaction of the contacting phases, i.e., on the DCHE design. The most commonly used designs of heat exchangers are the following [6]:

-

spray-type (gas phase flows upwards and comes into contact with the liquid phase, which is sprayed from the nozzles and flows downwards),

-

film-type (liquid phase flows downwards as a thin liquid film on the inside wall of the vertical tube while the air flows counter currently) [17,18,19,20],

-

bubbling-type (bubbling of the gas phase through a layer of the liquid located on a hole tray [21,22,23] or in a vertical channel [24,25].

Direct Contact Condensers (DCCs) have a variety of purposes. They can be used to heat the liquid for heat recovery. The hot liquid can be used to heat rooms, preheat raw materials, or melt solids such as ice. DCCs can be used to cool the gas to generate condensate. Condensate can be used to purge a reaction product, such as acids coabsorbed in the DCC, condense a particulate by converting it from a vapor to a liquid or solid, and grow particulate by condensing directly on the particulate surface to improve its capture or reclaim water in arid regions. Direct Contact Condensers also can reduce gas volume, suppress stack plumes, and lower energy requirements.

2.1. Type of Direct Contact Condensers

In direct-contact condensers, the gas and liquid come in direct contact. The cooling liquid is sprayed into the gas region to start a rapid condensation, which maximizes the thermal efficiency of condensers. The heat is transferred from a gas to a liquid, and the condensate temperature is the same as that of the cooling liquid leaving the condenser. The condensate cannot be reused as feed water if the cooling water is not pure and free from harmful impurities. The occurrence of the other gases strongly impacts the heat transfer rate and condensation efficiency. This process is one of the important issues investigated experimentally or numerically to determine overall efficiency and properly design Direct Contact Condensers. The general classification of condensers is presented in Figure 1.

In a parallel flow jet type condenser, the exhaust steam and cooling water find their entry at the top of the condenser and then flow downwards, and condensate and water are finally collected at the bottom (Figure 2).

The steam and cooling water enter the condenser from opposite directions in a counter jet type condenser. Generally, the exhaust steam travels upward and meets the cooling water, which flows downwards. In this low-level jet-type condenser (counter jet type condenser), presented in Figure 3, the exhaust steam enters slightly lower than in a parallel flow jet-type condenser, and the cooling water is supplied from the top of the condenser chamber (Figure 3). The direction of the steam is upward, and the cooling water is downward. An air pump creates a vacuum and is placed on top of the condenser. The vacuum sucks the cooling water, and a hollow cone plate collects the falling water, which joins the second series of streams and meets the exhaust steam entering from below. The resulting condensate is delivered to the tank through a vertical pipe by the condensate pump. Another solution of counter jet type condensers is called barometric condenser and is presented in Figure 4. In this type, the shell is placed at the height of about 10.363 m above the hot well; thus, there is no need to provide an extraction pump. Provision of providing injection pump is observed, where water under pressure is unavailable.

In Figure 4, the discharge pipe is connected to the bottom of the condenser shell. The exhaust steam enters the system in the lower part of the condenser, with the flow direction pointing upwards. Cooling water enters at the top and is collected by a punched cone plate. An air pump creates the vacuum on top of the shell. Steam and cooling water mix together and are carried through a discharge pipe to the tank. The difference between low and high-level jet condensers is that there is no pump between the tank and the discharge pipe in the high-level type.

The last type of jet condenser is an ejector flow jet type condenser (Figure 5). Here the exhaust steam and cooling water mix in hollow truncated cones. Due to this decreased pressure, exhaust steam and associated air are drawn through the truncated cones, finally leading to the diverging cone. In the diverging cone, a portion of kinetic energy is converted into pressure energy which is more than the atmospheric, so that condensate consisting of condensed steam, cooling water, and the air is discharged into the hot well. The exhaust steam inlet is provided with a non-return valve which does not allow the water from the hot well to rush back to the engine in case of cooling water supply to the condenser.

The cooling cycle makes use of a steam ejector condenser. The steam ejector condenser is classified into two types based on the mixing method in the primary nozzle exit [7,26]. The first one is the constant pressure jet ejector (CPJE), and the other one is the constant area jet ejector (CAJE). The CPJE performs better than the CAJE due to better turbulent mixing [7,27]. In addition to having no moving parts, the steam ejector condenser benefits from lower maintenance and capital cost than the compressor.

2.2. Water and CO₂ Separation

After the exhaust passes through the Direct Contact Condenser (DCC) for condensation, the condensate water from the DCC consists of a proportion of non-condensable gases such as CO₂, air, or other gases. The stream is passed through the separator or non-condensable gas removal system, which separates the water and the non-condensable gases. By this method, the separated CO₂ can be sent to the CCU unit for further utilization, or the separated air gases can be removed from the system. Gas separation from the DCC outlet stream can be carried out in various methods. The axial flow cyclone separator is the most commonly used gas-liquid separation method widely used in industries. Kou et al. [28] simulated and experimentally proved gas-liquid separation using an axial flow cyclone separator. The experiment is conducted by passing the gas-liquid mixture stream into the cylindrical axial flow separator. A guide vane at the bottom of the cyclone separator produces centrifugal force in the fluid passing through it. Once the fluid passes into the separator, the centrifugal force created in the fluid separates the gas and liquid due to the density difference. While the liquid is collected at the bottom, the gas escapes through the top of the separator [28,29]. Ji et al. [29] experimentally proved that the efficiency of the cyclone separator could be improved by combining components to the cyclone separator. The combined cyclone separator includes components such as a steady flow element, leaf grind element, and folding plate element, which increases the efficiency of gas-liquid separation by more than 95%. Chemical looping is one of the methods of splitting the H₂O and CO₂ in the exhaust gas. The exhaust, which consists of H₂O and CO₂ undergoes a chemical reaction with the metal oxide used in chemical looping and produces different components. Farooqui et al. [30] state the process of chemical looping with cerium oxide (CeO₂). The H₂O and CO₂ are pressurized, and the temperature is raised up to 500 °C by compression. By integrating chemical looping, oxidation occurs with CeO₂, which splits H₂O into Hydrogen and CO₂ into carbon monoxide. The separated components from the exhaust of the chemical looping is further used for dimethyl ether (DME) production. This is considered one of the methods for CCU technology using chemical looping. Wotzka et al. [31] presented the possibility of separating CO₂ and water with the application of a microporous membrane. The separation of carbon dioxide and water using an MFI zeolite membrane treated with amine is analyzed experimentally and with molecular simulation. For experimental purposes, the liquid water is heated up to 120 °C, mixed with CO₂ in an evaporator, and further sent to separation. The performance of membrane separation is analyzed under different factors.

3. Experimental Facilities for Direct Contact Condensers Investigation

3.1. Description of Experiments

When considering direct contact condensers, researchers were directed to several topics. The first one covers various physical aspects of the direct contact condensation phenomenon in different construction variants, as in downcommerless trays for the steam–water system, direct contact condensation in a moving steam-water interface, in the case of the steam jet in subcooled water flow in a rectangular mix chamber or in a vertical square cross-section pipe. Additionally, visualization studies involving high-speed cameras were presented. There can also be distinguished direct contact condensation in the presence of non-condensable gas.

Other studies were devoted to analyzing heat transfer coefficient or volumetric heat transfer in direct contact condensers. Then, various construction aspects and their impact on condenser performance were analyzed. Finally, a few cases of DCC performance in the presence of non-condensable gases were given. Their short description, with emphasis on applied fluids (liquids and gases), is shown in

Table 1. Main areas investigated in experimental studies on direct contact condensers.

Author(s)	Fluid(s)	Capacity	Operating Conditions	Remarks
Zong et al. [32]	Steam–water	Water mass flux at nozzle outlet 6–18 × 10−3 kg/m2 s	Pwater = 0.1−0.5 MPa, steam mass flux at nozzle throat 200–600 kg/m2 s	The flow field was filmed. Proposed an empirical correlation for the average heat transfer coefficient calculation
Xu et al. [33]	Steam–water	Maximum steam flow rate is 0.03 kg/s.	Steam inlet pressure 0.2–0.7 MPa Steam inlet temperature 110–170 C	Five types of plume shapes were identified visually
Mahood et al. [34]	Pentane, liquid-, vapour-water	Mass flow rate < 0.38 kg/min	Temperatures < 50 °C	Mass flow rate ratio has a significant effect on the direct contact condenser output
Ma et al. [35]	Pure steam, steam-Nitrogen and steam-Argon	Coolant mass flow rate: 0 to 8.5 t/h	Pressure in the primary loop 0.2–3.1 MPa The temperature in the primary loop 123–237 °C	The condensation heat transfer coefficient increased with pressure,

.

In the following paragraphs, experimental studies on direct contact heat exchangers are presented. They are grouped according to the previous section into the parallel flow, counter flow, and ejector flow condensers.

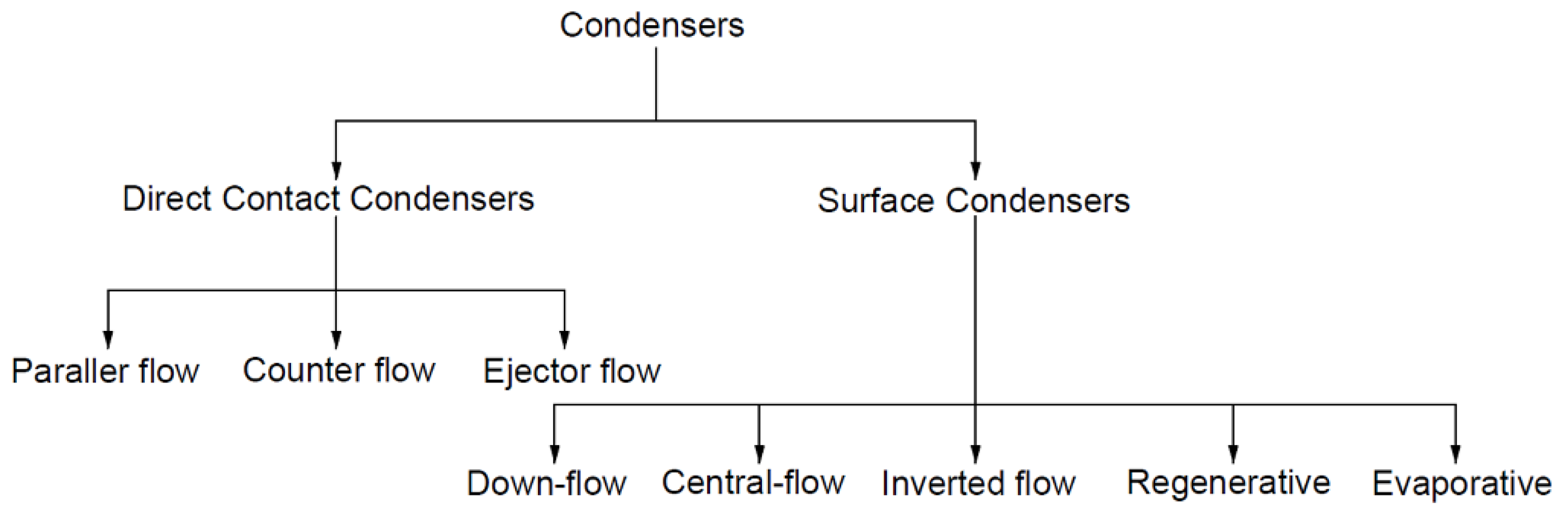
3.2. Parallel Flow Condensers

The Thermochemical Power Group (TPG) at the Polytechnic School of the University of Genoa developed and implemented the contact condenser test rig [36,37,38,39] (

Table 2. The equipment in the test rig of the TPG [36,37,38,39].

Device	Rating Parameters	Comments
Water pump	0.75 kW	Centrifugal
Recirculation pump	0.33 kW	Centrifugal
Water heater	7.5 kW	Electric
Air compressor capacity	10 g/s	Maximum

). It was intended for studies on the humid air turbine cycle where water introduction in a gas turbine circuit is provided by a pressurised saturator (i.e., humidification tower or saturation tower).

Changing input variables at the levels given in

Table 3. Experimental conditions in [36,37,38,39].

Quantity	Range	Unit
System	Air-steam
Column diameter	80	mm
Column height	200–1800	mm
Inlet air flow	5, 7.5 and 10	g/s
Inlet water flow	5, 7.5 and 10	g/s
Air temperature	100, 200 and 300	°C
Column pressure	3, 4, 5	bar

, the authors performed 162 tests in total. Data analysis was provided using two types of correlations for the non-dimensional outlet air temperature, i.e., based on polynomial correlation:

$$T_{adim}=c_0+c_1{x}_1+c_2{x}_1^2+c_3{x}_1^3+c_4{x}_2+c_5{x}_2^2+c_6{x}_2^3+\dots ,$$

(1)

and applying non-dimensional parameters, as non-dimensional temperature (T*), mass flow (M*) and the Reynolds number of inlet air (Re*):

$$\mathsf{\Delta }{T}_{adim}^{\ast }=4.5259\times {\left(M^{\ast }\right)}^{0.0326}\times {\left(T^{\ast }\right)}^{-0.4645}\times {\left(R{e}^{\ast }\right)}^{-0.1027},$$

(2)

and:

$$\mathsf{\Delta }{T}_{adim}^{\ast }=4.8198\times {\left(M^{\ast }\right)}^{0.0277}\times {\left(T^{\ast }\right)}^{-0.4667}\times {\left(R{e}^{\ast }\right)}^{-0.1108}.$$

(3)

Equation (5) was derived based on enthalpy balance and assuming an adiabatic saturation process. The standard deviation of 2.5 K and 2.8 K were obtained in the first and second case, respectively. Hence, presented relationships can be used when designing structured packing saturators.

In the work [39] the same rig was used to validate the numerical code TRANSAT developed to simulate the transient performance of direct contact heat exchangers. The error for water temperature was less than 1%.

Zare et al. [40] analysed a steam-water system with a vertical square cross-section pipe supplying equipment (

Table 4. The test rig equipment in the study of Zare et al. [40].

Device	Rating Parameters	Comments
Water pump	1 kW	Centrifugal
Water tank	0.5 m3	-
Water heater	6 kW	-
Steam generator capacity	90 kg/h	Maximum
Steam generator pressure	5 bar	Maximum

). The high-speed camera (set at 100 fps) photographed the studied phenomenon.

Based on experimental data and employing a genetic algorithm, authors developed an empirical correlation for the average heat transfer coefficient steam-water der direct contact condensation:

$$N{u}_{av}=\frac{h_{av}D}{{\lambda }_w}=2083\times B^{1.47}{\left(\frac{G_0}{G_m}\right)}^{-1.51}\times R{e}^{0.525}$$

(4)

with:

λ_w—thermal conductivity of water, W/(m·K),

D—hydraulic diameter of the test section, m,

B—condensation driving potential, -

G_m—critical steam mass flux, G_m = 275 kg/m² s at an atmospheric condition

G₀—Steam mass flux, kg/m2 s.

Under experimental conditions (

Table 5. The test conditions in [40].

Parameter	Value/Unit
Cross section of the test section	8 × 8 cm
Height of the test section	50 cm
Water flow rate	1–7 m3/h
Water temperature	20–50 °C
Steam pressure	0.05–0.4 MPa
Steam temperature	108–146 °C
Steam mass flux	200–540 kg/m2 s

) the calculated average heat transfer coefficient was within the range of 0.716–3.131 MW/(m² K).

Datta et al. [41] investigated direct contact condensation during subcooled water injection into a horizontal pipe supplied with steam. The test section was made of stainless steel. A steam tank was used as a steam accumulator (

Table 6. The test rig equipment in [41].

Quantity	Value	Unit
Test column diameter	66.65	mm
Test column length	2050	mm
Steam generator capacity	200	kg/h
Maximum steam pressure	16	bar
Steam tank length	1070	mm
Steam tank diameter	343	mm

). Three pressure and five temperature sensors were mounted along the test section to provide their temporal variations.

During experiments, steam and water pressure varied from 2 to 3 bar and from 3 to 6 bar, respectively. Supplying water temperature was maintained about 30 °C. Steam temperature was from 120.2 °C to 133.5 °C. Authors observed higher pressure peaks (up to 6.08 bar) in the test section when the rising pressure difference between its inlet and water section was up to 3 bar.

Karapantsios et al. [42,43] considered a steam—air system using a vertical and transparent column 2660 mm high with 50 mm of internal diameter. They divided the column into the inlet (300 mm), intermediate (900 mm), and measurement (1400 mm) sections. Inlet steam pressure was maintained constant at 1.5 bar. The water flow rate was changed within the range of 26 to 416 g/s.

They defined a condensation heat transfer coefficient:

$$h_c=\frac{L}{\Delta T}\frac{\Delta W_c}{\Delta x },$$

(5)

with:

L—latent heat, J/kg,

ΔW_c—condensation rate, kg/s·m.

ΔT—temperature difference, K,

Δx—distance between measuring points, m.

Then the cumulative heat transfer coefficient was analyzed, assuming as ΔT the logarithmic mean temperature difference. During experiments, it varied between 500 and 2000 W/m² K for the entire condensing region (at heights between 0 and 690 mm from the steam entry).

The steam condensation subatmospheric conditions in the concurrent flow packing tower were investigated by Chen et al. [44]. As the direct contact condenser, they used a stainless steel 1000 mm high column with 300 mm of internal diameter. A steam generator with 0–144 kW of heating power and a 1.5 kW vacuum pump (6 × 10⁻² Pa and flow rate of 15 L/s) were used.

During an impact of steam temperature T_cond, steam flow G_in, inlet water temperature T_in, and water flow L_w on the condensation process was studied. These parameters were set at values given in

Table 7. Operating conditions during experiments in the study of Chen et al. [44].

Parameter	Value
Tcond (°C)	47.5, 50.0, 52.5, 55.0, 60.0
Gin (kg/h)	68.6, 74.6, 80.6, 86.6, 92.6
Tin (°C)	22–32 (0.5 interval)
Lw (m3/h)	2.40, 2.15, 1.90, 1.65

.

The authors analyzed several parameters, such as condensation rate (R), degree of subcooling (ΔT), number of liquid-phase heat transfer units (NTUL), and the total volume heat transfer coefficient K_V. The relationship gives the latter one:

$$K_V=\frac{c_{pL}{G}_L \left(T_{out}-T_{in}\right)}{\Delta T_m V},$$

(6)

with:

cp_L—specific heat at constant pressure, J/(kgK),

G_L—mass flow rate of cooling water, kg/s,

T_in—inlet temperature of cooling water, K,

T_out—outlet temperature of cooling water, K,

ΔT_m—logarithmic average temperature difference during condensation, K,

V—volume from the liquid distributor to the stable liquid level of the tower bottom, m³.

During experiments, K_V varied from 80 to 250 kW/(m³ K). After fitting to experimental data, authors provided the correlation in the form:

$$K_V=50{\left(T_r{F}_{LG}\right)}^{-1.512},$$

(7)

with F_LG given by the equation:

$$F_{LG}=\frac{G_L}{G_{S,in}}\sqrt{\frac{{\rho }_S}{{\rho }_L}}.$$

(8)

Ma et al. [35] analyzed steam condensation in the presence of non-condensable gas (steam-nitrogen and steam argon) in relation to pure steam and estimated the heat transfer coefficient in relation to various conditions (pressure, gas content). The test section was the 1669 mm high tube with 5 mm and 8 mm inner and outer diameters, respectively. It was placed in a cylindrical container, 3660 mm high and with an internal diameter of 40 mm.

The test section was the tube-in-tube type, made of an inner tube with an outer diameter of 34 mm and an outer condensing tube with an inner diameter of 60 mm, and located in the axial centre of a stainless steel vessel with an inner diameter of 0.4 m and a height of 3.66 m. At its bottom were electrical heaters with power controlled from 0 to 60 kW, used to heat water. The condensing section had a height of 1.669 m. The thickness of the inner and outer tubes was 5 mm and 8 mm, respectively. A 60 kW electric heater was used to heat up water. The mass fraction of N₂/Ar was between 5% and 90%. Other experimental conditions are given in

Table 8. The test conditions during experiments during pure steam condensation and steam condensation with Nitrogen/Argon.

Parameter	Steam	N/Ar	Unit
Pressure in the primary loop	0.21–3.12	0.21–4.12	MPa
Temperature in the primary loop	123–237	80–267	°C
Pressure in the coolant loop	2.01–2.46	0.40–3.2	MPa
Temperature difference between the inlet and outlet of the condensing section	9.0–12.6	10–20	°C
Average temperature difference between the primary loop and the coolant loop	45.1–80.6	27–83	°C
Pressure in the primary loop	0.21–3.12	0.21–4.12	MPa
Temperature in the primary loop	123–237	80–267	°C

.

During pure steam condensation, when increasing the bulk pressure from 0.21 MPa to 3.12 MPa, the average condensation heat transfer coefficient, h_c, increased from 1.74 kW/(m² K) to 8.95 kW/(m² K). The introduction of non-condensable gases significantly influenced obtained results. In the presence of N₂ with a mass fraction of 11.5% h_c increased from 0.99 kW/(m² K) to 4.37 kW/(m² K) under the system pressure rise from 0.21 MPa to 3.11 MPa. They also noticed that under constant pressure, the condensation heat transfer coefficient decreases along with the increase of non-condensable gas share. They gave a case for 4.12 MPa bulk pressure and the mass fraction of N₂ increased from 8.41% to 81.5% when h_c decreased from 6.12 kW/(m² K) to 0.54 kW/(m² K).

3.3. Counter Flow Condensers

Genic [45] analyzed a water and steam system (

Table 9. The test conditions during experiments in the study of Genic [45].

Quantity	Range	Unit
System	Steam-water
Column diameter	DN 300, 323.9/309.7	mm
Water flow rates at the column inlet	3.0–13.6	m3/h
Steam flow rate	203–1070	kg/h
Inlet water temperature	20–30	°C
Water outlet temperature	39–98	°C
Steam at the inlet	102–117	°C
Working pressure in a column	100.1–101.8	kPa

) comprising a 300 mm diameter column for water deaerators with downcommerless trays.

The author derived experimental correlation for the number of transfer units for the liquid phase (NTU_L), with a correlation ratio of 0.925 and standard deviation of 15.9%, in the following form:

$$NT{U}_L=0.185{\left(\frac{G_L}{G_{S,in}}\sqrt{\frac{{\rho }_S}{{\rho }_L}}\right)}^{-1.48}$$

(9)

with:

G_L—mass flow rate of liquid, kg/s,

G_S,in—inlet mass flow rate of steam (vapour), kg/s,

ρ_L—liquid density, kg/m³,

ρ_S—steam (vapour) density, kg/m³.

In the next study [46] based on the same test rig, authors investigated heat transfer during direct-contact condensation on baffle trays. They presented the experimental correlation for Nusselt number based on dimensionless numbers:

$$Nu=5.8\times {10}^{-6}\times R{e}^{5/3}\times P{r}^{1/3}\times F{r}^{-2/3}$$

(10)

With a correlation ratio of 0.983 and a standard deviation of 13.3% sufficient for engineering design purposes.

In the study of Chen et al. [47], the authors investigated sonic steam jet condensation in sonic flow of water. Visualization of steam plumes was performed using a high-speed camera. Then digital image processing with Matlab software was applied. The test rig was set to provide the maximum steam flow rate of 126 kg/s (

Table 10. The additional equipment in the test rig of Chen et al. [47].

Device	Rating Parameters	Comments
Test section length	200 mm
Inner diameter of steam nozzle exit	5 mm
Diameter of the restricted channel	26 mm
Steam generator heater	90 kW	Maximum
Steam generator capacity	35 g/s	Maximum
Steam generator pressure	0.7 MPa	Maximum

). The test conditions are given in

Table 11. The test conditions during experiments of Chen et al. [47].

Parameter	Value/Unit
Steam inlet pressure	0.16–0.55 Mpa
Steam inlet temperature	115–155 °C
Steam mass flux	kg/(m2 s) 200–800
Water flow rate	kg/s 0.13–0.80
Water inlet temperature	50–70 °C

.

The authors distinguished five considered plume shapes: hemispherical, conical, contraction-expansion-contraction, ellipsoidal, and divergent, and presented a 3-D map of these shapes.

Introducing, as in previous studies, several dimensionless parameters authors derived experimental correlation for average heat transfer coefficient:

$$h_{av}=3.51\times {10}^{-3}\times c_p{G}_m{B}^{0.64}{\left(\frac{G_e}{G_m}\right)}^{-1.25}\times R{e}^{0.15}$$

(11)

Under presented experimental conditions, h_av varied Nusselt number:

$$N{u}_{av}=\frac{h_{av}{d}_e}{{\lambda }_w}=0.008B^{1.15}{\left(\frac{G_e}{G_m}\right)}^{-1.34}\times R{e}^{0.16}$$

(12)

with:

d_e—diameter of steam nozzle exit, mm,

G_m—critical steam mass flux,

G_e—steam mass flux, kg/m² s.

The presented model produced results with an accuracy of 20% when comparing the experimental data. The measured heat transfer coefficient was within the range of 1.6–5.5 MW/m² K.

Fei [48] and Xu [49] investigated bubbles’ uniformity and mixing time in a direct contact heat exchanger. They used a two-component system with heat transfer fluid (HTF) and R-245fa under the test conditions presented in

Table 12. The test conditions during experiments of Fei [48] and Xu [49].

Quantity	Range	Unit
Column diameter	480	mm
Column height	1500	mm
Flow rate of HTF	0–0.3	kg/s
Refrigerant flow rate	1−3	×104 m3/s

.

The authors concluded that there was a linear relationship between the flow patterns of a bubble swarm and heat transfer.

Xu et al. [33] investigated direct-contact condensation of the steam jet in water flow in pipes. The authors investigated the average heat transfer coefficient and Nusselt number. They also observed the plume’s shape and length using a high-speed camera. The test conditions are given in

Table 13. The test conditions during experiments of Xu et al. [33].

Quantity	Range	Unit
Height of the test section	mm	2000
Inner diameter of the test section	mm	80
Steam inlet pressure p	MPa	0.2–0.7
Steam inlet temperature Ts	°C	110–170
Steam mass flux Ge	kg/m2 s	150–500
Water flow rate Q	kg/s	0.14–6.65
Water temperature Tw	°C	20–70

.

Finally, they presented experimental correlations to obtain average heat transfer coefficients. For Reynolds numbers from 2456 to 29,473:

$$h_{av}=0.61C_p{G}_m{B}^{0.59}{\left(\frac{G_e}{G_m}\right)}^{-0.58}\times R{e}^{0.30}.$$

(13)

For 29,473 ≤ Re < 117,893:

$$h_{av}=7.21\times {10}^{-5}{C}_p{G}_m{B}^{0.35}{\left(\frac{G_e}{G_m}\right)}^{-0.55}\times R{e}^{1.10}.$$

(14)

B—condensation driving potential

C_p—water-specific heat, J/kgK

G_e—steam mass flux at nozzle exit, kg/m² s

G_m—critical steam mass flux, kg/m² s

Its value during experiments was within the range of 0.34–11.36 MW/m² K.

Mahood et al. [34] presented an experimental test facility for the investigation of a three-phase direct contact condenser using three phases (pentane, liquid-, vapor-water). A test section was built in the form of a 70 cm high Perspex vertical column with a 4 cm internal diameter and with seven thermocouples located along its height. The initial dispersed phase (liquid pentane) and continuous phase (water) temperature were from 37.6 °C to 41.7 °C and 19 °C, respectively.

The authors studied the impact of the mass flow rate ratio and temperature of the dispersed phase on the outlet conditions of the condenser and found that they depend mainly on the relation between dispersed and continuous mass flows. Additionally, the water temperature increased along with the column height.

In the next studies [50,51,52,53,54,55,56,57,58] they modified the test rig, locating thermocouples in different positions, and investigated the time-dependent volumetric heat transfer coefficient. In [50] they concluded that it decreases with time until steady-state conditions (at about 100 s in the considered case) are reached, according to the relationship:

$$U_v=\left(\frac{C_{pc}\left(1-\alpha \right){\rho }_c}{t}\right)ln\left[\frac{\left(T_{di}-T_{co}\right)+\left({\dot{m}}_d/{\dot{m}}_c\right)h_{fg}/C_{pc}}{T_{di}-T_{co}}\right]$$

(15)

with:

C_pc—specific heat of continuous phase, J/kgK

α—holdup ratio, -

ρ_c—density of continuous phase, kg/m³,

t—time, s,

T_di—dispersed phase inlet temperature, K

T_co—continuous phase outlet temperature, K,

h_fg—latent heat of condensation, J/kg.

Depending on the dispersed to continuous phases mass flow ratio, R, the initial value of U_v was from about 150 kW/m³ K at R = 6.5% to 780 kW/m³ K at R = 43.7%. Further, in [53] they confirmed that its value was not dependent on the initial dispersed temperature. In [54] the U_v was studied during the inception of the undesirable flooding phenomenon. Its value was from about 30 kW/m³ K to 60 kW/m³ K at T_di = 40°C to 60°C, respectively.

The next papers [55,56] were devoted to heat transfer by convection during direct contact condensation. Experiments showed that the unit heat transfer rate increased along with the mass flow rate ratio: from 100 kW/m³K to 200 kW/m³K at ${\dot{m}}_c$ = 0.05 kg/min to 200–400 kW/m³K at ${\dot{m}}_c$ = 0.38 kg/min.

In [51] authors developed their research determining the efficiency and capital cost of this heat exchanger. The heat transfer efficiency was given as:

$$H{T}_{eff}=\frac{T_{co}-T_{ci}}{T_{d,sat}-T_{ci}}\times 100\%,$$

(16)

with:

T_ci—continuous phase inlet temperature, K

T_co—continuous phase outlet temperature, K,

T_d,sat—vapour saturation temperature, K.

It was found that efficiency was controlled by means of the mass flow ratio (R). At higher values of R, the efficiency was above 50%.

This test rig with the different columns, 100 cm high with a 10 cm internal diameter, was also used [57] in investigations of the temperature distribution in the column condenser. The presented results showed a decrease in the continuous phase temperature down the height of the column. In [58,59] heat transfer measurements were performed depending on various parameters. The authors showed that the water (continuous phase) flow rate significantly affected the average volumetric heat transfer coefficient. During tests its value varied within the range of 20–60 kW/m³ K.

Observations of the transient behavior of a steam-water system with a packed column 1045 mm high and with an internal diameter of 325 mm were presented in [60]. The flow rate of cooling water was set at 120 L/h, 160 L/h, 350 L/h, 540 L/h, and 840 L/h, at a constant temperature of 28 °C.

The authors defined the volumetric heat transfer coefficient by the following equation:

$$h_v=\frac{Q_{water}}{V_e\times \Delta T_m},$$

(17)

with:

V_e—effective heat transfer volume of the column, m²,

ΔT_m—logarithmic mean temperature difference, K.

They reported that h_v increased from 1.47 kW/m³ K to 10.93 kW/m³ K with an increasing water flow rate from 120 L/h to 840 L/h. Additionally, time constant, referred to as the maximum attenuation of steam, shortened from 75 s to 13 s with the water flow rate rising within the same range.

Pommerenck et al. [61] used steam with volatile oils entrained in an air flow in the direct condenser with the sprayed water to analyze the recovery phenomenon for such oils. The condenser was built as a vertical PVC pipe with a 10 cm diameter. Water sprayer tips were mounted opposite at the same height. There were between 2 to 8 spray tips used during tests. Steam was introduced into the condenser through 2, 4, or 8 sprayers. The authors found that the direct contact condenser allowed better recovery in relation to the shell condenser. The direct condenser capture efficiency was found to be less depended on steam concentration than spray development.

3.4. Ejector Condensers

Yang et al. [32,60] investigated flow patterns and the influence of inlet water and steam parameters on pressure and temperature distributions in an ejector condenser under experimental conditions given in

Table 14. The experimental conditions in [32,60].

Parameter	Value	Unit
Inlet steam pressure	0.1–0.5	MPa
Inlet water pressure	0.1–0.5	MPa
Steam mass flux at the nozzle throat	200–600	kg/m2 s
Water mass flux at the nozzle outlet	6–18 × 10−3	kg/m2 s
Inlet water temperature [32]	293–333	K
Inlet water temperature [60]	288–333	K

.

The authors presented selected pressure and temperature distributions for stable and unstable flow patterns, providing input conditions.

Kwidzinski [62] investigated two-phase steam-water injectors. Four devices were used, each with different dimensions. During experiments motive steam pressure was from 60 to 430 kPa with flow rates from 75 to 130 kg/h. The water flow rate was between 1500 and 6500 kg/h at a water temperature of 14 to 40 °C. The average heat transfer coefficient for condensation in a mixing chamber of the condenser was given by:

$${\alpha }_{MC}=\frac{{\dot{m}}_{c2}\left(h_{V1}-h_{L2}\right)}{A_{MC}\Delta T_{MC}},$$

(18)

with:

${\dot{m}}_{c2}$—mass flow rate of condensate at the outlet of a mixing chamber, kg/s,

h_V1—steam enthalpy at the steam nozzle outlet, J/kg,

h_L2—liquid enthalpy at the mixing chamber outlet, J/kg,

ΔT_MC—logarithmic mean temperature difference between the vapour and liquid in the mixing chamber, K,

A_MC—surface area of the mixing chamber wall, m².

Depending on the device, it was found that α_MC varied from 250 kW/m² K to about 800 kW/m² K at the temperature difference (ΔT_MC) from 24 K to 68 K. Other experimental studies devoted to steam-ejector condensers were presented by Shah et al. [63,64,65]. The authors evaluated the effect of the mixing section length (110, 130, and 150 mm) on the transport process in the condenser. In addition, CFD simulations were performed.

As the source of steam, the electric 36 kW steam boiler with a 38 L tank generates saturated steam at a maximum flow rate of 52 kg/h (14.4 g/s) and pressure of 8 bar. The operating conditions during experiments are given in

Table 15. The experimental parameters of steam, water, and pressure in [63,64,65].

Parameter	Value	Unit
Steam inlet pressure	140–220	kPa
Steam inlet temperature	382–396	K
Water inlet pressure	96	kPa
Water inlet temperature	290	K
Ambient pressure	96	kPa

.

The authors didn’t present experimental correlations. However, several general outcomes were given. They observed an increasing water mass flow rate along with increasing inlet steam pressure. Additionally, under the same operating conditions, they obtainedhigher suction pressure and flow rate at a shorter length of the mixing section.

Reddick et al. [66] investigated a steam ejector’s performance in a mixture of steam and carbon dioxide (as non-condensable gas). The test rig included the 75 kW electric boiler (maximum pressure of 600 kPa), a 3 kW superheater, an ejector, a flash tank, and a condenser. Several operation variants were considered (

Table 16. The experimental conditions in [66].

Parameter	Value	Unit
Primary inlet pressure	350, 450, 550	kPa
Secondary in let pressure	50, 70, 90	kPa
Nozzle throat diameter	4.03, 4.23, 4.59, 5.09	mm

) and performance curves were then prepared.

When pure steam, without CO₂ entraining, was used, then it was observed that increasing the primary pressure, secondary pressure or nozzle diameter resulted in a higher value of critical pressure and lower critical entrainment ratio.

Entraining CO₂ resulted in different outcomes. Authors reported that the rising share of CO₂ resulted in an increased critical entrainment ratio, linearly. At the same time, the critical pressure was unchanged.

4. Measuring Systems in DCC Analysis

The main physical quantities measured in test rigs with direct contact condensers include temperature, pressure, and flow rate. A large variety of measurement methods and techniques can be applied here. However, from a practical and economical point of view, those that the authors found best in a given case were used. It should be emphasized here that none of the presented publications gave reasons for this or that choice. So, it may be worth giving a short presentation of various measurement methods with their main advantages and disadvantages and then presenting a short summary of findings.

The first criterion used when choosing a given sensor is based on the design of the test rig. From this, one can say if there is an electronic data acquisition system or not. If so, a sensor with an electric output signal should be used. If not, there can be applied simpler and cheaper solutions. Scientific experiments require data measurement and acquisition for further processing. Therefore, the presented description covers mainly measurement sensors with electric output signals, which can be used in modern data acquisition systems.

Regarding the temperature measurement, the temperature range of process fluids in the presented papers has not exceeded 300 °C [36]. Hence, thermocouples (TC) and resistance temperature detectors (RTD) could be useful. This is so because these kinds of sensors provide electrical-type output measurement signals that can be very easily transmitted and converted into computer measurement systems. Thermocouples can be used for a wide measurement range, from –270 °C to +1370 °C (K-type chrome–alumel thermocouple) to over 2000 °C (Pt-Rh thermocouples). The IEC 60584 standard defines classes 1 and 2 of tolerance. For class 1 of a measured temperature of 200 °C tolerance is from ±0.50 °C (type T) to ±1.50 °C (types E, J, K, and N). Due to the fact that the sensitive measuring point of the thermocouple (measuring junction) can be very small, with a diameter below 0.5 mm, the response time of these sensors can be very short. Protection of this junction against the negative impact of the external environment in a protective tube (sheath) results in a greater value of this response time [67,68].

The second kind of electrical temperature sensor are RTDs, which are more expensive, larger, and more fragile than thermocouples. Yet they have good accuracy, stability, and sensitivity [67,68]. At a temperature of 200 °C, according to the IEC 60751, the wire-wound A-class Pt100 sensor has a tolerance of ±0.44 °C. Protection of the sensitive part, platinum resistive wires, against the negative environmental impact results in a longer thermal time constant. Temperature measurement in direct contact condensers in presented test rigs was performed mainly by thermocouples. Additionally, RTDs were used but on a smaller scale. Their main parameters are given in

Table 17. Sensors for temperature measurement are used in experimental rigs with direct-contact condensers.

Type	Diameter [mm]	Accuracy	Reference
Pt100	n.a.	±0.1 °C	[47]
Pt100	n.a.	0.1 °C	[46]
Pt100	n.a.	0.1 °C	[69]
K	n.a.	±1 K	[50,51,52,53,54,55,56]
K	n.a.	±1.5 K	[39]
T	n.a.	0.1 °C	[42]
K	1.0	0.5 K	[62]
Pt100	0.48 mm	±0.1 °C	[66]
K	n.a.	1 °C	[64]
J	n.a.	0.5%	[41]
K	3.0	0.75%	[35]

.

As pressure measurement is considered, dominated piezoresistive absolute and differential pressure transducers [48,50], and piezoelectric transducers were used for pressure measurements. [49,66]. They have good accuracy and sensitivity.

The next very important measured quantity is the flow rate of various liquids and gases in the presented test rigs. Genić et al. [37] applied orifice flow meters manufactured following ISO 5167-1, with classical mercury U-tube manometers. When the water flow rate is to be considered, the most popular solution was the electromagnetic flow meter. However, in several cases, the turbine flow meter was also chosen (

Table 18. Devices used in water flow measurements.

Type	Range	Error	Reference
Rotameter	1–7 m3/h	0.1 m3/h	[40]
Electromagnetic	0.08–2.78 kg/s	0.2%	[60]
Electromagnetic	0.88–17.66 m3/h	0.5%	[47]
Electromagnetic	0–10 m3/h	1.0%	[41]
Rotameter	-	1.25%	[56]
Turbine	0.04–0.25 m3/h	1.0%	[47]
Turbine	0.6–6 m3/h	1.0%	[47]
Rotameter	1–10 m3/h	1.5%	[47]
Turbine	0.9–13.6 m3/h	0.15%	[47]

).

In steam flow measurement, vortex flow meters were the most popular (

Table 19. Devices used in steam flow measurements.

Type	Range	Error	Reference
Orifice	-	1.0 Pa	[64]
Vortex	7.5–73.9 g/s	1.0%	[57]
Vortex	30 to 300 m3/h	1.5%	[59]
Vortex	0–40 m3/h	0.75%	[28]
Vortex	0–120 m3/h	0.75%	[28]
Vortex	0–150 kg/h	1.0%	[59]
Vortex	-	2.0%	[61]
Orifice	-	1.5%	[61]

). However, despite the wide range of analysed studies, no selection guidelines were given by the authors.

The presented review shows various measurement techniques used in experiments with direct contact condensers. Despite the importance of this issue, authors presented a general overview and review about the selection of measurement equipment devoted to the test rig with the ejector condenser.

5. Numerical Modeling of Direct Contact Condensation

Numerical modeling of Direct Contact Condensation (DCC), which occurs in Direct Contact Condensers (DCCs), is challenging because of the phenomenon’s complexity. It requires taking into account the multiphase flow, often combined with turbulence. Computational Fluid Dynamics (CFD) can fully overcome these challenges, which is the most common tool for DCC modeling. There is no universal modeling framework for DCC because of the diversity of the phenomenon. Various flow regimes can occur (stratified flow, bubbly/droplets flow, etc.). The Euler-Euler interface tracking methods are suitable for liquid/vapour jet-type condensation, where the heat and mass transfer occurs mainly on the interface between phases. The most known clear interface tracking method is the Volume of Fluid (VOF). For drop-type direct condensation, where the vapor condenses on the surface of the droplets, methods allowing for a dispersed phase should be used. They can be based on the Euler-Euler and Euler-Lagrange approaches [69], but the Euler-Euler approach is often used. In this framework, two models are worth mentioning: the Mixture and the Eulerian two-fluid model. The Eulerian two-fluid model allows for modelling a mixed flow regime combined with interface tracking. Together with the k-ε model, it is often used for modeling steam/bubble jets submerged in subcooled water [70]. The major disadvantage of this model is extensive computational time. This section contains examples of numerical modeling of Direct Contact Condensation in various types of devices.

5.1. Numerical Analysis of DCC of Vapour Injected in the Liquid Tank

The direct contact condensation of steam from a vertical pipe into a water pool was examined numerically by Kunwoo Yi et al. [71]. The scheme of the geometrical model was presented in Figure 6. The presence of inert gas (air) was taken into account. The Star CCM+ solver was used. The Volume of Fluid model (VOF) was used to simulate multiphase flow. Reynolds-Averaged Navier-Stokes equations were closed using the k-ω SST model. The mixture of gas (steam and air) was assumed as an ideal gas. The evaporation/condensation model was used to model the direct contact condensation phenomenon. Mesh consists of mesh with 3 million polyhedral elements. The steam rate was 0.468 kg/m² s, and the flow was chugging. The tank was initially filled with water in 30% above the bottom of the suppression pool. The initial pressure in the suppression pool was atmospheric, and the temperature was 48.9 °C. As a result of the study, the influence of vertical tube pin holes on the behavior of chugging flow was investigated. The low steam flow rate in the blowdown pipe can prevent the chugging flow.

Multiphase CFD analysis of steam-water direct contact condensation in a Pressure Suppression Chamber was conducted by Tyler Dee Hughes [73]. The pressure Suppression Chamber is a crucial part of the BWR Reactor Core Cooling system. A 2D, axisymmetric model was developed using commercial Star CCM+ software based on the Finite Volume Method (FVM). The Eulerian two-fluid multiphase model with a segregated solver was used. Direct contact condensation was modelled based on the Hughes-Duffey Nusselt number correlation correlated to the liquid side:

$$Nu=\frac{2}{\pi }R{e}_t^{1/2}P{r}_l$$

(19)

with:

$R{e}_t$—turbulent Reynolds number, -,

$P{r}_l$—liquid Prandtl number, -,

The Standard k-ε turbulence model was used to model both phases’ behavior. The boundary conditions were assumed in accordance with the experimental environments. The physical properties of water and steam were computed based on IAPWS tables [74]. The simulation was transient First-order backward Euler implicit time step discretization and was applied; the Courrant Number did not exceed 10. For all fields, the second order discretization scheme was used. Simulation relaxation factors were presented in

Table 20. Simulation relaxation factor [71].

Solver Field	Relaxation Factor
Phase coupled velocity	0.56
Pressure	0.2
Volume Fraction	0.1
Energy	0.3
Turbulence	0.3

. Two types of meshes are considered: polygonal and structured. The temperature of the steam was 120 °C (Saturation temperature for 197 kPa pressure), and the mass flow was 34 kg/m² s. The average water temperature in the pool was 67 °C. The bubbling flow regime was observed numerically and experimentally. Figure 7 shows the condensation which occurs near the periphery of the bubble. In the simulation, rapid changes in the pressure were observed. The 2D axisymmetric structured mesh was the best for this type of calculation.

Roman Thiele [75] did the modeling of Direct Contact Condensation of saturated steam to subcooled water using the opensource, OpenFoam framework. The condensation occurs in the suppression pool, which is part of the Nuclear Power Plant. The solver uses the VOF method based on the cavitation model earlier developed by Kunz [76]. The governing equations are based on the volume continuity law. Pressure, velocity, and phase continuity equations were solved separately. Two-phase change models were developed to describe direct contact condensation: one based on the combustion approach and the second using inter-facial heat transfer. The simulation model of the facility was presented in Figure 8. The fluid properties were based on the IF97 database [74]. The steam temperature was 102 °C, and the corresponding saturation pressure was 1.1 bar. The liquid temperature was 22 °C with the same ambient pressure. Various steam mass flow rates were used for the time step and velocity dependence tests: 1.2 g/s, 4.9 g/s, and 12.4 g/s. The interface model better predicts the direct contact condensation phenomenon. It also shows great time-step stability. It should be considered for further development.

Jayachandran et al. [77] investigated numerically bubbling direct contact condensation of gas and liquid oxygen to capture heat and mass transfer effects. Direct contact condensation takes place as a result of mixing between hot gas mixture jet and subcooled liquid oxygen in booster turbopump exit of oxidizer-rich staged combustion cycle. To simplify the complex phenomenon, the gas mixture consists only of pure oxygen. The problem was solved using CFD methods with the ANSYS CFX solver based on the Finite Volume Method (FVM). For multiphase flow modeling, the two-fluid (particle-based) model was applied. The mean bubble diameter was taken from Anglart et al. [78]. RANS approach with separate equations for phases was used in the case of turbulence modeling. The two-equationsk-ε model was used for modeling turbulence on the liquid side, and the dispersed phase zero equation model was used for the vapor side [79]. The first-order upwind scheme was used to solve turbulence and advection schemes and the first-order backward Euler scheme to solve unsteady terms. The time step was 10⁻⁴ s. Direct Contact Condensation was modeled using the thermal phase change model, which is a two-resistance model. The Nusselt number for the vapor side was calculated using the zero-equation formula, and the liquid side was based on the Ranz Marshall model [80], which is expressed below:

$$Nu=2+0.6R{e}^{0.6}P{r}^{0.3}$$

(20)

The mass flow rate of steam and temperature were respectively 0.0051 kg/s and −293 °C. The liquid temperature was 208 °C, and the pressure in the tank was 0.1 MPa. Figure 9 presents the heat transfer coefficient for a typical cycle. The observed DCC heat transfer coefficient is approximately ten times higher than in film condensation (for oxygen). The maximum value of the heat transfer coefficient and the strongest pressure oscillations are achieved for the necking stage of bubbling DCC.

5.2. Numerical Analysis of Jet-Type Flow Direct Contact Condensers

The condensing ejector was the object of the numerical investigation conducted by Colarossi et al. [72]. The aim was to develop a CFD model of condensing ejector producing growth in static pressure in refrigeration systems based on a CO₂ working medium. Computation Fluid Dynamics supplemented with semiempirical correlations was used to create a numerical model. The open-source OpenFoam library was used and the Eulerian pseudo-fluid approach was applied. The thermodynamic non-equilibrium state of the working fluid was taken into account. Pressure and velocity fields were calculated implicitly using the PISO algorithm (Pressure Implicit with Splitting of Operators). Modified versions of the Homogeneous relaxation model (HRM) were used (originally HRM model has developed for modeling of Flash boiling phenomenon [81]). The HRM model is based on the total derivative which describes the mass fraction of vapour:

$$\frac{Dx}{Dt}=\frac{\overline{x}-x}{\theta }$$

(21)

with:

$x$—quality (mass fraction of vapour), -,

$\overline{x}$—equiblirum quality, -,

$t$- time, s,

$\theta$- timescale, s,

In considering the modified HRM model, the timescale is expressed as:

$$\theta ={\theta }_o{\alpha }^a{\psi }^b{\left(1-\alpha \right)}^a$$

(22)

with:

${\theta }_o, a, b$—model constants, -,

$\alpha$—vapour volume fraction, -,

$\psi$—dimensionless pressure difference, -.

The HRM model coefficient values for low-pressure conditions (below 10 bar) were taken from Downar-Zapolski et al. [82]. RANS equations were supplemented with the k-ε model. The 2D mesh consists of nearly 6100–6750 elements was used. The results show good agreement with the experimental data. Turbulence modeling was marked as the most challenging in the case of condensing ejectors modeling.

The three-dimensional CFD model of condensing ejectors was developed by Bergander et al. [83]. The Condensing Ejector is part of the second compression step in the refrigeration cycle. The article contains theoretical, numerical, and experimental analyses. The scheme of condensing the ejector and pressure distribution is presented in Figure 10. The working medium was R22. The study aims to calculate the exit pressure of the condensing ejector at given inlet boundary conditions. Operating parameters are presented in

Table 21. Operating parameters from Bergander et al. [83].

Parameter	Vapor Inlet	Liquid Inlet
Temperature (°C)	43	34
Pressure(MPa)	1.7	2.1
Massflow (kg/s)	0.016	0.077

. The temperature was taken from R22 tables based on pressure and enthalpy values presented by the authors.The pseudo-fluid approach was applied, considering a mixture of no thermodynamic-equilibrium conditions with a homogeneous relaxation model HRM. The prepared model can be used for flash-boiling and condensation modeling.

Zhang et al. [84] conducted a numerical and experimental study of steam-water ejectors in a trigeneration system for hydrogen production. Direct Contact Condensation takes place in the presence of non-condensable gas (air). The aim was to predict the performance of the ejector using CFD method. CFD solver available in ANSYS 18.2 version was used. For multiphase modeling, Euler-Euler two-fluid model was used. The species transport model was incorporated into the simulation to consider the inert gas’s presence. K-ω SST model with enhanced wall treatment accounted for the turbulent flow phenomenon. All equations were descretized using a high-order scheme. The thermal equilibrium model, a two-resistance model, was applied to model direct contact condensation [85]. The condensation rate per unit volume $\dot{m}$ from gas phase α to liquid phase β:

$$\dot{m}=\frac{h_{\alpha }{A}_{\alpha \beta }\left(T_s-T_{\alpha }\right)}{H_{S\beta }-H_w}$$

(23)

with:

$h_{\alpha }$—heat transfer coefficient at liquid side, W/(m² K),

$\overline{A_{\alpha \beta }}$—interface area per unit volume, 1/m,

$T_s$—saturation temperature, K,

$T_{\alpha }$—liquid phase temperature, K,

$H_{S\beta }$—specific enthalpy of steam, J/kg,

$H_w$—specific enthalpy of liquid-phase at the gas-liquid interface temperature, J/kg,

The heat transfer coefficient $h_{\alpha }$ for the liquid side was calculated based on the Nusselt Number expressed by the Hughmark model [86]:

$$Nu=2+0.6R{e}^{0.5}P{r}^{0.33}, 0\le Re<776.06, 0\le Pr<250$$

(24)

$$Nu=2+0.27R{e}^{0.62}P{r}^{0.33}, 776.06\le Re, 0\le Pr<250$$

(25)

The 3D mesh consisting of 141,376 hexahedral elements was created using ICEM CFD. The steam mass flowrate was 1.45 g/s. The temperature of the water was 8 °C. At the outlet, a 1 atm pressure boundary condition was assumed. Simulation parameters are summarized in

Table 22. Simulation parameters from Zhang et al. [84].

Parameter	Gas Inlet	Liquid Inlet	Outlet
Temperature (°C)	104.8 (steam) 20 (air)	9	-
Pressure(kPa)	120	100	100
Massflow (g/s)	1.45 (steam) 0–0.14 g/s (inert gas)	34.7–37.3

. Properties of water and steam were assumed based on the IAPWS-IF-1997 [74]. The density of air was calculated using the ideal-gas law. For a small amount of air, the performance of the ejector was improved. The achieved maximum value of condensation rate is 3252–2340 kg/m³ s, depending on the air concentration.

Shah et al. did a numerical and experimental investigation of steam pumps taking into account the direct contact phenomenon [63]. The task of the steam jet pump is to pump water. CFD, a three-dimensional model, was developed. Ansys Fluent 6.3 software was used. The multiphase flow was modeled using the Eulerian two-fluid model. The direct-contact condensation phenomenon was considered using the two-resistance model, developed earlier by [85]. The heat transfer coefficient of the liquid side was calculated based on the Hughmark Nusselt number correlation [86]. The heat transfer coefficient for steam bubbles was calculated according to the Brucker and Sparrow formula [87]. Steam is modeled using ideal gas relation. A realizable k-e model was used. Continuity and volume fraction equations were discretizated using second-order and first-order upwind schemes, respectively, and the remaining equations using Power law scheme. Mesh consists of 69,677 hexahedral and tetrahedral elements. Various steam inlet pressures were considered: 140, 160, 180, 200, 220 kPa. The steam temperature was saturated at mentioned pressures. The different water nozzle pressures were assumed: 93.56, 92.92, 91.87, 90.38, and 89.30 kPa. The water nozzle temperature was 17 °C. The static pressure and temperature charts along the length were prepared. ThThe temperature agreement between simulation results and experimental data can be observed. Considering conditions, it is possible to suck in the water from 2.12 m depth.

A numerical investigation of condensing water jet eductorwas done by Koirala et al. [88]. Mass and heat transfer in direct contact condensation occurs in two-phase flow were computationally studied using the CFD method. The aim of the study was to investigate the performance of the device as a direct contact condenser for various operational conditions. The eductor is part of a thermal desalination system. The motive fluid was water, and the sucked-in fluid was steam. The Eulerian model using ANSYS Fluent software was used to calculate multiphase flow. Fluid turbulence was taken into account using k-ωmixture model. Inlet and outlet pressure boundary conditions were applied and presented in

Table 23. Assumed boundary conditions from Koirala et al. [88].

Parameter	Gas Inlet	Liquid Inlet	Outlet
Temperature (°C)	100	25	-
Pressure(kPa)	45, 60, 80, 105	1000	100

. For direct contact condensation heat transfer calculations, two resistance models were applied. For mass transfer calculations, the thermal phase change model was used. Pressure based double precision solver was used. Under-relaxation factors of pressure, turbulent kinetic energy, and turbulent dissipation rate were respectively 0.1, 0.2 and 0.4. As a result of the study, the influence of back pressureand motive fluid temperature on the performance of eductor was investigated. Increasing back pressure decreased the flow of entertainment. Increasing the motive fluid temperature causes a lower entertainment ratio because a decrease in the condensation rate can be observed.

5.3. Other Works

CFD simulation of direct contact condenser in the presence of inert gas for Oxy-fuel CO₂ Capture process was developed by Takami et al. [89]. The scheme of the device is presented in Figure 11. The aim of the condenser is to separate steam and CO₂ through the condensation process. The goal of the investigation was to provide a better understanding of the separation process depending on various boundary conditions and different fluid properties. The process was conducted based on 2D CFD modeling using a COMSOL solver. The simulation parameters at inlets and outlets are presented in

Table 24. Simulation results and assumptions [89].

Parameter	Gas Inlet	Gas Outlet	Liquid Inlet	Liquid Outlet
Composition (%)	CO2 = 92.30 H20 = 5.76 O2 = 1.94	CO2 = 97.88 H20 = 1.2 O2 = 0.92	H20 = 100	H20 = 99.92 CO2 = 0.02
Temperature (°C)	50	27.8	25	51
Pressure(Pa)	100,000	101,325	150,000	101,325
Massflow (kg/s)	8.3	7.8	9.3	9.78

. Constant fluid properties were assumed. The triangular mesh with 27,054 elements was applied. The application of considering condenser allows for condensing 75% of water content from exhaust gases. Laminar flow regimes were observed in the middle of the condenser and zones near the walls.

Numerical modeling of a Direct Contact Condensation of steam in a horizontal pipe was conducted by Thomas Hofne et al. [90]. The study aimed to model the two-phase stratified steam-water flow experiment and compute new heat and mass transport models between water and steam. In this stratified flow pattern, condensation occurs mainly on the interface. The Eulerian two-fluid model was used. Algebraic Interfacial Area Density (AIAD) model was implemented in the Ansys CFX solver. The models allow for simulating momentum exchange depending on the character of the stratified flow. Three various DCC models, which express the correlations for Nusselt number calculation, were used: the Egorov model with the Ranz Marshall correlation, modified Hughes-Duffey with the Ranz Marshall correlation, and the Adapted Coste model. The Nusselt Number for the last one can be expressed as the following:

$$Nu=2.7R{e}_t^{0.875}P{r}_l^{1/2}$$

(26)

The gas temperature was 100 °C (saturation temperature), and the mass flow rate was 5.3 g/s. The water temperature was 20 °C (initially), and the mass flow rate was 13.8 g/s. No slip boundary conditions were applied, and the simulation was stationary. Mesh consisted of 1.3 million elements.

5.4. Numerical Analysis of DCC—Summary

Table 25. Overview of direct contact condensation models.

Authors	Device	Phases	Solution Metod	Multiphase Model	Turbulence Model	DCC Model
Yi et al. [71]	Suppression pool	Steam-water (air)	FVM	VOF	k-ω SST model	Evaporation/condensation
Hughes [73]	Suppression pool	Steam-water	FVM	Eulerian two-fluid	Standard k-ε	Interface method
Jayachandran et al. [77]	Suppression pool	Vapour-liquid (O2)	FVM	two-fluid (particle-based)	k-ε (liquid) 0 eq. (vapour [79])	Thermal phase change model (two-resistance model)
Thiele [75]	Suppression pool	Steam-water	FVM	VOF		combustion method, interface method
Colarossi et al. [72]	Ejector	Liquid-vapor (CO2)		Pseudo-fluid	Standard k-ε	modified HRM [82]
Bergander et al. [83]	Ejector	Liquid-vapor (R22)		Pseudo-fluid		modified HRM [82]
Zhang et al. [84]	Ejector	Steam(air)-water	FVM	Eulerian two-fluid	k-ω SST model	two-resistance model [85]
Shah et al. [63]	Ejector	Steam-water	FVM	Eulerian two-fluid	Realizable k-ε	two-resistance model [85]
Koirala [88]	Eductor	Water-steam	FVM	Eulerian two-fluid	k-ω	Thermal phase change model (two-resistance model)
Takami et al. [89]	Direct Contact Condenser	Water-Steam (CO2)
Hohne et al. [90]	Pipes	Water-steam	FVM	Eulerian two-fluid		Egorov model, Hughes-Duffey, Adapted Coste

and

Table 26. Overview of direct contact condensation simulation conditions.

Authors	Phases	Phase 1			Phase 2			Main Conclusion
		m [g/s]	P [kPa]	T [oC]	m [g/s]	P [kPa]	T °C]
Yi et al. [71]	Steam-Water(air)	-	101.3	48.9	-	-	-	It is possible to prevent the chugging flow
Hughes [73]	Steam-water	45.0	197.0	120.0	-	-	67.0	2D axisymmetric structured mesh was found to be the best for this type of calculation
Jayachandran et al. [77]	Vapour-liquid (O2)	5.1	-	−293.0	-	100	−208.0	Heat transfer coefficient is approximately 10 times higher than in film condensation
Thiele [75]	Steam-water	1.2, 4.9; 12.4	110.0	102.0	-	110.0	22.0	Interface model better predict DCC phenomenon
Colarossi et al. [72]	Liquid-vapor (CO2)	-	-	-	-	-	-	Turbulence modeling is the most challenging task in case of ejector modeling
Bergander et al. [83]	Liquid-vapor (R22)	77.0	2100.0	34.0	16.0	1700.0	43.0	Prepared model can be used for flash-boiling and condensation modeling
Zhang et al. [84]	Steam(air)-water	1.45, 0–0.14 (air)	120.0	104.8, 20 (air)	34.7–37.3	100	9.0	For the small amount of air, the performance of the ejector is improved
Shah et al. [63]	Steam-water	-	140, 160, 180, 200, 220	Satura-ted	100–700	-	17.0	Considering ejector allow to suck in the water from 2.12 m depth
Koirala [88]	Water-steam	-	1000.0	25.0	45, 60, 80, 105		100.00	Increasing a motive fluid temperature causes decreasing in the condensation
Takami et al. [89]	Water-Steam (CO2)	9.3	150.0	25.0	8.3	100	50.0	75% of water content from exhaust gas was condensed
Hohne et al. [90]	Water-steam	13.8		20	5.3		100.0	All considering models are in good agreement with experimental data

summarize the most important issues connected with the numerical modeling of direct contact condensation. Table 25 is an overview of the computational models (multiphase, turbulence, and condensation). Table 26 shows the simulation conditions in the listed research: mass flow rate, temperature, and pressure of phases. In the last column of Table 26, the main conclusions are presented. Still, the developed direct condensation CFD models need to be carefully calibrated and physically validated by the use of experimental results [91,92].

6. Conclusions

A wide range of applications of Direct Contact Condensers indicates the strong need to investigate these phenomena occurring during the direct contact condensation process. Computational and experimental studies are two more popular ways to explore and investigate heat and mass transfer processes. To date, the developed direct condensation models still need to be carefully calibrated and physically validated by the use of experimental results. On the other side, the experimental test rig’s conceptual design should be first analyzed by using available numerical results. The paper presented a comprehensive review of experimental and numerical investigations on the DirectContact Condensation process.

CFD computational methods are very helpful in the numerical analysis of direct contact condensers because of the phenomenon’s complexity. Multiphase, turbulent flow with phase change requires sophisticated methods to consider all crucial aspects. Commercial software (Ansys, CFX, STAR CCM+) are most often used. Numerical calculations mainly concern cases in nuclear reactor safety systems (suppression pools) and refrigeration and heating systems (condensing ejectors). Various boundary conditions and geometries cause the flow of structure occurring during direct contact to be very diverse (jet, bubbly/droplets flows). Because of the diversity of the flow patterns, there is no universal modeling framework. Pseudofluid multiphase approaches are often used for computational calculations of ejector condensers. The VOF model is used for modeling DCC in suppression pools, where vapor is injected into stationary liquid. The eulerian two-fluid model is suitable for a wide range of applications (ejectors, tanks, pipes, etc.). Two equations RANS models: the k-ε model and the k-ω SST modelare sufficiently accurate for turbulence modelling in case of direct contact condensation. For DCC heat and mass transfer calculation, interface methods are dominating. In this model, heat transport is most often calculated based on Nusselt number correlation, which allows for calculating the heat transfer coefficient. Another type of approach, mainly used in the numerical calculation of condensing ejectors, is HRM model. It is strongly based on empirical correlations but tuned with coefficients and is characterized by robustness and sufficient accuracy. The review of the numerical investigation shows that various types of direct contact condensation modelling approaches are still developing because of the immense diversity and complexity of the phenomenon.

Various measurement methods and techniques applied to direct contact condensation experiments are presented in the studies. In temperature measurement, thermocouples prevailed due to their short thermal time constant and small dimensions. Pressure measuring techniques are based mainly on piezoelectric or piezoresistive transducers. Water flow rate measurement was performed using mainly electromagnetic and turbine flow meters. For steam flow rate measurements, mainly vortex flow meters were used. The developed detailed guidelines for measurement equipment in DCC experimental campaign are complicated and should be designed individually for the selected type of Direct Contact Heat Exchanger and operating conditions.