Optimization of the Control of Electromagnetic Brakes in the Stand for Tuning Internal Combustion Engines Using ID Regulators of Fractional Order
Abstract
:1. Introduction: Fractional Calculus in Control Systems
- Integer controller–integer control object;
- Controller with fractional order–integer control object;
- Integer controller–control object with a fractional order;
- Controller with fractional order–control object with fractional order.
2. Fractional Order Regulators in the Control System of Electromagnetic Brakes in the Stand for Tuning of Internal Combustion Engines
- Elastic connections and losses in the clutch, gearbox and cardan shaft are combined into one element;
- Power losses and elastic connections in the differential are not taken into account.
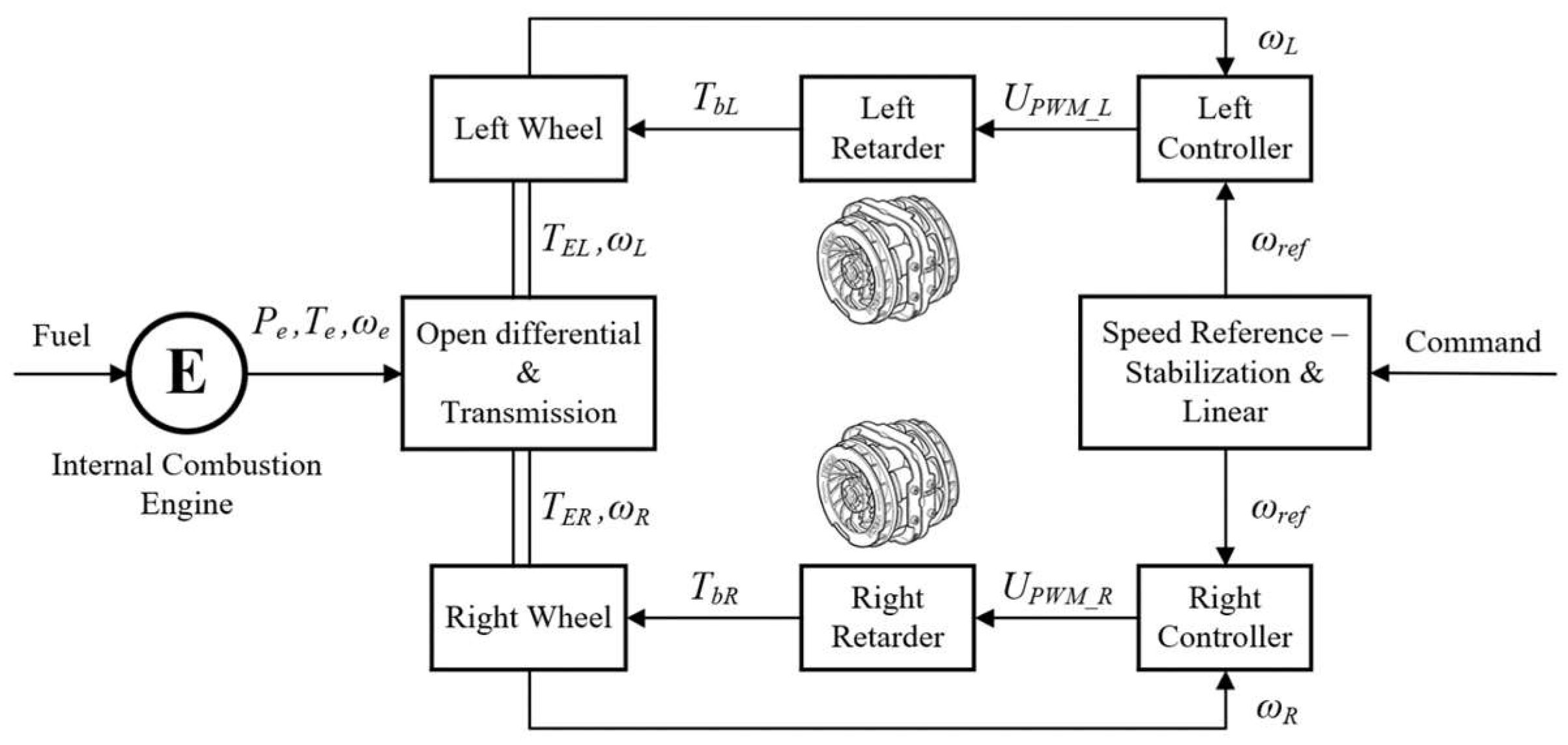
3. Experimental Studies for a Stand with Two Electromagnetic Retarders
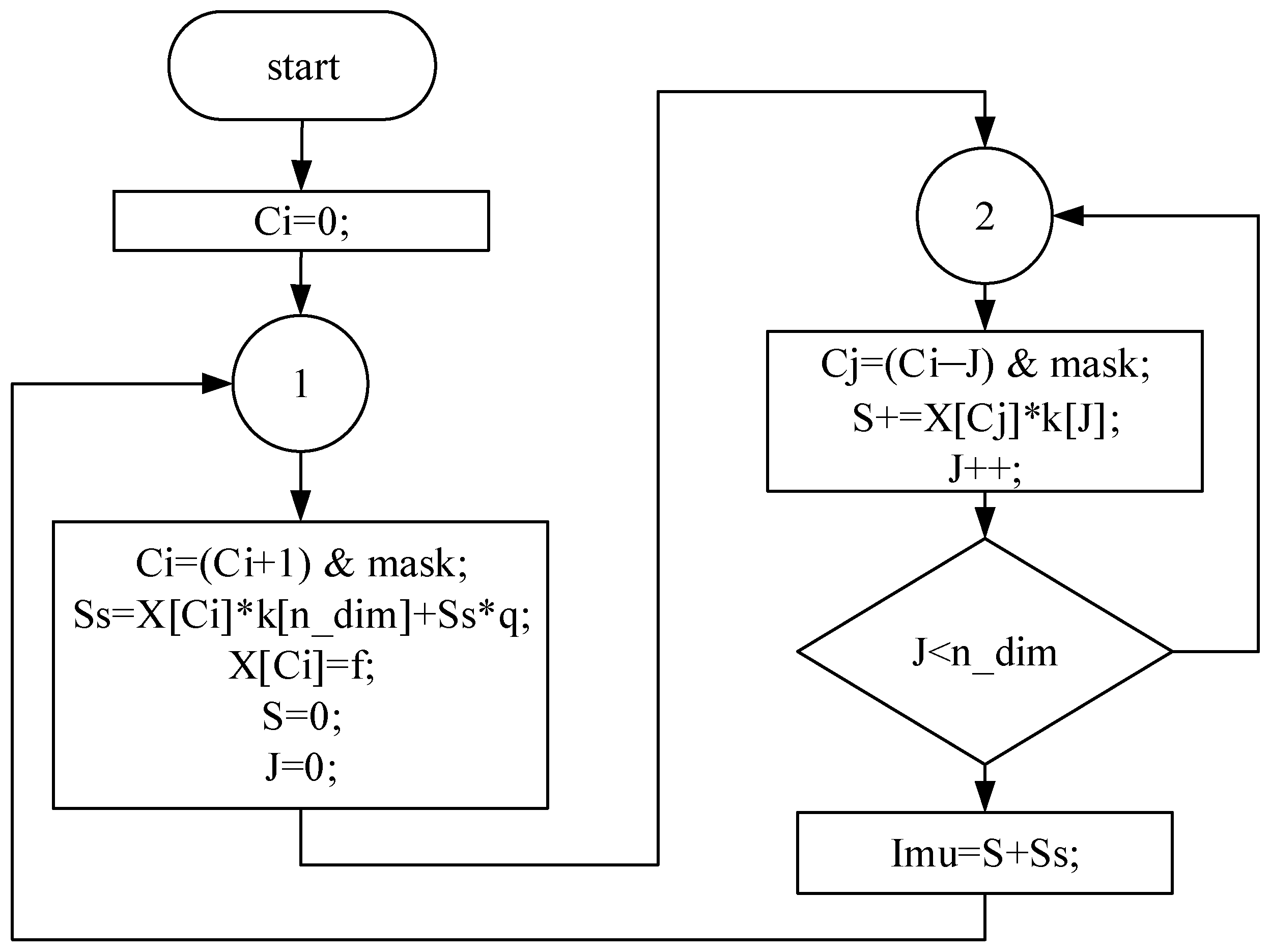
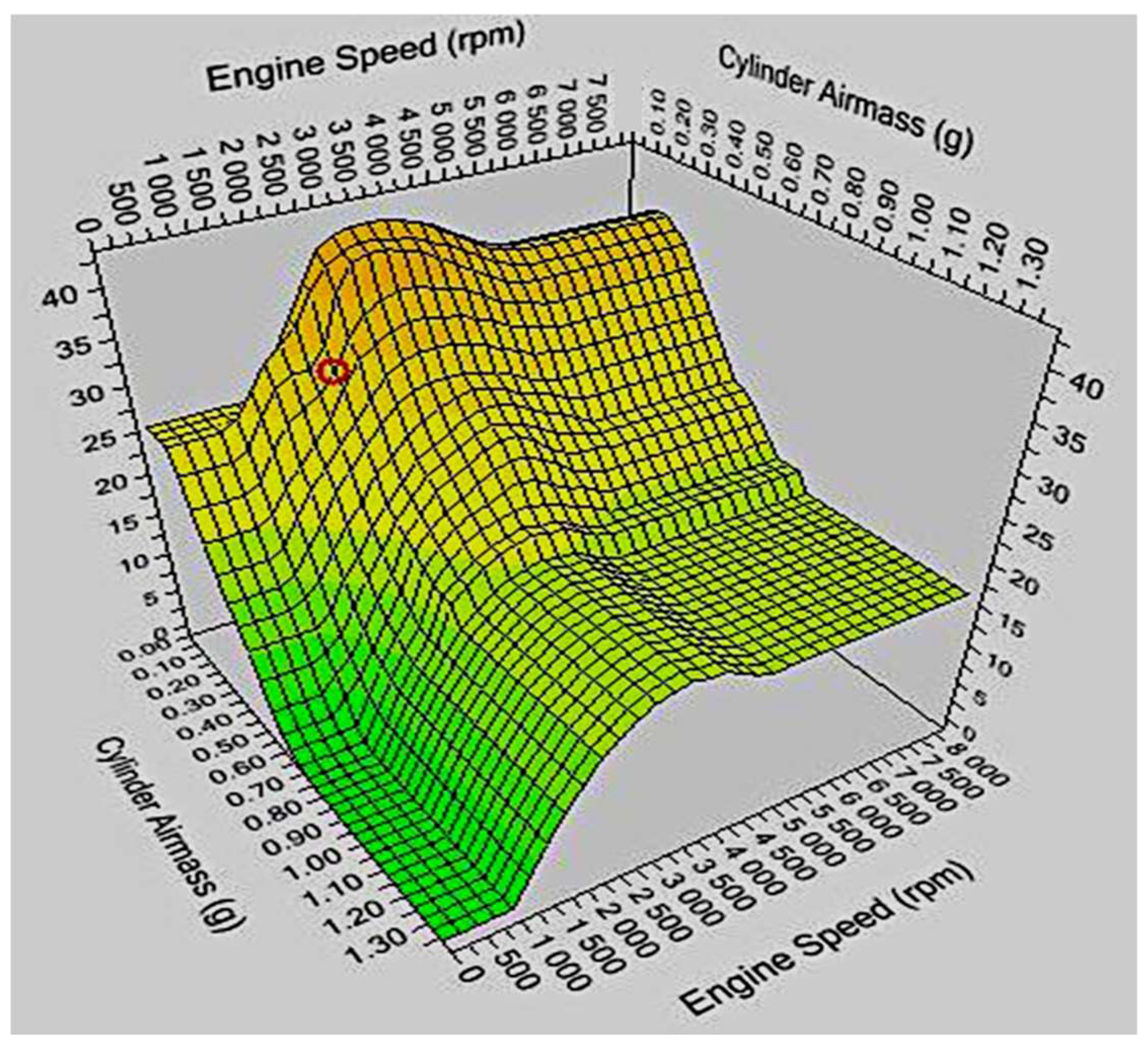
4. Identification of the Parameters of the Control Object Based on Preliminary Experimental Studies
5. Synthesis of an Optimal Control System for Electromagnetic Retarders
- For the Wco1 function in the “PID Controller” block of MATLAB Simulink, using the “Tune” procedure, the parameters of the classical PID controller were found, which turned out to be quite close to those found empirically: Kp = 65, Ki = 50, Kd = 15.
- Based on the Wco4 fractional order model, the circuit is tuned to a modular optimum with an equivalent transfer function:
- 3.
- Additionally, on the basis of the fractional order model Wco4, taking into account (10), a controller is synthesized that ensures the astatism of the closed loop of the fractional order µ = 1 + µco. From the relation
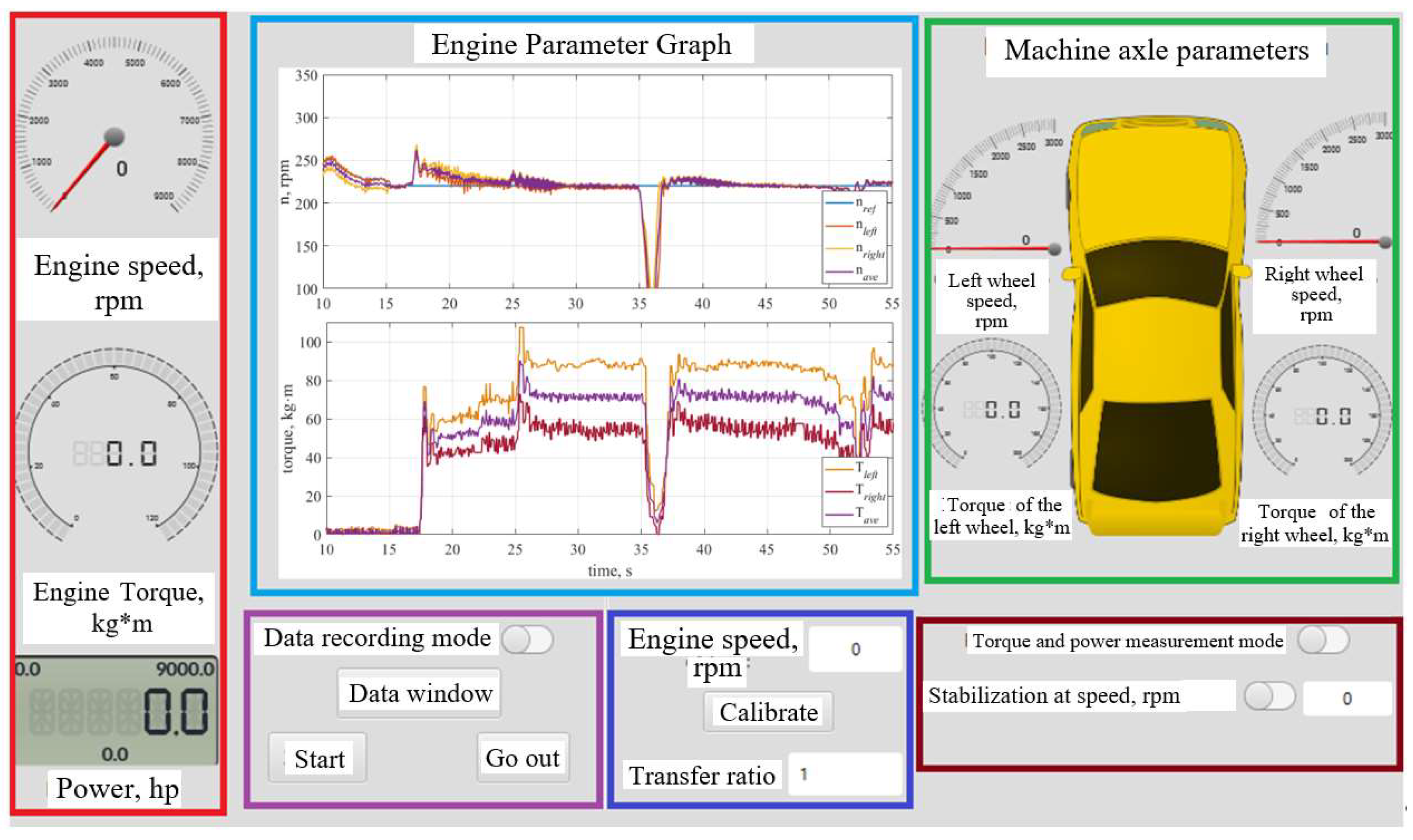
6. Experimental Studies of the Tuned Stand and Discussion of the Results
7. Results
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kimeu, J.M. Fractional Calculus: Definitions and Applications. Master′s Thesis, Western Kentucky University, Bowling Green, KY, USA, May 2009. [Google Scholar]
- Miller, D. Fractional Calculus. Ph.D. Thesis, West Virginia University, Morgantown, WV, USA, May 2004. [Google Scholar] [CrossRef]
- Lioville, J. Memoire sur l’integration des equations differentielles a indices fractionnaires. J. l’École R. Polytech. 1837, 15, 58–84. [Google Scholar]
- Lazarević, M. Advanced Topics on Applications of Fractional Calculus on Control Problems, System Stability and Modelin; Mladenov, V., Mastorakis, N., Eds.; World Scientific and Engineering Academy and Society: Belgrade, Serbia, 2014; p. 210. ISBN 978-960-474-348-3. [Google Scholar]
- Riemann, B. Versuch einer allgemeinen Auffasung der Integration und Differentiation. Gesammelte Math. Werke 1876, 62, 331–344. [Google Scholar]
- Sonin, N. On differentiation with arbitrary index. Mosc. Matem. Sb. 1869, 6, 1–38. [Google Scholar]
- Letnikov, A. An explanation of the concepts of the theory of differentiation of arbitrary index. Mosc. Matem. Sb. 1872, 6, 413–445. [Google Scholar]
- Laurent, H. Sur le calcul des derivees a indicies quelconques. Nouv. Ann. Math. 1884, 3, 240–252. [Google Scholar]
- Grünwald, A. Ueber "Begrenzte" Derivationen und Deren Anwendung. Zeitschrift für Mathematik und Physik: Organ Für angewandte Mathematik 1867, 12, Leipzig, Verlag Von B.G. Teubner. Available online: https://www.deutsche-digitale-bibliothek.de/item/57U4JANM6MPP2QDG3TKZTG5TKAI7AUBF (accessed on 9 December 2022).
- Heaviside, O. Electrical Papers; Macmillan Co.: London, UK; New York, NY, USA, 1894; Volume 2. [Google Scholar]
- Weyl, H. Bemerkungen zum begriff des differentialquotienten gebrochener ordnung. Vierteljschr. Naturforsch. Gesellsch. Zur. 1917, 62, 296–302. [Google Scholar]
- Marchaud, M.A. Sur les dérivées et sur les différences des fonctions de variables réelles. Thèses L’entre-Deux-Guerres. 1927, 78, 98. [Google Scholar]
- Caputo, M.; Mainardi, F. Linear models of dissipation in anelastic solids. Riv. Nuovo Cim. 1971, 1, 161–198. [Google Scholar] [CrossRef]
- Ross, B. Fractional Calculus and Its Applications, Proceedings of the International Conference Held at the University of New Haven, June 1974; Springer: Berlin/Heidelberg, Germany, 1974; Volume 457, p. 386. ISBN 978-3-540-07161-7. [Google Scholar] [CrossRef] [Green Version]
- Oldham, K.B.; Spanier, J. The Fractional Calculus, Mathematics in Science and Engineering; Academic Press: New York, NY, USA; London, UK, 1974; Volume 111, p. 234. [Google Scholar]
- Samko, S.; Kilbas, A.; Marichev, O. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers: Background and Theory; Nonlinear Physical Science; Springer: Beijing, China, 2013. [Google Scholar]
- Westerlund, E. Einstein’s Relativity—And What It Really Is; Preprint SE-39351: Kalmar, Sweden, 2003; p. 5. [Google Scholar]
- Ułanowicz, L.; Jastrzębski, G. The analysis of working liquid flow in a hydrostatic line with the use of frequency characteristics. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 949–956. [Google Scholar] [CrossRef]
- Caponetto, R.; Dongola, G.; Fortuna, L.; Petras, I. Fractional Order Systems: Modeling and Control Applications; World Scientific: Singapore, 2010; p. 178. [Google Scholar]
- Yamamoto, S.; Hashimoto, I. Present Status and Future Needs: The View from Japanese Industry. In Chemical Process Control Cpciv: Proceedings of the Fourth International Conference on Chemical Process Control, Padre Island, TX, USA, February 17–22 1991; Amer Inst. of Chemical Engineers: New York, NY, USA, 1991. [Google Scholar]
- Podlubny, I. Fractional-order systems and PIγDμ-controllers. IEEE Trans. Autom. Control. 1999, 1, 208–214. [Google Scholar] [CrossRef]
- Petras, I. The fractional-order controllers: Methods for their synthesis and application. J. Electr. Eng. 1999, 50, 284–288. [Google Scholar]
- Lozynskyy, O.; Lozynskyy, A.; Kopchak, B.; Paranchuk, Y.; Kalenyuk, P.; Marushchak, Y. Synthesis and research of electromechanical systems described by fractional order transfer functions. In Proceedings of the 2017 International Conference on Modern Electrical and Energy Systems (MEES), Kremenchuk, Ukraine, 15–17 November 2017; pp. 16–19. [Google Scholar] [CrossRef]
- Chen, Y.; Petras, I.; Xue, D. Fractional Order Control—A Tutorial. In Proceedings of the American Control Conference, St. Louis, MO, USA, 10–12 June 2009. [Google Scholar]
- Lurie, B. Three-Parameter Tunable Tilt-Integral-Derivative (TID) Controller; Jet Propulsion Lab. California Inst. of Tech.: Pasadena, CA, USA, 1994. [Google Scholar]
- Yessef, M.; Bossoufi, B.; Taoussi, M.; Motahhir, S.; Lagrioui, A.; Chojaa, H.; Lee, S.; Kang, B.-G.; Abouhawwash, M. Improving the Maximum Power Extraction from Wind Turbines Using a Second-Generation CRONE Controller. Energies 2022, 15, 3644. [Google Scholar] [CrossRef]
- Monje, C.; Vinagre, B.; Calderón, A. Auto-tuning of Fractional Lead-Lag Compensators. IFAC Proc. Vol. 2005, 38, 319–324. [Google Scholar] [CrossRef]
- Yu, J.; Zhao, Q.; Li, H.; Yue, X.; Wen, S. High-Performance Fractional Order PIMR-Type Repetitive Control for a Grid-Tied Inverter. Energies 2022, 15, 3854. [Google Scholar] [CrossRef]
- Monje, C.; Chen, Y.; Vinagre, M. Fractional-Order Systems and Controls: Fundamentals and Applications; Springer: London, UK, 2010. [Google Scholar]
- Calderón, A.; Vinagre, B.; Feliu, V. Fractional order control strategies for power electronic buck converters. Signal Process. 2006, 86, 2803–2819. [Google Scholar] [CrossRef]
- Kaczorek, T. The pointwise completeness and the pointwise degeneracy of fractional descriptor discrete-time linear systems. Bull. Pol. Acad. Sci. Tech. Sci. 2019, 67, 989–993. [Google Scholar] [CrossRef]
- Oustaloup, A.; Sabatier, J.; Lanusse, P. An overview of the Crone approach in system analysis, modeling and identification, observation and control. In Proceedings of the 17th World Congress IFAC, Soul, Republic of Korea, 6–11 July 2008; pp. 14254–14265. [Google Scholar] [CrossRef] [Green Version]
- Valério, D. Fractional Robust System Control. Ph.D. Thesis, Universidade Técnica de Lisboa Instituto Superior, Lisbon, Portugal, 2005. [Google Scholar]
- Vinagre, M.; Petras, I.; Merchan, P.; Dorcak, L. Two digital realizations of fractional controllers: Application to temperature control of a solid. In Proceedings of the European Control Conference, Porto, Portugal, 4–7 September 2001; pp. 1764–1767. [Google Scholar] [CrossRef]
- Chen, Y.; Moore, K. Discretization schemes for fractional-order differentiators and integrators. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2002, 49, 363–367. [Google Scholar] [CrossRef]
- Vinagre, B.; Chen, Q.; Petras, I. Two direct Tustin discretization methods for fractional-order differentiator/integrator. J. Frankl. Inst. 2003, 340, 349–362. [Google Scholar] [CrossRef]
- Oprz ˛edkiewicz, K.; Rosół, M.; Mitkowski, W. Modeling of Thermal Traces Using Fractional Order, a Discrete, Memory-Efficient Model. Energies 2022, 15, 2257. [Google Scholar] [CrossRef]
- Tseng, C. Design of fractional order digital FIR differentiator. IEEE Signal Process. Lett. 2001, 8, 77–79. [Google Scholar] [CrossRef]
- Hwang, C.; Leu, J.; Tsay, S. A note on time-domain simulation of feedback fractional-order systems. IEEE Trans. Autom. Control. 2002, 47, 625–631. [Google Scholar] [CrossRef]
- Podlubny, I.; Chechkin, A.; Skovranek, T. Matrix approach to discrete fractional calculus II: Partial fractional differential equations. J. Comput. Phys. 2021, 228, 3137–3153. [Google Scholar] [CrossRef] [Green Version]
- Oprzędkiewicz, K. Fractional order, discrete model of heat transfer process using time and spatial Grünwald-Letnikov operator. Bull. Pol. Ac. Tech. 2021, 69, 1–10. [Google Scholar] [CrossRef]
- Busher, V.; Aldairi, A. Synthesis and technical realization of the control systems with the digital fractional integral-differentiating regulators. East. Eur. J. Enterp. Technol. 2018, 4, 63–71. [Google Scholar] [CrossRef] [Green Version]
- Anwar, S. A parametric model of an eddy current electric machine for automotive braking applications. IEEE Trans. Control. Syst. Technol. 2004, 3, 422–427. [Google Scholar] [CrossRef]
- Liu, C.; Jiang, K.; Zhang, Y. Design and Use of an Eddy Current Retarder In an Automobile. Int. J. Automot. Technol. 2011, 4, 611–616. [Google Scholar] [CrossRef]
- Kalmakov, V.; Andreev, A. The Ignition System of a Car; GRANADAPRESS: Cheljabinsk, Russia, 2014. [Google Scholar]
- Kakaee, A.; Shojaeefard, M.; Zareei, J. Sensitivity and Effect of Ignition Timing on the Performance of a Spark Ignition Engine: An Experimental and Modeling Study. J. Combust. 2011, 2011, 678719. [Google Scholar] [CrossRef] [Green Version]
- Morselli, R.; Zanasi, R.; Sandoni, G. Detailed and Reduced Dynamic Models of Passive and Active Limited-slip Car Differentials. Math. Comput. Model. Dyn. Syst. 2006, 12, 347–362. [Google Scholar] [CrossRef]
- Tarasik, V.; Puzanova, O.; Kurstak, V. Differential drives modeling of mobile machines driving wheels. Vestnik Belorussko-Rossiyskogo Universiteta 2009, 24, 1–12. [Google Scholar] [CrossRef]
- Busher, V.; Horoshko, V. Dual Electromagnetic Retarder Control System for Tuning Internal Combustion Engines. In Proceedings of the 2019 IEEE International Conference on Modern Electrical and Energy Systems (MEES), Kremenchuk, Ukraine, 23–25 September 2019; pp. 26–29. [Google Scholar] [CrossRef]
- Busher, V.; Horoshko, V. Fractional Integral-differentiating Control in Speed Loop of Switched Reluctance Motor. Probl. Reg. Energetics 2019, 1, 46–54. [Google Scholar] [CrossRef]
- Busher, V.; Melnikova, L.; Horoshko, V. Synthesis and implementation of fractional-order controllers in a current circuit of the motor with series excitation, Eastern-European Journal of Enterprise Technologies. Ind. Control. Syst. 2019, 2, 63–72. [Google Scholar] [CrossRef] [Green Version]
- Busher, V.; Horoshko, V.; Shestaka, A.; Melnikova, L. Fractional Integrated Dual Electromagnetic Retarder Controller for Tuning Internal Combustion Engines. In Proceedings of the 2020 IEEE Problems of Automated Electrodrive. Theory and Practice (PAEP), Kremenchuk, Ukraine, 21–25 September 2020; pp. 218–223. [Google Scholar] [CrossRef]
- Kolimas, Ł.; Bieńkowski, K.; Łapczyński, S.; Szulborski, M.; Kozarek, Ł.; Birek, K. Control system and measurements of coil actuators parameters for magnetomotive micropump concept. Bull. Pol. Acad. Tech. 2020, 68, 893–901. [Google Scholar] [CrossRef]



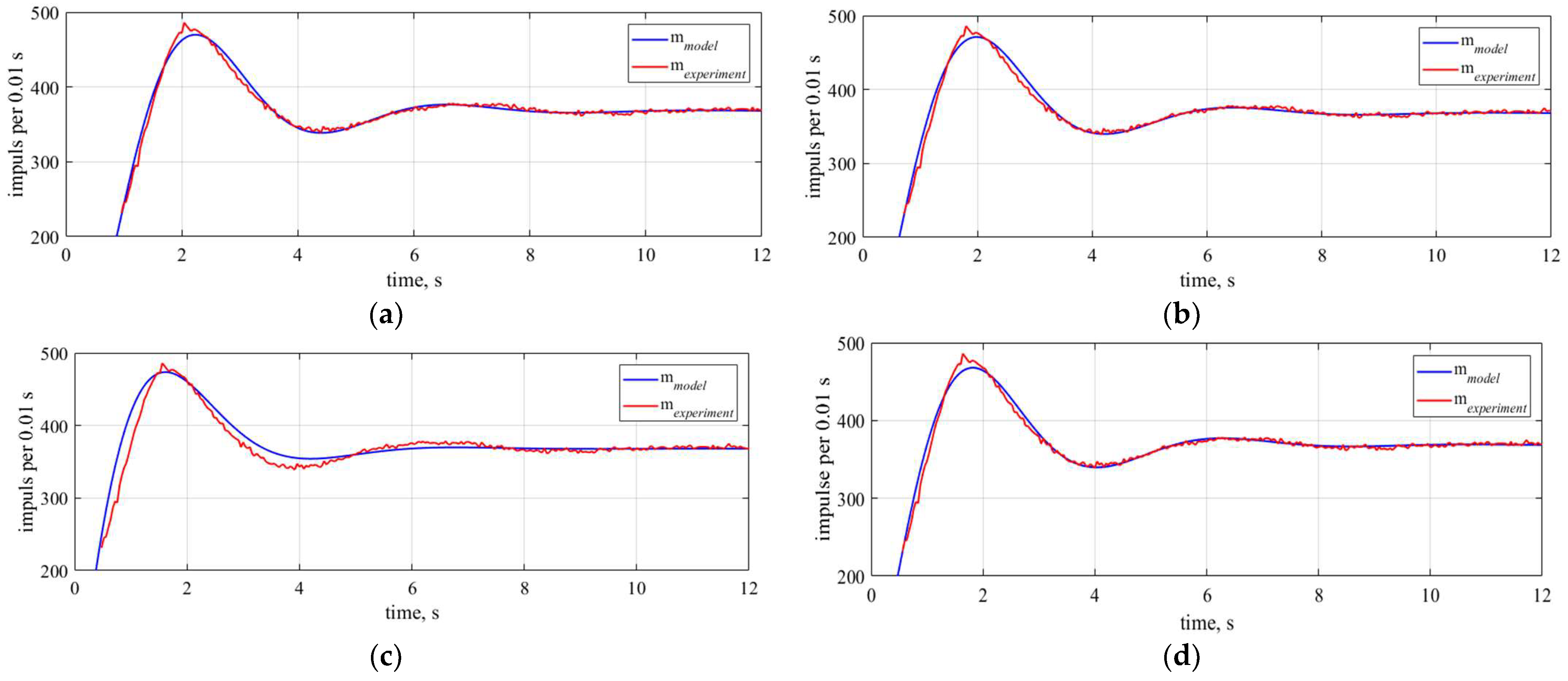
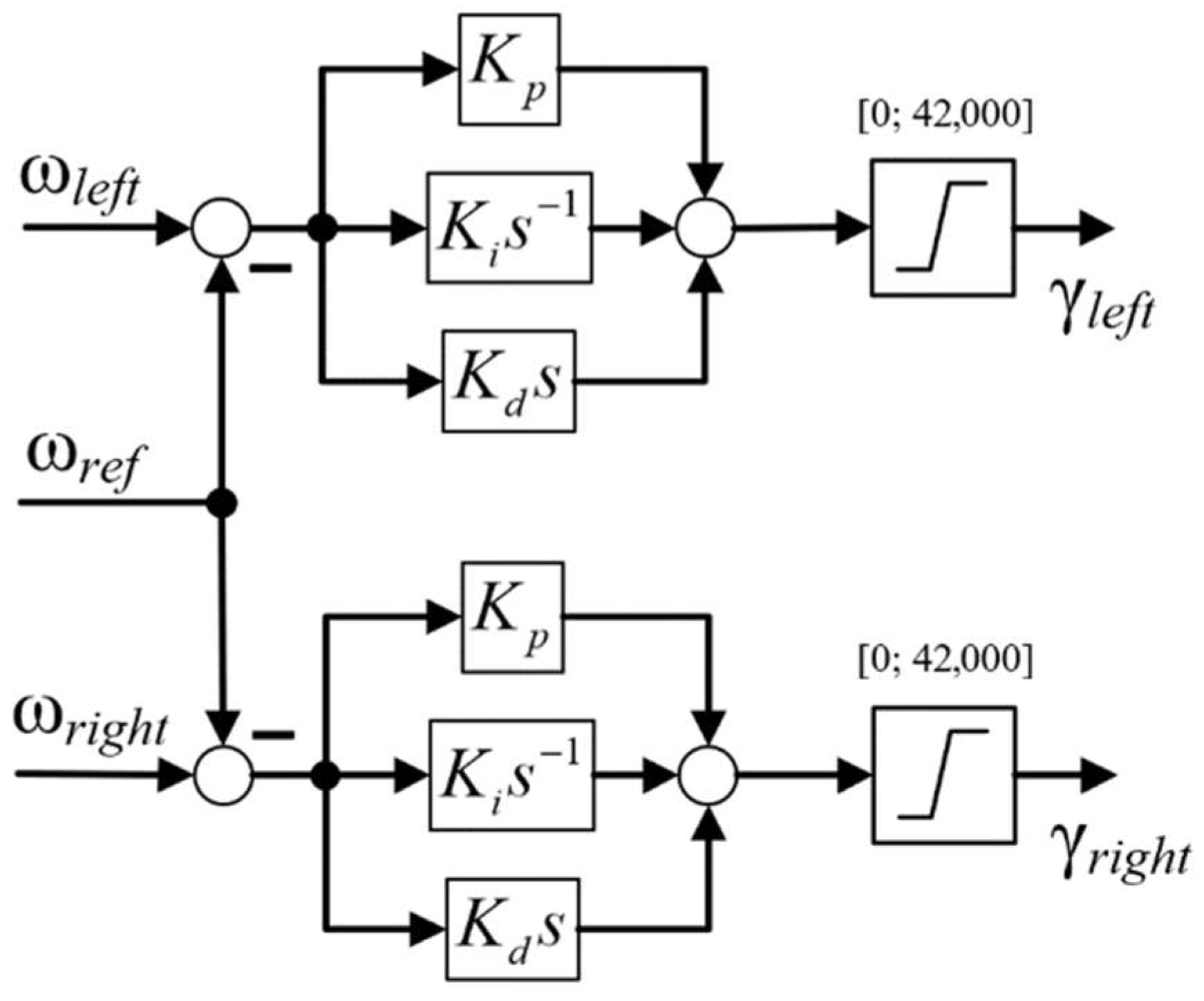
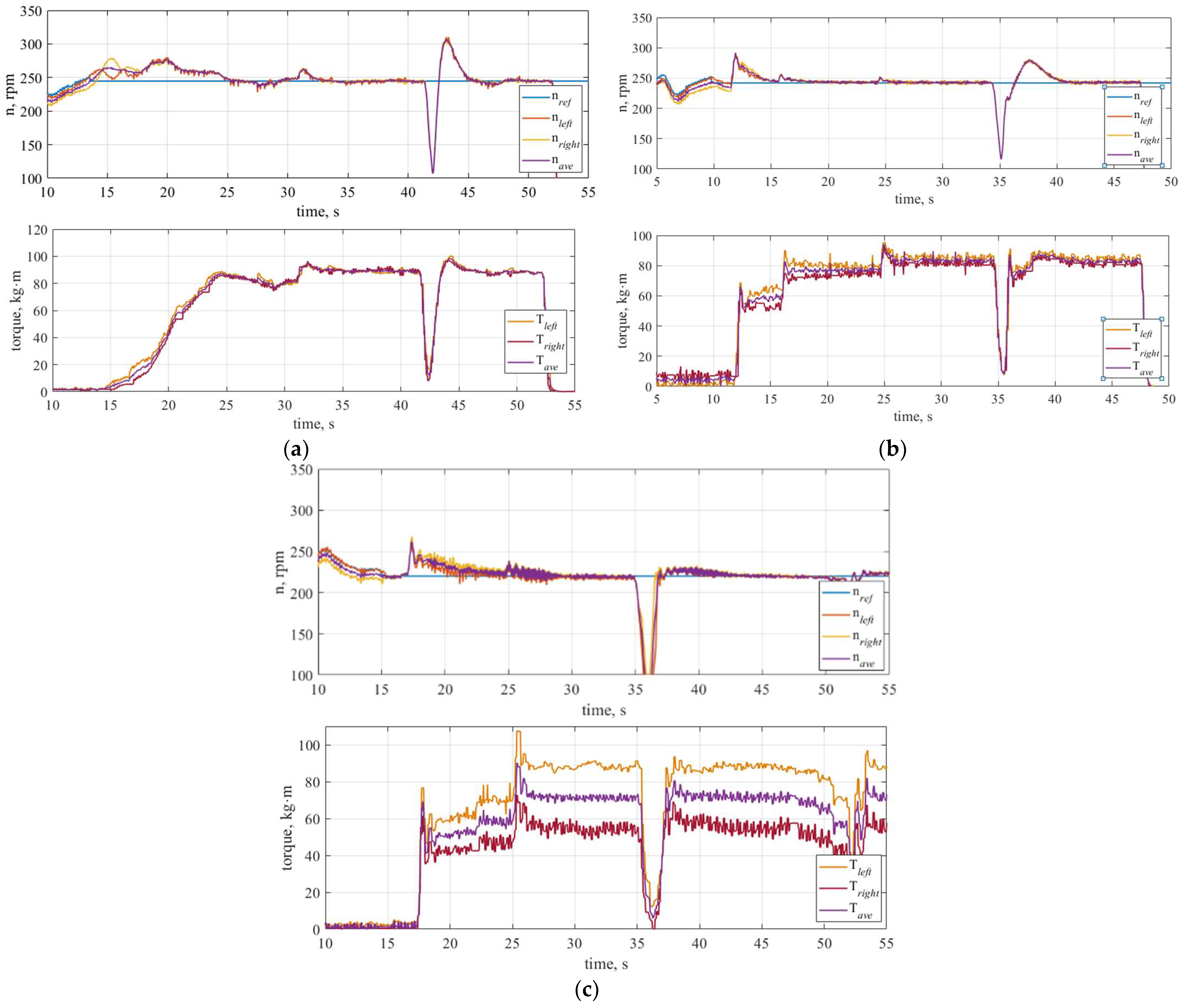



| Parameter | Transfer Function of the Control Object | |||
|---|---|---|---|---|
| Wco1 | Wco2 | Wco3 | Wco4 | |
| K | 0.03729 | 0.06666 | 0.04069 | 0.11514 |
| a1 | 0.7445 | 1.2856 | 0.2042 | 2.8951 |
| a2 | 0.3208 | 0.8804 | 0.04813 | 1.8987 |
| a3 | 0.7252 | – | – | – |
| µco | – | – | – | 0.6261 |
| F | 0.0130 | 0.0142 | 0.0275 | 0.0132 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Busher, V.; Zakharchenko, V.; Shestaka, A.; Kuznetsov, V.; Kuznetsov, V.; Nader, S. Optimization of the Control of Electromagnetic Brakes in the Stand for Tuning Internal Combustion Engines Using ID Regulators of Fractional Order. Energies 2022, 15, 9378. https://doi.org/10.3390/en15249378
Busher V, Zakharchenko V, Shestaka A, Kuznetsov V, Kuznetsov V, Nader S. Optimization of the Control of Electromagnetic Brakes in the Stand for Tuning Internal Combustion Engines Using ID Regulators of Fractional Order. Energies. 2022; 15(24):9378. https://doi.org/10.3390/en15249378
Chicago/Turabian StyleBusher, Victor, Vadim Zakharchenko, Anatoliy Shestaka, Valeriy Kuznetsov, Vitalii Kuznetsov, and Stanislaw Nader. 2022. "Optimization of the Control of Electromagnetic Brakes in the Stand for Tuning Internal Combustion Engines Using ID Regulators of Fractional Order" Energies 15, no. 24: 9378. https://doi.org/10.3390/en15249378






