Volumic Eddy-Current Losses in Conductive Massive Parts with Experimental Validations
Abstract
:1. Introduction
1.1. Preamble
1.2. Objectives of the Study of Volumic Eddy-Current Losses
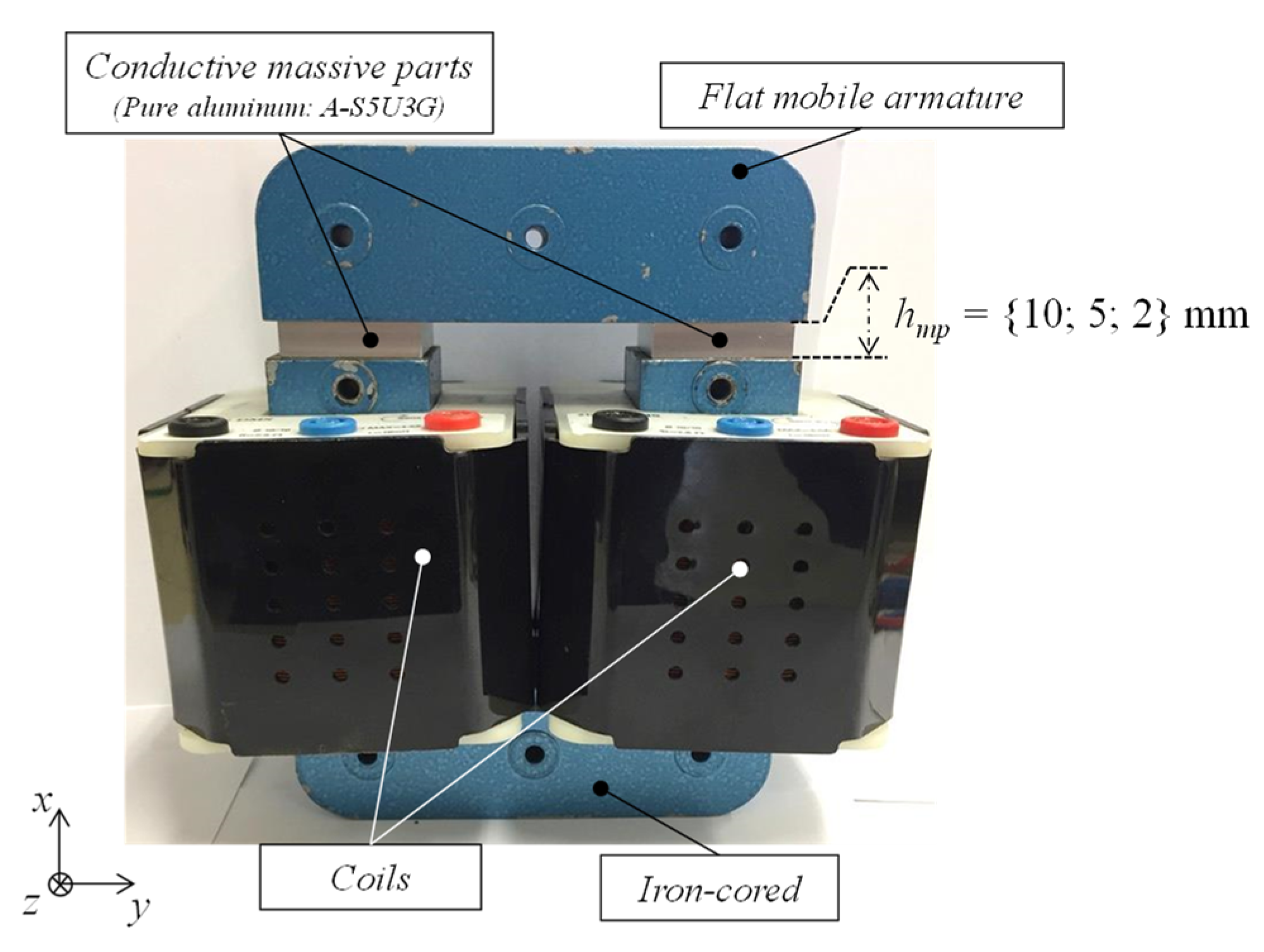
2. U-Shaped Electromagnetic Device and Conductive Massive Parts Description
2.1. Overall View
- to have a more or less intense magnetic field in the air gap;
- to be able to insert conductive massive parts of various thicknesses ;
- and to displace the conductive massive parts with respect to the magnetic circuit to apply a spatially non-uniform applied magnetic field to the studied materials.
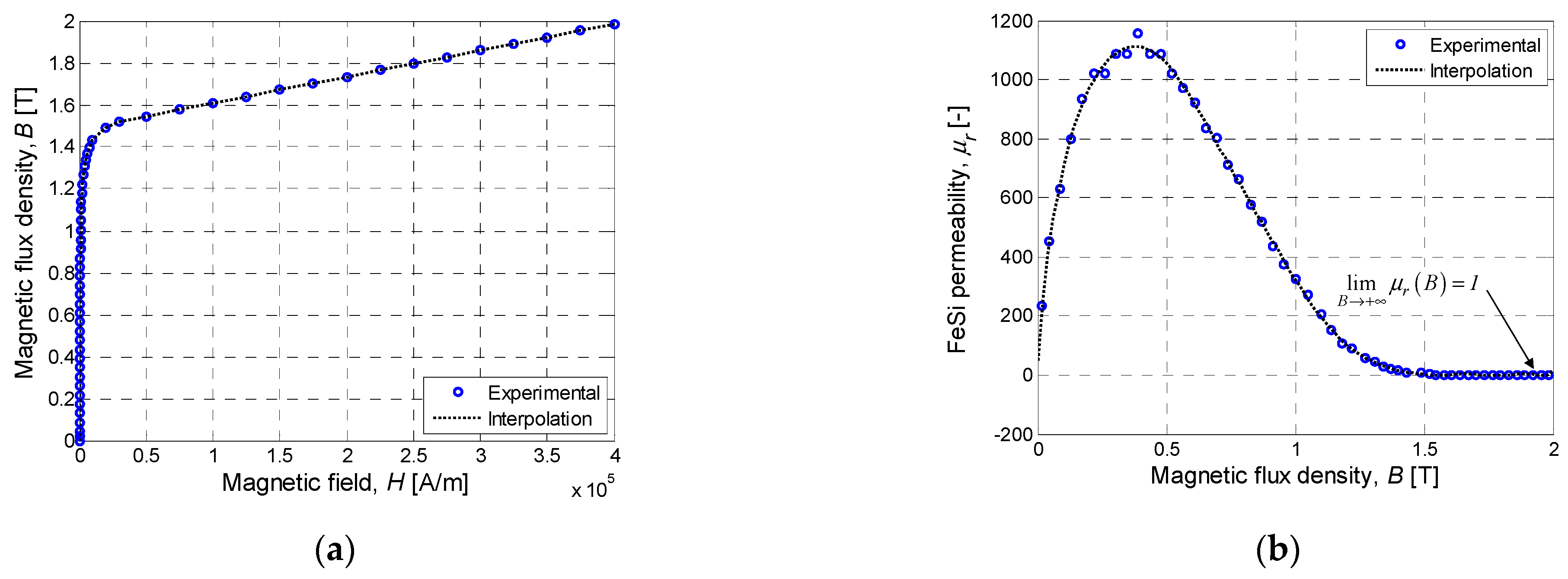
2.2. Ferromagnetic Circuit
2.3. Coils and Connections
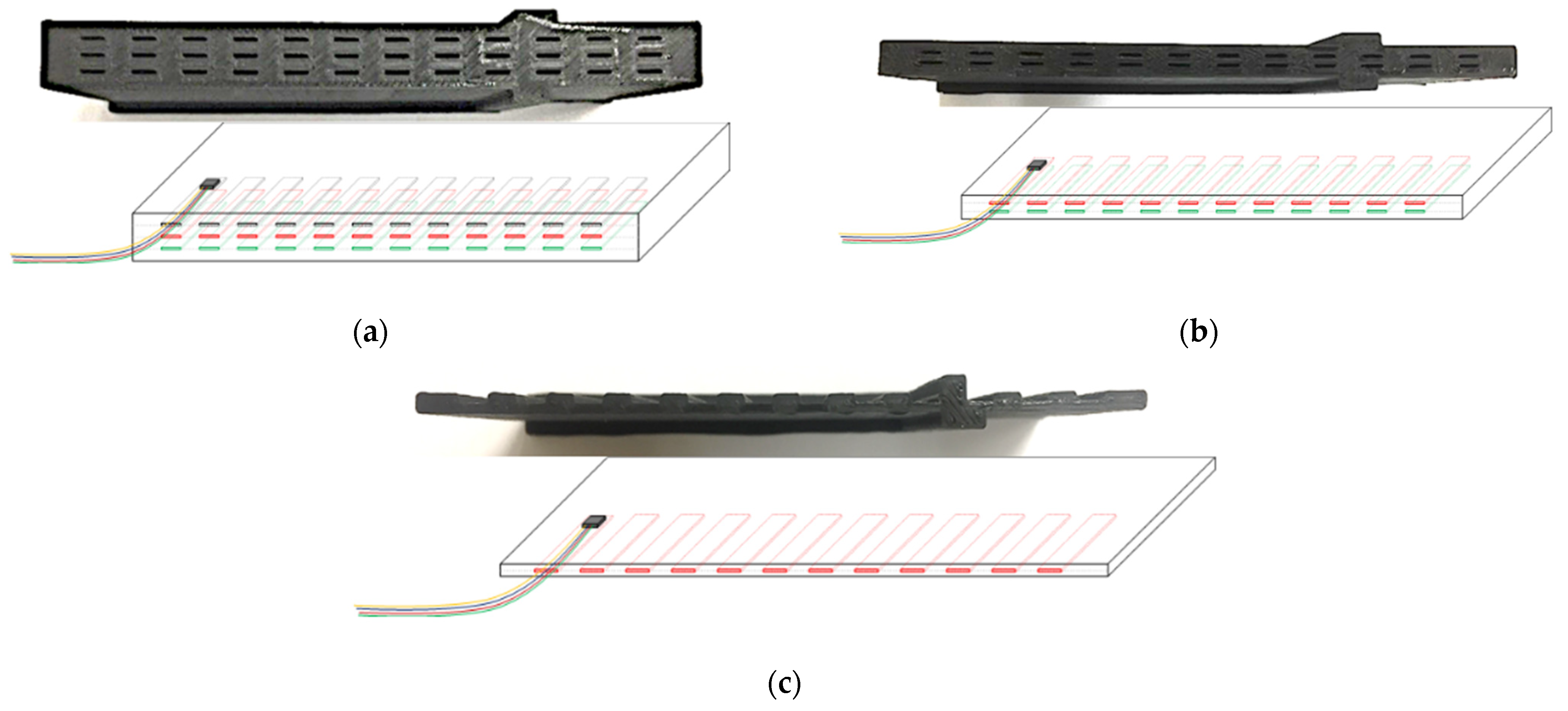
2.4. Conductive Massive Parts
3. Applied Magnetic Field Distribution with Experimental Validations
3.1. Instrumentation
3.1.1. Hall Effect Sensor
3.1.2. Sensor Supports
3.2. Experimental Measurements
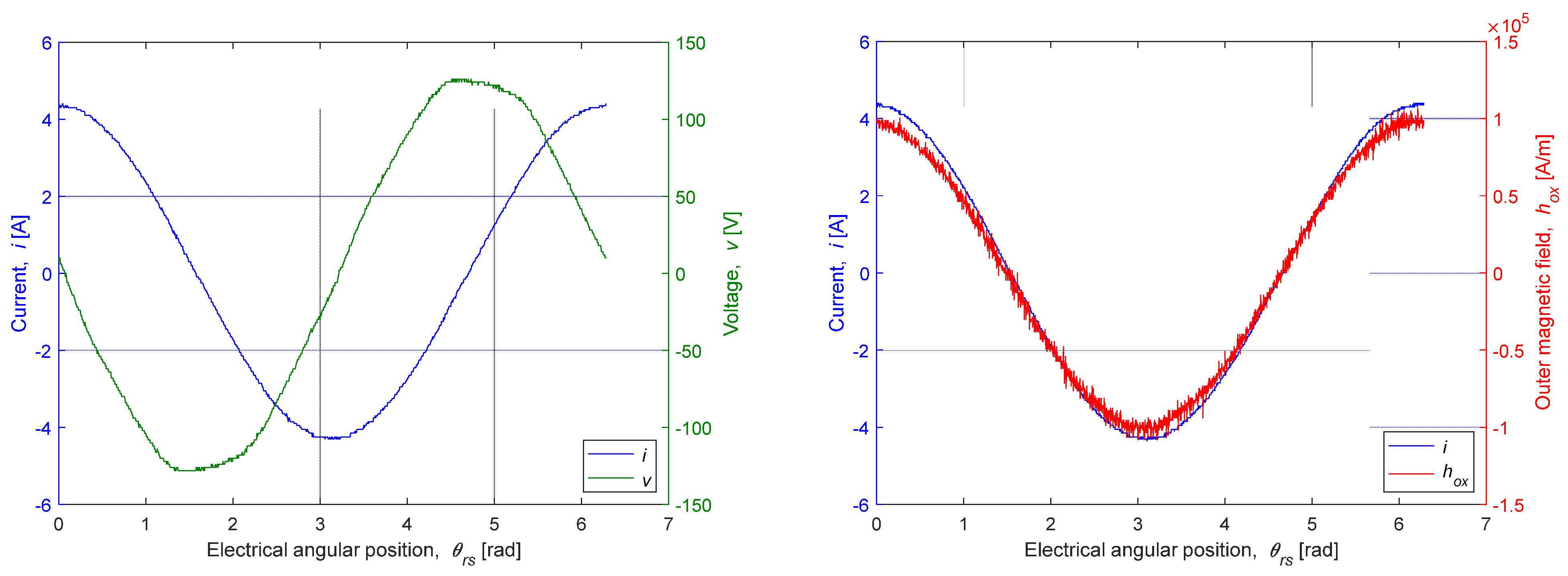
3.2.1. Temporal Evolutions of , , and
- and (only the fundamental components) have a phase shift of as demonstrated by (6);
- and are still in phase.
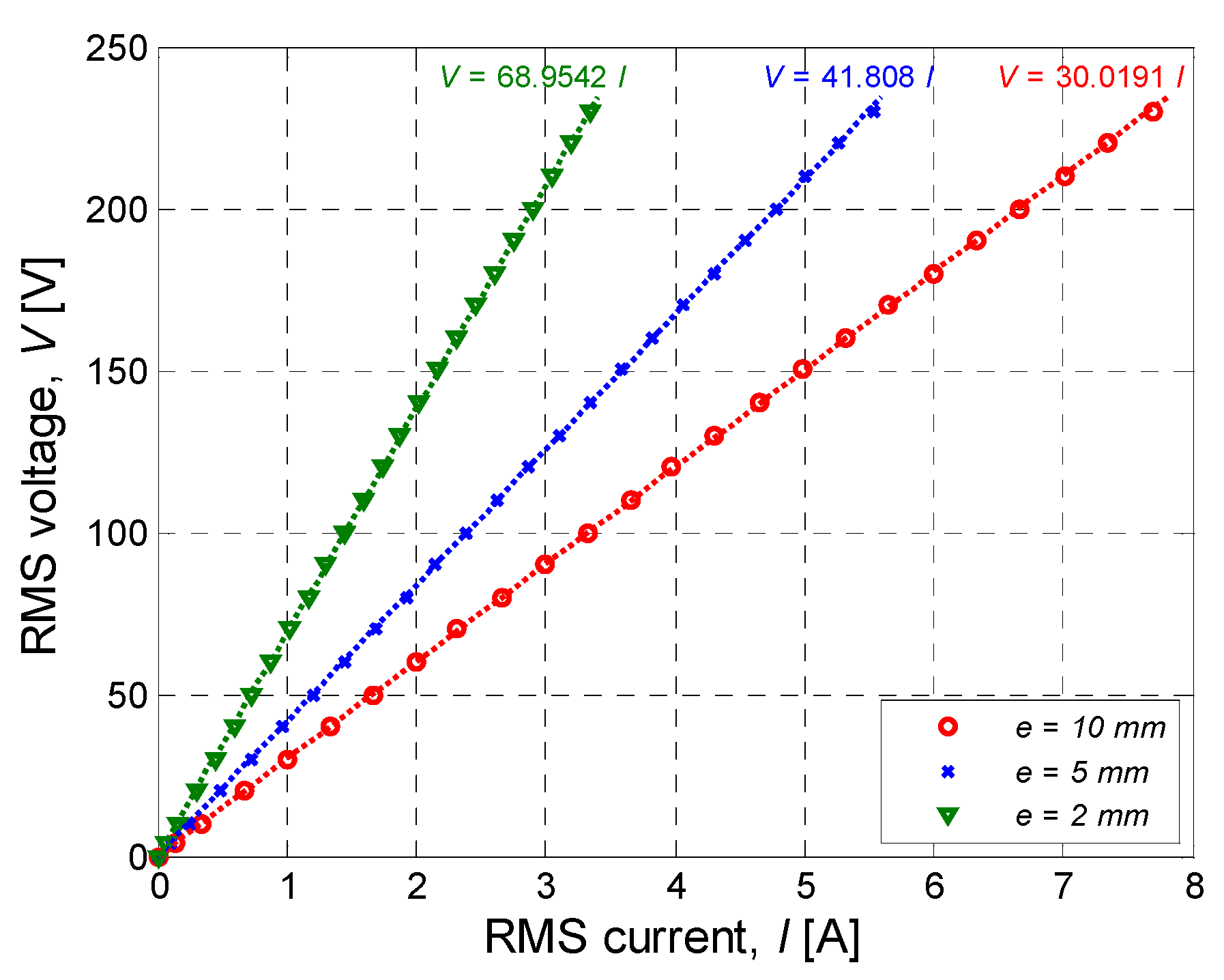
3.2.2. Linear Dependency of and
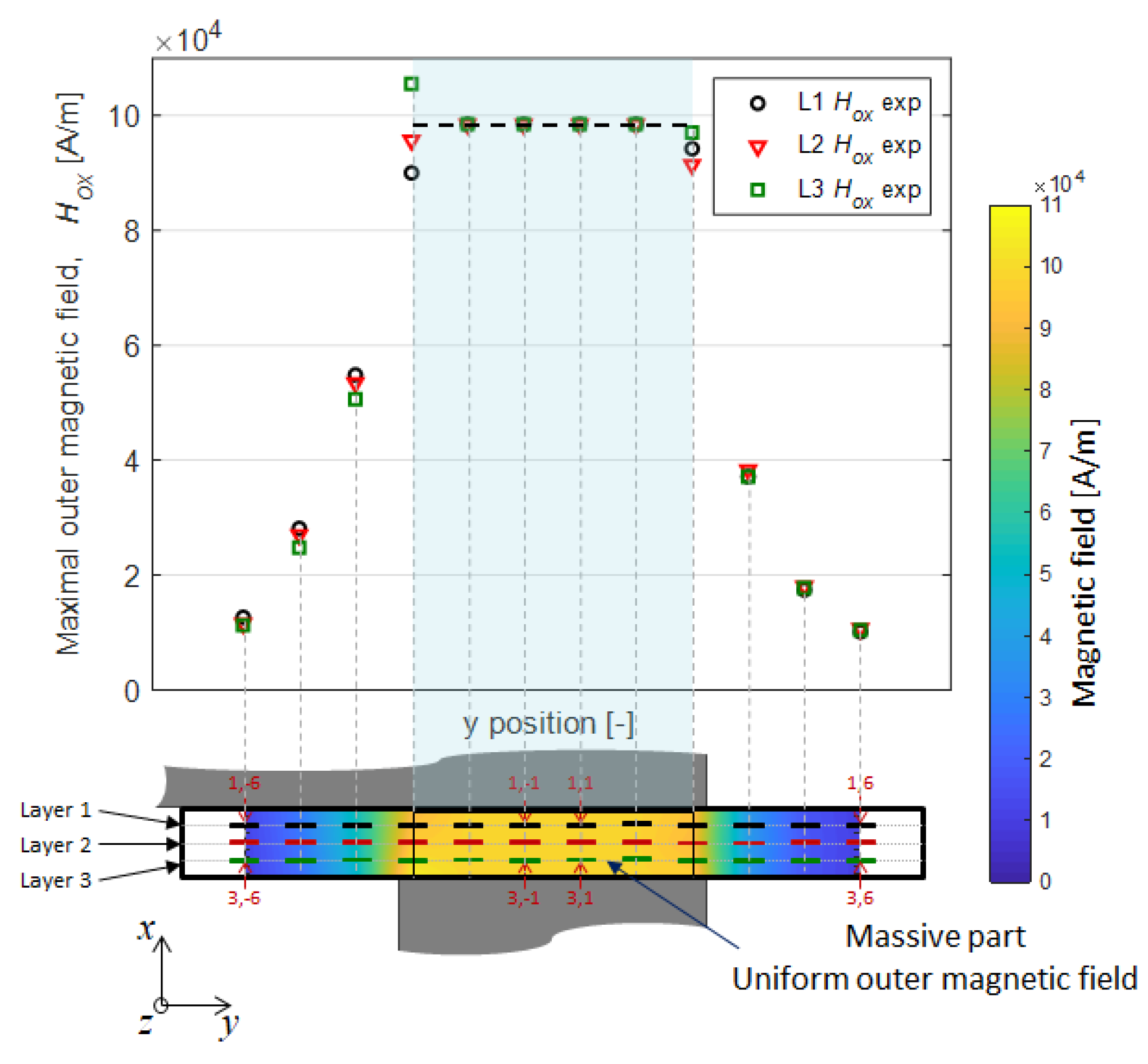
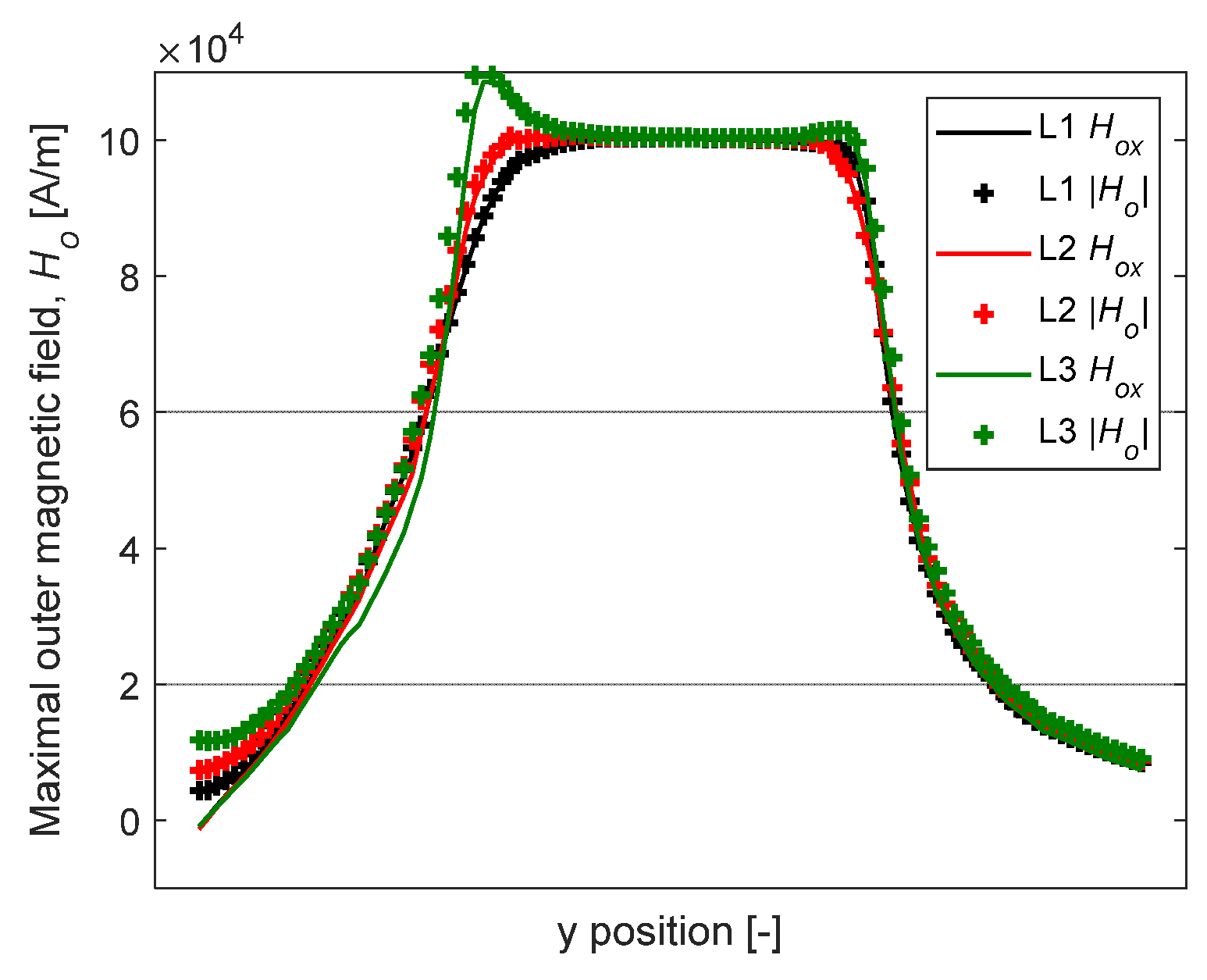
3.2.3. Spatial Evolution of
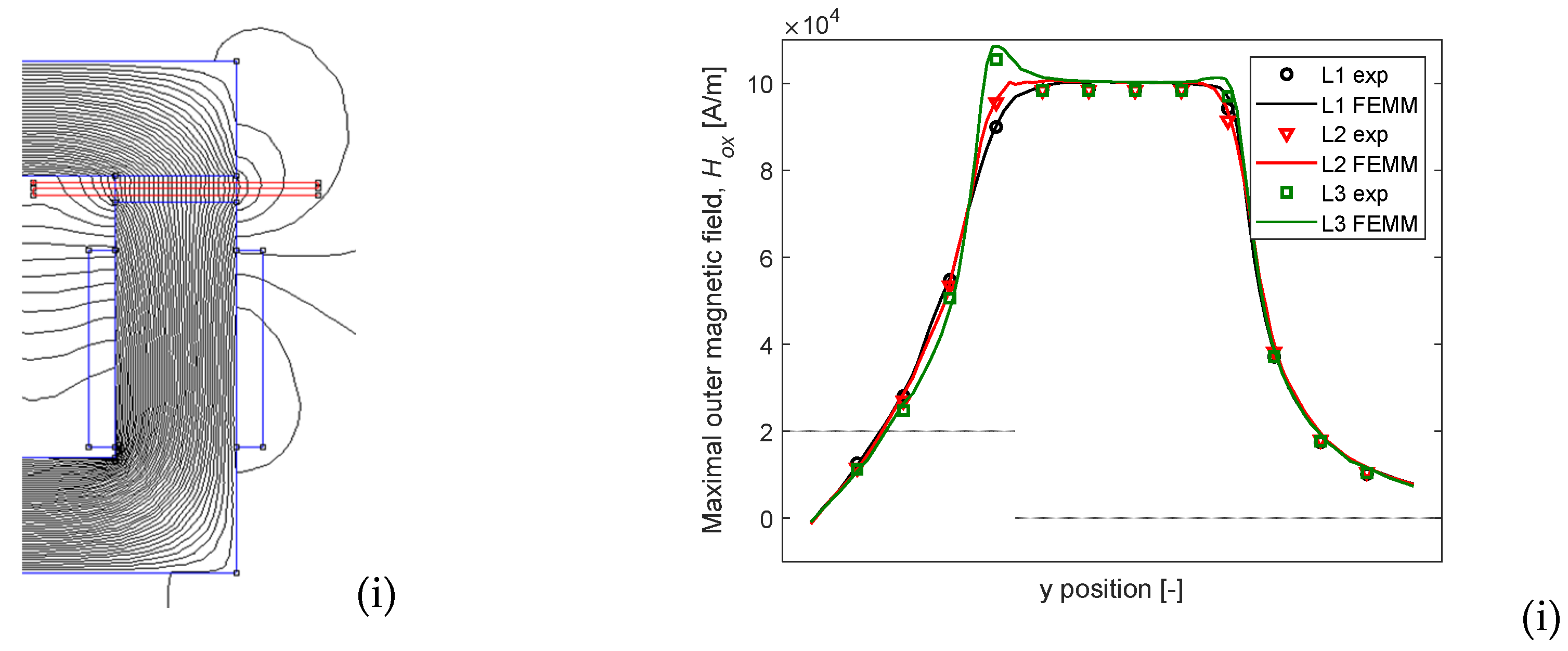
3.3. Comparison between Measurements and Numerical Results
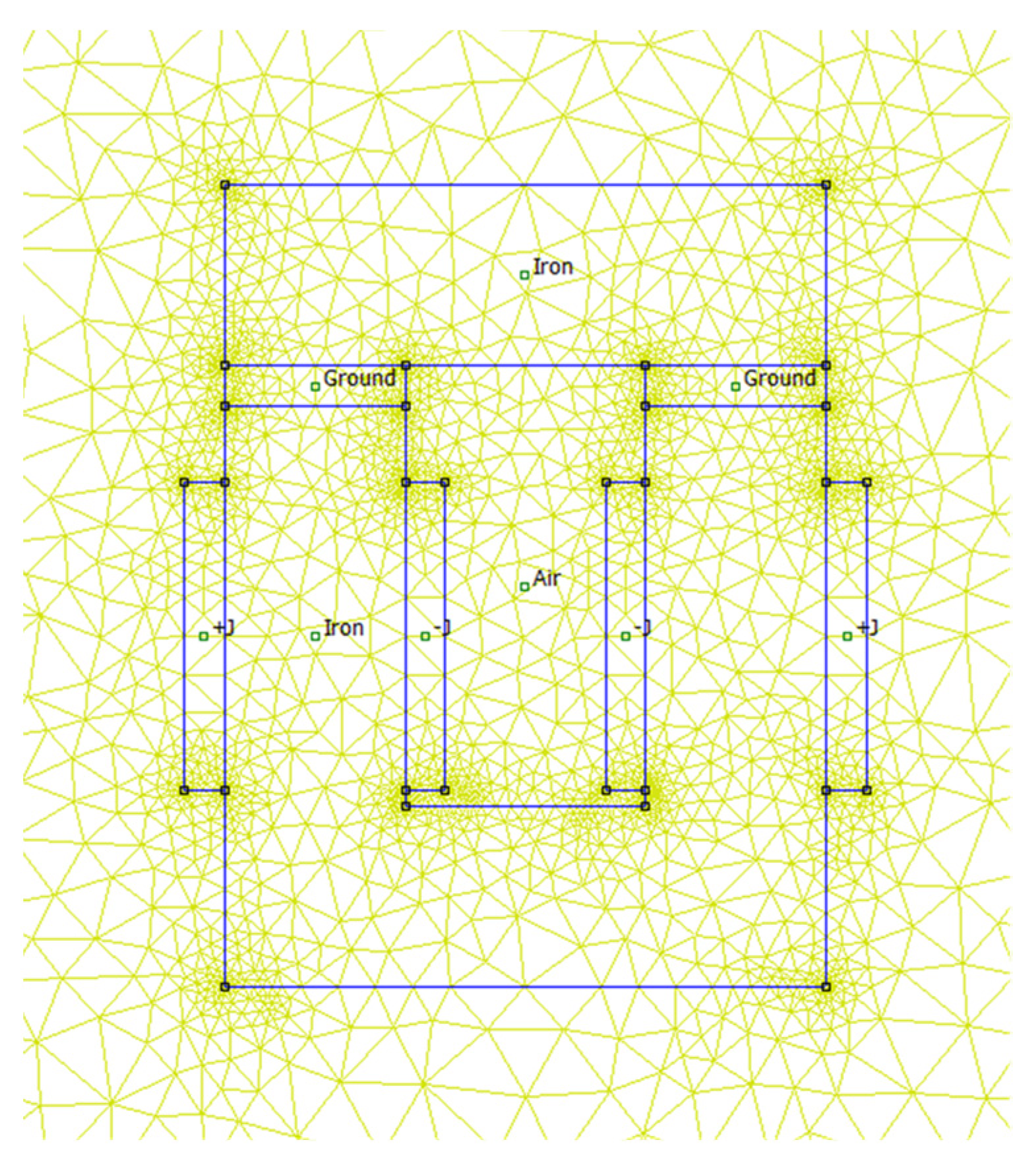
3.3.1. Numerical Modeling
- the model is supposed to be in 2D (i.e., the end effects are neglected);
- the magnetic materials are considered to be isotropic;
- the hysteresis effect is ignored;
- and the skin effect in all materials (e.g., copper and iron) is neglected.
3.3.2. Results Discussion
4. Eddy-Current Loss Calculation with Experimental Validations
4.1. Analytical Model
4.1.1. Introduction
4.1.2. Assumptions and Segmentation
- the studied materials are excited by a spatially uniform outer magnetic field supposed normal to the -plane, as shown in Figure 17a; i.e., with where is the unity vector of the three components;
- the eddy currents are induced only by and the effects of other magnetic field components on the eddy-current loss calculation can be neglected;
- the studied materials are rectangular-shaped only and considered to be isotropic (i.e., the magnetic permeability and the electrical conductivity of the conductive massive part are constant);
- and is assumed to be invariant to the operating temperature.
- the leakage fluxes at the edges of the conductive massive parts could be neglected (such as is independent of x, );
- and the electromagnet supplied with a sinusoidal voltage was not saturated.
- Therefore, the analytical model can be developed in 2D and the -plane. Hence,
- the resultant eddy-current density has two components, i.e., with and ;
- and the inner (or resulting) magnetic field in the conductive massive parts considering the skin effect with .
4.1.3. Resulting Magnetic Field
- ➢
- Governing Partial Differential Equation (PDE) in Cartesian Coordinate: In the quasi-stationary approximation, inside a linear (non)magnetic material without electromagnetic sources, the magnetodynamic PDE in terms of , resulting from Maxwell’s equations, is defined by
- ➢
- Definition of BCs: Since the conductive massive parts are excited by an outer sinusoidal spatially uniform magnetic field, the BCs can be considered homogeneous [see Section 3] and equal to (according to the Cartesian coordinates of Figure 17) on the edges, :
- -
- in the -axis:
- -
- in the -axis:
- ➢
- Magnetic Field Solution: By satisfying (14) and (15), the 2D final solution of (viz., the complex amplitude of ) in each conductive segment can be written as a Fourier series
4.1.4. Resultant Eddy-Current Density Distribution
4.1.5. Volumic Eddy-Current Losses
4.2. Experimental Validations
4.2.1. Power Conservation Method
- : the power consumed only by the electromagnet (i.e., without the studied materials);
- and, : the total power consumed by the electromagnet associated with the conductive massive parts.
4.2.2. Power Experimental Measurements
- ➢
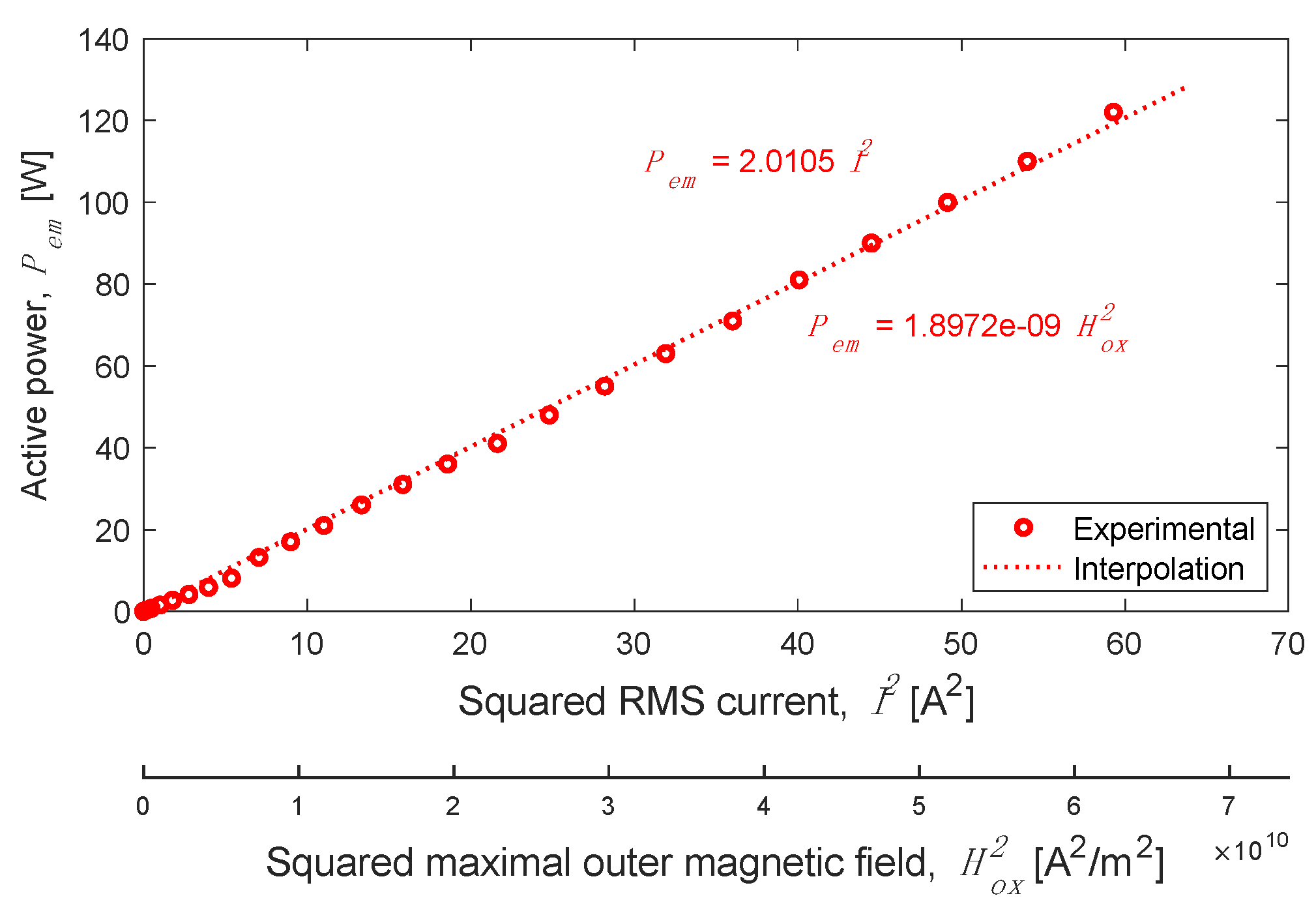
- Electromagnet Power Consumption: First, the electromagnetic device alone is characterized (see Figure 18a). The active power (without the conductive massive parts replaced by PLA) is then measured.
- ➢
- Total Power: Secondly, the conductive massive parts with(out) segmentation are introduced into the adjustable air gap. The total active power consumed by the electromagnet associated with the conductive massive parts (see Figure 18b) is then measured.
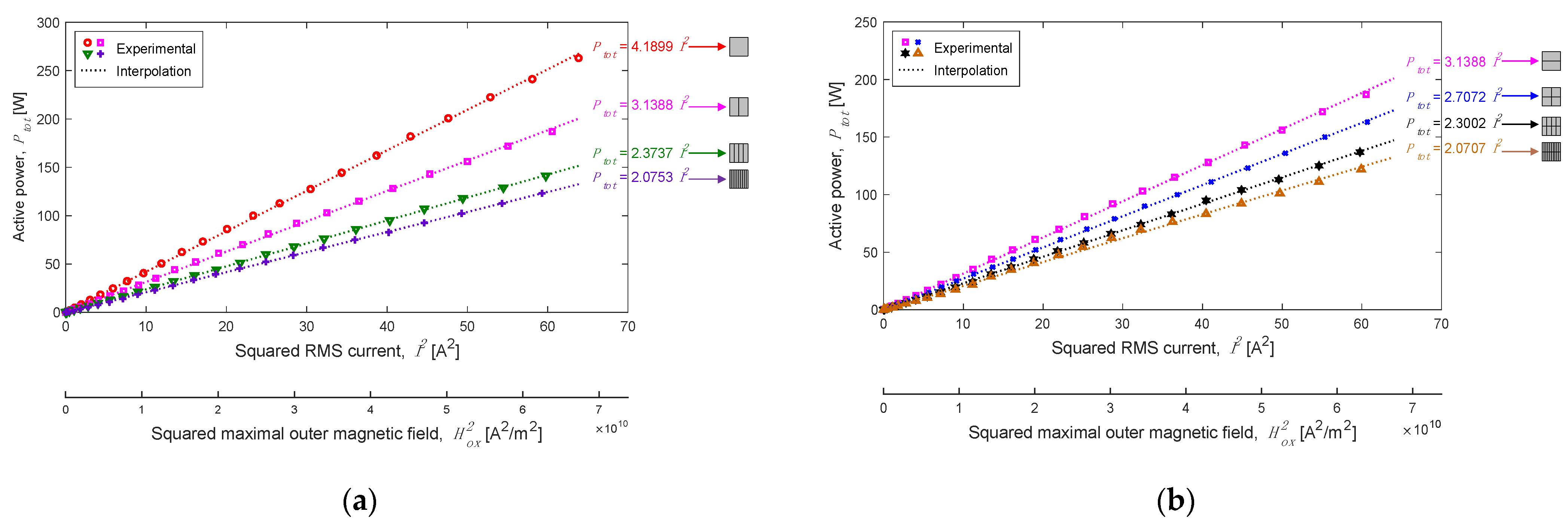
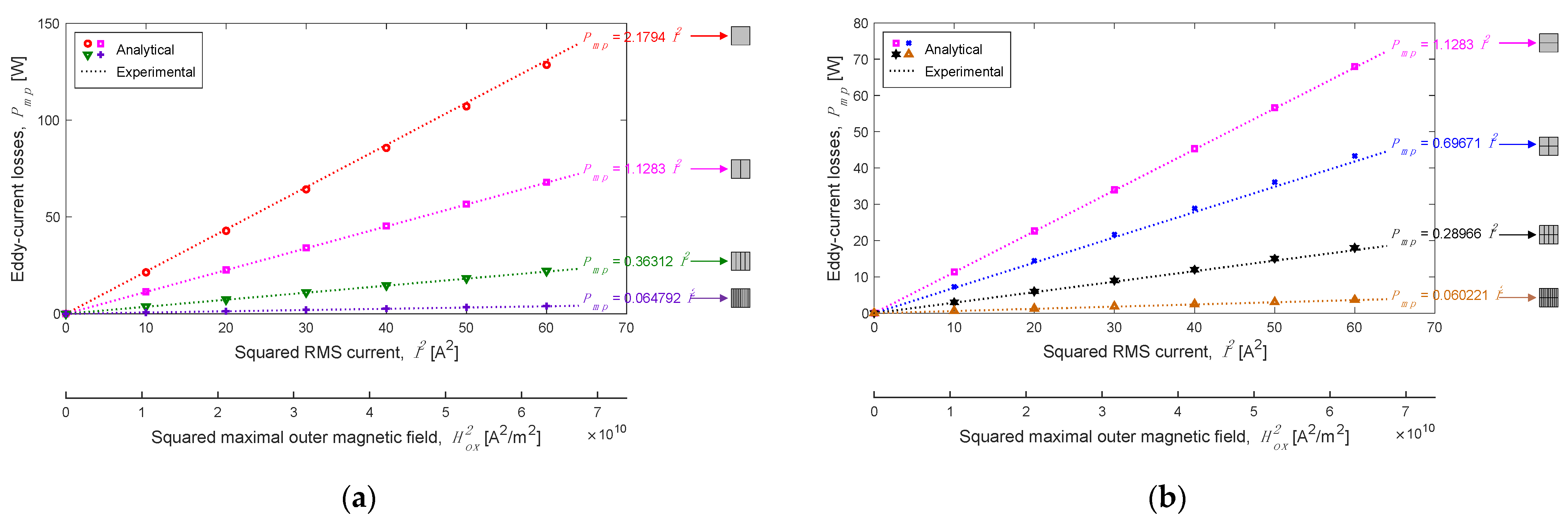
4.2.3. Analytical and Experimental Comparison of Volumic Eddy-Current Losses
- ➢
- Linear Dependency: Knowing and , the volumic eddy-current losses in conductive massive parts are determined from (26).
- -
- the experimental method;
- -
- and the variation of due to the heating of the conductive massive parts (which is assumed to be invariant to the operating temperature in the analytical model).
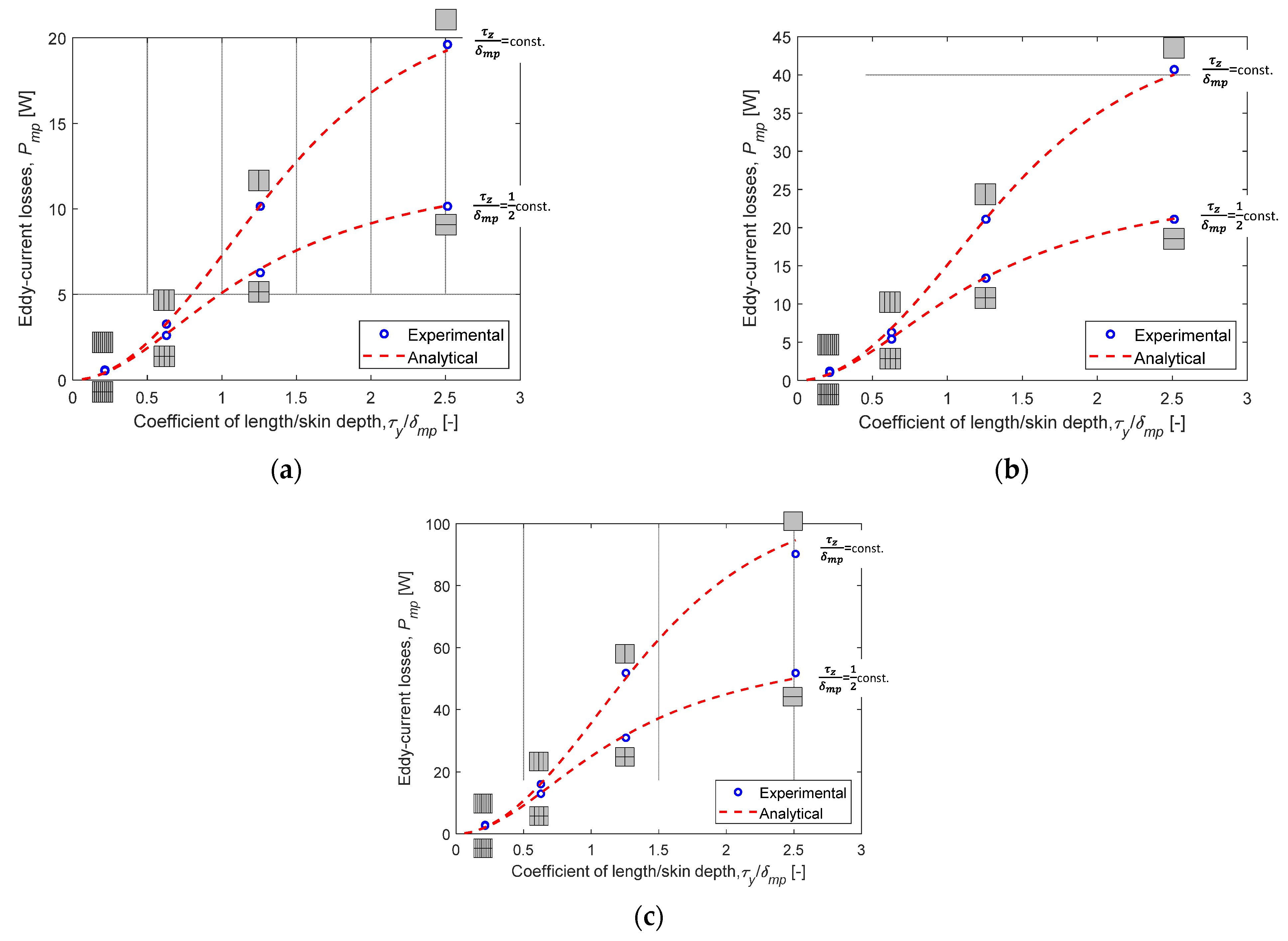
- ➢
- Coefficient of Length/Skin Depth Study: For this comparison analysis, = 3 A (viz., = 90 V). In order to study the segmentation influence on volumic eddy-current losses, they were plotted in relation to the coefficient of length/skin depth in both directions (such as in the -axis and in the -axis). In our study, the skin depth = 16 mm.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Stoll, R.L. The Analysis of Eddy Currents; Clarendon Press: Oxfort, UK, 1974. [Google Scholar]
- Sikora, R.; Purczynski, J.; Lipinski, W.; Gramz, M. Use of variational methods to the eddy current calculation in thin conducting plates. IEEE Trans. Magn. 1978, 14, 383–385. [Google Scholar] [CrossRef]
- Dresner, L. Eddy current heating of irregularly shaped plates by slow ramped fields. OAK Ridge Natl. Lab. (ORNL) 1978, 6968, 1–44. [Google Scholar]
- Vansompel, H.; Yarantseva, A.; Sergeant, P.; Crevecoeur, G. An inverse thermal modeling approach for thermal parameter and loss identification in an axial flux permanent magnet machine. IEEE Trans. Ind. Electron. 2019, 66, 1727–1735. [Google Scholar] [CrossRef]
- Benlamine, R.; Dubas, F.; Randi, S.A.; Lhotellier, D.; Espanet, C. 3-D numerical hybrid method for PM eddy-current losses calculation: Application to axial-flux PMSMs. IEEE Trans. Magn. 2015, 51, 8106110. [Google Scholar] [CrossRef] [Green Version]
- Jassal, A.; Polinder, H.; Ferreira, J.A. Literature survey of eddy-current loss analysis in rotating electrical machines. IET Electr. Power Appl. 2012, 6, 743–752. [Google Scholar] [CrossRef]
- Dubas, F.; Rahideh, A. Two-dimensional analytical permanent-magnet eddy-current loss calculations in slotless PMSM equipped with surface-inset magnets. IEEE Trans. Magn. 2014, 50, 6300320. [Google Scholar] [CrossRef]
- Tessarolo, A. A survey of state-of-the-art methods to compute rotor eddy-current losses in synchronous permanent magnet machines. In Proceedings of the IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Nottingham, UK, 20–21 April 2017. [Google Scholar] [CrossRef]
- Ouamara, D.; Dubas, F. Permanent-magnet eddy-current losses: A global revision of calculation and analysis. Math. Comput. Appl. 2019, 24, 67. [Google Scholar] [CrossRef] [Green Version]
- Sirimanna, S.; Balachandran, T.; Haran, K.A. Review on magnet loss analysis, validation, design considerations, and reduction strategies in permanent magnet synchronous motors. Energies 2022, 15, 6116. [Google Scholar] [CrossRef]
- Jara, W.; Lindh, P.; Tapia, J.A.; Petrov, I.; Repo, A.K.; Pyrhönen, J. Rotor eddy-current losses reduction in an axial flux permanent-magnet machine. IEEE Trans. Ind. Electron. 2016, 63, 4729–4737. [Google Scholar] [CrossRef]
- De Paula Machado Bazzo, T.; Kölzer, J.F.; Carlson, R.; Wurtz, F.; Gerbaud, L. Multiphysics design optimization of a permanent magnet synchronous generator. IEEE Trans. Ind. Electron. 2017, 64, 9815–9823. [Google Scholar] [CrossRef]
- Zheng, J.; Zhao, W.; Ji, J.; Zhu, J.; Gu, C.; Zhu, S. Design to reduce rotor losses in fault-tolerant permanent-magnet machines. IEEE Trans. Ind. Electron. 2018, 65, 8476–8487. [Google Scholar] [CrossRef]
- Zhu, S.; Hu, Y.; Liu, C.; Wang, K. Iron loss and efficiency analysis of interior PM machines for electric vehicle applications. IEEE Trans. Ind. Electron. 2018, 65, 114–123. [Google Scholar] [CrossRef]
- Martinek, G.; Lanz, M.; Schneider, G.; Goll, D. Determination of AC losses in segmented rare earth permanent magnets. J. Appl. Phys. 2020, 128, 113902. [Google Scholar] [CrossRef]
- Amara, Y.; Wang, J.; Howe, D. Analytical prediction of eddy-current loss in modular tubular permanent-magnet machines. IEEE Trans. Energy Convers. 2005, 20, 761–770. [Google Scholar] [CrossRef]
- Yamazaki, K.; Abe, A. Loss investigation of interior permanent-magnet motors considering carrier harmonics and magnet eddy currents. IEEE Trans. Ind. Appl. 2009, 45, 659–665. [Google Scholar] [CrossRef]
- Huang, W.; Bettayeb, A.; Kaczmarek, R.; Vannier, J. Optimization of magnet segmentation for reduction of eddy-current losses in permanent magnet synchronous machine. IEEE Trans. Energy Convers. 2010, 25, 381–387. [Google Scholar] [CrossRef] [Green Version]
- Mirzaei, M.; Binder, A.; Funieru, B.; Susic, M. Analytical calculations of induced eddy currents losses in the magnets of surface mounted PM machines with consideration of circumferential and axial segmentation effects. IEEE Trans. Magn. 2012, 48, 4831–4841. [Google Scholar] [CrossRef]
- Mirzaei, M.; Binder, A.; Deak, C. 3D analysis of circumferential and axial segmentation effect on magnet eddy-current losses in permanent magnet synchronous machines with concentrated windings. In Proceedings of the XIX International Conference on Electrical Machines—ICEM 2010, Rome, Italy, 6–8 September 2010. [Google Scholar] [CrossRef]
- Balamurali, A.; Lai, C.; Mollaeian, A.; Loukanov, V.; Kar, N.C. Analytical investigation into magnet eddy current losses in interior permanent magnet motor using modified winding function theory accounting for pulsewidth modulation harmonics. IEEE Trans. Magn. 2016, 52, 8106805. [Google Scholar] [CrossRef]
- Nair, S.S.; Wang, J.; Chin, R.; Chen, L.; Sun, T. Analytical prediction of 3-D magnet eddy current losses in surface mounted PM machines accounting slotting effect. IEEE Trans. Energy Convers. 2017, 32, 414–423. [Google Scholar] [CrossRef]
- Aoyama, Y.; Miyata, K.; Ohashi, K. Simulations and experiments on eddy current in Nd-Fe-B magnet. IEEE Trans. Magn. 2005, 41, 3790–3792. [Google Scholar] [CrossRef]
- Yamazaki, K.; Shina, M.; Miwa, M.; Hagiwara, J. Investigation of eddy current loss in divided Nd-Fe-B sintered magnets for synchronous motors due to insulation resistance and frequency. IEEE Trans. Magn. 2008, 44, 4269–4272. [Google Scholar] [CrossRef]
- Yogal, N.; Lehrmann, C.; Henke, M. Permanent magnet eddy current loss measurement at higher frequency and temperature effects under ideal sinusoidal and non-sinusoidal external magnetic fields. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021. [Google Scholar] [CrossRef]
- Deak, C.; Petrovic, L.; Binder, A.; Mirzaei, M.; Irimie, D.; Funieru, B. Calculation of eddy-current losses in permanent magnets of synchronous machines. In Proceedings of the IEEE International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Ischia, Italy, 11–13 June 2008. [Google Scholar] [CrossRef]
- Plait, A.; Dubas, F. 2-D eddy-current losses model and experimental validation through thermal measurements. IEEE Trans. Instrum. Meas. 2022; under review. [Google Scholar]
- Fukuma, A.; Kanazawa, S.; Miyagi, D.; Takahashi, N. Investigation of AC loss of permanent magnet of SPM motor considering hysteresis and eddy-current losses. IEEE Trans. Magn. 2005, 41, 1964–1967. [Google Scholar] [CrossRef] [Green Version]
- Kanazawa, S.; Takahashi, N.; Kubo, T. Measurement and analysis of AC loss of NdFeB sintered magnet. Electr. Eng. Jpn. 2006, 154, 869–875. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, B.; Zhang, C.; Liu, Y.; Gong, X. Eddy-current loss measurement of permanent magnetic material at different frequency. Int. J. Appl. Electromagn. Mech. 2019, 61, S13–S22. [Google Scholar] [CrossRef]
- Fratila, R.; Benabou, A.; Tounzi, A.; Mipo, J.C. A combined experimental and finite element analysis method for the estimation of eddy-current loss in NdFeB magnets. Sensors 2014, 14, 8505–8512. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Takahashi, N.; Shinagawa, H.; Miyagi, D.; Doi, Y.; Miyata, K. Analysis of eddy current losses of segmented Nd-Fe-B sintered magnets considering contact resistance. IEEE Trans. Magn. 2009, 45, 1234–1237. [Google Scholar] [CrossRef]
- Tong, W.; Hou, M.; Sun, L.; Wu, S. Analysis and experimental verification of segmented rotor structure on rotor eddy current loss of high-speed surface-mounted permanent magnet machine. In Proceedings of the IEEE International Magnetic Conference (INTERMAG), Lyon, France, 26–30 April 2021. [Google Scholar] [CrossRef]
- Meeker, D.C. Finite Element Method Magnetics Ver. 4.2. Available online: http://www.femm.info (accessed on 21 April 2019).
- Asensor Technology AB, Linear High Precision Analog Hall Sensors. Available online: https://www.asensor.eu (accessed on 8 November 2022).
- Plait, A.; Dubas, F. Electrical conductivity influence on eddy-current losses: Analytical study and experimental validation. In Proceedings of the IEEE International Conference on Electrical Machines and Systems (ICEMS), Gyeongju, Korea, 31 October–3 November 2021. (Best Paper Award from the IEEE ICEMS’22). [Google Scholar] [CrossRef]








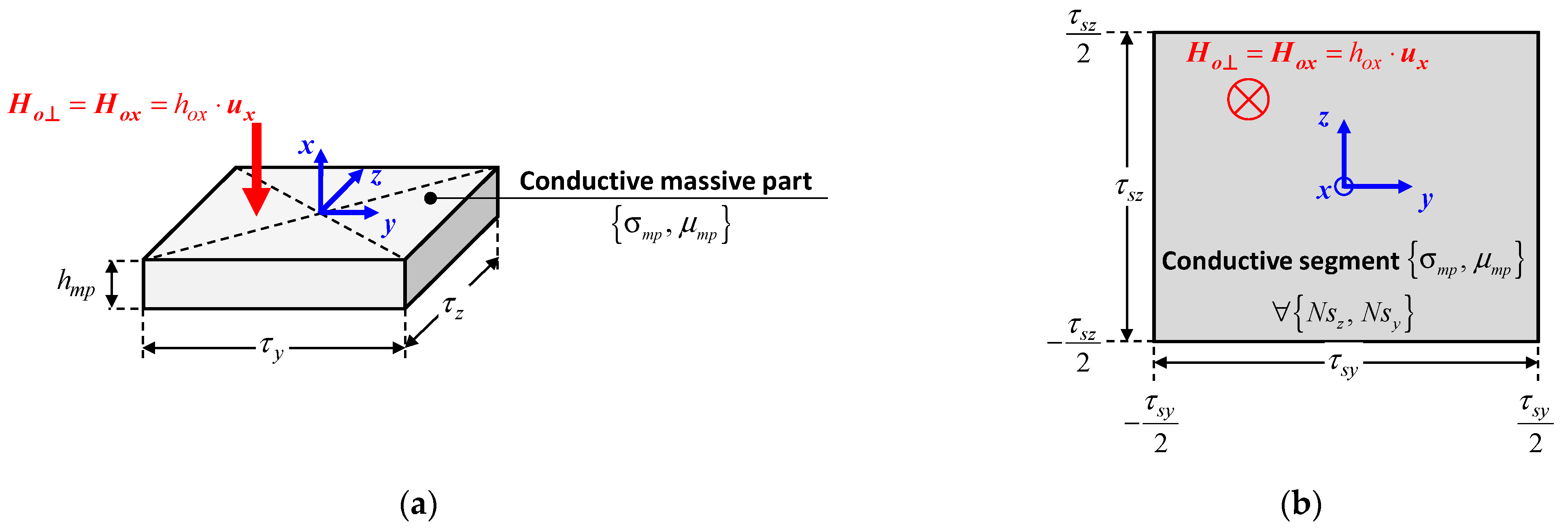

| Symbol | Quantity | Values | |
|---|---|---|---|
| Ferromagnetic circuit | Depth | 46 mm | |
| Width | 45 mm | ||
| Yoke height | 45 mm | ||
| Yoke length | 150 mm | ||
| Height overhang top | 19 mm | ||
| Height overhang bot | 4 mm | ||
| Vacuum permeability | 4π10−7 H/m | ||
| B(H) | FeSi ferromagnetic properties | Figure 3 | |
| Coils | Number of coils turns | 500 | |
| Maximal current (per coil) | 4.5 A | ||
| Coil height | 77 mm | ||
| Coil width | 10 mm | ||
| Conductors area | 700 mm² | ||
| Electrical resistance | 2.8 Ω | ||
| Inductance | 18 mH |
| (mm2) | (mm) | ||||
|---|---|---|---|---|---|
| {1,1} |  | 1600 | 160 | 2.513 | 2.513 |
| {1,2} |  | 800 | 120 | 1.257 | 2.513 |
| {1,4} |  | 400 | 100 | 0.628 | 2.513 |
| {1,10} |  | 160 | 88 | 0.251 | 2.513 |
| {2,1} |  | 800 | 120 | 2.513 | 1.257 |
| {2,2} |  | 400 | 80 | 1.257 | 1.257 |
| {2,4} |  | 200 | 60 | 0.628 | 1.257 |
| {2,10} |  | 80 | 48 | 0.251 | 1.257 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plait, A.; Dubas, F. Volumic Eddy-Current Losses in Conductive Massive Parts with Experimental Validations. Energies 2022, 15, 9413. https://doi.org/10.3390/en15249413
Plait A, Dubas F. Volumic Eddy-Current Losses in Conductive Massive Parts with Experimental Validations. Energies. 2022; 15(24):9413. https://doi.org/10.3390/en15249413
Chicago/Turabian StylePlait, Antony, and Frédéric Dubas. 2022. "Volumic Eddy-Current Losses in Conductive Massive Parts with Experimental Validations" Energies 15, no. 24: 9413. https://doi.org/10.3390/en15249413






