The Role of Computational Science in Wind and Solar Energy: A Critical Review
Abstract
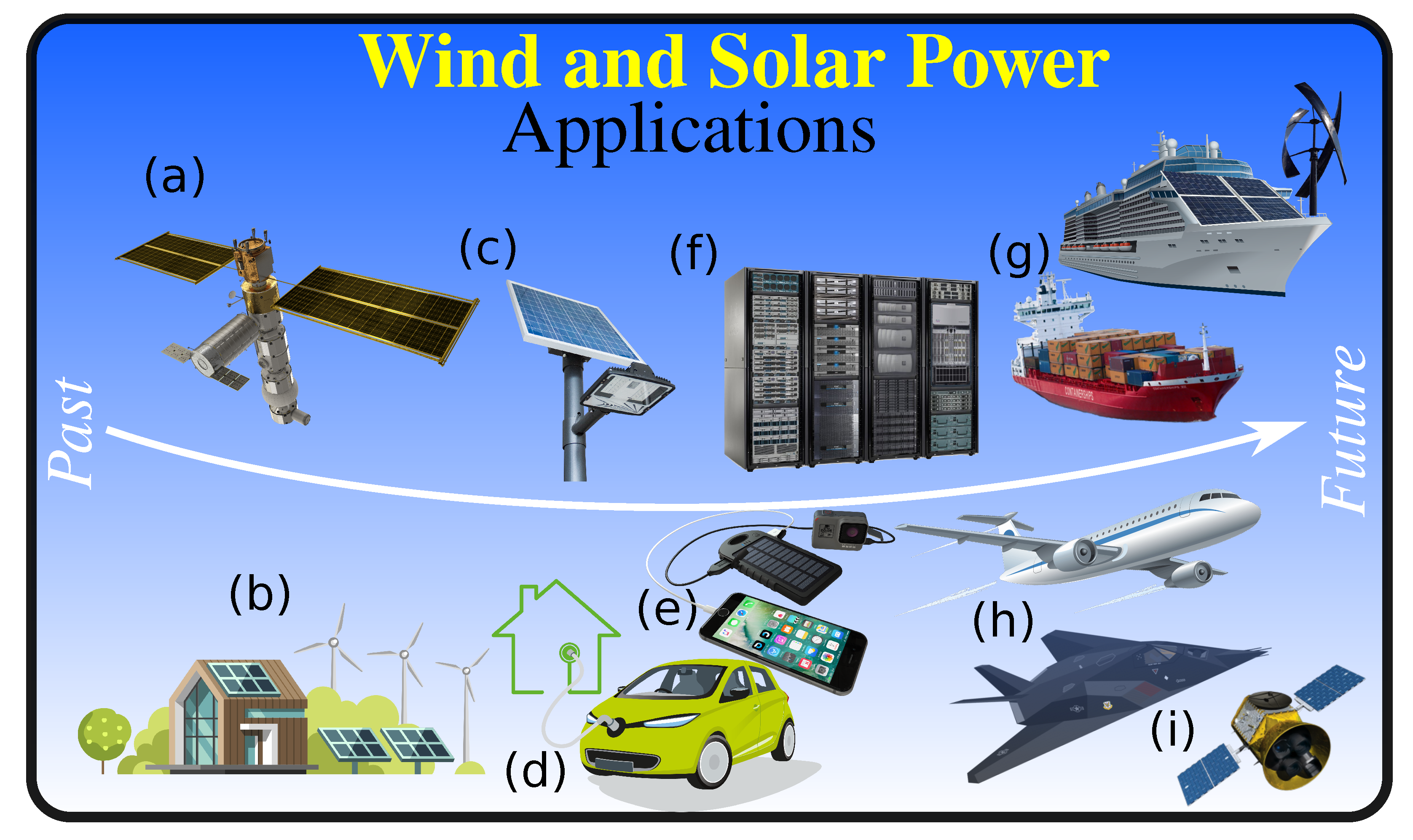
:1. Introduction
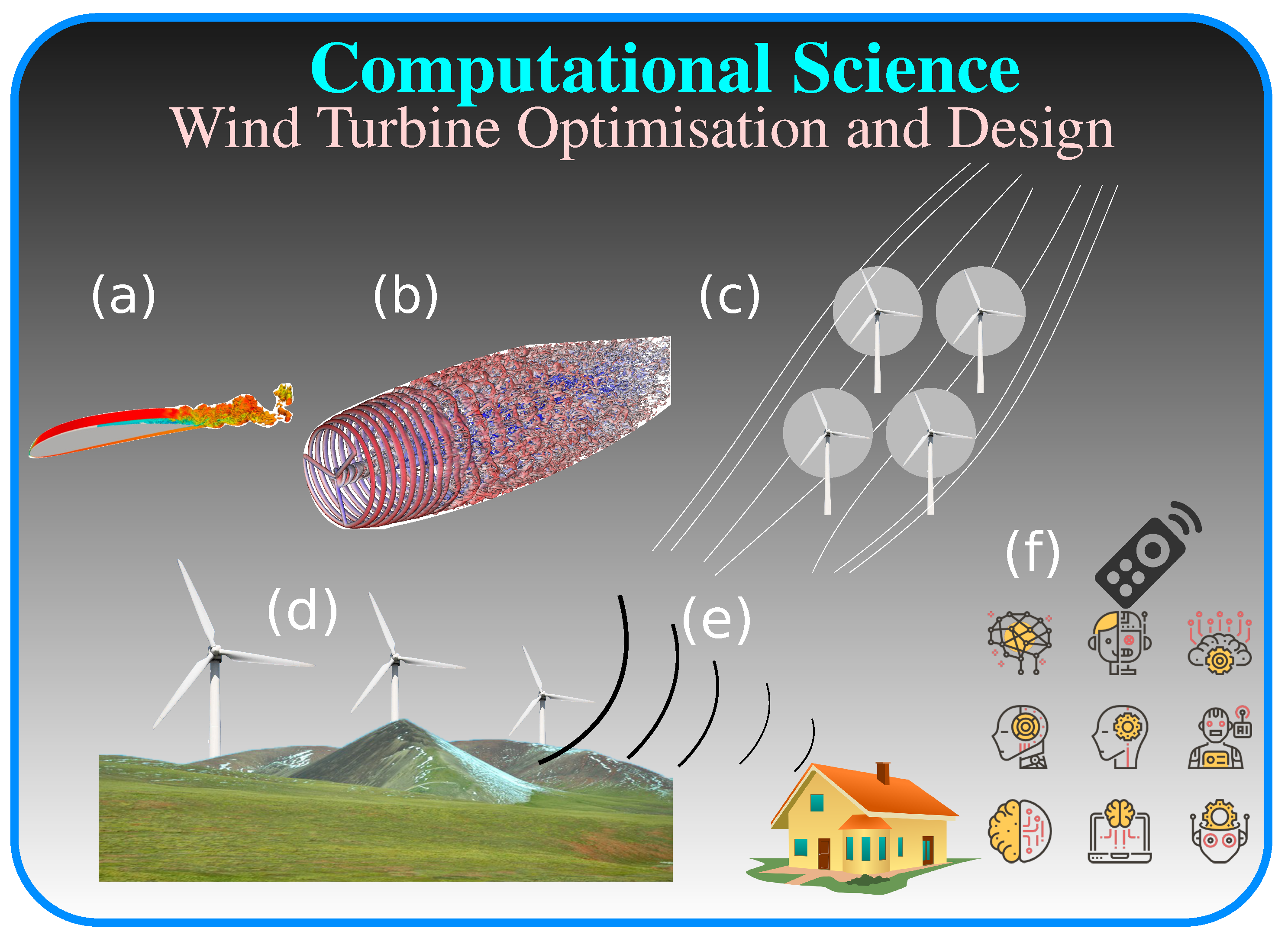
2. Challenges in Wind Energy
2.1. Technology Challenges
- An improved understanding of flow physics at an atmospheric and wind farms scale.
- Improvements regarding the aerodynamics of onshore and offshore turbines and hydrodynamics of offshore turbines. Furthermore, a better understanding of large wind turbines’ structural dynamics (aeroelastic effects in particular).
- Improved integration of wind power plants into the electricity grid.
2.2. Flow Physics
2.3. Aeroelastic Behaviour
2.4. Wind Farms
2.5. Other Challenges
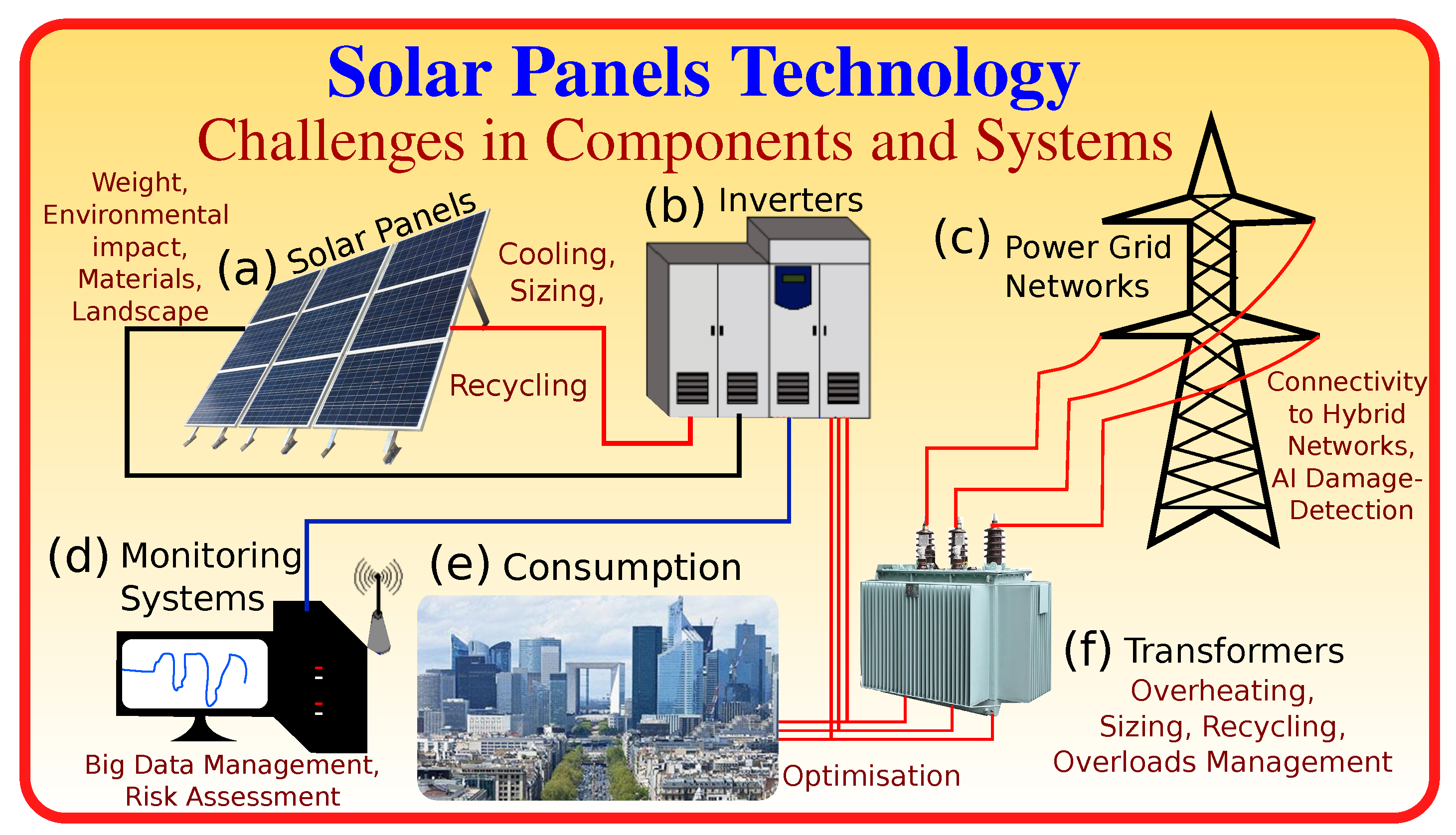
3. Challenges in Solar Energy
3.1. Intermittency
3.2. Air Pollution
3.3. Storage
3.4. Sustainability
3.5. Grid Connectivity and Management
4. Modelling and Simulation
4.1. Wind Energy
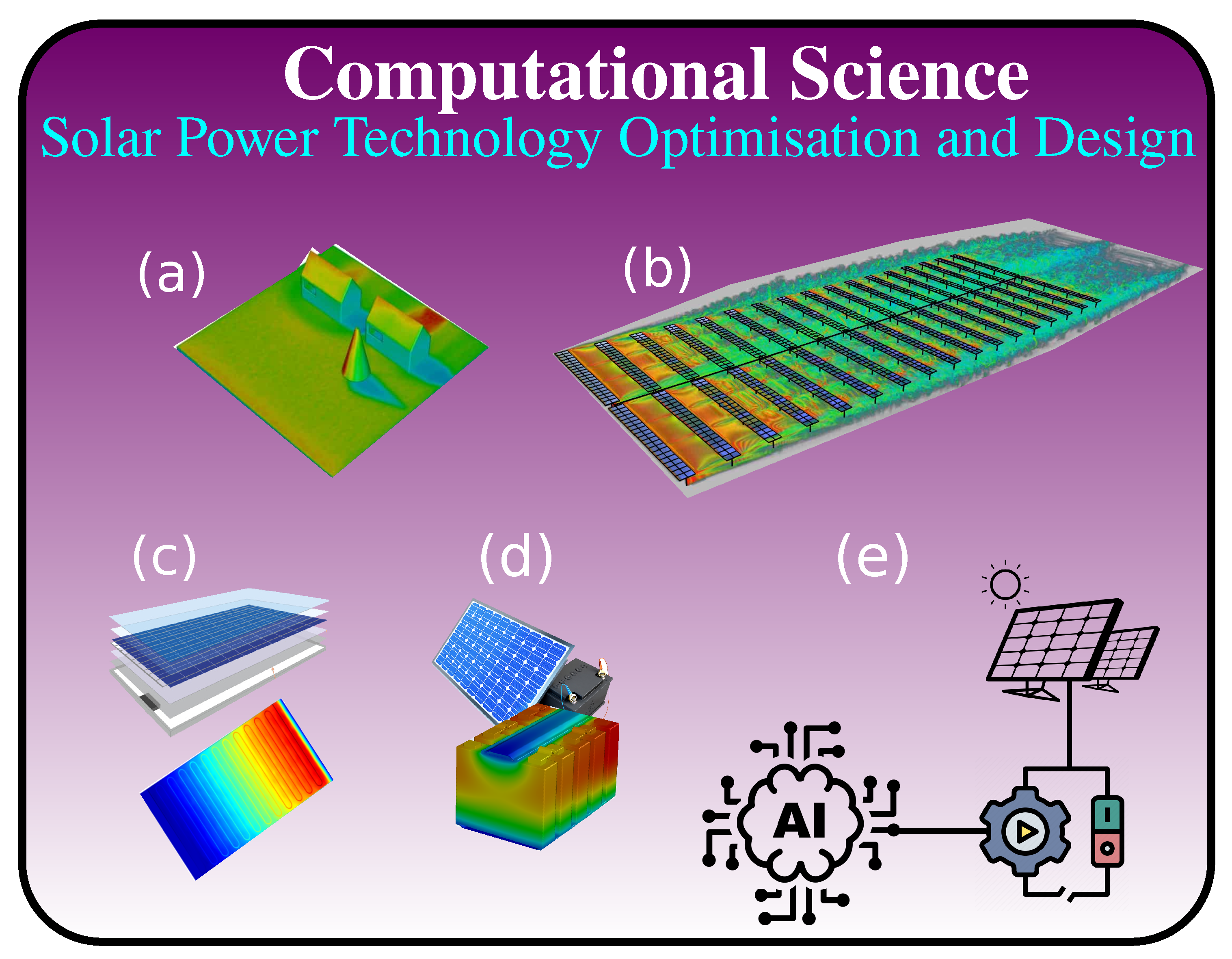
4.2. Solar Energy
- Reduced order models based on the integration of PV modules in operating cycles for different power types generation, e.g., thermodynamic cycles simulation software, Matlab/Simulink.
- Statistical [116], ML and AI models for an increased prediction accuracy (forecasting) and thus higher confidence in the PV system continuous production and performance, e.g., enhanced solar energy management and conversion.
- CFD and optimisation tools for enhanced efficiency of PV systems at the components level, i.e., materials, cooling technologies for energy storage, thermal isolation and regulation for thermal energy storage.
5. Artificial Intelligence and Optimisation
5.1. Machine Learning
5.2. Optimisation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Veers, P.; Dykes, K.; Lantz, E.; Barth, S.; Bottasso, C.L.; Carlson, O.; Clifton, A.; Green, J.; Green, P.; Holttinen, H.; et al. Grand challenges in the science of wind energy. Science 2019, 366, eaau2027. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wagner, B.; Hauer, C.; Schoder, A.; Habersack, H. A review of hydropower in Austria: Past, present and future development. Renew. Sustain. Energy Rev. 2015, 50, 304–314. [Google Scholar] [CrossRef]
- Creţan, R.; Vesalon, L. The Political Economy of Hydropower in the Communist Space: Iron Gates Revisited. Tijdschr. Voor Econ. Soc. Geogr. 2017, 108, 688–701. [Google Scholar] [CrossRef]
- Webber, M. The Political Economy of the Three Gorges Project. Geogr. Res. 2012, 50, 154–165. [Google Scholar] [CrossRef]
- Remus, C.; Guran, L.; Platon, D.; Turnock, D. Foreign Direct Investment and Social Risk in Romania: Progress in Less-favoured Areas. In Foreign Direct Investment and Regional Development in East Central Europe and the Former Soviet Union: A Collection of Essays in Memory of Professor Francis Frank Carter; Routledge: London, UK, 2005; pp. 305–348. [Google Scholar] [CrossRef]
- Vesalon, L.; Remus, C. Mono-industrialism and the Struggle for Alternative Development: The Case of the Roşia Montanǎ Gold-mining Project. Tijdschr. Voor Econ. Soc. Geogr. 2013, 104, 539–555. [Google Scholar] [CrossRef]
- Hernández-Callejo, L.; Gallardo-Saavedra, S.; Alonso-Gómez, V. A review of photovoltaic systems: Design, operation and maintenance. Sol. Energy 2019, 188, 426–440. [Google Scholar] [CrossRef]
- Parida, B.; Iniyan, S.; Goic, R. A review of solar photovoltaic technologies. Renew. Sustain. Energy Rev. 2011, 15, 1625–1636. [Google Scholar] [CrossRef]
- Shukla, A.; Buddhi, D.; Sawhney, R. Solar water heaters with phase change material thermal energy storage medium: A review. Renew. Sustain. Energy Rev. 2009, 13, 2119–2125. [Google Scholar] [CrossRef]
- Ackermann, T.; Prevost, T.; Vittal, V.; Roscoe, A.J.; Matevosyan, J.; Miller, N. Paving the Way: A Future Without Inertia Is Closer Than You Think. IEEE Power Energy Mag. 2017, 15, 61–69. [Google Scholar] [CrossRef]
- Nygaard, N.G.; Newcombe, A.C. Wake behind an offshore wind farm observed with dual-Doppler radars. J. Physics Conf. Ser. 2018, 1037, 072008. [Google Scholar] [CrossRef]
- Frank, M.; Drikakis, D.; Charissis, V. Machine-Learning Methods for Computational Science and Engineering. Computation 2020, 8, 15. [Google Scholar] [CrossRef] [Green Version]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Dbouk, T. A review about the engineering design of optimal heat transfer systems using topology optimization. Appl. Therm. Eng. 2017, 112, 841–854. [Google Scholar] [CrossRef]
- Subramaniam, V.; Dbouk, T.; Harion, J.L. Topology optimization of conjugate heat transfer systems: A competition between heat transfer enhancement and pressure drop reduction. Int. J. Heat Fluid Flow 2019, 75, 165–184. [Google Scholar] [CrossRef]
- Wang, M.; Wang, Q.; Zaki, T.A. Discrete adjoint of fractional-step incompressible Navier-Stokes solver in curvilinear coordinates and application to data assimilation. J. Comput. Phys. 2019, 396, 427–450. [Google Scholar] [CrossRef]
- Roth, R.; Ulbrich, S. A Discrete Adjoint Approach for the Optimization of Unsteady Turbulent Flows. Flow Turbul. Combust 2013, 90, 763–783. [Google Scholar] [CrossRef]
- Anderson, E.M.; Bhuiyan, F.H.; Mavriplis, D.J.; Fertig, R.S. Adjoint-Based High-Fidelity Structural Optimization of Wind-Turbine Blade for Load Stress Minimization. AIAA J. 2019, 57, 4057–4070. [Google Scholar] [CrossRef]
- Xiao, T.P.; Cifci, O.S.; Bhargava, S.; Chen, H.; Gissibl, T.; Zhou, W.; Giessen, H.; Toussaint, K.C.; Yablonovitch, E.; Braun, P.V. Diffractive Spectral-Splitting Optical Element Designed by Adjoint-Based Electromagnetic Optimization and Fabricated by Femtosecond 3D Direct Laser Writing. ACS Photonics 2016, 3, 886–894. [Google Scholar] [CrossRef]
- Marck, F. Fundamentals of Optimization; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- IEA. World Energy Outlook, Technical Report. 2018. Available online: https://www.iea.org/weo2018/ (accessed on 15 November 2022).
- BNEF. New Energy Outlook. 2019. Available online: https://about.bnef.com/new-energy-outlook/ (accessed on 15 November 2022).
- BPEE. BP Energy Outlook. 2018. Available online: https://www.bp.com/content/dam/bp/en/corporate/pdf/energy-economics/energy-outlook/bp-energy-outlook-2018.pdf (accessed on 15 November 2022).
- Sverre, A. Energy Transition Outlook 2018: A Global and Regional Forecast of the Energy Transition to 2050. 2018. Available online: https://eto.dnvgl.com/2018/ (accessed on 15 November 2022).
- GWEC. Global Wind Energy Council, 60.4 GW of Wind Energy Capacity Was Installed Globally in 2019. 2019. Available online: https://gwec.net/global-wind-report-2019/ (accessed on 15 November 2022).
- Mai, T.; Lantz, E.; Mowers, M.; Wiser, R. The Value of Wind Technology Innovation: Implications for the U.S. Power System, wind Industry, Electricity Consumers, and Environment, Technical Report. 2017. Available online: https://www.nrel.gov/docs/fy17osti/70032.pdf/ (accessed on 15 November 2022).
- IRENA. Global Energy Transformation: A Roadmap to 2050. 2018. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2018/Apr/IRENA_Report_GET_2018.pdf/ (accessed on 15 November 2022).
- Veers, P.S.; Ashwill, T.D.; Sutherland, H.J.; Laird, D.L.; Lobitz, D.W.; Griffin, D.A.; Mandell, J.F.; Musial, W.D.; Jackson, K.; Zuteck, M.; et al. Trends in the Design, Manufacture and Evaluation of Wind Turbine Blades. Wind Energy 2003, 6, 245–259. [Google Scholar] [CrossRef]
- Jamieson, P. Innovation in Wind Turbine Design; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Scott, S.; Capuzzi, M.; Langston, D.; Bossanyi, E.; McCann, G.; Weaver, P.M.; Pirrera, A. Effects of aeroelastic tailoring on performance characteristics of wind turbine systems. Renew. Energy 2017, 114, 887–903. [Google Scholar] [CrossRef]
- Bortolotti, P.; Bottasso, C.L.; Croce, A.; Sartori, L. Integration of multiple passive load mitigation technologies by automated design optimization—The case study of a medium-size onshore wind turbine. Wind Energy 2019, 22, 65–79. [Google Scholar] [CrossRef] [Green Version]
- Wyngaard, J.C. Toward Numerical Modeling in the “Terra Incognita”. J. Atmos. Sci. 2004, 61, 1816–1826. [Google Scholar] [CrossRef]
- Larsén, X.G.; Petersen, E.L.; Larsen, S.E. Variation of boundary-layer wind spectra with height. Q. J. R. Meteorol. Soc. 2018, 144, 2054–2066. [Google Scholar] [CrossRef] [Green Version]
- Sanz Rodrigo, J.; Chávez Arroyo, R.A.; Moriarty, P.; Churchfield, M.; Kosović, B.; Réthoré, P.E.; Hansen, K.S.; Hahmann, A.; Mirocha, J.D.; Rife, D. Mesoscale to microscale wind farm flow modeling and evaluation. WIREs Energy Environ. 2017, 6, e214. [Google Scholar] [CrossRef]
- Mann, J.; Angelou, N.; Arnqvist, J.; Callies, D.; Cantero, E.; Arroyo, R.C.; Courtney, M.; Cuxart, J.; Dellwik, E.; Gottschall, J.; et al. Complex terrain experiments in the New European Wind Atlas. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2017, 375, 20160101. [Google Scholar] [CrossRef] [Green Version]
- Han, X.; Liu, D.; Xu, C.; Shen, W.Z. Atmospheric stability and topography effects on wind turbine performance and wake properties in complex terrain. Renew. Energy 2018, 126, 640–651. [Google Scholar] [CrossRef]
- Calaf, M.; Meneveau, C.; Meyers, J. Large eddy simulation study of fully developed wind-turbine array boundary layers. Phys. Fluids 2010, 22, 015110. [Google Scholar] [CrossRef] [Green Version]
- Aitken, M.L.; Banta, R.M.; Pichugina, Y.L.; Lundquist, J.K. Quantifying Wind Turbine Wake Characteristics from Scanning Remote Sensor Data. J. Atmos. Ocean. Technol. 2014, 31, 765–787. [Google Scholar] [CrossRef]
- Hirth, B.D.; Schroeder, J.L.; Gunter, W.S.; Guynes, J.G. Measuring a Utility-Scale Turbine Wake Using the TTUKa Mobile Research Radars. J. Atmos. Ocean. Technol. 2012, 29, 765–771. [Google Scholar] [CrossRef] [Green Version]
- Menke, R.; Vasiljević, N.; Hansen, K.S.; Hahmann, A.N.; Mann, J. Does the wind turbine wake follow the topography? A multi-lidar study in complex terrain. Wind Energy Sci. 2018, 3, 681–691. [Google Scholar] [CrossRef] [Green Version]
- Wildmann, N.; Vasiljevic, N.; Gerz, T. Wind turbine wake measurements with automatically adjusting scanning trajectories in a multi-Doppler lidar setup. Atmos. Meas. Tech. 2018, 11, 3801–3814. [Google Scholar] [CrossRef] [Green Version]
- Lienard, C.; Boisard, R.; Daudin, C. Aerodynamic behavior of a floating offshore wind turbine. In Proceedings of the AIAA Scitech Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef] [Green Version]
- Sørensen, J.N.; Shen, W.Z.; Munduate, X. Analysis of wake states by a full-field actuator disc model. Wind Energy 1998, 1, 73–88. [Google Scholar] [CrossRef]
- Jonkman, J.M. Dynamics of offshore floating wind turbines—Model development and verification. Wind Energy 2009, 12, 459–492. [Google Scholar] [CrossRef]
- Koo, B.J.; Goupee, A.J.; Kimball, R.W.; Lambrakos, K.F. Model Tests for a Floating Wind Turbine on Three Different Floaters. J. Offshore Mech. Arct. Eng. 2014, 136, 020907. [Google Scholar] [CrossRef]
- Madsen, H.A.; Sørensen, N.N.; Bak, C.; Troldborg, N.; Pirrung, G. Measured aerodynamic forces on a full scale 2MW turbine in comparison with EllipSys3D and HAWC2 simulations. J. Phys. Conf. Ser. 2018, 1037, 022011. [Google Scholar] [CrossRef]
- Schepers, J.; Boorsma, K.; Sørensen, N.; Voutsinas; Sieros, G.; Rahimi, H.; Heisselmann, H.; Jost, E.; Lutz, T.; Maeder, T.; et al. Final results from the EU project AVATAR: Aerodynamic modelling of 10 MW wind turbines. J. Phys. Conf. Ser. 2018, 1037, 022013. [Google Scholar] [CrossRef]
- Shapiro, C.R.; Bauweraerts, P.; Meyers, J.; Meneveau, C.; Gayme, D.F. Model-based receding horizon control of wind farms for secondary frequency regulation. Wind Energy 2017, 20, 1261–1275. [Google Scholar] [CrossRef]
- Fleming, P.; Aho, J.; Gebraad, P.; Pao, L.; Zhang, Y. Computational fluid dynamics simulation study of active power control in wind plants. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 1413–1420. [Google Scholar] [CrossRef]
- Vali, M.; Petrović, V.; Steinfeld, G.; Pao, L.Y.; Kühn, M. An active power control approach for wake-induced load alleviation in a fully developed wind farm boundary layer. Wind Energy Sci. 2019, 4, 139–161. [Google Scholar] [CrossRef] [Green Version]
- Ellis, G.; Ferraro, G. The Social Acceptance of Wind Energy; Technical Report EUR 28182 EN; European Commission: Luxembourg, 2016. [CrossRef]
- Enevoldsen, P.; Sovacool, B.K. Examining the social acceptance of wind energy: Practical guidelines for onshore wind project development in France. Renew. Sustain. Energy Rev. 2016, 53, 178–184. [Google Scholar] [CrossRef]
- Taylor, J.; Klenk, N. The politics of evidence: Conflicting social commitments and environmental priorities in the debate over wind energy and public health. Energy Res. Soc. Sci. 2019, 47, 102–112. [Google Scholar] [CrossRef]
- Yanagisawa, T. Test of amorphous silicon solar cells: Characteristics degradation due to exposure to intermittent light at several constant ambient temperatures and the validity of the test method. Microelectron. Reliab. 1991, 31, 173–184. [Google Scholar] [CrossRef]
- Mitchell, C.S.; Perkins, G.M.; McNeil, I.J. Intermittent light studies to investigate electron mobility in dye-sensitized solar cells. Sol. Energy 2021, 213, 36–42. [Google Scholar] [CrossRef]
- Anand, V.P.; Indumathi, S.; Pesala, B. Solar power intermittency reduction using supercapacitors integrated with solar panels. J. Renew. Sustain. Energy 2015, 7, 043140. [Google Scholar] [CrossRef]
- Prasad, A.A.; Kay, M. Assessment of Simulated Solar Irradiance on Days of High Intermittency Using WRF-Solar. Energies 2020, 13, 385. [Google Scholar] [CrossRef] [Green Version]
- Manohar, M.; Koley, E.; Ghosh, S.; Mohanta, D.K.; Bansal, R. Spatio-temporal information based protection scheme for PV integrated microgrid under solar irradiance intermittency using deep convolutional neural network. Int. J. Electr. Power Energy Syst. 2020, 116, 105576. [Google Scholar] [CrossRef]
- Mani, M.; Pillai, R. Impact of dust on solar photovoltaic (PV) performance: Research status, challenges and recommendations. Renew. Sustain. Energy Rev. 2010, 14, 3124–3131. [Google Scholar] [CrossRef]
- Sulaiman, S.A.; Singh, A.K.; Mokhtar, M.M.M.; Bou-Rabee, M.A. Influence of Dirt Accumulation on Performance of PV Panels. Energy Procedia 2014, 50, 50–56. [Google Scholar] [CrossRef] [Green Version]
- Hussain, A.; Batra, A.; Pachauri, R. An experimental study on effect of dust on power loss in solar photovoltaic module. Renewables 2017, 4, 9. [Google Scholar] [CrossRef]
- Roumpakias, E.; Stamatelos, T. Surface Dust and Aerosol Effects on the Performance of Grid-Connected Photovoltaic Systems. Sustainability 2020, 12, 569. [Google Scholar] [CrossRef] [Green Version]
- Salamah, T.; Ramahi, A.; Alamara, K.; Juaidi, A.; Abdallah, R.; Abdelkareem, M.A.; Amer, E.C.; Olabi, A.G. Effect of dust and methods of cleaning on the performance of solar PV module for different climate regions: Comprehensive review. Sci. Total Environ. 2022, 827, 154050. [Google Scholar] [CrossRef]
- Bergin, M.H.; Ghoroi, C.; Dixit, D.; Schauer, J.J.; Shindell, D.T. Large Reductions in Solar Energy Production Due to Dust and Particulate Air Pollution. Environ. Sci. Technol. Lett. 2017, 4, 339–344. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Wagner, F.; Peng, W.; Yang, J.; Mauzerall, D.L. Reduction of solar photovoltaic resources due to air pollution in China. Proc. Natl. Acad. Sci. USA 2017, 114, 11867–11872. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Son, J.; Jeong, S.; Park, H.; Park, C.E. The effect of particulate matter on solar photovoltaic power generation over the Republic of Korea. Environ. Res. Lett. 2020, 15, 084004. [Google Scholar] [CrossRef]
- Stutz, B.; Le Pierres, N.; Kuznik, F.; Johannes, K.; Palomo Del Barrio, E.; Bédécarrats, J.P.; Gibout, S.; Marty, P.; Zalewski, L.; Soto, J.; et al. Storage of thermal solar energy. Comptes Rendus Phys. 2017, 18, 401–414. [Google Scholar] [CrossRef]
- Akkurt, N.; Aghakhani, S.; Mahmoud, M.Z.; Tag El Din, E.M. The influence of battery distance on a hybrid air-cooled cylindrical lithium-ion battery phase change material thermal management system for storing solar energy. J. Energy Storage 2022, 52, 104873. [Google Scholar] [CrossRef]
- Tao, J.; Yu, S. Review on feasible recycling pathways and technologies of solar photovoltaic modules. Sol. Energy Mater. Sol. Cells 2015, 141, 108–124. [Google Scholar] [CrossRef]
- Latunussa, C.E.; Ardente, F.; Blengini, G.A.; Mancini, L. Life Cycle Assessment of an innovative recycling process for crystalline silicon photovoltaic panels. Sol. Energy Mater. Sol. Cells 2016, 156, 101–111. [Google Scholar] [CrossRef]
- Perez-Gallardo, J.; Azzaro-Pantel, C.; Astier, S.A. Multi-objective Framework for Assessment of Recycling Strategies for Photovoltaic Modules based on Life Cycle Assessment. Waste Biomass Valor 2018, 9, 147–159. [Google Scholar] [CrossRef]
- Daljit Singh, J.K.; Molinari, G.; Bui, J.; Soltani, B.; Rajarathnam, G.P.; Abbas, A. Life Cycle Assessment of Disposed and Recycled End-of-Life Photovoltaic Panels in Australia. Sustainability 2021, 13, 11025. [Google Scholar] [CrossRef]
- Majewski, P.; Al-shammari, W.; Dudley, M.; Jit, J.; Lee, S.H.; Myoung-Kug, K.; Sung-Jim, K. Recycling of solar PV panels- product stewardship and regulatory approaches. Energy Policy 2021, 149, 112062. [Google Scholar] [CrossRef]
- Bo, C.; Chengbin, F.; Shangshang, C.; Hangyu, G.; Xun, X.; Jinsong, H. Recycling lead and transparent conductors from perovskite solar modules. Nat. Commun. 2021, 12, 5859. [Google Scholar] [CrossRef]
- Franco, M.A.; Groesser, S.N. A Systematic Literature Review of the Solar Photovoltaic Value Chain for a Circular Economy. Sustainability 2021, 13, 9615. [Google Scholar] [CrossRef]
- Phuangpornpitak, N.; Tia, S. Opportunities and Challenges of Integrating Renewable Energy in Smart Grid System. Energy Procedia 2013, 34, 282–290. [Google Scholar] [CrossRef] [Green Version]
- Nwaigwe, K.; Mutabilwa, P.; Dintwa, E. An overview of solar power (PV systems) integration into electricity grids. Mater. Sci. Energy Technol. 2019, 2, 629–633. [Google Scholar] [CrossRef]
- David, T.M.; Silva Rocha Rizol, P.M.; Guerreiro Machado, M.A.; Buccieri, G.P. Future research tendencies for solar energy management using a bibliometric analysis, 2000–2019. Heliyon 2020, 6, e04452. [Google Scholar] [CrossRef]
- Kharrazi, A.; Sreeram, V.; Mishra, Y. Assessment techniques of the impact of grid-tied rooftop photovoltaic generation on the power quality of low voltage distribution network—A review. Renew. Sustain. Energy Rev. 2020, 120, 109643. [Google Scholar] [CrossRef]
- Salem, W.; Ibrahim, W.G.; Abdelsadek, A.M.; Nafeh, A.A. Grid connected photovoltaic system impression on power quality of low voltage distribution system. Cogent Eng. 2022, 9, 2044576. [Google Scholar] [CrossRef]
- Fachrizal, R.; Ramadhani, U.H.; Munkhammar, J.; Widén, J. Combined PV–EV hosting capacity assessment for a residential LV distribution grid with smart EV charging and PV curtailment. Sustain. Energy Grids Netw. 2021, 26, 100445. [Google Scholar] [CrossRef]
- Soto, E.A.; Bosman, L.B.; Wollega, E.; Leon-Salas, W.D. Analysis of Grid Disturbances Caused by Massive Integration of Utility Level Solar Power Systems. Eng 2022, 3, 18. [Google Scholar] [CrossRef]
- Uroic, T.; Jasak, H. Block-selective algebraic multigrid for implicitly coupled pressure-velocity system. Comput. Fluids 2018, 167, 100–110. [Google Scholar] [CrossRef]
- Drikakis, D.; Rider, J. High-Resolution Methods for Incompressible and Low-Speed Flows; Springer: Berlin/Heidelberg, Germany, 2004; Volume 1. [Google Scholar] [CrossRef]
- Besson, J.; Foerch, R. Large scale Object-Oriented Finite Element code design. Comput. Methods Appl. Mech. Engng 1997, 142, 165–187. [Google Scholar] [CrossRef]
- Zimmermann, T.; Eyheramendy, D. Object-Oriented Finite Elements I. Principles of Symbolic Derivations and Automatic Programming. Comput. Methods Applied Mech. Eng. 1996, 132, 259–276. [Google Scholar] [CrossRef]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A Tensorial Approach to Computational Continuum Mechanics using Object Orientated Techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Antoniadis, A.F.; Drikakis, D.; Farmakis, P.S.; Fu, L.; Kokkinakis, I.; Nogueira, X.; Silva, P.A.; Skote, M.; Titarev, V.; Tsoutsanis, P. UCNS3D: An open-source high-order finite-volume unstructured CFD solver. Comput. Phys. Commun. 2022, 279, 108453. [Google Scholar] [CrossRef]
- Blazek, J. Computational Fluid Dynamics: Principles and Applications; Butterworth-Heinemann: Oxford, UK, 2015. [Google Scholar]
- Boris, J.; Grinstein, F.; Oran, E.; Kolbe, R. New insights into large eddy simulation. Fluid Dyn. Res. 1992, 10, 199–228. [Google Scholar] [CrossRef]
- Grinstein, F.F.; Margolin, L.G.; Rider, W.J. Implicit Large Eddy Simulation: Computing Turbulent Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Drikakis, D. Advances in turbulent flow computations using high-resolution methods. Prog. Aerosp. Sci. 2003, 39, 405–424. [Google Scholar] [CrossRef]
- Drikakis, D.; Hahn, M.; Mosedale, A.; Thornber, B. Large eddy simulation using high-resolution and high-order methods. Phil. Trans. Roy. Soc. A 2009, 367, 2985–2998. [Google Scholar] [CrossRef]
- Rider, W.; Margolin, L. From numerical analysis to implicit subgrid turbulence modeling. In Proceedings of the 16th AIAA Computational Fluid Dynamics Conference, Orlando, FL, USA, 23–26 June 2003; pp. 2003–4101. [Google Scholar] [CrossRef]
- Margolin, L.G.; Rider, W.J. The design and construction of implicit LES models. Int. J. Numer. Methods Fluids 2005, 47, 1173–1179. [Google Scholar] [CrossRef]
- Margolin, L.G.; Rider, W.J.; Grinstein, F.F. Modeling turbulent flow with implicit LES. J. Turbul. 2006, 7, 27. [Google Scholar] [CrossRef]
- Fureby, C.; Grinstein, F.F. Recent progress on MILES for high Reynolds number flows. J. Fluids Eng. 2002, 124, 848–861. [Google Scholar] [CrossRef]
- Grinstein, F.F.; Fureby, C.; DeVore, C.R. On MILES based on flux-limiting algorithms. Int. J. Numer. Methods Fluids 2005, 47, 1043–1051. [Google Scholar] [CrossRef]
- Bose, S.T.; Park, G.I. Wall-Modeled Large-Eddy Simulation for Complex Turbulent Flows. Annu. Rev. Fluid Mech. 2018, 50, 535–561. [Google Scholar] [CrossRef] [PubMed]
- Spalart, P.; Jou, W.; Strelets, M.; Allmaras, S. Comments of feasibility of LES for wings, and on a hybrid RANS/LES approach. In Proceedings of the International Conference on DNS/LES, Ruston, LA, USA, 4–8 August 1997. [Google Scholar]
- Spalart, P.R. Detached-Eddy Simulation. Annu. Rev. Fluid Mech. 2009, 41, 181–202. [Google Scholar] [CrossRef]
- Menter, F.R. Review of the shear-stress transport turbulence model experience from an industrial perspective. Int. J. Comput. Fluid Dyn. 2009, 23, 305–316. [Google Scholar] [CrossRef]
- Jiang, L.; Tabor, G.; Gao, G. A new turbulence model for separated flows. Int. J. Comp. Fluid Dyn. 2011, 25, 427–438. [Google Scholar] [CrossRef]
- Speziale, C.G. Analytical Methods for the Development of Reynolds-Stress Closures in Turbulence. Ann. Rev. Fluid Mech. 1991, 23, 107–157. [Google Scholar] [CrossRef]
- Wilcox, D.C. Simulating transition with a two-equation turbulence model. AIAA.J. 1994, 32, 247–255. [Google Scholar] [CrossRef]
- Balachandar, S.; Eaton, J.K. Turbulent Dispersed Multiphase Flow. Annu. Rev. Fluid Mech. 2010, 42, 111–133. [Google Scholar] [CrossRef]
- Fox, R.O. Large-Eddy-Simulation Tools for Multiphase Flows. Annu. Rev. Fluid Mech. 2012, 44, 47–76. [Google Scholar] [CrossRef]
- Yeoh, G.H.; Tu, J. Computational Techniques for Multiphase Flows, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Roekaerts, D.; Vervisch, L. (Eds.) Computational Fluid Dynamics of Turbulent Combustion; BPG, ERCOFTAC: Vienna, Austria, 2015. [Google Scholar]
- Sommerfeld, M.; van Wachem, B.; Oliemans, R. (Eds.) Best Practice Guidelines for Computational Fluid Dynamics of Dispersed Multi-Phase Flows; BPG, ERCOFTAC: Vienna, Austria, 2008. [Google Scholar]
- Peters, B.; Baniasadi, M.; Baniasadi, M.; Besseron, X.; Donoso, A.E.; Mohseni, M.; Pozzetti, G. XDEM multi-physics and multi-scale simulation technology: Review of DEM–CFD coupling, methodology and engineering applications. Particuology 2019, 44, 176–193. [Google Scholar] [CrossRef] [Green Version]
- Drew, D.A. Mathematical Modelling of Two-Phase Flow. Ann. Rev. Fluid Mech. 1983, 15, 261–291. [Google Scholar] [CrossRef]
- Fox, R.O. On multiphase turbulence models for collisional fluid–particle flows. J. Fluid Mech. 2014, 742, 368–424. [Google Scholar] [CrossRef]
- Riella, M.; Kahraman, R.; Tabor, G. Reynolds-Averaged Two-Fluid Model prediction of moderately dilute fluid-particle flow over a backward-facing step. Int. J. Multiph. Flow 2018, 106, 95–108. [Google Scholar] [CrossRef]
- Riella, M.; Kahraman, R.; Tabor, G.R. Fully coupled pressure-based two-fluid solver for the solution of turbulent fluid-particle systems. Submitt. J. Comp. Phys 2019, 192, 104275. [Google Scholar] [CrossRef]
- Pasari, S.; Nandigama, V.S.S.K. Statistical Modeling of Solar Energy. In Enhancing Future Skills and Entrepreneurship; Sangwan, K.S., Herrmann, C., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 157–165. [Google Scholar]
- Bourdoucen, H.; Gastli, A. Analytical Modelling and Simulation of Photovoltaic Panels and Arrays. J. Eng. Res. 2007, 4, 75–81. [Google Scholar] [CrossRef] [Green Version]
- Campana, P.E.; Li, H.; Yan, J. Dynamic modelling of a PV pumping system with special consideration on water demand. Appl. Energy 2013, 112, 635–645. [Google Scholar] [CrossRef] [Green Version]
- Vogt, M.R.; Holst, H.; Winter, M.; Brendel, R.; Altermatt, P.P. Numerical Modeling of c-Si PV Modules by Coupling the Semiconductor with the Thermal Conduction, Convection and Radiation Equations. Energy Procedia 2015, 77, 215–224. [Google Scholar] [CrossRef] [Green Version]
- Premalatha, N.; Valan Arasu, A. Prediction of solar radiation for solar systems by using ANN models with different back propagation algorithms. J. Appl. Res. Technol. 2016, 14, 206–214. [Google Scholar] [CrossRef] [Green Version]
- Vinod; Kumar, R.; Singh, S. Solar photovoltaic modeling and simulation: As a renewable energy solution. Energy Rep. 2018, 4, 701–712. [Google Scholar] [CrossRef]
- Lee, M.; Hong, T. Hybrid agent-based modeling of rooftop solar photovoltaic adoption by integrating the geographic information system and data mining technique. Energy Convers. Manag. 2019, 183, 266–279. [Google Scholar] [CrossRef]
- Mitchell, T.M. Machine Learning; McGraw Hill: Burr Ridge, IL, USA, 1997; Volume 45, pp. 870–877. [Google Scholar]
- Xie, T.; Ghiaasiaan, S.; Karrila, S. Artificial neural network approach for flow regime classification in gas–liquid–fiber flows based on frequency domain analysis of pressure signals. Chem. Eng. Sci. 2004, 59, 2241–2251. [Google Scholar] [CrossRef]
- Al-Rawahi, N.; Meribout, M.; Al-Naamany, A.; Al-Bimani, A.; Meribout, A. A neural network algorithm for density measurement of multiphase flow. Multiph. Sci. Technol. 2012, 24, 89–103. [Google Scholar] [CrossRef]
- Asproulis, N.; Drikakis, D. An artificial neural network-based multiscale method for hybrid atomistic-continuum simulations. Microfluid. Nanofluidics 2013, 15, 559–574. [Google Scholar] [CrossRef]
- Lee, C.; Kim, J.; Babcock, D.; Goodman, R. Application of neural networks to turbulence control for drag reduction. Phys. Fluids 1997, 9, 1740–1747. [Google Scholar] [CrossRef] [Green Version]
- Ghaboussi, J.; Garrett, J., Jr.; Wu, X. Knowledge-based modeling of material behavior with neural networks. J. Eng. Mech. 1991, 117, 132–153. [Google Scholar] [CrossRef]
- Unger, J.F.; Könke, C. Coupling of scales in a multiscale simulation using neural networks. Comput. Struct. 2008, 86, 1994–2003. [Google Scholar] [CrossRef]
- Unger, J.F.; Könke, C. Neural networks as material models within a multiscale approach. Comput. Struct. 2009, 87, 1177–1186. [Google Scholar] [CrossRef]
- Waszczyszyn, Z.; Ziemiański, L. Neural networks in mechanics of structures and materials–new results and prospects of applications. Comput. Struct. 2001, 79, 2261–2276. [Google Scholar] [CrossRef]
- Zimmerman, D.C.; Hasselman, T.; Anderson, M. Approximation and calibration of nonlinear structural dynamics. Nonlinear Dyn. 2005, 39, 113–128. [Google Scholar] [CrossRef]
- Kerschen, G.; Worden, K.; Vakakis, A.F.; Golinval, J.C. Past, present and future of nonlinear system identification in structural dynamics. Mech. Syst. Signal Process. 2006, 20, 505–592. [Google Scholar] [CrossRef] [Green Version]
- Asproulis, N.; Drikakis, D. Nanoscale materials modelling using neural networks. J. Comput. Theor. Nanosci. 2009, 6, 514–518. [Google Scholar] [CrossRef]
- Srivastava, A.N.; Han, J. Machine Learning and Knowledge Discovery for Engineering Systems Health Management; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Napolitano, M.R.; Chen, C.I.; Naylor, S. Aircraft failure detection and identification using neural networks. J. Guid. Control. Dyn. 1993, 16, 999–1009. [Google Scholar] [CrossRef]
- Napolitano, M.R.; Neppach, C.; Casdorph, V.; Naylor, S.; Innocenti, M.; Silvestri, G. Neural-network-based scheme for sensor failure detection, identification, and accommodation. J. Guid. Control. Dyn. 1995, 18, 1280–1286. [Google Scholar] [CrossRef]
- Napolitano, M.R.; An, Y.; Seanor, B.A. A fault tolerant flight control system for sensor and actuator failures using neural networks. Aircr. Des. 2000, 3, 103–128. [Google Scholar] [CrossRef]
- Chen, Y.; Lee, M. Neural networks-based scheme for system failure detection and diagnosis. Math. Comput. Simul. 2002, 58, 101–109. [Google Scholar] [CrossRef]
- Nanduri, A.; Sherry, L. Anomaly detection in aircraft data using Recurrent Neural Networks (RNN). In Proceedings of the 2016 Integrated Communications Navigation and Surveillance (ICNS), Herndon, VA, USA, 19–21 April 2016; IEEE: Piscataway, NJ, USA, 2016; p. 5C2-1. [Google Scholar]
- Esau, I. On application of artificial neural network methods in large-eddy simulations with unresolved urban surfaces. Mod. Appl. Sci. 2010, 4, 3. [Google Scholar] [CrossRef] [Green Version]
- Paez, T.L.; Hunter, N. Dynamical System Modeling via Signal Reduction and Neural Network Simulation; Technical Report; Sandia National Labs.: Albuquerque, NM, USA, 1997. [Google Scholar]
- Smaoui, N. A Model for the Unstable Manifold of the Bursting Behavior in the 2D Navier–Stokes Flow. SIAM J. Sci. Comput. 2001, 23, 824–839. [Google Scholar] [CrossRef]
- Smaoui, N.; Al-Enezi, S. Modelling the dynamics of nonlinear partial differential equations using neural networks. J. Comput. Appl. Math. 2004, 170, 27–58. [Google Scholar] [CrossRef] [Green Version]
- Lin, H.; Chen, W.; Tsutsumi, A. Long-term prediction of nonlinear hydrodynamics in bubble columns by using artificial neural networks. Chem. Eng. Process. Process Intensif. 2003, 42, 611–620. [Google Scholar] [CrossRef]
- Bakker, R.; De Korte, R.; Schouten, J.; Van Den Bleek, C.; Takens, F. Neural networks for prediction and control of chaotic fluidized bed hydrodynamics: A first step. Fractals 1997, 5, 523–530. [Google Scholar] [CrossRef]
- Bakker, R.; Schouten, J.C.; Giles, C.L.; Takens, F.; Bleek, C.M.v.d. Learning chaotic attractors by neural networks. Neural Comput. 2000, 12, 2355–2383. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ladický, L.U.; Jeong, S.; Solenthaler, B.; Pollefeys, M.; Gross, M. Data-driven fluid simulations using regression forests. ACM Trans. Graph. 2015, 34, 199. [Google Scholar] [CrossRef]
- Wang, Z.; Xiao, D.; Fang, F.; Govindan, R.; Pain, C.C.; Guo, Y. Model identification of reduced order fluid dynamics systems using deep learning. Int. J. Numer. Methods Fluids 2018, 86, 255–268. [Google Scholar] [CrossRef]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016, 113, 3932–3937. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lui, H.F.; Wolf, W.R. Construction of reduced-order models for fluid flows using deep feedforward neural networks. J. Fluid Mech. 2019, 872, 963–994. [Google Scholar] [CrossRef] [Green Version]
- Pan, S.; Duraisamy, K. Long-time predictive modeling of nonlinear dynamical systems using neural networks. Complexity 2018, 2018, 4801012. [Google Scholar] [CrossRef]
- Owhadi, H. Bayesian numerical homogenization. Multiscale Model. Simul. 2015, 13, 812–828. [Google Scholar] [CrossRef] [Green Version]
- Raissi, M.; Karniadakis, G.E. Hidden physics models: Machine learning of nonlinear partial differential equations. J. Comput. Phys. 2018, 357, 125–141. [Google Scholar] [CrossRef] [Green Version]
- Baydin, A.G.; Pearlmutter, B.A.; Radul, A.A.; Siskind, J.M. Automatic differentiation in machine learning: A survey. J. Mach. Learn. Res. 2018, 18, 1–43. [Google Scholar]
- Scholten, D.; Bosman, R. The geopolitics of renewables; exploring the political implications of renewable energy systems. Technol. Forecast. Soc. Change 2016, 103, 273–283. [Google Scholar] [CrossRef] [Green Version]
- Blondeel, M.; Bradshaw, M.J.; Bridge, G.; Kuzemko, C. The geopolitics of energy system transformation: A review. Geography Compass 2021, 15, e12580. [Google Scholar] [CrossRef]
- Su, C.W.; Khan, K.; Umar, M.; Zhang, W. Does renewable energy redefine geopolitical risks? Energy Policy 2021, 158, 112566. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drikakis, D.; Dbouk, T. The Role of Computational Science in Wind and Solar Energy: A Critical Review. Energies 2022, 15, 9609. https://doi.org/10.3390/en15249609
Drikakis D, Dbouk T. The Role of Computational Science in Wind and Solar Energy: A Critical Review. Energies. 2022; 15(24):9609. https://doi.org/10.3390/en15249609
Chicago/Turabian StyleDrikakis, Dimitris, and Talib Dbouk. 2022. "The Role of Computational Science in Wind and Solar Energy: A Critical Review" Energies 15, no. 24: 9609. https://doi.org/10.3390/en15249609
APA StyleDrikakis, D., & Dbouk, T. (2022). The Role of Computational Science in Wind and Solar Energy: A Critical Review. Energies, 15(24), 9609. https://doi.org/10.3390/en15249609






