New Energy Power System Static Security and Stability Region Calculation Research Based on IPSO-RLS Hybrid Algorithm
Abstract
:1. Introduction
- A unique mathematical notion and formulations of the proposed grid and its SSR were presented to improve the proposed new energy power system’s reliability through the study of static security and stability.
- This research developed and integrated the benefits of the IPSO algorithm and the RLS method to determine the crucial security stability operation region of the new energy power system more rapidly and precisely. In addition, a unique hybrid IPSO-RLS algorithm for finding the region of greatest static security and stability was developed.
- The SSSR of the system was fitted and examined by IPSO-RLS, all by different energy in the new energy 118 bus system with varying power output.
2. Static Security and Stability Analysis
2.1. Static Security and Stability Analysis
2.2. SSSR-Surface
- (1)
- Equality constraint
- (2)
- Inequality constraint
3. Methodology
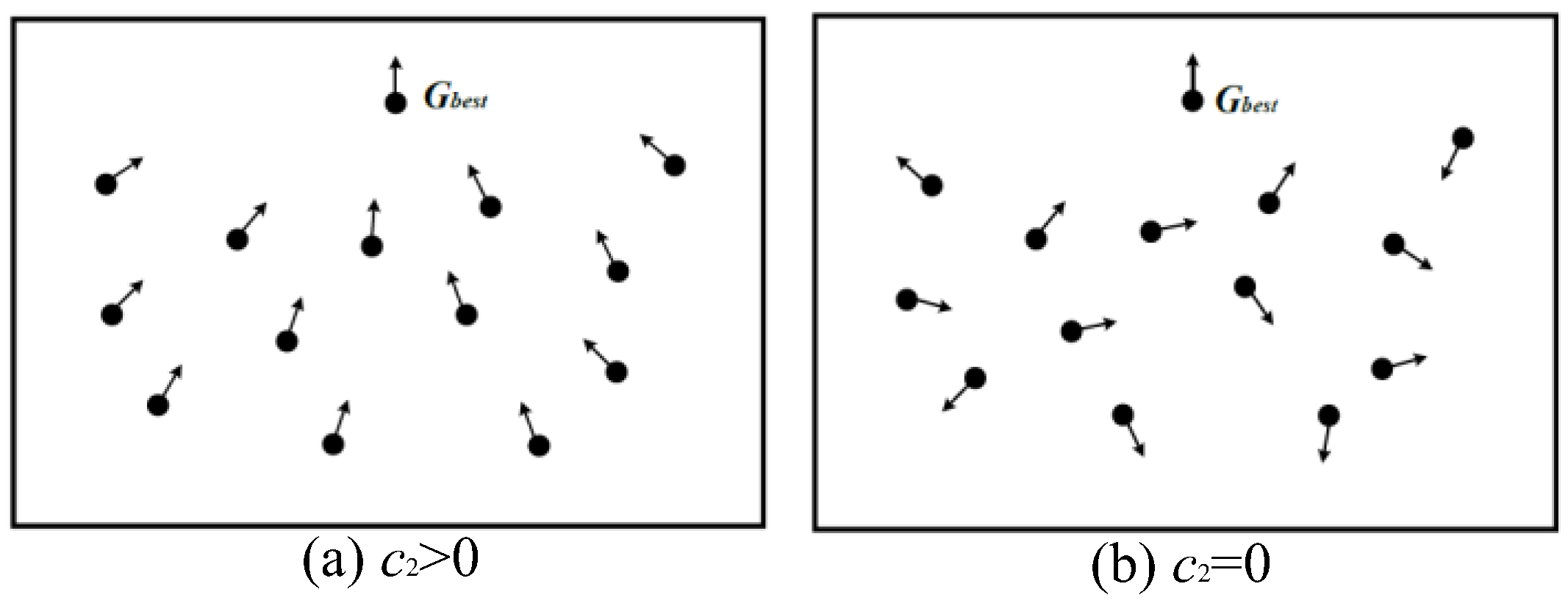
3.1. Overview of IPSO
3.2. RLS Method
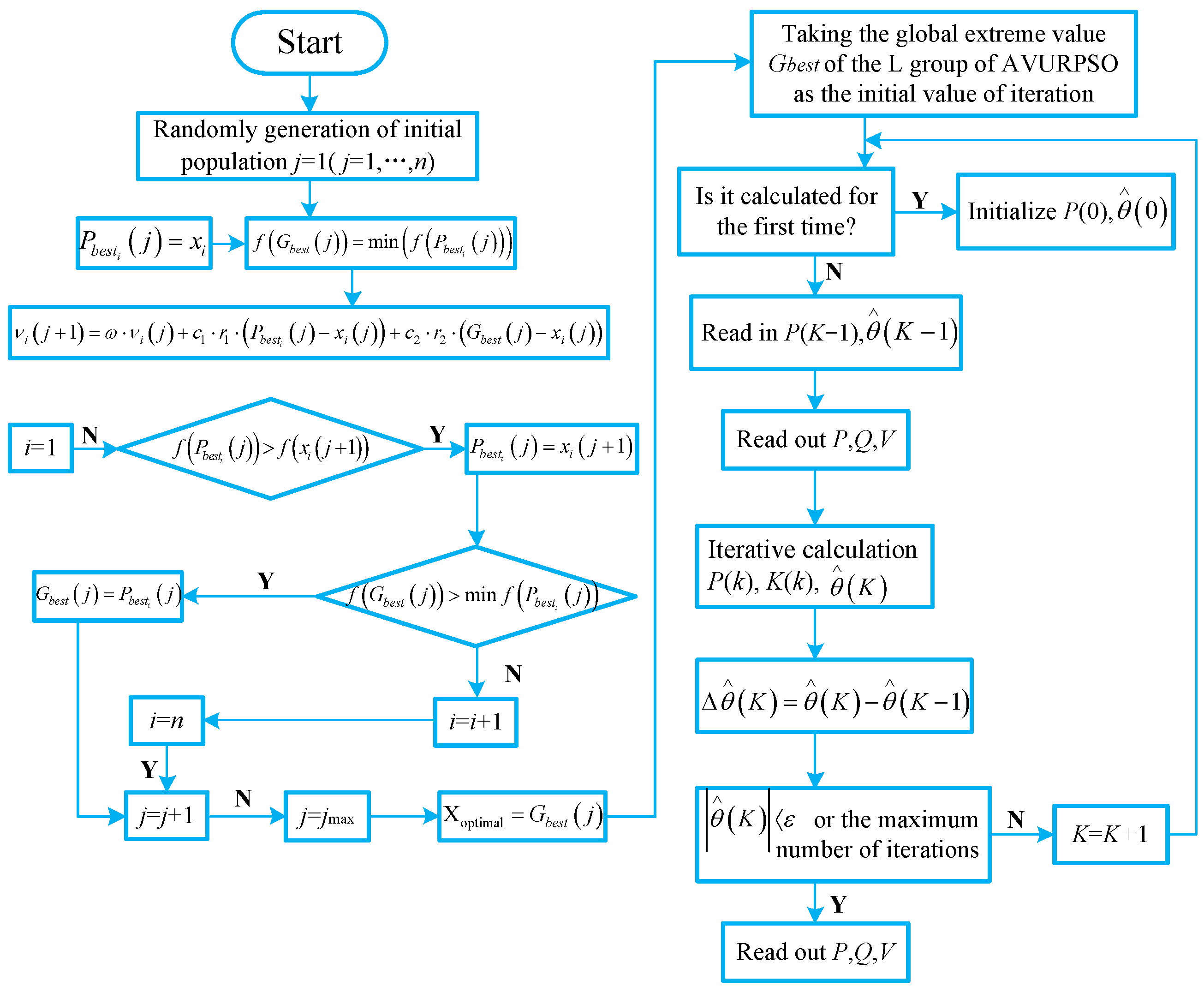
3.3. The Parameter Identification Basis on IPSO-RLS
4. Test System Simulation Results and Discussions
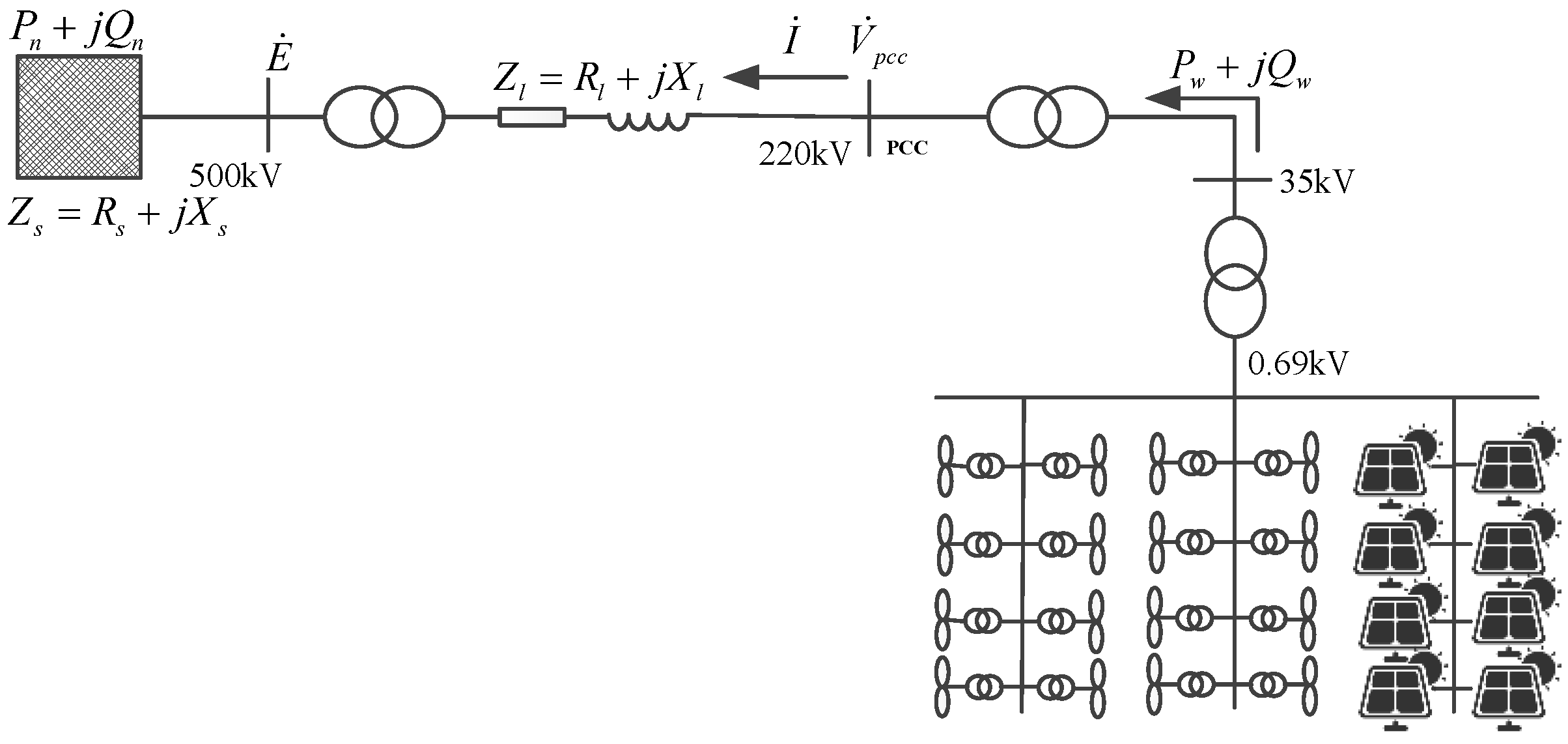
4.1. Introduction of New England 118 Bus System
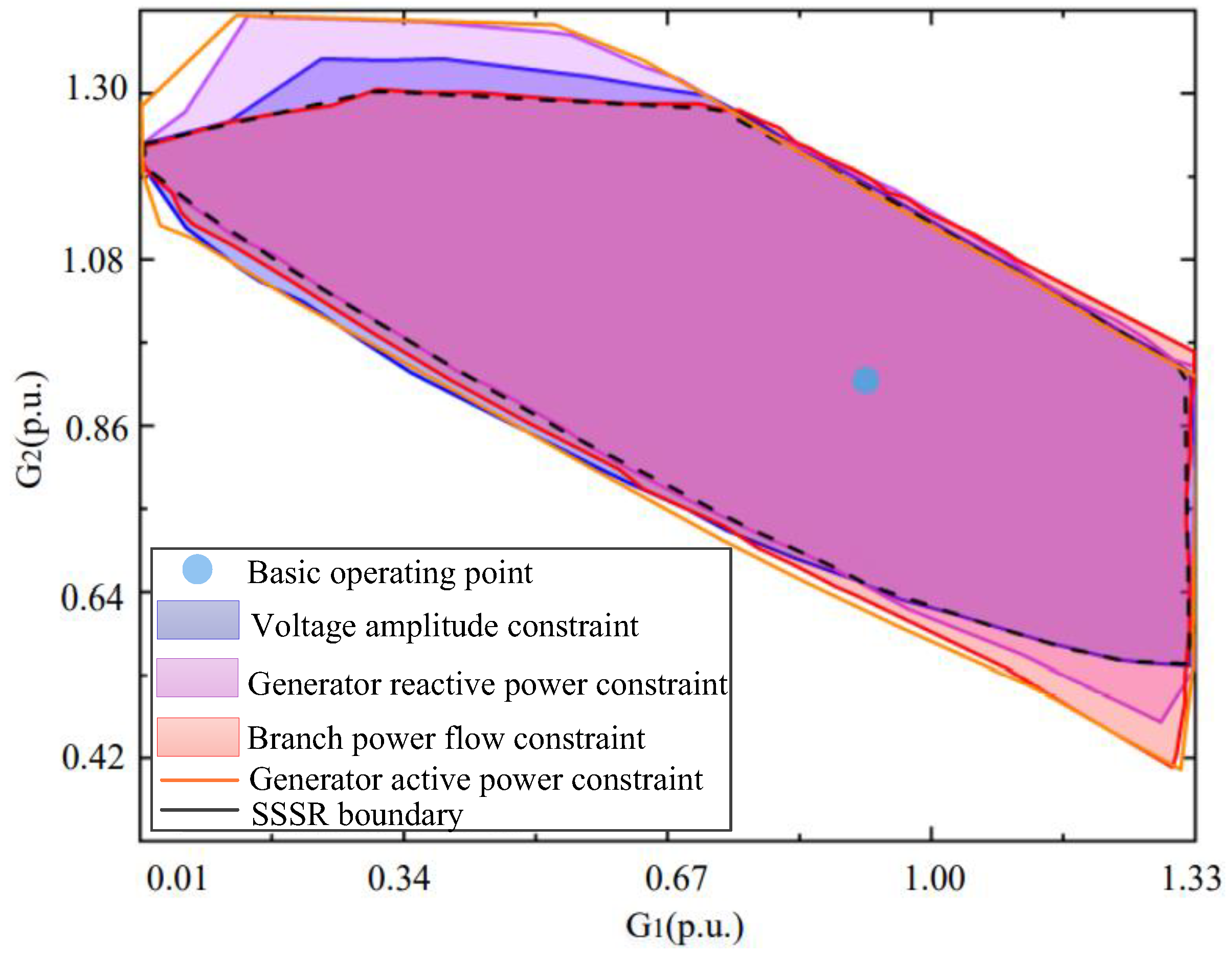
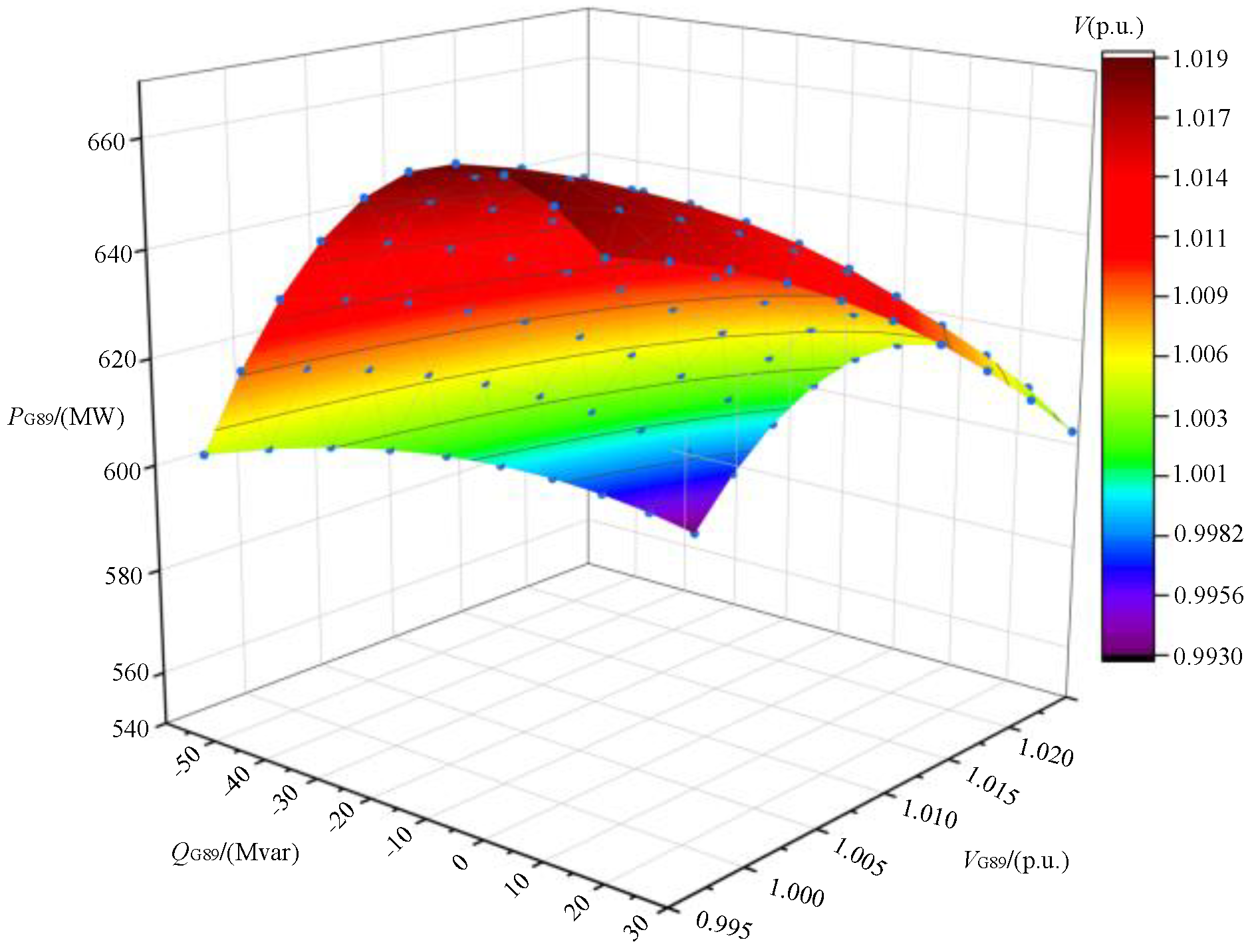
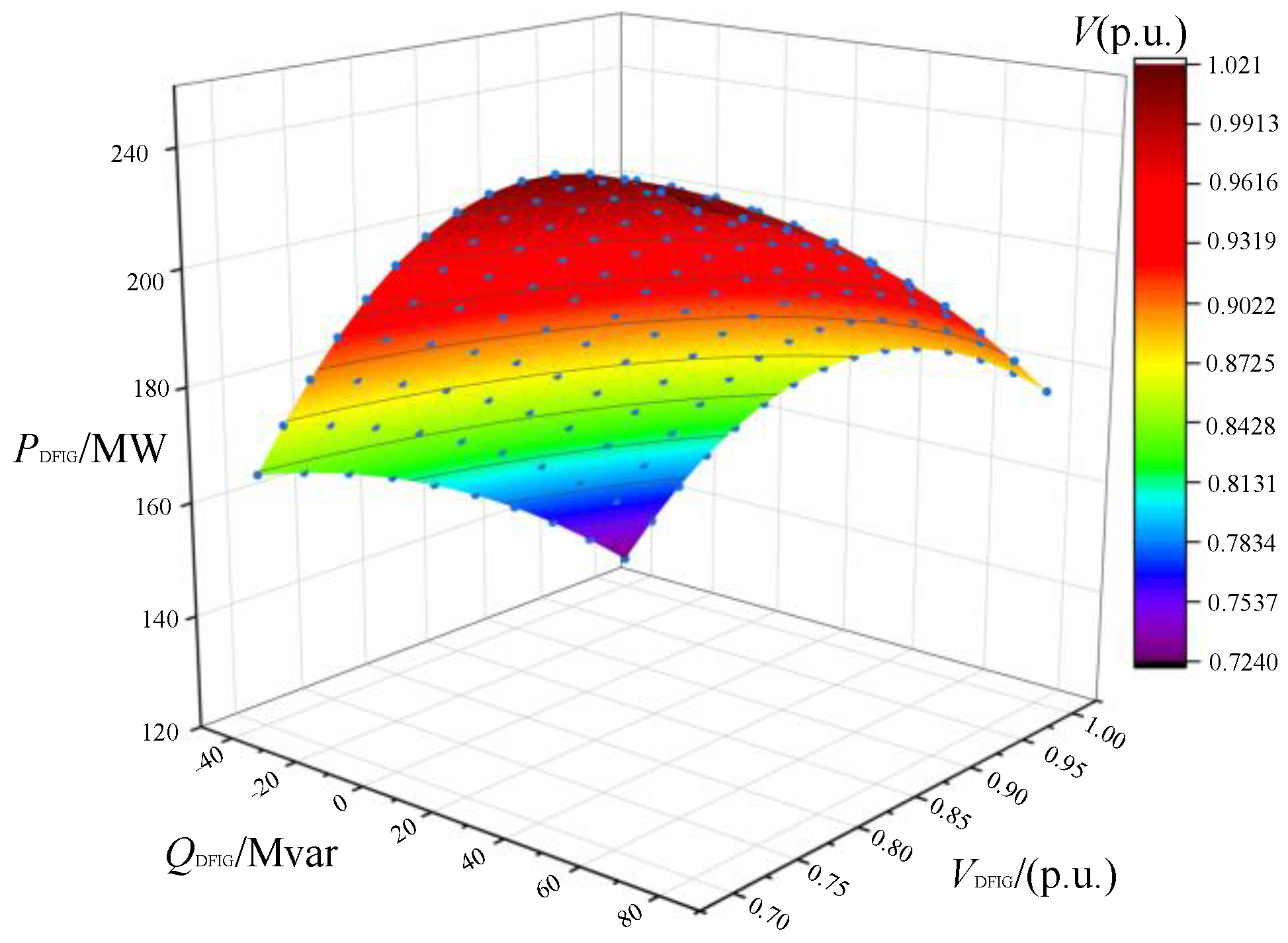
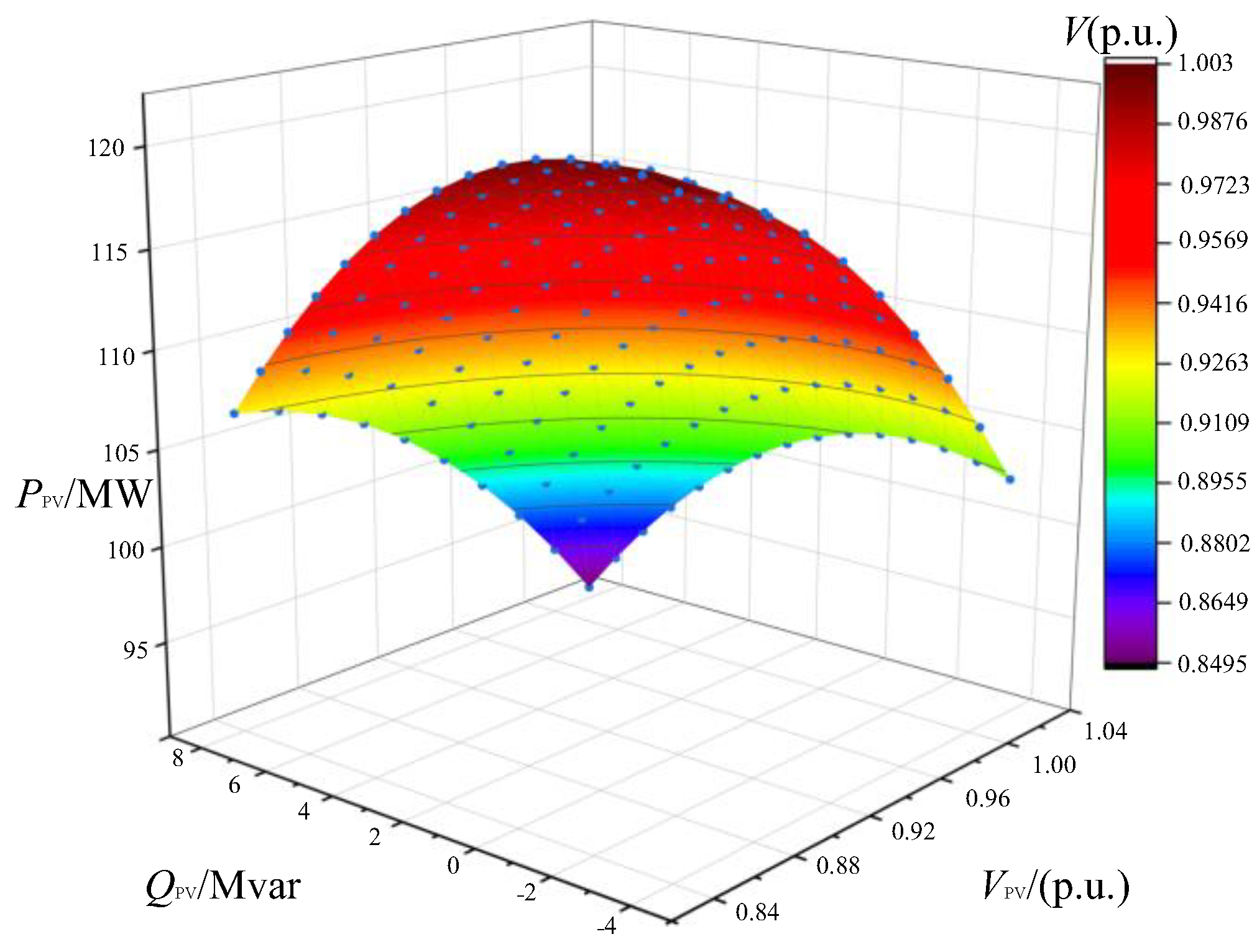
4.2. SSSR-Surface Calculation
4.3. Comparison and Analysis for Conclusions
5. Conclusions
- The new energy power system’s IPSO-RLS static security and stability region critical point search optimization model constructed can greatly reduce the optimization space of the critical point search, while ensuring the accuracy and precision of the searched critical point, achieve an effective dimensionality reduction of the high-dimensional space security and stability region critical point search, and improve the search efficiency of the critical point.
- The critical value, fitting error, and safety distance of different generator operation points are obtained by comparing the static safety and stability regions of three different generator sets. According to the safe distance from the critical value to the operating point, it can be judged whether the point is in the safe and stable region and whether it is a weak link. For traditional generator sets, operation point 15 is a relatively weak link. For wind turbines, operation points 4 and 6 are relatively weak compared with operation points 8, 10, and 15. For photovoltaic units, operation points 4 and 14 are weak links. The fitting error in engineering is less than 5%. The error verification results obtained in this paper are reasonable, which proves that this method can be applied in engineering practice.
- The proposed static security stability region boundary search method based on the IPSO-RLS algorithm effectively avoids the complex optimization process of the traditional “point-by-point method”. While ensuring the error, convergence accuracy, and convergence speed, the effectiveness of the proposed method in obtaining the static security and stability region of the new energy power system is verified, which also lays a foundation for practical research.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhu, H.; Goh, H.H.; Zhang, D.; Ahmad, T.; Liu, H.; Wang, S.; Li, S.; Liu, T.; Dai, H.; Wu, T. Key technologies for smart energy systems: Recent developments, challenges, and research opportunities in the context of carbon neutrality. J. Clean. Prod. 2022, 331, 129809. [Google Scholar] [CrossRef]
- You, Y.; Yi, L. Energy industry Carbon neutrality transition path: Corpus-based AHP-DEMATEL system modelling. Energy Rep. 2022, 8, 25–39. [Google Scholar] [CrossRef]
- Shabani, H.R.; Kalantar, M. Real-time transient stability detection in the power system with high penetration of DFIG-based wind farms using transient energy function. Int. J. Electr. Power Energy Syst. 2021, 133, 107319. [Google Scholar] [CrossRef]
- Boričić, A.; Torres, J.L.R.; Popov, M. Fundamental study on the influence of dynamic load and distributed energy resources on power system short-term voltage stability. Int. J. Electr. Power Energy Syst. 2021, 131, 107141. [Google Scholar] [CrossRef]
- Adetokun, B.B.; Muriithi, C.M.; Ojo, J.O. Voltage stability assessment and enhancement of power grid with increasing wind energy penetration. Int. J. Electr. Power Energy Syst. 2020, 120, 105988. [Google Scholar] [CrossRef]
- Wang, J.; Xu, J.; Liao, S.; Sima, L. Coordinated Optimization of Integrated Electricity-Gas Energy System Considering Uncertainty of Renewable Energy Output. Auto. Elect. Power Syst. 2019, 43, 2–9. [Google Scholar]
- Dong, X.; Tang, Y.; Bu, G.; Shen, C.; Song, G.; Wang, Z.; Gan, D.; Hou, J.; Wang, B.; Zhao, B.; et al. Confronting problem and challenge of large-scale AC-DC hybrid power grid operation. Proc. Chin. Soc. Electr. Eng. 2019, 39, 3107–3119. [Google Scholar]
- Li, B.; Chao, P.; Li, W.; Xu, S.; Liu, X.; Li, Z. Transient overvoltage calculation method of wind power transmission system via UHVDC. Electr. Mach. Control 2021, 25, 11–18. [Google Scholar]
- Tu, J.; Zhang, J.; Liu, M.; Yi, J. Study on Wind Turbine Generators Tripping Caused by HVDC Contingencies of Wind-Thermal-Bundled HVDC Transmission Systems. Power Syst. Technol. 2015, 39, 3333–3338. [Google Scholar]
- Wu, Y.; Hu, M.; Liao, M.; Liu, F.; Xu, C. Risk assessment of renewable energy-based island microgrid using the HFLTS-cloud model method. J. Clean. Prod. 2021, 284, 125362. [Google Scholar] [CrossRef]
- Hnyilicza, E.; Lee, S.; Schweppe, F.C. Steady-State Security Regions: Set-the Oretic Approach. In Proceedings of the Conference of Power Industry Computer Application, New Orleans, LA, USA, 2–4 June 1975; pp. 347–355. [Google Scholar]
- Galiana, J.J.F.D. Quantitative Analysis of Steady State Stability in Power Networks. IEEE Trans. Power Appar. Syst. 1981, 1, 318–326. [Google Scholar]
- Phillipe, V.G.; Saraiva, J.T. State-of-the-art of transmission expansion planning: A survey from restructuring to renewable and distributed electricity markets. Int. J. Elect. Power Energy Syst. 2019, 111, 411–424. [Google Scholar]
- Maihemuti, S.; Wang, W.; Wang, H.; Wu, J. Voltage Security Operation Region Calculation Based on Improved Particle Swarm Optimization and Recursive Least Square Hybrid Algorithm. J. Mod. Power Syst. Clean Energy 2021, 9, 138–147. [Google Scholar] [CrossRef]
- Lin, W.; Jiang, H.; Yang, Z. Time-line security regions in high dimension for renewable accommodations. arXiv 2022, arXiv:10.48550/arXiv.2201.01019. [Google Scholar]
- Chertkov, M.; Backhaus, S.; Lebedev, V. Cascading of fluctuations in interdependent energy infrastructures: Gas-grid coupling. Appl. Energy 2015, 160, 541–551. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Jia, H.; Chiang, H.-D.; Yu, D.C.; Wang, D. Dynamic Modeling and Interaction of Hybrid Natural Gas and Electricity Supply System in Microgrid. IEEE Trans. Power Syst. 2015, 30, 1212–1221. [Google Scholar] [CrossRef]
- Martinez-Mares, A.; Fuerte-Esquivel, C.R. A Unified Gas and Power Flow Analysis in Natural Gas and Electricity Coupled Networks. IEEE Trans. Power Syst. 2012, 27, 2156–2166. [Google Scholar] [CrossRef]
- Kumari, B.A.; Vaisakh, K. Ensuring expected security cost with flexible resources using modified DE algorithm based dynamic optimal power flow. Appl. Soft Comput. 2022, 124, 124–136. [Google Scholar] [CrossRef]
- Tunç, C.; Tunç, O. On the stability, integrability and boundedness analyses of systems of integro-differential equations with time-delay retardation. Rev. Real Acad. Cienc. Exactas Físicas Y Naturales. Ser. A Math. 2021, 115, 1–17. [Google Scholar] [CrossRef]
- Tunç, O.; Tunç, C. Solution estimates to Caputo proportional fractional derivative delay integro-differential equations. Rev. Real Acad. Cienc. Exactas Físicas Y Naturales. Ser. A Math. 2023, 117, 1–13. [Google Scholar] [CrossRef]
- Zeng, X.; Yu, Y.; Huang, C. Steady-state security region (SSR) and its visualization of bulk high voltage power system. In Proceedings of the International Conference on Power System Technology, Kunming, China, 13–17 October 2002; Volume 2, pp. 1259–1263. [Google Scholar] [CrossRef]
- Jun, X.; Yan, C.; Baoqiang, Z. Concavity and convexity of distribution system security region: Theorem proof and determination algorithm. Proc. Chin. Soc. Electr. Eng. 2021, 41, 5153–5167. [Google Scholar]
- Robert, F.; Guvenis, A.; Halpin, T. Statistical power transmission network design. IEEE Trans. Circuits Syst. 1982, 29. [Google Scholar]
- Wu, F.; Kumagai, S. Steady-State Security Regions of Power Systems. IEEE Trans. Circuits Syst. 1982, 29, 703–711. [Google Scholar] [CrossRef]
- Liu, C. A new method for the construction of maximal steady-state security regions of power systems. IEEE Trans. Power Syst. 1986, 1, 19–26. [Google Scholar] [CrossRef]
- Xue, L.; Linwei, Z.; Tao, J. General algorithm for exploring security region boundary in power systems using lagrange multiplier. Proc. Chin. Soc. Electr. Eng. 2021, 41, 5139–5153. [Google Scholar]
- Tao, J.; Zhang, M.; Cui, X.; Li, Y.; Shi, Q. A novel optimization model to explore static voltage stability region boundary in bulk power systems. Trans. China Electrotech. Soc. 2018, 33, 4167–4179. [Google Scholar]
- Yu, Y.; Liu, Y.; Qin, C.; Yang, T. Theory and Method of Power System Integrated Security Region Irrelevant to Operation States: An Introduction. Engineering 2020, 6, 754–777. [Google Scholar] [CrossRef]
- Zhang, Q.; Zheng, H.; Wang, J. A method for calculating static voltage stability margin of power system based on aq bus. Power Syst. Technol. 2019, 43, 714–721. [Google Scholar]
- Xia, S.; Bai, X.; Chen, S.; Guo, Z. Solving for dynamic security region based on Taylor series trajectory sensitivity. Electr. Power Autom. Equip. 2018, 38, 157–164. [Google Scholar]
- Tinoco, R.A.G.; Passos Filho, J.A.; Peres, W.; Henriques, R. A new particle swarm optimization-based methodology for determining online static security regions. Int. Trans. Electr. Energy Syst. 2021, 31, e12790. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, G.; Wang, T. Kernel feature identification based on improved ant colony optimization algorithm for transient stability assessment. Trans. China Electrotech. Soc. 2010, 25, 154–160. [Google Scholar]
- Russell, S.J.; Norvig, P. Artificial Intelligence: A Modern Approach; Pearson Education Limited: London, UK, 2016. [Google Scholar]
- Shuai, H.; Fang, J.; Ai, X.; Wen, J.; He, H. Optimal Real-Time Operation Strategy for Microgrid: An ADP-Based Stochastic Nonlinear Optimization Approach. IEEE Trans. Sustain. Energy 2019, 10, 931–942. [Google Scholar] [CrossRef] [Green Version]
- Sun, M.; Konstantelos, I.; Strbac, G. A deep learning-based feature extraction frame-work for system security assessment. IEEE Trans Smart Grid 2018, 10, 5007–5020. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Y.; Bu, S.; Dong, Z.Y.; Zhang, R. Online power system dynamic security assessment with incomplete PMU measurements: A robust white-box model. IET Gener. Transm. Distrib. 2019, 13, 662–668. [Google Scholar] [CrossRef]
- Gomez, F.R.; Rajapakse, A.D.; Annakkage, U.D.; Fernando, I.T. Support Vector Machine-Based Algorithm for Post-Fault Transient Stability Status Prediction Using Synchronized Measurements. IEEE Trans. Power Syst. 2011, 26, 1474–1483. [Google Scholar] [CrossRef]
- Hou, K.; Shao, G.; Wang, H.; Le Zheng, L.; Zhang, Q.; Wu, S.; Hu, W. Research on practical power system stability analysis algorithm based on modified SVM. Prot. Control. Mod. Power Syst. 2018, 3, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Guan, L. A data mining technique based on pattern discovery and k-Nearest Neighbor classifier for transient stability assessment. Int. Power Eng. Conf. 2007, 118–123. [Google Scholar]
- Zhang, Y.; Xu, Y.; Dong, Z.Y.; Xu, Z.; Wong, K.P. Intelligent Early Warning of Power System Dynamic Insecurity Risk: Toward Optimal Accuracy-Earliness Tradeoff. IEEE Trans. Ind. Inform. 2017, 13, 2544–2554. [Google Scholar] [CrossRef]
- Ren, C.; Xu, Y.; Zhang, Y. Post-disturbance transient stability assessment of power systems towards optimal accuracy-speed tradeoff. Prot. Control. Mod. Power Syst. 2018, 3, 19. [Google Scholar] [CrossRef] [Green Version]
- Acharjee, P. Optimal power flow with UPFC using security constrained self-adaptive differential evolutionary algorithm for restructured power system. Int. J. Electr. Power Energy Syst. 2016, 76, 69–81. [Google Scholar] [CrossRef]
- Maihemuti, S.; Wang, W.; Wang, H.; Wu, J.; Zhang, X. Dynamic Security and Stability Region Under Different Renewable Energy Permeability in IENGS System. IEEE Access 2021, 9, 19800–19817. [Google Scholar] [CrossRef]
- Abdulkhader, H.K.; Jacob, J.; Mathew, A.T. Robust type-2 fuzzy fractional order PID controller for dynamic stability enhancement of power system having RES based microgrid penetration. Int. J. Electr. Power Energy Syst. 2019, 110, 357–371. [Google Scholar] [CrossRef]
- Veerasamy, V.; Wahab, N.I.A.; Ramachandran, R.; Othman, M.L.; Hizam, H.; Devendran, V.S.; Irudayaraj, A.X.R.; Vinayagam, A. Recurrent network based power flow solution for voltage stability assessment and improvement with distributed energy sources. Appl. Energy 2021, 302, 117524. [Google Scholar] [CrossRef]
- Honghai, K.; Fuqing, S.; Yurui, C.; Kai, W.; Zhiyi, H. Reactive power optimization for distribution network system with wind power based on improved multi-objective particle swarm optimization algorithm. Electr. Power Syst. Res. 2022, 213, 108731. [Google Scholar] [CrossRef]
- Haidar, A.M.; Mustafa, M.; Ibrahim, F.A.; Ahmed, I.A. Transient stability evaluation of electrical power system using generalized regression neural networks. Appl. Soft Comput. 2011, 11, 3558–3570. [Google Scholar] [CrossRef]
- Belkacem Mahdad, K. Srairi. Application of a combined superconducting fault current limiter and STATCOM to enhancement of power system transient stability. Phys. C Supercond. 2013, 495, 160–168. [Google Scholar] [CrossRef]
- Rautray, S.; Choudhury, S.; Mishra, S.; Rout, P. A Particle Swarm Optimization based Approach for Power System Transient Stability Enhancement with TCSC. Procedia Technol. 2012, 6, 31–38. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Ju, P.; Wu, F.; Lei, S.; Pan, X. Sequential steady-state security region-based transmission power system resilience enhancement. Renew. Sustain. Energy Rev. 2021, 151, 111533. [Google Scholar] [CrossRef]
- Kyomugisha, R.; Muriithi, C.M.; Edimu, M. Multiobjective optimal power flow for static voltage stability margin improvement. Heliyon 2021, 7, e08631. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, Q.; Li, P. Online prediction and correction control of static voltage stability index based on Broad Learning System. Expert Syst. Appl. 2022, 199, 117184. [Google Scholar] [CrossRef]
- Kenned, Y. Particle swarm optimization. Proc. IEEE Int. Conf. Neural Netw. 1995, 4, 1942–1948. [Google Scholar]
- Jing, X.C.; Bing, L.C. Parameter Identification of Permanent Magnet Synchronous Motor Based on RLS. Small Spec. Electr. Mach. 2012, 40, 30–33. [Google Scholar]
- Singh, S.K.; Sinha, N.; Goswami, A.K.; Nidul, S. Robust estimation of power system harmonics using a hybrid firefly based recursive least square algorithm. Int. J. Electr. Power Energy Syst. 2016, 80, 287–296. [Google Scholar] [CrossRef]
- Reichbach, N.; Kuperman, A. Recursive-least-squares-based real-time estimation of supercapacitor parameters. IEEE Trans. Energy Convers. 2016, 31, 1–3. [Google Scholar] [CrossRef]



| Operation Point | Pcr (p.u.) | Qcr (p.u.) | Vcr (p.u.) | Fitting Curves Error/% | SSSD (p.u.) |
|---|---|---|---|---|---|
| 1 | 0.9312 | 2.8871 | 0.9911 | −0.2017 | 1.5342 |
| 2 | 0.9524 | 1.4586 | 0.9972 | 0.0549 | 2.0311 |
| 3 | 0.9625 | 1.0752 | 0.9989 | −0.3228 | 1.4573 |
| 4 | 0.9690 | 0.9374 | 0.9999 | 0.1859 | 1.0033 |
| 5 | 0.9752 | 0.8505 | 1.0008 | −0.4429 | 2.1595 |
| 6 | 0.9827 | 0.7829 | 1.0017 | 0.3093 | 1.6086 |
| 7 | 0.9931 | 0.7304 | 1.0027 | −0.5601 | 1.9926 |
| 8 | 1.0028 | 0.7172 | 1.0031 | 0.4226 | 2.6413 |
| 9 | 1.0122 | 0.7307 | 1.0031 | −0.6727 | 1.6592 |
| 10 | 1.0216 | 0.7665 | 1.0027 | 0.5235 | 2.1323 |
| 11 | 1.0311 | 0.8241 | 1.0020 | −0.7792 | 1.4323 |
| 12 | 1.0404 | 0.9059 | 1.0010 | 0.6096 | 1.8308 |
| 13 | 1.0495 | 1.0169 | 0.9999 | −0.878 | 1.2709 |
| 14 | 1.0509 | 1.0390 | 0.9997 | 0.6980 | 1.5990 |
| 15 | 1.0463 | 1.9576 | 0.9966 | −0.0622 | 0.9413 |
| Operation Point | Pcr (p.u.) | Qcr (p.u.) | Vcr (p.u.) | Fitting Curves Error/% | SSSD (p.u.) |
|---|---|---|---|---|---|
| 1 | 0.7196 | 0.7163 | 0.7621 | −1.2763 | 1.8258 |
| 2 | 0.9029 | 1.2612 | 0.8389 | 0.2017 | 0.8852 |
| 3 | 1.1996 | 0.8812 | 0.9635 | −1.2407 | 1.7748 |
| 4 | 1.1903 | 1.1832 | 1.0049 | 0.0427 | 0.6101 |
| 5 | 1.1529 | 1.7650 | 1.0590 | −1.2161 | 1.7396 |
| 6 | 1.1306 | 1.5295 | 1.0735 | −0.1512 | 0.6213 |
| 7 | 1.1019 | 1.0500 | 1.0636 | −1.1647 | 1.6662 |
| 8 | 1.0607 | 0.8486 | 1.0550 | −0.3385 | 0.8442 |
| 9 | 1.0254 | 0.7549 | 1.0505 | −1.1257 | 1.6103 |
| 10 | 1.0016 | 0.7132 | 1.0503 | −0.5537 | 0.7921 |
| 11 | 0.9890 | 0.6991 | 1.0524 | −1.0804 | 1.5455 |
| 12 | 0.9854 | 0.7001 | 1.0554 | −0.7543 | 1.0791 |
| 13 | 0.9886 | 0.7086 | 1.0584 | −1.0295 | 1.4726 |
| 14 | 0.9945 | 0.7171 | 1.0601 | −0.9748 | 1.3940 |
| 15 | 0.8261 | 2.0639 | 0.9909 | 0.1756 | 0.7510 |
| Operation Point | Pcr (p.u.) | Qcr (p.u.) | Vcr (p.u.) | Fitting Curves Error/% | SSSD (p.u.) |
|---|---|---|---|---|---|
| 1 | 1.0036 | 0.9034 | 0.9033 | 0.7672 | 2.60478 |
| 2 | 1.0149 | 0.6799 | 0.9822 | −1.0495 | 1.9041 |
| 3 | 0.9905 | 0.9162 | 0.9952 | 0.8154 | 2.4507 |
| 4 | 0.9930 | 0.9684 | 1.0026 | −1.1201 | 0.7842 |
| 5 | 0.9943 | 1.1746 | 1.0085 | 0.8409 | 2.3764 |
| 6 | 0.9953 | 1.5128 | 1.0142 | −1.1797 | 1.6939 |
| 7 | 0.9965 | 1.7546 | 1.0196 | 0.8615 | 2.3198 |
| 8 | 0.9983 | 1.7194 | 1.0216 | −1.2282 | 1.6271 |
| 9 | 1.0000 | 1.6058 | 1.0216 | 0.8566 | 2.3330 |
| 10 | 1.0013 | 1.4786 | 1.0200 | −1.2652 | 1.5795 |
| 11 | 1.0024 | 1.3182 | 1.0172 | 0.8258 | 2.4199 |
| 12 | 1.0033 | 1.1239 | 1.0138 | −1.2908 | 1.5483 |
| 13 | 1.0040 | 0.8990 | 1.0098 | 0.7685 | 2.6003 |
| 14 | 1.0041 | 0.8584 | 1.0091 | −1.3051 | 0.9312 |
| 15 | 0.9990 | 1.0107 | 0.9752 | 0.7042 | 2.8379 |
| Power Units | Algorithms | Vcr (p.u.) | Qcr (p.u.) | Pcr (p.u.) | SSSD (p.u.) |
|---|---|---|---|---|---|
| Synchronous unit | PSO | 0.7794 | 0.6785 | 1.3115 | 1.452 |
| IPSO | 0.9195 | 0.7529 | 1.6387 | 1.599 | |
| IPSO-RLS | 1.0408 | 0.9736 | 1.8372 | 1.826 | |
| Wind power unit | PSO | 0.5185 | 3.7169 | 2.6012 | 1.912 |
| IPSO | 0.7228 | 4.3085 | 2.9887 | 2.178 | |
| IPSO-RLS | 0.8034 | 4.8361 | 3.0613 | 2.422 | |
| PV power unit | PSO | 0.6026 | 1.4287 | 1.6012 | 1.951 |
| IPSO | 0.6974 | 1.5857 | 1.8107 | 2.201 | |
| IPSO-RLS | 0.7829 | 1.732 | 1.9744 | 2.656 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maihemuti, S.; Wang, W.; Wu, J.; Wang, H.; Muhedaner, M. New Energy Power System Static Security and Stability Region Calculation Research Based on IPSO-RLS Hybrid Algorithm. Energies 2022, 15, 9655. https://doi.org/10.3390/en15249655
Maihemuti S, Wang W, Wu J, Wang H, Muhedaner M. New Energy Power System Static Security and Stability Region Calculation Research Based on IPSO-RLS Hybrid Algorithm. Energies. 2022; 15(24):9655. https://doi.org/10.3390/en15249655
Chicago/Turabian StyleMaihemuti, Saniye, Weiqing Wang, Jiahui Wu, Haiyun Wang, and Muladi Muhedaner. 2022. "New Energy Power System Static Security and Stability Region Calculation Research Based on IPSO-RLS Hybrid Algorithm" Energies 15, no. 24: 9655. https://doi.org/10.3390/en15249655
APA StyleMaihemuti, S., Wang, W., Wu, J., Wang, H., & Muhedaner, M. (2022). New Energy Power System Static Security and Stability Region Calculation Research Based on IPSO-RLS Hybrid Algorithm. Energies, 15(24), 9655. https://doi.org/10.3390/en15249655





