Fractal Characterization of Multimodal, Multiscale Images of Shale Rock Fracture Networks
Abstract
:1. Introduction
- Length distribution prevails over fractal geometry, and large fractures dominate global connectivity for:
- Connectivity is controlled by fractures much smaller than the system size when:
- The system is self-similar when the transition between regimes and connectivity properties are scale invariant as
2. Materials and Methods
2.1. Sample Image Dataset
2.2. Sample Descriptions
2.3. Image-Based Fractal Dimension Estimation
2.3.1. Segmentation
2.3.2. Box-Counting Method
2.4. Connectivity Properties
3. Results and Discussion
3.1. Fractal Dimension
3.2. Connectivity
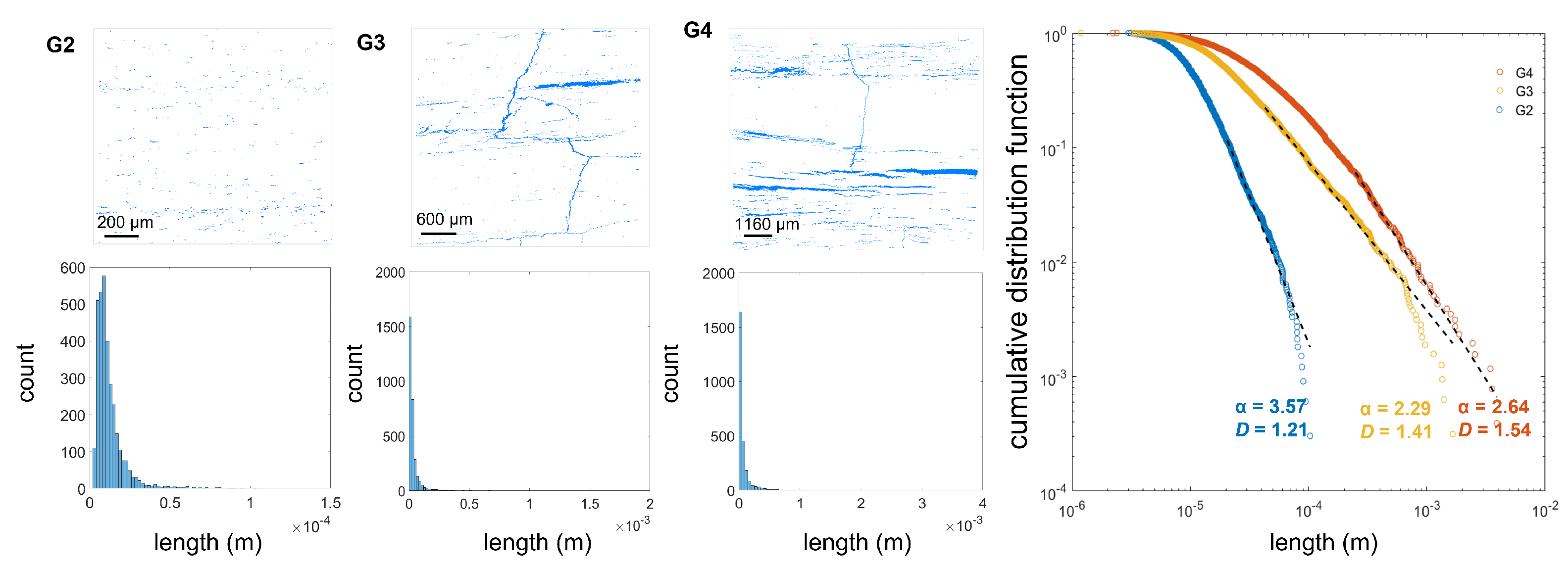
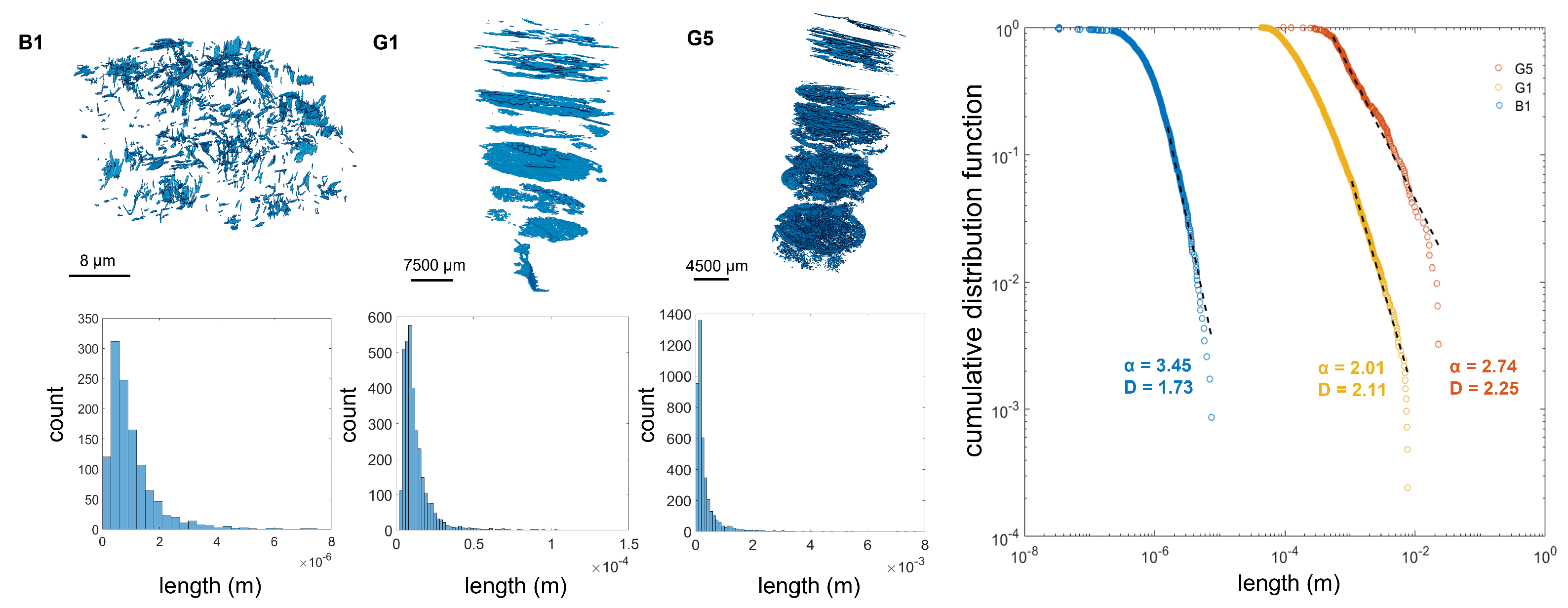
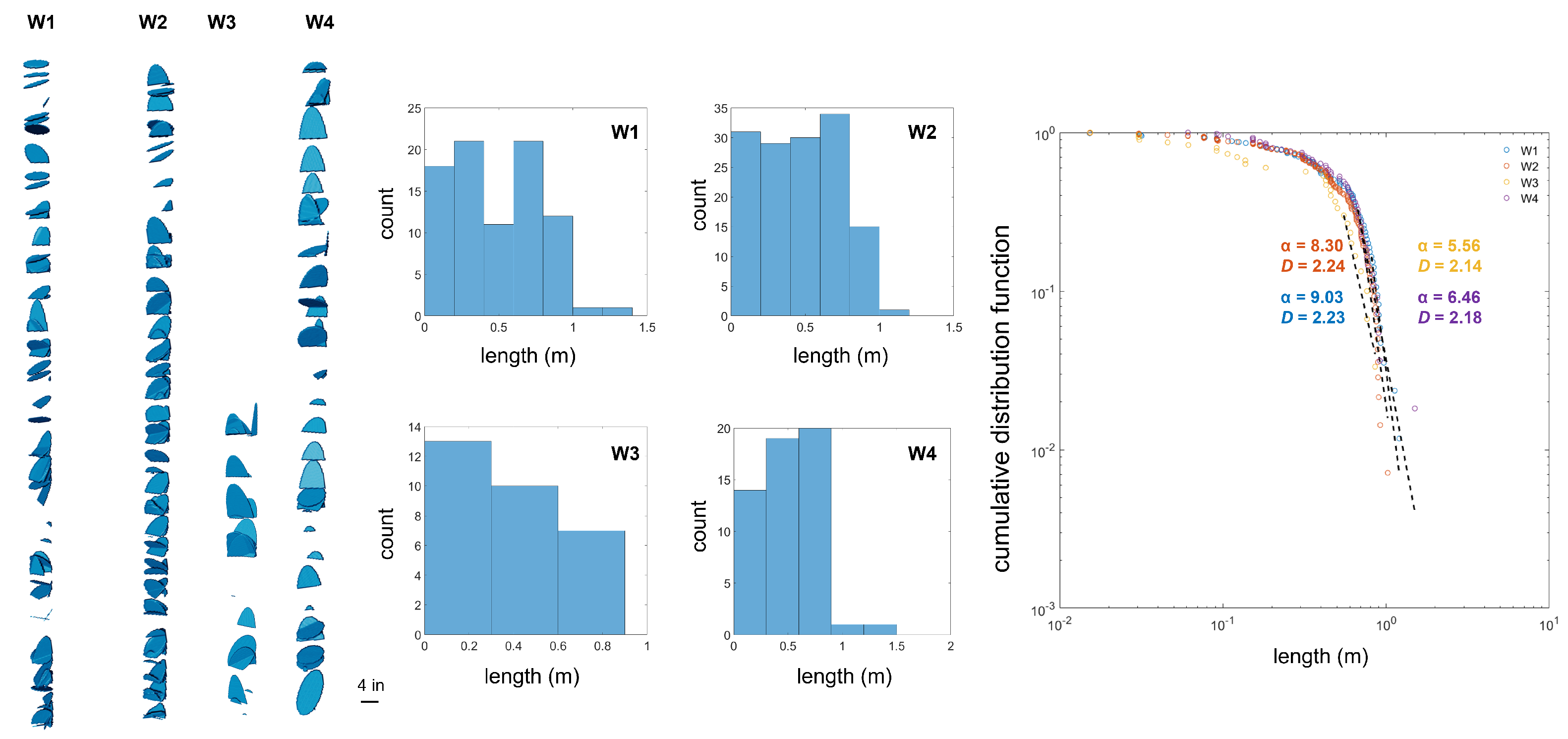
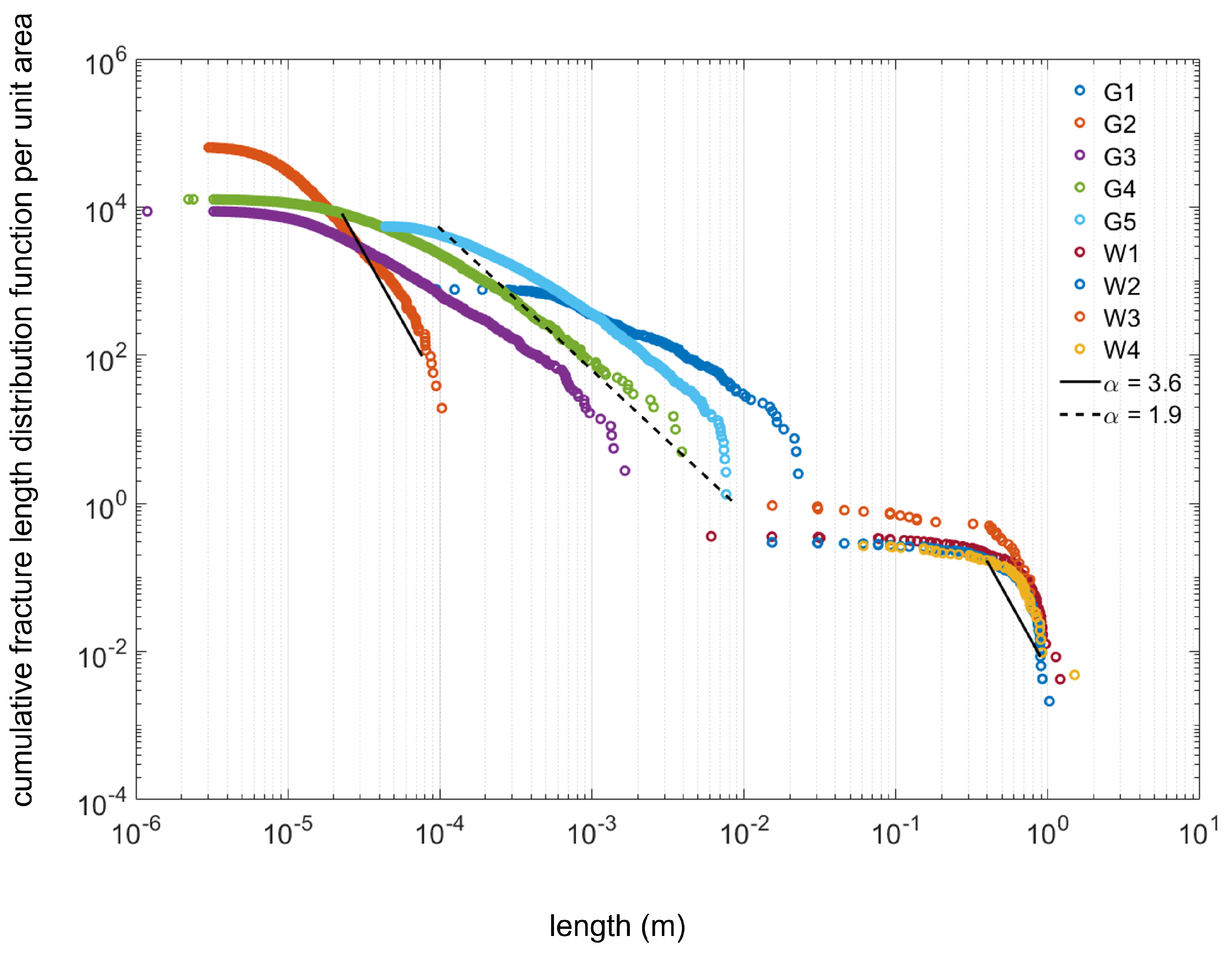
3.3. Multiscale Length Distribution
4. Conclusions
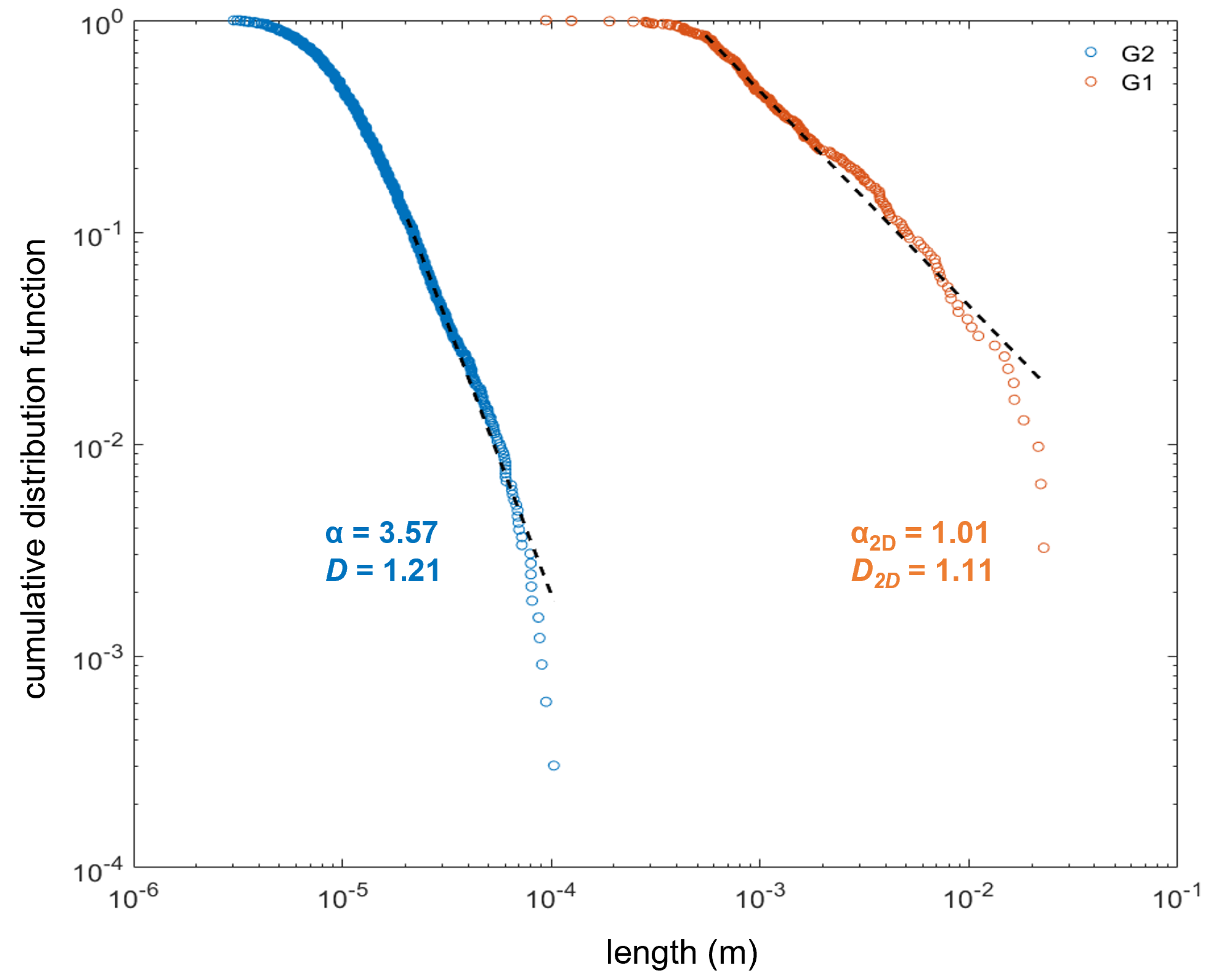
- Throughout a sample size range spanning from 10−6 to 100 m, most sample systems show a power-law exponent > 3, suggesting that fractures one or more orders of magnitude smaller than the system size control connectivity and classic rules of percolation theory apply. These fractal fracture network samples also fall in the > D + 1 category, indicating that connectivity decreases with system scale. These samples belong to the natural/hydraulically fractured group.
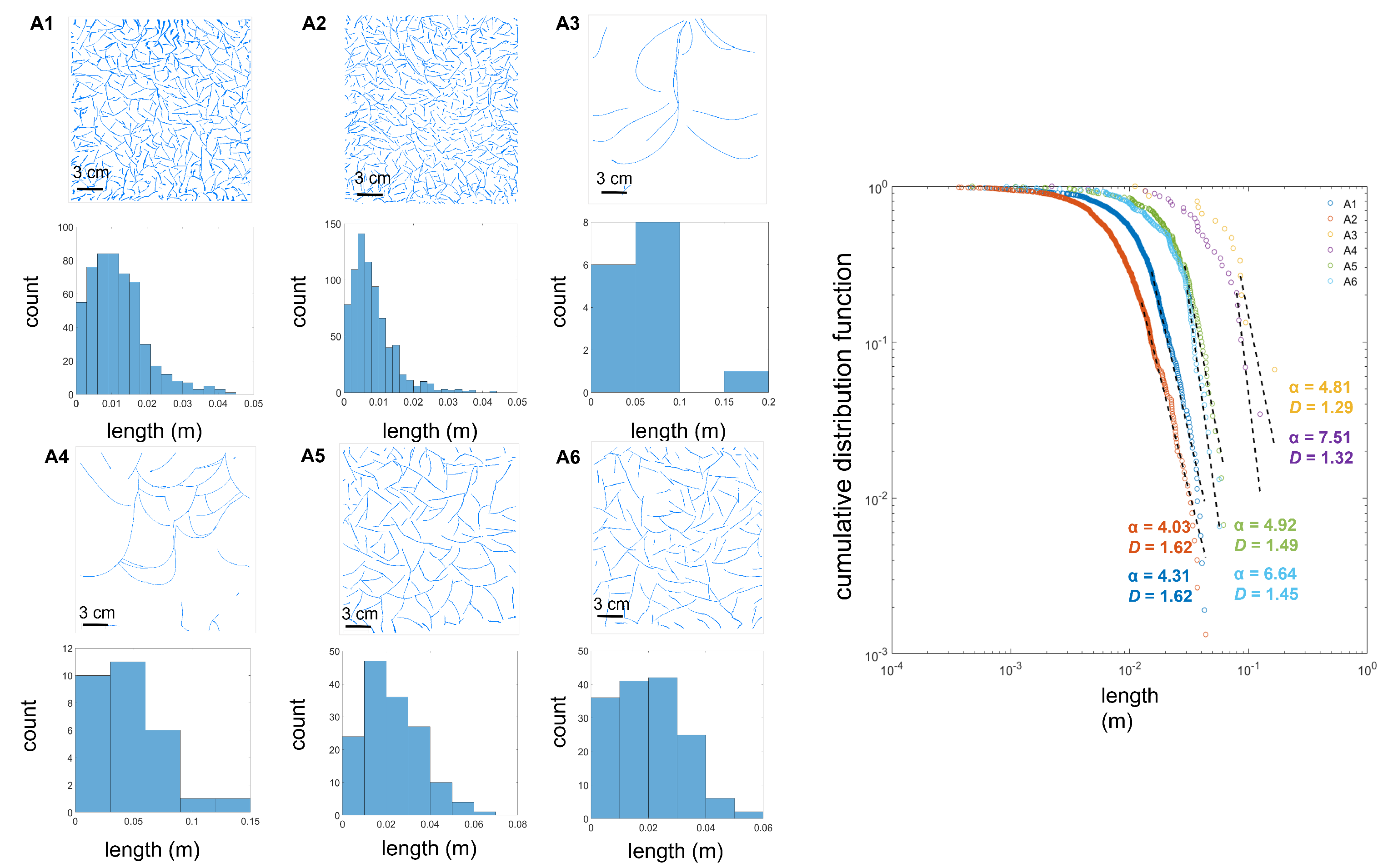
- Fractures in the samples matured using pyrolysis (G1, G3, G4, and G5) correlate with a different connectivity regime than the natural/hydraulic fractures. These fractures fit power-law exponents such that 2 < < 3, suggesting that a combination of small and large fractures interact to determine connectivity, but they also conform to < D + 1, such that larger fractures prevail in system connectivity. This effect increases with system scale. Given the fracture length distribution shown on their histograms and their segmented images, it is probable that the larger fractures (of the same order of magnitude as system length) are more dominant than smaller fractures (one or more orders of magnitude smaller than the system).
- The distribution and abundance of organic matter of the shale samples has a direct and predominant effect on the distribution and clustering of the resulting fracture networks if the rock is (naturally or artificially) matured. In the samples included in this study, this effect resulted in large fractures located within the laminations of samples with a large amount of organic matter. These fractures dominate connectivity. In the case of hydraulic fracturing, the process is correlated to the mechanical features of the rock and the fracturing parameters that overall produces fracture networks with connectivity most likely dominated by smaller system size fractures.
- Gelatin is found to be an accurate rock analog for maturation-induced fractures as validated through multiscale connectivity trends.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| power-law function exponent | |
| D | fractal dimension |
| cdf | cumulative distribution function |
| HI | heat-induced organic matter maturation |
| N, HF | natural and hydraulically fractured rock samples |
References
- Gale, J.F.W.; Holder, J. Natural fractures in some US shales and their importance for gas production. In Petroleum Geology: From Mature Basins to New Frontiers, Proceedings of the 7th Petroleum Geology Conference; Geological Society of London: London, UK, 2010. [Google Scholar] [CrossRef]
- Allix, P.; Burnham, A.; Fowler, T.; Herron, M.; Kleinberg, R.; Symington, B. Coaxing oil from shale. Oilfield Rev. 2010, 22, 4–15. [Google Scholar]
- Akkutlu, I.Y.; Fathi, E. Multiscale gas transport in shales with local kerogen heterogeneities. SPE J. 2012, 17, 1002–1011. [Google Scholar] [CrossRef] [Green Version]
- Aljamaan, H.; Alnoaimi, K.; Kovscek, A. In-depth experimental investigation of shale physical and transport properties. In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 12–14 August 2013; pp. 1120–1129. [Google Scholar]
- Aljamaan, H.; Ross, C.M.; Kovscek, A.R. Multiscale Imaging of Gas Storage in Shales. SPE J. 2017, 22, 1760–1777. [Google Scholar] [CrossRef]
- Alnoaimi, K.R.; Duchateau, C.; Kovscek, A. Characterization and measurement of multi-scale gas transport in shale core samples. In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 25–27 August 2014; pp. 1140–1158. [Google Scholar]
- Vega, B.; Andrews, J.C.; Liu, Y.; Gelb, J.; Kovscek, A. Nanoscale visualization of gas shale pore and textural features. In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 12–14 August 2013; pp. 1603–1613. [Google Scholar]
- Sondergeld, C.H.; Ambrose, R.J.; Rai, C.S.; Moncrieff, J. Micro-structural studies of gas shales. In Proceedings of the SPE Unconventional Gas Conference, Pittsburgh, PA, USA, 23–25 February 2010. [Google Scholar]
- Elgmati, M.M.; Zhang, H.; Bai, B.; Flori, R.E.; Qu, Q. Submicron-pore characterization of shale gas plays. In Proceedings of the North American Unconventional Gas Conference and Exhibition, The Woodlands, TX, USA, 14–16 June 2011. [Google Scholar]
- Curtis, M.E.; Ambrose, R.J.; Sondergeld, C.H. Structural characterization of gas shales on the micro-and nano-scales. In Proceedings of the Canadian Unconventional Resources and International Petroleum Conference, Calgary, AB, Canada, 19–21 October 2010. [Google Scholar]
- Energy Technology Perspectives. IEA Energy Technology Perspectives 2008–Scenarios and Strategies to 2050; International Energy Agency: Paris, France, 2008. [Google Scholar]
- Nuttall, B.C.; Drahovzal, J.A.; Eble, C.; Bustin, R.M. CO2 sequestration in gas shales of Kentucky. In Proceedings of the Oral Presentation at AAPG Annual Convention, Calgary, AB, Canada, 19–22 June 2005; pp. 19–22. [Google Scholar]
- Khosrokhavar, R.; Griffiths, S.; Wolf, K.H. Shale Gas Formations and Their Potential for Carbon Storage: Opportunities and Outlook. Environ. Process. 2014, 1, 595–611. [Google Scholar] [CrossRef] [Green Version]
- Tao, Z.; Clarens, A. Estimating the Carbon Sequestration Capacity of Shale Formations Using Methane Production Rates. Environ. Sci. Technol. 2013, 47, 11318–11325. [Google Scholar] [CrossRef] [PubMed]
- Mohagheghian, E.; Hassanzadeh, H.; Chen, Z. CO2 sequestration coupled with enhanced gas recovery in shale gas reservoirs. J. CO2 Util. 2019, 34, 646–655. [Google Scholar] [CrossRef]
- Godec, M.; Koperna, G.; Petrusak, R.; Oudinot, A. Potential for enhanced gas recovery and CO2 storage in the Marcellus Shale in the Eastern United States. Int. J. Coal Geol. 2013, 118, 95–104. [Google Scholar] [CrossRef]
- Lord, A.S.; Kobos, P.H.; Borns, D.J. Geologic storage of hydrogen: Scaling up to meet city transportation demands. Int. J. Hydrog. Energy 2014, 39, 15570–15582. [Google Scholar] [CrossRef] [Green Version]
- Tarkowski, R.; Uliasz-Misiak, B.; Tarkowski, P. Storage of hydrogen, natural gas, and carbon dioxide – Geological and legal conditions. Int. J. Hydrog. Energy 2021, 46, 20010–20022. [Google Scholar] [CrossRef]
- Gale, J.; Laubach, S.; Olson, J.; Eichhubl, P.; Fall, A. Natural fractures in shale: A review and new observations. AAPG Bull. 2014, 98, 2165–2216. [Google Scholar] [CrossRef]
- Gale, J.F.W.; Elliott, S.J.; Laubach, S.E. Hydraulic Fractures in Core From Stimulated Reservoirs: Core Fracture Description of HFTS Slant Core, Midland Basin, West Texas. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Houston, TX, USA, 23–25 July 2018. [Google Scholar] [CrossRef]
- Darcel, C.; Bour, O.; Davy, P.; de Dreuzy, J.R. Connectivity properties of two-dimensional fracture networks with stochastic fractal correlation. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Gasparrini, M.; Sassi, W.; Gale, J.F. Natural sealed fractures in mudrocks: A case study tied to burial history from the Barnett Shale, Fort Worth Basin, Texas, USA. Mar. Pet. Geol. 2014, 55, 122–141. [Google Scholar] [CrossRef] [Green Version]
- Gale, J.; Reed, R.; Holder, J. Natural fractures in the Barnett Shale and their importance for hydraulic fracture treatments. AAPG Bull. 2007, 91, 603–622. [Google Scholar] [CrossRef]
- Davy, P.; Bour, O.; Dreuzy, J.R.D.; Darcel, C. Flow in multiscale fractal fracture networks. In Fractal Analysis for Natural Hazards; Geological Society of London: London, UK, 2006. [Google Scholar] [CrossRef]
- Mandelbrot, B. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mandelbrot, B. Form, chance and dimension. In Chance and Dimension; Freeman: San Francisco, CA, USA, 1977; pp. 1–234. [Google Scholar]
- Barton, C.; Zoback, M. Self-similar distribution and properties of macroscopic fractures at depth in crystalline rock in the Cajon Pass Scientific Drill Hole. J. Geophys. Res. Solid Earth 1992, 97, 5181–5200. [Google Scholar] [CrossRef]
- Watanabe, K.; Takahashi, H. Fractal geometry characterization of geothermal reservoir fracture networks. J. Geophys. Res. Solid Earth 1995, 100, 521–528. [Google Scholar] [CrossRef]
- Xia, Y.; Cai, J.; Wei, W.; Hu, X.; Wang, X.; Ge, X. A new method for calculating fractal dimensions of porous media based on pore size distribution. Fractals 2018, 26, 1850006. [Google Scholar] [CrossRef]
- Velde, B.; Dubois, J.; Moore, D.; Touchard, G. Fractal patterns of fractures in granites. Earth Planet. Sci. Lett. 1991, 104, 25–35. [Google Scholar] [CrossRef]
- Miao, T.; Yang, S.; Long, Z.; Yu, B. Fractal analysis of permeability of dual-porosity media embedded with random fractures. Int. J. Heat Mass Transf. 2015, 88, 814–821. [Google Scholar] [CrossRef]
- Bonnet, E.; Bour, O.; Odling, N.; Davy, P.; Main, I.; Cowie, P.; Berkowitz, B. Scaling of fracture systems in geological media. Rev. Geophys. 2001, 39, 347–383. [Google Scholar] [CrossRef] [Green Version]
- Hazra, B.; Wood, D.; Kumar, S.; Saha, S.; Dutta, S.; Kumari, P.; Singh, A. Fractal disposition, porosity characterization and relationships to thermal maturity for the Lower Permian Raniganj basin shales, India. J. Nat. Gas Sci. Eng. 2018, 59, 452–465. [Google Scholar] [CrossRef]
- Chelidze, T.; Gueguen, Y. Evidence of fractal fracture. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1990, 27, 223–225. [Google Scholar] [CrossRef]
- Vignes-Adler, M.; Page, A.L.; Adler, P. Fractal analysis of fracturing in two African regions, from satellite imagery to ground scale. Tectonophysics 1991, 196, 69–86. [Google Scholar] [CrossRef]
- Chabani, A.; Trullenque, G.; Ledésert, B.A.; Klee, J. Multiscale Characterization of Fracture Patterns: A Case Study of the Noble Hills Range (Death Valley, CA, USA), Application to Geothermal Reservoirs. Geosciences 2021, 11, 280. [Google Scholar] [CrossRef]
- Kim, T.; Ross, C.; Guan, K.; Burnham, A.; Kovscek, A. Permeability and Porosity Evolution of Organic-Rich Shales from the Green River Formation as a Result of Maturation. SPE J. 2020, 25, 1377–1405. [Google Scholar] [CrossRef]
- Vega, B.; Yang, J.; Tchelepi, H.; Kovscek, A. Investigation of Stress Field and Fracture Development During Shale Maturation Using Analog Rock Systems. Transp. Porous Media 2019, 131, 503–535. [Google Scholar] [CrossRef]
- Ling, B.; Khan, H.J.; Druhan, J.L.; Battiato, I. Multi-Scale Microfluidics for Transport in Shale Fabric. Energies 2021, 14, 21. [Google Scholar] [CrossRef]
- Vega, B.; Ross, C.M.; Kovscek, A.R. Imaging-Based Characterization of Calcite-Filled Fractures and Porosity in Shales. SPE J. 2015, 20, 810–823. [Google Scholar] [CrossRef]
- Vega, B.; Kovscek, A. A systematic study of internal gas generation in shale source rocks using analog experiments. J. Pet. Sci. Eng. 2019, 173, 209–221. [Google Scholar] [CrossRef]
- Clauset, A.; Shalizi, C.R.; Newman, M.E.J. Power-Law Distributions in Empirical Data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef] [Green Version]
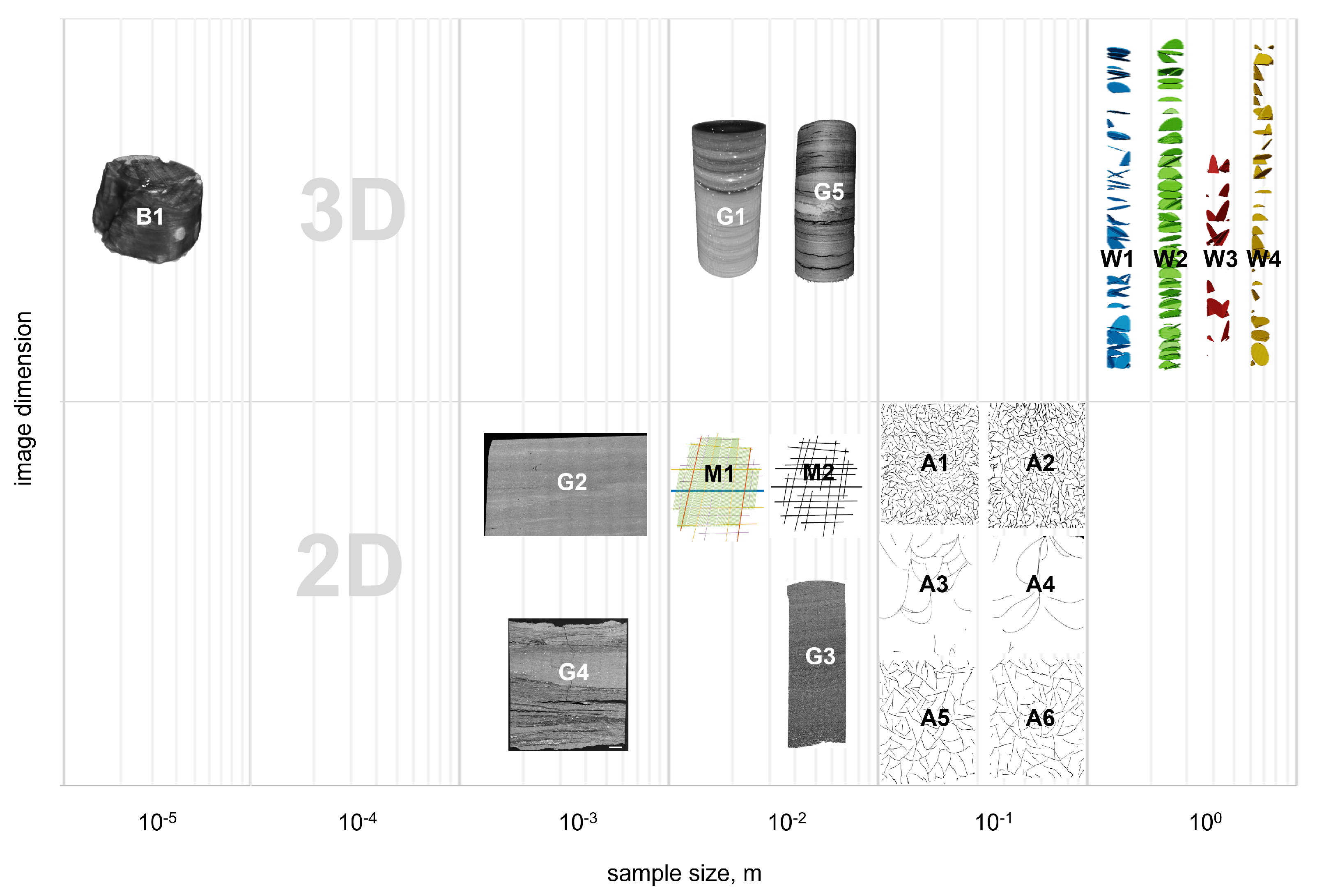



| Sample | Sample Size Length Units | Image Resolution | Euclidean Dimension | Image Modality | Fracture Origin | Data Provenance |
|---|---|---|---|---|---|---|
| B1 | m | 31.2 nm/vx | 3 | nano-CT | N | [40] |
| G1 * | cm | 30.58 m/vx | 3 | micro-CT | HI | [37] |
| G2 * | mm | 540 nm/px | 2 | SEM | HI | [37] |
| G3 | mm | 540 nm/px | 2 | SEM | HI | [37] |
| G4 | mm | 540 nm/px | 2 | SEM | HI | [37] |
| G5 | mm | 5.11 m/vx | 3 | micro-CT | HI | [37] |
| W1 | m | 0.3 × 0.3 × 2.4 mm/vx | 3 | tabular data | N, F | unpublished |
| W2 | m | 0.3 × 0.3 × 2.4 mm/vx | 3 | tabular data | N, F | unpublished |
| W3 | m | 0.3 × 0.3 × 2.4 mm/vx | 3 | tabular data | N, F | unpublished |
| W4 | m | 0.3 × 0.3 × 2.4 mm/vx | 3 | tabular data | N, F | unpublished |
| A1 | cm | 60.8 m/px | 2 | DSLR camera | N/A | [38] |
| A2 | cm | 60.8 m/px | 2 | DSLR camera | N/A | [38] |
| A3 | cm | 60.8 m/px | 2 | DSLR camera | N/A | [38] |
| A4 | cm | 60.8 m/px | 2 | DSLR camera | N/A | [38] |
| A5 | cm | 60.8 m/px | 2 | DSLR camera | N/A | [38] |
| A6 | cm | 60.8 m/px | 2 | DSLR camera | N/A | [38] |
| M1 | mm | 244.7 m/px | 2 | graphics | N/A | [39] |
| M2 | mm | 117.1 m/px | 2 | graphics | N/A | [39] |
| Sample | Alpha () | D | Connectivity Dominance |
|---|---|---|---|
| B1 | 3.45 | 1.73 | small fractures |
| G1 | 2.01 | 2.11 | transitional towards large fractures |
| G2 | 3.57 | 1.21 | small fractures |
| G3 | 2.29 | 1.41 | transitional toward large fractures |
| G4 | 2.64 | 1.54 | self-similar, invariant |
| G5 | 2.74 | 2.25 | transitional toward large fractures |
| W1 | 9.03 | 2.23 | small fractures |
| W2 | 8.30 | 2.24 | small fractures |
| W3 | 5.56 | 2.14 | small fractures |
| W4 | 6.46 | 2.18 | small fractures |
| A1 | 4.31 | 1.62 | small fractures |
| A2 | 4.03 | 1.62 | small fractures |
| A3 | 4.81 | 1.29 | small fractures |
| A4 | 7.51 | 1.32 | small fractures |
| A5 | 4.92 | 1.49 | small fractures |
| A6 | 6.64 | 1.45 | small fractures |
| M1 | 23.89 | 1.76 | small fractures |
| M2 | 2.58 | 1.56 | self-similar, invariant |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vega, B.; Kovscek, A.R. Fractal Characterization of Multimodal, Multiscale Images of Shale Rock Fracture Networks. Energies 2022, 15, 1012. https://doi.org/10.3390/en15031012
Vega B, Kovscek AR. Fractal Characterization of Multimodal, Multiscale Images of Shale Rock Fracture Networks. Energies. 2022; 15(3):1012. https://doi.org/10.3390/en15031012
Chicago/Turabian StyleVega, Bolivia, and Anthony R. Kovscek. 2022. "Fractal Characterization of Multimodal, Multiscale Images of Shale Rock Fracture Networks" Energies 15, no. 3: 1012. https://doi.org/10.3390/en15031012
APA StyleVega, B., & Kovscek, A. R. (2022). Fractal Characterization of Multimodal, Multiscale Images of Shale Rock Fracture Networks. Energies, 15(3), 1012. https://doi.org/10.3390/en15031012






