Effective Thermal Conductivity and Borehole Thermal Resistance in Selected Borehole Heat Exchangers for the Same Geology
Abstract
:1. Introduction
- -
- Material research [26].
- -
- Depth maximization for specific BHE construction [27], in terms of the type of pipe material and rock stability.
- -
- Utilizing old/abandoned/closed boreholes drilled for different reasons [28].
- -
- Operational parameters optimization [29] such as the type of heat carrier, its flow rate and velocity, inlet temperature, heating power (optimized for coefficient of performance of geothermal heat pump).
- -
- -
- Borehole axis, noting BHEs can be drilled either vertically or directionally (obliquely) using the BHE construction technology GRD, with such wells having been drilled under buildings and town infrastructure in Pałecznica [38].
- -
- -
- -
- -
- -
- -
- China, Xi’an, eight deep borehole heat exchanger constructions with a depth between 2–2.8 km and a temperature approximately 70–90 °C [57].
- -
- -
- The thermal resistance of the borehole Rb, [66].
- -
2. Essence of the Thermal Response Test and Research Objectives
2.1. Theoretical Foundation of the Thermal Response Test
2.2. Test Subjects
3. Interpretation Methods for Thermal Response Test Results
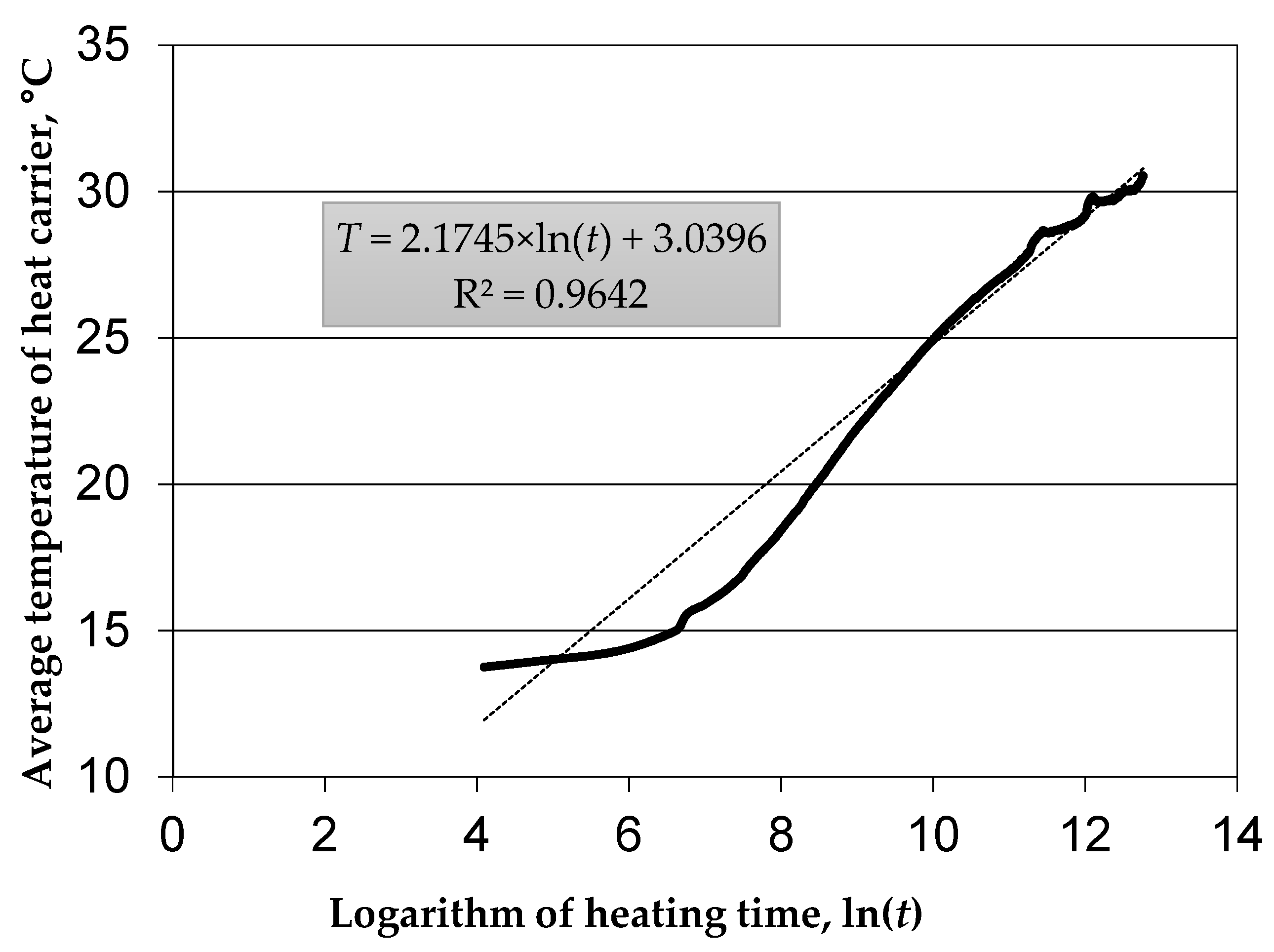
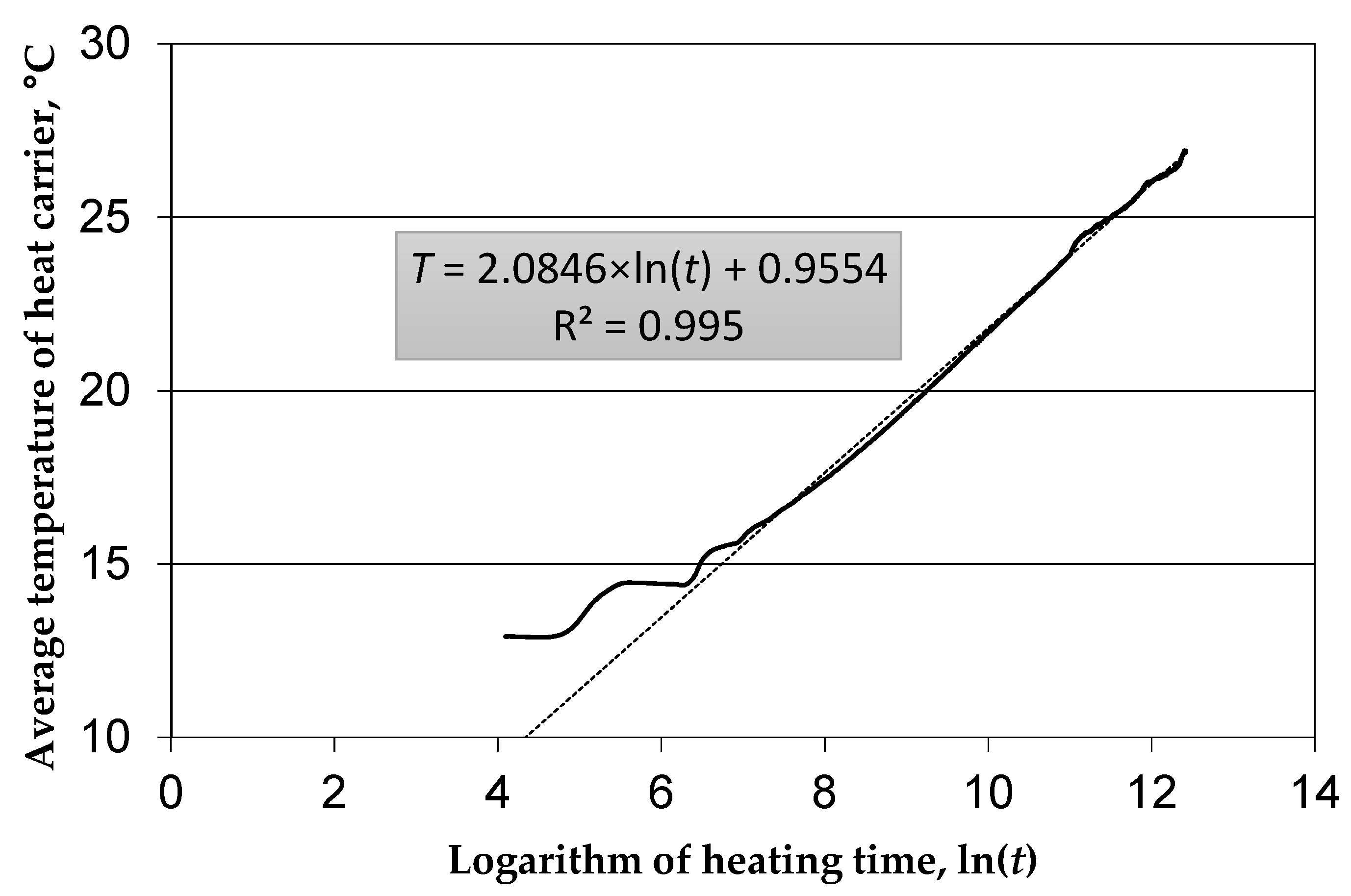
3.1. Classic Method (cm) of Determining Parameters from Thermal Response Tests
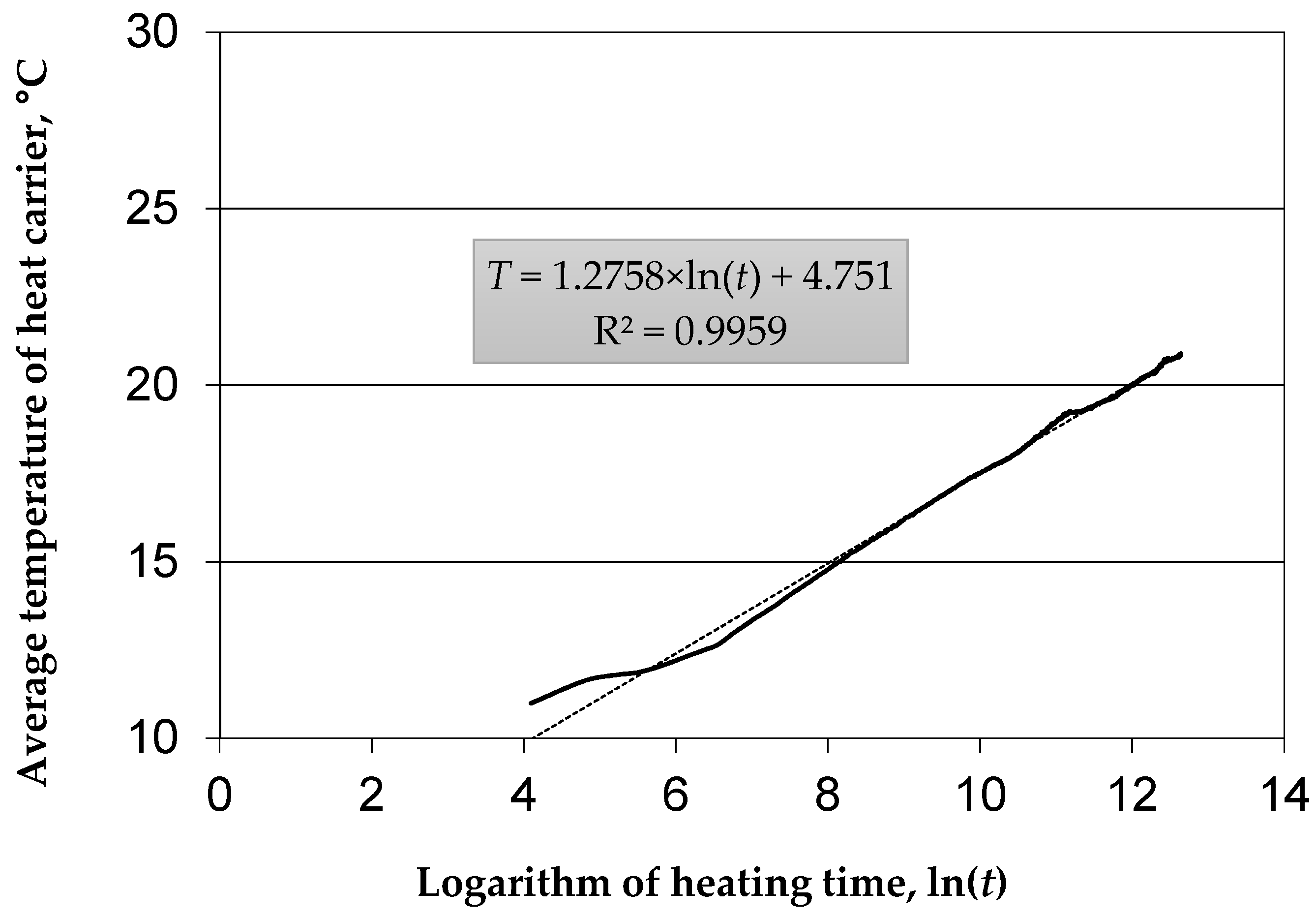
3.2. Point Method (pm) of Determining Parameters from Thermal Response Tests
- -
- Having the following data: ln(t1) or ln(t2) and Tav, the slope coefficient k and the intersection point of the line with the vertical axis (point b) are determined for a given time range. The intersection point is the point where the regression line, taken through known values ln(t1) or ln(t2) and Tav, intersects the vertical axis. That is,
- -
- Then, the following equation can be written:
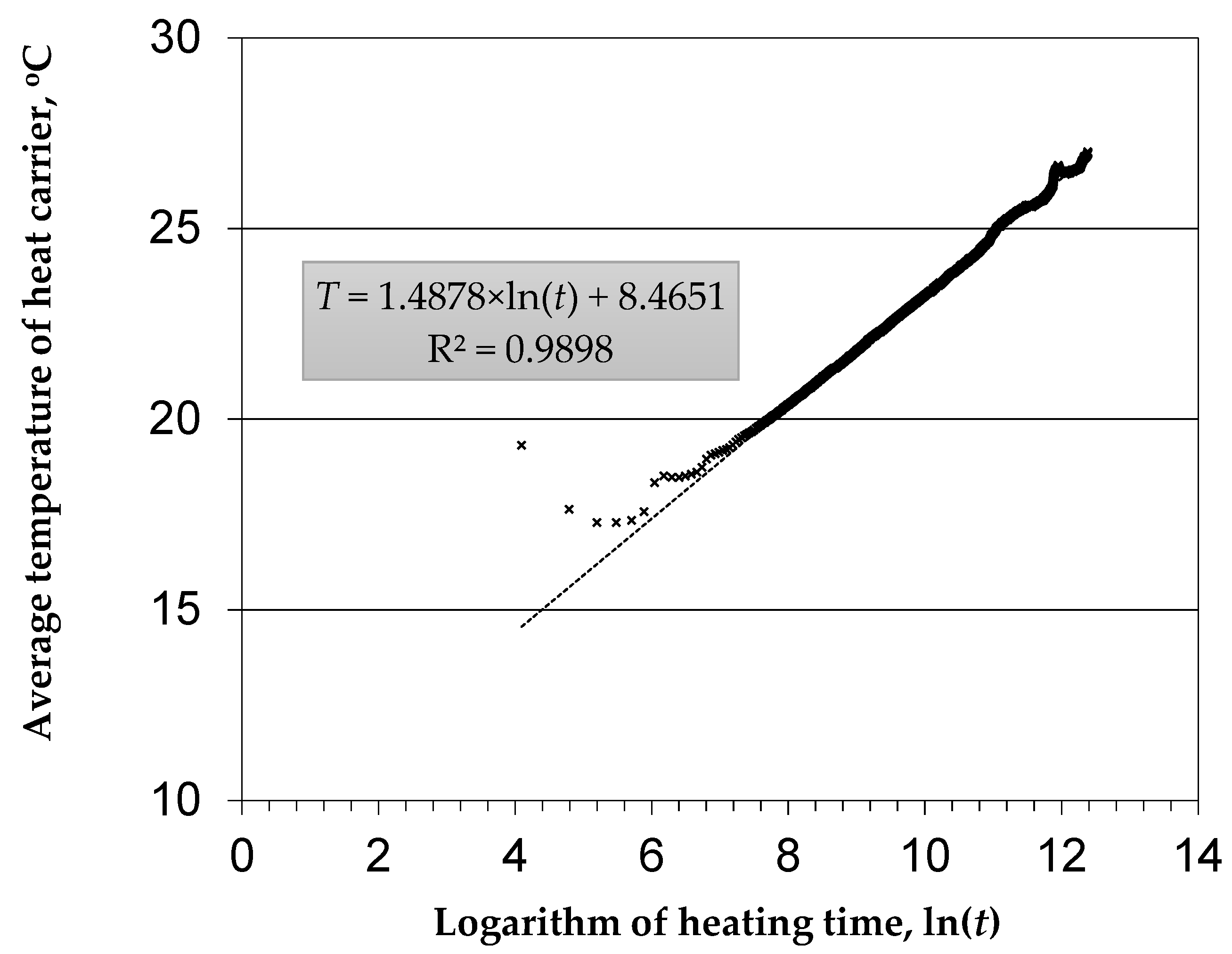
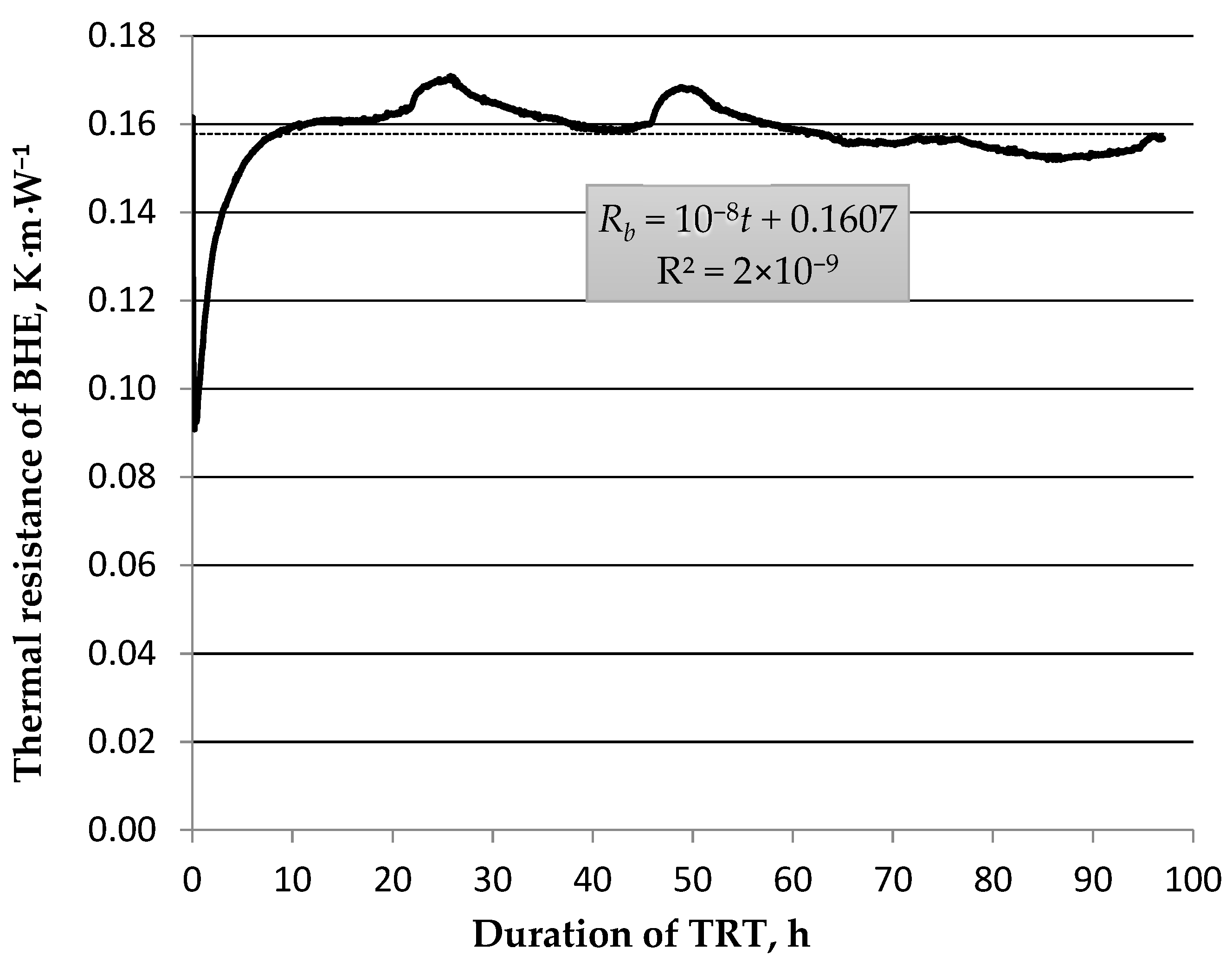
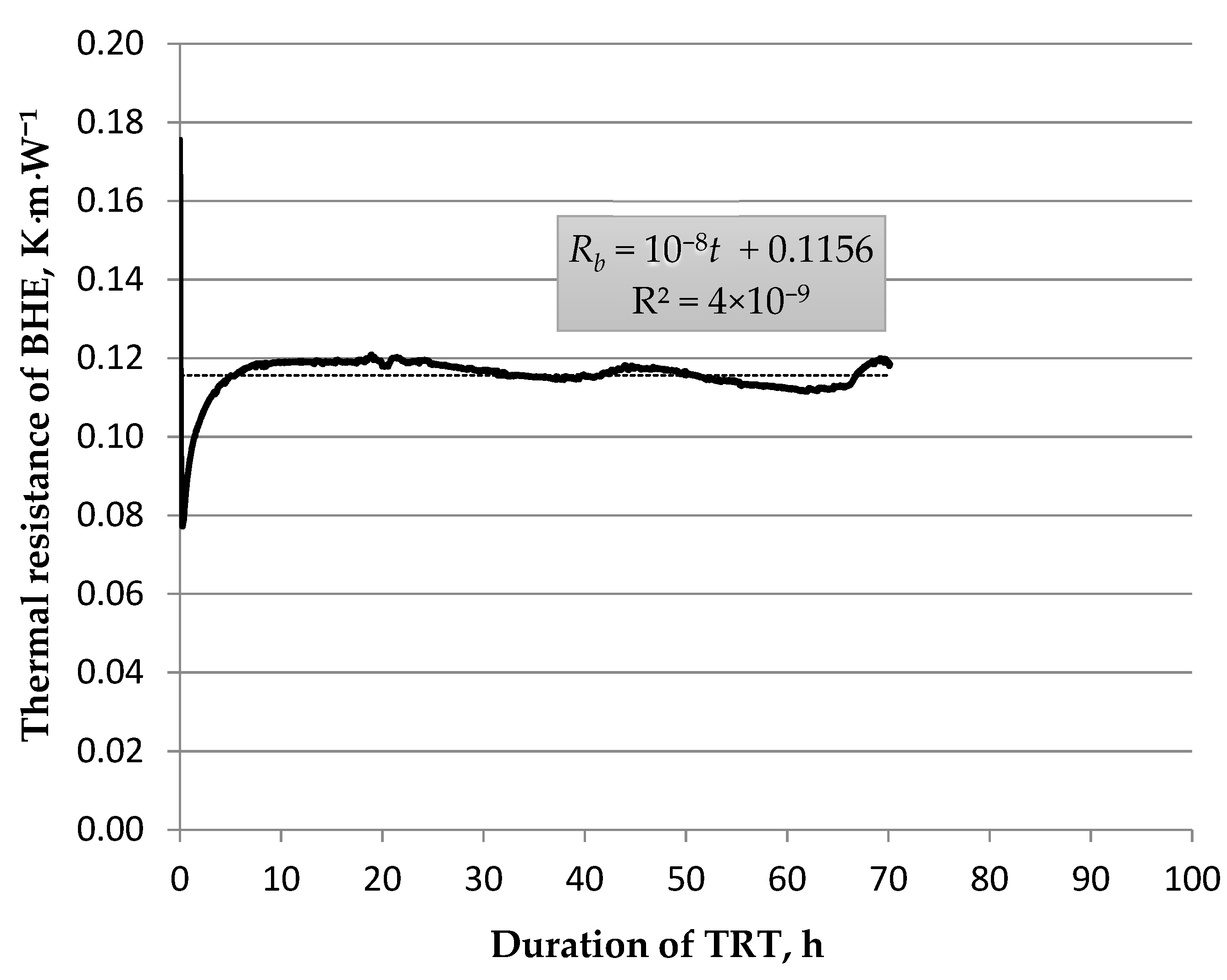
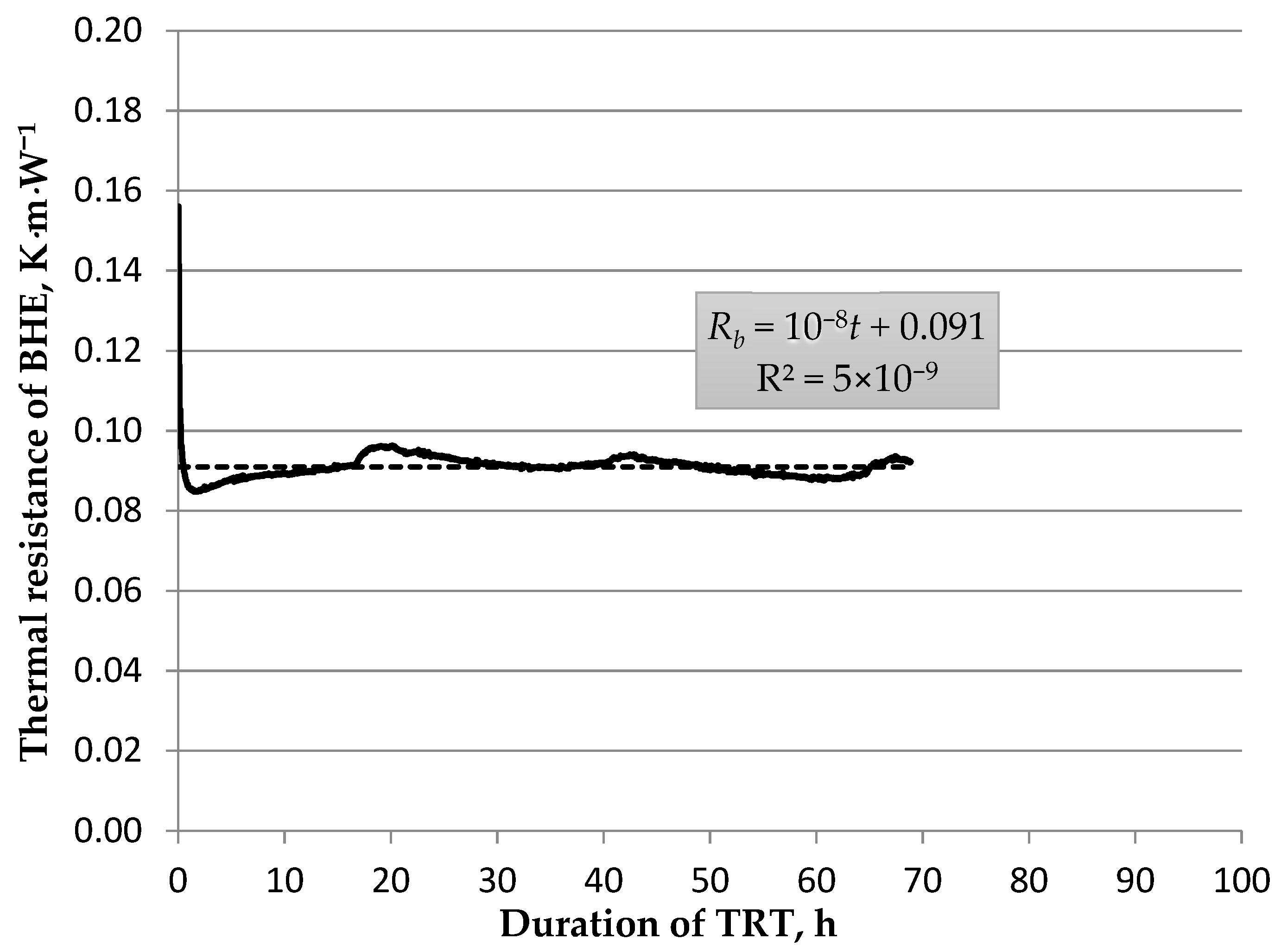
3.3. Constant Borehole Resistivity Method (cbrm) of Determining Parameters from Thermal Response Tests
4. Test Results
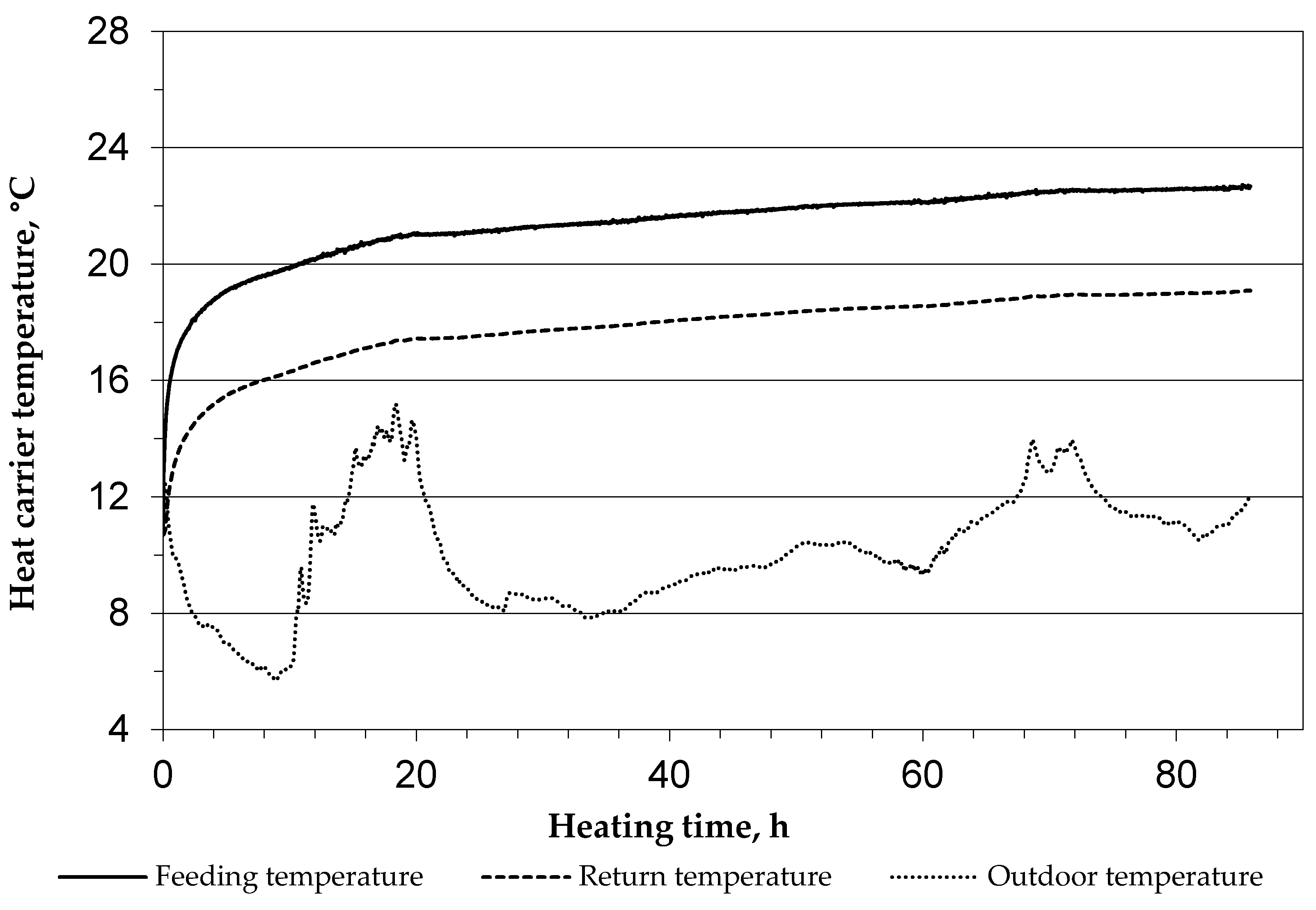
- The time from the onset of heating, s.
- The fluid temperature inlet to the exchanger, °C.
- The fluid temperature returning from the exchanger, °C.
- The outside (atmospheric) temperature, °C.
- The temporary flow rate, dm3/min.
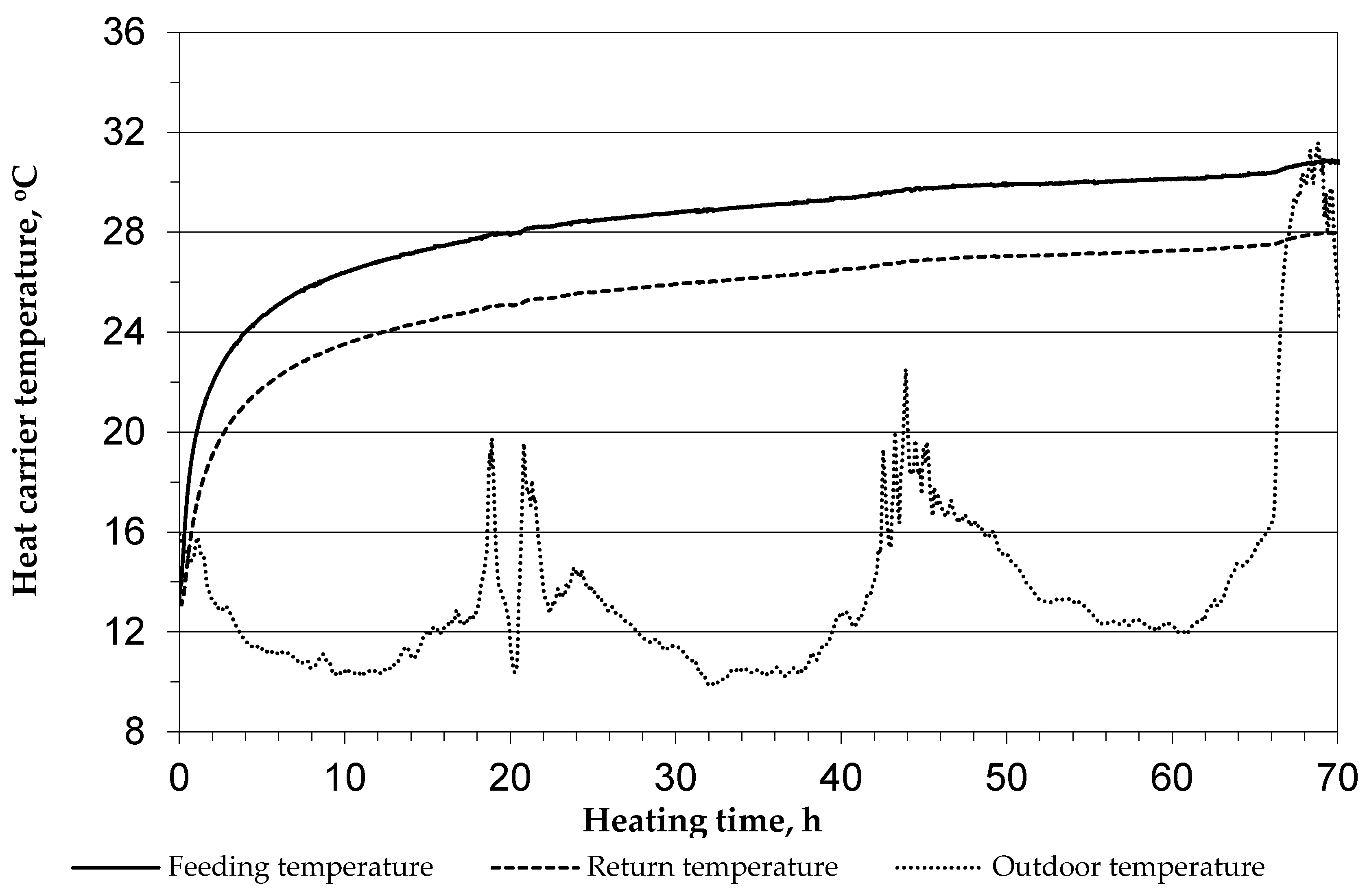
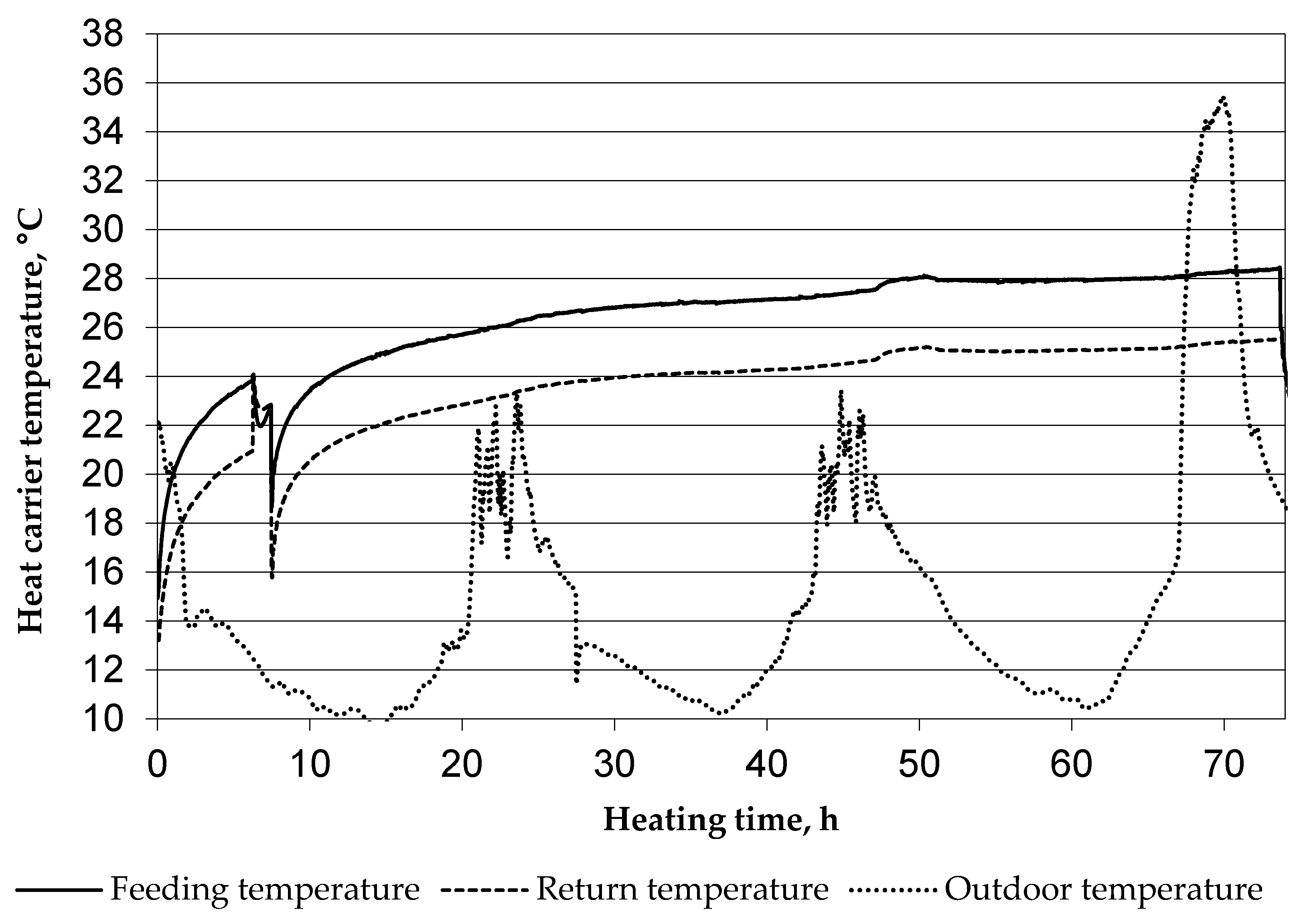
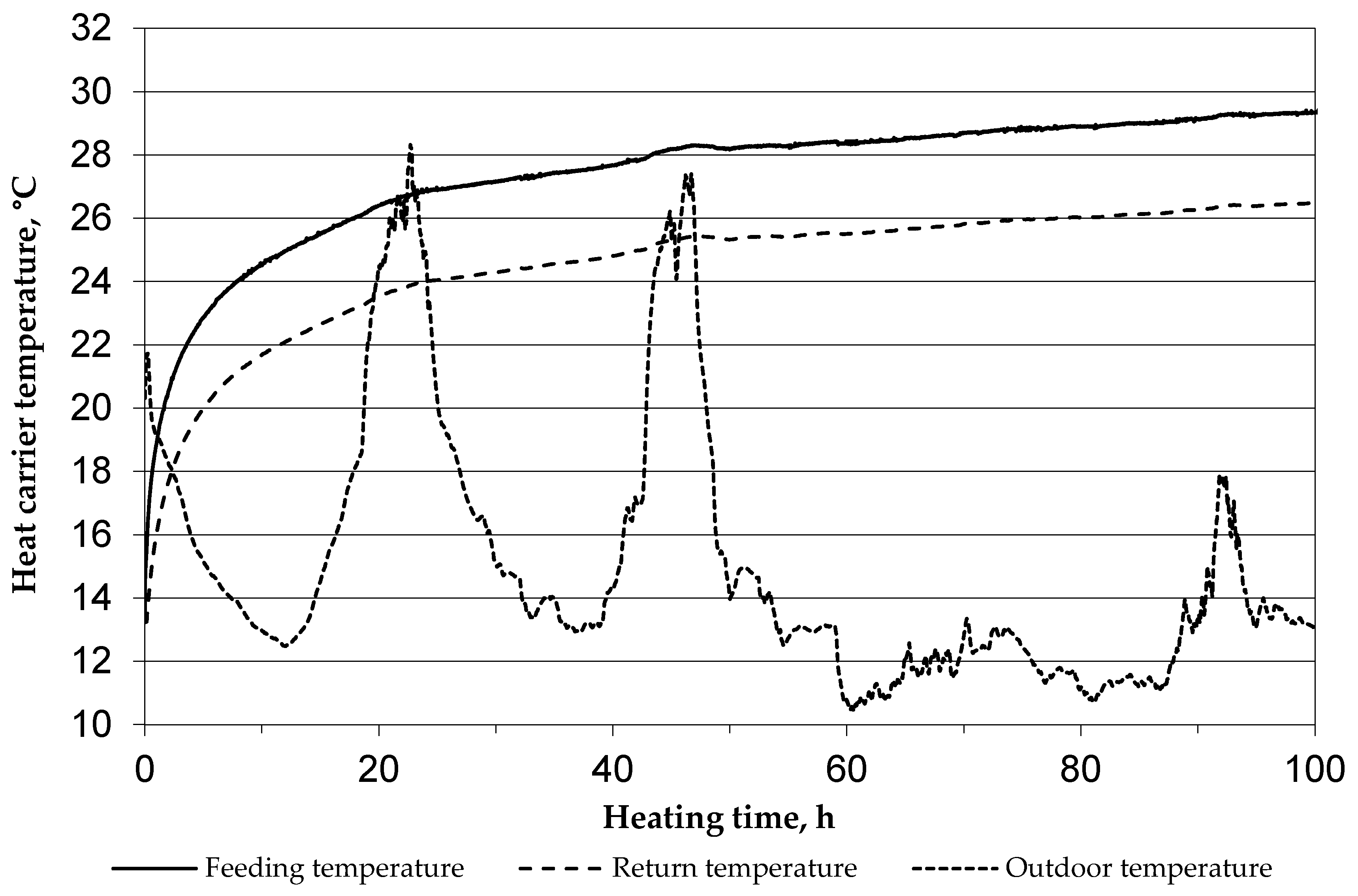
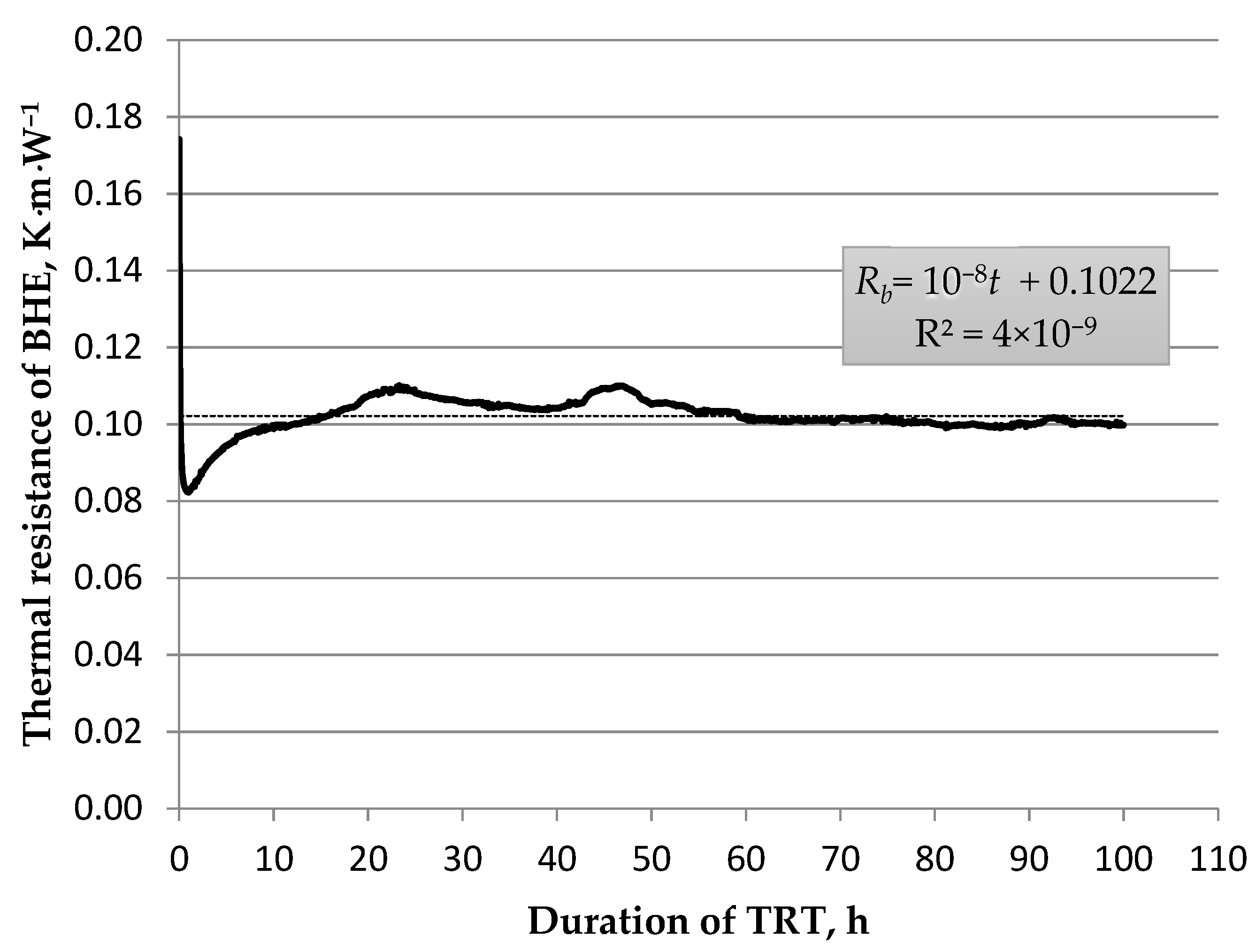
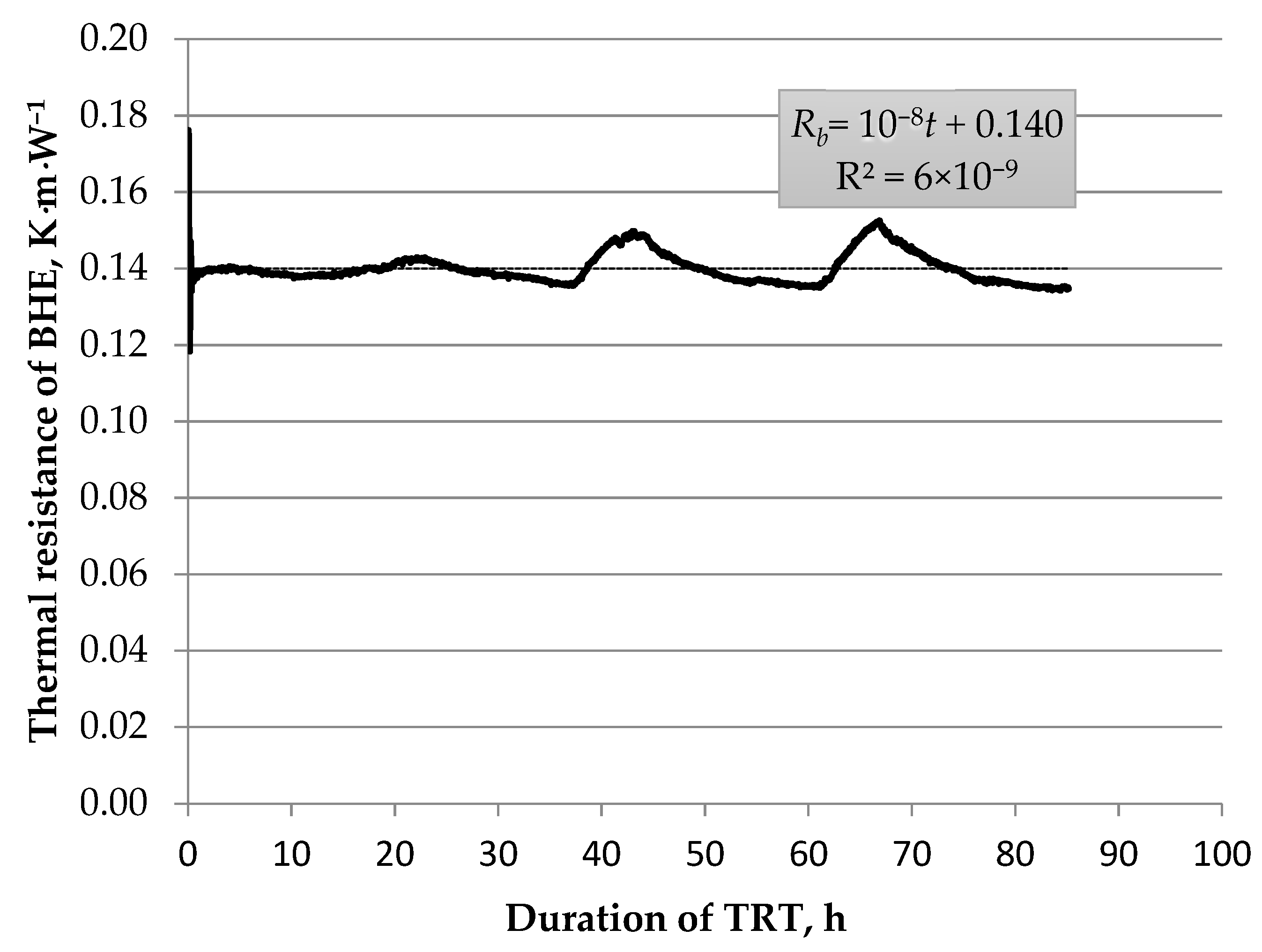
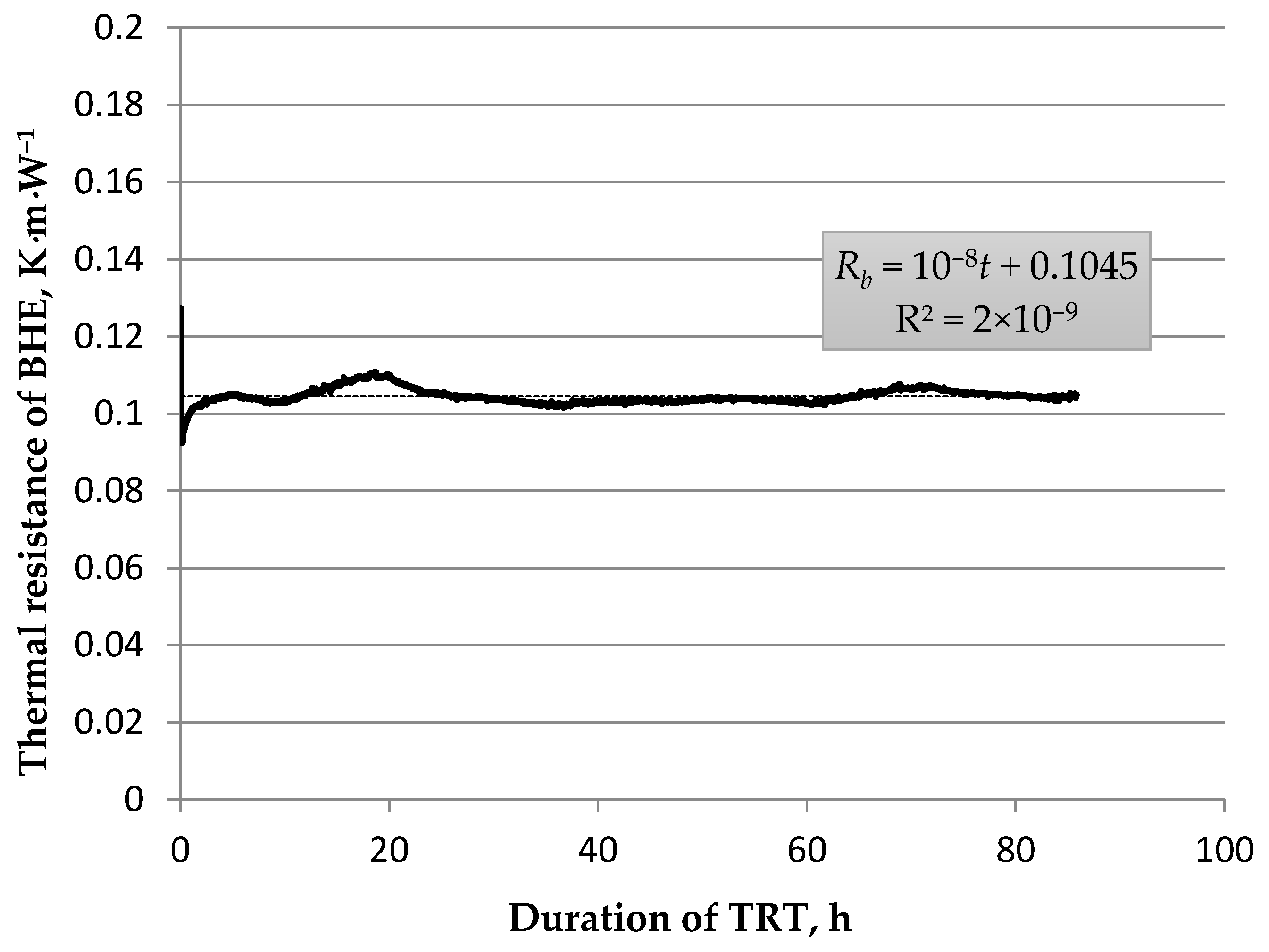
Analysis of the TRT Results
5. Data Interpretation and Results
6. Conclusions
- The measurements were conducted for two locations, i.e., for two different geological profiles, and thus are limited. For a more robust and broad analysis, more tests should be performed, both on the already tested wells (with different test parameters) and in other locations. The matter of selecting the most advantageous BHE design and construction in terms of test results has not been determined conclusively.
- The best effective thermal conductivity λeff result is observed for the BHE with a single U-pipe with gravel as the grout, for the classic method, and its value equals 2802 W·K−1·m−1. For the constant borehole resistivity method, the F1 exchanger (double U-pipe) has the best result (2.724 W·K−1·m−1). However, according to the point-based method, the F2 exchanger (single U-pipe) turns out to be the best borehole heat exchanger. These values are considered to be very high, which suggests the potential for very efficient results of the heat pump operation for the given geological structure.
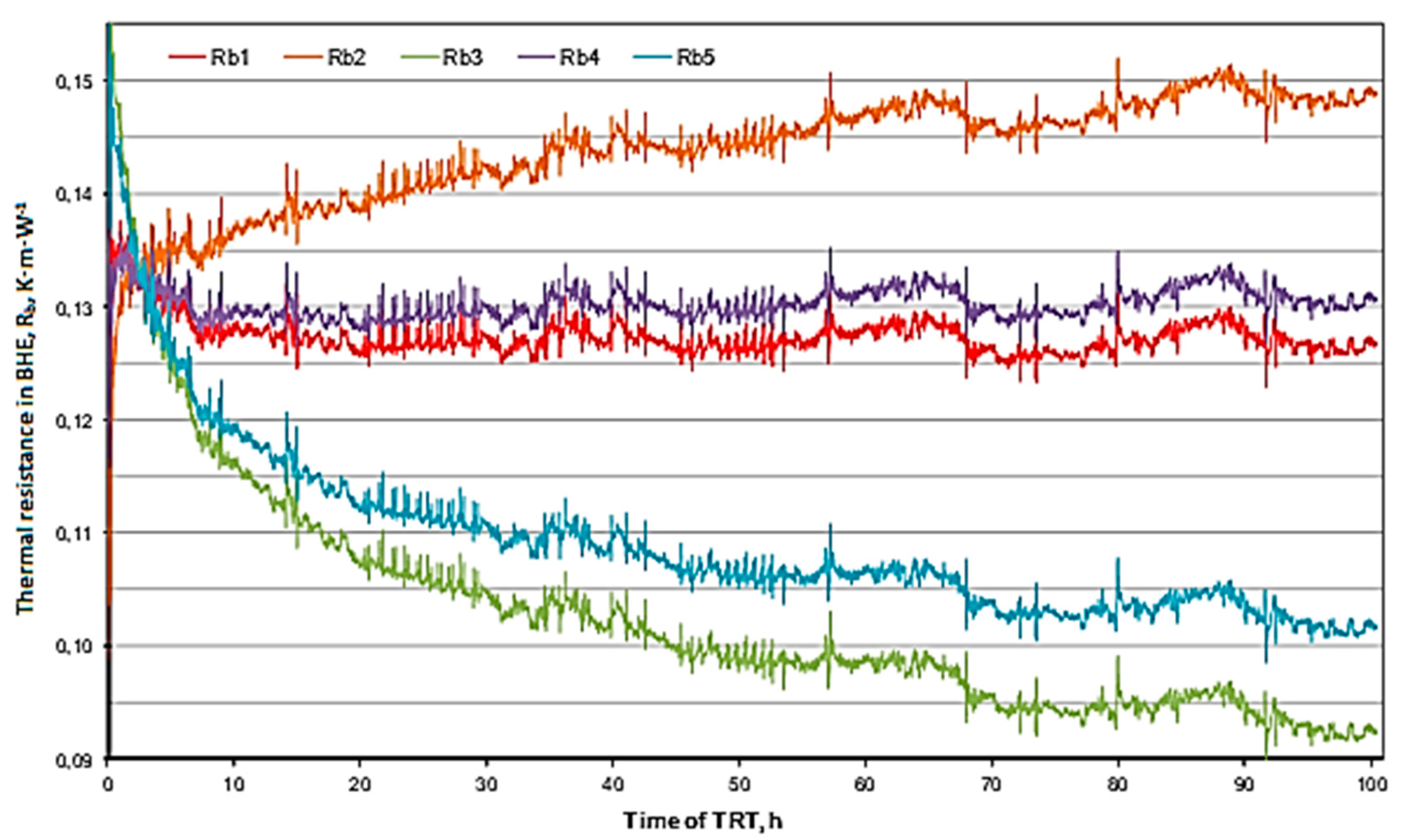
- The LG-4a borehole (BHE with a single U-pipe with gravel as the grout) has the best thermal resistance, at 0.045 K·m·W−1 for the classic method. For the point-based and the constant borehole resistivity methods, the results indicate that the LG-3a borehole heat exchanger has the lowest thermal resistance.
- To compare the influence of the BHE construction on the thermal conductivity and resistance coefficient characteristics, one can use the Folusz boreholes, where one of the designs is a single U-tube and the other a double U-tube. In this case, it is clear that a single U-tube achieves better thermal resistance values, while a double U-tube achieves better conductivity. In industrial practice, a double U-tube is considered a better, albeit more expensive, design. However, many parameters can influence TRT results. One of the important factors for the borehole thermal resistance Rb is the sealing effectiveness (even and precise distribution of the grout). With a double U-tube, sealing/filling the borehole is more difficult than with a single U-tube.
- The new method for determining the characteristic coefficients from the thermal response test gives different results compared to the old (classic) method. The largest standard deviation for thermal conductivity can be observed in the LG-4a well, where it was as high as 0.397 W·m−1·K−1. The values of the remaining standard deviations are much lower, which may indicate a good relationship between thermal conductivity calculations for both methods. Thermal resistance is also characterized by small standard deviations. However, with the LG-4a well it can be seen that there may be significant differences in individual cases, most likely depending on the thermal response test duration.
- The constant thermal resistivity method provides outcomes that do not depend in any way on the test duration. Therefore, it can be theorized that it may be a more reliable and accurate method, yielding better borehole heat exchanger coefficients from the thermal response test (λeff and Rb). However, this is speculative and it must be supported by a greater number of measurements than currently are available to be conclusive. This is the subject of future work being carried out in borehole heat exchanger fields B and C of the AGH UST Geoenergetics Laboratory.
- Further research on the centric design of the BHE is merited. Theoretically, the centric design should be the most advantageous (the lowest Rb value), but simultaneously it is the most difficult to properly seal with filling material. Hence, practical problems may indicate that this type of design should not be used. It is, however, the most advantageous in terms of heat carrier hydraulics and must be used in deep BHEs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| ∆Ti | Difference between feed temperature and return temperature for record i (K). |
| α | Ground thermal diffusivity (m2·s−1). |
| γ | Euler constant (γ = 0.5772156). |
| λ | Ground thermal conductivity (W·m−1·K−1). |
| λcm | Ground thermal conductivity (classic method) (W·K−1·m−1). |
| λpm | Ground thermal conductivity (point method) (W·K−1·m−1). |
| λcbrm | Ground thermal conductivity (constant borehole resistivity method) (W·K−1·m−1). |
| ρ | Density of rocks (kg·m−3). |
| ρi | Density of heat carrier for record i, which is dependent on temperature ρi = f(T) (kg·m−3). |
| H | Borehole heat exchanger depth (m). |
| P | Thermal power (W). |
| Pchi | Temporary heating power for record i (W). |
| Rb.cm | Borehole thermal resistance (classic method) (K·m·W−1). |
| Rb.pm | Borehole thermal resistance (point-based method) (K·m·W−1). |
| Rb.cbrm | Borehole thermal resistance (constant borehole resistivity method) (K·m·W−1). |
| T0 | Average natural temperature of geological profile of the borehole (K). |
| Tf | Feed temperature (K). |
| Tr | Return temperature (K). |
| T(t1) | Average heat carrier temperature at time t1 (K). |
| T(t2) | Average heat carrier temperature at time t2 (K). |
| Tz | Inlet temperature (at the inflow to the borehole heat exchanger) (K). |
| Tp | Return temperature (at the outflow of the borehole heat exchanger) (K). |
| Tśr(reg) | Temperature from the linear regression function (T(t1) or T(t2)) (K). |
| , Q | Heat carrier flow rate (m3·s−1). |
| Heat carrier flow rate for record i (m3·s−1). | |
| ci | Specific heat of heat carrier for record i, which is dependent on temperature ci = f(T) (J·kg−1·K−1). |
| cv | Volumetric specific heat (J·m−3·K−1). |
| k | Coefficient of inclination of (straight) lines of trends, representing the function of the heat carrier temperature vs. the natural logarithm of time of TRT. |
| kcm | Slope of regression line (classic method). |
| kpm | Slope of regression line (point-based method). |
| kcbrm | Slope of regression line (constant borehole resistivity method). |
| n | Number of records registered during the heating phase of the TRT. |
| q | Unit heat loss rate for borehole heat exchanger (W·m−1). |
| r | Radius (m). |
| rb | Borehole radius (m). |
| u | Auxiliary variable. |
| t | Time (s). |
| t1 | Starting time (s). |
| t2 | Ending time (s). |
References
- Qian, X.; Yang, Y.; Lee, S.W. Design and Evaluation of the Lab-Scale Shell and Tube Heat Exchanger (STHE) for Poultry Litter to Energy Production. Processes 2020, 8, 500. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, P.; Liu, Y.; Sun, S.; Peng, D. An improved evaluation method for thermal performance of borehole heat exchanger. Renew. Energy 2015, 77, 142–151. [Google Scholar] [CrossRef]
- Qian, X.; Lee, S.W.; Yang, Y. Heat Transfer Coefficient Estimation and Performance Evaluation of Shell and Tube Heat Exchanger Using Flue Gas. Processes 2021, 9, 939. [Google Scholar] [CrossRef]
- Nordell, B. Borehole Heat Store Design Optimization. Ph.D. Thesis, Division of Water Resources Engineering, Luleå University of Technology, Luleå, Sweden, 1994. [Google Scholar]
- Bujok, P.; Klempa, M.; Koziorek, J.; Rado, R.; Porzer, M. Evaluation of influence of climate conditions on rock mass energy balance in the research area of VSB—TU Ostrava. AGH Drill. Oil Gas 2012, 29/1, 97–107. [Google Scholar]
- Koohi-Fayegh, S.; Rosen, M.A. Examination of thermal interaction of multiple vertical ground heat exchangers. Appl. Energy 2012, 97, 962–969. [Google Scholar] [CrossRef]
- Schüppler, S.; Zorn, R.; Steger, H.; Blum, P. Uncertainty analysis of wireless temperature measurement (WTM) in borehole heat exchangers. Geothermics 2021, 90, 102019. [Google Scholar] [CrossRef]
- Cassaso, A.; Sethi, R. Sensitivity analysis on the performance of a ground source heat pump equipped with a double U-pipe borehole heat exchanger. Energy Procedia 2014, 59, 301–308. [Google Scholar] [CrossRef] [Green Version]
- Drysdale, R. Thermal Performance and Sustainability of Borehole Heat Exchangers within Building Clusters. Master’s Thesis, The University of Western Ontario, London, ON, Canada, 2019. [Google Scholar]
- Pollard, H.J.; Lee, F. Long term monitoring of borehole temperature profiles using a thermistor array in the Ball State University ground-source geothermal system. In Proceedings of the Conference 50th Annual GSA North-Central Section Meeting, Champaign, IL, USA, 18 April 2016. [Google Scholar]
- Dijkshoorn, L.; Speer, S.; Pechnig, R. Measurements and Design Calculations for a Deep Coaxial Borehole Heat Exchanger in Aachen, Germany. Int. J. Geophys. 2013, 2013, 916541. [Google Scholar] [CrossRef]
- Gehlin, S.; Andersson, O.; Bjelm, L.; Alm, P.G.; Rosberg, J.E. Country Update for Sweden. In Proceedings of the World Geothermal Congress 2015, Melbourne, Australia, 16–24 April 2015. [Google Scholar]
- Hellstrom, G. Ground Heat Storage Thermal Analyses of Duct Storage Systems Theory; Dept. of Mathematical Physics, University of Lund: Lund, Sweden, 1991. [Google Scholar]
- Eskilson, P. Thermal Analysis of Heat Extraction Boreholes; Dept. of Mathematical Physics, University of Lund: Lund, Sweden, 1987. [Google Scholar]
- Rybach, L.; Eugster, W.J. Sustainability aspects of geothermal heat pump operation, with experience from Switzerland. Geothermics 2010, 39, 365–369. [Google Scholar] [CrossRef]
- Rybach, L.; Hopkirk, R.J. Experience with Borehole Heat Exchangers in Switzerland; Institute of Geophysics ETH-Hoenggerberg: Zurich, Switzerland, 1994. [Google Scholar]
- Weber, J.; Ganz, B.; Schellschmidt, R.; Sanner, B.; Schulz, R. Geothermal Energy Use in Germany. In Proceedings of the World Geothermal Congress 2015, Melbourne, Australia, 16–24 April 2015. [Google Scholar]
- Schulte, D.O. Modeling insulated borehole heat exchangers. Environ. Earth Sci. 2016, 75, 910. [Google Scholar] [CrossRef]
- Kurevija, T.; Macenić, M.; Sabolić, T.; Jovanović, D. Defining geoexchange extraction rates in the same geological environment for different borehole geometry settings—Pilot results from the happen—Horizon 2020 project. Min.-Geol.-Pet. Eng. Bull. 2021, 36, 99–113. [Google Scholar] [CrossRef]
- Raymond, J.; Malo, M.; Tanguay, D.; Grasby, S.; Bakhteyar, F. Direct Utilization of Geothermal Energy from Coast to Coast: A Review of Current Applications and Research in Canada. In Proceedings of the World Geothermal Congress 2015, Melbourne, Australia, 16–24 April 2015. [Google Scholar]
- Giordano, N. Efficiency evaluation of borehole heat exchangers in Nunavik, Québec, Canada. In Proceedings of the 25th International Congress of Refrigeration, Montréal, QC, Canada, 24–30 August 2019. [Google Scholar]
- Boyd, T.L.; Sifford, A.; Lund, J.W. The United States of America Country Update 2015. In Proceedings of the World Geothermal Congress 2015, Melbourne, Australia, 16–24 April 2015; pp. 1–12. [Google Scholar]
- Cortes, D.; Nasirian, A.; Dai, S. Smart Ground-Source Borehole Heat Exchanger Backfills: A Numerical Study: SEG-2018. In Energy Geotechnics; Ferrari, A., Laloui, L., Eds.; Springer Series in Geomechanics and Geoengineering; Springer: Berlin/Heidelberg, Germany, 2019; pp. 27–34. [Google Scholar]
- Sasada, M. Geothermal heat pumps in Japan. In Proceedings of the Japan International Geothermal Symposium; Geothermal Research Society of Japan: Tokyo, Japan, 2012; Available online: http://www.geothermal-energy.org/pdf/IGAstandard/Japan/2012/p17-Masakatsu_Sasada(Eng-Jpn).pdf? (accessed on 27 June 2021).
- Fang, L.; Diao, N.; Shao, Z.; Cui, P.; Zhu, K.; Fang, Z. Thermal analysis models of deep borehole heat exchangers. In Proceedings of the IGSHPA Research Track 2018, Stockholm, Sweden, 18–20 September 2018; International Ground Source Heat Pump Association: Springfield, IL, USA, 2018. [Google Scholar]
- Javadi, H.; Ajatrostaghi, S.; Rosen, M.A.; Pourfallah, M.A. Comprehensive Review of Backfill Materials and Their Effects on Ground Heat Exchanger Performance. Sustainability 2018, 10, 4486. [Google Scholar] [CrossRef] [Green Version]
- Walch, A. Quantifying the technical geothermal potential from shallow borehole heat exchangers at regional scale. Renew. Energy 2020, 165, 369–380. [Google Scholar] [CrossRef]
- Caulk, R.; Tomac, I. Reuse of Abandoned Oil and Gas Wells for Geothermal Energy Production. Renew. Energy 2017, 112, 388–397. [Google Scholar] [CrossRef] [Green Version]
- Pan, S.; Kong, Y.; Chen, C.; Pang, Z.; Wang, J. Optimization of the utilization of deep borehole heat exchangers. Geotherm. Energy 2020, 8, 6. [Google Scholar] [CrossRef]
- Sliwa, T.; Rosen, M.A. Natural and artificial methods for regeneration of heat resources for borehole heat exchangers to enhance the sustainability of underground thermal storages: A review. Sustainability 2015, 7, 13104–13125. [Google Scholar] [CrossRef] [Green Version]
- Beier, R.A.; Acuña, J.; Mogensen, P.; Palm, B. Borehole resistance and vertical temperature profiles in coaxial borehole heat exchangers. Appl. Energy 2013, 102, 665–675. [Google Scholar] [CrossRef]
- Zarrella, A.; De Carli, M. Heat transfer analysis of short helical borehole heat exchangers. Appl. Energy 2013, 102, 1477–1491. [Google Scholar] [CrossRef]
- Zarrella, A.; Capozza, A.; De Carli, M. Analysis of short helical and double U-tube borehole heat exchangers: A simulation-based comparison. Appl. Energy 2013, 112, 358–370. [Google Scholar] [CrossRef]
- Li, M.; Lai, A.C.K. Heat-source solutions to heat conduction in anisotropic media with application to pile and borehole ground heat exchangers. Appl. Energy 2012, 96, 451–458. [Google Scholar] [CrossRef]
- Barbaresi Maioli, V.; Bovo, M.; Tinti, F.; Torreggiani, D.; Tassinari, P. Application of basket geothermal heat exchangers for sustainable greenhouse cultivation. Renew. Sustain. Energy Rev. 2020, 129, 109928. [Google Scholar] [CrossRef]
- Sliwa, T.; Kucper, M. Accessing Earth’s heat using Geothermal Radial Drilling for borehole heat exchangers. AGH Drill. Oil Gas 2017, 34, 495–512. [Google Scholar] [CrossRef] [Green Version]
- Mendrinos, D.; Katsantonis, S.; Karytsas, C. Pipe materials for borehole heat exchangers. In Proceedings of the European Geothermal Congress 2016 (EGC2016), Strasbourg, France, 19–23 September 2016. [Google Scholar]
- Sliwa, T.; Gaweł, M. Ohorona atmosfernogo povìtrâ zavdâki vikoristannû vìdnovlûvanih džerel energìï v sistemah opalennâ ta oholodžennâ u gromads’kih ob’êktah u gmìnì Palečnìca. In Improvement of Energy Management in Typical Public Buildings of the City and Oblast Ivano-Frankivsk; Good Polish Practices of Utilizing Energy Saving in Infrastructural Facilities, Kraków–Zakopane, 9–12 September 2013; AGH University of Science and Technology: Kraków, Poland, 2013; pp. 1–11. [Google Scholar]
- Gonet, A.; Sliwa, T.; Złotkowski, A.; Sapińska-Śliwa, A.; Macuda, J. The Analysis of Expansion Thermal Response Test (TRT) for Borehole Heat Exchangers (BHE). In Proceedings of the Thirty-Seventh Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 30 January–1 February 2012; Stanford University: Stanford, CA, USA, 2012; p. 194. [Google Scholar]
- Alberti, L.; Angelotti, A.; Antelmi, M.; La Licata, I. A Numerical Study on the Impact of Grouting Material on Borehole Heat Exchangers Performance in Aquifers. Energies 2017, 10, 703. [Google Scholar] [CrossRef] [Green Version]
- Yoon, S.; Lee, S.R.; Xue, J.; Zosseder, K.; Go, G.H.; Park, H. Evaluation of the Thermal Efficiency and a Cost analysis of Different Types of Ground Heat Exchangers in Energy Piles. Energy Convers. Manag. 2015, 105, 393–402. [Google Scholar] [CrossRef]
- Lund, J.W.; Toth, A.N. Direct Utilization of Geothermal Energy 2020 Worldwide Review. In Proceedings of the World Geothermal Congress 2020, Reykjavik, Iceland, 26 April–2 May 2020; International Geothermal Association: San Francisco, CA, USA, 2020. [Google Scholar]
- Lund, J.W.; Gawell, K.; Boyd, T.L.; Jennejohn, D. The United States of America Country Update 2010. In Proceedings of the World Geothermal Congress 2010, Bali, Indonesia, 25–30 April 2010; pp. 1–18. [Google Scholar]
- Lee, K.S. Underground Thermal Energy Storage; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; p. 152. [Google Scholar]
- Morita, K.; Bollmeier, S.W.; Mizogami, H. An experiment to prove the concept of the downhole coaxial heat exchanger (DCHE) in Hawaii. Geotherm. Resour. Counc. Trans. 1992, 16, 9–17. [Google Scholar]
- Morita, K.; Matsubayashi, O.; Kusunoki, K. Down-hole coaxial heat exchanger using insulated inner pipe for maximum heat extraction. Geotherm. Resour. Counc. Trans. 1985, 9, 17–23. [Google Scholar]
- Schneider, D.; Strothöffer, T.; Broßmann, E. Die 2800 m von Prenzlau oder die tiefste Erdwärmesonde der Welt. Geotherm. Energ. 1996, 16, 10–12. [Google Scholar]
- Clauser, C. Numerical Simulation of Reactive Flowing Hot Aquifers; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Rybach, L.; Eugster, W. Reliable long term performance of BHE systems and market penetration—The Swiss success story. In Proceedings of the 2nd Stockton International Geothermal Conference 1998, Galloway, NJ, USA, 16–17 March 1998; pp. 41–57. [Google Scholar]
- Rybach, L.; Hopkirk, R.J. Shallow and Deep Borehole Heat Exchangers—Achievements and Prospects. In Proceedings of the World Geothermal Congress 1995, Florence, Italy, 18–31 May 1995; pp. 2133–2138. [Google Scholar]
- Kohl, T.; Salton, M.; Rybach, L. Data Analysis of the Deep Borehole Heat Exchanger Plant Weissbad (Switzerland). In Proceedings of the World Geothermal Congress 2000, Kyushu-Tohoku, Japan, 28 May–10 June 2000; pp. 3459–3464. [Google Scholar]
- Kohl, T.; Brenni, R.; Eugster, W. System performance of a deep borehole heat exchanger. Geothermics 2002, 31, 687–708. [Google Scholar] [CrossRef]
- Signorelli, S.; Andenmatten Bertoud, N.; Kohl, T.; Rybach, L. Projekt Statistik Geothermische Nutzung der Schweiz für die Jahre 2002 und 2003; Geowatt AG: Zürich, Switzerland, 2004. [Google Scholar]
- Signorelli, S.; Wagner, R.; Kohl, T.; Rybach, L. Statistik der Geothermischen Nutzung in der Schweiz, Überarbeitung der Geothermiestatistik von 1990 bis 2006; Geowatt AG: Zürich, Switzerland, 2014. [Google Scholar]
- Sliwa, T.; Kotyza, J. Selection of Optimal Construction of Borehole Heat Exchangers Based on Jachowka 2K Well to a Depth 2870 m. In Methodology and Technology of Obtaining Usable Energy from a Single Geothermal Borehole; Sokolowski, J., Ed.; Instytut Gospodarki Surowcami Mineralnymi i Energia PAN, Pracownia Geosynoptyki i Geotermii: Krakow, Poland, 2000; pp. 251–284. (In Polish) [Google Scholar]
- Sokołowski, J.; Ludwikowski, B.; Pawlik, E. On the necessity to evaluate geothermal resources in counties lying within the small Poland and Silesia voivodeships. Techn. Posz. 1999, 2, 17–23. (In Polish) [Google Scholar]
- Deng, J.; Wei, Q.; He, S.; Liang, M.; Zhang, H. What Is the Main Difference between Medium-Depth Geothermal Heat Pump Systems and Conventional Shallow-Depth Geothermal Heat Pump Systems? Field Tests and Comparative Study. Appl. Sci. 2019, 9, 5120. [Google Scholar] [CrossRef] [Green Version]
- Sapińska-Śliwa, A.; Rosen, M.A.; Gonet, A.; Sliwa, T. Deep Borehole Heat Exchangers—A Conceptual and Comparative Review. Int. J. Air-Cond. Refrig. 2016, 24, 1630001. [Google Scholar] [CrossRef]
- Gehlin, S. Thermal Response Teast, Meathod Development and Evaluation. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 2002. [Google Scholar]
- Gonet, A.; Sliwa, T.; Stryczek, S.; Sapińska-Śliwa, A.; Jaszczur, M.; Pająk, L.; Złotkowski, A. Metodyka Identyfikacji Potencjału Cieplnego Górotworu wraz z Technologią Wykonywania i Eksploatacji Otworowych Wymienników Ciepła (Methodology for the Identification of Potential Heat of the Rock Mass along with Technology Implementation and Operation of the Borehole Heat Exchangers; Wydawnictwa AGH: Kraków, Poland, 2011. (In Polish) [Google Scholar]
- Sliwa, T. Badania Podziemnego Magazynowania Ciepła za Pomocą Kolektorów Słonecznych i Wymienników Otworowych Ciepła (Research on Underground Thermal Energy Storage by Use Solar Collectors and Borehole Heat Exchangers; Wydawnictwa AGH: Kraków, Poland, 2012. [Google Scholar]
- Czekalski, D.; Obstawski, P. Procedura testowania pionowego wymiennika gruntowego w warunkach eksploatacyjnych. Ciepłownictwo Ogrzew. Went. 2006, 37/4, 18–21. (In Polish) [Google Scholar]
- Gonet, A.; Sliwa, T. Thermal response test on example of borehole heat exchangers in Ecological Park of Education and Amusement “OSSA”. In Proceedings of the XIV International Scientific-Technical Conference “New Knowledge in the Area of Drilling, Production, Transport and Storage Hydrocarbons”; Technicka Univerzita Kosice: Kosice, Slovakia, 2008; pp. 42–47. [Google Scholar]
- Sapińska-Śliwa, A.; Sliwa, T.; Twardowski, K.; Szymski, K.; Gonet, A.; Żuk, P. Method of Averaging the Eective Thermal Conductivity Based on Thermal Response Tests of Borehole Heat Exchangers. Energies 2020, 13, 3737. [Google Scholar] [CrossRef]
- Luo, J.; Tuo, J.; Huang, H.; Zhu, Y.Q.; Jiao, Y.Y.; Xiang, W.; Rohn, J. Influence of groundwater levels on effective thermal conductivity of the ground and heat transfer rate of borehole heat exchangers. Appl. Therm. Eng. 2018, 128, 508–516. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, H.; Fan, J.; Sun, P.; Sun, S.; Kong, X. The coupled two-step parameter estimation procedure for borehole thermal resistance in thermal response test. Renew. Energy 2020, 154, 672–683. [Google Scholar] [CrossRef]
- Rybach, L. Shallow Systems; Geowatt AG: Zurich, Switzerland, 2012. [Google Scholar]
- Spitler, J.; Gehlin, S. Thermal response testing for ground source heat pump systems—An historical review. Renew. Sustain. Energy Rev. 2015, 50, 1125–1137. [Google Scholar] [CrossRef]
- Badenes, B.; Mateo Pla, M.Á.; Lemus-Zúñiga, L.G.; Sáiz Mauleón, B.; Urchueguía, J.F. On the Influence of Operational and Control Parameters in Thermal Response Testing of Borehole Heat Exchangers. Energies 2017, 10, 1328. [Google Scholar] [CrossRef] [Green Version]
- Perina, T. Derivation of the Theis (1935) Equation by Substitution. Ground Water 2010, 48, 6–7. [Google Scholar] [CrossRef]
- Sliwa, T.; Sojczyńska, A.; Rosen, M.A.; Kowalski, T. Evaluation of temperature profiling quality in determining energy efficiencies of borehole heat exchangers. Geothermics 2019, 78, 129–137. [Google Scholar] [CrossRef]
- Sapińska-Sliwa, A.; Rosen, M.A.; Gonet, A.; Kowalczyk, J.; Sliwa, T. A New Method Based on Thermal Response Tests for Determining Effective Thermal Conductivity and Borehole Resistivity for Borehole Heat Exchangers. Energies 2019, 12, 1072. [Google Scholar] [CrossRef] [Green Version]
- Pawlikowski, B. Dokumentacja Geologiczna Wierceń dla Przyszłej Instalacji Otworowych Wymienników ciepła w Celach Naukowo-Badawczych; AGH: Kraków, Poland, 2008. (In Polish) [Google Scholar]
- Sliwa, T.; Sapińska-Śliwa, A.; Knez, D.; Bieda, A.; Kowalski, T.; Złotkowski, A. Borehole Heat Exchangers: Production and Storage of Heat in the Rock Mass; Laboratory of Geoenergetics book series; Drilling, Oil and Gas Foundation: Kraków, Poland, 2016; Volume 2, p. 175. [Google Scholar]
- Śliwa, T.; Gonet, A. Otworowe wymienniki ciepła jako źródło ciepła lub chłodu na przykładzie Laboratorium Geoenergetyki WWNiG AGH (Borehole heat exchangers as heat or cool source on the basis of Laboratory of Geoenergetics of Drilling, Oil and Gas Faculty in AGH University of Science and Technology). Wiert. Naft. Gaz 2011, 28, 419–430. (In Polish) [Google Scholar]
- Sanner, B.; Hellström, G.; Spitler, J.; Gehlin, S. Thermal Response Test—Current Status and World-Wide Application. In Proceedings of the World Geothermal Congress 2005, Antalya, Turkey, 24–29 April 2005. [Google Scholar]
- Lamarche, L.; Raymond, J.; Pambou, C.H. Evaluation of the Internal and Borehole Resistances during Thermal Response Tests and Impact on Ground Heat Exchanger Design. Energies 2018, 11, 38. [Google Scholar] [CrossRef] [Green Version]
- Sapińska-Śliwa, A. Efektywność Pozyskiwania Ciepła z Górotworu w Aspekcie Sposobu Udostępniania Otworami Wiertniczymi (Effectiveness of Heat Recovery from Rock Mass in the Context of the Production Method by Means of Boreholes); Rozprawy Monografie Number 364; Wydawnictwa AGH: Kraków, Poland, 2019; p. 319. (In Polish) [Google Scholar]
- Grygieńcza, A. Analiza Metod Oceny Mocy Grzewczej Otworowych Wymienników Ciepła (Analysis of Estimation Methods of Borehole Heat Exchangers Power Rating). Master’s Thesis, AGH University of Science and Technology, Drilling, Oil and Gas Faculty, Krakow, Poland, 2009. (In Polish). [Google Scholar]










| Number | The Depth of the Layer’s Top, m | The Depth of the Layer’s Bottom, m | Thickness, m | Lithology | Stratigraphy | Thermal Conductivity, λ, W·m−1·K−1 | Specific Volumetric Heat, cv, MJ·m−3·K−1 |
|---|---|---|---|---|---|---|---|
| 1 | 1.8 | 2.2 | 0.4 | Anthropogenic land (dark gray gully with rubble) | Quaternary (Pleistocene, Holocene) | 1.600 | 2.000 |
| 2 | 2.2 | 2.6 | 0.4 | Silts (gray soil) | 1.600 | 2.200 | |
| 3 | 2.6 | 4.0 | 1.4 | Fine and dusty sand slightly muddied | 1.000 | 2.000 | |
| 4 | 4.0 | 6.0 | 2.0 | Fine sand | 1.200 | 2.500 | |
| 5 | 6.0 | 15.0 | 9.0 | Sandy gravel and gravel | 1.800 | 2.400 | |
| 6 | 15.0 | 30.0 | 15.0 | Gray clay | Tertiary (Miocene) | 2.200 | 2.300 |
| 7 | 30.0 | 78.0 | 48.0 | Gray shale | 2.100 | 2.300 | |
| Weighted mean | 2.039 | 2.309 | |||||
| Parameter | LG-1a | LG-2a | LG-3a | LG-4a | LG-5a |
|---|---|---|---|---|---|
| Construction | Casing pipes PE with diameter 90 mm and wall thickness 5.4 mm, inner pipe PE with diameter 40 mm and wall thickness 2.4 mm | Single U-pipe PE with diameter 40 mm and wall thickness 2.4 mm | Single U-pipe PE with diameter 40 mm and wall thickness 2.4 mm | Single U-pipe PE with diameter 40 mm and wall thickness 2.4 mm | Double U-pipe PE with diameter 32 mm and wall thickness 2.4 mm |
| BHE number | 1 | 2 | 3 | 4 | 5 |
| Construction (Illustration) |  | 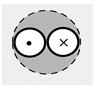 |  | 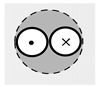 | 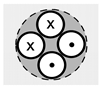 |
| Depth of BHE, m, | 76.2 | ||||
| Sealing used with borehole | Cement slurry seal | Cement slurry seal | Cement slurry seal (ThermoChem) with increased thermal conductivity | Gravel on granulation between 8 and 16 mm and two clay corks—Compactonit | Cement slurry seal |
| Heat conductivity of fill material (hardened grout), λ, W·m−1·K−1 | 1.2 | 1.2 | 2.0 | 1.8 | 1.2 |
| Number | The Depth of the Layer’s Top, m | The Depth of the Layer’s Bottom, m | Thickness, m | Lithology | Thermal Conductivity, λ, W·m−1·K−1 | Specific Volumetric Heat, cv, MJ·m−3·K−1 |
|---|---|---|---|---|---|---|
| 1 | 0 | 2.0 | 2.0 | Sandy clay and stone gravel | 1.60 | 2.400 |
| 2 | 2 | 7.0 | 5.0 | Rubble stratified with clay | 1.60 | 2.400 |
| 3 | 7 | 12.5 | 5.5 | Shales, claystones | 2.10 | 2.300 |
| 4 | 12.5 | 45.5 | 32.0 | Sandstone stratified with siltstones and claystones | 2.30 | 2.000 |
| 5 | 45.5 | 100.0 | 54.5 | Sandy gravel and gravel | 2.30 | 2.000 |
| Weighted mean | 2.24 | 2.045 | ||||
| BHE Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| T0, °C | 12.68 | 12.73 | 12.72 | 13.18 | 12.71 | 10.17 | 10.33 |
| H, m | 76.2 | 100.0 | |||||
| q, W·m−1 | 52.36 | 40.00 | |||||
| BHE NUMBER | BHE NAME | INFLOW TEMPERATURE, °C | OUTFLOW TEMPERATURE, °C | AVERAGE FLOW TEMPERATURE, °C | HEAT CARRIER VOLUMETRIC FLOW RATE, DM3/MIN | TEMPERATURE DIFFERENCE (INFLOW TO OUTFLOW), °C |
|---|---|---|---|---|---|---|
| 1 | LG-1a | 31.261 | 28.394 | 29.828 | 20.00 | 2.867 |
| 2 | LG-2a | 30.848 | 27.941 | 29.395 | 19.99 | 2.907 |
| 3 | LG-3a | 28.336 | 25.462 | 26.899 | 20.00 | 2.874 |
| 4 | LG-4a | 28.044 | 25.168 | 26.606 | 19.89 | 2.876 |
| 5 | LG-5a | 28.704 | 25.824 | 27.264 | 20.00 | 2.880 |
| 6 | F1 | 23.392 | 19.749 | 21.571 | 20.00 | 3.643 |
| 7 | F2 | 22.486 | 18.899 | 20.693 | 20.00 | 3.587 |
| BHE Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Number of Max/Min Values |
|---|---|---|---|---|---|---|---|---|
| BHE Name | LG-1a | LG-2a | LG-3a | LG-4a | LG-5a | F1 | F2 | |
| BHE Construction |  |  |  | 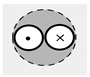 |  | 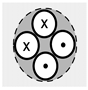 |  | |
| Coaxial | Single U-Pipe + Cement | Single U-Pipe + Thermal Cement | Single U-Pipe + Gravel | Double U-Pipe | Double U-Pipe | Single U-Pipe | ||
| k | 2.1745 | 2377 | 2.085 | 1.488 | 2.081 | 1.216 | 1.276 | - |
| λcm | 1.917 | 1.753 | 2.003 | 2.802 ↑ | 1.962 | 2.701 | 2.600 | 1 |
| λcbrm | 2.121 ↑ | 1.829 ↑ | 1.981 | 2.716 | 1.980 | 2.724 | 2.617 | 2 |
| λpm | 1.905 | 2.403 | 2.072 ↑ | 2.075 | 1.980 | 2.802 ↑ | 2.910 ↑ | 3 |
| λavr | 1.981 | 1.995 | 2.019 | 2.531 | 1.974 | 2.742 | 2709 | - |
| Standard deviation | 0.121 | 0.355 | 0.047 | 0.397 | 0.000 | 0.053 | 0.174 | - |
| Rb.cm | 0.151 | 0.151 | 0.124 | 0.045 ↓ | 0.135 | 0.125 ↓ | 0.112 | 2 |
| Rb.cbrm | 0.161 | 0.116 ↓ | 0.091 ↓ | 0.134 | 0.102 | 0.140 | 0.104 ↓ | 3 |
| Rb.pm | 0.138 ↓ | 0.147 | 0.093 | 0.097 | 0.099 ↓ | 0.141 | 0.113 | 2 |
| Rb.avr | 0.150 | 0.138 | 0.103 | 0.092 | 0112 | 0.135 | 0.110 | - |
| Standard deviation | 0.012 | 0.019 | 0.019 | 0.045 | 0.020 | 0.009 | 0.005 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sliwa, T.; Leśniak, P.; Sapińska-Śliwa, A.; Rosen, M.A. Effective Thermal Conductivity and Borehole Thermal Resistance in Selected Borehole Heat Exchangers for the Same Geology. Energies 2022, 15, 1152. https://doi.org/10.3390/en15031152
Sliwa T, Leśniak P, Sapińska-Śliwa A, Rosen MA. Effective Thermal Conductivity and Borehole Thermal Resistance in Selected Borehole Heat Exchangers for the Same Geology. Energies. 2022; 15(3):1152. https://doi.org/10.3390/en15031152
Chicago/Turabian StyleSliwa, Tomasz, Patryk Leśniak, Aneta Sapińska-Śliwa, and Marc A. Rosen. 2022. "Effective Thermal Conductivity and Borehole Thermal Resistance in Selected Borehole Heat Exchangers for the Same Geology" Energies 15, no. 3: 1152. https://doi.org/10.3390/en15031152
APA StyleSliwa, T., Leśniak, P., Sapińska-Śliwa, A., & Rosen, M. A. (2022). Effective Thermal Conductivity and Borehole Thermal Resistance in Selected Borehole Heat Exchangers for the Same Geology. Energies, 15(3), 1152. https://doi.org/10.3390/en15031152








