Estimating of Non-Darcy Flow Coefficient in Artificial Porous Media
Abstract
:1. Introduction
| Eq. N | Ref. No | |
|---|---|---|
| 1 | [25] | |
| 2 | [18] | |
| 3 | [19] | |
| 4 | [27] | |
| 5 | [33] | |
| 6 | [23] | |
| 7 | [32] | |
| 8 | [31] | |
| 9 | [21] | |
| 10 | [34] | |
| 11 | [35] | |
| 12 | [35] | |
| 13 | [24] |
2. Formulation
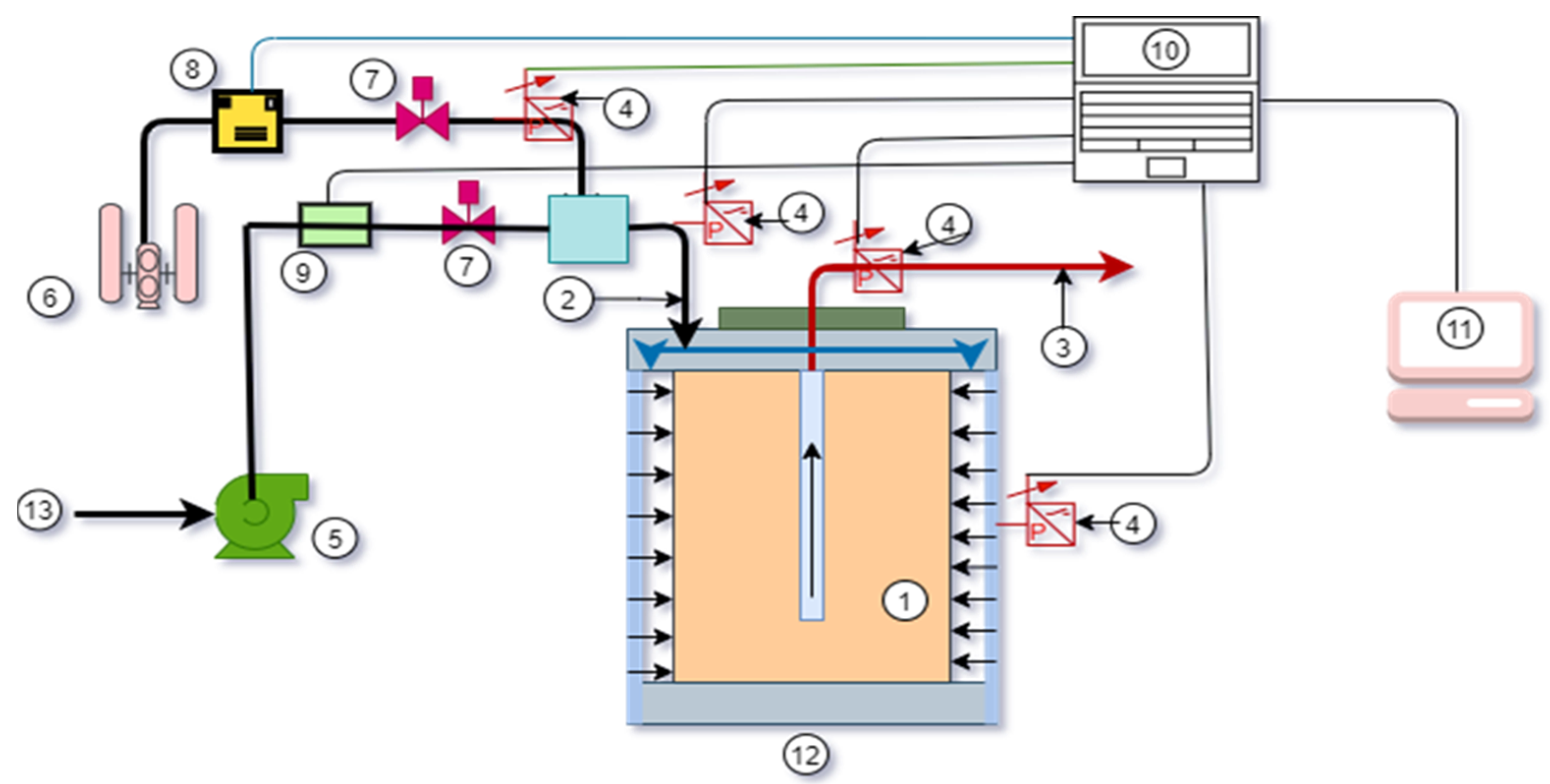
3. Experimental Procedure
3.1. Preparation of the Samples
3.2. Performing the Flow Experiments
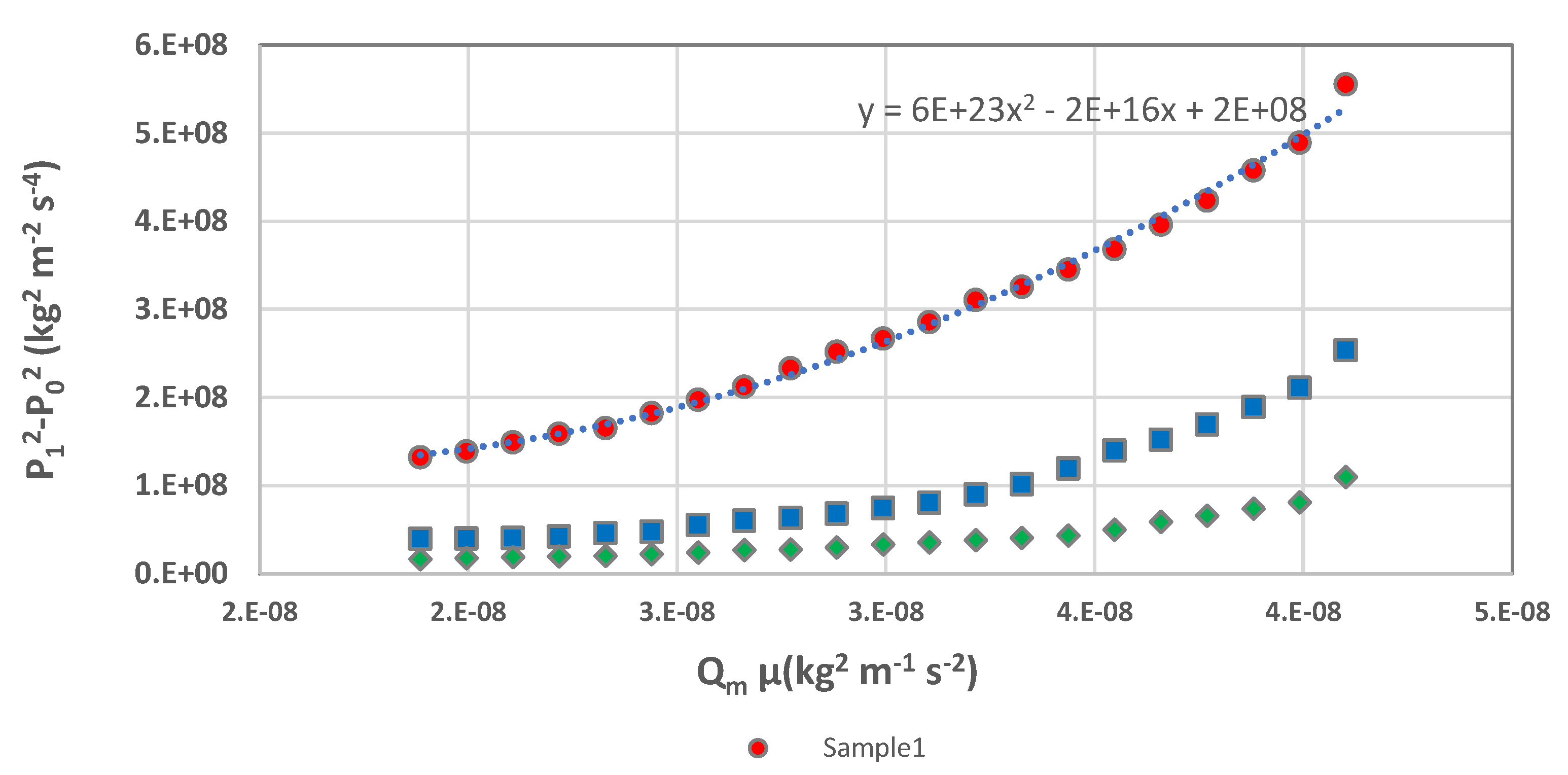
4. Non-Darcy Flow Regime
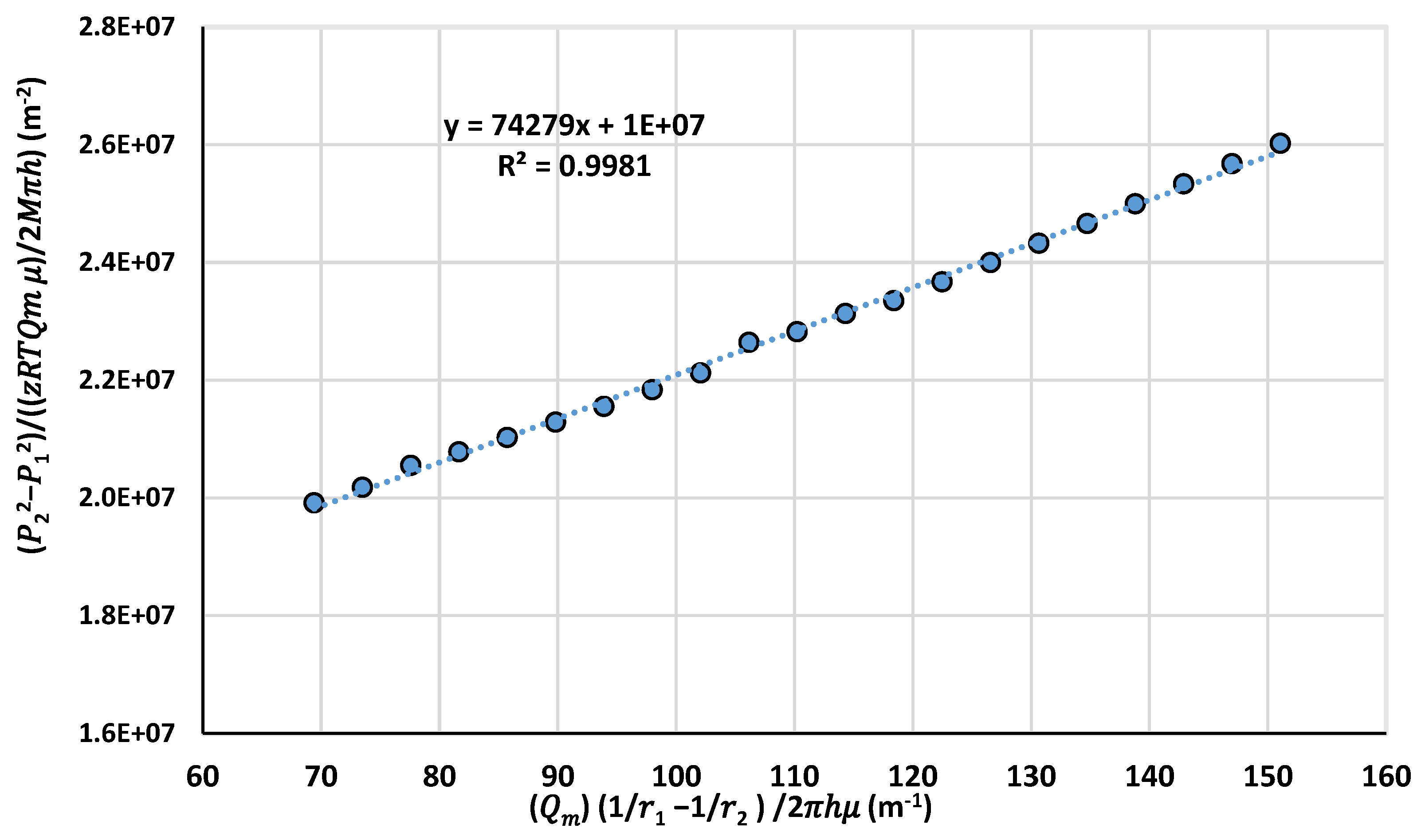
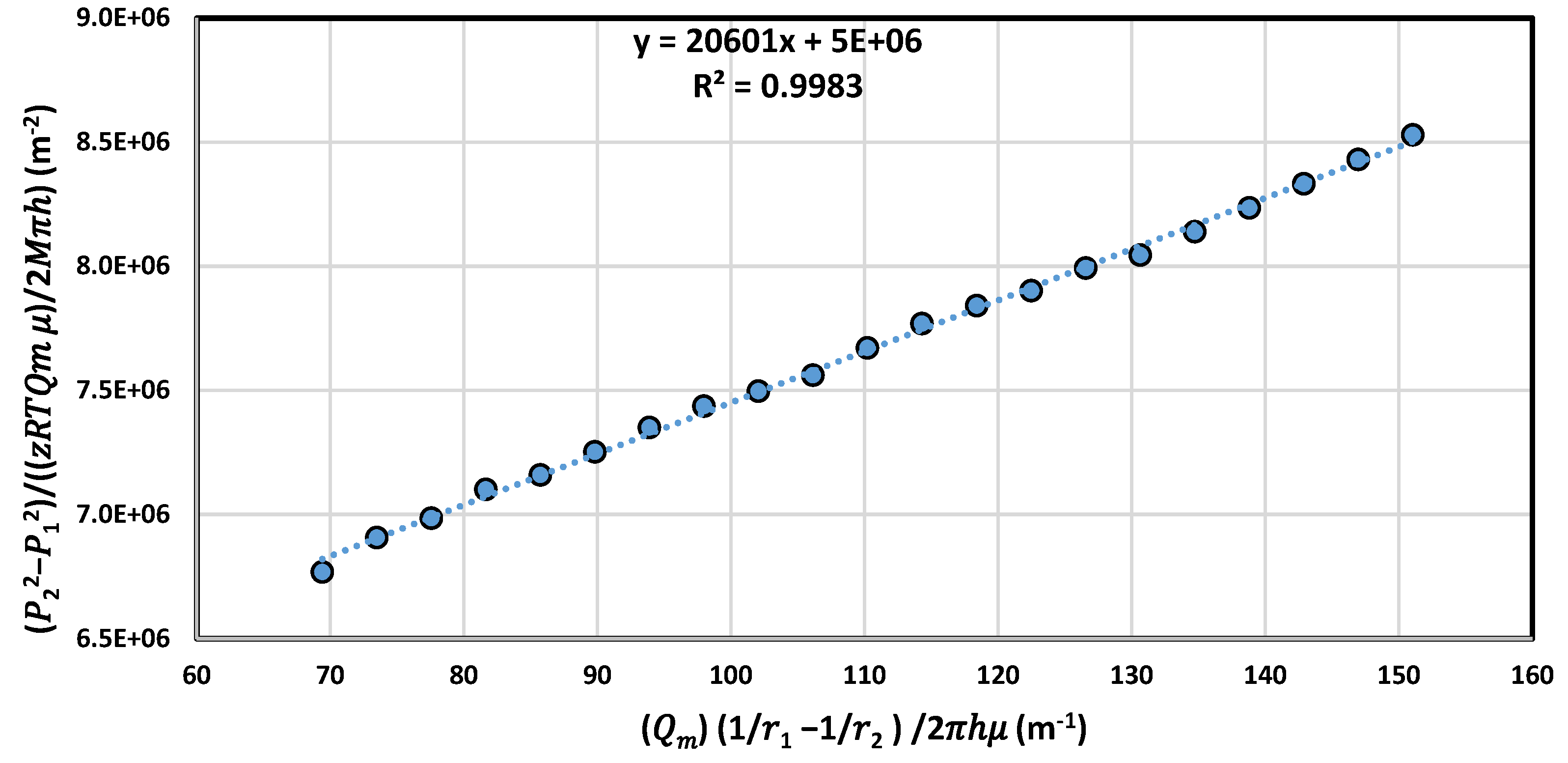
4.1. Calculating Non-Darcy Coefficient β
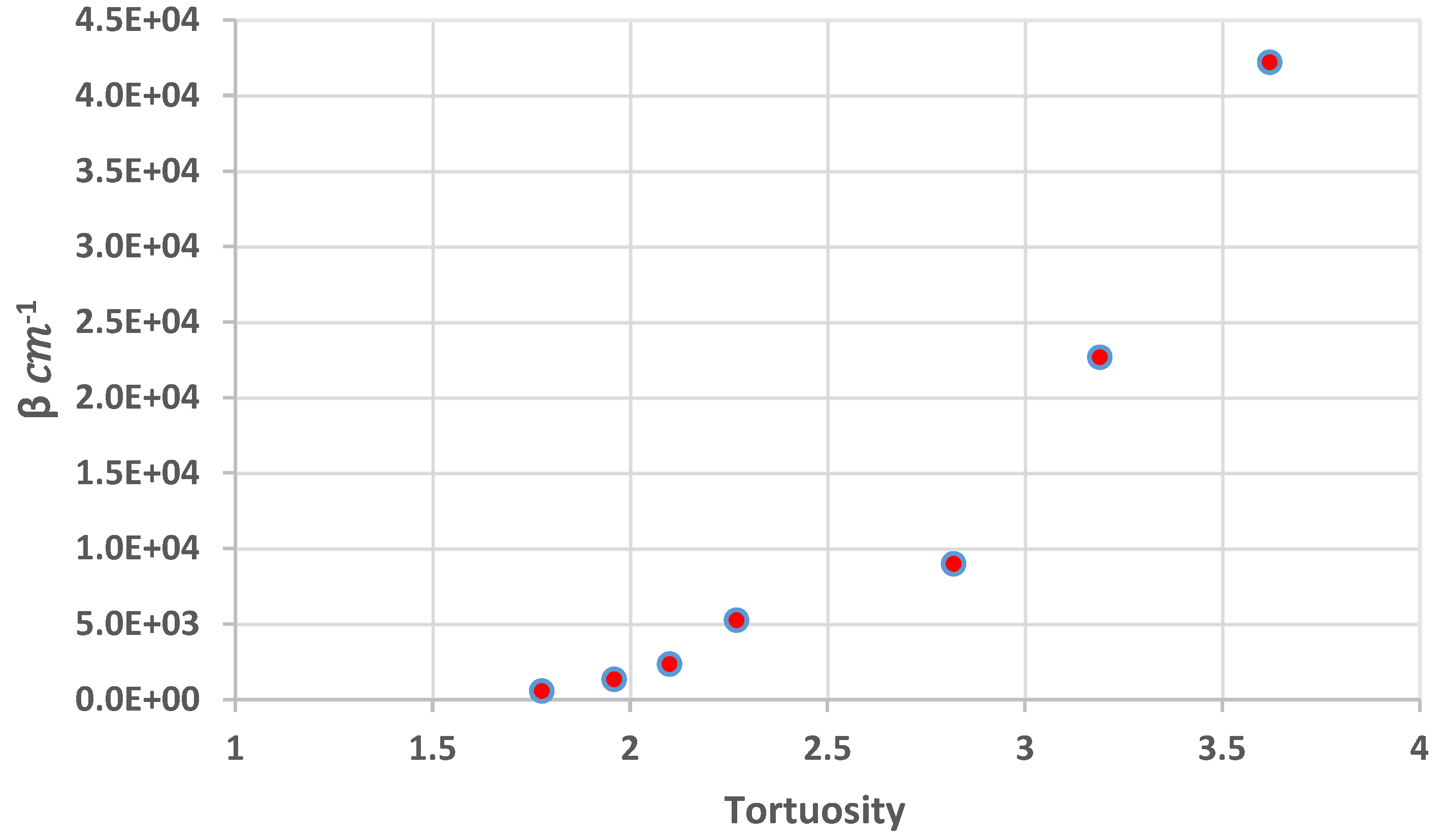
4.2. Effect of Permeability, Porosity, Median Pore Diameter
4.3. Forchheimer Number
5. Conclusions
- This study conducted a radial flow experiment to investigate the existence of non-Darcy flow and calculate the non-Darcy “inertia” coefficient. Seven artificial samples were used. The flow rate of the air ranged from 3 LPM to 99 LPM, and in total, 231 run were conducted.
- Using the mean of pressure square difference versus plot the non-Darcy behavior was conformed. This resulted in lines better fit to a polynomial.
- The non-Darcy coefficient β was calculated for each sample from the experimental results of the pressure gradient and using linear regression. The β measurement results were between 276,180.32 and 19,589.15 .
- The non-Darcy coefficient decreases with the increase in the median pore diameter and the porosity. When the median pore diameter at 25.31 µm non-Darcy coefficient β 276,180.32 and at median pore diameter 181 µm non-Darcy coefficient β = 19,589.15 .
- Forchheimer numbers for airflow at varied flow rates are determined using experimental permeability and non-Darcy coefficient data.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| flow area, | |
| zRT/M, J | |
| molecular weight | |
| pressure, Pa | |
| volumetric flow rate, | |
| mass flow rate, kg | |
| temperature, K | |
| seepage velocity, Darcy’s velocity, m | |
| fluid velocity, superficial velocity, m | |
| compressibility coefficient | |
| non-Darcy flow coefficient, | |
| porosity, adimensional | |
| fluid viscosity, Pa s | |
| fluid density, kg | |
| air density at the air compressor | |
| volumetric flow rate |
References
- Zeng, Z.; Grigg, R. A Criterion for Non-Darcy Flow in Porous Media. Transp. Porous Media 2006, 63, 57–69. [Google Scholar] [CrossRef]
- Whitaker, S. Advances in theory of fluid motion in porous media. Ind. Eng. Chem. 1969, 61, 14–28. [Google Scholar] [CrossRef]
- Hassnizadeh, M.; Gray, W. General conservation equations for multi-phase systems: 1. Averaging procedure. Adv. Water Resour. 1979, 2, 131–144. [Google Scholar] [CrossRef]
- Green, C.T.; Stonestrom, D.A.; Bekins, B.A.; Akstin, K.C.; Schulz, M.S. Percolation and transport in a sandy soil under a natural hydraulic gradient. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef] [Green Version]
- Forchheimer, P. Wasserbewegung durch Boden. Z. Ver. Dtsch. Ing. 1901, 45, 1781–1788. [Google Scholar]
- Kadi, K.S. Non-Darcy Flow In Dissolved Gas-Drive Reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 24–27 September 1980. [Google Scholar]
- Belhaj, H.; Agha, K.; Nouri, A.; Butt, S.; Vaziri, H.; Islam, M.R. Numerical Modeling of Forchheimer’s Equation to Describe Darcy and Non-Darcy Flow in Porous Media. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Jakarta, Indonesia, 9–11 September 2003. [Google Scholar]
- Rushing, J.; Newsham, K.; Fraassen, K.V. Measurement of the Two-Phase Gas Slippage Phenomenon and Its Effect on Gas Relative Permeability in Tight Gas Sands. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 5–8 October 2003. [Google Scholar]
- Katz, D.; Cornell, D.; Vary, J.; Kobayashi, R. Handbook of Natural Gas Engineering; Mcgraw-Hill Book Company: New York, NY, USA, 1959. [Google Scholar]
- Holditch, S.A.; Morse, R.A. The Effects of Non-Darcy Flow on the Behavior of Hydraulically Fractured Gas Wells. J. Pet. Technol. 1979, 28, 1169–1179. [Google Scholar] [CrossRef]
- Guppy, K.H.; Cinco-Ley, H.; Ramey, H.J. Pressure buildup analysis of fractured wells producing at high flowrates. J. Pet. Technol. 1982, 34, 2656–2666. [Google Scholar] [CrossRef]
- Martins, J.P.; Milton-Tayler, D.; Leung, H.K. The Effects of Non-Darcy Flow in Propped Hydraulic Fractures. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 23–26 September 1990. [Google Scholar]
- David, C.; Donald, K. An analysis of high-velocity gas flow through porous media. Ind. Eng. Chem. 1953, 10, 2145–2152. [Google Scholar]
- Shiri, Y.; Hassani, H. Two-component Fluid Front Tracking in Fault Zone and Discontinuity with Permeability Heterogeneity. Rud. -Geol. -Naft. Zb. 2021, 36, 19–30. [Google Scholar] [CrossRef]
- Shiri, Y.; Shiri, A. Numerical Investigation of Fluid Flow Instabilities in Pore-Scale with Heterogeneities in Permeability and Wettability. Rud. -Geol. -Naft. Zb. 2021, 36, 143–156. [Google Scholar] [CrossRef]
- Faez, M.; Ramezanzadeh, A.; Ghavami-Riabi, R.; Tokhmechi, B. The evaluation of the effect of fracture geometry on permeability based on laboratory study and numerical modelling. Rud. -Geol. -Naft. Zb. 2021, 36, 155–164. [Google Scholar] [CrossRef]
- Namdari, S.; Baghbanan, A.; Hashemolhosseini, H. Investigation of the effect of the discontinuity direction on fluid flow in porous rock masses on a large-scale using hybrid FVM-DFN and streamline simulation. Rud. -Geol. -Naft. Zb. 2021, 36, 49–59. [Google Scholar] [CrossRef]
- Ergun, S. Fluid flow through packed column. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- John, J.; Donald, K. Applications of unsteady state gas flow calculations. In Proceedings of the Research Conference “Flow of Natural Gas from Reservoirs”, Ann Arbor, MI, USA, 30 June–1 July 1955. [Google Scholar]
- Cooke, C.J. Conductivity of Fracture Proppants in Multiple Layers. J. Pet. Technol. 1973, 25, 1101–1107. [Google Scholar] [CrossRef]
- Macdonald, I.F.; El-Sayed, M.S.; Mow, K.; Dullien, F.A.L. Flow through Porous Media—The Ergun Equation Revisited. Ind. Eng. Chem. Fundam. 1979, 18, 199–208. [Google Scholar] [CrossRef]
- Kutasov, I.M. Equation Predicts Non-Darcy Flow Coefficient. Oil Gas J. 1993, 91, 66–67. [Google Scholar]
- Liu, X.; Civan, F.; Evans, R. Correlation of the Non-Darcy Flow Coefficient. J. Can. Pet. Technol. 1995, 34, PETSOC-95-10-05. [Google Scholar] [CrossRef]
- Coles, M.E.; Hartman, K.J. Non-Darcy Measurements in Dry Core and the Effect of Immobile Liquid. In Proceedings of the SPE Gas Technology Symposium, Calgary, AB, Canada, 15–18 March 1998. [Google Scholar]
- Pascal, H.; Quillian, R.G. Analysis Of Vertical Fracture Length And Non-Darcy Flow Coefficient Using Variable Rate Tests. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 24–27 September 1980. [Google Scholar]
- Cornell, D.; Katz, D.L. Flow of Gases through Consolidated Porous Media. Ind. Eng. Chem. 1953, 45, 2145–2152. [Google Scholar] [CrossRef]
- Geertsma, J. Estimating the Coefficient of Inertial Resistance in Fluid Flow Through Porous Media. Soc. Pet. Eng. J. 1974, 14, 445–450. [Google Scholar] [CrossRef]
- Evans, E.; Evans, R. Influence of an Immobile or Mobile Saturation on Non-Darcy Compressible Flow of Real Gases in Propped Fractures. J. Pet. Technol. 1988, 40, 1345–1351. [Google Scholar] [CrossRef]
- Whitney, D.D. Characterization of the Non-Darcy Flow Coefficient in Propped Hydraulic Fractures. Master’s Thesis, University of Oklahoma, Norman, OK, USA, 1988. [Google Scholar]
- Li, D. Analytical Study of the Wafer Non-Darcy Flow Experiments. In Proceedings of the SPE Western Regional/AAPG Pacific Section Joint Meeting, Anchorage, AK, USA, 8–10 May 2002. [Google Scholar]
- Tek, M.R.; Coats, K.H.; Katz, D.L. Turbulence on Flow of Natural Gas Through Porous Reservoirs. J. Pet. Technol. 1962, 14, 799–806. [Google Scholar] [CrossRef]
- Yao, Y.; Li, G.; Qin, P. Seepage features of high-velocity non-Darcy flow in highly productive reservoirs. J. Nat. Gas Sci. Eng. 2015, 27, 1732–1738. [Google Scholar] [CrossRef]
- Core, J. Using the Inertial Coefficient, B, To Characterize Heterogeneity in Reservoir Rock. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 27–30 September 1987. [Google Scholar]
- Li, D.; Svec, R.K.; Engler, T.W.; Grigg, R.B. Modeling and Simulation of the Wafer Non-Darcy Flow Experiments. In Proceedings of the SPE Western Regional Meeting, Bakersfield, CA, USA, 8–10 March 2001. [Google Scholar]
- Thauvin, F.; Mohanty, K.K. Network Modeling of Non-Darcy Flow Through Porous Media. Transp. Porous Media 1998, 31, 19–37. [Google Scholar] [CrossRef]
- Shachi, S.; Yadav, B.K.; Rahman, M.A.; Pal, M. Migration of CO2 through Carbonate Cores: Effect of Salinity, Pressure, and Cyclic Brine-CO2 Injection. J. Environ. Eng. 2020, 146, 04019114. [Google Scholar] [CrossRef]
- Ahammad, M.J.; Alam, J.; Rahman, M.; Butt, S.D. Numerical simulation of two-phase flow in porous media using a wavelet based phase-field method. Chem. Eng. Sci. 2017, 173, 230–241. [Google Scholar] [CrossRef]
- Sajjad Rabbani, H.; Osman, Y.; Almaghrabi, I.; Azizur Rahman, M.; Seers, T. The Control of Apparent Wettability on the Efficiency of Surfactant Flooding in Tight Carbonate Rocks. Processes 2019, 7, 684. [Google Scholar] [CrossRef] [Green Version]
- Ding, L.; Cui, L.; Jouenne, S.; Gharbi, O.; Pal, M.; Bertin, H.; Rahman, M.A.; Romero, C.; Guérillot, D. Estimation of Local Equilibrium Model Parameters for Simulation of the Laboratory Foam-Enhanced Oil Recovery Process Using a Commercial Reservoir Simulator. ACS Omega 2020, 5, 23437–23449. [Google Scholar] [CrossRef]
- Rahman, M.; Mustafiz, S.; Koksal, M.; Islam, M. Quantifying the skin factor for estimating the completion efficiency of perforation tunnels in petroleum wells. J. Pet. Sci. Eng. 2007, 58, 99–110. [Google Scholar] [CrossRef]
- Rahman, M.; Mustafiz, S.; Biazar, J.; Koksal, M.; Islam, M. Investigation of a novel perforation technique in petroleum wells—Perforation by drilling. J. Frankl. Inst. 2007, 344, 777–789. [Google Scholar] [CrossRef]
- Zheng, L.; Rahman, M.; Ahammad, M.J.; Butt, S.D.; Alam, J. Experimental and Numerical Investigation of a Novel Technique for Perforation in Petroleum Reservoir. In Proceedings of the SPE International Conference and Exhibition on Formation Damage Control, Lafayette, LA, USA, 19–21 February 2016. [Google Scholar] [CrossRef]
- Abobaker, E.; Elsanoose, A.; Khan, F.; Rahman, M.A.; Aborig, A.; Noah, K. A New Evaluation of Skin Factor in Inclined Wells with Anisotropic Permeability. Energies 2021, 14, 5585. [Google Scholar] [CrossRef]
- Ahammad, J.; Rahman, A.; Butt, S.; Alam, M. An Experimental Development to Characterise the Flow Phenomena at the Near-Wellbore Region. In Proceedings of the ASME 2019 38th International Conference on Ocean, Offshore and Arctic Engineering, Glasgow, UK, 9–14 June 2019. [Google Scholar]
- Abobaker, E.; Elsanoose, A.; Rahman, M.A.; Aborig, A.; Zhang, Y.; Sripal, E. Investigation-the-Effect-Mixing-Grain-Size-and-Epoxy-Glue-Content-on-Index-Properties-of-Synthetic-Sandstone-Sample. In Proceedings of the Canadian Society for Mechanical Engineering International Congress, Charlottetown, PE, Canada, 21–24 June 2020. [Google Scholar]


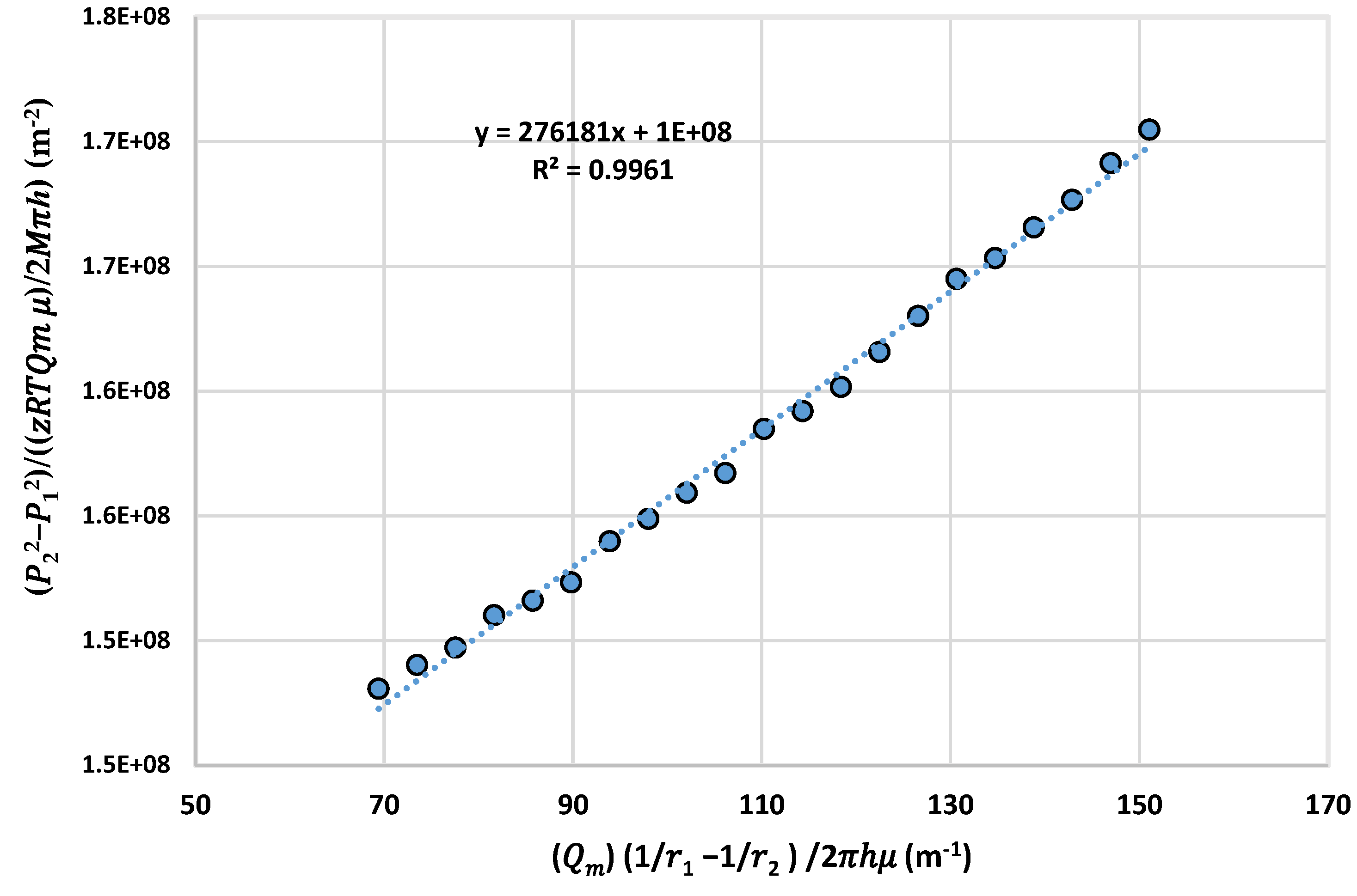


| Sample No. | The Index Properties for the Samples | |||
|---|---|---|---|---|
| Permeability (mD) | Porosity (%) | Tortuosity | MPD (µm) | |
| Sample 1 | 2035.95 | 33 | 3.62 | 25.31 |
| Sample 2 | 3981.50 | 29.23 | 3.19 | 32.14 |
| Sample 3 | 6292.66 | 27 | 2.82 | 45.27 |
| Sample 4 | 8127.04 | 26.6 | 2.27 | 60.6101 |
| Sample 5 | 12,281.50 | 25.8 | 2.10 | 81 |
| Sample 6 | 16,320.24 | 25.5 | 1.96 | 100 |
| Sample 7 | 26,151.72 | 25 | 1.7765 | 181.7485 |
| Sample No | Geertsma [27] | Tek [31] | |
|---|---|---|---|
| Sample 1 | 276,180.32 | 440,041.83 | 14,556.91 |
| Sample 2 | 210,821.61 | 153,871.68 | 5708.06 |
| Sample 3 | 169,710.87 | 122,395.33 | 2954.77 |
| Sample 4 | 119,204.17 | 29,141.28 | 1957.57 |
| Sample 5 | 73,103.274 | 17,068.78 | 1117.16 |
| Sample 6 | 38,663.54 | 10,077.68 | 742.99 |
| Sample 7 | 19,589.15 | 4165.19 | 377.27 |
| Q LPM/s | Sample 3 | Sample 4 | Sample 5 | Sample 7 |
|---|---|---|---|---|
| 3 | 0.0682 | 0.0573 | 0.0124 | 0.0073 |
| 9 | 0.2041 | 0.1708 | 0.0369 | 0.0146 |
| 15 | 0.3389 | 0.2829 | 0.0613 | 0.0218 |
| 21 | 0.4729 | 0.3938 | 0.0854 | 0.0291 |
| 27 | 0.606 | 0.5033 | 0.1093 | 0.0362 |
| 33 | 0.738 | 0.6116 | 0.1329 | 0.0434 |
| 39 | 0.869 | 0.7185 | 0.1564 | 0.0506 |
| 45 | 1.000 | 0.8243 | 0.1797 | 0.0578 |
| 51 | 1.129 | 0.9288 | 0.2027 | 0.0649 |
| 57 | 1.258 | 1.032 | 0.2256 | 0.0720 |
| 63 | 1.386 | 1.134 | 0.2483 | 0.0791 |
| 69 | 1.512 | 1.235 | 0.2707 | 0.0862 |
| 75 | 1.638 | 1.335 | 0.2929 | 0.0932 |
| 81 | 1.764 | 1.434 | 0.3150 | 0.1003 |
| 87 | 1.888 | 1.531 | 0.3369 | 0.1073 |
| 93 | 2.0116 | 1.628 | 0.3586 | 0.1143 |
| 99 | 2.1344 | 1.723 | 0.3801 | 0.1213 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elsanoose, A.; Abobaker, E.; Khan, F.; Rahman, M.A.; Aborig, A.; Butt, S.D. Estimating of Non-Darcy Flow Coefficient in Artificial Porous Media. Energies 2022, 15, 1197. https://doi.org/10.3390/en15031197
Elsanoose A, Abobaker E, Khan F, Rahman MA, Aborig A, Butt SD. Estimating of Non-Darcy Flow Coefficient in Artificial Porous Media. Energies. 2022; 15(3):1197. https://doi.org/10.3390/en15031197
Chicago/Turabian StyleElsanoose, Abadelhalim, Ekhwaiter Abobaker, Faisal Khan, Mohammad Azizur Rahman, Amer Aborig, and Stephen D. Butt. 2022. "Estimating of Non-Darcy Flow Coefficient in Artificial Porous Media" Energies 15, no. 3: 1197. https://doi.org/10.3390/en15031197
APA StyleElsanoose, A., Abobaker, E., Khan, F., Rahman, M. A., Aborig, A., & Butt, S. D. (2022). Estimating of Non-Darcy Flow Coefficient in Artificial Porous Media. Energies, 15(3), 1197. https://doi.org/10.3390/en15031197









