Photovoltaic System with a Battery-Assisted Quasi-Z-Source Inverter: Improved Control System Design Based on a Novel Small-Signal Model
Abstract
:1. Introduction
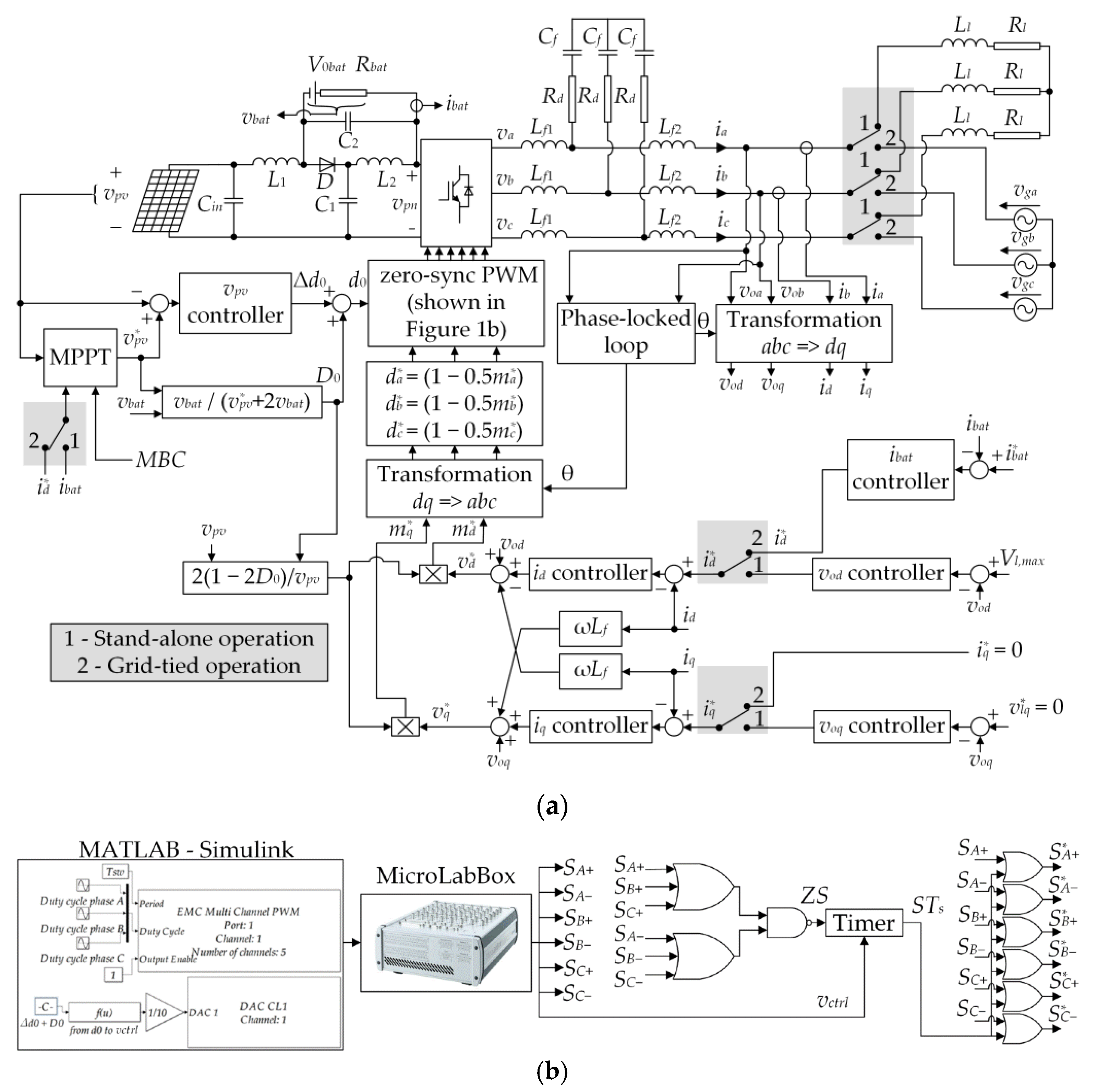
2. System Configuration
2.1. Grid-Tied Operation
2.2. Stand-Alone Operation
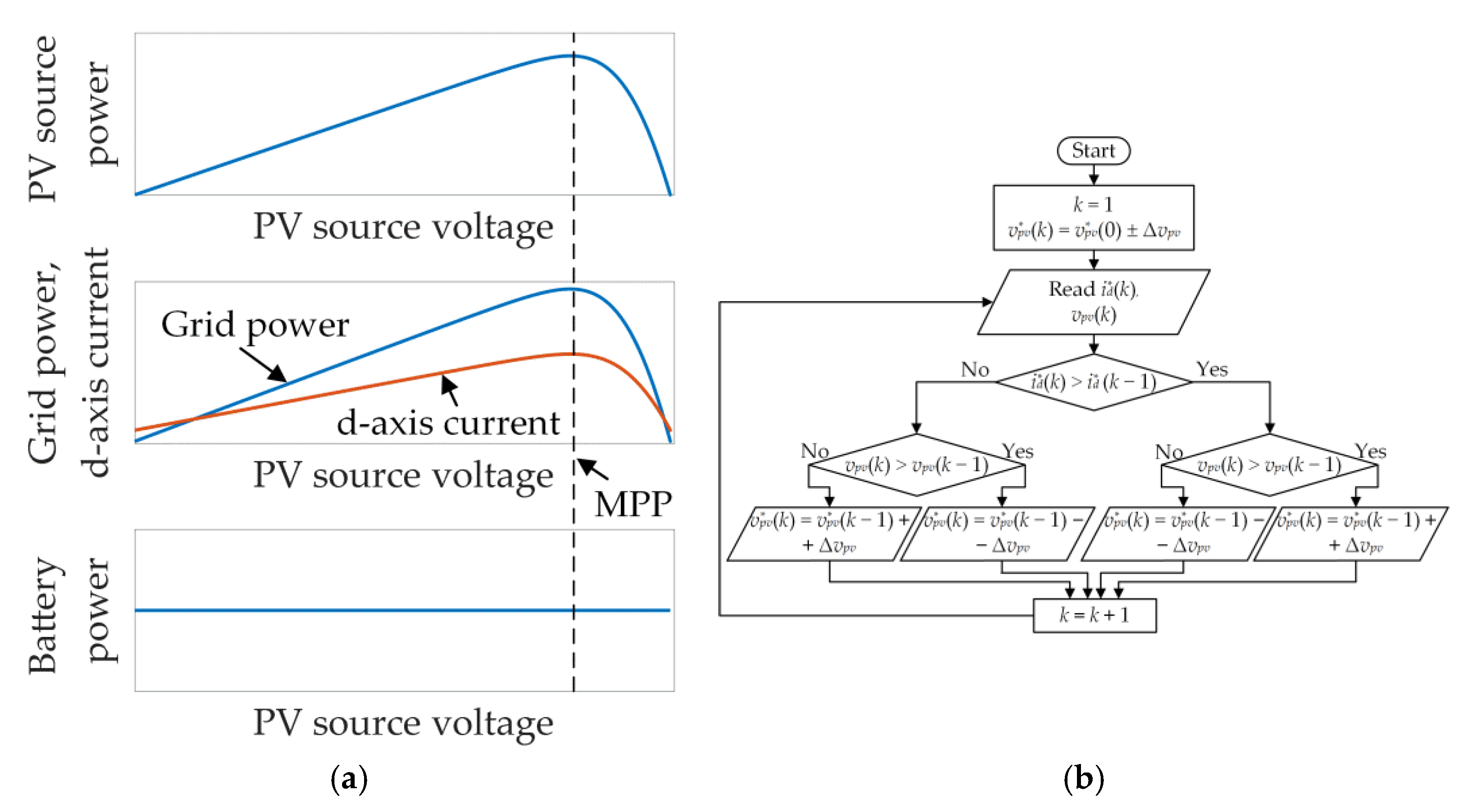
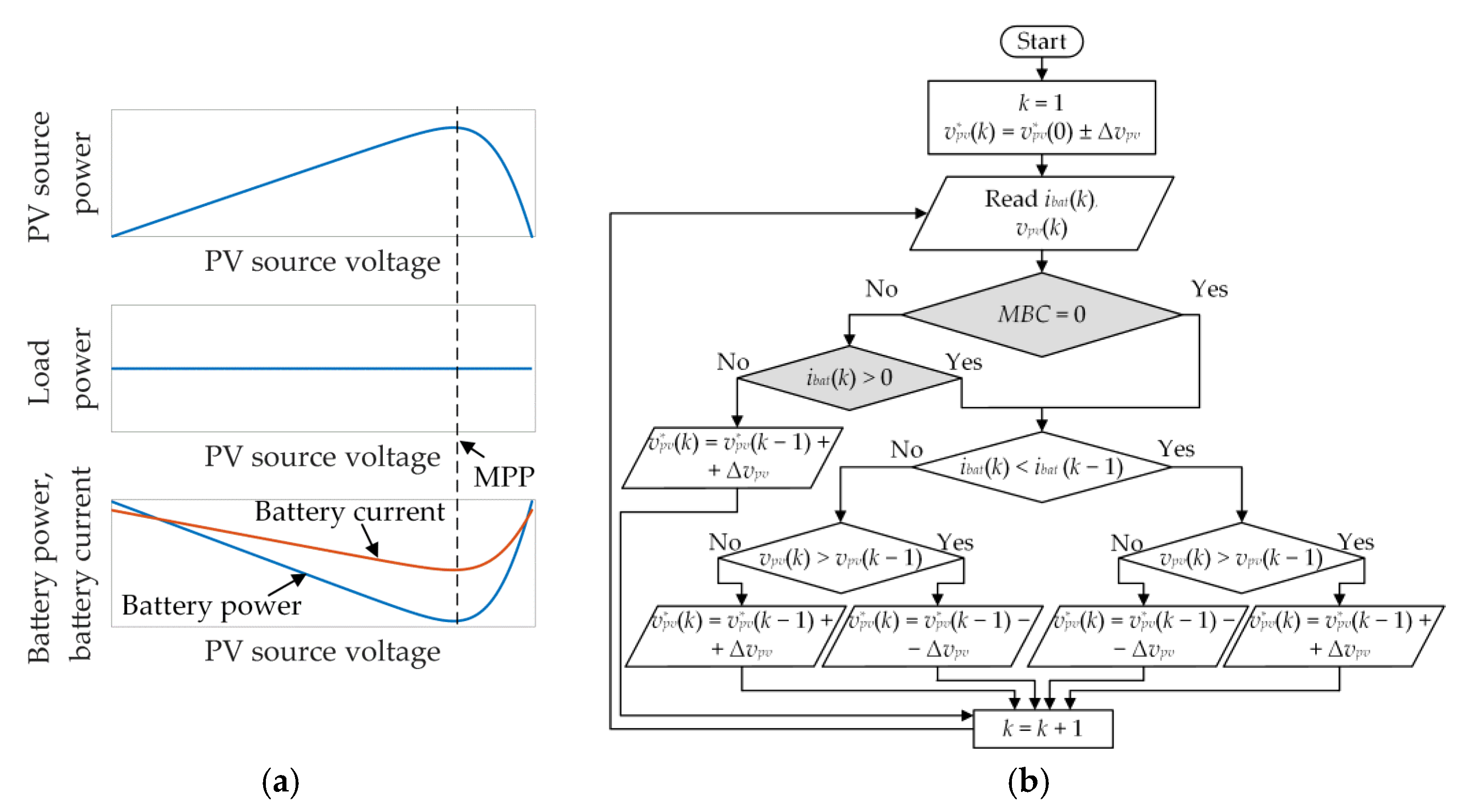
2.3. Maximum Power Point Tracking of the Photovoltaic Source
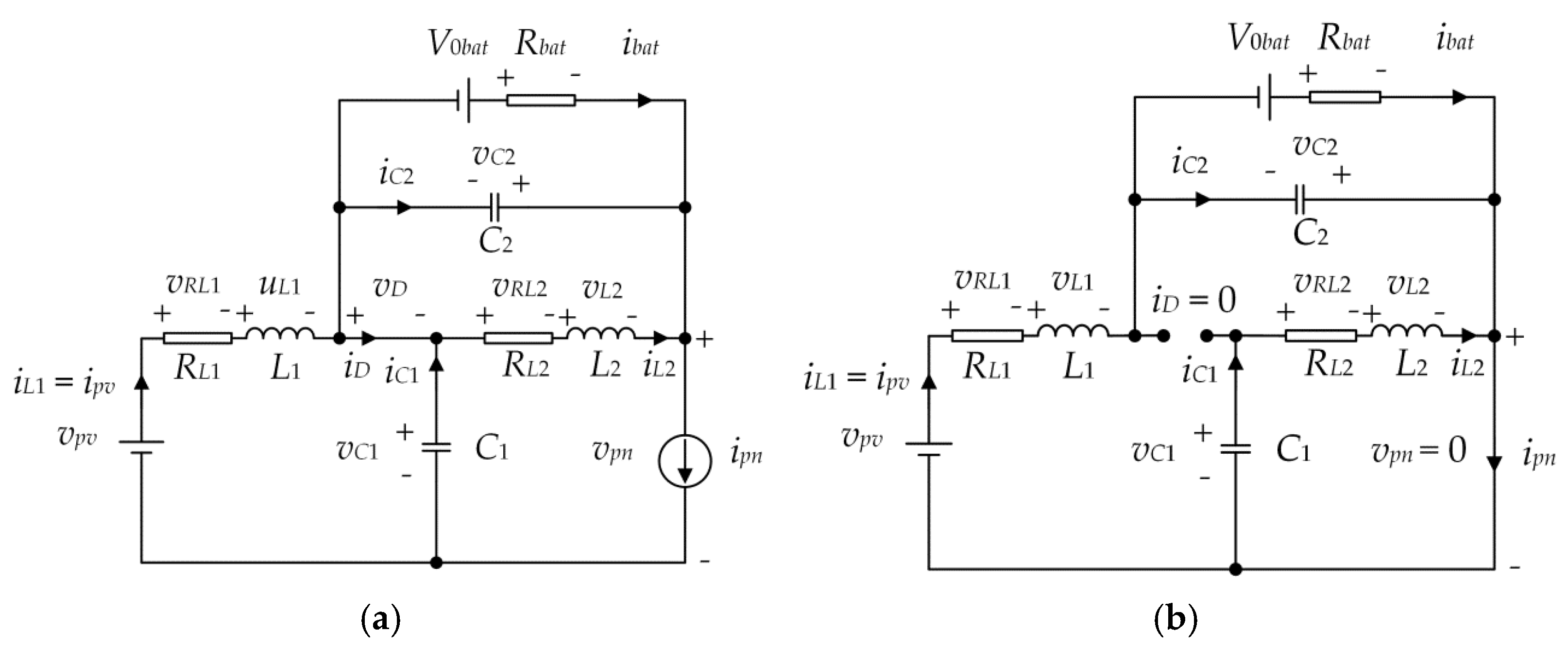
3. Small-Signal Model of the System
4. Control Schemes for the Grid-Tied Operation and Stand-Alone Operation
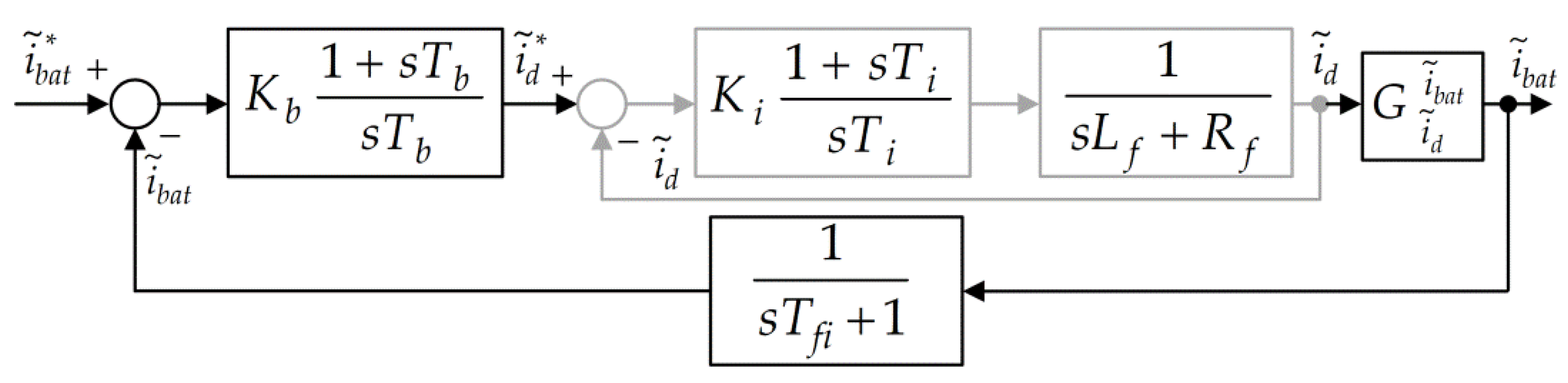
4.1. Control of the Battery Current for the Grid-Tied Operation
4.2. Control of the Inverter Output Voltage for the Stand-Alone Operation
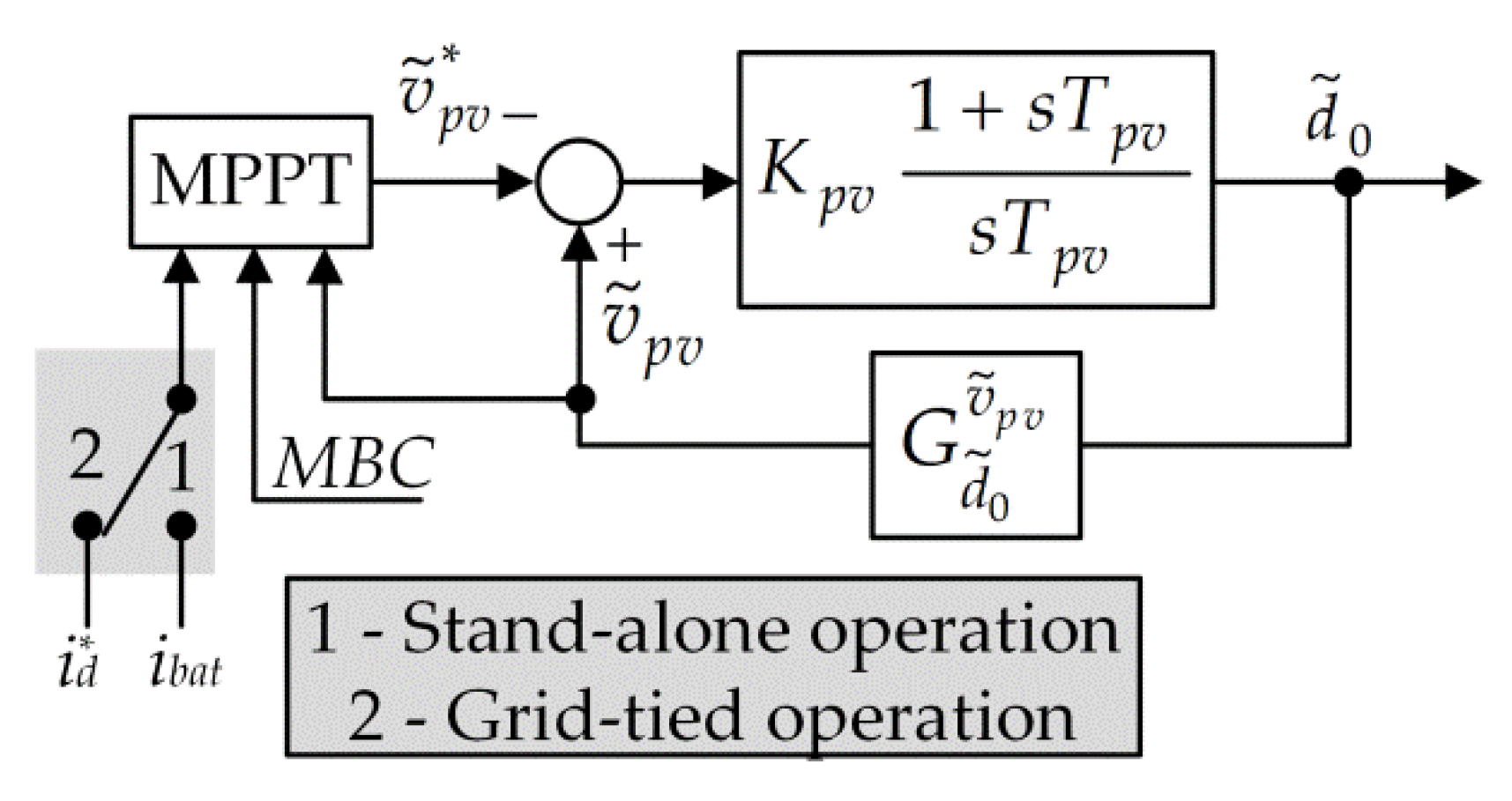
4.3. Control of the Photovoltaic Source Voltage and Maximum Power Point Tracking
5. Experimental Implementation of the System
5.1. Laboratory Setup
- DC power supply Chroma 62050H 600S, programmed to emulate 16 series-connected PV panels KC200GT (Kyocera).
- qZSI impedance network with L1 = L2 = 20.2 mH (unsaturated), RL = 0.5 Ω (at 25 °C)), and C1 = C2 = 50 μF (ESR = 7.8 mΩ).
- qZSI three-phase inverter bridge (IXBX75N170 IGBTs (IXYS) and SKHI 22B(R) drivers (Semikron)).
- LCL filter at the qZSI output stage (Lf1 = 8.64 mH, Lf2 = 4.32 mH, Rf1 = 0.1036 Ω, Rf2 = 0.0518 Ω, Cf = 4 μF, Rd = 10 Ω), with the design details given in Appendix A.
- MicroLabBox controller board (dSpace) for the qZSI control.
- A symmetric three-phase resistive load.
- The battery system composed of 22 lead-acid batteries connected in series with a total open-circuit voltage amounting to about 270 V.
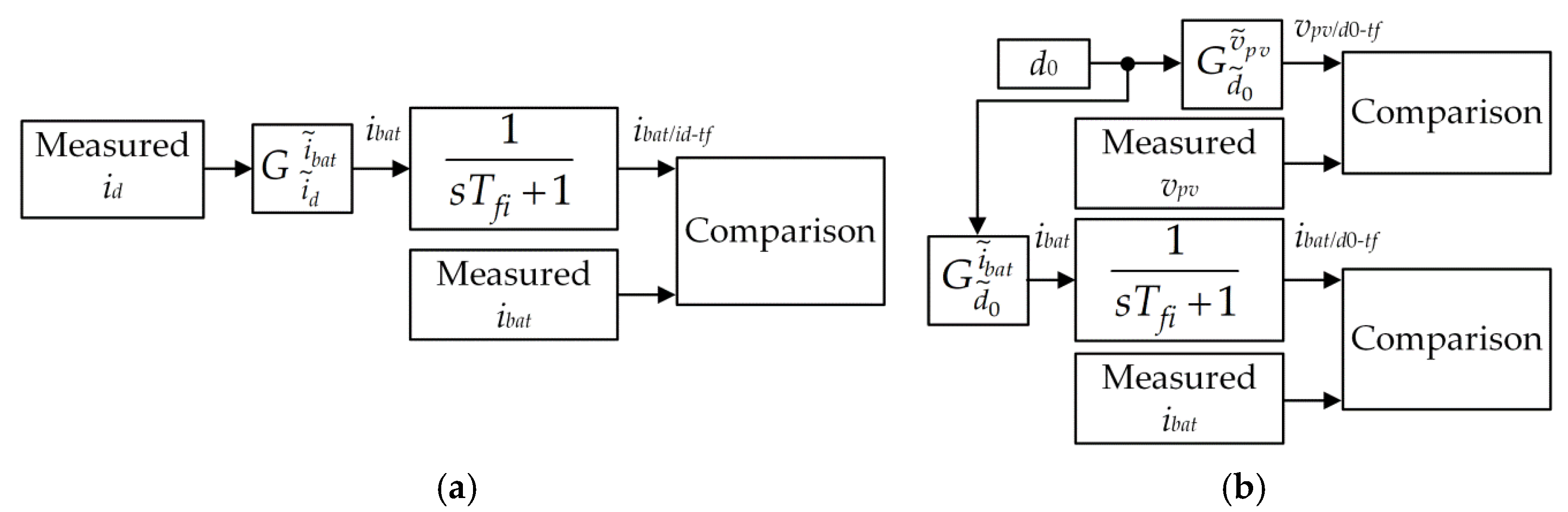
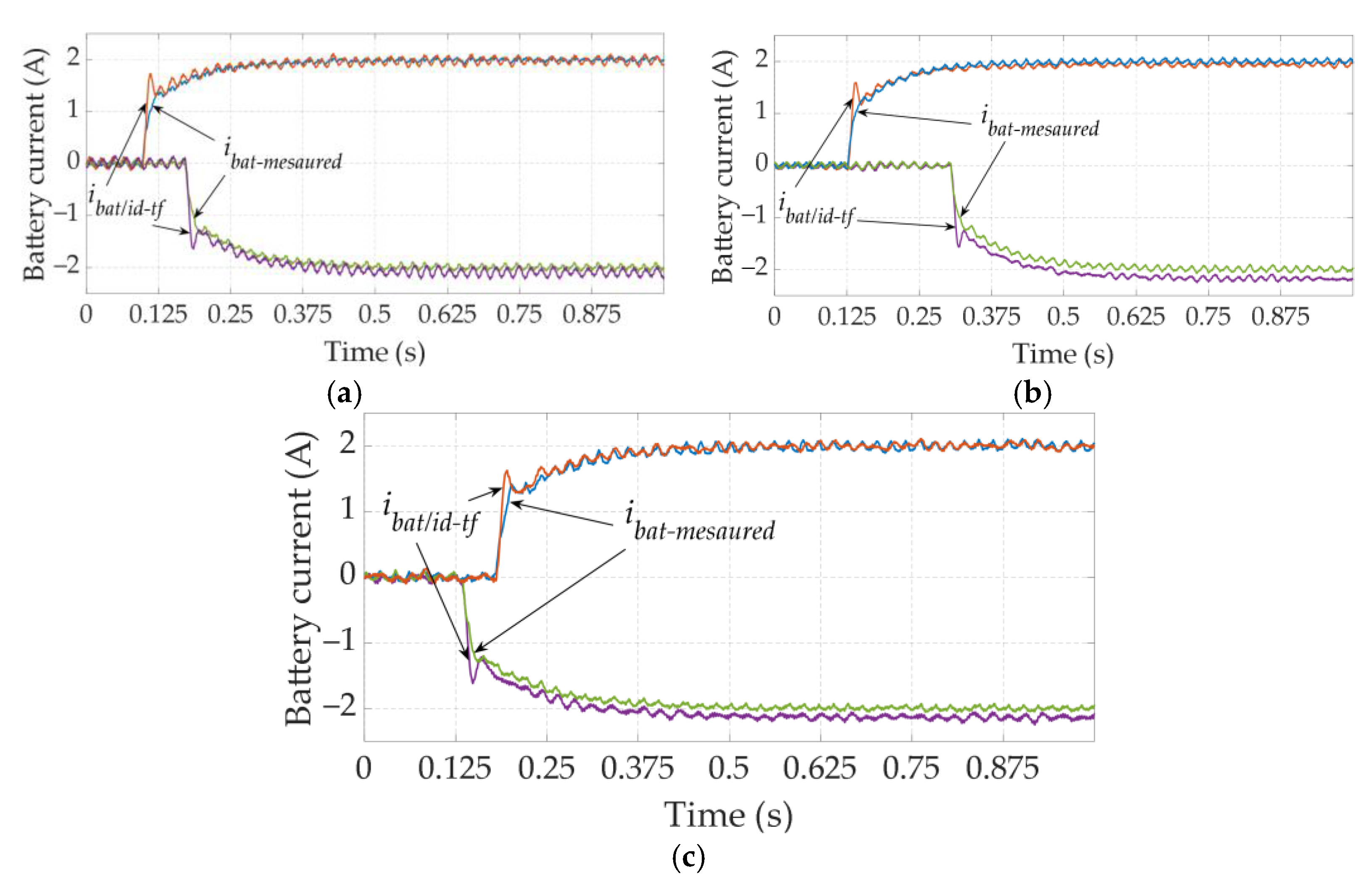
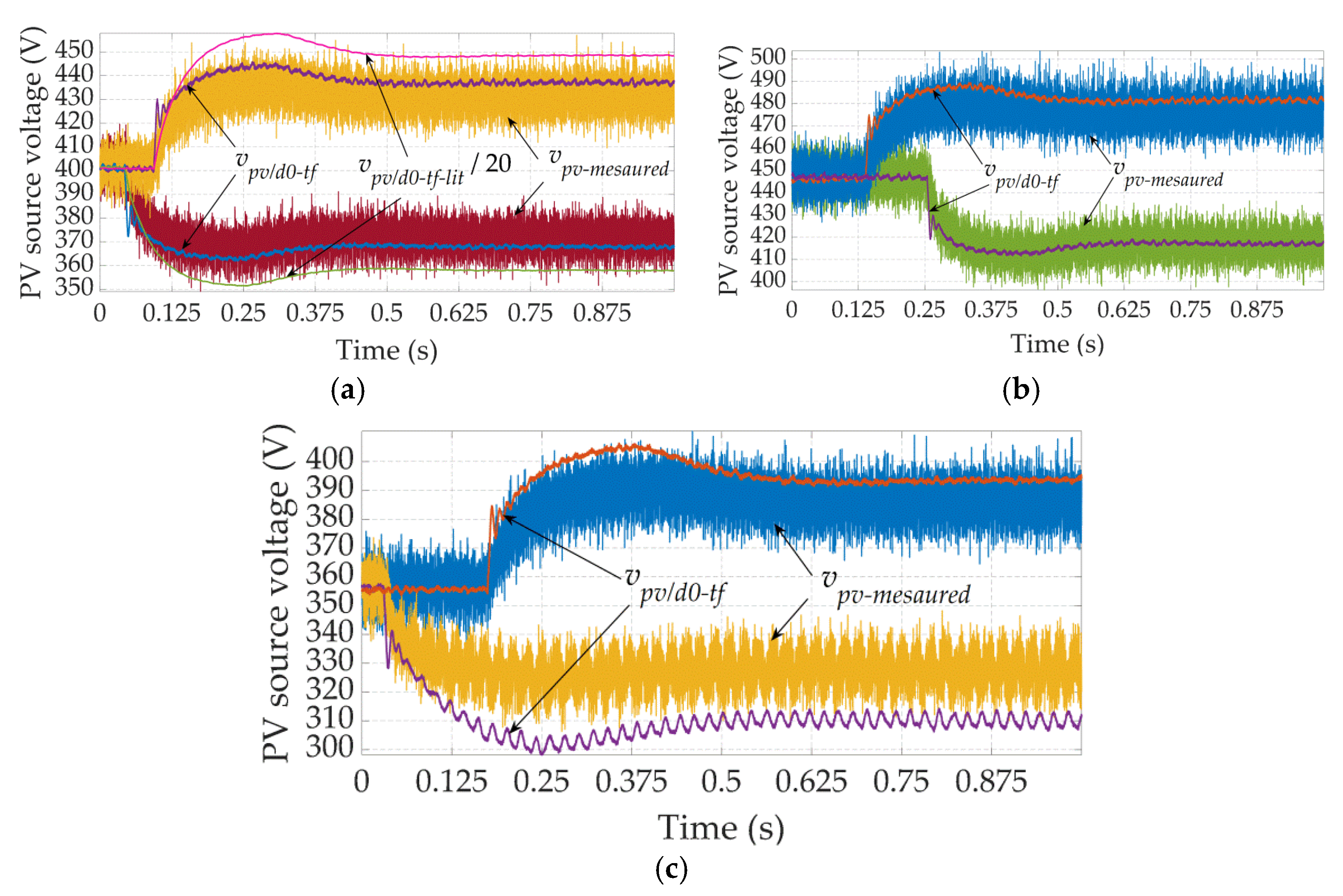
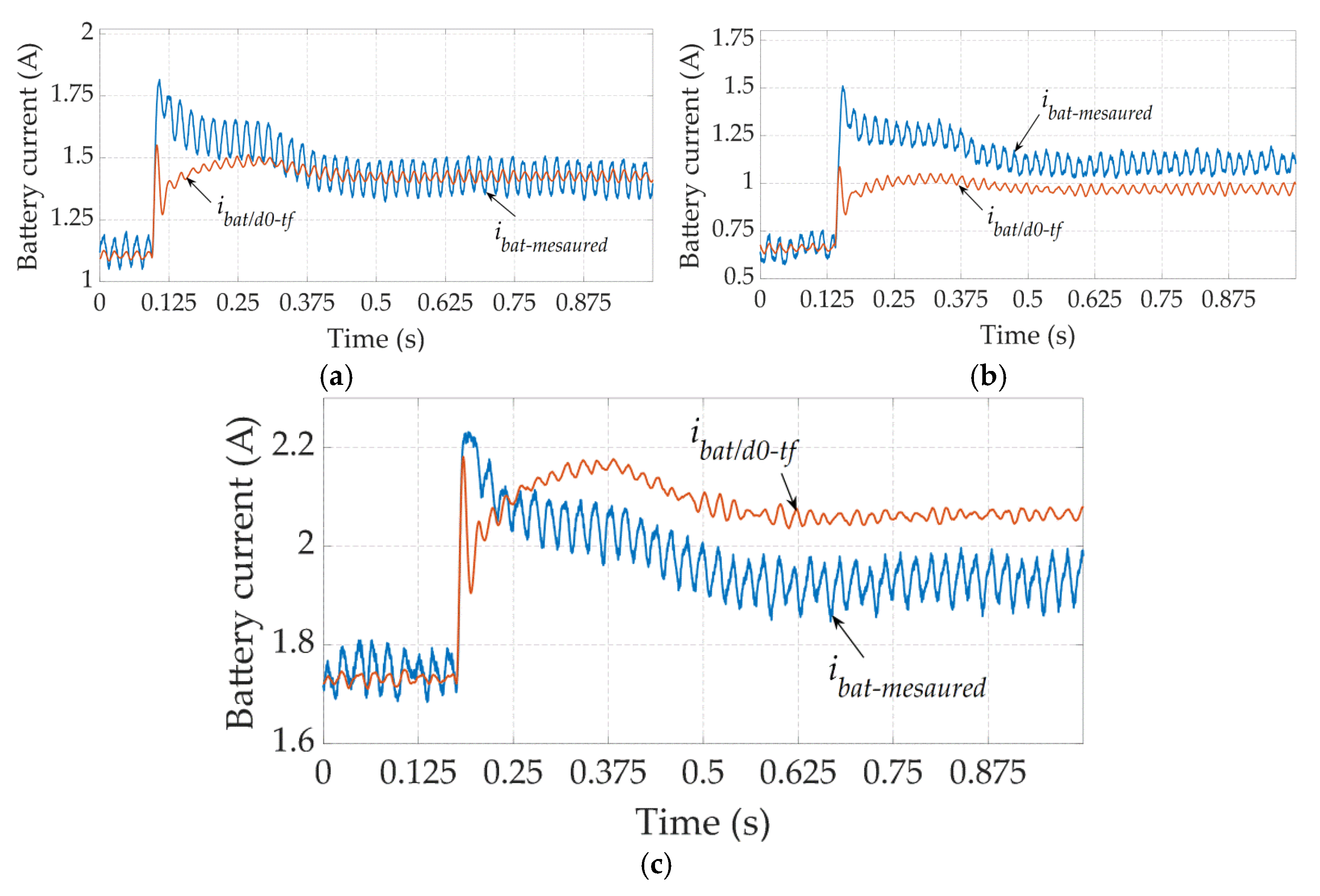
5.2. Accuracy Verification of the Proposed Transfer Functions
5.3. Tuning of the PI Controllers
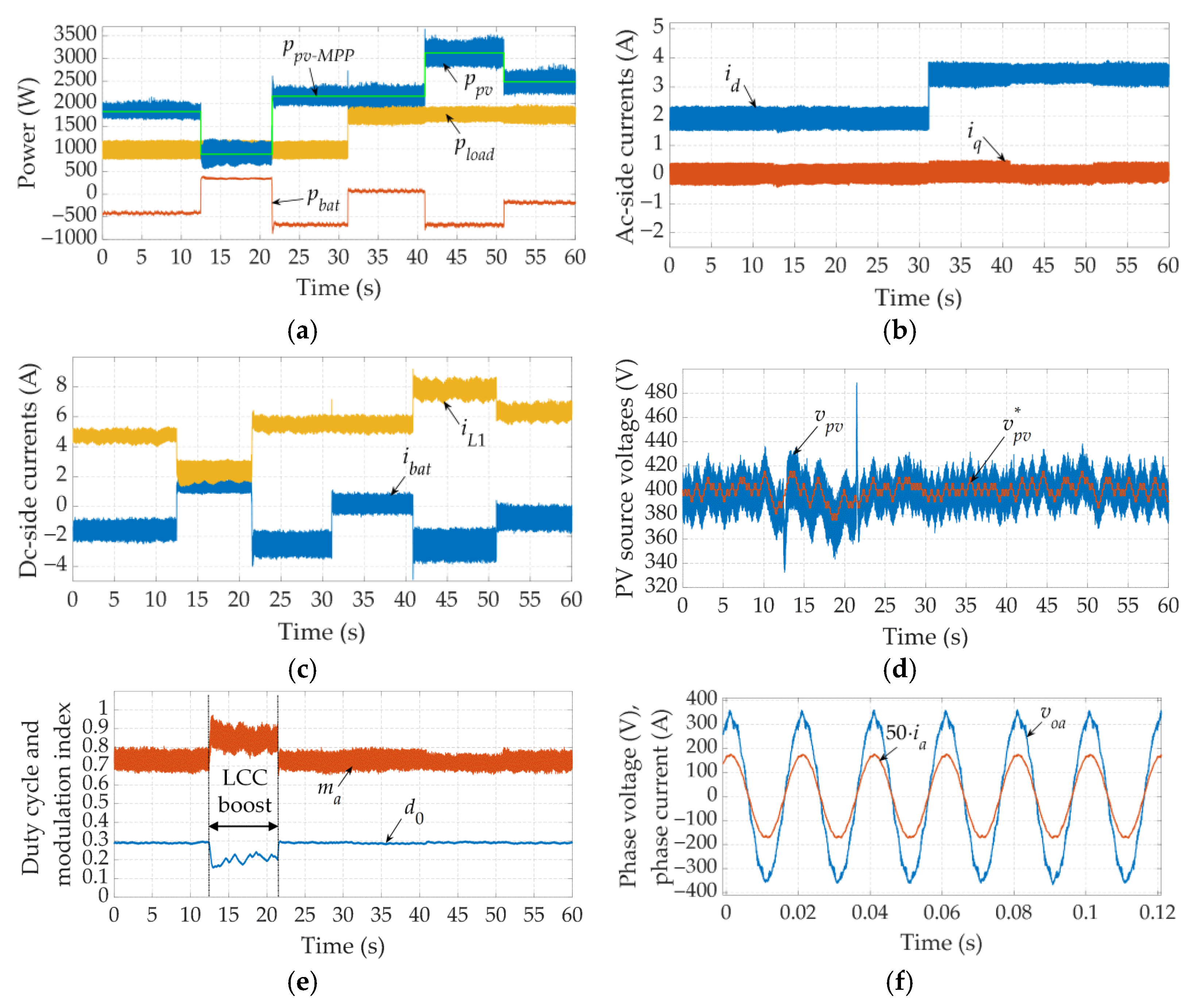
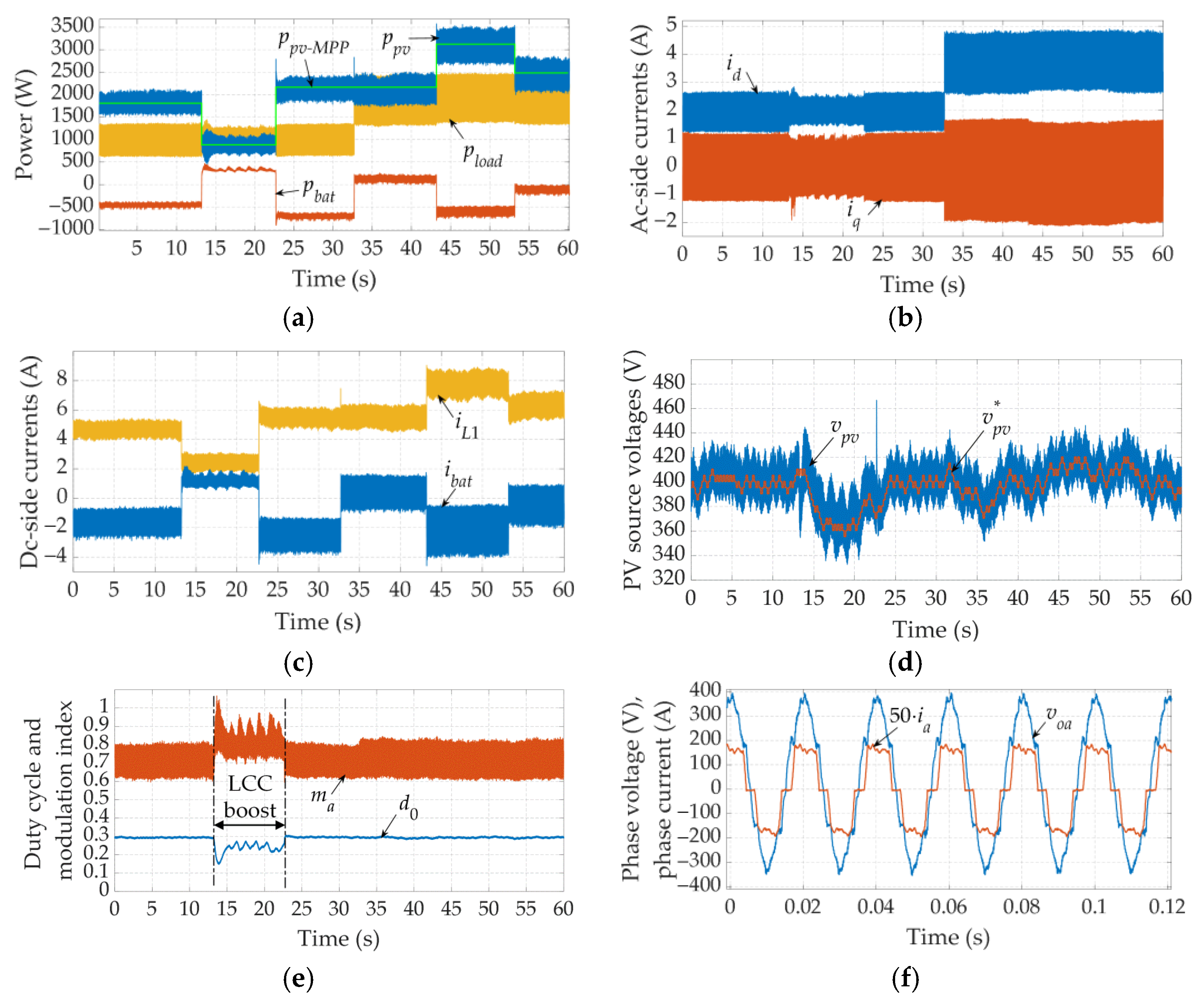
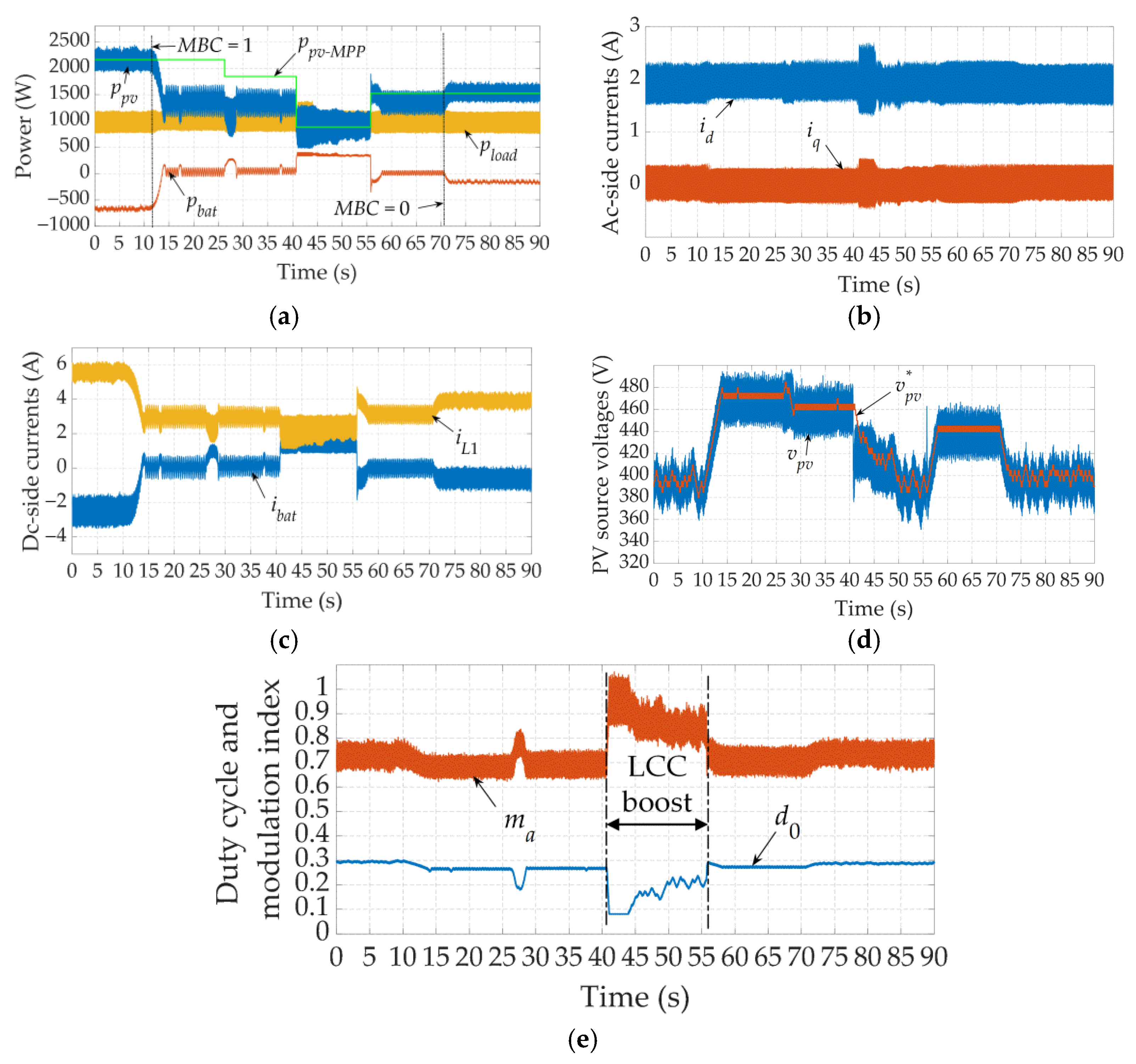
6. Experimental Results
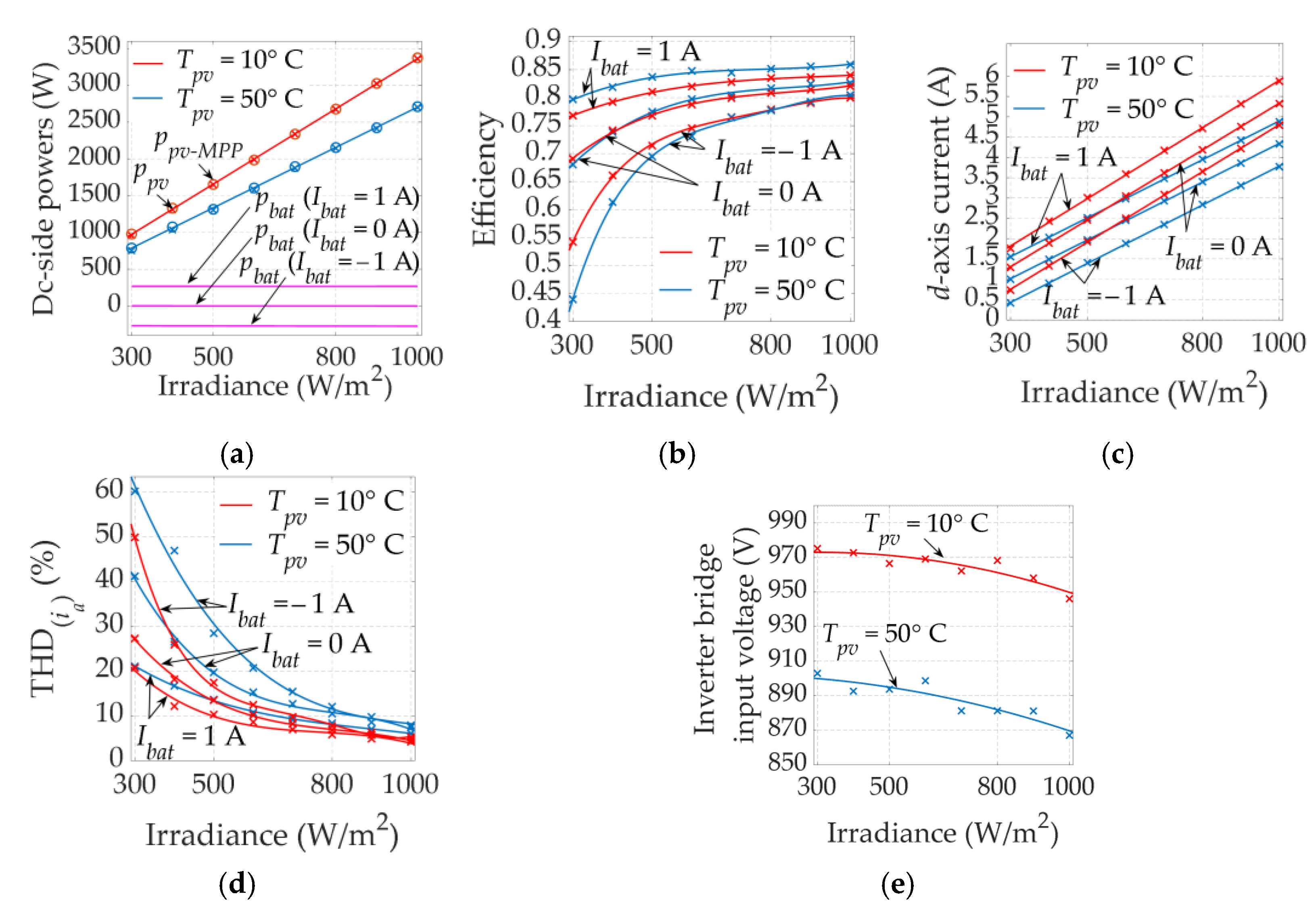
6.1. Steady-State Analysis
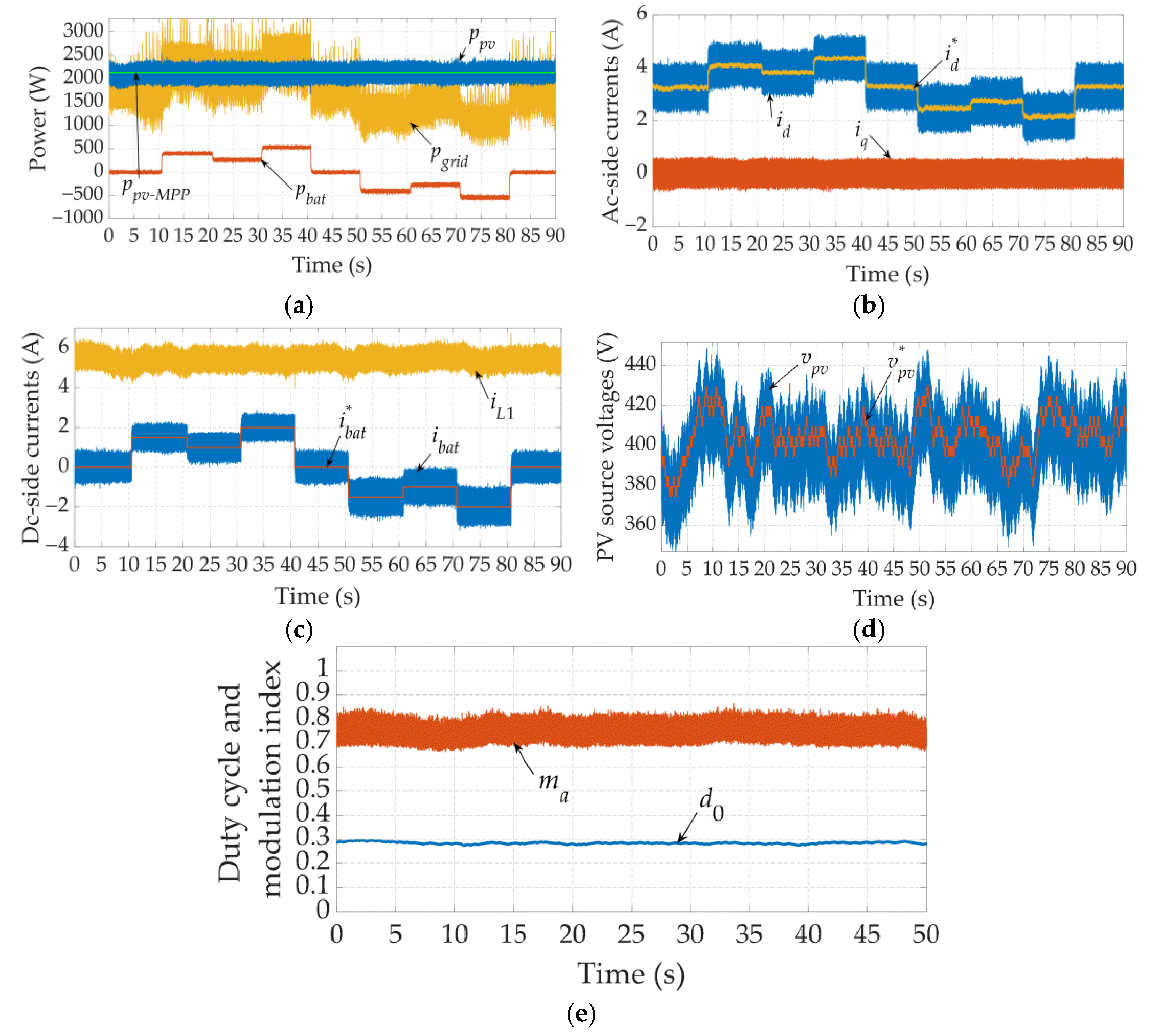
6.2. Dynamic Analysis
6.2.1. Grid-Tied Operation
6.2.2. Stand-Alone Operation
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B

References
- Bianconi, E.; Calvente, J.; Giral, R.; Mamarelis, E.; Petrone, G.; Ramos-Paja, C.A.; Spagnuolo, G.; Vitelli, M. A fast current-based MPPT technique employing sliding mode control. IEEE Trans. Ind. Electron. 2013, 60, 1168–1178. [Google Scholar] [CrossRef]
- Errouissi, R.; Al-Durra, A.; Muyeen, S.M. A robust continuous-time MPC of a DC–DC boost converter interfaced with a grid-connected photovoltaic system. IEEE J. Photovolt. 2016, 6, 1619–1629. [Google Scholar] [CrossRef] [Green Version]
- Jain, C.; Singh, B. A three-phase grid tied SPV system with adaptive DC link voltage for CPI voltage variations. IEEE Trans. Sustain. Energy 2016, 7, 337–344. [Google Scholar] [CrossRef]
- Anderson, J.; Peng, F.Z. Four quasi-Z-source inverters. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 2743–2749. [Google Scholar]
- Monjo, L.; Sainz, L.; Mesas, J.J.; Pedra, J. State-space model of quasi-z-source inverter-PV systems for transient dynamics studies and network stability assessment. Energies 2021, 14, 4150. [Google Scholar] [CrossRef]
- Monjo, L.; Sainz, L.; Mesas, J.J.; Pedra, J. Quasi-Z-source inverter-based photovoltaic power system modeling for grid stability studies. Energies 2021, 14, 508. [Google Scholar] [CrossRef]
- Ge, B.; Abu-Rub, H.; Peng, F.Z.; Lei, Q.; Almeida, A.T.d.; Ferreira, F.J.T.E.; Sun, D.; Liu, Y. An energy-stored quasi-z-source inverter for application to photovoltaic power system. IEEE Trans. Ind. Electron. 2013, 60, 4468–4481. [Google Scholar] [CrossRef]
- Ge, B.; Peng, F.Z.; Abu-Rub, H.; Ferreira, F.J.T.E.; Almeida, A.T.d. Novel energy stored single-stage photovoltaic power system with constant DC-link peak voltage. IEEE Trans. Sustain. Energy 2014, 5, 28–36. [Google Scholar] [CrossRef]
- Abu-Rub, H.; Iqbal, A.; Ahmed, S.M.; Peng, F.Z.; Li, Y.; Baoming, G. Quasi-Z-source inverter-based photovoltaic generation system with maximum power tracking control using ANFIS. IEEE Trans. Sustain. Energy 2013, 4, 11–20. [Google Scholar] [CrossRef]
- Grgić, I.; Bašić, M.; Vukadinović, D.; Bubalo, M. Fixed-duty-cycle control of a quasi-z-source inverter in a battery-assisted photovoltaic system. In Proceedings of the 2019 20th International Symposium on Power Electronics (Ee), Novi Sad, Serbia, 23–26 October 2019; pp. 1–6. [Google Scholar]
- Khajesalehi, J.; Sheshyekani, K.; Hamzeh, M.; Afjei, E. High-performance hybrid photovoltaic -battery system based on quasi-Z-source inverter: Application in microgrids. IET Gener. Transm. Distrib. 2015, 9, 895–902. [Google Scholar] [CrossRef]
- Li, F.; Ge, B.; Sun, D.; Bi, D.; Peng, F.Z.; Haitham, A.R. Quasi-Z source inverter with battery based PV power generation system. In Proceedings of the 2011 International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011; pp. 1–5. [Google Scholar]
- Liu, Y.; Ge, B.; Abu-Rub, H.; Iqbal, A.; Peng, F. Modeling and controller design of quasi-Z-Source inverter with battery based photovoltaic power system. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 3119–3124. [Google Scholar]
- Liu, Y.; Ge, B.; Abu-Rub, H.; Peng, F.Z. Control system design of battery-assisted quasi-z-source inverter for grid-tie photovoltaic power generation. IEEE Trans. Sustain. Energy 2013, 4, 994–1001. [Google Scholar] [CrossRef]
- Liu, Y.; Ge, B.; Abu-Rub, H.; Peng, F.Z. Modelling and controller design of quasi-Z-source inverter with battery-based photovoltaic power system. IET Power Electron. 2014, 7, 1665–1674. [Google Scholar] [CrossRef]
- Sun, D.; Ge, B.; Bi, D.; Peng, F.Z. Analysis and control of quasi-Z source inverter with battery for grid-connected PV system. Int. J. Electr. Power Energy Syst. 2013, 46, 234–240. [Google Scholar] [CrossRef]
- Sun, D.; Ge, B.; Peng, F.Z.; Rub, H.A.; Almeida, A.T.D. Power flow control for quasi-Z source inverter with battery based PV power generation system. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; pp. 1051–1056. [Google Scholar]
- De Oliveira-Assis, L.; Soares-Ramos, E.P.P.; Sarrias-Mena, R.; García-Triviño, P.; González-Rivera, E.; Sánchez-Sainz, H.; Llorens-Iborra, F.; Fernández-Ramírez, L.M. Simplified model of battery energy-stored quasi-Z-source inverter-based photovoltaic power plant with Twofold energy management system. Energy 2021, 122563. [Google Scholar] [CrossRef]
- Babaa, S.E.; Armstrong, M.; Pickert, V. Overview of maximum power point tracking control methods for PV systems. J. Power Energy Eng. 2014, 2, 59–72. [Google Scholar] [CrossRef] [Green Version]
- Eltawil, M.A.; Zhao, Z. MPPT techniques for photovoltaic applications. Renew. Sustain. Energy Rev. 2013, 25, 793–813. [Google Scholar] [CrossRef]
- Tofoli, F.L.; de Castro Pereira, D.; de Paula, W.J. Comparative study of maximum power point tracking techniques for photovoltaic systems. Int. J. Photoenergy 2015, 2015, 812582. [Google Scholar] [CrossRef]
- Yazdani, A.; Iravani, R. Voltage-Sourced Converters in Power Systems: Modeling, Control, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Dannehl, J.; Wessels, C.; Fuchs, F.W. Limitations of voltage-oriented pi current control of grid-connected PWM rectifiers with LCL filters. IEEE Trans. Ind. Electron. 2009, 56, 380–388. [Google Scholar] [CrossRef]
- Grgić, I.; Vukadinović, D.; Bašić, M.; Bubalo, M. Efficiency boost of a quasi-z-source inverter: A novel shoot-through injection method with dead-time. Energies 2021, 14, 4216. [Google Scholar] [CrossRef]
- LEM. Current Transducer LA 55-P/SP52. Available online: https://www.lem.com/sites/default/files/products_datasheets/la_55-p_sp52.pdf (accessed on 12 December 2021).
- LEM. Voltage Transducer DVL 500. Available online: https://www.lem.com/sites/default/files/products_datasheets/dvl_500.pdf (accessed on 12 December 2021).
- LEM. Voltage Transducer CV 3-500. Available online: https://www.lem.com/sites/default/files/products_datasheets/cv_3-500.pdf (accessed on 12 December 2021).
- Golestan, S.; Guerrero, J.M.; Vasquez, J.C. Three-phase PLLs: A review of recent advances. IEEE Trans. Power Electron. 2017, 32, 1894–1907. [Google Scholar] [CrossRef] [Green Version]
- Vukadinović, D.; Nguyen, T.D.; Nguyen, C.H.; Vu, N.L.; Bašić, M.; Grgić, I. Hedge-algebra-based phase-locked loop for distorted utility conditions. J. Control. Sci. Eng. 2019, 2019, 3590527. [Google Scholar] [CrossRef]
- Bollipo, R.B.; Mikkili, S.; Bonthagorla, P.K. Hybrid, optimal, intelligent and classical PV MPPT techniques: A review. CSEE J. Power Energy Syst. 2021, 7, 9–33. [Google Scholar] [CrossRef]
- Hohm, D.P.; Ropp, M.E. Comparative study of maximum power point tracking algorithms. Prog. Photovolt. Res. Appl. 2003, 11, 47–62. [Google Scholar] [CrossRef]
- Shen, M.; Peng, F.Z. Operation modes and characteristics of the z-source inverter with small inductance or low power factor. IEEE Trans. Ind. Electron. 2008, 55, 89–96. [Google Scholar] [CrossRef]
- Liske, A.; Clos, G.; Braun, M. Analysis and modeling of the quasi-Z-source-inverter. In Proceedings of the IECON 2011—37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, VIC, Australia, 7–10 November 2011; pp. 1197–1202. [Google Scholar]
- Kayiranga, T.; Li, H.; Lin, X.; Shi, Y.; Li, H. Abnormal operation state analysis and control of asymmetric impedance network-based quasi-z-source PV inverter (AIN-qZSI). IEEE Trans. Power Electron. 2016, 31, 7642–7650. [Google Scholar] [CrossRef]
- Vukosavic, S.N. Grid-Side Converters Control and Design, 1st ed.; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Wei, X.; Xiao, L.; Yao, Z.; Gong, C. Design of LCL filter for wind power inverter. In Proceedings of the 2010 World Non-Grid-Connected Wind Power and Energy Conference, Nanjing, China, 5–7 November 2010; pp. 1–6. [Google Scholar]
- Liserre, M.; Blaabjerg, F.; Hansen, S. Design and control of an LCL-filter-based three-phase active rectifier. IEEE Trans. Ind. Appl. 2005, 41, 1281–1291. [Google Scholar] [CrossRef]






| Rbat (Ω) | Rfn (Ω) | RL (Ω) | Ibat (A) | IL1 (A) | D0 | V0bat (V) | VC1 (V) | Ma |
|---|---|---|---|---|---|---|---|---|
| 0.7 | 87 | 0.5 | 0 | 4.5 | 0.284 | 268 | 679 | 0.72 |
| Rbat (Ω) | Rfn (Ω) | RL (Ω) | Ibat (A) | IL1 (A) | D0 | V0bat (V) | VC1 (V) | Ma |
|---|---|---|---|---|---|---|---|---|
| 0.7 | 87 | 0.5 | 1.15 | 4.5 | 0.283 | 270 | 672 | 0.73 |
| Z (W/m2) | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
| STE50°C (%) | 96.9 | 97.2 | 99.23 | 98.44 | 98.94 | 99.53 | 99.5 | 99.63 |
| STE10°C (%) | 98.81 | 98.92 | 99.87 | 100 | 100 | 99.81 | 99.9 | 99.72 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grgić, I.; Vukadinović, D.; Bašić, M.; Bubalo, M. Photovoltaic System with a Battery-Assisted Quasi-Z-Source Inverter: Improved Control System Design Based on a Novel Small-Signal Model. Energies 2022, 15, 850. https://doi.org/10.3390/en15030850
Grgić I, Vukadinović D, Bašić M, Bubalo M. Photovoltaic System with a Battery-Assisted Quasi-Z-Source Inverter: Improved Control System Design Based on a Novel Small-Signal Model. Energies. 2022; 15(3):850. https://doi.org/10.3390/en15030850
Chicago/Turabian StyleGrgić, Ivan, Dinko Vukadinović, Mateo Bašić, and Matija Bubalo. 2022. "Photovoltaic System with a Battery-Assisted Quasi-Z-Source Inverter: Improved Control System Design Based on a Novel Small-Signal Model" Energies 15, no. 3: 850. https://doi.org/10.3390/en15030850
APA StyleGrgić, I., Vukadinović, D., Bašić, M., & Bubalo, M. (2022). Photovoltaic System with a Battery-Assisted Quasi-Z-Source Inverter: Improved Control System Design Based on a Novel Small-Signal Model. Energies, 15(3), 850. https://doi.org/10.3390/en15030850








