Generalized Extreme Value Statistics, Physical Scaling and Forecasts of Oil Production from All Vertical Wells in the Permian Basin
Abstract
:1. Introduction
2. Results
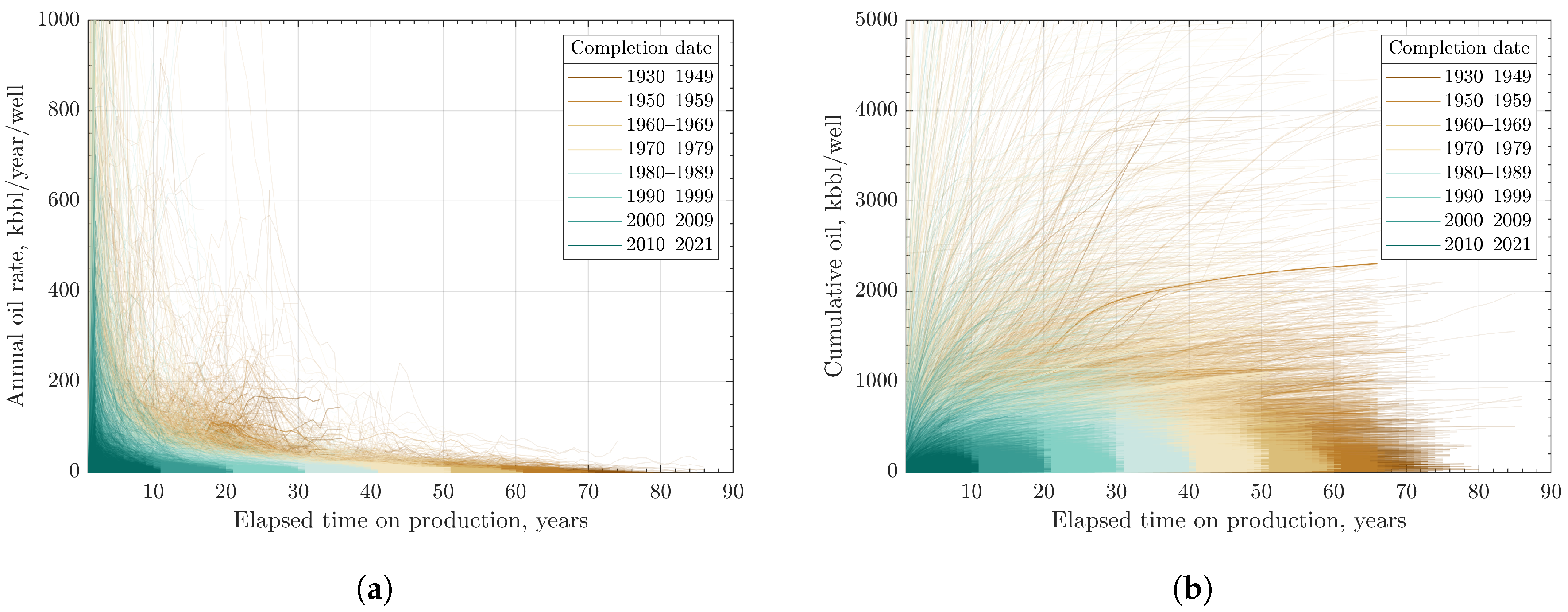
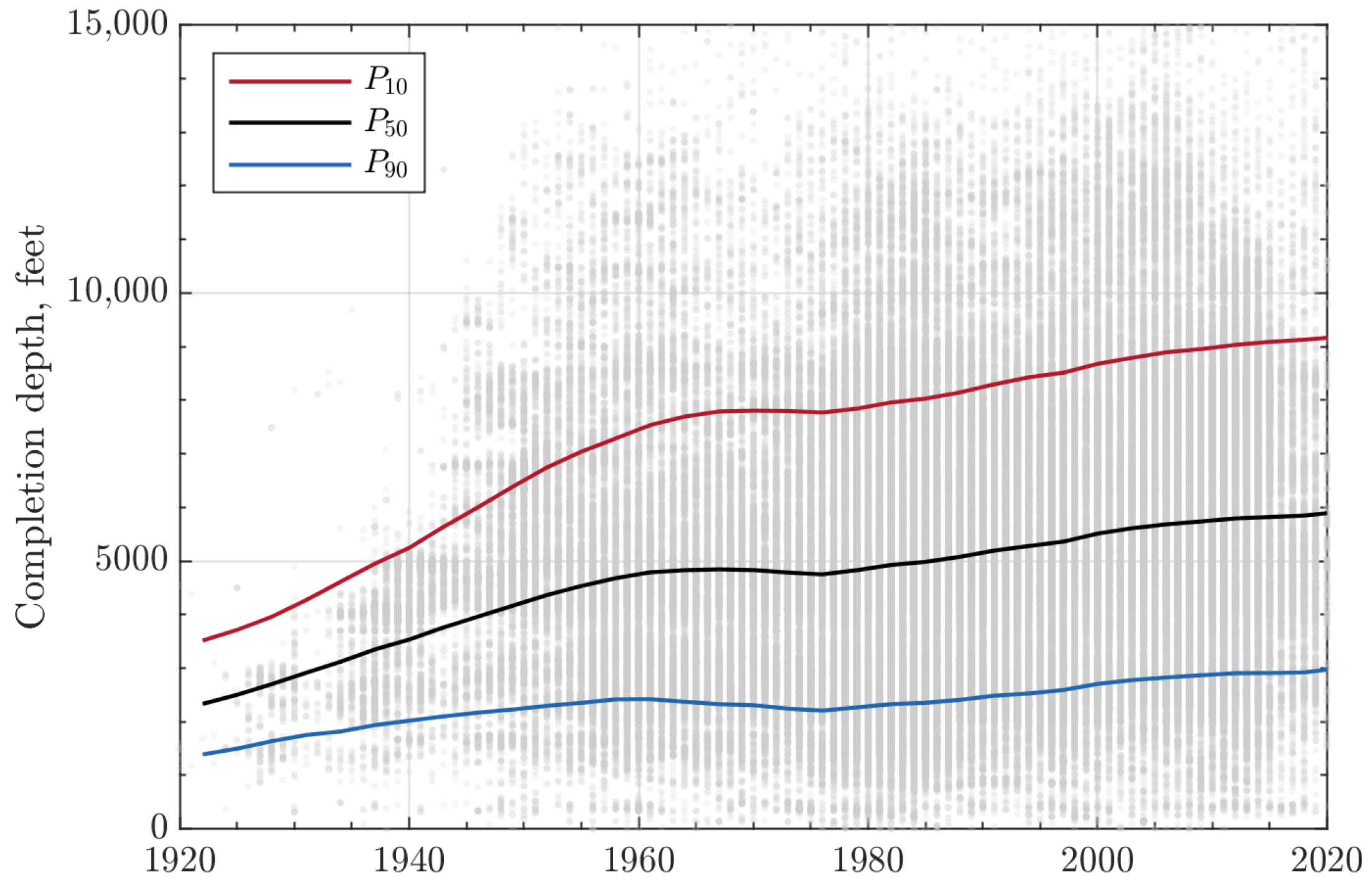
2.1. Exploratory Data Analysis
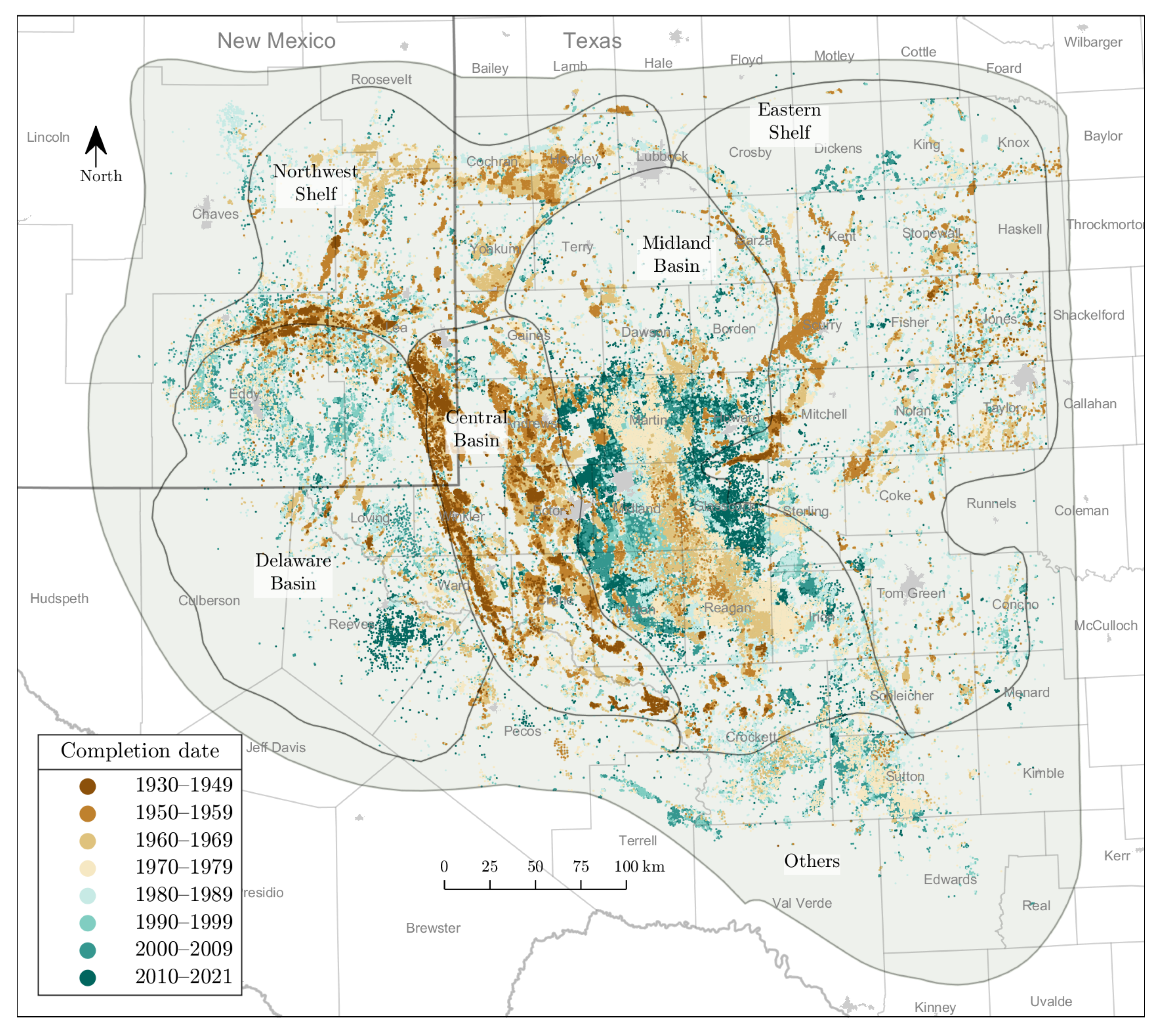
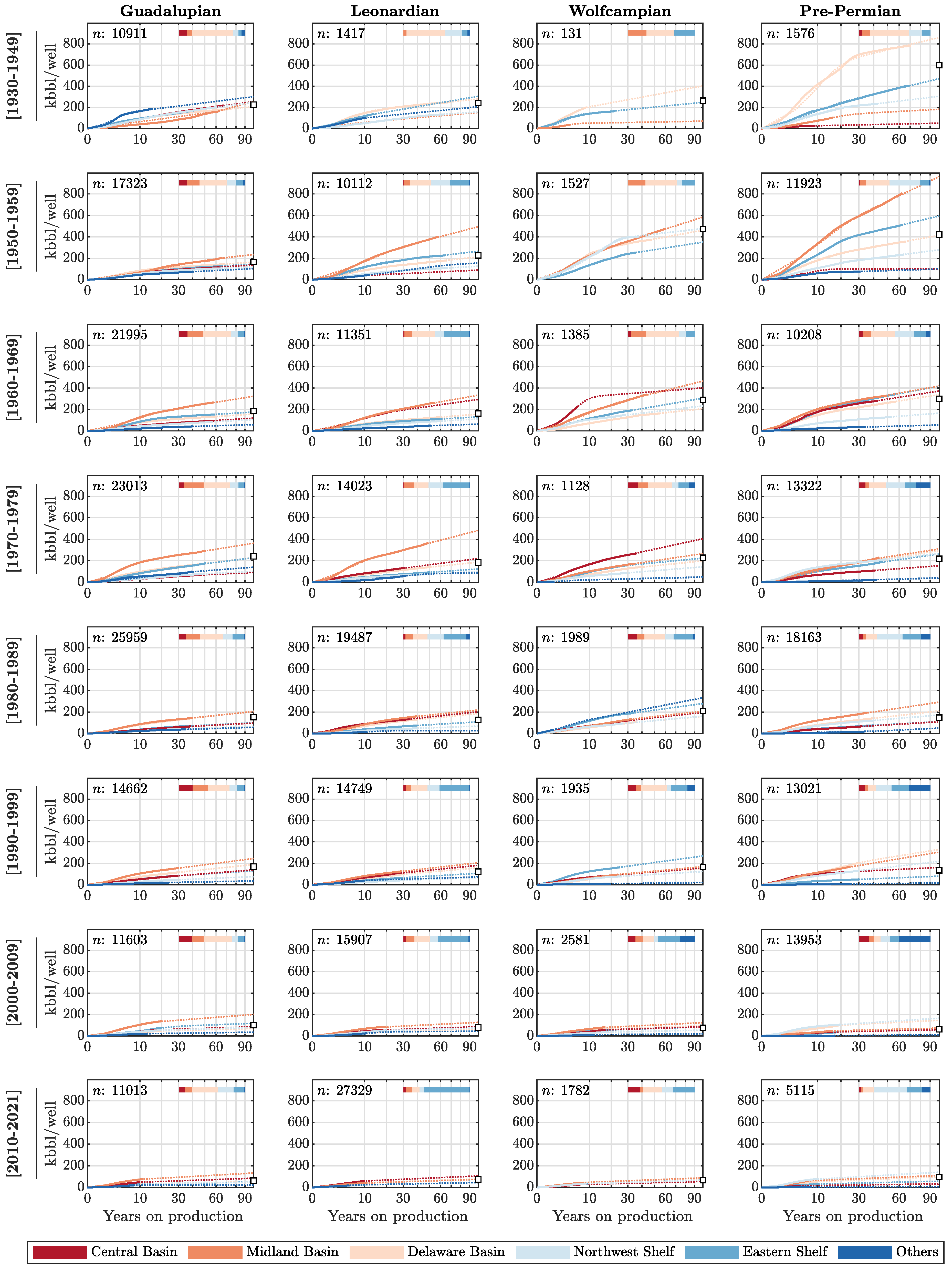
2.2. Design of Well Cohorts
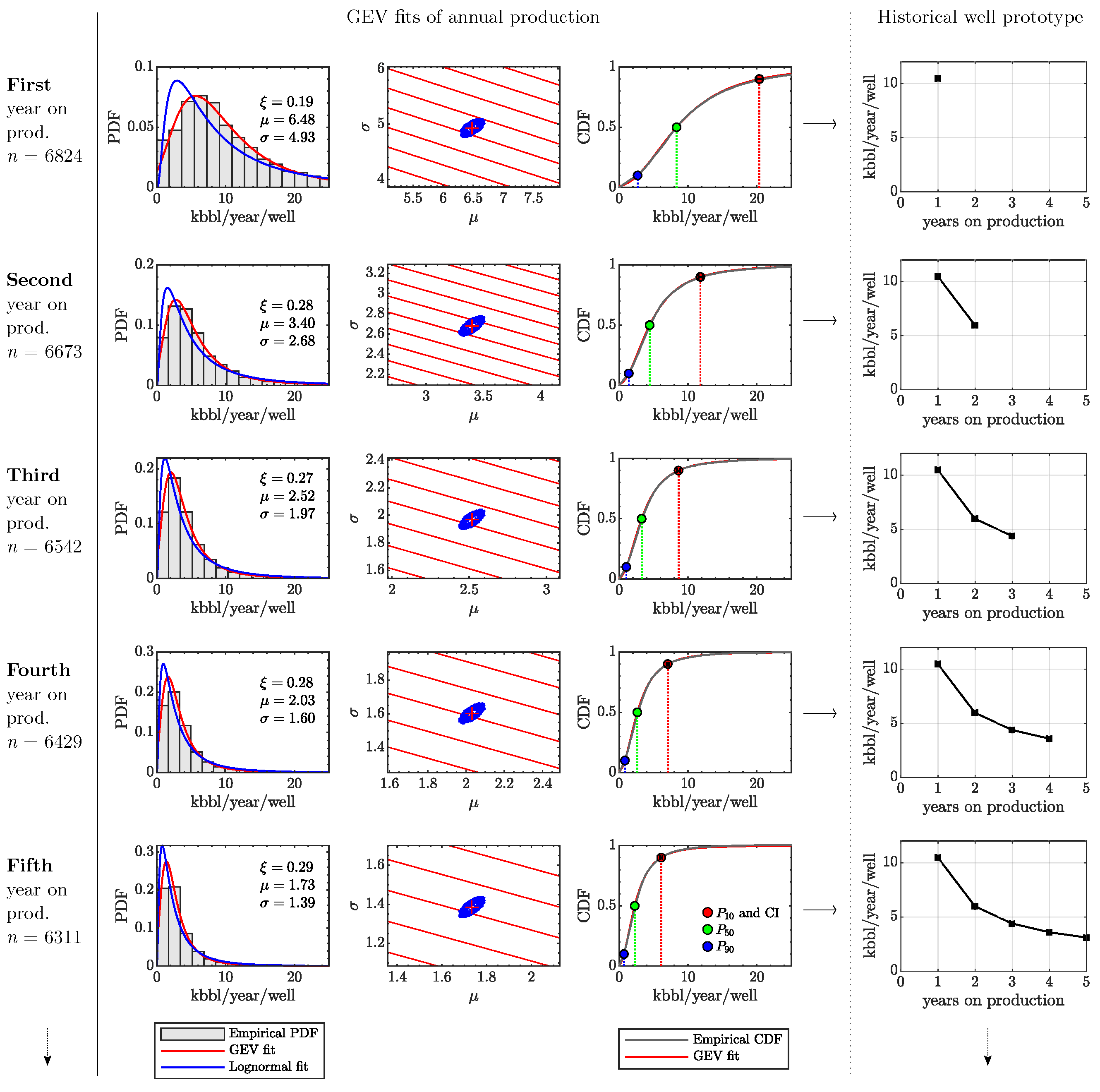
2.3. GEV Statistics and Historical Well Prototypes
2.4. Physical Scaling and Extended Well Prototypes
2.5. Probability of Well Survival
2.6. Total Field Forecast
3. Discussion
4. Materials and Methods
- Design of well cohorts: We divide nearly half a million vertical wells in the Permian into 192 spatiotemporal well cohorts. The number 192 is the multiplication of four reservoir ages, six sub-plays, and eight completion date intervals detailed in Table 2.
- Perform GEV statistics and historical well prototypes: For each cohort, we sample years on production and fit a generalized extreme value distribution using Equation (1) to find the location parameter, , scale parameter, , and shape parameter, . Using Equations (2) and (3), we calculate the expected value or mean, , the upper bound, , and the lower bound, , of the GEV distributions. We then connect each value of annual ’s to construct a historical well prototype, see Figure 7.
- Perform physical scaling and extended well prototypes: We use the physical scaling approach to extend the historical well prototypes for several more decades. In Appendix A, we derive the new physical scaling for conventional vertical wells. First, we convert the annual oil rate into the cumulative mass produced using Equation (A31). Next, we scale the cumulative mass with along the x-axis and by along the y-axis, so that the scaling result matches the master curve in Equation (A34).
- Estimate probability of well survival: We calculate the survival probability of each sub-region of the Permian using Equation (4), where and are the numbers of active and inactive wells in year-i:To estimate the maximum time of well survival, we fit the probability of survival with Equation (5) and find the intercept of the curve fit to the probability equal to zero:
- Complete total field forecast: We replace the actual reported field production rate from all existing vertical wells in the Permian with the corresponding extended well prototypes. The summation of all prototypes becomes the total basin-wide forecast of the conventional Permian wells.
5. Conclusions
- We have provided a transparent hybrid method of forecasting conventional oil production at a basin scale.
- A combination of GEV statistics of very large data sets with physical scaling matches historical production data almost perfectly and gives a smooth, optimal prediction of the future in the least-square sense.
- Our spatiotemporal well cohorts are a combination of different reservoir ages, sub-plays, and completion date intervals.
- The estimated ultimate recovery (EUR) from all 484,759 existing vertical wells in the Permian is about 34 billion barrels of oil.
- We observed that the vertical wells in the Permian can last between 10 and 100 years, depending on which sub-play and reservoir these wells penetrate.
- In practice, no large reservoir has been found in the Permian since the 1970s.
- Today, operators need to drill wells that are twice as deep as the 1930s’ wells but that produce 4–12 times less.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| EUR | Estimated Ultimate Recovery |
| GEV | Generalized Extreme Value |
| GOR | Gas to Oil Ratio |
| ODE | Ordinary Differential Equation |
| PDE | Partial Differential Equation |
| RF | Recovery Factor |
Appendix A. Physical Scaling for Conventional Wells
Appendix A.1. One-Dimensional Pressure Diffusion Equation in Radial Coordinates: Constant Pressure—Bounded Reservoir
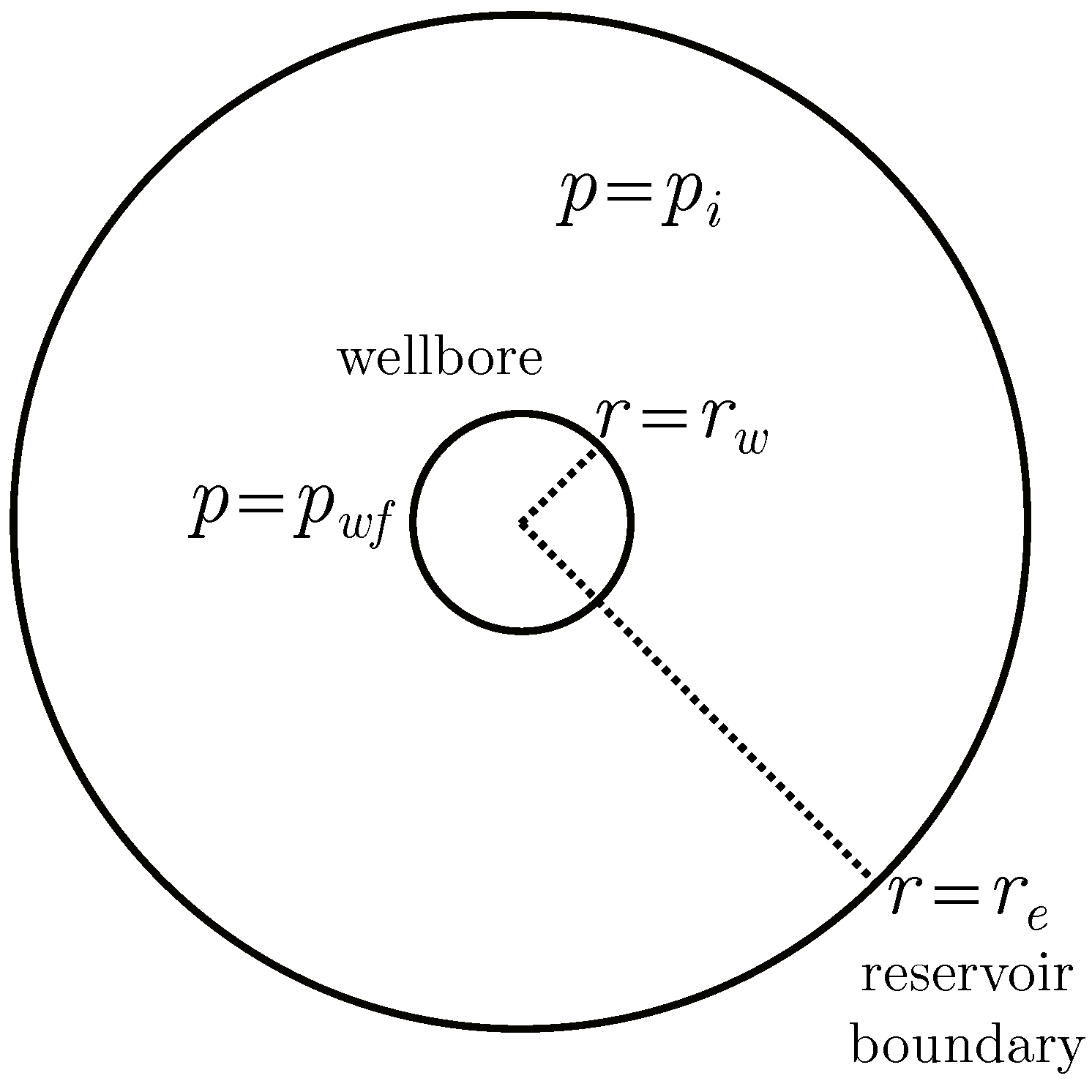
Appendix A.2. Discretization Techniques and Numerical Solutions

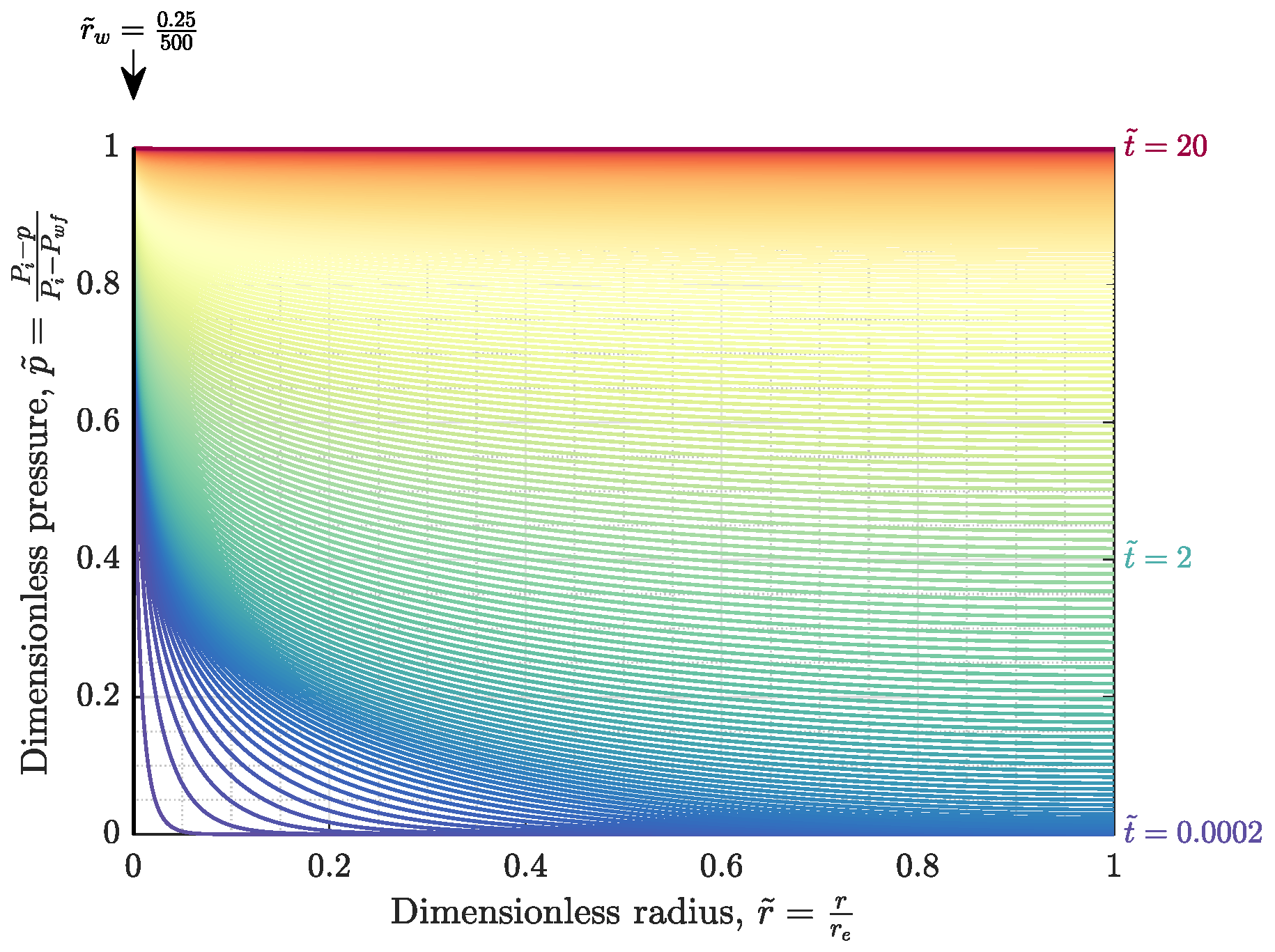
Appendix A.3. Calculating Recovery Factor

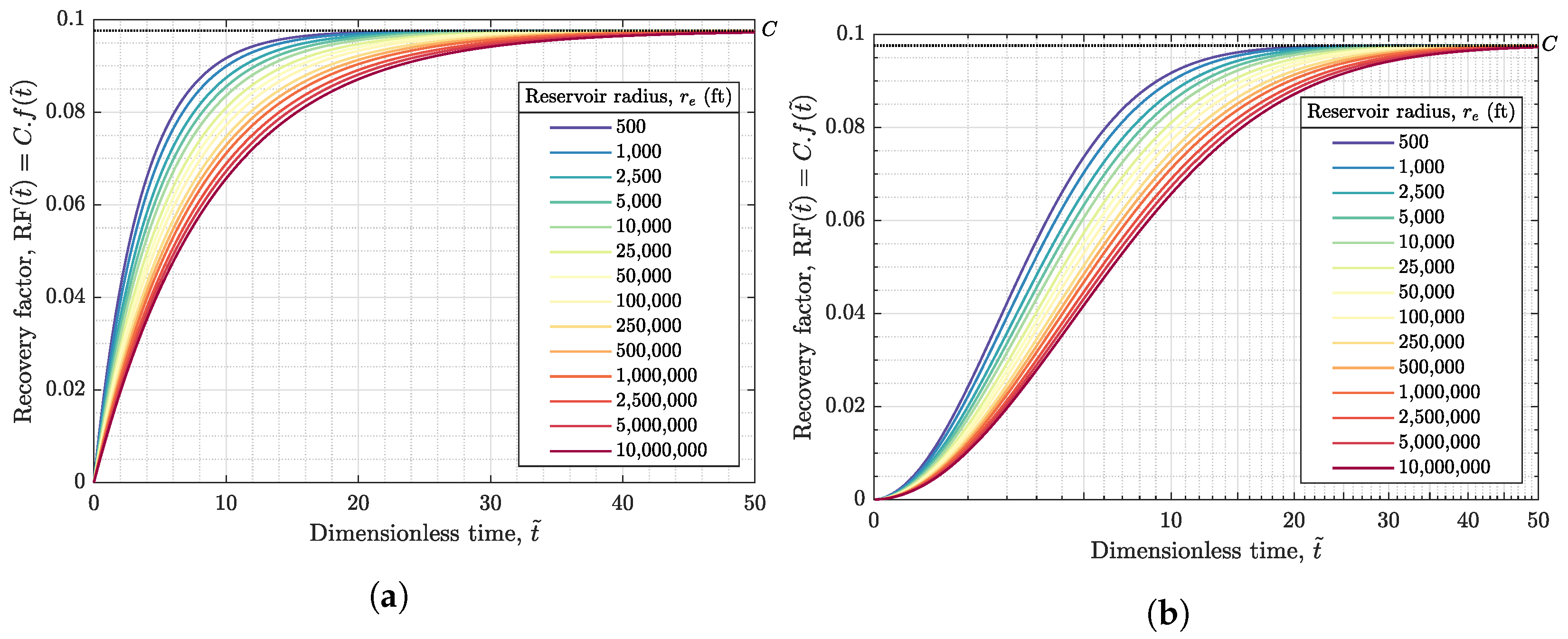
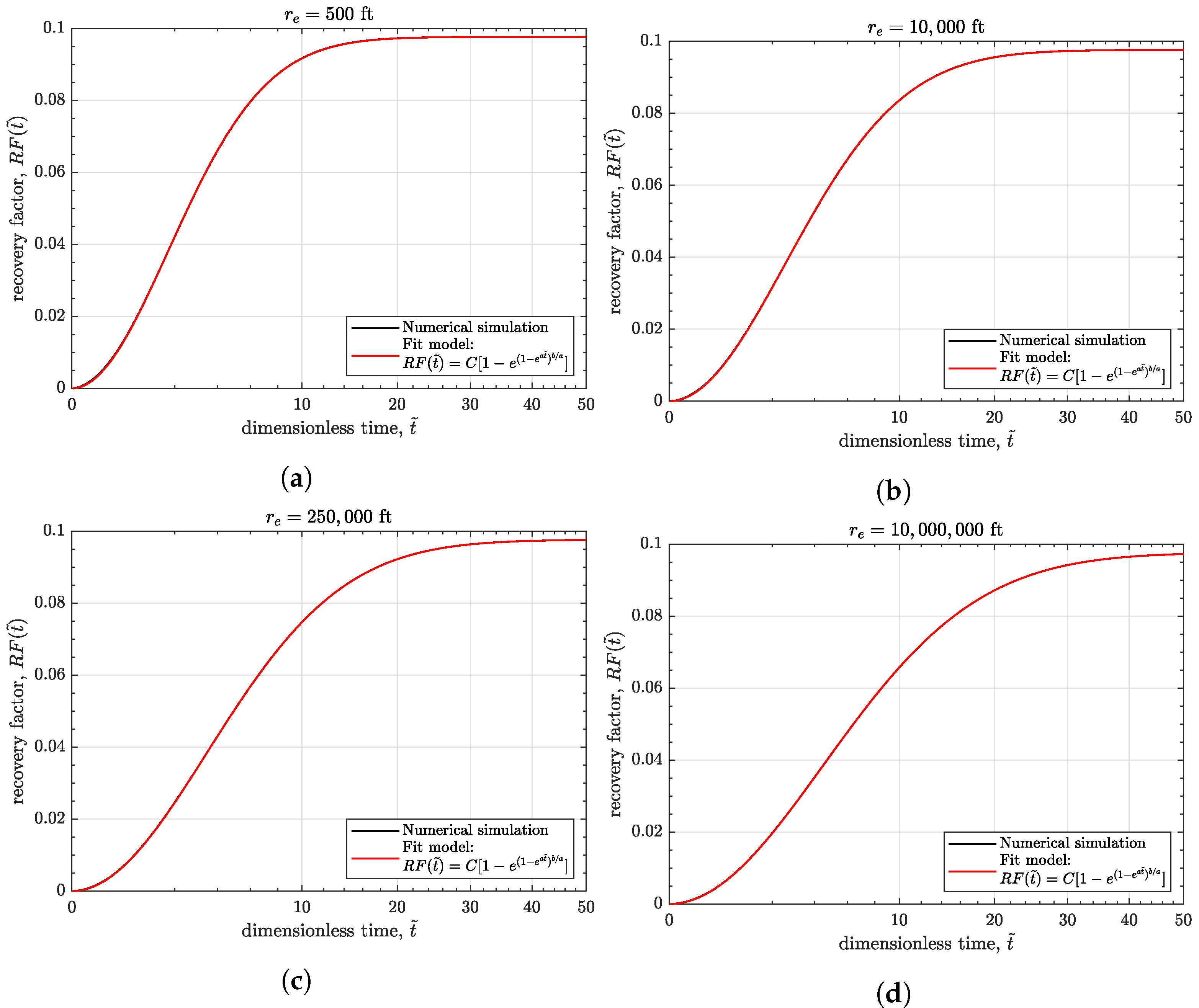
Appendix A.4. Semi-Analytical Solution of Oil Recovery Factor in Radial Flow: Bounded-Reservoir Constant-Pressure
| (ft) | a | b | ||
|---|---|---|---|---|
| 500 | 0.00050 | −7.6 | −0.00296 | 0.284 |
| 1000 | 0.00025 | −8.3 | −0.00235 | 0.257 |
| 2500 | 0.00010 | −9.2 | −0.00179 | 0.228 |
| 5000 | 0.000050 | −9.9 | −0.00149 | 0.210 |
| 10,000 | 0.000025 | −10.6 | −0.00126 | 0.195 |
| 25,000 | 0.000010 | −11.5 | −0.00103 | 0.178 |
| 50,000 | 0.0000050 | −12.2 | −0.00090 | 0.167 |
| 100,000 | 0.0000025 | −12.9 | −0.00079 | 0.157 |
| 250,000 | 0.0000010 | −13.8 | −0.00068 | 0.145 |
| 500,000 | 0.00000050 | −14.5 | −0.00061 | 0.138 |
| 1,000,000 | 0.00000025 | −15.2 | −0.00055 | 0.131 |
| 2,500,000 | 0.00000010 | −16.1 | −0.00048 | 0.123 |
| 5,000,000 | 0.000000050 | −16.8 | −0.00043 | 0.117 |
| 10,000,000 | 0.000000025 | −17.5 | −0.00040 | 0.112 |


Appendix A.5. Physical Scaling for Conventional Wells and Validations

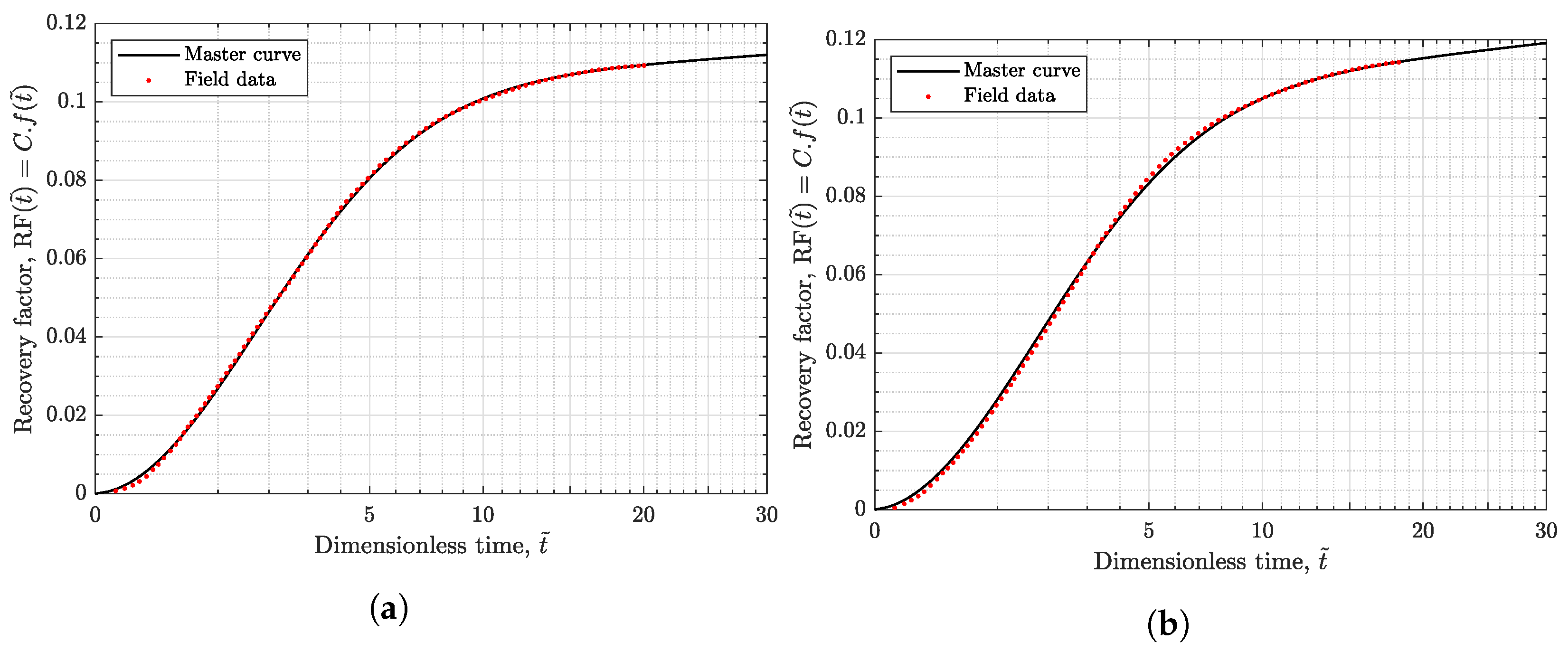
References
- Dancy, J.R. From the Drake Well to the Santa Rita# 1: The History of the US Permian Basin: A Miracle of Technological Innovation. ONE J. 2017, 3, 1183. [Google Scholar]
- Tang, C.M. Permian Basin. Available online: https://www.britannica.com/place/Permian-Basin (accessed on 19 September 2021).
- Vertrees, C.D. Permian Basin. Available online: https://www.tshaonline.org/handbook/entries/permian-basin (accessed on 19 September 2021).
- Smith, T. The Permian Basin—A Brief Overview. GEOExpro 2013, 9, 1. [Google Scholar]
- Enverus. Permian Basin: Ultimate Guide for Permian News, Information, Facts & Statistics. Available online: https://www.enverus.com/permian-basin/ (accessed on 19 September 2021).
- Fed, D. Energy in the Eleventh District: Permian Basin. Available online: https://www.dallasfed.org/research/energy11/permian.aspx (accessed on 19 September 2021).
- EIA. Assumptions to the Annual Energy Outlook 2021: Oil and Gas Supply Module. US Energy Information Administration: Annual Energy Outlook. 2021; p. 5. Available online: https://www.eia.gov/outlooks/aeo/ (accessed on 1 December 2021).
- Gaswirth, S.B.; French, K.L.; Pitman, J.K.; Marra, K.R.; Mercier, T.J.; Leathers-Miller, H.M.; Schenk, C.J.; Tennyson, M.E.; Woodall, C.A.; Brownfield, M.E.; et al. Assessment of Undiscovered Continuous Oil and Gas Resources in the Wolfcamp Shale and Bone Spring Formation of the Delaware Basin, Permian Basin Province, New Mexico and Texas, 2018; US Geological Survey: Denver, CO, USA, 2018. Available online: https://pubs.er.usgs.gov/publication/fs20183073 (accessed on 1 December 2021). [CrossRef]
- Patzek, T.W.; Male, F.; Marder, M. From the Cover: Cozzarelli Prize Winner: Gas production in the Barnett Shale obeys a simple scaling theory. Proc. Natl. Acad. Sci. USA 2013, 110, 19731–19736. [Google Scholar] [CrossRef] [Green Version]
- Patzek, T.W.; Male, F.; Marder, M. A simple model of gas production from hydrofractured horizontal wells in shales. AAPG Bull. 2014, 98, 2507–2529. [Google Scholar] [CrossRef]
- Eftekhari, B.; Marder, M.; Patzek, T.W. Field data provide estimates of effective permeability, fracture spacing, well drainage area and incremental production in gas shales. J. Nat. Gas Sci. Eng. 2018, 56, 141–151. [Google Scholar] [CrossRef]
- Marder, M.; Eftekhari, B.; Patzek, T.W. Solvable Model for Dynamic Mass Transport in Disordered Geophysical Media. Phys. Rev. Lett. 2018, 120, 138302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Patzek, T.W.; Saputra, W.; Kirati, W.; Marder, M. Generalized Extreme Value Statistics, Physical Scaling, and Forecasts of Gas Production in the Barnett Shale. Energy Fuels 2019, 33, 12154–12169. [Google Scholar] [CrossRef]
- Haider, S.; Patzek, T.W. The key physical factors that yield a good horizontal hydrofractured gas well in mudrock. Energies 2020, 13, 2348. [Google Scholar] [CrossRef]
- Patzek, T.W.; Saputra, W.; Kirati, W. A Simple Physics-Based Model Predicts Oil Production from Thousands of Horizontal Wells in Shales. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9–11 October 2017. [Google Scholar]
- Saputra, W.; Kirati, W.; Patzek, T. Generalized Extreme Value Statistics, Physical Scaling and Forecasts of Oil Production in the Bakken Shale. Energies 2019, 12, 3641. [Google Scholar] [CrossRef] [Green Version]
- Saputra, W.; Kirati, W.; Patzek, T. Physical Scaling of Oil Production Rates and Ultimate Recovery from All Horizontal Wells in the Bakken Shale. Energies 2020, 13, 2052. [Google Scholar] [CrossRef] [Green Version]
- Male, F.; Islam, A.W.; Patzek, T.W.; Ikonnikova, S.; Browning, J.; Marder, M.P. Analysis of gas production from hydraulically fractured wells in the Haynesville Shale using scaling methods. J. Unconv. Oil Gas Resour. 2015, 10, 11–17. [Google Scholar] [CrossRef]
- Saputra, W.; Kirati, W.; Patzek, T.W. Generalized extreme value statistics, physical scaling and forecasts of gas production in the Haynesville shale. J. Nat. Gas Sci. Eng. 2021, 94, 104041. [Google Scholar] [CrossRef]
- Marder, M.; Chen, C.H.; Patzek, T. Simple models of the hydrofracture process. Phys. Rev. E 2015, 92, 062408. [Google Scholar] [CrossRef] [Green Version]
- Eftekhari, B.; Marder, M.; Patzek, T.W. Estimation of Effective Permeability, Fracture Spacing, Drainage Area, and Incremental Production from Field Data in Gas Shales with Nonnegligible Sorption. SPE Reserv. Eval. Eng. 2020, 23, 664–683. [Google Scholar] [CrossRef]
- Saputra, W.; Kirati, W.; Hughes, D.; Patzek, T.W. Forecast of Economic Gas production in the Marcellus. AAPG Bull. 2021. under review. [Google Scholar]
- Saputra, W. Physics-Guided Data-Driven Production Forecasting in Shales. Doctoral Dissertation, KAUST Research Repository. 2021. Available online: https://repository.kaust.edu.sa/handle/10754/673816 (accessed on 17 December 2021). [CrossRef]
- Fréchet, M. Sur la loi de probabilité de l’écart maximum. Ann. Soc. Math. Polon. 1927, 6, 93–116. [Google Scholar]
- Weibull, W. A statistical distribution function of wide applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar] [CrossRef]
- Gumbel, E.J. Statistical theory of extreme values and some practical applications. NBS Appl. Math. Ser. 1954, 33, 19–32. [Google Scholar]
- Saputra, W.; Albinali, A.A. Validation of the Generalized Scaling Curve Method for EUR Prediction in Fractured Shale Oil Wells. In Proceedings of the SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, Dammam, Saudi Arabia, 23–26 April 2018. [Google Scholar]
- Arps, J. Analysis of Decline Curves. Trans. AIME 1945, 160, 228–247. [Google Scholar] [CrossRef]
- Saputra, W.; Kirati, W.; Patzek, T.W. Forecast of economic tight oil and gas production in Permian Basin. AAPG Bull. 2021. submitted. [Google Scholar] [CrossRef]
- Boltzmann, L. Zur Integration der Diffusionsgleichung bei variabeln Diffusionscoefficienten. Annalen der Physik 1894, 289, 959–964. [Google Scholar] [CrossRef] [Green Version]
- Zimmerman, R.W. Imperial College Lectures in Petroleum Engineering, The-Volume 5: Fluid Flow in Porous Media; World Scientific: Singapore, 2018; pp. 23–122. [Google Scholar]
- Muskat, M. The Flow of Compressible Fluids Through Porous Media and Some Problems in Heat Conduction. Physics 1934, 5, 71–94. [Google Scholar] [CrossRef]
- Everdingen, A.V.; Hurst, W. The Application of the Laplace Transformation to Flow Problems in Reservoirs. J. Pet. Technol. 1949, 1, 305–324. [Google Scholar] [CrossRef]
- Ehlig-Economides, C.A. Well Test Analysis for Wells Produced at a Constant Pressure. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1979. [Google Scholar]
- Darcy, H. Les Fontaines Publiques de la ville de Dijon: Exposition et Application; Victor Dalmont: Paris, France, 1856. [Google Scholar]
- Hubbert, M.K. Darcy’s law and the field equations of the flow of underground fluids. Trans. AIME 1956, 207, 222. [Google Scholar] [CrossRef]
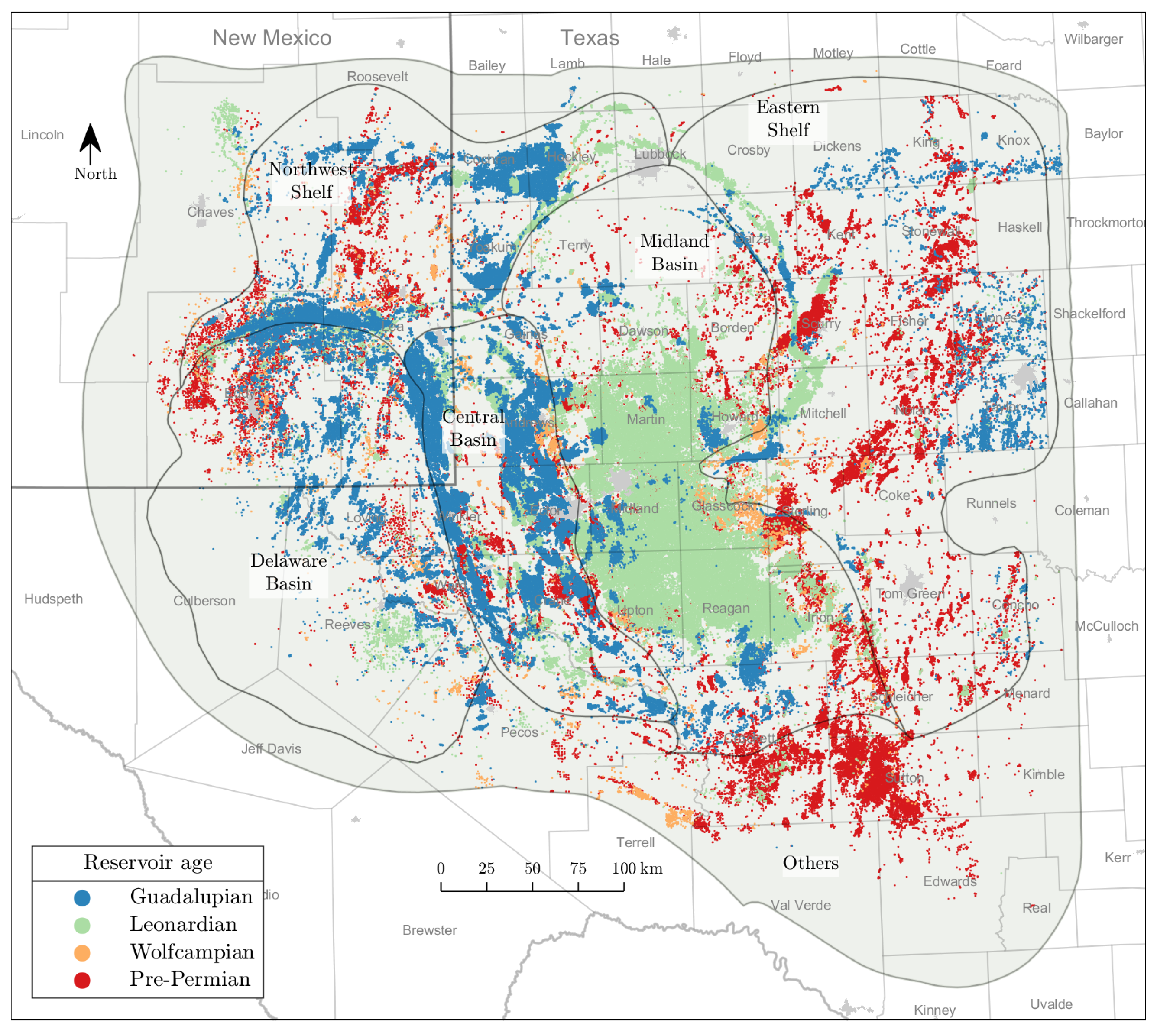
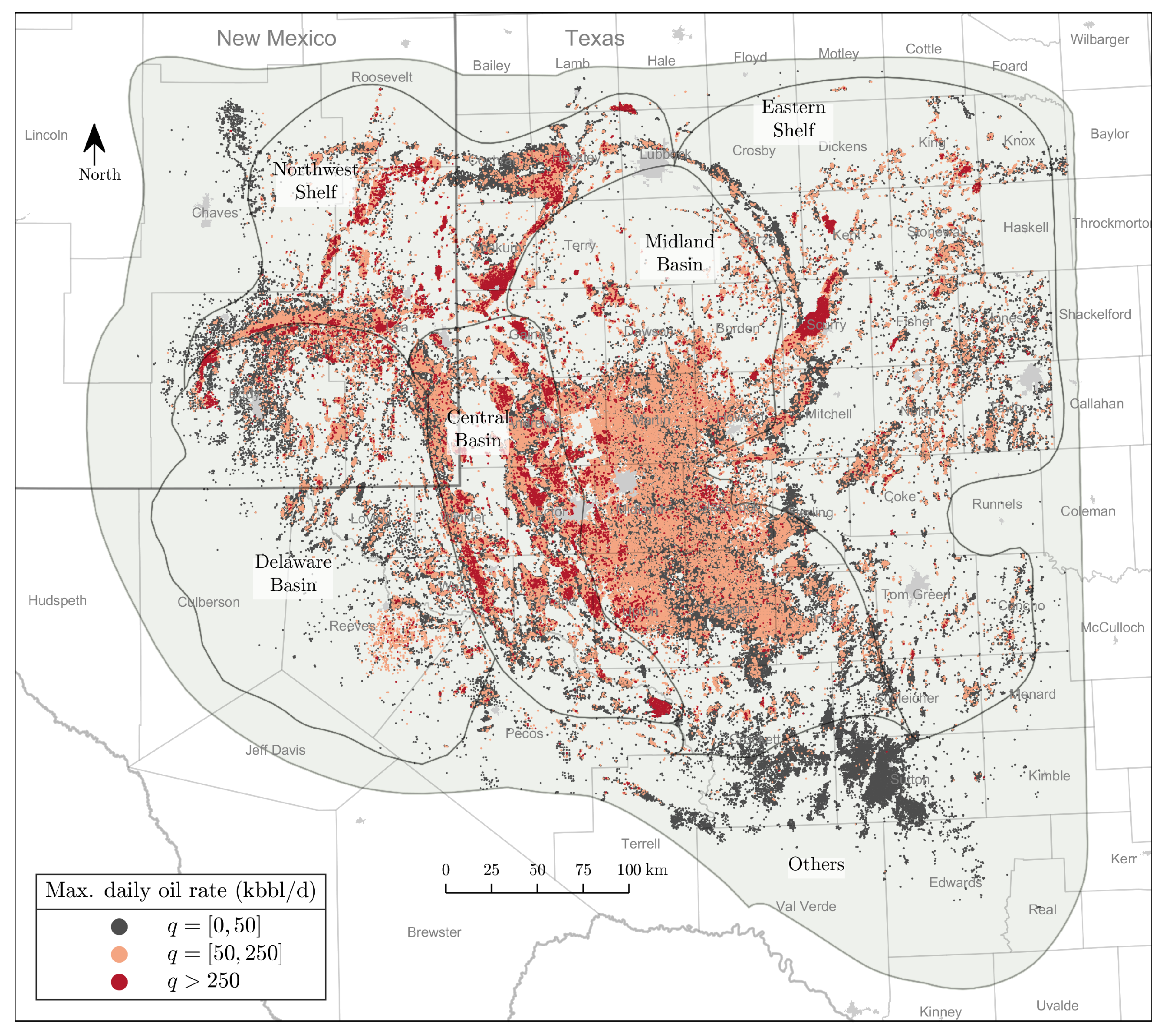

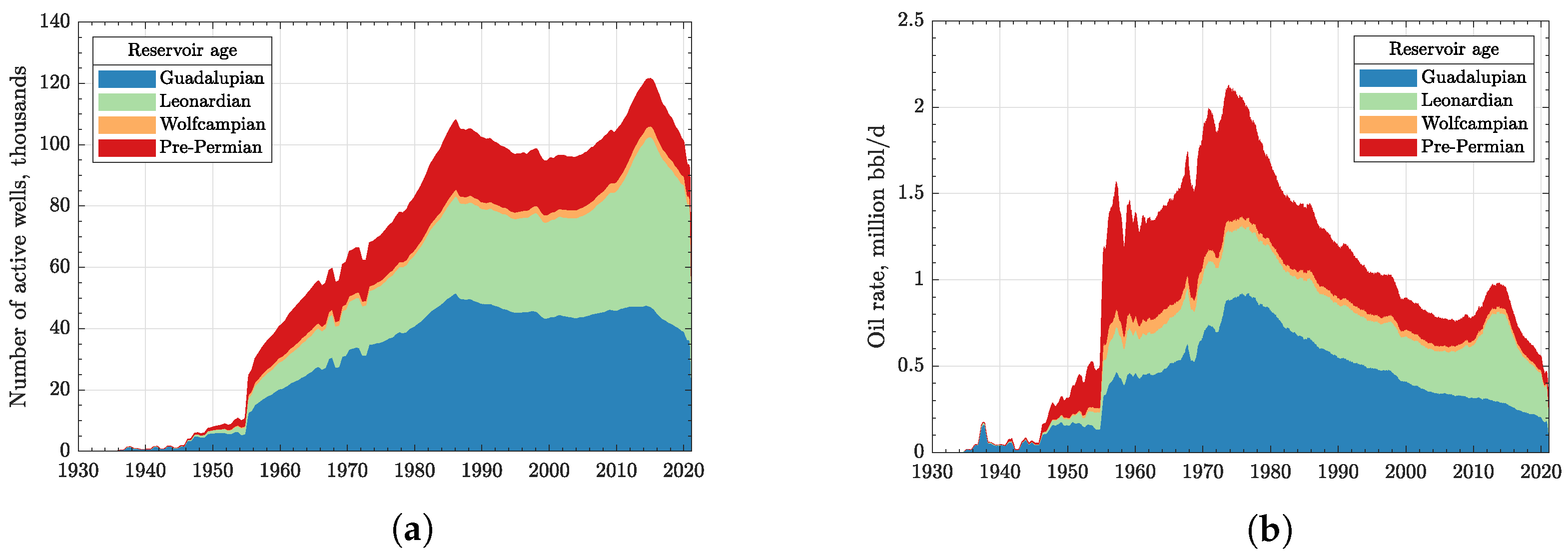



| No | Reservoir Age | Time (m.y.) | Reservoir Name | Areal Extent | ||||
|---|---|---|---|---|---|---|---|---|
| Delaware Basin | Northwest Shelf | Central Basin | Eastern Shelf | Midland Basin | ||||
| 1 | Guadalupian | 251 | Bell Canyon | ⊠ | ☐ | ☐ | ☐ | ☐ |
| Delaware | ⊠ | ☐ | ☐ | ☐ | ☐ | |||
| Capitan | ☐ | ☐ | ⊠ | ☐ | ☐ | |||
| Tansill | ☐ | ⊠ | ⊠ | ⊠ | ⊠ | |||
| Yates | ☐ | ⊠ | ⊠ | ⊠ | ⊠ | |||
| Seven Rivers | ☐ | ⊠ | ⊠ | ⊠ | ⊠ | |||
| Queen | ☐ | ⊠ | ⊠ | ⊠ | ⊠ | |||
| Grayburg | ☐ | ⊠ | ⊠ | ⊠ | ⊠ | |||
| San Andres | ☐ | ⊠ | ⊠ | ⊠ | ☐ | |||
| Holt | ☐ | ☐ | ⊠ | ☐ | ☐ | |||
| Brushy Canyon | ⊠ | ☐ | ☐ | ☐ | ⊠ | |||
| 2 | Leonardian | 275 | Bone Spring | ⊠ | ☐ | ☐ | ☐ | ☐ |
| Spraberry | ☐ | ☐ | ☐ | ☐ | ⊠ | |||
| Dean | ☐ | ☐ | ☐ | ☐ | ⊠ | |||
| Glorieta | ☐ | ⊠ | ⊠ | ⊠ | ☐ | |||
| Paddock | ☐ | ⊠ | ☐ | ☐ | ☐ | |||
| Blinebry | ☐ | ⊠ | ☐ | ☐ | ☐ | |||
| Clear Fork | ☐ | ⊠ | ⊠ | ⊠ | ☐ | |||
| Tubb | ☐ | ⊠ | ⊠ | ⊠ | ☐ | |||
| Drinkard | ☐ | ⊠ | ☐ | ☐ | ☐ | |||
| Yeso | ☐ | ⊠ | ☐ | ☐ | ☐ | |||
| Abo | ☐ | ⊠ | ⊠ | ⊠ | ☐ | |||
| 3 | Wolfcampian | 290 | Wolfcamp | ⊠ | ⊠ | ⊠ | ⊠ | ⊠ |
| 4 | Pre-Permian | 302–495 | Pennsylvanian | ⊠ | ⊠ | ⊠ | ⊠ | ⊠ |
| Cisco | ⊠ | ⊠ | ⊠ | ⊠ | ⊠ | |||
| Canyon | ⊠ | ⊠ | ⊠ | ⊠ | ⊠ | |||
| Strawn | ⊠ | ⊠ | ⊠ | ⊠ | ⊠ | |||
| Atoka | ⊠ | ⊠ | ⊠ | ⊠ | ⊠ | |||
| Morrow | ⊠ | ⊠ | ⊠ | ⊠ | ⊠ | |||
| Barnett | ⊠ | ⊠ | ⊠ | ⊠ | ⊠ | |||
| Mississippian | ⊠ | ⊠ | ⊠ | ⊠ | ⊠ | |||
| Devonian | ⊠ | ⊠ | ⊠ | ⊠ | ⊠ | |||
| Silurian | ⊠ | ⊠ | ⊠ | ⊠ | ⊠ | |||
| Fusselman | ⊠ | ⊠ | ⊠ | ⊠ | ⊠ | |||
| Ordovician | ⊠ | ⊠ | ⊠ | ⊠ | ⊠ | |||
| Montoya | ⊠ | ⊠ | ⊠ | ⊠ | ⊠ | |||
| Simpson | ⊠ | ☐ | ⊠ | ☐ | ⊠ | |||
| Ellenburger | ⊠ | ⊠ | ⊠ | ⊠ | ☐ | |||
| 4 Reservoir Ages | 6 Sub-Plays | 8 Completion Dates |
|---|---|---|
| Guadalupian | Central Basin | 1930–1949 |
| Leonardian | Midland Basin | 1950–1959 |
| Wolfcampian | Delaware Basin | 1960–1969 |
| Pre-Permian | Northwest Shelf | 1970–1979 |
| Eastern Shelf | 1980–1989 | |
| Others | 1990–1999 | |
| 2000–2009 | ||
| 2010–2021 |
| Guadalupian | Leonardian | Wolfcampian | Pre-Permian | Mean | |
|---|---|---|---|---|---|
| Delaware Basin | 70 | 47 | 35 | 20 | 43 |
| Northwest Shelf | 95 | 78 | 47 | 31 | 63 |
| Central Basin | 78 | 87 | 44 | 57 | 67 |
| Eastern Shelf | 50 | 91 | 48 | 39 | 57 |
| Midland Basin | 94 | 77 | 40 | 50 | 65 |
| Others | 45 | 27 | 10 | 19 | 25 |
| Mean | 72 | 68 | 37 | 36 | 53 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saputra, W.; Kirati, W.; Patzek, T. Generalized Extreme Value Statistics, Physical Scaling and Forecasts of Oil Production from All Vertical Wells in the Permian Basin. Energies 2022, 15, 904. https://doi.org/10.3390/en15030904
Saputra W, Kirati W, Patzek T. Generalized Extreme Value Statistics, Physical Scaling and Forecasts of Oil Production from All Vertical Wells in the Permian Basin. Energies. 2022; 15(3):904. https://doi.org/10.3390/en15030904
Chicago/Turabian StyleSaputra, Wardana, Wissem Kirati, and Tadeusz Patzek. 2022. "Generalized Extreme Value Statistics, Physical Scaling and Forecasts of Oil Production from All Vertical Wells in the Permian Basin" Energies 15, no. 3: 904. https://doi.org/10.3390/en15030904
APA StyleSaputra, W., Kirati, W., & Patzek, T. (2022). Generalized Extreme Value Statistics, Physical Scaling and Forecasts of Oil Production from All Vertical Wells in the Permian Basin. Energies, 15(3), 904. https://doi.org/10.3390/en15030904






