Reactive Transport: A Review of Basic Concepts with Emphasis on Biochemical Processes
Abstract
:1. Introduction


2. Basic Equations
2.1. Transport
- Advection, that is, the displacement of solutes dragged by fluid flow. Note that, unless flow is solved at the pore scale, advection is represented with a mean fluid flux (mean over a volume that depends on the level of detail with which flow has been solved).
- Dispersion includes two processes: molecular diffusion (i.e., Brownian motion causes a solute mass flux away from high concentration regions, given by Fick’s Law) and velocity fluctuations with respect to the mean fluid flux, which causes the solute to spread (also written by a Fick’s-like Law). We will revisit this term in Section 4.
- External sources, solute mass that leaves/enters the medium with fluid sink and sources, .
- Chemical reactions, which may cause concentration to increase (e.g., mineral dissolution) or decrease (e.g., precipitation).
2.2. Reactions

2.3. Coupled Transport and Reactions
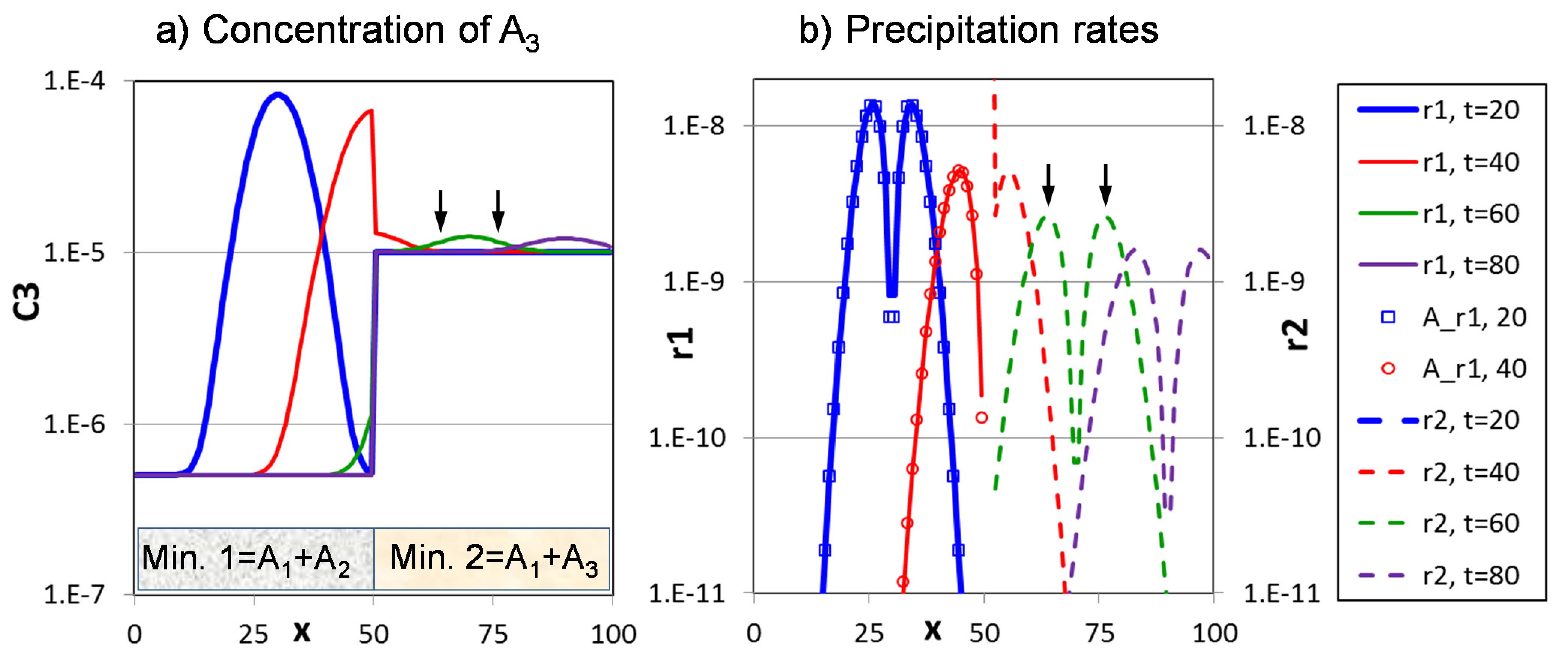
3. Basic Reactive Transport Paradigms
3.1. Sorption. Conceptual Issue No. 6: Each Species Travels at a Different Velocity
3.2. Kinetic Reactions. Conceptual Issue No. 7: Kinetics Are Important and Complex
3.3. Equilibrium. Conceptual Issue No. 8: The Rate of Fast Reactions Is Controlled by Mixing and Access to Reaction Sites
4. Representing the Impact of Unknown Heterogeneity on Transport
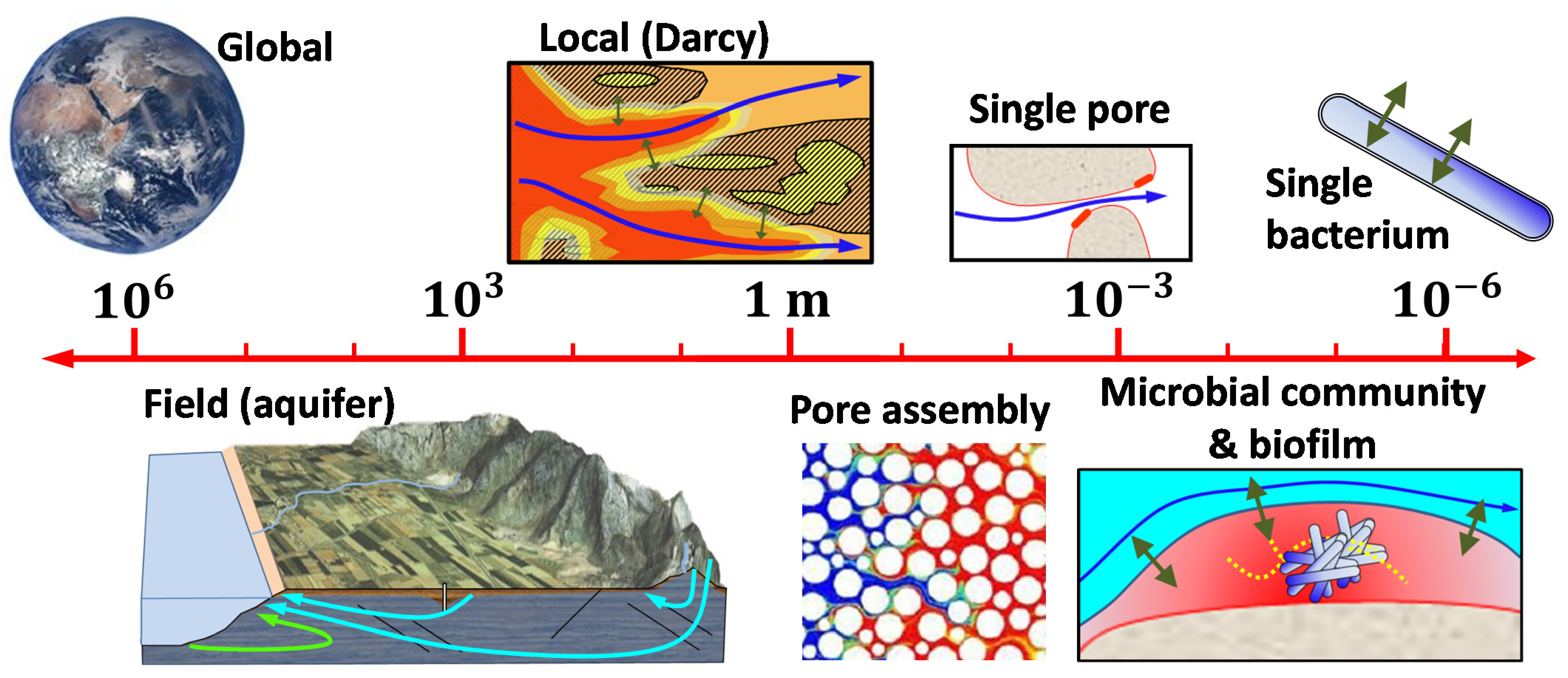
4.1. The Search for an Effective Transport Equation

4.2. Lessons Learned, Formal Upscaling, and On-Going Efforts

5. Biochemical Reactions. Conceptual Issue No. 10: Biochemical Reactions Involve Microorganisms
5.1. Organic Carbon Decay and Redox Sequence
5.2. Traditional Kinetic Models (Monod and Michaelis–Menten)
5.3. Microbial Based Kinetic Models
5.4. Genomics Based Metabolic Models
5.5. Biofilm Modeling
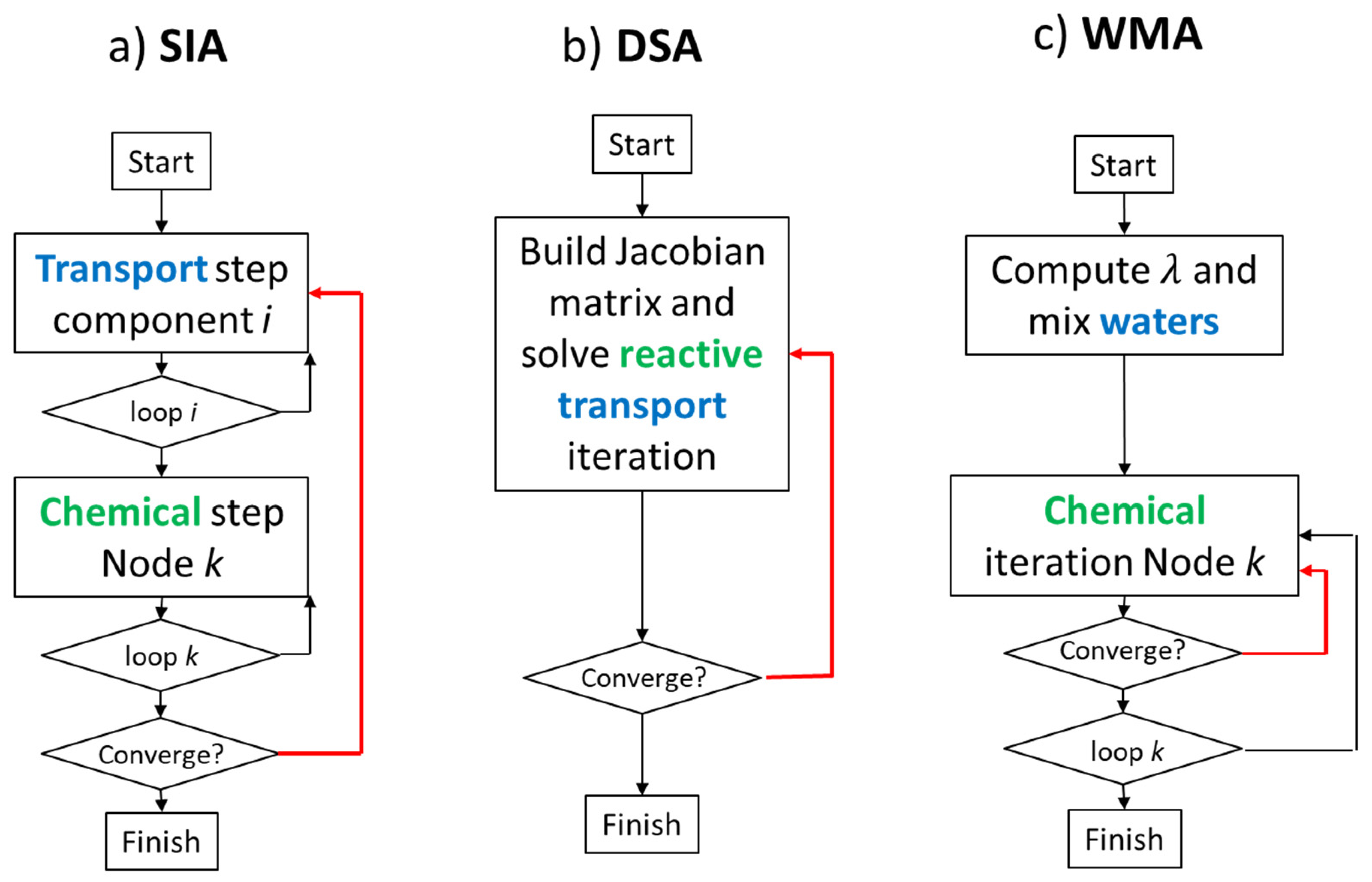
6. Solution Methods and Tools
7. Discussion and Conclusions
| No. | Conceptual Issue |
|---|---|
| 1 | RT is multidisciplinary and requires interdisciplinarity |
| RT requires not only expertise on flow, hydrogeochemistry, biology, transport or numerics, but also close interaction between experts to understand interactions among processes. | |
| 2 | Diffusion controls microscales; advection controls macroscales; the Peclet number is ambiguous |
| The ADE characteristic length is D/q. Pe is not a property of the equation, but of one model scale. Several scales may be relevant in practice. Better compare these to D/q, which leads to the above statement for diffusion coefficients and GW flux (Section 3.2). | |
| 3 | It is important to select the appropriate set of species and reactions |
| Selection of species and reactions requires understanding geochemistry, where it can be helped by speciation codes (Section 2.2), and biochemistry, where selection of biological reaction is more difficult, though at least they should be thermodynamically favorable (Section 5.1). | |
| 4 | Equilibrium reactions reduce the size and complexity of RT problems |
| The number of components, or the number of transport equations to be solved, equals the number of species minus the number of equilibrium reactions (Section 2.2 and 2.3). | |
| 5 | Mineral zones variations lead to sharp fronts in aqueous chemistry |
| The set of equilibrium reactions in any subdomain (loosely, mineral zone) determines the chemical system and the equations that need to be solved (set of mass action laws, components, etc.) and, thus, water chemistry (Section 3.3). Note that varying microbial communities may have a similar effect (redox zonation). | |
| 6 | Each species travels at a different velocity |
| Solid species do not move, whereas aqueous species do. Exchanging species are retarded with respect to wa-ter while mobilizing others (Section 3.1). This hinders the accuracy of Lagrangian methods and leads to non-linear dependence between total concentration of a component () and its aqueous part () in the transport equation (Equation (22)). | |
| 7 | Kinetics are important and complex |
| Equilibrium constants are well-known, the gist of RT often lies on the adopted kinetic laws and their parameters (Section 2.2 and Section 5). Since kinetic rates are often variable, beware of the Damköhler number (Section 5.2). | |
| 8 | The rate of fast reactions is controlled by mixing and access to reaction sites |
| For cases with only aqueous and mineral reaction in equilibrium reaction rates can be expressed by Equation (32), which implies that mixing rates need to be accurately modeled for accurate RT. | |
| 9 | Solutes are displaced by advection, spread by dispersion, diluted by mixing |
| The ADE is a poor representation of transport as it does not distinguish dispersion from mixing. This has been acknowledged for conservative transport, but it is even more relevant for RT. | |
| 10 | Biochemical reactions involve microorganisms |
| Microorganisms mean complex kinetic rate laws. Moreover, they can create biofilms that alter heterogeneity and flow and transport characteristics of the porous media. Yet, accurate biochemistry requires acknowledging both microbial communities and biofilms. | |
| 11 | Select an appropriate solution method for efficient and accurate RT |
| Solution methods may control the way mixing, and thus fast reactions, are represented, whether chemical localization can be reproduced, etc. Therefore, not only for efficiency, but also for conceptual consistence, an appropriate solution method needs to be adopted. |
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Notation
| Activity | |
| Concentration | |
| Dispersion-diffusion coefficient | |
| Volumetric sinks and sources | |
| Equilibrium constant | |
| Michaelis–Menten or Monod factor | |
| Darcy flux | |
| Reaction rate | |
| Reactions contribut. to a species | |
| Stoichiometric coefficient | |
| Component concentration | |
| Component matrix | |
| Density of a phase | |
| porosity | |
| Dispersivity | |
| Activity coefficient | |
| Kinetic rate constant | |
| Subscripts | |
| Primary, secondary species | |
| Aqueous phase | |
| Equilibrium | |
| External | |
| Kinetic | |
| Porous medium | |
| Solid phase | |
| Water |
References
- Li, L. Watershed Reactive Transport. Rev. Mineral. Geochem. 2019, 85, 381–418. [Google Scholar] [CrossRef] [Green Version]
- Valhondo, C.; Martinez-Landa, L.; Carrera, J.; Ayora, C.; Nödler, K.; Licha, T. Evaluation of EOC removal processes during artificial recharge through a reactive barrier. Sci. Total Environ. 2018, 612, 985–994. [Google Scholar] [CrossRef] [PubMed]
- Barbieri, M.; Carrera, J.; Sanchez-Vila, X.; Ayora, C.; Cama, J.; Köck-Schulmeyer, M.; López De Alda, M.; Barceló, D.; Tobella Brunet, J.; Hernández García, M. Microcosm experiments to control anaerobic redox conditions when studying the fate of organic micropollutants in aquifer material. J. Contam. Hydrol. 2011, 126, 330–345. [Google Scholar] [CrossRef] [PubMed]
- Šimůnek, J.; van Genuchten, M.T.; Šejna, M. Development and Applications of the HYDRUS and STANMOD Software Packages and Related Codes. Vadose Zo. J. 2008, 7, 587–600. [Google Scholar] [CrossRef] [Green Version]
- Werner, A.D.; Bakker, M.; Post, V.E.A.; Vandenbohede, A.; Lu, C.; Ataie-Ashtiani, B.; Simmons, C.T.; Barry, D.A. Seawater intrusion processes, investigation and management: Recent advances and future challenges. Adv. Water Resour. 2013, 51, 3–26. [Google Scholar] [CrossRef]
- Berkowitz, B.; Cortis, A.; Dentz, M.; Scher, H. Modeling Non-fickian transport in geological formations as a continuous time random walk. Rev. Geophys. 2006, 44, 1–49. [Google Scholar] [CrossRef] [Green Version]
- Liger, E.; Charlet, L.; Van Cappellen, P. Surface catalysis of uranium(VI) reduction by iron(II). Geochim. Cosmochim. Acta 1999, 63, 2939–2955. [Google Scholar] [CrossRef]
- Rubin, J.; James, R.V. Dispersion-affected transport of reacting solutes in saturated porous media: Galerkin Method applied to equilibrium-controlled exchange in unidirectional steady water flow. Water Resour. Res. 1973, 9, 1332–1356. [Google Scholar] [CrossRef]
- Grovea, D.B.; Wood, W.W. Prediction and Field Verification of Subsurface-Water Quality Changes During Artificial Recharge, Lubbock, Texas. Groundwater 1979, 17, 250–257. [Google Scholar] [CrossRef]
- Lichtner, P.C. Continuum model for simultaneous chemical reactions and mass transport in hydrothermal systems. Geochim. Cosmochim. Acta 1985, 49, 779–800. [Google Scholar] [CrossRef]
- Cao, T.; Han, D.; Song, X. Past, present, and future of global seawater intrusion research: A bibliometric analysis. J. Hydrol. 2021, 603, 126844. [Google Scholar] [CrossRef]
- Rubin, J. Transport of reacting solutes in porous media: Relation between mathematical nature of problem formulation and chemical nature of reactions. Water Resour. Res. 1983, 19, 1231–1252. [Google Scholar] [CrossRef]
- Steefel, C.I.; DePaolo, D.J.; Lichtner, P.C. Reactive transport modeling: An essential tool and a new research approach for the Earth sciences. Earth Planet. Sci. Lett. 2005, 240, 539–558. [Google Scholar] [CrossRef]
- Gaus, I. Role and impact of CO2-rock interactions during CO2 storage in sedimentary rocks. Int. J. Greenh. Gas Control 2010, 4, 73–89. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, T.; Sun, S. A tutorial review of reactive transport modeling and risk assessment for geologic CO2 sequestration. Comput. Geosci. 2019, 127, 1–11. [Google Scholar] [CrossRef]
- Cama, J.; Soler, J.M.; Ayora, C. Acid Water–Rock–Cement Interaction and Multicomponent Reactive Transport Modeling. Rev. Mineral. Geochem. 2019, 85, 459–498. [Google Scholar] [CrossRef]
- Amos, R.T.; Blowes, D.W.; Bailey, B.L.; Sego, D.C.; Smith, L.; Ritchie, A.I.M. Waste-rock hydrogeology and geochemistry. Appl. Geochem. 2015, 57, 140–156. [Google Scholar] [CrossRef]
- Cumberland, S.A.; Douglas, G.; Grice, K.; Moreau, J.W. Uranium mobility in organic matter-rich sediments: A review of geological and geochemical processes. Earth-Sci. Rev. 2016, 159, 160–185. [Google Scholar] [CrossRef] [Green Version]
- Liang, S.-Y.; Lin, W.-S.; Chen, C.-P.; Liu, C.-W.; Fan, C. A Review of Geochemical Modeling for the Performance Assessment of Radioactive Waste Disposal in a Subsurface System. Appl. Sci. 2021, 11, 5879. [Google Scholar] [CrossRef]
- Gaucher, E.C.; Blanc, P. Cement/clay interactions—A review: Experiments, natural analogues, and modeling. Waste Manag. 2006, 26, 776–788. [Google Scholar] [CrossRef] [Green Version]
- MacQuarrie, K.T.B.; Mayer, K.U. Reactive transport modeling in fractured rock: A state-of-the-science review. Earth-Sci. Rev. 2005, 72, 189–227. [Google Scholar] [CrossRef]
- Dignac, M.-F.; Derrien, D.; Barré, P.; Barot, S.; Cécillon, L.; Chenu, C.; Chevallier, T.; Freschet, G.T.; Garnier, P.; Guenet, B.; et al. Increasing soil carbon storage: Mechanisms, effects of agricultural practices and proxies. A review. Agron. Sustain. Dev. 2017, 37, 14. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Maher, K.; Navarre-Sitchler, A.; Druhan, J.; Meile, C.; Lawrence, C.; Moore, J.; Perdrial, J.; Sullivan, P.; Thompson, A.; et al. Expanding the role of reactive transport models in critical zone processes. Earth-Sci. Rev. 2017, 165, 280–301. [Google Scholar] [CrossRef] [Green Version]
- Arndt, S.; Jørgensen, B.B.; LaRowe, D.E.; Middelburg, J.J.; Pancost, R.D.; Regnier, P. Quantifying the degradation of organic matter in marine sediments: A review and synthesis. Earth-Sci. Rev. 2013, 123, 53–86. [Google Scholar] [CrossRef]
- Regnier, P.; Dale, A.W.; Arndt, S.; LaRowe, D.E.; Mogollón, J.; Van Cappellen, P. Quantitative analysis of anaerobic oxidation of methane (AOM) in marine sediments: A modeling perspective. Earth-Sci. Rev. 2011, 106, 105–130. [Google Scholar] [CrossRef]
- Langergraber, G. Modeling of Processes in Subsurface Flow Constructed Wetlands: A Review. Vadose Zo. J. 2008, 7, 830–842. [Google Scholar] [CrossRef] [Green Version]
- Patil, V.; McPherson, B.J. Modeling Coupled Reactive Transport through Fault Zones: A Critical Review. Environ. Eng. Sci. 2021, 38, 165–180. [Google Scholar] [CrossRef]
- Deng, H.; Navarre-Sitchler, A.; Heil, E.; Peters, C. Addressing Water and Energy Challenges with Reactive Transport Modeling. Environ. Eng. Sci. 2021, 38, 109–114. [Google Scholar] [CrossRef]
- Ajayi, T.; Gupta, I. A review of reactive transport modeling in wellbore integrity problems. J. Pet. Sci. Eng. 2019, 175, 785–803. [Google Scholar] [CrossRef]
- Abd, A.S.; Abushaikha, A.S. Reactive transport in porous media: A review of recent mathematical efforts in modeling geochemical reactions in petroleum subsurface reservoirs. SN Appl. Sci. 2021, 3, 401. [Google Scholar] [CrossRef]
- Hommel, J.; Coltman, E.; Class, H. Porosity–Permeability Relations for Evolving Pore Space: A Review with a Focus on (Bio-)geochemically Altered Porous Media. Transp. Porous Media 2018, 124, 589–629. [Google Scholar] [CrossRef] [Green Version]
- Molins, S.; Knabner, P. Multiscale Approaches in Reactive Transport Modeling. Rev. Mineral. Geochem. 2019, 85, 27–48. [Google Scholar] [CrossRef] [Green Version]
- Ladd, A.J.C.; Szymczak, P. Reactive Flows in Porous Media: Challenges in Theoretical and Numerical Methods. Annu. Rev. Chem. Biomol. Eng. 2021, 12, 543–571. [Google Scholar] [CrossRef]
- Seigneur, N.; Mayer, K.U.; Steefel, C.I. Reactive Transport in Evolving Porous Media. Rev. Mineral. Geochem. 2019, 85, 197–238. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Min, T.; Liu, Y.; Chen, L.; Tao, W.Q. Pore-scale study of effects of different Pt loading reduction schemes on reactive transport processes in catalyst layers of proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2021, 46, 20037–20053. [Google Scholar] [CrossRef]
- Meakin, P.; Tartakovsky, A.M. Modeling and simulation of pore-scale multiphase fluid flow and reactive transport in fractured and porous media. Rev. Geophys. 2009, 47, 1–47. [Google Scholar] [CrossRef]
- Xiong, Q.; Baychev, T.G.; Jivkov, A.P. Review of pore network modelling of porous media: Experimental characterisations, network constructions and applications to reactive transport. J. Contam. Hydrol. 2016, 192, 101–117. [Google Scholar] [CrossRef]
- Yeh, G.T.; Tripathi, V.S. A critical evaluation of recent developments in hydrogeochemical transport models of reactive multichemical components. Water Resour. Res. 1989, 25, 93–108. [Google Scholar] [CrossRef]
- Saaltink, M.W.; Carrera, J.; Ayora, C. On the behavior of approaches to simulate reactive transport. J. Contam. Hydrol. 2001, 48, 213–235. [Google Scholar] [CrossRef]
- Steefel, C.I.; Appelo, C.A.J.; Arora, B.; Jacques, D.; Kalbacher, T.; Kolditz, O.; Lagneau, V.; Lichtner, P.C.; Mayer, K.U.; Meeussen, J.C.L.; et al. Reactive Transport Codes for Subsurface Environmental Simulation; Springer: Berlin/Heidelberg, Germany, 2015; Volume 19, ISBN 1059601494. [Google Scholar]
- Dai, Z.; Samper, J. Inverse problem of multicomponent reactive chemical transport in porous media: Formulation and applications. Water Resour. Res. 2004, 40, 40. [Google Scholar] [CrossRef]
- Majdalani, S.; Fahs, M.; Carrayrou, J.; Ackerer, P. Reactive transport parameter estimation: Genetic algorithm vs. Monte carlo approach. AIChE J. 2009, 55, 1959–1968. [Google Scholar] [CrossRef]
- Torlapati, J.; Clement, T.P. Using Parallel Genetic Algorithms for Estimating Model Parameters in Complex Reactive Transport Problems. Processes 2019, 7, 640. [Google Scholar] [CrossRef] [Green Version]
- Bear, J. Dynamics of Fluids in Porous Media (Dover Civil and Mechanical Engineering); Elsevier: New York, NY, USA, 1972. [Google Scholar]
- Olivella, S.; Carrera, J.; Gens, A.; Alonso, E.E. Nonisothermal multiphase flow of brine and gas through saline media. Transp. Porous Media 1994, 15, 271–293. [Google Scholar] [CrossRef]
- Cordes, C.; Kinzelbach, W. Continuous groundwater velocity fields and path lines in linear, bilinear, and trilinear finite elements. Water Resour. Res. 1992, 28, 2903–2911. [Google Scholar] [CrossRef]
- Saaltink, M.W.; Batlle, F.; Ayora, C.; Carrera, J.; Olivella, S. RETRASO, a code for modeling reactive transport in saturated and unsaturated porous media. Geol. Acta 2004, 2, 235–251. [Google Scholar] [CrossRef]
- Friedly, J.C.; Rubin, J. Solute transport with multiple equilibrium-controlled or kinetically controlled chemical reactions. Water Resour. Res. 1992, 28, 1935–1953. [Google Scholar] [CrossRef]
- Prigogine, I.; Defay, R. On the Number of Independent Constituents and the Phase Rule. J. Chem. Phys. 1947, 15, 614–615. [Google Scholar] [CrossRef]
- Lasaga, A.C. Kinetic Theory in the Earth Sciences; Princeton University Press: Princeton, NJ, USA, 2014. [Google Scholar]
- Appelo, C.A.J.; Postma, D. Geochemistry, Groundwater and Pollution, 2nd ed.; CRC Press: London, UK, 2005; Volume 59. [Google Scholar]
- Wolery, T.J. Calculation of Chemical Equilibrium between Aqueous Solution and Minerals: The EQ 3/6 Software Package; Lawrence Livermore Laboratory, University of California: Livermore, CA, USA, 1979. [Google Scholar]
- Parkhurst, D.L.; Thorstenson, D.C.; Plummer, N. PHREEQE: A Computer Program for Geochemical Calculations; U.S. Geological Survey, Water Resources Division: Reston, VA, USA, 1980.
- Krupka, K.M.; Cantrell, K.J.; McGrail, B.P. Thermodynamic Data for Geochemical Modeling of Carbonate Reactions Associated with CO2 Sequestration–Literature Review; U.S. Department of Energy: Washington, DC, USA, 2010.
- Blanc, P.; Vieillard, P.; Gailhanou, H.; Gaboreau, S.; Marty, N.; Claret, F.; Madé, B.; Giffaut, E. ThermoChimie database developments in the framework of cement/clay interactions. Appl. Geochem. 2015, 55, 95–107. [Google Scholar] [CrossRef]
- Martinez, J.S.; Santillan, E.-F.; Bossant, M.; Costa, D.; Ragoussi, M.-E. The new electronic database of the NEA Thermochemical Database Project. Appl. Geochem. 2019, 107, 159–170. [Google Scholar] [CrossRef]
- Palandri, J.L.; Kharaka, Y.K. A Compilation of Rate Parameters of Water-Mineral Interaction Kinetics for Application to Geochemical Modeling; U.S. Geological Survey: Reston, VA, USA, 2004.
- Marty, N.C.M.; Claret, F.; Lassin, A.; Tremosa, J.; Blanc, P.; Madé, B.; Giffaut, E.; Cochepin, B.; Tournassat, C. A database of dissolution and precipitation rates for clay-rocks minerals. Appl. Geochem. 2015, 55, 108–118. [Google Scholar] [CrossRef]
- Li, L.; Steefel, C.I.; Kowalsky, M.B.; Englert, A.; Hubbard, S.S. Effects of physical and geochemical heterogeneities on mineral transformation and biomass accumulation during biostimulation experiments at Rifle, Colorado. J. Contam. Hydrol. 2010, 112, 45–63. [Google Scholar] [CrossRef]
- Kim, S.; Gindulyte, A.; Zhang, J.; Thiessen, P.A.; Bolton, E.E. PubChem Periodic Table and Element pages: Improving access to information on chemical elements from authoritative sources. Chem. Teach. Int. 2021, 3, 57–65. [Google Scholar] [CrossRef]
- Molins, S.; Carrera, J.; Ayora, C.; Saaltink, M.W. A formulation for decoupling components in reactive transport problems. Water Resour. Res. 2004, 40, W103011–W1030113. [Google Scholar] [CrossRef]
- Steefel, C.I.; MacQuarrie, K.T.B. Approaches to modeling reactive transport in porous media. Rev. Mineral. Geochem. 1996, 34, 83–125. [Google Scholar]
- Saaltink, M.W.; Ayora, C.; Carrera, J. A mathematical formulation for reactive transport that eliminates mineral concentrations. Water Resour. Res. 1998, 34, 1649–1656. [Google Scholar] [CrossRef]
- Saaltink, M.W.; Carrera Ramirez, J.; Ayora, C. Numerical solutions of reactive transport equations. In Geochemical Modeling of Groundwater, Vadose and Geothermal Systems; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Marinoni, M.; Carrayrou, J.; Lucas, Y.; Ackerer, P. Thermodynamic equilibrium solutions through a modified Newton Raphson method. AIChE J. 2017, 63, 1246–1262. [Google Scholar] [CrossRef]
- Carrayrou, J.; Bertagnolli, C.; Fahs, M. Algorithms for activity correction models for geochemical speciation and reactive transport modeling. AIChE J. 2022, 68, e17391. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Appelo, C.A.J. PHREEQC (Version 3)—A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations; U.S. Geological Survey: Reston, VA, USA, 2013.
- Bea, S.A.; Carrera, J.; Ayora, C.; Batlle, F.; Saaltink, M.W. CHEPROO: A Fortran 90 object-oriented module to solve chemical processes in Earth Science models. Comput. Geosci. 2009, 35, 1098–1112. [Google Scholar] [CrossRef]
- Kulik, D.A.; Wagner, T.; Dmytrieva, S.V.; Kosakowski, G.; Hingerl, F.F.; Chudnenko, K.V.; Berner, U.R. GEM-Selektor geochemical modeling package: Revised algorithm and GEMS3K numerical kernel for coupled simulation codes. Comput. Geosci. 2013, 17, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Leal, A.M.M.; Kyas, S.; Kulik, D.A.; Saar, M.O. Accelerating Reactive Transport Modeling: On-Demand Machine Learning Algorithm for Chemical Equilibrium Calculations. Transp. Porous Media 2020, 133, 161–204. [Google Scholar] [CrossRef]
- Kräutle, S.; Knabner, P. A new numerical reduction scheme for fully coupled multicomponent transport-reaction problems in porous media. Water Resour. Res. 2005, 41, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Kräutle, S.; Knabner, P. A reduction scheme for coupled multicomponent transport-reaction problems in porous media: Generalization to problems with heterogeneous equilibrium reactions. Water Resour. Res. 2007, 43, 1–15. [Google Scholar] [CrossRef]
- De Simoni, M.; Carrera, J.; Sánchez-Vila, X.; Guadagnini, A. A procedure for the solution of multicomponent reactive transport problems. Water Resour. Res. 2005, 41, 1–16. [Google Scholar] [CrossRef]
- Michael, H.A.; Charette, M.A.; Harvey, C.F. Patterns and variability of groundwater flow and radium activity at the coast: A case study from Waquoit Bay, Massachusetts. Mar. Chem. 2011, 127, 100–114. [Google Scholar] [CrossRef]
- Moore, W.S. Determining coastal mixing rates using radium isotopes. Cont. Shelf Res. 2000, 20, 1993–2007. [Google Scholar] [CrossRef]
- Appelo, C.A.J.; Van Der Weiden, M.J.J.; Tournassat, C.; Charlet, L. Surface Complexation of Ferrous Iron and Carbonate on Ferrihydrite and the Mobilization of Arsenic. Environ. Sci. Technol. 2002, 36, 3096–3103. [Google Scholar] [CrossRef] [PubMed]
- Valocchi, A.J.; Street, R.L.; Roberts, P.V. Transport of ion-exchanging solutes in groundwater: Chromatographic theory and field simulation. Water Resour. Res. 1981, 17, 1517–1527. [Google Scholar] [CrossRef]
- Charbeneau, R.J. Groundwater contaminant transport with adsorption and ion exchange chemistry: Method of characteristics for the case without dispersion. Water Resour. Res. 1981, 17, 705–713. [Google Scholar] [CrossRef]
- Appelo, C.A.J. Some Calculations on Multicomponent Transport with Cation Exchange in Aquifers. Groundwater 1994, 32, 968–975. [Google Scholar] [CrossRef]
- Appelo, C.A.J. Cation and proton exchange, pH variations, and carbonate reactions in a freshening aquifer. Water Resour. Res. 1994, 30, 2793–2805. [Google Scholar] [CrossRef]
- Steefel, C.I.; Carroll, S.; Zhao, P.; Roberts, S. Cesium migration in Hanford sediment: A multisite cation exchange model based on laboratory transport experiments. J. Contam. Hydrol. 2003, 67, 219–246. [Google Scholar] [CrossRef]
- Tournassat, C.; Gailhanou, H.; Crouzet, C.; Braibant, G.; Gautier, A.; Lassin, A.; Blanc, P.; Gaucher, E.C. Two cation exchange models for direct and inverse modelling of solution major cation composition in equilibrium with illite surfaces. Geochim. Cosmochim. Acta 2007, 71, 1098–1114. [Google Scholar] [CrossRef] [Green Version]
- Bradbury, M.H.; Baeyens, B. A generalised sorption model for the concentration dependent uptake of caesium by argillaceous rocks. J. Contam. Hydrol. 2000, 42, 141–163. [Google Scholar] [CrossRef]
- Shiri, J.; Keshavarzi, A.; Kisi, O.; Iturraran-Viveros, U.; Bagherzadeh, A.; Mousavi, R.; Karimi, S. Modeling soil cation exchange capacity using soil parameters: Assessing the heuristic models. Comput. Electron. Agric. 2017, 135, 242–251. [Google Scholar] [CrossRef]
- Kashi, H.; Emamgholizadeh, S.; Ghorbani, H. Estimation of Soil Infiltration and Cation Exchange Capacity Based on Multiple Regression, ANN (RBF, MLP), and ANFIS Models. Commun. Soil Sci. Plant Anal. 2014, 45, 1195–1213. [Google Scholar] [CrossRef]
- Möri, A.; Alexander, W.R.; Geckeis, H.; Hauser, W.; Schäfer, T.; Eikenberg, J.; Fierz, T.; Degueldre, C.; Missana, T. The colloid and radionuclide retardation experiment at the Grimsel Test Site: Influence of bentonite colloids on radionuclide migration in a fractured rock. Colloids Surfaces A Physicochem. Eng. Asp. 2003, 217, 33–47. [Google Scholar] [CrossRef]
- Painter, S.; Cvetkovic, V.; Turner, D.R. Effect of heterogeneity on radionuclide retardation in the alluvial aquifer near Yucca Mountain, Nevada. Ground Water 2001, 39, 326–338. [Google Scholar] [CrossRef]
- Trinchero, P.; Cvetkovic, V.; Selroos, J.-O.; Bosbach, D.; Deissmann, G. Upscaling of radionuclide transport and retention in crystalline rocks exhibiting micro-scale heterogeneity of the rock matrix. Adv. Water Resour. 2020, 142, 103644. [Google Scholar] [CrossRef]
- Domenech, C.; Arcos, D.; Sellin, P. Review on Cation Exchange Selectivity Coefficients for MX-80 Bentonite. 2005. Available online: https://inis.iaea.org/search/search.aspx?orig_q=RN:38093000 (accessed on 22 November 2021).
- White, A.F.; Peterson, M.L. Role of Reactive-Surface-Area Characterization in Geochemical Kinetic Models. In Chemical Modeling of Aqueous Systems II; ACS Symposium Series; American Chemical Society: Washington, DC, USA, 1990; Volume 416, pp. 35–461. ISBN 9780841217294. [Google Scholar]
- Maher, K.; Steefel, C.I.; DePaolo, D.J.; Viani, B.E. The mineral dissolution rate conundrum: Insights from reactive transport modeling of U isotopes and pore fluid chemistry in marine sediments. Geochim. Cosmochim. Acta 2006, 70, 337–363. [Google Scholar] [CrossRef]
- Valhondo, C.; Carrera, J.; Ayora, C.; Tubau, I.; Martinez-Landa, L.; Nödler, K.; Licha, T. Characterizing redox conditions and monitoring attenuation of selected pharmaceuticals during artificial recharge through a reactive layer. Sci. Total Environ. 2015, 512–513, 240–250. [Google Scholar] [CrossRef]
- Sanchez-Vila, X.; Donado, L.D.; Guadagnini, A.; Carrera, J. A solution for multicomponent reactive transport under equilibrium and kinetic reactions. Water Resour. Res. 2010, 46, 1–13. [Google Scholar] [CrossRef]
- Wigley, T.M.L.; Plummer, L.N. Mixing of carbonate waters. Geochim. Cosmochim. Acta 1976, 40, 989–995. [Google Scholar] [CrossRef]
- Sanford, W.E.; Konikow, L.F. Simulation of calcite dissolution and porosity changes in saltwater mixing zones in coastal aquifers. Water Resour. Res. 1989, 25, 655–667. [Google Scholar] [CrossRef]
- Rezaei, M.; Sanz, E.; Raeisi, E.; Ayora, C.; Vázquez-Suñé, E.; Carrera, J. Reactive transport modeling of calcite dissolution in the fresh-salt water mixing zone. J. Hydrol. 2005, 311, 282–298. [Google Scholar] [CrossRef]
- Kitanidis, P.K. The concept of the Dilution Index. Water Resour. Res. 1994, 30, 2011–2026. [Google Scholar] [CrossRef]
- Carrera, J.; Vázquez-Suñé, E.; Castillo, O.; Sánchez-Vila, X. A methodology to compute mixing ratios with uncertain end-members. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef] [Green Version]
- Valocchi, A.J. Validity of the Local Equilibrium Assumption for Modeling Sorbing Solute Transport through Homogeneous Soils. Water Resour. Res. 1985, 21, 808–820. [Google Scholar] [CrossRef]
- Carrera, J. An overview of uncertainties in modelling groundwater solute transport. J. Contam. Hydrol. 1993, 13, 23–48. [Google Scholar] [CrossRef]
- Lallemand-Barres, A.; Peaudecerf, P. Recherche des relations entre la valeur de la dispersivite macroscopique d’un milieu acquifere, ses autres characteristiques et les conditions de mesure. Bull. Bur. Rech. Geollogiques Minier. 1978, 3/4, 277–287. [Google Scholar]
- Gelhar, L.W.; Welty, C.; Rehfeldt, K.R. A critical review of data on field-scale dispersion in aquifers. Water Resour. Res. 1992, 28, 1955–1974. [Google Scholar] [CrossRef]
- Guimerà, J.; Carrera, J. A comparison of hydraulic and transport parameters measured in low- permeability fractured media. J. Contam. Hydrol. 2000, 41, 261–281. [Google Scholar] [CrossRef]
- Sánchez-Vila, X.; Carrera, J. Directional effects on convergent flow tracer tests. Math. Geol. 1997, 29, 551–569. [Google Scholar] [CrossRef]
- Neuman, S.P. On the tensorial nature of advective porosity. Adv. Water Resour. 2005, 28, 149–159. [Google Scholar] [CrossRef]
- Gelhar, L.W.; Axness, C.L. Three-dimensional stochastic analysis of macrodispersion in aquifers. Water Resour. Res. 1983, 19, 161–180. [Google Scholar] [CrossRef]
- Dagan, G. Solute transport in heterogeneous porous formations. J. Fluid Mech. 1984, 145, 151–177. [Google Scholar] [CrossRef]
- Neuman, S.P.; Winter, C.L.; Newman, C.M. Stochastic theory of field-scale fickian dispersion in anisotropic porous media. Water Resour. Res. 1987, 23, 453–466. [Google Scholar] [CrossRef]
- Frippiat, C.C.; Holeyman, A.E. A comparative review of upscaling methods for solute transport in heterogeneous porous media. J. Hydrol. 2008, 362, 150–176. [Google Scholar] [CrossRef]
- Einstein, A. On the Motion of Small Particles Suspended in Liquids at Rest Required by the Molecular-Kinetic Theory of Heat. Ann. Phys. 1905, 17, 208. [Google Scholar]
- Salamon, P.; Fernàndez-Garcia, D.; Gómez-Hernández, J.J. Modeling mass transfer processes using random walk particle tracking. Water Resour. Res. 2006, 42, 1–14. [Google Scholar] [CrossRef]
- Noetinger, B.; Roubinet, D.; Russian, A.; Le Borgne, T.; Delay, F.; Dentz, M.; de Dreuzy, J.R.; Gouze, P. Random Walk Methods for Modeling Hydrodynamic Transport in Porous and Fractured Media from Pore to Reservoir Scale. Transp. Porous Media 2016, 115, 345–385. [Google Scholar] [CrossRef] [Green Version]
- Fernàndez-Garcia, D.; Sanchez-Vila, X. Optimal reconstruction of concentrations, gradients and reaction rates from particle distributions. J. Contam. Hydrol. 2011, 120–121, 99–114. [Google Scholar] [CrossRef]
- Sole-Mari, G.; Bolster, D.; Fernàndez-Garcia, D.; Sanchez-Vila, X. Particle density estimation with grid-projected and boundary-corrected adaptive kernels. Adv. Water Resour. 2019, 131, 103382. [Google Scholar] [CrossRef] [Green Version]
- Tartakovsky, A.M.; Meakin, P.; Scheibe, T.D.; Eichler West, R.M. Simulations of reactive transport and precipitation with smoothed particle hydrodynamics. J. Comput. Phys. 2007, 222, 654–672. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Neuman, S.P. Effects of Peclet number on pore-scale mixing and channeling of a tracer and on directional advective porosity. Geophys. Res. Lett. 2008, 35, 1–4. [Google Scholar] [CrossRef]
- Yoon, H.; Kang, Q.; Valocchi, A.J. Lattice boltzmann-based approaches for pore-scale reactive transport. Rev. Mineral. Geochem. 2015, 80, 393–431. [Google Scholar] [CrossRef]
- Berkowitz, B.; Scher, H. Anomalous Transport in Random Fracture Networks. Phys. Rev. Lett. 1997, 79, 4038. [Google Scholar] [CrossRef]
- Le Borgne, T.; Gouze, P. Non-Fickian dispersion in porous media: 2. Model validation from measurements at different scales. Water Resour. Res. 2008, 44, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Bijeljic, B.; Mostaghimi, P.; Blunt, M.J. Signature of non-fickian solute transport in complex heterogeneous porous media. Phys. Rev. Lett. 2011, 107, 20–23. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Benson, D.A.; Wheatcraft, S.W.; Meerschaert, M.M. Application of a fractional advection-dispersion equation. Water Resour. Res. 2000, 36, 1403–1412. [Google Scholar] [CrossRef] [Green Version]
- Schumer, R.; Benson, D.A.; Meerschaert, M.M.; Baeumer, B. Fractal mobile/immobile solute transport. Water Resour. Res. 2003, 39, 1–13. [Google Scholar] [CrossRef]
- Oldham, K.B.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and lntegration to Arbitrary Order; Elsevier: Amsterdam, The Netherlands, 1974; Volume 111. [Google Scholar]
- Barker, J.A. A generalized radial flow model for hydraulic tests in fractured rock. Water Resour. Res. 1988, 24, 1796–1804. [Google Scholar] [CrossRef] [Green Version]
- Carrera, J.; Sànchez-Vila, X.; Benet, I.; Medina, A.; Galarza, G.; Guimerà, J. On matrix diffusion: Formulations, solution methods and qualitative effects. Hydrogeol. J. 1998, 6, 178–190. [Google Scholar] [CrossRef]
- Dentz, M.; Berkowitz, B. Transport behavior of a passive solute in continuous time random walks and multirate mass transfer. Water Resour. Res. 2003, 39, 1–20. [Google Scholar] [CrossRef]
- Silva, O.; Carrera, J.; Dentz, M.; Kumar, S.; Alcolea, A.; Willmann, M. A general real-time formulation for multi-rate mass transfer problems. Hydrol. Earth Syst. Sci. 2009, 13, 1399–1411. [Google Scholar] [CrossRef] [Green Version]
- Haggerty, R.; Gorelick, S.M. Multiple-Rate Mass Transfer for Modeling Diffusion and Surface Reactions in Media with Pore-Scale Heterogeneity. Water Resour. Res. 1995, 31, 2383–2400. [Google Scholar] [CrossRef]
- Babey, T.; de Dreuzy, J.-R.; Casenave, C. Multi-Rate Mass Transfer (MRMT) models for general diffusive porosity structures. Adv. Water Resour. 2015, 76, 146–156. [Google Scholar] [CrossRef]
- De Dreuzy, J.R.; Rapaport, A.; Babey, T.; Harmand, J. Influence of porosity structures on mixing-induced reactivity at chemical equilibrium in mobile/immobile Multi-Rate Mass Transfer (MRMT) and Multiple INteracting Continua (MINC) models. Water Resour. Res. 2013, 49, 8511–8530. [Google Scholar] [CrossRef] [Green Version]
- Fernandez-Garcia, D.; Sanchez-Vila, X. Mathematical equivalence between time-dependent single-rate and multiratemass transfer models. Water Resour. Res. 2015, 51, 3166–3180. [Google Scholar] [CrossRef] [Green Version]
- Battiato, I.; Tartakovsky, D.M.; Tartakovsky, A.M.; Scheibe, T. On breakdown of macroscopic models of mixing-controlled heterogeneous reactions in porous media. Adv. Water Resour. 2009, 32, 1664–1673. [Google Scholar] [CrossRef]
- Battiato, I.; Tartakovsky, D.M.; Tartakovsky, A.M.; Scheibe, T.D. Hybrid models of reactive transport in porous and fractured media. Adv. Water Resour. 2011, 34, 1140–1150. [Google Scholar] [CrossRef]
- Sadhukhan, S.; Gouze, P.; Dutta, T. A simulation study of reactive flow in 2-D involving dissolution and precipitation in sedimentary rocks. J. Hydrol. 2014, 519, 2101–2110. [Google Scholar] [CrossRef]
- Scheibe, T.D.; Schuchardt, K.; Agarwal, K.; Chase, J.; Yang, X.; Palmer, B.J.; Tartakovsky, A.M.; Elsethagen, T.; Redden, G. Hybrid multiscale simulation of a mixing-controlled reaction. Adv. Water Resour. 2015, 83, 228–239. [Google Scholar] [CrossRef] [Green Version]
- Tartakovsky, A.M.; Tartakovsky, D.M.; Scheibe, T.D.; Meakin, P. Hybrid simulations of reaction-diffusion systems in porous media. SIAM J. Sci. Comput. 2008, 30, 2799–2816. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Tartakovsky, G.D.; Scheibe, T.D. Effects of incomplete mixing on multicomponent reactive transport. Adv. Water Resour. 2009, 32, 1674–1679. [Google Scholar] [CrossRef]
- Van Leemput, P.; Vandekerckhove, C.; Vanroose, W.; Roose, D. Accuracy of hybrid Lattice Boltzmann/Finite differences schemes for reaction-diffusion systems. Multiscale Model. Simul. 2007, 6, 838–857. [Google Scholar] [CrossRef]
- Le Borgne, T.; Dentz, M.; Villermaux, E. Stretching, coalescence, and mixing in porous media. Phys. Rev. Lett. 2013, 110, 204501. [Google Scholar] [CrossRef]
- Willmann, M.; Carrera, J.; Sanchez-Vila, X.; Silva, O.; Dentz, M. Coupling of mass transfer and reactive transport for nonlinear reactions in heterogeneous media. Water Resour. Res. 2010, 46, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Luquot, L.; Andreani, M.; Gouze, P.; Camps, P. CO2 percolation experiment through chlorite/zeolite-rich sandstone (Pretty Hill Formation—Otway Basin–Australia). Chem. Geol. 2012, 294–295, 75–88. [Google Scholar] [CrossRef]
- Soler-Sagarra, J.; Luquot, L.; Martínez-Pérez, L.; Saaltink, M.W.; De Gaspari, F.; Carrera, J. Simulation of chemical reaction localization using a multi-porosity reactive transport approach. Int. J. Greenh. Gas Control 2016, 48, 59–68. [Google Scholar] [CrossRef]
- Becker, M.W.; Shapiro, A.M. Tracer transport in fractured crystalline rock: Evidence of nondiffusive breakthrough tailing. Water Resour. Res. 2000, 36, 1677–1686. [Google Scholar] [CrossRef] [Green Version]
- Luo, J.; Cirpka, O.A. How well do mean breakthrough curves predict mixing-controlled reactive transport? Water Resour. Res. 2011, 47, 1–12. [Google Scholar] [CrossRef]
- Soler-Sagarra, J.; Hakoun, V.; Dentz, M.; Carrera, J. The Multi-Advective Water Mixing Approach for Transport through Heterogeneous Media. Energies 2021, 14, 6562. [Google Scholar] [CrossRef]
- De Dreuzy, J.R.; Carrera, J.; Dentz, M.; Le Borgne, T. Time evolution of mixing in heterogeneous porous media. Water Resour. Res. 2012, 48, 1–11. [Google Scholar] [CrossRef] [Green Version]
- de Dreuzy, J.-R.; Carrera, J. On the validity of effective formulations for transport through heterogeneous porous media. Hydrol. Earth Syst. Sci. 2016, 20, 1319–1330. [Google Scholar] [CrossRef] [Green Version]
- Neuman, S.P.; Tartakovsky, D.M. Perspective on theories of non-Fickian transport in heterogeneous media. Adv. Water Resour. 2009, 32, 670–680. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, F.; Yin, S.; Wallace, C.D.; Soltanian, M.R.; Dai, Z.; Ritzi, R.W.; Ma, Z.; Zhan, C.; Lü, X. Application of upscaling methods for fluid flow and mass transport in multi-scale heterogeneous media: A critical review. Appl. Energy 2021, 303, 117603. [Google Scholar] [CrossRef]
- Sherman, T.; Engdahl, N.B.; Porta, G.; Bolster, D. A review of spatial Markov models for predicting pre-asymptotic and anomalous transport in porous and fractured media. J. Contam. Hydrol. 2021, 236, 103734. [Google Scholar] [CrossRef]
- Koltermann, C.E.; Gorelick, S.M. Heterogeneity in sedimentary deposits: A review of structure-imitating, process-imitating, and descriptive approaches. Water Resour. Res. 1996, 32, 2617–2658. [Google Scholar] [CrossRef]
- Riva, M.; Guadagnini, A.; Fernandez-Garcia, D.; Sanchez-Vila, X.; Ptak, T. Relative importance of geostatistical and transport models in describing heavily tailed breakthrough curves at the Lauswiesen site. J. Contam. Hydrol. 2008, 101, 1–13. [Google Scholar] [CrossRef]
- Kitanidis, P.K. Prediction by the method of moments of transport in a heterogeneous formation. J. Hydrol. 1988, 102, 453–473. [Google Scholar] [CrossRef]
- Dentz, M.; Kinzelbach, H.; Attinger, S.; Kinzelbach, W. Temporal behavior of a solute cloud in a heterogeneous porous medium 1. Point-like injection. Water Resour. Res. 2000, 36, 3591–3604. [Google Scholar] [CrossRef]
- Dentz, M.; Gouze, P.; Carrera, J. Effective non-local reaction kinetics for transport in physically and chemically heterogeneous media. J. Contam. Hydrol. 2011, 120, 222–236. [Google Scholar] [CrossRef] [Green Version]
- Luquot, L.; Gouze, P.; Niemi, A.; Bensabat, J.; Carrera, J. CO2-rich brine percolation experiments through Heletz reservoir rock samples (Israel): Role of the flow rate and brine composition. Int. J. Greenh. Gas Control 2016, 48, 44–58. [Google Scholar] [CrossRef]
- Cirpka, O.A.; Chiogna, G.; Rolle, M.; Bellin, A. Transverse mixing in three-dimensional nonstationary anisotropic heterogeneous porous media. Water Resour. Res. 2015, 51, 241–260. [Google Scholar] [CrossRef]
- Willingham, T.W.; Werth, C.J.; Valocchi, A.J. Evaluation of the effects of porous media structure on mixing-controlled reactions using pore-scale modeling and micromodel experiments. Environ. Sci. Technol. 2008, 42, 3185–3193. [Google Scholar] [CrossRef] [PubMed]
- Attinger, S.; Dentz, M.; Kinzelbach, W. Exact transverse macro dispersion coefficients for transport in heterogeneous porous media. Stoch. Environ. Res. Risk Assess. 2004, 18, 9–15. [Google Scholar] [CrossRef]
- Rolle, M.; Eberhardt, C.; Chiogna, G.; Cirpka, O.A.; Grathwohl, P. Enhancement of dilution and transverse reactive mixing in porous media: Experiments and model-based interpretation. J. Contam. Hydrol. 2009, 110, 130–142. [Google Scholar] [CrossRef]
- Le Borgne, T.; Dentz, M.; Carrera, J. Lagrangian statistical model for transport in highly heterogeneous velocity fields. Phys. Rev. Lett. 2008, 101, 090601. [Google Scholar] [CrossRef] [Green Version]
- Le Borgne, T.; Dentz, M.; Carrera, J. Spatial Markov processes for modeling Lagrangian particle dynamics in heterogeneous porous media. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2008, 78, 026308. [Google Scholar] [CrossRef]
- Dentz, M.; Kang, P.K.; Comolli, A.; Le Borgne, T.; Lester, D.R. Continuous Time Random Walks for the Evolution of Lagrangian Velocities. Phys. Rev. Fluids 2016, 1, 074004. [Google Scholar] [CrossRef]
- De Anna, P.; Le Borgne, T.; Dentz, M.; Tartakovsky, A.M.; Bolster, D.; Davy, P. Flow intermittency, dispersion, and correlated continuous time random walks in porous media. Phys. Rev. Lett. 2013, 110, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Kang, P.K.; Dentz, M.; Le Borgne, T.; Juanes, R. Spatial Markov model of anomalous transport through random lattice networks. Phys. Rev. Lett. 2011, 107, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Kang, P.K.; De Anna, P.; Nunes, J.P.; Bijeljic, B.; Blunt, M.J.; Juanes, R. Pore-scale intermittent velocity structure underpinning anomalous transport through 3-D porous media. Geophys. Res. Lett. 2014, 41, 6184–6190. [Google Scholar] [CrossRef]
- Kang, P.K.; Dentz, M.; Le Borgne, T.; Lee, S.; Juanes, R. Anomalous transport in disordered fracture networks: Spatial Markov model for dispersion with variable injection modes. Adv. Water Resour. 2017, 106, 80–94. [Google Scholar] [CrossRef] [Green Version]
- Thullner, M.; Regnier, P. Microbial controls on the biogeochemical dynamics in the subsurface. Rev. Mineral. Geochem. 2019, 85, 265–302. [Google Scholar] [CrossRef] [Green Version]
- Rittmann, B.E.; McCarty, P.L. Environmental Biotechnology: Principles and Applications. 2001. Available online: https://www.academia.edu/28898814/Environmental_Biotechnology (accessed on 22 November 2021).
- Stumm, W. Aquatic Chemistry: Chemical Equilibria and Rates in Natural Waters; Wiley: Chichester, UK, 1996. [Google Scholar]
- Christensen, T.H.; Bjerg, P.L.; Banwart, S.A.; Jakobsen, R.; Heron, G.; Albrechtsen, H.J. Characterization of redox conditions in groundwater contaminant plumes. J. Contam. Hydrol. 2000, 45, 165–241. [Google Scholar] [CrossRef]
- Geyer, K.M.; Kyker-Snowman, E.; Grandy, A.S.; Frey, S.D. Microbial carbon use efficiency: Accounting for population, community, and ecosystem-scale controls over the fate of metabolized organic matter. Biogeochemistry 2016, 127, 173–188. [Google Scholar] [CrossRef] [Green Version]
- Cirpka, O.A.; Valocchi, A.J. Two-dimensional concentration distribution for mixing-controlled bioreactive transport in steady state. Adv. Water Resour. 2007, 30, 1668–1679. [Google Scholar] [CrossRef]
- Michaelis, L.; Menten, M.L.; Goody, R.S.; Johnson, K.A. Die Kinetik der Invertinwirkung/The kinetics of invertase action. Biochemistry 1913, 49, 352. [Google Scholar]
- Monod, J. The Growth of Bacterial Cultures. Annu. Rev. Microbiol. 1949, 3, 371–394. [Google Scholar] [CrossRef] [Green Version]
- Liu, S. Bioprocess Engineering: Kinetics, Sustainability, and Reactor Design, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Appelo, C.A.J.; Postma, D. Geochemistry, Groundwater and Pollution; CRC Press: Boca Raton, FL, USA, 2004; ISBN 9781439833544. [Google Scholar]
- Widdowson, M.A.; Molz, F.J.; Benefield, L.D. A numerical transport model for oxygen- and nitrate-based respiration linked to substrate and nutrient availability in porous media. Water Resour. Res. 1988, 24, 1553–1565. [Google Scholar] [CrossRef]
- Van Cappellen, P.; Gaillard, J.F. Biogeochemical dynamics in aquatic sediments. Rev. Mineral. 1996, 34, 335–376. [Google Scholar] [CrossRef]
- Brun, A.; Engesgaard, P. Modelling of transport and biogeochemical processes in pollution plumes: Literature review and model development. J. Hydrol. 2002, 256, 211–227. [Google Scholar] [CrossRef]
- Curtis, G.P. Comparison of approaches for simulating reactive solute transport involving organic degradation reactions by multiple terminal electron acceptors. Comput. Geosci. 2003, 29, 319–329. [Google Scholar] [CrossRef]
- Jin, Q.; Bethke, C.M. A new rate law describing microbial respiration. Appl. Environ. Microbiol. 2003, 69, 2340–2348. [Google Scholar] [CrossRef] [Green Version]
- Schafer, D.; Schafer, W.; Kinzelbach, W. Simulation of reactive processes related to biodegradation in aquifers 1. Structure of the three-dimensional reactive transport model. Contam. Hydrol. 1998, 31, 167–186. [Google Scholar] [CrossRef]
- Postma, D.; Jakobsen, R. Redox zonation: Equilibrium constraints on the Fe(III)/SO4-reduction interface. Geochim. Cosmochim. Acta 1996, 60, 3169–3175. [Google Scholar] [CrossRef]
- Thullner, M.; Regnier, P.; Van Cappellen, P. Modeling microbially induced carbon degradation in redox-stratified subsurface environments: Concepts and open questions. Geomicrobiol. J. 2007, 24, 139–155. [Google Scholar] [CrossRef]
- Mayer, K.U.; Benner, S.G.; Frind, E.O.; Thornton, S.F.; Lerner, D.N. Reactive transport modeling of processes controlling the distribution and natural attenuation of phenolic compounds in a deep sandstone aquifer. J. Contam. Hydrol. 2001, 53, 341–368. [Google Scholar] [CrossRef]
- Rolle, M.; Clement, T.P.; Sethi, R.; Di Molfetta, A. A kinetic approach for simulating redox-controlled fringe and core biodegradation processes in groundwater: Model development and application to a landfill site in Piedmont, Italy. Hydrol. Process. 2008, 22, 4905–4921. [Google Scholar] [CrossRef]
- Van Breukelen, B.M.; Griffioen, J.; Röling, W.F.M.; Van Verseveld, H.W. Reactive transport modelling of biogeochemical processes and carbon isotope geochemistry inside a landfill leachate plume. J. Contam. Hydrol. 2004, 70, 249–269. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Van Cappellen, P. A multicomponent reactive transport model of early diagenesis: Application to redox cycling in coastal marine sediments. Geochim. Cosmochim. Acta 1996, 60, 2993–3014. [Google Scholar] [CrossRef]
- Torres, E.; Couture, R.M.; Shafei, B.; Nardi, A.; Ayora, C.; Van Cappellen, P. Reactive transport modeling of early diagenesis in a reservoir lake affected by acid mine drainage: Trace metals, lake overturn, benthic fluxes and remediation. Chem. Geol. 2015, 419, 75–91. [Google Scholar] [CrossRef]
- Arora, B.; Şengör, S.S.; Spycher, N.F.; Steefel, C.I. A reactive transport benchmark on heavy metal cycling in lake sediments. Comput. Geosci. 2015, 19, 613–633. [Google Scholar] [CrossRef]
- Paraska, D.W.; Hipsey, M.R.; Ursula Salmon, S. Sediment diagenesis models: Review of approaches, challenges and opportunities. Environ. Model. Softw. 2014, 61, 297–325. [Google Scholar] [CrossRef]
- Dash, S.; Borah, S.S.; Kalamdhad, A.S. Study of the limnology of wetlands through a one-dimensional model for assessing the eutrophication levels induced by various pollution sources. Ecol. Modell. 2020, 416, 108907. [Google Scholar] [CrossRef]
- Ng, G.H.C.; Rosenfeld, C.E.; Santelli, C.M.; Yourd, A.R.; Lange, J.; Duhn, K.; Johnson, N.W. Microbial and Reactive Transport Modeling Evidence for Hyporheic Flux-Driven Cryptic Sulfur Cycling and Anaerobic Methane Oxidation in a Sulfate-Impacted Wetland-Stream System. J. Geophys. Res. Biogeosci. 2020, 125, e2019JG005185. [Google Scholar] [CrossRef]
- Greskowiak, J.; Prommer, H.; Massmann, G.; Nützmann, G. Modeling seasonal redox dynamics and the corresponding fate of the pharmaceutical residue phenazone during artificial recharge of groundwater. Environ. Sci. Technol. 2006, 40, 6615–6621. [Google Scholar] [CrossRef]
- Ben Moshe, S.; Weisbrod, N.; Furman, A. Optimization of soil aquifer treatment (SAT) operation using a reactive transport model. Vadose Zone J. 2021, 20, e20095. [Google Scholar] [CrossRef]
- Rodríguez-Escales, P.; Fernàndez-Garcia, D.; Drechsel, J.; Folch, A.; Sanchez-Vila, X. Improving degradation of emerging organic compounds by applying chaotic advection in Managed Aquifer Recharge in randomly heterogeneous porous media. Water Resour. Res. 2017, 53, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Pagel, H.; Poll, C.; Ingwersen, J.; Kandeler, E.; Streck, T. Modeling coupled pesticide degradation and organic matter turnover: From gene abundance to process rates. Soil Biol. Biochem. 2016, 103, 349–364. [Google Scholar] [CrossRef]
- Tang, J.Y. On the relationships between the Michaelis-Menten kinetics, reverse Michaelis-Menten kinetics, equilibrium chemistry approximation kinetics, and quadratic kinetics. Geosci. Model Dev. 2015, 8, 3823–3835. [Google Scholar] [CrossRef] [Green Version]
- Kindred, J.S.; Celia, M.A. Contaminant transport and biodegradation: 2. Conceptual model and test simulations. Water Resour. Res. 1989, 25, 1149–1159. [Google Scholar] [CrossRef]
- Langergraber, G.; Rousseau, D.P.L.; García, J.; Mena, J. CWM1: A general model to describe biokinetic processes in subsurface flow constructed wetlands. Water Sci. Technol. 2009, 59, 1687–1697. [Google Scholar] [CrossRef]
- Thullner, M.; Van Cappellen, P.; Regnier, P. Modeling the impact of microbial activity on redox dynamics in porous media. Geochim. Cosmochim. Acta 2005, 69, 5005–5019. [Google Scholar] [CrossRef]
- Huang, J.; Xu, Q.; Wang, X.; Xi, B.; Jia, K.; Huo, S.; Liu, H.; Li, C.; Xu, B. Evaluation of a modified monod model for predicting algal dynamics in Lake Tai. Water 2015, 7, 3626. [Google Scholar] [CrossRef] [Green Version]
- Stolpovsky, K.; Martinez-Lavanchy, P.; Heipieper, H.J.; Van Cappellen, P.; Thullner, M. Incorporating dormancy in dynamic microbial community models. Ecol. Modell. 2011, 222, 3092–3102. [Google Scholar] [CrossRef]
- Joergensen, R.G.; Wichern, F. Alive and kicking: Why dormant soil microorganisms matter. Soil Biol. Biochem. 2018, 116, 419–430. [Google Scholar] [CrossRef]
- Mancuso, M.A.; Fioreze, M. Numerical simulation of flow and biokinetic processes in subsurface flow constructed wetlands: A systematic review. J. Urban Environ. Eng. 2018, 12, 120–127. [Google Scholar] [CrossRef]
- Yuan, C.; Huang, T.; Zhao, X.; Zhao, Y. Numerical models of subsurface flow constructed wetlands: Review and future development. Sustainability 2020, 12, 3498. [Google Scholar] [CrossRef] [Green Version]
- Llorens, E.; Saaltink, M.W.; Poch, M.; García, J. Bacterial transformation and biodegradation processes simulation in horizontal subsurface flow constructed wetlands using CWM1-RETRASO. Bioresour. Technol. 2011, 102, 928–936. [Google Scholar] [CrossRef] [PubMed]
- Llorens, E.; Saaltink, M.W.; García, J. CWM1 implementation in RetrasoCodeBright: First results using horizontal subsurface flow constructed wetland data. Chem. Eng. J. 2011, 166, 224–232. [Google Scholar] [CrossRef]
- Pálfy, T.G.; Langergraber, G. The verification of the constructed wetland model no. 1 implementation in HYDRUS using column experiment data. Ecol. Eng. 2014, 68, 105–115. [Google Scholar] [CrossRef]
- Langergraber, G.; Šimůnek, J. Modeling Variably Saturated Water Flow and Multicomponent Reactive Transport in Constructed Wetlands. In Reactive Transport Modeling: Applications in Subsurface Energy and Environmental Problems; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2018. [Google Scholar]
- Reed, D.C.; Algar, C.K.; Huber, J.A.; Dick, G.J. Gene-centric approach to integrating environmental genomics and biogeochemical models. Proc. Natl. Acad. Sci. USA 2014, 111, 1879–1884. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Louca, S.; Hawley, A.K.; Katsev, S.; Torres-Beltran, M.; Bhatia, M.P.; Kheirandish, S.; Michiels, C.C.; Capelle, D.; Lavik, G.; Doebeli, M.; et al. Integrating biogeochemistry with multiomic sequence information in a model oxygen minimum zone. Proc. Natl. Acad. Sci. USA 2016, 113, 5925–5933. [Google Scholar] [CrossRef] [Green Version]
- Pagel, H.; Ingwersen, J.; Poll, C.; Kandeler, E.; Streck, T. Micro-scale modeling of pesticide degradation coupled to carbon turnover in the detritusphere: Model description and sensitivity analysis. Biogeochemistry 2014, 117, 185–204. [Google Scholar] [CrossRef]
- Price, P.B.; Sowers, T. Temperature dependence of metabolic rates for microbial growth, maintenance, and survival. Proc. Natl. Acad. Sci. USA 2004, 101, 4631–4636. [Google Scholar] [CrossRef] [Green Version]
- Reed, J.L.; Patel, T.R.; Chen, K.H.; Joyce, A.R.; Applebee, M.K.; Herring, C.D.; Bui, O.T.; Knight, E.M.; Fong, S.S.; Palsson, B.O. Systems approach to refining genome annotation. Proc. Natl. Acad. Sci. USA 2006, 103, 17480–17484. [Google Scholar] [CrossRef] [Green Version]
- Schuetz, R.; Kuepfer, L.; Sauer, U. Systematic evaluation of objective functions for predicting intracellular fluxes in Escherichia coli. Mol. Syst. Biol. 2007, 3, 119. [Google Scholar] [CrossRef]
- Feist, A.M.; Palsson, B. The growing scope of applications of genome-scale metabolic reconstructions using Escherichia coli. Nat. Biotechnol. 2008, 26, 659–667. [Google Scholar] [CrossRef] [Green Version]
- Fang, Y.; Scheibe, T.D.; Mahadevan, R.; Garg, S.; Long, P.E.; Lovley, D.R. Direct coupling of a genome-scale microbial in silico model and a groundwater reactive transport model. J. Contam. Hydrol. 2011, 122, 96–103. [Google Scholar] [CrossRef]
- Satpathy, S.; Sen, S.K.; Pattanaik, S.; Raut, S. Review on bacterial biofilm: An universal cause of contamination. Biocatal. Agric. Biotechnol. 2016, 7, 56–66. [Google Scholar] [CrossRef]
- Flemming, H.C.; Neu, T.R.; Wozniak, D.J. The EPS matrix: The “House of Biofilm Cells”. J. Bacteriol. 2007, 189, 7945–7947. [Google Scholar] [CrossRef] [Green Version]
- Flemming, H.C.; Wingender, J. The biofilm matrix. Nat. Rev. Microbiol. 2010, 8, 623–633. [Google Scholar] [CrossRef]
- Deng, W.; Cardenas, M.B.; Kirk, M.F.; Altman, S.J.; Bennett, P.C. Effect of permeable biofilm on micro-and macro-scale flow and transport in bioclogged pores. Environ. Sci. Technol. 2013, 47, 11092–11098. [Google Scholar] [CrossRef]
- Wang, J.; Carrera, J.; Saaltink, M.W.; Valhondo, C. A general and efficient numerical solution of reactive transport with multirate mass transfer. Comput. Geosci. 2022, 158, 104953. [Google Scholar] [CrossRef]
- Orgogozo, L.; Golfier, F.; Buès, M.A.; Quintard, M.; Koné, T. A dual-porosity theory for solute transport in biofilm-coated porous media. Adv. Water Resour. 2013, 62, 266–279. [Google Scholar] [CrossRef]
- Taylor, S.W.; Milly, P.C.D.; Jaffé, P.R. Biofilm growth and the related changes in the physical properties of a porous medium: 2. Permeability. Water Resour. Res. 1990, 26, 2161–2169. [Google Scholar] [CrossRef]
- Cunningham, A.B.; Characklls, W.G.; Abedeen, F.; Crawford, D. Influence of Biofilm Accumulation on Porous Media Hydrodynamics. Environ. Sci. Technol. 1991, 25, 1305–1311. [Google Scholar] [CrossRef]
- Cunningham, A.B.; Sharp, R.R.; Hiebert, R.; James, G. Subsurface biofilm barriers for the containment and remediation of contaminated groundwater. Bioremediat. J. 2003, 7, 151–164. [Google Scholar] [CrossRef]
- Thullner, M. Comparison of bioclogging effects in saturated porous media within one- and two-dimensional flow systems. Ecol. Eng. 2010, 36, 176–196. [Google Scholar] [CrossRef]
- Morales, V.L.; Parlange, J.Y.; Steenhuis, T.S. Are preferential flow paths perpetuated by microbial activity in the soil matrix? A review. J. Hydrol. 2010, 393, 29–36. [Google Scholar] [CrossRef]
- Carles Brangarí, A.; Sanchez-Vila, X.; Freixa, A.; Romaní, A.M.; Rubol, S.; Fernàndez-Garcia, D. A mechanistic model (BCC-PSSICO) to predict changes in the hydraulic properties for bio-amended variably saturated soils. Water Resour. Res. 2017, 53, 93–109. [Google Scholar] [CrossRef]
- Carrel, M.; Morales, V.L.; Dentz, M.; Derlon, N.; Morgenroth, E.; Holzner, M. Pore-Scale Hydrodynamics in a Progressively Bioclogged Three-Dimensional Porous Medium: 3-D Particle Tracking Experiments and Stochastic Transport Modeling. Water Resour. Res. 2018, 54, 2183–2198. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, Z.; Liu, C.; Liu, Y.; Bailey, V.L. Multiscale Investigation on Biofilm Distribution and Its Impact on Macroscopic Biogeochemical Reaction Rates. Water Resour. Res. 2017, 53, 8698–8714. [Google Scholar] [CrossRef]
- Seifert, D.; Engesgaard, P. Use of tracer tests to investigate changes in flow and transport properties due to bioclogging of porous media. J. Contam. Hydrol. 2007, 93, 58–71. [Google Scholar] [CrossRef] [PubMed]
- Kone, T.; Golfier, F.; Orgogozo, L.; Oltéan, C.; Lefèvre, E.; Block, J.C.; Buès, M.A. Impact of biofilm-induced heterogeneities on solute transport in porous media. Water Resour. Res. 2014, 50, 9103–9119. [Google Scholar] [CrossRef]
- Carrayrou, J.; Hoffmann, J.; Knabner, P.; Kräutle, S.; de Dieuleveult, C.; Erhel, J.; Van der Lee, J.; Lagneau, V.; Mayer, K.U.; MacQuarrie, K.T.B. Comparison of numerical methods for simulating strongly nonlinear and heterogeneous reactive transport problems—the MoMaS benchmark case. Comput. Geosci. 2010, 14, 483–502. [Google Scholar] [CrossRef] [Green Version]
- Parkhurst, D.L.; Wissmeier, L. PhreeqcRM: A reaction module for transport simulators based on the geochemical model PHREEQC. Adv. Water Resour. 2015, 83, 176–189. [Google Scholar] [CrossRef]
- Prommer, H.; Barry, D.A.; Zheng, C. MODFLOW/MT3DMS-based reactive multicomponent transport modeling. Ground Water 2003, 41, 247–257. [Google Scholar] [CrossRef]
- Nardi, A.; Idiart, A.; Trinchero, P.; de Vries, L.M.; Molinero, J. Interface COMSOL-PHREEQC (iCP), an efficient numerical framework for the solution of coupled multiphysics and geochemistry. Comput. Geosci. 2014, 69, 10–21. [Google Scholar] [CrossRef]
- Mao, X.; Prommer, H.; Barry, D.A.; Langevin, C.D.; Panteleit, B.; Li, L. Three-dimensional model for multi-component reactive transport with variable density groundwater flow. Environ. Model. Softw. 2006, 21, 615–628. [Google Scholar] [CrossRef]
- Šimůnek, J.; Šejna, M.; Saito, H.; Sakai, M.; van Genuchten, M.T. The HYDRUS-1D Software Package for Simulating the One-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media. Univ. Calif.-Riverside Res. Rep. 2005, 3, 1–240. [Google Scholar]
- Yeh, G.-T.; Tsai, C.-H.P. HYDROGEOCHEM 7.1: A Three-Dimensional Model of Coupled Fluid Flow, Thermal Transport, HYDROGEOCHEMical Transport, and Geomechanics through Multiple Phase Systems Version 7.1 (A Three Dimensional THMC Processes Model). Grad. Inst. Appl. Geol. Natl. Cent. Univ. Jhongli 2015, 1. [Google Scholar] [CrossRef]
- Xu, T.; Spycher, N.; Sonnenthal, E.; Zhang, G.; Zheng, L.; Pruess, K. TOUGHREACT Version 2.0: A simulator for subsurface reactive transport under non-isothermal multiphase flow conditions. Comput. Geosci. 2010, 37, 763–774. [Google Scholar] [CrossRef] [Green Version]
- Samper, J.; Xu, T.; Yang, C. A sequential partly iterative approach for multicomponent reactive transport with CORE2D. Comput. Geosci. 2009, 13, 301. [Google Scholar] [CrossRef] [Green Version]
- van der Lee, J.; De Windt, L.; Lagneau, V.; Goblet, P. Module-oriented modeling of reactive transport with HYTEC. Comput. Geosci. 2003, 29, 265–275. [Google Scholar] [CrossRef]
- Raoof, A.; Nick, H.M.; Hassanizadeh, S.M.; Spiers, C.J. PoreFlow: A complex pore-network model for simulation of reactive transport in variably saturated porous media. Comput. Geosci. 2013, 61, 160–174. [Google Scholar] [CrossRef]
- Kolditz, O.; Bauer, S.; Bilke, L.; Böttcher, N.; Delfs, J.O.; Fischer, T.; Görke, U.J.; Kalbacher, T.; Kosakowski, G.; McDermott, C.I.; et al. OpenGeoSys: An open-source initiative for numerical simulation of thermo-hydro-mechanical/chemical (THM/C) processes in porous media. Environ. Earth Sci. 2012, 67, 589–599. [Google Scholar] [CrossRef]
- Fahs, M.; Carrayrou, J.; Younes, A.; Ackerer, P. On the efficiency of the direct substitution approach for reactive transport problems in porous media. Water Air Soil Pollut. 2008, 193, 299–308. [Google Scholar] [CrossRef]
- Mayer, K.U.; Benner, S.G.; Blowes, D.W.; Frind, E.O. The reactive transport model MIN3P: Application to acid mine drainage generation and treatment-nickel rim mine site, Sudbury, Ontario. In Mining and Environment; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1, pp. 145–154. [Google Scholar]
- Hammond, G.E.; Lichtner, P.C.; Lu, C.; Mills, R.T. PFLOTRAN: Reactive Flow & Transport Code for Use on Laptops to Leadership-Class Supercomputers. In Groundwater Reactive Transport Models; Zhang, F., Yeh, G.-H., Parker, J.C., Eds.; Bentham Science: Sharjah, United Arab Emirates, 2012; Volume 19, pp. 141–159. [Google Scholar]
- Steefel, C.I. CrunchFlow: User’s Manual; Earth Sciences Division, Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2009. [Google Scholar]
- Su, D.; Mayer, K.U.; MacQuarrie, K.T.B. MIN3P-HPC: A High-Performance Unstructured Grid Code for Subsurface Flow and Reactive Transport Simulation. Math. Geosci. 2021, 53, 517–550. [Google Scholar] [CrossRef]
- Beisman, J.J.; Maxwell, R.M.; Navarre-Sitchler, A.K.; Steefel, C.I.; Molins, S. ParCrunchFlow: An efficient, parallel reactive transport simulation tool for physically and chemically heterogeneous saturated subsurface environments. Comput. Geosci. 2015, 19, 403–422. [Google Scholar] [CrossRef]
- Amir, L.; Kern, M. Jacobian Free Methods for Coupling Transport with Chemistry in Heterogenous Porous Media. Water 2021, 13, 370. [Google Scholar] [CrossRef]
- Erhel, J.; Sabit, S. Analysis of a global reactive transport model and results for the MoMaS benchmark. Math. Comput. Simul. 2017, 137, 286–298. [Google Scholar] [CrossRef] [Green Version]
- Kees, C.E.; Miller, C.T. Higher order time integration methods for two-phase flow. Adv. Water Resour. 2002, 25, 159–177. [Google Scholar] [CrossRef]
- Equilibria, J.P. Open Archive Toulouse Archive Ouverte (OATAO). Mater. Sci. Forum 2006, 508, 621–628. [Google Scholar] [CrossRef] [Green Version]
- Fahs, M.; Younes, A.; Ackerer, P. An Efficient Implementation of the Method of Lines for Multicomponent Reactive Transport Equations. Water Air Soil Pollut. 2011, 215, 273–283. [Google Scholar] [CrossRef]
- Soler-Sagarra, J.; Saaltink, M.W.; Nardi, A.; De Gaspari, F.; Carrera, J. Water Mixing Approach (WMA) for reactive transport modeling. Adv. Water Resour. 2021, preprint. [Google Scholar] [CrossRef]
- Pelizardi, F.; Bea, S.A.; Carrera, J.; Vives, L. Identifying geochemical processes using End Member Mixing Analysis to decouple chemical components for mixing ratio calculations. J. Hydrol. 2017, 550, 144–156. [Google Scholar] [CrossRef]
- Neuman, S.P. A Eulerian-Lagrangian numerical scheme for the dispersion-convection equation using conjugate space-time grids. J. Comput. Phys. 1981, 41, 270–294. [Google Scholar] [CrossRef]
- Neuman, S.P. Adaptive Eulerian–Lagrangian finite element method for advection–dispersion. Int. J. Numer. Methods Eng. 1984, 20, 321–337. [Google Scholar] [CrossRef]
- Goode, D.J.; Konikow, L.F. Modification of a Method-of-Characteristics Solute-Transport Model to Incorporate Decay and Equilibrium-Controlled Sorption or Ion Exchange; U.S. Geological Survey: Reston, VA, USA, 1989.
- Konikow, L.F.; Bredehoeft, J.D. Computer Model of Two-Dimensional Solute Transport and Dispersion in Ground Water; U.S. Geological Survey: Reston, VA, USA, 1984.
- Bell, L.S.J.; Binning, P.J. A split operator approach to reactive transport with the forward particle tracking Eulerian Lagrangian localized adjoint method. Adv. Water Resour. 2004, 27, 323–334. [Google Scholar] [CrossRef]
- Ramasomanana, F.; Younes, A.; Fahs, M. Modeling 2D Multispecies Reactive Transport in Saturated/Unsaturated Porous Media with the Eulerian–Lagrangian Localized Adjoint Method. Water Air Soil Pollut. 2012, 223, 1801–1813. [Google Scholar] [CrossRef]
- Cirpka, O.A.; Frind, E.O.; Helmig, R. Numerical methods for reactive transport on rectangular and streamline-oriented grids. Adv. Water Resour. 1999, 22, 711–728. [Google Scholar] [CrossRef]
- Benson, D.A.; Meerschaert, M.M. Simulation of chemical reaction via particle tracking: Diffusion-limited versus thermodynamic rate-limited regimes. Water Resour. Res. 2008, 44, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Berkowitz, B.; Dror, I.; Hansen, S.K.; Scher, H. Measurements and models of reactive transport in geological media. Rev. Geophys. 2016, 54, 930–986. [Google Scholar] [CrossRef] [Green Version]
- Aquino, T.; Dentz, M. Chemical Continuous Time Random Walks. Phys. Rev. Lett. 2017, 119, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Perez, L.J.; Hidalgo, J.J.; Dentz, M. Reactive Random Walk Particle Tracking and Its Equivalence With the Advection-Diffusion-Reaction Equation. Water Resour. Res. 2019, 55, 847–855. [Google Scholar] [CrossRef] [Green Version]
- Wright, E.E.; Sund, N.L.; Richter, D.H.; Porta, G.M.; Bolster, D. Upscaling bimolecular reactive transport in highly heterogeneous porous media with the LAgrangian Transport Eulerian Reaction Spatial (LATERS) Markov model. Stoch. Environ. Res. Risk Assess. 2021, 35, 1529–1547. [Google Scholar] [CrossRef]
- Ding, D.; Benson, D.A.; Fernàndez-Garcia, D.; Henri, C.V.; Hyndman, D.W.; Phanikumar, M.S.; Bolster, D. Elimination of the Reaction Rate “Scale Effect”: Application of the Lagrangian Reactive Particle-Tracking Method to Simulate Mixing-Limited, Field-Scale Biodegradation at the Schoolcraft (MI, USA) Site. Water Resour. Res. 2017, 53, 10411–10432. [Google Scholar] [CrossRef]
- Dentz, M.; Castro, A. Effective transport dynamics in porous media with heterogeneous retardation properties. Geophys. Res. Lett. 2009, 36, L03403–L03407. [Google Scholar] [CrossRef]
- Bolster, D.; Paster, A.; Benson, D.A. A particle number conserving Lagrangian method for mixing-driven reactive transport. Water Resour. Res. 2016, 52, 1518–1527. [Google Scholar] [CrossRef] [Green Version]
- Paster, A.; Bolster, D.; Benson, D.A. Connecting the dots: Semi-analytical and random walk numerical solutions of the diffusion-reaction equation with stochastic initial conditions. J. Comput. Phys. 2014, 263, 91–112. [Google Scholar] [CrossRef]
- Perez, L.J.; Hidalgo, J.J.; Dentz, M. Upscaling of Mixing-Limited Bimolecular Chemical Reactions in Poiseuille Flow. Water Resour. Res. 2019, 55, 249–269. [Google Scholar] [CrossRef] [Green Version]
- Sole-Mari, G.; Fernàndez-Garcia, D.; Rodríguez-Escales, P.; Sanchez-Vila, X. A KDE-Based Random Walk Method for Modeling Reactive Transport With Complex Kinetics in Porous Media. Water Resour. Res. 2017, 53, 9019–9039. [Google Scholar] [CrossRef]
- Schmidt, M.J.; Pankavich, S.; Benson, D.A. A Kernel-based Lagrangian method for imperfectly-mixed chemical reactions. J. Comput. Phys. 2017, 336, 288–307. [Google Scholar] [CrossRef] [Green Version]
- Tartakovsky, A.M.; Trask, N.; Pan, K.; Jones, B.; Pan, W.; Williams, J.R. Smoothed particle hydrodynamics and its applications for multiphase flow and reactive transport in porous media. Comput. Geosci. 2016, 20, 807–834. [Google Scholar] [CrossRef] [Green Version]
- Sole-Mari, G.; Schmidt, M.J.; Bolster, D.; Fernàndez-Garcia, D. Random-Walk Modeling of Reactive Transport in Porous Media With a Reduced-Order Chemical Basis of Conservative Components. Water Resour. Res. 2021, 57, 1–19. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carrera, J.; Saaltink, M.W.; Soler-Sagarra, J.; Wang, J.; Valhondo, C. Reactive Transport: A Review of Basic Concepts with Emphasis on Biochemical Processes. Energies 2022, 15, 925. https://doi.org/10.3390/en15030925
Carrera J, Saaltink MW, Soler-Sagarra J, Wang J, Valhondo C. Reactive Transport: A Review of Basic Concepts with Emphasis on Biochemical Processes. Energies. 2022; 15(3):925. https://doi.org/10.3390/en15030925
Chicago/Turabian StyleCarrera, Jesús, Maarten W. Saaltink, Joaquim Soler-Sagarra, Jingjing Wang, and Cristina Valhondo. 2022. "Reactive Transport: A Review of Basic Concepts with Emphasis on Biochemical Processes" Energies 15, no. 3: 925. https://doi.org/10.3390/en15030925
APA StyleCarrera, J., Saaltink, M. W., Soler-Sagarra, J., Wang, J., & Valhondo, C. (2022). Reactive Transport: A Review of Basic Concepts with Emphasis on Biochemical Processes. Energies, 15(3), 925. https://doi.org/10.3390/en15030925







