The Impact of Water Hammer on Hydraulic Power Units
Abstract
:1. Introduction
2. The Water Hammer Phenomenon—Literature Review
2.1. 2nd Half of the XIX Century—First General Theories
2.2. 1st Half of the XX Century—Early Applied Studies
2.3. 2nd Half of the XX Century—Theories in Modern Times
2.4. Present Day: Current Research
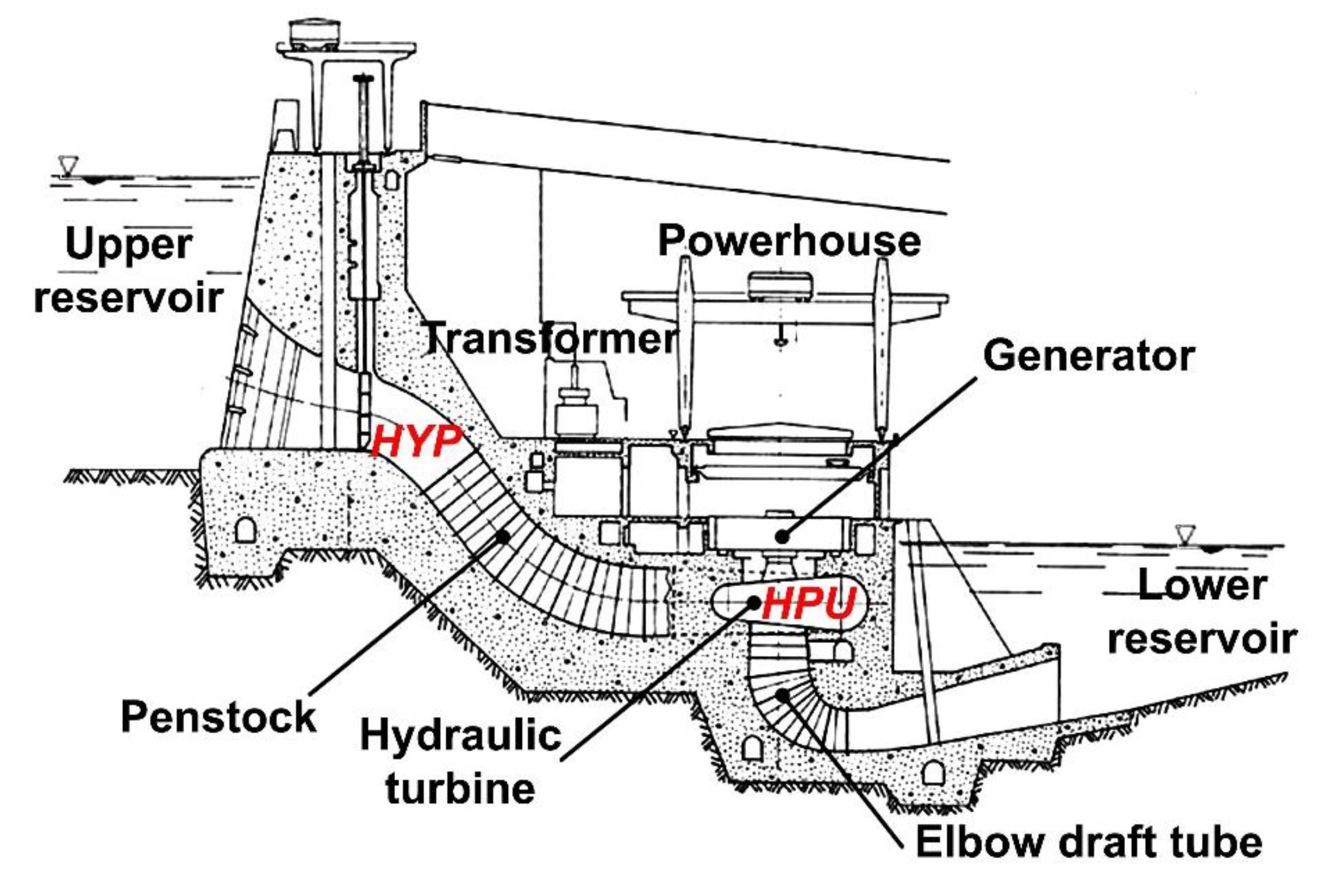
3. In Situ Experimental Investigations of the Main Parameters Associated with the Water Hammer Phenomenon
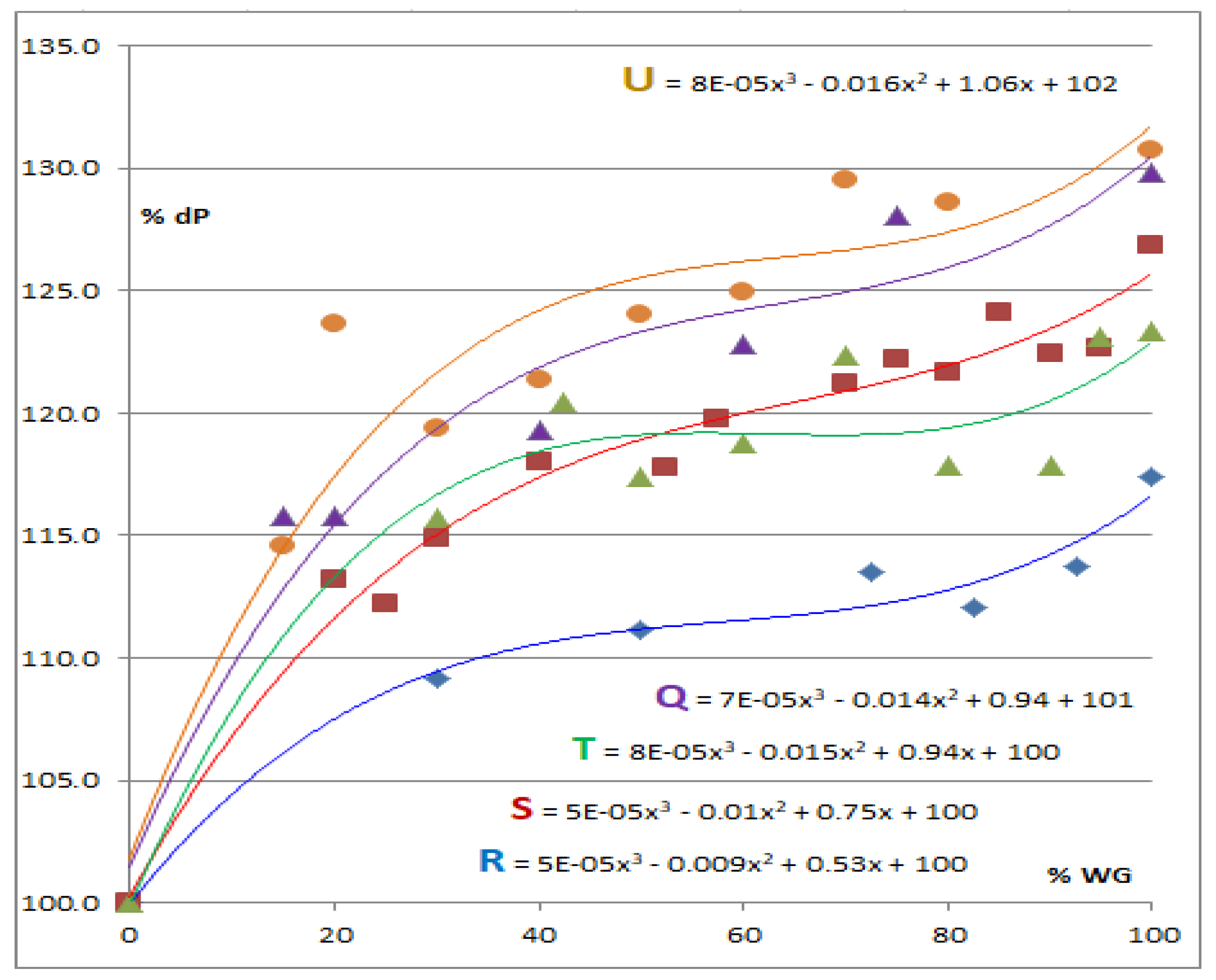
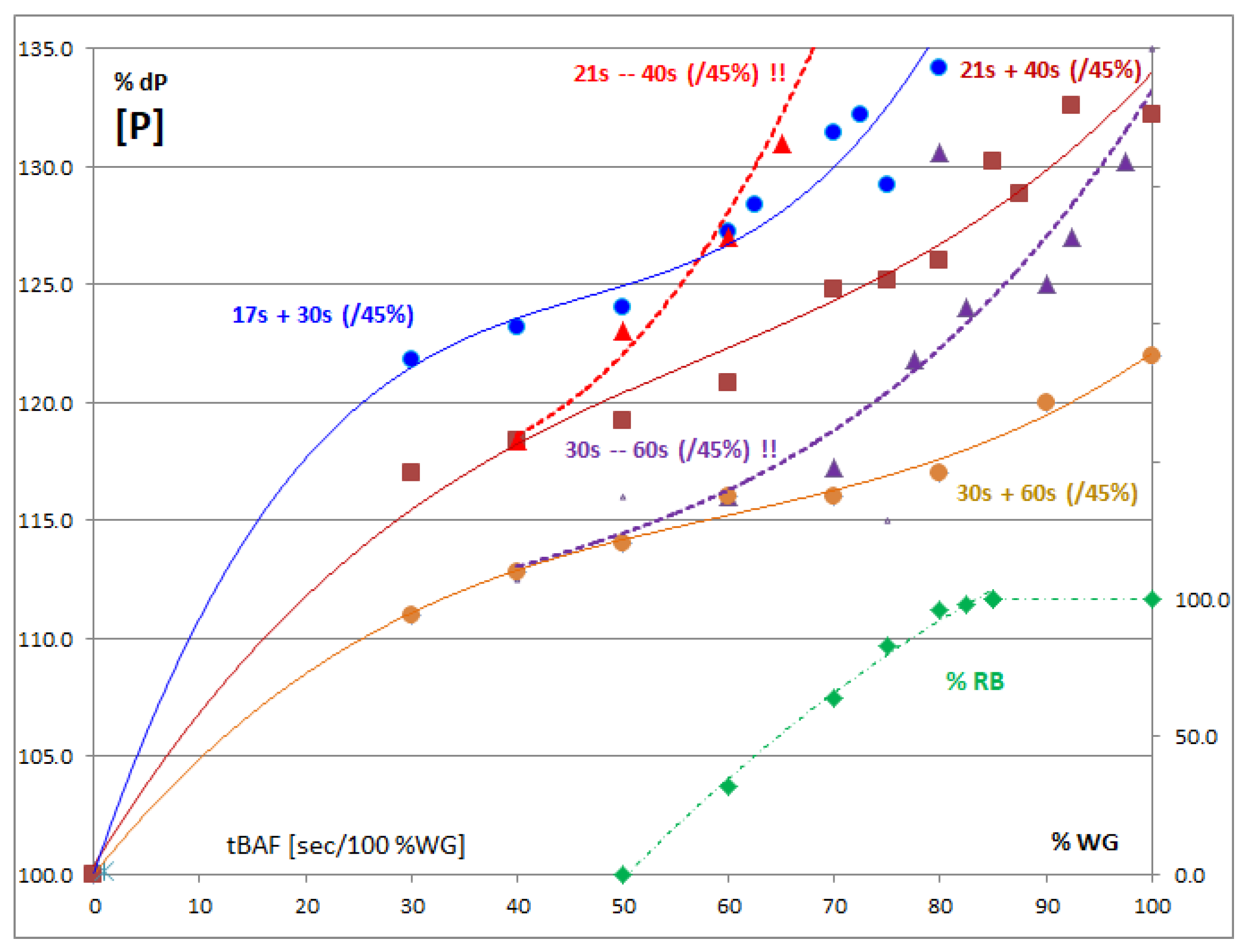
3.1. Overpressure Evolution and Trends
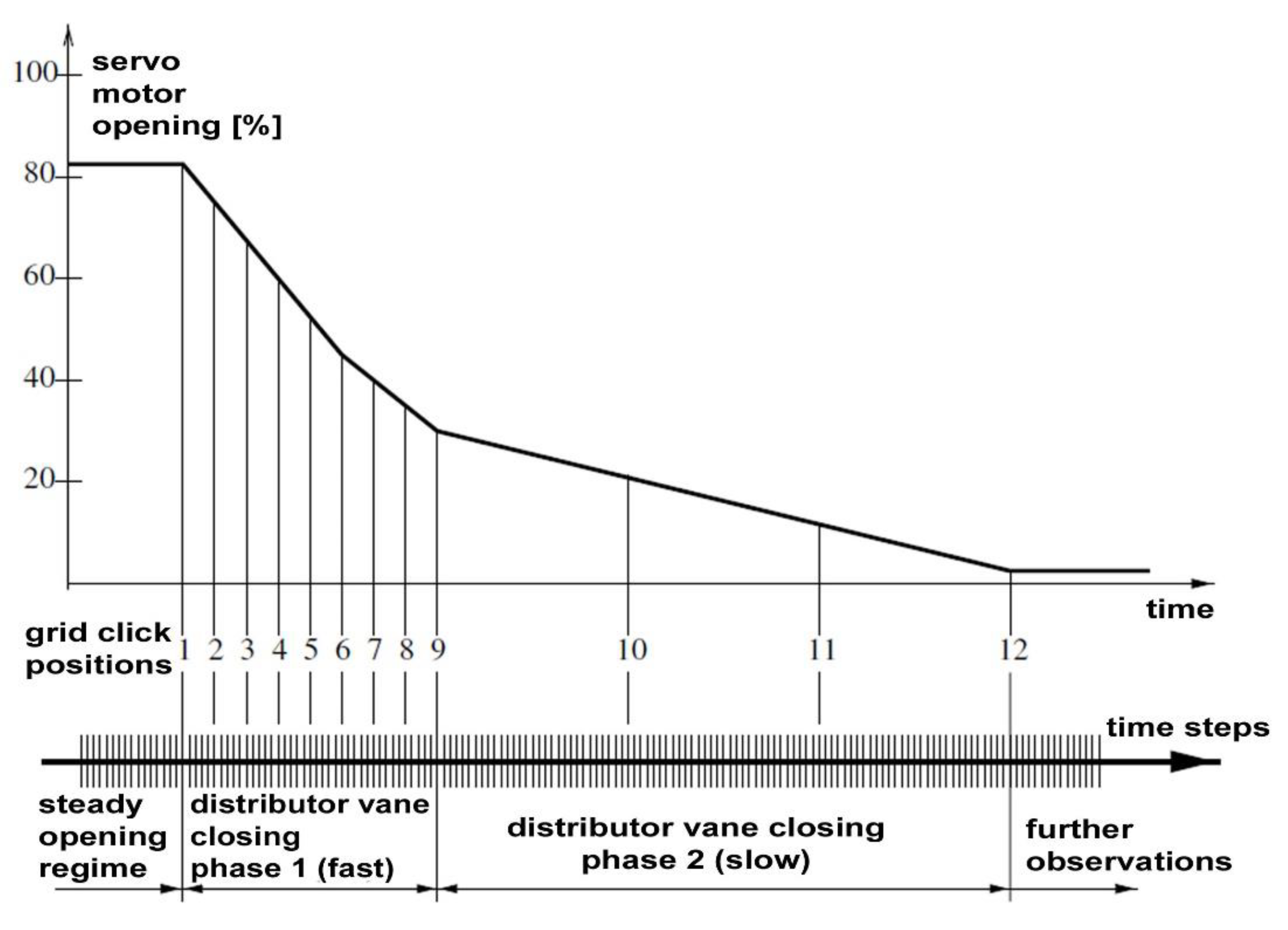
3.2. Influence of Rapid Closure on Overpressure
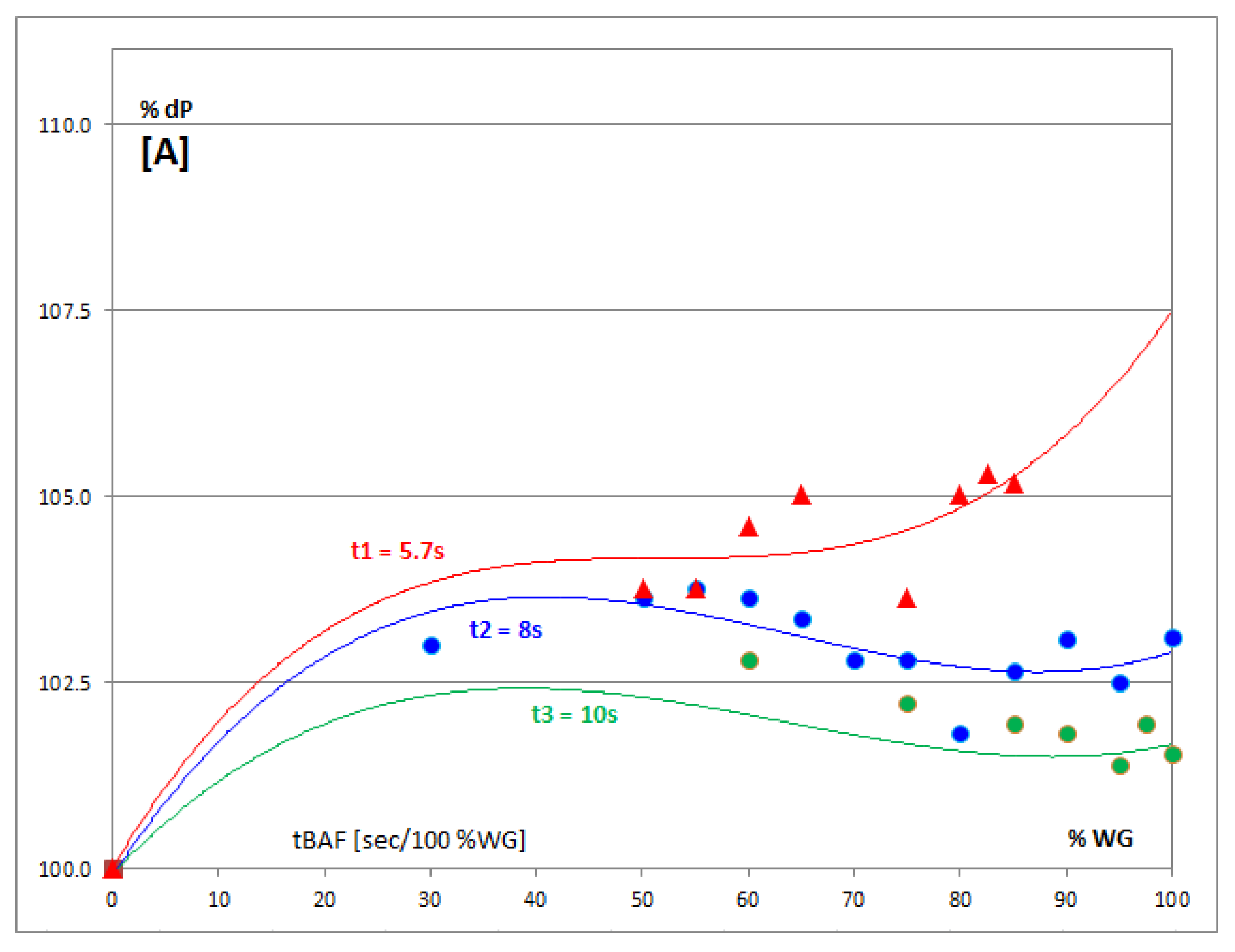
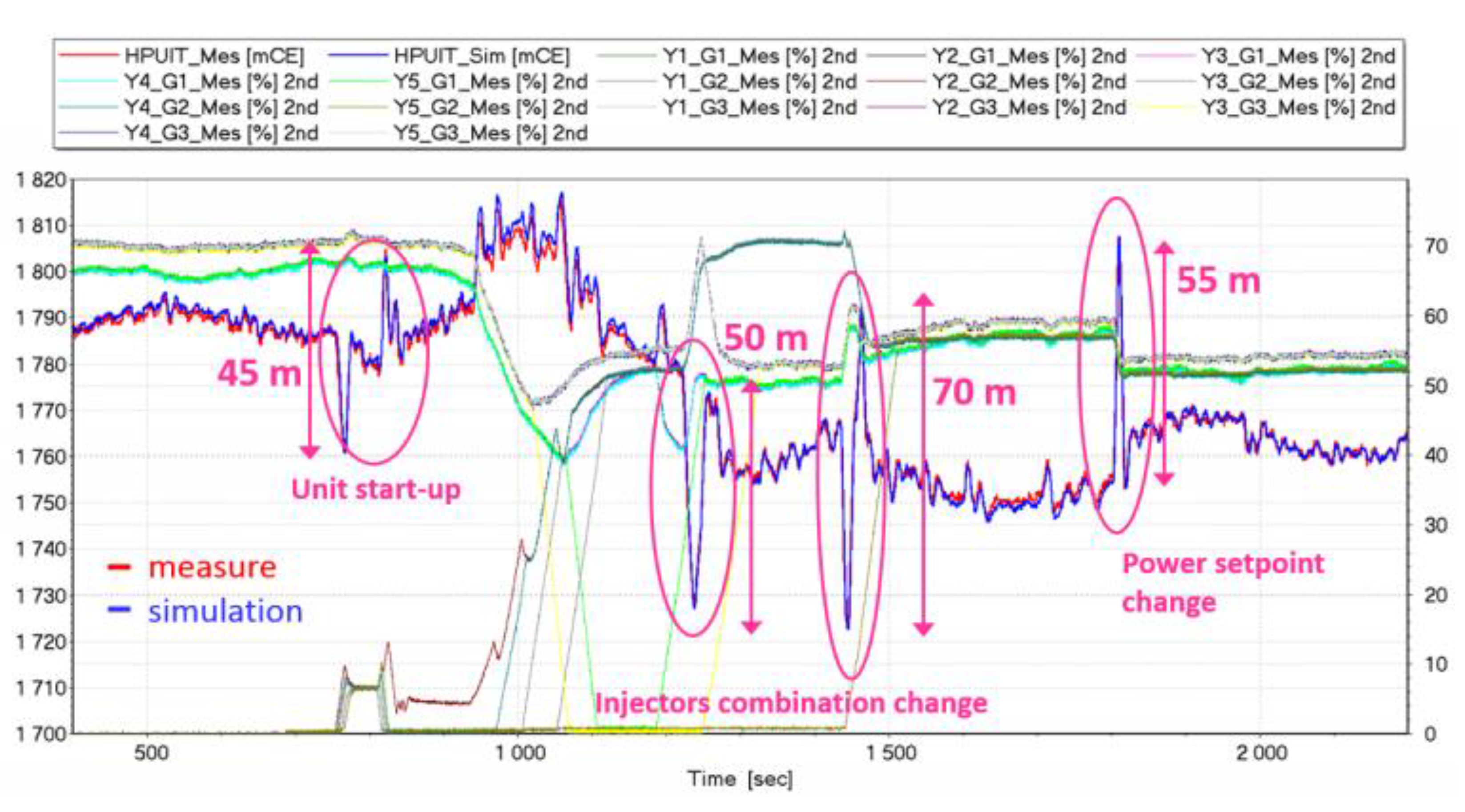
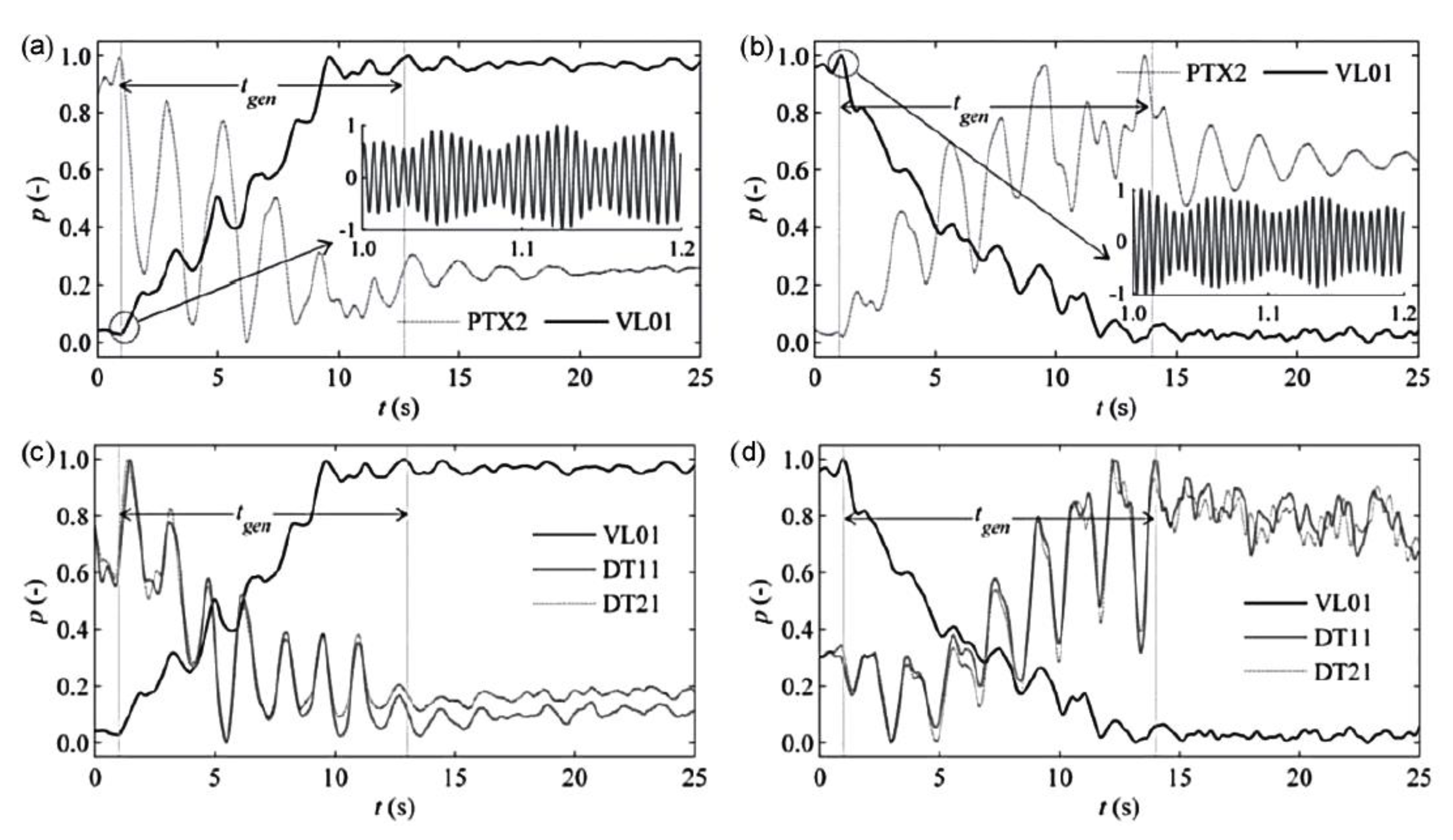
3.3. Temporal Analysis—Main Factors Interaction
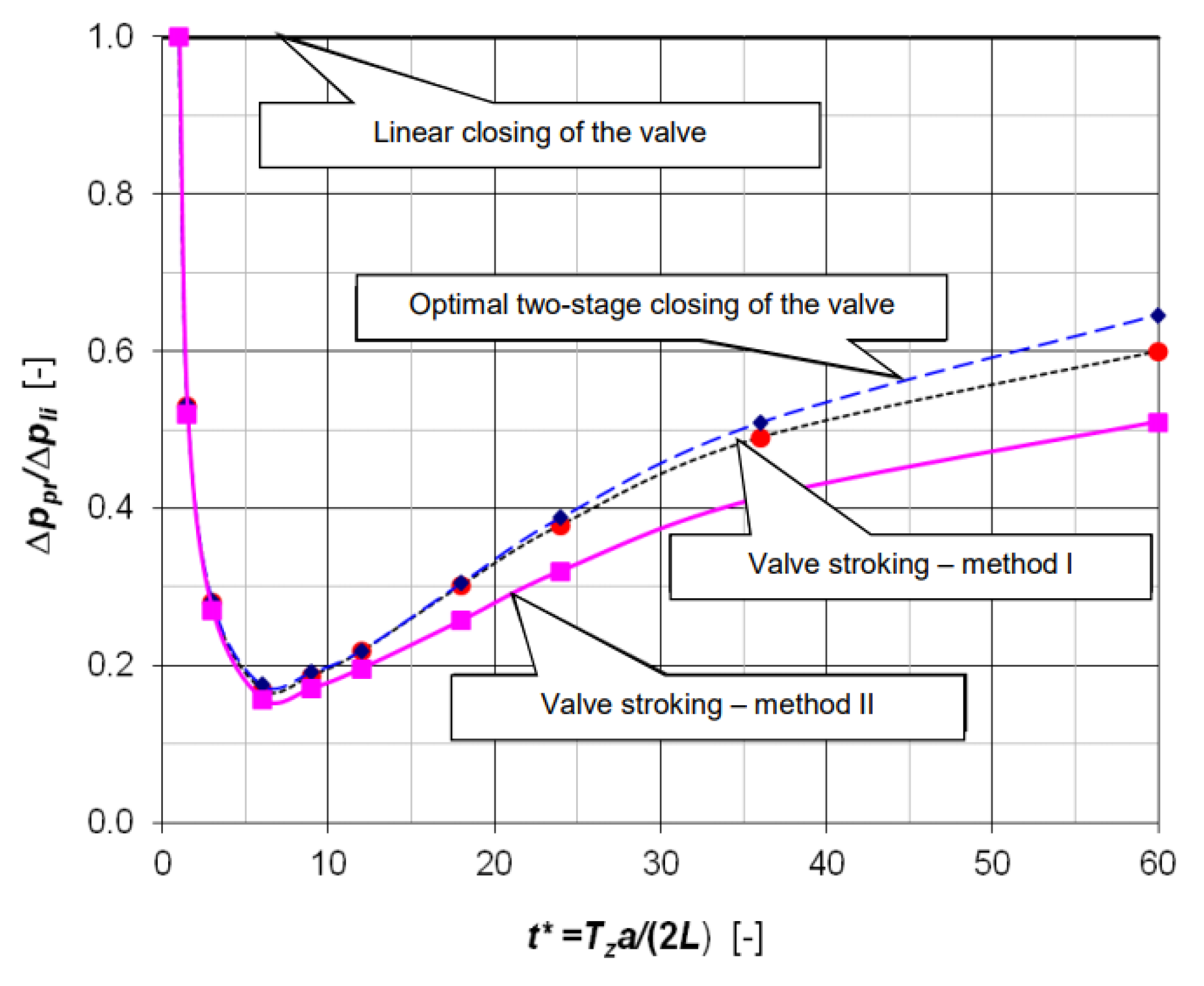
3.4. Second Slope Influence
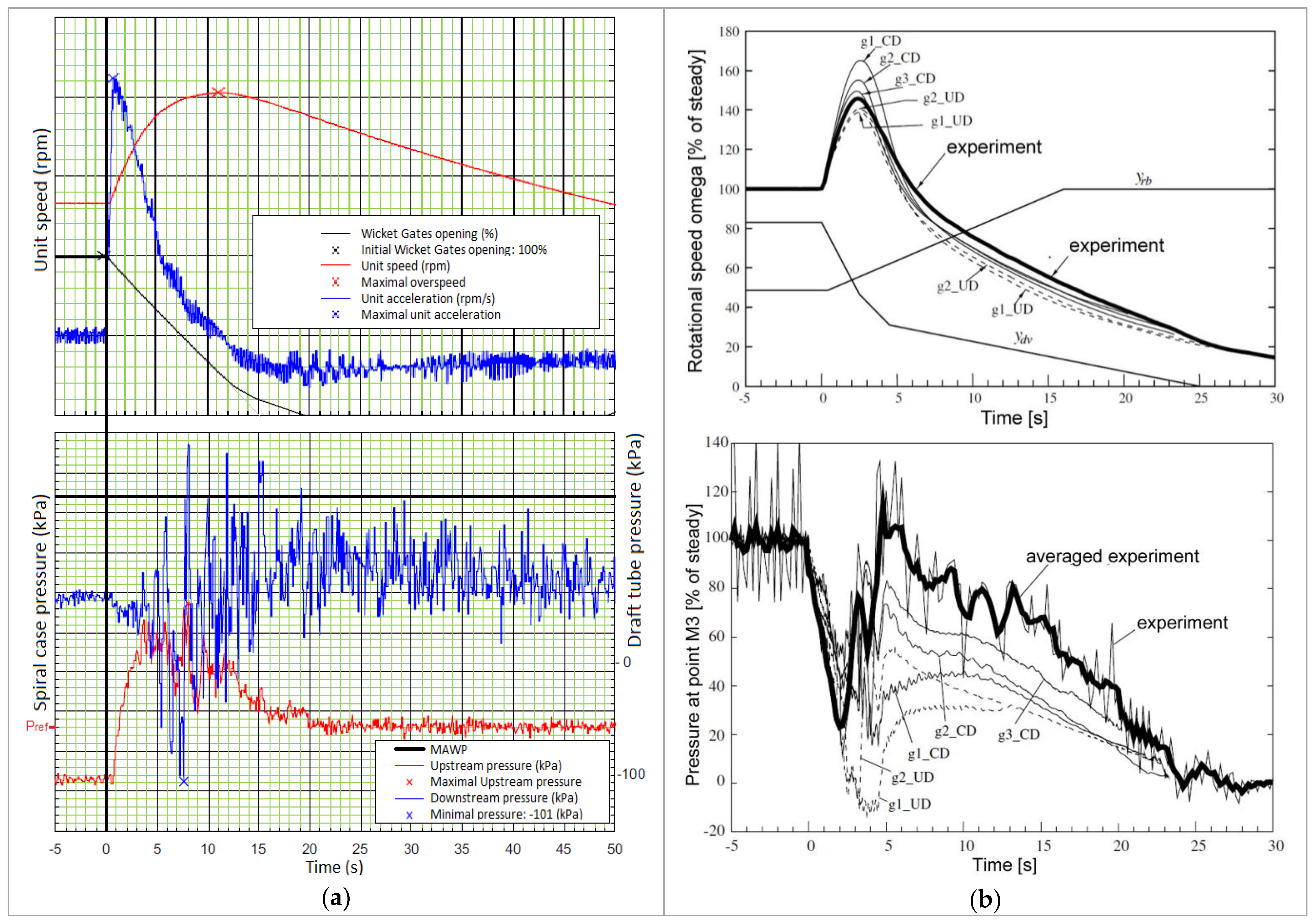
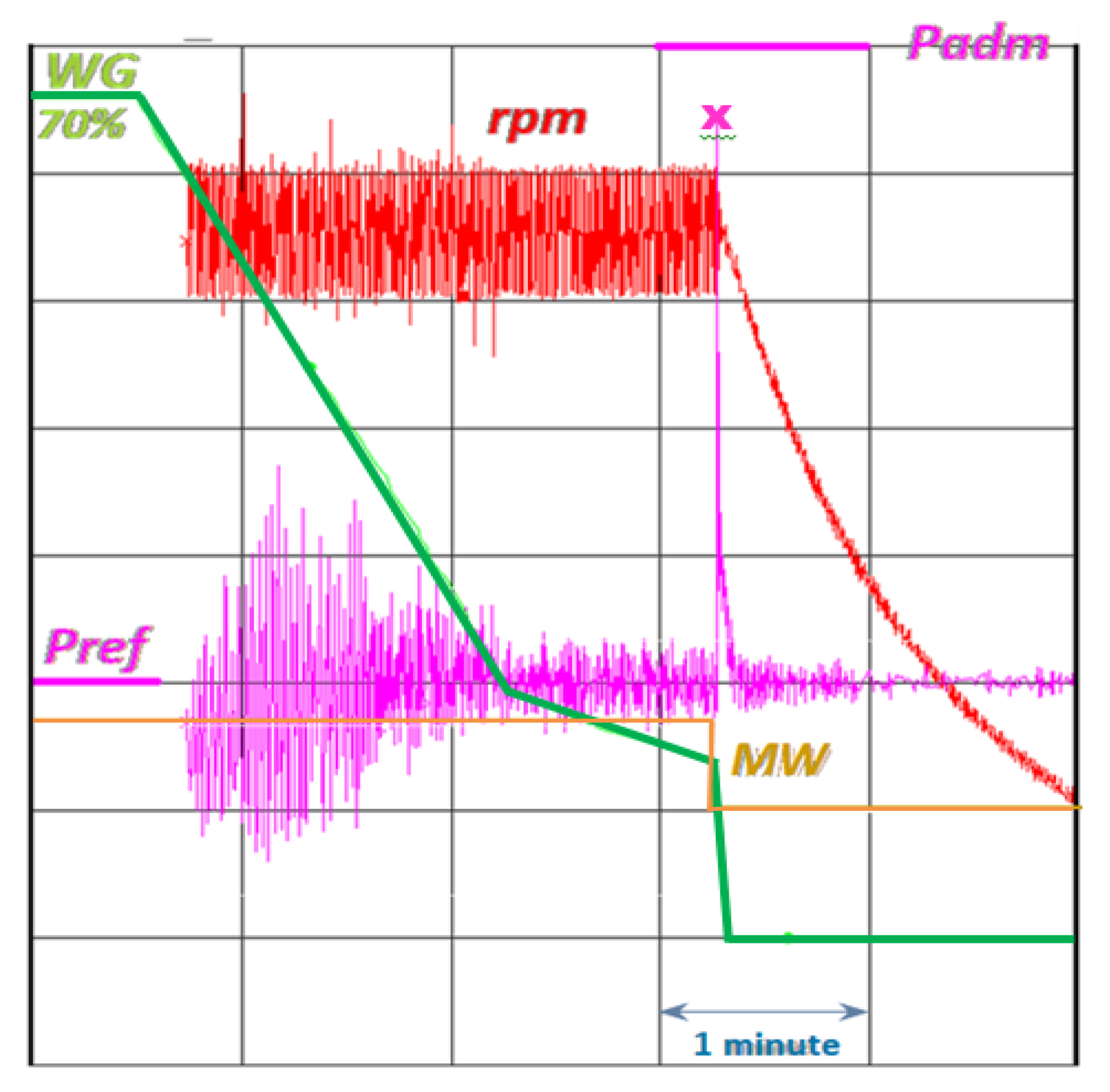
3.5. Overpressure in Closing Sequence from Speed-No-Load
3.6. Overpressure during Speed Regulation
4. Accidents in Hydropower Plants
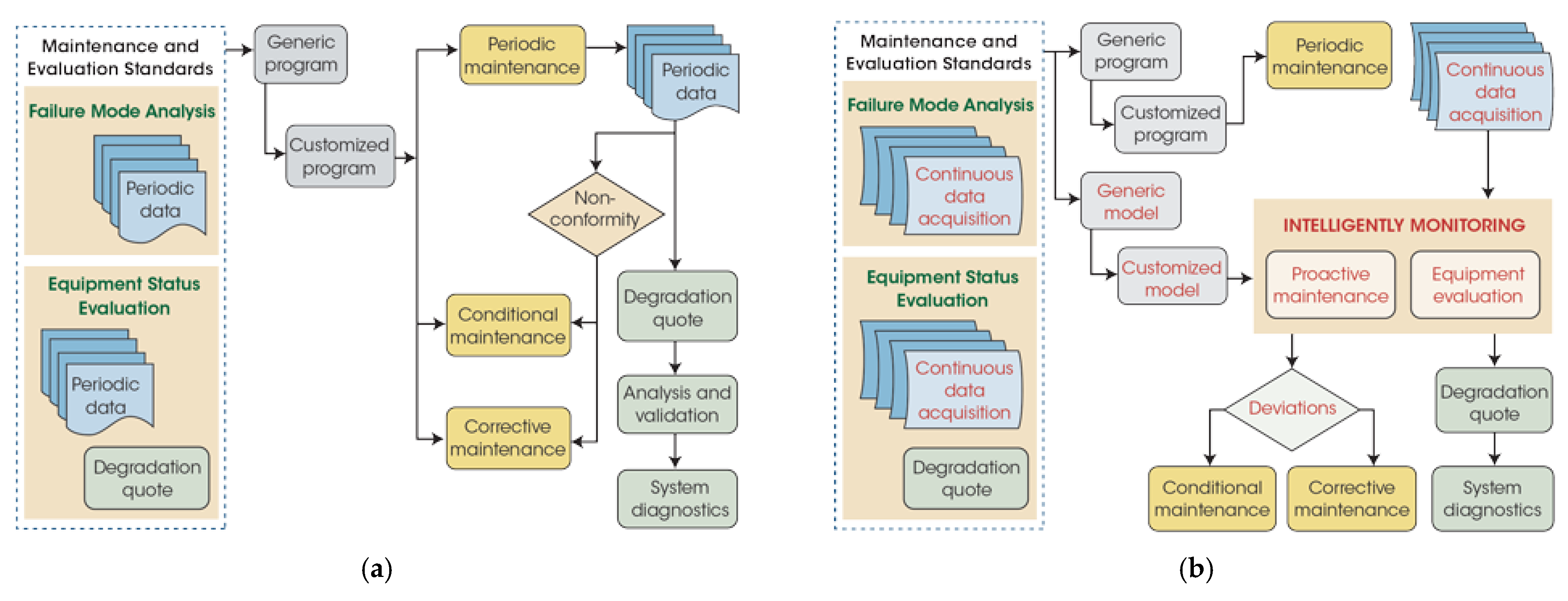
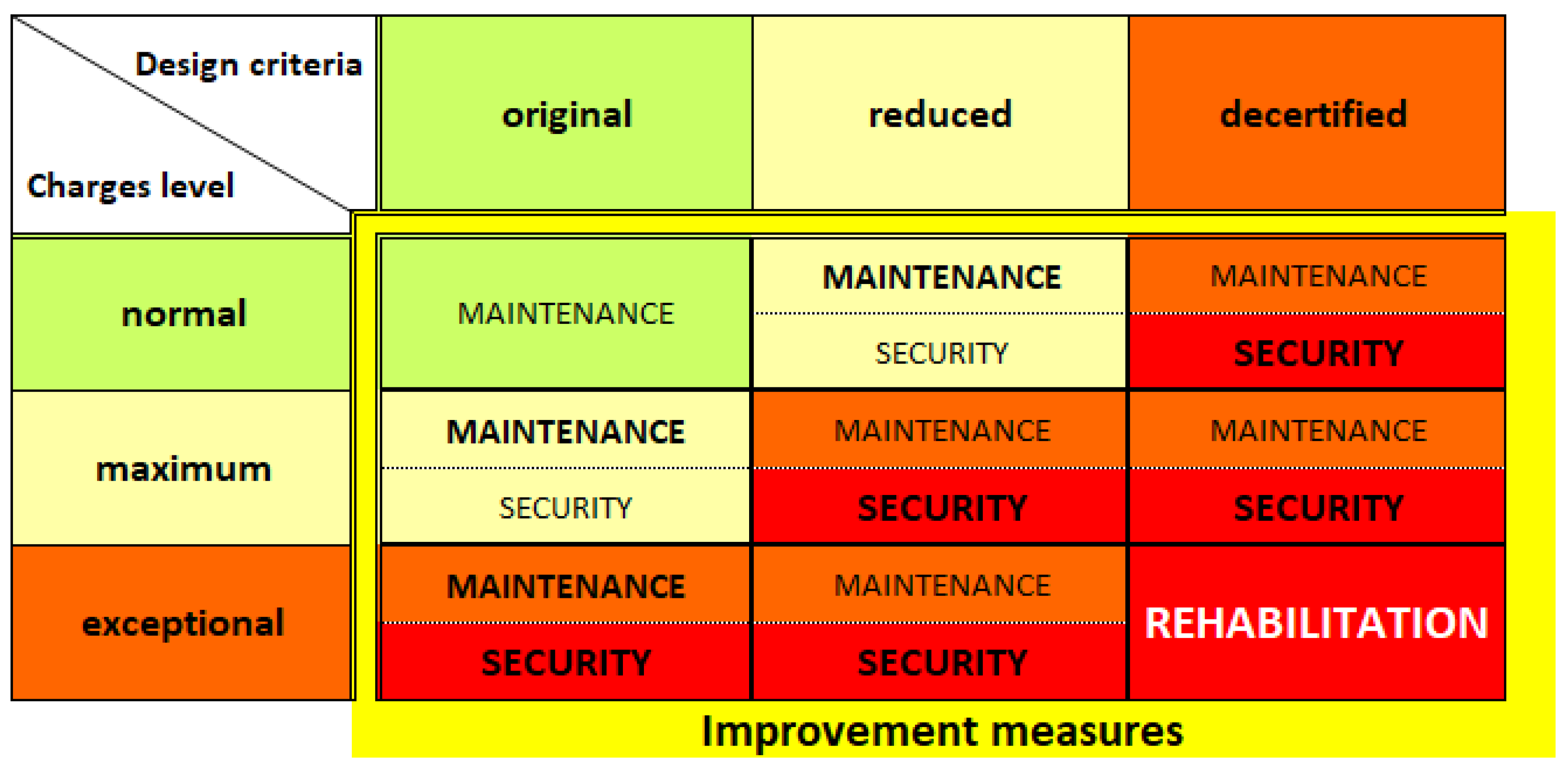
5. Discussion and Recommendations
- A further analysis remains to be undertaken in order to clearly separate the contribution of each factor.
- Concerning the temporal analysis of the factors influencing overpressure, more attention need to be paid to the existing recorded data in order to formalize the cause- effect relationships between overpressure and each factor as well as the totality of factors.
- A supplementary validation by experiments on a test bench will help to identify the influence of main parameters on overpressure.
- The results obtained shall be validated with tests in the power plants of another producer.
- The results obtained during the tests shall be compared with the theoretical models as well.
- In order to complete the present study, additional tests are recommended to investigate the influence of the following parameters on water hammer: (1) closing low; (2) unit overspeed; (3) effective flow rate established in the HYP at the moment of pressure peak; (4) tendency of the hydraulic forces on moving wicket gate during load rejection; (5) behavior of the turbine runner in overspeed; (6) HYP resonance phenomenon; (7) transient flow between wicket gate; (8) air injection downstream from the runner; (9) effect of a surge tank.
- The particular cases observed during the test campaign need more investigation and reconfirmation.
6. Conclusions and Perspectives
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- March, P. Flexible Operation of Hydropower Plants; Report No. 3002011185; Electric Power Research Institute (EPRI): Palo Alto, CA, USA, 2017. [Google Scholar]
- Dreyer, M.; Nicolet, C.; Gaspoz, A.; Biner, D.; Rey-Mermet, S.; Saillen, C.; Boulicaut, B. Digital clone for penstock fatigue monitoring. IOP Conf. Ser. Earth Environ. Sci. 2019, 405, 012013. [Google Scholar] [CrossRef]
- Quaranta, E.; Aggidis, G.; Boes, R.M.; Comoglio, C.; De Michele, C.; Ritesh Patro, E.; Georgievskaia, E.; Harby, A.; Kougiasi, I.; Muntean, S.; et al. Assessing the energy potential of modernizing the European hydropower fleet. Energy Convers. Manag. 2021, 246, 114655. [Google Scholar] [CrossRef]
- Henry, P. Turbomachines Hydrauliques: Choix Illustré de Réalisations Marquantes, 1st ed.; Presses Polytechniques et Universitaires Romandes (PPUR): Lausanne, Switzerland, 1992. [Google Scholar]
- Vitruvius Pollio, M. The Ten Books on Architecture; Harvard University Press: Cambridge, UK, 1914; Book VIII, Chapter VI, Sections 5–8; pp. 244–246, (Translated by Morgan, M.H.). [Google Scholar]
- Rouse, H. Highlights: History of Hydraulics. In IIHR-Hydroscience & Engineering, Books at Iowa 38; University of Iowa: Iowa, IA, USA, 1983. [Google Scholar]
- Menabrea, L.-F. Note sur les effects de choc de l’eau dans les conduites, C.R. Hebd. Seances Acad. Sci. 1858, 47, 221–224. [Google Scholar]
- Michaud, J. Coups de belier dans les conduites—Etude des moyens employees pour en atteneur les effects. Bull. Soc. Vaud. Ing. Arch. 1878, 43, 56–64. [Google Scholar]
- Von Kries, J. Ueber die Beziehungen zwischen Druck und Geschwindigkeit, welche bei der Wellenbewegung in elastischen Schläuchen bestehen [On the relationships between pressure and velocity, which exist in connection with wave motion in elastic tubing]. In Festschrift of the 56th Convention of German Scientists and Physicians; Akademische Verlagsbuchhandlung: Tübingen, Germany, 1883; pp. 67–88. (In German) [Google Scholar]
- Joukowsky, N. Über den hydraulischen Stoss in Wasserleitungsröhren [On hydraulic shock in water pipes]. In Mémoires de l’Académie Impériale des Sciences de St.-Pétersbourg; 8th series; Académie Impériale des Sciences: Saint Petersburg, Russia, 1898; Volume 9, pp. 1–71. (In German) [Google Scholar]
- Tijsseling, A.S.; Anderson, A. The Joukowsky equation for fluids and solids. J. Sci. Comput. 2006, 1–11. Available online: https://www.researchgate.net/publication/254810250_The_Joukowsky_equation_for_fluids_and_solids (accessed on 9 December 2021).
- Tijsseling, A.S.; Anderson, A. A precursor in waterhammer analysis—rediscovering Johannes von Kries. In Proceedings of the 9th International Conference on Pressure Surges, Chester, UK, 24–26 March 2016; pp. 739–751. [Google Scholar]
- Tijsseling, A.S.; Anderson, A. Johannes von Kries and the history of water hammer. ASCE J. Hydraul. Eng. 2007, 133, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Walters, T.A.; Leishear, R.A. When the Joukowsky Equation Does Not Predict Maximum Water Hammer Pressures. In Proceedings of the ASME 2018 Pressure Vessels and Piping Conference, Prague, Czech Republic, 15–20 July 2018. [Google Scholar]
- Bouchayer, A. Établissement Des Conduites Forcées. Houille Blanche 1902, 1, 212–218. [Google Scholar] [CrossRef] [Green Version]
- Bouchayer, A. Hydraulique. Des ruptures dans les conduites. Houille Blanche 1911, 10, 73–79. [Google Scholar] [CrossRef] [Green Version]
- De Sparre, C. Note Au Sujet Des Coups De Bélier. Houille Blanche 1904, 3, 302–308. [Google Scholar] [CrossRef] [Green Version]
- De Sparre, C. Remarques au sujet de l’emploi de la méthode de M. Allievi pour le calcul des coups de belier. Houille Blanche 1905, 4, 159–166. [Google Scholar] [CrossRef] [Green Version]
- De Sparre, C. Sur les Effets de Résonance dans les coups de Bélier pour le cas des hautes chutes. Houille Blanche 1907, 6, 277–279. [Google Scholar] [CrossRef] [Green Version]
- De Sparre, C. L’étude des Coups de Bélier Dans les Canalisations Métalliques Sous Pression. Houille Blanche 1919, 16, 57–58. [Google Scholar] [CrossRef] [Green Version]
- Camichel, C.; Eydoux, D.; Gariel, M. Étude théorique et expérimentale des coups de bélier. Essais faits à l’institut électrotechnique de Toulouse et à l’usine hydroélectrique de Soulom. Ann. De La Fac. Des. Sci. De Toulouse 1916, 3, 1–251. [Google Scholar] [CrossRef]
- Camichel, C.; Eydoux, D. L’étude des Coups de Bélier Dans les Canalisations Métalliques Sous Pression. Houille Blanche 1920, 17, 127–131. [Google Scholar] [CrossRef] [Green Version]
- Allievi, L. Theory of Water-Hammer; R. Garroni Typography: Rome, Italy, 1925. [Google Scholar]
- Parmakian, J. Waterhammer Analysis; Dover Publications: New York, NY, USA, 1963. [Google Scholar]
- Ramos, H.M.; Almeida, A.B. Dynamic orifice model on waterhammer analysis of high or medium heads of small hydropower schemes. J. Hydraul. Res. 2001, 39, 429–436. [Google Scholar] [CrossRef]
- Ramos, H.M.; Almeida, A.B. Parametric Analysis of Waterhammer Effects in Small Hydropower Schemes. ASCE J. Hydraul. Eng. 2002, 128, 689–697. [Google Scholar] [CrossRef]
- Selz, A. Recertification of Pressure Vessels and Pressure Systems. J. Press. Vessel Technol. 1986, 108, 514–517. [Google Scholar] [CrossRef]
- Levina, S.M.; Vasil’chenko, K.I. General Problem of Condition and Remaining-Life Assessment of Metallic Structures in Water-Delivery Runs of Hydraulic Turbines at HPP. Power Technol. Eng. 2014, 48, 102–111. [Google Scholar] [CrossRef]
- Levina, S.M.; Novkunskii, A.A.; Shevchenko, Y.V. Estimate of Remaining Operating Lifetime of Penstock Metal Lining with Due Regard for Its Actual Thickness. Power Technol. Eng. 2016, 50, 248–253. [Google Scholar] [CrossRef]
- Kahraman, G. Investigation of the Effect of Operating Conditions Change on Water Hammer in Hydroelectric Power Plants. J. Fail. Anal. Preven. 2020, 20, 1987–1991. [Google Scholar] [CrossRef]
- Cassano, S.; Nicolet, C.; Sossan, F. Reduction of Penstock Fatigue in a Medium-Head Hydropower Plant Providing Primary Frequency Control. In Proceedings of the 55th International Universities Power Engineering Conference (UPEC), Turin, Italy, 1–4 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Adamkowski, A.; Lewandowski, M.; Lewandowski, S. Fatigue life analysis of hydropower pipelines using the analytical model of stress concentration in welded joints with angular distortions and considering the influence of water hammer damping. Thin Wall Struct. 2021, 159, 107350. [Google Scholar] [CrossRef]
- Suresh, S. Fatigue of Materials, 2nd ed.; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Schijve, J. Fatigue of Structures and Materials, 2nd ed.; Springer: Dordrecht, NL, USA, 2009. [Google Scholar]
- Pachoud, A.J.; Manso, P.A.; Schleiss, A.J. New methodology for safety assessment of steel-lined pressure shafts using high-strength steel. Int. J. Hydropower Dams 2017, 24, 80–88. [Google Scholar]
- Pachoud, A.J. Influence of Geometrical Imperfections and Flaws at Welds of Steel Liners on Fatigue Behavior of Pressure Tunnels and Shafts in Anisotropic Rock. Ph.D. Thesis, No. 7305. Ecole Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2017. [Google Scholar]
- Pachoud, A.J.; Berthod, R.; Manso, P.A.; Schleiss, A.J. Advanced models for stress evaluation and safety assessment in steel-lined pressure tunnels. Int. J. Hydropower Dams 2018, 25, 77–82. [Google Scholar]
- Gagnon, M.; Nicolle, J.; Morissette, J.; Lawrence, M. A look at Francis runner blades response during transients. IOP Conf. Ser. Earth Environ. Sci. 2016, 49, 052005. [Google Scholar] [CrossRef] [Green Version]
- Thibault, D.; Gagnon, M.; Godin, S. The effect of materials properties on the reliability of hydraulic turbine runners. Int. J. Fluid Mach. Syst. 2015, 8, 254–263. [Google Scholar] [CrossRef] [Green Version]
- Gagnon, M.; Tahan, A.; Bocher, P.; Thibault, D. Influence of load spectrum assumptions on the expected reliability of hydroelectric turbines: A case study. Struct. Saf. 2014, 50, 1–8. [Google Scholar] [CrossRef]
- Liu, X.; Luo, Y.; Wang, Z. A review on fatigue damage mechanism in hydro turbines. Renew. Sustain. Energy Rev. 2016, 54, 1–14. [Google Scholar] [CrossRef]
- Trivedi, C.; Bhupendra, G.; Cervantes, J.M. Effect of transients on Francis turbine runner life: A review. J. Hydraul. Res. 2013, 51, 121–132. [Google Scholar] [CrossRef]
- Savin, O.; Baroth, J.; Badina, C.; Charbonnier, S.; Bérenguer, C. Damage due to start-stop cycles of turbine runners under high-cycle fatigue. Int. J. Fatigue 2021, 153, 106458:1–106458:11. [Google Scholar] [CrossRef]
- Hydraulic Power Committee. Effect of Speed Regulation and Water Hammer on the Design of Relief Valves, Penstocks and Surge Tanks. In Report of Hydraulic Power Committee; National Electric Light Association: New York, NY, USA, 1927; 26p. [Google Scholar]
- United States Department of the Interior Bureau of Reclamation (US-DIBR). Welded Steel Penstock; Engineering Monograph; U.S. Government Printing Office: Washington, WA, USA, 1977.
- Chaudry, M.H. Applied Hydraulic Transients, 3rd ed.; Springer: New York, NY, USA, 2014. [Google Scholar]
- Selek, B.; Kirkgöz, M.S.; Selek, Z. Comparison of computed water hammer pressures with test results for the Çatalan power plant in Turkey. Can. J. Civ. Eng. 2004, 31, 78–85. [Google Scholar] [CrossRef]
- Mandair, S. 1D and 3D Water-Hammer Models: The Energetics of High Friction Pipe Flow and Hydropower Load Rejection. Ph.D. Thesis, No. 7305. University of Toronto, Toronto, ON, Canada, 2020. [Google Scholar]
- Mandair, S.; Morissette, J.F.; Magnan, R.; Karney, B. MOC-CFD coupled model of load rejection in hydropower station. IOP Conf. Ser. Earth Environ. Sci. 2021, 774, 012021. [Google Scholar] [CrossRef]
- Aminikhah, H. Solution of Wave Equation in Radial Form by VIM, International Scholarly Research Network. ISRN Comput. Math. 2012. [Google Scholar] [CrossRef] [Green Version]
- Wichowski, R. Comparative Analysis of Water-Hammer calculation by the Approximate and the Complete Methods of Characteristics. Period. Polytech. Ser. Civil. Eng. 1991, 35, 107–125. [Google Scholar]
- Salmasi, F.; Abraham, J. The Method of Characteristics Applied to the Sensitivity Analysis for Water Hammer Problems. New Approaches Eng. Res. 2021, 9, 50–63. [Google Scholar] [CrossRef]
- Afshar, M.H.; Rohani, M. Water hammer simulation by implicit method of characteristic. Int. J. Press. Vessels Pip. 2008, 85, 851–859. [Google Scholar] [CrossRef]
- Iliev, V.; Popovski, P.; Markov, Z. Water Hammer Analysis Using Characteristics Method and Numerical Simulation. Mech. Eng. Sci. J. 2013, 31, 53–62. [Google Scholar]
- Pal, S.; Hanmaiahgari, P.R.; Karney, B.W. An Overview of the Numerical Approaches to Water Hammer Modelling: The Ongoing Quest for Practical and Accurate Numerical Approaches. Water 2021, 13, 1597. [Google Scholar] [CrossRef]
- Bakken, B.H.; Bjørkvoll, T. Hydropower unit start-up costs. IEEE Power Eng. Soc. Summer Meet. 2002, 3, 1522–1527. [Google Scholar] [CrossRef]
- Gagnon, M.; Tahan, S.A.; Bocher, P.; Thibault, D. Impact of start-up scheme on Francis runner life expectancy. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012107. [Google Scholar] [CrossRef]
- Bergant, A.; Simpson, A.R.; Tijsseling, A.S. Water hammer with column separation: A review of research in the twentieth century. In Centre for Analysis Scientific Computing and Applications; Report No. 0434; Eindhoven University of Technology: Eindhoven, Poland, 2004. [Google Scholar]
- Wylie, E.B.; Streeter, V.L. Fluid Transients in Systems; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Marples, E.I.B. The Significance of Surge Diagrams. Proceedings of the Institution of Mechanical Engineers. Conf. Proc. 1965, 180, 3–11. [Google Scholar] [CrossRef]
- Bergant, A.; Vítkovský, J.P.; Simpson, A.R.; Lambert, M.F.; Tijsseling, A.S. Discrete vapour cavity model with efficient and accurate convolution type unsteady friction term. In Proceedings of the 23rd IAHR Symposium on Hydraulic Machinery and Systems IAHR2006, Yokohama, Japan, 17–21 October 2006. [Google Scholar]
- Bergant, A.; Tijsseling, A.S.; Vítkovský, J.P.; Simpson, A.R.; Lambert, M.F. Discrete Vapour Cavity Model with Improved Timing of Opening and Collapse of Cavities. In Proceedings of the 2nd IAHR International Meeting of the Work Group on Cavitation and Dynamic Problems in Hydraulic Machinery and Systems, IAHRWG2007, Timişoara, Romania, 24–26 October 2007. [Google Scholar]
- Santoro, V.C.; Crimì, A.; Pezzinga, G. Developments and Limits of Discrete Vapor Cavity Models of Transient Cavitating Pipe Flow: 1D and 2D Flow Numerical Analysis. ASCE J. Hydraul. Eng. 2018, 144, 04018047. [Google Scholar] [CrossRef]
- Zhao, L.; Yang, Y.; Wang, T.; Zhou, L.; Li, Y.; Zhang, M. A Simulation Calculation Method of a Water Hammer with Multpoint Collapsing. Energies 2020, 13, 1103. [Google Scholar] [CrossRef] [Green Version]
- Liou, J.C.P. Numerical Properties of the Discrete Gas Cavity Model for Transients. ASME J. Fluids Eng. 2000, 122, 636–639. [Google Scholar] [CrossRef]
- Bergant, A.; Karadžić, U.; Vítkovský, J.; Vušanović, I.; Simpson, A.R. A Discrete Gas-Cavity model that Considers the Friction Effects of Unsteady Pipe Flow. Stroj. Vestn J. Mech. E 2005, 51, 692–710. [Google Scholar]
- Zhou, L.; Wang, H.; Bergant, A.; Tijsseling, A.S.; Liu, D.; Guo, S. Godunov-Type Solutions with Discrete Gas Cavity Model for Transient Cavitating Pipe Flow. ASCE J. Hydraul. Eng. 2018, 144, 04018017. [Google Scholar] [CrossRef] [Green Version]
- Bergant, A.; Simpson, A.R. Interface model for transient cavitating flow in pipelines. In Unsteady Flow and Fluid Transients; Bettess, R., Watts, J., Eds.; Balkema: Rotterdam, The Netherlands, 1992; pp. 333–342. [Google Scholar]
- Himr, D. Investigation and Numerical Simulation of a Water Hammer with Column Separation. ASCE J. Hydraul. Eng. 2015, 141, 04014080. [Google Scholar] [CrossRef]
- Ilić, J.; Petković, A.; Božić, I. Numerical Analyses of Water Hammer and Water-Mass Oscillations in a Hydropower Plant for the Most Extreme Operational Regimes. FME Trans. 2019, 47, 7–15. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, J.; Li, G.H.; Yu, X.D. Influence Mechanism of Geometric Characteristics of Water Conveyance System on Extreme Water Hammer during Load Rejection in Pumped Storage Plants. Energies 2019, 12, 2854. [Google Scholar] [CrossRef] [Green Version]
- Adamkowski, A.; Lewandowski, M. Experimental examination of unsteady friction models for transient pipe flow simulation. ASME J. Fluids Eng. 2006, 128, 1351–1363. [Google Scholar] [CrossRef]
- Adamkowski, A.; Lewandowski, M. A New Method for Numerical Prediction of Liquid Column Separation Accompanying Hydraulic Transients in Pipelines. ASME J. Fluids Eng. 2009, 131, 071302. [Google Scholar] [CrossRef]
- Bergant, A.; Simpson, A.R. Pipeline Column Separation Flow Regimes. ASCE J. Hydraul. Eng. 1999, 125, 835–848. [Google Scholar] [CrossRef] [Green Version]
- Karadžić, U.; Bulatović, V.; Bergant, A. Valve-Induced Water Hammer and Column Separation in a Pipeline Apparatus. Stroj. Vestn. J. Mech. E 2014, 60, 742–754. [Google Scholar] [CrossRef] [Green Version]
- Vítkovský, J.; Stephens, M.; Bergant, A.; Simpson, A.R.; Lambert, M.F. Numerical Error in Weighting Function-Based Unsteady Friction Models for Pipe Transients. ASCE J. Hydraul. Eng. 2006, 132, 709–721. [Google Scholar] [CrossRef] [Green Version]
- Ghidaoui, M.S.; Zhao, M.; McInnis, D.A.; Axworthy, D.H. A review of water hammer theory and practice. Appl. Mech. Rev. 2005, 58, 49–76. [Google Scholar] [CrossRef]
- Ramos, H.M. Special Concerns Related to the Runaway Effect in Francis Turbines. Hydro Rev. 2010, 1. Available online: https://www.renewableenergyworld.com/baseload/special-concerns-related-to-the-runaway-effect-in-francis-turbines/#gref (accessed on 9 December 2021).
- Li, X.Q.; Chang, J.S.; Chen, P. Wicket Gate Closure Control Law to Improve the Transient of a Water Turbine. In Advanced Materials Research; Zhou, C.C., Ma, G.J., Liao, R., Wang, J.W., Eds.; Trans Tech Publications: Bäch, Switzerland, 2013; Volume 732. [Google Scholar] [CrossRef]
- Zheng, T.; Tian, Z.; Gui, S.; Li, J.; Zou, H.Q. Hydraulic transient process research technology and engineering application on the complex water tunnel conveyance system of hydropower station. In Proceedings of the 2014 ISFMFE—6th International Symposium on Fluid Machinery and Fluid Engineering, Wuhan, China, 22–25 October 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Chen, D.Y.; Zhang, X.G.; Wu, Y.H.; Li, H.H. Dynamic analysis and modelling of a Francis hydro-energy generation system in the load rejection transient. IET Renew. Power Gener. 2016, 10, 1140–1148. [Google Scholar] [CrossRef]
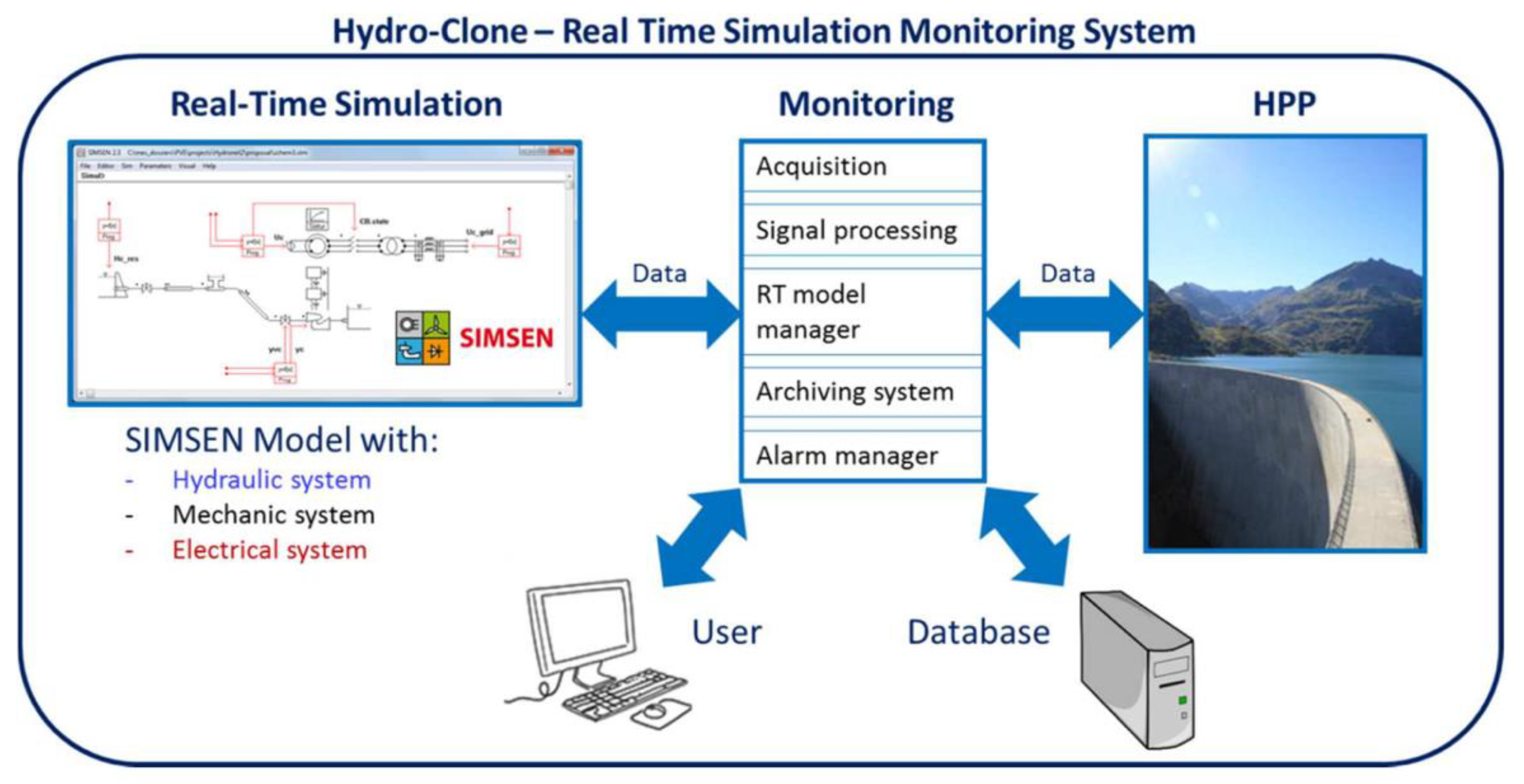
- Nicolet, C.; Dreyer, M.; Béguin, A.; Bollaert, E.; Torrent, S.; Dayer, J.-D. Hydraulic Transient Survey at Cleuson-Dixence with Real-Time Hydro-Clone Monitoring System. In Proceedings of the HYDRO 2018 Conference, Gdansk, Poland, 15–17 October 2018. [Google Scholar]
- Pejović, S.; Gajić, A. The Rules for Hydraulic Transient Design Analysis: Guide for Designers and Manufacturers: Recommendations for Investors and Managers; CSPSAG Press: Toronto, ON, Canada, 2018. [Google Scholar]
- Bergant, A.; Mazij, J.; Karadžić, U. Design of Water Hammer Control Strategies in Hydropower Plants. Appl. Eng. Lett. 2018, 1, 27–33. [Google Scholar] [CrossRef]
- Dollon, Q. Identification des Caractéristiques du Comportement Dynamique des Roues de Turbines Hydroélectriques par l’Étude des Régimes Transitoires; Devis de Recherche, DGA1033; ETS: Montréal, QC, Canada, 2019. [Google Scholar]
- Dreyer, M.; Nicolet, C.; Gaspoz, A.; Gonçalves, N.; Rey-Mermet, S.; Boulicaut, B. Monitoring 4.0 of penstocks: Digital twin for fatigue assessment. IOP Conf. Ser. Earth Environ. Sci. 2021, 774, 012009. [Google Scholar] [CrossRef]
- Klun, M.; Zupan, D.; Lopatič, J.; Kryžanowski, A. On the Application of Laser Vibrometry to Perform Structural Health Monitoring in Non-Stationary Conditions of a Hydropower Dam. Sensors 2019, 19, 3811. [Google Scholar] [CrossRef] [Green Version]
- Lupa, S.I.; Gagnon, M.; Abdul–Nour, G. Water Hammer Interaction between Hydraulic Power Generators and Hydraulic Passages; World Congress on Engineering Asset Management (WCEAM 2021): Bonito, Brasilia, 2021. [Google Scholar]
- Kolšek, T.; Duhovnik, J.; Bergant, A. Simulation of unsteady flow and runner rotation during shut-down of an axial water turbine. J. Hydraul. Res. 2006, 44, 129–137. [Google Scholar] [CrossRef]
- Trivedi, C.; Cervantes, M.J.; Bhupendrakumr, G.; Dahlhaug, O.G. Pressure measurements on a high-head Francis turbine during load acceptance and rejection. J. Hydraul. Res. 2014, 52, 283–297. [Google Scholar] [CrossRef]
- Hirschberg, S.; Spiekemann, G.; Dones, R. Severe Accidents in the Energy Sector; Technical Report No. 98–16; Paul Scherrer Institute: Viligen, Switzerland, 1998. [Google Scholar]
- Hirschberg, S.; Burgherr, P.; Spiekerman, G.; Dones, R. Severe accidents in the energy sector: Comparative perspective. J. Hazard. Mater. 2004, 111, 57–65. [Google Scholar] [CrossRef]
- Bonin, C.C. Water Hammer Damage to Oigawa power station. J. Eng. Power. 1960, 82, 111–116. [Google Scholar] [CrossRef]
- Adamkowski, A. Case Study: Lapino Powerplant Penstock Failure. ASCE J. Hydraul. Eng. 2001, 127, 547–555. [Google Scholar] [CrossRef]
- Adamkowski, A.; Lewandowski, M.; Lewandowski, S. Przyczyny i skutki niekontrolowanego uderzenia hydraulicznego [Causes and effects of the uncontrolled water hammer]. Energetika Wodna 2020, 36, 32–39. (In Polish) [Google Scholar]
- Fortov, V.; Fedorov, M.; Elistratov, V. Scientific and Technical Problems of the Hydropower Industry after the Accident at the Sayano-Shushenskaya Hydropower Plant. Her. Russ. Acad. Sci. 2011, 81, 333–340. [Google Scholar] [CrossRef]
- Hamill, F.A. Sayano Shushenskaya accident—Presenting a possible direct cause. Int. Water Power Dam Constr. 2010, 30–36. Available online: https://www.waterpowermagazine.com/features/featuresayano-shushenskaya-accident-presenting-a-possible-direct-cause/ (accessed on 9 December 2021).
- Bellendir, E.; Semenov, Y.; Shtengel, V. First results of inspection of structural components at the Sayano-Shushenskaya HPP after the failure of 17 August 2009. Power Technol. Eng. 2011, 44, 335–341. [Google Scholar] [CrossRef]
- Kogan, K. Abnormal operating modes and reability of modern generating sets. Power Technol. Eng. 2010, 44, 202–207. [Google Scholar]
- Belash, I. Cause of the failure of the no. 2 hydraulic generating set at the Sayano-Shushenskaya HPP: Criticality of reability enhancement for water–power equipments. Power Technol. Eng. 2010, 44, 165–170. [Google Scholar] [CrossRef]
- Berlin, V.; Murav’ev, O. Technical aspects of the failure of the second generating set at the Sayano-Shushenskaya HPP. Power Technol. Eng. 2010, 44, 263–268. [Google Scholar] [CrossRef]
- Hamill, F.A. Sayano Shushenskaya 2009 accident update. Hydrolink 2020, 2, 50–53. [Google Scholar]
- Adamkowski, A.; Lewandowski, M. Preventing destructive effects of water hammer in hydropower plant penstocks. In Proceedings of the ACI’s Hydropower Development Conference: Europe 2015, Salzburg, Austria, 23–24 September 2015. [Google Scholar]
- Nicolet, C.; Béguin, A.; Bollaert, E.; Boulicaut, B.; Gros, G. Real-time simulation monitoring system for hydro plant transient surveys. Int. J. Hydropower Dams 2015, 22, 62–69. [Google Scholar]
- Lupa, S.I. Hydro-Quebec Manages Delicate Balance of Old and New Systems. Hydro. Rev. 2015, 34, 10. [Google Scholar]
- Kougias, I.; Aggidis, G.; Avellan, F.; Deniz, S.; Lundin, U.; Moro, A.; Muntean, S.; Novara, D.; Pérez-Díaz, J.I.; Quaranta, E.; et al. Analysis of emerging technologies in the hydropower sector. Renew. Sustain. Energy Rev. 2019, 113, 109257. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lupa, S.-I.; Gagnon, M.; Muntean, S.; Abdul-Nour, G. The Impact of Water Hammer on Hydraulic Power Units. Energies 2022, 15, 1526. https://doi.org/10.3390/en15041526
Lupa S-I, Gagnon M, Muntean S, Abdul-Nour G. The Impact of Water Hammer on Hydraulic Power Units. Energies. 2022; 15(4):1526. https://doi.org/10.3390/en15041526
Chicago/Turabian StyleLupa, Sorin-Ioan, Martin Gagnon, Sebastian Muntean, and Georges Abdul-Nour. 2022. "The Impact of Water Hammer on Hydraulic Power Units" Energies 15, no. 4: 1526. https://doi.org/10.3390/en15041526
APA StyleLupa, S.-I., Gagnon, M., Muntean, S., & Abdul-Nour, G. (2022). The Impact of Water Hammer on Hydraulic Power Units. Energies, 15(4), 1526. https://doi.org/10.3390/en15041526








