Numerical Analysis on the Hydraulic Thrust and Dynamic Response Characteristics of a Turbine Pump
Abstract
:1. Introduction
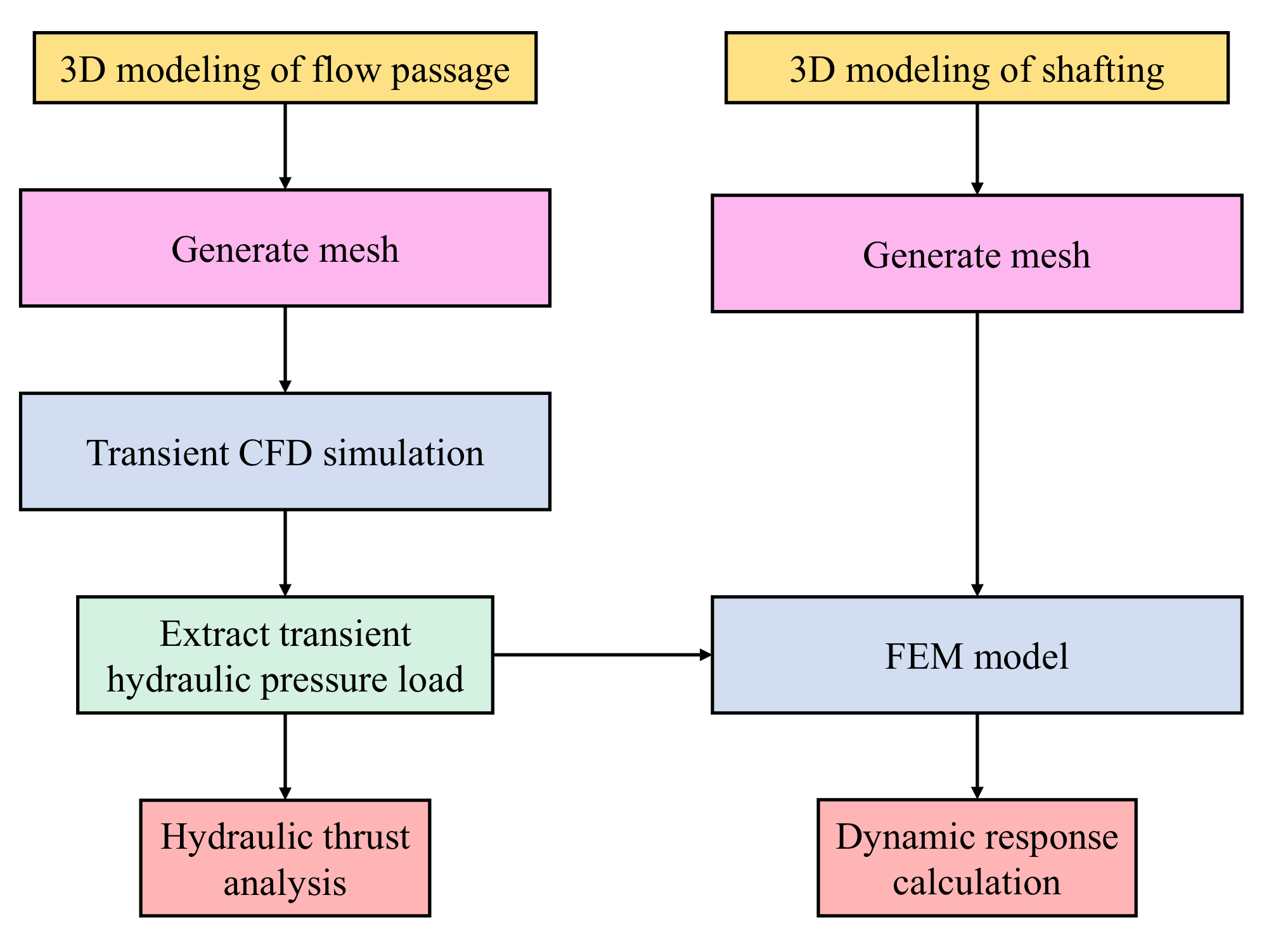
2. Objective and Methods
2.1. Turbine Pump Flow Model
2.2. CFD Simulation Theory and Setup
2.3. Shafting FEM Model and Setup
3. Results and Discussion
3.1. Hydraulic Performance
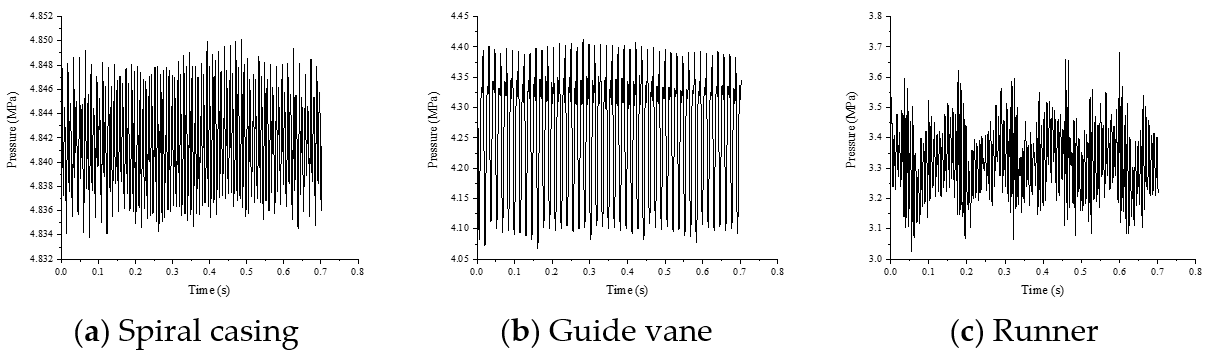
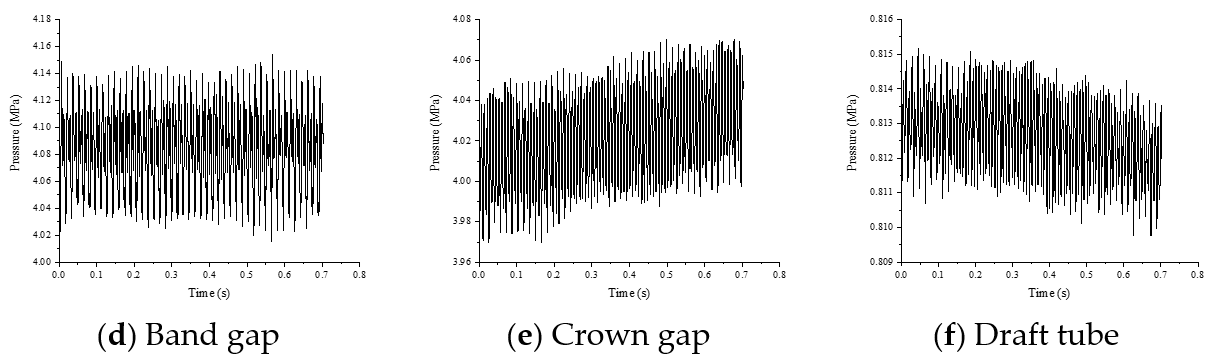
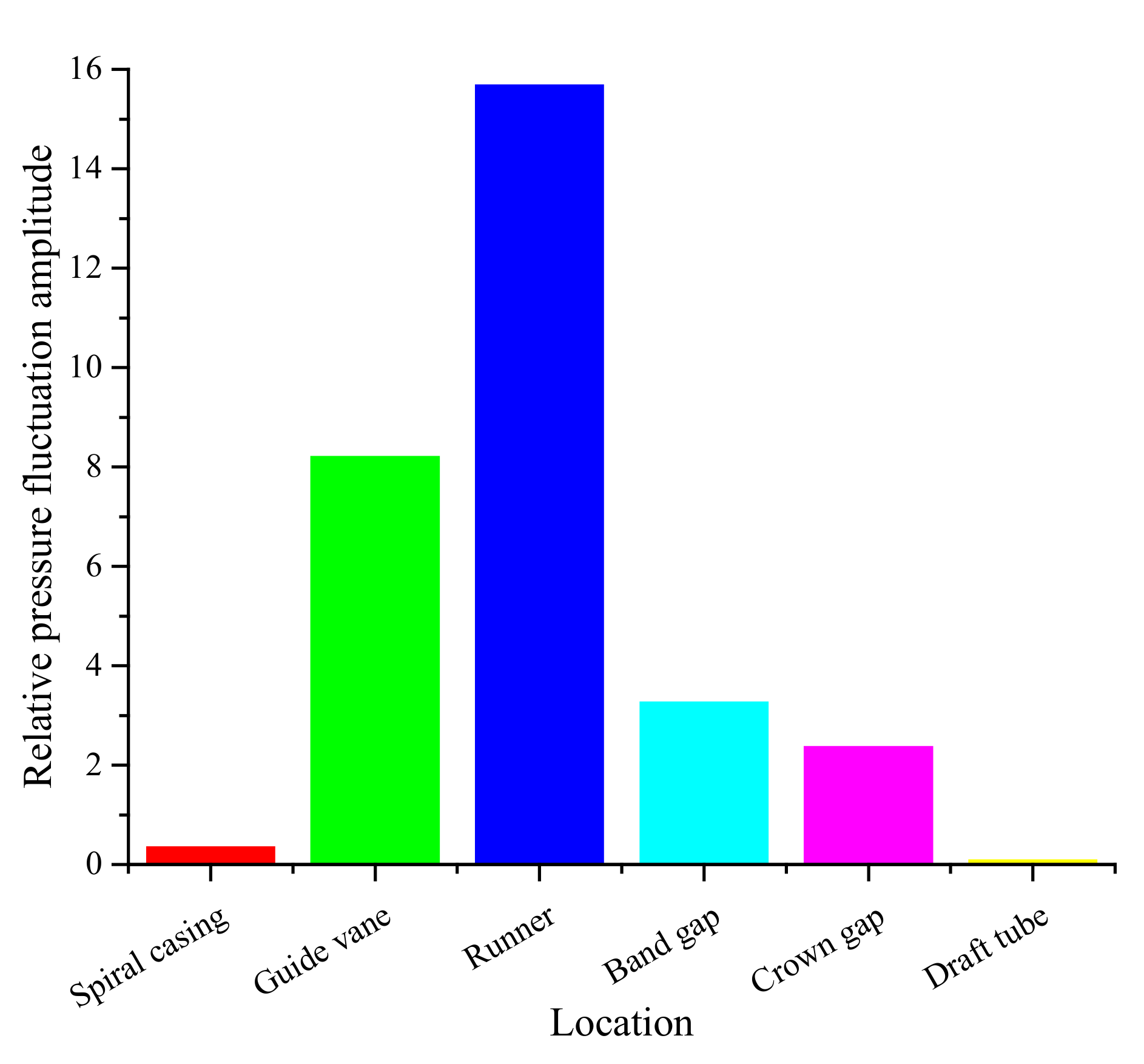
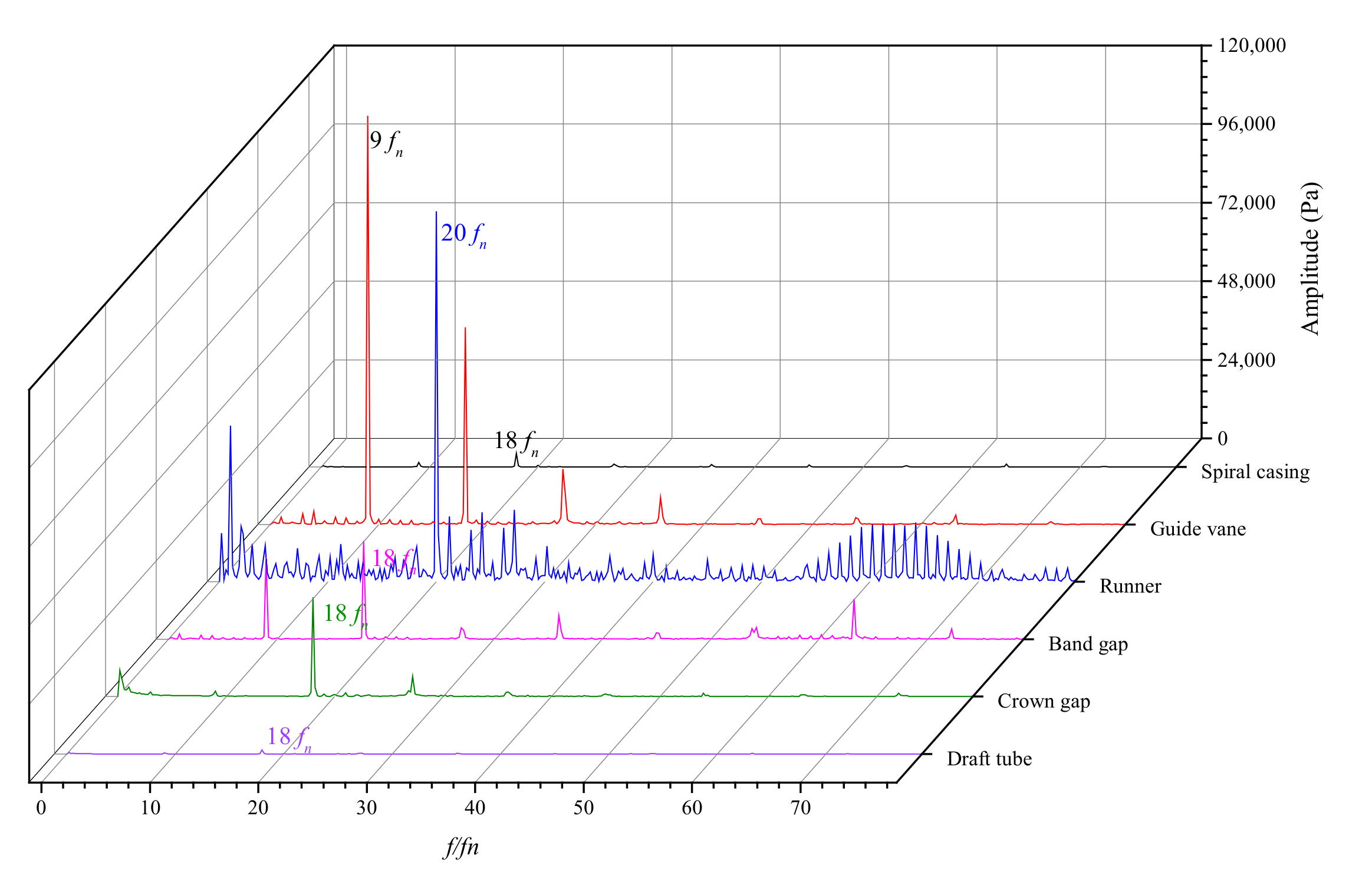
3.2. Pressure Pulsation Characteristics
3.3. Hydraulic Thrust
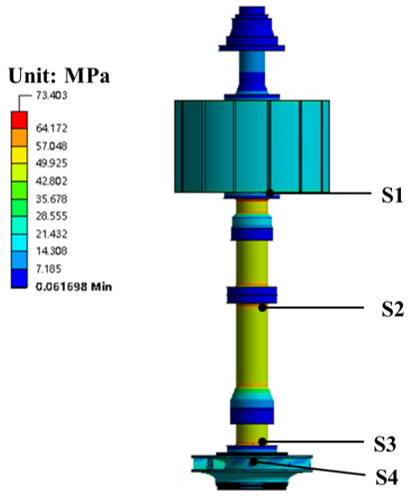
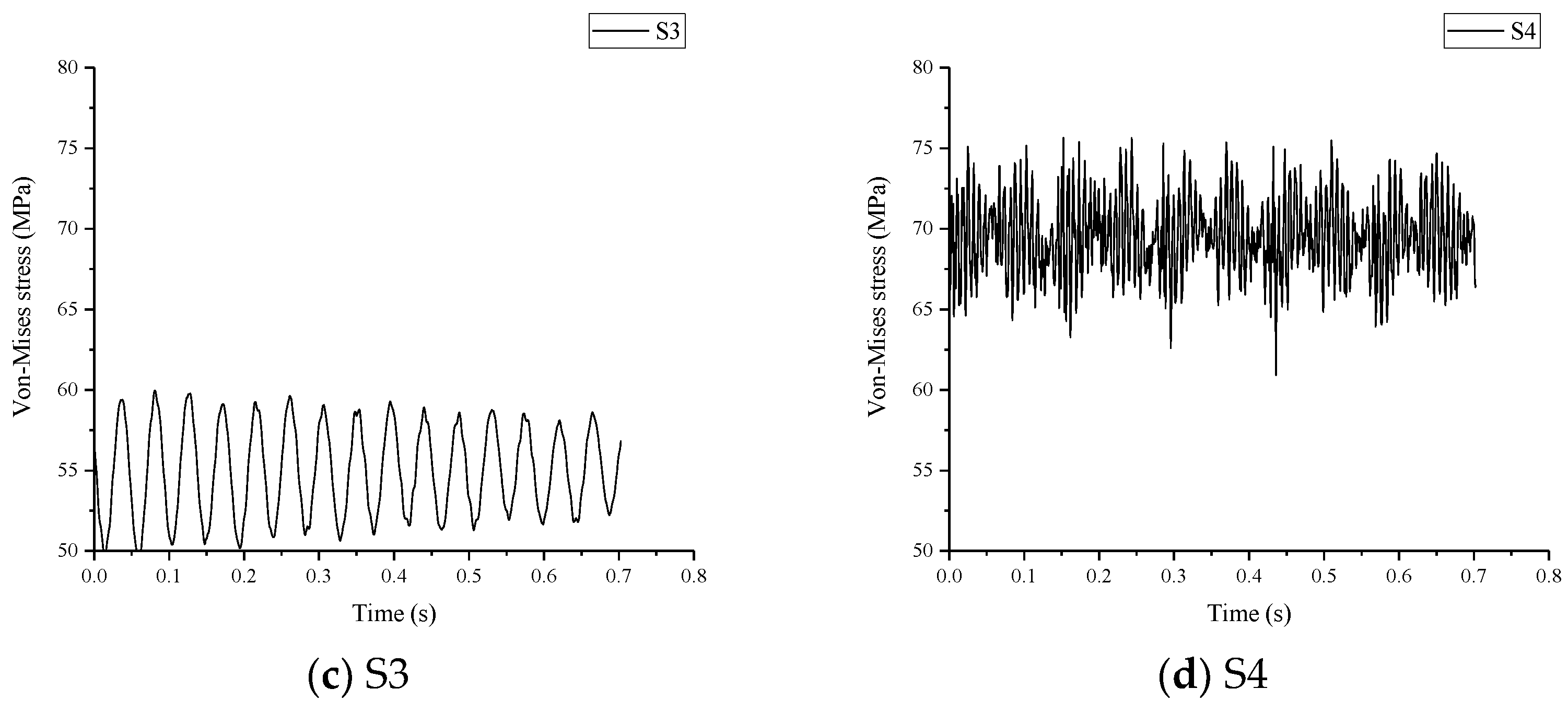
3.4. Dynamic Response of the Shafting
4. Conclusions
- (a)
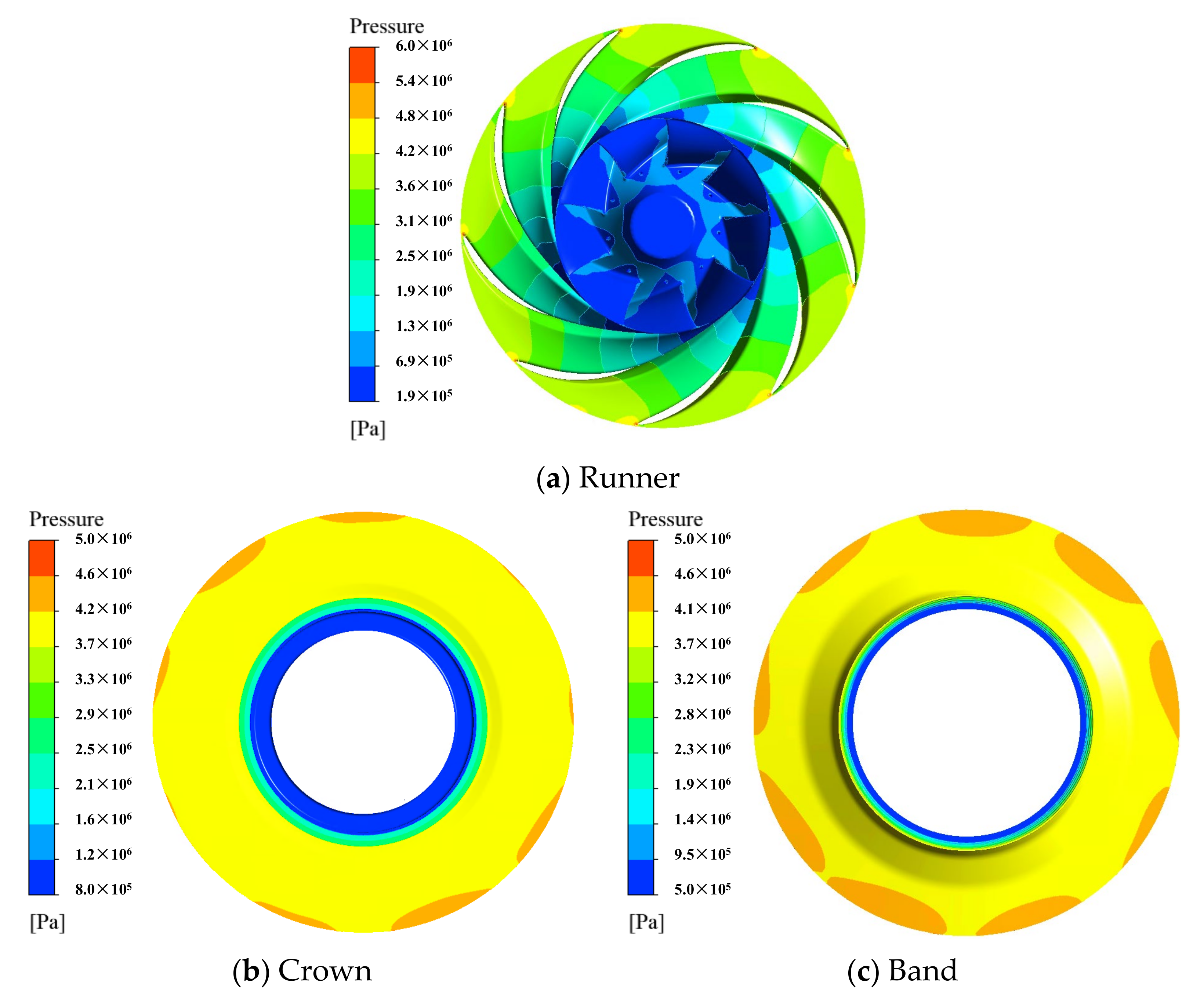
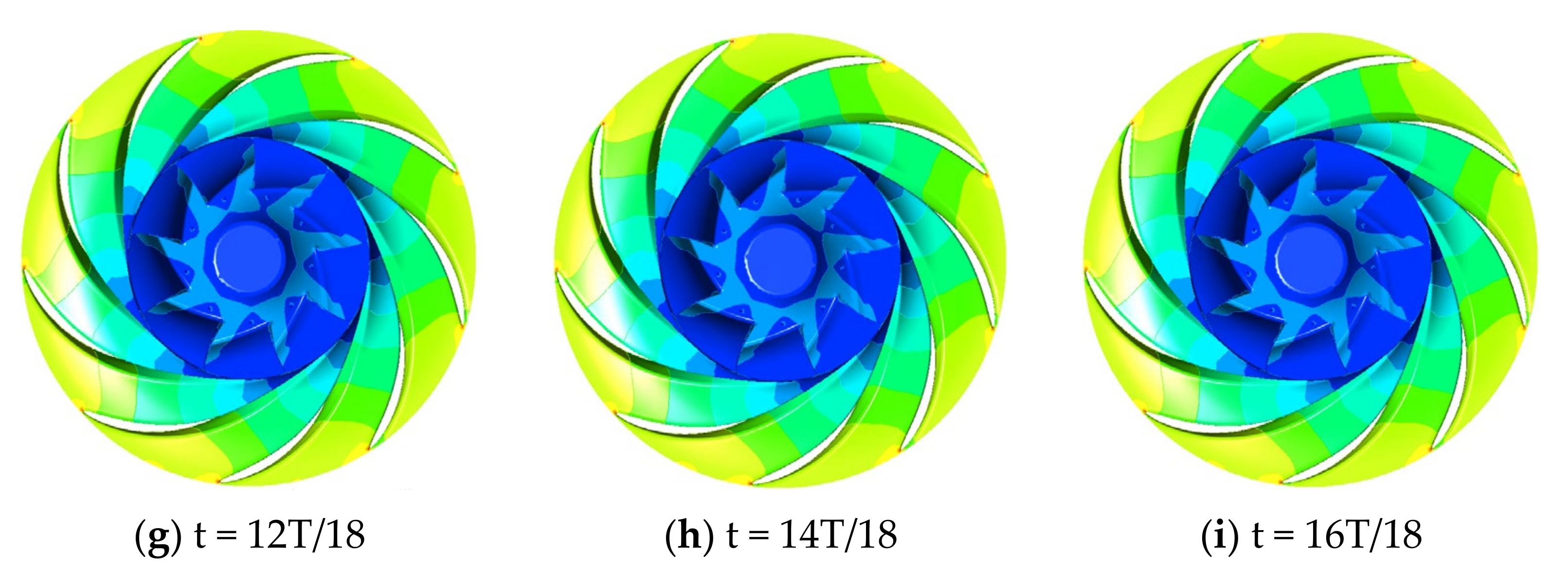
- The hydraulic performance calculated by the CFD shows good agreement with the designed parameters; the pressure distribution in the flow passage is symmetrically distributed and gradually decreases from the spiral casing to the draft tube, and the pressure distribution on the runner surface is stable in one rotating circle.
- (b)
- The streamline is smooth in the whole flow passage with one vortex rope in the draft tube. The pressure fluctuation of the runner reaches 16% of the head, which is greater than other flow passages. The typical dominant frequencies are found in the runner and the guide vane; the guide vane passing frequency in the runner and the runner blade frequency in the guide vane.
- (c)
- The radial hydraulic thrust is much smaller than the axial hydraulic thrust. The axial hydraulic thrust fluctuates from about 155 t to 175 t, and the dominant frequency is only 0.4. The unit has the risk of resonance caused by axial hydraulic thrust in the start-up and shutdown processes. The radial hydraulic thrust fluctuates from about 2 t to 13 t.
- (d)
- The runner has asymmetrical deformation in the axial and radial direction. The maximum stress on the shafting is about 73 MPa, the amplitude of the dynamic stress on the shafting is about 10 MPa, and the dominant frequency of the dynamic stress on the runner is 20.
Author Contributions
Funding
Institutional Review Board statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- National Energy Administration. Medium and Long Term Development Planning of Pumped Storage (2021–2035); National Energy Administration: Beijing, China, 2021.
- Li, D.; Wang, H.; Qin, Y.; Han, L.; Wei, X.; Qin, D. Entropy production analysis of hysteresis characteristic of a pump-turbine model. Energy Convers. Manag. 2017, 149, 175–191. [Google Scholar] [CrossRef]
- Moazeni, F.; Khazaei, J. Optimal energy management of water-energy networks via optimal placement of pumps-as-turbines and demand response through water storage tanks. Appl. Energy 2021, 283, 116335. [Google Scholar] [CrossRef]
- Sambito, M.; Piazza, S.; Freni, G. Stochastic Approach for Optimal Positioning of Pumps As Turbines (PATs). Sustainability 2021, 13, 12318. [Google Scholar] [CrossRef]
- Zhai, L.; Luo, Y.; Wang, Z.; Liu, X.; Xiao, Y. A review on the large tilting pad thrust bearings in the hydropower units. Renew. Sustain. Energy Rev. 2017, 69, 1182–1198. [Google Scholar] [CrossRef]
- Ji, X.-Y.; Li, X.-B.; Su, W.-T.; Lai, X.; Zhao, T.-X. On the hydraulic axial thrust of Francis hydro-turbine. J. Mech. Sci. Technol. 2016, 30, 2029–2035. [Google Scholar] [CrossRef]
- Kazakov, Y.A.; Pelinskii, A.A. Experimental investigation of the axial force in a submersible, electric well pump. Chem Petrol Eng. 1970, 6, 262–263. [Google Scholar] [CrossRef]
- Xia, L.; Cheng, Y.; Yang, Z.; You, J.; Yang, J.; Qian, Z. Evolutions of Pressure Fluctuations and Runner Loads during Runaway Processes of a Pump-Turbine. J. Fluids Eng. 2017, 139, 091101. [Google Scholar] [CrossRef]
- Liu, D.; You, G.; Wang, F.; Zhang, J. Calculation and analysis of axial thrust acting on turning wheel of flow-mixing reversible hydraulic turbines. J. Hohai Univ. (Nat. Sci.) 2004, 5, 557–561. [Google Scholar]
- Mao, Z.; Tao, R.; Chen, F.; Bi, H.; Cao, J.; Luo, Y.; Fan, H.; Wang, Z. Investigation of the Starting-Up Axial Hydraulic Force and Structure Characteristics of Pump Turbine in Pump Mode. J. Mar. Sci. Eng. 2021, 9, 158. [Google Scholar] [CrossRef]
- Mao, X.L.; Lu, J.H.; Yang, J.G.; Wei, D.; Li, T.; Zhang, N. Analysis of Inter-blade Vortex and Runner Blades Force of Pump Turbine during Load Rejection Period. IOP Conf. Ser. Earth Environ. Sci. 2021, 701, 012033. [Google Scholar] [CrossRef]
- Fu, X.; Li, D.; Wang, H.; Zhang, G.; Li, Z.; Wei, X. Numerical Simulation of the Transient Flow in a Pump-Turbine during the Load Rejection Process with Special Emphasis on the Cavitation Effect. J. Fluids Eng. 2020, 142, 1–12. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, Z.; Liu, X.; Xiao, Y.; Chen, C.; Wang, H.; Yan, J. Numerical prediction of pressure pulsation for a low head bidirectional tidal bulb turbine. Energy 2015, 89, 730–738. [Google Scholar] [CrossRef]
- Liu, S.; Li, S.; Wu, Y. Pressure Fluctuation Prediction of a Model Kaplan Turbine by Unsteady Turbulent Flow Simulation. J. Fluids Eng. 2009, 131, 101102. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, L. Simulations and Measurements of Pressure Oscillations Caused by Vortex Ropes. J. Fluids Eng. 2006, 128, 649–655. [Google Scholar] [CrossRef]
- Ahn, S.-H.; Zhou, X.; He, L.; Luo, Y.; Wang, Z. Numerical estimation of prototype hydraulic efficiency in a low head power station based on gross head conditions. Renew. Energy 2020, 153, 175–181. [Google Scholar] [CrossRef]
- Ahn, S.-H.; Xiao, Y.; Wang, Z.; Zhou, X.; Luo, Y. Numerical prediction on the effect of free surface vortex on intake flow characteristics for tidal power station. Renew. Energy 2017, 101, 617–628. [Google Scholar] [CrossRef]
- Hanjalic, K.; Launder, B.E. A Reynolds stress model of turbulence and its application to thin shear flows. J. Fluid Mech. 1972, 52, 609–638. [Google Scholar] [CrossRef]
- Wilcox, D.C. Formulation of the k-w Turbulence Model Revisited. AIAA J. 2008, 46, 2823–2838. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Xiao, Y.; Wang, Z.; Luo, Y.; Cao, L. Unsteady Flow and Pressure Pulsation Characteristics Analysis of Rotating Stall in Centrifugal Pumps under Off-Design Conditions. J. Fluids Eng. 2018, 140, 021105. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Wang, Z.; Xiao, R.; Luo, Y. Analysis of dynamic stresses in Kaplan turbine blades. Eng. Comput. 2007, 24, 753–762. [Google Scholar] [CrossRef]
- Dompierre, F.; Sabourin, M. Determination of turbine runner dynamic behaviour under operating condition by a two-way staggered fluid-structureinteraction method. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012085. [Google Scholar] [CrossRef]
- Pei, J.; Yuan, S.; Yuan, J. Dynamic stress analysis of sewage centrifugal pump impeller based on two-way coupling method. Chin. J. Mech. Eng. 2014, 27, 369–375. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, Z.; Zhou, L.; Peng, G.; Sun, G. Computation of Static and Dynamic Stresses of a Bulb Tubular Turbine. In Proceedings of the 2008 ASME Fluids Engineering Conference, Jacksonville, FL, USA, 10–14 August 2008. [Google Scholar]
- Trivedi, C.; Cervantes, M.J. Fluid-structure interactions in Francis turbines: A perspective review. Renew. Sustain. Energy Rev. 2017, 68, 87–101. [Google Scholar] [CrossRef]
- Terentiev, L. The Turbulence Closure Model Based on Linear Anisotropy Invariant. Doctoral Thesis, Friedrich-Alexander University, Erlangen-Nuremberg, Germany, 2006. [Google Scholar]
- Huang, B.; Zhao, B.; Wang, L.; Wang, P.; Zhao, H.; Guo, P.; Yang, S.; Wu, D. The effects of heave motion on the performance of a floating counter-rotating type tidal turbine under wave-current interaction. Energy Convers. Manag. 2022, 252, 115093. [Google Scholar] [CrossRef]
- Zhou, D.; Sun, X. Influences of Geometrical Parameters of Upstream Deflector on Performance of a H-Type Vertical Axis Marine Current Turbine. Energies 2021, 14, 4087. [Google Scholar] [CrossRef]
- Menter, F.; Rumsey, C. Assessment of two-equation turbulence models for transonic flows. In Proceedings of the Fluid Dynamics Conference, Colorado Springs, CO, USA, 20–23 June 1994. [Google Scholar]
- ANSYS. ANSYS® Academic Research Mechanical; Version 18.1; Help System, Mechanical APDL Documentation; ANSYS, Inc.: Canonsburg, PA, USA, 2017. [Google Scholar]
- Bathe, K.-J. Finite Element Procedures; Prentice Hall: Hoboken, NJ, USA; Pearson Education, Inc.: London, UK, 2016. [Google Scholar]
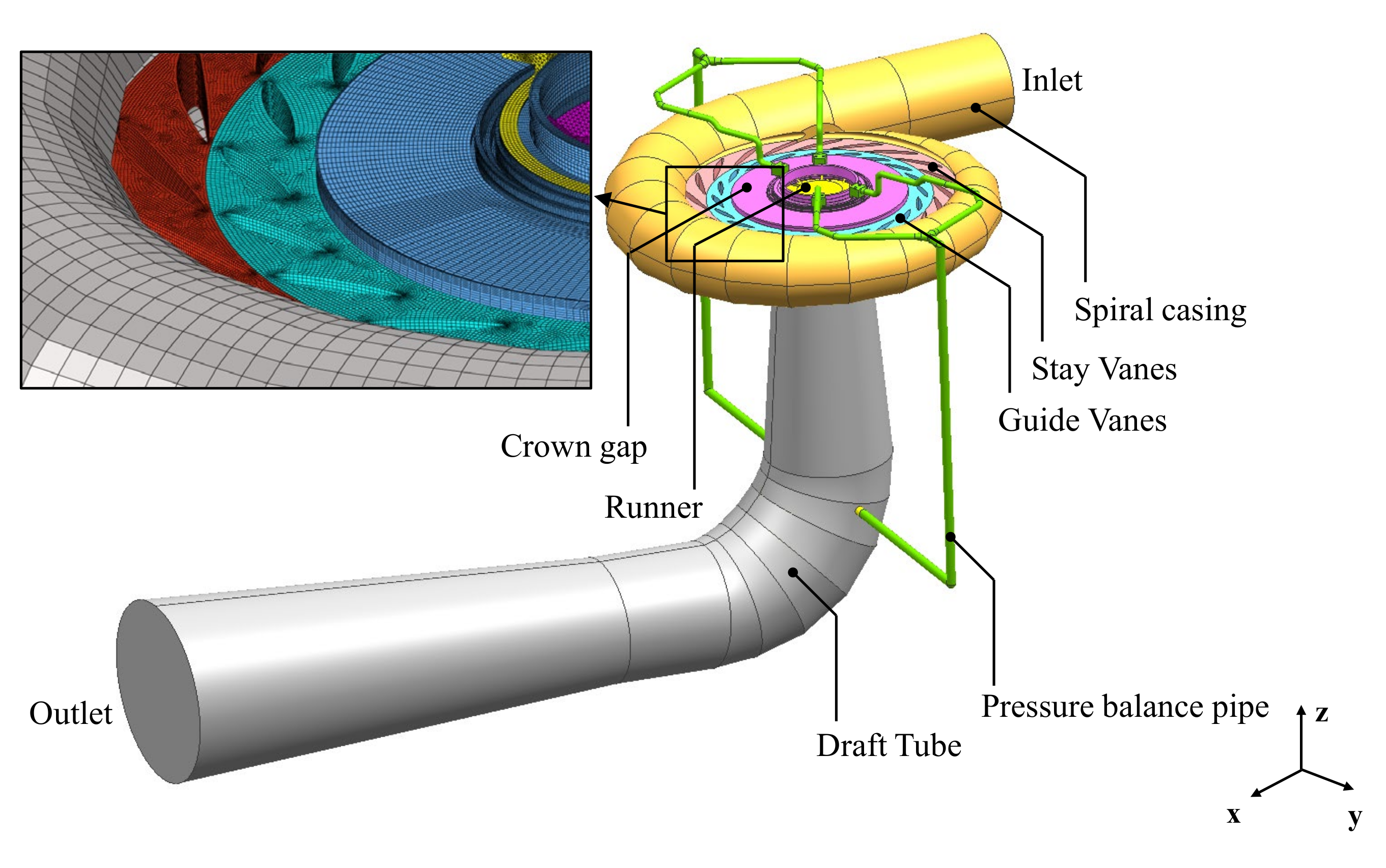
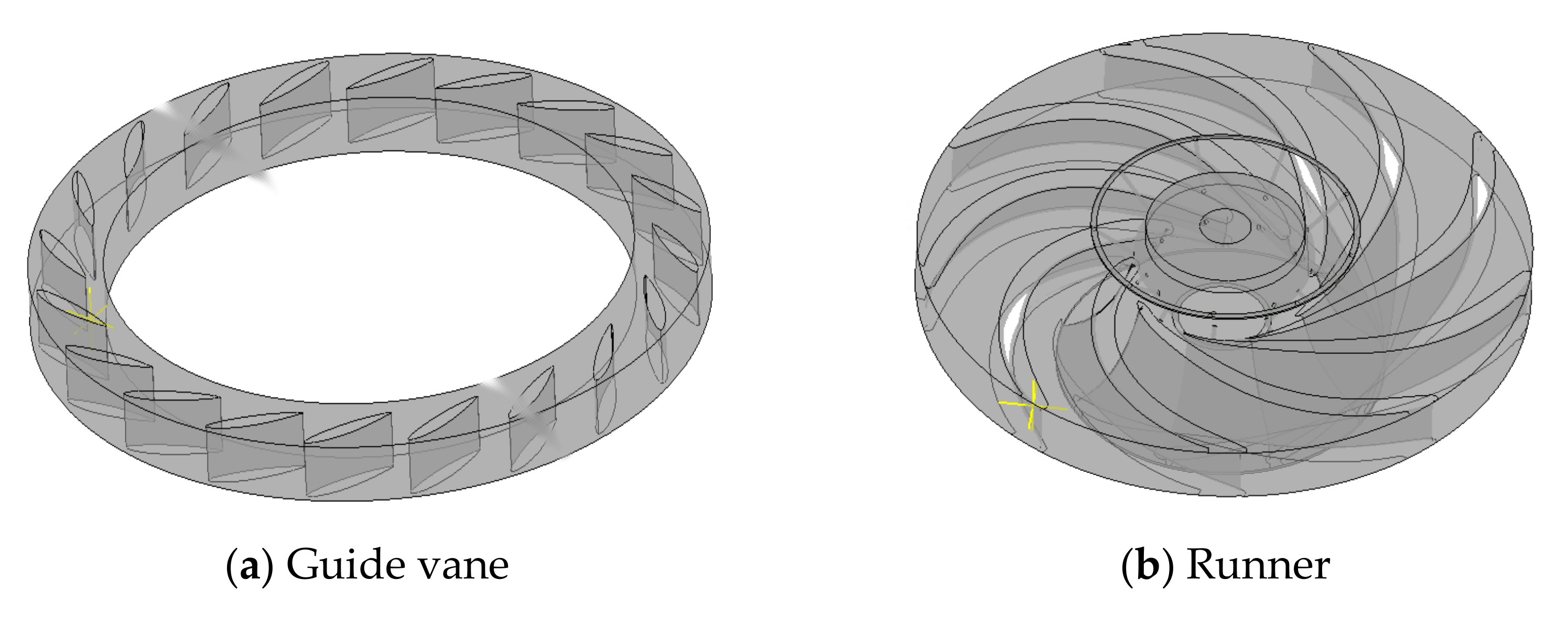
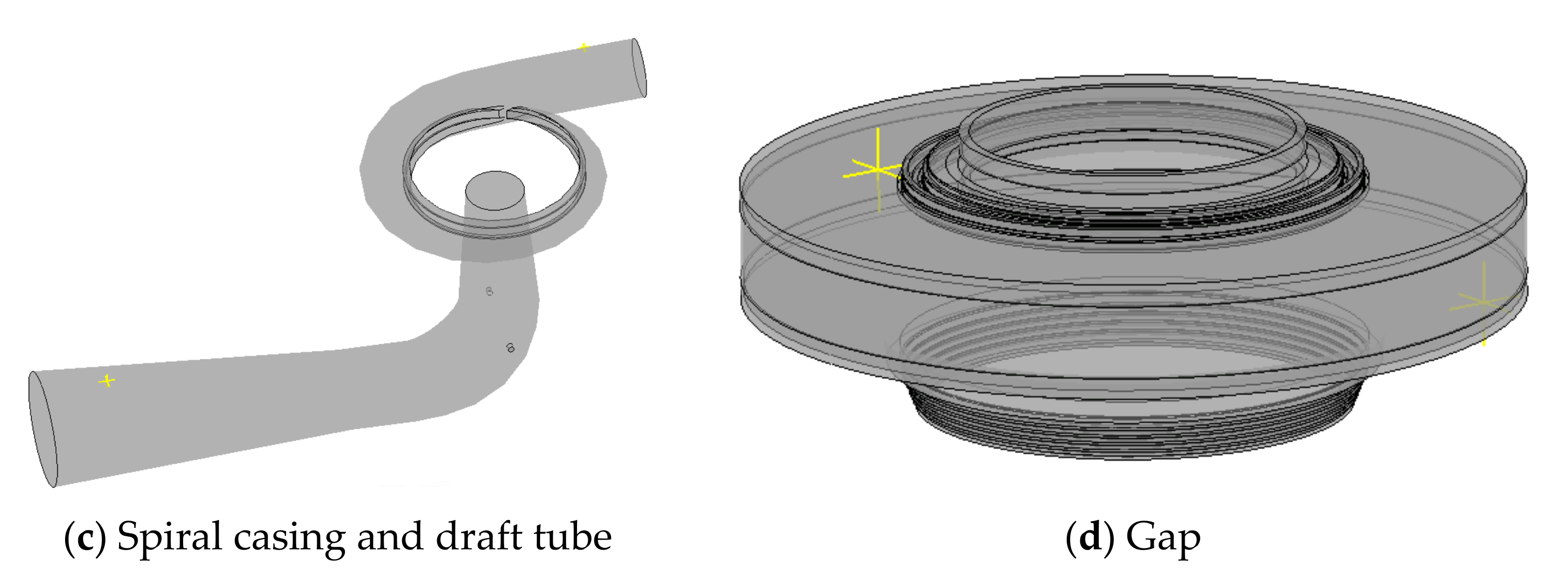
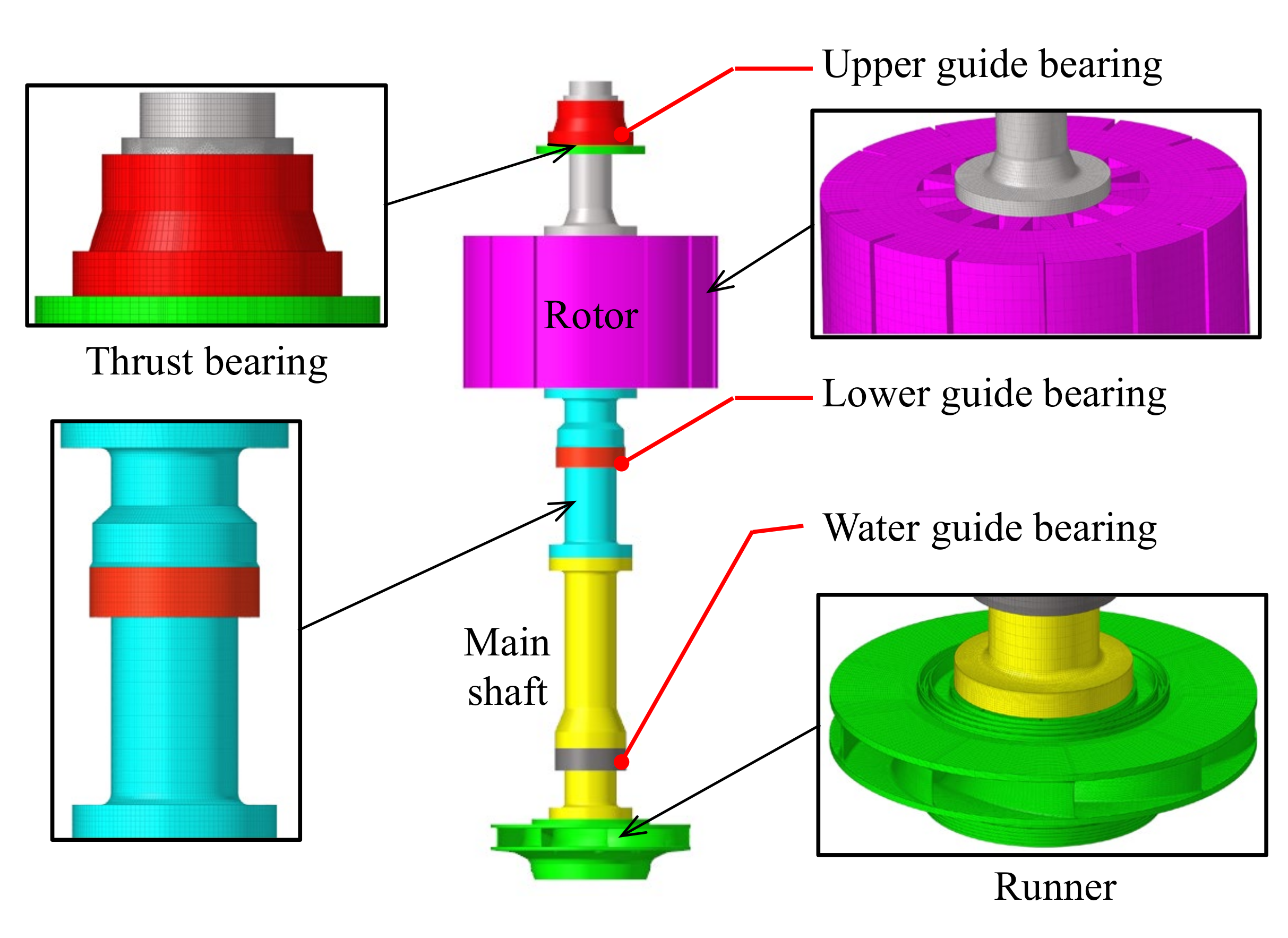






| Component | Element Type | Element Number |
|---|---|---|
| Spiral casing | Hexahedral | 72,588 |
| Stay vanes | Hexahedral | 579,660 |
| Guide vanes | Hexahedral | 434,160 |
| Runner | Hybrid | 2,086,433 |
| Crown gap and band gap | Hexahedral | 753,330 |
| Pressure balance pipe | Hexahedral | 295,652 |
| Draft tube | Hybrid | 1,162,188 |
| Total | - | 5,384,011 |
| Item | Head (m) | Discharge (m3/s) | Power (MW) |
|---|---|---|---|
| Simulation | 429.60 | 78.27 | 297.80 |
| Designed Parameter | 430.00 | 79.16 | 306.10 |
| Error (%) | −0.09% | −1.12% | −2.71% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, L.; Cao, J.; Li, X.; Zhou, X.; Hu, H.; Wang, T.; Gui, S.; Lai, W.; Zhu, Z.; Wang, Z.; et al. Numerical Analysis on the Hydraulic Thrust and Dynamic Response Characteristics of a Turbine Pump. Energies 2022, 15, 1580. https://doi.org/10.3390/en15041580
Kong L, Cao J, Li X, Zhou X, Hu H, Wang T, Gui S, Lai W, Zhu Z, Wang Z, et al. Numerical Analysis on the Hydraulic Thrust and Dynamic Response Characteristics of a Turbine Pump. Energies. 2022; 15(4):1580. https://doi.org/10.3390/en15041580
Chicago/Turabian StyleKong, Linghua, Jingwei Cao, Xiangyang Li, Xulei Zhou, Haihong Hu, Tao Wang, Shuxin Gui, Wenfa Lai, Zhongfeng Zhu, Zhengwei Wang, and et al. 2022. "Numerical Analysis on the Hydraulic Thrust and Dynamic Response Characteristics of a Turbine Pump" Energies 15, no. 4: 1580. https://doi.org/10.3390/en15041580
APA StyleKong, L., Cao, J., Li, X., Zhou, X., Hu, H., Wang, T., Gui, S., Lai, W., Zhu, Z., Wang, Z., & Liu, Y. (2022). Numerical Analysis on the Hydraulic Thrust and Dynamic Response Characteristics of a Turbine Pump. Energies, 15(4), 1580. https://doi.org/10.3390/en15041580






