Control Strategy of Interlinking Converter in Hybrid Microgrid Based on Line Impedance Estimation
Abstract
:1. Introduction
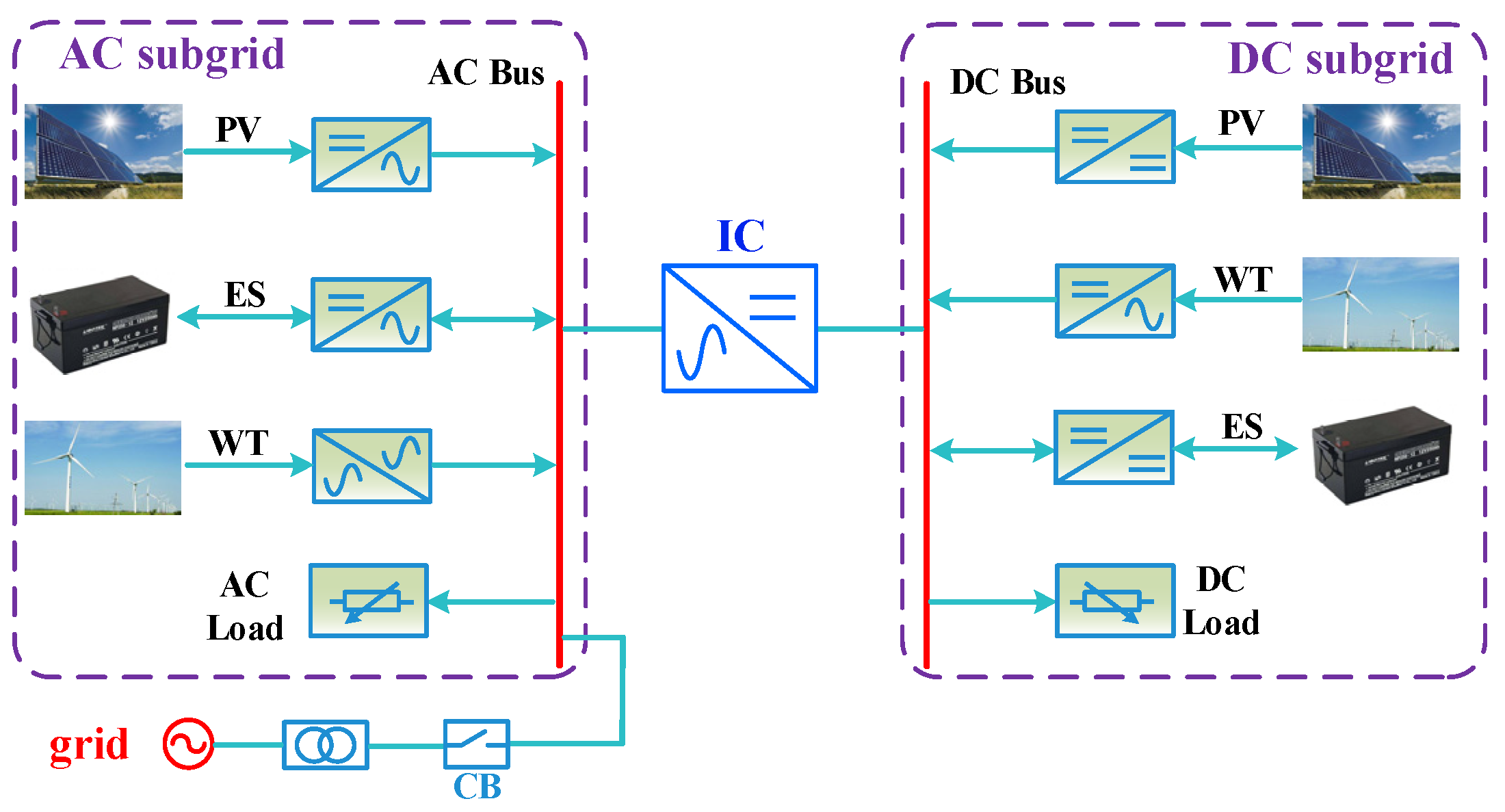
2. Structure and Control Strategy of Hybrid Microgrid
2.1. Structure of Hybrid Microgrid
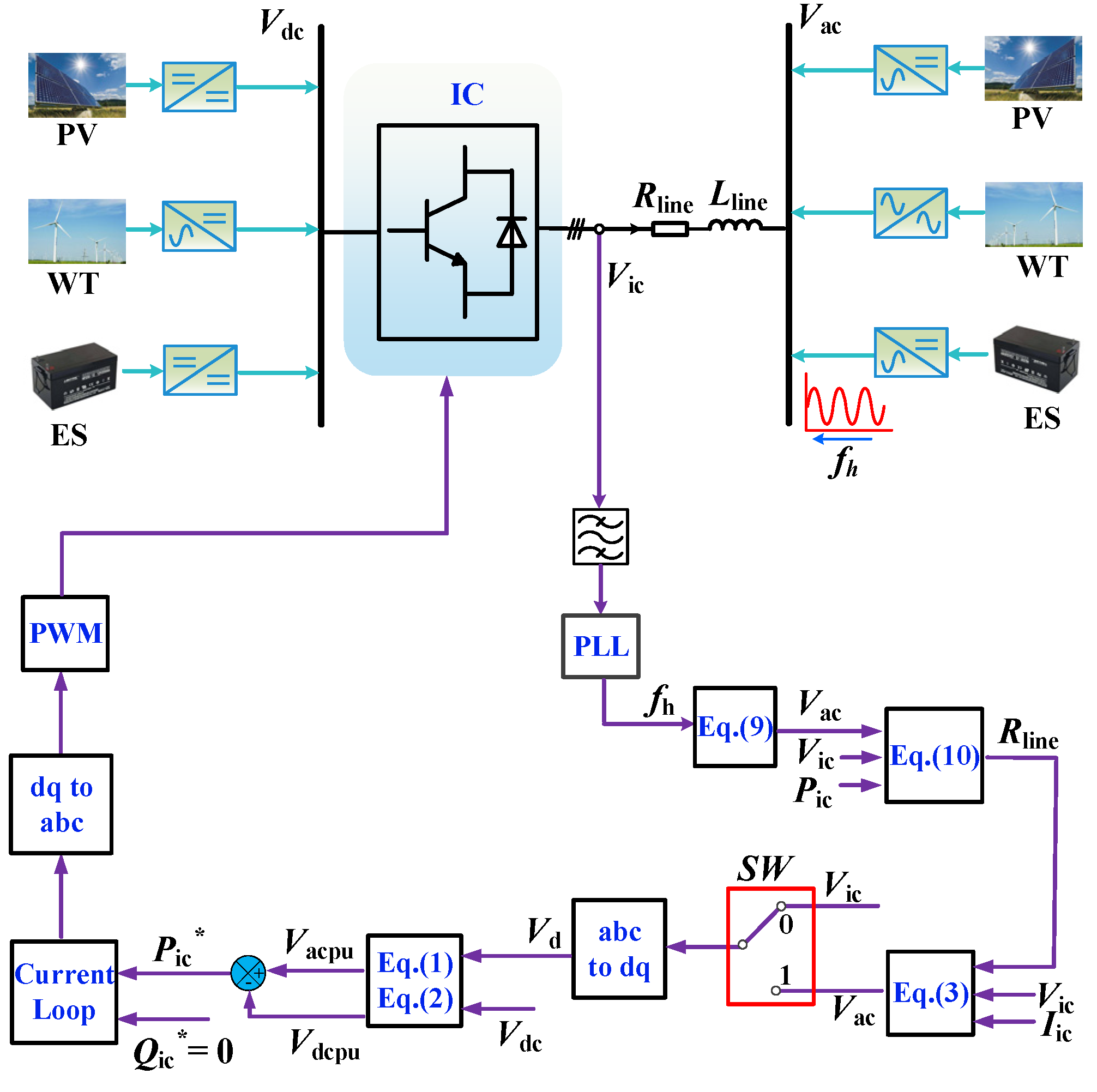
2.2. Traditional Normalized Droop Control of IC
3. Line Resistance Estimation Method
3.1. Relationship between IC Transmitted Power and Line Impedance
3.2. Estimation of Line Impedance by Means of Harmonic Signal Injection
3.3. Influence of Line Reactance
4. Control Strategy of IC Based on Line Impedance Compensation
5. Hardware-in-the-Loop (HIL) Verification
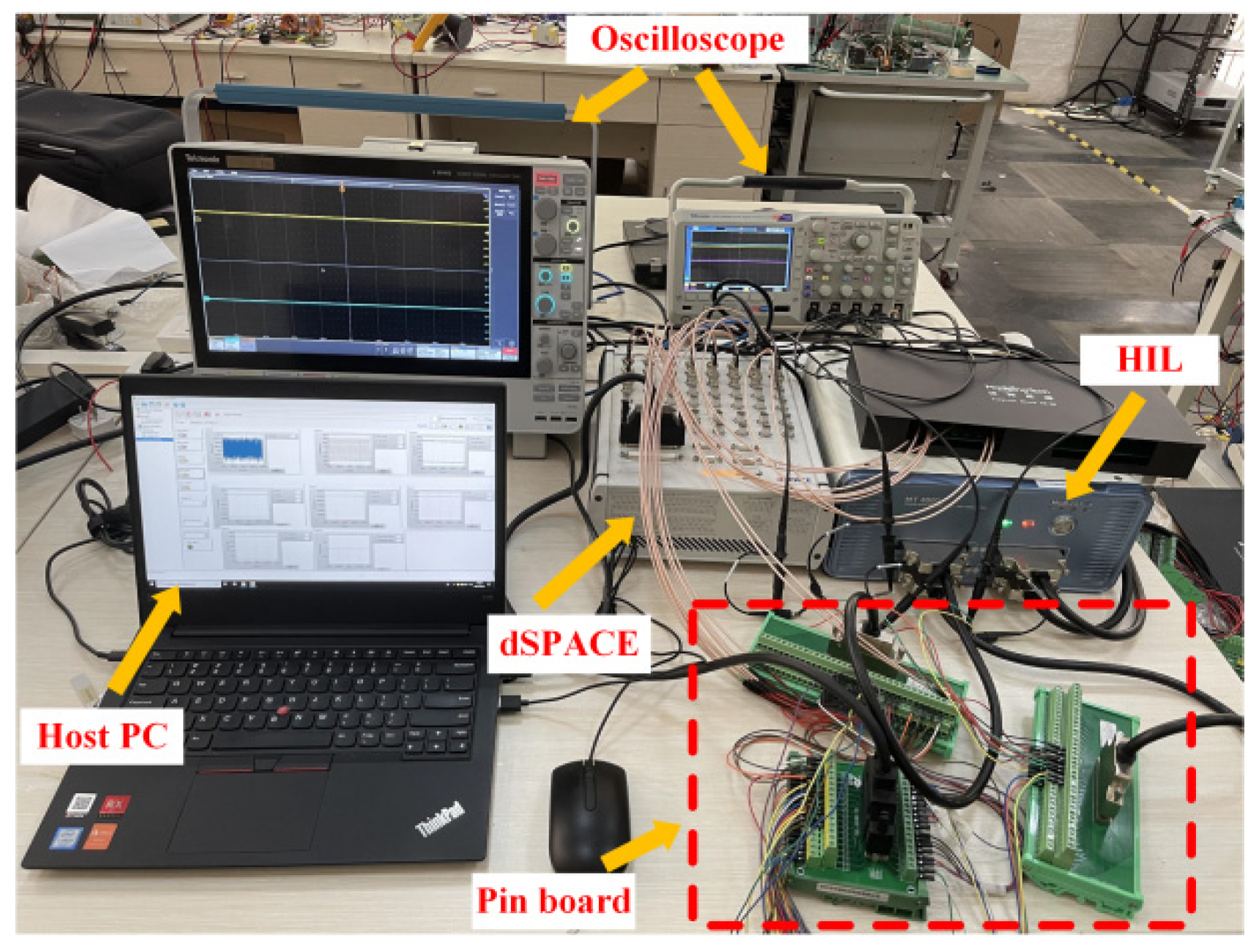
5.1. Details of the HIL Platform
5.2. Case Study
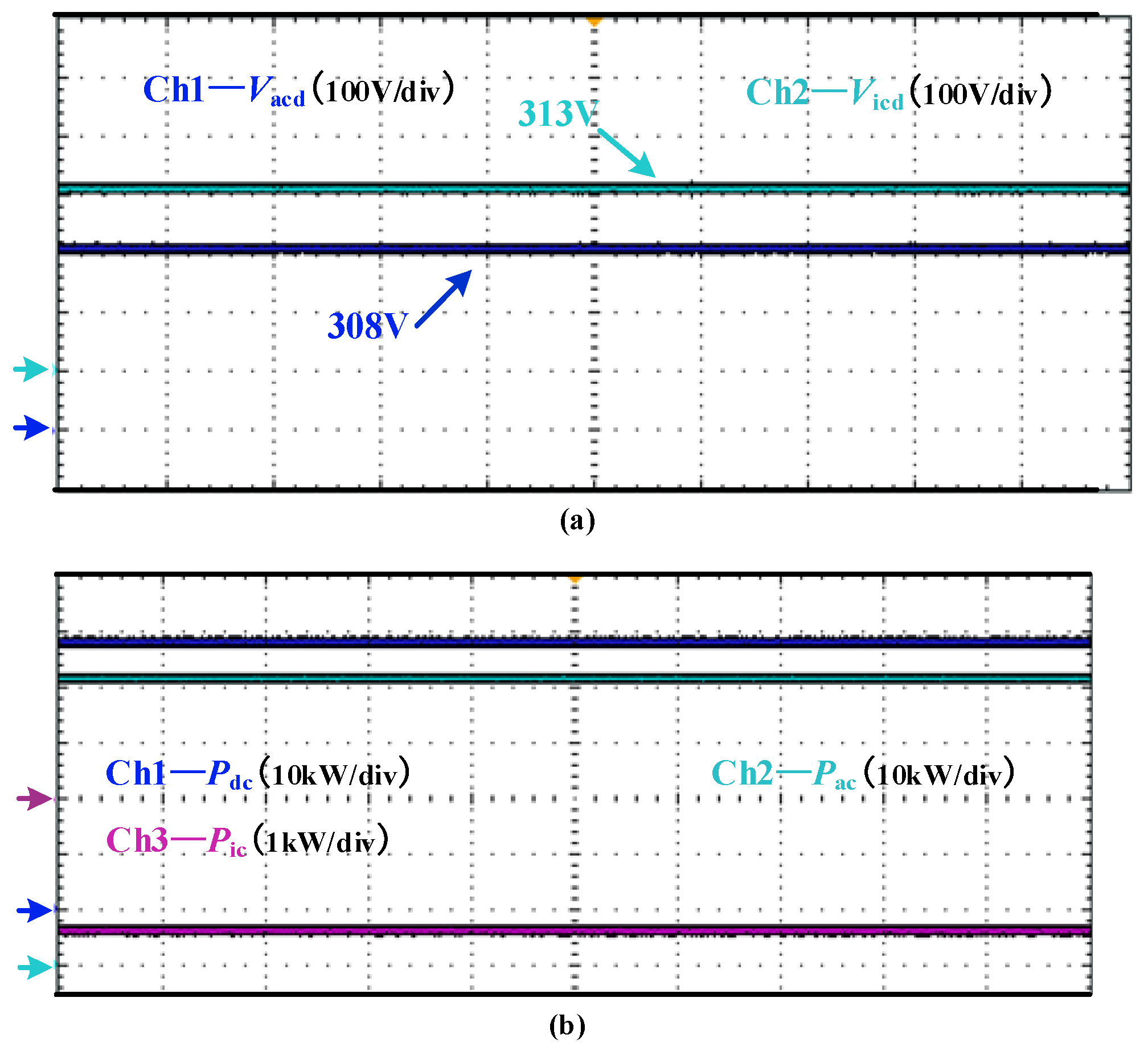
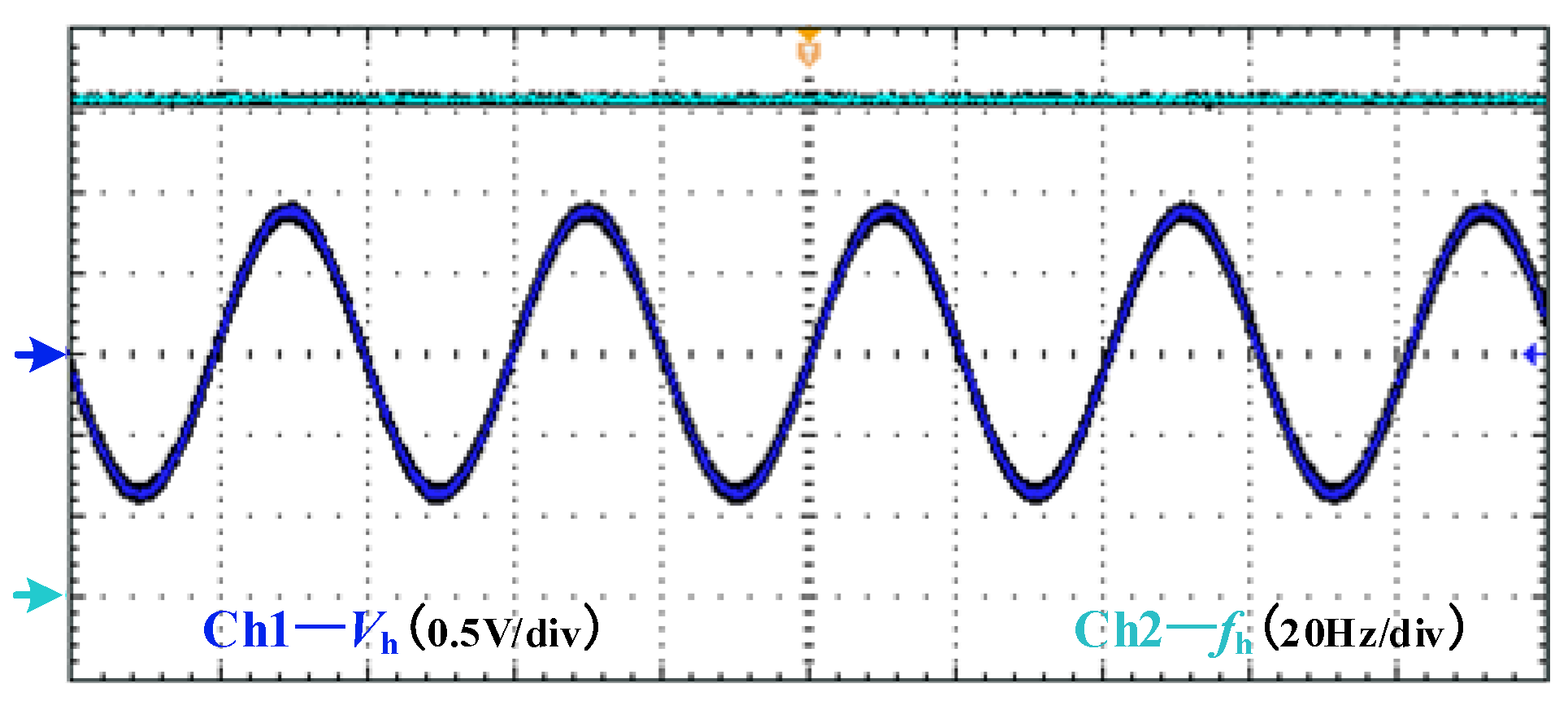
5.2.1. Impact on the Power Quality When Injecting Harmonics
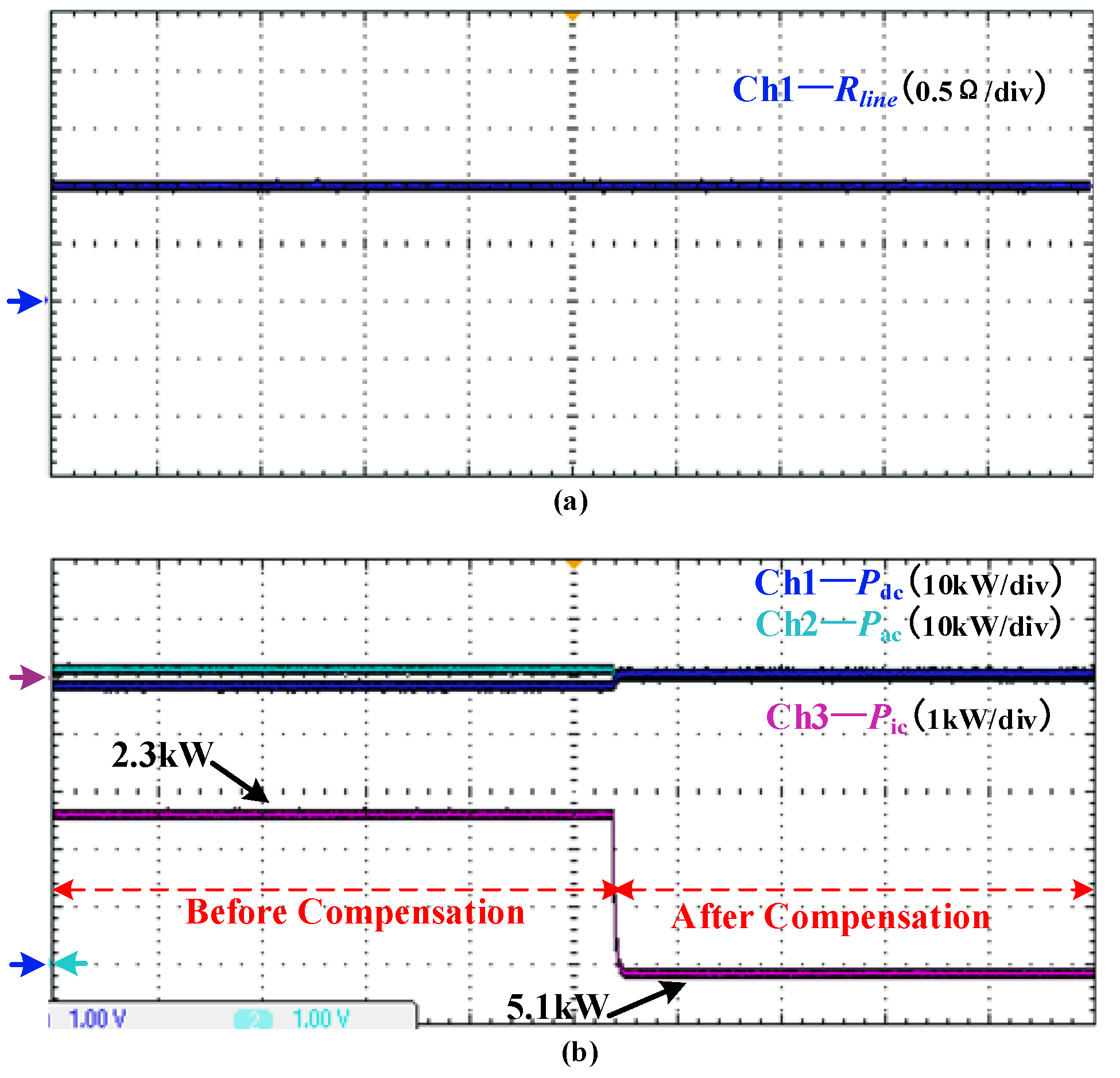
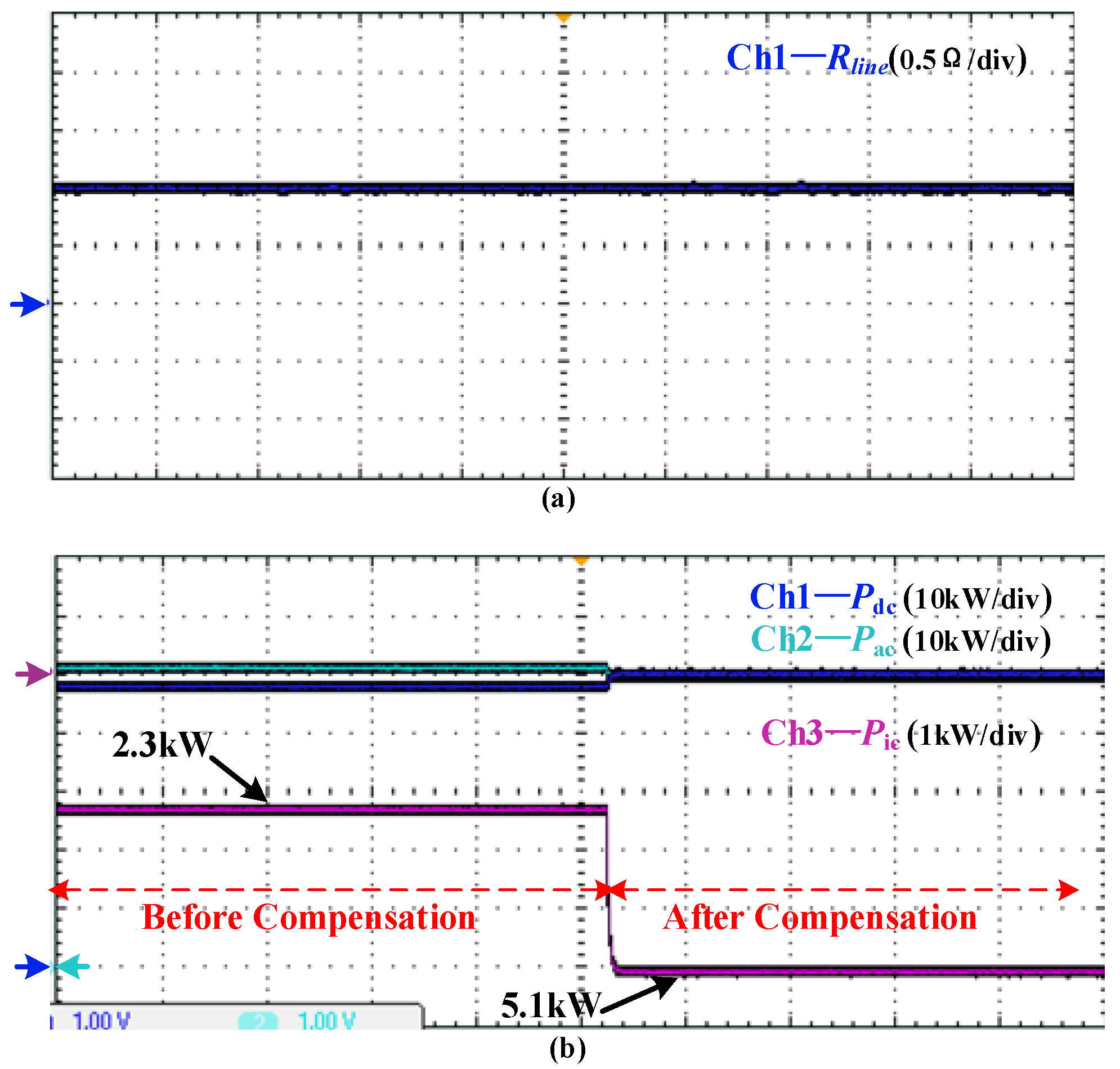
5.2.2. Case 1 (Rline = 1 Ω, Xline = 0 Ω)
5.2.3. Case 2 (Rline = 1 Ω, Xline = 0.125 Ω)
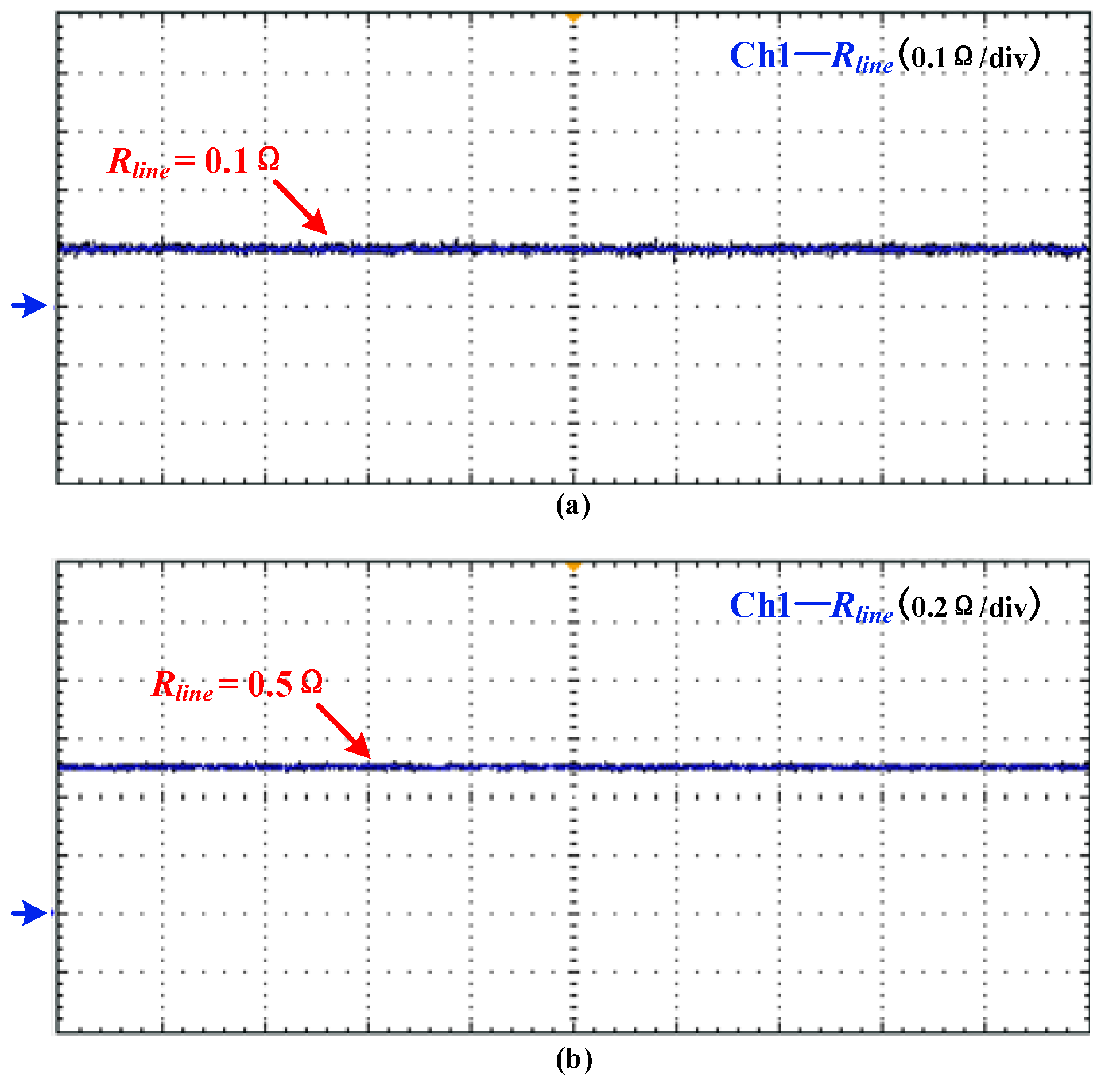
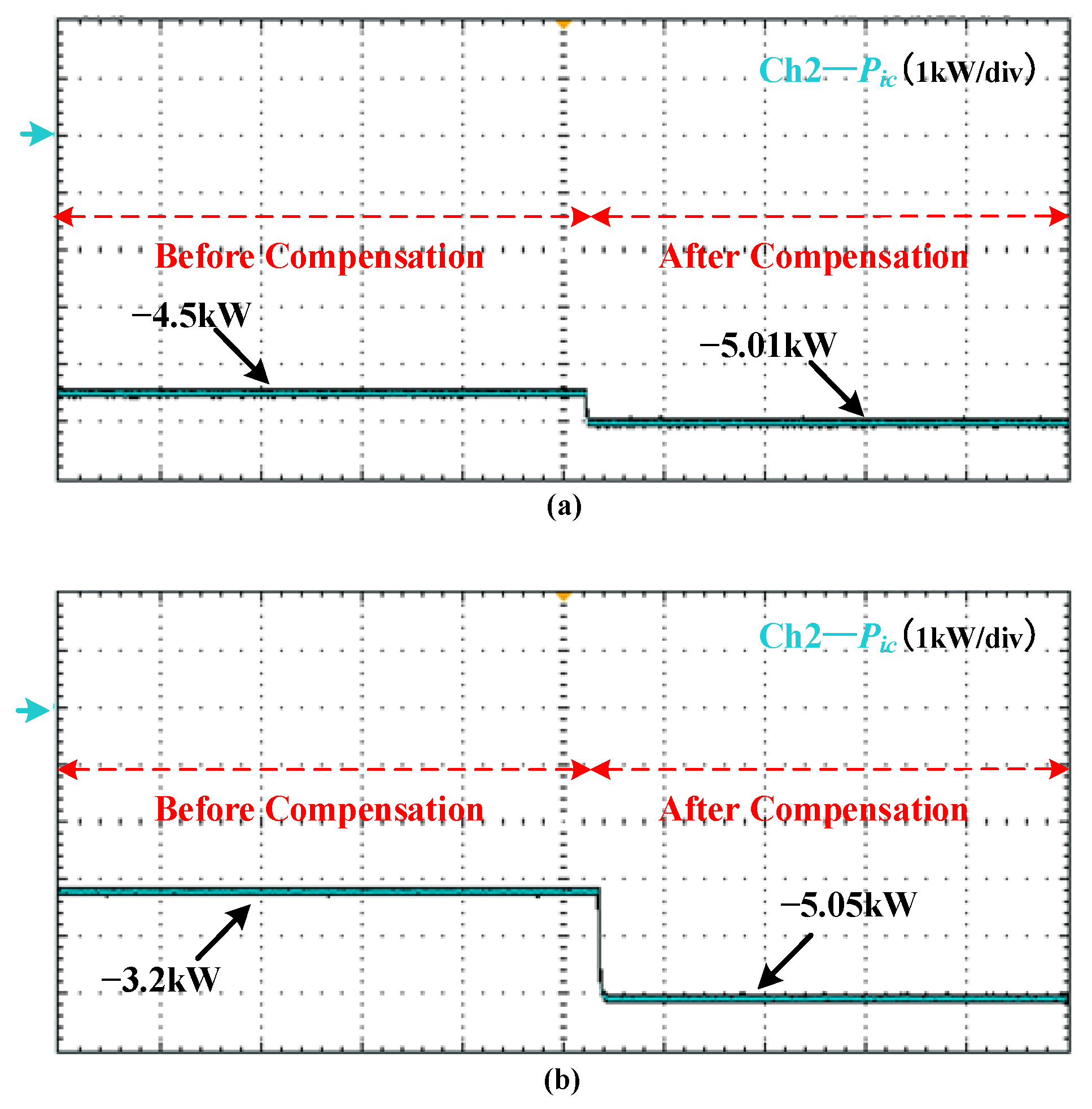
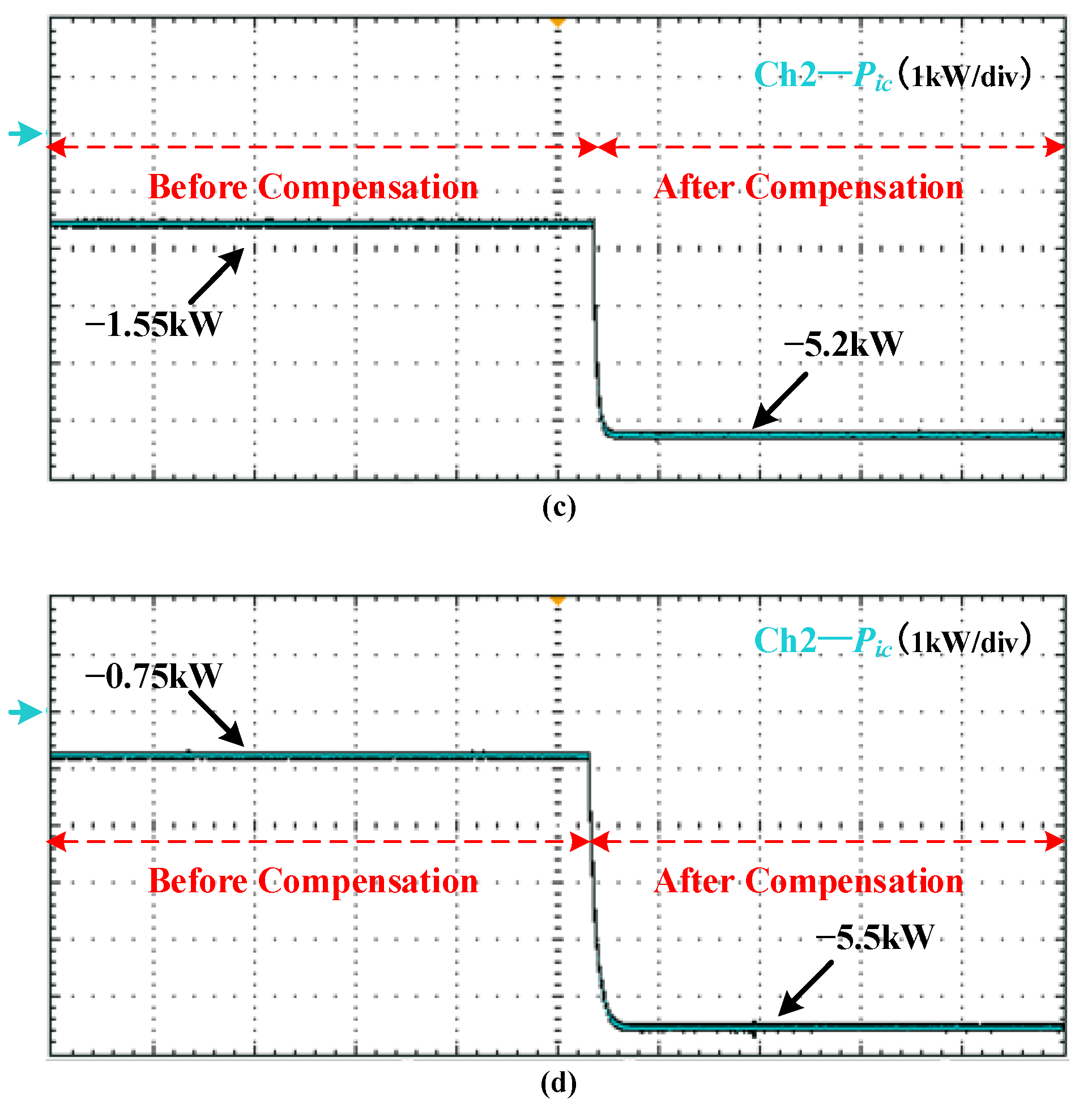
5.2.4. Case 3 (Different Line Resistances)
5.3. Discussions about the Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nikkhajoei, H.; Lasseter, R.H. Distributed generation interface to the CERTS microgrid. IEEE Trans. Power Delivery 2009, 24, 1598–1608. [Google Scholar] [CrossRef]
- Lasseter, R.H.; Paigi, P. Microgrid: A conceptual solution. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), Aachen, Germany, 20–25 June 2004; pp. 4285–4290. [Google Scholar]
- Xia, Y.; Wei, W.; Yu, M.; Peng, Y.; Tang, J. Decentralized multi-time scale power control for a hybrid AC/DC microgrid with multiple subgrids. IEEE Trans. Power Electron. 2018, 33, 4061–4072. [Google Scholar] [CrossRef]
- Liu, X.; Wang, P.; Loh, P.C. A hybrid AC/DC microgrid and its coordination control. IEEE Trans. Smart Grid 2011, 2, 278–286. [Google Scholar]
- Lu, X.; Guerrero, J.M.; Sun, K.; Vasquez, J.C.; Teodorescu, R.; Huang, L. Hierarchical Control of Parallel AC-DC Converter Interfaces for Hybrid Microgrids. IEEE Trans. Smart Grid 2014, 5, 683–692. [Google Scholar] [CrossRef] [Green Version]
- Peyghami, S.; Mokhtari, H.; Blaabjerg, F. Autonomous Operation of a Hybrid AC/DC Microgrid with Multiple Interlinking Converters. IEEE Trans. Smart Grid 2018, 9, 6480–6488. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Li, D.; Wang, Y.; Yan, X. Self-adaptable reactive power-voltage controller for virtual synchronous generators. J. Eng. 2019, 9, 2969–2973. [Google Scholar] [CrossRef]
- Jin, C.; Loh, P.C.; Wang, P.; Mi, Y.; Blaabjerg, F. Autonomous operation of hybrid ac–dc microgrids. In Proceedings of the 2010 IEEE International Conference on Sustainable Energy Technologies (ICSET), Kandy, Sri Lanka, 6–9 December 2010; pp. 1–7. [Google Scholar]
- Loh, P.C.; Li, D.; Chai, Y.K.; Blaabjerg, F. Autonomous Operation of Hybrid Microgrid with AC and DC Subgrids. IEEE Trans. Power Electron. 2013, 28, 2214–2223. [Google Scholar] [CrossRef]
- Loh, P.C.; Li, D.; Chai, Y.K.; Blaabjerg, F. Autonomous control of interlinking converter with energy storage in hybrid AC–DC microgrid. IEEE Trans. Ind. Appl. 2013, 49, 1374–1382. [Google Scholar] [CrossRef]
- Li, X.; Guo, L.; Li, Y.; Guo, Z.; Hong, C.; Zhang, Y.; Wang, C. A Unified Control for the DC-AC Interlinking Converters in Hybrid AC/DC Microgrids. IEEE Trans. Smart Grid 2018, 9, 6540–6553. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Berbel, N.; Matas, J.; de Vicuna, L.G.; Miret, J. Decentralized control for parallel operation of distributed generation inverters using resistive output impedance. IEEE Trans. Ind. Electron. 2017, 54, 994–1004. [Google Scholar] [CrossRef]
- Zhang, B.; Cao, G.; Ren, C.; Wang, J.; Han, X. Autonomous control strategy of bidirectional AC/DC converter in low voltage hybrid microgrid. In Proceedings of the 12th IEEE Conference on Industrial Electronics and Applications (ICIEA), Siem Reap, Cambodia, 18–20 June 2017; pp. 1564–1569. [Google Scholar]
- Xiao, H.; Luo, A.; Shuai, Z.; Jin, G.; Huang, Y. An improved control method for multiple bidirectional power converters in hybrid AC/DC microgrid. IEEE Trans. Smart Grid 2016, 7, 340–347. [Google Scholar] [CrossRef]
- Lin, P.; Wang, P.; Jin, C.; Xiao, J.; Li, X.; Guo, F.; Zhang, C. A Distributed Power Management Strategy for Multi-Paralleled Bidirectional Interlinking Converters in Hybrid AC/DC Microgrids. IEEE Trans. Smart Grid 2019, 10, 5696–5711. [Google Scholar] [CrossRef]
- Asiminoaei, L.; Teodorescu, R.; Blaabjerg, F.; Borup, U. A digital controlled PV-inverter with grid impedance estimation for ENS detection. IEEE Trans. Power Electron. 2005, 20, 1480–1490. [Google Scholar] [CrossRef]
- Asiminoaei, L.; Teodorescu, R.; Blaabjerg, F.; Borup, U. Implementation and test of an online embedded grid impedance estimation technique for PV inverters. IEEE Trans Ind. Electron. 2005, 52, 1136–1144. [Google Scholar] [CrossRef]
- Liserre, M.; Blaagjerg, F.; Teodorescu, R. Grid impedance detection via excitation of LCL-filter resonance. In Proceedings of the Fourtieth IAS Annual Meeting. Conference Record of the 2005 Industry Applications Conference, Hong Kong, China, 2–6 October 2005; pp. 910–916. [Google Scholar]
- Liserre, M.; Blaabjerg, F.; Teodorescu, R. Grid Impedance Estimation via Excitation of LCL-Filter Resonance. IEEE Trans. Ind. Appl. 2007, 43, 1401–1407. [Google Scholar] [CrossRef]
- Ghorbal, M.J.; Ghzaiel, W.; Slama-Belkhodja, I.; Guerrero, J.M. Online detection and estimation of grid impedance variation for Distributed Power Generation. In Proceedings of the 2012 16th IEEE Mediterranean Electrotechnical Conference, Yasmine Hammamet, Tunisia, 25–28 March 2012; pp. 555–560. [Google Scholar]
- Ciobotaru, M.; Teodorescu, R.; Rodriguez, P.; Timbus, A.; Blaabjerg, F. Online grid impedance estimation for single-phase grid-connected systems using PQ variations. In Proceedings of the 2007 IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 2306–2312. [Google Scholar]
- Timbus, A.V.; Rodriguez, P.; Teodorescu, R.; Ciobotaru, M. Line Impedance Estimation Using Active and Reactive Power Variations. In Proceedings of the 2007 IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 1273–1279. [Google Scholar]
- Gu, H.; Guo, X.; Wang, D.; Wu, W. Real-time grid impedance estimation technique for grid-connected power converters. In Proceedings of the 2012 IEEE International Symposium on Industrial Electronics, Hangzhou, China, 28–31 May 2012; pp. 1621–1626. [Google Scholar]
- Guerrero, J.M.; de Vicuna, L.G.; Matas, J.; Castilla, M.; Miret, J. Output impedance design of parallel-connected UPS inverters with wireless load-sharing control. IEEE Trans. Ind. Electron. 2005, 52, 1126–1135. [Google Scholar] [CrossRef]
- He, J.; Li, Y.W.; Guerrero, J.M.; Blaabjerg, F.; Vasquez, J.C. An Islanding Microgrid Power Sharing Approach Using Enhanced Virtual Impedance Control Scheme. IEEE Trans. Power Electron. 2013, 28, 5272–5282. [Google Scholar] [CrossRef]
- Engler, A.; Soultanis, N. Droop control in LV-grids. In Proceedings of the 2005 International Conference on Future Power Systems, Amsterdam, The Netherlands, 18 November 2005; pp. 1–6. [Google Scholar]

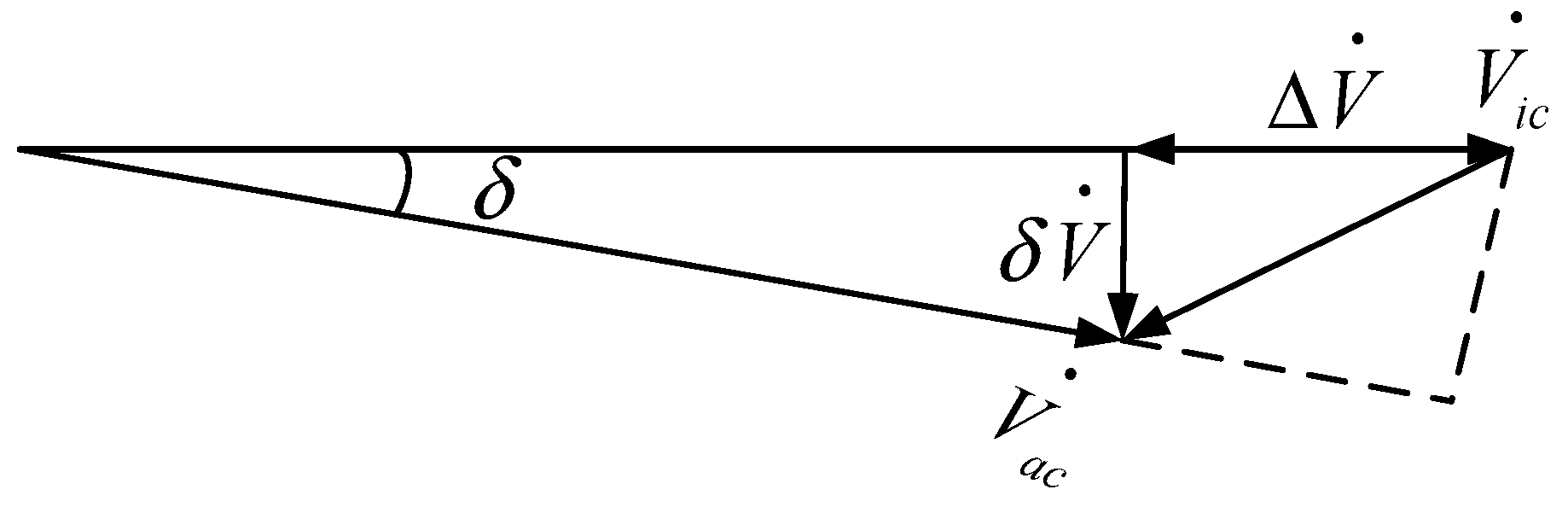


| Type of Line | R (Ω/km) | X (Ω/km) | R/X |
|---|---|---|---|
| Line for the low-voltage | 0.642 | 0.083 | 7.7 |
| Line for the medium-voltage | 0.161 | 0.190 | 0.85 |
| Line for the high-voltage | 0.06 | 0.191 | 0.31 |
| Subsystem | Parameter | Value |
|---|---|---|
| AC sub-grid | Rated power PacN | 50 kW |
| RMS rated voltage (phase to ground) | 220 V | |
| Droop coefficient mac | 0.002 V/W | |
| Filter capacitance | 220 μF | |
| Filter inductance | 5 mH | |
| IC | Capacitor on DC side | 4700 μF |
| Filter inductance | 3 mH | |
| DC sub-grid | Rated power PdcN | 50 kW |
| Rated voltage | 700 V | |
| Droop coefficient mdc | 0.002 V/W |
| THD (%) | Vacd (V) | |
|---|---|---|
| Before injection | 0.05 | 308 |
| After injection | 0.56 | 308 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Deng, C.; Li, G. Control Strategy of Interlinking Converter in Hybrid Microgrid Based on Line Impedance Estimation. Energies 2022, 15, 1664. https://doi.org/10.3390/en15051664
Wang C, Deng C, Li G. Control Strategy of Interlinking Converter in Hybrid Microgrid Based on Line Impedance Estimation. Energies. 2022; 15(5):1664. https://doi.org/10.3390/en15051664
Chicago/Turabian StyleWang, Can, Can Deng, and Guiyuan Li. 2022. "Control Strategy of Interlinking Converter in Hybrid Microgrid Based on Line Impedance Estimation" Energies 15, no. 5: 1664. https://doi.org/10.3390/en15051664
APA StyleWang, C., Deng, C., & Li, G. (2022). Control Strategy of Interlinking Converter in Hybrid Microgrid Based on Line Impedance Estimation. Energies, 15(5), 1664. https://doi.org/10.3390/en15051664






