Technical and Economic Assessment of Supermarket and Power Substation Waste Heat Integration into Existing District Heating Systems
Abstract
:1. Introduction
- Development of the detailed hourly model based on the pinch analysis for different waste heat sources: Supermarkets and power transformers.
- Optimization of waste heat connection to the district heating network by considering different connection pipe diameters and the calculation of system cost in correlation to the distance between the waste heat source and district heating network.
- Cost analysis of optimal connection and comparison of waste heat sources with respect to temperature regimes in the network.
2. Materials and Methods
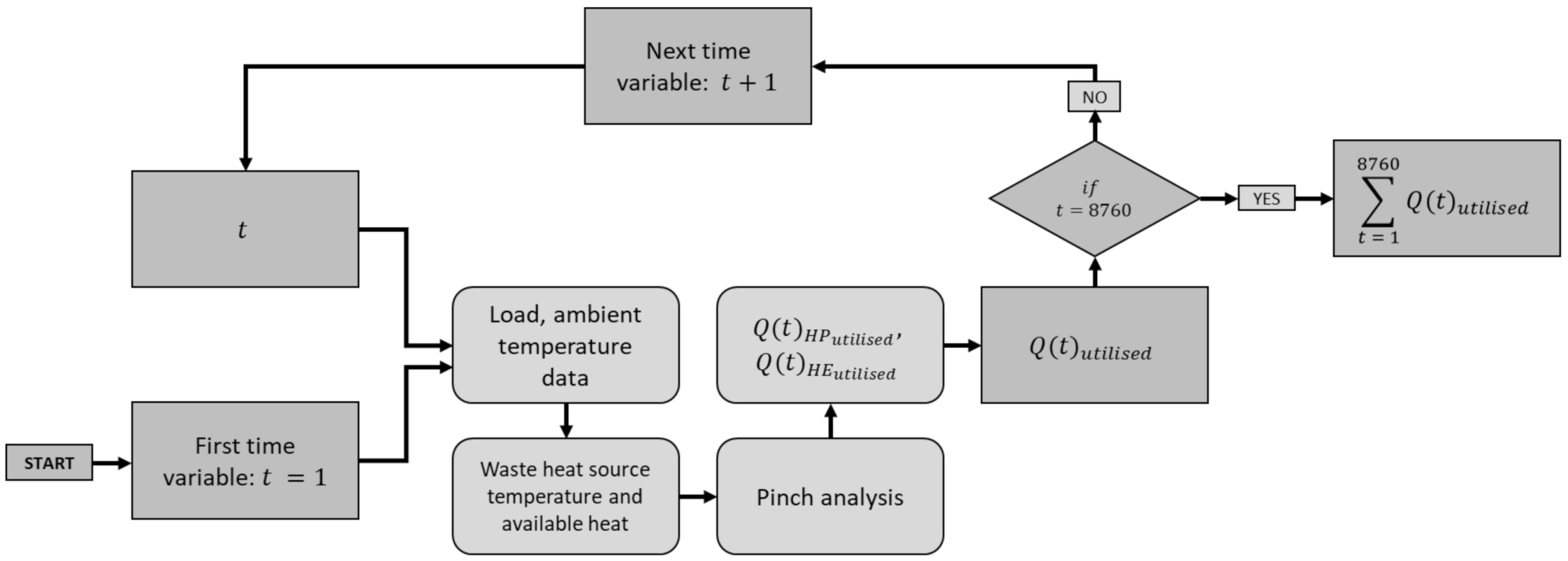
2.1. Time Variable Approach
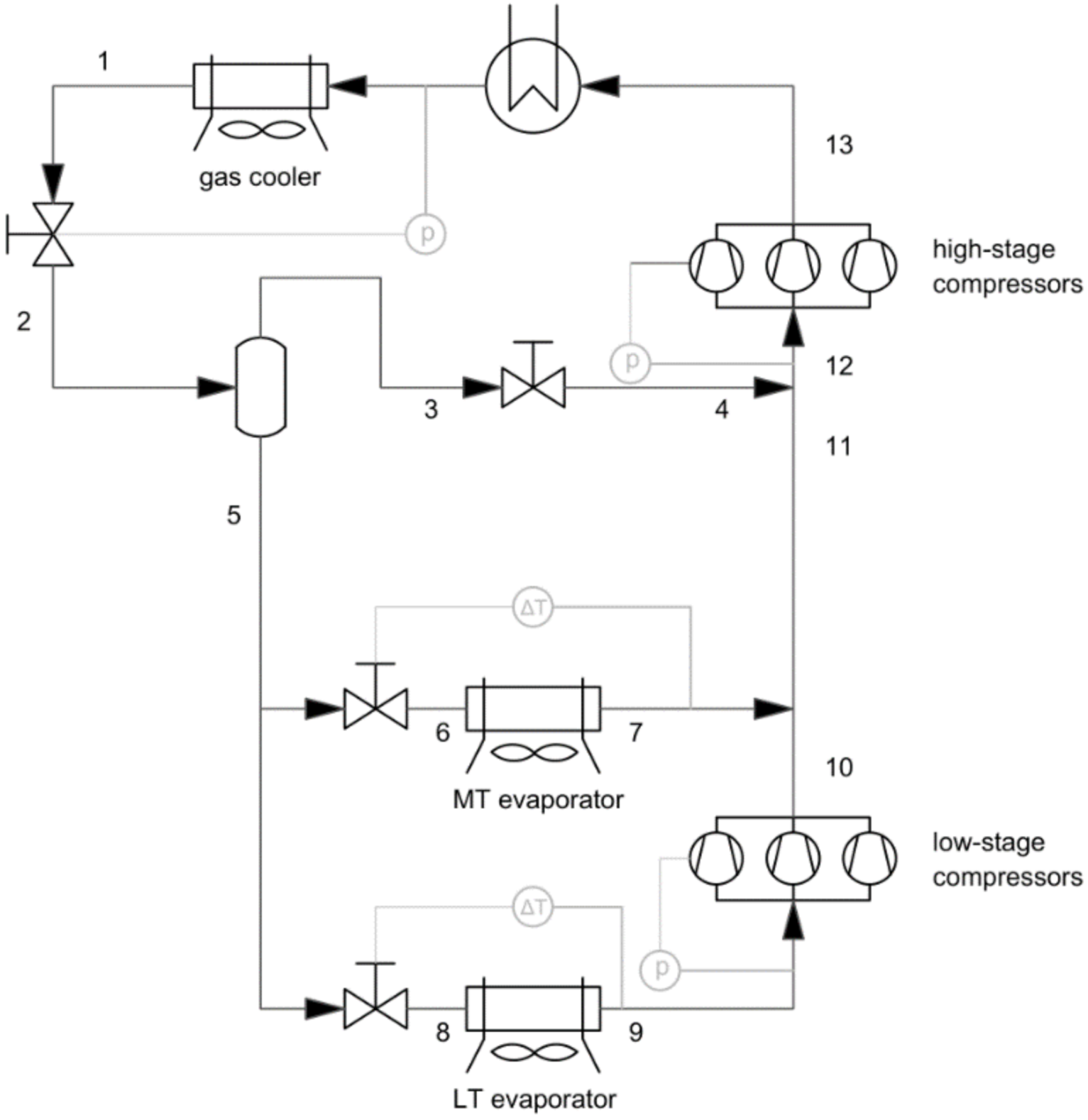
2.2. Supermarket Refrigeration
- Temperature levels of waste heat source (points 1 and 13);
- Available waste heat load (enthalpy difference between points 1 and 13);
- Coefficient of performance (COP) of refrigeration cycle.
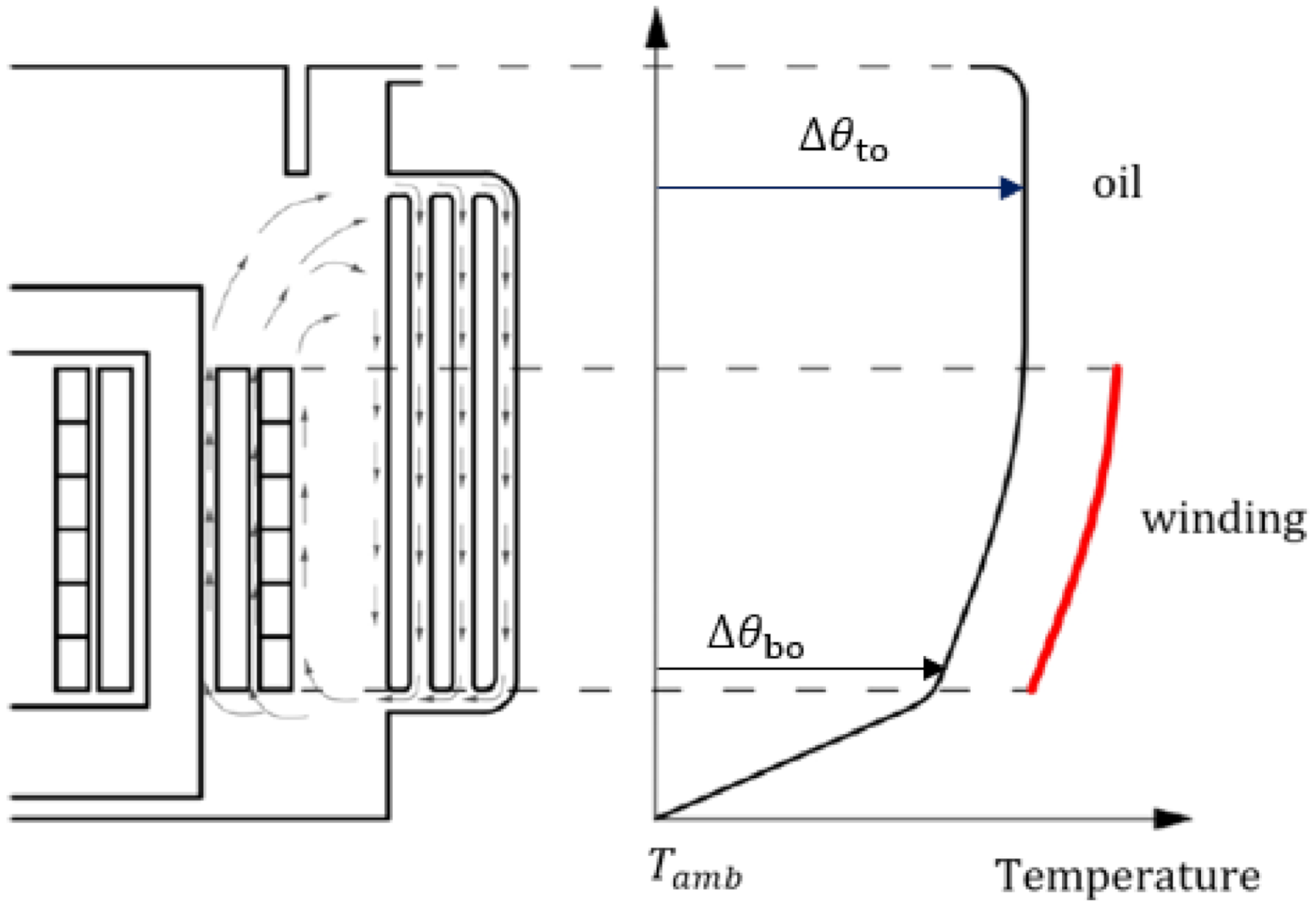
2.3. Power Substation
2.4. Pinch Method Analysis
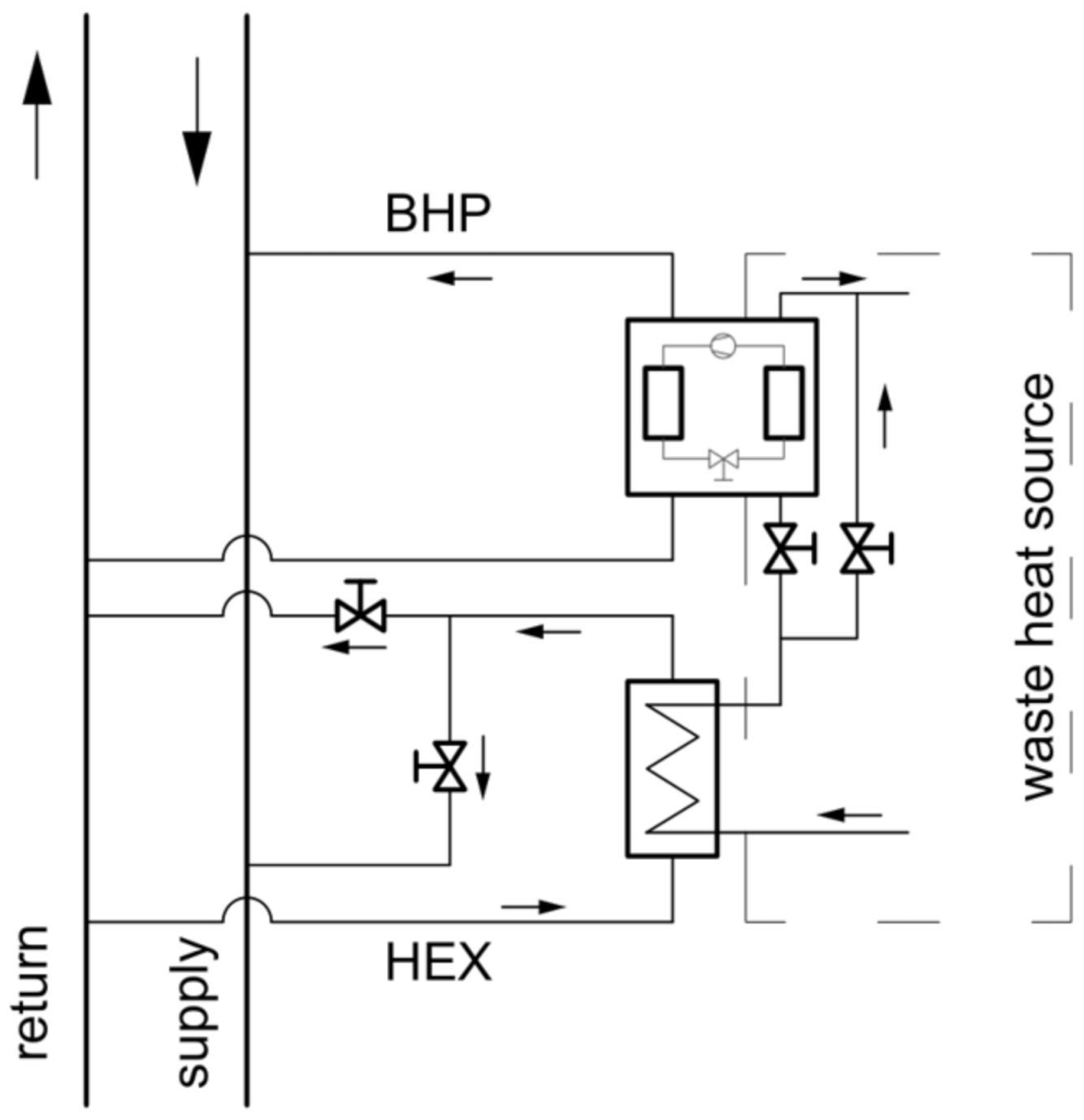
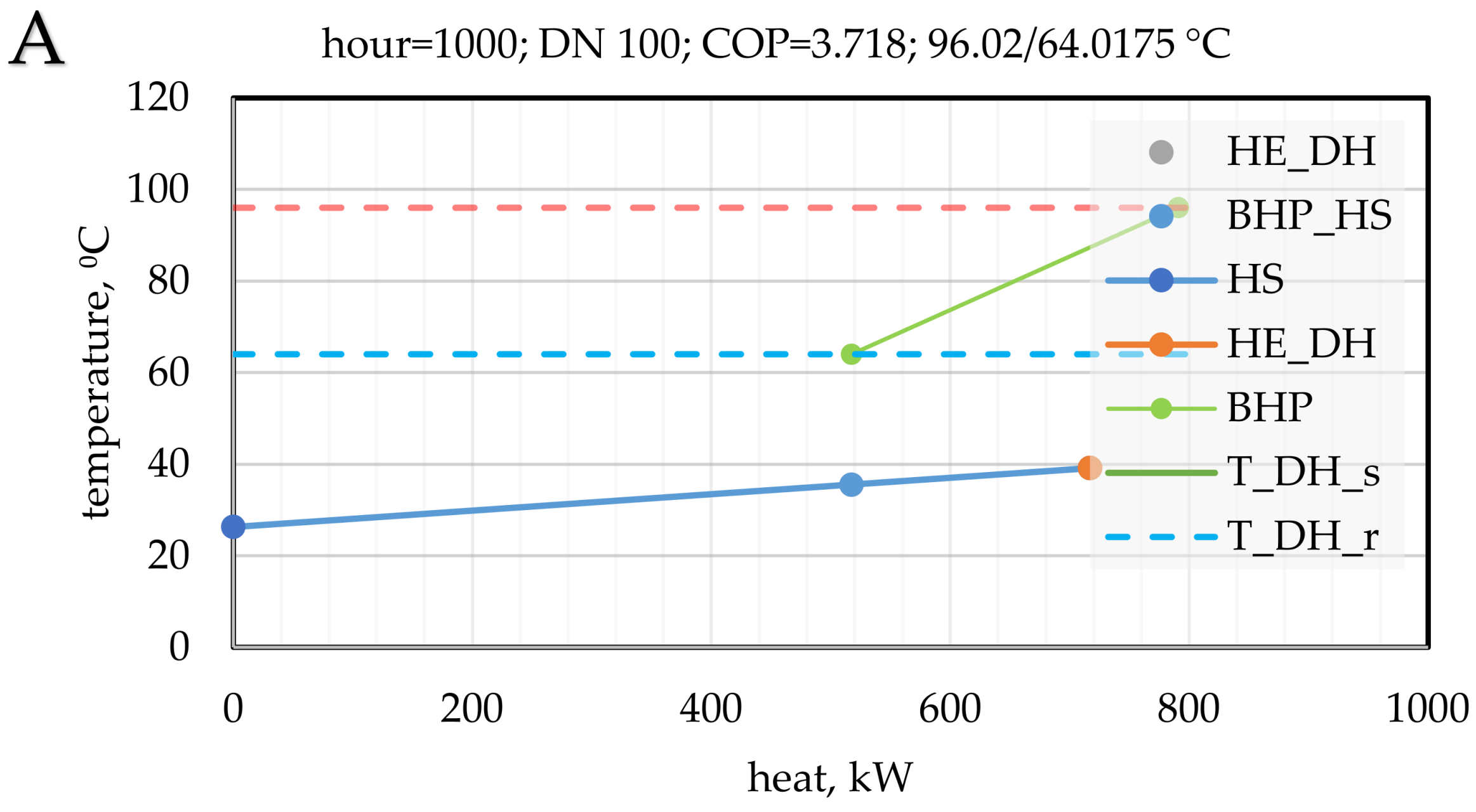
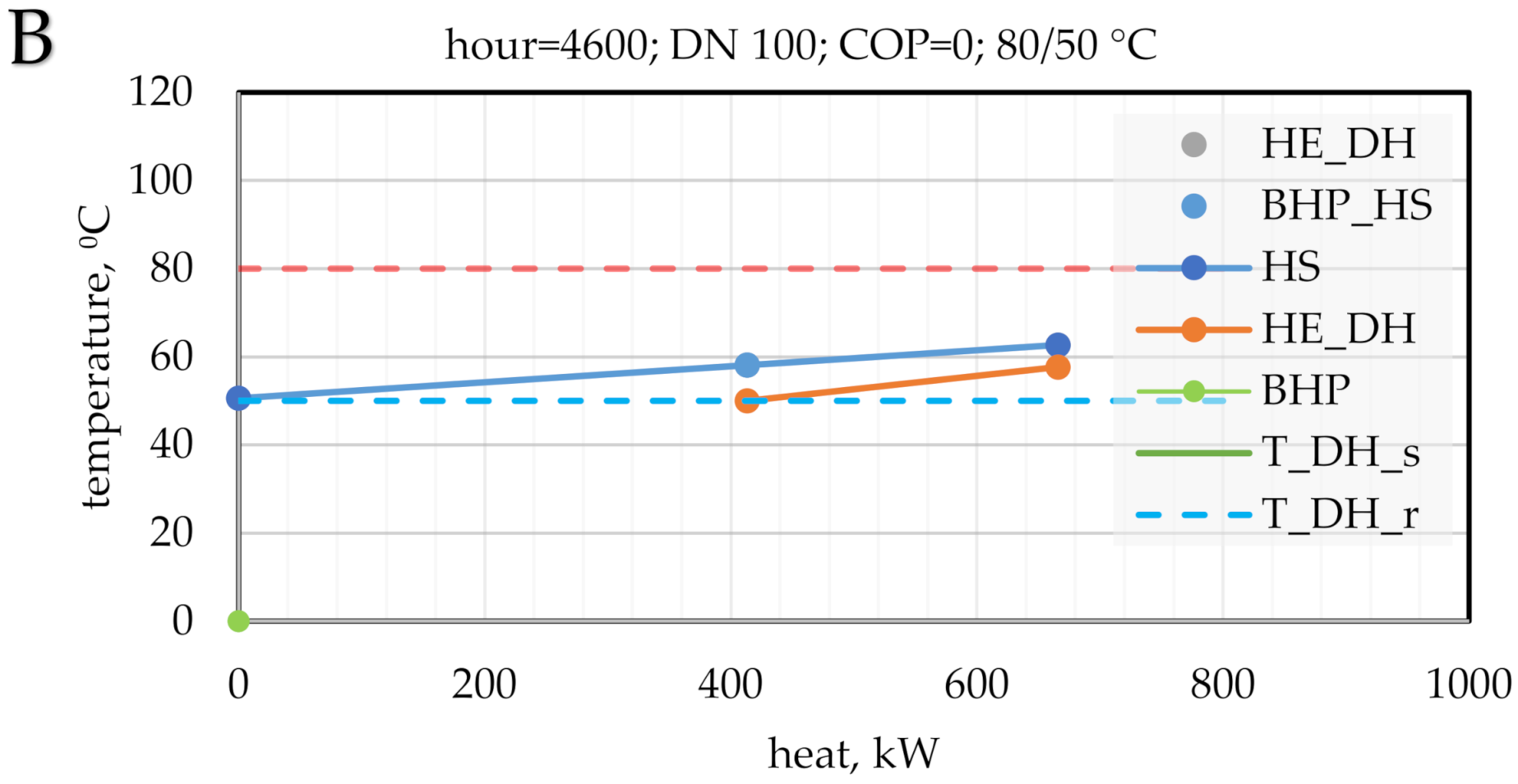
2.5. Booster Heat Pump
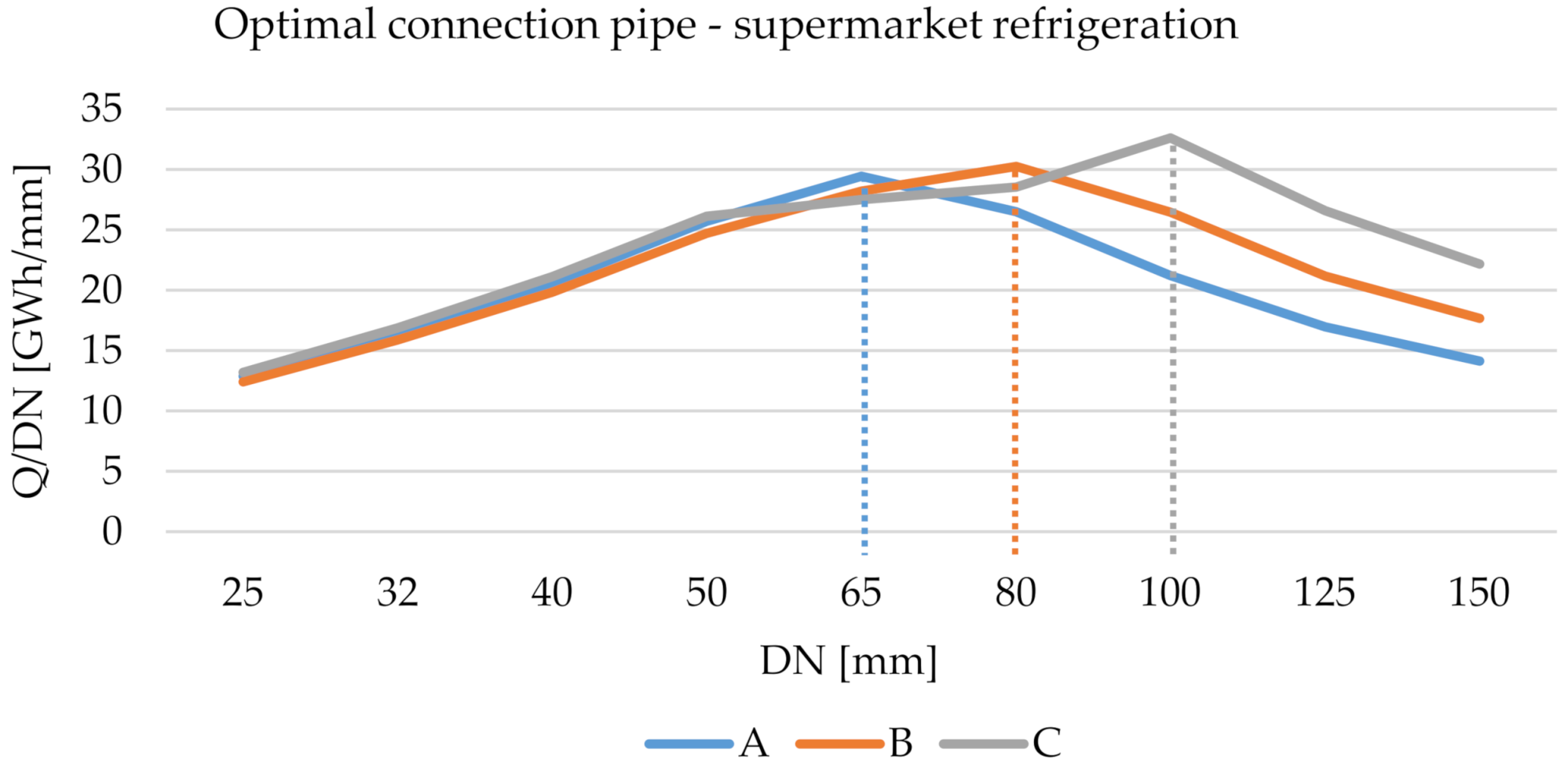
2.6. Connection Pipe Diameter Analysis
2.7. Techno-Economic Analysis
2.8. Case Study and Input Data
3. Results
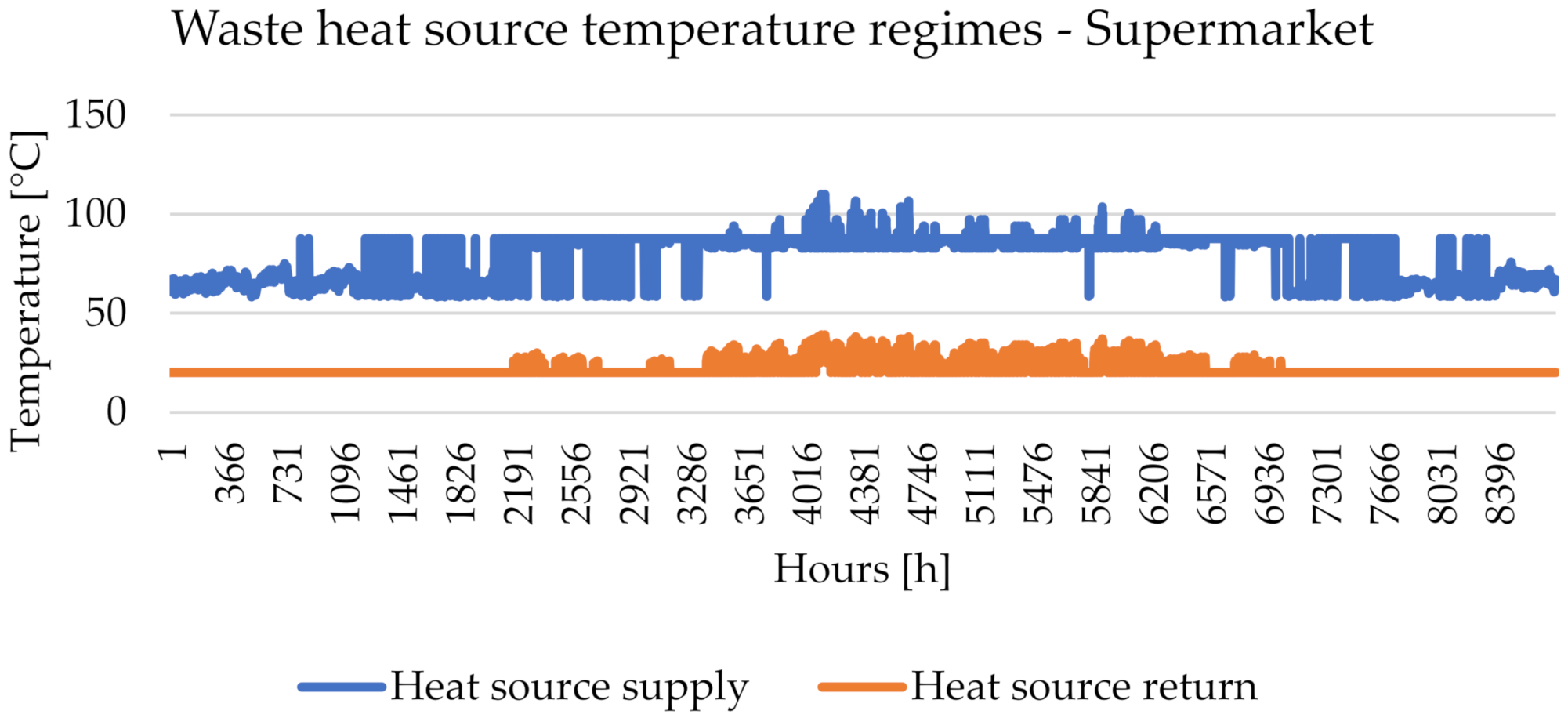
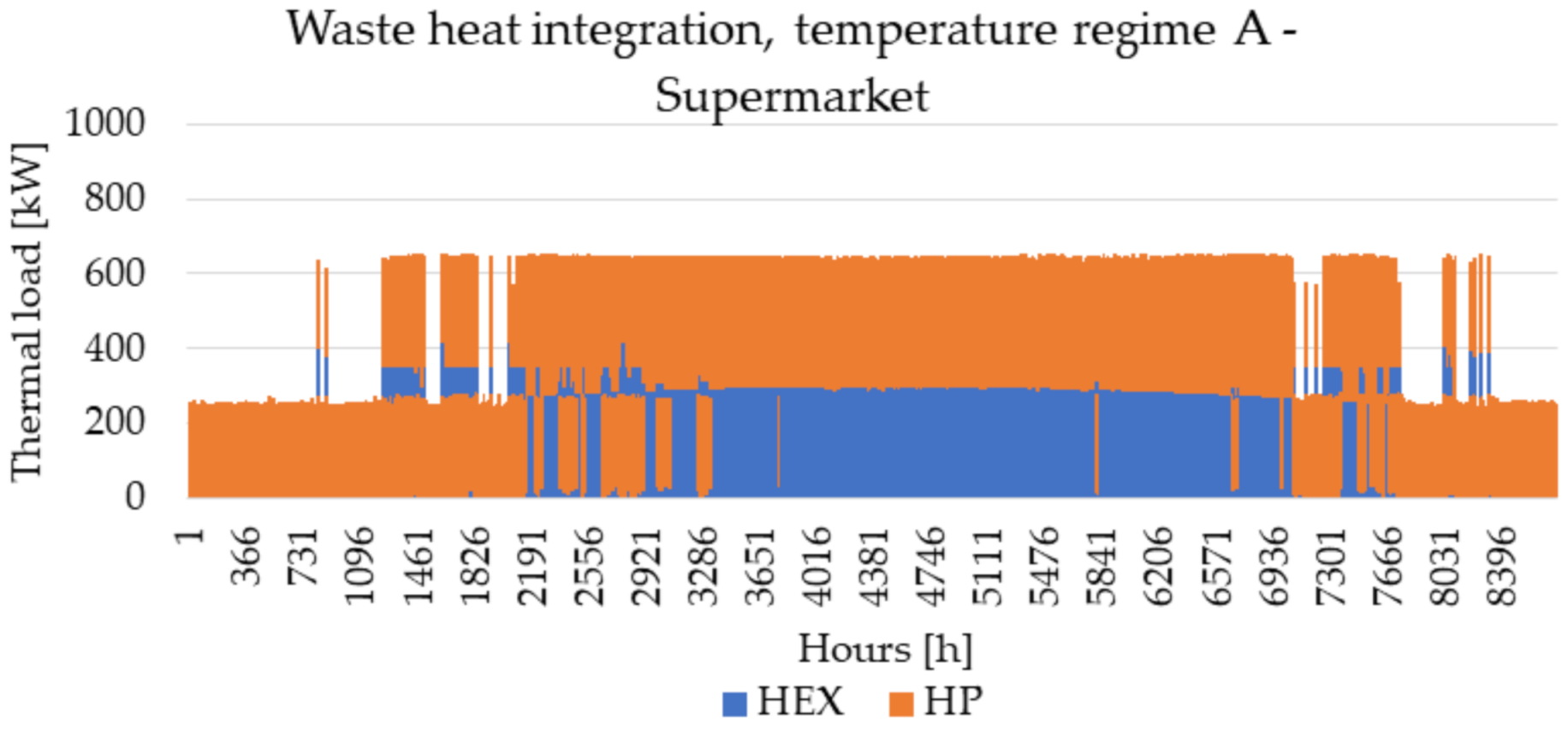
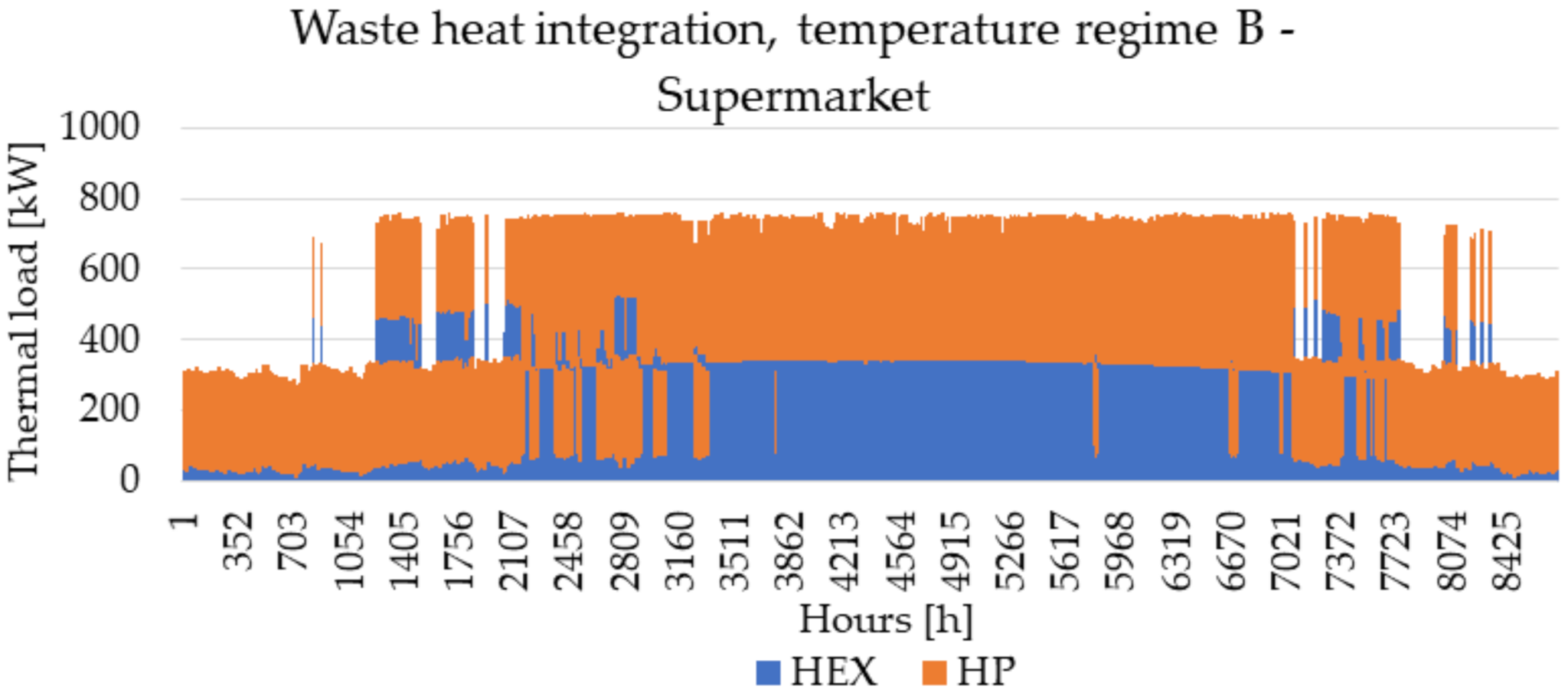
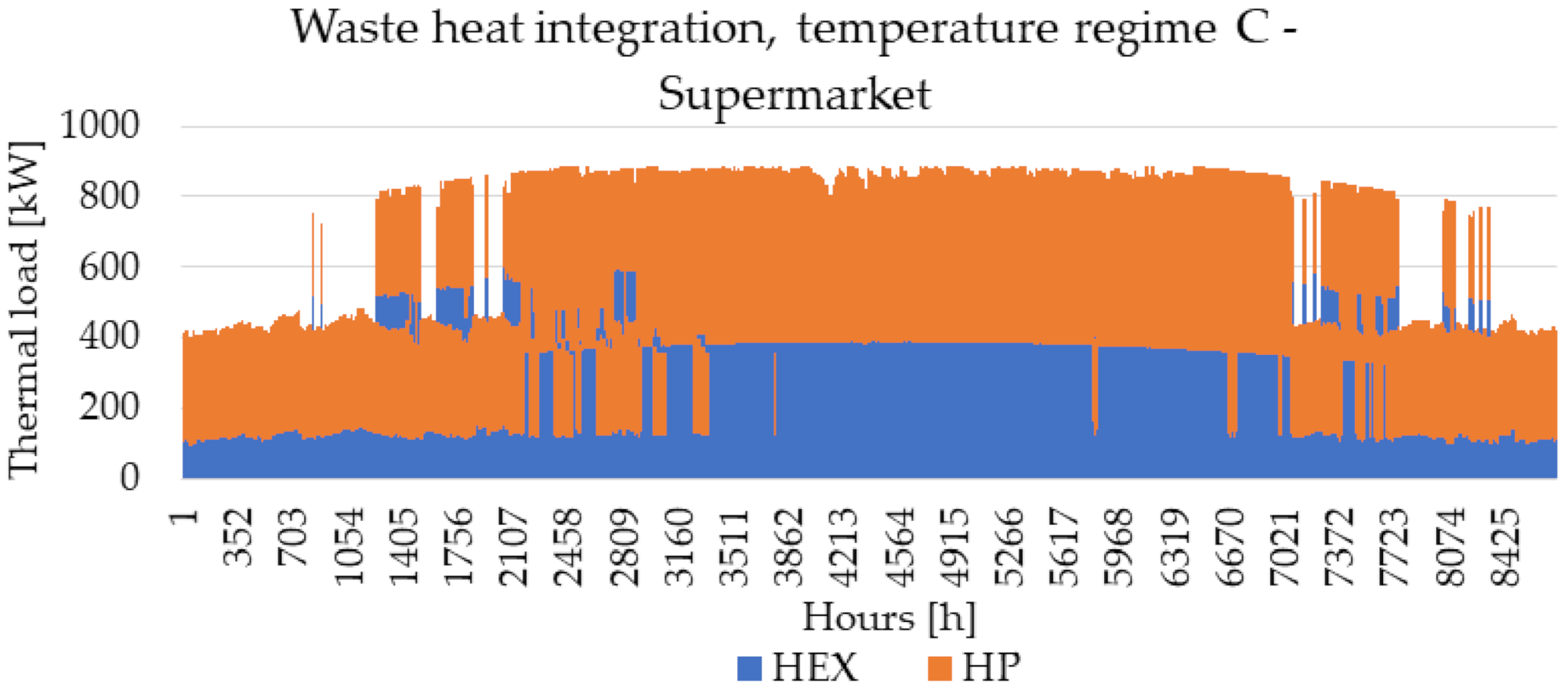
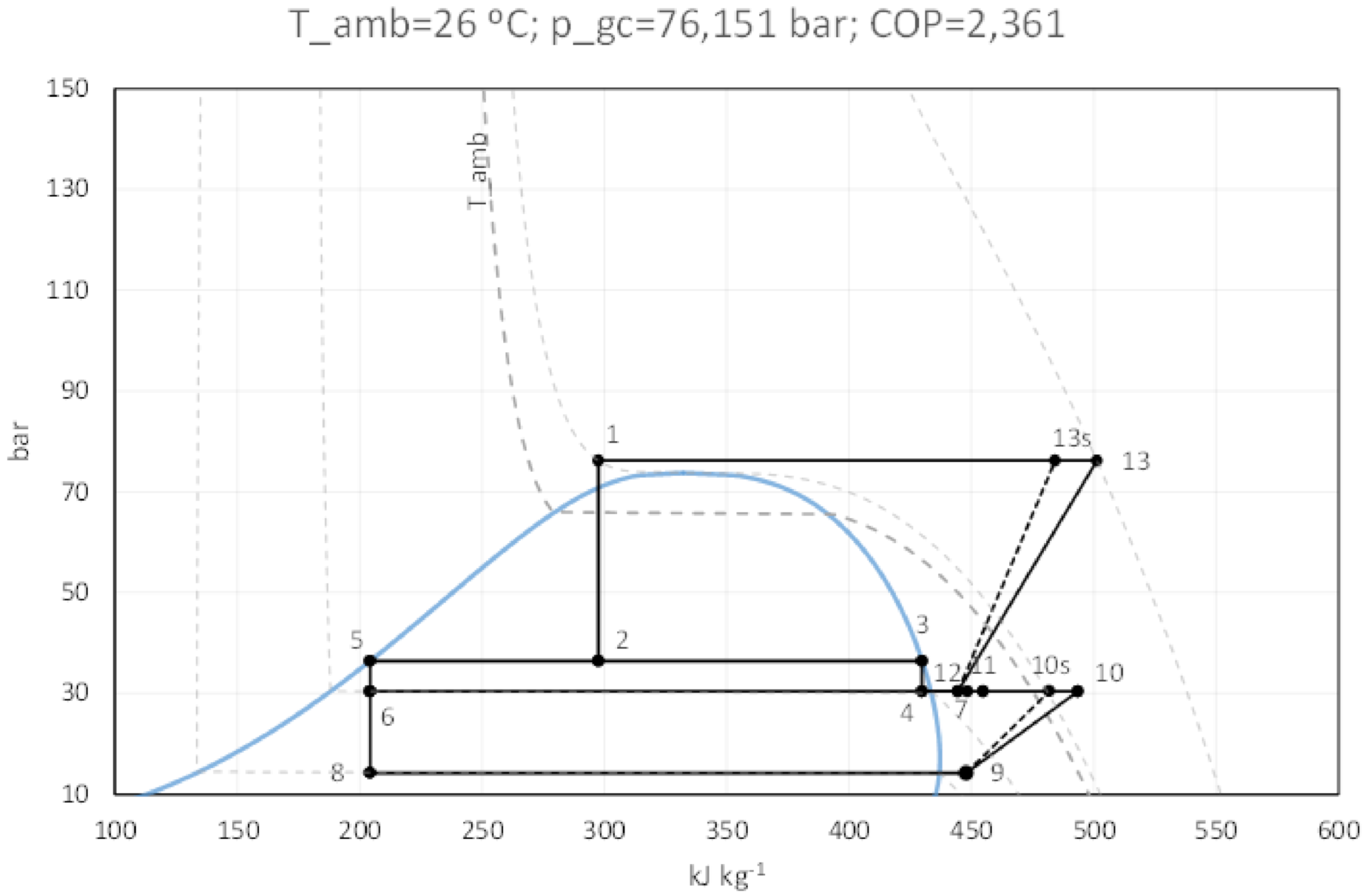
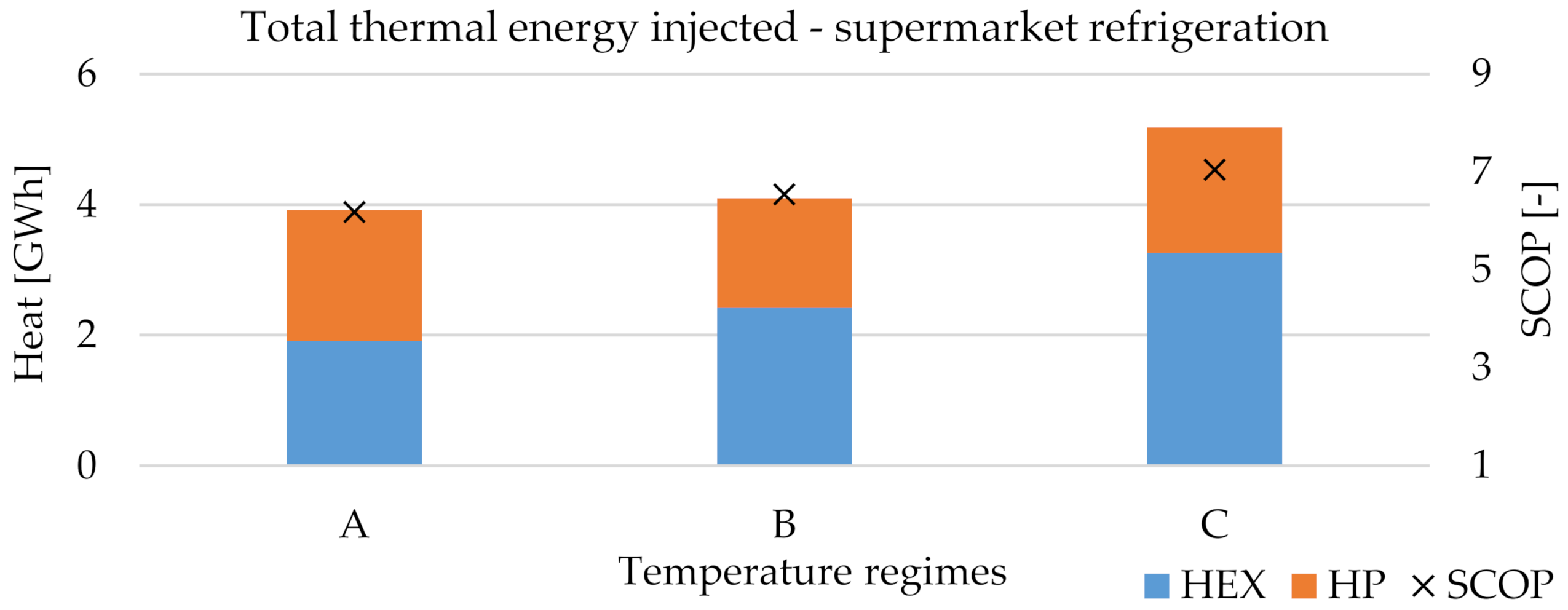
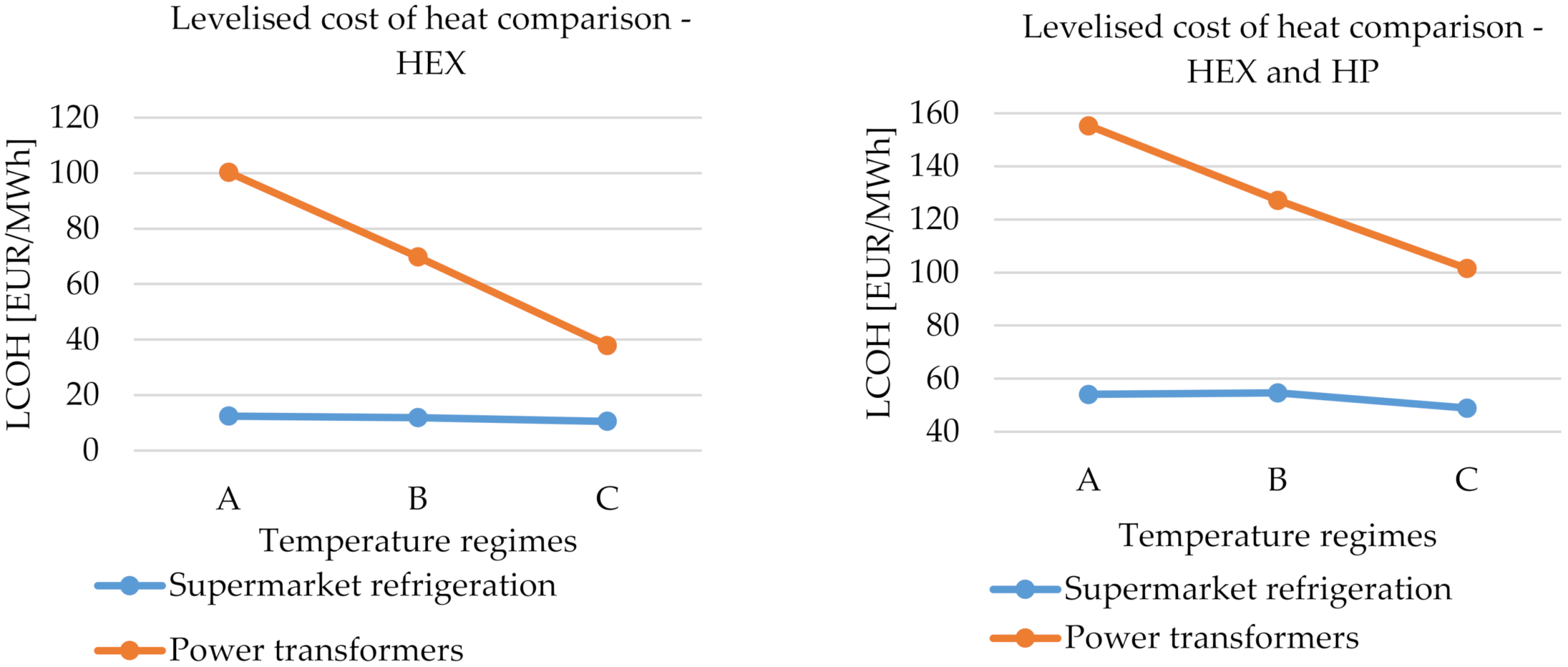
3.1. Supermarket Refrigeration
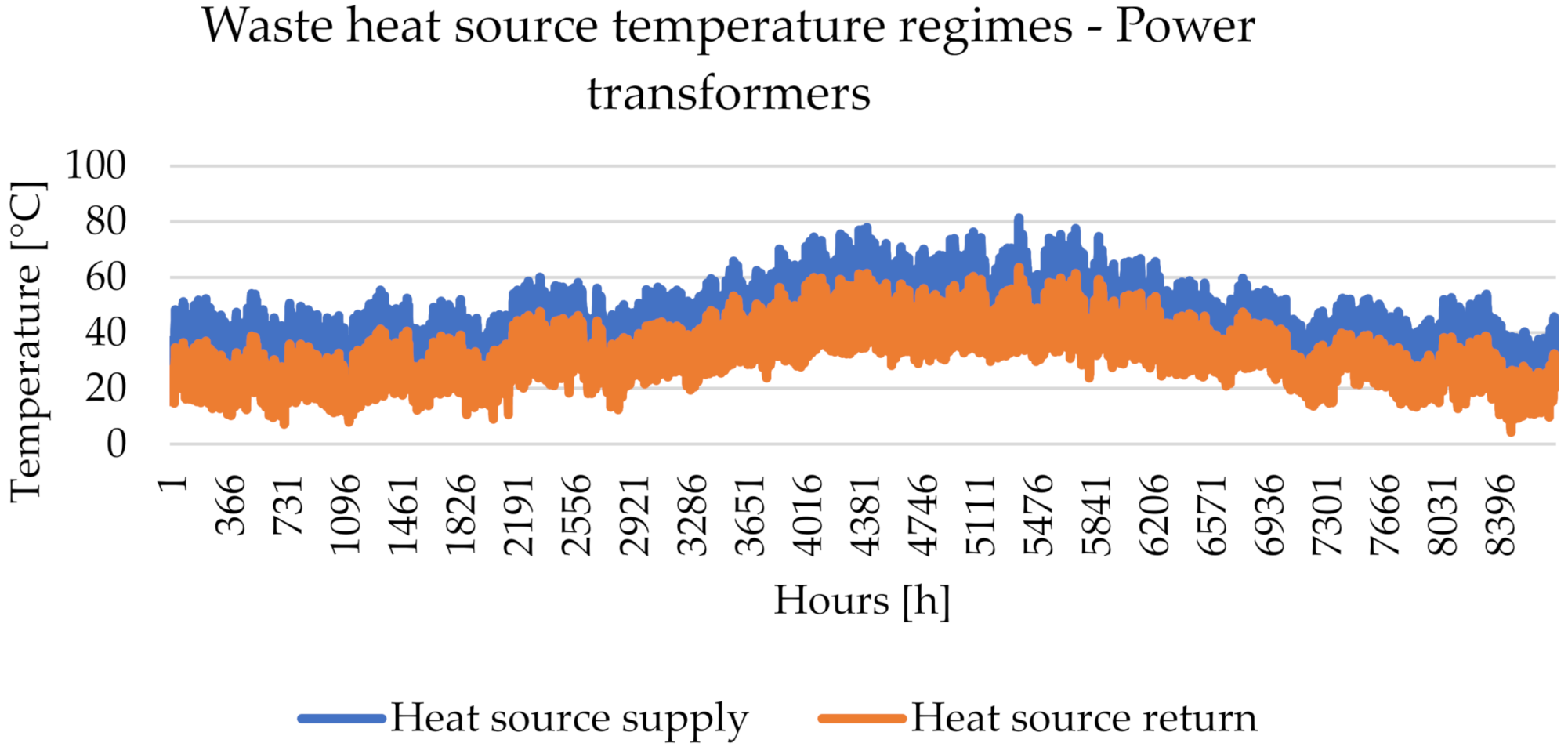
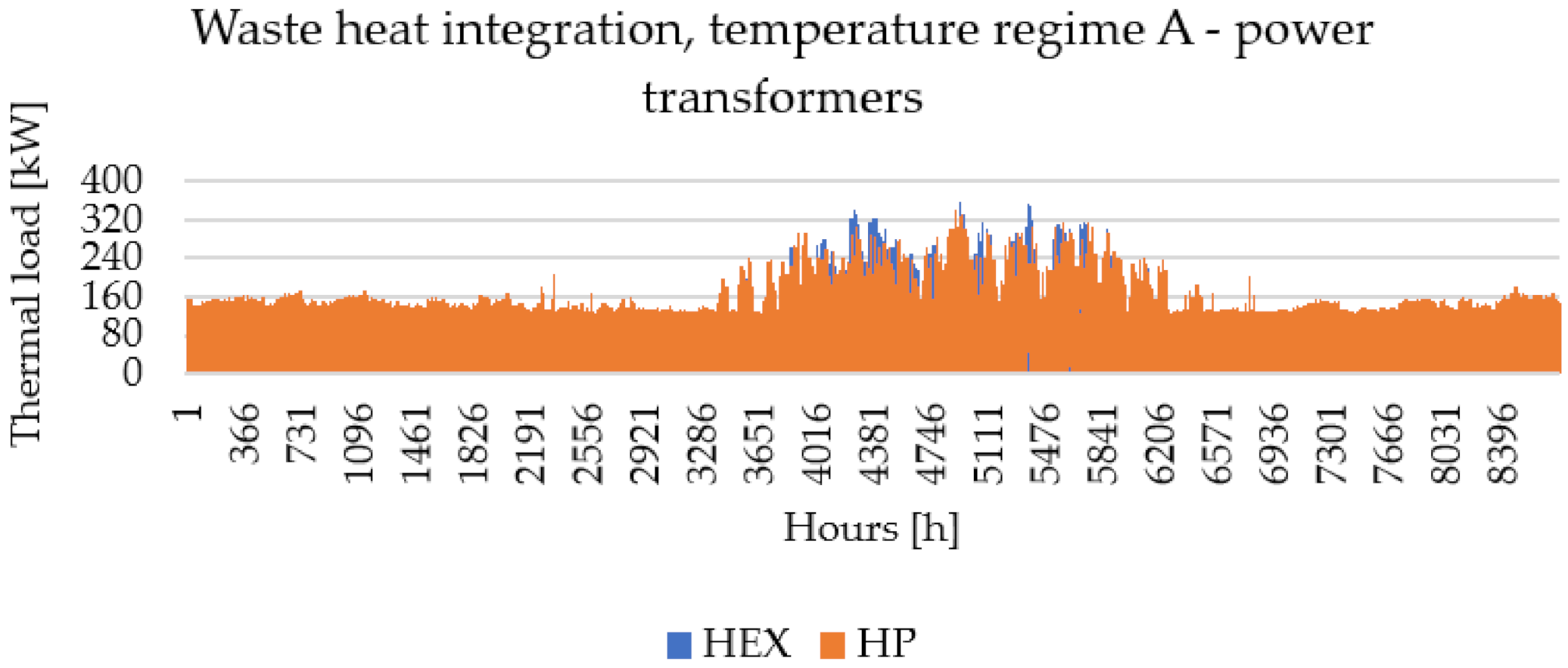
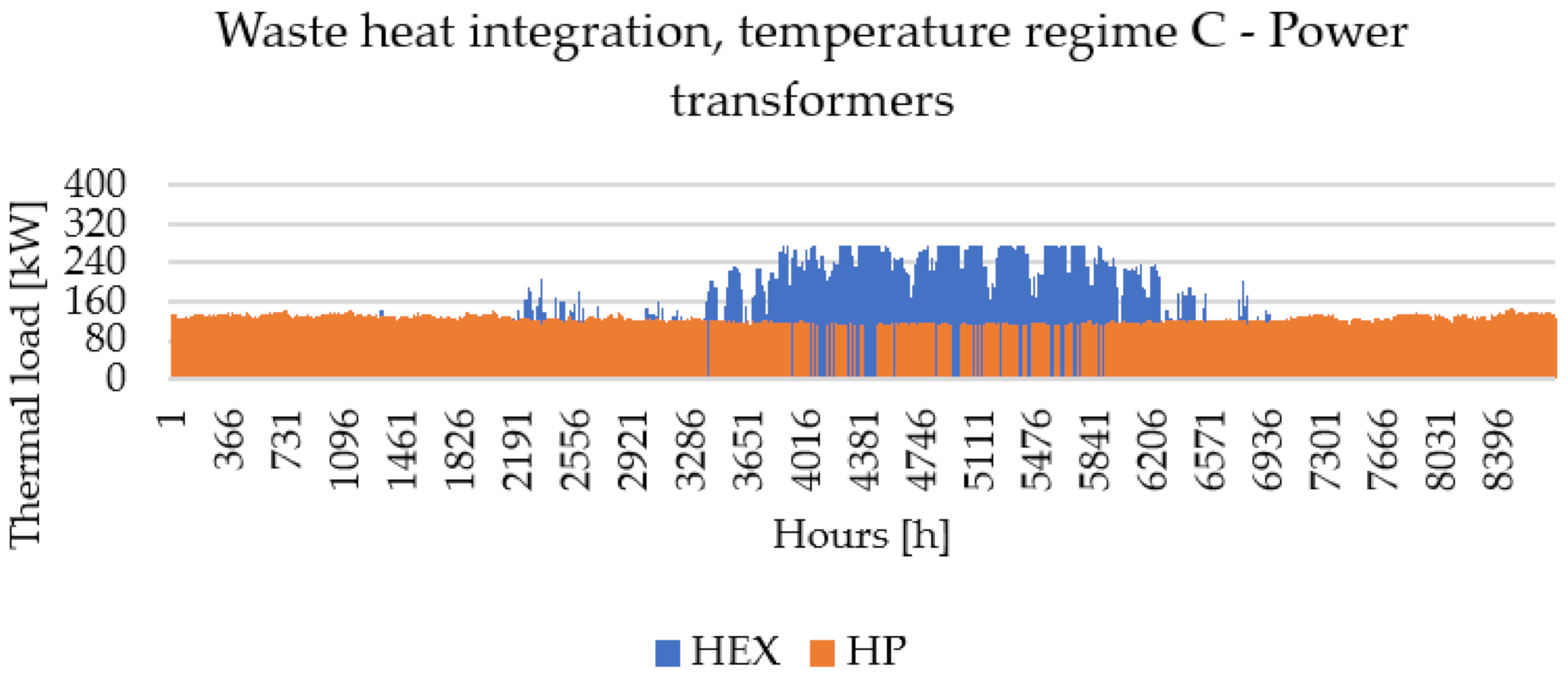
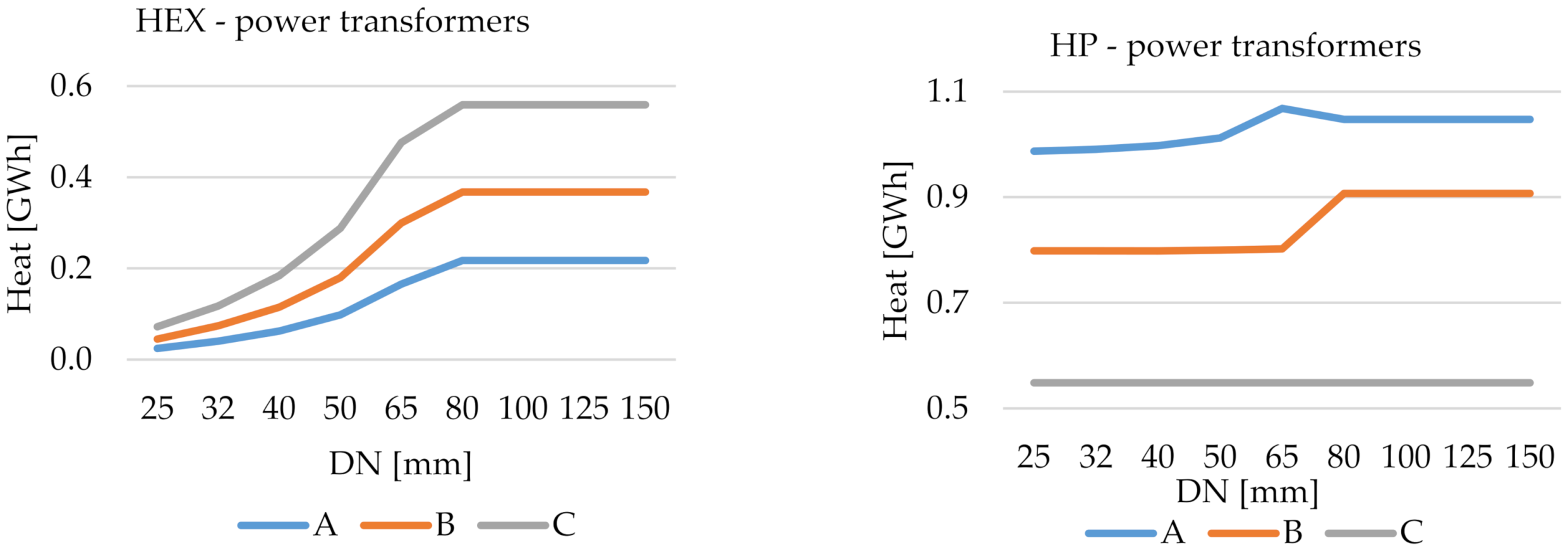
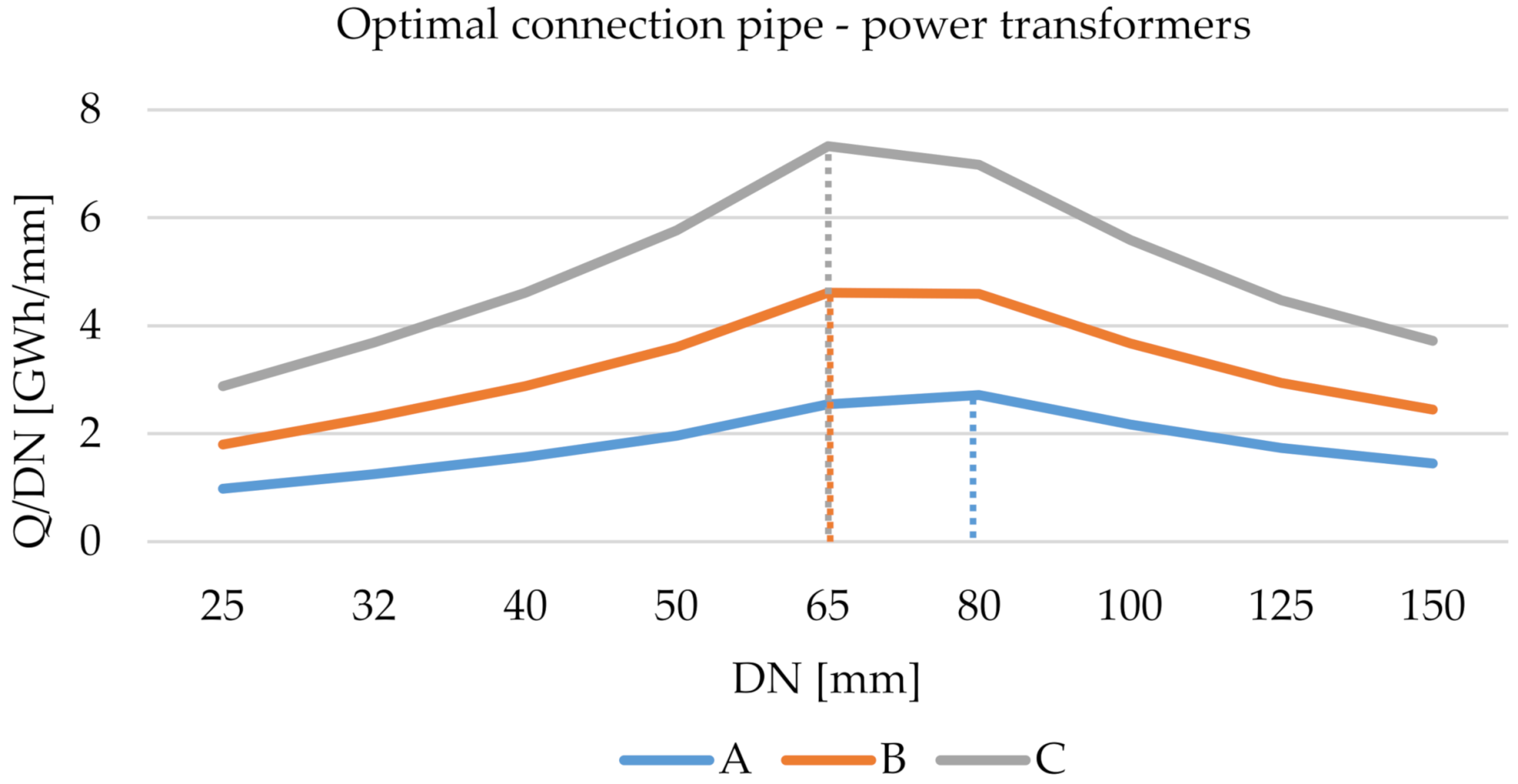
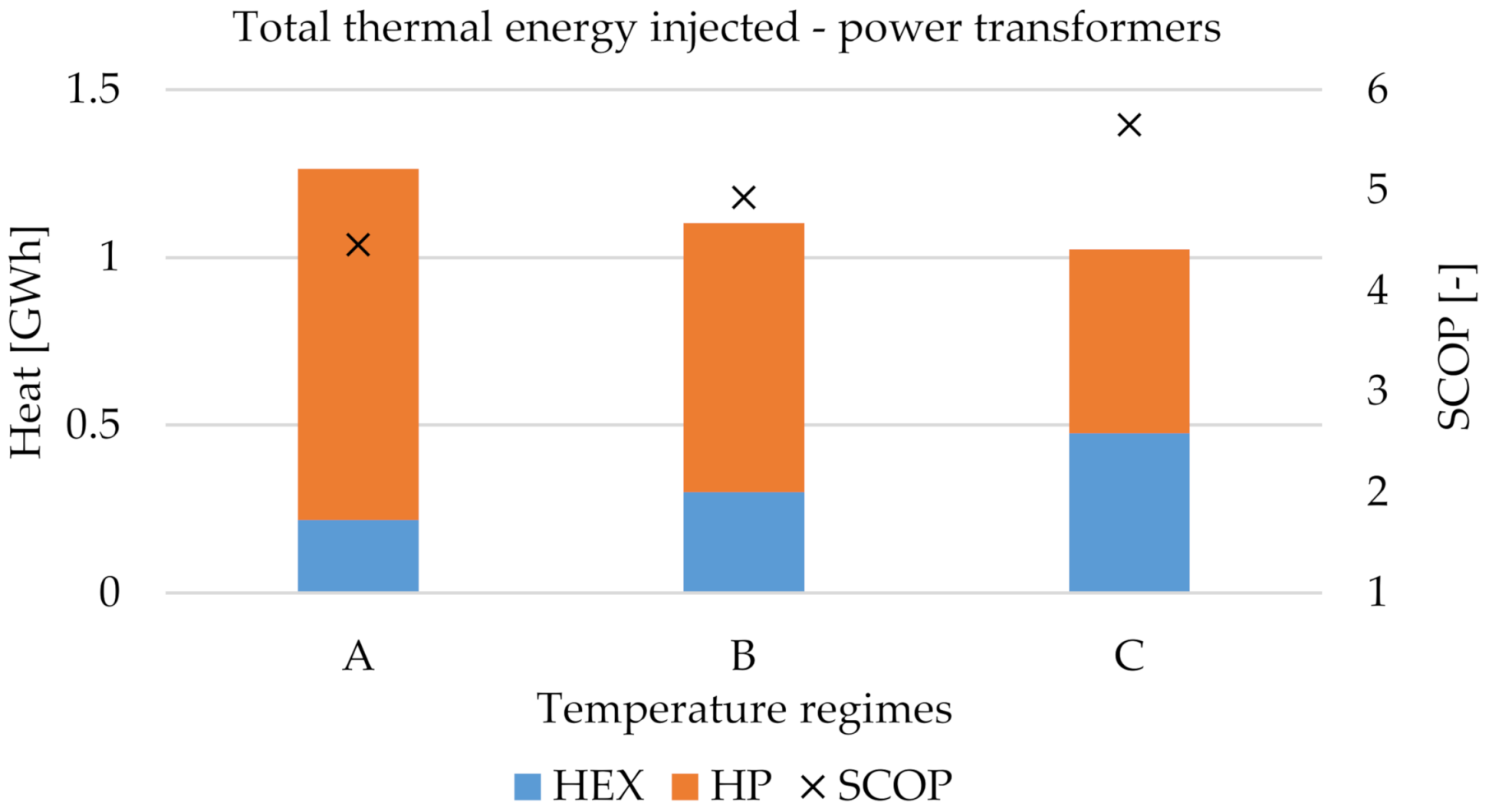
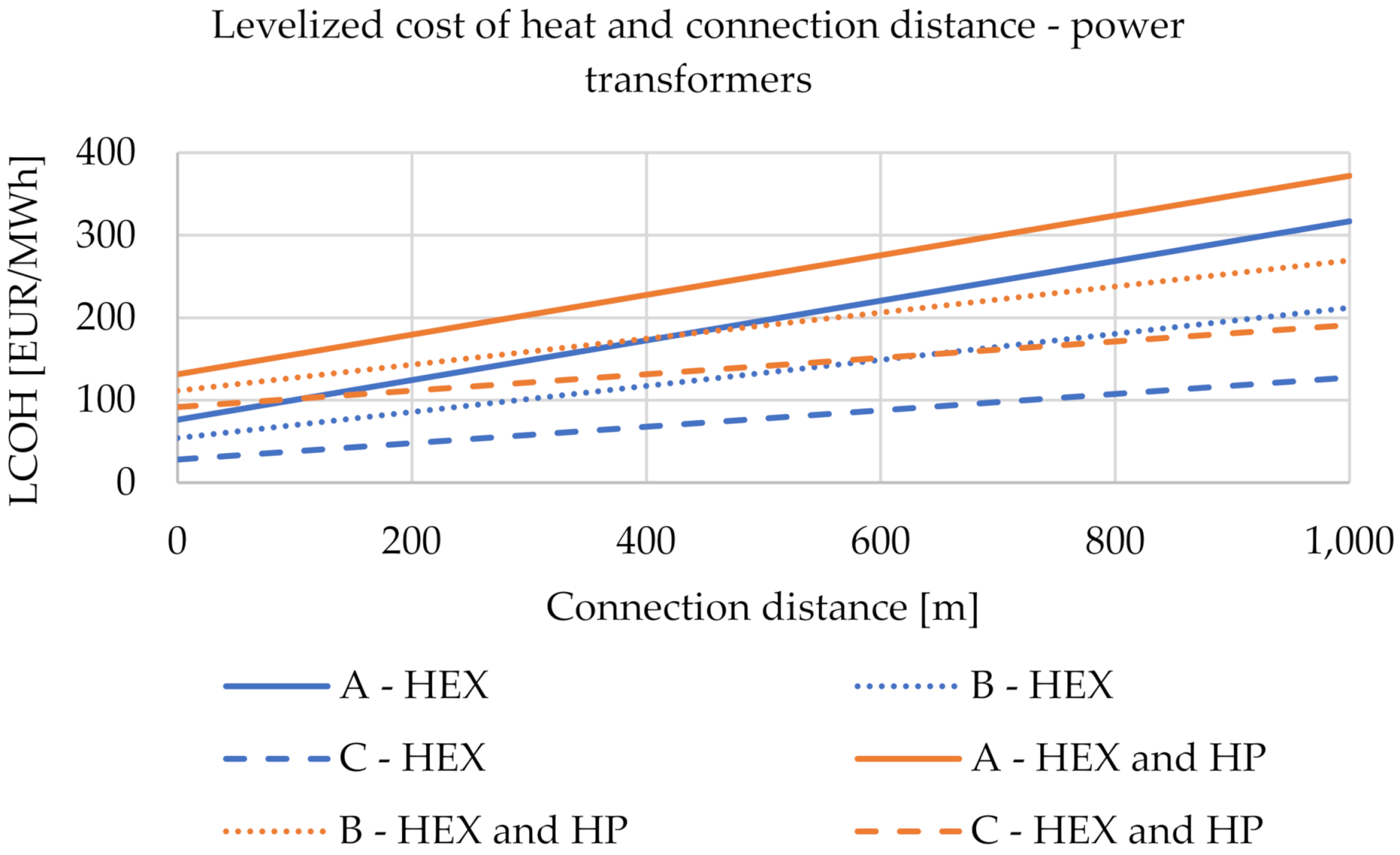
3.2. Power Substations
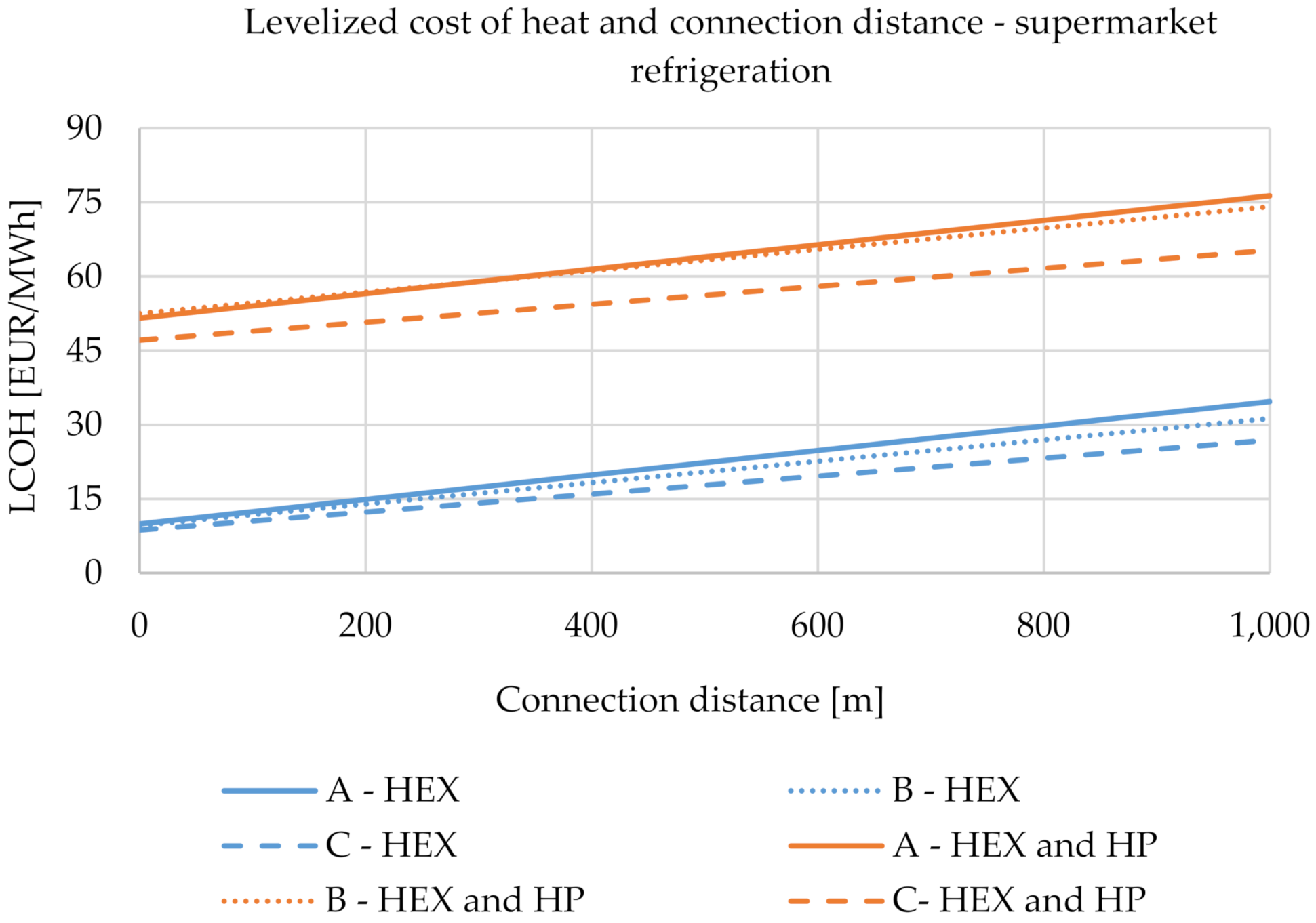
3.3. Techno-Economic Analysis
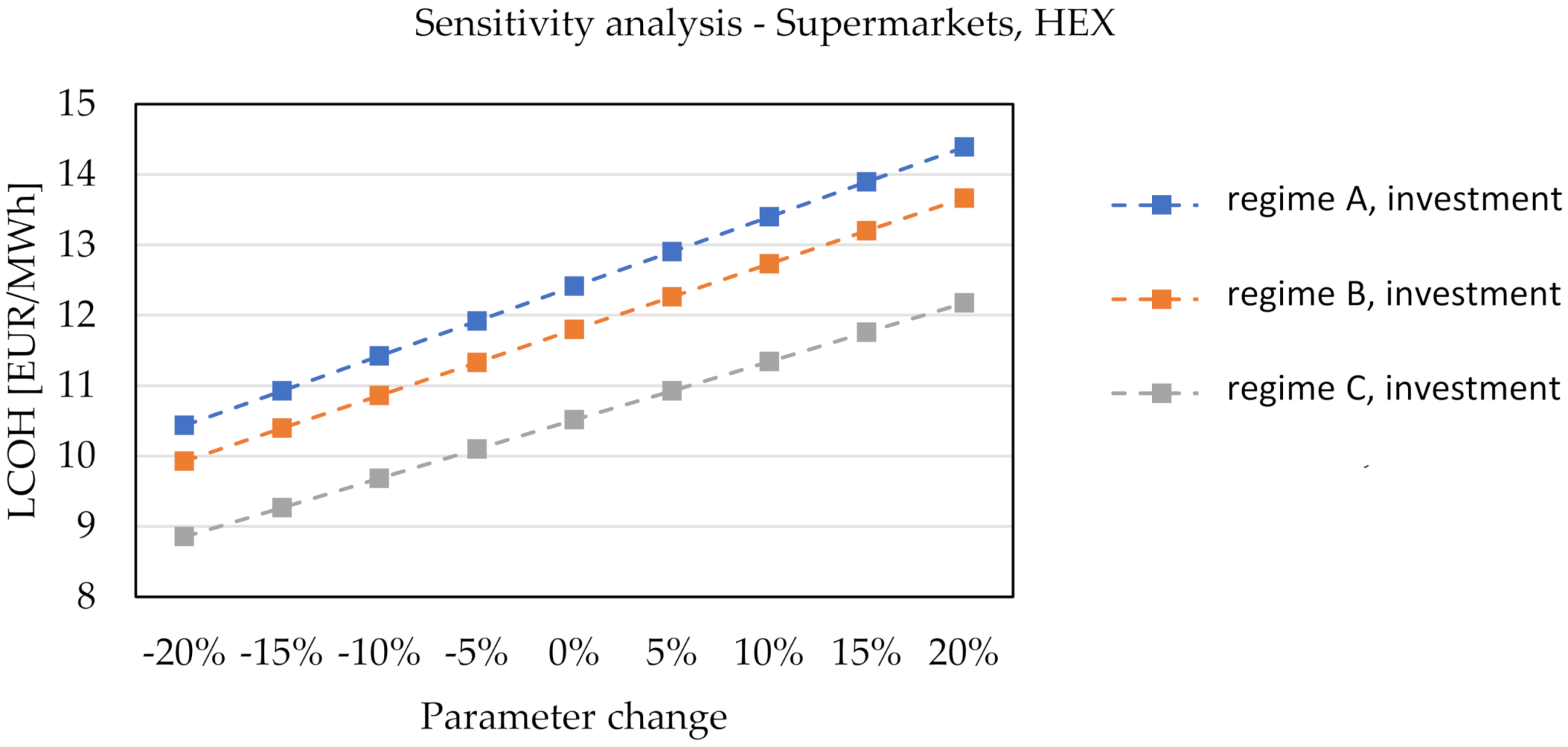
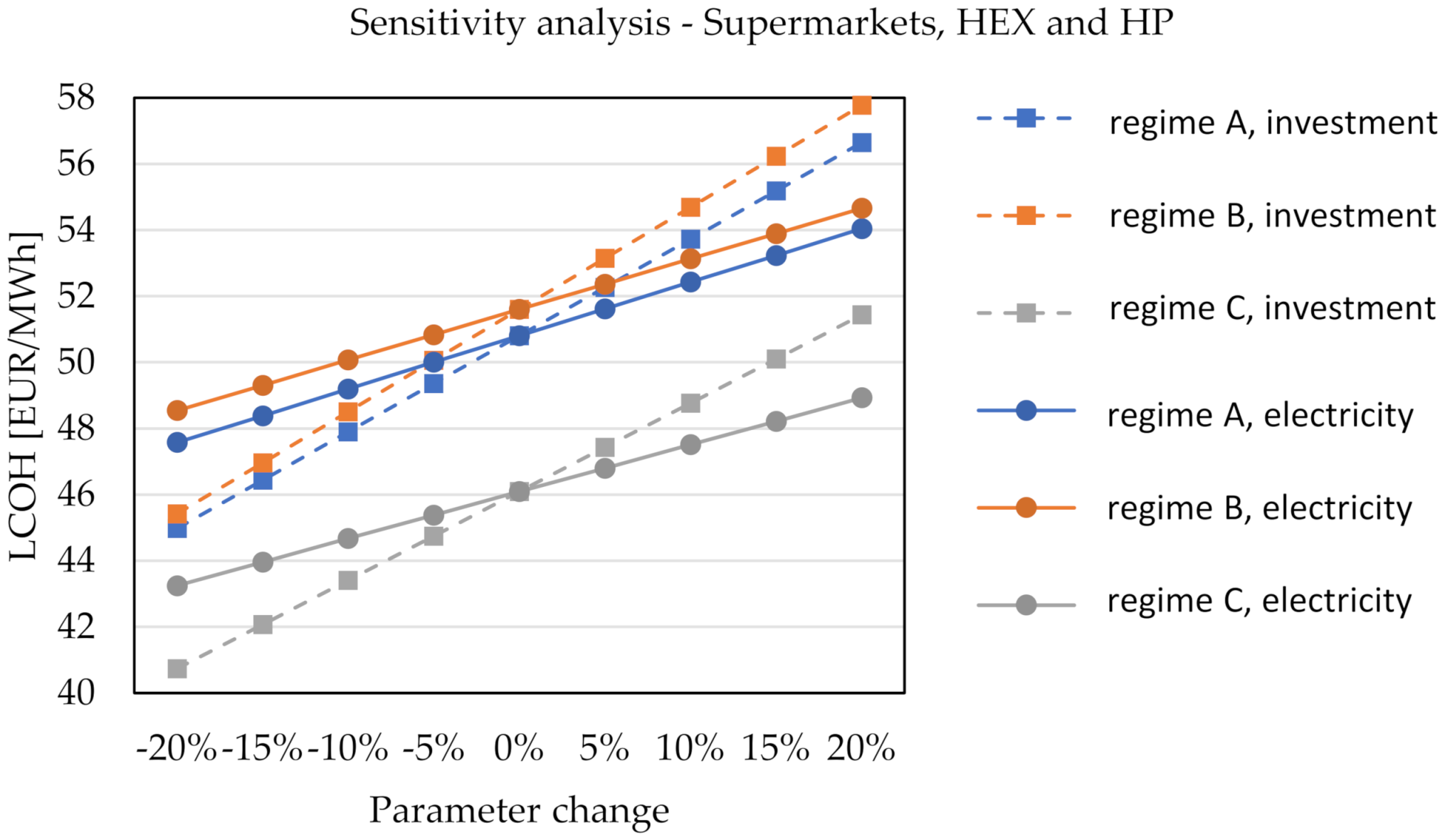
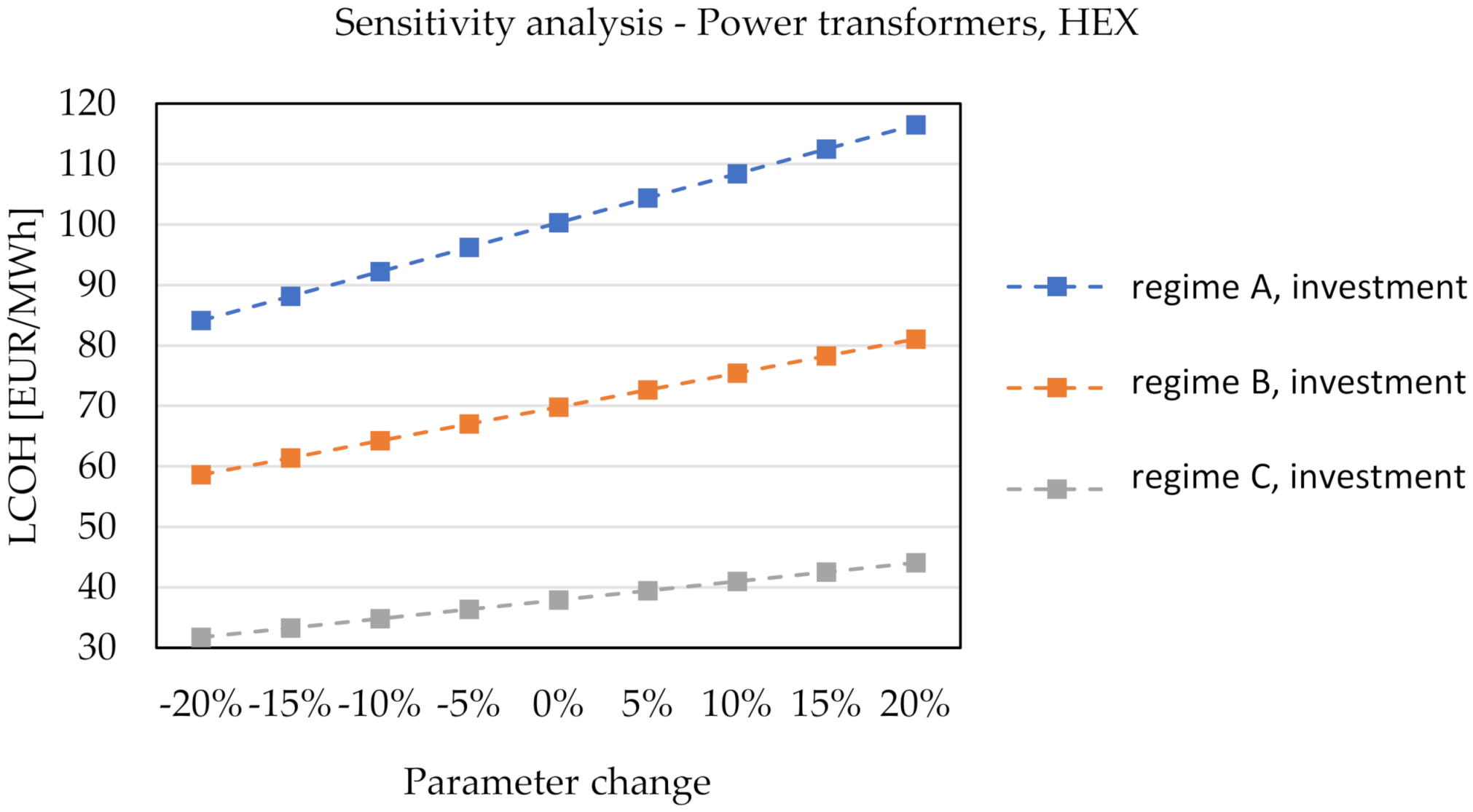
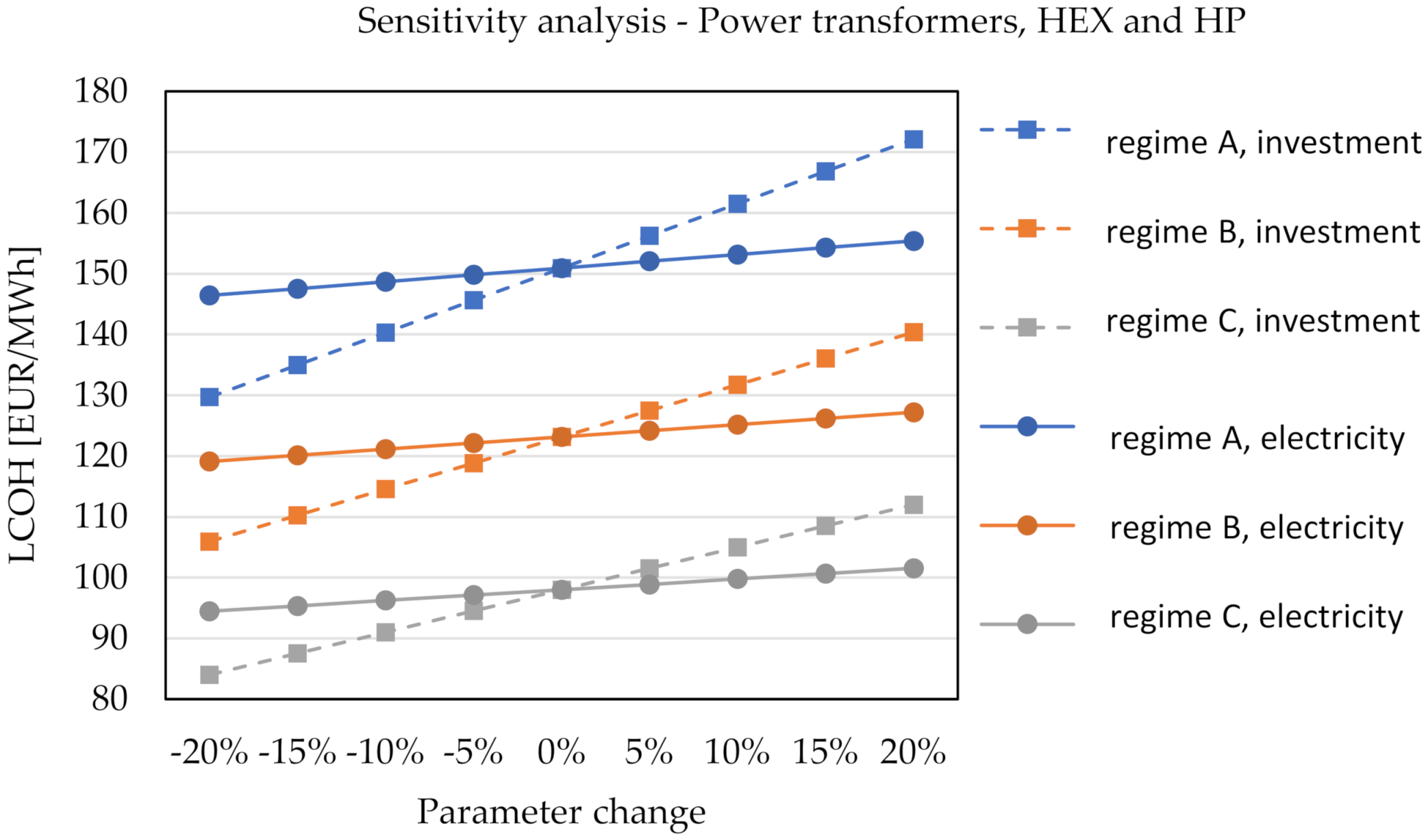
3.4. Sensitivity Analysis
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Frederiksen, S.; Werner, S. District Heating and Cooling, 1st ed.; Studentlitteratur AB: Lund, Sweden, 2013. [Google Scholar]
- Mikulandrić, R.; Krajačić, G.; Duić, N.; Khavin, G.; Lund, H.; Mathiesen, B.V. Performance Analysis of a Hybrid District Heating System: A Case Study of a Small Town in Croatia. J. Sustain. Dev. Energy Water Environ. Syst. 2015, 3, 282–302. [Google Scholar] [CrossRef]
- Weiss, R.; Saastamoinen, H.; Ikäheimo, J.; Abdurafikov, R.; Sihvonen, T.; Shemeikka, J. Decarbonised District Heat, Electricity and Synthetic Renewable Gas in Wind- and Solar-Based District Energy Systems. J. Sustain. Dev. Energy Water Environ. Syst. 2021, 9, 2. [Google Scholar] [CrossRef]
- Sorknæs, P.; Østergaard, P.A.; Thellufsen, J.Z.; Lund, H.; Nielsen, S.; Djørup, S.; Sperling, K. The benefits of 4th generation district heating in a 100% renewable energy system. Energy 2020, 213, 119030. [Google Scholar] [CrossRef]
- Lund, H.; Duic, N.; Østergaard, P.A.; Mathiesen, B.V. Smart energy systems and 4th generation district heating. Energy 2016, 110, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Lund, H.; Østergaard, P.A.; Chang, M.; Werner, S.; Svendsen, S.; Sorknæs, P.; Thorsen, J.E.; Hvelplund, F.; Mortensen, B.O.G.; Mathiesen, B.V.; et al. The status of 4th generation district heating: Research and results. Energy 2018, 164, 147–159. [Google Scholar] [CrossRef]
- Puschnigg, S.; Jauschnik, G.; Moser, S.; Volkova, A.; Linhart, M. A review of low-temperature sub-networks in existing district heating networks: Examples, conditions, replicability. Energy Rep. 2021, 7, 18–26. [Google Scholar] [CrossRef]
- Buffa, S.; Cozzini, M.; D’Antoni, M.; Baratieri, M.; Fedrizzi, R. 5th generation district heating and cooling systems: A review of existing cases in Europe. Renew. Sustain. Energy Rev. 2019, 104, 504–522. [Google Scholar] [CrossRef]
- Bilardo, M.; Sandrone, F.; Zanzottera, G.; Fabrizio, E. Modelling a fifth-generation bidirectional low temperature district heating and cooling (5GDHC) network for nearly Zero Energy District (nZED). Energy Rep. 2021, 7, 8390–8405. [Google Scholar] [CrossRef]
- Wirtz, M.; Kivilip, L.; Remmen, P.; Müller, D. Quantifying Demand Balancing in Bidirectional Low Temperature Networks. Energy Build. 2020, 224, 110245. [Google Scholar] [CrossRef]
- Penkovskii, A.; Stennikov, V.; Kravets, A. Bi-level modeling of district heating systems with prosumers. Energy Rep. 2020, 6, 89–95. [Google Scholar] [CrossRef]
- Postnikov, I. Methods for optimization of time redundancy of prosumer in district heating systems. Energy Rep. 2020, 6, 214–220. [Google Scholar] [CrossRef]
- Stennikov, V.; Penkovskii, A. The pricing methods on the monopoly district heating market. Energy Rep. 2020, 6, 187–193. [Google Scholar] [CrossRef]
- Østergaard, P.A.; Andersen, A.N. Booster heat pumps and central heat pumps in district heating. Appl. Energy 2016, 184, 1374–1388. [Google Scholar] [CrossRef]
- Balboa-Fernández, M.; de Simón-Martín, M.; González-Martínez, A.; Rosales-Asensio, E. Analysis of District Heating and Cooling systems in Spain. Energy Rep. 2020, 6, 532–537. [Google Scholar] [CrossRef]
- Simeoni, P.; Ciotti, G.; Cottes, M.; Meneghetti, A. Integrating industrial waste heat recovery into sustainable smart energy systems. Energy 2019, 175, 941–951. [Google Scholar] [CrossRef]
- Papapetrou, M.; Kosmadakis, G.; Cipollina, A.; La Commare, U.; Micale, G. Industrial waste heat: Estimation of the technically available resource in the EU per industrial sector, temperature level and country. Appl. Therm. Eng. 2018, 138, 207–216. [Google Scholar] [CrossRef]
- Al-Janabi, A.; Al-Azri, N. Effect of recovering the industrial waste heat in Oman on energy and environment. Energy Rep. 2020, 6, 526–531. [Google Scholar] [CrossRef]
- Varga, Z.; Palotai, B. Comparison of low temperature waste heat recovery methods. Energy 2017, 137, 1286–1292. [Google Scholar] [CrossRef]
- Miró, L.; Brückner, S.; Cabeza, L.F. Mapping and discussing Industrial Waste Heat (IWH) potentials for different countries. Renew. Sustain. Energy Rev. 2015, 51, 847–855. [Google Scholar] [CrossRef] [Green Version]
- Yuan, M.; Thellufsen, J.Z.; Sorknæs, P.; Lund, H.; Liang, Y. District heating in 100% renewable energy systems: Combining industrial excess heat and heat pumps. Energy Convers. Manag. 2021, 244, 114527. [Google Scholar] [CrossRef]
- Doračić, B.; Pavičević, M.; Pukšec, T.; Quoilin, S.; Duić, N. Utilizing excess heat through a wholesale day ahead heat market–The DARKO model. Energy Convers. Manag. 2021, 235, 114025. [Google Scholar] [CrossRef]
- Wheatcroft, E.; Wynn, H.; Lygnerud, K.; Bonvicini, G.; Leonte, D. The Role of Low Temperature Waste Heat Recovery in Achieving 2050 Goals: A Policy Positioning Paper. Energies 2020, 13, 2107. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, S.; Hansen, K.; Lund, R.; Moreno, D. Unconventional Excess Heat Sources for District. Energies 2020, 13, 5068. [Google Scholar] [CrossRef]
- Ebrahimi, K.; Jones, G.F.; Fleischer, A.S. A review of data center cooling technology, operating conditions and the corresponding low-grade waste heat recovery opportunities. Renew. Sustain. Energy Rev. 2014, 31, 622–638. [Google Scholar] [CrossRef]
- Huang, P.; Copertaro, B.; Zhang, X.; Shen, J.; Löfgren, I.; Rönnelid, M.; Fahlen, J.; Andersson, D.; Svanfeldt, M. A review of data centers as prosumers in district energy systems: Renewable energy integration and waste heat reuse for district heating. Appl. Energy 2019, 258, 114109. [Google Scholar] [CrossRef]
- Oró, E.; Taddeo, P.; Salom, J. Waste heat recovery from urban air cooled data centres to increase energy efficiency of district heating networks. Sustain. Cities Soc. 2019, 45, 522–542. [Google Scholar] [CrossRef]
- Wahlroos, M.; Pärssinen, M.; Rinne, S.; Syri, S.; Manner, J. Future views on waste heat utilization–Case of data centers in Northern Europe. Renew. Sustain. Energy Rev. 2018, 82, 1749–1764. [Google Scholar] [CrossRef]
- Khosravi, A.; Laukkanen, T.; Vuorinen, V.; Syri, S. Waste heat recovery from a data centre and 5G smart poles for low-temperature district heating network. Energy 2021, 218, 119468. [Google Scholar] [CrossRef]
- Giunta, F.; Sawalha, S. Techno-economic analysis of heat recovery from supermarket’s CO2 refrigeration systems to district heating networks. Appl. Therm. Eng. 2021, 193, 117000. [Google Scholar] [CrossRef]
- Mateu-Royo, C.; Sawalha, S.; Mota-Babiloni, A.; Navarro-Esbrí, J. High temperature heat pump integration into district heating network. Energy Convers. Manag. 2019, 210, 112719. [Google Scholar] [CrossRef]
- Arnaudo, M.; Giunta, F.; Dalgren, J.; Topel, M.; Sawalha, S.; Laumert, B. Heat recovery and power-to-heat in district heating networks–A techno-economic and environmental scenario analysis. Appl. Therm. Eng. 2021, 185, 116388. [Google Scholar] [CrossRef]
- Gross, M.; Karbasi, B.; Reiners, T.; Altieri, L.; Wagner, H.-J.; Bertsch, V. Implementing prosumers into heating networks. Energy 2021, 230, 120844. [Google Scholar] [CrossRef]
- Maouris, G.; Escriva, E.J.S.; Acha, S.; Shah, N.; Markides, C.N. CO2 refrigeration system heat recovery and thermal storage modelling for space heating provision in supermarkets: An integrated approach. Appl. Energy 2020, 264, 114722. [Google Scholar] [CrossRef]
- Petrovic, S.; Bühler, F.; Radoman, U. Power transformers as excess heat sources. In Proceedings of the 32nd International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems (ECOS 2019), Wrocław, Poland, 23–28 June 2019. [Google Scholar]
- Trbusic, M.; Marusa, R.; Pihler, J.; Hamler, A. Utilization of dissipated heat of power transformers. Transform. Mag. 2019, 6, 84–93. [Google Scholar]
- Gilfanov, K.H.; Tien, N.; Gaynullin, R.N.; Hallyyev, I. Energy efficient heat supply system for electric power facilities. E3S Web Conf. 2019, 124, 01011. [Google Scholar] [CrossRef] [Green Version]
- Ninikas, K.; Hytiris, N.; Emmanuel, R.; Aaen, B. Recovery and Valorisation of Energy from Wastewater Using a Water Source Heat Pump at the Glasgow Subway: Potential for Similar Underground Environments. Resources 2019, 8, 169. [Google Scholar] [CrossRef] [Green Version]
- Ninikas, K.; Hytiris, N.; Emmanuel, R.; Aaen, B. The Performance of an ASHP System Using Waste Air to Recover Heat Energy in a Subway System. Clean Technol. 2019, 1, 154–163. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.; Hendel, M. Urban water networks as an alternative source for district heating and emergency heat-wave cooling. Energy 2018, 145, 79–87. [Google Scholar] [CrossRef] [Green Version]
- Somogyi, V.; Sebestyén, V.; Domokos, E. Assessment of wastewater heat potential for district heating in Hungary. Energy 2018, 163, 712–721. [Google Scholar] [CrossRef]
- Nagpal, H.; Spriet, J.; Murali, M.; McNabola, A. Heat Recovery from Wastewater—A Review of Available Resource. Water 2021, 13, 1274. [Google Scholar] [CrossRef]
- Karampour, M.; Sawalha, S.; Arias, J. Eco-Friendly Supermarkets—An Overview; Report 2; Shecco: Bruxelles, Belgium, 2016; pp. 1–53. [Google Scholar]
- Meesenburg, W.; Christian, J.; Kruse, R.; Ali, Z.A. Flexible heat supply from supermarket refrigeration systems. In Proceedings of the SES Conference, Aalborg, Denmark, 6–7 October 2020. [Google Scholar]
- Uzbašić, I. Projekt Demonstracijskog Rashladnog Uređaja s Ugljikovim Dioksidom Kao Radnom Tvari. Ph.D. Thesis, Sveučilište u Zagrebu, Zagreb, Croatia, 2015. [Google Scholar]
- Liao, S.; Zhao, T.; Jakobsen, A. A correlation of optimal heat rejection pressures in transcritical carbon dioxide cycles. Appl. Therm. Eng. 2000, 20, 831–841. [Google Scholar] [CrossRef]
- Dorotić, H.; Pukšec, T.; Duić, N. Economical, environmental and exergetic multi-objective optimization of district heating systems on hourly level for a whole year. Appl. Energy 2019, 251, 113394. [Google Scholar] [CrossRef]
- Jensen, J.K.; Ommen, T.; Reinholdt, L.; Markussen, W.B.; Elmegaard, B. Heat pump COP, part 2: Generalized COP estimation of heat pump processes. Refrig. Sci. Technol. 2018, 2018, 1255–1264. [Google Scholar] [CrossRef]
- Best, I.; Orozaliev, J.; Vajen, K. Economic comparison of low-temperature and ultra-low-temperature district heating for new building developments with low heat demand densities in Germany. Int. J. Sustain. Energy Plan. Manag. 2018, 16, 45–60. [Google Scholar] [CrossRef]
- Cortella, G.; Lollini, R.; Noris, F.; D’Agaro, P.; Saro, O. Re-Conceptualizing Shopping Malls from Consumerism to Energy Conservation; Researchgate: Berlin, Germany, 2014; pp. 582–589. [Google Scholar]
- Majnarić, L. Procjena Ugroženosti Stanovništva, Materijalnih i Kulturnih Dobara i Okoliša od Katastrofa i Velikih Nesreća za Područje Grada Zagreba. Ph.D. Thesis, Karlovac University of Applied Sciences, Karlovac, Croatia, 2016. [Google Scholar]
- Hrvatska Elektroprivreda. Podaci za Izračun 2019. HEP. Available online: https://www.hep.hr/ods/opskrbljivaci/pravila-primjene-nadomjesnih-krivulja-opterecenja/podaci-za-izracun-2019/613 (accessed on 20 November 2021).
- Huld, T.; Müller, R.; Gambardella, A. A new solar radiation database for estimating PV performance in Europe and Africa. Solar Energy 2012, 86, 1803–1815. [Google Scholar] [CrossRef]
- Aromada, S.A.; Eldrup, N.H.; Normann, F.; Øi, L.E. Techno-Economic Assessment of Different Heat Exchangers for CO2 Capture. Energies 2020, 13, 6315. [Google Scholar] [CrossRef]
- Danish Energy Agency and Energinet, Technology Data for Generation of Electricity and District Heating, Copenhagen. 2020. Available online: https://ens.dk/en/our-services/projections-and-models/technology-data/technology-data-generation-electricity-and (accessed on 24 November 2021).
- Eurostat, Electricity Prices for Non-Household Consumers, Second Half 2020. 2021. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Electricity_price_statistics (accessed on 4 December 2021).


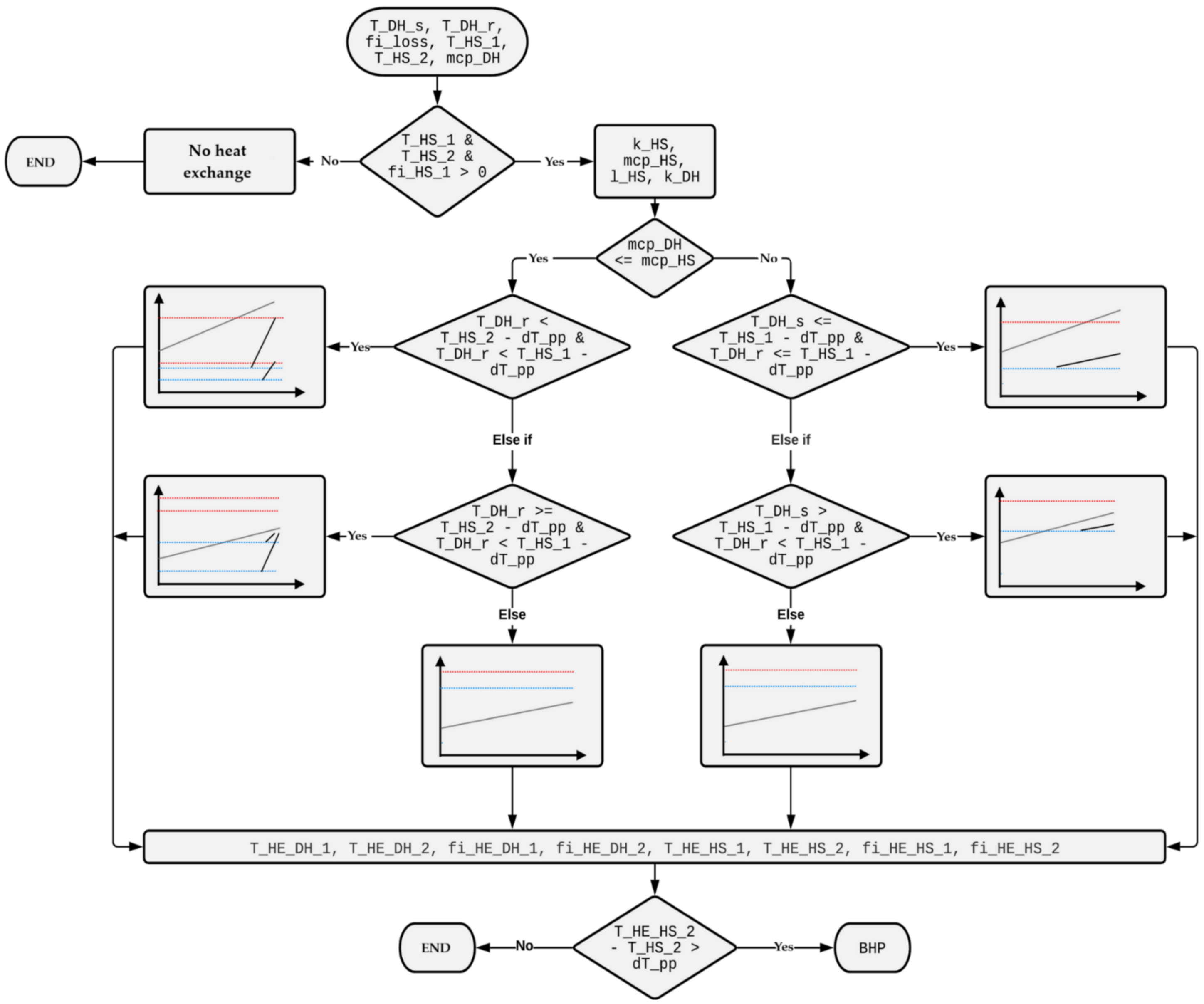

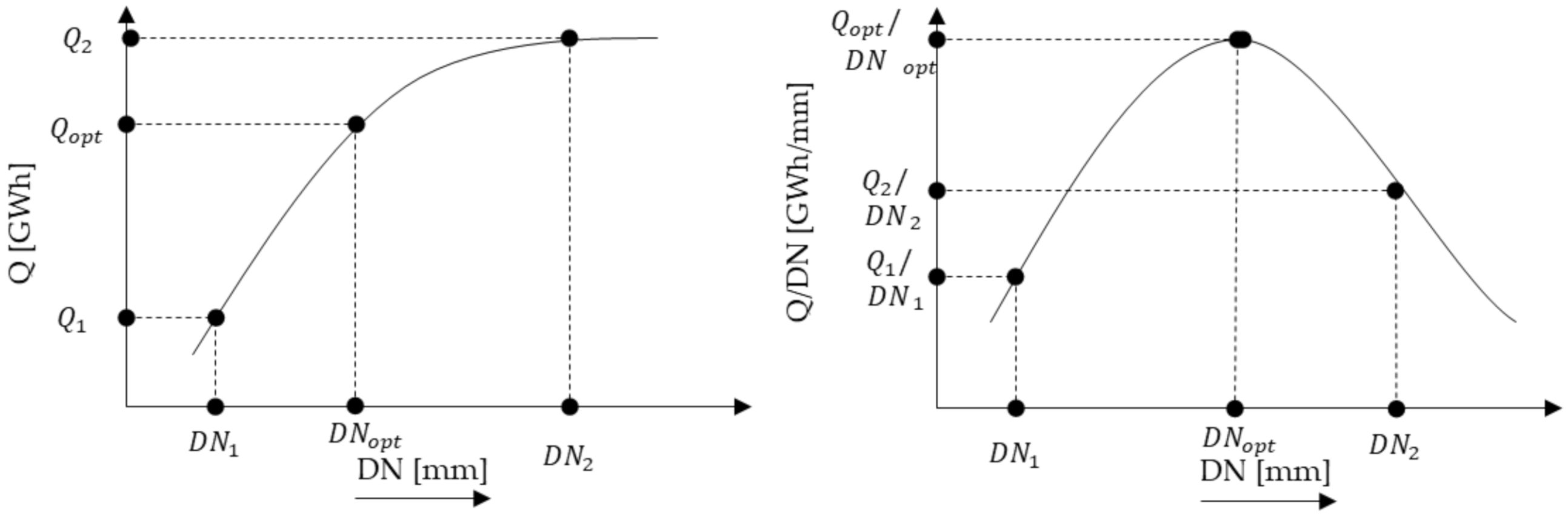

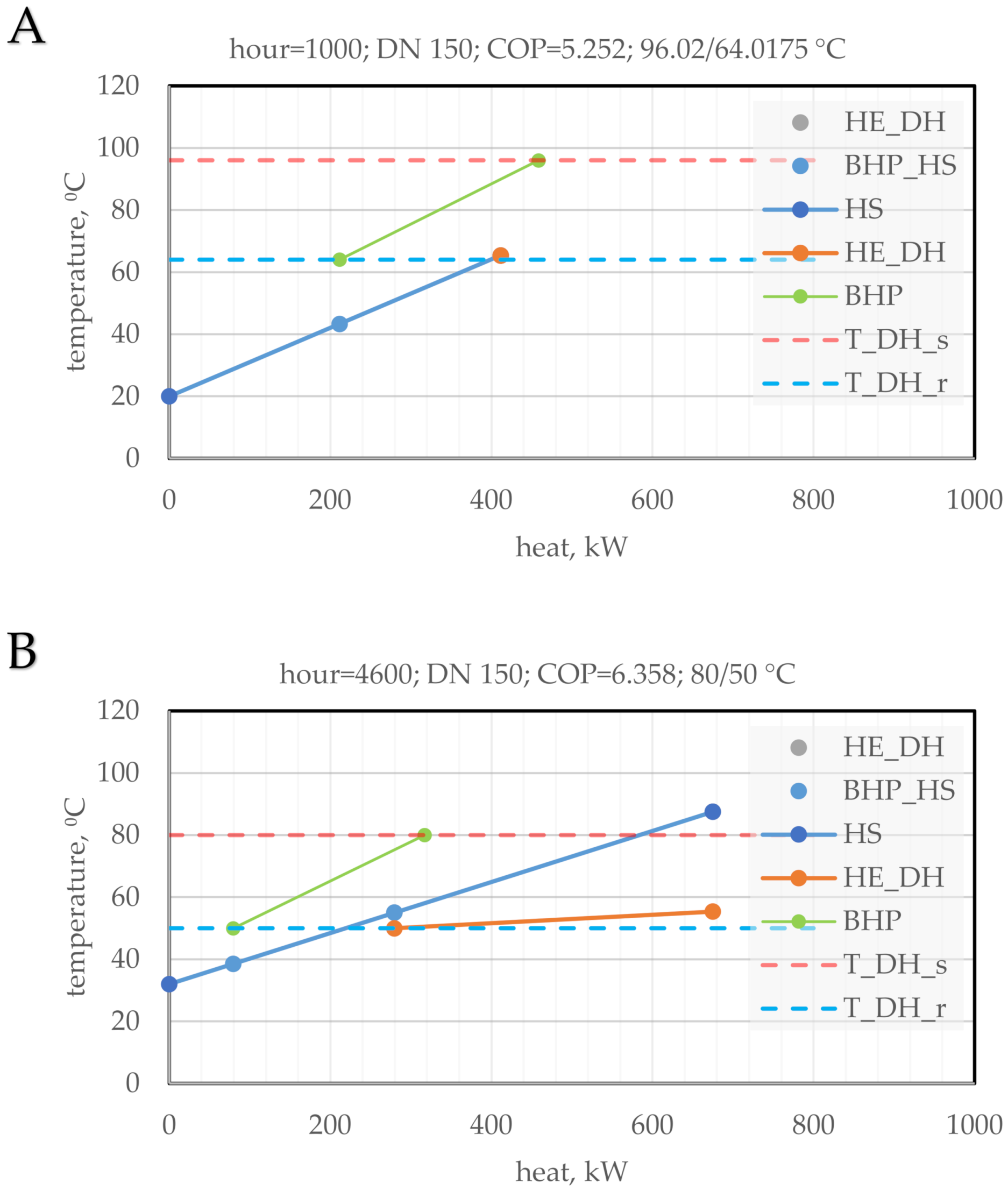
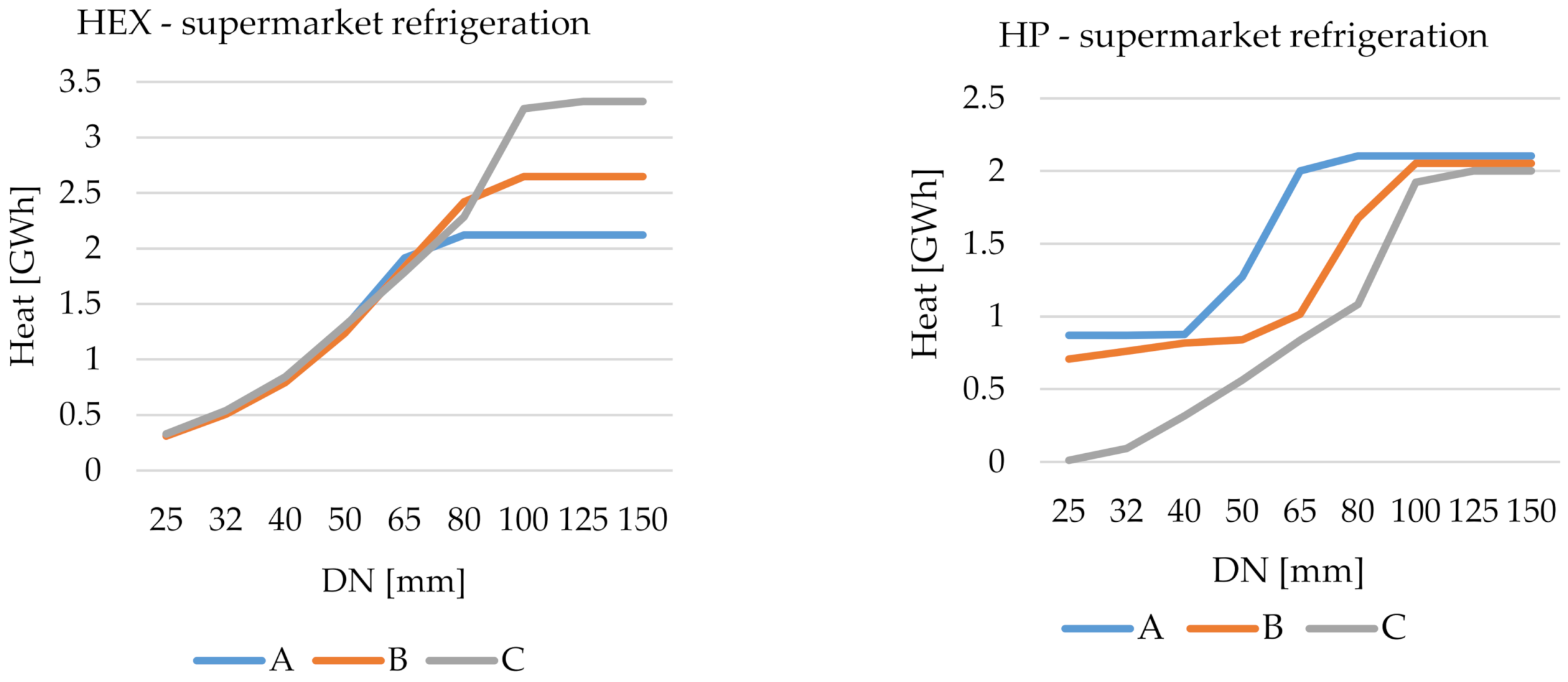
| Label | Unit | Description |
|---|---|---|
| T_DH_s | °C | Supply temperature of DH |
| T_DH_r | °C | Return temperature of DH |
| fi_loss | kW | Available heat after heat recovery |
| T_HS_1 | °C | Inlet temperature of heat sources |
| T_HS_2 | °C | Outlet temperature of heat sources |
| mcp_DH | W/K | DH–Thermal capacity |
| fi_HS_1 | kW | Inlet heat of heat sources |
| k_HS | K/W | Inverse value of thermal capacity–HS |
| mcp_HS | W/K | HS–Thermal capacity |
| 1_HS | K | Temperature drop of HS as a result of heat exchange |
| k_DH | K/W | Inverse value of thermal capacity–DH |
| dT_pp | Pinch temperature difference | |
| T_HE_DH_1 | °C | Inlet temperature of HEX–DH side |
| T_HE_DH_2 | °C | Outlet temperature of HEX–DH side |
| fi_HE_DH_1 | W | Inlet heat of HEX–DH side |
| fi_HE_DH_2 | W | Outlet heat of HEX–DH side |
| T_HE_HS_1 | °C | Inlet temperature of HEX–HS side |
| T_HE_HS_2 | °C | Outlet temperature of HEX–HS side |
| fi_HE_HS_1 | kW | Inlet heat of HEX |
| fi_HE_HS_1 | kW | Outlet heat of HEX |
| −30 | 14.7 | −5 | 30.5 | 20 | 123 |
| 220 | 23.8 | 63 | 200 | 36 | 236 |
| Label | Value | Unit | Name |
|---|---|---|---|
| 4187.00 | J kg−1 K−1 | Specific thermal capacity of water | |
| 1000.00 | kg K−1 | Water density | |
| 1.00 | m s−1 | Water flow rate | |
| 25–150 | mm | Connection pipe diameter |
| Label | Value | Unit | Name |
|---|---|---|---|
| 0.10 | - | Discount rate | |
| 20 | year | Life expectancy | |
| 0.04 | - | Part operative expenditures for HEX into an investment [54] | |
| 1.24 | MEUR MW−1 | Specific price of BHP [55] | |
| - | kW | Nominal power of BHP, from load duration of source | |
| 2.000 | EUR kWh−1 | Fixed operative expenditures for BHP [55] | |
| 2.7 | EUR MWh−1 | Variable operative expenditures for BHP | |
| - | MWh | Electricity for BHP, from calculation | |
| 0.1 | EUR kWh−1 | Electricity price for non-households [56] | |
| MEUR MW−1 | Specific price for HEX, nominal power for HEX |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dorotić, H.; Čuljak, K.; Miškić, J.; Pukšec, T.; Duić, N. Technical and Economic Assessment of Supermarket and Power Substation Waste Heat Integration into Existing District Heating Systems. Energies 2022, 15, 1666. https://doi.org/10.3390/en15051666
Dorotić H, Čuljak K, Miškić J, Pukšec T, Duić N. Technical and Economic Assessment of Supermarket and Power Substation Waste Heat Integration into Existing District Heating Systems. Energies. 2022; 15(5):1666. https://doi.org/10.3390/en15051666
Chicago/Turabian StyleDorotić, Hrvoje, Kristijan Čuljak, Josip Miškić, Tomislav Pukšec, and Neven Duić. 2022. "Technical and Economic Assessment of Supermarket and Power Substation Waste Heat Integration into Existing District Heating Systems" Energies 15, no. 5: 1666. https://doi.org/10.3390/en15051666
APA StyleDorotić, H., Čuljak, K., Miškić, J., Pukšec, T., & Duić, N. (2022). Technical and Economic Assessment of Supermarket and Power Substation Waste Heat Integration into Existing District Heating Systems. Energies, 15(5), 1666. https://doi.org/10.3390/en15051666








