Universal Model to Predict Expected Direction of Products Quality Improvement
Abstract
:1. Introduction
2. Literature Review
3. Model
3.1. Concept of Model
3.2. Assumptions and Conditions of the Model Ensuring Its Versatility
- The product for verification should be the current existing product [1];
- The type (kind) of products for verification should not be limited;
- The product quality level should be calculated separately according to the assessments from individual customers.
3.3. Characterization of Model
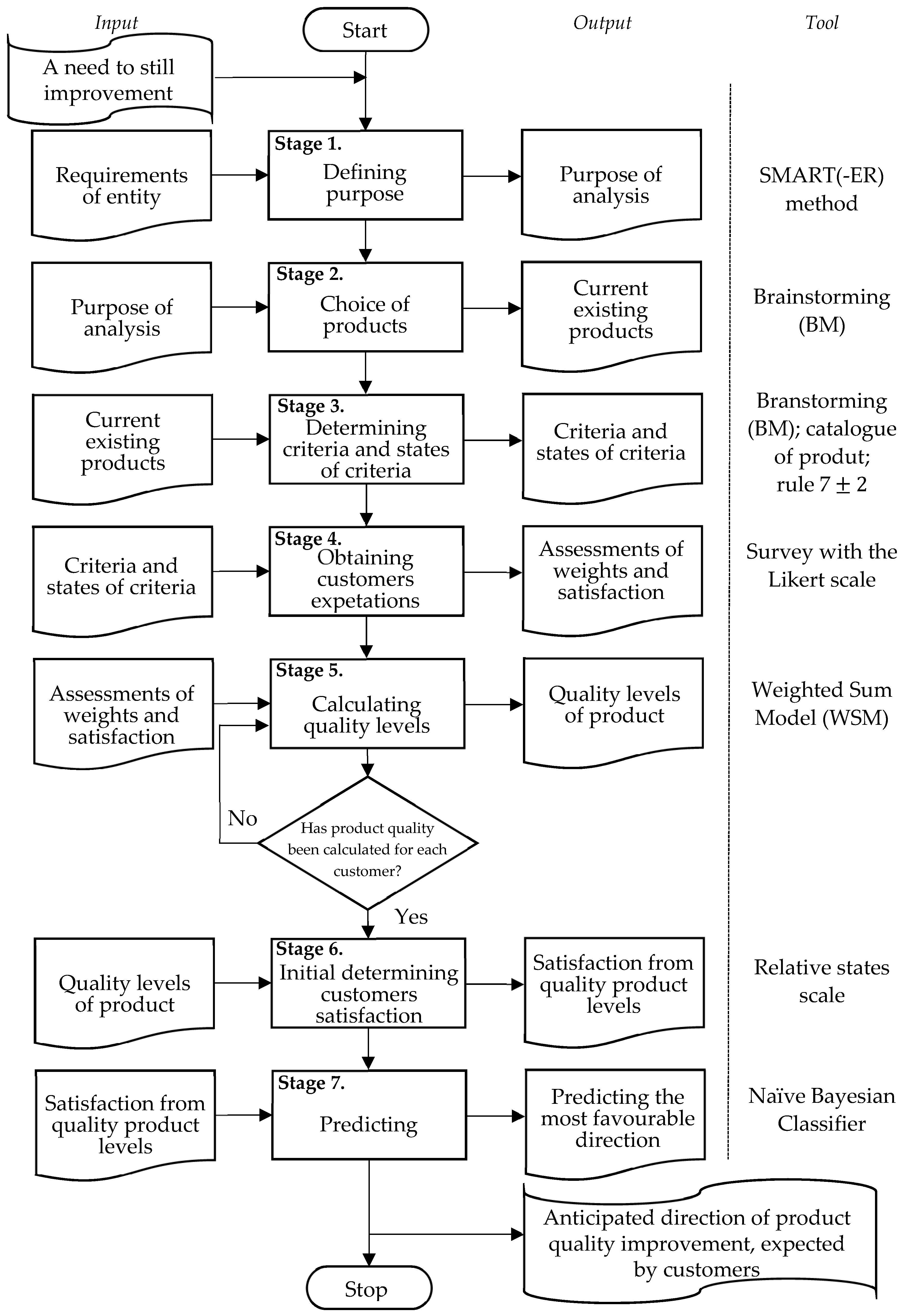
- Stage 1. Definition of purpose
- Stage 2. Choice of products
- Stage 3. Determining criteria and state of criteria
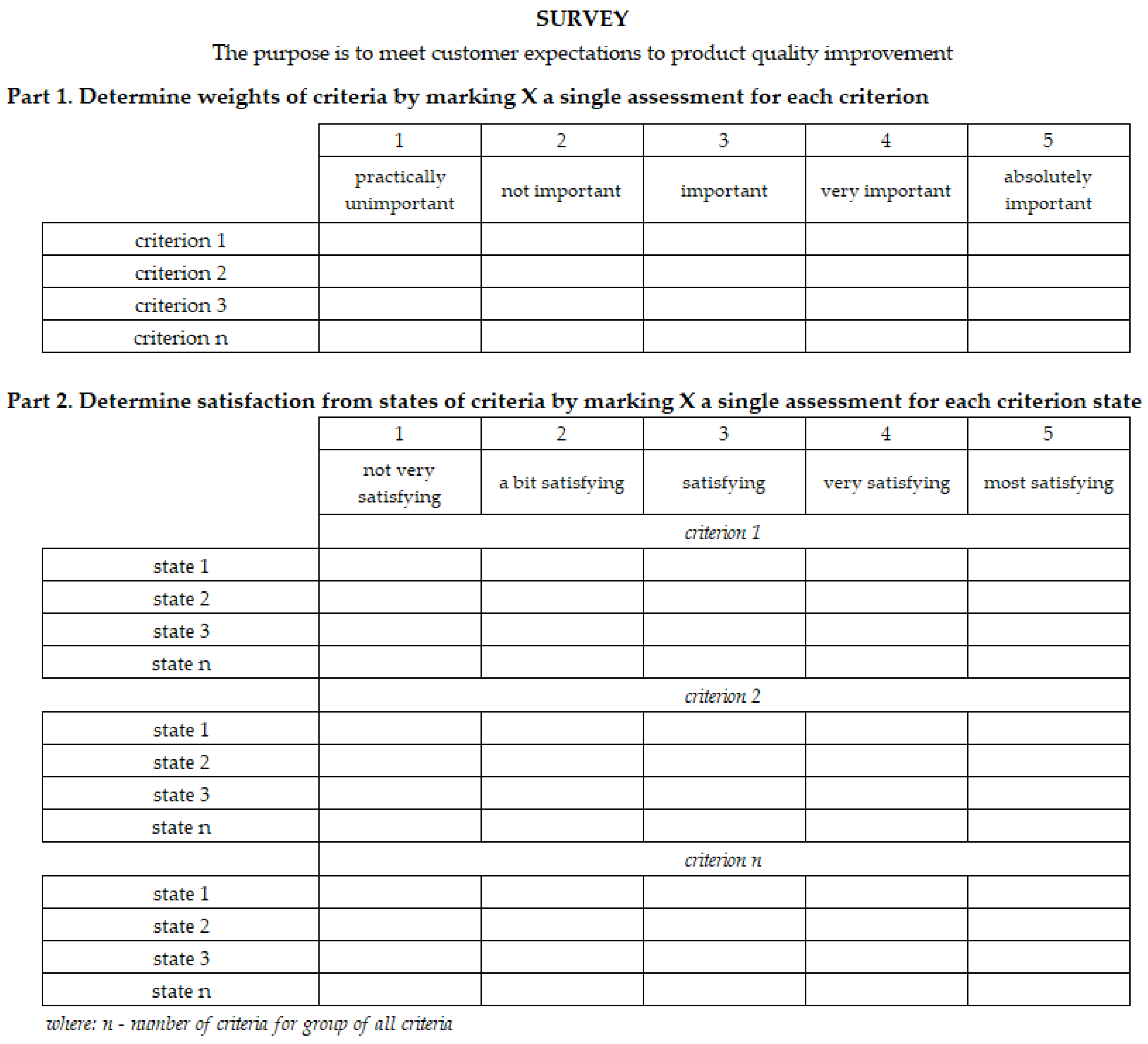
- Stage 4. Obtaining customer expectations
- Stage 5. Calculating the quality level
- Stage 6. Initial determination of customer satisfaction
- Stage 7. Predicting the expected direction of product quality improvement
4. Test of Model
- Rated power (Wp);
- Short-circuit current (current at maximum load) (A);
- Maximum (output) current (A);
- Open-circuit voltage (no load, open circuit) (V);
- Efficiency (%);
- Front glass (mm);
- Dimensions (mm);
- Number of cells;
- Temperature coefficient of intensity (%/C);
- Visibility;
- Degree of integration;
- Light reflection;
- Fractality;
- Pattern (texture).
5. Discussion
- Estimating product quality according to assessment of the importance of criteria and assessments of satisfaction with states of these criteria;
- Determining customers’ satisfaction with product quality levels;
- Predicting the direction of eventual changes in the product to meet customers’ satisfaction;
- Reduction in waste sources by determining adequate improvement actions;
- Sustainable development of existing products, which can be in the maturity or decline phase;
- Possibility to predict the direction of products improvement based on a small number of customers;
- Possibility to use the model by any entity;
- Possibility to use the model for any product.
- Supporting entity in making the right decision during the process of improving the product;
- Low-cost model, which can also be supported by a software program;
- Choice of the appropriate direction of product improvement;
- Support for planning and design activities;
- Predicting ahead of the competition the direction of product improvement.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Siwiec, D.; Pacana, A. A Pro-environmental method of sample size determination to predict the quality level of products considering current customers’ expectations. Sustainability 2021, 13, 5542. [Google Scholar] [CrossRef]
- Pacana, A.; Pasternak-Malicka, M.; Zawada, M.; Radon-Cholewa, A. Decision support in the production of packaging films by cost-quality analysis. Przemysl Chem. 2016, 95, 1042–1044. [Google Scholar] [CrossRef]
- Siwiec, D.; Pacana, A. Model of choice photovoltaic panels considering customers’ expectations. Energies 2021, 14, 5977. [Google Scholar] [CrossRef]
- Ulewicz, R.; Siwiec, D.; Pacana, A.; Tutak, M.; Brodny, J. Multi-criteria method for the selection of renewable energy sources in the polish industrial sector. Energies 2021, 14, 2386. [Google Scholar] [CrossRef]
- Tawalbeh, M.; Al-Othman, A.; Kafiah, F.; Abdelsalam, E.; Almomani, F.; Alkasrawi, M. Environmental impacts of solar photovoltaic systems: A critical review of recent progress and future outlook. Sci. Total Environ. 2021, 759, 143528. [Google Scholar] [CrossRef] [PubMed]
- López, G.; Ramírez, D.; Alonso-Montesinos, J.; Sarmiento, J.; Polo, J.; Martín-Chivelet, N.; Marzo, A.; Batlles, F.J.; Ferrada, P. Design of a low-cost multiplexer for the study of the impact of soiling on PV panel performance. Energies 2021, 14, 4186. [Google Scholar] [CrossRef]
- Shaito, A.; Hammoud, M.; Kawtharani, F.; Kawtharani, A.; Reda, H. Power enhancement of a PV module using different types of phase change materials. Energies 2021, 14, 5195. [Google Scholar] [CrossRef]
- Amaral, T.G.; Pires, V.F.; Pires, A.J. Fault detection in PV tracking systems using an image processing algorithm based on PCA. Energies 2021, 14, 7278. [Google Scholar] [CrossRef]
- Pandey, A.; Pandey, P.; Tumuluru, J.S. Solar energy production in India and commonly used technologies—An overview. Energies 2022, 15, 500. [Google Scholar] [CrossRef]
- Trela, M.; Dubel, A. Net-metering vs. net-billing from the investors perspective—Impacts of changes in RES financing in Poland on the profitability of a joint photovoltaic panels and heat pump system. Energies 2022, 15, 227. [Google Scholar] [CrossRef]
- Kshatri, S.S.; Dhillon, J.; Mishra, S.; Tariq, R.; Sharma, N.K.; Bajaj, M.; Rehman, A.U.; Shafiq, M.; Choi, J.-G. Reliability analysis of bifacial PV panel-based inverters considering the effect of geographical location. Energies 2022, 15, 170. [Google Scholar] [CrossRef]
- Kusznier, J.; Wojtkowski, W. IoT solutions for maintenance and evaluation of photovoltaic systems. Energies 2021, 14, 8567. [Google Scholar] [CrossRef]
- Aguilar, F.J.; Ruiz, J.; Lucas, M.; Vicente, P.G. Analiza i optymalizacja wydajności słonecznego klimatyzatora on-grid. Energies 2021, 14, 8054. [Google Scholar] [CrossRef]
- Al Siyabi, I.; Al Mayasi, A.; Al Shukaili, A.; Khanna, S. Effect of soiling on solar photovoltaic performance under desert climatic conditions. Energies 2021, 14, 659. [Google Scholar] [CrossRef]
- Griffin, A.; Hauser, J. The voice of the customer. Mark. Sci. 1991, 12, 1–27. [Google Scholar] [CrossRef]
- Ben Hamad, K.; Luta, D.N.; Raji, A.K. A grid-tied fuel cell multilevel inverter with low harmonic distortions. Energies 2021, 14, 688. [Google Scholar] [CrossRef]
- El-Bayeh, C.Z.; Zellagui, M.; Shirzadi, N.; Eicker, U. A novel optimization algorithm for solar panels selection towards a self-powered EV parking lot and its impact on the distribution system. Energies 2021, 14, 4515. [Google Scholar] [CrossRef]
- Mutani, G.; Todeschi, V. Optimization of costs and self-sufficiency for roof integrated photovoltaic technologies on residential buildings. Energies 2021, 14, 4018. [Google Scholar] [CrossRef]
- Stamatellos, G.; Zogou, O.; Stamatelos, A. Energy performance optimization of a house with grid-connected rooftop PV installation and air source heat pump. Energies 2021, 14, 740. [Google Scholar] [CrossRef]
- Abdallah, R.; Natsheh, E.; Juaidi, A.; Samara, S.; Manzano-Agugliaro, F. A multi-level world comprehensive neural network model for maximum annual solar irradiation on a flat surface. Energies 2020, 13, 6422. [Google Scholar] [CrossRef]
- Nguyen, D.P.N.; Lauwaert, J. Calculating the energy yield of si-based solar cells for belgium and vietnam regions at arbitrary tilt and orientation under actual weather conditions. Energies 2020, 13, 3180. [Google Scholar] [CrossRef]
- Gutiérrez Galeano, A.; Bressan, M.; Jiménez Vargas, F.; Alonso, C. Shading ratio impact on photovoltaic modules and correlation with shading patterns. Energies 2018, 11, 852. [Google Scholar] [CrossRef] [Green Version]
- Mousavi Maleki, S.A.; Hizam, H.; Gomes, C. Estimation of hourly, daily and monthly global solar radiation on inclined surfaces: Models re-visited. Energies 2017, 10, 134. [Google Scholar] [CrossRef] [Green Version]
- Gazda, A.; Pacana, A.; Malindzak, D. Study on improving the quality of stretch film by Taguchi method. Przemysl Chem. 2013, 92, 980–982. [Google Scholar]
- Garcia, A.Q.; Nishiumi, N.; Saito, A.; Matsumura, E.; Senda, J. Economic, environmental and energetic analysis of a distributed generation system composed by waste gasification and photovoltaic panels. Energies 2021, 14, 3889. [Google Scholar] [CrossRef]
- Chatterji, E.; Bazilian, D. Smart meter data to optimize combined roof-top solar and battery systems using a stochastic mixed integer programming model. IEEE Access 2020, 8, 1333843–1333853. [Google Scholar] [CrossRef]
- Niri, M.; Liu, K.; Apachitei, G.; Ramirez, L.; Lain, M.; Widanage, D.; Marco, J. Machine learning for optimised and clean Li-ion battery manufacturing: Revealing the dependency between electrode and cell characteristics. J. Clean. Prod. 2021, 324, 129272. [Google Scholar] [CrossRef]
- Liu, K.; Hu, X.; Meng, J.; Guerrero, J.; Teodorescu, R. RUBoost-based ensemble machine learning for electrode quality classification in Li-ion battery manufacturing. IEEE/ASME Trans. Mechatron. 2021, 10, 1–10. [Google Scholar] [CrossRef]
- Liu, K.; Peng, Q.; Sun, H.; Fei, M.; Ma, H.; Hu, T. A transferred recurrent neural network for battery calendar health prognostics of energy-transportation systems. IEEE Trans. Ind. Inf. 2022. [Google Scholar] [CrossRef]
- Liu, K.; Tang, X.; Teodorescu, R.; Gao, F.; Meng, J. Future ageing trajectory prediction for lithium-ion battery considering the knee point effect. IEEE Trans. Ind. Inf. 2022. [Google Scholar] [CrossRef]
- Liu, K.; Hu, X.; Zhou, H.; Tong, L.; Widanage, W.; Marco, J. Feature analyses and modeling of lithium-ion battery manufacturing based on random forest classification. IEEE/ASME Trans. Mechatron. 2021, 26, 2944–2955. [Google Scholar] [CrossRef]
- Lawlor, K.B.; Hornyak, M.J. Smart goals: How the application of smart goals can contribute to achievement of student learning outcomes. Dev. Bus. Simul. Exp. Learn. 2012, 39, 259–267. [Google Scholar]
- Kohn, N.; Smith, S. Collaborative fixation: Effects of others’ ideas on brainstorming. Appl. Cognit. Psychol. 2011, 25, 359–371. [Google Scholar] [CrossRef]
- Pacana, A.; Siwiec, D.; Bednarova, L. Analysis of the incompatibility of the product with fluorescent method. Metalurgija 2019, 58, 337–340. [Google Scholar]
- Joshi, A.; Kale, S.; Chandel, S.; Pal, D.K. Likert scale: Explored and explained. Curr. J. Appl. Sci. Technol. 2015, 7, 396–403. [Google Scholar] [CrossRef]
- Chmielarz, W.; Zborowski, M. On the assessment of e-banking websites supporting sustainable development goals. Energies 2022, 15, 378. [Google Scholar] [CrossRef]
- Garcia-Ayllon, S.; Hontoria, E.; Munier, N. The contribution of MCDM to SUMP: The case of Spanish cities during 2006–2021. Int. J. Environ. Res. Public Health 2022, 19, 294. [Google Scholar] [CrossRef] [PubMed]
- Tran, N.H.; Yang, S.-H.; Tsai, C.Y.; Yang, N.C.; Chang, C.-M. Developing transportation livability-related indicators for green urban road rating system in Taiwan. Sustainability 2021, 13, 14016. [Google Scholar] [CrossRef]
- Othman, A.A.; Obaid, A.K.; Al-Manmi, D.A.M.; Pirouei, M.; Salar, S.G.; Liesenberg, V.; Al-Maamar, A.F.; Shihab, A.T.; Al-Saady, Y.I.; Al-Attar, Z.T. Insights for landfill site selection using GIS: A case study in the Tanjero River Basin, Kurdistan Region, Iraq. Sustainability 2021, 13, 12602. [Google Scholar] [CrossRef]
- Siwiec, D.; Pacana, A. Model supporting development decisions by considering qualitative–Environmental aspects. Sustainability 2021, 13, 9067. [Google Scholar] [CrossRef]
- Sugahara, S.; Ueno, M. Exact learning augmented naive bayes classifier. Entropy 2021, 23, 1703. [Google Scholar] [CrossRef]
- Chen, H.; Hu, S.; Hua, R.; Zhaon, X. Improved naive Bayes classification algorithm for traffic risk management. EURASIP J. Adv. Signal. Process. 2021, 30, 1–12. [Google Scholar] [CrossRef]
- Zhang, W.; Gao, F. An improvement to naïve bayes for text classification. Procedia Eng. 2011, 15, 2160–2164. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Zhu, M.; Yang, Y. A Bayesian classifier learning algorithm based on optimization model. Math. Probl. Eng. 2013, 2013, 975953. [Google Scholar] [CrossRef]
- Hansen, E.; Bush, R.J. Understanding customer quality requirements—Model and application. Ind. Mark. Manag. 1999, 28, 119–130. [Google Scholar] [CrossRef]
- Huang, Y.M. On the general evaluation of customer requirements during conceptual design. J. Mech. Des. 1999, 121, 92–97. [Google Scholar] [CrossRef]
- Roder, B.; Heidl, M.J.; Birkhofer, H. Pre-acquisition clustering of requirements–Helping Customers to realize what they want. Des. Harm. 2013, 7, 407–416. [Google Scholar]
- Stylidis, K.; Rossi, M.; Wickman, C.; Söderberg, R. The communication strategies and customer’s requirements definition at the early design stages: An empirical study on italian luxury automotive brands. Procedia CIRP 2016, 50, 553–558. [Google Scholar] [CrossRef] [Green Version]
- Ostasz, G.; Czerwinska, K.; Pacana, A. Quality management of aluminum pistons with the use of quality control points. Manag. Syst. Prod. Eng. 2020, 28, 29–33. [Google Scholar] [CrossRef] [Green Version]
- Madzik, P.; Chocholakova, A. Structured transfer of customer’s requirements into product quality attributes—A University Case Study. Qual. Access Success 2016, 17, 38–45. [Google Scholar]
- Gupta, M.; Shri, C. Understanding customer requirements of corrugated industry using Kano model. Int. J. Qual. Reliab. Manag. 2018, 35, 1653–1670. [Google Scholar] [CrossRef]
- Pacana, A.; Siwiec, D. Model to predict quality of photovoltaic panels considering customers’ expectations. Energies 2022, 15, 1101. [Google Scholar] [CrossRef]
- Mu, E.; Pereyra-Rojas, M. Practical decision making. In Springer Briefs in Operations Research, Appendix A: Practical Questions Related to AHP Modeling; Springer Nature: Basel, Switzerland, 2017; pp. 105–106. [Google Scholar]
- Chan, F.T.S.; Kumar, N. Global supplier development considering risk factors using fuzzy extended AHP-based approach. Omega 2007, 35, 417–431. [Google Scholar] [CrossRef]
- Wang, L.; Chu, J.; Wu, J. Selection of optimum maintenance strategies based on a fuzzy analytic hierarchy process. Int. J. Prod. Econ. 2007, 107, 151–163. [Google Scholar] [CrossRef]
- Gawilk, R. Stratification of research target group and selection of experts for AHP-based decision making model. Stud. Mater. Misc. Oecon. 2016, 20, 193–200. [Google Scholar]
- Pacana, A.; Siwiec, D. Universal model to support the quality improvement of industrial products. Materials 2021, 14, 7872. [Google Scholar] [CrossRef] [PubMed]
- Jie, Y.; Ji, X.; Yue, A.; Chen, J.; Deng, Y.; Chen, J.; Zhang, Y. Combined multi-layer feature fusion and edge detection method for distributed photovoltaic power station identification. Energies 2020, 13, 6742. [Google Scholar] [CrossRef]
- Guzman Razo, D.E.; Müller, B.; Madsen, H.; Wittwer, C. A genetic algorithm approach as a self-learning and optimization tool for PV power simulation and digital twinning. Energies 2020, 13, 6712. [Google Scholar] [CrossRef]
- Lucchi, E.; Polo Lopez, C.S.; Franco, G. A conceptual framework on the integration of solar energy systems in heritage sites and buildings. IOP Conf. Ser. Mater. Sci. Eng. 2020, 949, 1. [Google Scholar] [CrossRef]
- Sánchez-Pantoja, N.; Vidal, R.; Pastor, M.C. EU-funded projects with actual implementation of renewable energies in cities. Analysis of their concern for aesthetic impact. Energies 2021, 14, 1627. [Google Scholar] [CrossRef]
- Wall, M.; Probst, M.; Roecker, C.; Dubois, M.; Horvat, M.; Jorgensen, O.; Kappel, K. Achieving solar energy in architecture-IEA SHC Task 41. Energy Procedia 2012, 30, 1250–1260. [Google Scholar] [CrossRef] [Green Version]
- Sanchez-Pantoja, N.; Pastor, M.; Vidal, R. Aesthetic impact of solar energy systems. Renew. Sustain. Energy Rev. 2018, 98, 227–238. [Google Scholar] [CrossRef]
- Ferreira, A.C.; Silva, A.; Teixeira, J.C.; Teixeira, S. Multi-objective optimization of solar thermal systems applied to portuguese dwellings. Energies 2020, 13, 6739. [Google Scholar] [CrossRef]
- Yildirim, M.A.; Nowak-Ocłoń, M. Modified maximum power point tracking algorithm under time-varying solar irradiation. Energies 2020, 13, 6722. [Google Scholar] [CrossRef]


| Criteria of PV | Range of Quality Criteria (1) | Range of Quality Criteria (2) | Range of Quality Criteria (3) |
|---|---|---|---|
| rated power (Wp) | |||
| short-circuit current (A) | |||
| maximum current (A) | |||
| open-circuit voltage (V) | |||
| efficiency (%) | |||
| front glass (mm) | |||
| dimensions (mm) | |||
| number of cells | |||
| temp. coeff. of inten. (%/C) | |||
| visibility | partially visible | visible | practically invisible |
| degree of integration | not integrated | partially integrated | integrated |
| light reflection | small | average | big |
| fractality | small | average | big |
| pattern (texture) | plain | porous | transparent |
| Quality Level from Criteria States (1) | Quality Level from Criteria States (2) | Quality Level from Criteria States (3) | |||
|---|---|---|---|---|---|
| 0.11 | very satisfying | 0.09 | a bit satisfying | 0.14 | a bit satisfying |
| 0.11 | very satisfying | 0.13 | very satisfying | 0.13 | very satisfying |
| 0.09 | a bit satisfying | 0.08 | not very satisfying | 0.10 | a bit satisfying |
| 0.11 | very satisfying | 0.09 | a bit satisfying | 0.14 | absolutely satisfying |
| 0.09 | a bit satisfying | 0.08 | not very satisfying | 0.11 | very satisfying |
| 0.10 | a bit satisfying | 0.08 | not very satisfying | 0.13 | very satisfying |
| 0.10 | a bit satisfying | 0.13 | very satisfying | 0.09 | a bit satisfying |
| Quality Level | Customers’ Satisfaction (NBC Class) | A Priori Value | Average Value | Standard Deviation |
|---|---|---|---|---|
| Quality level from criteria states (1) | very satisfying | 0.428571 | 0.108333 | 0.000024 |
| a bit satisfying | 0.571429 | 0.090750 | 0.000024 | |
| Quality level from criteria states (2) | very satisfying | 0.285714 | 0.139500 | 0.000013 |
| not very satisfying | 0.428571 | 0.079667 | 0.000020 | |
| a bit satisfying | 0.285714 | 0.087000 | 0.000002 | |
| Quality level from criteria states (3) | absolutely satisfying | 0.285714 | 0.137000 | 0.000008 |
| very satisfying | 0.428571 | 0.125333 | 0.000176 | |
| a bit satisfying | 0.285714 | 0.093000 | 0.000098 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ostasz, G.; Siwiec, D.; Pacana, A. Universal Model to Predict Expected Direction of Products Quality Improvement. Energies 2022, 15, 1751. https://doi.org/10.3390/en15051751
Ostasz G, Siwiec D, Pacana A. Universal Model to Predict Expected Direction of Products Quality Improvement. Energies. 2022; 15(5):1751. https://doi.org/10.3390/en15051751
Chicago/Turabian StyleOstasz, Grzegorz, Dominika Siwiec, and Andrzej Pacana. 2022. "Universal Model to Predict Expected Direction of Products Quality Improvement" Energies 15, no. 5: 1751. https://doi.org/10.3390/en15051751
APA StyleOstasz, G., Siwiec, D., & Pacana, A. (2022). Universal Model to Predict Expected Direction of Products Quality Improvement. Energies, 15(5), 1751. https://doi.org/10.3390/en15051751








