Damping of Subsynchronous Resonance in Utility DFIG-Based Wind Farms Using Wide-Area Fuzzy Control Approach
Abstract
:1. Introduction
- Design of a WAMS-based fuzzy control scheme that considers the communication time latencies originating from PMU measurements.
- Decrease in the subsynchronous resonance for utility DFIG wind farms.
- The proposed control scheme does not require adjusting the parameters of the controller.
2. Modeling of the IEEE Second Benchmark including DFIG Wind Farms
2.1. IEEE Second Benchmark
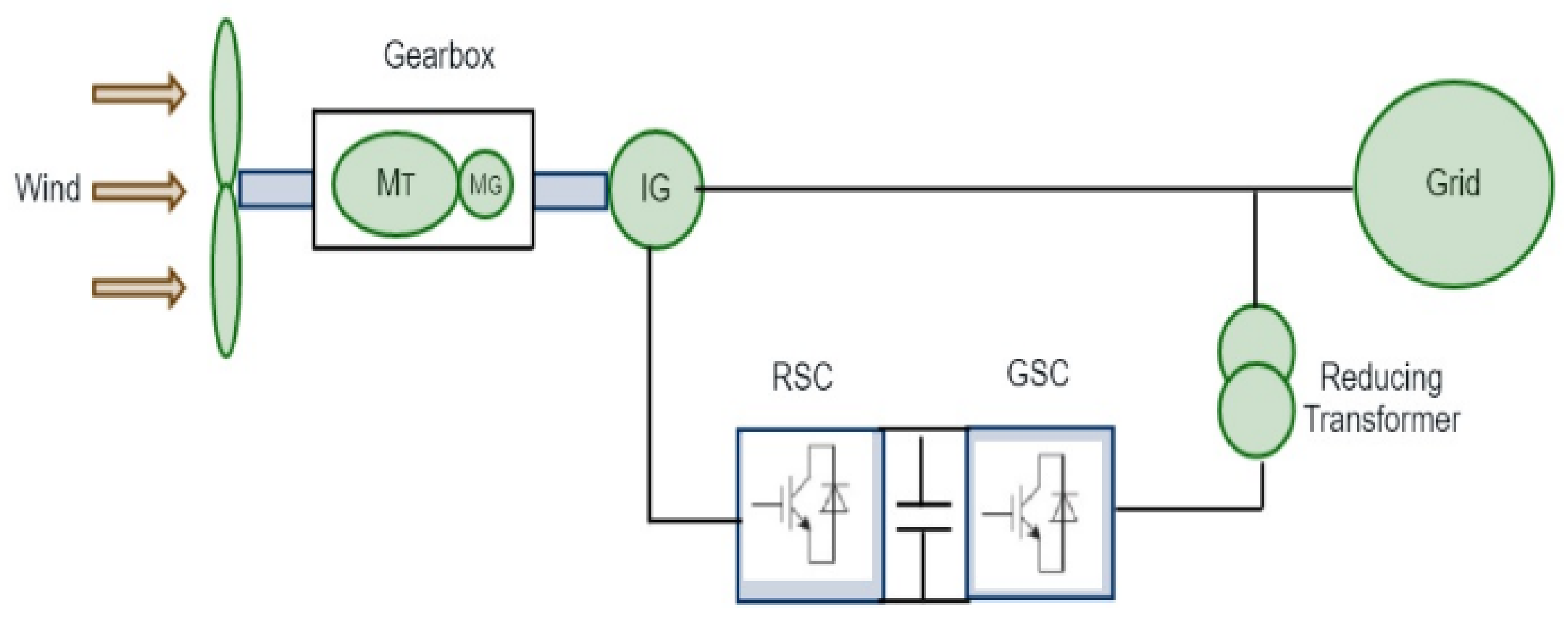
2.2. Model of DFIG-Based Wind Farm
3. Definition of SSR
4. Modeling of Wide-Area Fuzzy Controller in the System under Study
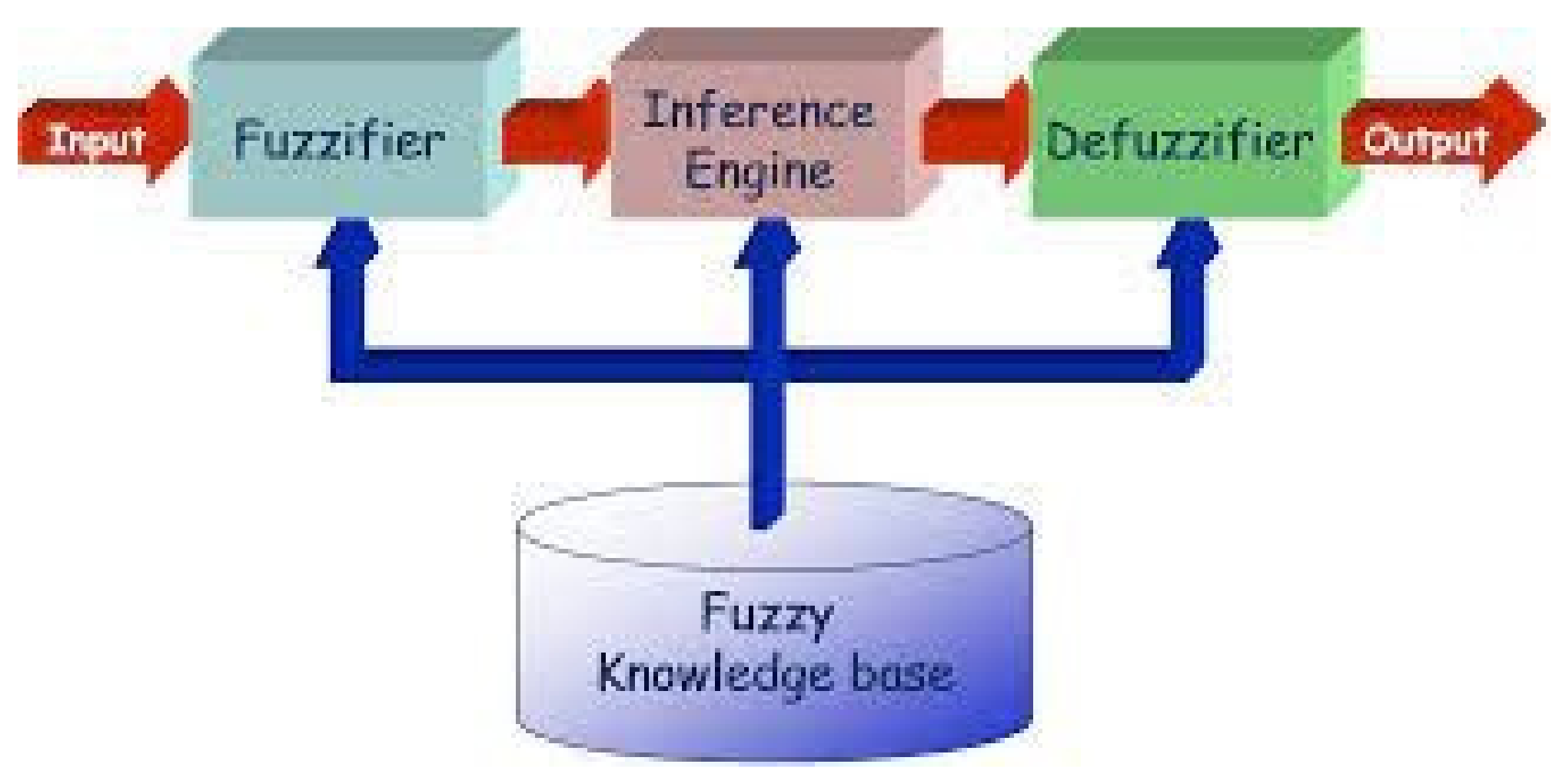
4.1. Review of Fuzzy Logic
4.2. Review on Wide-Area Measurement Systems
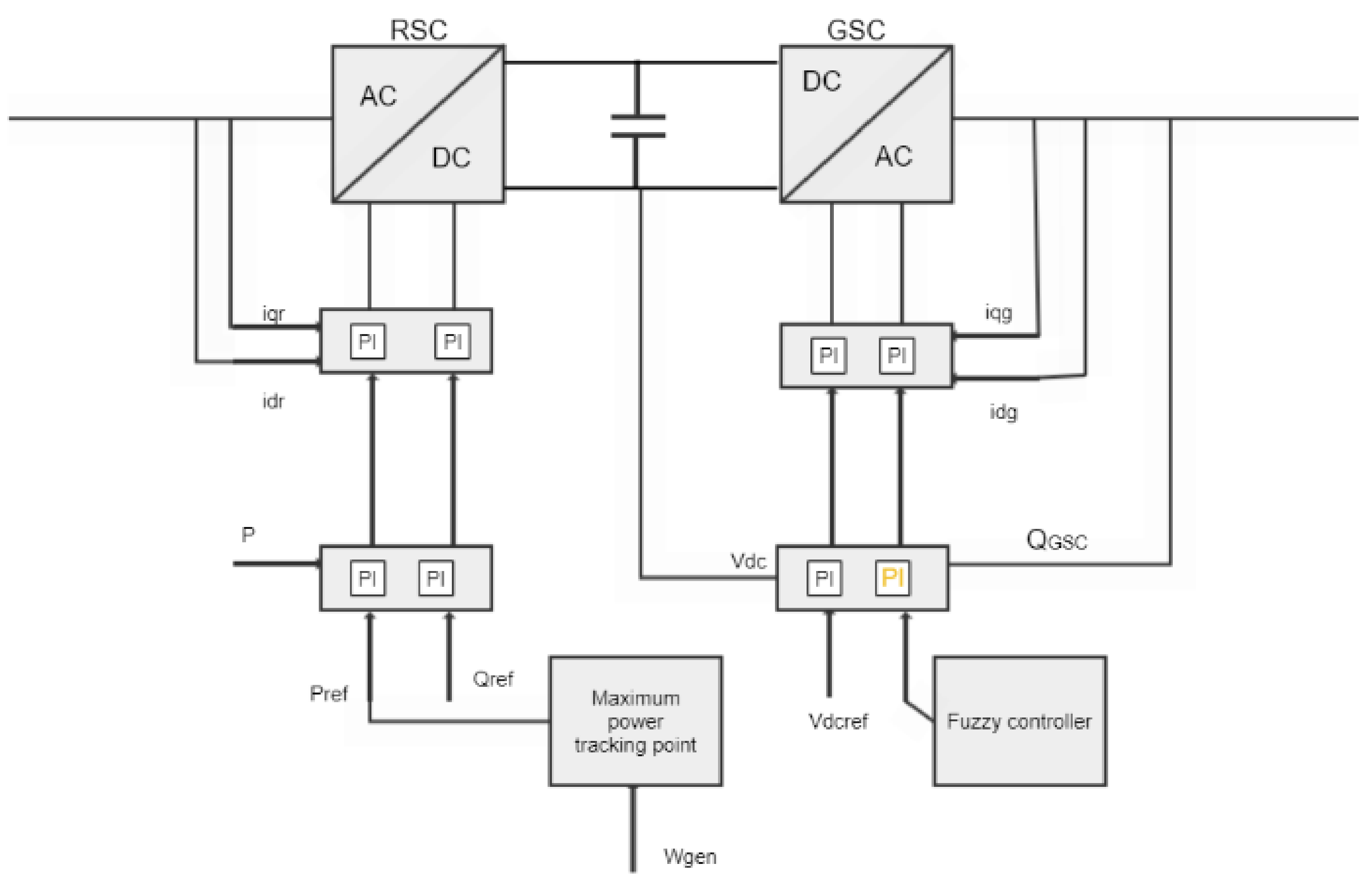
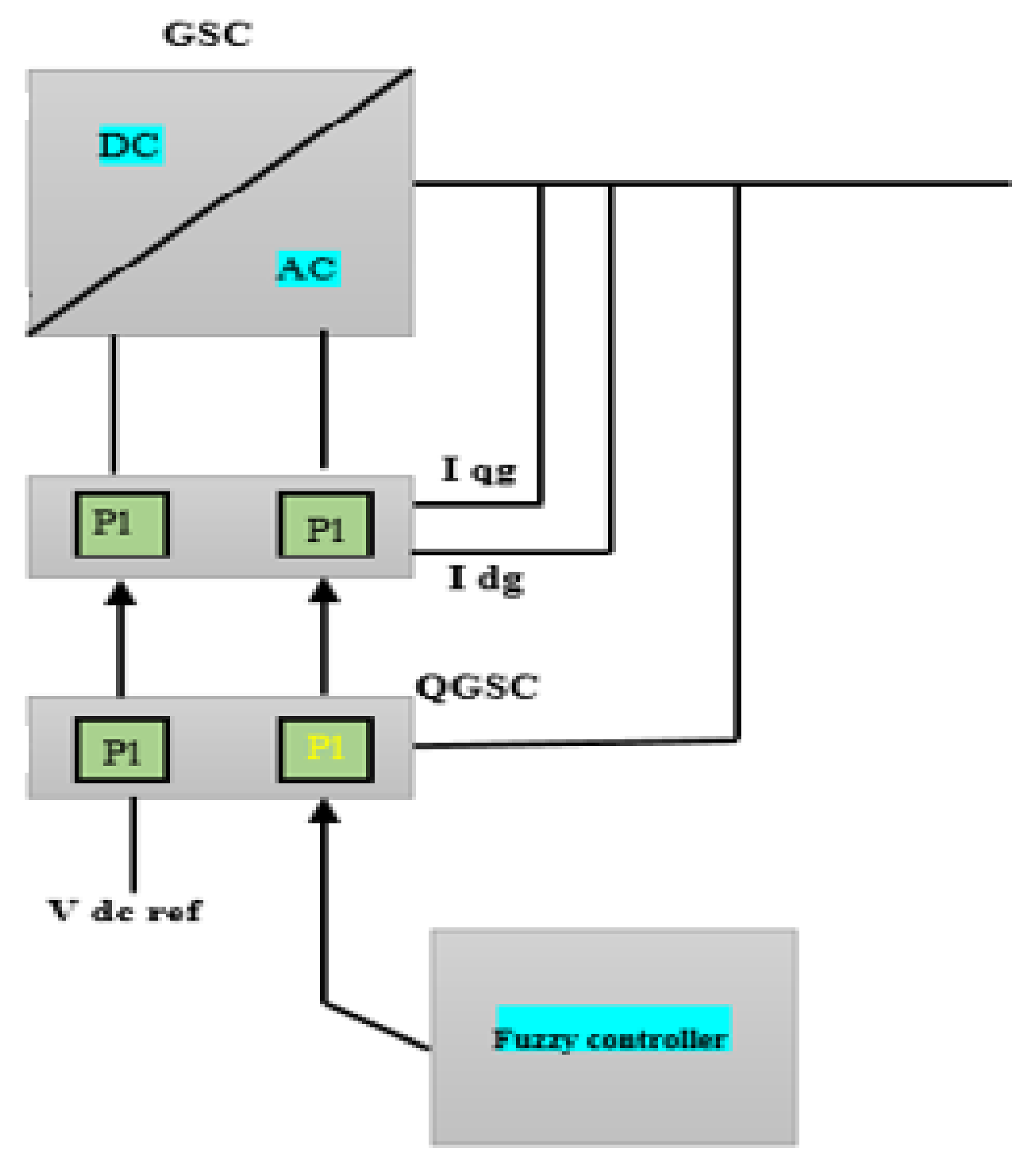
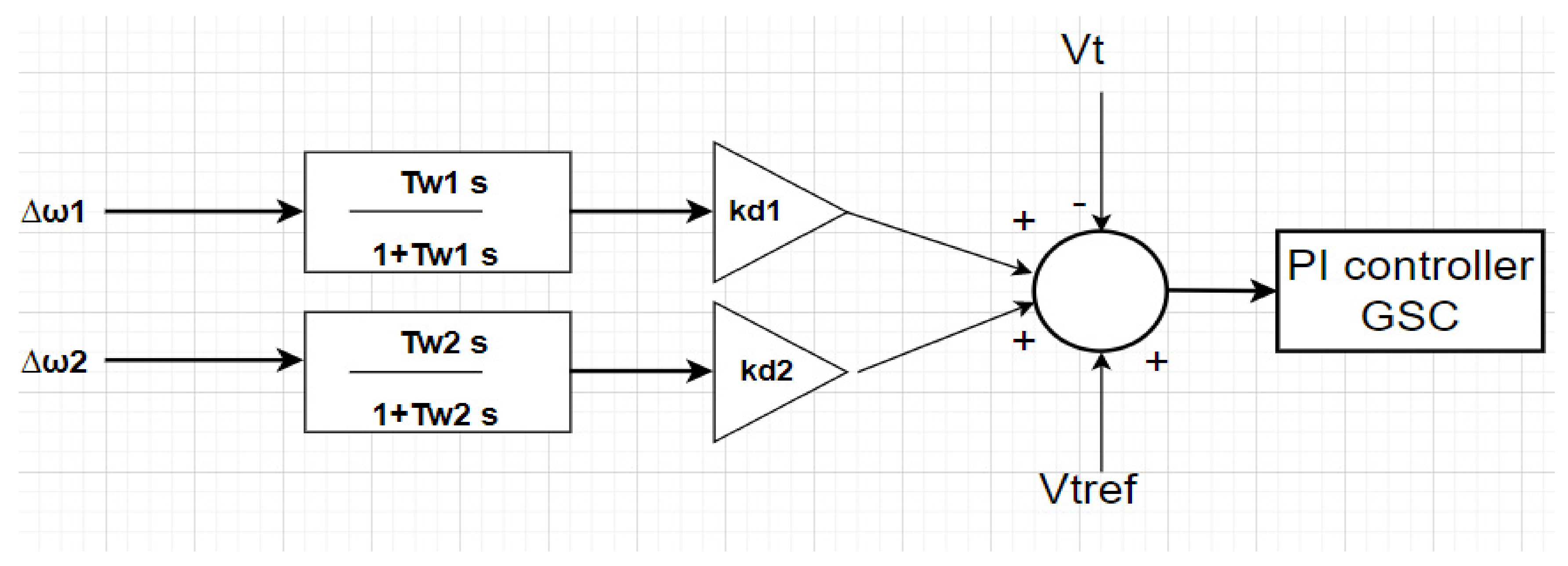
4.3. Fuzzy Controller Based on Wide-Area Measurement System
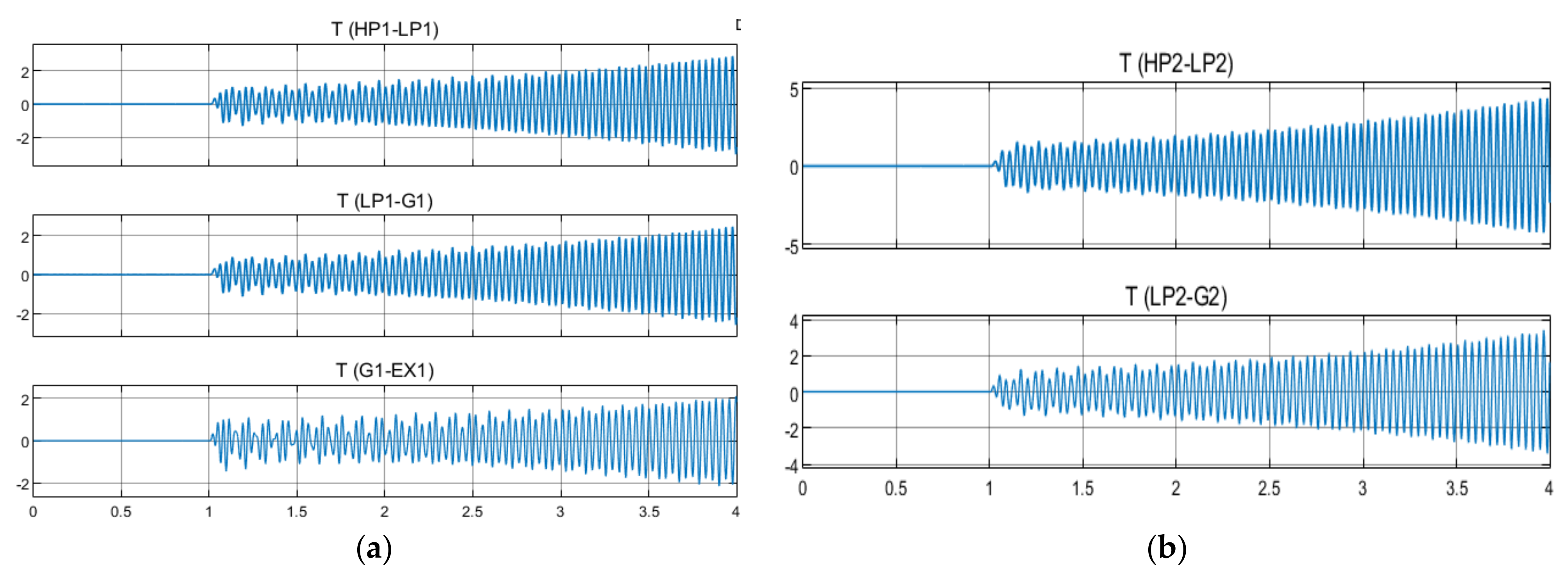
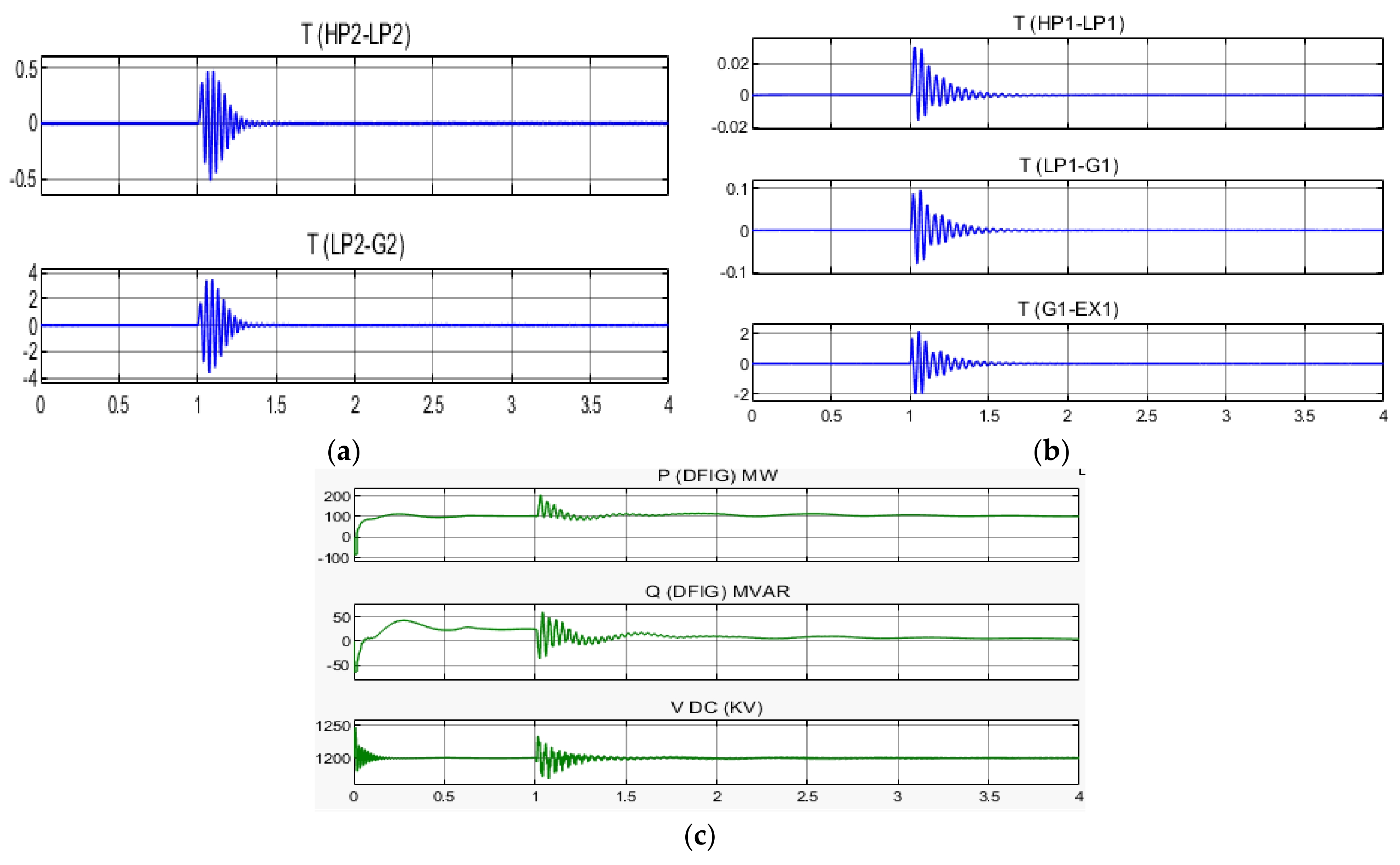
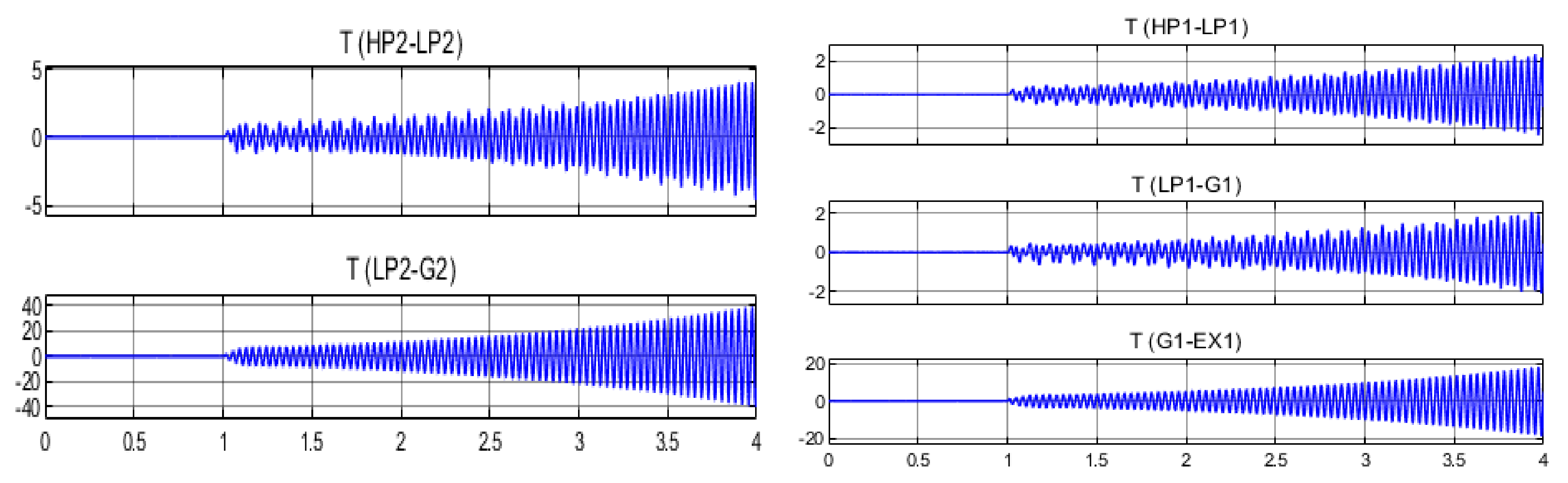
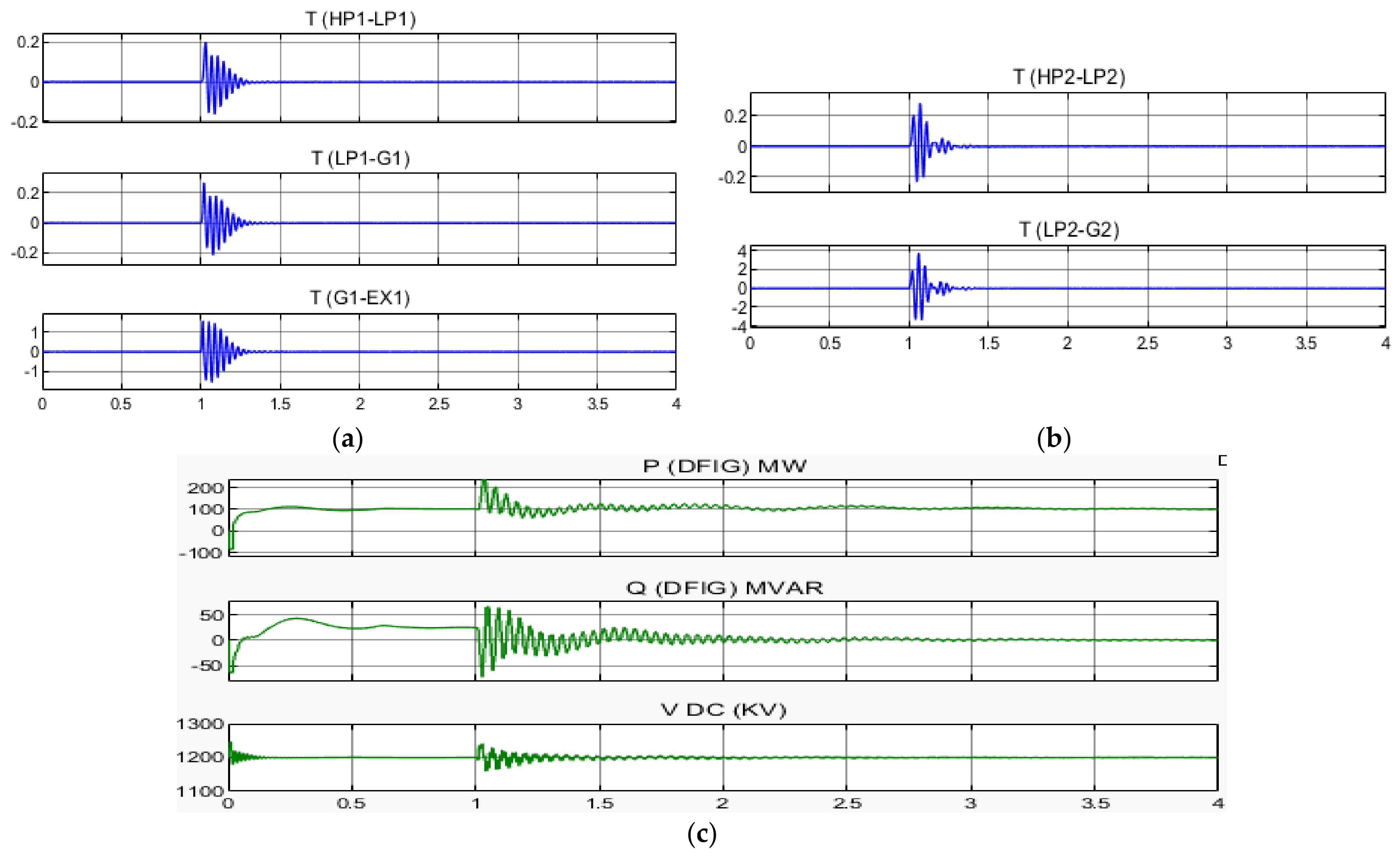
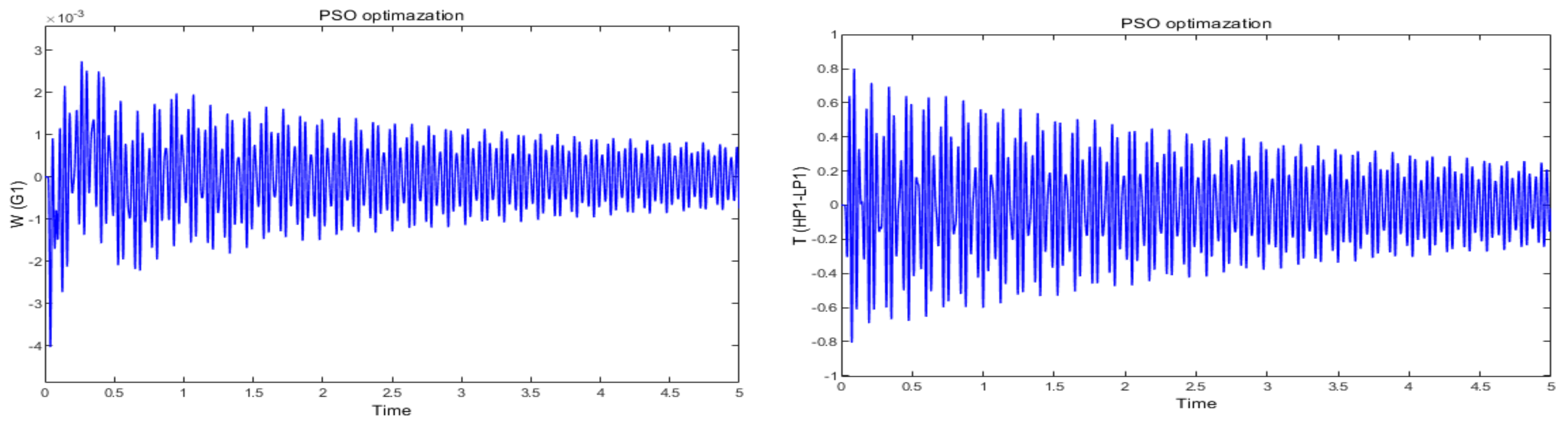
5. Simulation Result
5.1. Wide-Area Fuzzy Controller without Time Delay
5.2. Wide-Area Fuzzy Controller with Time Delay
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Systems Parameters
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| KGEN-EXC | 2.82 pu/rad | HIP | 0.155589 |
| KLPB-GEN | 70.858 pu/rad | HLPB | 0.884215 |
| KHP-IP | 19.303 pu/rad | HEXC | 0.0342165 |
| KIP-LPA | 34.929 pu/rad | HHP | 0.092897 |
| KLPA-LPB | 52.038 pu/rad | HLPA | 0.858670 |
| HGEN | 0.868495 | ||
| Parameter | Lower Bound | Upper Bound |
|---|---|---|
| Base Power | 2 MW | 100 MW |
| Based voltage (VLL) | 690 V | 690 V |
| Xls | 0.09231 | 0.09231 |
| Xlr | 0.09955 | 0.09955 |
| Rs | 0.00488 | 0.00488 |
| XM | 3.95279 | 3.95279 |
| Xtg | 0.3 (0.189 mH) | 0.3 (0.189/50 mH) |
| DC-link base voltage | 1.2 KV | 1.2 KV |
| DC-link capacitor | 14 mF | 0.7 F |
References
- Mohammadpour, H.A.; Santi, E. Modeling and control of gate-controlled series capacitor interfaced with a DFIG-based wind farm. IEEE Trans. Ind. Electron. 2014, 62, 1022–1033. [Google Scholar] [CrossRef]
- Xu, L.; Wang, Y. Dynamic modeling and control of DFIG-based wind turbines under unbalanced network conditions. IEEE Trans. Power Syst. 2007, 22, 314–323. [Google Scholar] [CrossRef]
- Hughes, F.M.; Anaya-Lara, O.; Jenkins, N.; Strbac, G. A power system stabilizer for DFIG-based wind generation. IEEE Trans. Power Syst. 2006, 21, 763–772. [Google Scholar] [CrossRef]
- Bialasiewicz, J.T.; Muljadi, E. The wind farm aggregation impact on power quality. In Proceedings of the 32nd Annual Conference on IEEE Industrial Electronics IECON 2006, Paris, France, 7–10 November 2006; pp. 4195–4200. [Google Scholar]
- Yan, G.; Wang, D.; Jia, Q.; Hu, W. Equivalent Modeling of Dfig-Based Wind Farms for Sub-Synchronous Resonance Analysis. Energies 2020, 13, 5426. [Google Scholar] [CrossRef]
- Fateh, D.; Birjandi, A.A.M.; Guerrero, J.M. A subsynchronous resonance prevention for DFIG-based wind farms. Turk. J. Electr. Eng. Comput. Sci. 2020, 28, 2670–2685. [Google Scholar] [CrossRef]
- Sewdien, V.; Wang, X.; Rueda Torres, J.; van der Meijden, M. Critical review of mitigation solutions for SSO in modern transmission grids. Energies 2020, 13, 3449. [Google Scholar] [CrossRef]
- Liu, H.; Xie, X.; Zhang, C.; Li, Y.; Liu, H.; Hu, Y. Quantitative SSR analysis of series-compensated DFIG-based wind farms using aggregated RLC circuit model. IEEE Trans. Power Syst. 2016, 32, 474–483. [Google Scholar] [CrossRef]
- Jiao, Y.; Li, F.; Dai, H.; Nian, H. Analysis and mitigation of sub-synchronous resonance for doubly fed induction generator under VSG control. Energies 2020, 13, 1582. [Google Scholar] [CrossRef] [Green Version]
- Naduvathuparambil, B.; Valenti, M.C.; Feliachi, A. Communication delays in wide-area measurement systems; Cat. No. 02EX540. In Proceedings of the IEEE Thirty-Fourth Southeastern Symposium on System Theory, Huntsville, AL, USA, 19 March 2002; pp. 118–122. [Google Scholar]
- Mohammadpour, H.A.; Santi, E. Analysis of sub-synchronous resonance (SSR) in doubly-fed induction generator (DFIG)-based wind farms. Synth. Lect. Power Electron. 2015, 5, 58–64. [Google Scholar] [CrossRef]
- Wang, L.; Xie, X.; Jiang, Q.; Liu, H.; Li, Y.; Liu, H. Investigation of SSR in practical DFIG-based wind farms connected to a series-compensated power system. IEEE Trans. Power Syst. 2018, 30, 2772–2780. [Google Scholar] [CrossRef]
- Alatar, F.; Mehrizi-Sani, A. Frequency scan–based mitigation approach of subsynchronous control interaction in type-3 wind turbines. Energies 2021, 14, 4626. [Google Scholar] [CrossRef]
- Vajpayee, S.; Panda, N.R.; Behera, P.; Swain, S.C. Implementation of PLL algorithm in DFIG based wind turbine connected to utility grid. In Proceedings of the IEEE 2020 Second International Conference on Inventive Research in Computing Applications (ICIRCA), Coimbatore, India, 15–17 July 2020; pp. 549–553. [Google Scholar]
- Musarrat, M.N.; Fekih, A.; Islam, M.R. An improved fault ride through scheme and control strategy for DFIG-based wind energy systems. IEEE Trans. Appl. Supercond. 2021, 31, 5401906. [Google Scholar] [CrossRef]
- Qiu, M.; Su, H.; Chen, M.; Ming, Z.; Yang, L.T. Balance of security strength and energy for a PMU monitoring system in smart grid. Commun. Protoc. Algorithms Smart Grid 2012, 50, 142–149. [Google Scholar] [CrossRef]
- Joint Working Group from the CIGRE Study Committees. Challenges with Series Compensation Applications in Power Systems when Overcompensating Lines. Electra, April 2021. Available online: https://electra.cigre.org/315-april-2021(accessed on 25 July 2021).
- Impram, S.; Nese, S.V.; Oral, B. Challenges of renewable energy penetration on power system flexibility: A survey. Energy Strategy Rev. 2020, 31, 100539. [Google Scholar] [CrossRef]
- Zhang, J.; Li, H.; Chen, D.; Xu, B.; Mahmud, M.A. Flexibility assessment of a hybrid power system: Hydroelectric units in balancing the injection of wind power. Renew. Energy 2021, 171, 1313–1326. [Google Scholar] [CrossRef]
- Fan, L.; Miao, Z. Mitigating SSR using DFIG-based wind generation. IEEE Trans. Sustain. Energy 2012, 3, 349–358. [Google Scholar] [CrossRef]
- Mohammadpour, H.A.; Ghaderi, A.; Mohammadpour, H.; Santi, E. SSR damping in wind farms using observed-state feedback control of DFIG converters. Electr. Power Syst. Res. 2015, 123, 57–66. [Google Scholar] [CrossRef]
- Din, Z.; Zhang, J.; Bassi, H.; Rawa, M.; Song, Y. Impact of phase locked loop with different types and control dynamics on resonance of DFIG system. Energies 2020, 13, 1039. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Xie, X.; Liu, H.; Liu, H.; Li, Y.; Zhang, C. Mitigation of sub-synchronous control interaction in wind power systems with GA-SA tuned damping controller. IFAC-PapersOnLine 2017, 50, 8740–8745. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, Q.; Yang, R.; Tao, G.; Liu, Z. H∞ current damping control of DFIG based wind farm for sub-synchronous control interaction mitigation. Int. J. Electr. Power Energy Syst. 2018, 98, 509–519. [Google Scholar] [CrossRef]
- Liu, H.; Xie, X.; Li, Y.; Liu, H.; Hu, Y. Mitigation of SSR by embedding subsynchronous notch filters into DFIG converter controllers. IET Gener. Transm. Distrib. 2017, 11, 2888–2896. [Google Scholar] [CrossRef]
- Yan, X.; Chang, W.; Cui, S.; Rassol, A.; Jia, J.; Sun, Y. Recurrence of sub-synchronous oscillation accident of hornsea wind farm in UK and its suppression strategy. Energies 2021, 14, 7685. [Google Scholar] [CrossRef]
- Irwin, G.D.; Jindal, A.K.; Isaacs, A.L. Sub-synchronous control interactions between type 3 wind turbines and series compensated AC transmission systems. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–6. [Google Scholar]
- Raju, D.K.; Umre, B.S.; Junghare, A.S.; Babu, B.C. Mitigation of subsynchronous resonance with fractional-order PI based UPFC controller. Mech. Syst. Signal. Process. 2017, 85, 698–715. [Google Scholar] [CrossRef]
- Raju, D.K.; Umre, B.S.; Junghare, A.S.; Thakre, M.P.; Motamarri, R.; Somu, C. Fractional-order PI based STATCOM and UPFC controller to diminish subsynchronous resonance. SpringerPlus 2016, 5, 1599. [Google Scholar]
- Raju, D.K.; Umre, B.S.; Junghare, A.S.; Babu, B.C. Improved control strategy for subsynchronous resonance mitigation with fractional-order pi controller. Int. J. Emerg. Electr. Power Syst. 2016, 17, 683–692. [Google Scholar] [CrossRef]
- Dhenuvakonda, K.R.; Singh, A.R.; Thakre, M.P.; Umre, B.S.; Kumar, A.; Bansal, R.C. Effect of SSSC-based SSR controller on the performance of distance relay and adaptive approach using synchronized measurement. Int. Trans. Electr. Energy Syst. 2018, 28, e2620. [Google Scholar] [CrossRef] [Green Version]






| A | B | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| P | N | ZE | P | N | ZE | ||||
| G1 | PL | PL | PM | PL | G2 | PL | PL | PM | PL |
| PM | PL | PS | PM | PM | PL | PS | PM | ||
| PS | PM | ZE | PS | PS | PM | ZE | PS | ||
| ZE | PM | NM | ZE | ZE | PM | NM | ZE | ||
| NS | ZE | NM | NS | NS | ZE | NM | NS | ||
| NM | NS | NL | NM | NM | NS | NL | NM | ||
| NL | NM | NL | NL | NL | NM | NL | NL | ||
| Communication Data Delays | Associated Delay (ms) |
|---|---|
| Telephone Lines | 200–350 |
| Satellite link | 500–700 |
| Time Delay | PL | PM | PS | ZE | NS | NM | NL | ||
|---|---|---|---|---|---|---|---|---|---|
| M | P | PM | NL | PL | PM | PM | NM | PM | |
| N | NL | ZE | PM | NL | NS | NM | PS | ||
| ZE | NS | PS | NM | ZE | PL | NM | NL | ||
| L | P | ZE | PM | PL | NM | NL | NM | PM | |
| N | PL | ZE | NM | NM | PM | PS | NM | ||
| ZE | PS | NL | ZE | PL | NM | ZE | PL | ||
| Optimization Methods | ||
|---|---|---|
| PSO | 0.64 | 0.38 |
| ICA | 0.72 | 0.57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bostani, Y.; Jalilzadeh, S.; Mobayen, S.; Rojsiraphisal, T.; Bartoszewicz, A. Damping of Subsynchronous Resonance in Utility DFIG-Based Wind Farms Using Wide-Area Fuzzy Control Approach. Energies 2022, 15, 1787. https://doi.org/10.3390/en15051787
Bostani Y, Jalilzadeh S, Mobayen S, Rojsiraphisal T, Bartoszewicz A. Damping of Subsynchronous Resonance in Utility DFIG-Based Wind Farms Using Wide-Area Fuzzy Control Approach. Energies. 2022; 15(5):1787. https://doi.org/10.3390/en15051787
Chicago/Turabian StyleBostani, Yaser, Saeid Jalilzadeh, Saleh Mobayen, Thaned Rojsiraphisal, and Andrzej Bartoszewicz. 2022. "Damping of Subsynchronous Resonance in Utility DFIG-Based Wind Farms Using Wide-Area Fuzzy Control Approach" Energies 15, no. 5: 1787. https://doi.org/10.3390/en15051787
APA StyleBostani, Y., Jalilzadeh, S., Mobayen, S., Rojsiraphisal, T., & Bartoszewicz, A. (2022). Damping of Subsynchronous Resonance in Utility DFIG-Based Wind Farms Using Wide-Area Fuzzy Control Approach. Energies, 15(5), 1787. https://doi.org/10.3390/en15051787








