Extraction of Time-Domain Characteristics and Selection of Effective Features Using Correlation Analysis to Increase the Accuracy of Petroleum Fluid Monitoring Systems

Abstract

In the current paper, a novel technique is represented to control the liquid petrochemical and petroleum products passing through a transmitting pipe. A simulation setup, including an X-ray tube, a detector, and a pipe, was conducted by Monte Carlo N Particle-X version (MCNPX) code to examine a two-by-two mixture of four diverse petroleum products (ethylene glycol, crude oil, gasoline, and gasoil) in various volumetric ratios. As the feature extraction system, twelve time characteristics were extracted from the received signal, and the most effective ones were selected using correlation analysis to present reasonable inputs for neural network training. Three Multilayers perceptron (MLP) neural networks were applied to indicate the volume ratio of three kinds of petroleum products, and the volume ratio of the fourth product can be feasibly achieved through the results of the three aforementioned networks. In this study, increasing accuracy was placed on the agenda, and an RMSE < 1.21 indicates this high accuracy. Increasing the accuracy of predicting volume ratio, which is due to the use of appropriate characteristics as the neural network input, is the most important innovation in this study, which is why the proposed system can be used as an efficient method in the oil industry.

1. Introduction

Poly-pipelines are mostly applied in the petrochemical industry for oil transmission or its derivatives to distribution centers. Using a pipeline to transport diverse petroleum fluids is highly economic; however, some problems such as mixing various petroleum fluids indicate the significance of extending a sustainable, non-invasive technique to control and detect the interference region. Due to the mentioned issue, a number of verifications have been conducted, which are concisely demonstrated. Salgado et al. established a petrochemical product density detection system, including a CS-137 source and a NaI detector [1]. The MCNPX code was utilized in such an examination. Via an artificial neural network, the scholars could predict the density of petroleum products with high accuracy independent of fluid admixture. Likewise, for Monte Carlo code validation, they staged a laboratory structure using a cesium source, a glass pipe, and a sodium iodide detector. Various volume percentages were simulated for both oil and water fluids. They could determine the volume percentages with 99% accuracy [2]. In other analyses, the authors simulated two-phase [3,4,5] and three-phase [6,7,8] at diverse volumetric percentages and flow regimes. It is worth noting that with different neural networks, such as MLP [9,10], RBF [11,12], an adaptive neuro-fuzzy inference system [13], the Jaya algorithm [14], and the GMDH neural network [15], the mentioned parameters were determined. Although the mentioned studies were able to obtain the volume percentages and types of flow regimes, not using the feature extraction techniques from the received signals reduced the accuracy and increased the computational cost in the presented systems. Nowadays, the application of characteristic derivation methods such as time-domain [16,17], frequency domain [18], and time-frequency domain [19] is of high significance for the authors. In all concerned investigations, the authors have provided various characteristics to distinguish the kind of flow regimes and detect the volume percentages. Sattari et al. applied a GMDH neural network to detect the kind of flow regimes and volume percentages [20]. By MCNPX code, these researchers simulated a frame including a CS-137 source, a Pyrex pipe, and a NaI detector. They derived the time domain features of the detected signal and regarded them as neural network inputs. They could classify all flow regimes and predict volume percentages with an RMSE < 1.1.

Currently, due to numerous advantages, using X-ray tubes is of high prominence for authors. The utilization of X-ray tubes as a source has the following benefits rather than the other sources such as radioisotopes. The X-ray tube can adjust the distributed photon energy, while the photon emission energy is stable in radioisotopes. It is highly noted that the radioisotope functions decline over time; however, the X-ray tube does not work this way. The X-ray tube can be turned on and off, which is highly prominent for individual health when dealing with these instruments. They are also more feasible to transport than radioisotopes. In previous research, Roshani et al. presented a fluid controlling system passing over transfer tubes [21]. Although they forecasted the volumetric ratio of petroleum products with significant precision, seemingly one of the issues in this study is the lack of using characteristic derivation methods. More studies have been performed for detecting the volume percentages of two-phase [22,23] and three-phase [24,25] flows by X-ray tubes. As the scholars believe, the characteristic extraction methods enhance the precision of detecting the sort of flow regimes and volume percentages. The simulated structure in this study becomes validated with numerous experiments in our preceding work [11]. The experiments and, therefore, the simulations have been carried out inside the static situation. The actual running situation is dynamic; however, the reference points for schooling the detection device are fixed, and it is able to be taken into consideration as a static situation. These constant points have been used for schooling the detection device so that you can decide the volume ratio in the detection device in an actual situation. In [26], prompt gamma-ray neutron activation evaluation for the quantitative evaluation was taken into consideration for rapid, non-intrusive and online measurements of multiphase oil/gas/seawater flow. In this study, all the simulations have been taken into consideration in a static situation before being utilized in an actual situation. In [27], the feasibility of the usage of detection of transmitted and scattered gamma radiation for characterization of produced water from offshore oil wells has been demonstrated. By the approach of transmitted and scattered gamma rays and calibration measurements, the salinity and sort of salt within the produced water have been determined. All of the simulations have been in a. static situation; however, they were eventually utilized in an actual situation.

Increasing the accuracy of diagnostic systems is one of the most important challenges for researchers in this field. Inspired by former research, in this study, it is attempted to provide a high-accuracy controlling system that recognizes the volume ratio of diverse oil products. This increase in accuracy has been achieved by extracting time characteristics and finding the most appropriate ones using correlation analysis as well as designing a suitable neural network. The recent paper will be proposed as follows. First, the structure of the simulation will be illustrated in detail. The second section represents the feature extraction technique to derive the received signal features. In the next part, the MLP neural network will be mentioned, and the results, as well as the precision of the designed networks, will be indicated. Finally, the conclusion is proposed in the last section.

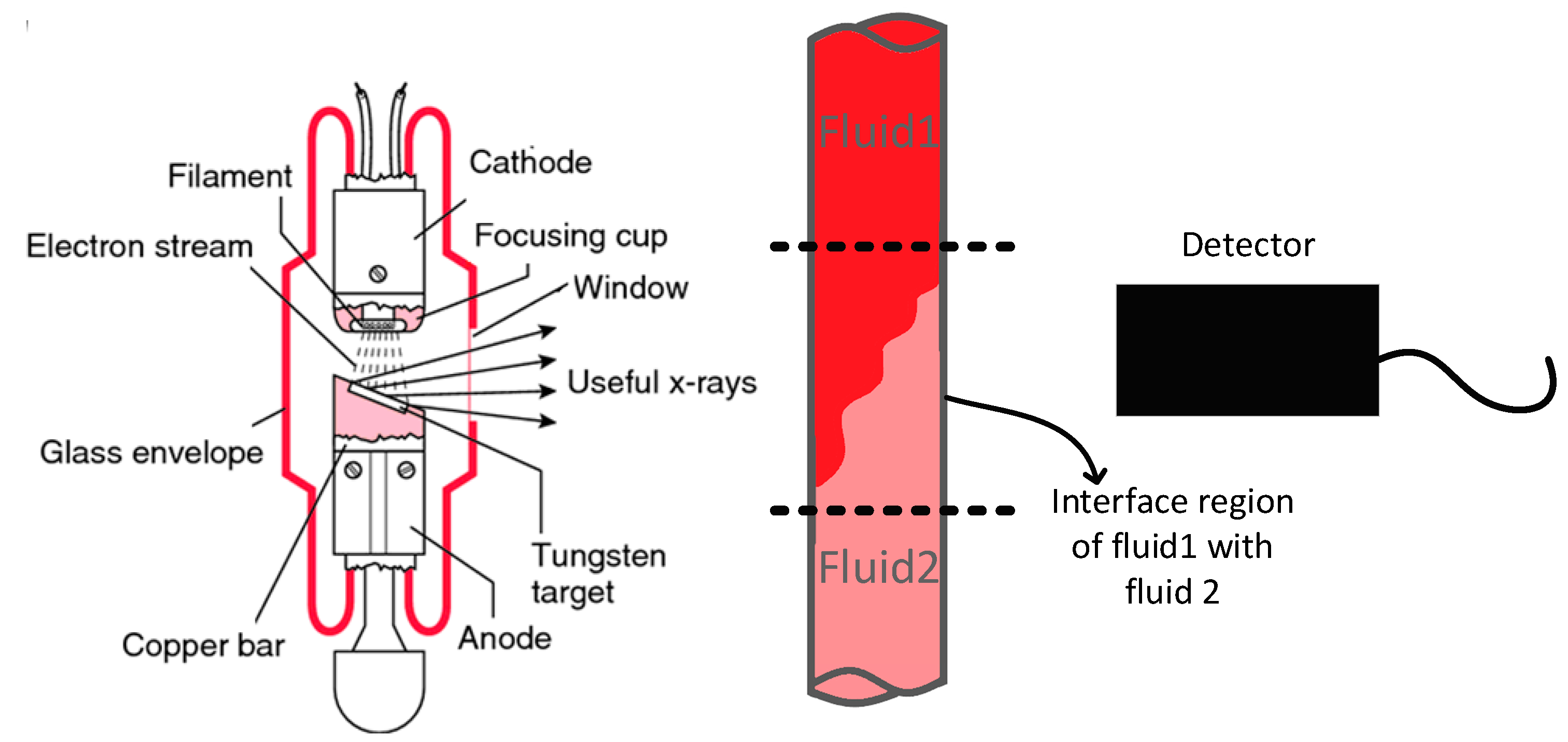
2. Simulation System

The simulation setup includes an X-ray tube, a pipe, and a NaI detector (Figure 1) and was conducted through MCNPX code [28]. A normal industrial X-ray tube was applied in this study. The electron source and a tungsten/rubidium target are embedded in X-ray tubes as the cathode and anode, respectively. Likewise, the shields with an output window, as well as a filter against the output window, are utilized. A perfect X-ray tube simulation by MCNPX code is time-demanding, in which an emitted electron from the cathode responds to the anode and generates an X-ray emission. Since the calculation of photons passing MCNPX code is lower than the electron, in this study, a source of photons mounted in an X-ray tube’s shield was considered for a cathode–anode collection. TASMIC, a free package proposed by Hernandez et al. [29], was utilized. It is worth noting that numerous investigations have been performed on X-ray spectra generation by both theoretical and MCNP techniques [30,31]. Figure 2 indicates the normalized conducted X-ray spectrum, as well as the characteristics of X-ray peaks in relevance to the tungsten target (Kα1, Kα2, Kβ1, and Kβ2). The previously mentioned photon source was embedded in a cylinder serving as an X-ray tube layer. The circular profile on the X-ray tube acting as the output window is 5 cm. It is highly important to mention that the cylindrical shape commonly constitutes the X-ray tube shields made up of lead or steel to prevent the converse radiation diffusions generated by X-ray. On the shield surface, a section is left open, as the output window, in order to release the congenial generated X-ray photons. To filter low-energy photons in this research, an aluminum filter having a thickness of 2.5 mm was mounted against the output window.

Transmitting pipes are applied to transmit different petroleum products, in some sections of which are followed by each other and are combined together. This zone is known as the interface region. In this study, four kinds of petroleum products—ethylene glycol, crude oil, gasoil, and gasoline—with densities of 1.114, 0.975, 0.826, and 0.721 g·cm⁻¹, respectively, are considered as crossing fluids through the pipe. By combining two-by-two of the total of the mentioned products, six admixtures will be achieved. Different volume ratios from 0% to 100% with 5% steps were simulated for six various whole states (in the current study, 118 simulations have been conducted). Data from all the simulations were gathered by an NaI detector using a pulse height tally (tally type F8) in Monte Carlo code and applied for future processing. Pseudo-random number generators (PRNG), which are intensively used in many stochastic algorithms in particle simulations and artificial neural networks, were used in MCNP code. Furthermore, the “STOP” card was used for obtaining the desired error in simulations.

3. Feature Extraction

There are various methods for extracting the characteristics of a signal, including the extraction of characteristics in the time domain, in the frequency domain, and combined methods in the time-frequency domain, as well as innovative methods. The purpose of feature extraction is to reduce the size of the signals while preserving the signal properties as well as better interpreting the signals. In this research, the feature extraction technique in the time domain was used. For this purpose, twelve features were extracted from the received signal as follows:

• Average value:

  $$m=\frac{1}{N}{\sum }_{n=1}^{N}x\left(n\right)$$

  (1)
• Standard deviation:

  $$STD=\sqrt{\frac{1}{N-1}{\sum }_{n=1}^N{\left|x_n-m\right|}^2}$$

  (2)
• Fourth-order moment:

  $$m_4=\frac{1}{N}{\sum }_{n=1}^N{\left[x\left(n\right)-m\right]}^4$$

  (3)
• Root mean square:

  $$RMS=\sqrt{m^2+{\sigma }^2}$$

  (4)
• Skewness:

  $$g_1=\frac{m_3}{{\sigma }^3}, m_3=\frac{1}{N}{\sum }_{n=1}^N{\left[x_n-m\right]}^3$$

  (5)
• Kurtosis:

  $$g_2=\frac{m_4}{{\sigma }^4}$$

  (6)
• Median:

  $$\{\begin{array}{ccc}odd\hfill & median=x_k& k=\frac{n+1}{2}\\ even& median=\frac{1}{2}\left(x_k+x_{k+1}\right)& k=\frac{n}{2}\end{array}$$

  (7)
• Waveform length (WL):

  $$\mathrm{WL}={\sum }_{n=0}^{N-1}\left|x_{n+1}-x_n\right|$$

  (8)
• Absolute value of the summation of square root (ASS):

  $$\mathrm{ASS}=\left|{\sum }_{n=1}^N{\left(x_n\right)}^{0.5}\right|$$

  (9)
• Mean value of the square root (MSR):

  $$\mathrm{MSR}=\frac{1}{N}{\sum }_{n=1}^N{\left(x_n\right)}^{0.5}$$

  (10)
• Absolute value of the summation of the ^{exp th} root (ASM):

  $$\mathrm{ASM}=|\frac{{\sum }_{n=1}^N{\left(x_n\right)}^{exp}}{N}|, exp=\{\begin{array}{cc}0.05& if (n>0.25·N and n<0.75·N)\\ 0.75& otherwise\end{array}$$

  (11)
• Maximum value:

  $$\mathrm{Max}=\mathrm{MAX} \left(x_n\right)$$

  (12)

One of the most important challenges of this research is to determine the most effective characteristic for determining the volume ratio of each oil product. Correlation analysis was used for this purpose. The result of the correlation analysis between the extracted characteristics is shown in Figure 3. As shown in this figure, many features are very similar to each other, and their selection as the network input is ineffective. However, the characteristics of the fourth-order moment, skewness, and kurtosis are the least similar to each other, so these characteristics have been selected as the input of the neural network.

4. Artificial Neural Network

In the past few decades, various advanced computational methods have been applied in various fields of study such as chemical engineering [32,33,34,35,36,37], electrical and computer engineering [38,39,40,41], civil engineering [42,43,44], mechanical engineering [45,46,47,48,49,50,51], petroleum engineering [52,53,54,55,56,57,58,59,60,61,62,63], and environmental engineering [64,65], etc. The ANN has been demonstrated to be the most potent technique for classification and prediction among the aforementioned computational methods. A type of neural network is based on a computational unit called a perceptron. A perceptron takes vectors of inputs with real values and calculates a linear combination of these inputs. If the result is more than a threshold value, the perceptron output will be equal to 1 and otherwise equal to −1. Perceptron output is determined by the following equation [66,67]:

$$y=f({\sum }_{i=1}^u{w}_i{x}_i+w_i)$$

(13)

In case the perceptron has two inputs x₁ and x₂, it divides the page into two parts, and the equation of the dividing line is determined as follows:

$$w_1{x}_1+w_2{x}_2+w_0=0$$

(14)

Therefore, the perceptron can be considered as a hyperplane in the n-dimensional space of the samples. Perceptron sets a value of 1 for samples on one side of the page and −1 for values on the other side of the screen and can only learn examples that are linearly separable. Such examples are cases that can be completely separated by a hyperplane. The purpose of training a perceptron is to find the values of its weights, so that the perceptron generates the correct values for the training examples. Different kinds of numerical calculations [68,69,70,71,72,73,74,75,76,77,78] and soft computing [79,80,81,82,83,84,85,86] have been used in various fields such as electrical engineering problems [87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102], computer sciences problems [103,104], and basic sciences [105,106,107,108,109], etc. In this paper, the perceptron learning algorithm is as follows—this algorithm is shown in Figure 4 as a flowchart:

• Random values are attributed to weights.
• Perceptron is applied to each training sample. If the samples are evaluated incorrectly, the values of perceptron weights are corrected.
• Is all the training properly evaluated?
• Yes, the end of the algorithm.
• No, back to step 2.

Networks made of one neuron have limitations. These networks do not have the ability to implement nonlinear functions. Other networks have been suggested to solve this problem. Multilayer perceptron (MLP) networks are among the most useful neural networks. This network is able to perform a nonlinear mapping with high accuracy, and this is what is proposed in engineering problems as the main solution. This network represents feed forward networks, and the output is calculated directly from the input without any feedback. The neuron model in the MLP network includes a nonlinear activation function. The important point to emphasize here is that the activation function must be continuous and derivable at all points. The nonlinearity of the activation function is very important because, otherwise, the network performance will be reduced to the level of the single-layer perceptron.

The obtained data are divided into three categories: training, validation and testing data.

Training dataset: The data that the network sees and learns with. The model fits with these data.

Validation dataset: The dataset that is used as input for the network validating during training to evaluate the training process. The neural network sees these dates but is not trained with them.

Testing dataset: The dataset is injected into the neural network at the end of the training process to test the final performance of the designed network.

The use of the validation test data in the network training process will give us the reassurance to avoid under-fitting and over-fitting problems.

The used validation methods and training processes in this paper are well-known methods in most modeling and optimization problems, which have been used in many studies [110,111,112,113,114,115]. In several studies [116,117,118,119,120,121,122,123,124,125], different mathematical methods such as feature extraction, feature reduction, feature selection, correlation analysis, and numerical calculation, etc., have been used. In this study, feature extraction in the time domain and correlation analysis were used in order to present a novel metering system.

5. Results Verification

In this study, the characteristics selected using correlation analysis were used as neural network inputs to determine the volume ratio. Three artificial neural networks were established to predict the volume ratios of ethylene glycol, crude oil, and gasoil. The structure of these networks is shown in Figure 5. By recognizing the volume ratio of the three given products, the ratio of the fourth product, i.e., gasoline, can be feasibly estimated. The features of the designed networks are visible in

Table 1. The characteristics of designed networks.

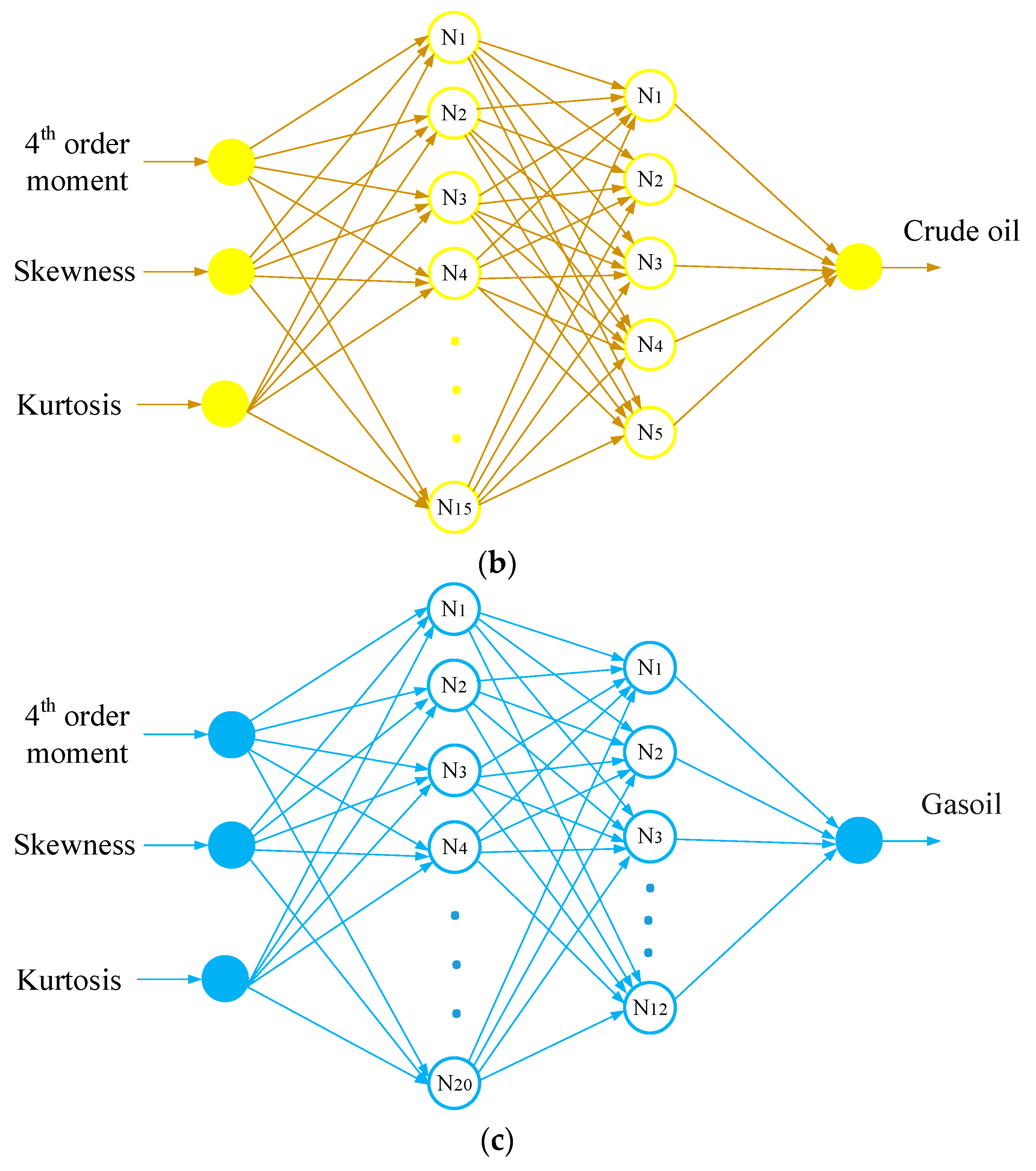
ANN Kind	MLP
	Ethylene Glycol	Gasoil	Crude Oil
No. of neurons in input layer	3	3	3
No. of neurons in the 1st hidden layer	24	20	15
No. of neurons in the 2nd hidden layer	11	12	5
No. of neurons in the output layer	1	1	1
No. of epoch	500	480	640
Activation function used for each hidden neuron	Tansig	Tansig	Tansig

.

Regression and error histogram diagrams in relevance to training, validation, and test data are obvious in Figure 6, Figure 7 and Figure 8 to display the precision of the designated networks. Regarding these three figures, in the regression diagram, the closer the red circles (representing the network output) to the black line (representing the target output), the higher the accuracy of the designed network. The error histogram plot also clearly shows the scatter of error between the desired output and the network output. The most prominent scale for assessing the operation of artificial neural networks is prediction precision. Some of the most significant prediction precision criteria calculated in this study are:

$$\mathrm{Root} \mathrm{Mean} \mathrm{Square} \mathrm{Error} \left(\mathrm{RMSE}\right)=\frac{{\sum }_{j=1}^N{\left(e_j\right)}^2}{N}$$

(15)

$$\mathrm{Mean} \mathrm{Absolut} \mathrm{Error} \left(\mathrm{MAE}\right)=\frac{1}{N}{\sum }_{j=1}^N\left|e\right|$$

(16)

where e is the error, and N presents the data number.

The amount of these calculated errors for all three implemented networks and for training, validation and test data is shown in

Table 2. The estimated error for established networks.

	Train Data		Validation Data		Test Data
	RMSE	MAE	RMSE	MAE	RMSE	MAE
Ethylene glycol	0.91	0.68	1.16	1.03	1.13	0.99
Crude oil	0.27	0.14	0.94	0.76	1.07	0.86
Gasoil	0.21	0.15	1.21	1.06	1.03	0.89

. The volume ratio of three products, namely ethylene glycol, crude oil, and gasoil, were obtained using an artificial neural network. The volume percentage of the fourth product (gasoline) can be easily calculated by subtracting the volume percentage of the three products from 100% of the pipe volume, which is shown graphically in Figure 9. The general process of the article to determine the percentage of volume ratios can be seen in Figure 10. The steps of determining the volume ratio include data acquisition, extracting time-domain features, introducing the most appropriate characteristics using correlation analysis, using selected features as neural network input for training, and finally, volume ratio prediction.

6. Discussion

In this study, for designing neural networks with high accuracy, networks with a different number of layers, from one layer to four layers, and with a different number of neurons in each layer were designed and their accuracy was examined. The design of these neural networks was achieved with the help of MATLAB R2018b software, and in this software, there is a function called “newff” for designing the multilayer perceptron neural network. No pre-designed toolboxes have been used and all the steps of training, validation, and testing of the network have been programmed step by step. The Levenberg–Marquardt algorithm has been used to train neural networks. This function does not provide users with any information about parameters such as momentum and learning rate, and the important challenge in using this function is to design a suitable structure to predict the target output with high accuracy. The high accuracy obtained in this research is a strong reason for the high performance of designed networks.

7. Conclusions

In the proposed article, the monitoring system consists of an X-ray tube, a NaI detector, and a pipe that has been simulated by MCNPX code. By simulating the combination of four petroleum products in diverse volume ratios and data collection registered by the detector, the time domain feature extraction method was utilized to derive the data characteristics, and a correlation analysis was applied to determine efficient ones. After that, the derived specifications were applied for implementing three MLP neural networks to predict the volume ratio of ethylene glycol, crude oil and gasoil. The designed networks were able to predict the volume ratio of ethylene glycol, crude oil and gasoil with RMSE less than 1.16, 1.07, and 1.21, respectively. It is highly noted that after estimating the volume ratio of three products, the volume ratio of the fourth product is feasibly estimated. Although the X-ray tube and radioisotopes have been utilized in previous research, applying the time-domain feature extraction technique and correlation analysis are the most important novelties of the proposed investigation, in which a high precision in determining the volumetric ratio (RMSE of less than 1.21) is the most profound result of applying this method. The use of frequency and time-frequency characteristics, as well as the use of different neural networks such as GMDH and RBF, can be a good clue for researchers in future research.