Control Strategy Assessment for Improving PEM Fuel Cell System Efficiency in Fuel Cell Hybrid Vehicles
Abstract
:1. Introduction
2. Methodology
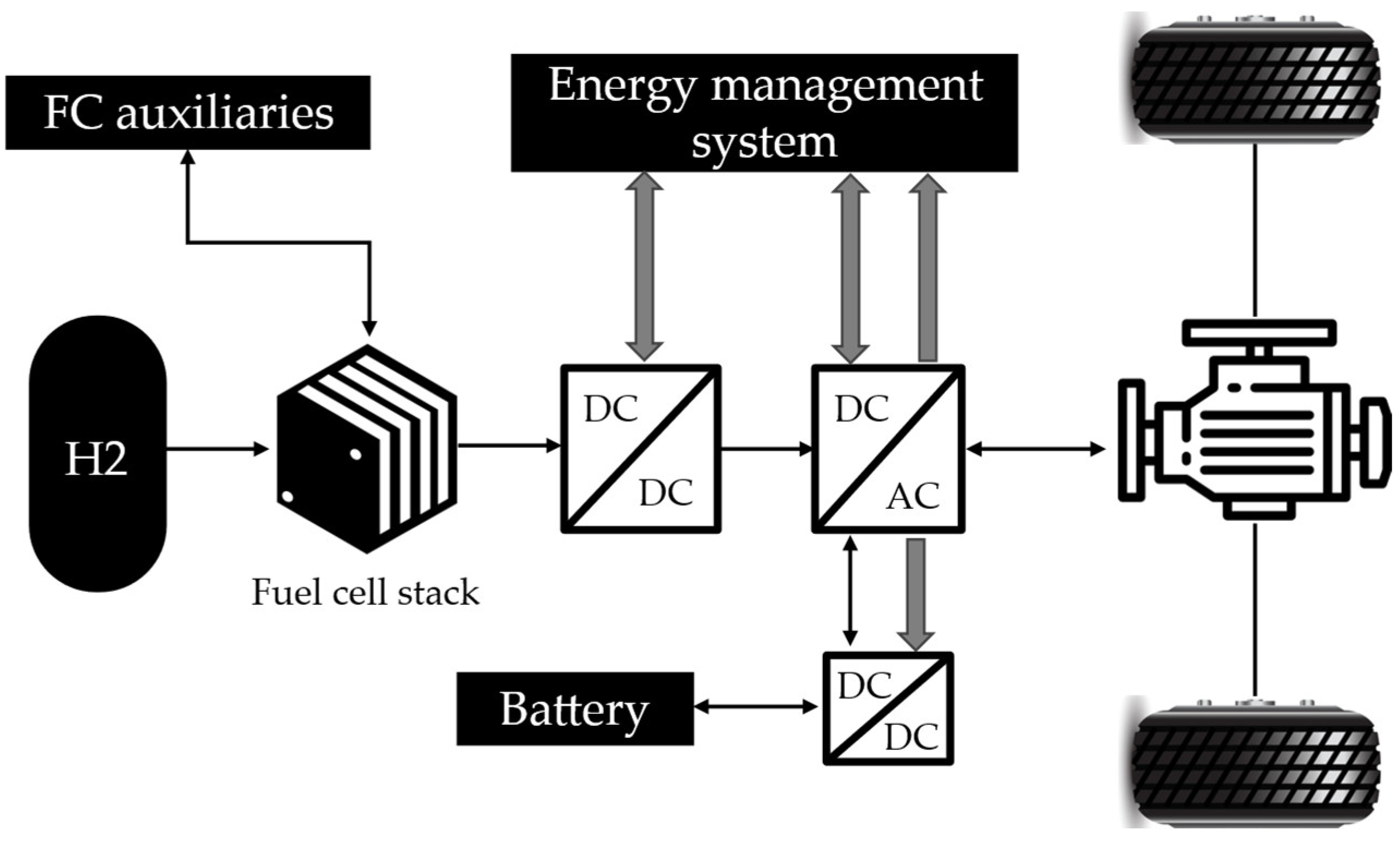
2.1. Powertrain Model
2.1.1. Battery Model
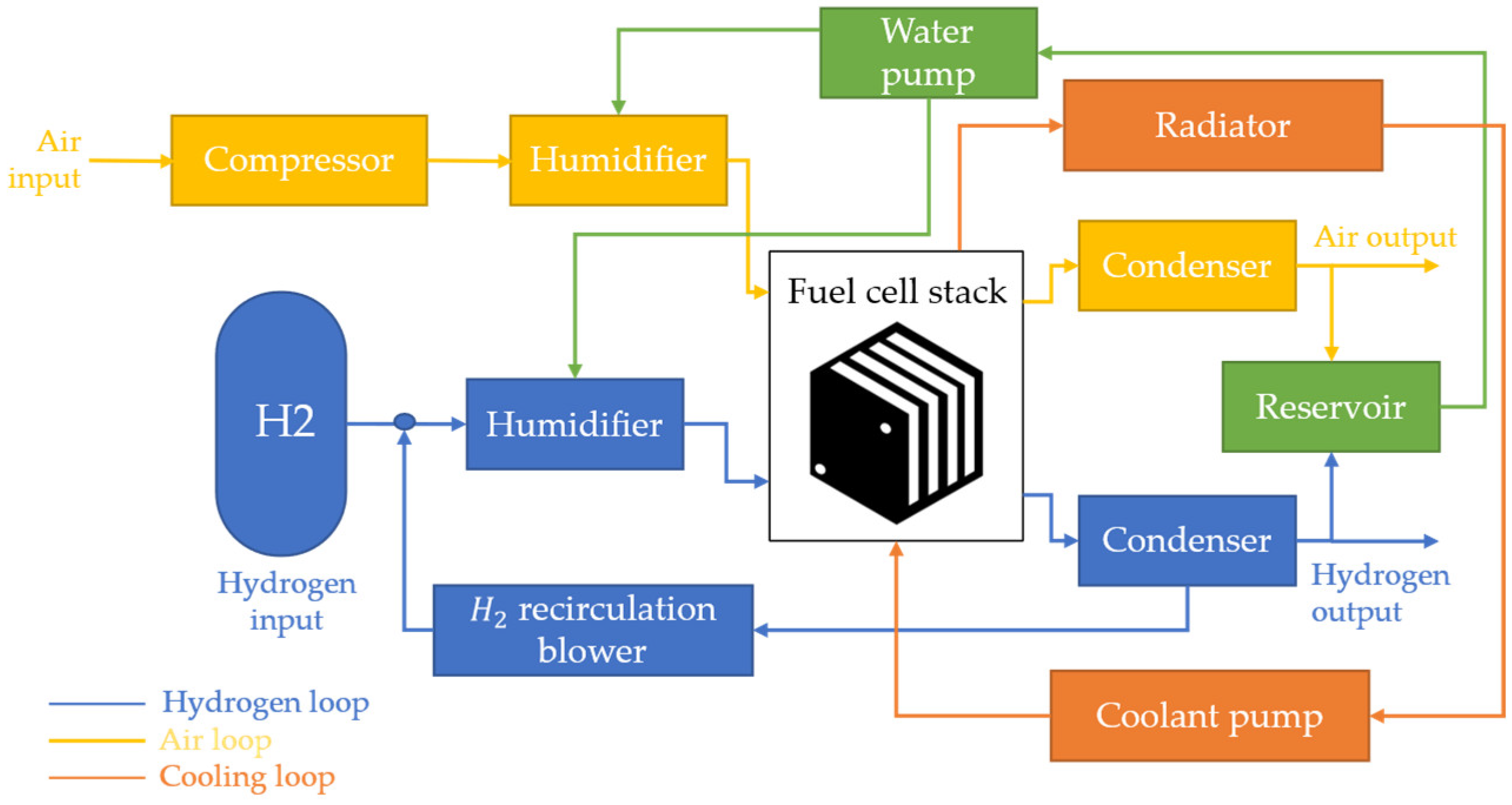
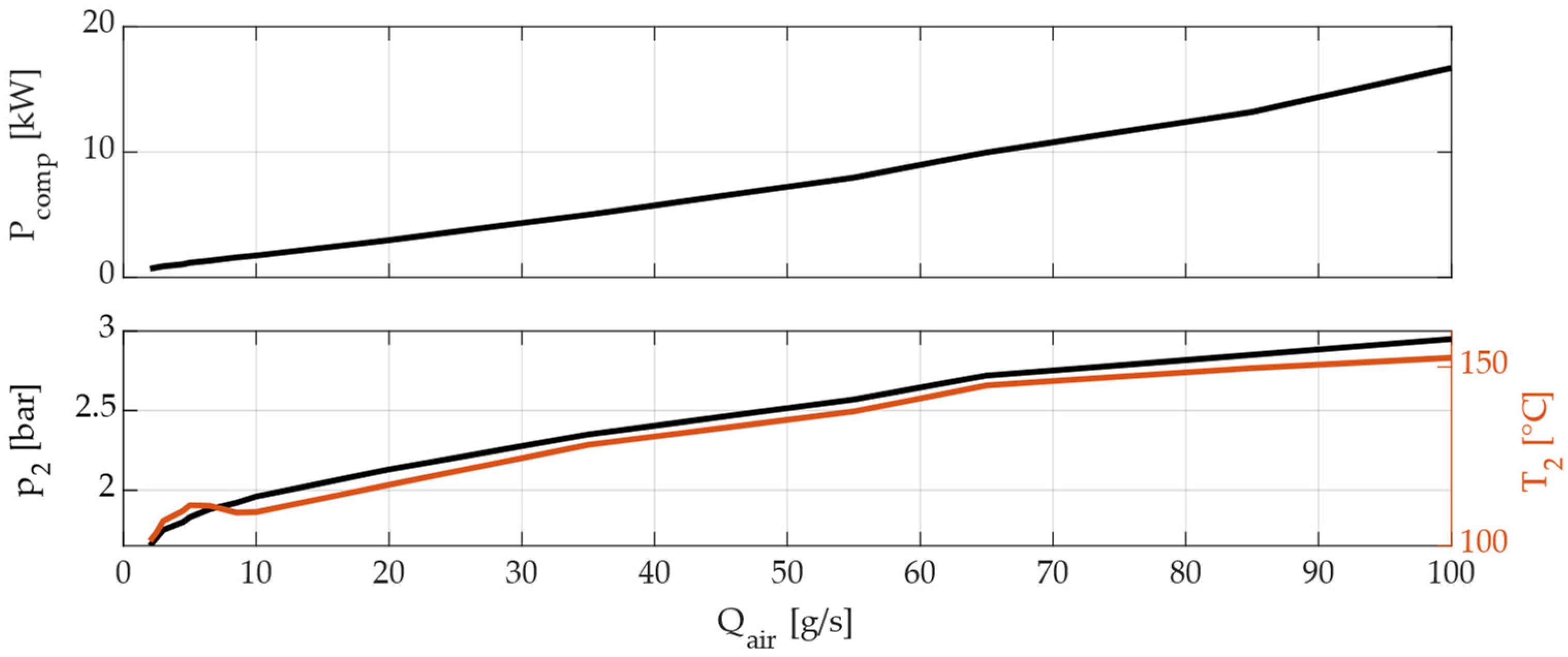
2.1.2. Fuel Cell System Model
2.2. Energy Management Strategies
2.2.1. Constant Power
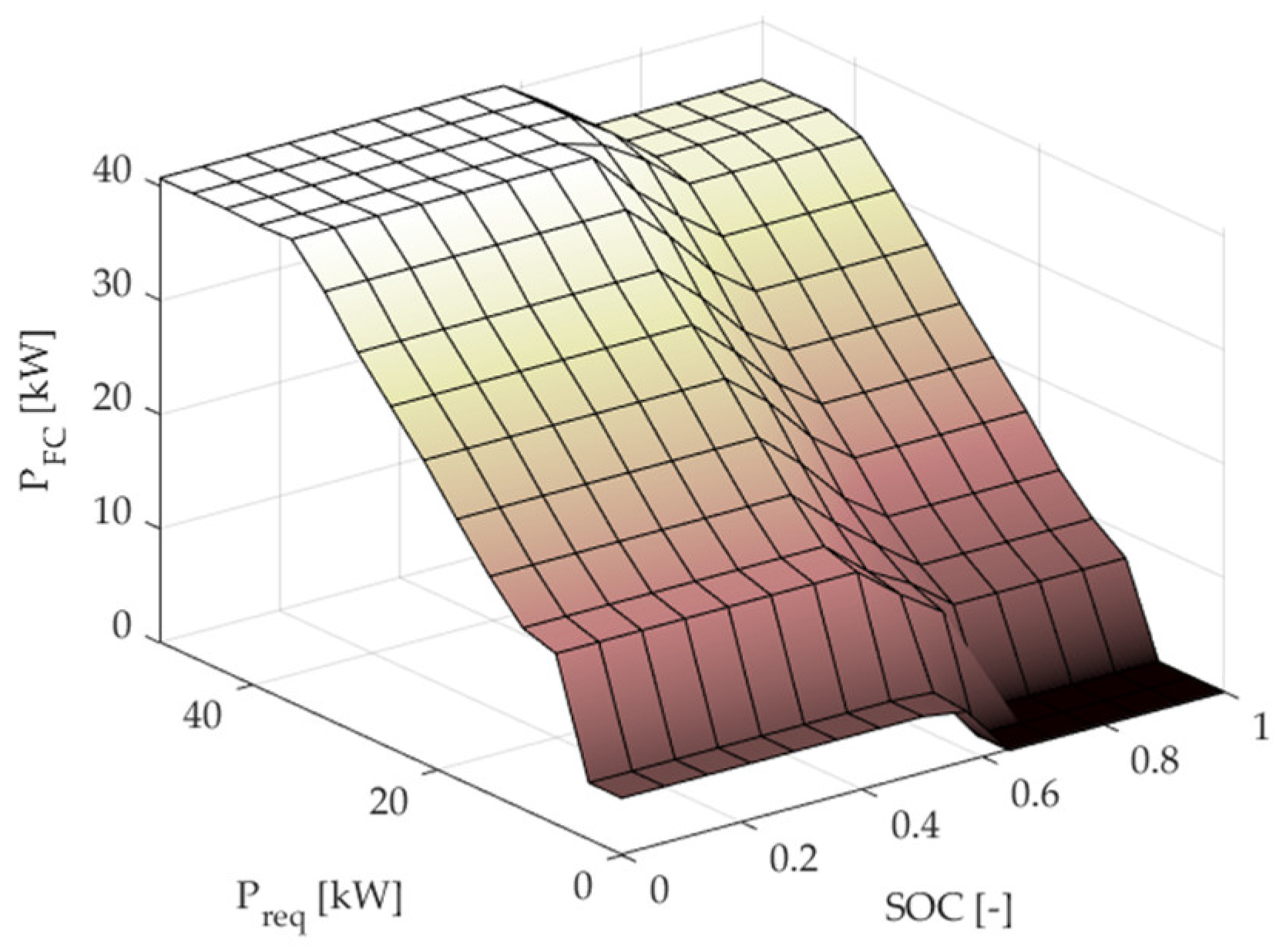
2.2.2. Baseline Mode-Based
2.2.3. Fuzzy Logic Control-Based
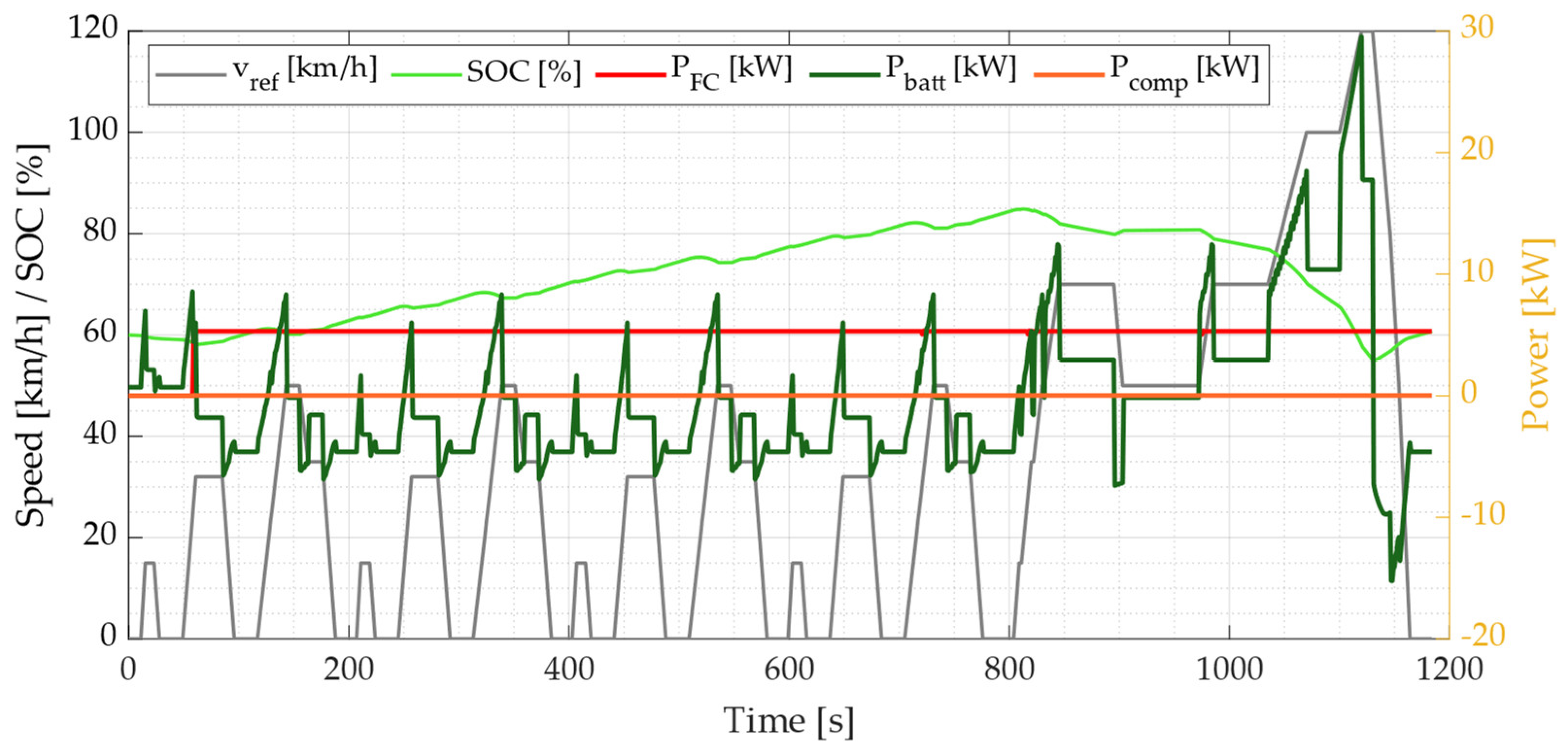
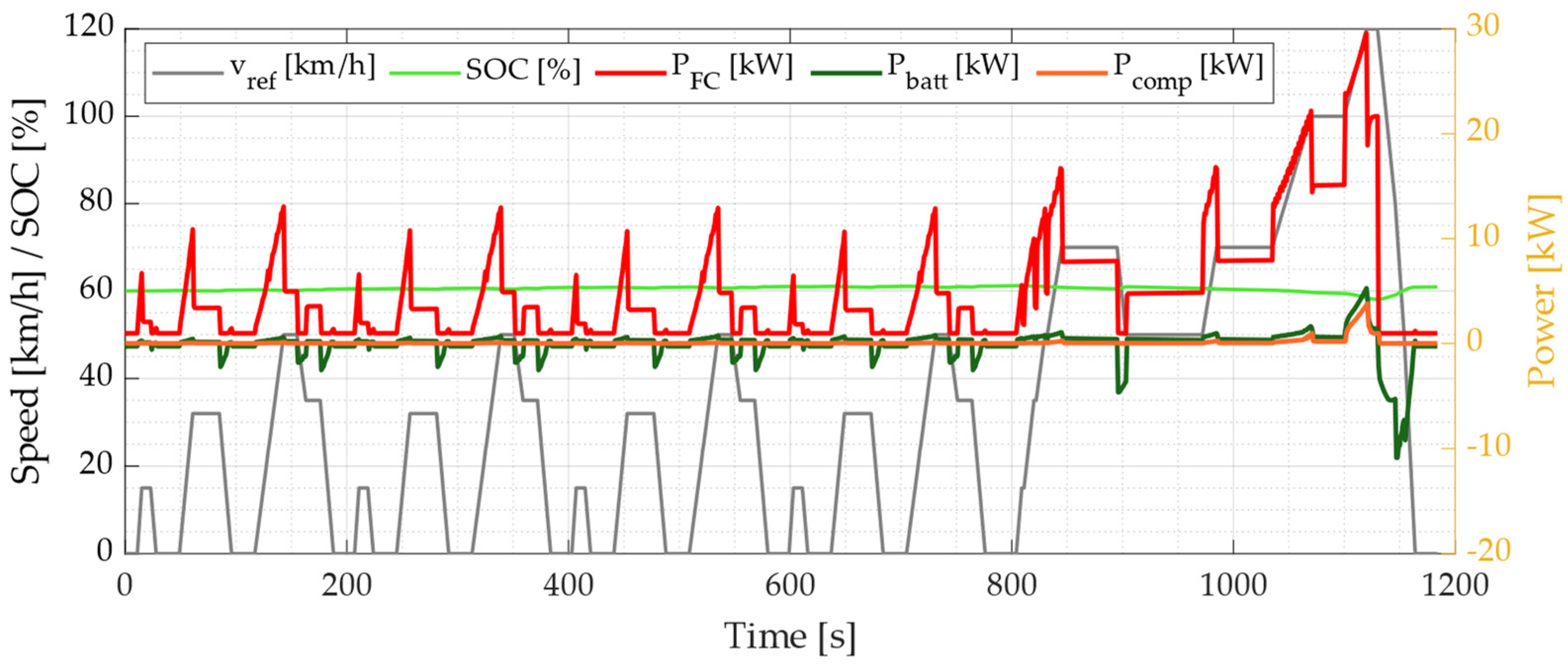
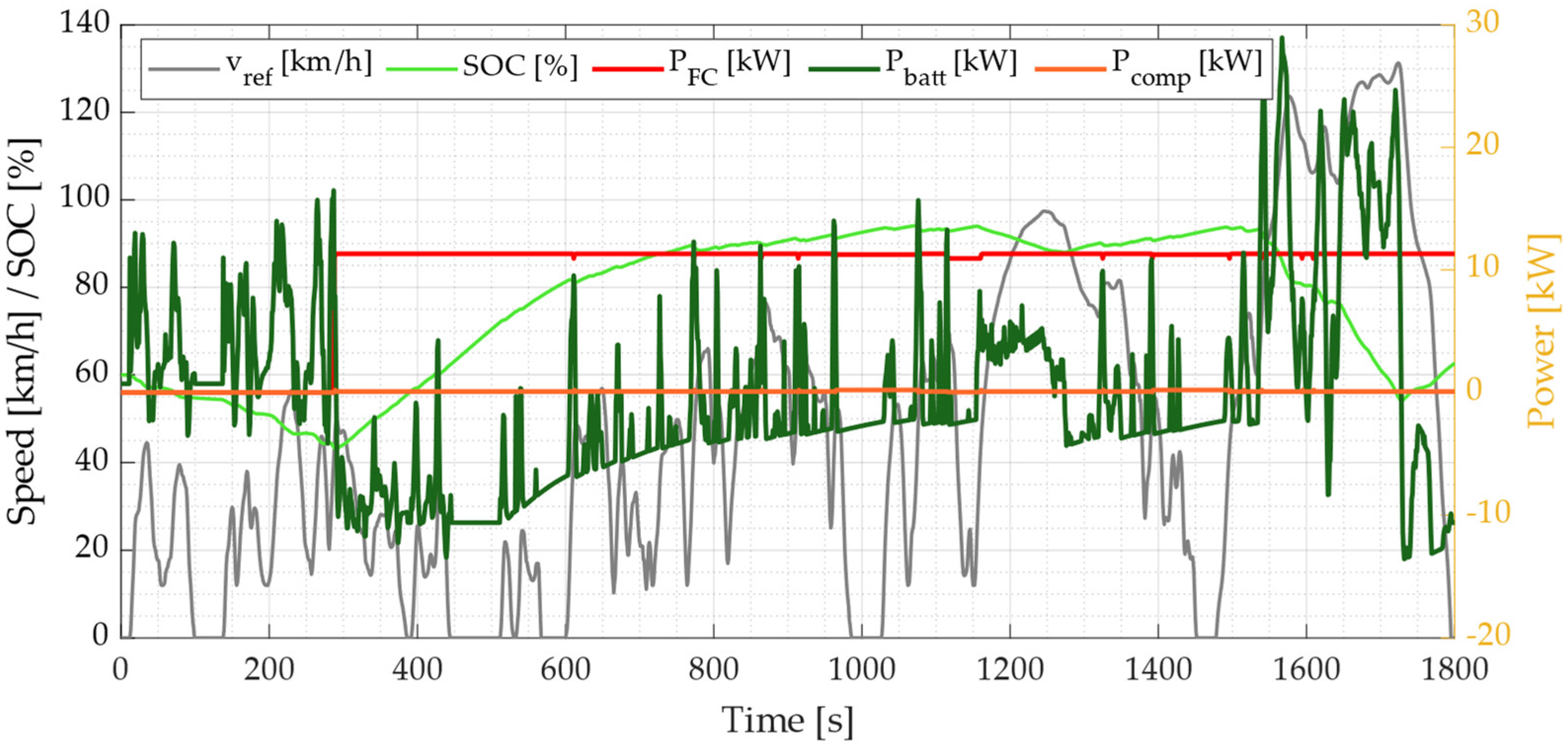
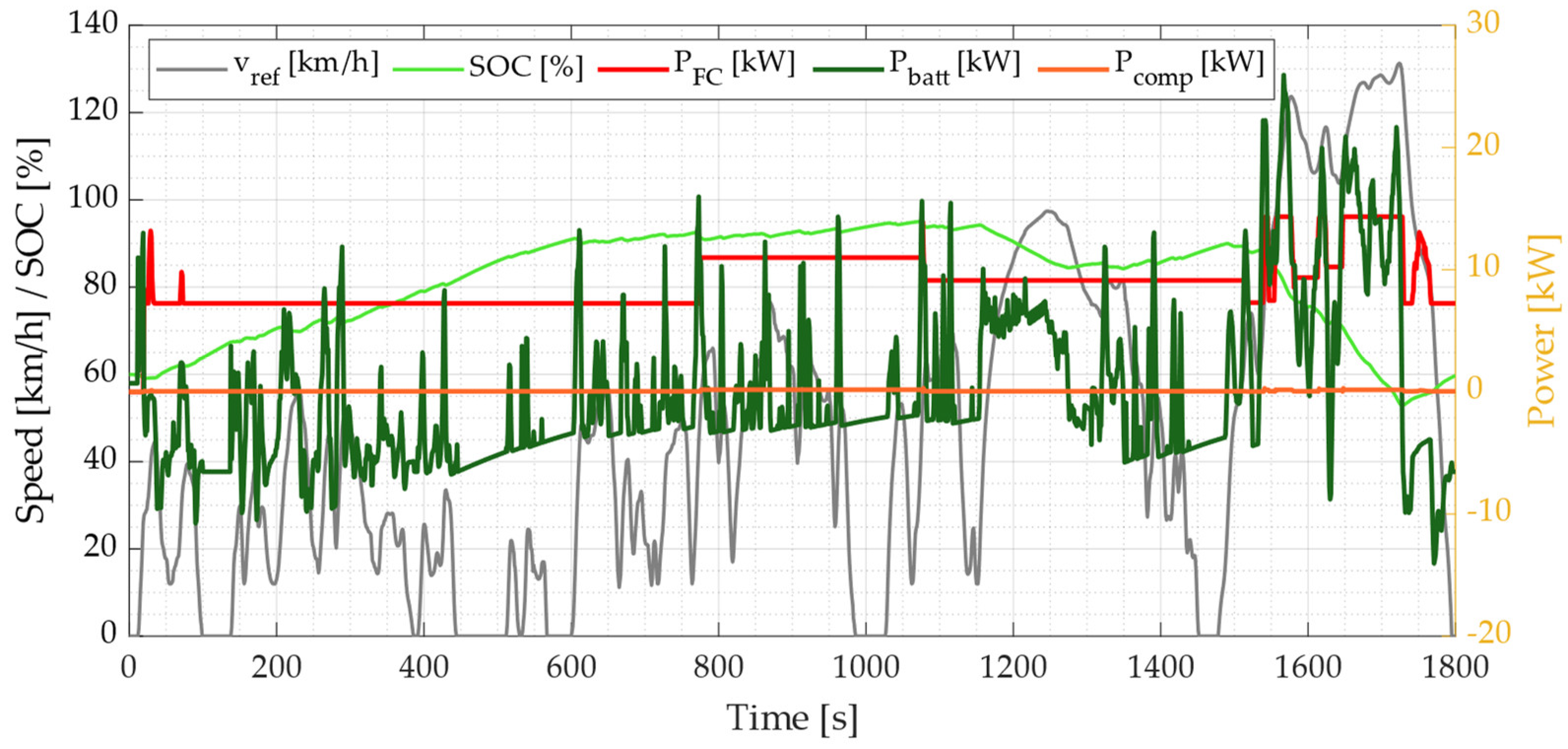
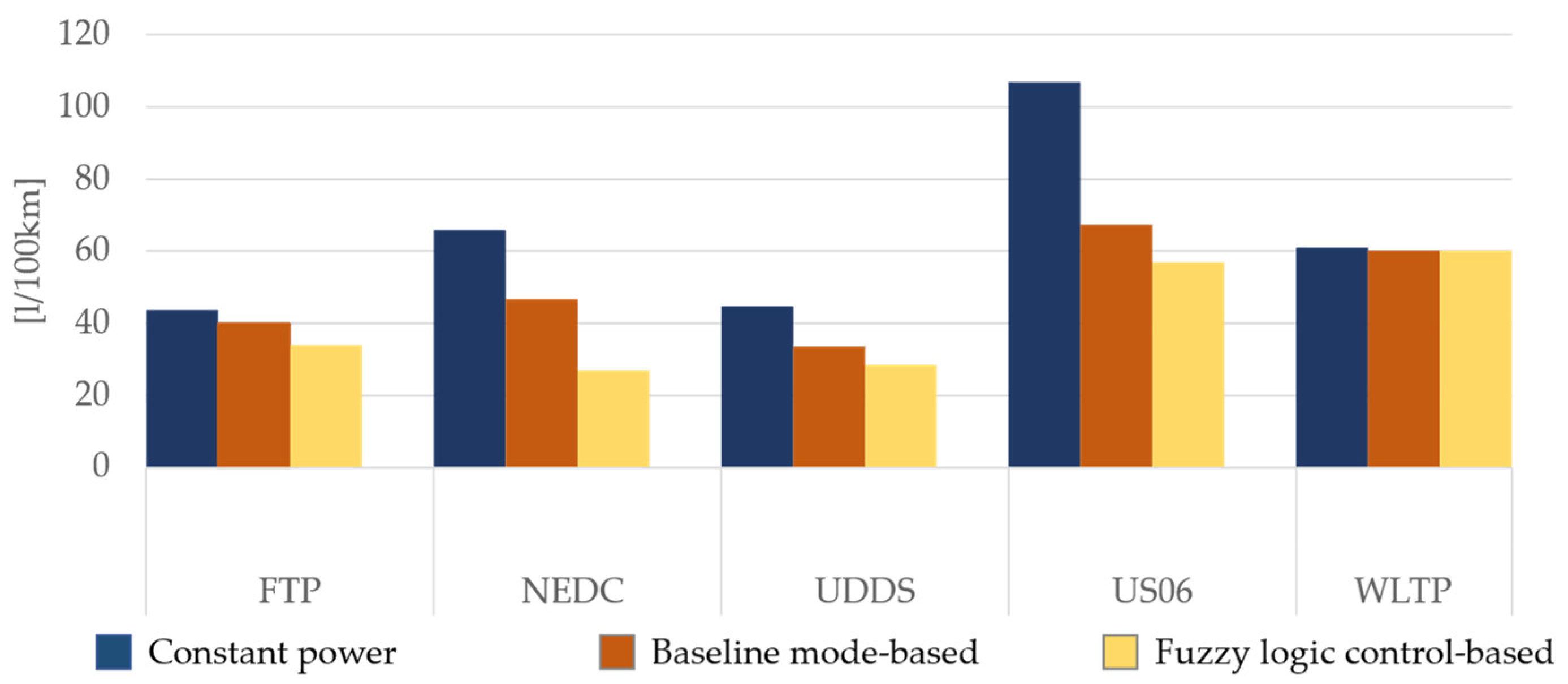
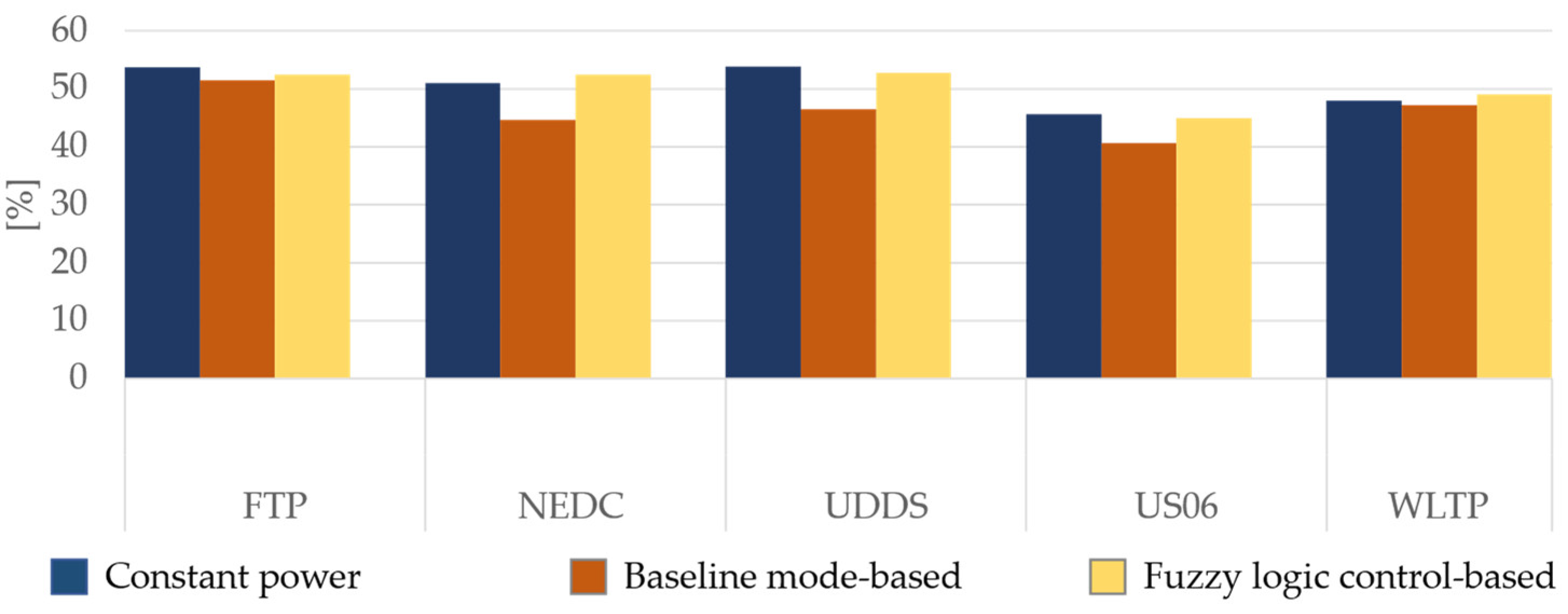
3. Results
3.1. Simulation Results
3.2. Control Strategy Performance Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FCHV | Fuel cell hybrid vehicle |
| PEM | Proton-exchange membrane fuel cell |
| ICE | Internal combustion engine |
| EV | Electric vehicle |
| FTP | Federal test procedure |
| NEDC | New European driving cycle |
| UDDS | Urban dynamometer driving schedule |
| US06 | Supplemental federal Test Procedure |
| WLTP | Worldwide harmonized light-duty vehicle test procedure |
| OCV | Open circuit voltage |
| SOC | State of charge |
| LHV | Lower heating value |
| CS | Charge sustaining |
References
- Ajanovic, A.; Haas, R. Economic and environmental prospects for battery electric-and fuel cell vehicles: A review. Fuel Cells 2019, 19, 515–529. [Google Scholar] [CrossRef] [Green Version]
- Bishop, J.; Martin, N.P.; Boies, A.M. Cost-effectiveness of alternative powertrains for reduced energy use and CO2 emissions in passenger vehicles. Appl. Energy 2014, 124, 44–61. [Google Scholar] [CrossRef]
- Tanç, B.; Arat, H.T.; Baltacıoğlu, E.; Aydın, K. Overview of the next quarter century vision of hydrogen fuel cell electric vehicles. Int. J. Hydrogen Energy 2019, 44, 10120–10128. [Google Scholar] [CrossRef]
- Thomas, C. Fuel cell and battery electric vehicles compared. Int. J. Hydrogen Energy 2009, 34, 6005–6020. [Google Scholar] [CrossRef] [Green Version]
- Khaligh, A.; Li, Z. Battery, Ultracapacitor, Fuel Cell, and Hybrid Energy Storage Systems for Electric, Hybrid Electric, Fuel Cell, and Plug-In Hybrid Electric Vehicles: State of the Art. IEEE Trans. Veh. Technol. 2010, 59, 2806–2814. [Google Scholar] [CrossRef]
- Hames, Y.; Kaya, K.; Baltacioglu, E.; Turksoy, A. Analysis of the control strategies for fuel saving in the hydrogen fuel cell vehicles. Int. J. Hydrogen Energy 2018, 43, 10810–10821. [Google Scholar] [CrossRef]
- Bethoux, O. Hydrogen Fuel Cell Road Vehicles: State of the Art and Perspectives. Energies 2020, 13, 5843. [Google Scholar] [CrossRef]
- Zhao, H.; Burke, A. Fuel Cell Powered Vehicles. In Encyclopedia of Automotive Engineering; Wiley: Hoboken, NJ, USA, 2013; pp. 1–18. [Google Scholar]
- Carello, M.; Pinheiro, H.D.C.; Longega, L.; Di Napoli, L. Design and Modelling of the Powertrain of a Hybrid Fuel Cell Electric Vehicle. SAE Tech. Pap. Ser. 2021, 3, 2878–2892. [Google Scholar] [CrossRef]
- Hilkert, M. Pathways for a Transition to a Sustainable Hydrogen Transportation Fuel Infrastructure in California; Karlsruhe Institute of Technology (KIT): Karlsruhe, Germany, 2004. [Google Scholar]
- Davis, S.C.; Williams, S.E.; Boundy, R.G.; Moore, S.A. 2016 Vehicle Technologies Market Report; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2017. [Google Scholar]
- Xu, N.; Kong, Y.; Chu, L.; Ju, H.; Yang, Z.; Xu, Z.; Xu, Z. Towards a Smarter Energy Management System for Hybrid Vehicles: A Comprehensive Review of Control Strategies. Appl. Sci. 2019, 9, 2026. [Google Scholar] [CrossRef] [Green Version]
- Biswas, A.; Emadi, A. Energy Management Systems for Electrified Powertrains: State-of-the-Art Review and Future Trends. IEEE Trans. Veh. Technol. 2019, 68, 6453–6467. [Google Scholar] [CrossRef]
- Tran, D.-D.; Vafaeipour, M.; El Baghdadi, M.; Barrero, R.; Van Mierlo, J.; Hegazy, O. Thorough state-of-the-art analysis of electric and hybrid vehicle powertrains: Topologies and integrated energy management strategies. Renew. Sustain. Energy Rev. 2020, 119, 109596. [Google Scholar] [CrossRef]
- Odeim, F.; Roes, J.; Heinzel, A. Power Management Optimization of an Experimental Fuel Cell/Battery/Supercapacitor Hybrid System. Energies 2015, 8, 6302–6327. [Google Scholar] [CrossRef] [Green Version]
- Santucci, A.; Sorniotti, A.; Lekakou, C. Power split strategies for hybrid energy storage systems for vehicular applications. J. Power Sources 2014, 258, 395–407. [Google Scholar] [CrossRef] [Green Version]
- Sundstrom, O.; Stefanopoulou, A. Optimal power split in fuel cell hybrid electric vehicle with different battery sizes, drive cycles, and objectives. In Proceedings of the 2006 IEEE Conference on Computer Aided Control System Design, 2006 IEEE International Conference on Control Applications, 2006 IEEE International Symposium on Intelligent Control, Munich, Germany, 4–6 October 2006; pp. 1681–1688. [Google Scholar]
- Enang, W.; Bannister, C. Modelling and control of hybrid electric vehicles (A comprehensive review). Renew. Sustain. Energy Rev. 2017, 74, 1210–1239. [Google Scholar] [CrossRef] [Green Version]
- Anselma, P. Optimization-Driven Powertrain-Oriented Adaptive Cruise Control to Improve Energy Saving and Passenger Comfort. Energies 2021, 14, 2897. [Google Scholar] [CrossRef]
- Anselma, P.G.; Kollmeyer, P.; Lempert, J.; Zhao, Z.; Belingardi, G.; Emadi, A. Battery state-of-health sensitive energy management of hybrid electric vehicles: Lifetime prediction and ageing experimental validation. Appl. Energy 2021, 285, 116440. [Google Scholar] [CrossRef]
- Hemi, H.; Ghouili, J.; Cheriti, A. Combination of Markov chain and optimal control solved by Pontryagin’s Minimum Principle for a fuel cell/supercapacitor vehicle. Energy Convers. Manag. 2015, 91, 387–393. [Google Scholar] [CrossRef]
- Peng, H.; Chen, Z.; Li, J.; Deng, K.; Dirkes, S.; Gottschalk, J.; Ünlübayir, C.; Thul, A.; Löwenstein, L.; Pischinger, S.; et al. Offline optimal energy management strategies considering high dynamics in batteries and constraints on fuel cell system power rate: From analytical derivation to validation on test bench. Appl. Energy 2021, 282, 116152. [Google Scholar] [CrossRef]
- Han, J.; Park, Y.; Kum, D. Optimal adaptation of equivalent factor of equivalent consumption minimization strategy for fuel cell hybrid electric vehicles under active state inequality constraints. J. Power Sources 2014, 267, 491–502. [Google Scholar] [CrossRef]
- Zhang, W.; Li, J.; Xu, L.; Ouyang, M. Optimization for a fuel cell/battery/capacity tram with equivalent consumption minimization strategy. Energy Convers. Manag. 2017, 134, 59–69. [Google Scholar] [CrossRef]
- Rahmeh, H.; Bonfitto, A.; Ruzimov, S. Fuzzy Logic vs Equivalent Consumption Minimization Strategy for Energy Management in P2 Hybrid Electric Vehicles. In International Design Engineering Technical Conferences and Computers and Information in Engineering Conference; American Society of Mechanical Engineers: New York, NY, USA, 2020; Volume 83938, p. V004T04A026. [Google Scholar]
- Hegde, S.; Bonfitto, A.; Rahmeh, H.; Amati, N.; Tonoli, A. Optimal Selection of Equivalence Factors for ECMS in Mild Hybrid Electric Vehicles. In International Design Engineering Technical Conferences and Computers and Information in Engineering Conference; American Society of Mechanical Engineers: New York, NY, USA, 2021; Volume 85369, p. V001T01A019. [Google Scholar]
- Amin; Bambang, R.T.; Rohman, A.S.; Dronkers, C.J.; Ortega, R.; Sasongko, A. Energy Management of Fuel Cell/Battery/Supercapacitor Hybrid Power Sources Using Model Predictive Control. IEEE Trans. Ind. Inform. 2014, 10, 1992–2002. [Google Scholar] [CrossRef]
- Ezemobi, E.; Yakhshilikova, G.; Ruzimov, S.; Castellanos, L.M.; Tonoli, A. Adaptive Model Predictive Control Including Battery Thermal Limitations for Fuel Consumption Reduction in P2 Hybrid Electric Vehicles. World Electr. Veh. J. 2022, 13, 33. [Google Scholar] [CrossRef]
- Zhou, Y.; Ravey, A.; Péra, M.-C. Real-time cost-minimization power-allocating strategy via model predictive control for fuel cell hybrid electric vehicles. Energy Convers. Manag. 2021, 229, 113721. [Google Scholar] [CrossRef]
- Pereira, D.F.; Lopes, F.D.C.; Watanabe, E.H. Nonlinear Model Predictive Control for the Energy Management of Fuel Cell Hybrid Electric Vehicles in Real Time. IEEE Trans. Ind. Electron. 2021, 68, 3213–3223. [Google Scholar] [CrossRef]
- Hofman, T.; Steinbuch, M.; Van Druten, R.; Serrarens, A. Rule-based energy management strategies for hybrid vehicles. Int. J. Electr. Hybrid Veh. 2007, 1, 71. [Google Scholar] [CrossRef]
- Ehsani, M.; Gao, Y.; Longo, S.; Ebrahimi, K.M. Modern Electric, Hybrid Electric, and Fuel Cell Vehicles; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Li, Q.; Su, B.; Pu, Y.; Han, Y.; Wang, T.; Yin, L.; Chen, W. A State Machine Control Based on Equivalent Consumption Minimization for Fuel Cell/ Supercapacitor Hybrid Tramway. IEEE Trans. Transp. Electrif. 2019, 5, 552–564. [Google Scholar] [CrossRef]
- Radica, G.; Tolj, I.; Markota, D.; Lototskyy, M.V.; Pasupathi, S.; Yartys, V. Control strategy of a fuel-cell power module for electric forklift. Int. J. Hydrogen Energy 2021, 46, 35938–35948. [Google Scholar] [CrossRef]
- Trovão, J.P.F.; Pereirinha, P.J.G. Control scheme for hybridised electric vehicles with an online power follower management strategy. IET Electr. Syst. Transp. 2015, 5, 12–23. [Google Scholar] [CrossRef]
- Li, C.-Y.; Liu, G.-P. Optimal fuzzy power control and management of fuel cell/battery hybrid vehicles. J. Power Sources 2009, 192, 525–533. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, C.-H.; Cui, N.-X. Fuzzy energy management strategy for a hybrid electric vehicle based on driving cycle recognition. Int. J. Automot. Technol. 2012, 13, 1159–1167. [Google Scholar] [CrossRef]
- Hemi, H.; Ghouili, J.; Cheriti, A. A real time fuzzy logic power management strategy for a fuel cell vehicle. Energy Convers. Manag. 2014, 80, 63–70. [Google Scholar] [CrossRef]
- Derakhshan, M.; Shirazi, K.H. Optimized fuzzy controller for a power–torque distribution in a hybrid vehicle with a parallel configuration. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2014, 228, 1654–1674. [Google Scholar] [CrossRef]
- Zhang, P.; Yan, F.; Du, C. A comprehensive analysis of energy management strategies for hybrid electric vehicles based on bibliometrics. Renew. Sustain. Energy Rev. 2015, 48, 88–104. [Google Scholar] [CrossRef]
- ISO 23274-1; Hybrid-Electric Road Vehicles—Exhaust Emissions and Fuel Consumption Measurements—Part 1: Non-Externally Chargeable Vehicles. ISO: Geneva, Switzerland, 2019.
- Tudoroiu, R.E.; Zaheeruddin, M.; Tudoroiu, N.; Radu, S.M. SOC Estimation of a Rechargeable Li-Ion Battery Used in Fuel-Cell Hybrid Electric Vehicles—Comparative Study of Accuracy and Robustness Performance Based on Statistical Criteria. Part I: Equivalent Models. Batteries 2020, 6, 42. [Google Scholar] [CrossRef]
- Haraldsson, K.; Alvfors, P. Effects of ambient conditions on fuel cell vehicle performance. J. Power Sources 2005, 145, 298–306. [Google Scholar] [CrossRef]






| Item | Parameter | Value | Unit |
|---|---|---|---|
| Vehicle | Mass | 1191 | kg |
| Cargo mass | 136 | kg | |
| Aerodynamic drag coefficient | 0.335 | - | |
| Rolling resistance coefficient | 0.013 | ||
| Frontal area | 2 | ||
| Weight distribution (front/rear) | 0.6/0.4 | - | |
| Center of Gravity height | 0.5 | m | |
| Wheelbase | 2.6 | m | |
| Wheel radius | 190 | mm | |
| e-motor | Continuous power | 45 | kW |
| Peak torque | 240 | Nm | |
| Peak power | 75 | kW | |
| DC-DC | Efficiency | 0.95 | - |
| DC-AC | Efficiency | 0.95 | - |
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Type | - | Li-Ion | |
| Mass | 27.5 | kg | |
| Nominal capacity | 6 | Ah | |
| Nominal voltage | 320 | V | |
| Number of modules | - | 25 | - |
| Heat exchange area | A | 0.032 | |
| Specific heat capacity | 795 | ||
| Heat transfer capacity | h | 5 |
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Max. output power | 50 | kW | |
| No. of cells | - | 300 | - |
| Fuel cell stack mass | 100 | kg | |
| Active area | 280 | ||
| pressure | - | 350 | bar |
| Hydrogen lower heating value | 33.3 | kWh/kg |
| Item | Parameter | Value | Unit |
|---|---|---|---|
| Battery | [0.55, 0.95] | - | |
| 0.6 | - | ||
| Fuel cell | 7 | kW | |
| 10 | kW | ||
| 50 | kW |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luciani, S.; Tonoli, A. Control Strategy Assessment for Improving PEM Fuel Cell System Efficiency in Fuel Cell Hybrid Vehicles. Energies 2022, 15, 2004. https://doi.org/10.3390/en15062004
Luciani S, Tonoli A. Control Strategy Assessment for Improving PEM Fuel Cell System Efficiency in Fuel Cell Hybrid Vehicles. Energies. 2022; 15(6):2004. https://doi.org/10.3390/en15062004
Chicago/Turabian StyleLuciani, Sara, and Andrea Tonoli. 2022. "Control Strategy Assessment for Improving PEM Fuel Cell System Efficiency in Fuel Cell Hybrid Vehicles" Energies 15, no. 6: 2004. https://doi.org/10.3390/en15062004
APA StyleLuciani, S., & Tonoli, A. (2022). Control Strategy Assessment for Improving PEM Fuel Cell System Efficiency in Fuel Cell Hybrid Vehicles. Energies, 15(6), 2004. https://doi.org/10.3390/en15062004







