Data-Driven Air-Fuel Path Control Design for Robust RCCI Engine Operation
Abstract
:1. Introduction
1.1. Fuel Flexible RCCI Concept
- 1.
- Realizing high brake thermal efficiencies (above 50%);
- 2.
- Stable engine operations over the entire load range;
- 3.
- Acceptable tailpipe total hydrocarbon (THC) and CO emissions;
- 4.
- Robust performance during highly dynamic drive cycles and varying ambient conditions.
1.2. RCCI Control Challenges
1.3. Research Objective and Main Contributions
- A new, data-driven combustion uncertainty model based on individual cylinder FRF system identification. This model quantifies the cylinder-to-cylinder variations;
- Robust MIMO feedback control design using the developed uncertainty model. This allows for a systematic trade-off between fast and robust performance for all cylinders;
- Additional control design details on achieved input–output decoupling and robust stability. This includes air–fuel path interaction analysis and robust stability analysis of the single feedback controller for varying operating points;
- New experimental results for the six-cylinder diesel-E85 RCCI engine around three operating points; in addition to earlier transient results, the potential of the RCCI engine controller is demonstrated to compensate for disturbed intake manifold temperature and to increase the high load RCCI range due to the reduced cylinder-to-cylinder variations.
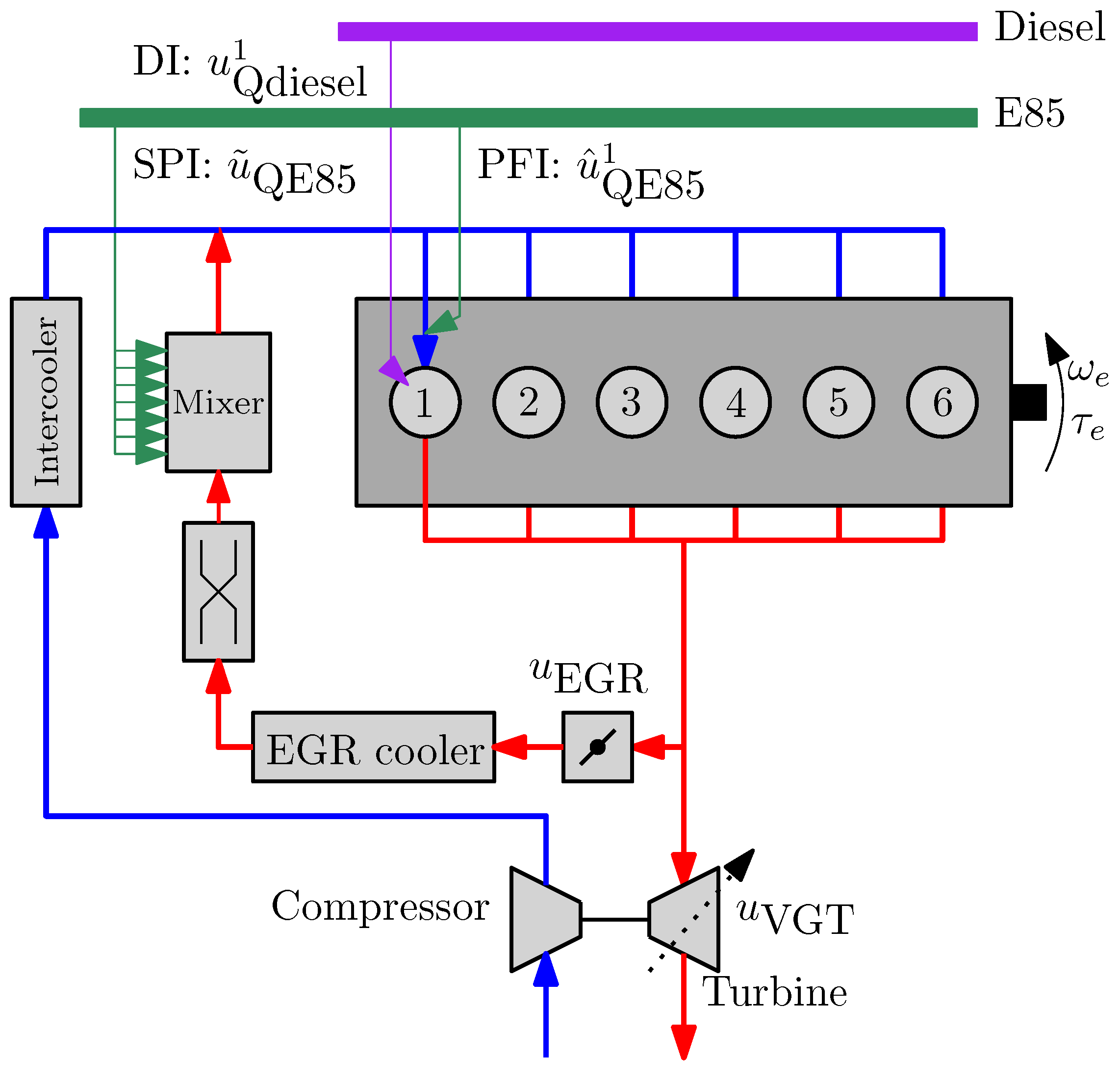
2. Experimental Setup
- E85 injection system with port fuel injection (PFI) for all cylinders as well as single point injection (SPI) capability;
- Modified piston;
- Modified turbocharger with a variable geometry turbine (VGT);
- Pressure sensor in each cylinder.
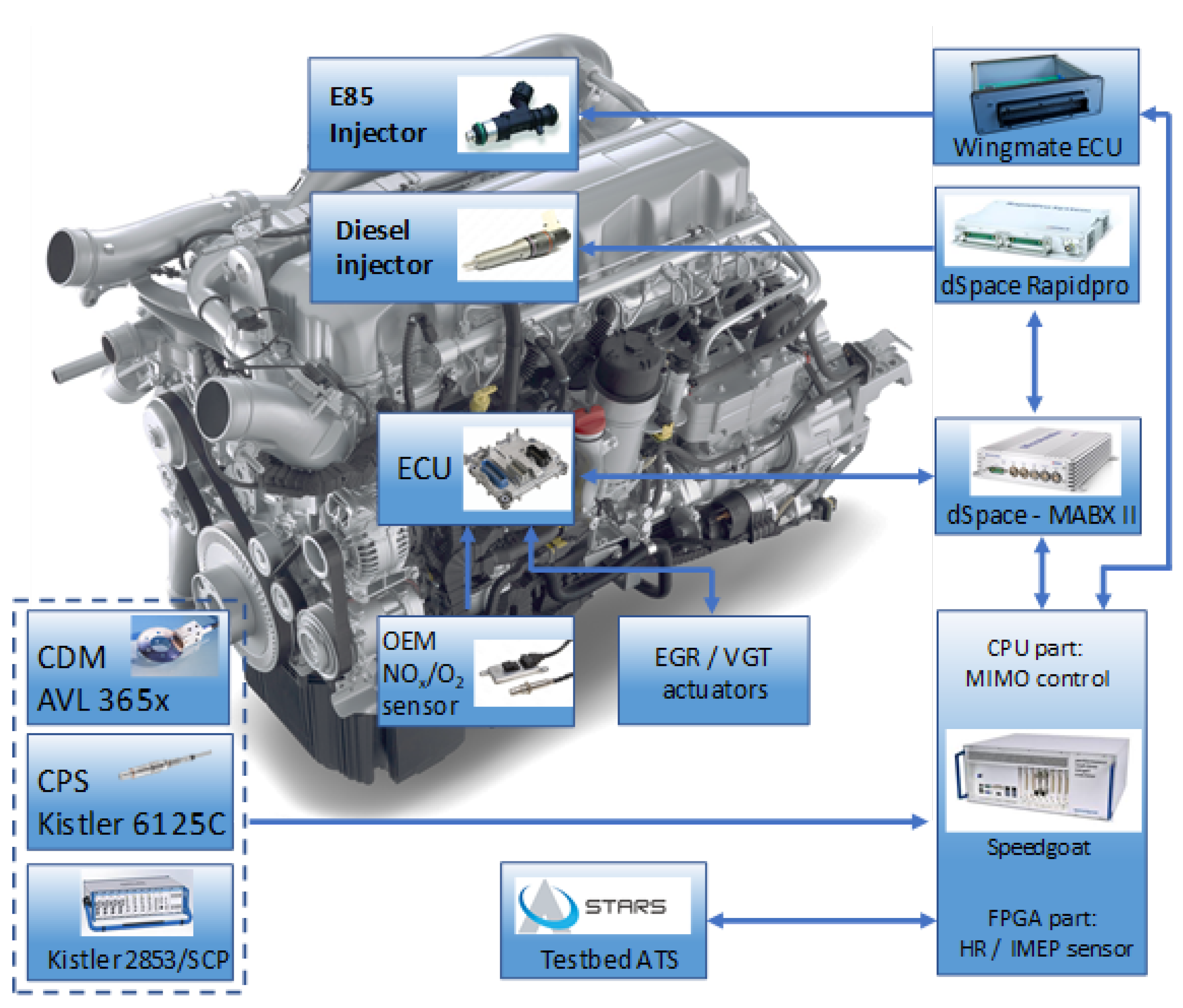
2.1. Data Acquisition
2.2. Real-Time Control System
- Wingmate ECU controls the E85 PFI and SPI injectors, such that the desired injection timing and quantity is realized;
- dSPACE MABXII realizes the desired VGT and EGR valve position and diesel injection timing and quantity for the individual cylinders.
2.3. Engine Operating Points
3. RCCI Control
3.1. RCCI Control Problem
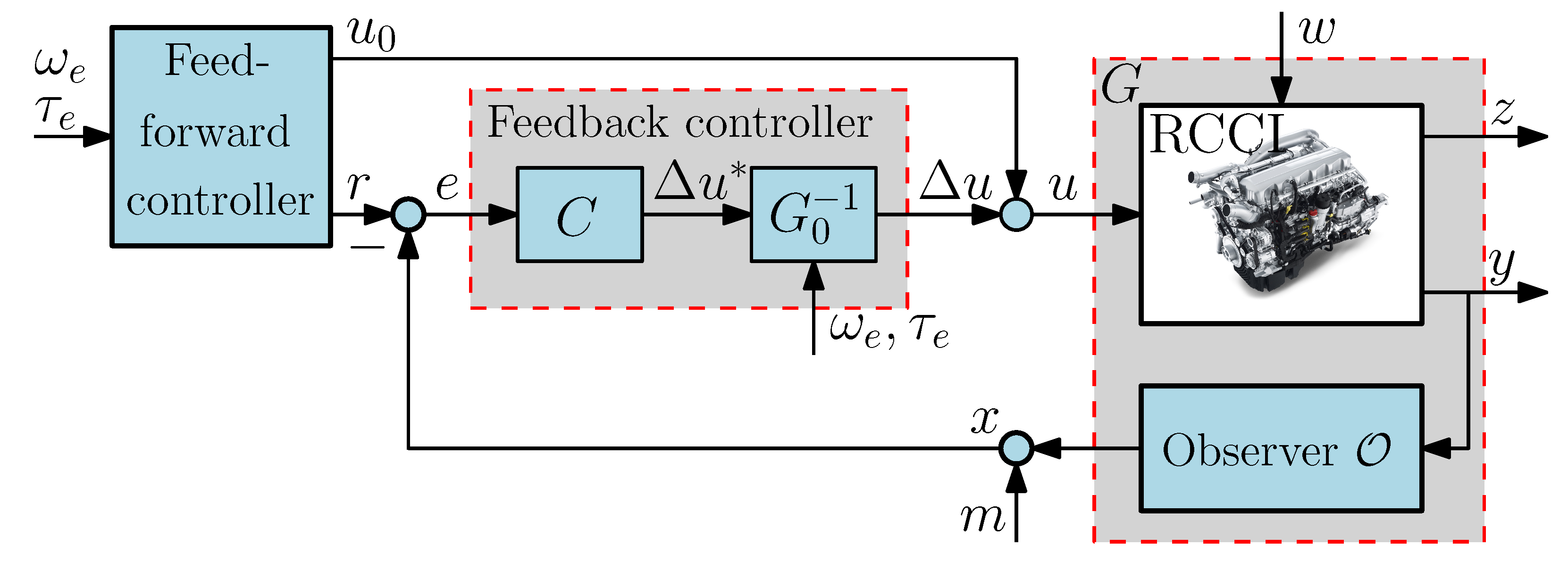
3.2. RCCI Engine Control Architecture
3.3. Feedforward Controller
- Net indicated mean effective pressure (IMEPn) is a cylinder individual measure for engine load and is an indicator for misfires and partial combustion;
- Energy-based blend-ratio is defined as:where denotes the cylinder individual mass flow and LHV the lower heating value of the fuel. This quantity has a strong link with THC and CO emissions and combustion stability;
- Combustion phasing (CA50) is an important indicator for the mixing period and for combustion stability. Moreover, CA50 is closely linked to thermal efficiency;
- Exhaust manifold pressure is associated with EGR mass flow and pumping losses;
- EGR ratio is given by:with EGR mass flow and compressor fresh air flow . It is linked to the oxygen content in the intake manifold.
3.4. Multivariable Feedback Controller
3.4.1. Next-Cycle Fuel Path Control
3.4.2. Air Path Control
4. Feedback Control Design
- 1.
- Multiple-input multiple-output (MIMO) system identification;
- 2.
- Static decoupling design;
- 3.
- Robust loop shaping using a combustion uncertainty model;
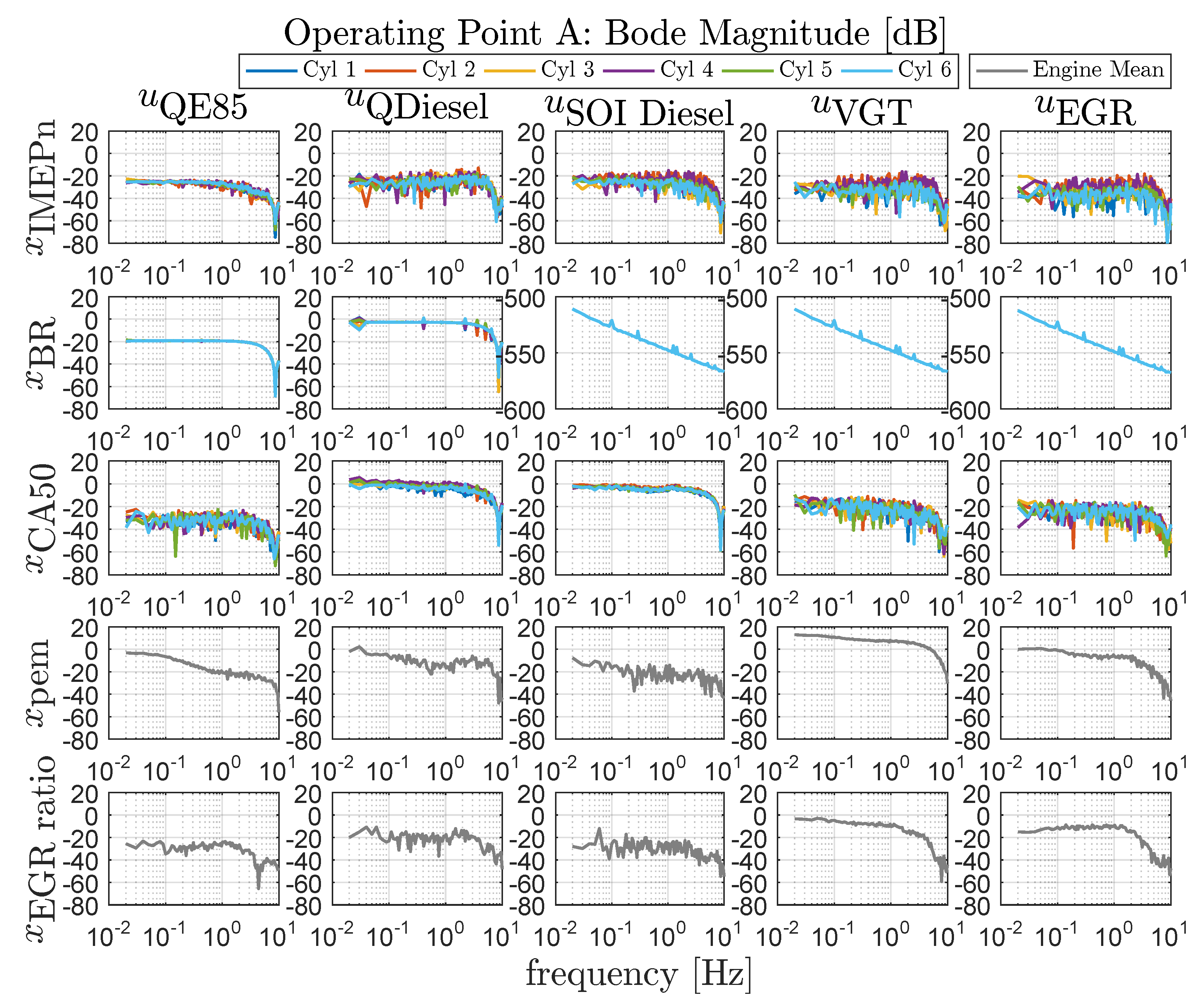
4.1. MIMO System Identification
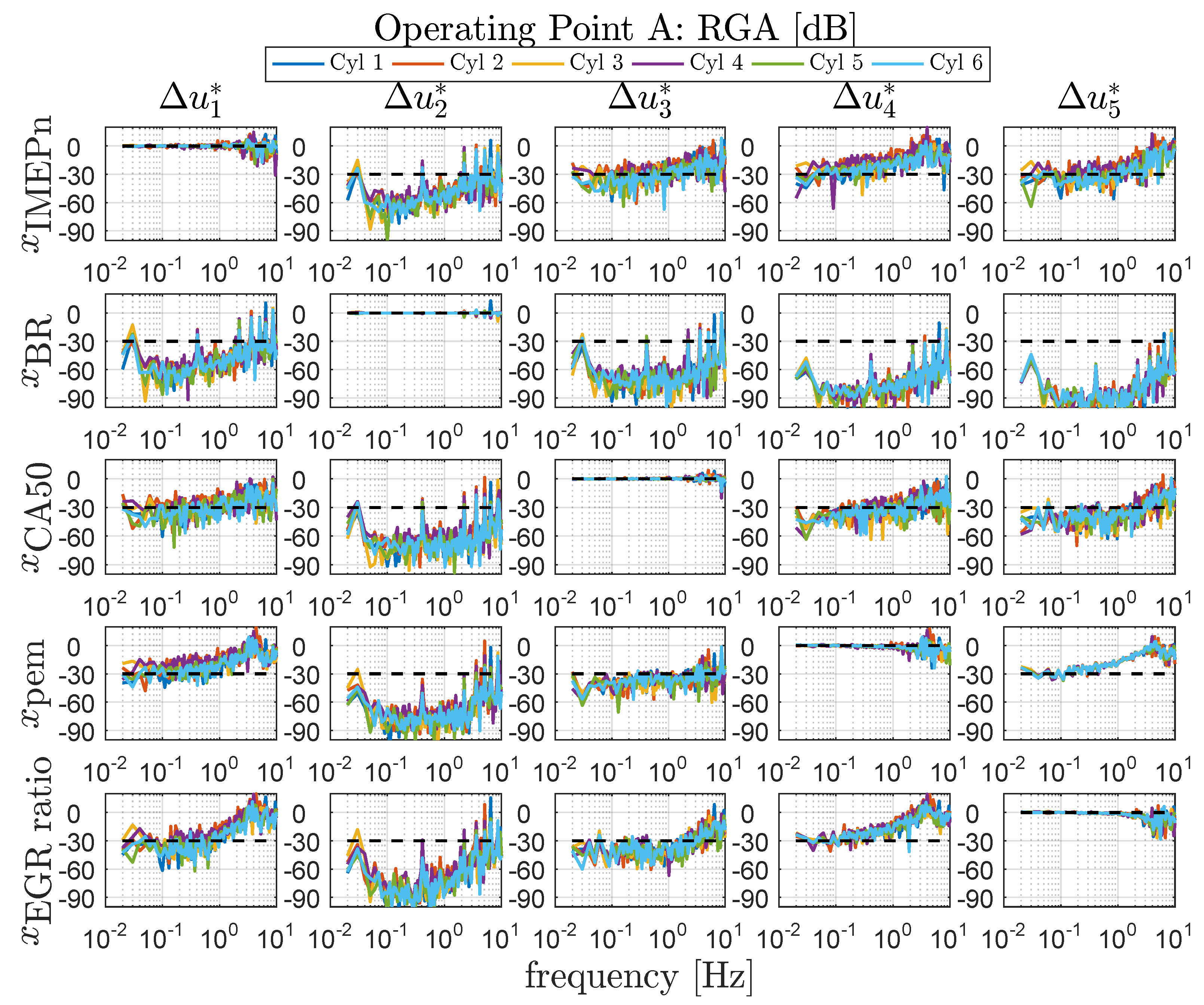
4.2. Static Decoupling Design
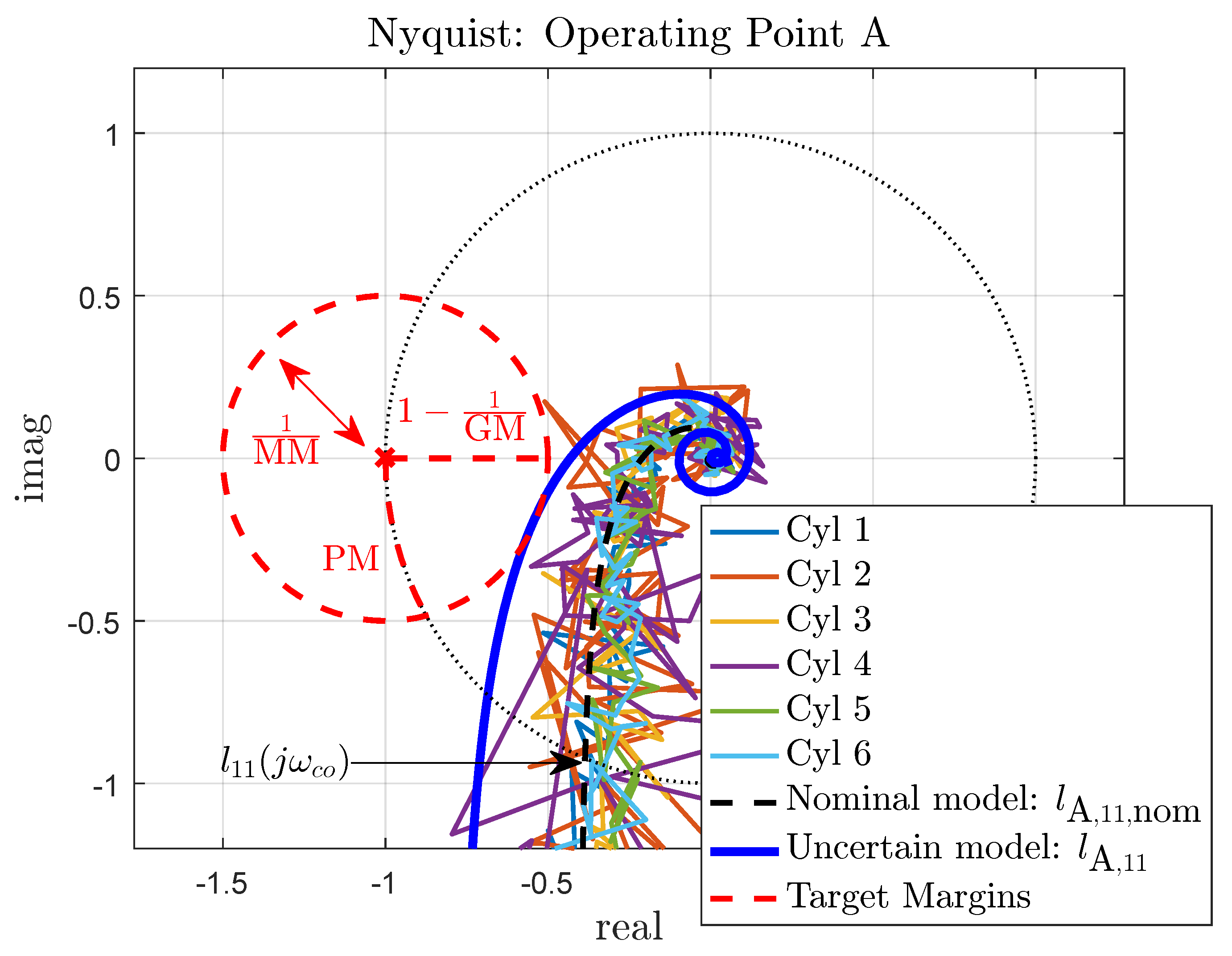
4.3. Robust Loop Shaping
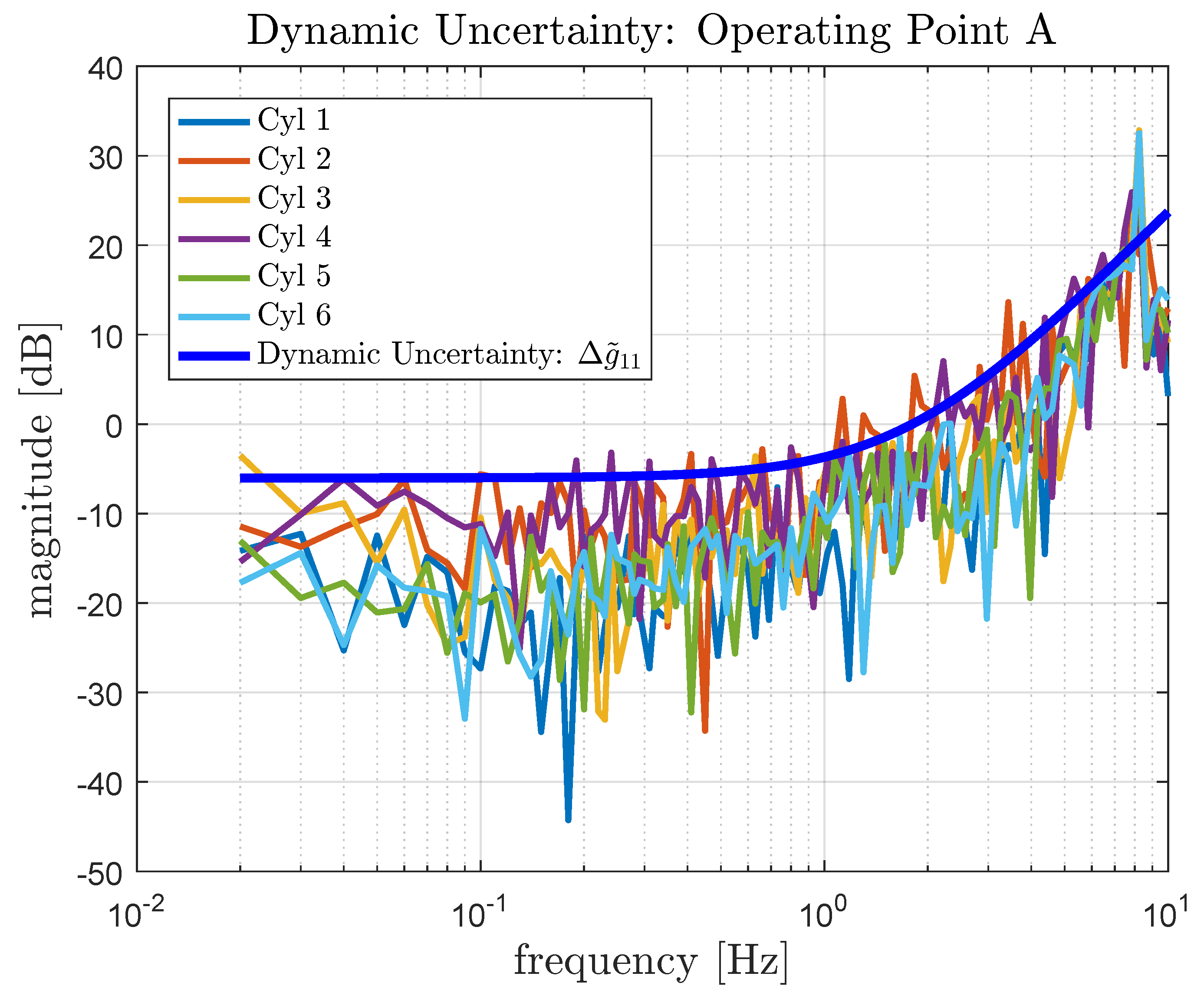
4.3.1. Dynamic Uncertainty Model
4.3.2. SISO Feedback Controller Design
5. Experimental Results
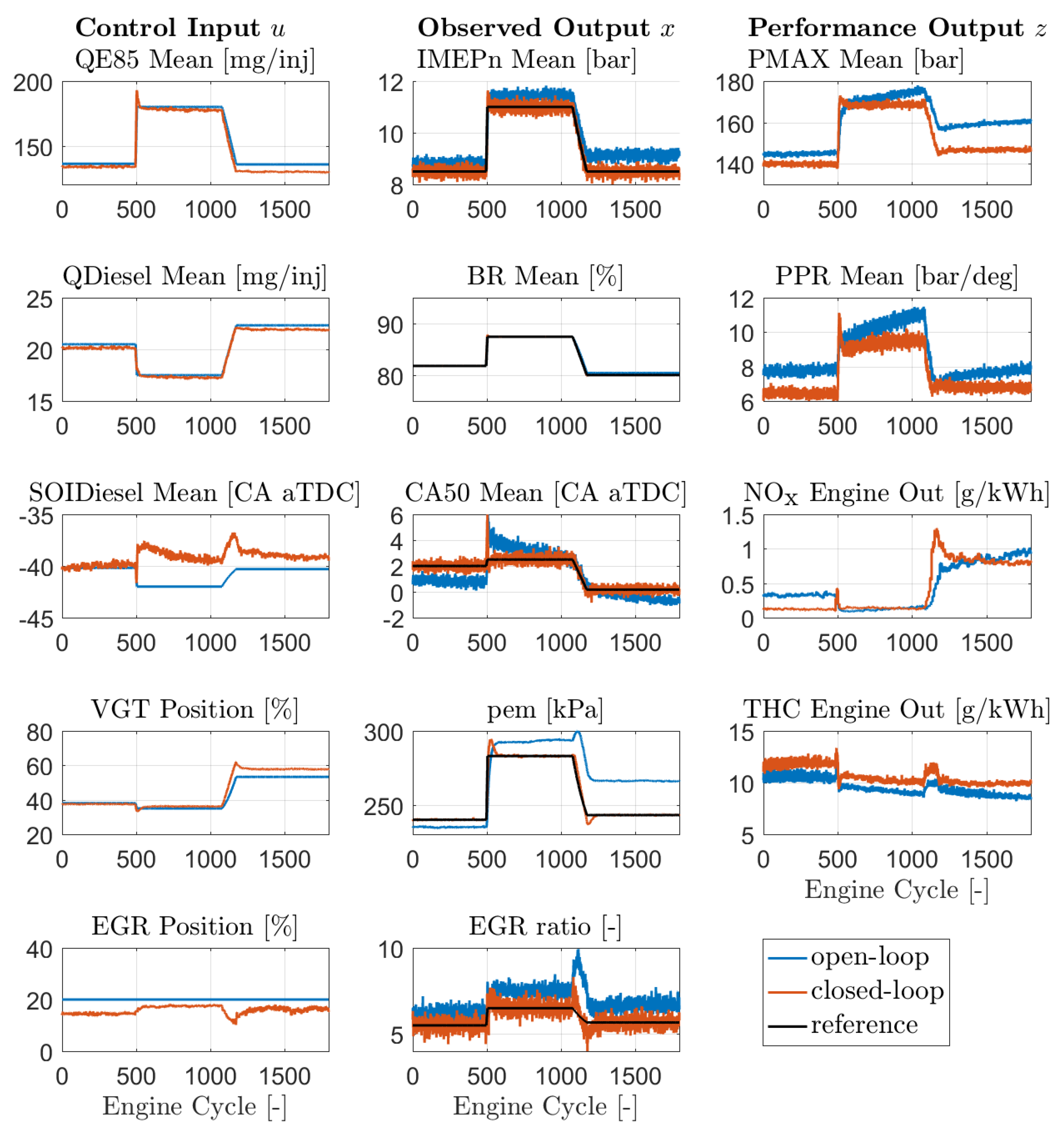
5.1. Transient RCCI Engine Performance
5.2. Disturbed Intake Manifold Temperature
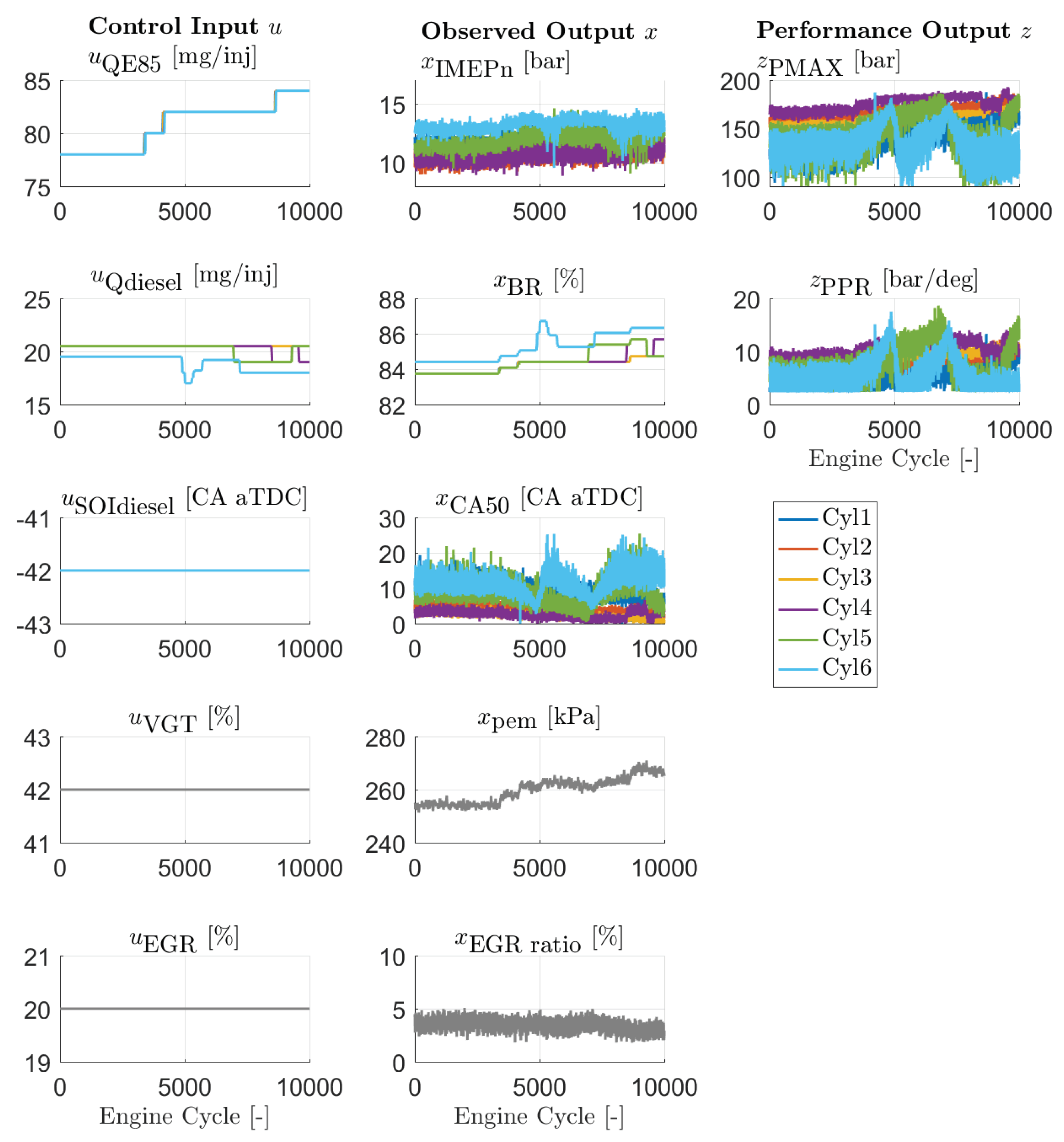
5.3. Increased RCCI Load Range
6. Conclusions
- Cylinder individual models of the complex RCCI combustion process can be efficiently identified following the frequency response function (FRF) method. The resulting data-driven models also capture wall wetting phenomena and sensor and actuator dynamics and are crucial input to derive a system uncertainty model;
- Effective input–output decoupling is realized using a static decoupling matrix. In experiments, minimal interaction between the five control loops is observed;
- Robust RCCI engine operation is demonstrated for the proposed closed-loop RCCI engine controller. This controller gives good reference tracking behavior for varying engine speed and load during transients and compensates for the effect of unknown external disturbances, such as the studied intake manifold temperature variations;
- Closed-loop engine control enables RCCI load range increase due to enhanced safety margins. At = 1000 rpm, the maximal load range was increased by 14.7% up to BMEP = 14.8 bar.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Robust Stability Analysis for Operating Points B and C
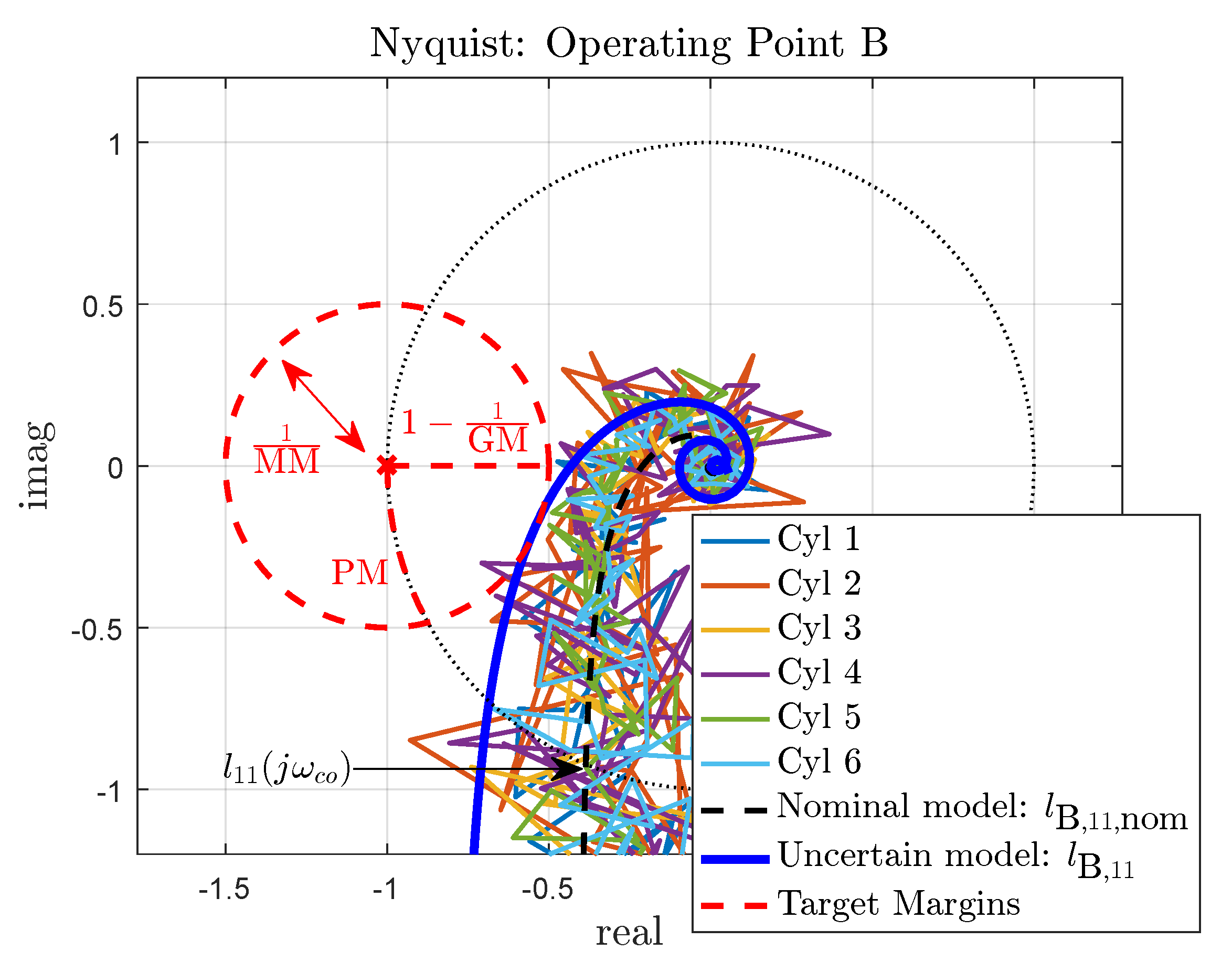

Appendix B. Load Increase for Open-Loop Controlled RCCI Engine
References
- A Fundamental Transport Transformation: Commission Presents Its Plan for Green, Smart and Affordable Mobility; Press Release; European Commission: Brussels, Belgium, 2020.
- Andersson, Ö.; Börjesson, P. The green house gas emissions of an electrified vehicle combined with renewable fuels: Life cycle assessment and policy implications. Appl. Energy 2021, 189, 116621. [Google Scholar] [CrossRef]
- Reitz, R.D.; Duraisamy, G. Review of high efficiency and clean reactivity controlled compression ignition (RCCI) combustion in internal combustion engines. Prog. Energy Combust. Sci. 2015, 46, 12–71. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Z.; Xia, M.; Liu, H.; Wang, X.; Yao, M. Experimental study on combustion and emissions of dual fuel RCCI mode fueled with biodiesel/n-butanol, biodiesel/2,5-dimethylfuran and biodiesel/ethanol. Energy 2018, 148, 824–838. [Google Scholar] [CrossRef]
- Han, J.; Somers, L.; Cracknell, R.; Joedicke, A.; W, R.; Mohan, V.R.R. Experimental investigation of ethanol/diesel dual-fuel combustion in a heavy-duty diesel engine. Fuel 2020, 275, 117867. [Google Scholar] [CrossRef]
- Paykani, A.; Garcia, A.; Shahbakhti, M.; Rahnama, P.; Reitz, R.D. Reactivity controlled compression ignition engine: Pathways towards commercial viability. Appl. Energy 2021, 282, 116174. [Google Scholar] [CrossRef]
- Willems, F. Is cylinder pressure-based control required to meet future HD legislation? IFAC-Pap. Online 2018, 51, 111–118. [Google Scholar] [CrossRef]
- Olsson, J.-O.; Tunestal, P.; Johansson, B. Closed-Loop Control of an HCCI Engine; SAE Technical Paper 2001-01-1031; SAE: Warrendale, PA, USA, 2001. [Google Scholar]
- Strandh, P.; Bengtsson, J.; Johansson, R.; Tunestal, P.; Johansson, B. Cycle-to-Cycle Control of a Dual-Fuel HCCI Engine; SAE Technical Paper 2004-01-0941; SAE: Warrendale, PA, USA, 2004. [Google Scholar]
- Hanson, R.; Reitz, R. Transient RCCI Operation in a Light-Duty Multi-Cylinder Engine. SAE Int. J. Engines 2013, 6, 1694–1705. [Google Scholar] [CrossRef]
- Maurya, R.; Agarwal, A. Experimental Investigation of Closed-Loop Control of HCCI Engine Using Dual Fuel Approach; SAE Technical Paper 2013-01-1675; SAE: Warrendale, PA, USA, 2013. [Google Scholar]
- Arora, J.; Shahbakhti, M. Real-Time Closed-Loop Control of a Light-Duty RCCI Engine During Transient Operations; SAE Technical Paper 2017-01-0767; SAE: Warrendale, PA, USA, 2017. [Google Scholar]
- Raut, A.; Irdmousa, B.K.; Shahbakhti, M. Dynamic modeling and model predictive control of an RCCI engine. Control Eng. Pract. 2018, 81, 129–144. [Google Scholar] [CrossRef]
- Guardiola, C.; Pla, B.; Bares, P.; Barbier, A. Closed-loop control of a dual-fuel engine working with different combustion modes using in-cylinder pressure feedback. Int. J. Engine Res. 2020, 21, 484–496. [Google Scholar] [CrossRef]
- Willems, F.; Kupper, F.; Ramesh, S.; Indrajuana, A.; Doosje, E. Coordinated Air-Fuel Path Control in a Diesel-E85 RCCI Engine; SAE Technical Paper 2019-01-1175; SAE: Warrendale, PA, USA, 2019. [Google Scholar]
- Benajes, J.; García, A.; Monsalve-Serrano, J.; Villalta, D. Benefits of E85 versus gasoline as low reactivity fuel for an automotive diesel engine operating in reactivity controlled compression ignition combustion mode. Energy Convers. Manag. 2018, 159, 85–95. [Google Scholar] [CrossRef]
- Splitter, D.; Hanson, R.; Kokjohn, S.; Reitz, R. Reactivity Controlled Compression Ignition (RCCI) Heavy-Duty Engine Operation at Mid-and High-Loads with Conventional and Alternative Fuels; SAE Technical Paper 2011-01-0363; SAE: Warrendale, PA, USA, 2011. [Google Scholar]
- Zhang, Y.; Sagalovich, I.; Ojeda, W.D.; Ickes, A.; Wallner, T.; Wickman, D.D. Development of Dual-Fuel Low Temperature Combustion Strategy in a Multi-Cylinder Heavy-Duty Compression Ignition Engine Using Conventional and Alternative Fuels. SAE Int. J. Engines 2013, 6, 1481–1489. [Google Scholar] [CrossRef]
- Verhaegh, J.; Kupper, F.; Willems, F. Frequency Response Based Multivariable Feedback Control Design for Transient RCCI Engine Operation. IFAC-Pap. Online 2020, 53, 14008–14015. [Google Scholar] [CrossRef]
- Willems, R.; Willems, F.; Deen, N.; Somers, B. Heat release rate shaping for optimal gross indicated efficiency in a heavy-duty RCCI engine fueled with E85 and diesel. Fuel 2021, 288, 119656. [Google Scholar] [CrossRef]
- Xia, L.; de Jager, B.; Donkers, M.; Willems, F. Robust constrained optimization for RCCI engines using nested penalized particle swarm. Control Eng. Pract. 2020, 99, 104411. [Google Scholar] [CrossRef]
- Pintelon, R.; Schoukens, J. System Identification: A Frequency Domain Approach; IEEE Press: New York, NY, USA, 2001. [Google Scholar]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control: Analysis and Design, 2nd ed.; Wiley: West Sussex, UK, 2015. [Google Scholar]
- Eriksson, L.; Nielsen, L. Modeling and Control of Engines and Drivelines; Automotive Series; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Vlaswinkel, M.; de Jager, B.; Willems, F. Data-Based Control Structure Selection for RCCI Engines with Electrically Assisted Turbocharger. In Proceedings of the 19th European Control Conference (ECC 2021), Rotterdam, The Netherlands, 29 June–2 July 2021; pp. 491–496. [Google Scholar]
- Poussin, O.; Gaillard, P.; García, A.; Monsalve-Serrano, J.; Martinez-Boggio, S. Dual-Fuel RCCI Diesel-Gasoline Hybrid Truck Concept to Achieve the Future Emissions Targets. In Proceedings of the 9th Aachen Colloquium China Automobile and Engine Technology, Beijing, China, 13–15 November 2019. [Google Scholar]




| Ref. | Controlled Parameter | Control Input | Control Strategy | Change or Disturbance |
|---|---|---|---|---|
| [8] | CA50, IMEPn | PID | , IMEPn | |
| [9] | CA50 | PID, LQG | , | |
| [10] | CA50 | PID | BMEP | |
| [11] | CA50, IMEP | PID | IMEP | |
| [12] | MFB50, IMEP | PI | IMEP | |
| [13] | CA50, IMEP | MPC | IMEP | |
| [14] | CC, IMEP, PPR | PI | IMEP |
| Parameter | Unit | Value or Spec |
|---|---|---|
| Number of cylinders | - | 6 (in line) |
| Total displacement volume | ℓ | 13 |
| Compression ratio | - | 15:1 |
| DI fuel rail pressure | bar | 500 |
| PFI/SPI fuel rail pressure | bar | 4.5 |
| DI fuel | - | Diesel (EN590) |
| PFI/SPI fuel | - | E85 |
| Parameter | Unit | A | B | C |
|---|---|---|---|---|
| Engine speed | rpm | 1000 | 1000 | 1300 |
| Net indicated mean effective pressure IMEPn | bar | 8.5 | 11.5 | 8.5 |
| Total injected E85 quantity | mg/inj | 136 | 180 | 125 |
| Diesel DI injection quantity | mg/inj | 20.5 | 18.0 | 23.0 |
| Diesel DI injection timing | deg CA aTDC | —40 | —42 | —40 |
| E85 PFI injection timing | deg CA aTDC | —295 | —295 | —295 |
| VGT position | % open | 38 | 35 | 56 |
| EGR position | % open | 20 | 20 | 20 |
| Energy-based blend ratio | % | 81.8 | 87.0 | 78.6 |
| Air fuel ratio | - | 2.3 | 2.2 | 2.5 |
| Intake manifold pressure | bar | 1.98 | 2.40 | 2.05 |
| Intake manifold temperature | C | 32.5 | 34.0 | 32.0 |
| Quantity | Limit |
|---|---|
| Peak in-cylinder pressure | 200 bar |
| Peak in-cylinder pressure rise rate | 15 bar/deg CA |
| Combustion stability cov(IMEPn) | 5% |
| Operating Point q | [rpm] | [s] | a | b |
|---|---|---|---|---|
| A | 1000 | 0.1200 | 6.745 | 6.745 |
| B | 1000 | 0.1200 | 6.745 | 6.745 |
| C | 1300 | 0.0923 | 10.321 | 10.321 |
| Output | Resp. Time | PM | GM | MM | |
|---|---|---|---|---|---|
| [cycles] | [Hz] | [deg] | [dB] | [dB] | |
| Design Target | |||||
| Operating point A | |||||
| 8 | 0.27 | 86.5 | 14.5 | 2.5 | |
| 11 | 0.32 | 97.8 | inf | 0.5 | |
| 9 | 0.26 | 77.2 | 15.6 | 1.6 | |
| 32 | 0.10 | 76.5 | 13.6 | 2.1 | |
| 28 | 0.11 | 94.1 | 6.4 | 5.6 | |
| Operating point B | |||||
| 8 | 0.32 | 70.6 | 11.2 | 3.2 | |
| 12 | 0.32 | 97.8 | Inf | 0.5 | |
| 10 | 0.30 | 78.9 | 16.3 | 1.7 | |
| 29 | 0.10 | 83.3 | 12.6 | 2.4 | |
| 35 | 0.12 | 94.2 | 6.4 | 5.6 | |
| Operating point C | |||||
| 10 | 0.30 | 79.4 | 16.4 | 1.8 | |
| 11 | 0.32 | 99.5 | Inf | 0.4 | |
| 10 | 0.24 | 75.4 | 18.1 | 1.2 | |
| 25 | 0.10 | 74.6 | 15.1 | 1.7 | |
| 30 | 0.13 | 95.6 | 7.9 | 5.0 | |
| SISO Controller | |||
|---|---|---|---|
| 0.25 | 2.00 | n/a | |
| 0.25 | 2.00 | n/a | |
| 0.25 | 2.00 | n/a | |
| 0.5 | 0.79 | 0.0159 | |
| 0.5 | 0.79 | 0.0159 |
| Performance Criteria | |||||
|---|---|---|---|---|---|
| Average absolute error | 0.24 | 0.01 | 0.45 | 1.01 | 0.26 |
| Standard deviation | 0.31 | 0.03 | 0.58 | 2.41 | 0.34 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verhaegh, J.; Kupper, F.; Willems, F. Data-Driven Air-Fuel Path Control Design for Robust RCCI Engine Operation. Energies 2022, 15, 2018. https://doi.org/10.3390/en15062018
Verhaegh J, Kupper F, Willems F. Data-Driven Air-Fuel Path Control Design for Robust RCCI Engine Operation. Energies. 2022; 15(6):2018. https://doi.org/10.3390/en15062018
Chicago/Turabian StyleVerhaegh, Jan, Frank Kupper, and Frank Willems. 2022. "Data-Driven Air-Fuel Path Control Design for Robust RCCI Engine Operation" Energies 15, no. 6: 2018. https://doi.org/10.3390/en15062018
APA StyleVerhaegh, J., Kupper, F., & Willems, F. (2022). Data-Driven Air-Fuel Path Control Design for Robust RCCI Engine Operation. Energies, 15(6), 2018. https://doi.org/10.3390/en15062018






