Characterization of Two-Phase Flow from Pore-Scale Imaging Using Fractal Geometry under Water-Wet and Mixed-Wet Conditions
Abstract
:1. Introduction
2. Materials and Method
2.1. High Resolution Image Datasets from Core Flooding Experiments
2.2. Wettability Characterization from Image Datasets
2.3. Fractal-Based Analysis and Phase Properties
2.3.1. Fractal Dimension Calculation for Two-Phase Flow
2.3.2. Lacunarity Calculation for Two-Phase Flow
2.3.3. Succolarity Calculation for Two-Phase Flow
3. Results
3.1. Phase Configuration Characterized by Fractal Dimension and Lacunarity during Multiphase Flow
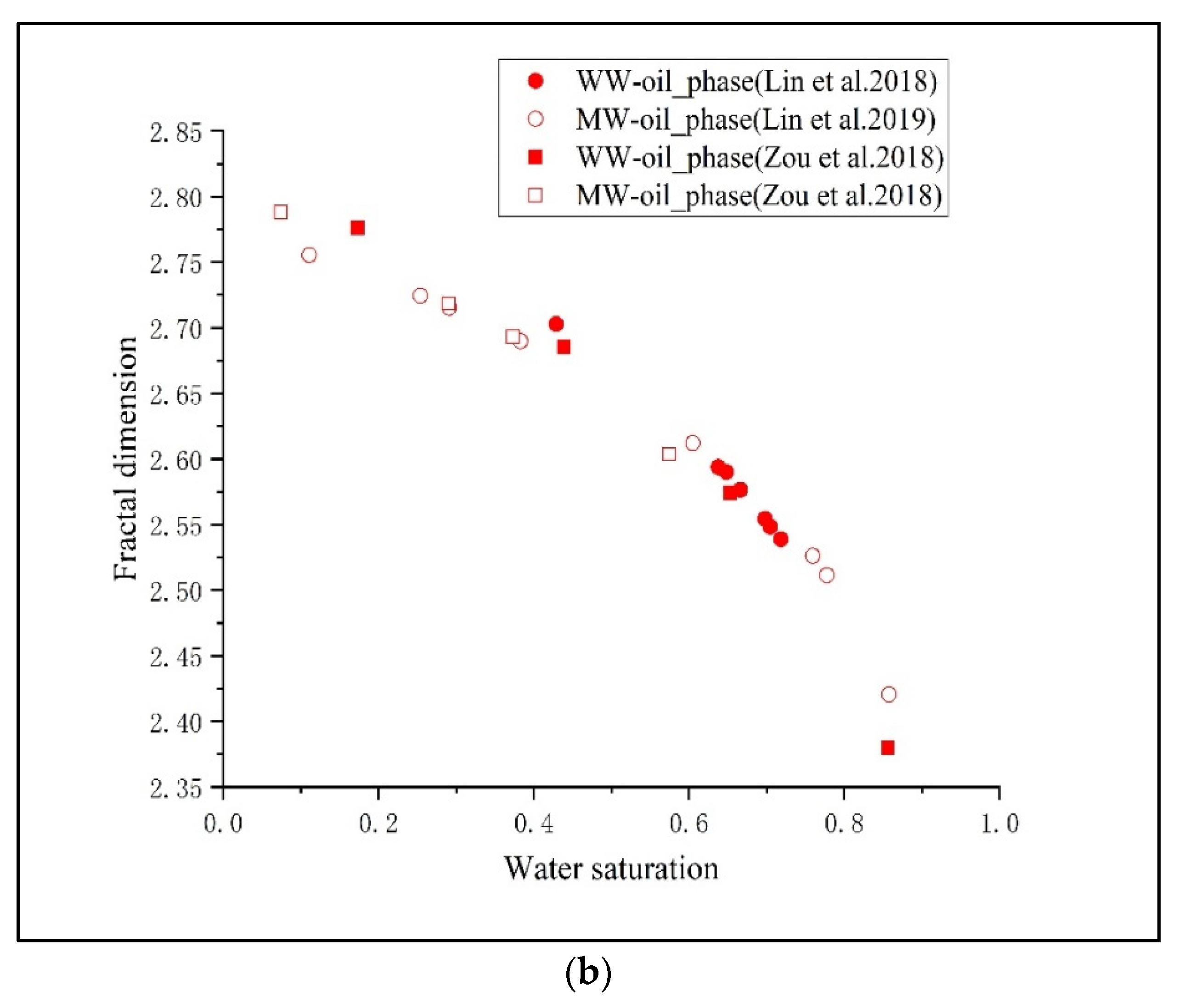
3.1.1. Fluid Complexity Characterized by Fractal Dimension
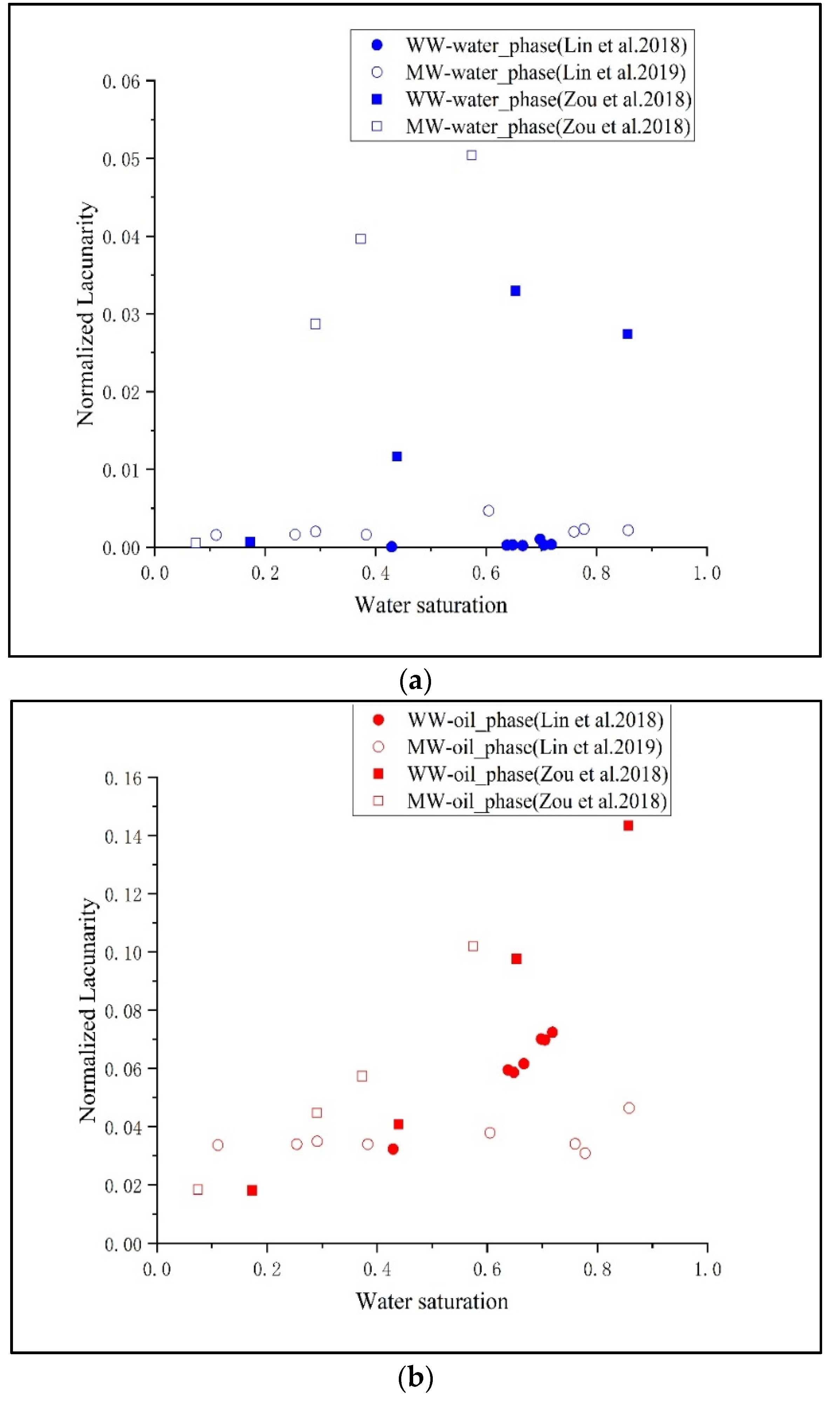
3.1.2. Fluid Heterogeneity Characterized by Normalized Lacunarity
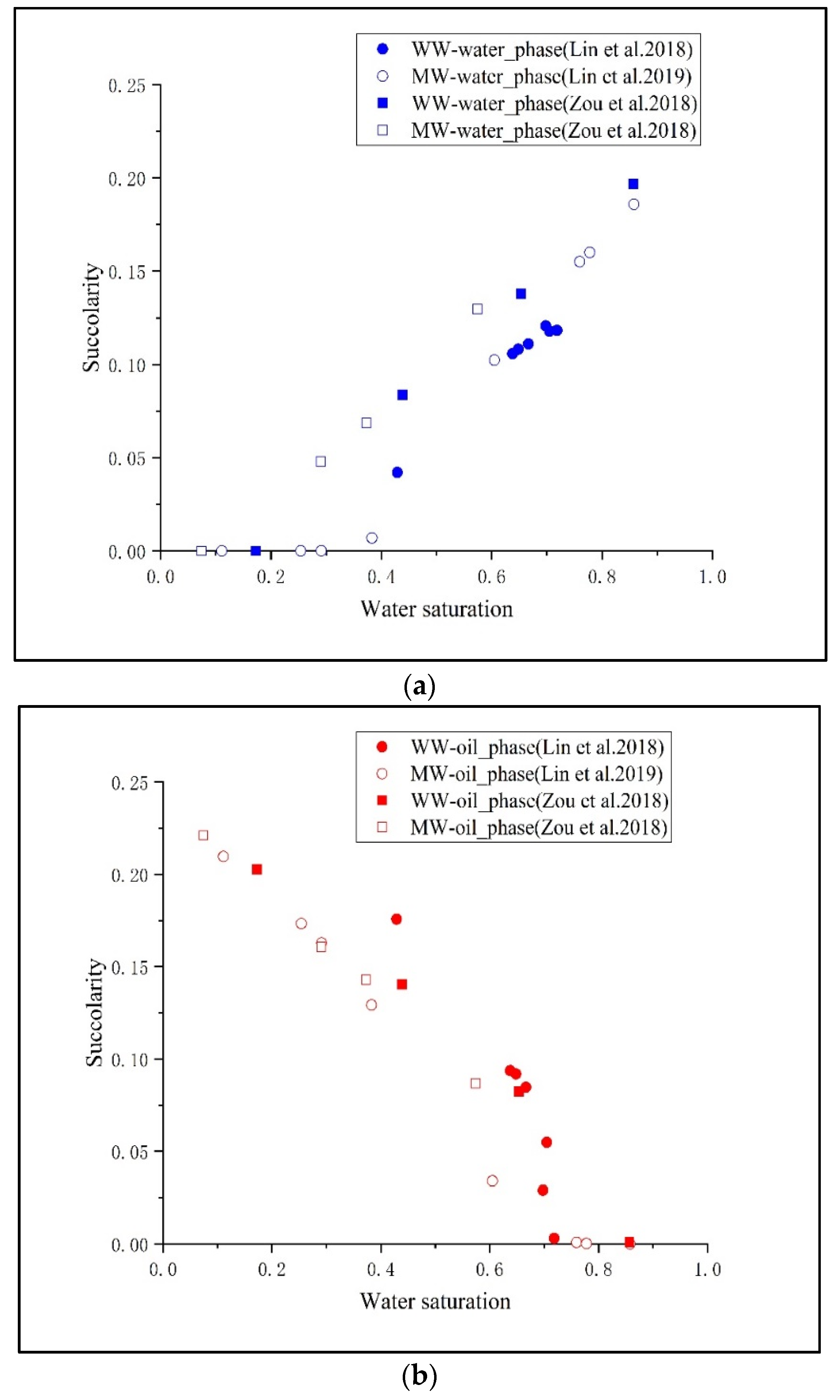
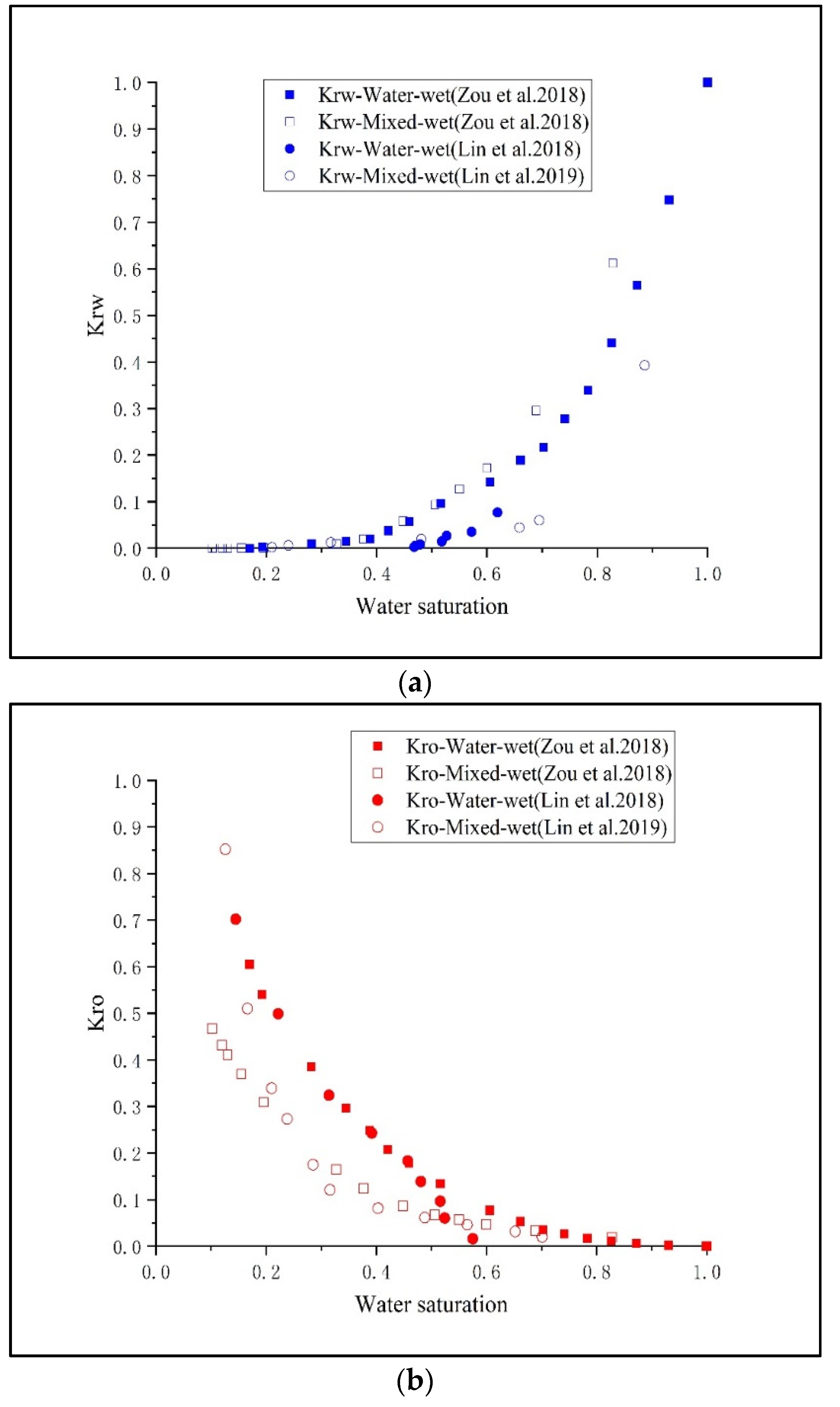
3.2. Flow Capacity Characterized by Succolarity and Relative Permeability Curves
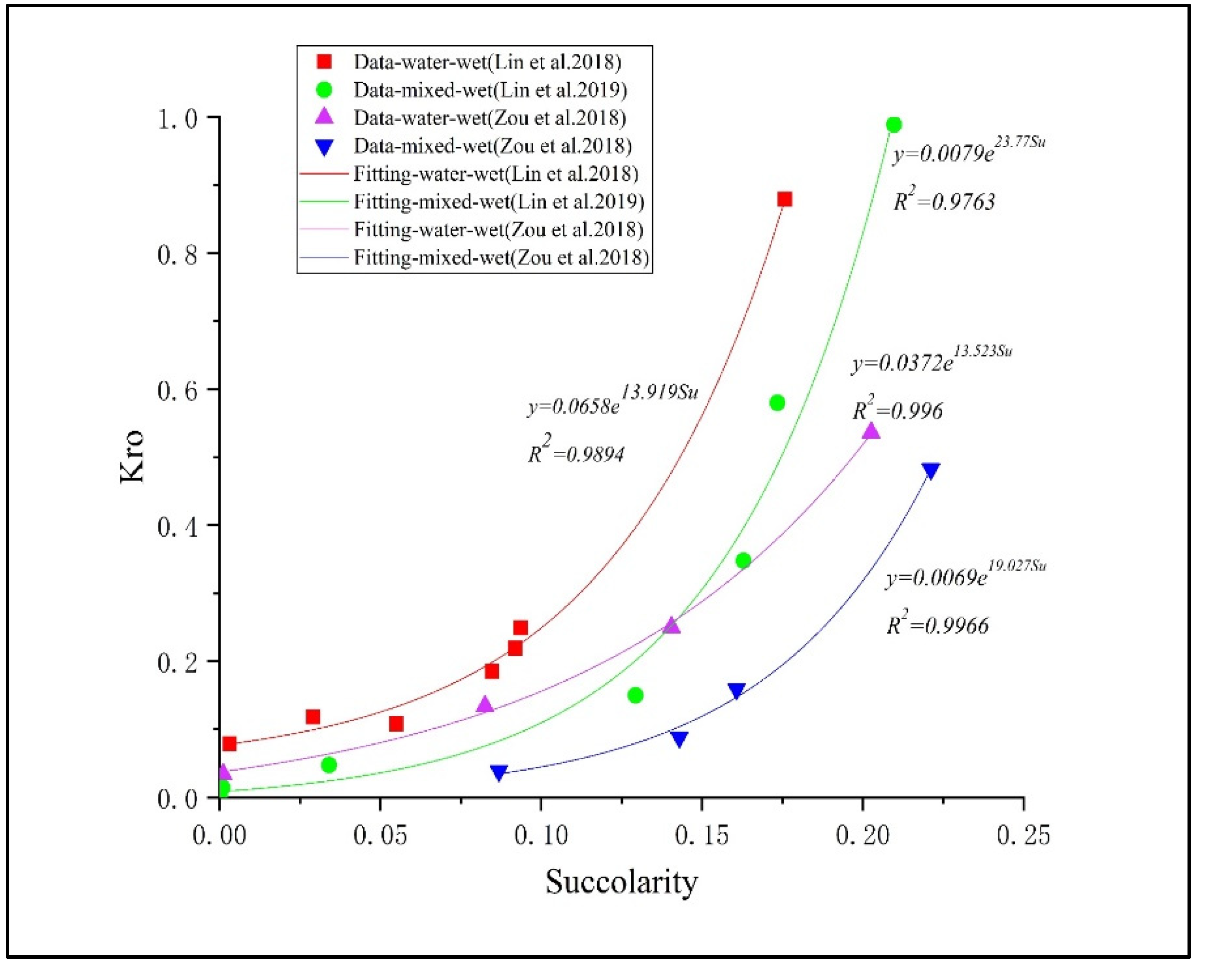
3.3. The Relationship between Succolarity and Relative Permeability
4. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blunt, M.J.; Bijeljic, B.; Dong, H.; Gharbi, O.; Iglauer, S.; Mostaghimi, P.; Paluszny, A.; Pentland, C. Pore-Scale Imaging and Modelling. Adv. Water Resour. 2013, 51, 197–216. [Google Scholar] [CrossRef] [Green Version]
- Morrow, N.; Buckley, J. Improved Oil Recovery by Low-Salinity Waterflooding. J. Pet. Technol. 2011, 63, 106–112. [Google Scholar] [CrossRef]
- Iglauer, S.; Paluszny, A.; Pentland, C.H.; Blunt, M. Residual CO2 imaged With X-Ray Micro-Tomography. Geophys. Res. Lett. 2011, 38, L21403. [Google Scholar] [CrossRef] [Green Version]
- Molnar, I.L.; Gerhard, J.I.; Willson, C.S.; O’Carroll, D.M. Wettability Effects on Primary Drainage Mechanisms and NAPL Distribution: A Pore-Scale Study. Water Resour. Res. 2020, 56, 2019–025381. [Google Scholar] [CrossRef] [Green Version]
- Morrow, N.R. Wettability and Its Effect on Oil Recovery. J. Pet. Technol. 1990, 42, 1476–1484. [Google Scholar] [CrossRef]
- Mohammadi, M.-R.; Bahmaninia, H.; Ansari, S.; Hemmati-Sarapardeh, A.; Norouzi-Apourvari, S.; Schaffie, M.; Ranjbar, M. Evaluation of Asphaltene Adsorption on Minerals of Dolomite and Sandstone Formations in Two and Three-Phase Systems. Adv. Geo-Energy Res. 2021, 5, 39–52. [Google Scholar] [CrossRef]
- Anderson, W.G. Wettability Literature Survey Part 5: The Effects of Wettability on Relative Permeability. J. Pet. Technol. 1987, 39, 1453–1468. [Google Scholar] [CrossRef]
- Anderson, W. Wettability Literature Survey-Part 6: The Effects of Wettability on Waterflooding. J. Pet. Technol. 1987, 39, 1605–1622. [Google Scholar] [CrossRef]
- Abdallah, W.; Buckley, J.S.; Carnegie, A.; Edwards, J.; Herold, B.; Fordham, E.; Graue, A.; Habashy, T.; Seleznev, N.; Signer, C.; et al. Fundamentals of Wettability. Oilfield Rev. 1986, 19, 44–61. [Google Scholar]
- Zhao, B.; MacMinn, C.W.; Juanes, R. Wettability Control on Multiphase Flow in Patterned Microfluidics. Proc. Natl. Acad. Sci. USA 2016, 113, 10251–10256. [Google Scholar] [CrossRef] [Green Version]
- Blunt, M.J.; Lin, Q.; Akai, T.; Bijeljic, B. A Thermodynamically Consistent Characterization of Wettability in Porous Media Using High-Resolution Imaging. J. Colloid Interface Sci. 2019, 552, 59–65. [Google Scholar] [CrossRef] [PubMed]
- Berg, S.; Ott, H.; Klapp, S.A.; Schwing, A.; Neiteler, R.; Brussee, N.; Makurat, A.; Leu, L.; Enzmann, F.; Schwarz, J.-O.; et al. Real-Time 3D Imaging of Haines Jumps in Porous Media Flow. Proc. Natl. Acad. Sci. USA 2013, 110, 3755–3759. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berg, S.; Rücker, M.; Ott, H.; Georgiadis, A.; van der Linde, H.; Enzmann, F.; Kersten, M.; Armstrong, R.; de With, S.; Becker, J.; et al. Connected Pathway Relative Permeability from Pore-Scale Imaging of Imbibition. Adv. Water Resour. 2016, 90, 24–35. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Herring, A.; Arns, C.; Berg, S.; Armstrong, R.T. Pore-Scale Characterization of Two-Phase Flow Using Integral Geometry. Transp. Porous Media 2017, 118, 99–117. [Google Scholar] [CrossRef]
- Zou, S.; Armstrong, R.T.; Arns, J.; Arns, C.H.; Hussain, F. Experimental and Theoretical Evidence for Increased Ganglion Dynamics During Fractional Flow in Mixed-Wet Porous Media. Water Resour. Res. 2018, 54, 3277–3289. [Google Scholar] [CrossRef]
- McClure, J.E.; Armstrong, R.T.; Berrill, M.A.; Schlüter, S.; Berg, S.; Gray, W.G.; Miller, C.T. Geometric State Function for Two-Fluid Flow in Porous Media. Phys. Rev. Fluids 2018, 3, 084306. [Google Scholar] [CrossRef]
- Gao, Y.; Raeini, A.Q.; Selem, A.M.; Bondino, I.; Blunt, M.J.; Bijeljic, B. Pore-Scale Imaging with Measurement of Relative Permeability and Capillary Pressure on the Same Reservoir Sandstone Sample under Water-Wet and Mixed-Wet Conditions. Adv. Water Resour. 2020, 146, 103786. [Google Scholar] [CrossRef]
- Gao, Y.; Raeini, A.Q.; Blunt, M.J.; Bijeljic, B. Dynamic Fluid Configurations in Steady-State Two-Phase Flow in Bentheimer Sandstone. Phys. Rev. E 2021, 103, 013110. [Google Scholar] [CrossRef]
- Zou, S.; Liu, Y.; Cai, J.; Armstrong, R.T. Influence of Capillarity on Relative Permeability in Fractional Flows. Water Resour. Res. 2020, 56, 2020–027624. [Google Scholar] [CrossRef]
- Armstrong, R.T.; Porter, M.L.; Wildenschild, D. Linking Pore-Scale Interfacial Curvature to Column-Scale Capillary Pressure. Adv. Water Resour. 2012, 46, 55–62. [Google Scholar] [CrossRef]
- Andrew, M.; Bijeljic, B.; Blunt, M.J. Pore-Scale Contact Angle Measurements at Reservoir Conditions Using X-Ray Microtomography. Adv. Water Resour. 2014, 68, 24–31. [Google Scholar] [CrossRef] [Green Version]
- Sun, C.; McClure, J.; Berg, S.; Mostaghimi, P.; Armstrong, R.T. Universal Description of Wetting on Multiscale Surfaces Using Integral Geometry. J. Colloid Interface Sci. 2021, 608, 2330–2338. [Google Scholar] [CrossRef] [PubMed]
- Armstrong, R.T.; McClure, J.E.; Berrill, M.A.; Rücker, M.; Schlüter, S.; Berg, S. Beyond Darcy’s law: The role of phase topology and ganglion dynamics for two-fluid flow. Phys. Rev. E 2016, 94, 043113. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wood, D.A. Techniques Used to Calculate Shale Fractal Dimensions Involve Uncertainties and Imprecisions That Require More Careful Consideration. Adv. Geo-Energy Res. 2021, 5, 153–165. [Google Scholar] [CrossRef]
- Xia, Y.; Wei, W.; Liu, Y.; Cai, Z.; Zhang, Q.; Cai, J. A Fractal-Based Approach to Evaluate the Effect of Microstructure on the Permeability of Two-Dimensional Porous Media. Appl. Geochem. 2021, 131, 105013. [Google Scholar] [CrossRef]
- Armstrong, R.T.; McClure, J.; Robins, V.; Liu, Z.; Arns, C.H.; Schlüter, S.; Berg, S. Porous Media Characterization Using Minkowski Functionals: Theories, Applications and Future Directions. Transp. Porous Media 2019, 130, 305–335. [Google Scholar] [CrossRef]
- Yu, B.; Liu, W. Fractal Analysis of Permeabilities for Porous Media. AIChE J. 2004, 50, 46–57. [Google Scholar] [CrossRef]
- Krohn, C.E. Fractal Measurements of Sandstones, Shales, and Carbonates. J. Geophys. Res. Earth Surf. 1988, 93, 3297–3305. [Google Scholar] [CrossRef]
- Katz, A.J.; Thompson, A.H. Fractal Sandstone Pores: Implications for Conductivity and Pore Formation. Phys. Rev. Lett. 1985, 54, 1325–1328. [Google Scholar] [CrossRef]
- Xia, Y.; Cai, J.; Perfect, E.; Wei, W.; Zhang, Q.; Meng, Q. Fractal Dimension, Lacunarity and Succolarity Analyses on CT Images of Reservoir Rocks for Permeability Prediction. J. Hydrol. 2019, 579, 124198. [Google Scholar] [CrossRef]
- De Melo, R.H.C.; Conci, A. How Succolarity Could Be Used as Another Fractal Measure in Image Analysis. Telecommun. Syst. 2013, 52, 1643–1655. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1982; Volume 1. [Google Scholar]
- Roy, A.; Perfect, E.; Dunne, W.M.; Odling, N.; Kim, J.-W. Lacunarity Analysis of Fracture Networks: Evidence for Scale-Dependent Clustering. J. Struct. Geol. 2010, 32, 1444–1449. [Google Scholar] [CrossRef]
- Kim, J.-W.; Sukop, M.; Perfect, E.; Pachepsky, Y.; Choi, H. Geometric and Hydrodynamic Characteristics of Three-Dimensional Saturated Prefractal Porous Media Determined with Lattice Boltzmann Modeling. Transp. Porous Media 2011, 90, 831–846. [Google Scholar] [CrossRef]
- Cousins, T.A.; Ghanbarian, B.; Daigle, H. Three-Dimensional Lattice Boltzmann Simulations of Single-Phase Permeability in Random Fractal Porous Media with Rough Pore–Solid Interface. Transp. Porous Media 2018, 122, 527–546. [Google Scholar] [CrossRef]
- Ahrenholz, B.; Tölke, J.; Lehmann, P.; Peters, A.; Kaestner, A.; Krafczyk, M.; Durner, W. Prediction of Capillary Hysteresis in a Porous Material Using Lattice-Boltzmann Methods and Comparison to Experimental Data and a Morphological Pore Network Model. Adv. Water Resour. 2008, 31, 1151–1173. [Google Scholar] [CrossRef]
- Kumar, M.; Fogden, A. Patterned Wettability of Oil and Water in Porous Media. Langmuir 2010, 26, 4036–4047. [Google Scholar] [CrossRef] [PubMed]
- Latham, S.; Varslot, T.; Sheppard, A. Image Registration: Enhancing and Calibrating X-Ray Micro-CT Imaging. In Proceedings of the International Symposium of the Society of Core Analysts, Abu Dhabi, United Arab Emirates, 29 October–2 November 2008; pp. 1–12. [Google Scholar]
- Sheppard, A.; Latham, S.; Middleton, J.; Kingston, A.; Myers, G.; Varslot, T.; Fogden, A.; Sawkins, T.; Cruikshank, R.; Saadatfar, M.; et al. Techniques in Helical Scanning, Dynamic Imaging and Image Segmentation for Improved Quantitative Analysis with X-Ray Micro-CT. Nucl. Instruments Methods Phys. Res. Sect. B Beam Interactions Mater. Atoms 2014, 324, 49–56. [Google Scholar] [CrossRef] [Green Version]
- Sheppard, A.; Sok, R.M.; Averdunk, H. Techniques for Image Enhancement and Segmentation of Tomographic Images of Porous Materials. Phys. A Stat. Mech. Appl. 2004, 339, 145–151. [Google Scholar] [CrossRef]
- Lin, Q.; Bijeljic, B.; Pini, R.; Blunt, M.J.; Krevor, S. Imaging and Measurement of Pore-Scale Interfacial Curvature to Determine Capillary Pressure Simultaneously with Relative Permeability. Water Resour. Res. 2018, 54, 7046–7060. [Google Scholar] [CrossRef]
- Lin, Q.; Bijeljic, B.; Berg, S.; Pini, R.; Blunt, M.J.; Krevor, S. Minimal Surfaces in Porous Media: Pore-Scale Imaging of Multiphase Flow in an Altered-Wettability Bentheimer Sandstone. Phys. Rev. E 2019, 99, 063105. [Google Scholar] [CrossRef] [Green Version]
- Foroughi, S.; Bijeljic, B.; Lin, Q.; Raeini, A.Q.; Blunt, M.J. Pore-by-Pore Modeling, Analysis, and Prediction of Two-Phase Flow in Mixed-Wet Rocks. Phys. Rev. E 2020, 102, 023302. [Google Scholar] [CrossRef] [PubMed]
- Zou, S.; Armstrong, R.T. Multiphase Flow Under Heterogeneous Wettability Conditions Studied by Special Core Analysis and Pore-Scale Imaging. SPE J. 2019, 24, 1234–1247. [Google Scholar] [CrossRef]
- Crawford, J.; Matsui, N. Heterogeneity of the Pore and Solid Volume of Soil: Distinguishing a Fractal Space from Its Non-Fractal Complement. Geoderma 1996, 73, 183–195. [Google Scholar] [CrossRef]
- Perfect, E.; Donnelly, B. Bi-Phase Box Counting: An Improved Method for Fractal Analysis of Binary Images. Fractals 2015, 23, 1540010. [Google Scholar] [CrossRef] [Green Version]
- Allain, C.; Cloitre, M. Characterizing the Lacunarity of Random and Deterministic Fractal Sets. Phys. Rev. A 1991, 44, 3552–3558. [Google Scholar] [CrossRef]
- Kovscek, A.R.; Wong, H.; Radke, C.J. A Pore-Level Scenario for the Development of Mixed Wettability in Oil Reservoirs. AIChE J. 1993, 39, 1072–1085. [Google Scholar] [CrossRef] [Green Version]
- Diao, Z.; Li, S.; Liu, W.; Liu, H.; Xia, Q. Numerical Study of the Effect of Tortuosity and Mixed Wettability on Spontaneous Imbibition in Heterogeneous Porous Media. Capillarity 2021, 4, 50–62. [Google Scholar] [CrossRef]

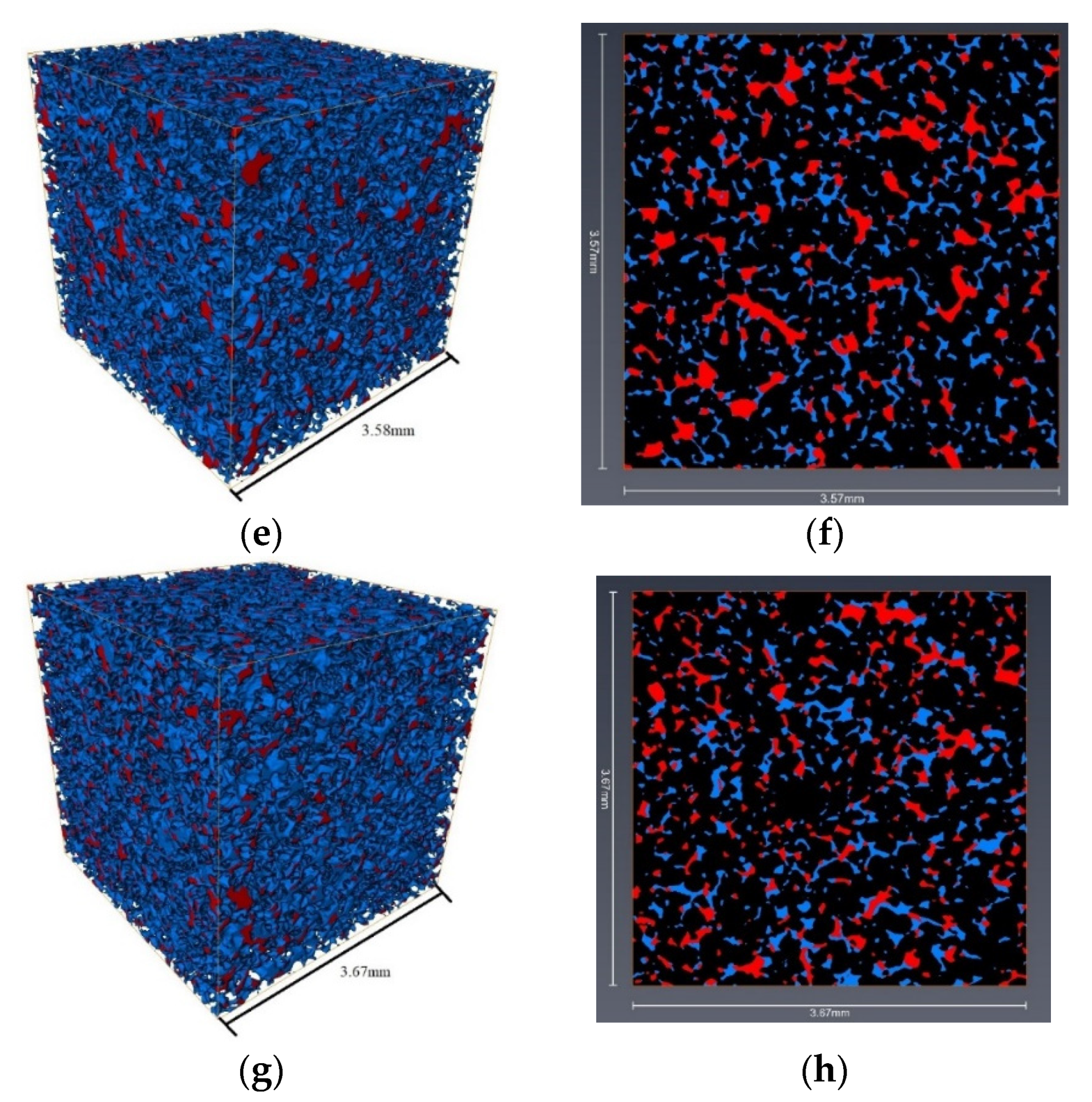
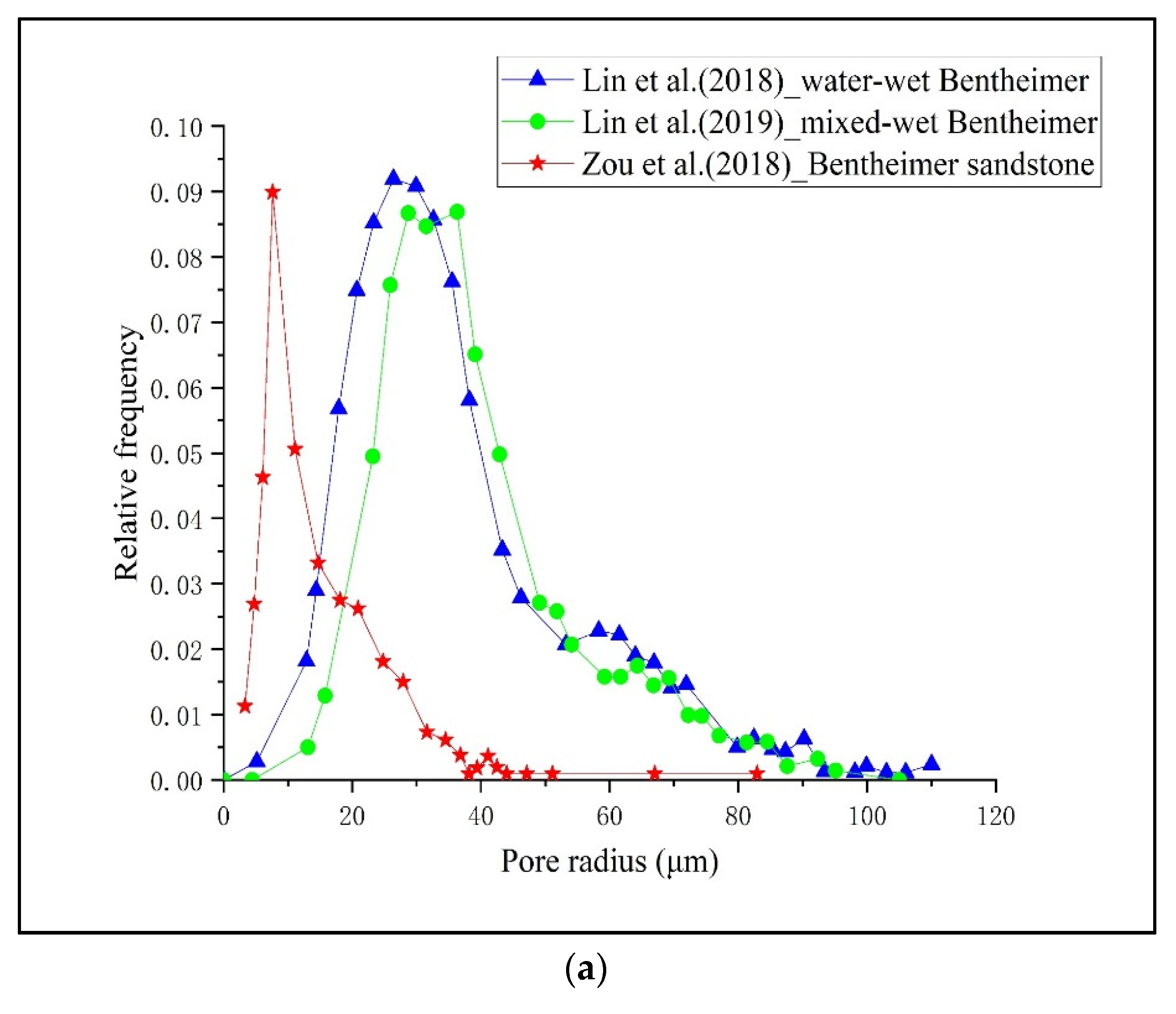
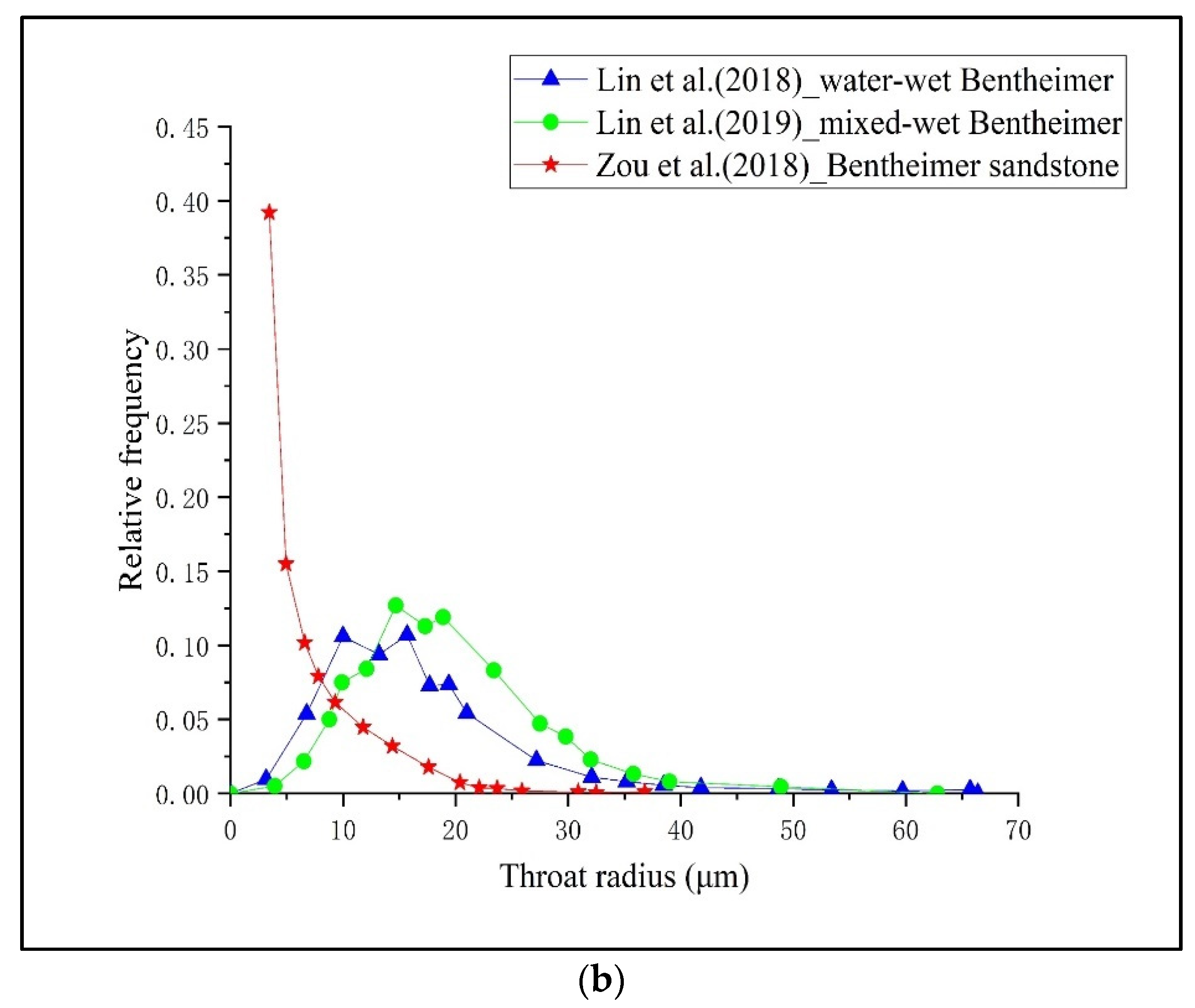
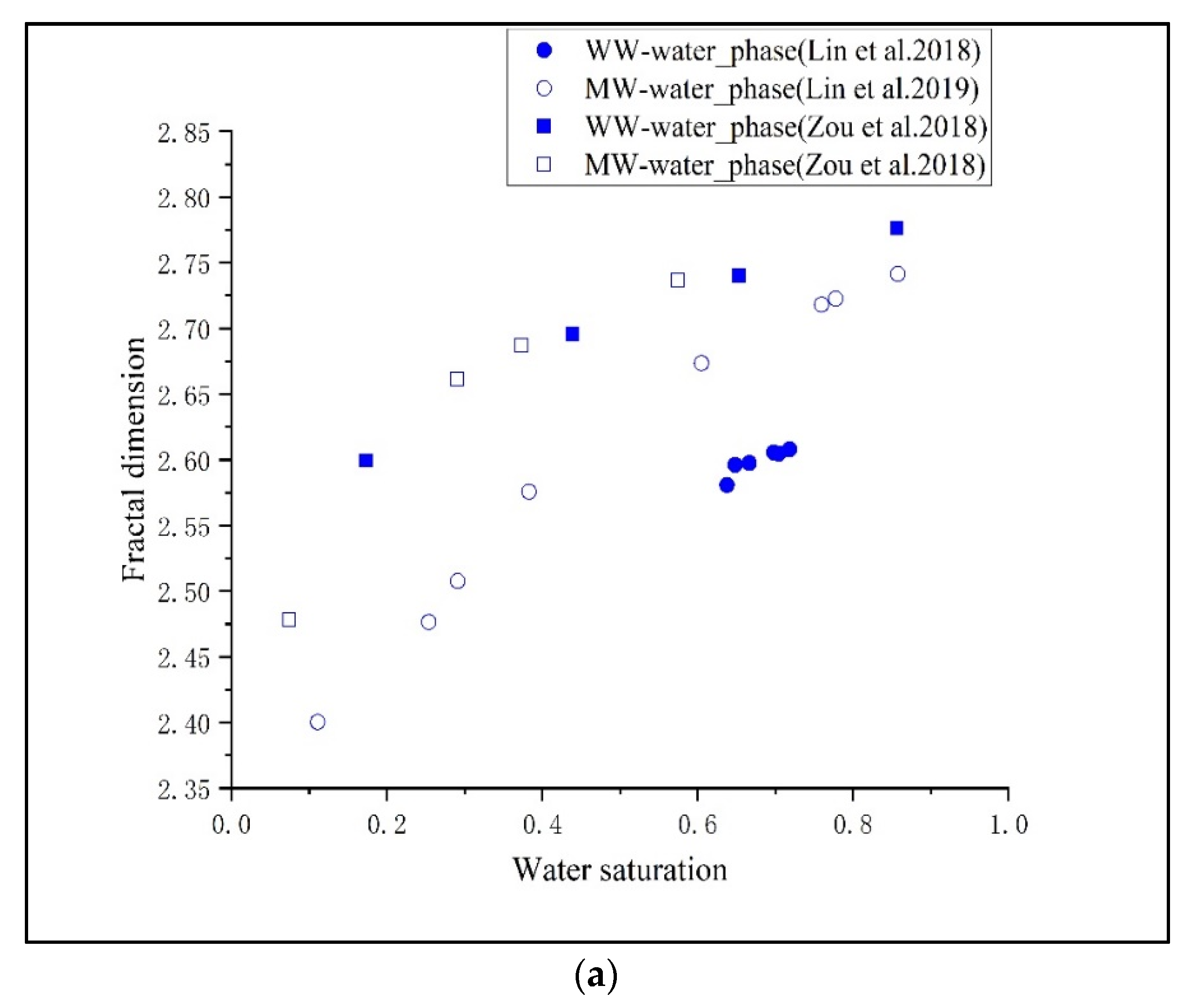
| Work | Porosity Based on CT Image | Total Flow Rate (mL/min) | Imaging Resolution (μm) |
|---|---|---|---|
| Zou et al. [15]—Water-wet | 0.245 | 1 | 5.56 |
| Zou et al. [15]—Mixed-wet | 0.245 | 1 | 5.56 |
| Lin et al. [41]—Water-wet | 0.348 | 0.02 | 3.58 |
| Lin et al. [42]—Mixed-wet | 0.231 | 0.03 | 3.58 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, S.; Xu, P.; Xie, C.; Deng, X.; Tang, H. Characterization of Two-Phase Flow from Pore-Scale Imaging Using Fractal Geometry under Water-Wet and Mixed-Wet Conditions. Energies 2022, 15, 2036. https://doi.org/10.3390/en15062036
Zou S, Xu P, Xie C, Deng X, Tang H. Characterization of Two-Phase Flow from Pore-Scale Imaging Using Fractal Geometry under Water-Wet and Mixed-Wet Conditions. Energies. 2022; 15(6):2036. https://doi.org/10.3390/en15062036
Chicago/Turabian StyleZou, Shuangmei, Peixing Xu, Congjiao Xie, Xuan Deng, and Haodong Tang. 2022. "Characterization of Two-Phase Flow from Pore-Scale Imaging Using Fractal Geometry under Water-Wet and Mixed-Wet Conditions" Energies 15, no. 6: 2036. https://doi.org/10.3390/en15062036
APA StyleZou, S., Xu, P., Xie, C., Deng, X., & Tang, H. (2022). Characterization of Two-Phase Flow from Pore-Scale Imaging Using Fractal Geometry under Water-Wet and Mixed-Wet Conditions. Energies, 15(6), 2036. https://doi.org/10.3390/en15062036






