Manual Operation Evaluation Based on Vectorized Spatio-Temporal Graph Convolutional for Virtual Reality Training in Smart Grid
Abstract
:1. Introduction
2. Literature Review
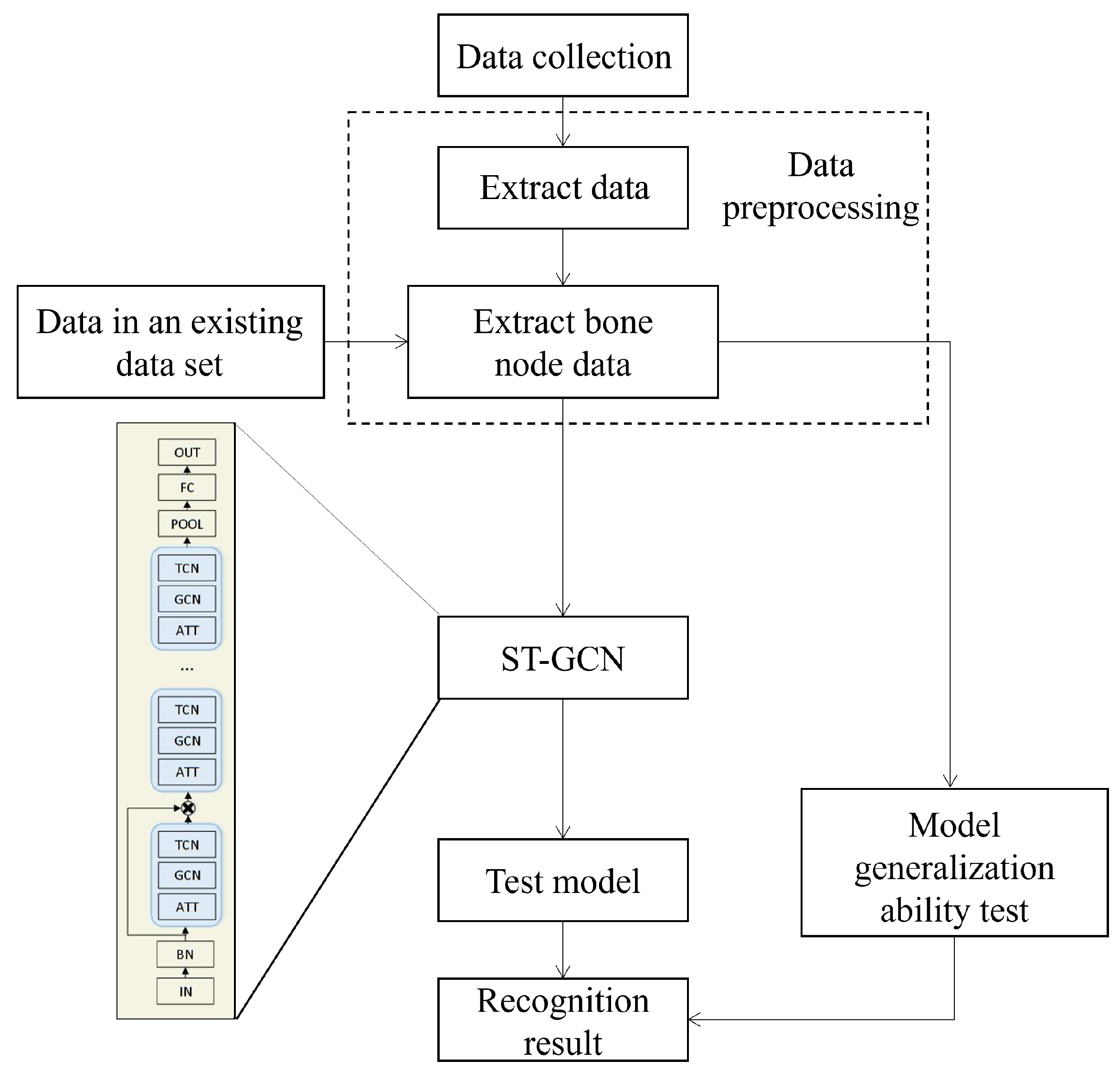
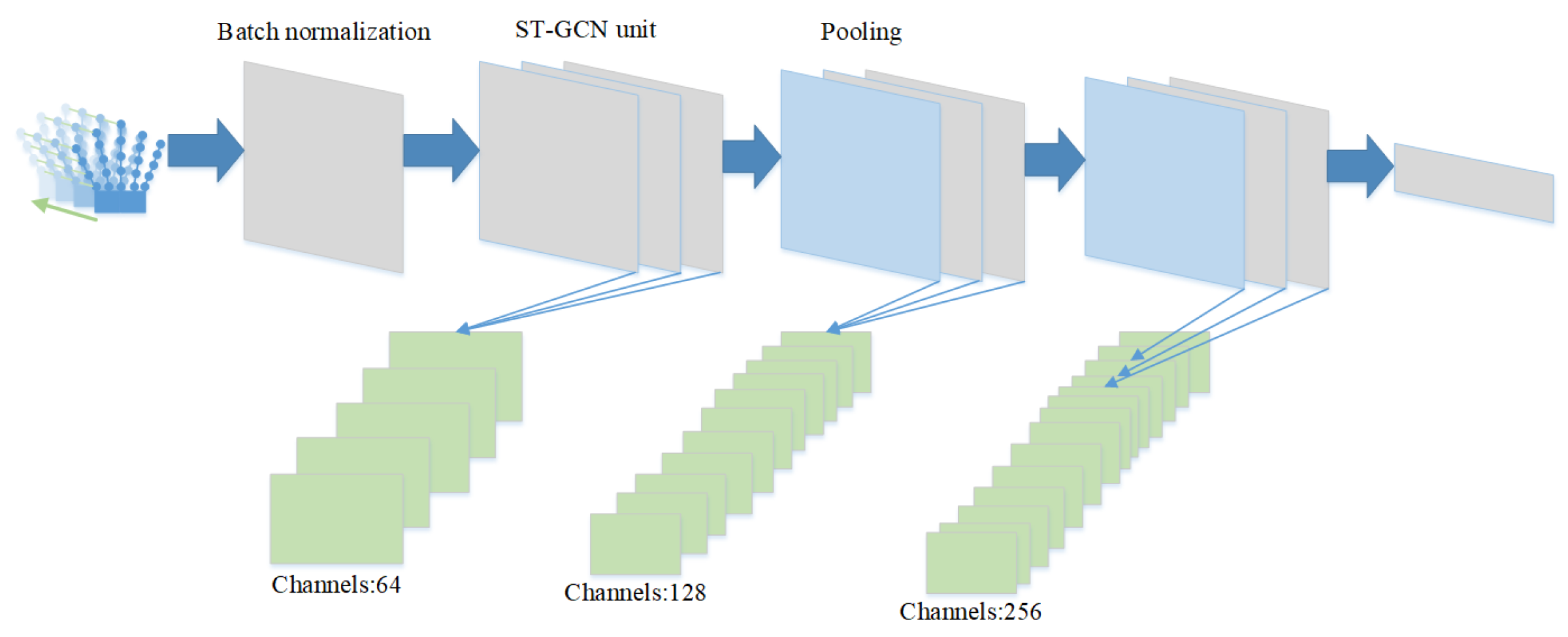
3. Vectorized Spatio-Temporal Graph Convolutional for VR Action Evaluation Method
3.1. Algorithm Refinement Process Design
3.2. Algorithm Refinement Process Design
3.3. Construction of Hand Vector Graph
3.4. Construction of Hand Vector Graph
3.5. Attention Mechanism
3.6. Partitioning Strategy
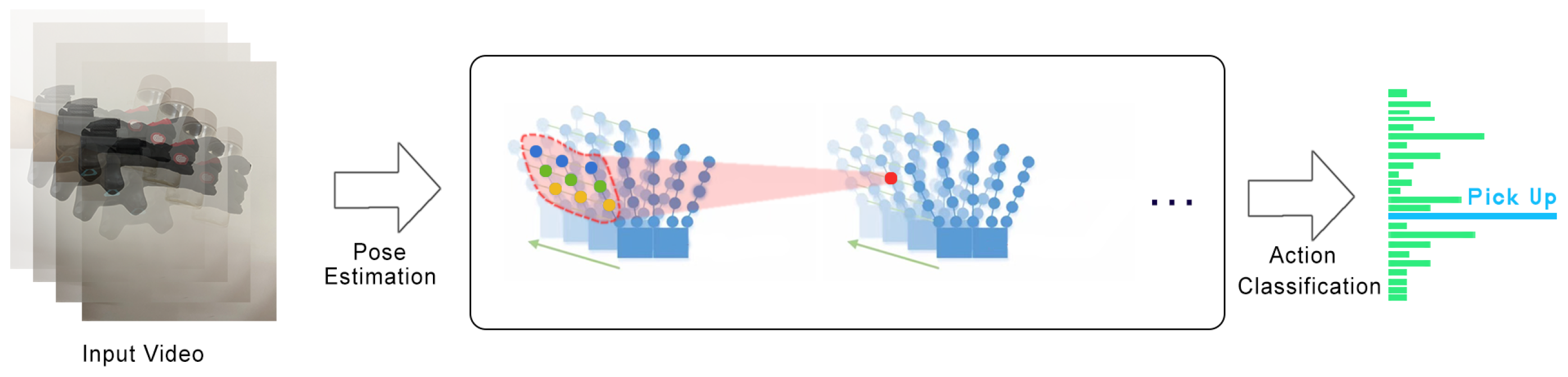
4. Application Instances
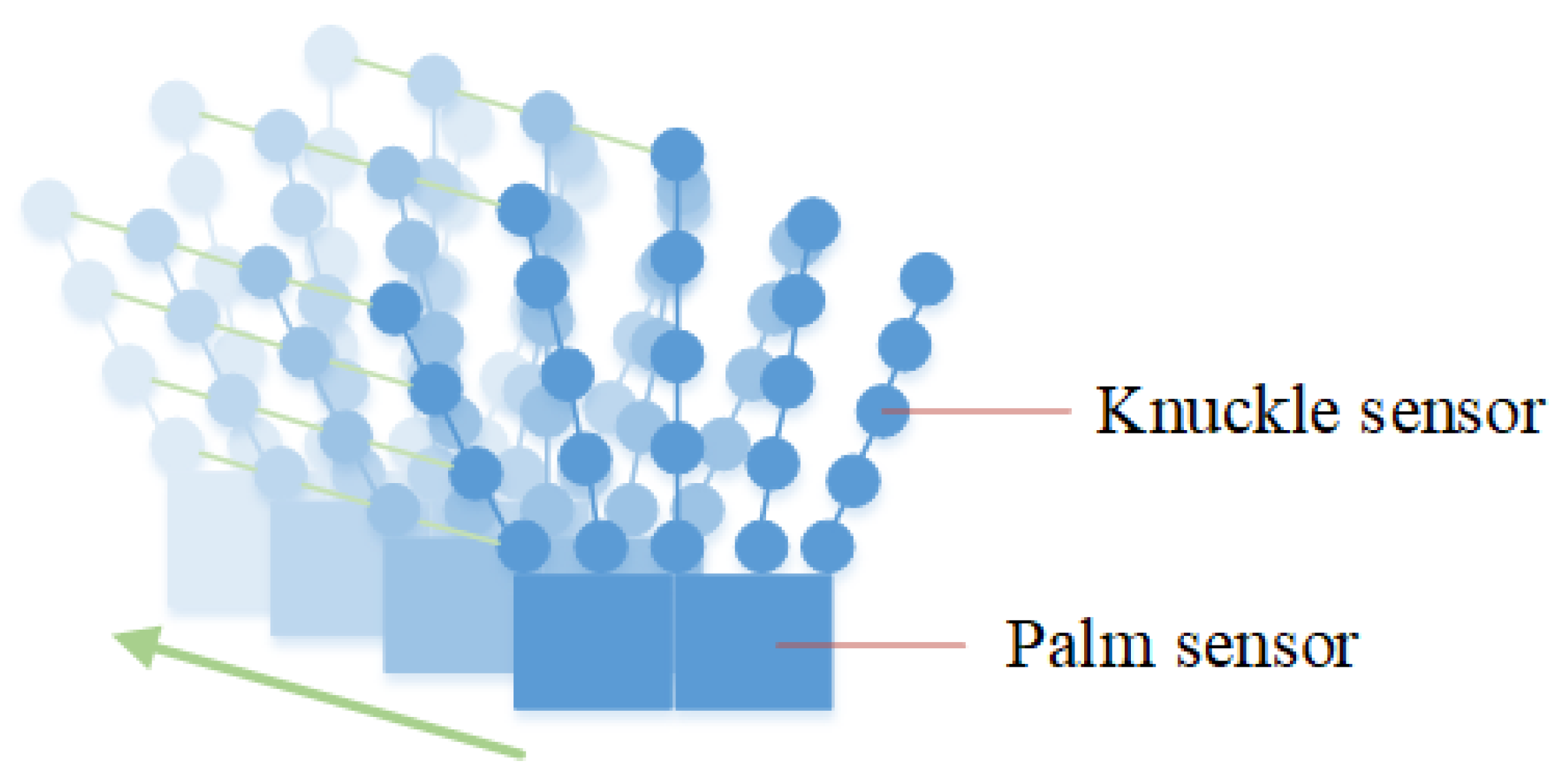
4.1. Method of Action Data Acquisition
4.2. Experiment and Result Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Osti, F.; de Amicis, R.; Sanchez, C.A.; Tilt, A.B.; Prather, E.; Liverani, A. A VR training system for learning and skills development for construction workers. Virtual Real. 2021, 25, 523–538. [Google Scholar] [CrossRef]
- Hagita, K.; Kodama, Y.; Takada, M. Simplified virtual reality training system for radiation shielding and measurement in nuclear engineering. Prog. Nucl. Energy 2020, 118, 103127. [Google Scholar] [CrossRef]
- Cikajlo, I.; Pogačnik, M. Movement analysis of pick-and-place virtual reality exergaming in patients with Parkinson’s disease. Technol. Health Care 2020, 28, 391–402. [Google Scholar] [CrossRef] [PubMed]
- Peng, Z.; Huang, Q.; Zhang, L.; Jafri, A.R.; Zhang, W.; Li, K. Humanoid on-line pattern generation based on parameters of off-line typical walk patterns. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 3758–3763. [Google Scholar]
- Seidenari, L.; Varano, V.; Berretti, S.; Bimbo, A.; Pala, P. Recognizing actions from depth cameras as weakly aligned multi-part bag-of-poses. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Portland, OR, USA, 23–28 June 2013; pp. 479–485. [Google Scholar]
- Leightley, D.; Yap, M.H.; Coulson, J.; Barnouin, Y.; McPhee, J.S. Benchmarking human motion analysis using kinect one: An open source dataset. In Proceedings of the 2015 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA), Hong Kong, China, 16–19 December 2015; pp. 1–7. [Google Scholar]
- Liu, Y.; Lu, G.; Yan, P. Exploring Multi-feature Based Action Recognition Using Multi-dimensional Dynamic Time Warping. In Information Science and Applications (ICISA) 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 421–429. [Google Scholar]
- Liu, X.; Feng, X.; Pan, S.; Peng, J.; Zhao, X. Skeleton tracking based on Kinect camera and the application in virtual reality system. In Proceedings of the 4th International Conference on Virtual Reality, Hong Kong, China, 24–26 February 2018; pp. 21–25. [Google Scholar]
- Wang, C.; Wang, Y.; Yuille, A.L. An approach to pose-based action recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 915–922. [Google Scholar]
- Devanne, M.; Wannous, H.; Berretti, S.; Pala, P.; Daoudi, M.; Del Bimbo, A. 3-d human action recognition by shape analysis of motion trajectories on riemannian manifold. IEEE Trans. Cybern. 2014, 45, 1340–1352. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zanfir, M.; Leordeanu, M.; Sminchisescu, C. The moving pose: An efficient 3d kinematics descriptor for low-latency action recognition and detection. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, NSW, Australia, 1–8 December 2013; pp. 2752–2759. [Google Scholar]
- Zhao, X.; Huang, Q.; Peng, Z.; Li, K. Kinematics mapping and similarity evaluation of humanoid motion based on human motion capture. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE Cat. No. 04CH37566), Sendai, Japan, 28 September–2 October 2004; Volume 1, pp. 840–845. [Google Scholar]
- Li, G.; Li, C. Learning skeleton information for human action analysis using Kinect. Signal Process. Image Commun. 2020, 84, 115814. [Google Scholar] [CrossRef]
- Slama, R.; Wannous, H.; Daoudi, M.; Srivastava, A. Accurate 3D action recognition using learning on the Grassmann manifold. Pattern Recognit. 2015, 48, 556–567. [Google Scholar] [CrossRef] [Green Version]
- Presti, L.L.; La Cascia, M.; Sclaroff, S.; Camps, O. Gesture modeling by hanklet-based hidden markov model. In Proceedings of the Asian Conference on Computer Vision, Singapore, 1–5 November 2014; pp. 529–546. [Google Scholar]
- Kim, K.; Cho, Y.K. Effective inertial sensor quantity and locations on a body for deep learning-based worker’s motion recognition. Autom. Constr. 2020, 113, 103126. [Google Scholar] [CrossRef]
- Liu, Y.; You, X. Specific action recognition method based on unbalanced dataset. In Proceedings of the 2019 IEEE 2nd International Conference on Information Communication and Signal Processing (ICICSP), Weihai, China, 28–30 September 2019; pp. 454–458. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Li, C.; Zhong, Q.; Xie, D.; Pu, S. Skeleton-based action recognition with convolutional neural networks. In Proceedings of the 2017 IEEE International Conference on Multimedia & Expo Workshops (ICMEW), Hong Kong, China, 10–14 July 2017; pp. 597–600. [Google Scholar]
- Kim, Y.; Kim, D. A CNN-based 3D human pose estimation based on projection of depth and ridge data. Pattern Recognit. 2020, 106, 107462. [Google Scholar] [CrossRef]
- Li, C.; Hou, Y.; Wang, P.; Li, W. Joint distance maps based action recognition with convolutional neural networks. IEEE Signal Process. Lett. 2017, 24, 624–628. [Google Scholar] [CrossRef] [Green Version]
- Du, Y.; Wang, W.; Wang, L. Hierarchical recurrent neural network for skeleton based action recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1110–1118. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Yan, S.; Xiong, Y.; Lin, D. Spatial temporal graph convolutional networks for skeleton-based action recognition. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LI, USA, 2–7 February 2018. [Google Scholar]
- Li, M.; Chen, S.; Chen, X.; Zhang, Y.; Wang, Y.; Tian, Q. Actional-structural graph convolutional networks for skeleton-based action recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3595–3603. [Google Scholar]
- Li, T.; Sun, J.; Wang, L. An intelligent optimization method of motion management system based on BP neural network. Neural Comput. Appl. 2021, 33, 707–722. [Google Scholar] [CrossRef]
- Slembrouck, M.; Luong, H.; Gerlo, J.; Schütte, K.; Cauwelaert, D.V.; Clercq, D.D.; Vanwanseele, B.; Veelaert, P.; Philips, W. Multiview 3D markerless human pose estimation from openpose skeletons. In Proceedings of the International Conference on Advanced Concepts for Intelligent Vision Systems, Auckland, New Zealand, 10–14 February 2020; pp. 166–178. [Google Scholar]
- Xu, X.; Chen, H.; Moreno-Noguer, F.; Jeni, L.A.; Torre, F.D.L. 3d human shape and pose from a single low-resolution image with self-supervised learning. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 284–300. [Google Scholar]
- Wang, J.; Jin, S.; Liu, W.; Liu, W.; Qian, C.; Luo, P. When human pose estimation meets robustness: Adversarial algorithms and benchmarks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 11855–11864. [Google Scholar]
- Shi, X.; Qin, P.; Zhu, J.; Xu, S.; Shi, W. Lower limb motion recognition method based on improved wavelet packet transform and unscented kalman neural network. Math. Probl. Eng. 2020, 2020, 5684812. [Google Scholar] [CrossRef] [PubMed]
- Xue, Y.; Yu, Y.; Yin, K.; Li, P.; Xie, S.; Ju, Z. Human In-hand Motion Recognition Based on Multi-modal Perception Information Fusion. IEEE Sens. J. 2022. [Google Scholar] [CrossRef]
- Li, Q.; Liu, Y.; Zhu, J.; Chen, Z.; Liu, L.; Yang, S.; Zhu, G.; Zhu, B.; Li, J.; Jin, R.; et al. Upper-Limb Motion Recognition Based on Hybrid Feature Selection: Algorithm Development and Validation. JMIR mHealth uHealth 2021, 9, e24402. [Google Scholar] [CrossRef] [PubMed]
- Guo, R.; Cui, J.; Zhao, W.; Li, S.; Hao, A. Hand-by-hand mentor: An AR based training system for piano performance. In Proceedings of the 2021 IEEE Conference on Virtual Reality and 3D User Interfaces Abstracts and Workshops (VRW), Lisbon, Portugal, 27 March–1 April 2021; pp. 436–437. [Google Scholar]


| A1: drink water | A2: eat meal | A3: brush teeth | A4: brush hair | A5: drop |
| A6: pick up | A7: throw | A8: sit down | A9: stand up | A10: clapping |
| A11: reading | A12: writing | A13: tear up paper | A14: put on jacket | A15: take off jacket |
| A16: put on a shoe | A17: take off a shoe | A18: put on glasses | A19: take off glasses | A20: put on a hat/cap |
| A21: take off a hat/cat | A22: cheer up | A23: hand waving | A24: kicking something | A25: reach into pocket |
| A31: point to something | A32: taking a selfie | A33: check time (from watch) | A34: rub two hands | A35: nod head/bow |
| A36: shake hands | A37: wipe face | A38: salute | A39: put palms together | A40: cross hands in front |
| A41: sneeze/cough | A42: staggering | A43: falling down | A44: headache | A45: chest pain |
| A46: back pain | A47: neck pain | A48: nausea | A49: fan self | A50: punch/slap |
| A51: kicking | A52: pushing | A53: pat on back | A54: point finger | A55: hugging |
| A56: giving object | A57: touch pocket | A58: shaking hands | A59: walking towards | A60: walking apart |
| Action Type | Sample Number | Training Number | Accuracy Rate TOP1 | Accuracy Rate TOP5 |
|---|---|---|---|---|
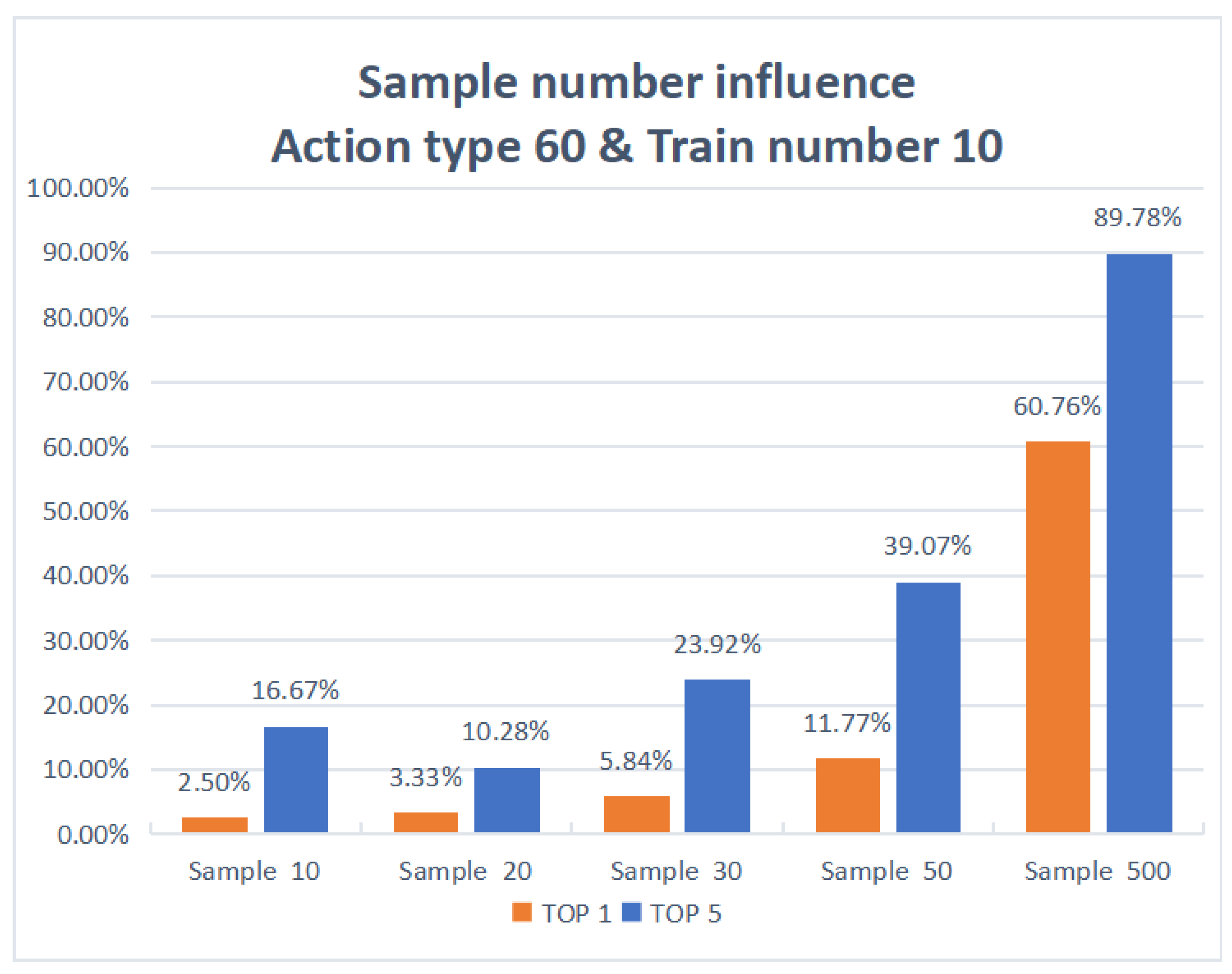
| 60 | 10 | 10 | 2.50% | 16.67% |
| 60 | 20 | 10 | 3.33% | 10.28% |
| 60 | 30 | 10 | 5.84% | 23.92% |
| 60 | 40 | 10 | 9.77% | 35.40% |
| 60 | 50 | 10 | 11.77% | 39.07% |
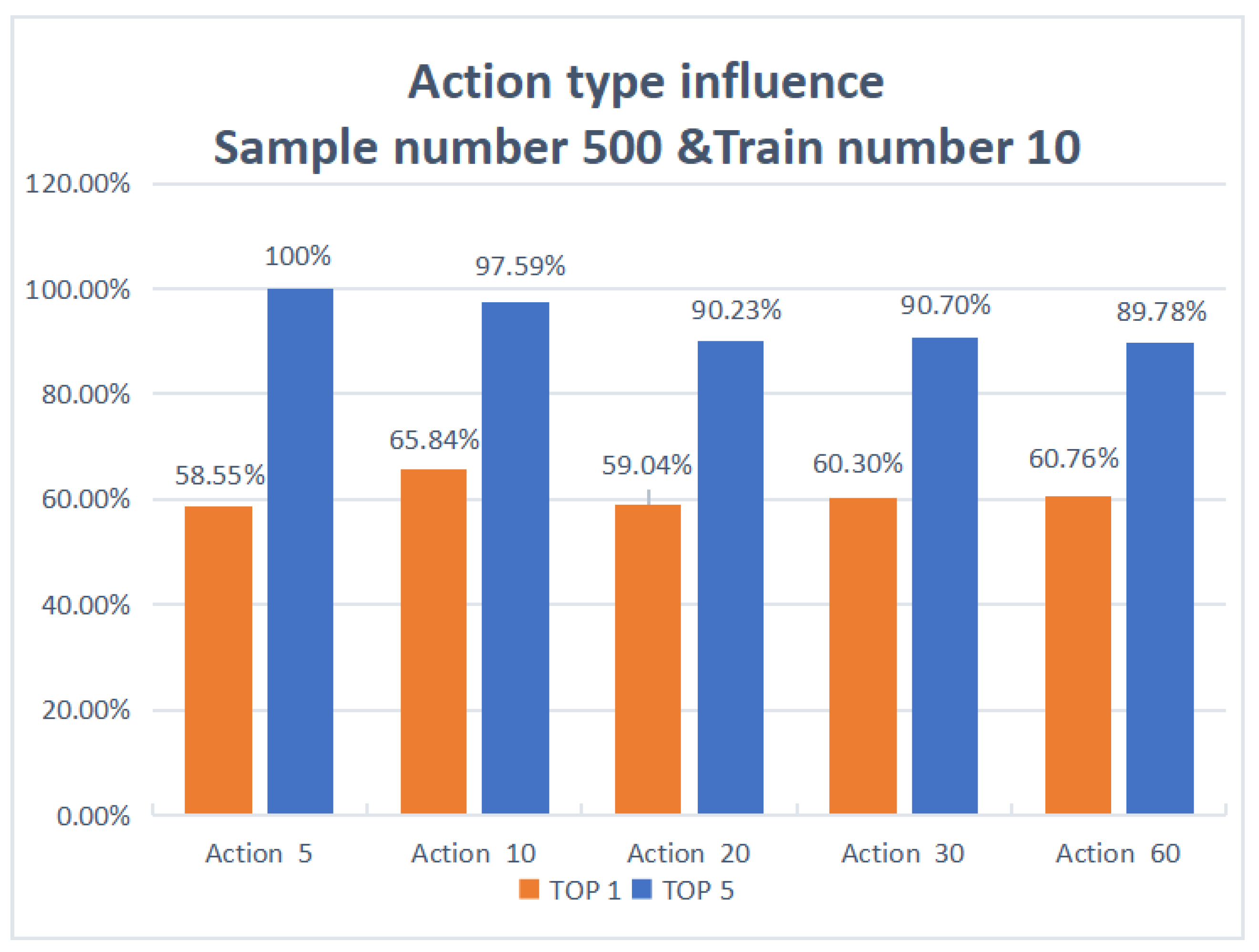
| 5 | 500 | 10 | 58.55% | 100% |
| 10 | 500 | 10 | 65.84% | 97.59% |
| 20 | 500 | 10 | 59.04% | 90.23% |
| 30 | 500 | 10 | 60.30% | 90.70% |
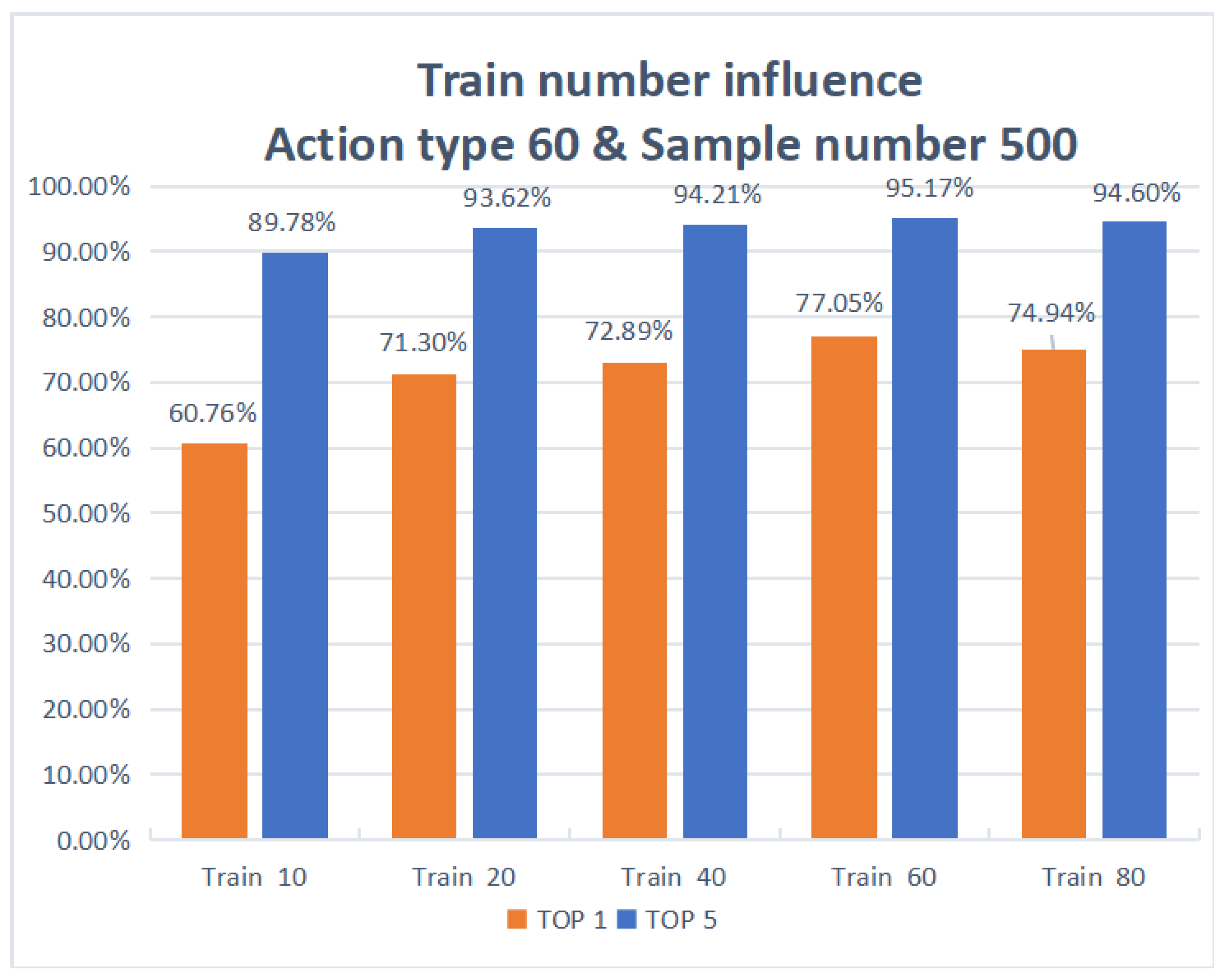
| 60 | 500 | 10 | 60.76% | 89.78% |
| 60 | 500 | 20 | 71.30% | 93.62% |
| 60 | 500 | 40 | 72.89% | 94.21% |
| 60 | 500 | 60 | 77.05% | 95.17% |
| 60 | 500 | 80 | 74.94% | 94.60% |
| 5 | 500 | 160 | 67.04% | 100% |
| 60 | 1000 | 80 | 82.84% | 97.44% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, F.; Liu, Y.; Zhan, W.; Xu, Q.; Chen, X. Manual Operation Evaluation Based on Vectorized Spatio-Temporal Graph Convolutional for Virtual Reality Training in Smart Grid. Energies 2022, 15, 2071. https://doi.org/10.3390/en15062071
He F, Liu Y, Zhan W, Xu Q, Chen X. Manual Operation Evaluation Based on Vectorized Spatio-Temporal Graph Convolutional for Virtual Reality Training in Smart Grid. Energies. 2022; 15(6):2071. https://doi.org/10.3390/en15062071
Chicago/Turabian StyleHe, Fangqiuzi, Yong Liu, Weiwen Zhan, Qingjie Xu, and Xiaoling Chen. 2022. "Manual Operation Evaluation Based on Vectorized Spatio-Temporal Graph Convolutional for Virtual Reality Training in Smart Grid" Energies 15, no. 6: 2071. https://doi.org/10.3390/en15062071
APA StyleHe, F., Liu, Y., Zhan, W., Xu, Q., & Chen, X. (2022). Manual Operation Evaluation Based on Vectorized Spatio-Temporal Graph Convolutional for Virtual Reality Training in Smart Grid. Energies, 15(6), 2071. https://doi.org/10.3390/en15062071





