1. Introduction
1.1. The Need for Measurements of Slow Flows
Measurements of slow and very slow flows have been gaining prominence in recent years, including in connection with the growing requirements concerning the energy efficiency of buildings. Precise control of air flow in rooms allows reduction in the costs of ventilation and air conditioning while meeting the requirements of industry standards [
1,
2,
3,
4]. Buildings such as museums, libraries, archives, and many others house valuable historical objects, most of which are sensitive, or very sensitive, to microclimatic conditions [
5,
6]. The key preventive measures in these buildings include continuous control of the quantity and quality of air flowing around historic objects. This is of great importance in view of their protection against mechanical, chemical, and microbiological degradation [
5,
7,
8,
9]. Special air flow conditions must be met in buildings with increased cleanliness requirements, e.g., in hospitals, factories producing electronic components, or cold rooms [
2,
4,
10,
11].
The buildings designed and constructed today, especially industrial and public utility buildings, usually have a well-developed network of mechanical ventilation tailored to their structure and purpose. Older buildings, especially historical and recently renovated buildings, have a ventilation network that results from a compromise between functionality and interference in the structure, as well as the visual and practical qualities, of the building. Such a solution requires, at least, periodic inspection of the ventilation conditions, especially in spaces that are not connected directly to the ventilation network or show signs of insufficient ventilation [
1,
2,
3,
4].
There are several types of anemometers that are usually chosen for studying air distribution in enclosed spaces (mainly vane anemometers and hot-wire anemometers); observations with the use of a marker (e.g., propylene glycol suspension) are also made [
1,
4,
5,
12,
13]. Anemometric methods are suitable for velocities above ~0.10 m/s (hot-wire anemometers) or above ~0.25 m/s (vane anemometers), providing information on instantaneous local flow velocity values. The direction and/or sense of the velocity vector is often inferred indirectly from the observation of measurement conditions. Marker-based methods allow us to visualize air flow in rooms to some extent, providing mainly qualitative information. Combining marker-based methods with optical techniques, such as LDA [
14] or PIV [
15], provides quantitative information on velocity vectors (LDA) or velocity vector fields (PIV) in the studied areas. However, this is an extremely costly approach, and therefore, it is rarely used.
This paper shows that a thermal wave anemometer and a proprietary measurement method can be used for the study of air distribution in enclosed spaces [
16]. The test results presented below show that this device has the potential to perform reliable measurements at a velocity of 0.01 m/s. Moreover, due to its design, it naturally provides information about the sense of the velocity vector. In quasi-stationary conditions, it can also be used to determine the direction of the velocity vector.
1.2. Motivation of the Study
A thermal wave anemometer is an instrument for precise measurements of the velocity of flowing gases and gas mixtures. Until now, this device has only been used in laboratory conditions due to the requirement of stationary flow conditions. However, the measurement method proposed in [
16] suggests that this device can be used to measure the velocity of slowly changing flows with a moderate intensity of longitudinal disturbances. In the present work, which is a continuation of [
16], it was checked whether the proposed approach can potentially be used to perform measurements in the presence of moderate transverse disturbances, whether the spatial arrangement of the transmitter and detectors affects the measurement uncertainty, and whether this method allows velocity measurements in the range below the diffusion velocity.
2. Materials and Methods
2.1. Basics of the Thermal Time-of-Flight Method
The basis for determining the velocity of a flowing gas stream, using the thermal wave method, is the measurement of the temperature wave propagation time in the tested flow over a known distance (usually between two detectors). Two interconnected phenomena are involved in the process of propagation of a temperature wave in flowing gas: wave drift with the flow velocity and thermal diffusion.
There are many approaches to determining the velocity of a flowing gas. This diversity results from usage of:
various types of electric current waveforms heating the wave transmitter, such as:
○ a rectangular signal [
27,
28],
○ a pseudo-stochastic signal [
29],
○ a signal composed of the sum of sinusoidal waveforms with various appropriately selected frequencies and amplitudes [
30],
○ a rectangular multifrequency binary sequence (MBS) signal [
31,
32];
various methods for determining the time-of-flight of the thermal wave, such as:
○ the determination of mutual correlation of signals on the detectors and calculation of the phase shift of the signals [
21,
28,
29,
31,
34],
○ the harmonic analysis of temperature waveforms followed by the determination of phase shifts of individual harmonics [
28,
29,
31].
All these methods, although based on the physics of flow, propagation of waves, and heat transfer, are burdened with the phenomenon of the so-called aerodynamic shadow formed behind the transmitter and first detector [
35,
36]. In fact, the very design of the thermal wave anemometer probe results in its mediocre aerodynamic behaviour [
37], and simply changing the geometry cannot solve the problem completely [
36]. Thus, although the thermal wave method belongs to the class of absolute methods, in practice, it is necessary to introduce a calibration function that corrects the negative impact of the aerodynamic shadow phenomenon.
2.2. The Proprietary Measurement Method
In [
16], the authors proposed a measurement method that uses a transmitter and only one thermal wave detector. It is, therefore, applicable in the case of most thermal wave anemometer probes. It is based on the analysis of the time interval between two characteristic points of voltage signals: on the transmitter and on the first detector. The time interval, thus determined after reference to the distance between the transmitter and receiver, is the first approximation of the measured flow velocity
vNT1′. A simple correction using the Belehradek power function [
38] (1) provides a good approximation of the sought value of the inflow velocity
v∞ for velocities above the apparent diffusion velocity
vp. This method requires a single calibration of the probe in order to determine the parameters of the power function.
The proposed approach is semi-empirical, as it partially abstracts from the physics of the processes of diffusion and dispersion of thermal waves, as well as transport and heat exchange. The characteristic point related to the transmitter (N)—the beginning of the voltage signal rise—may not be the same as the beginning of the temperature rise of the transmitter wire [
39]. Similarly, the inflection point of the rising edge of the voltage signal at the detector (T) is only an approximation of the time of arrival of the thermal wave. However, apart from other metrological reasons, these points were selected because their determination is the easiest with automatic methods and has lowest uncertainties. Moreover, the only measured value related to the flow is the moment of occurrence of the aforementioned point on the detector.
2.3. Measurement Stand
Measurements were carried out on two measuring stands. The first was the TANPOZ wind tunnel (Strata Mechanics Research Institute of the Polish Academy of Sciences, Krakow, Poland) [
40]. The inflow velocity was controlled using a Schmidt thermal anemometer (model SS 20.500), whose measurement range is 0.07–2.50 m/s, and measurement uncertainty is 1.5% of the indicated value but not less than 0.02 m/s.
A series of measurements, primarily for the velocity range below the diffusion velocity, was carried out on the second measurement stand—a specially designed measurement setup for generating the lowest flow velocities, based on a water piston driven by a Mariotte cylinder [
41]. This measurement setup, after a modification that involved increasing the cross-section of the outlet pipe, allows one to obtain flow velocities from 0.01 to 0.20 m/s, with the stability from 5 to 2% and uncertainty of velocity determination from 10 to 3%, respectively.
For the generation and detection of temperature waves, a computer-controlled digital anemometer-thermometer (CCC2002) was used [
42]. Each of the three probes used consisted of the transmitter and the two wave detectors made of tungsten wire: 8 µm in diameter and 6 mm in length (transmitter) and 3 µm in diameter and 3 mm in length (detectors). The transmitter operated in a constant temperature-anemometer (CTA) mode with a rectangular input. The overheating ratio of transmitter wire alternated between 1.0 and 1.8. The wave frequency was set to 1.0 Hz.
Data acquisition from both anemometers (Schmidt and thermal wave) was performed at a sampling rate of 10 kHz with 16-bit resolution.
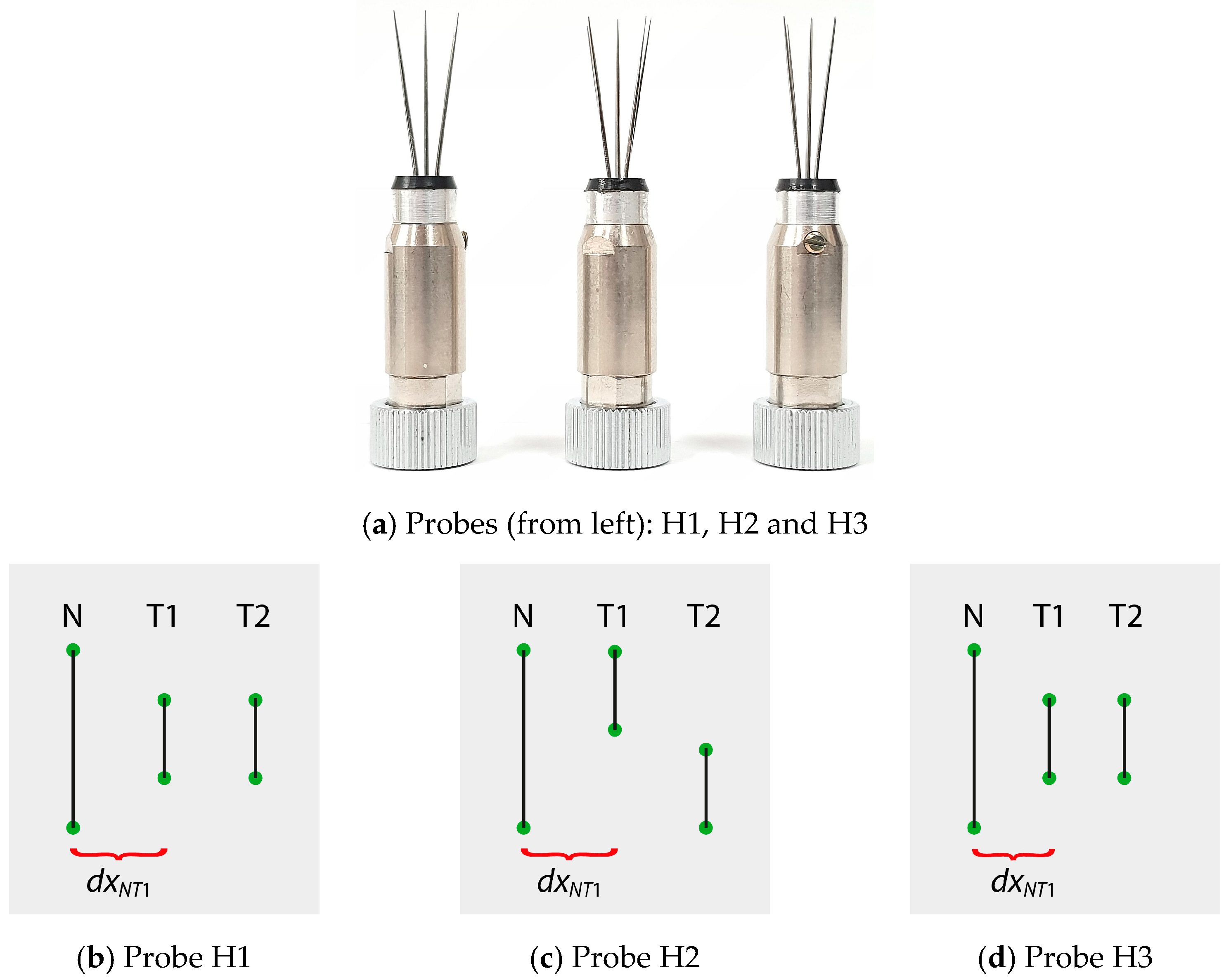
The geometric configuration of probes is shown in
Figure 1. The distance of the detector T1 from the transmitter N (denoted as
dxNT1) was 3.7 mm (probe H1 and H2) or 2.8 mm (probe H3).
In [
16], the measurement results for the H1 probe are presented. They were performed in the TANPOZ wind tunnel, with the optimal spatial configuration of the probe in relation to the flow direction. For comparative purposes, one series of measurements carried out using probes H2 and H3 in similar measurement conditions and one series of measurements using probe H1 inclined by an angle of
α = 7° in the direction of the inflow were carried out. Additionally, in order to supplement the results obtained in the TANPOZ wind tunnel with the lowest flow velocity range, a series of measurements with the H1 probe on the water piston stand was also performed [
41].
3. Results
3.1. Probe H1, α = 0°
The collected measurement data were analysed using the method described in [
16]. The results of the H1 probe presented therein are shown in
Figure 2 for comparative purposes. The following excerpts summarize the relevant results described in [
16]:
Figure 2a “compares the inflow velocity measured with the Schmidt anemometer (horizontal axis) with the velocity determined with the thermal wave anemometer (vertical axis). The figure also includes a dashed line that shows the ideal relationship of the two velocities (ratio 1:1). If the velocity values determined with the use of the thermal wave anemometer were close to the actual values, the measurement points (squares) should appear on this straight line.”
The graph in
Figure 2a presents that “the higher the inflow velocity, the greater the difference between the results of the measurements using the thermal wave anemometer and the actual values. The presentation of these deviations as a function of the velocity in the wind tunnel reveals their exponential character (
Figure 2b). The imposition of a correction in the form of a power function (1) on the measurement results leads to a significant improvement in the indications of the thermal wave anemometer.” Measurement points with the applied correction (using:
a = 0.409;
n = 1.650;
vp = 0.055 m/s) are marked in
Figure 2 with circles.
“
Figure 2c shows a graph of the relative differences (expressed as a percentage value) between the velocity values corrected using the power function and the set values in the wind tunnel (residual values). Deviations of the corrected velocity values from the set values amount to about 1% for velocities above 0.5 m/s, and increase to about 4% with a decrease in velocity. The increase is systematic, hence it may be possible to apply another form of the power function to reduce the value of the deviations in the range of lowest velocities. The higher deviations in the range of lowest velocities may also result from the metrological properties of the instrument used as a reference, the Schmidt anemometer.”
3.2. Probe H1, α = 7°
Figure 3 presents the results of measurements with the H1 probe inclined by an angle of
α = 7° in the direction of the flow. The same values of
a,
n i
vp as in the previous case were used to determine the series of points with the correction (circles). The purpose of this series of measurements was simply to check whether the proposed method shows a significant directional sensitivity.
Despite a slightly smaller number of measurement points than in the previous series, the chart in
Figure 3c shows that in the area of low velocities, i.e., below 0.7 m/s, the values of residuals (relative velocity deviations) do not change visibly, while in the remaining area, the residual values increased to approx. 4%. This result is fully acceptable, considering that, in the case of the measurement method, using information from both detectors a probe deviation of 7 degrees would result in a loss of signal on the second detector and, consequently, no results at a velocity of approx. 2 m/s.
3.3. Probe H2, α = 0°
The analysis of the H2 probe measurements revealed that changing from probe H1 to H2 did not cause significant qualitative changes in the obtained results (
Figure 4). Changing the probe geometry only required finding new values of parameters
a and
n from Equation (1):
a = 0.503,
n = 1.600.
The value of the parameter vp = 0.055 m/s remained unchanged because the measurements were carried out under almost identical thermodynamic conditions, so the velocity of the thermal wave did not change measurably.
3.4. Probe H3, α = 0°
In the case of changing from probe H1 to H3, even the results were improved (
Figure 5). If a better suited form of the power function was used for calibration, the probe would likely provide the most accurate results. The found values of parameters
a and
n from Equation (1) for the H3 probe are:
a = 0.723,
n = 1.659.
Table 1 summarizes the values of parameters
a and
n for all the probes. It shows that the distances between the wires have the strongest impact on these parameters, followed by the design of the probe.
3.5. Probe H1, α = 0°, Very Low Velocities
The results of H1 probe measurements (α = 0°) for velocities from 0.00 to 0.18 m/s are shown in
Figure 6.
Figure 6a shows that for velocities close to the velocity of thermal diffusion and lower, the sensitivity of the described method drops drastically. This is related to the diffusion deformation of the shape of the heat marker, the intensity of which is directly proportional to time. The longer it takes to transport the marker to the detector, the “fuzzier” the recorded thermal signal.
Even though sensitivity decreased in the lowest velocity area, the dependence
vNT1′(
v∞) remains unambiguous. We can, therefore, propose a correction, as a result of which an inverse relationship is obtained, i.e.,
v∞(
vNT1′) in the form of an analytical function. This correction requires a more complex form than relation (1). Among the many that were tested, the best results were obtained by the “two-phase exponential decay function with time offset” (2). It is worth noting that the need to adjust six different parameters requires at least seven measurement points.
The result of applying such a correction is shown in
Figure 6. An analysis of
Figure 6b shows that the measured value deviations from the set values did not exceed 1% in the velocity range from 0.050 to 0.200 m/s. Taking into account the specificity of the medium, this is a very good result and, interestingly, much better than those obtained earlier in a similar velocity range (see
Figure 2,
Figure 3,
Figure 4 and
Figure 5). Therefore, this is a rationale for modifying the dependence (1) to ensure that the measurement results are more consistent with the actual conditions.
For the velocity range from 0.015 to 0.031 m/s, these deviations are from 15 to 5%, respectively. Despite the low sensitivity of the method in this velocity range, the obtained deviations allow one to assume that properly performed measurements would provide reliable results, even for velocities of 0.010 m/s.
3.6. Probe H1, α = 0°, Modification of Function (1)
In
Section 3.5 above, an analysis of the applicability of the proposed measurement method was carried out for velocities below 0.2 m/s. It turned out that obtaining high consistency of measured and set velocities is possible. In particular, for velocities in the range of 0.05–0.20 m/s, the relative deviations did not exceed 1%. Therefore, a repeated analysis of the data collected using the H1 probe (
α = 0°) was performed for the velocity range of 0.05–2.50 m/s. It was found that the application of the correction, in the form of a 2nd order polynomial (3) instead of the dependence (1), allows one to maintain a 1% band of relative deviations of the measured and set velocities for velocities above 0.2 m/s. This is shown in
Figure 7.
This observation leads to the final form of the calibration function (4):
3.7. Signal Amplitude on Detectors
Depending on the design of the thermal wave anemometer, it may show greater or lesser sensitivity to deviations from the optimal position in relation to the flow direction. In the case of the H1 probe, tilting it forward or backward (
Figure 8) leads to faster deterioration and loss of the signal, especially on the T2 detector, than in the case of rotation around its axis (
Figure 9).
The graphs in
Figure 8 and
Figure 9 show that the measurement methods using only one detector, including the one proposed in this paper, are less affected by non-optimal probe orientation, with respect to the flow direction and slight transverse flow disturbance, than methods using both detectors.
In the case of quasi-stationary (and very slowly changing) flows, it is also conceivable to apply the knowledge of the probe’s angular “characteristics” to determine the direction and sense of the flow. For this purpose, the measurements should be carried out in an active manner that involves manipulating the orientation of the probe in space in order to find the optimal direction, i.e., the direction for which the signal amplitude, at one or both of the detectors, is the highest. This concept, however, requires a separate study.
The presented angular relationships show certain asymmetries. There are two reasons for this. One is the asymmetry of the probe design. The probes are made by hand; therefore, slight differences are possible, e.g., in the diameters or the spacing of the brackets. The aerodynamic properties of the H1 probe [
44,
45] are the second reason.
3.8. Measurement Uncertainties
For the inflow velocity (
v∞) range 0.00 ÷ 0.25 m/s, its measurement uncertainties varied from 10 to 3% of the measured values, respectively [
41]. For the remaining range (up to 2.5 m/s) measurement, uncertainty was equal to 1.5% of the measured value but not less than 0.02 m/s. Every velocity value was calculated and averaged over a considerable period of time. Therefore, its uncertainties resulted directly from the equipment used.
The voltage signals were measured with the uncertainty of less than 1 mV. In the case of direct presentation (
Figure 8 and
Figure 9), it was increased to 3 mV to take into account small flow disturbances occurring randomly in the wind tunnel.
The uncertainty of the directly measured velocities (
vNT1′) was estimated to be less than 1.0% of the measured value. However, due to the above mentioned flow disturbances and the
vNT1′ calculation method [
16], it was considered as equal to 1.5%.
In the case of determining the angle, its uncertainty was 1°.
4. Conclusions
The proposed measurement method allows the existing measuring probes, with different spatial configurations, to be used without interfering with their design. It is relatively unaffected by deviations from the optimal flow direction. In the simplest case (amendment (1)), it is necessary to know only three parameters of a given probe (dxNT1, a, n). The fourth one (vp) depends mainly on gas viscosity, so if there is no significant change in the gas composition, nor its density, it is not necessary to determine vp before every series of measurements, but it does allow a higher precision of results. On the other hand, the use of the full form of the calibration function (4) allows one to assume that the obtained measurement results will be characterized by deviations of relative values not exceeding 1% of the measured value in the velocity range of 0.05–2.50 m/s. Unfortunately, in the velocity range below 0.05 m/s, the residual values of the calibration function increase rapidly, reaching the value of 15% for the velocity of 0.015 m/s.
It should be emphasized that the values listed above are true for quasi-stationary conditions or very slowly changing flows. Although the proposed method enables the measurements of flows with a low level of longitudinal and transverse disturbances, it is necessary to further verify how these disturbances affect the measurement accuracy.
For velocities close to the velocity of thermal diffusion and lower, the sensitivity of the described method drops drastically. Nevertheless, it is possible to obtain reliable measurement results in the range of the lowest velocities. In order to increase the sensitivity of the method, apart from the characteristic point related to the rising edge of the signal on the detector, it would probably be necessary to also take into account the voltage pulse width data registered by it.
The presented measurement method makes it possible to determine the velocity vector. However, this requires further study, in particular, on the design of a miniature polar mount, which automatically determines the optimal positioning of the probe in relation to the flow.
Funding
This work was performed in 2020–2021 as a part of statutory works carried out at the Strata Mechanics Research Institute of the Polish Academy of Sciences in Krakow (Poland), funded by the Ministry of Science and Higher Education.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The author expresses his gratitude to Andrzej Rachalski for valuable technical guidance, and to Waldemar Wodziak and Tymoteusz Piga for assisting with the measurements.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
| CTA | Constant temperature Anemometer |
| LDA | Laser Doppler Anemometer |
| MBS | Multifrequency Binary Sequence |
| PIV | Particle Image Velocimetry |
| SMRI PAS | Strata Mechanics Research Institute of the Polish Academy of Sciences (Krakow, Poland) |
| TANPOZ | name of the wind tunnel in SMRI PAS |
| TTOF | Thermal Time-of-Flight Method |
Parameters
| v∞ | inflow velocity |
| vNT1′ | measured velocity, [m/s] |
| vNT1 | measured velocity with applied correction, [m/s] |
| vp | apparent velocity of thermal wave propagation in the current medium; its value results from the thermal diffusivity of the actual medium, the heat wave frequency and the measurement method, [m/s] |
| a, n | parameters of the Belehradek function, which are determined during fitting, [(m/s)1–n], [–] |
| A0, …, A5 | parameters of the “two-phase exponential decay function with time offset”, [m/s], …, [m/s] |
| B0, B1, B2 | parameters of the 2nd order polynomial, [m/s], [–], [–] |
References
- Cheremisinoff, N.P. Ventilation and Indoor Air Quality Control. Handb. Air Pollut. Prev. Control. 2002, 188–280. [Google Scholar] [CrossRef]
- Legg, R. Indoor Design Conditions. In Air Conditioning System Design; Elsevier: Amsterdam, The Netherlands, 2017; pp. 53–65. [Google Scholar]
- Ma, N.; Aviv, D.; Guo, H.; Braham, W.W. Measuring the Right Factors: A Review of Variables and Models for Thermal Comfort and Indoor Air Quality. Renew. Sustain. Energy Rev. 2021, 135, 110436. [Google Scholar] [CrossRef]
- Ashrae.Org. Available online: https://www.ashrae.org/ (accessed on 13 December 2021).
- Camuffo, D. Measuring Wind and Indoor Air Motions. In Microclimate for Cultural Heritage; Elsevier: Amsterdam, The Netherlands, 2019; pp. 483–511. [Google Scholar]
- Elkadi, H.; Al-Maiyah, S.; Fielder, K.; Kenawy, I.; Martinson, D.B. The Regulations and Reality of Indoor Environmental Standards for Objects and Visitors in Museums. Renew. Sustain. Energy Rev. 2021, 152, 111653. [Google Scholar] [CrossRef]
- Finlayson-Pitts, B.J.; Pitts, J.N. Indoor Air Pollution: Sources, Levels, Chemistry, and Fates. Chem. Up. Low. Atmos. 2000, 844–870. [Google Scholar] [CrossRef]
- Fabbri, K.; Bonora, A. Two New Indices for Preventive Conservation of the Cultural Heritage: Predicted Risk of Damage and Heritage Microclimate Risk. J. Cult. Herit. 2021, 47, 208–217. [Google Scholar] [CrossRef]
- Boeri, A.; Longo, D.; Fabbri, K.; Pretelli, M.; Bonora, A.; Boulanger, S. Library Indoor Microclimate Monitoring with and without Heating System. A Bologna University Library Case Study. J. Cult. Herit. 2022, 53, 143–153. [Google Scholar] [CrossRef]
- Xue, K.; Cao, G.; Liu, M.; Zhang, Y.; Pedersen, C.; Mathisen, H.M.; Stenstad, L.I.; Skogås, J.G. Experimental Study on the Effect of Exhaust Airflows on the Surgical Environment in an Operating Room with Mixing Ventilation. J. Build. Eng. 2020, 32, 101837. [Google Scholar] [CrossRef]
- Duret, S.; Hoang, H.M.; Flick, D.; Laguerre, O. Experimental Characterization of Airflow, Heat and Mass Transfer in a Cold Room Filled with Food Products. Int. J. Refrig. 2014, 46, 17–25. [Google Scholar] [CrossRef]
- Sui, X.; Tian, Z.; Liu, H.; Chen, H.; Wang, D. Field Measurements on Indoor Air Quality of a Residential Building in Xi’an under Different Ventilation Modes in Winter. J. Build. Eng. 2021, 42, 103040. [Google Scholar] [CrossRef]
- Calautit, J.K.; Hughes, B.R. Measurement and Prediction of the Indoor Airflow in a Room Ventilated with a Commercial Wind Tower. Energy Build. 2014, 84, 367–377. [Google Scholar] [CrossRef]
- Goodfellow, H.D.; Wang, Y. Industrial Ventilation Design Guidebook. In Engineering Design and Applications; Academic Press: Cambridge, MA, USA, 2021; Volume 2, ISBN 9780128166734. [Google Scholar]
- Cao, X.; Liu, J.; Jiang, N.; Chen, Q. Particle Image Velocimetry Measurement of Indoor Airflow Field: A Review of the Technologies and Applications. Energy Build. 2014, 69, 367–380. [Google Scholar] [CrossRef] [Green Version]
- Sobczyk, J.; Rachalski, A.; Wodziak, W. A Semi-Empirical Approach to Gas Flow Velocity Measurement by Means of the Thermal Time-of-Flight Method. Sensors 2021, 21, 5679. [Google Scholar] [CrossRef] [PubMed]
- Bradbury, L.J.S.; Castro, I.P. A Pulsed-Wire Technique for Velocity Measurements in Highly Turbulent Flows. J. Fluid Mech. 1971, 49, 657–691. [Google Scholar] [CrossRef]
- Tombach, I.H. An Evaluation of the Heat Pulse Anemometer for Velocity Measurement in Inhomogeneous Turbulent Flow. Rev. Sci. Instrum. 1973, 44, 141–148. [Google Scholar] [CrossRef]
- Avirav, Y.; Guterman, H.; Ben-Yaakov, S. Implementation of Digital Signal Processing Techniques in the Design of Thermal Pulse Flowmeters. IEEE Trans. Instrum. Meas. 1990, 39, 761–766. [Google Scholar] [CrossRef]
- Mathioulakis, E.; Grignon, M.; Poloniecki, J.G. A Pulsed-Wire Technique for Velocity and Temperature Measurements in Natural Convection Flows. Exp. Fluids 1994, 18, 82–86. [Google Scholar] [CrossRef]
- Jan, K.; Jerzy, P.; Józef, R.; Zdzisław, S.A.; Bolesław, S. Heat Waves In Flow Metrology. In Proceedings of the Flow Measurement of Fluids; North-Holland Publishing Company: Groningen, The Netherlands, 1978; pp. 403–407. [Google Scholar]
- Rachalski, A. High-Precision Anemometer with Thermal Wave. Rev. Sci. Instrum. 2006, 77, 095107. [Google Scholar] [CrossRef]
- Kovasznay, L.S.G. Hot-Wire Investigation of the Wake behind Cylinders at Low Reynolds Numbers. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1949, 198, 174–190. [Google Scholar] [CrossRef]
- Walker, R.E.; Westenberg, A.A. Absolute Low Speed Anemometer. Rev. Sci. Instrum. 1956, 27, 844–848. [Google Scholar] [CrossRef]
- Kiełbasa, J. Measurments of Steady Flow Velocity Using the Termal Wave Method. Arch. Min. Sci. 2005, 50, 191–208. [Google Scholar]
- Byon, C. Numerical and Analytic Study on the Time-of-Flight Thermal Flow Sensor. Int. J. Heat Mass Transf. 2015, 89, 454–459. [Google Scholar] [CrossRef]
- Biernacki, Z. A System of Wave Thermoanemometer with a Thermoresistive Sensor. Sens. Actuators A Phys. 1998, 70, 219–224. [Google Scholar] [CrossRef]
- Rachalski, A.; Poleszczyk, E.; Zięba, M. Use of the Thermal Wave Method for Measuring the Flow Velocity of Air and Carbon Dioxide Mixture. Measurement 2017, 95, 210–215. [Google Scholar] [CrossRef]
- Berthet, H.; Jundt, J.; Durivault, J.; Mercier, B.; Angelescu, D. Time-of-Flight Thermal Flowrate Sensor for Lab-on-Chip Applications. Lab Chip 2011, 11, 215–223. [Google Scholar] [CrossRef] [PubMed]
- Rachalski, A. Absolute Measurement of Low Gas Flow by Means of the Spectral Analysis of the Thermal Wave. Rev. Sci. Instrum. 2013, 84, 25105. [Google Scholar] [CrossRef] [PubMed]
- Bujalski, M.; Rachalski, A.; Ligęza, P.; Poleszczyk, E. The Use of Multifrequency Binary Sequences MBS Signal in the Anemometer with Thermal Wave. In Proceedings of the Measurement 2015; Institute of Measurement Science Slovak Academy of Sciences: Smolenice, Slovakia, 2015; pp. 297–300. [Google Scholar]
- Henderson, I.A.; Mcghee, J. Compact Symmetrical Binary Codes For System Identification. Math. Comput. Model. 1990, 14, 213–218. [Google Scholar] [CrossRef]
- Mosse, C.A.; Roberts, S.P. Microprocessor-Based Time-of-Flight Respirometer. Med. Biol. Eng. Comput. 1987, 25, 34–40. [Google Scholar] [CrossRef]
- Engelien, E.; Ecin, O.; Viga, R.; Hosticka, B.J.; Grabmaier, A. Calibration-Free Volume Flow Measurement Principle Based on Thermal Time-of-Flight (TToF). Proc. Procedia Eng. 2011, 25, 765–768. [Google Scholar] [CrossRef] [Green Version]
- Ong, L.; Wallace, J. The Velocity Field of the Turbulent Very near Wake of a Circular Cylinder. Exp. Fluids 1996, 20, 441–453. [Google Scholar] [CrossRef]
- Kiełbasa, J. Measurement of Aerodynamic and Thermal Footprints. Arch. Min. Sci. 1999, 44, 71–84. (In Polish) [Google Scholar]
- Gawor, M.; Sobczyk, J.; Wodziak, W.; Ligęza, P.; Rachalski, A.; Jamróz, P.; Socha, K.; Palacz, J. Flow Velocity Distribution in the Probe Area of the Anemometer with Thermal Wave. Trans. Strat. Mech. Res. Inst. 2019, 21, 49–53. (In Polish) [Google Scholar]
- Help Online—Origin Help—Belehradek. Available online: https://www.originlab.com/doc/Origin-Help/Belehradek-FitFunc (accessed on 28 June 2021).
- Durst, F.; Al-Salaymeh, A.; Bradshaw, P.; Jovanović, J. The Development of a Pulsed-Wire Probe for Measuring Flow Velocity with a Wide Bandwidth. Int. J. Heat Fluid Flow 2003, 24, 1–13. [Google Scholar] [CrossRef]
- Bujalski, M.; Gawor, M.; Sobczyk, J. Closed-Circuit Wind Tunnel with Air Temperature and Humidity Stabilization, Adapted for Measurements by Means of Optical Methods; Prace Instytutu Mechaniki Górotworu PAN: Krakow, Poland, 2013. (In Polish) [Google Scholar]
- Piga, T.; Rachalski, A.; Wodziak, W.; Sobczyk, J. Experimental Setup for Very Low Velocity Gas Flow Generation. Meas. Sci. Rev. 2022. in preparation. [Google Scholar]
- Ligȩza, P. Four-Point Non-Bridge Constant-Temperature Anemometer Circuit. Exp. Fluids 2000, 29, 505–507. [Google Scholar] [CrossRef]
- Rachalski, A.; Jamróz, P. Unpublished Research, Krakow, Poland. 2019.
- Gawor, M.; Sobczyk, J.; Wodziak, W.; Ligęza, P.; Rachalski, A.; Jamróz, P.; Socha, K.; Palacz, J. Distribution of Flow Velocity in the Vicinity of the Thermal Wave Anemometer Probe; Prace Instytutu Mechaniki Górotworu PAN: Krakow, Poland, 2019. (In Polish) [Google Scholar]
- Sobczyk, J. Experimental Study of the Flow Field Disturbance in the Vicinity of Single Sensor Hot-Wire Anemometer. EPJ Web Conf. 2018, 180, 02094. [Google Scholar] [CrossRef]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).