Collaborative Charging Scheduling of Hybrid Vehicles in Wireless Rechargeable Sensor Networks
Abstract
:1. Introduction
- We propose a novel charging system for WRSN that uses one WCV, a set of WCV-carried drones, and wireless charging in large and/or hostile areas. As far as we know, we are the first to explore the collaborative charging scheduling problem for the complicated wireless charging system.
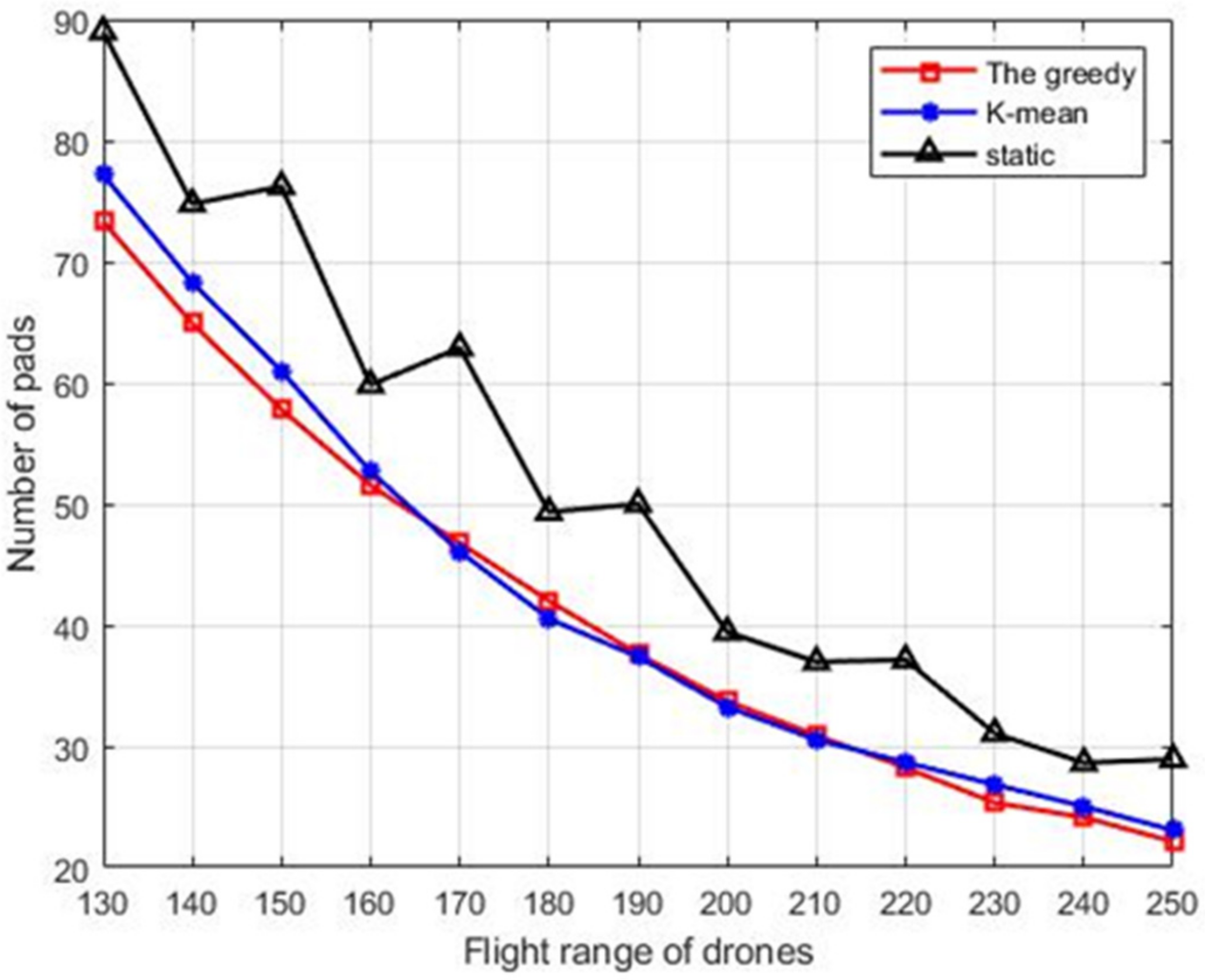
- We elaborate the problem of pad deployment to minimize the pad cost for charging all sensors considering the energy limitation of drones, locations of sensors, and terrain of the sensing region, and propose three near-optimal schemes to solve the problem.
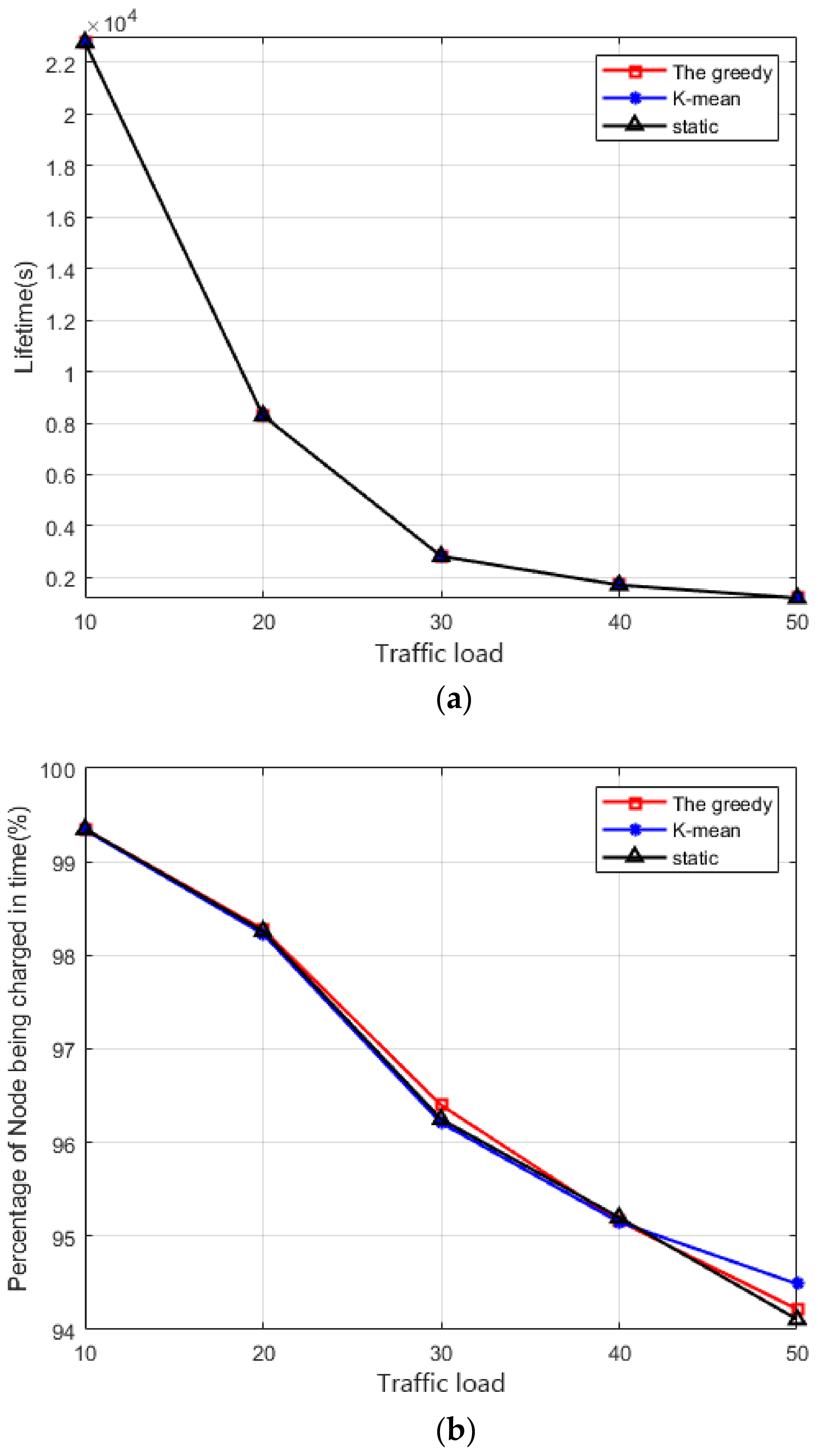
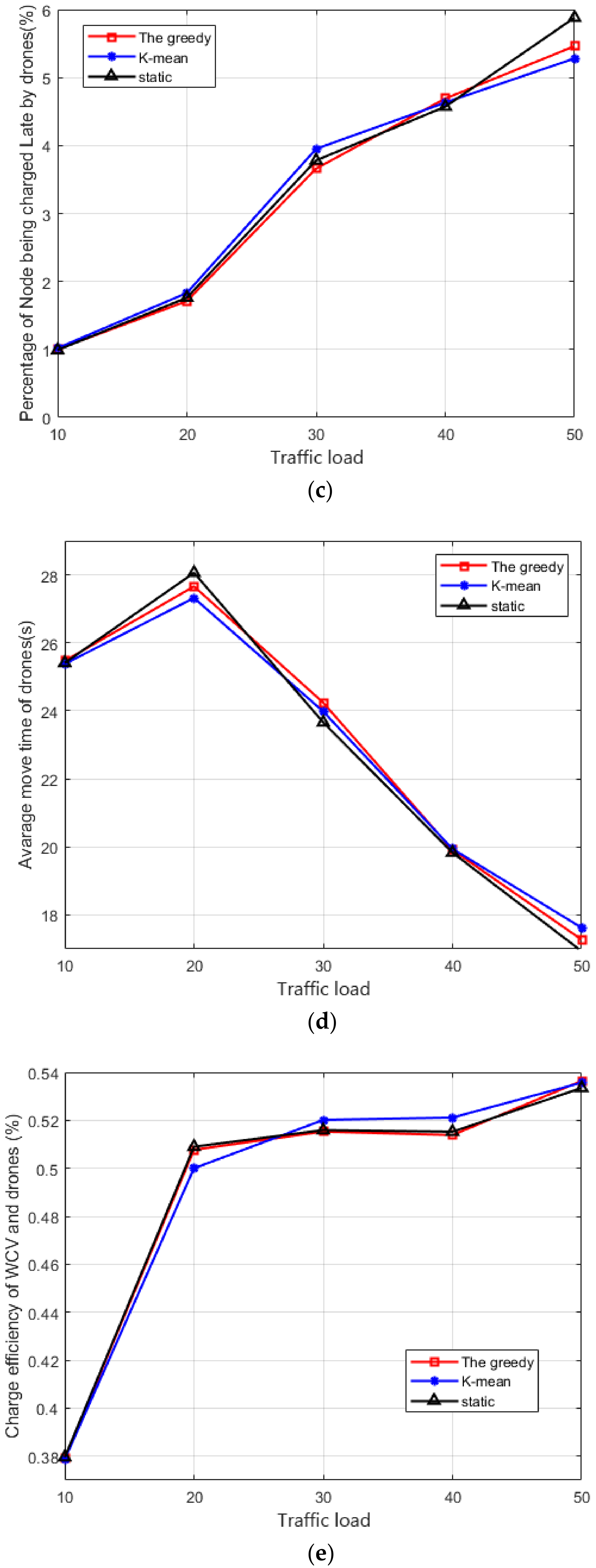
- Taking the nonstop sensing tasks of WRSN into account, we then elucidate the charging schedule problem to serve the maximum number of charged sensors under the limitations of both the energy of drones and the deadlines of sensors with the help of pads. Meanwhile, we design an approximation scheduling algorithm to solve the problem.
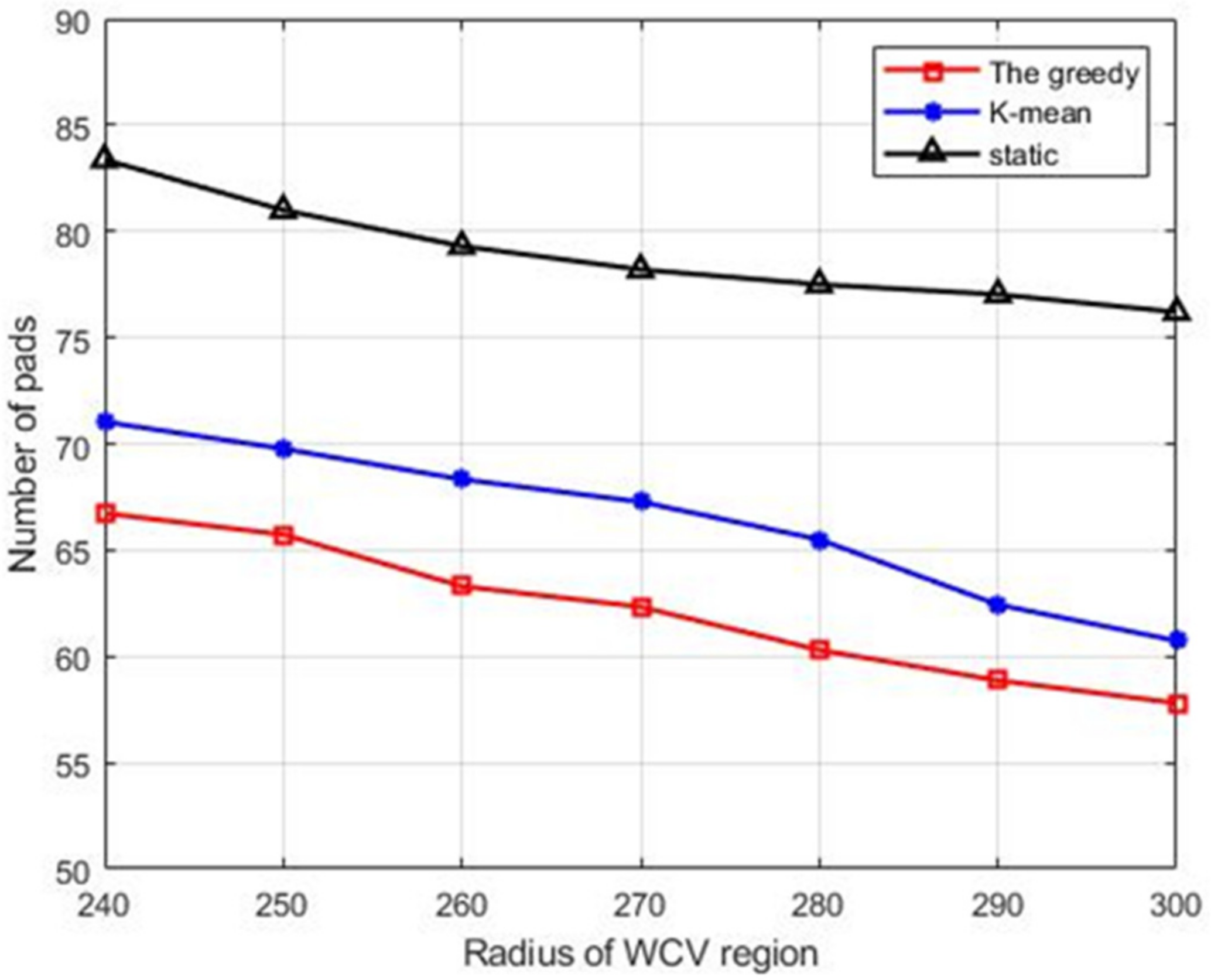
- We also conduct extensive simulation for the proposed algorithms. The first part of the simulation results demonstrates that a greedy scheme can reduce the number of pads compared with the other two schemes. The second part of the simulation results shows that the scheduling of vehicles leads to better performance of the WRSN.
2. Related Work
3. Preliminaries
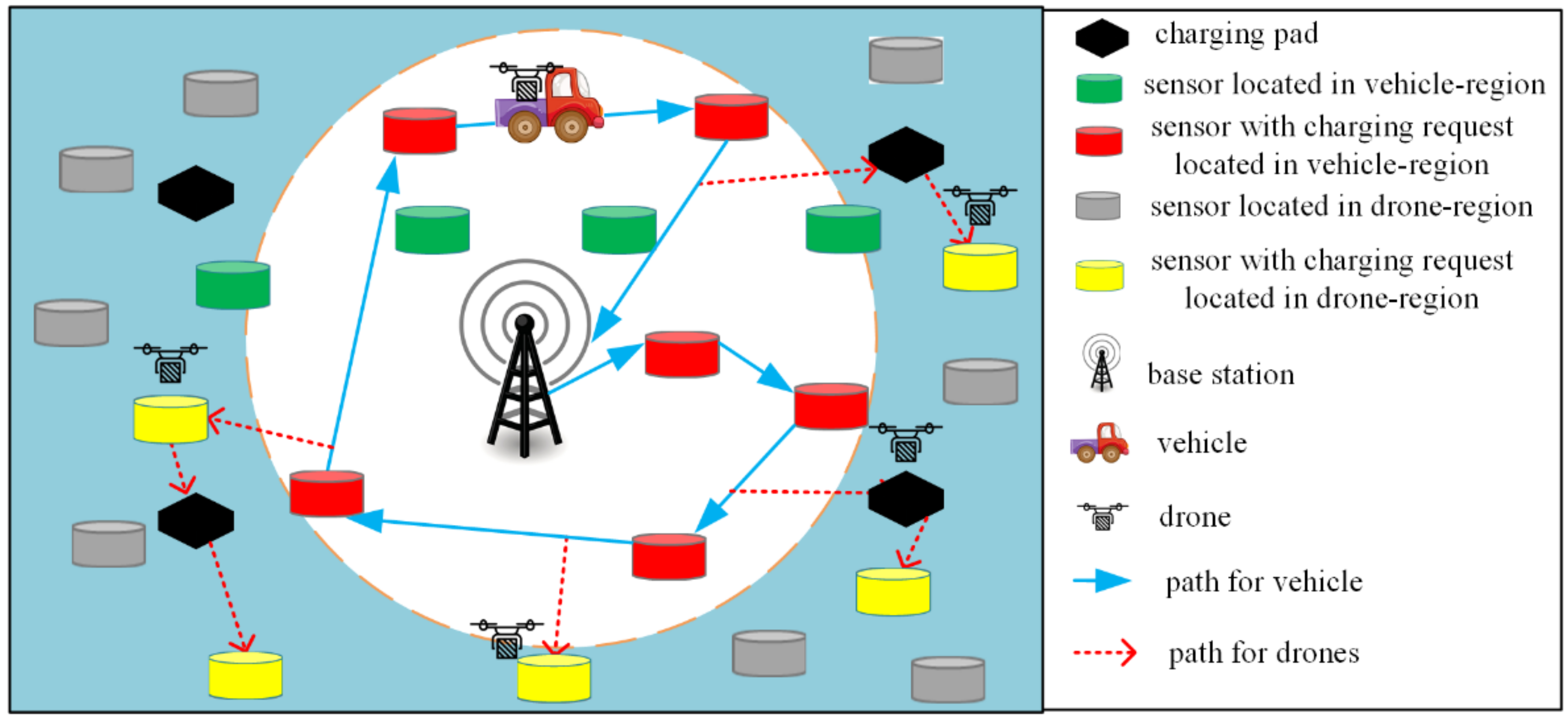
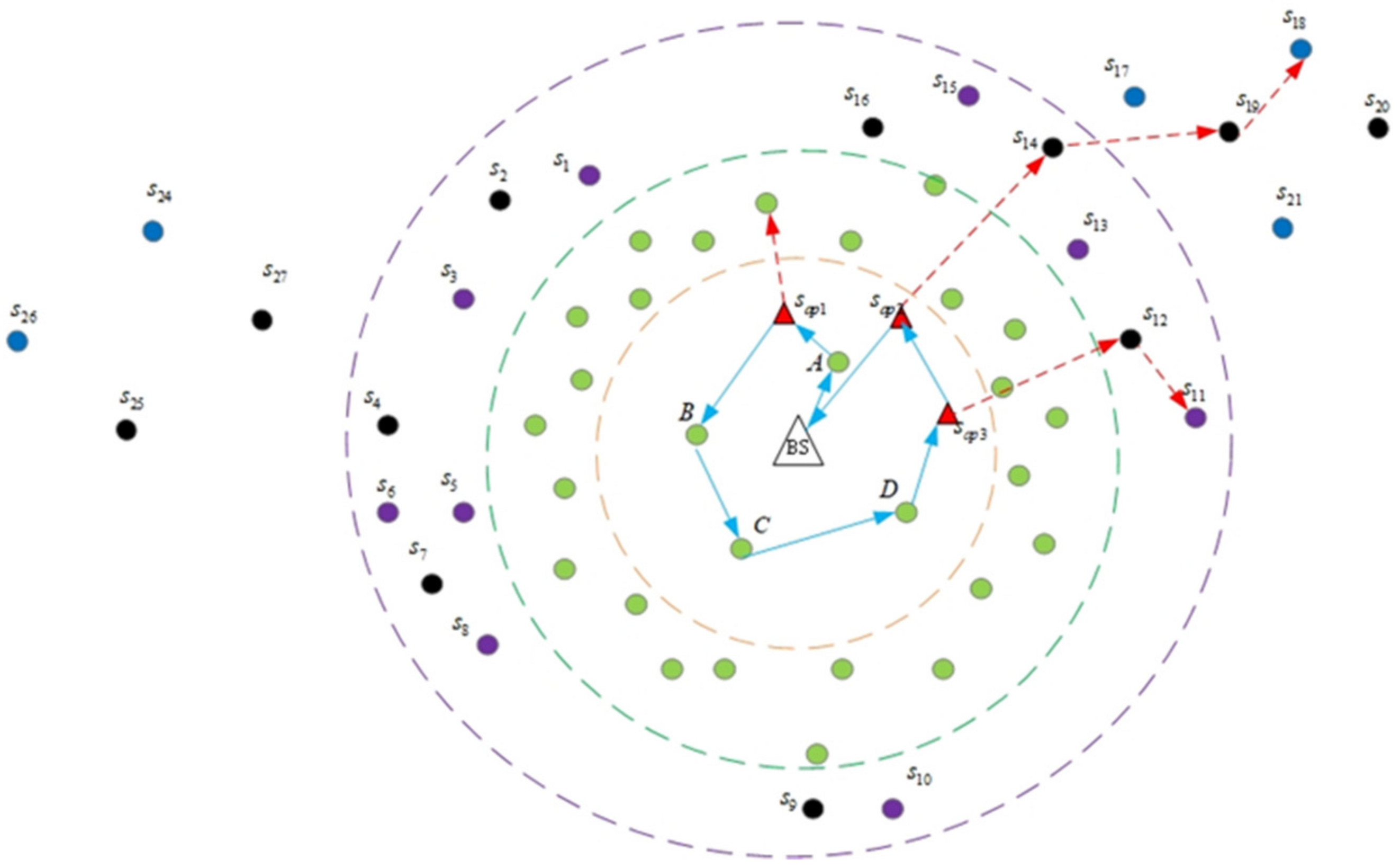
3.1. System Model
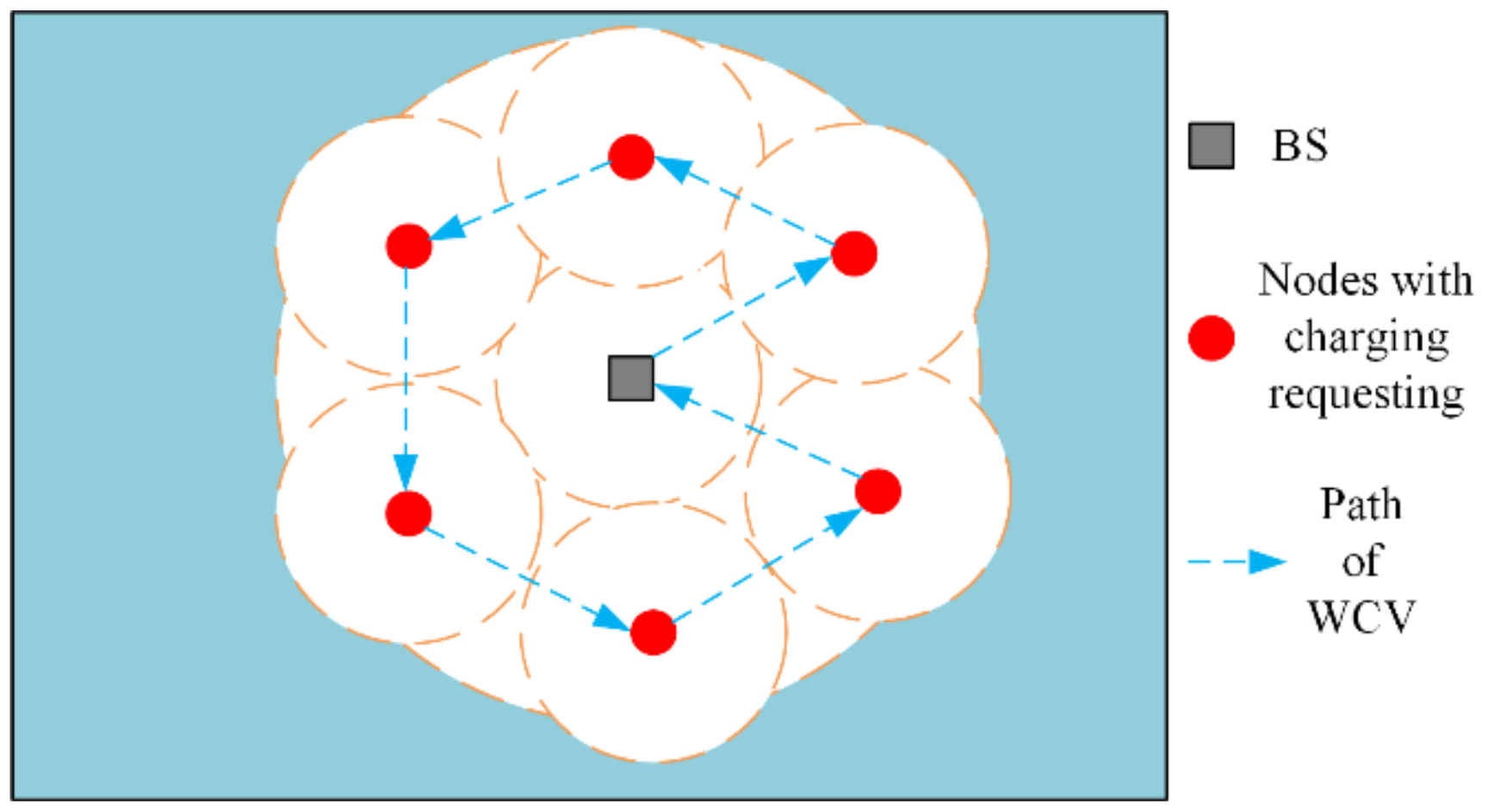
- The sensing region is vast and complex, and the WCV can move freely in its safe middle area (the white area in Figure 1), but cannot access its surrounding hazardous area (the blue area in Figure 1). Therefore, the sensors located in the middle area are charged by the WCV, while those located in the surrounding area are only charged by the drones, assisted by the pads.
- The BS is located in the center of the region and serves as a data sink and the service station of the WCV and drones. The WCV carrying several drones starts to charge sensors from BS along a predefined path. When the WCV reaches the release point, a drone is launched to charge the assigned sensors, assisted by the pads. After finishing the assignment, the WCV carried by drones returns to the BS, waiting for the next charging task.
- The drones charge only one sensor at a time through direct flight. However, when their residual energy cannot take them to the next sensors or return them to a safe area, the drones need to fly to the nearest pads to replenish their energy.
- The pads considered here are stationary and located in the given deployed region. These pads connect with the drones automatically and charge them wirelessly when the drones land on them. It is assumed that every pad only supports the landing of only one drone at one time.
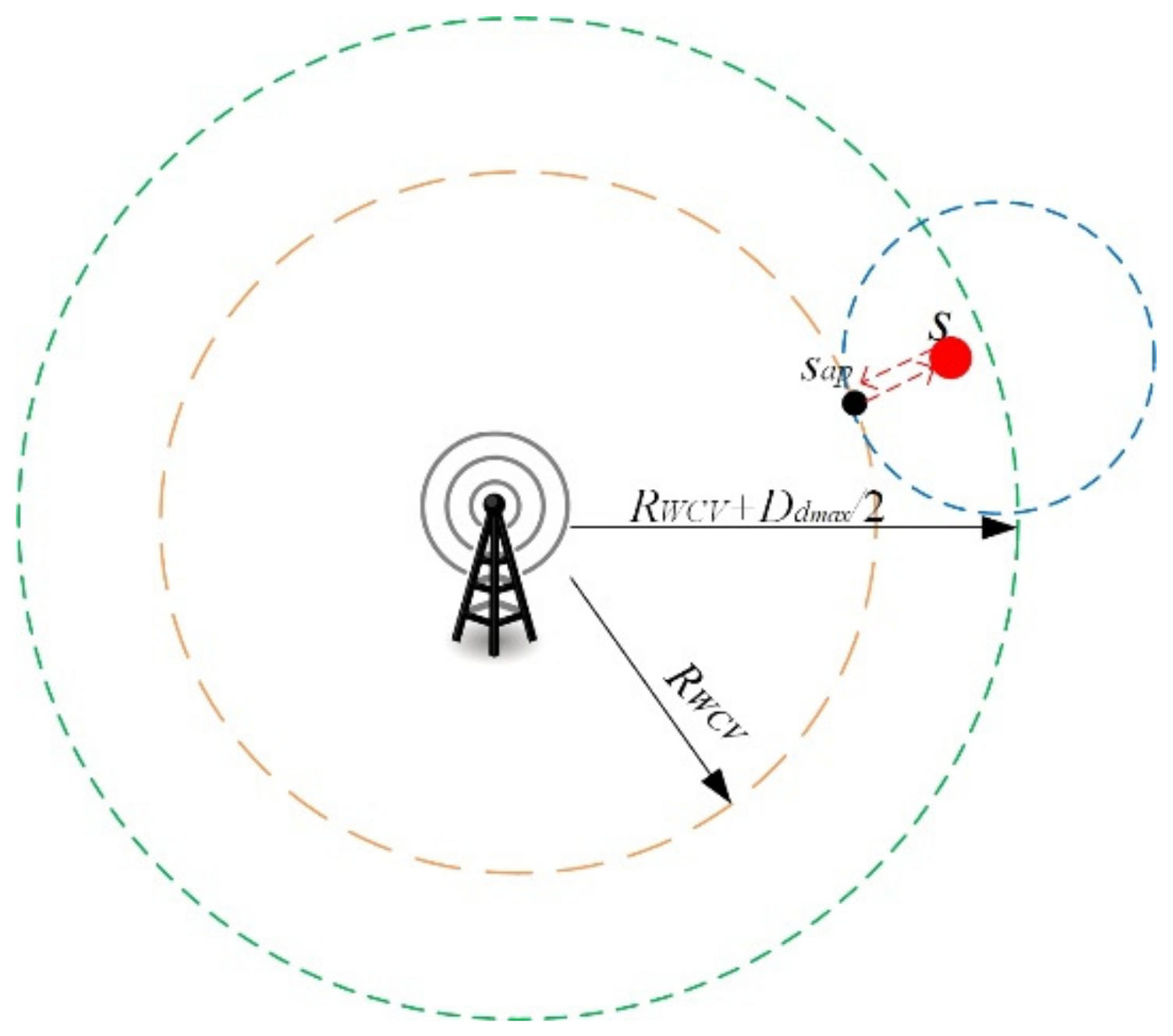
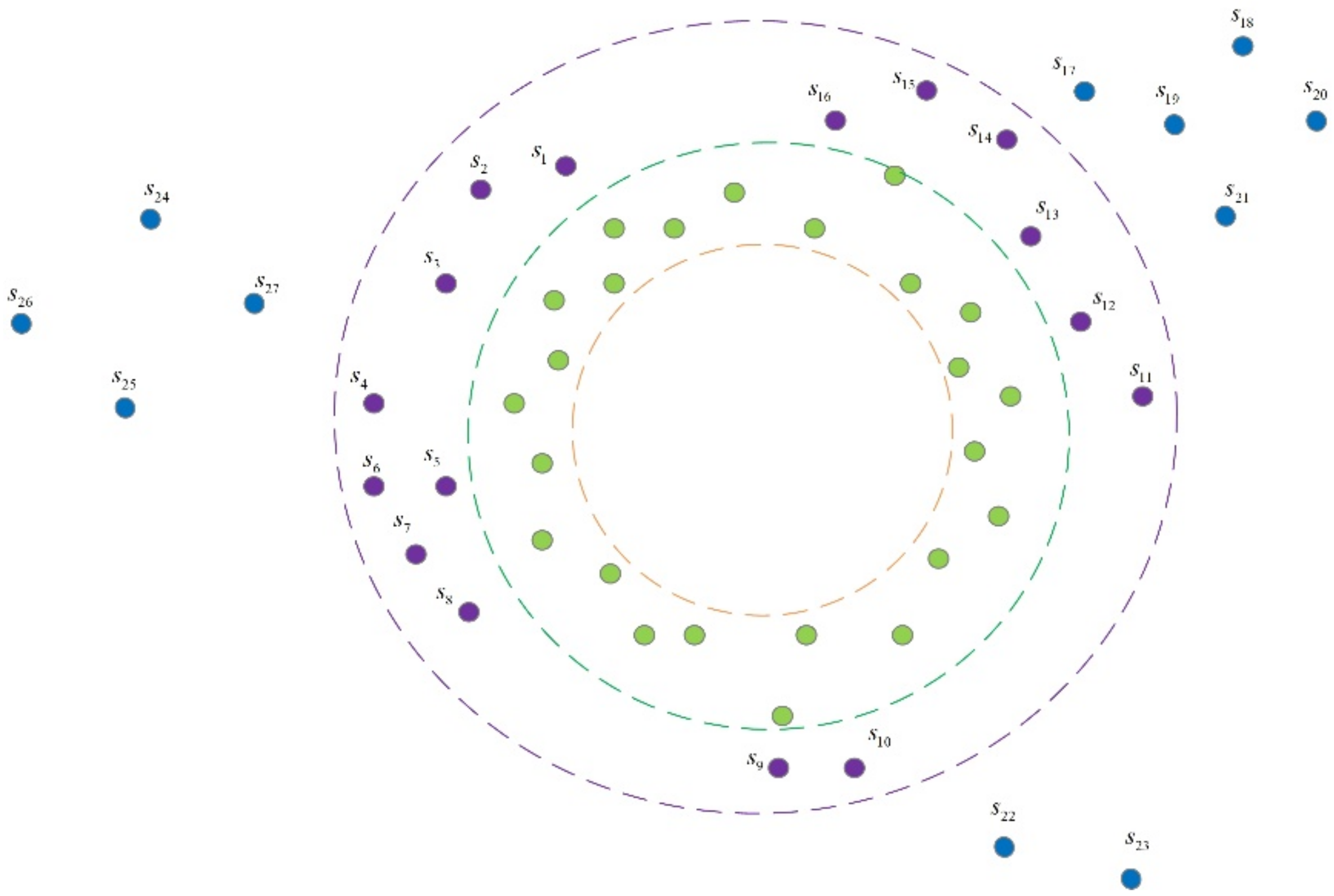
3.2. Region Division
3.2.1. WCV Region
3.2.2. Drone-Pad Region
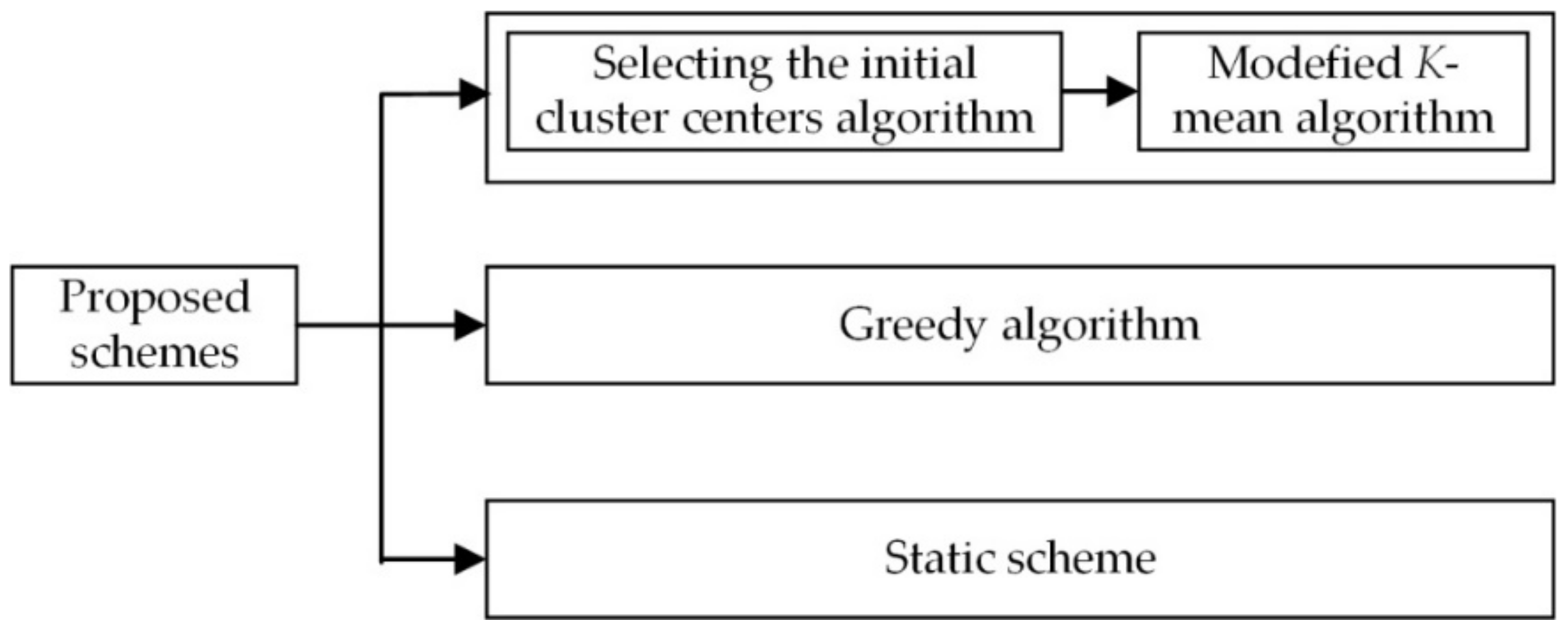
4. Proposed Schemes
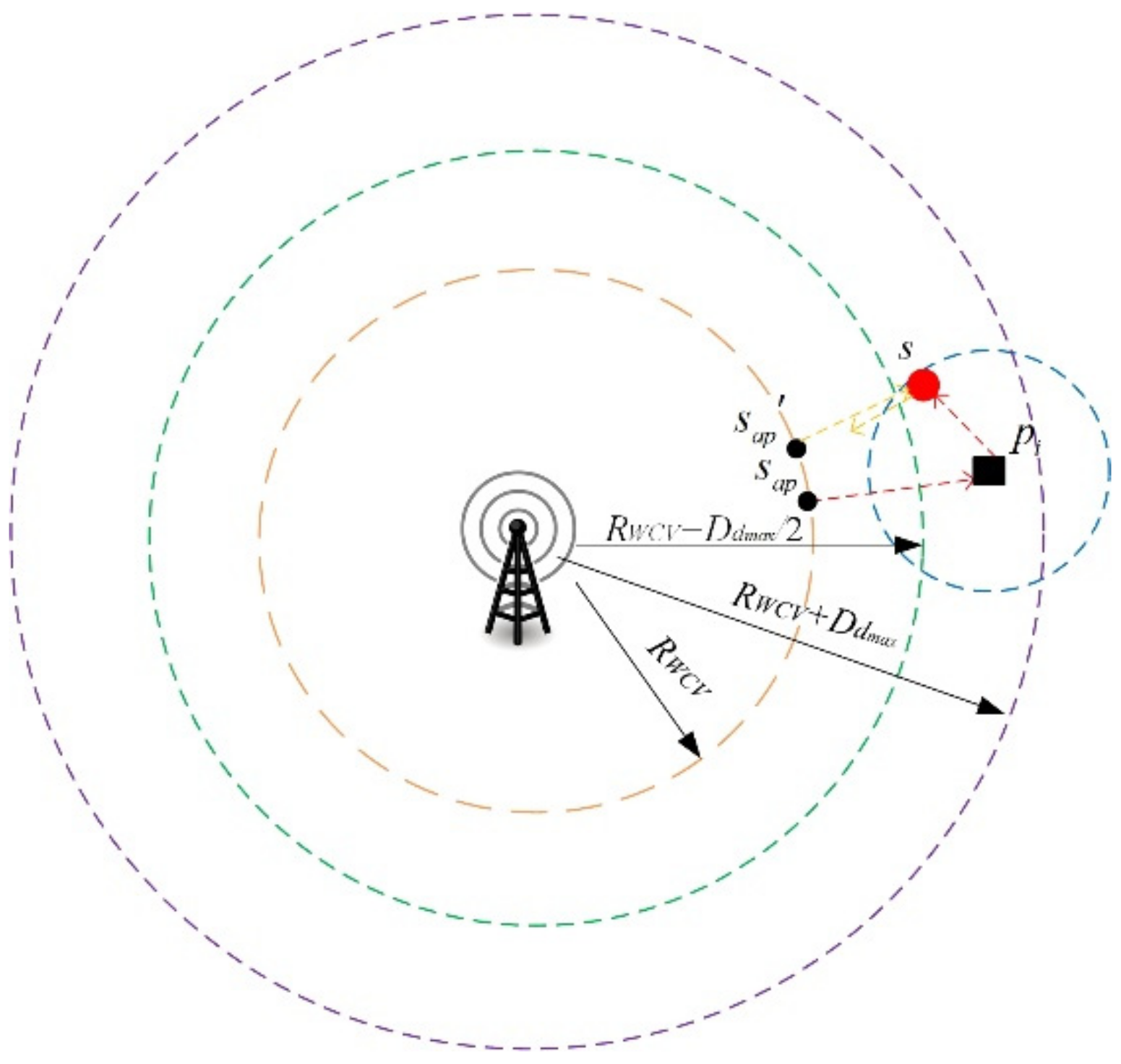
4.1. Definition of Pad Deployment Problem
4.2. Problem Formulation for Pad Deployment
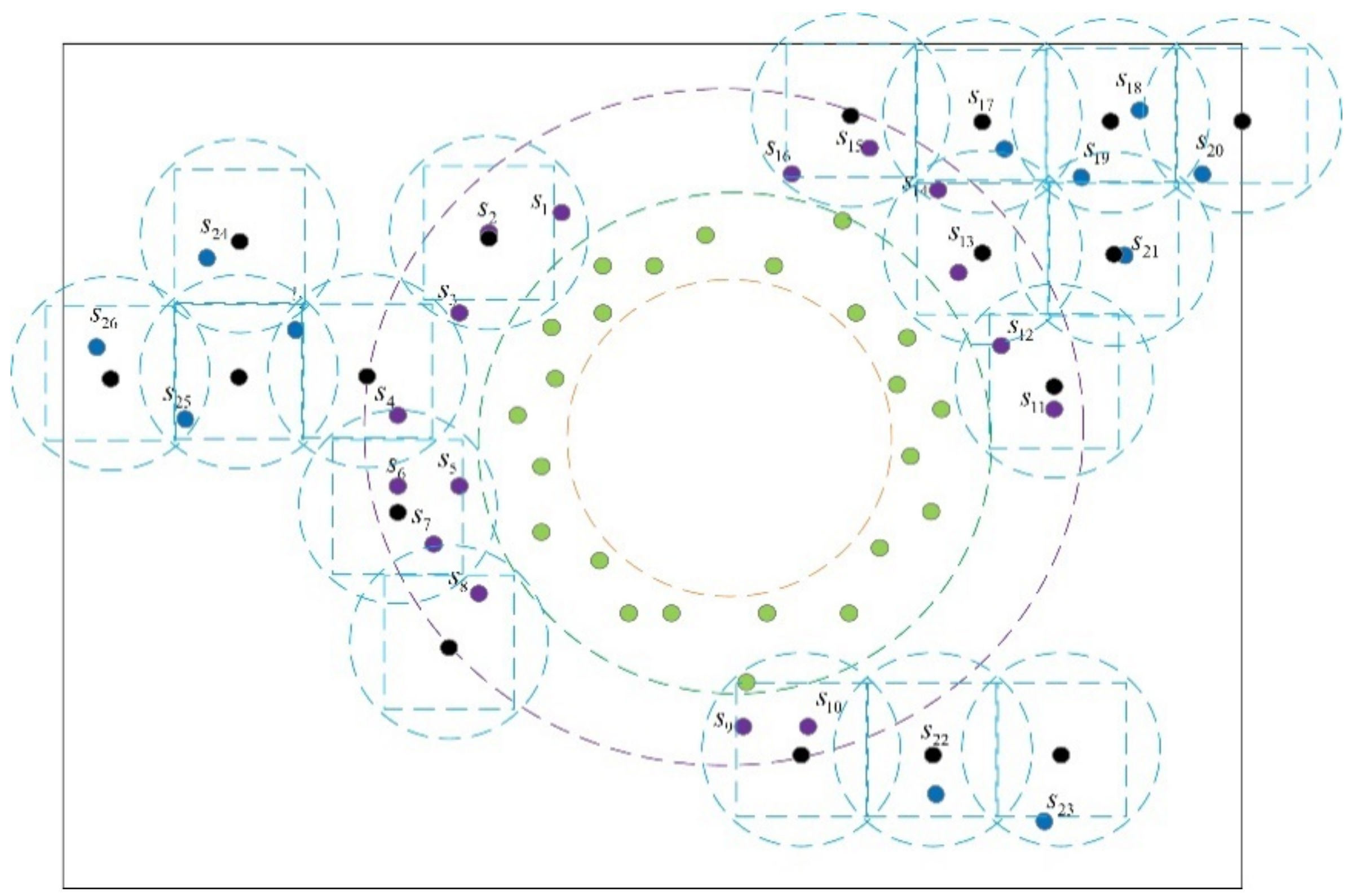
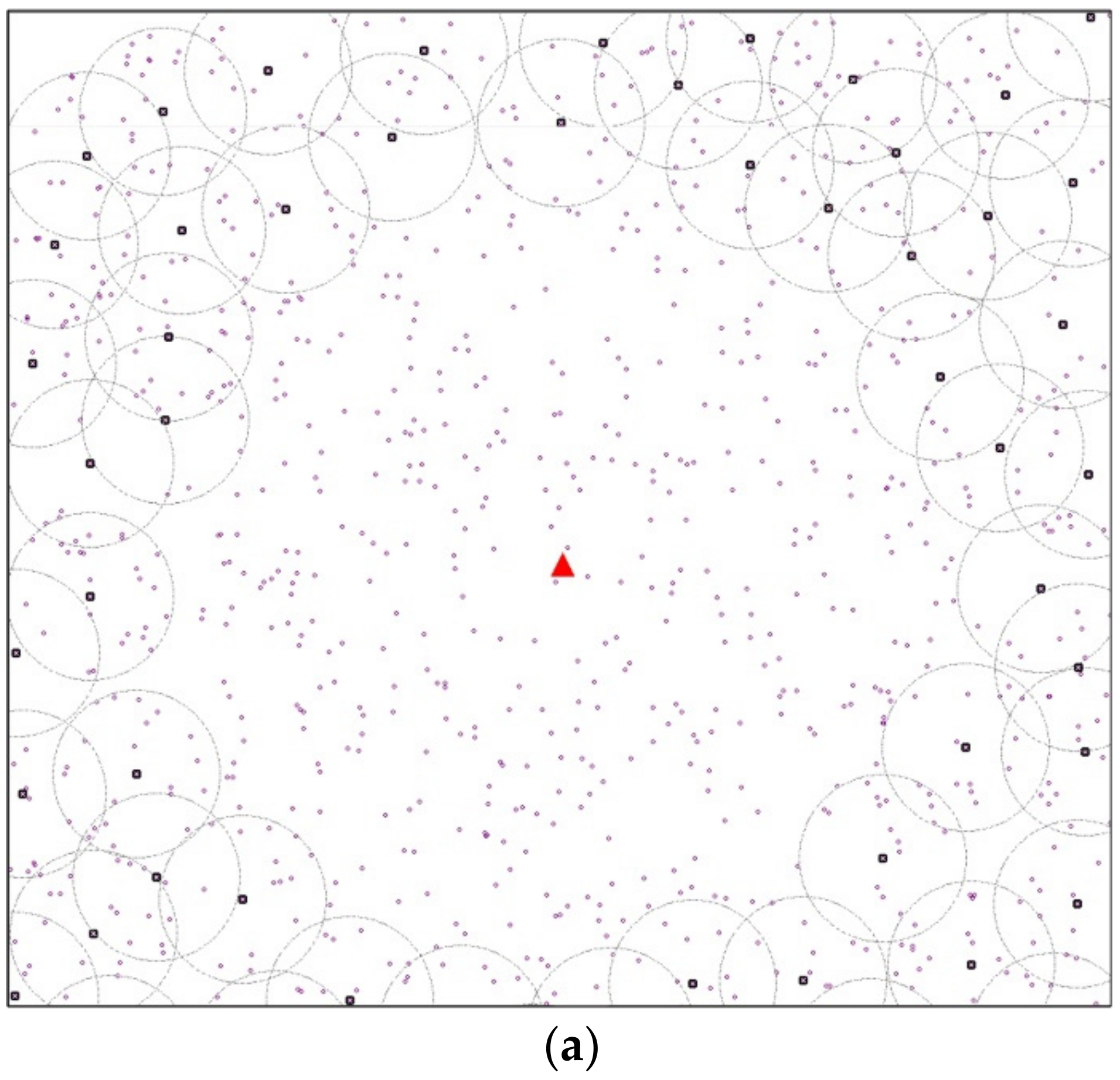
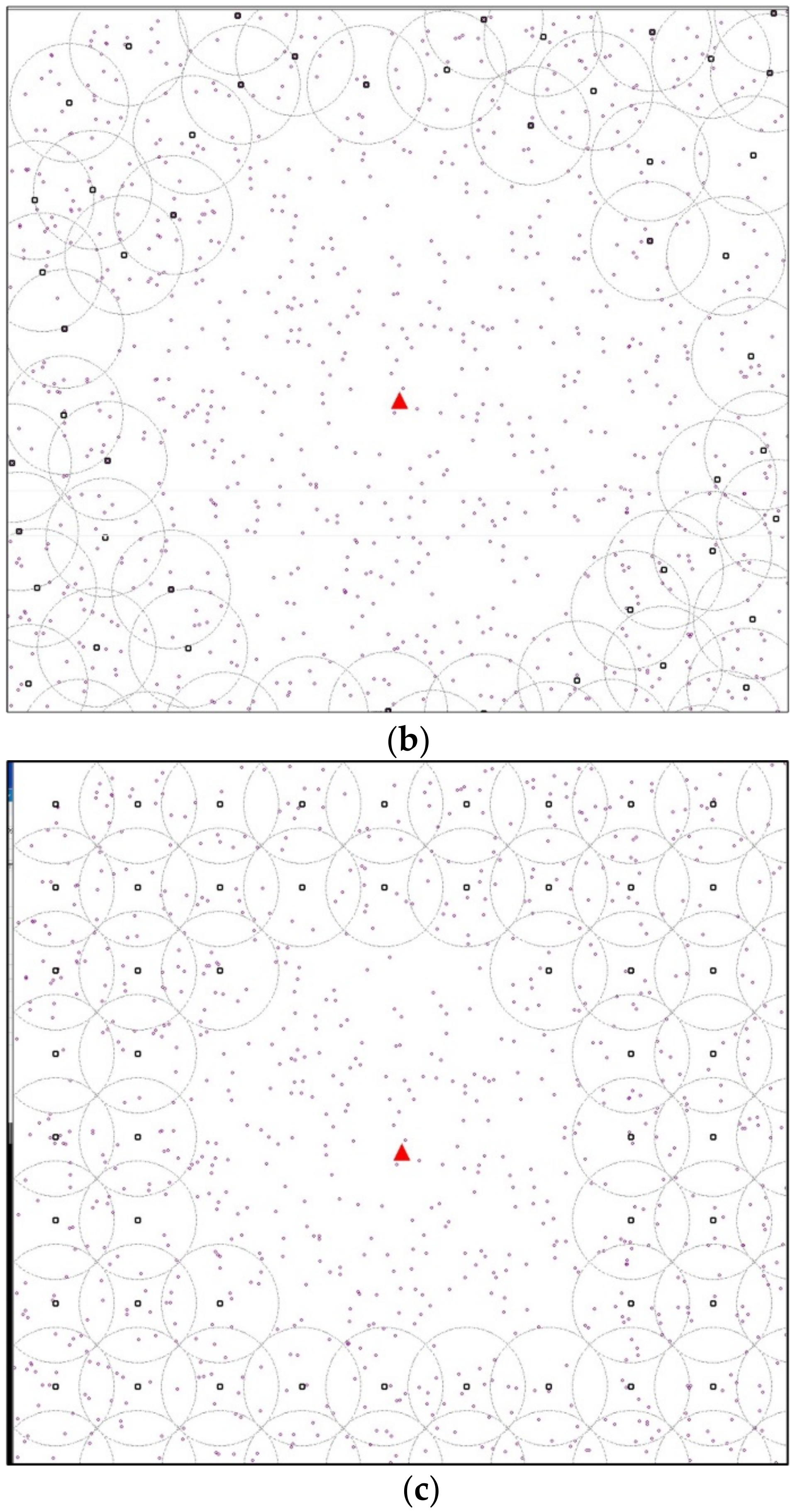
4.3. Modified K-Mean Scheme
| Algorithm 1 Selecting the initial cluster centers algorithm |
| Input: Sensor node set V of the drone-pad region with a center set C = ∅, initial cluster number K, Set Vc= ∅. |
| Output: An initial cluster center set C. |
| Step 1: Select a node s1 randomly in V as the first cluster center, c = s1. |
| Cc |
| for each s in set V |
| Compute dist(s, c) |
| if dist(s, c) ≤ dmax/2 |
| Vc s |
| V = V/Vc |
| Step 2: Select a node s in V with the maximum value of max(min(dist(s, ci))) as the cluster center, c = s. |
| C c |
| Vc = ∅ |
| for each s in set V |
| Compute dist(s, c) |
| if dist(s, c) ≤ dmax/2 |
| Vc s |
| V = V/Vc |
| Step 3: Repeat Step 2 until |C|= K. |
| Step 4: Output the Set C. |
| Algorithm 2 Modified K-mean algorithm |
| Input: Sensor node set V of the drone-pad region, an initial cluster center set C, K = |C|. |
| Output: A final cluster center set C. |
| Step 1: for each c in set C |
| for each s in set V |
| Compute dist(s, c) |
| Step 2: According the result of Step 1, assign each s in set V into the nearest cluster, i.e., if dist(s, ci) = min{dist(s, ci), i = 1, 2, 3,… K}, then sCi. |
| Step 3: Compute new cluster centers , j = 1, 2, 3, …, K. |
| Step 4: Compute cluster criterion function . |
| Step 5: if |
| go to Step 6. |
| else go to Step 1. |
| Step 6: Output set C. |
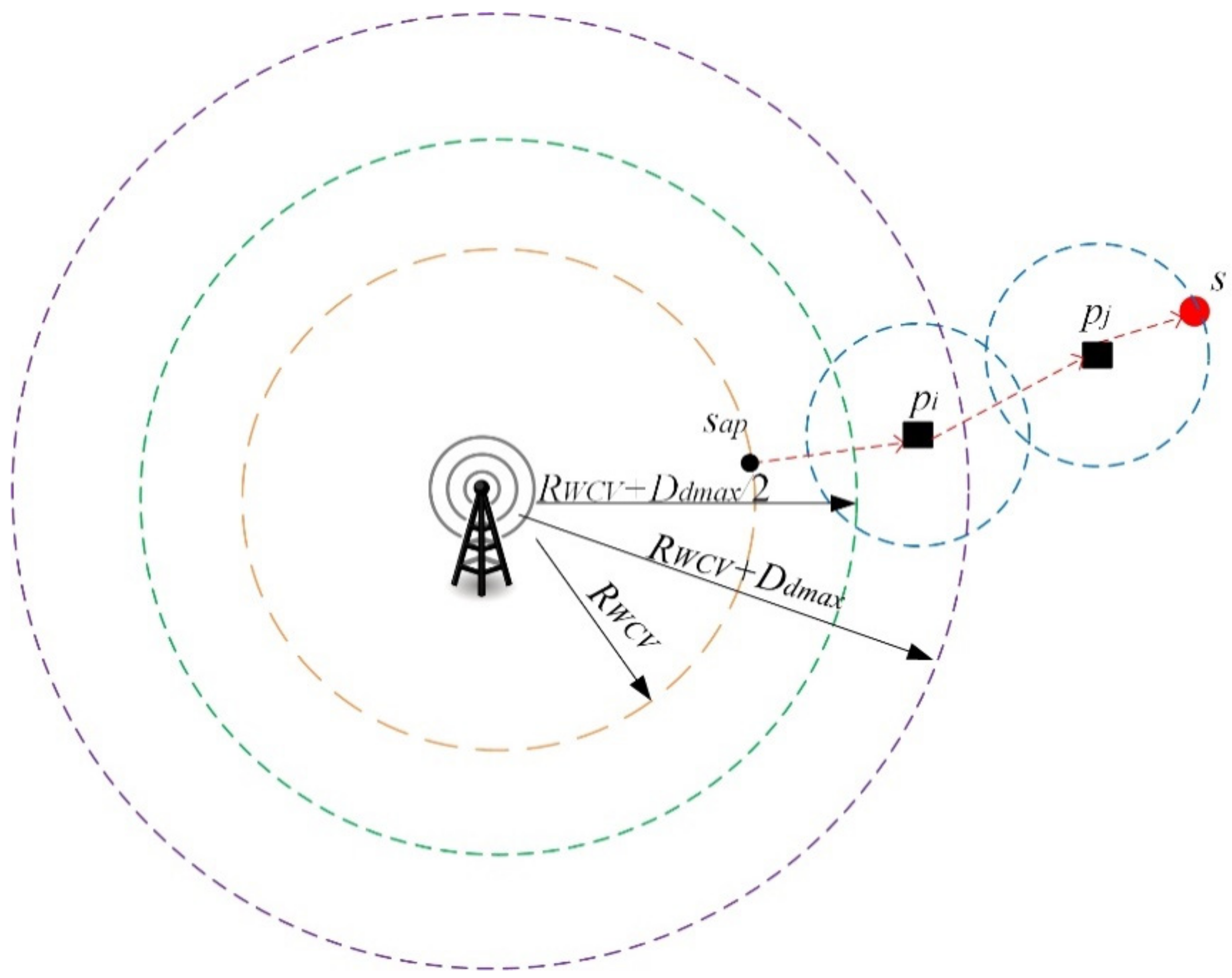
4.4. Greedy Scheme
| Algorithm 3 Greedy algorithm |
| Input: Purple node set with Vp = {sp1, sp2, …, spN}, blue node set Vb = {sb1, sb2, …, sbM} with a node set C = ∅. |
| Output: a selected node set C. |
| Step 1: Create a graph G2 = (V2, E2) by adding an edge between si and sj in Vp if, and only if, d(si, sj) ≤ Ddmax/2. |
| Create a graph G1 = (V1, E1) by adding an edge between si and sj in Vp if, and only if, Ddmax/2 ≤ d(si, sj) ≤ Ddmax. |
| Step 2: Calculate N(v) of each uncolored node v in V1 of G1. |
| Calculate NP(v) for every purple node v in V2 of G2. |
| Select a purple node v in G1 with the maximum NP(v) value in G2. |
| Set v.color = black. |
| . |
| Set u.color = gray for each node u in NP(v). |
| Step 3: For each node v in set C |
| for each purple node x in N(v) of G1 |
| Calculate NP(x) of each node x in V2 of G2. |
| Select the node x with the maximum NP(x) value. Set x.color = black. |
| . |
| Set y.color = gray for each node y in NP(x). |
| Step 4: Repeat Step 3 until there are no purple nodes in G2. |
| Step 5: Set V = VbC |
| Step 6: Create a graph G2 = (V2, E2) by putting an edge between si and sj in V if, and only if, d(si, sj)≤ Ddmax/2. |
| Create a graph G1 = (V1, E1) by putting an edge between si and sj in V if, and only if, Ddmax/2 ≤ d(si, sj) ≤ Ddmax. |
| Step 7: For each node v in set C |
| Set v.color = black. |
| Calculate NB(v) for every blue node v in V2 of G2. |
| Set u.color = gray for each node u in NB(v). |
| Step 8: For each node v in set C |
| for each blue node x in N(v) of G1 |
| Calculate NB(x) of each node x in V2 of G2. |
| Select the node x with the maximum NB(x) value. |
| Set x.color = black. |
| . |
| Set y.color = gray for each node y in NP(x). |
| Step 9: Repeat Step 8 until there are no blue nodes in G2. |
| Step 10: Output the nodes in black (i.e., set C). |
4.5. Static Scheme
4.6. Scheduling for the WCV and Drones
4.6.1. Scheduling Problem
4.6.2. Scheduling for the WCV
5. Simulations
5.1. Performance of the Proposed Deployment Schemes
5.2. Performance of the Scheduling Based on Deployment Schemes
5.3. Statistical Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Lazarescu, M.T. Design and Field Test of a WSN Platform Prototype for Long-Term Environmental Monitoring. Sensors 2015, 15, 9481–9518. [Google Scholar] [CrossRef] [Green Version]
- Muñoz-Gea, J.P.; Manzanares-Lopez, P.; Malgosa-Sanahuja, J.; Garcia-Haro, J. Design and implementation of a P2P communication infrastructure for WSN-based vehicular traffic control applications. J. Syst. Architect. 2013, 59, 923–930. [Google Scholar] [CrossRef]
- Liu, X.; Liu, A.; Li, Z.; Tian, S.; Choi, Y.; Sekiya, H.; Li, J. Distributed cooperative communication nodes control and optimization reliability for resource-constrained WSNs. Neurocomputing 2017, 270, 122–136. [Google Scholar] [CrossRef]
- Temene, N.; Sergiou, C.; Georgiou, C.; Vassiliou, V. A survey on mobility in wireless sensor networks. Ad Hoc Netw. 2022, 125, 102726. [Google Scholar] [CrossRef]
- Gao, X.; Fan, J.; Wu, F.; Chen, G. Cooperative sweep coverage problem with mobile sensors. IEEE Trans. Mobile Comput. 2022, 21, 480–494. [Google Scholar] [CrossRef]
- Yogi, A.Y.; Noritaka, S.; Hiromi, M. Multiple Route Construction with Path-overlap Avoidance for Mobile Relay on WSN. Eng. Lett. 2015, 23, 299–306. [Google Scholar]
- Yalçın, S.; Erdem, E. BTA-MM: Burst traffic awareness-based adaptive mobility model with mobile sinks for heterogeneous wireless sensor networks. ISA Trans. 2021. [Google Scholar] [CrossRef]
- Lu, Y.; Sun, N.; Pan, X. Mobile sink-based path optimization strategy in wireless sensor networks using artificial bee colony algorithm. IEEE Access 2019, 7, 11668–11678. [Google Scholar] [CrossRef]
- Khedr, A.M.; Al Aghbari, Z.; Khalifa, B.E. Fuzzy-based multi-layered clustering and ACO-based multiple mobile sinks path planning for optimal coverage in WSNs. IEEE Sens. J. 2022, 1. [Google Scholar] [CrossRef]
- Al-Kaseem, B.R.; Taha, Z.K.; Abdulmajeed, S.W.; Al-Raweshidy, H.S. Optimized energy—Efficient path planning strategy in WSN with multiple mobile sinks. IEEE Access 2021, 9, 82833–82847. [Google Scholar] [CrossRef]
- Al-Behadili, H.A.; AlWane, S.K.; Al-Yasir, Y.I.; Parchin, N.O.; Olley, P.; Abd-Alhameed, R.A. Use of multiple mobile sinks in wireless sensor networks for large-scale areas. IET Wirel. Sens. Syst. 2020, 10, 175–180. [Google Scholar] [CrossRef]
- Zhang, Z.; Glaser, S.; Bales, R.; Conklin, M.; Rice, R.; Marks, D. Insights into mountain precipitation and snowpack from a basin-scale wireless-sensor network. Water Resour. Res. 2017, 53, 6626–6641. [Google Scholar] [CrossRef]
- Faustine, A.; Mvuma, A.N.; Mongi, H.J.; Gabriel, M.C.; Tenge, A.J.; Kucel, S.B. Wireless Sensor Networks for Water Quality Monitoring and Control within Lake Victoria Basin: Prototype Development. Wirel. Sens. Netw. 2014, 06, 281–290. [Google Scholar] [CrossRef]
- Lee, H.-S.; Kim, D.-Y.; Lee, J.-W. Radio and Energy Resource Management in Renewable Energy-Powered Wireless Networks with Deep Reinforcement Learning. IEEE Trans. Wirel. Commun. 2022, 1. [Google Scholar] [CrossRef]
- Zareei, M.; Vargas-Rosales, C.; Villalpando-Hernandez, R.; Azpilicueta, L.; Anisi, M.H.; Rehmani, M.H. The effects of an Adaptive and Distributed Transmission Power Control on the performance of energy harvesting sensor networks. Comput. Netw. 2018, 137, 69–82. [Google Scholar] [CrossRef] [Green Version]
- Bao, X.; Han, L.; He, X.; Tan, W.; Fan, T. Optimizing Maximum Monitoring Frequency and Guaranteeing Target Coverage and Connectivity in Energy Harvesting Wireless Sensor Networks. Mob. Inf. Syst. 2019, 2019, 6312589. [Google Scholar] [CrossRef] [Green Version]
- Jin, Y.; Xu, J.; Wu, S.; Xu, L.; Yang, D.; Xia, K. Bus network assisted drone scheduling for sustainable charging of wireless rechargeable sensor network. J. Syst. Architect. 2021, 116, 102059. [Google Scholar] [CrossRef]
- Chen, J.; Yu, C.W.; Ouyang, W. Efficient Wireless Charging Pad Deployment in Wireless Rechargeable Sensor Networks. IEEE Access 2020, 8, 39056–39077. [Google Scholar] [CrossRef]
- Chen, Y.; Gu, Y.; Li, P.; Lin, F. Minimizing the number of wireless charging PAD for unmanned aerial vehicle–based wireless rechargeable sensor networks. Int. J. Distrib. Sens. Netw. 2021, 17, 155014772110559. [Google Scholar] [CrossRef]
- Nguyen, P.L.; La, V.Q.; Nguyen, A.D.; Nguyen, T.H.; Nguyen, K. An on-demand charging for connected target coverage in WRSNs using fuzzy logic and Q-learning. Sensors 2021, 21, 5520. [Google Scholar] [CrossRef]
- Zhong, P.; Xu, A.; Zhang, S.; Zhang, Y.; Chen, Y. EMPC: Energy-minimization path construction for data collection and wireless charging in WRSN. Pervasive Mob. Comput. 2021, 73, 101401. [Google Scholar] [CrossRef]
- Chawra, V.K.; Gupta, G.P. Hybrid meta-heuristic techniques based efficient charging scheduling scheme for multiple mobile wireless chargers based wireless rechargeable sensor networks. Peer Peer Netw. Appl. 2021, 14, 1303–1315. [Google Scholar] [CrossRef]
- Li, Y.; Zhong, L.; Lin, F. Predicting-scheduling-Tracking: Charging nodes with non-deterministic mobility. IEEE Access 2021, 9, 2213–2228. [Google Scholar] [CrossRef]
- Simica, M.; Bila, C.; Vojisavljevic, V. Investigation in wireless power transmission for UAV charging. In Proceedings of the 19th International Conference on Knowledge Based and Intelligent Information and Engineering Systems, Singapore, 7–9 September 2015; pp. 1846–1855. [Google Scholar]
- Wu, T.; Yang, P.; Dai, H.; Li, P.; Rao, X. Near optimal bounded route association for drone-enabled rechargeable WSNs. Comput. Netw. 2018, 145, 107–117. [Google Scholar] [CrossRef]
- Wang, Y.; Hua, M.; Liu, Z.; Zhang, D.; Dai, H.; Hu, Y. Joint Scheduling and Trajectory Design for UAV-Aided Wireless Power Transfer System. Lect. Notes Inst. Comput. Sci. Soc. Inform. Telecommun. Eng. 2019, 278, 3–17. [Google Scholar] [CrossRef]
- Wu, P.; Xiao, F.; Sha, C.; Huang, H.; Sun, L. Trajectory Optimization for UAVs’ Efficient Charging in Wireless Rechargeable Sensor Networks. IEEE Trans. Veh. Technol. 2020, 69, 4207–4220. [Google Scholar] [CrossRef]
- Liang, S.; Fang, Z.; Sun, G.; Lin, C.; Li, J.; Li, S.; Wang, A. Charging UAV deployment for improving charging performance of wireless rechargeable sensor networks via joint optimization approach. Comput. Netw. 2021, 201, 108573. [Google Scholar] [CrossRef]
- Lin, C.; Yang, W.; Dai, H.; Li, T.; Wang, Y.; Wang, L.; Wu, G.; Zhang, Q. Near Optimal Charging Schedule for 3-D Wireless Rechargeable Sensor Networks. IEEE Trans. Mob. Comput. 2021, 11. [Google Scholar] [CrossRef]
- Gonzalez, T.F. Clustering to minimize the maximum intercluster distance. Theor. Comput. Sci. 1985, 38, 293–306. [Google Scholar] [CrossRef] [Green Version]
- He, L.; Kong, L.; Gu, Y.; Pan, J.; Zhu, T. Evaluating the on-demand mobile charging in wireless sensor networks. IEEE Trans. Mobile Comput. 2015, 14, 1861–1875. [Google Scholar] [CrossRef]
- Hu, W.; Zhang, M.; Li, Z.; Popov, S.; Leeson, M.S.; Xu, T. High-dimensional feature based non-coherent detection for multi-intensity modulated ultraviolet communications. J. Lightwave Technol. 2021, 1. [Google Scholar] [CrossRef]



| WCV | Drone | Pad | WCV-Carried Drones | |
|---|---|---|---|---|
| [20,21,22,23] | Used | Not used | Not used | Not used |
| [28] | Not used | Used | Not used | Not used |
| [19,29] | Not used | Used | Used | Not used |
| [17] | Used | Not used | Not used | Used |
| Our work | Used | Not used | Used | Used |
| Symbol | Definition |
|---|---|
| Ctotal | Total moving distance of the WCV |
| emax_WCV | Maximum capacity of the WCV |
| emax_sn | Maximum capacity of each sensor’s battery |
| emin_sn | Minimum capacity of each sensor’s battery |
| PWCV | Energy consumption rate of the WCV |
| RWCV | Radius of the WCV region |
| sapi | The ith stop for releasing drones |
| Ddmax | Maximum flight distance of drones |
| si | The ith sensor |
| pi | The ith pad |
| S | Nodes with charging requesting |
| SWCV | Nodes with charging requesting in the WCV region |
| nmax | Maximum number of sensors with charging requests in each charging circle |
| P | Set of pads |
| K | Number of clusters |
| Parameter | Values |
|---|---|
| Network size (m2) | 1000 × 1000 |
| Network density | 500–1000 |
| Ddmax (m) | 130–250 |
| RWCV (m) | 240–250 |
| Parameter | Values |
|---|---|
| Simulation time (s) | 100,000 |
| Network size (m2) | 1000 × 1000 |
| Network density | 1000 |
| Number of drones carried by WCVs | 10 |
| RWCV (m) | 300 |
| Ddmax (m) | 130 |
| Traffic load ([0, x/network density]) | 10–50 |
| Energy capacity of WCVs (J) | 100,000 |
| Battery capacity of drones (J) | 300 |
| Battery capacity of nodes (J) | 100 |
| Speed of drones (m/s) | 35 |
| Speed of WCVs (m/s) | 10 |
| Energy threshold of nodes (%) | 30 |
| Energy consumption rate of drones when flying (J/s) | 10 |
| Energy consumption rate of drones when hovering for charging nodes (J/s) | 1 |
| Energy consumption rate of moving WCVs (J/m) | 10 |
| Charging rate (J/s) | 5 |
| Initial energy of nodes (%) | 100 |
| Network traffic (number of events sensed by nodes per second) | 50 |
| Transmission range of nodes (m) | 60 |
| Packet length (kB) | 10 |
| Time of transmitting packets for one hop (s) | 0.01 |
| (a) For lifetime | |||||
| Traffic load | Scheme | Standard deviation | Standard error | 95% confidence interval for mean difference | |
| Lower bound | Upper bound | ||||
| 50 | Greedy | 381.039 | 70.757 | 1072.96 | 1362.84 |
| K-mean | 381.039 | 70.757 | 1072.96 | 1362.84 | |
| Static | 381.039 | 70.757 | 1072.96 | 1362.84 | |
| (b) For percentage of nodes being charged in time | |||||
| Traffic load | Scheme | Standard deviation | Standard error | 95% confidence interval for mean difference | |
| Lower bound | Upper bound | ||||
| 50 | Greedy | 0.0423121555 | 0.0078571700 | 0.916271629 | 0.948460995 |
| K-mean | 0.0260250457 | 0.0048327297 | 0.930337912 | 0.950136708 | |
| Static | 0.0436544840 | 0.0081064342 | 0.914372664 | 0.947583219 | |
| (c) For percentage of nodes being charged late by drones | |||||
| Traffic load | Scheme | Standard deviation | Standard error | 95% confidence interval for mean difference | |
| Lower bound | Upper bound | ||||
| 50 | Greedy | 0.0538552643 | 0.0101776883 | 0.047403424 | 0.089169207 |
| K-mean | 0.0419137735 | 0.0079209587 | 0.045383824 | 0.077888753 | |
| Static | 0.0613234300 | 0.0115890390 | 0.050628263 | 0.098185751 | |
| (d) For average move time of drones | |||||
| Traffic load | Scheme | Standard deviation | Standard error | 95% confidence interval for mean difference | |
| Lower bound | Upper bound | ||||
| Static | 4.7321464 | 0.8787375 | 18.599545 | 22.199569 | |
| 50 | Greedy | 6.1110782 | 1.1347987 | 15.093313 | 19.742373 |
| K-mean | 5.2972658 | 0.9836776 | 15.936389 | 19.966333 | |
| Static | 5.0301260 | 0.9340709 | 15.174031 | 19.000747 | |
| (e) For charge efficiency of WCV and drones | |||||
| Traffic load | Scheme | Standard deviation | Standard error | 95% confidence interval for mean difference | |
| Lower bound | Upper bound | ||||
| 50 | Greedy | 0.0004073624 | 0.0000756453 | 0.005210727 | 0.005520632 |
| K-mean | 0.0004491571 | 0.0000834064 | 0.005188956 | 0.005530657 | |
| Static | 0.0003572805 | 0.0000663453 | 0.005199698 | 0.005471503 | |
| (f) For charge efficiency of drones | |||||
| Traffic load | Scheme | Standard deviation | Standard error | 95% confidence interval for mean difference | |
| Lower bound | Upper bound | ||||
| 50 | Greedy | 0.0119598979 | 0.0022208973 | 0.350430434 | 0.359529038 |
| K-mean | 0.0168365753 | 0.0031264735 | 0.341796321 | 0.354604902 | |
| Static | 0.0084270088 | 0.0015648562 | 0.354756708 | 0.361167633 | |
| (a) For lifetime | |||||||
| Traffic load | Between schemes | Mean difference | Standard error | Significance | 95% confidence interval for mean difference | ||
| Lower bound | Upper bound | ||||||
| 50 | Greedy | K-mean | 0.000 | 100.066 | 1.000 | −198.99 | 198.99 |
| Static | 0.000 | 100.066 | 1.000 | −198.99 | 198.99 | ||
| K-mean | Greedy | 0.000 | 100.066 | 1.000 | −198.99 | 198.99 | |
| Static | 0.000 | 100.066 | 1.000 | −198.99 | 198.99 | ||
| Static | Greedy | 0.000 | 100.066 | 1.000 | −198.99 | 198.99 | |
| K-mean | 0.000 | 100.066 | 1.000 | −198.99 | 198.99 | ||
| (b) For percentage of nodes being charged in time | |||||||
| Traffic load | Between schemes | Mean difference | Standard error | Significance | 95% confidence interval for mean difference | ||
| Lower bound | Upper bound | ||||||
| 50 | Greedy | K-mean | −0.0078709981 | 0.0100267865 | 0.435 | −0.027810363 | 0.012068366 |
| Static | 0.0013883706 | 0.0100267865 | 0.890 | −0.018550994 | 0.021327735 | ||
| K-mean | Greedy | 0.0078709981 | 0.0100267865 | 0.435 | −0.012068366 | 0.027810363 | |
| Static | 0.0092593688 | 0.0100267865 | 0.358 | −0.010679996 | 0.029198733 | ||
| Static | Greedy | −0.0013883706 | 0.0100267865 | 0.890 | −0.021327735 | 0.018550994 | |
| K-mean | −0.0092593688 | 0.0100267865 | 0.358 | −0.029198733 | 0.010679996 | ||
| (c) For percentage of nodes being charged late by drones | |||||||
| Traffic load | Between schemes | Mean difference | Standard error | Significance | 95% confidence interval for mean difference | ||
| Lower bound | Upper bound | ||||||
| 50 | Greedy | K-mean | 0.0066500268 | 0.0141570418 | 0.640 | −0.021518046 | 0.034818099 |
| Static | −0.0061206913 | 0.0141570418 | 0.667 | −0.034288764 | 0.022047381 | ||
| K-mean | Greedy | −0.0066500268 | 0.0141570418 | 0.640 | −0.034818099 | 0.021518046 | |
| Static | −0.0127707181 | 0.0141570418 | 0.370 | −0.040938791 | 0.015397354 | ||
| Static | Greedy | 0.0061206913 | 0.0141570418 | 0.667 | −0.022047381 | 0.034288764 | |
| K-mean | 0.0127707181 | 0.0141570418 | 0.370 | −0.015397354 | 0.040938791 | ||
| (d) For average move time of drones | |||||||
| Traffic load | Between schemes | Mean difference | Standard error | Significance | 95% confidence interval for mean difference | ||
| Lower bound | Upper bound | ||||||
| 50 | Greedy | K-mean | −0.5335184 | 1.4440402 | 0.713 | −3.405151 | 2.338114 |
| Static | 0.3304540 | 1.4440402 | 0.820 | −2.541178 | 3.202086 | ||
| K-mean | Greedy | 0.5335184 | 1.4440402 | 0.713 | −2.338114 | 3.405151 | |
| Static | 0.8639724 | 1.4440402 | 0.551 | −2.007660 | 3.735605 | ||
| Static | Greedy | −0.3304540 | 1.4440402 | 0.820 | −3.202086 | 2.541178 | |
| K-mean | −0.8639724 | 1.4440402 | 0.551 | −3.735605 | 2.007660 | ||
| (e) For charge efficiency of WCV and drones | |||||||
| Traffic load | Between schemes | Mean difference | Standard error | Significance | 95% confidence interval for mean difference | ||
| Lower bound | Upper bound | ||||||
| 50 | Greedy | K-mean | 0.0000058733 | 0.0001067100 | 0.956 | −0.000206331 | 0.000218078 |
| Static | 0.0000300789 | 0.0001067100 | 0.779 | −0.000182126 | 0.000242283 | ||
| K-mean | Greedy | −0.0000058733 | 0.0001067100 | 0.956 | −0.000218078 | 0.000206331 | |
| Static | 0.0000242056 | 0.0001067100 | 0.821 | −0.000187999 | 0.000236410 | ||
| Static | Greedy | −0.0000300789 | 0.0001067100 | 0.779 | −0.000242283 | 0.000182126 | |
| K-mean | −0.0000242056 | 0.0001067100 | 0.821 | −0.000236410 | 0.000187999 | ||
| (f) For charge efficiency of drones | |||||||
| Traffic load | Between schemes | Mean difference | Standard error | Significance | 95% confidence interval for mean difference | ||
| Lower bound | Upper bound | ||||||
| 50 | Greedy | K-mean | 0.0067791244 * | 0.0033819123 | 0.048 | 0.000053821 | 0.013504428 |
| Static | −0.0029824341 | 0.0033819123 | 0.380 | −0.009707738 | 0.003742869 | ||
| K-mean | Greedy | −6.7791244294 × 10−3 | 0.0033819123 | 0.048 | −0.013504428 | −0.000053821 | |
| Static | −9.7615585278 × 10−3 | 0.0033819123 | 0.005 | −0.016486862 | −0.003036255 | ||
| Static | Greedy | 0.0029824341 | 0.0033819123 | 0.380 | −0.003742869 | 0.009707738 | |
| K-mean | 0.0097615585 * | 0.0033819123 | 0.005 | 0.003036255 | 0.016486862 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.-J.; Yu, C.-W. Collaborative Charging Scheduling of Hybrid Vehicles in Wireless Rechargeable Sensor Networks. Energies 2022, 15, 2256. https://doi.org/10.3390/en15062256
Chen J-J, Yu C-W. Collaborative Charging Scheduling of Hybrid Vehicles in Wireless Rechargeable Sensor Networks. Energies. 2022; 15(6):2256. https://doi.org/10.3390/en15062256
Chicago/Turabian StyleChen, Jing-Jing, and Chang-Wu Yu. 2022. "Collaborative Charging Scheduling of Hybrid Vehicles in Wireless Rechargeable Sensor Networks" Energies 15, no. 6: 2256. https://doi.org/10.3390/en15062256
APA StyleChen, J.-J., & Yu, C.-W. (2022). Collaborative Charging Scheduling of Hybrid Vehicles in Wireless Rechargeable Sensor Networks. Energies, 15(6), 2256. https://doi.org/10.3390/en15062256







