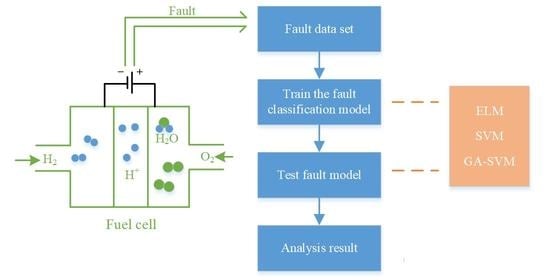
Research on Fuel Cell Fault Diagnosis Based on Genetic Algorithm Optimization of Support Vector Machine †
Abstract
:1. Introduction
2. Fault Classification Method
2.1. Extreme Learning Machine Theory
2.2. Support Vector Machine Theory
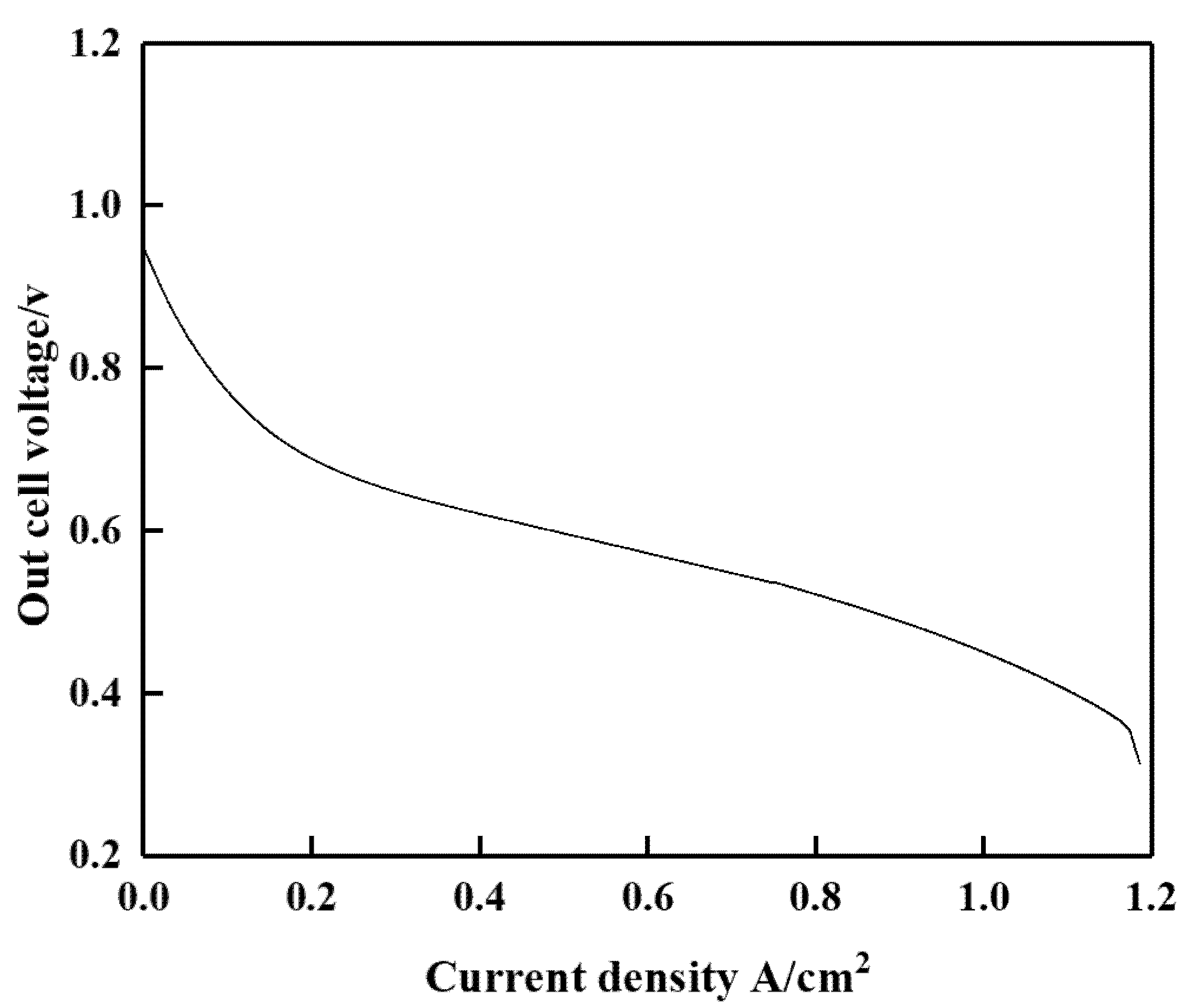
3. Fault Simulation of Fuel Cell System
4. Fault Diagnosis of Fuel Cell System
4.1. ELM Fault Classification Method
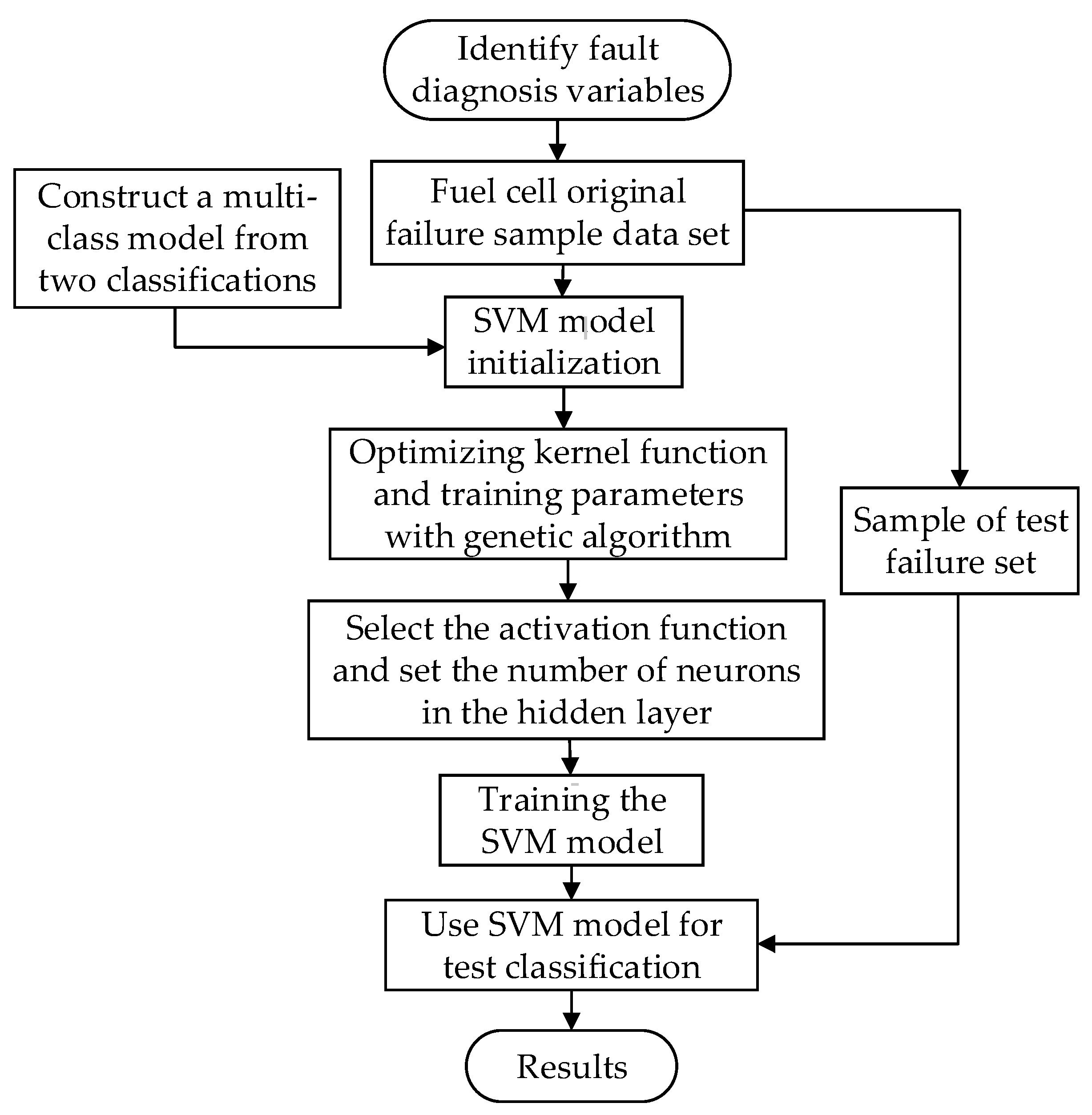
4.2. Support Vector Machine Fault Classification Method
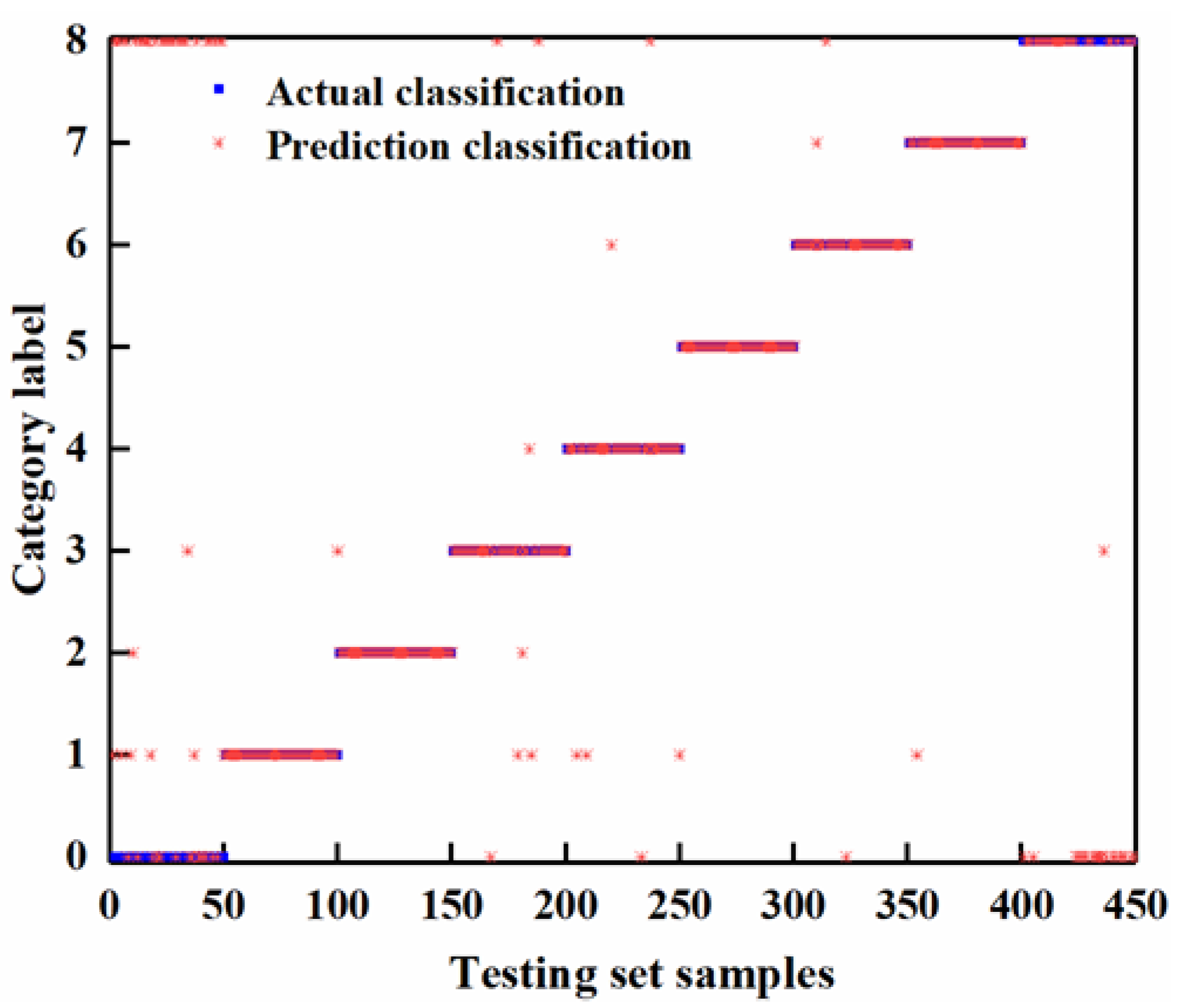
4.3. GA-SVM Fault Classification Method
4.4. Comparison and Analysis of Failure Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PEMFC | Proton exchange membrane fuel cell |
| SOFC | Solid oxide fuel cell |
| His | Health indices |
| EIA-PSO | Effective informed adaptive particle swarm optimization |
| DS | Dempster-Shafer |
| HSMMs | Hidden semi-Markov models |
| SVM | Support vector machine |
| LS-SVM | Least squares support vector machine |
| ELM | Extreme learning machine |
| GA | Genetic algorithm |
| GA-SVM | Genetic algorithm support vector machine |
| BPNN | Back propagation neural network |
References
- Hissel, D.; Candusso, D.; Harel, F. Fuzzy-clustering durability diagnosis of polymer electrolyte fuel cells dedicated to transportation applications. IEEE Trans. Veh. Technol. 2007, 56, 2414–2420. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Z.; Guan, C. Optimization of sizing and frequency control in battery/supercapacitor hybrid energy storage system for fuel cell ship. Energy 2020, 197, 117285. [Google Scholar] [CrossRef]
- Simon Araya, S.; Zhou, F.; Lennart Sahlin, S.; Thomas, S.; Jeppesen, C.; Knudsen Kær, S. Fault Characterization of a Proton Exchange Membrane Fuel Cell Stack. Energies 2019, 12, 152. [Google Scholar] [CrossRef] [Green Version]
- Won, J.; Oh, H.; Hong, J.; Kim, M.; Lee, W.Y.; Choi, Y.Y.; Han, S.B. Hybrid diagnosis method for initial faults of air supply systems in proton exchange membrane fuel cells. Renew. Energy 2021, 180, 343–352. [Google Scholar] [CrossRef]
- Liu, J.; Luo, W.; Yang, X.; Wu, L. Robust model-based fault diagnosis for PEM fuel cell air-feed system. IEEE Trans. Ind. Electron. 2016, 66, 3261–3270. [Google Scholar] [CrossRef] [Green Version]
- Zuo, B.; Zhang, Z.; Cheng, J.; Huo, W.; Zhong, Z.; Wang, Z. Data-driven flooding fault diagnosis method for proton-exchange membrane fuel cells using deep learning technologies. Energy Convers. Manag. 2022, 251, 115004. [Google Scholar] [CrossRef]
- Zhou, S.; Jin, J.; Wei, Y. Research on Online Diagnosis Method of Fuel Cell Centrifugal Air Compressor Surge Fault. Energies 2021, 14, 3071. [Google Scholar] [CrossRef]
- Lim, I.S.; Park, J.Y.; Choi, E.J.; Kim, M.S. Efficient fault diagnosis method of PEMFC thermal management system for various current densities. Int. J. Hydrogen Energy 2021, 46, 2543–2554. [Google Scholar] [CrossRef]
- Zhuo, S.; Gaillard, A.; Xu, L.; Liu, C.; Paire, D.; Gao, F. An Observer-Based Switch Open-Circuit Fault Diagnosis of DC–DC Converter for Fuel Cell Application. IEEE Trans. Ind. Appl. 2020, 56, 3159–3167. [Google Scholar] [CrossRef]
- Shao, M.; Zhu, X.J. An artificial neural network ensemble method for fault diagnosis of proton exchange membrane fuel cell system. Energy 2014, 67, 268–275. [Google Scholar] [CrossRef]
- Li, Q.; Chen, W.R.; Liu, Z.X.; Guo, A.; Huang, J. Nonlinear multivariable modeling of locomotive proton exchange membrane fuel cell system. Int. J. Hydrogen Energy 2014, 39, 13777–13786. [Google Scholar] [CrossRef]
- Liu, J.; Li, Q.; Chen, W.; Yan, Y.; Wang, X. A fast fault diagnosis method of the PEMFC system based on extreme learning machine and dempster–shafer evidence theory. IEEE Trans. Transp. Electrif. 2019, 5, 271–284. [Google Scholar] [CrossRef]
- Wu, X.J.; Ye, Q.W. Fault diagnosis and prognostic of solid oxide fuel cells. J. Power Sources 2016, 321, 47–56. [Google Scholar] [CrossRef]
- Zhao, X.; Xu, L.F.; Li, J.Q.; Fang, C.; Ouyang, M.G. Faults diagnosis for PEM fuel cell system based on multi-sensor signals and principle component analysis method. Int. J. Hydrogen Energy 2017, 42, 18524–18531. [Google Scholar] [CrossRef]
- Djeziri, M.; Djedidi, O.; Benmoussa, S.; Bendahan, M.; Seguin, J.L. Failure Prognosis Based on Relevant Measurements Identification and Data-Driven Trend-Modeling: Application to a Fuel Cell System. Processes 2021, 9, 328. [Google Scholar] [CrossRef]
- Du, R.B.; Wei, X.Z.; Wang, X.Y.; Chen, S.Q.; Yuan, H.; Dai, H.F.; Ming, P.W. A fault diagnosis model for proton exchange membrane fuel cell based on impedance identification with differential evolution algorithm. Int. J. Hydrogen Energy 2021, 46, 38795–38808. [Google Scholar] [CrossRef]
- Zhang, X.; Guo, X. Fault diagnosis of proton exchange membrane fuel cell system of tram based on information fusion and deep learning. Int. J. Hydrogen Energy 2021, 46, 30828–30840. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part I: Fault Diagnosis With Model-Based and Signal-Based Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef] [Green Version]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part II: Fault Diagnosis With Knowledge-Based and Hybrid/Active Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3768–3774. [Google Scholar] [CrossRef]
- Li, Y.; Zeng, Y.J.; Qing, Y.Y.; Huang, G.B. Learning local discriminative representations via extreme learning machine for machine fault diagnosis. Neurocomputing 2020, 409, 275–285. [Google Scholar] [CrossRef]
- Yuan, X.; Liu, Z.; Miao, Z.; Zhao, Z.; Zhou, F.; Song, Y. Fault diagnosis of analog circuits based on IH-PSO optimized support vector machine. IEEE Access 2019, 7, 137945–137958. [Google Scholar] [CrossRef]
- Pukrushpan, J.T.; Stefanopoulou, A.; Peng, H. Control of Fuel Cell Power Systems: Principles, Modeling, Analysis and Feedback Design; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Escobet, A.; Nebot, A.; Mugica, F. PEM fuel cell fault diagnosis via a hybrid methodology based on fuzzy and pattern recognition techniques. Eng. Appl. Artif. Intell. 2014, 36, 40–53. [Google Scholar] [CrossRef] [Green Version]
- Rosich, A.; Sarrate, R.; Nejjari, F. On-line model-based fault detection and isolation for PEM fuel cell stack systems. Appl. Math. Model. 2014, 38, 2744–2757. [Google Scholar] [CrossRef]
- Kamal, M.; Yu, D.; Yu, D.; Yu, D. Fault detection and isolation for PEM fuel cell stack with independent RBF model. Eng. Appl. Artif. Intell. 2014, 28, 52–63. [Google Scholar] [CrossRef]
- Liu, J.W.; Li, Q.; Chen, W.R.; Yan, Y.; Wang, X.T. Research on the fault diagnosis of a polymer electrolyte membrane fuel cell system. Energies 2020, 13, 2531. [Google Scholar]






| Symbol | Parameter | Value |
|---|---|---|
| Effective activation area | Afc | 280 cm2 |
| Number of cells | n | 381 |
| Anode volume | Van | 0.005 m3 |
| Cathode volume | Vca | 0.01 m3 |
| Membrane thickness | tm | 0.01275 cm |
| Compressor diameter | dc | 0.2286 m |
| Compressor and motor inertia | JCP | 5 × 10−5 kg × m2 |
| Compressor motor circuit resistance | Rcm | 1.2 Ω |
| Motor electric constant | kv | 0.0153 V/(rad/s) |
| Motor torque constant | kt | 0.225 N × m/A |
| Motor mechanical efficiency | ƞcm | 98% |
| Supply manifold volume | Vsm | 0.02 m3 |
| Supply manifold outlet orifice constant | Ksm,out | 0.36293 × 10−5 kg/(s × Pa) |
| Return manifold volume | Vrm | 0.005 m3 |
| Motor electric constant | kv | 0.0153 V/(rad/s) |
| Motor torque constant | kt | 0.225 N × m/A |
| Fault ID | Fault Description | Type | Magnitude |
|---|---|---|---|
| Fault 0 | Normal state | Parametric unchanged | 0 |
| Fault 1 | Sudden increase in friction of compressor mechanical parts | Abrupt change | Flow coefficient increased by 10% |
| Fault 2 | The temperature of the compressor motor is too high | Abrupt change | Internal resistance increased by 100% |
| Fault 3 | Flooding failure in stack | Abrupt change | Reduce water flow by 50% |
| Fault 4 | Air leak in the air supply manifold | Abrupt change | Reduce air flow by 50% |
| Fault 5 | The cooler temperature control failure | Gradual change | Temperature increment of 10 K |
| Fault 6 | The humidifier control failure | Gradual change | Humidity increase by 20% |
| Fault 7 | The stack temperature control failure | Gradual change | Temperature increment of 10 K |
| Fault 8 | Air leak in the outlet manifold | Abrupt change | Reduce gas flow by 30% |
| Classification | Fault 0 | Fault 1 | Fault 2 | Fault 3 | Fault 4 | Fault 5 | Fault 6 | Fault 7 | Fault 8 | Average |
|---|---|---|---|---|---|---|---|---|---|---|
| ELM | 76% | 68% | 86% | 78% | 84% | 90% | 66% | 80% | 80% | 78.67% |
| SVM | 28% | 98% | 100% | 86% | 88% | 100% | 94% | 98% | 58% | 83.33% |
| GA-SVM | 86% | 88% | 100% | 100% | 100% | 86% | 100% | 100% | 84% | 98% |
| Classification | Time |
|---|---|
| ELM | 0.36 s |
| SVM | 0.41 s |
| GA-SVM | 0.18 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huo, W.; Li, W.; Sun, C.; Ren, Q.; Gong, G. Research on Fuel Cell Fault Diagnosis Based on Genetic Algorithm Optimization of Support Vector Machine. Energies 2022, 15, 2294. https://doi.org/10.3390/en15062294
Huo W, Li W, Sun C, Ren Q, Gong G. Research on Fuel Cell Fault Diagnosis Based on Genetic Algorithm Optimization of Support Vector Machine. Energies. 2022; 15(6):2294. https://doi.org/10.3390/en15062294
Chicago/Turabian StyleHuo, Weiwei, Weier Li, Chao Sun, Qiang Ren, and Guoqing Gong. 2022. "Research on Fuel Cell Fault Diagnosis Based on Genetic Algorithm Optimization of Support Vector Machine" Energies 15, no. 6: 2294. https://doi.org/10.3390/en15062294
APA StyleHuo, W., Li, W., Sun, C., Ren, Q., & Gong, G. (2022). Research on Fuel Cell Fault Diagnosis Based on Genetic Algorithm Optimization of Support Vector Machine. Energies, 15(6), 2294. https://doi.org/10.3390/en15062294