Numerical Prediction of Tower Loading of Floating Offshore Wind Turbine Considering Effects of Wind and Wave
Abstract
:1. Introduction
2. Numerical Model and Load Calculation
2.1. The Load Calculation by Using Coupled Model
2.2. Prediction of Tower Moment Induced by Platform Motion
2.3. The Load Calculation Based on the Uncoupled Approach
3. Prediction of Tower Bending Moment of FOWT by Coupled and Uncoupled Approaches
3.1. Onsite Measurement and Metocean Conditions
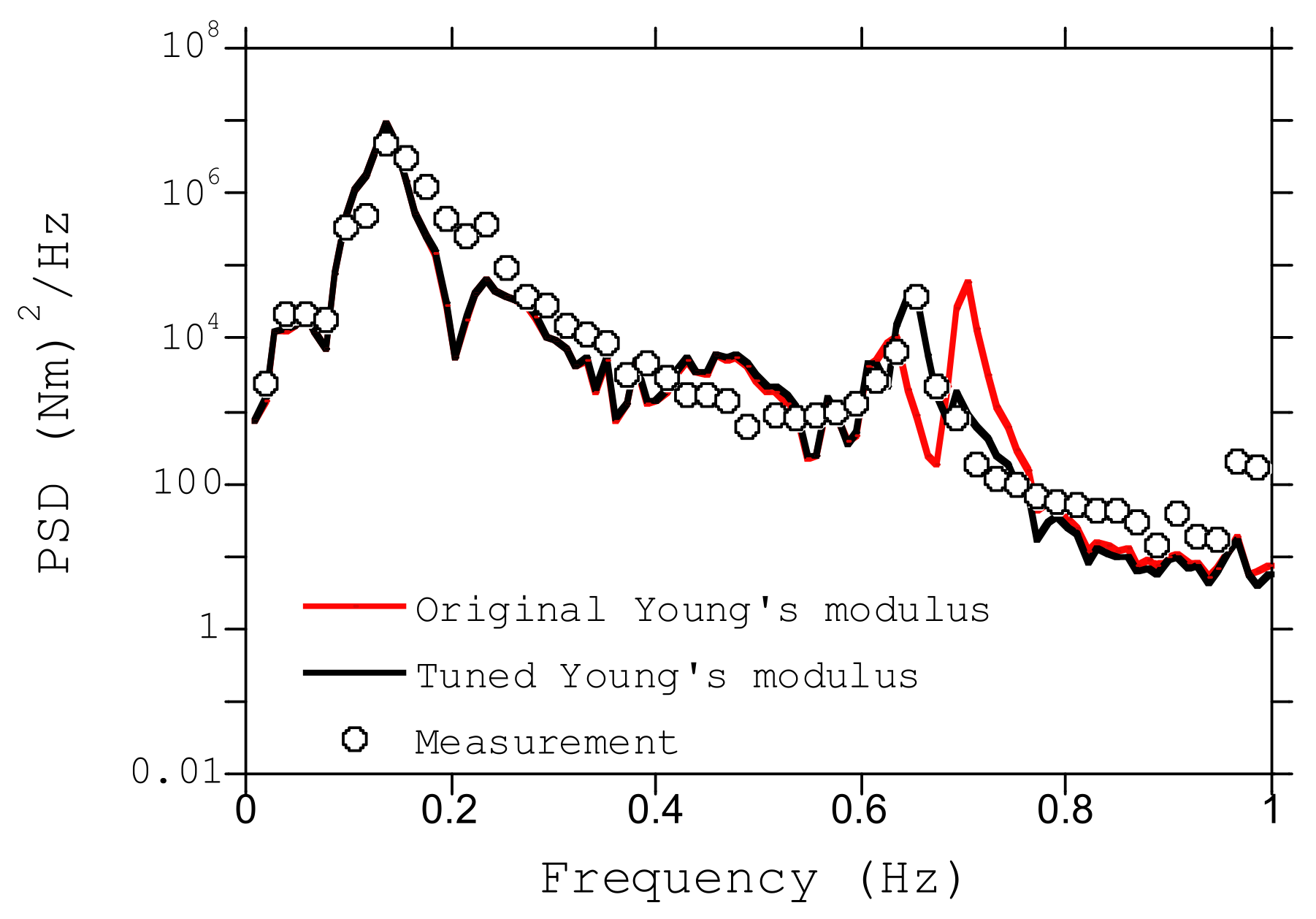
3.2. The Effect of Flexibility and Boundary Condition of Platform on the Tower First Mode Frequency
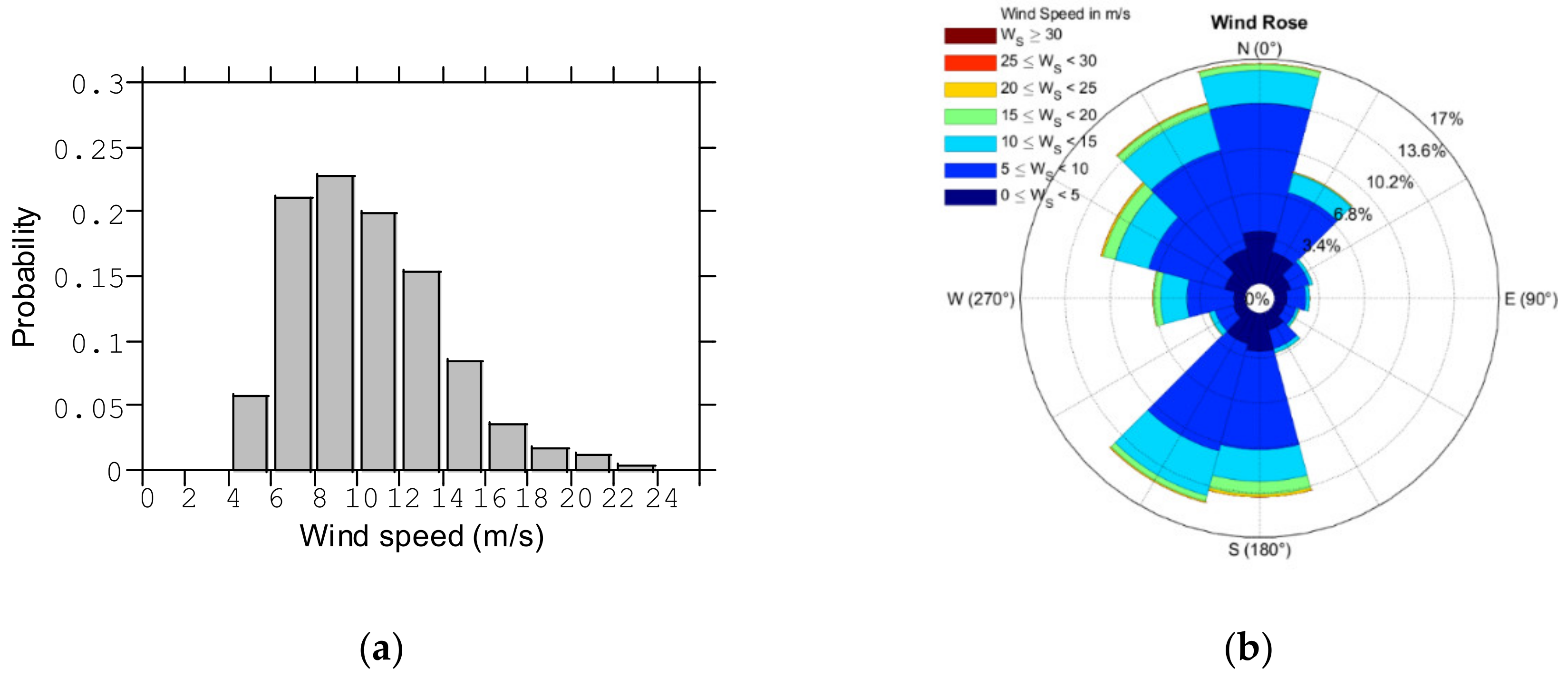
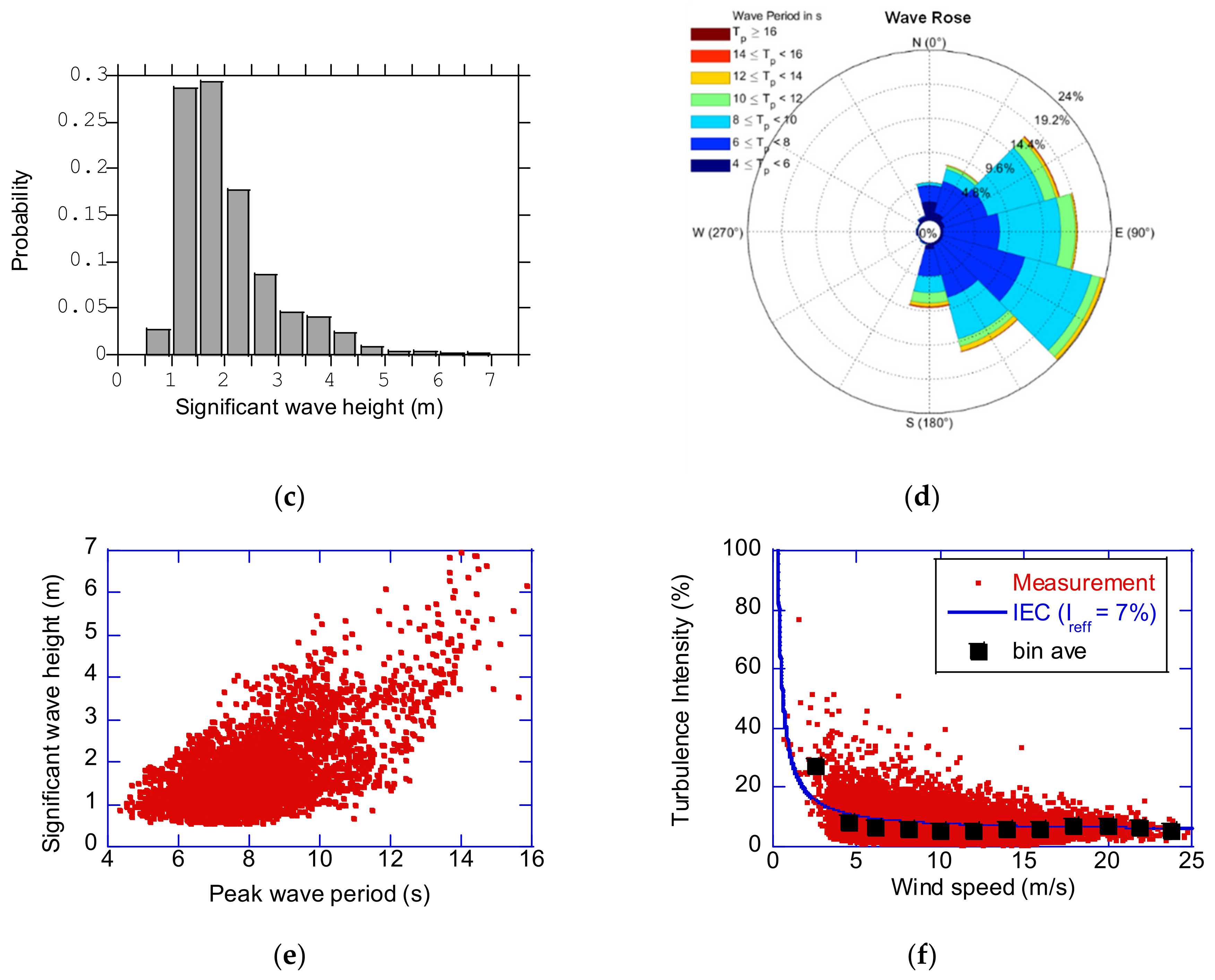
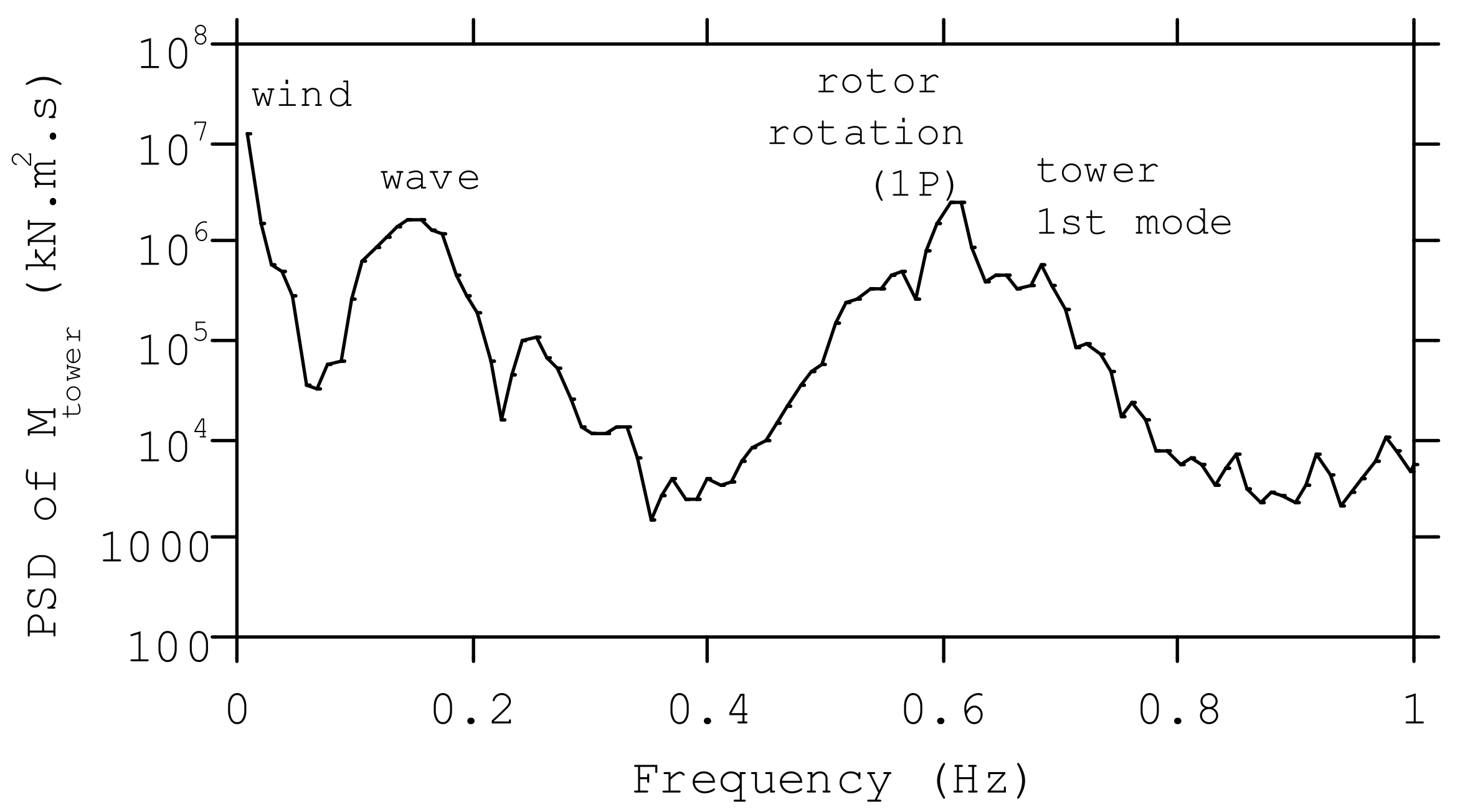
3.3. The Characteristics of Wind and Wave Actions
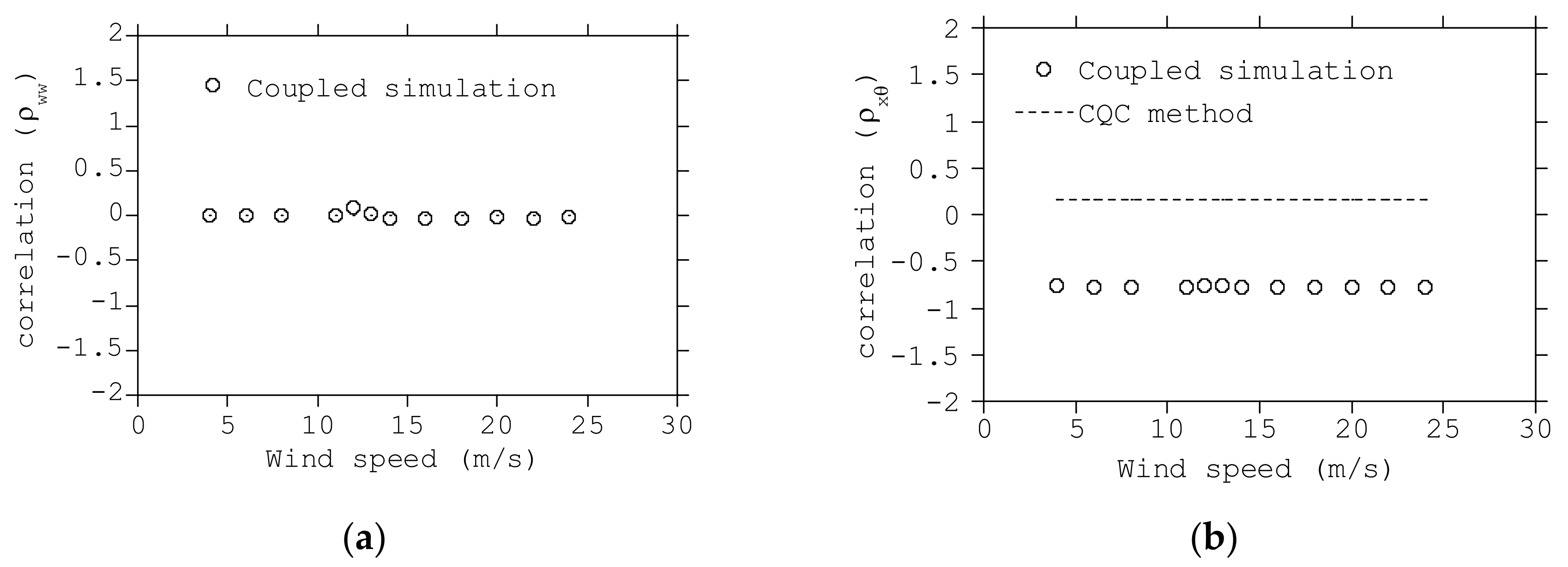
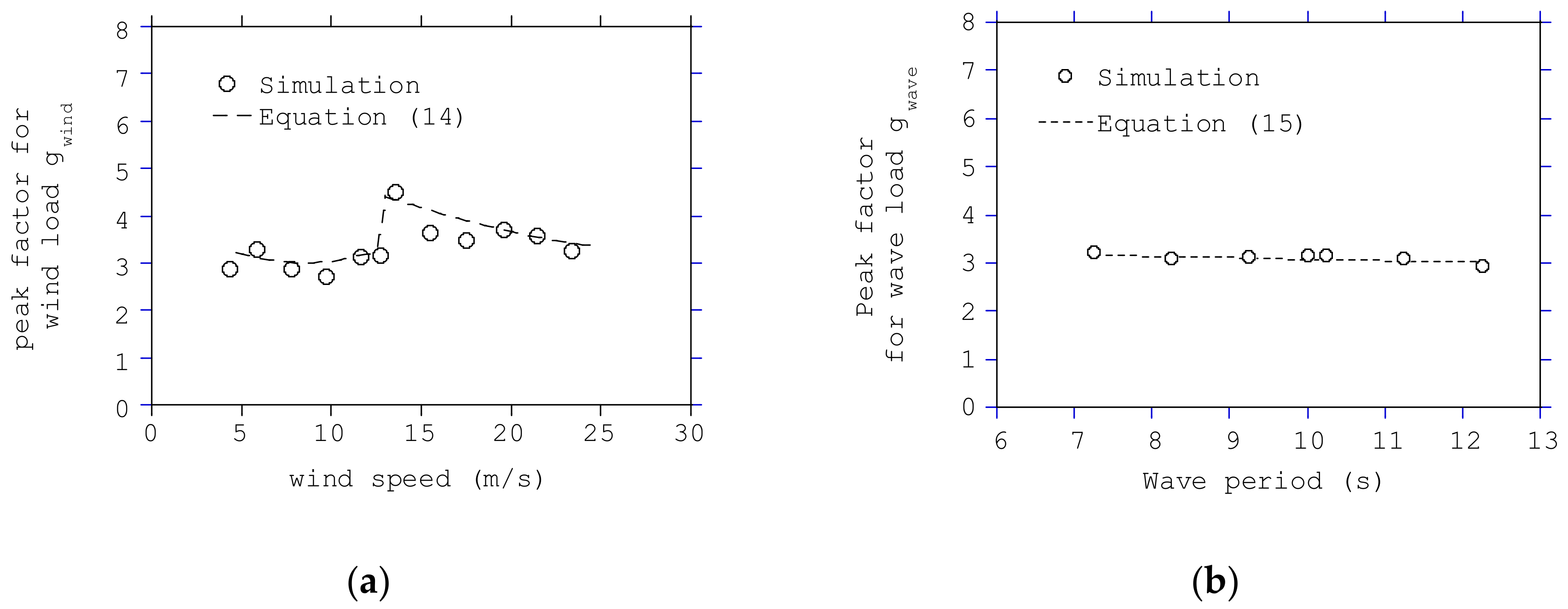
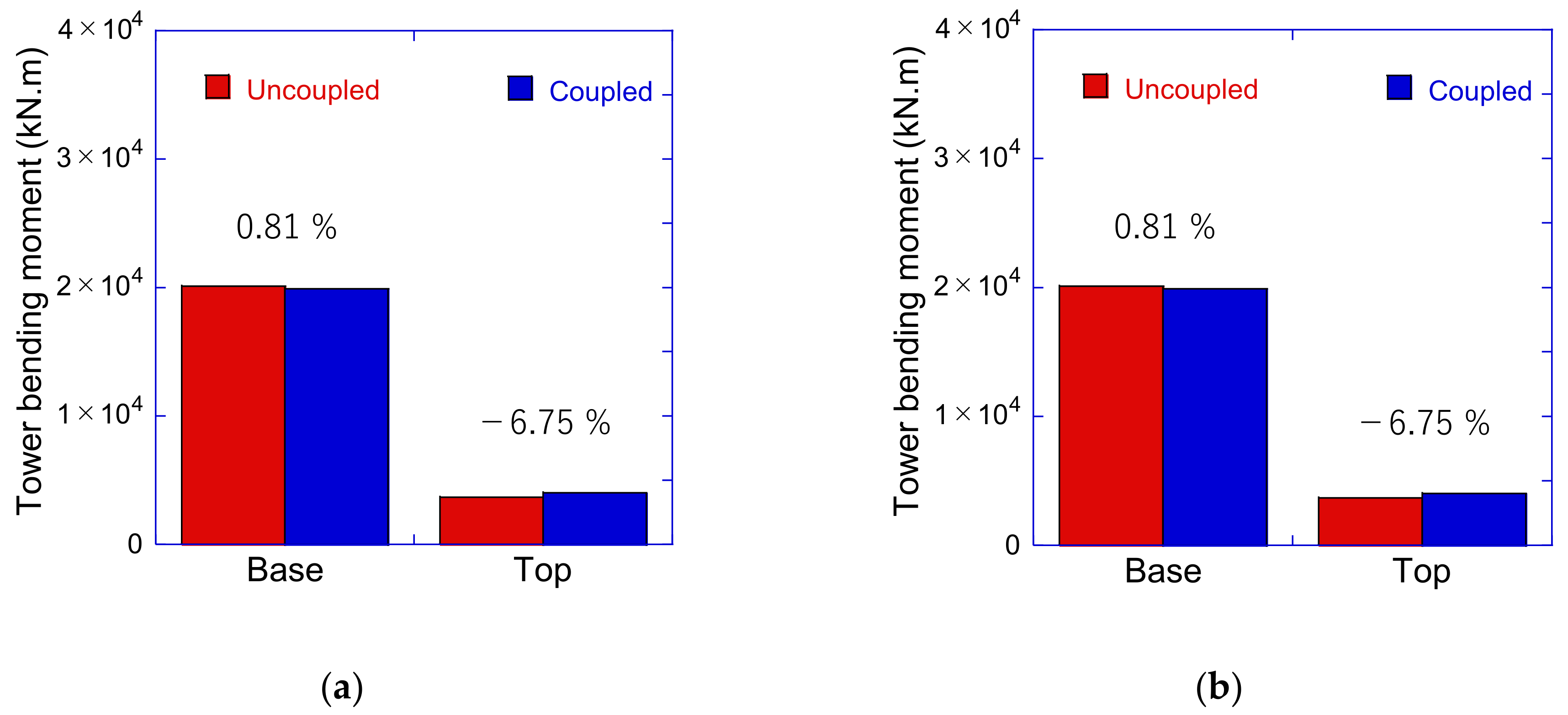
3.4. Comparison between Coupled and Uncoupled Approach for the Extreme Sea States
4. Conclusions
- The elasticity and the bottom boundary condition of the platform had to be considered to accurately predict the tower first mode frequency. When performing the dynamic simulation of FOWTs by using rigid platform model such as FAST, the effect of the elasticity of platform could be considered by tuning the Young’s modulus of the tower material to fit the tower first model frequency obtained by the finite element method. The predicted power spectrum density of the fore-aft tower base moment by using the proposed method shows good agreement with the measurement;
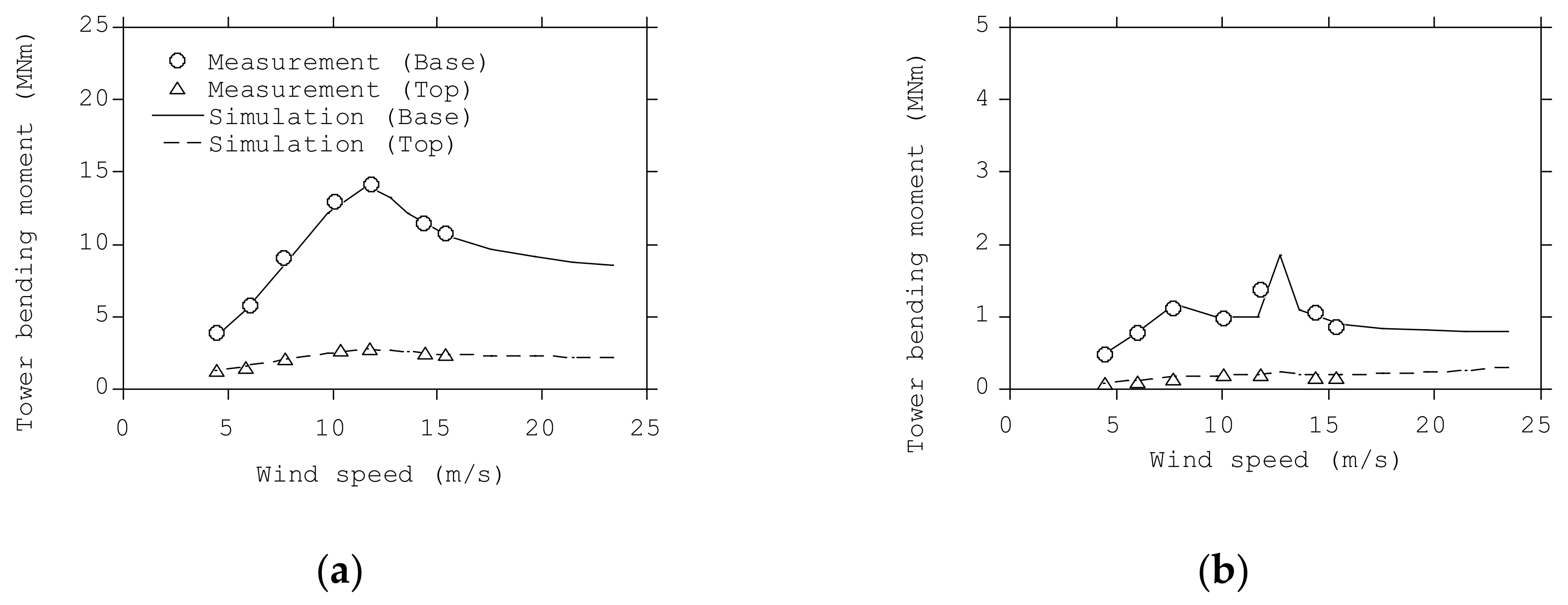
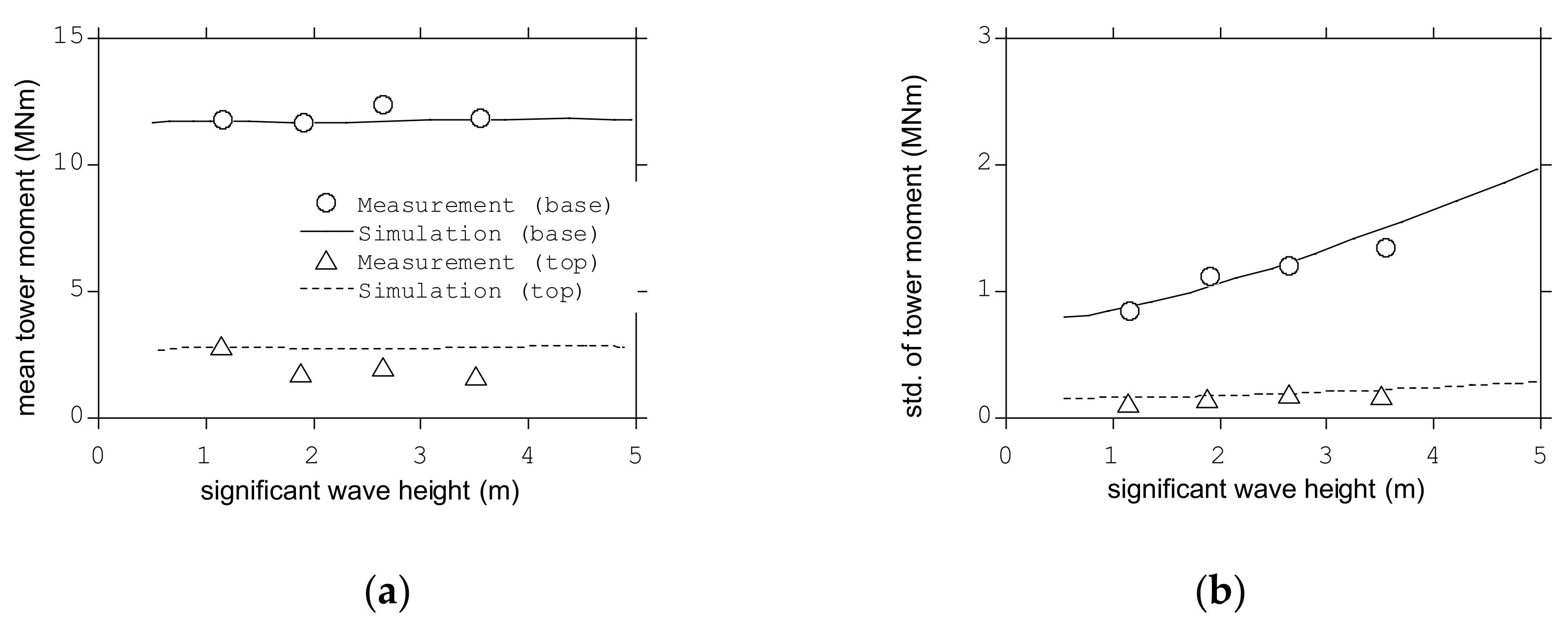
- The difference of the wind load between the bottom fixed wind turbine and floating wind turbine was observed only in the mean component and can be corrected by considering the hydrostatic stiffness of platform and mooring stiffness, since the fluctuating wind load of wind turbine tower on semi-submersible platforms did not show difference from that on fixed foundations;
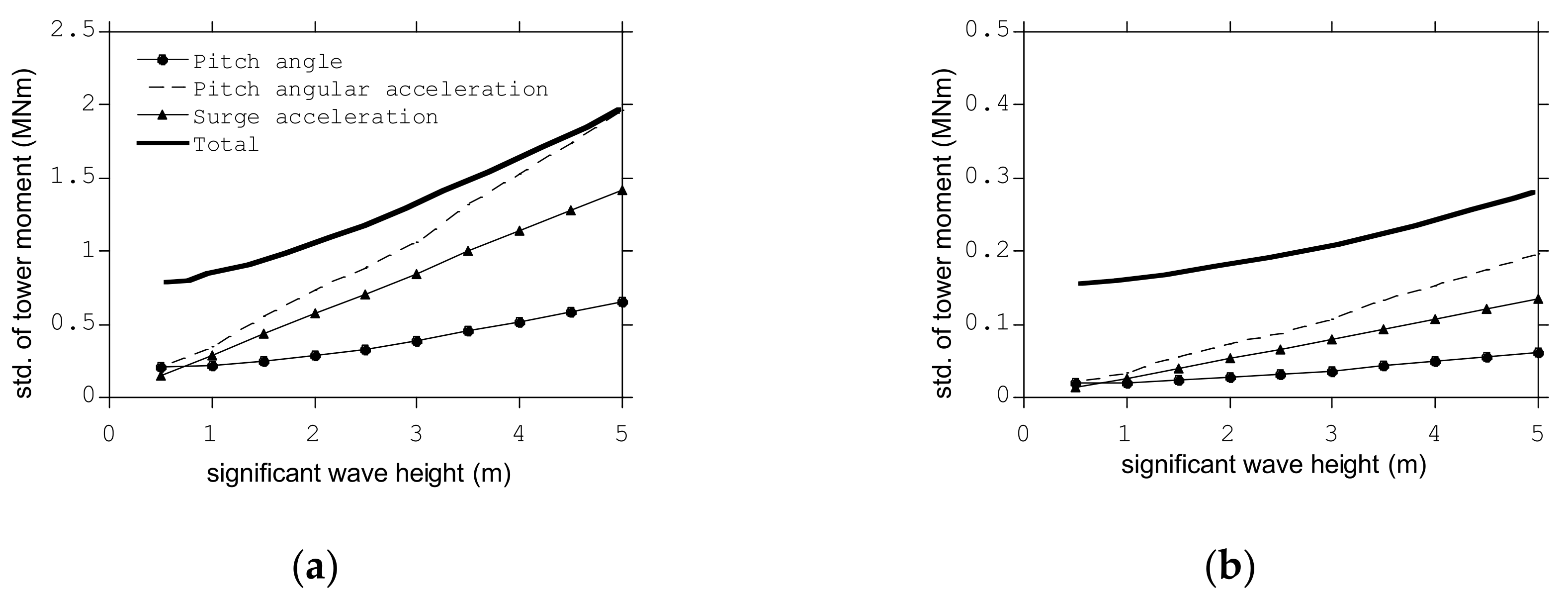
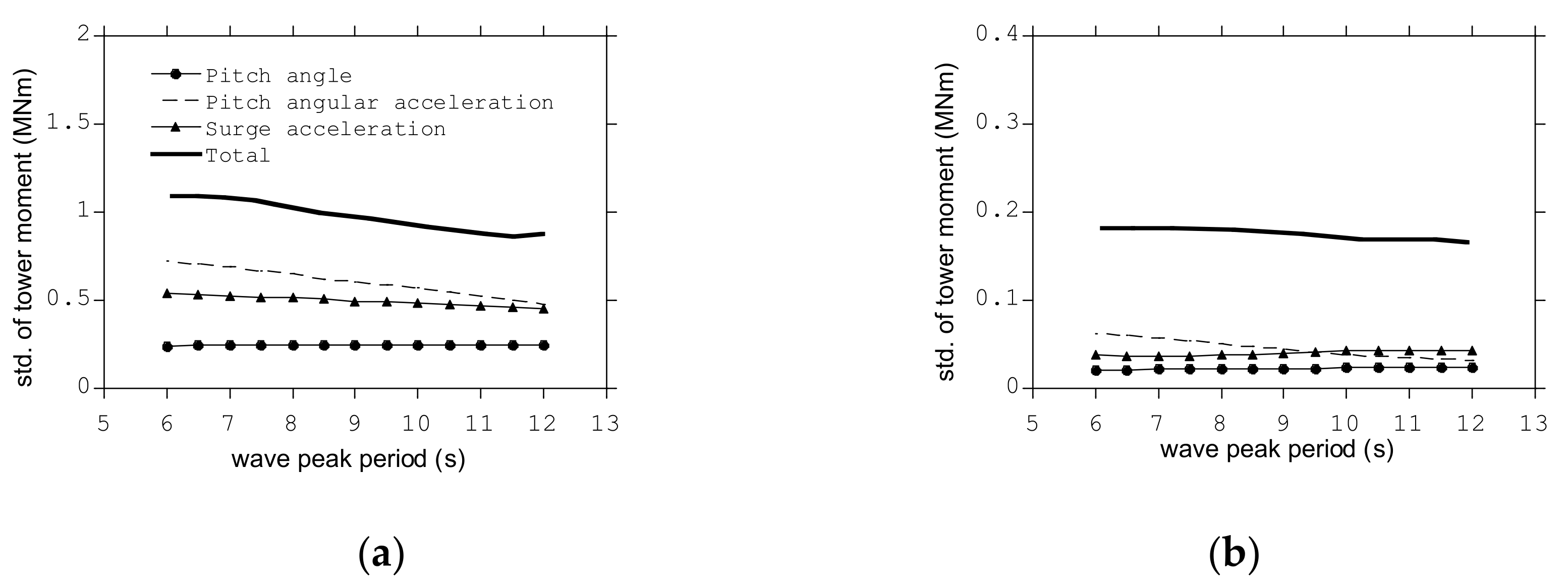
- The standard deviation of the fore-aft tower moment increased as the significant wave heights increased when the mean wind speed and peak wave period were fixed. On the other hand, the standard deviation of the fore-aft tower bending moment decreased as the peak wave periods increased when the mean wind speed and significant wave height were fixed. It was found that the increase of the significant wave height causes the increase of the pitch and surge motions of the platform resulting in the increase of the fluctuating fore-aft tower moment, and the increase of the peak wave period caused the decrease of the pitch and surge accelerations of the platform resulting in the decrease of the fluctuating fore-aft tower moment;
- The predicted tower loading in extreme sea states during power production by the proposed uncoupled approach show good agreement with those by the coupled approach, and the simulation time was reduced to 1/40 for FOWTs on semi-submersible platforms because the effect of wind action and wave action can be calculated separately.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dhingra, T.; Sengar, A.; Sajith, S. A fuzzy analytic hierarchy process-based analysis for prioritization of barriers to offshore wind energy. J. Clean. Prod. 2022, 345, 131111. [Google Scholar] [CrossRef]
- Dokur, E.; Erdogan, N.; Salari, M.E.; Karakuzu, C.; Murphy, J. Offshore Wind Speed Short-Term Forecasting Based on a Hybrid Method: Swarm Decomposition and Meta-Extreme Learning Machine. Available online: https://ssrn.com/abstract=4000338 (accessed on 14 March 2022).
- Calautit, K.; Aquino, A.; Calautit, J.K.; Nejat, P.; Jomehzadeh, F.; Hughes, B.R. A review of numerical modelling of multi-scale wind turbines and their Environment. Computation 2018, 6, 24. [Google Scholar] [CrossRef] [Green Version]
- Buljac, A.; Kozmar, H.; Yang, W.; Kareem, A. Concurrent wind, wave and current loads on a monopile-supported offshore wind turbine. Eng. Struct. 2022, 255, 113950. [Google Scholar] [CrossRef]
- Dinh, Q.V.; Doan, Q.V.; Ngo-Duc, T.; Dinh, V.N.; Duc, N.D. Offshore wind resource in the context of global climate change over a tropical area. Appl. Energy 2022, 308, 118369. [Google Scholar] [CrossRef]
- Lerche, J.; Lindhard, S.; Enevoldsen, P.; Velaayudan, A.; Teizer, J.; Neve, H.H.; Wandahl, S. What can be learned from variability in offshore wind projects. Energy Strategy Rev. 2022, 39, 100794. [Google Scholar] [CrossRef]
- Wang, C.M.; Utsunomiya, T.; Wee, S.C.; Choo, Y.S. Research on floating wind turbines: A literature survey. IES J. Part A Civ. Struct. Eng. 2010, 3, 267–277. [Google Scholar] [CrossRef] [Green Version]
- Twidell, J.; Gaudiosi, G. (Eds.) Offshore Wind Power; Multi-Science Publishing Co. Ltd.: Essex, UK, 2009. [Google Scholar]
- Goupee, A.J.; Koo, B.J.; Kimball, R.W.; Lambrakos, K.F.; Dagher, H.J. Experimental comparison of three floating wind turbine concepts. J. Offshore Mech. Arct. Eng. 2014, 136, 020906. [Google Scholar] [CrossRef]
- Tang, Y.G.; Song, K.; Wang, B. Experiment study of dynamics response for wind turbine system of floating foundation. China Ocean Eng. 2015, 29, 835–846. [Google Scholar] [CrossRef]
- Robertson, A.N.; Jonkman, J.M. Loads analysis of several offshore floating wind turbine concepts. In Proceedings of the International Society of Offshore and Polar Engineers 2011 Conference, Maui, HI, USA, 19–24 June 2011; Available online: https://www.nrel.gov/docs/fy12osti/50539.pdf (accessed on 14 March 2022).
- IEC TS 61400-3-2; Wind Energy Generation Systems—Part 3-2: Design Requirements for Floating Offshore Wind Turbines, Edition 1.0. International Electrotechnical Commission: Geneva, Switzerland, 5 April 2019.
- Zhang, S.; Ishihara, T. Effects of Multidirectional Sea States and Flexible Foundation on Dynamic Response of Floating Offshore Wind Turbine System. In Proceedings of the First International Symposium on Flutter and its Application, Tokyo, Japan, 15–17 May 2016. [Google Scholar]
- Robertson, A.N.; Gueydon, S.; Bachynski, E.; Wang, L.; Jonkman, J.; Alarcón, D.; Amet, E.; Beardsell, A.; Bonnet, P.; Boudet, B.; et al. OC6 Phase I: Investigating the underprediction of low frequency hydrodynamic loads and responses of a floating wind turbine. J. Phys. Conf. Ser. 2020, 1618, 032033. [Google Scholar] [CrossRef]
- Robertson, A.N.; Fabian, W.; Jonkman, J.M.; Wojciech, W.P.; Habib, D. OC5 Project Phase II: Validation of global loads of the DeepCwind floating semisubmersible wind turbine. Energy Procedia 2017, 137, 38–57. [Google Scholar] [CrossRef]
- Kvittem, M.I.; Moan, T. Time domain analysis procedures for fatigue assessment of a semi-submersible wind turbine. Mar. Struct. 2015, 40, 38–59. [Google Scholar] [CrossRef] [Green Version]
- Long, M.; Yanping, H.; Tao, Z. Research on Dynamic Response Characteristics of 6 MW Spar-Type Floating Offshore Wind Turbine. J. Shanghai Jiaotong Univ. (Sci.) 2018, 23, 505–514. [Google Scholar] [CrossRef]
- Xu, N.; Ishihara, T. Prediction of tower loading of floating offshore wind turbine systems in the extreme wind and wave conditions. Wind. Eng. 2014, 38, 463–476. [Google Scholar] [CrossRef]
- Jonkman, J.M.; Buhl, M.L., Jr. Loads Analysis of a Floating Offshore Wind Turbine Using Fully Coupled Simulation. In Proceedings of the Wind Power 2007 Conference & Exhibition, Los Angeles, CA, USA, 3–6 June 2007; Available online: https://www.nrel.gov/docs/fy07osti/41714.pdf (accessed on 14 March 2022).
- Ishihara, T.; Zhang, S. Prediction of dynamic response of semi- submersible floating offshore wind turbine using augmented Morison’s equation with frequency dependent hydrodynamic coefficients. Renew. Energy 2019, 131, 1186–1207. [Google Scholar] [CrossRef]
- Yoshida, S. Variable speed-variable pitch controllers for aero-servo-elastic simulations of wind turbine support structures. J. Fluid Sci. Technol. 2011, 6, 300–312. [Google Scholar] [CrossRef] [Green Version]
- Yamaguchi, A.; Yousefi, I.; Ishihara, T. Reduction of the fluctuating load on wind turbine by using a combined nacelle acceleration feedback and Lidar-based feedforward control. Energies 2020, 13, 4558. [Google Scholar] [CrossRef]
- Liu, Y.; Ishihara, T. Prediction of dynamic response of semi-submersible floating offshore wind turbines by a novel hydrodynamic coefficient model. J. Phys. Conf. Ser. 2019, 1356, 012035. [Google Scholar] [CrossRef]
- Jonkman, J.M.; Buhl, M.L., Jr. A Quantitative Comparison of the Responses of Three Floating Platforms. In Proceedings of the European Offshore Wind 2009 Conference and Exhibition, Stockholm, Sweden, 14–16 September 2009; Available online: https://www.nrel.gov/docs/fy10osti/46726.pdf (accessed on 14 March 2022).
- Yamaguchi, A.; Taki, S.; Ishihara, T. Metocean measurement at Fukushima offshore site. In Proceedings of the Grand Renewable Energy 2018, Yokohama, Japan, 17–22 June 2018. [Google Scholar] [CrossRef]
- IEC61400-1; Wind Energy Generation Systems—Part 1: Design Requirements, Edition 4.0. International Electrotechnical Commission: Geneva, Switzerland, 8 February 2019.
- Michael, S. ABAQUS/Standard User’s Manual, Version 6.9; Dassault Systmes Simulia Corp.: Providence, RI, USA, 2009. [Google Scholar]
- Yamaguchi, A.; Sarli, P.W.; Ishihara, T. Extreme load estimation of the wind turbine tower during power production. Wind Eng. 2019, 45, 93–106. [Google Scholar] [CrossRef]
- Kiureghian, A.D. A response spectrum method for random vibration analysis of mdf systems. Earthq. Eng. Struct. Dyn. 1981, 9, 419–435. [Google Scholar] [CrossRef]
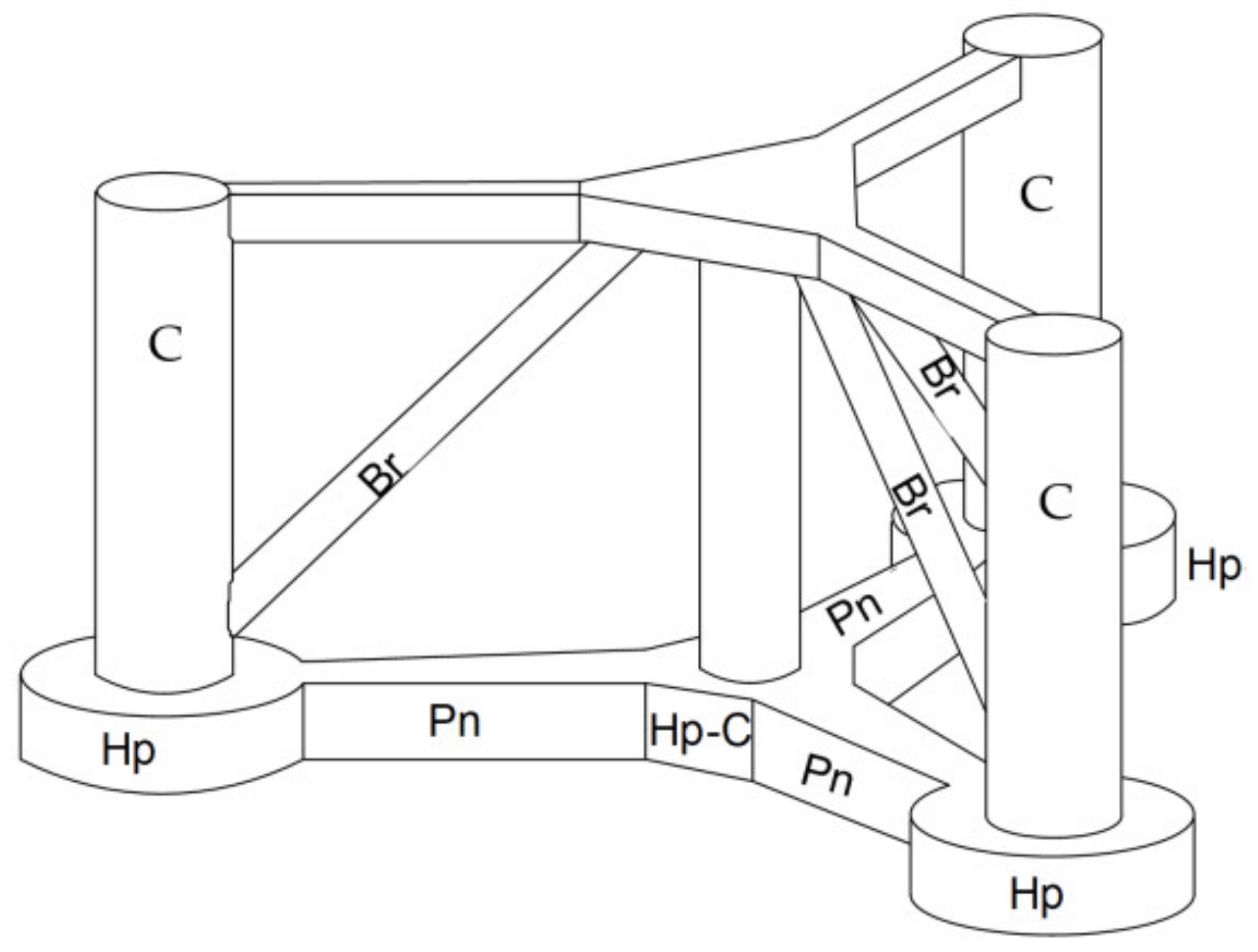
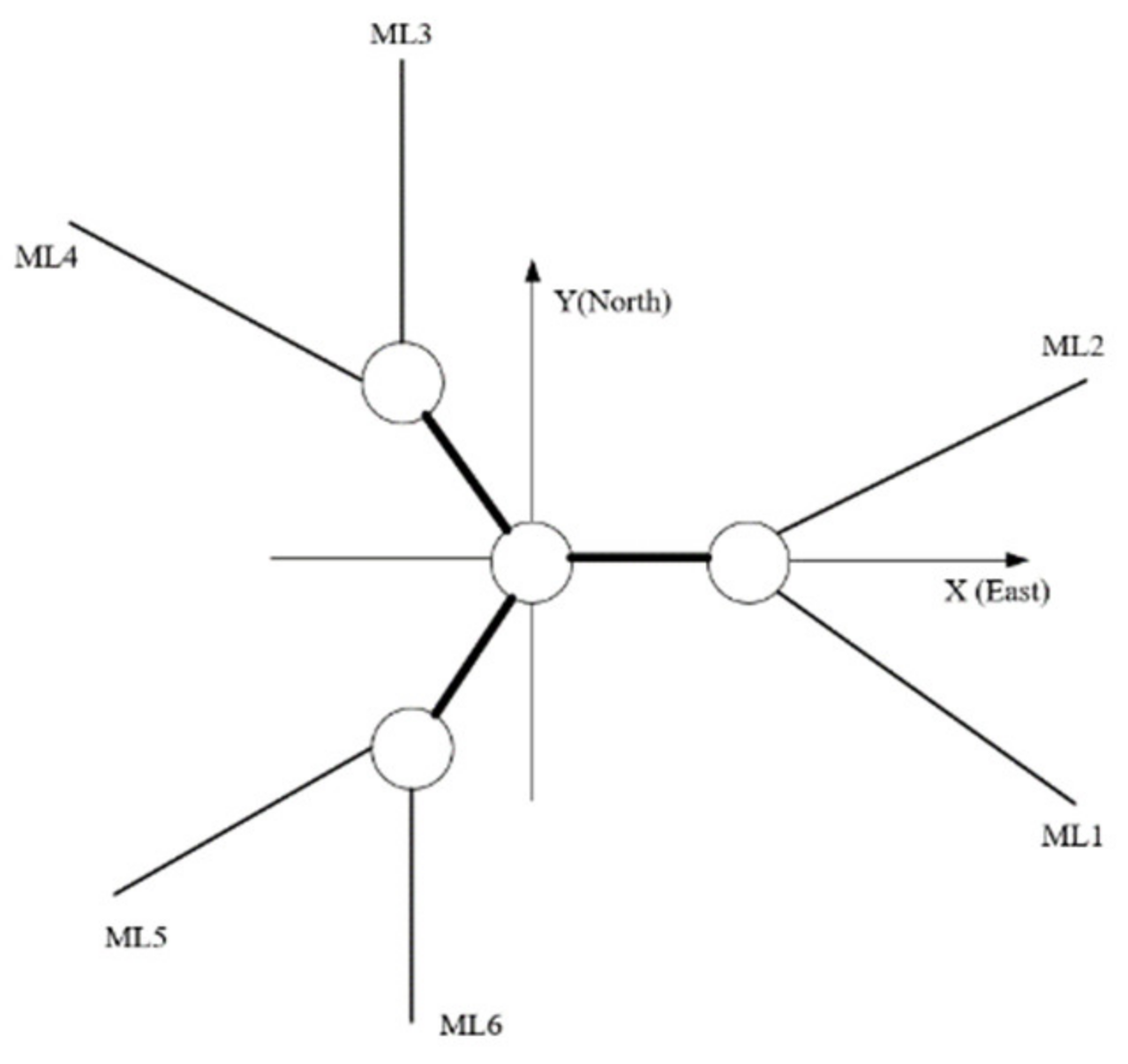




| Dimension and Weight | Value |
|---|---|
| Dimension of the nacelle | Length × Width × Height = 11.5 × 3.5 × 4.9 m |
| Mass of the nacelle | 75,168 kg |
| Length of blade | 39 m |
| Mass of rotor | 41,038 kg |
| Control Parameter | Value |
|---|---|
| Optimal mode gain for torque control | 0.1717 Nm/(rad/s)2 |
| Minimum generator speed | 1087.8 rpm |
| Optimum mode maximum speed | 1920.8 rpm |
| Pitch PI control proportional gain | 0.0169 s |
| Pitch PI control integral gain | 0.0090 |
| Rated power | 2 MW |
| Rated torque | 12,083.6 Nm |
| Rated generated speed | 1715 rpm |
| Components of Platform | Cd in the Normal Direction | Cd in the Axial Direction |
|---|---|---|
| C and Br | 0.65 | 0 |
| Hp | 0.65 | 17.5 |
| Hp-C | 0.65 | 4.0 |
| Pn-x | 2.2 | 0 |
| Pn-y | 7.0 | 0 |
| Mooring Line Properties | Value |
|---|---|
| Number of mooring lines | 6 |
| Angle between adjacent lines | 60 degrees |
| Depth to anchors below SWL | 120 m |
| Depth to fairleads below SWL | 13.3 m |
| Upstretched mooring line length | 680 m |
| Equivalent mooring line diameter | 0.249 m |
| Equivalent mooring line mass density | 382.00 kg/m |
| Equivalent mooring line mass in water | 332.08 kg/m |
| Equivalent mooring line extensional stiffness | 1.76 GN/m |
| Case | Boundary Condition | Platform Flexibility | First Mode Eigenfrequency |
|---|---|---|---|
| 1 | Fixed | Rigid | 0.773 Hz |
| 2 | Fixed | Flexible | 0.619 Hz |
| 3 | Free | Rigid | 0.740 Hz |
| 4 | Free | Flexible | 0.665 Hz |
| Measurement | 0.664 Hz | ||
| Wind-Wave MISALIGNMENT (deg.) | Significant Wave Height (m) | Wave Peak Period (s) | Mean Wind Speed (m/s) | |
|---|---|---|---|---|
| 0 | 6.1 | 7.0, 10.0, 13.0 | 4–24 | 7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamaguchi, A.; Danupon, S.; Ishihara, T. Numerical Prediction of Tower Loading of Floating Offshore Wind Turbine Considering Effects of Wind and Wave. Energies 2022, 15, 2313. https://doi.org/10.3390/en15072313
Yamaguchi A, Danupon S, Ishihara T. Numerical Prediction of Tower Loading of Floating Offshore Wind Turbine Considering Effects of Wind and Wave. Energies. 2022; 15(7):2313. https://doi.org/10.3390/en15072313
Chicago/Turabian StyleYamaguchi, Atsushi, Subanapong Danupon, and Takeshi Ishihara. 2022. "Numerical Prediction of Tower Loading of Floating Offshore Wind Turbine Considering Effects of Wind and Wave" Energies 15, no. 7: 2313. https://doi.org/10.3390/en15072313
APA StyleYamaguchi, A., Danupon, S., & Ishihara, T. (2022). Numerical Prediction of Tower Loading of Floating Offshore Wind Turbine Considering Effects of Wind and Wave. Energies, 15(7), 2313. https://doi.org/10.3390/en15072313






