A Review of Energy-Efficient and Sustainable Construction Scheduling Supported with Optimization Tools

Abstract

This article reviews the accomplishments of studies in which optimization tools were used to develop energy-efficient and sustainable construction schedules. With the increase in global awareness of environmental issues, the construction industry has been forced to explore innovative techniques to make the building process more energy-efficient and sustainable. Project managers can use optimization tools in their scheduling procedures to address these issues in the early stages of the project. Therefore, this paper examines different optimization-based construction scheduling methods and their impact on schedule energy efficiency and the three key sustainability goals: economic viability, social equity, and environmental protection. Such a review has not yet been conducted to the best of our knowledge. This research aims to fill the gap and contribute to understanding advanced optimization tools that can pave the way to energy-efficient and sustainable scheduling practices. After a brief introduction, the background of optimization-based construction scheduling techniques that aim to improve construction management and incorporate these aspects into the decision-making process is explained. Then, these approaches are addressed in detail. It is determined for each study whether it adopted energy efficiency goals and which sustainability dimensions it considered within the proposed optimization model. The results of this study indicate a wide heuristic algorithms application for complex scheduling problems. Meanwhile, mathematical programming is still quite unexplored, especially methods that utilize algebraic modeling languages. This study provides a foundation for further research by addressing the current reach in development and possible knowledge gaps that could be researched in future studies. The paper also discusses the advantages and limitations of different approaches and illustrates the potential for utilizing these methods. Supported by the main review findings, conclusions and recommendations for further research are provided.

1. Introduction

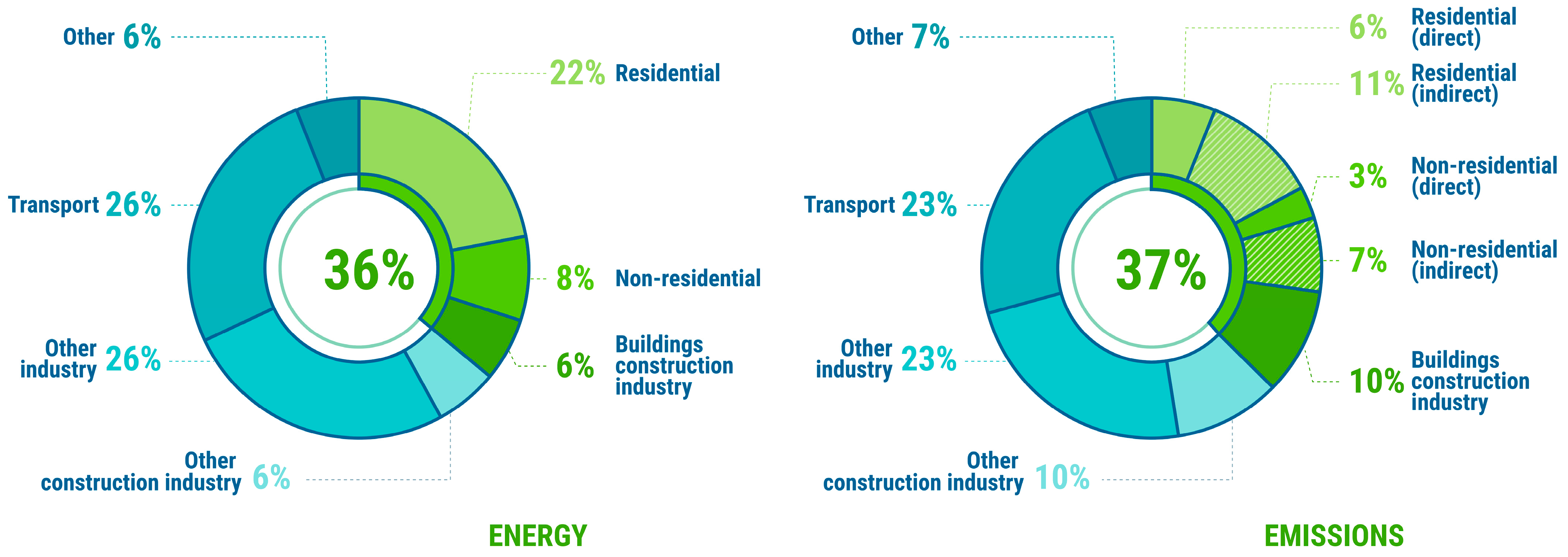
According to the United Nations Environment Programme report for 2021 [1], the operation of the buildings and construction industry in 2020 generated around 37% (11.7 gigatons) of global energy-related carbon dioxide emissions and consumed 149 exajoules or 36% of global energy (Figure 1). In 2015, this sector was responsible for 38% (13.1 gigatons) of CO₂ emissions and required 144 exajoules of energy. Energy demand peaked at 150 exajoules in 2019. The slowdown in global energy demand for the operation of the buildings and construction industry and the reduction in emissions reflect the impact of the COVID-19 pandemic. Thus, the ascent of construction projects postponed due to pandemics can be expected in the post-pandemic era. Therefore, energy demand will increase and environmental problems, often related to the construction sector, may arise.

Due to astonishing amounts of energy and greenhouse gas emissions related to the construction sector, considerable attention is paid to enhancing the construction project’s energy efficiency and sustainability [2]. Generally speaking, sustainable construction is often associated with building design, and there are significant innovations that minimize utility costs and provide a better quality of life. Buildings nowadays are designed to consume less energy for heating/cooling with proper isolation and ventilation. There are also technologically advanced materials and renewable energy sources that can be used to produce near-zero energy buildings. In contrast, energy efficiency and sustainability during the construction phase are somewhat relatively overlooked or mainly remain acknowledged just as some set of general principles that point in that direction.

Construction sites can be dynamic environments and often include many different participants working together. Additionally, budgetary constraints, deadlines, environmental conditions to be concerned, and resource shortages must be considered, affecting energy efficiency and sustainability of the construction phase [3]. Maintaining all this information and their in-between correlation can be a rather difficult task for most (even) experienced project managers. In this study, optimization-based construction scheduling methods are addressed to tackle these issues and manage all project constraints. In the early project planning phase, it is possible to consider all the project objectives with a particular optimization model to achieve the best overall solution.

The modeled scheduling problem can be used to calculate an optimal construction schedule that ensures that the project is sustainable and saves energy. Since the construction projects are often carried out in a dynamic environment, an energy-efficient and sustainable construction schedule can ensure that the project meets all deadlines, even if parameters change during the execution period. In other words, sustainable scheduling is not only about delivering a result according to expectations, within the available budget, and on time, but also about ensuring that the practice of project updates and re-optimizations is sustainable in the long run [4].

This review makes an original contribution to the field of construction project management, addressing the creative approaches for producing optimal construction schedules through the utilization of optimization tools. The methods are explained with particular attention to optimization techniques that improve the project’s energy efficiency and different sustainability dimensions (economic, social, and environmental). To the best of our knowledge, such a literature review has not yet been comprehensively done. At the same time, the main contribution intends to appoint to a literature gap in the area of energy-efficient and sustainable construction project management as well as provide insights and possibilities for further research studies.

This review paper presents various optimization-based scheduling methods that ensure energy-efficient and sustainable construction scheduling. After a brief introduction, Section 2 sets the foundation for energy efficiency and sustainability in construction scheduling supported with optimization tools. In Section 3, an extensive literature review is performed and explained. Afterward, in Section 4, the literature review results and most important findings are stated and discussed in Section 5. Supported by the main review findings, conclusions and recommendations for further research are drawn in Section 6. A list of abbreviations used in the continuation of this paper is shown in

Table 1. Abbreviations.

ACS	Ant Colony System
API	Application Programming Interface
AP/OA/ER	Augmented Penalty/Outer-Approximation/Equality-Relaxation
BB	Branch-and-Bound
BIM	Building Information Modeling
CH	Constructive Heuristics
DEA	Data Envelopment Analysis
FBI	Forensic-Based Investigation
GA	Genetic Algorithm
GAMS	General Algebraic Modeling System
GRASP-HH	Greedy Randomized Adaptive Search Procedure Based Hyper-heuristics
HS	Harmony Search
IFC	International Foundation Classes
IPLSFM	Interior Point Line Search Filter Method
LP	Linear Programming
MACROS	Multiobjective Automated Construction Resource Optimization System
MASCA	Multi-Attributed Schedule Crashing Algorithm
MAWA	Modified Adaptive Weighting Approach
MILP	Mixed-Integer Linear Programming
MINLP	Mixed-Integer Nonlinear Programming
MOSP	Multi-Objective Scheduling Problem
NLP	Nonlinear Programming
NPV	Net Present Value
PGSL	Probabilistic Global Search Lausanne
PMT	Project Management Tool
PSO	Particle Swarm Optimization
RAP	Resource Allocation Problem
RCPSP	Resource-Constrained Project Scheduling Problem
RLP	Resource Leveling Problem
SA	Simulated Annealing
SDA	Sustainability Development Ability
TCTP	Time-Cost Tradeoff Problem
TS	Tabu Search
VBA	Visual Basic for Applications
WO	Whale Optimization

.

2. Background of Energy Efficiency and Sustainability Criteria in Optimization-Supported Construction Scheduling

Efficient energy use in high-demand markets, such as the construction industry, can make a global difference in reducing greenhouse gas emissions. One way to achieve energy efficiency is to reduce the amount of energy required to construct and operate buildings through innovative and efficient technology or production processes. The benefits of energy efficiency are manifold. First, new technologies and techniques can reduce project costs and make the construction phase more efficient. In addition, the use of energy-efficient building materials, equipment, and machinery can also reduce environmental impact. Therefore, the energy-efficient construction sector could improve air quality, reduce climate change impacts, and improve indoor conditions.

The appropriate optimization models were developed to ensure energy-efficient construction scheduling practice. The optimization tools can be used in early project phases, so a large amount of energy can be conserved by applying an efficient solving algorithm. Energy efficiency can also be seen as “not consumed energy” or even as the cheapest form of energy on a construction site. So, every optimization model with an objective to reduce energy consumption leads to energy-efficient construction scheduling practice.

Sustainability and energy efficiency are closely related, and their goals generally overlap. In a broader sense, sustainability is how companies manage economic, social, and environmental concerns that ensure that their business can continue operating regardless of obstacles such as resource scarcity, ecological disasters, and social and political events [5]. Another definition states that the needs of the present are met without compromising the ability of future generations to meet their own needs [6].

The economic, social, and environmental criteria are also called sustainability pillars or dimensions [7]. These dimensions are intertwined and affect each other, so project managers need to find a balanced and harmonized combination of all three dimensions. Therefore, sustainable construction scheduling is part of the sustainable management of change that uses innovative approaches, taking into account the construction project’s economic, social, and environmental impacts, the building to be delivered, and the resulting consequences for the present and future generations [8].

The economic segment of sustainability is sometimes the only dimension considered by stakeholders since the company’s economic growth strengthens the company’s position in the market. Sometimes this segment can conflict with environmental and social dimensions. Hence, it is vital to find a compromise solution. Optimization tools can minimize overall project costs within the assigned timeframe through innovative scheduling techniques. To assure these objectives, TCTP and RCPSP model formulations can be used. The TCTP aims to reduce overall project costs within the project deadline, while the RCPSP also considers the availability of specific resources through resource constraints. If there are restrictions on the availability of human resources, we can say that the model also contributes to the project’s social sustainability.

Social sustainability is probably the most challenging dimension to define since it deals with human (or societal) well-being and can be observed subjectively. A construction company needs to maintain a healthy organizational culture, positive labor practices, respect human rights, and take care of the safety and health of all project participants. By utilizing an adequate optimization model, project managers can assure satisfying allocation of the human workforce and reduce daily resource fluctuations. For this purpose, project managers can develop RAP and RLP optimization models. Solving these scheduling problems could, in early phases, ensure rational use of human resources, provide job stability, and reduce overtime work.

The goals for achieving environmental sustainability are to reduce transportation needs, reduce greenhouse gas emissions by reducing energy consumption, protect against air and water pollution, reduce waste, and recycle and reuse materials or resources [9]. The optimization methods can contribute to the fulfillment of these objectives in the early project scheduling stages by developing multicriteria tradeoff problems. In the multicriteria planning problem, project managers can specify the objective function for each project goal, i.e., duration, cost, construction quality, safety, environmental impact, and energy consumption, and obtain solution sets. By analyzing the output data, project managers can better understand the relationship between the different objectives and choose the best solution from all aspects.

The literature review was conducted in five steps: (i) formulation of research questions and objectives, (ii) search for relevant literature, (iii) screening of literature that was found and decision on inclusion, (iv) data extraction, description of particular approach with corresponding study findings, and (v) analysis and data synthesis. The objective was to find optimization-supported scheduling techniques that could improve the project’s energy efficiency and sustainability. Web of Science and Scopus online scientific databases were used to find suitable approaches. The keywords construction, project management, scheduling, optimization, sustainability, and energy efficiency were used. Afterward, the material was refined to include studies relevant to study design. The studies were thoroughly examined, and the methodology used for each study was described. Finally, the findings of included studies were reported in a meaningful way to address the extent to which this field was examined and the knowledge gaps.

In the aspect of TCTP and RCPSP models found in the literature, only research papers that integrate optimization tools with PMTs according to precisely defined criteria in the article [4] will be considered. There are multiple reasons for that. The integrated approach ensures not only that the initial construction schedule is economically sustainable but also provides sustainable scheduling practice in the long run. Since the construction projects are dynamic and often require weekly (or even daily) updates and reviews, integrating optimization techniques with PMTs can provide a novel scheduling practice. That practice facilitates updating schedules and re-applying optimization to achieve optimal schedules based on newly appeared circumstances.

This rule is difficult to apply from social, environmental, and energy efficiency standpoints because data on these criteria are rather challenging to quantify [10]. Furthermore, most commercial PMTs incorporate no such information for construction project management, but this issue will be discussed afterward in this paper. The advanced approaches dealing with energy efficiency and different sustainability dimensions in construction scheduling through optimization tools will be addressed in detail in the next chapter.

3. Literature Review

Table 2. Summary of accomplishments in energy-efficient and sustainable construction scheduling.

Reference	Energy Efficiency Criteria	Economic Criteria	Social Criteria	Environmental Criteria	Solving Method
Hegazy [11]		√			GA
Hegazy [12]			√		GA
Kandil and El-Rayes [13]		√			GA
Hebert and Deckro [14]		√			Simplex
Zhang and Ng [15]		√			ACS
Anagnostopoulos and Koulinas [16,17]		√	√		GA [16], GRASP-HH [17]
Anagnostopoulos and Koulinas [18,19,20]			√		SA [18], TA [19], TS [20]
Moselhi and Roofigari-Esfahan [21]		√			MASCA, HS
Tereso et al. [22]		√	√		CH, BB
Tiwari and Johari [23]		√	√		BB
Liu et al. [24]		√	√		Simulation, PSO
Kaiafa and Chassiakos [25]		√	√		GA
Barrientos et al. [26]		√	√	√	GA
Zheng et al. [27]		√		√	GA
Zheng [28]		√		√	GA
Yi et al. [29]		√		√	Simulation, GA
San Cristobal [30]		√	√		Simplex
Zaki et al. [31]		√	√	√	SA
Habibi et al. [32]		√	√	√	GA, PSO
Panwar and Jha [33]		√	√	√	GA
Kannimuthu et al. [34]		√	√		PGSL
Banihashemi and Khalilzadeh [35]		√	√	√	DEA
Rosłon et al. [36]	√	√	√	√	TS
Erdal and Kanit [37]			√		GA
Dasović and Klanšek [38]		√			AP/OA/ER
He et al. [39]	√	√	√		GA
He et al. [40]		√	√		GA
Xie et al. [41]		√	√		GA
ElMenshawy and Marzouk [42]		√			GA
Wang et al. [43]		√	√		GA
Nguyen et al. [44]		√	√		WO
Nguyen et al. [45]	√	√	√	√	FBI
Lotfi et al. [46]	√	√	√	√	IPLSFM

summarizes research studies that represent current accomplishments in the field of using optimization tools for energy-efficient and sustainable construction scheduling. For each study, it was ruled which sustainability criteria, along with energy efficiency, has been processed in the corresponding optimization model. Additionally, it was determined which algorithm was used for solving the optimization problem.

In his studies, Hegazy [11,12] programmed GA as a VBA macro program to solve different scheduling problems within commercial PMT, an early version of MS Project. The said studies were devoted to solving TCTP [11] and simultaneous RAP and RLP [12], the tasks that typically occur on a construction site for which optimization techniques can be beneficial. Since the optimization tool was implemented within the PMT, this approach showed a high level of automation in obtaining an optimal construction schedule. The scheduling process was facilitated while considering the economic and social aspects of the construction project. The author notes that the downside of using GA is its random nature, so there is no guarantee that the results are exactly optimal. Moreover, a more efficient programming language than VBA, such as C++, was proposed. The applicability of this approach was shown on small-scale construction projects, so it is not completely clear whether or not this approach would be helpful on projects with a higher number of activities and the number of tasks up to which this approach can be employed.

Kandil and El-Rayes [13] demonstrated their own multi-objective automated construction resource optimization system named MACROS. It was created in C++ programming language, connected to MS Project and MS Access, and used obtained data to formulate and solve MOSP. In their case, the build quality was also included as one of the objectives for the optimization model. The same limitations apply to GA used in their application. The abilities of their system were shown on the practical example of a highway construction project consisting of 180 activities. The MACROS requires weighting factors for each project objective, i.e., time, cost, and quality. In a way, more freedom was given to the project manager to decide which of these objectives was more important. On the other hand, this process can be tedious since various combinations of weighting factors should be tried before deciding the schedule to be implemented on-site.

One of the early attempts to combine mathematical programming and PMT was presented in a study by Hebert and Deckro [14]. They developed an LP model for solving TCTP in MS Excel, using the simplex algorithm within Excel Solved add-in. The model had an objective to reduce the overall project duration for a certain number of days by incurring minimal additional cost. The functionalities of their system were demonstrated on a small-scale project. The optimal schedule was then exported to MS Project for further analysis. Complex spreadsheet-based optimization models tend to complicate the data manipulation process and result in scalability issues. In other words, a minor change in project details, e.g., change of activity duration, activity precedence relations, or introducing additional project activities, would lead to excessive model modifications. That would be highly impractical on the construction site since the schedules are often updated each week or even daily.

Zhang and Ng [15] presented their MAWA system. Their program aimed to solve TCTP by applying the ACS algorithm. The system minimizes cost and project duration simultaneously, and it was developed using VBA programming language within MS Project. Afterward, the optimized output data could be exported to MS Excel for further inspection. The authors note that their approach facilitates the construction scheduling process with user-friendly and efficient MAWA as well as encourages project managers to use their MAWA system to rationalize economic expenditures on the construction site.

The series of papers by Anagnostopoulos and Koulinas [17] demonstrated how to solve different scheduling problems, e.g., RAP and RLP [18,19,20], and RCPSP [16,17], through the utilization of varying heuristic methods such as SA, GA, ACS, TS, and GRASP-HH. All the models and algorithms were programmed within the MS Project VBA programming language. These studies aimed to reduce overall project costs and more efficient use of human resources, thus achieving economic and social sustainability in construction scheduling. The authors suggest further improvements of their studies to use more efficient and sophisticated hyper-heuristic techniques.

Moselhi and Roofigari-Esfahan [21] connected MATLAB and MS Project for solving TCTP. This was one of the early contributions to integrating specialized optimization software with PMTs. Their MASCA and an HS method were used to solve the scheduling problem. The MASCA has an option to open the MS Project file and transfer data to a spreadsheet, which is afterward used in MATLAB to calculate cost slopes of critical activities. The authors point out that their approach is mainly helpful for linear projects with repetitive construction activities.

Tereso et al. [22] used BB and CH algorithms to solve RCPSP. The authors developed an add-in function for MS Project in C Sharp (C#) language, and the end-user can choose which of the algorithms will be applied. The system was demonstrated on a small-scale construction project, so the study did not record any variations in results obtained by heuristics and mathematical programming methods. The only difference noted was that the BB method solved the optimization problem within a single run, while the heuristics required sensitivity analysis of algorithm search parameters.

A MILP model was demonstrated to solve both TCTP and RCPSP simultaneously in a study by Tiwari and Johari [23]. Like Hebert and Deckro’s [14], their approach used optimization tools from MS Excel. First, a regular TCTP was solved using Simplex LP from the Excel Solver tool. As stated on the Excel Solver developer’s site [47], the Simplex LP commercial algorithm, usually used for LP models, can also engage the BB technique to solve MILP problems. Afterward, MS Project was used to perform an analysis of resource utilization. This step aims to verify if an optimal schedule can be achieved with available human resources and, therefore, assure social and economic sustainability of the schedule.

With the emerging rise of BIM technologies, Liu et al. [24] introduced their system that can utilize data obtained from BIM design for scheduling purposes. The system has three components, i.e., (i) MS Access database regarding project resources; (ii) 3D model of a building designed in Autodesk Revit; (iii) MS Project schedule. The authors integrated all the components through the Autodesk Revit API function. Their system can simulate the construction process, reduce possible human errors, and keep the construction site safe for all participants. A PSO model assured the optimality of the generated construction schedule. As possible upgrades for their system, the authors suggest improvements in normative for resource usage, introducing site and weather conditions in an equation, and advancements in system automation.

Kaiafa and Chassiakos [25] developed multi-objective RCPSP in MS Excel and used GA procedure programmed as a VBA macro program to solve construction scheduling problems. Besides minimizing project duration and overall costs, the model also considers resource over allocation and daily resource fluctuations. It was found that the algorithm’s efficiency decreases with the number of project activities but that even the slightest schedule improvements can lead to a notable return, i.e., cost reductions and better technique of human resource allocation. Therefore, the project schedule can be improved from economic and social perspectives.

An in-depth analysis of railroad infrastructure construction projects was presented in a paper by Barrientos et al. [26]. The goal was to facilitate the decision-making process during railways construction projects with special attention to environmental impacts, such as carbon and water footprint, as well as economic and social indicators. Some of the social indicators for the project were working conditions, health and safety on the construction site, human rights, governance, community infrastructure, and the possibility of job creation. All the data for each project activity were plugged into MIVES (engl. Value Integrated Model for Sustainable Evaluations). Afterward, GA was used to optimize the schedule based on all three sustainability criteria. The algorithm produced different execution alternatives that can be analyzed after that. The system was developed as a web application in R and Python programming languages for the backend. The frontend was programmed in JavaScript. The limitations of this approach are excessive manual labor entering environmental and social impacts for each activity that are difficult to measure anyhow. The author proposes standardization of these measures.

In their study, Zheng et al. [27] presented their MOSP that takes into account the impact of construction on the environment. The model was based on hybrid GA under a fuzzy environment. The aim was to minimize project time, cost of penalties, and reduction of construction impact on the environment for multiple projects at once. The model was tested on a hydropower station construction project in China and demonstrated its benefits in an economic and environmental sense. In the continuation of his work, Zheng [28] added build quality as another objective for scheduling problems. The author suggests further research on models including even more dimensions and improvement of heuristic algorithm’s efficiency for NP-hard problems.

Yi et al. [29] presented another approach for solving MOSP with particular attention to project completion time, cost, build quality, and environmental impact for technical tender evaluation. Their system can import schedule network data from different PMTs, such as MS Project and Primavera P6, and then perform an enumerative analysis to find the optimal schedule based on weights set on each project objective. Afterward, GA is used to find a set of sub-optimal solutions that do not exceed constraints imposed for each activity. The third step was to run the simulation to compute the project performance indicators′ variability and select the most probable case scenario. Their system can make selecting more favorable bidders easier and set the basis for negotiating better contractual obligations.

San Cristobal’s paper [30] presented an optimization model that calculates the best construction schedule based on construction project duration, overall project costs, quality of construction elements, and work safety. The author notes that safety has become one of the critical elements contributing to overall project success, so an integer LP formulation for time-cost-quality-safety tradeoff analysis was developed. The model capabilities were demonstrated on a road construction project in Spain. His approach can use alternative solutions if some activities have not been completed as planned initially. The author notes how complex this analysis can be as some project objectives can conflict, so quality or safety criteria can result in longer project duration and higher costs. Furthermore, future research should explore what would be the best practice for measuring and quantifying abstract terms, i.e., quality and safety.

The paper presented by Zaki et al. [31] demonstrates a model for reaching sustainable development on construction projects throughout different life cycle phases. They used a simulation-based optimization model and SA for scheduling the stages of many projects maintaining the correct order of building phases. Their concept is based on SDA introduced by Zhang et al. [48]. The SDA model calculates the feasibility of a construction project while managing the project sustainability criteria. Although it is interesting to see how sustainability criteria values are behaving throughout the construction life cycle, it is unclear how these measures are quantified or calculated.

Habibi et al. [32] present their optimization model for simultaneous scheduling and material ordering problem while considering sustainability. Their framework consists of two phases: (i) collecting environmental and social data for the project; and (ii) mathematical model formulation for solving scheduling and ordering problems based on acquired data while also maximizing project NPV. Modified GA and PSO algorithms were utilized to solve the problem, and the results were compared to those obtained by an exact mathematical method called the augmented ε-constraint method. For more extensive problems, the exact method could not provide results in a reasonable time due to model complexity. For future research, the authors suggest the use of new meta-heuristic techniques and analysis of results compared to previously used algorithms.

Panwar and Jha [33] developed a MOSP emphasizing environmental impact and human resources′ well-being. A multi-objective scheduling model was developed in MATLAB based on non-dominated sorting GA to optimize all project objectives simultaneously. The environmental impact was calculated as the amount of greenhouse gas emissions (in kg CO₂ equivalent) for different modes of execution for each activity. Additionally, the model minimizes resource fluctuations since large fluctuations lead to periods of high resource utilization and, consequently, higher costs and poor safety on construction sites. The authors note that their approach allows project managers better representation of construction projects and facilitates more sustainable decision-making techniques from a social, economic, and environmental viewpoint. Adding additional resource types in the model and other project objectives were proposed, i.e., quality, safety, and cash flow. Moreover, further research on the interrelation of various objectives was suggested to better understand the implications of incorporating one goal over another.

Another approach of optimizing time, cost, and quality through the use of a multimode RCPSP model was presented by Kannimuthu et al. [34]. The proposed framework has four stages: (i) integer-programming model for optimizing multiple objectives; (ii) building quality assessment and evaluation of performance scores for each project activity; (iii) collecting data for different activity execution modes; (iv) solving the optimization problem. The last stage set of near-optimal solutions (Pareto front) is generated by applying the PGSL algorithm, and, after that, the project manager finds a compromise solution. The authors mention that the algorithm is more efficient than GA or SA when the number of variables increases. The significant contribution of this paper lies in a thorough and concise method of quantifying quality by each activity.

Banihashemi and Khalilzadeh [35] demonstrated their DEA approach for solving the time-cost-quality-environmental impact tradeoff problem. The DEA method examined different activity execution modes and chose the best based on mentioned project objectives. The functionalities were demonstrated on a project of water supply construction project and gave promising results. The most-efficient execution mode indeed leads to the highest construction quality with minimal cost and environmental footprint and, therefore, to more sustainable scheduling practice. The authors emphasize challenges in collecting data and estimations for four project factors in different modes of activity execution.

In their study, Rosłon et al. [36] presented their multimode RCPSP model and in-depth analysis from an investor’s point of view. The model allows maximization of NPV of the building while also considering building safety, comfort, health and hygiene, durability, and sustainability. Their approach to optimizing the construction schedule was completely different from those previously described. In this approach, the authors tried to select the best construction schedule that also considers sustainability over the building’s whole life cycle. The TS algorithm included in OptQuest Engine was used to solve the optimization problem, and the results were presented in MS Project. This approach can be beneficial for “design and build” projects or for consulting companies managing investments to maximize project value and minimize expenses during the building operation phase.

Erdal and Kanit [37] developed software for optimal resource allocation and critical path identification as well as minimization of overall project duration under resource-constrained conditions. To solve the optimization problem, GA was used. The software has two main parts: (i) project input data (i.e., activities, precedence relations, resource types, resource quantities by activity); (ii) optimization tool and post-optimization analysis visual reports. The authors claim that the critical path method is somewhat different if the resources are limited and that, in their case, represents the most extended project duration under constrained resources. It remains open why costs were not considered a resource type since money is one of the essential resources in most cases.

Dasović and Klanšek [38] presented their system that integrates state-of-the-art algorithms from the GAMS and PMT for sustainable and cost-efficient construction scheduling. The TCTP model was developed in the high-level modeling system GAMS, which was also used to export results to spreadsheets. They created a data transformation tool within the spreadsheet to automatically present the results within commercial PMT. This way, a dynamical system was constructed that allows schedule re-optimization upon project changes (e.g., delays, activity prolongation, additional tasks). Further development should aim toward a two-way connection between software for an even better user experience.

The RAP approach with multiple project objectives was presented in He et al. [39]. The GA algorithm was used to obtain the best tradeoff between project duration, cost, and energy consumption and afterward, present the optimal scheme of resource arrangement. The optimization was performed in MATLAB. The method was demonstrated on an industrial plant office building in China. The obtained optimal schedule was then used to simulate the construction process in the BIM tool to review the solution and avoid possible errors.

Two similar approaches for scheduling optimization of prefabricated construction projects were presented by He et al. [40] and Xie et al. [41]. In both studies, GA was used for solving optimization problems. The TCTP model in [40] was used to develop an optimal schedule for producing prefabricated buildings, including the production process, logistics, and transportation and assembling the structure on construction sites with limited resources for each of these processes. The RCPSP formulation presented in [41] was proven effective in experimental analysis on examples of automatically generated projects with various project sizes. The model was developed in MATLAB to help project managers develop prefabricated construction schedules with minimal project duration and reasonable resource usage.

ElMenshawy and Marzouk [42] presented their automated BIM schedule generation approach for TCTP. The authors have developed a VBA macro for MS Excel to read quantities from the BIM model developed in Revit and accordingly create project activities. To solve the optimization problem, the authors used an add-in tool in MS Excel called SolveXL. The results were afterward modified so the results could be imported to Primavera PMT. The method was applied to the construction of a residential building in Egypt consisting of 47 activities. The authors note that the results were sensitive to the algorithm parameters. It was suggested that future research include other PMTs such as MS Project or cost management software to facilitate the generation of input parameters from BIM tools.

A time-cost-quality tradeoff model was presented by Wang et al. [43]. Their optimization model adopts a quantitative research method and contains two steps: (i) identifying objective function and model decision variables and (ii) identifying model input data and execution of Non-Dominated Sorting GA. The model was developed in Python and tested on a construction project with 20 activities. The presented model facilitates identifying the highest quality solution within a specified duration and budget. The authors suggest a further model extension to incorporate objectives such as sustainability and safety.

Nguyen et al. present their innovative approach for a tradeoff between time, cost, and quality [44], and, furthermore, safety and environmental impact (reducing diesel and electricity consumption) [45]. The system [45] starts with a 3D model of construction and environment in Autodesk Revit. The data from the BIM model are connected through visual programming in Dynamo to a spreadsheet database afterward used for multiobjective optimization in MATLAB. Results can also be visualized for finding the best solution for a construction project. The FBI population-based heuristic algorithm [49] inspired by the police investigation process was used to solve the optimization problem. The study [44] used algorithm WO based on the behavior of humpback whales. The authors suggest user-friendly software integrating various software platforms used in this study for further development.

A robust approach with five different objective dimensions was proposed by Lotfi et al. [46]. Model functionalities were demonstrated on an example of building underpass bridge construction in Iran. The model aims to cover sustainable development goals such as more efficient energy consumption, environmental pollution reduction, and assuring quality, along with the usual goals of minimizing project duration and costs. The NLP model was developed in GAMS and solved with an open-source BONMIN solver. Although the BONMIN solver is generally used for solving MINLP problems, it contains algorithms that can be applied to NLP problems (Ipopt and FilterSQP). The paper gives excellent insights on the in-between correlation of different project objectives. Furthermore, a novel approach that uses the augmented ε-constraint method for solving multi-objective problems was explained. As the authors claim, this method records different Pareto front solutions and optimizes each objective individually while presenting other goals as constraints.

4. Findings

The findings and results of the previously described studies are presented to better represent the potential savings in construction projects. Each study uses a case study of some sort to demonstrate the effectiveness of its optimization-based scheduling technique. The results are presented in three different categories. First, the results of TCTP models are presented, and separately, the results of resource-oriented optimization models such as RLP, RAP, and RCPSP are presented. Afterward, the results of MOSP models are described.

The results of the TCTP examples are presented in

Table 3. Results of reviewed TCTP models.

Ref.	Case Example	No. of Activities	Optimization Results
[11]	Literature example	18	Duration reduced 35%, cost reduction 4%
[14]	Textbook example	15	Duration reduced 14%, increase of 175 cost units
[15]	Literature example	18	Duration reduced 9%, cost reduction 15%
[21]	Literature example	7	Duration reduced 36%, cost reduction 13%
[23]	Literature example	5	Duration reduced by 17%, increase of 250 cost units
[38]	Literature example	29	Duration reduced 20%, cost reduction 6%
[42]	Residential building project	47	Duration reduced 14%, cost reduction 2%

. The type of case study used to support the study results and the number of project activities were indicated for each reference. In addition, the results achieved with the optimization model are provided to show potential savings in terms of project duration and total project cost.

It can be noted that the case study projects all involved under 50 activities and had a considerable duration and cost reductions. The studies [14,23] were formulated somewhat differently, and their approaches increased overall project costs. Their models required a reduction of project duration by a certain number of days and then minimized additional costs. So additional costs are inevitable for their method. Surprisingly, only a minority of TCTP model formulations from Table 3 used all generalized precedence relationships. Most studies used only Finish-to-Start (FS) relationship without lead/lag time. Studies [14,38,42] used all other generalized precedence relations along with the possibility of lead/lag times. The table shows that TCTP models can theoretically reduce project duration by up to 36% and total project cost by up to 15% for literature examples.

The results of the resource-oriented optimization models examined in this study are summarized in

Table 4. Results of reviewed resource-oriented optimization models.

Ref.	Case Example	No. of Activities	Optimization Results
[12]	Literature example	20	10% duration and 20% resource moment reduction
[16]	Experimental analysis on automatically generated networks	30	Up to 11% reduced project duration
		40	Up to 10% reduced project duration
		50	Up to 8% reduced project duration
		60	Up to 7% reduced project duration
[17]	Literature examples and automatically generated network	15	24% reduced project duration
		17	14% reduced project duration
		20	12% reduced project duration
		15–65	From 4–9% reduced project duration
[20]	Literature example	10	Same duration, daily resource use reduced from 17 to 10
[24]	Generated from BIM model	20	15% reduced project duration
[25]	Literature example	10	Duration prolonged 22%, daily resource usage reduced from 14 to 8 with lower day-to-day resource fluctuations
[36]	Residential building project	26	Building NPV increased by 16%

. The optimization models formulated as RLP and RAP, such as [12,20], show a significant reduction in daily resource consumption and also reduced day-to-day fluctuations. Anagnostopoulos and Koulinas [16,17] investigated different heuristic methods in their RCPSP models, namely GA and GRASP-HH. They performed an experimental analysis on automatically generated projects with a different number of activities, resource availabilities, and diverse complexities of the project network. Better performance of the algorithm was found on projects with fewer activities, higher resource availability, and lower project network complexity.

The MOSP model formulations described in the previous chapter are somewhat more difficult to analyze as there are different combinations of objective functions, i.e., project duration, cost, quality, environmental impact, safety, and energy consumption. Therefore, it is quite challenging to compare these approaches since these objectives affect each other, and introducing new dimensions into the model formulation could impair other objectives. That is evident in [33] where, in one case, the objectives of time, cost, environment, and resource moment were considered and then compared with the results where the objective of resource moment was excluded. By considering this objective, the project duration increased from 85 to 97 days, but on the other hand, the costs and environmental impacts were lower.

The study [13] shows that the highest priority given to project execution quality leads to a 60% higher total cost than the minimal project cost. On the other hand, the minimum price leads to a 33% longer project duration than the shortest possible duration. Zheng et al. [27] used a practical example of a hydropower station project to show that their method can shorten the project duration by 9%, reduce the penalty cost by 167%, and reduce the environmental impact by 200%. The approach presented by Kannimuthu et al. [34] was demonstrated on a residential construction project in India. It is shown that reducing the project duration by 13 days can result in a 1.61% lower project cost and 3.31% improvement in construction quality. The tradeoff between time, cost, quality, and environmental impact presented in [35] resulted in a 26% improvement in project duration, 20% improvement in overall project costs, 5% improvement in quality, and 16% improvement in environmental impact. The model for a time-cost-quality tradeoff [43] found the shortest project duration of 84 days with an 85% quality rating. With a 4.5% increase in project cost, the quality was improved to 94%.

In summary, the results in this chapter indicate that there are great opportunities for the use of optimization tools in construction scheduling. Based on the project goals and defined objectives, one of the methods studied could be used to achieve an energy-efficient and sustainable project schedule.

5. Discussion

This paper presented achievements on energy efficiency and sustainable construction scheduling practices supported by optimization tools. All examined studies can be mainly deployed in four categories: (i) macro application programmed within PMT; (ii) spreadsheet-based models for project scheduling problems; (iii) new scheduling software; and (iv) use of algebraic modeling optimization systems. Each of these approaches has its advantages and limitations.

As presented in studies [11,12,15,16,17,18,19,20,22], the algorithms programmed within PMT can be compelling as they offer a high level of automation. Results can be reviewed in a matter of seconds as the optimization is performed within PMT. The limitation is that they are often developed to solve particular scheduling problems that only use data stored within PMT. Thus, this approach can perhaps be suitable for achieving economic or social sustainability through TCTP, RAP, and RLP formulations. Everything beyond that would require extensive programming leaving an open question on how to include external data on, for example, environmental impacts or quality.

Scheduling problems can also be modeled within spreadsheets that offer optimization tools. Because of the widespread spreadsheet usage on construction sites and familiar environments, it can also be convenient to develop an optimization model for solving small-scale construction scheduling problems, as demonstrated in studies [14,23,25]. Spreadsheets usually have limitations on the number of variables and constraints that may not be sufficient for complex scheduling problems. Additionally, there is a problem of entering or displaying data with more than two dimensions often used for multi-objective trade-off problems. So, this would make any kind of multidimensional tradeoff analysis more difficult. In addition to that, spreadsheet-based models can lead to issues with scalability.

Robust and well-developed scheduling software (e.g., [13,45]) with optimization capabilities can undoubtedly help project managers in their intention to incorporate energy-efficient and sustainable scheduling practices. In many cases, this newly developed software can read and store data in different data formats or even PMTs, so the whole data flow is fully automated. The development of this kind of software requires a high level of programming skills. Since most software is often developed to solve specific scheduling problems, including anything outside the original scope can be challenging and require initial program code changes. Furthermore, most studies that used this approach included only one solving algorithm.

Algebraic modeling languages provide the most flexibility for project managers, as demonstrated in studies [21,33,38,46]. Specialized optimization tools provide numerous state-of-the-art commercial and open-source algorithms. They can use data stored in various file formats and solve different scheduling problems. It is no surprise that most authors dealing with multi-objective tradeoff problems have opted for this approach. Although the original model formulation requires advanced programming knowledge, the model can be easily used on different projects by changing input data. Further improvements could be made in the form of an additional user-friendly system that would not require programming skills from end-users. Therefore, this approach could be available to a wide range of project management and facilitate the process of obtaining an energy-efficient and sustainable construction project schedule.

Altogether, what particularly stands out is that most authors used heuristic search methods for solving their scheduling problems, especially GA. Heuristic methods can solve a large share of scheduling problems within a reasonable time. The problem with heuristic methods is that they can, in some cases, obtain only a near-optimal solution due to the random nature of the algorithm. Mathematical programming could be used to ensure that the solution is optimal. On the other hand, exact mathematical methods can be time-consuming and use a lot of processing power. In many cases, a basic personal computer can solve various scheduling problems. There are also open-access supercomputers available for solving more complex scheduling problems. Further studies should investigate mathematical programming techniques for solving complex (non) linear continuous and/or discrete formulations of different scheduling problems.

It is no surprise that almost all studies, to some extent, considered the economic sustainability dimension since every construction company tends to reduce overall project costs and maximize profits. That does not necessarily mean that other sustainability dimensions were not considered, but commonly they were not directly included in the optimization model. Even so, to reduce their spending, construction companies often must introduce new technologies or more energy-efficient mechanization and even mitigate environmental impact. Another idea for upgrading optimization models for cost-optimal schedules is to address the ecological effects in the objective function and set a model to minimize greenhouse gas emissions per unit of construction costs.

Some studies that have developed innovative multi-objective tradeoff analyses [36,45,46] certainly brought most of the energy efficiency and sustainability criteria in their optimization models. It is interesting to see all these objectives in one model and how they affect each other. The multi-objective models allow project managers to set weights on different project objectives and incorporate energy efficiency and sustainability indicators in their scheduling practice. There are only a few issues with this approach. Namely, calculating environmental impact, social equity, and quality indicators for different task execution modes can be challenging as there are still no standards that could be used. A good starting point for establishing a framework for a standardized method for calculating greenhouse gas emissions on construction sites is provided in a report by Obernosterer et al. [50]. This framework could enable project managers to take the necessary steps to reduce emissions and, thus, strive for a CO₂-neutral construction site.

These results are important first steps toward energy-efficient and sustainable scheduling techniques. This work can be valuable in construction project management as it provides a good basis for further research in this field. This work has again shown that heuristic methods are predominantly used in solving complex scheduling problems. On the other hand, mathematical programming is still quite unexplored, especially methods that use algebraic modeling languages. Future studies should focus on developing a user-friendly application for construction scheduling. The application should be publicly available and easy to use to facilitate use on the construction site. More research should focus on the ability to ensure continuous project optimality. In other words, if the changes occur during project execution, it should be beneficial to update project input parameters and re-optimize the construction schedule.

6. Conclusions

This paper has provided an overview of current optimization-supported construction scheduling practices that deal especially with the problems of energy efficiency and sustainability. The literature review results confirm that optimization tools can be used to improve energy efficiency during the construction phase. Additionally, appropriate optimization problem formulations can ensure that the project supports the company’s economic development, protects the environment, and provides social equity. The findings of this review add to our understanding of energy efficiency and different sustainability dimensions, along with their in-between correlation on construction projects. It is essential to address all these issues in the early stages of projects and incorporate them into the scheduling strategy.

These results provide a step towards automated optimization-based construction scheduling systems to enhance modern-day project management. All construction companies should aspire to energy efficiency and sustainable project management because the advantages are manifold. Incorporating these tools in everyday project management would reduce overall project costs and give construction companies a strategic edge over the competition. Furthermore, energy-efficient construction projects would reduce energy demand and therefore, minimize construction costs and environmental impacts. Social sustainability can improve project participants′ general safety and health, avoid occupational overburn of the human workforce, and lead to a better business climate.

The optimization-based construction scheduling techniques were reviewed in this paper and have been proven effective. Optimization tools can objectively verify all possible solutions for scheduling problems, find the best balance of energy efficiency and sustainability criteria, and implement a solution that best suits the strategic plans of the construction company. These approaches can be utilized on most construction projects, and it is time for project managers to incorporate these criteria in their scheduling practices and, therefore, take a step towards an energy-efficient and sustainable future.