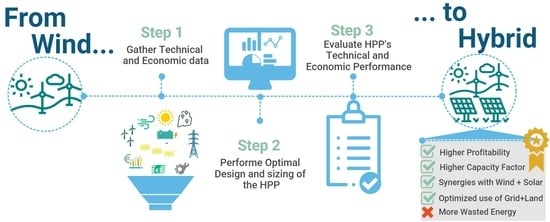
From Wind to Hybrid: A Contribution to the Optimal Design of Utility-Scale Hybrid Power Plants
Abstract
:1. Introduction
- A methodology to characterize the energy contribution and economic viability of hybrid power plants in utility-scale applications, providing insights both to plant owners/developers and grid operators.
- A decision-aid tool for renewable power plant developers to use in assessing the optimal hybrid plant configuration that maximizes the project’s financial performance, given the local resources and area availability, costs, and market prices.
2. Overview of Hybrid Renewable Power Plants
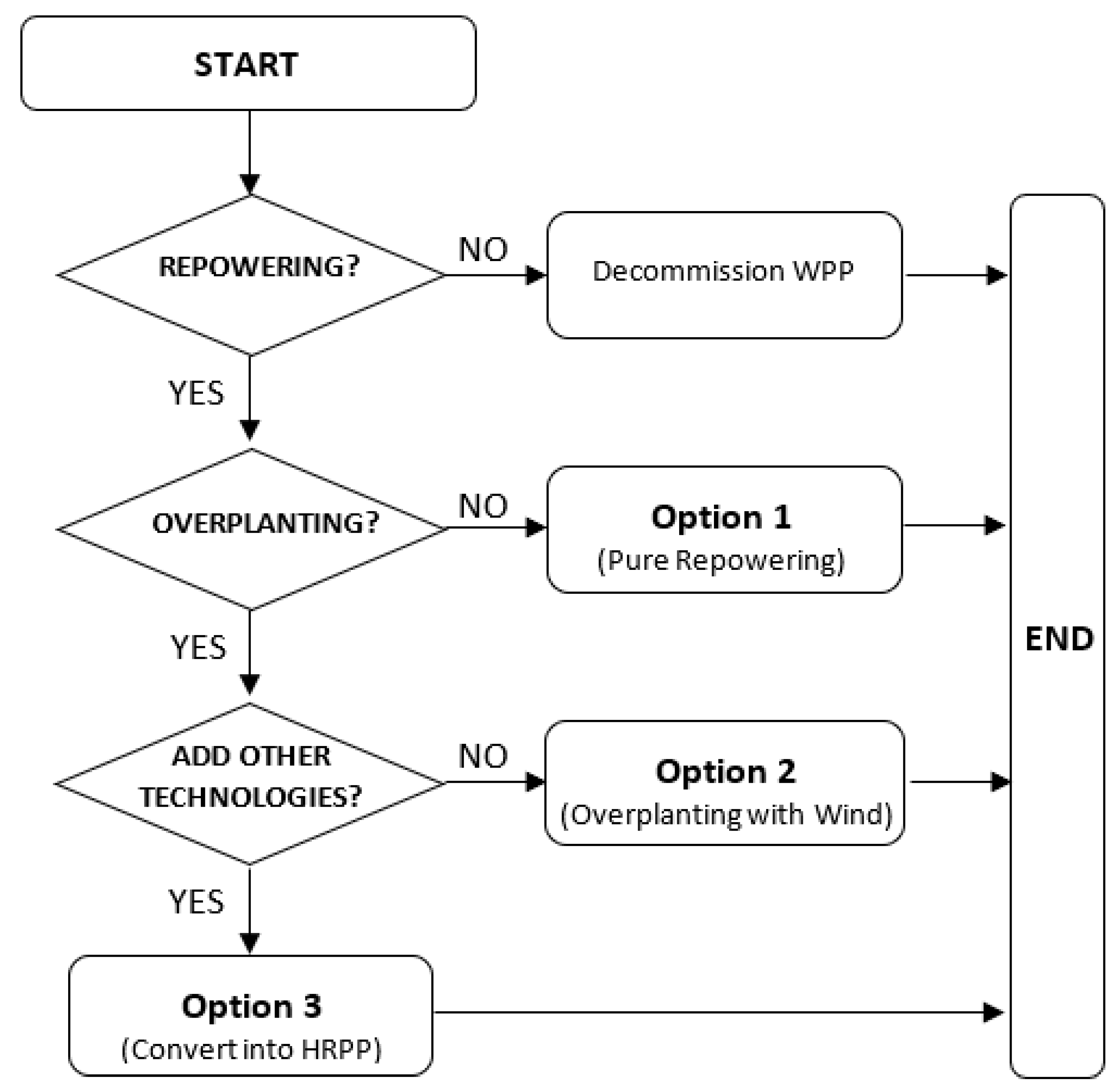
- Comparing the obtained results with the industry’s standard practices. These typically include repowering or overplanting with single technologies. The premise is that by comparing with standard industry practices, the proposed methodology and the results obtained could highlight the added value of HRPPs and better inform stakeholders and decision-makers in the energy sector.
- Applying it to different case studies, with different complementarity profiles of renewable production and DA market prices at different timescales. The premise is that, by considering different case studies, the results obtained could provide more insights into the debate on the technical and economic feasibility of hybrid power plants.
- Considering the capacity addition of wind, solar PV, and battery technologies when performing an HRPP sizing optimization for day-ahead market (DAM) participation, rather than focusing mainly on the design of the storage system [26,27,28]. The hypothesis here is that considering all technologies in the optimization exercise allows the model to have a more comprehensive view of the problem, thus obtaining holistically optimized decisions. Failing to do so may lead to solutions that are not as efficient when considering technical and economic perspectives.
3. Methodology
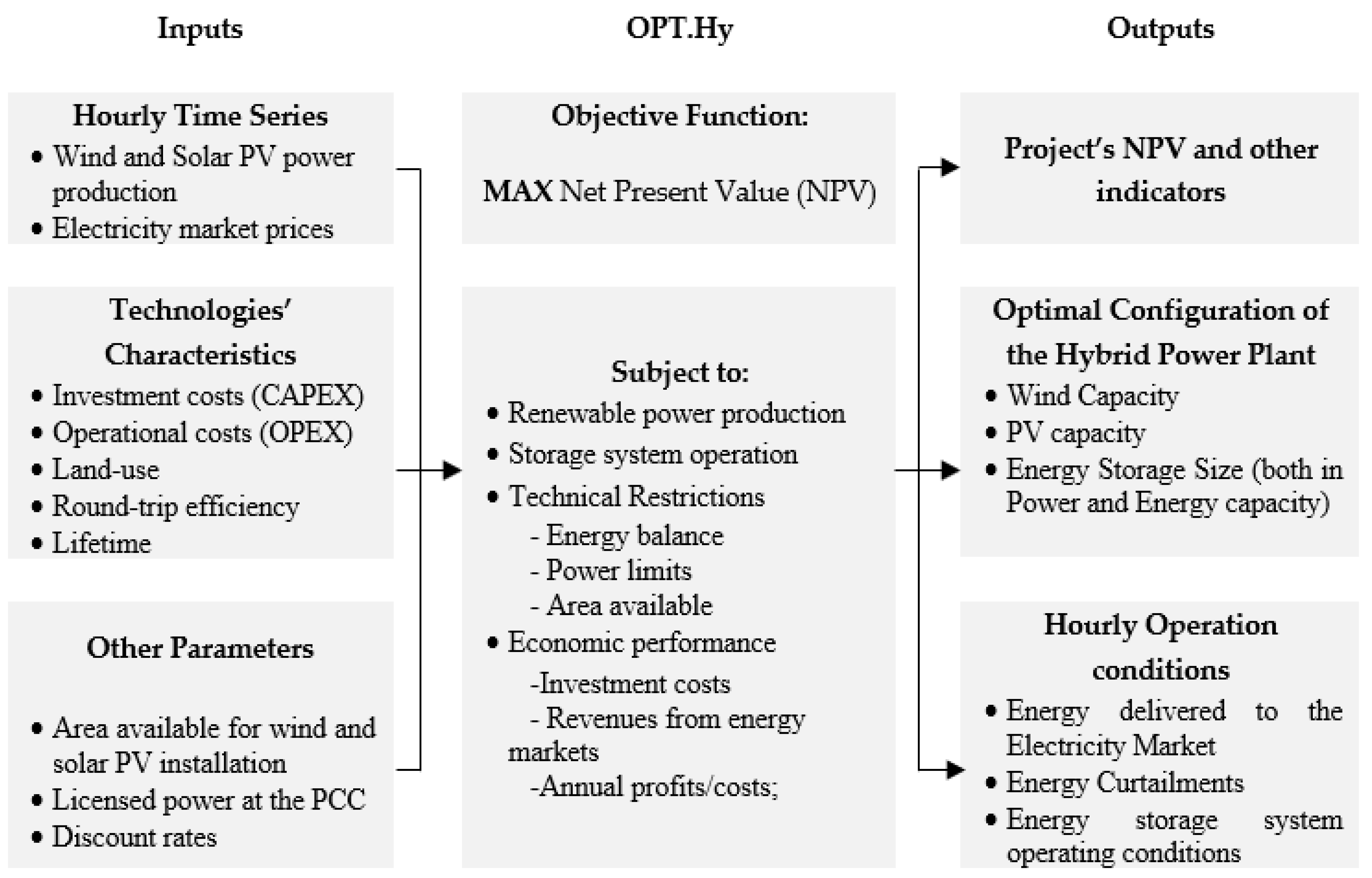
3.1. Problem Formulation
3.2. Optimal Design and Sizing of Hybrid Power Plants (OPT.Hy)
3.2.1. Variable Renewable Generation
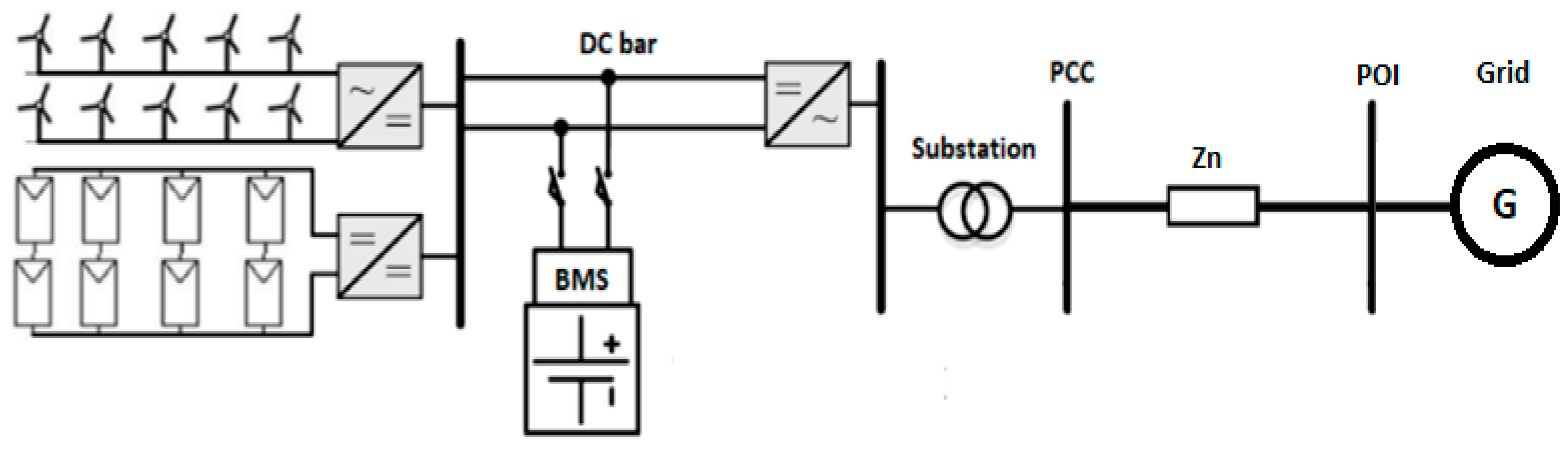
3.2.2. Energy Storage System
3.2.3. Technical Restrictions
3.2.4. Economic Performance
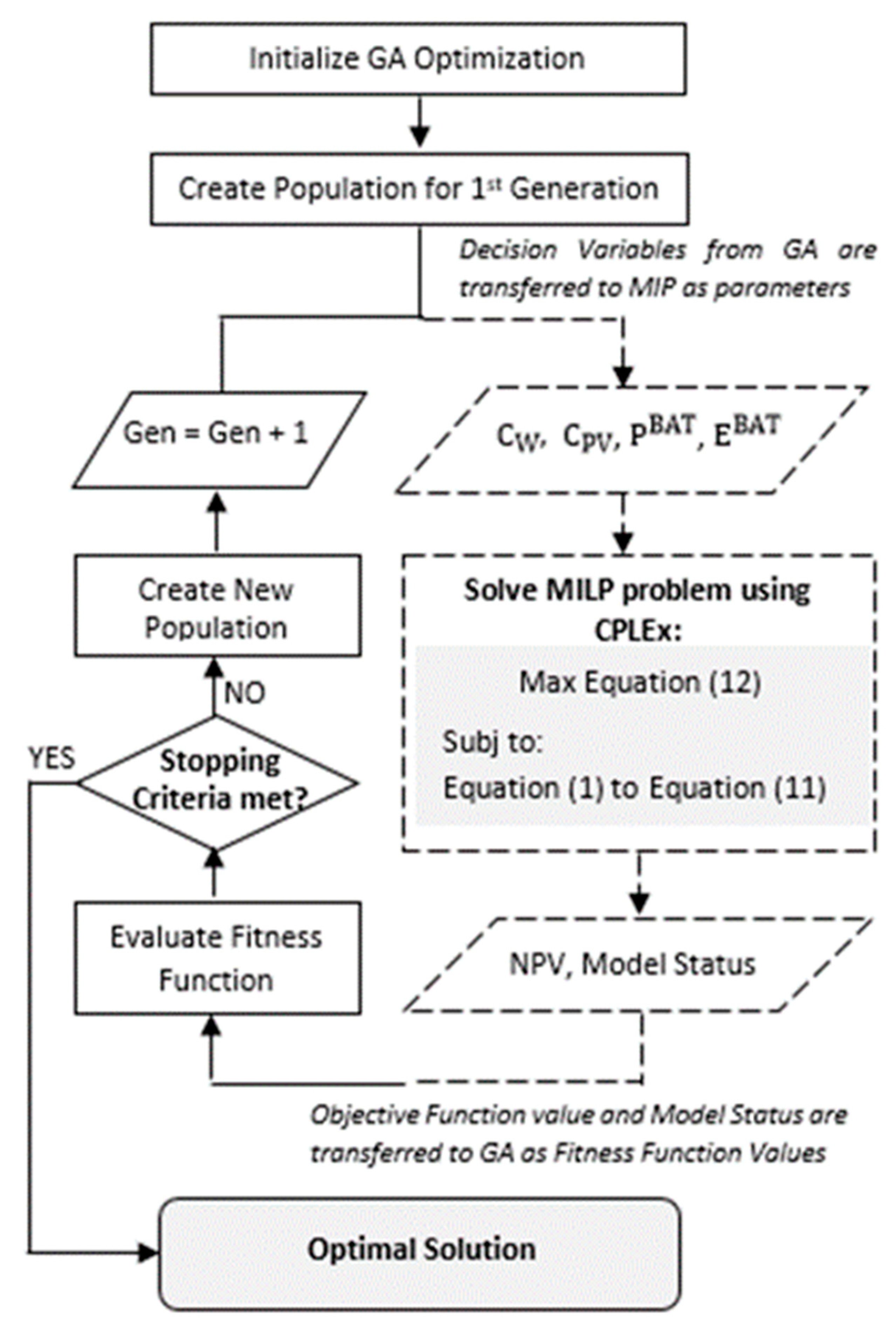
3.3. Optimization Formulation and Solving Method
| STEP 1 | A 1st candidate solution is arbitrarily created by the GA algorithm; |
| STEP 2 | The candidate solution is transferred as input parameters to the MILP model; |
| STEP 3 | The MILP model is solved using the CPLEX; |
| STEP 4 | The feasibility of the solution and its respective objective function value is transferred as the fitness function value for the GA algorithm; A very large penalty is added to the fitness function if the candidate solution is infeasible; |
| STEP 5 | Repeat STEPs 2 to 4 until stopping criteria is met. |
3.4. Application of the OPT.Hy Methodology
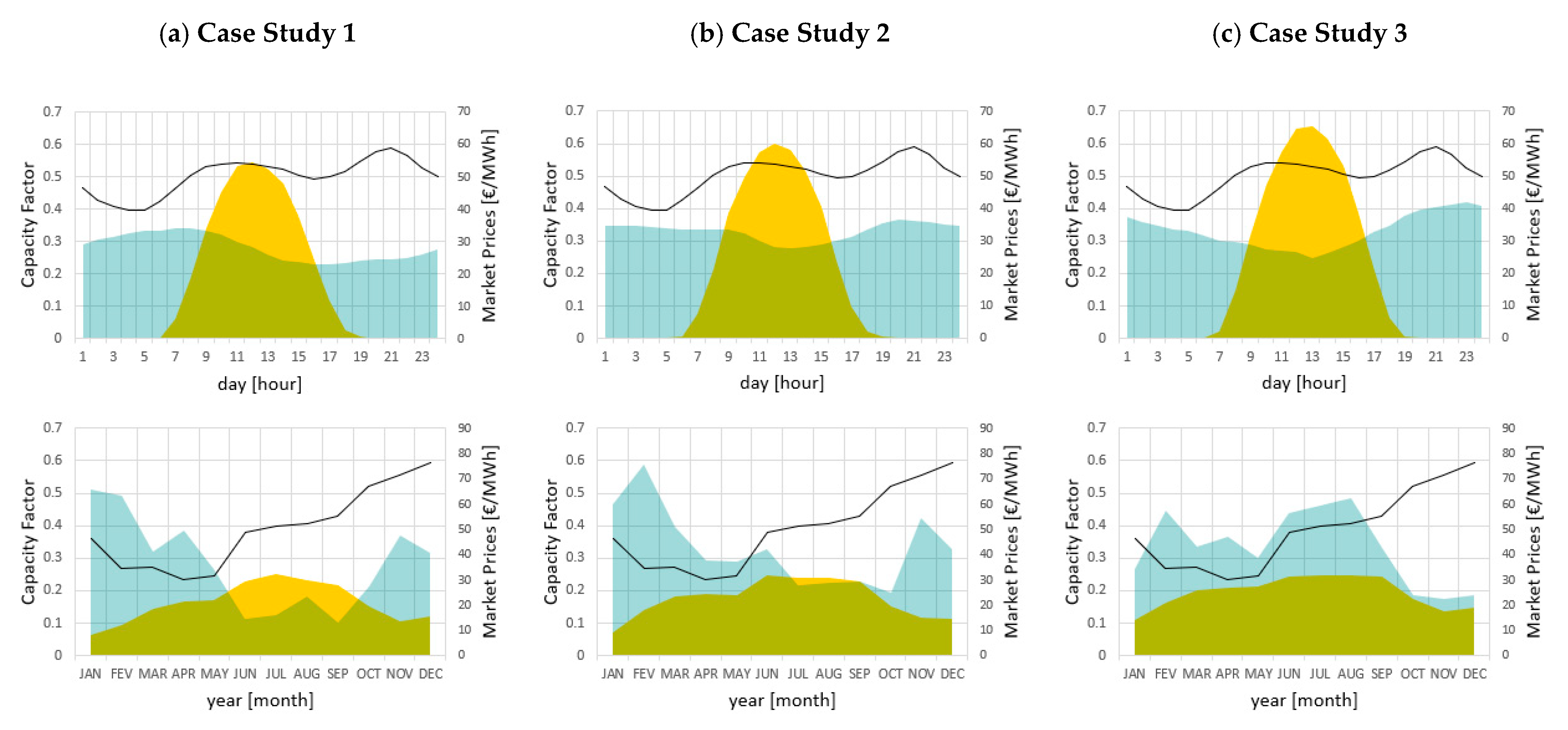
3.4.1. Case Study Selection and Scenario Construction
3.4.2. Input Data
- An MCP (measure–correlation–prediction) method was used to create the time series of wind power production used in this work. The MCP method is based on a neuronal network technique using real and numerical weather prediction data [48].
- The photovoltaic geographical information system (PVGIS) tool was used to gather the hourly PV power data of the selected case studies [49]. The optimized slope and azimuth option were used for each HRPP location, as well as crystalline silicon PV panels, considering 14% of the system’s losses (related to losses in cables and power inverters, among other factors).
- The time series for day-ahead market (DAM) prices used in this study refers to the Iberian market (MIBEL) [50]. A correction factor was introduced so that the average market price reflects recent market trends (an average price of 53.40 €/MWh from 2017 to 2019).
4. Results
- Case Study 1: the pure repowering option (Opt1) in this case study originates the supply of 49.4 GWh of energy per year, on average, to the energy market, which corresponds to a load factor for the interconnection line of 28%. The energy produced had an average market price of 46.16 €/MWh. When considering overcapacity, the results demonstrate that adding wind capacity (Opt2) over the PCC limit is not optimal. Instead, the optimal decision is to add 25 MW of PV technology (Opt3). The addition of PV technology would originate the supply of 80.6 GWh/year to the energy market, increasing the load factor of the interconnection line to 46%. The average market price per MWh produced also increased by 6.26 €/MWh, assuming the value of 52.42 €/MWh. This allowed an increase of NPV from 15.6 to 23.7 M€. However, the internal rate of return (IRR) decreases in the Opt3 scenario compared with the pure repowering option, going from 20% in Opt1 to 14% in the Opt3 scenario.
- Case Study 2: the pure repowering option (Opt1) in this case study originates the supply of 57.9 GWh/year to the energy market, corresponding to a load factor for the connection line of 33%. When considering the overcapacity scenario with wind technology only (Opt2), the results show that 10% of overcapacity increases the economic performance of the WPP. This result translates into a supply of 61.81 GWh to the energy market, an interconnection line load factor equal to 35%, and an average market price of 49.38 €/MWh. However, the Opt3 scenario for Case Study 2 reveals that the optimal decision is to repower the initial 20 MW of wind technology and add 23 MW of PV technology. This decision results in a supply of 88.4 GWh annually to the energy market, increases the interconnection line’s load factor from 35% to 50%, and the average market price for the produced energy from 49.38 to 53.73 €/MWh. The NPV of the project also increases from 22.3 M€ in the Opt2 scenario to 27.4 M€. As in Case Study 1, the IRR of the hybrid project is lower (16%) in Opt3 compared with the 25% and 23% of Opt1 and Opt2, respectively.
- Case Study 3: the pure repowering option (Opt1) in this case study originates the production of 58.1 GWh yearly, which corresponds to a connection line load factor of 33%. The Opt2 scenario shows the added value of installing an overcapacity of 20%, i.e., adding 4 MW to the original wind plant. The decision to add 4 MW of wind technology increases the energy produced to 66.7 GWh yearly, which also increases the load factor of the connection line to 38%. As in Case Study 2, the Opt3 scenario shows that the optimal decision is to repower the 20 MW of wind technology and add 24 MW of PV technology. In this scenario, the highest NPV is achieved (29 M€), with 90.9 GWh per year being supplied to the energy market, a load factor of 52%, with an average market price of 54.44 €/MWh.
5. Discussion
5.1. Technical and Environmental Domains
- Higher renewable installed capacity and yearly capacity factor: the concept of an HRPP allows for an increase in renewable energy systems (RES) installed capacity. In all three case studies, the initial WPP capacity doubled when the plant was converted to an HRPP, maintaining the maximum injected power as prescribed. Consequently, a higher energy value is delivered yearly to the network, increasing the capacity factor of the (hybrid) power plant compared with keeping the plant as a wind power plant.
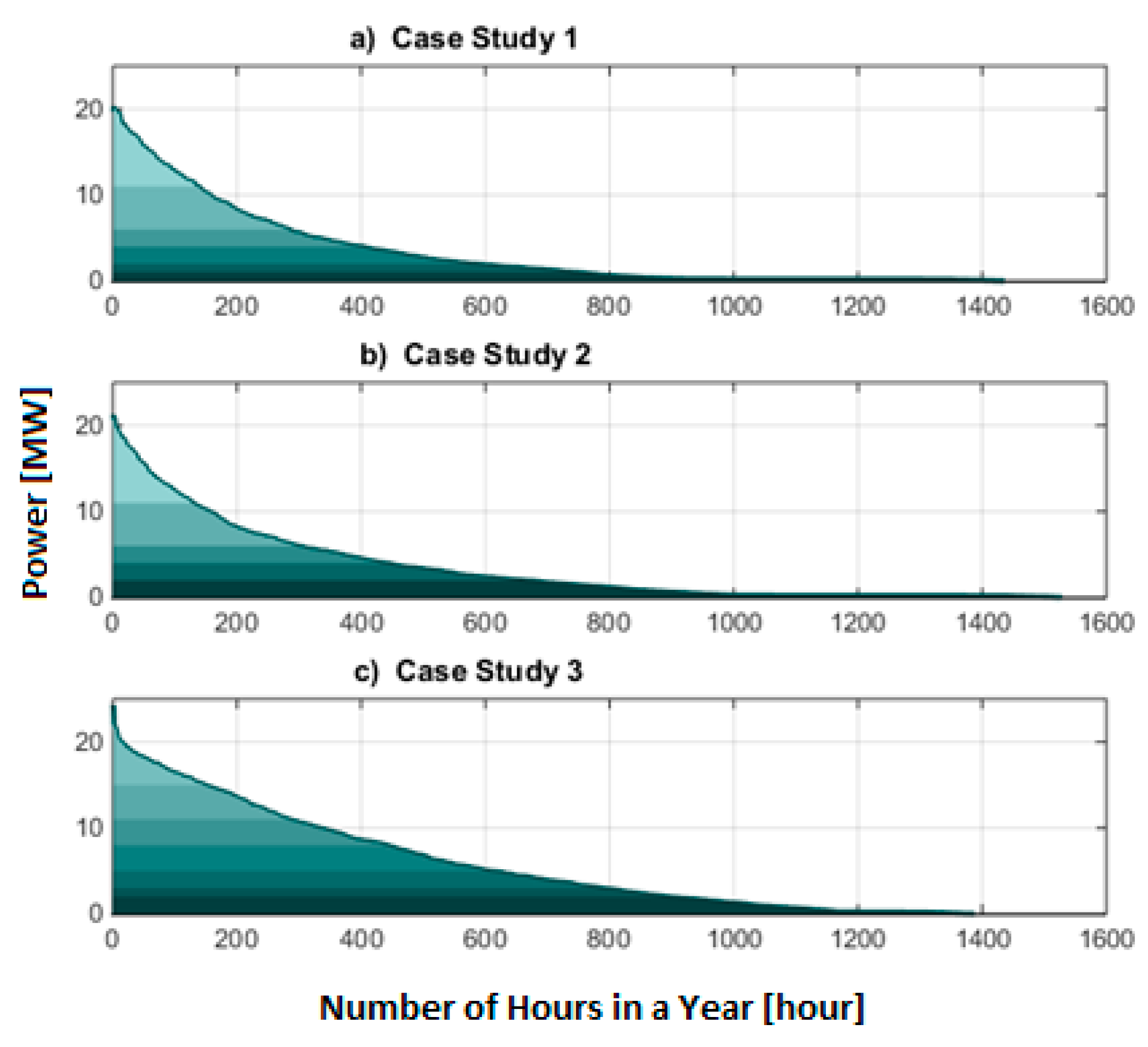
- Higher curtailment levels: converting an existing WPP into an HRPP originates higher curtailment energy, especially if no storage system is installed. This result was expected due to the increase in installed capacity (above the permitted power), which allows for the generation of higher amounts of energy and, for a short annual period (<5% hours of the year, approximately), the power produced will be above the allowed interconnection grid capacity, making curtailment inevitable. For that reason, all three case studies show an increase in curtailed energy when a hybrid solution is in place compared with the reference scenario.
5.2. Economic Domain
- Higher energy marginal value: adding solar PV technology to a WPP yields a higher correlation between the power plant’s daily profile and market prices. Thus, a higher market value per MWh produced is achieved, as demonstrated by the increase in the energy produced marginal value from the wind to the hybrid scenario in all three case studies. This increase in value is expected to occur in most Southern European locations due to existing complementarity between wind and PV generation profiles. The site-depending relevance is proven by the results of the three case studies with distinct wind and PV profiles.
- Higher investment costs: the results show that investing in an HRPP is more capital-intensive than pure repowering due to the solar PV technology capacity. The high investment costs can be considered to be a barrier to small stakeholders with limited access to capital. Furthermore, the higher investment costs of the HRPP option compared with the pure repowering option also decreases the IRR of the project.
- Higher profitability of the investments: when comparing an HRPP with the other options (e.g., repowering, or repowering plus wind overcapacity), even though investment costs are higher, the profitability of the hybrid solution is also higher, as shown by the presented net present values obtained for all three case studies. Moreover, a hybrid mix of energy sources can represent higher flexibility in adapting to changes in environmental conditions, thus offering investors a potential mitigation effect on long-term risks linked to climate changes and new consequent regulations.
5.3. Technical and Economic Domains
- Storage systems are economically unattractive when trading only at DAM: the main benefits of adding storage systems to the HRPP—more stable energy output and less curtailed energy—to enhance the HRPP’s participation in DAM do not offset the current investment costs it requires, discouraging developers from investing in distributed storage systems under simulated actual conditions.
5.4. Technical, Economic, and Environmental Domains
- Increased network and land-use efficiency: installing capacity over the (permitted) maximum limit while maintaining the technical injection power limits (of whichever technology) allows us, on the one hand, to optimize the use of existing grid infrastructure and, on the other, to contribute to deploying a representative share of PV capacity. At the same time, land use is optimized as there is a higher installed capacity per area unit, avoiding the need to commit additional land to electricity production purposes.
- Spark collaborations between the solar and wind sector: although this work was conducted mainly from wind power plant owners/operators/investors’ point of view, the results show an opportunity for solar developers as well. In the context of hybridizing current wind parks, PV solar developers have an opportunity to join forces with wind promotors and bypass some of the legal requirements of installing new plants, such as environmental impact assessments and connection node auctions, since all the licensing and investments in grid infrastructure and substations are already in place.
6. Conclusions
- A higher installed capacity and average yearly capacity factor, increasing the contribution from RES in power systems.
- The optimal use of grid and land, contributing to the economic and environmental sustainability of power systems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Acronyms | Round-trip efficiency of the energy storage system (%) | ||
| HRPP | Hybrid renewable power plants | Hourly day-ahead electricity market prices (€/MWh) | |
| WPP | Wind power plant | Integer Variables | |
| DAM | Day-ahead market | Number of wind turbines to be installed (#) | |
| PCC | Point of common coupling | Solar PV capacity to be installed (MW) | |
| POI | Point of interconnection | Power capacity of the storage system to be installed (MW) | |
| NPV | Net present value | Energy capacity of the storage system to be installed (MWh) | |
| MILP | Mixed-integer linear problem | Positive Variables | |
| GA | Genetic algorithm | Hourly power produced by the HRPP (MW) | |
| Sets | Hourly energy stored in the battery system (MWh) | ||
| Set for years in the project’s lifetime | Hourly charging power in the battery system (MW) | ||
| Set for hours in a year | Hourly discharging power in the battery system (MW) | ||
| Parameters | Hourly power delivered to the electricity grid (MW) | ||
| Area available for wind and PV installation (km2) | Hourly power curtailed (MW) | ||
| Land use for MW of wind technology installed (km2/MW) | Yearly revenues (M€) | ||
| Land use for MW of solar PV technology installed (km2/MW) | Yearly operational costs per technology type (M€) | ||
| Licensed power at the point of common coupling (MW) | Investment costs per technology type (M€) | ||
| Discount rate (%) | Original WPP wind power capacity (MW) | ||
| Inflation rate (%) | Total investment costs (M€) | ||
| Normalized hourly annual production profile for the wind technology | Binary Variables | ||
| Normalized hourly annual production profile for the solar PV technology | Binary variable linked to the storage system operation. It assumes the value 1 when the battery is in discharge mode and 0 otherwise. | ||
| Random parameter modeling the interannual variability of wind power production | Real Variables | ||
| Random parameter modeling the interannual variability of solar PV power production | NPV | Net present value of the project (M€) | |
References
- European Union. A European Green Deal: Striving to Be the First Climate-Neutral Continent. 2019. Available online: https://ec.europa.eu/info/strategy/priorities-2019-2024/european-green-deal_en (accessed on 3 September 2020).
- de Doile, G.N.D.; Junior, P.R.; Rocha, L.C.S.; Bolis, I.; Janda, K.; Junior, L.M.C. Hybrid wind and solar photovoltaic generation with energy storage systems: A systematic literature review and contributions to technical and economic regulations. Energies 2021, 14, 6521. [Google Scholar] [CrossRef]
- Lian, J.; Zhang, Y.; Ma, C.; Yang, Y.; Chaima, E. A review on recent sizing methodologies of hybrid renewable energy systems. Energy Convers. Manag. 2019, 199, 112027. [Google Scholar] [CrossRef]
- Hansen, A.D.; Das, K.; Sørensen, P.; Singh, P.; Gavrilovic, A. European and Indian Grid Codes for Utility Scale Hybrid Power Plants. Energies 2021, 14, 4335. [Google Scholar] [CrossRef]
- DL-76/2019; Diário da República, 1.a Série—N.o 106—3 de Junho de 2019. D. Repub. 2019, pp. 2792–2865. Available online: https://dre.pt/dre/detalhe/decreto-lei/76-2019-122476954 (accessed on 3 June 2019).
- Han, S.; Zhang, L.; Liu, Y.; Zhang, H.; Yan, J.; Li, L.; Lei, X.; Wang, X. Quantitative evaluation method for the complementarity of wind-solar-hydro power and optimization of wind-solar ratio. Appl. Energy 2019, 236, 973–984. [Google Scholar] [CrossRef]
- Pérez Odeh, R.; Watts, D.; Negrete-Pincetic, M. Portfolio applications in electricity markets review: Private investor and manager perspective trends. Renew. Sustain. Energy Rev. 2018, 81, 192–204. [Google Scholar] [CrossRef]
- Dykes, K.; King, J.; Diorio, N.; King, R.; Gevorgian, V.; Corbus, D.; Blair, N.; Anderson, K.; Stark, G.; Turchi, C.; et al. Opportunities for Research and Development of Hybrid Power Plants. 2020. Available online: https://www.nrel.gov/docs/fy20osti/75026.pdf (accessed on 29 September 2021).
- Couto, A.; Estanqueiro, A. Exploring Wind and Solar PV Generation Complementarity to Meet Electricity Demand. Energies 2020, 13, 4132. [Google Scholar] [CrossRef]
- Schindler, D.; Dieter, H.; Jung, C. On the spatiotemporal variability and potential of complementarity of wind and solar resources. Energy Convers. Manag. 2020, 218, 113016. [Google Scholar] [CrossRef]
- Ren, G.; Wan, J.; Liu, J.; Yu, D. Spatial and temporal assessments of complementarity for renewable energy resources in China. Energy 2019, 177, 262–275. [Google Scholar] [CrossRef]
- Couto, A.; Estanqueiro, A. Assessment of wind and solar PV local complementarity for the hybridization of the wind power plants installed in Portugal. J. Clean. Prod. 2021, 319, 128728. [Google Scholar] [CrossRef]
- Blechinger, P.; Cader, C.; Bertheau, P.; Huyskens, H.; Seguin, R.; Breyer, C. Global analysis of the techno-economic potential of renewable energy hybrid systems on small islands. Energy Policy 2016, 98, 674–687. [Google Scholar] [CrossRef]
- Grau, L.; Jung, C.; Schindler, D. Sounding out the repowering potential of wind energy—A scenario-based assessment from Germany. J. Clean. Prod. 2021, 293, 126094. [Google Scholar] [CrossRef]
- de Bona, J.C.; Ferreira, J.C.E.; Ordoñez Duran, J.F. Analysis of scenarios for repowering wind farms in Brazil. Renew. Sustain. Energy Rev. 2021, 135, 110197. [Google Scholar] [CrossRef]
- Wang, S.; Jia, R.; Shi, X.; Luo, C.; An, Y.; Huang, Q.; Guo, P.; Wang, X.; Lei, X. Research on Capacity Allocation Optimization of Commercial Virtual Power Plant (CVPP). Energies 2022, 15, 1303. [Google Scholar] [CrossRef]
- Akter, H.; Howlader, H.O.R.; Nakadomari, A.; Islam, M.R.; Saber, A.Y.; Senjyu, T. A Short Assessment of Renewable Energy for Optimal Sizing of 100% Renewable Energy Based Microgrids in Remote Islands of Developing Countries: A Case Study in Bangladesh. Energies 2022, 15, 1084. [Google Scholar] [CrossRef]
- Hatata, A.Y.; Osman, G.; Aladl, M.M. An optimization method for sizing a solar / wind / battery hybrid power system based on the arti fi cial immune system. Sustain. Energy Technol. Assess. 2018, 27, 83–93. [Google Scholar] [CrossRef]
- Ma, T.; Javed, M.S. Integrated sizing of hybrid PV-wind-battery system for remote island considering the saturation of each renewable energy resource. Energy Convers. Manag. 2019, 182, 178–190. [Google Scholar] [CrossRef]
- Ramli, M.A.M.; Bouchekara, H.R.E.H.; Alghamdi, A.S. Optimal sizing of PV/wind/diesel hybrid microgrid system using multi-objective self-adaptive differential evolution algorithm. Renew. Energy 2018, 121, 400–411. [Google Scholar] [CrossRef]
- Cai, W.; Li, X.; Maleki, A.; Pourfayaz, F.; Rosen, M.A.; Alhuyi, M.; Tien, D. Optimal sizing and location based on economic parameters for an off-grid application of a hybrid system with photovoltaic, battery and diesel technology. Energy 2020, 201, 117480. [Google Scholar] [CrossRef]
- Duchaud, J.L.; Notton, G.; Fouilloy, A.; Voyant, C. Wind, solar and battery micro-grid optimal sizing in Tilos Island. Energy Procedia 2019, 159, 22–27. [Google Scholar] [CrossRef]
- Zhang, W.; Maleki, A.; Rosen, M.A.; Liu, J. Sizing a stand-alone solar-wind-hydrogen energy system using weather forecasting and a hybrid search optimization algorithm. Energy Convers. Manag. 2019, 180, 609–621. [Google Scholar] [CrossRef]
- Chiacchio, F.; Famoso, F.; Cedola, L. Performance and Economic Assessment of a Grid-Connected Photovoltaic Power Plant with a Storage System: A Comparison between the North and the South of Italy. Energies 2019, 12, 2356. [Google Scholar] [CrossRef] [Green Version]
- Bakhtvar, M.; Al-Hinai, A. Robust operation of hybrid solar–wind power plant with battery energy storage system. Energies 2021, 14, 3781. [Google Scholar] [CrossRef]
- Małkowski, R.; Jaskólski, M.; Pawlicki, W. Operation of the hybrid photovoltaic-battery system on the electricity market-simulation, real-time tests and cost analysis. Energies 2020, 16, 1402. [Google Scholar] [CrossRef] [Green Version]
- Nasrolahpour, E.; Zareipour, H.; Rosehart, W.D.; Electric, A.; Operator, S. Battery investment by a strategic wind producer: A scenario-based decomposition approach. Electr. Power Syst. Res. 2020, 182, 106255. [Google Scholar] [CrossRef]
- Wang, G.; Ciobotaru, M.; Agelidis, V.G. Optimal capacity design for hybrid energy storage system supporting dispatch of large-scale photovoltaic power plant. J. Energy Storage 2015, 3, 25–35. [Google Scholar] [CrossRef]
- Yang, B.; Guo, Y.; Xiao, X.; Tian, P. Bi-level Capacity Planning of Wind-PV-Battery Hybrid Generation System Considering Return on Investment. Energies 2020, 13, 3046. [Google Scholar] [CrossRef]
- Carvalho, D.B.; Guardia, E.C.; Lima, J.W.M. Technical-economic analysis of the insertion of PV power into a wind-solar hybrid system. Sol. Energy 2019, 191, 530–539. [Google Scholar] [CrossRef]
- Al-Shereiqi, A.; Al-Hinai, A.; Albadi, M.; Al-Abri, R. Optimal sizing of a hybrid wind-photovoltaic-battery plant to mitigate output fluctuations in a grid-connected system. Energies 2020, 13, 3015. [Google Scholar] [CrossRef]
- Al-Shereiqi, A.; Al-Hinai, A.; Albadi, M.; Al-Abri, R. Optimal sizing of hybrid wind-solar power systems to suppress output fluctuation. Energies 2021, 14, 5377. [Google Scholar] [CrossRef]
- Nuvvula, R.S.S.; Elangovan, D.; Teegala, K.S.; Madurai Elavarasan, R.; Islam, M.R.; Inapakurthi, R. Optimal Sizing of Battery-Integrated Hybrid Renewable Energy Plant Load Factors of Various Sectors. Energies 2021, 14, 5368. [Google Scholar] [CrossRef]
- Sohani, A.; Dehnavi, A.; Sayyaadi, H.; Hoseinzadeh, S.; Goodarzi, E.; Garcia, D.A.; Groppi, D. The real-time dynamic multi-objective optimization of a building integrated photovoltaic thermal (BIPV/T) system enhanced by phase change materials. J. Energy Storage 2022, 46, 103777. [Google Scholar] [CrossRef]
- Durante, F.; Gianfreda, A.; Ravazzolo, F.; Rossini, L. A multivariate dependence analysis for electricity prices, demand and renewable energy sources. Inf. Sci. 2022, 590, 74–89. [Google Scholar] [CrossRef]
- Correa-Quezada, R.; del Tituaña-Castillo, M.d.C.; Río-Rama, M.d.l.C.; Álvarez-García, J. Effects of Increased Renewable Energy Consumption on Electricity Prices: Evidence for Six South American Countries. Energies 2022, 15, 620. [Google Scholar] [CrossRef]
- Oosthuizen, A.M.; Inglesi-Lotz, R.; Thopil, G.A. The relationship between renewable energy and retail electricity prices: Panel evidence from OECD countries. Energy 2022, 238, 1790. [Google Scholar] [CrossRef]
- Gomes, I.L.R.; Pousinho, H.M.I.; Melício, R.; Mendes, V.M.F. Stochastic coordination of joint wind and photovoltaic systems with energy storage in day-ahead market. Energy 2017, 124, 310–320. [Google Scholar] [CrossRef]
- Ciez, R.E.; Whitacre, J.F. Comparative techno-economic analysis of hybrid micro-grid systems utilizing different battery types. Energy Convers. Manag. 2016, 112, 435–444. [Google Scholar] [CrossRef] [Green Version]
- Talent, O.; Du, H. Optimal sizing and energy scheduling of photovoltaic-battery systems under different tariff structures. Renew. Energy 2018, 129, 513–526. [Google Scholar] [CrossRef]
- Grossmann, I.E. Minlp Optimization Strategies and Algorithms for Process Synthesis. Found. Comput. Process Des. 1990, 105–132. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.927.7660&rep=rep1&type=pdf (accessed on 20 May 2020).
- Li, B.; Roche, R.; Miraoui, A. Microgrid sizing with combined evolutionary algorithm and MILP unit commitment. Appl. Energy 2017, 188, 547–562. [Google Scholar] [CrossRef] [Green Version]
- Fossati, J.P.; Galarza, A.; Martín-Villate, A.; Fontán, L. A method for optimal sizing energy storage systems for microgrids. Renew. Energy 2015, 77, 539–549. [Google Scholar] [CrossRef]
- Gan, L.K.; Shek, J.K.H.; Mueller, M.A. Optimised operation of an off-grid hybrid wind-diesel-battery system using genetic algorithm. Energy Convers. Manag. 2016, 126, 446–462. [Google Scholar] [CrossRef] [Green Version]
- Lip, W.; Shiun, J.; Ra, S.; Alwi, W.; Erniza, N.; Rozali, M.; Shin, W.; Abdul-manan, Z. An MILP model for cost-optimal planning of an on-grid hybrid power system for an eco-industrial park. Energy 2016, 116, 1423–1441. [Google Scholar] [CrossRef]
- Lamedica, R.; Santini, E.; Ruvio, A.; Palagi, L.; Rossetta, I. A MILP methodology to optimize sizing of PV-Wind renewable energy systems. Energy 2018, 165, 385–398. [Google Scholar] [CrossRef] [Green Version]
- Mazzeo, D.; Matera, N.; De Luca, P.; Baglivo, C.; Congedo, M.; Oliveti, G. A literature review and statistical analysis of photovoltaic-wind hybrid renewable system research by considering the most relevant 550 articles: An upgradable matrix literature database. J. Clean. Prod. 2021, 295, 126070. [Google Scholar] [CrossRef]
- Couto, A.; Wind Power Production Timeseries. LNEG Internal Communication. 2019. Available online: https://www.researchgate.net/figure/Wind-power-time-series-all-hourly-wind-energy-production-time-series-have-been_fig3_226527334 (accessed on 22 January 2022).
- European Commission Joint Research Centre. Photovoltaic Geographical Information Systems. 2019. Available online: https://re.jrc.ec.europa.eu/pvg_tools/en/tools.html (accessed on 3 August 2019).
- OMIE. Market Results. 2020. Available online: http://www.omie.es/en/inicio (accessed on 20 October 2020).
- NREL. Land Use by System Technology. 2016. Available online: https://www.nrel.gov/analysis/tech-size.html (accessed on 5 July 2019).
- DGEG. Direção Geral de Energia e Geologia. Available online: http://www.dgeg.gov.pt/ (accessed on 19 February 2020).
- European Association for Storage of Energy. Electrochemical Energy Storage: Flow Battery. pp. 1–2. Available online: www.ease-storage.eu (accessed on 20 July 2019).


| Case Study | Capacity Factor | Correlations | |||||
|---|---|---|---|---|---|---|---|
| Wind–Solar | Wind–DAM | Hybrid–DAM | |||||
| Day | Year | Day | Year | Day | Year | ||
| CS1 | Low | −0.04 | −0.91 | −0.57 | −0.25 | 0.24 | −0.42 |
| CS2 | Average | −0.86 | −0.61 | −0.08 | −0.26 | 0.38 | −0.48 |
| CS3 | High | −0.82 | 0.70 | 0.08 | −0.57 | 0.43 | −0.52 |
| Parameter | Value | Unit | |
|---|---|---|---|
| Symbol | Description | ||
| Area available for wind and PV installation | 2.5 | km2 | |
| Interannual variability of wind power production | - | ||
| Interannual variability of solar PV power production | - | ||
| Licensed power at the point of common coupling | 20 | MW | |
| Discount rate | 7 | % | |
| Inflation rate: | |||
| Year 1 (REF) | 1 | % | |
| Year 2 | 1.2 | % | |
| Year 3 | 0.8 | % | |
| Year 4 | 1.2 | % | |
| Year ≥ Year 5—Lifetime | 1.3 | % | |
| Technology | CAPEX | OPEX | Land Use | Round-Trip Efficiency | Lifetime | REF |
|---|---|---|---|---|---|---|
| [M€/MW] | [%CAPEX/Year] | [km2/MW] | [%] | [Years] | ||
| Wind: | 1.00 | 3.00 | 0.050 | - | 25 | [51,52] |
| PV: | 0.70 | 1.70 | 0.025 | - | 25 | |
| Battery: | 0.75 | 15 | [53] | |||
| Energy | 0.25 | 1.25 | - | |||
| Power | 0.90 | 0.03 | - |
| Energetic Indicators | Economic Indicators | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Additional Capacity | Energy → Market | Load Factor | Curtailed Energy | Investment Cost | Market Revenue | Marginal Value | IRR | NPV | |||||
| MW | MWh | GWh/Year | % | GWh/Year | M€ | M€/Year | €/MWh | % | M€ | ||||
| W | PV | PBAT | EBAT | ||||||||||
| CS1 | Opt1 | - | - | - | - | 49.4 | 28.1 | 0 | 10.0 | 2.281 | 46.16 | 20 | 15.6 |
| Opt2 | 0 | - | - | - | |||||||||
| Opt3 | 0 | 25 | 0 | 0 | 80.6 | 45.9 | 4.707 | 27.5 | 4.223 | 52.42 | 14 | 23.7 | |
| CS2 | Opt1 | - | - | - | - | 57.9 | 32.9 | 0 | 10.0 | 2.858 | 49.35 | 25 | 22.2 |
| Opt2 | 2 | - | - | - | 61.8 | 35.2 | 2.089 | 12.0 | 3.052 | 49.38 | 23 | 22.3 | |
| Opt3 | 0 | 23 | 0 | 0 | 88.4 | 50.3 | 5.019 | 26.1 | 4.751 | 53.73 | 16 | 27.4 | |
| CS3 | Opt1 | - | - | - | - | 58.1 | 33.1 | 0 | 10.0 | 2.904 | 49.97 | 26 | 22.8 |
| Opt2 | 4 | - | - | - | 66.7 | 38.0 | 3.298 | 14.0 | 3.317 | 49.76 | 21 | 23.3 | |
| Opt3 | 0 | 24 | 0 | 0 | 90.9 | 51.8 | 8.121 | 26.8 | 4.953 | 54.44 | 17 | 29.0 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, A.R.; Estanqueiro, A. From Wind to Hybrid: A Contribution to the Optimal Design of Utility-Scale Hybrid Power Plants. Energies 2022, 15, 2560. https://doi.org/10.3390/en15072560
Silva AR, Estanqueiro A. From Wind to Hybrid: A Contribution to the Optimal Design of Utility-Scale Hybrid Power Plants. Energies. 2022; 15(7):2560. https://doi.org/10.3390/en15072560
Chicago/Turabian StyleSilva, Ana Rita, and Ana Estanqueiro. 2022. "From Wind to Hybrid: A Contribution to the Optimal Design of Utility-Scale Hybrid Power Plants" Energies 15, no. 7: 2560. https://doi.org/10.3390/en15072560
APA StyleSilva, A. R., & Estanqueiro, A. (2022). From Wind to Hybrid: A Contribution to the Optimal Design of Utility-Scale Hybrid Power Plants. Energies, 15(7), 2560. https://doi.org/10.3390/en15072560