Utility-Scale Storage Integration in the Maltese Medium-Voltage Distribution Network
Abstract
:1. Introduction
2. Methodology
2.1. Analysis of the Net-Demand and Selection of Case Scenario
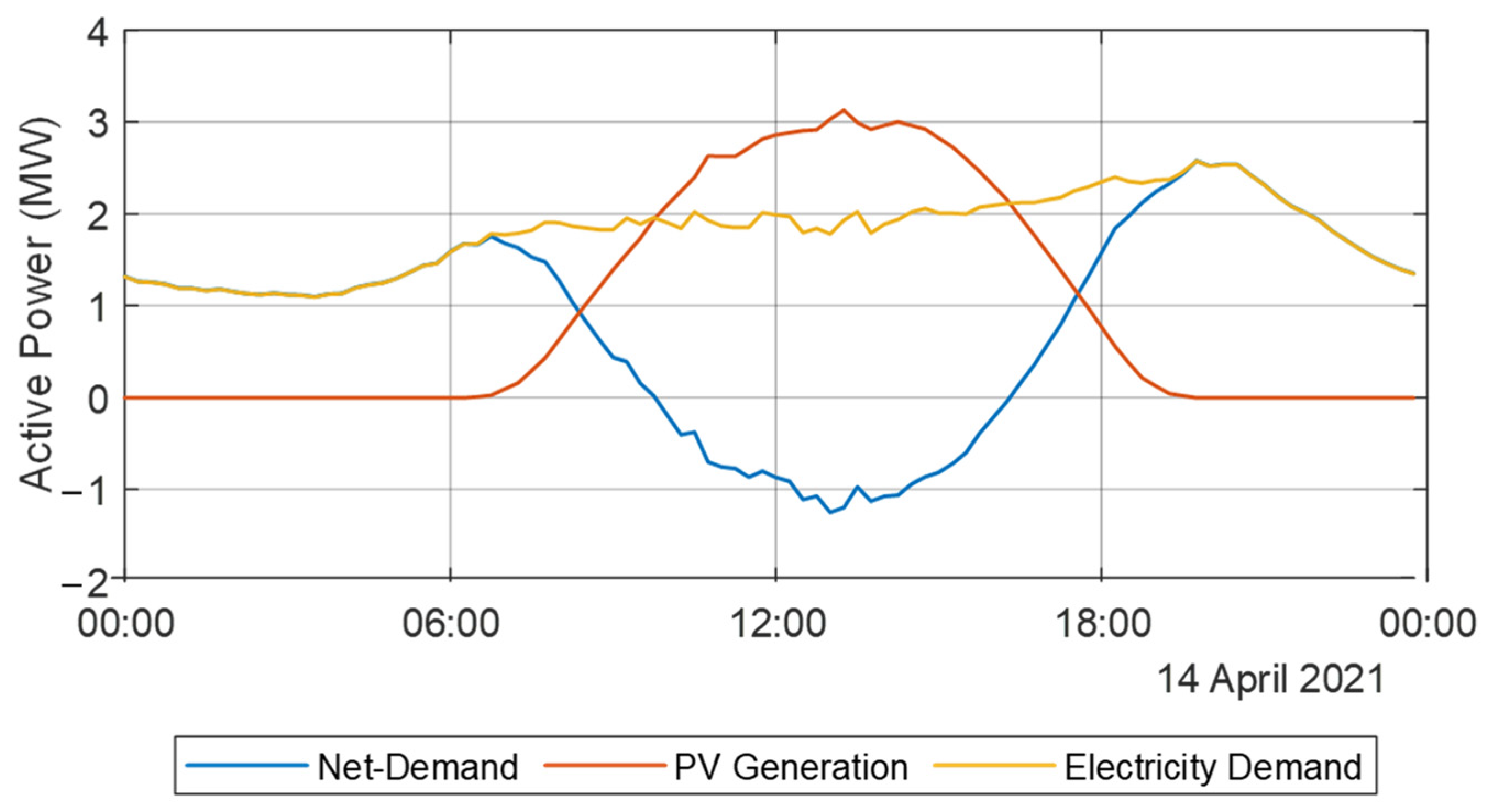
2.1.1. Analysis of the Net-Demand
2.1.2. Selection of Case Scenario
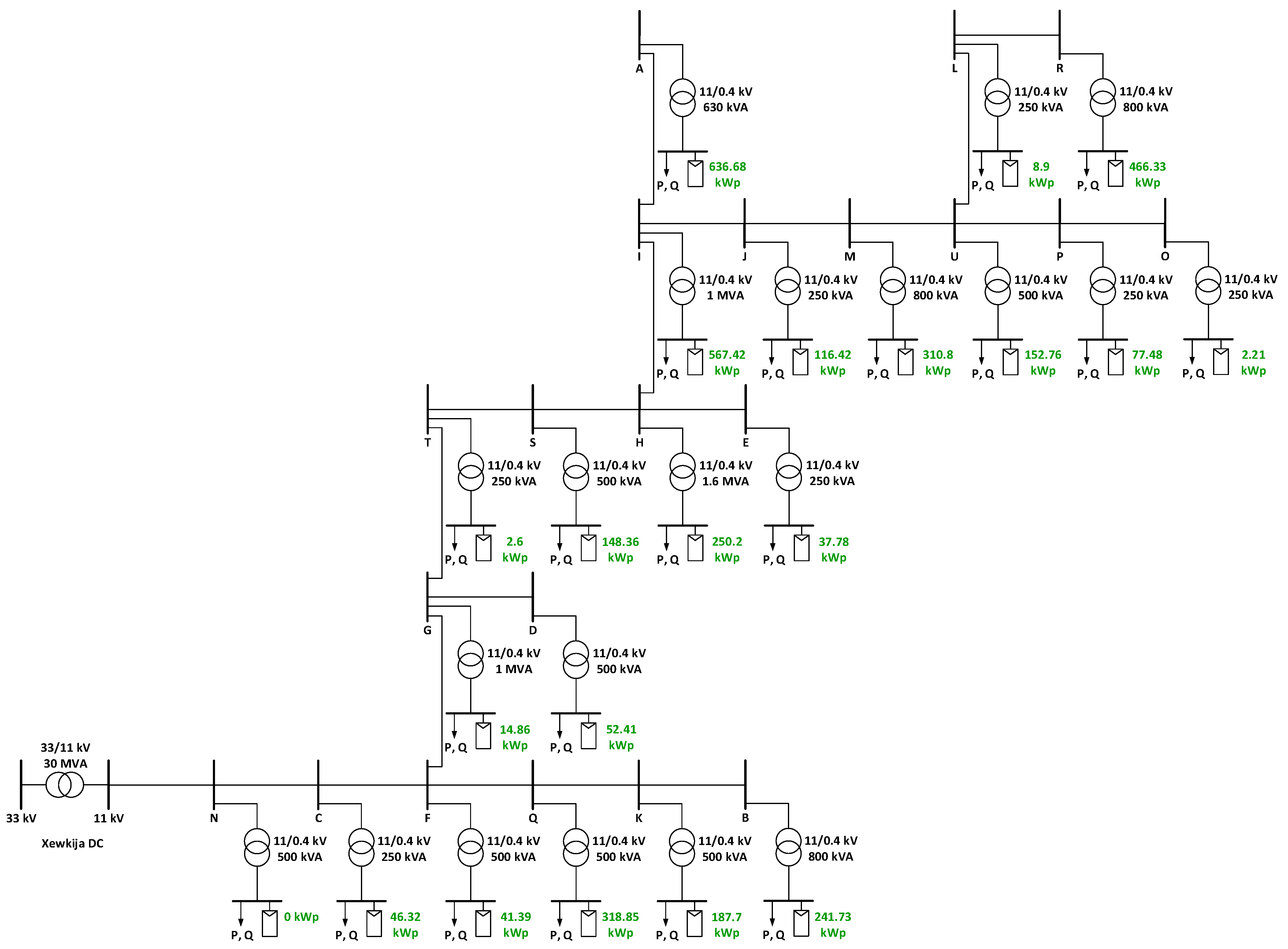
2.2. Gozo Network Simulation Model
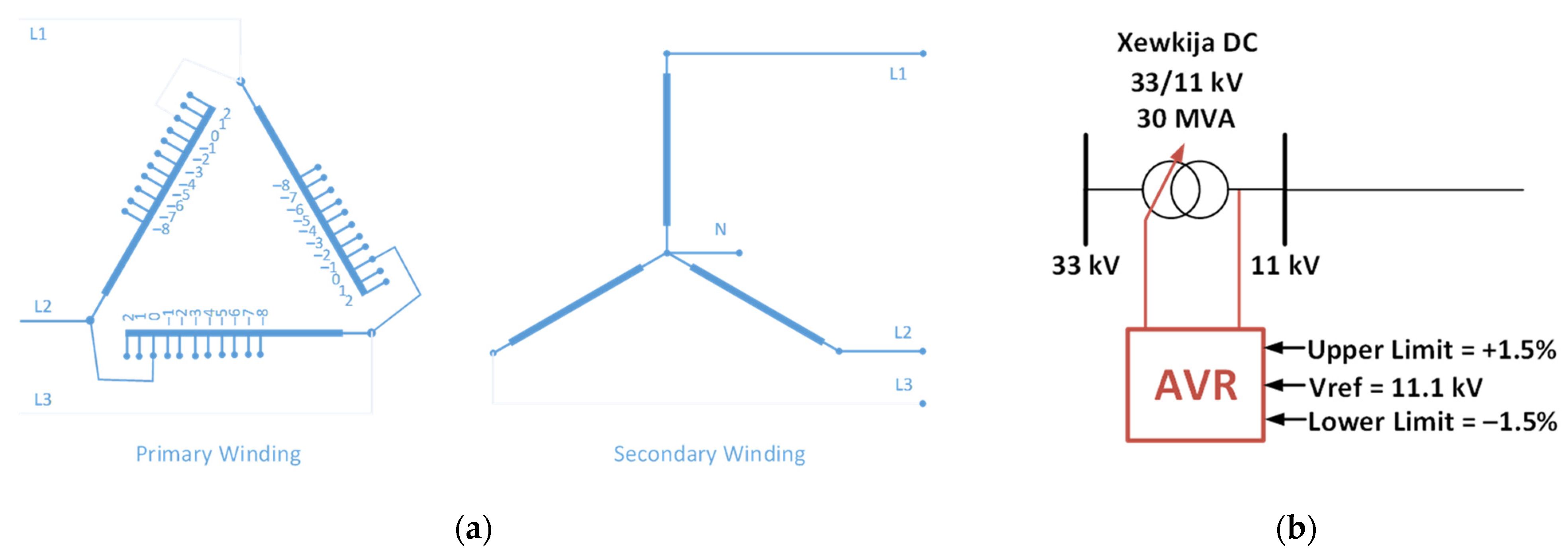
2.2.1. Slack Bus
2.2.2. Decentralized PV Generation Capacity
2.2.3. On-Load Tap Changer (OLTC)
2.3. Utility-Scale Battery Storage Systems
- The self-discharge rate was considered negligible.
- Round-trip energy efficiency is 85% (includes the battery and power electronic converter efficiencies).
- The efficiency of the power electronic converter does not vary with the output power from the BESS.
- The state of charge (SoC) varies between 20% and 80% to prolong the lifetime of the battery banks.
- Other battery-specific characteristics were not considered.
- The BESS is assumed to be discharged at the start of the simulation (initial SoC of 20%).
2.3.1. Utility-Scale BESS Sizing Strategy for Peak Shaving Functionality
2.3.2. Centralized Utility-Scale Storage Strategy
2.3.3. Decentralized Utility-Scale Storage Strategy
3. Simulation Results
3.1. OLTC Tap Positions
3.2. BUF Sizing Strategy
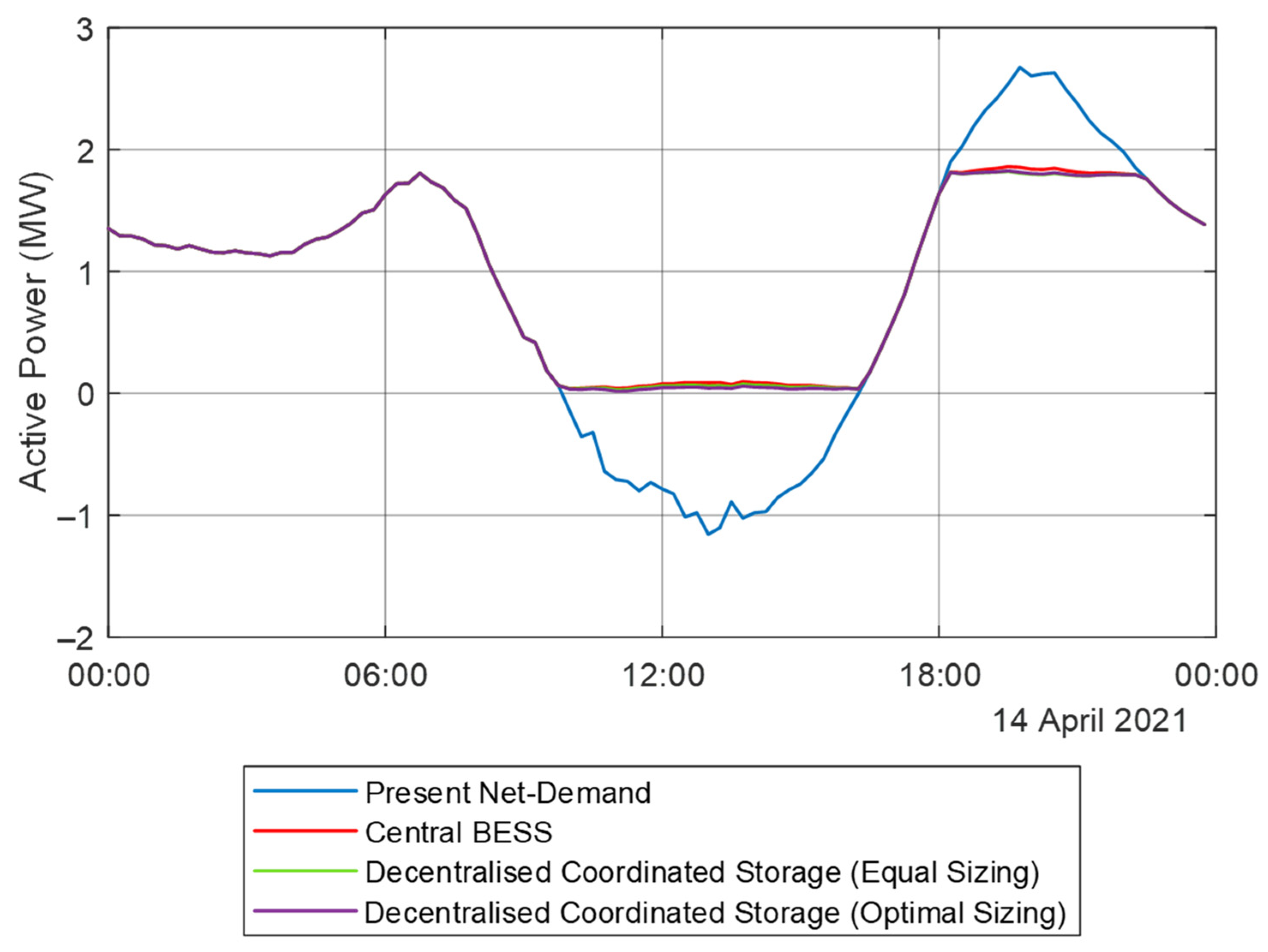
3.2.1. Net Demand Characteristics
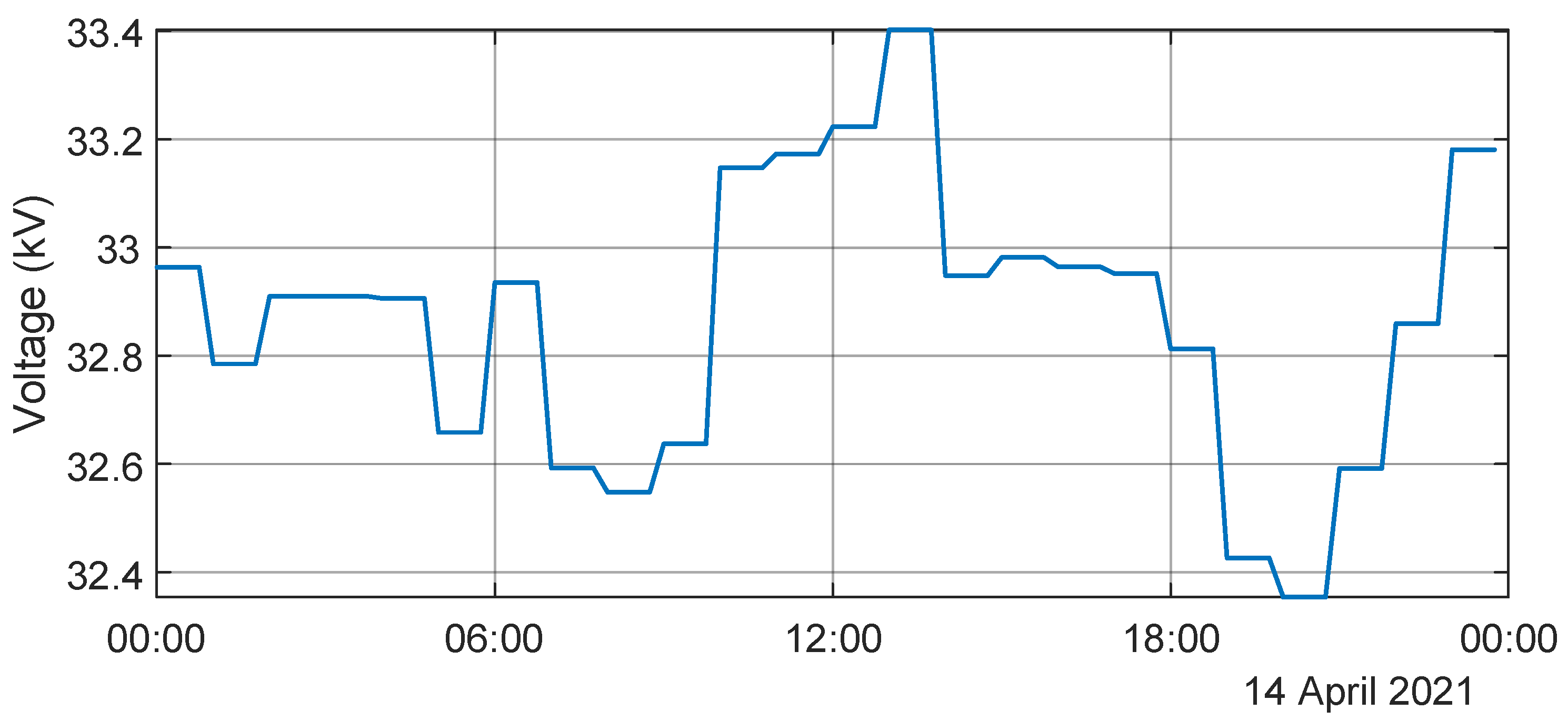
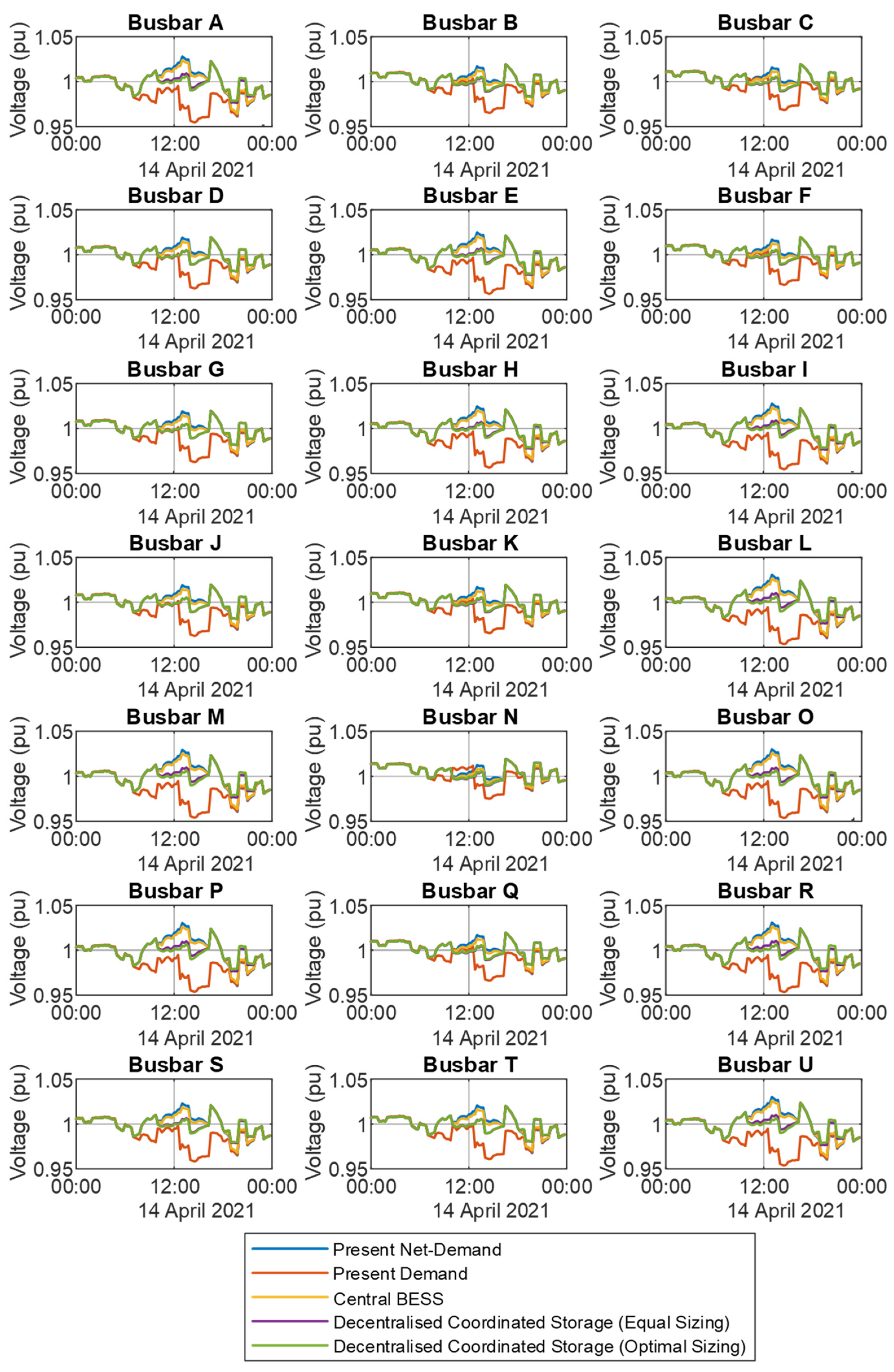
3.2.2. Xewkija DC Voltage Profile
3.2.3. Substation Voltage Profiles
3.3. Zero Reverse Power at Xewkija DC
3.3.1. Net Demand Characteristics
3.3.2. Xewkija DC Voltage Profile
3.3.3. Substation Voltage Profiles
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Eurostat, Share of Renewable Energy in Gross Final Energy Consumption by Sector. 2020. Available online: https://ec.europa.eu/eurostat/databrowser/product/view/NRG_IND_REN (accessed on 20 February 2022).
- Energy & Water Agency. National Strategy for Research and Innovation in Energy and Water (2021–2030); Energy & Water Agency: Qormi, Malta, 2020. [Google Scholar]
- Micallef, A.; Spiteri-Staines, C. Voltage rise mitigation and low voltage ride through capabilities for grid-connected low voltage microgrids. In Proceedings of the 19th European Conference on Power Electronics and Applications (EPE’17), Warsaw, Poland, 11–14 September 2017. [Google Scholar]
- European Commission; Directorate-General for Energy; Andrey, C.; Barberi, P.; Nuffel, L.; Gérard, F.; Gorenstein Dedecca, J.; Rademaekers, K.; El Idrissi, Y.; Crenes, M.; et al. Study on Energy Storage: Contribution to the Security of the Electricity Supply in Europe. Publications Office. 2020. Available online: https://data.europa.eu/doi/10.2833/077257 (accessed on 20 January 2022).
- Khezri, R.; Mahmoudi, A.; Aki, H. Optimal planning of solar photovoltaic and battery storage systems for grid-connected residential sector: Review, challenges and new perspectives. Renew. Sustain. Energy Rev. 2022, 153, 111763. [Google Scholar] [CrossRef]
- Castillo, A.; Gayme, D.F. Grid-scale energy storage applications in renewable energy integration: A survey. Energy Convers. Manag. 2014, 87, 885–894. [Google Scholar] [CrossRef]
- Mohamad, F.; Teh, J.; Lai, C.-M.; Chen, L.-R. Development of Energy Storage Systems for Power Network Reliability: A Review. Energies 2018, 11, 2278. [Google Scholar] [CrossRef] [Green Version]
- Killer, M.; Farrokhseresht, M.; Paterakis, N.G. Implementation of large-scale Li-ion battery energy storage systems within the EMEA region. Appl. Energy 2020, 260, 114166. [Google Scholar] [CrossRef]
- Saboori, H.; Hemmati, R.; Abbasi, V. Multistage distribution network expansion planning considering the emerging energy storage systems. Energy Convers. Manag. 2015, 105, 938–945. [Google Scholar] [CrossRef]
- Danish, S.M.S.; Ahmadi, M.; Danish, M.S.S.; Mandal, P.; Yona, A.; Senjyu, T. A coherent strategy for peak load shaving using energy storage systems. J. Energy Storage 2020, 32, 101823. [Google Scholar] [CrossRef]
- Lange, C.; Rueß, A.; Nuß, A.; Öchsner, R.; März, M. Dimensioning battery energy storage systems for peak shaving based on a real-time control algorithm. Appl. Energy 2020, 280, 115993. [Google Scholar] [CrossRef]
- Kichou, S.; Markvart, T.; Wolf, P.; Silvestre, S.; Chouder, A. A simple and effective methodology for sizing electrical energy storage (EES) systems based on energy balance. J. Energy Storage 2022, 49, 104085. [Google Scholar] [CrossRef]
- Conlon, T.; Waite, M.; Modi, V. Assessing new transmission and energy storage in achieving increasing renewable generation targets in regional grid. Appl. Energy 2019, 250, 1085–1098. [Google Scholar] [CrossRef]
- Park, H. A Stochastic Planning Model for Battery Energy Storage Systems Coupled with Utility-Scale Solar Photovoltaics. Energies 2021, 14, 1244. [Google Scholar] [CrossRef]
- Yao, M.; Cai, X. Energy Storage Sizing Optimization for Large-Scale PV Power Plant. IEEE Access 2021, 9, 75599–75607. [Google Scholar] [CrossRef]
- Wei, W.; Wang, Y.; Dai, S.; Chen, C.; Chen, L. Energy Storage Economic Optimization Scheduling Method for Multi-Scene Demand of Peak and Frequency Modulation. Energies 2021, 14, 8605. [Google Scholar] [CrossRef]
- Hong, Z.; Wei, Z.; Li, J.; Han, X. A novel capacity demand analysis method of energy storage system for peak shaving based on data-driven. J. Energy Storage 2021, 39, 102617. [Google Scholar] [CrossRef]
- Alamri, A.; Alowaifeer, M.; Meliopoulos, A.P.S. Energy Storage Sizing and Probabilistic Reliability Assessment for Power Systems Based on Composite Demand. IEEE Trans. Power Syst. 2022, 37, 106–117. [Google Scholar] [CrossRef]
- Regional, Geospatial, Energy and Transport Statistics Unit, Electricity Supply: 2016–2020; News Release 181/2021; National Statistics Office: New Castle, PA, USA, 2021.
- Enemalta Corporation. The Network Code. Malta. 2013. Available online: https://www.enemalta.com.mt/wp-content/uploads/2018/05/Network-Code-EMC-Approved-October-2013-1.pdf (accessed on 5 October 2021).
- Staffell, I.; Pfenninger, S. The increasing impact of weather on electricity supply and demand. Energy 2018, 145, 65–78. [Google Scholar] [CrossRef]
- Eurostat, Cooling and Heating Degree Days by Country—Monthly Data. Available online: http://appsso.eurostat.ec.europa.eu/nui/show.do?dataset=nrg_chdd_m (accessed on 18 November 2021).

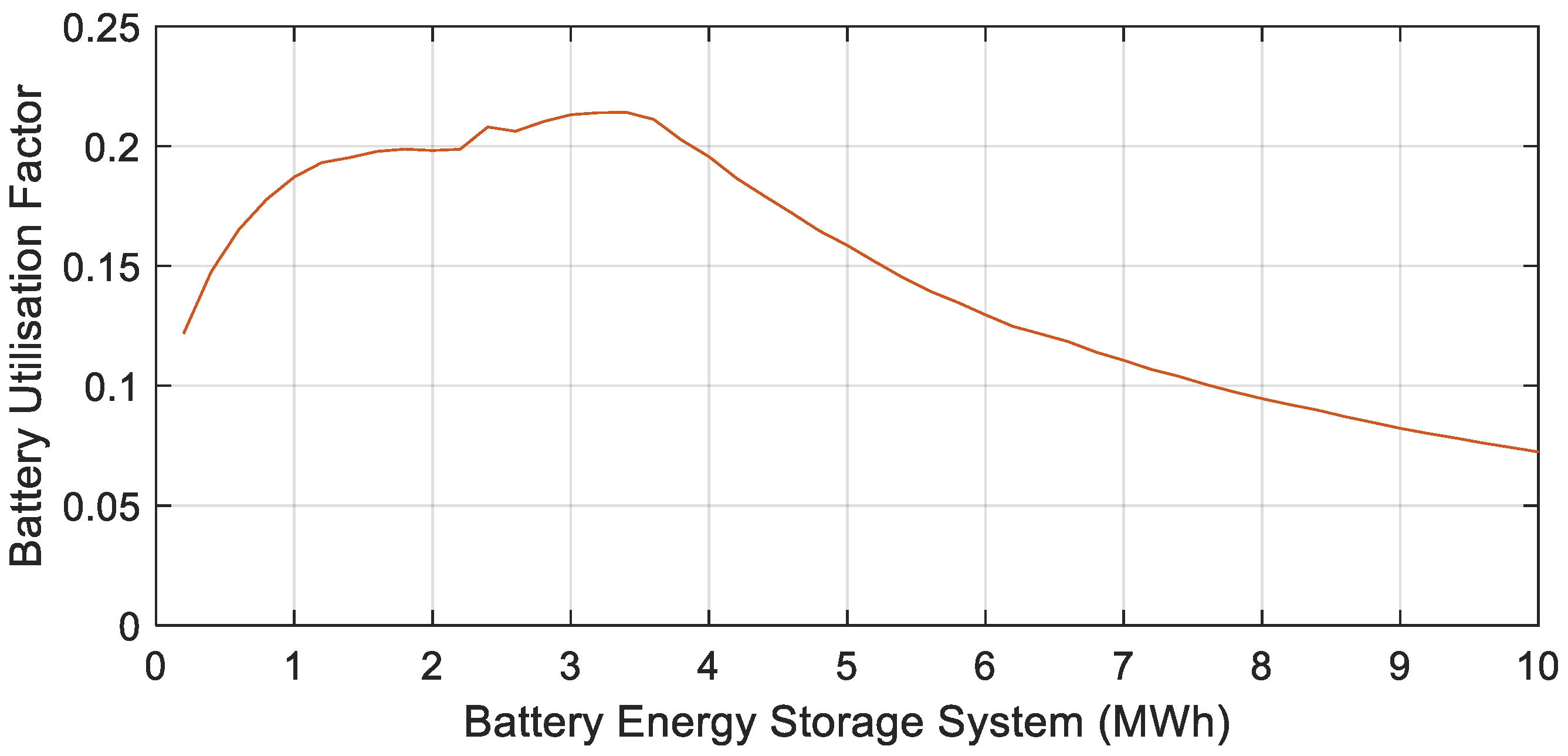
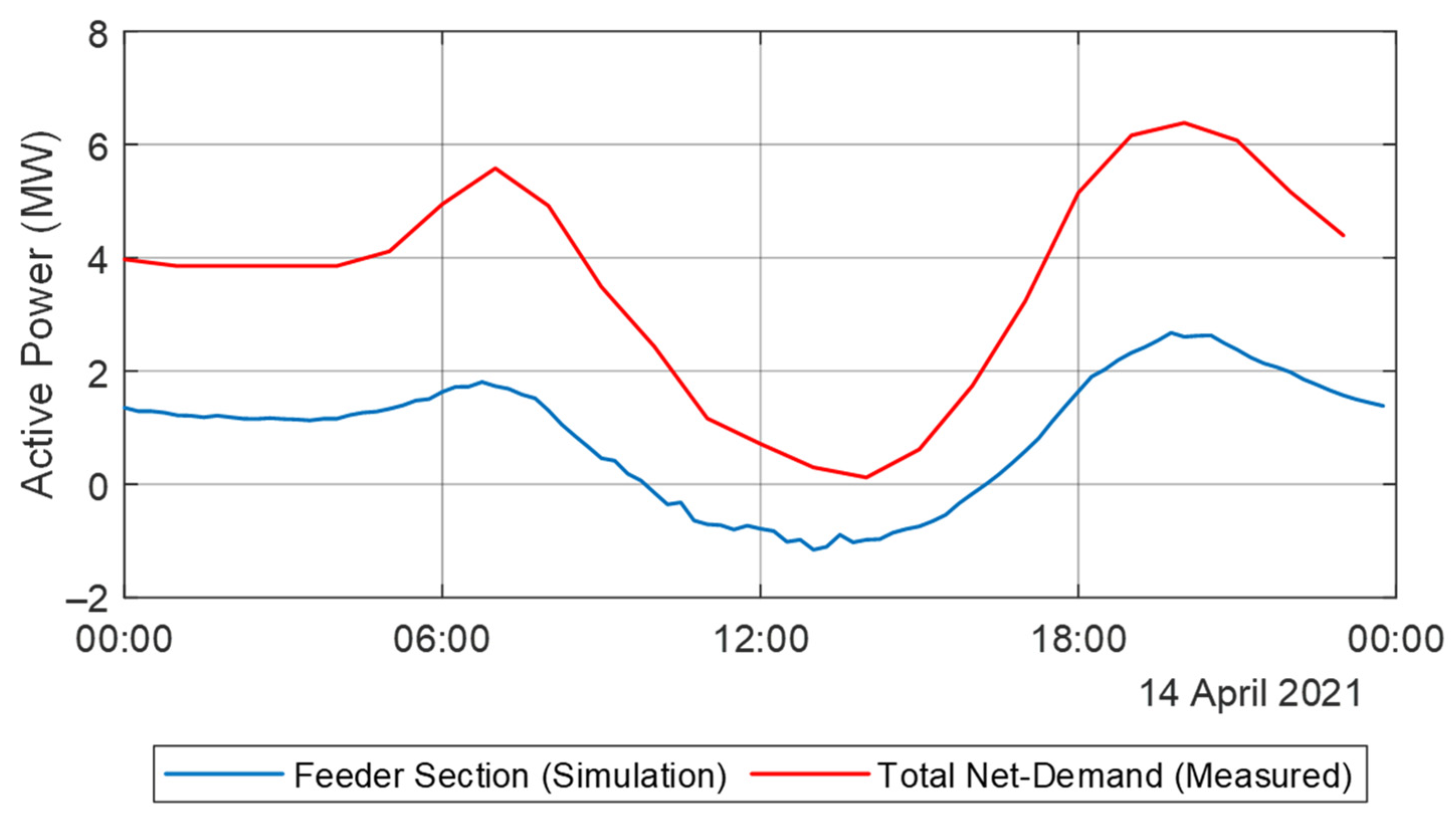


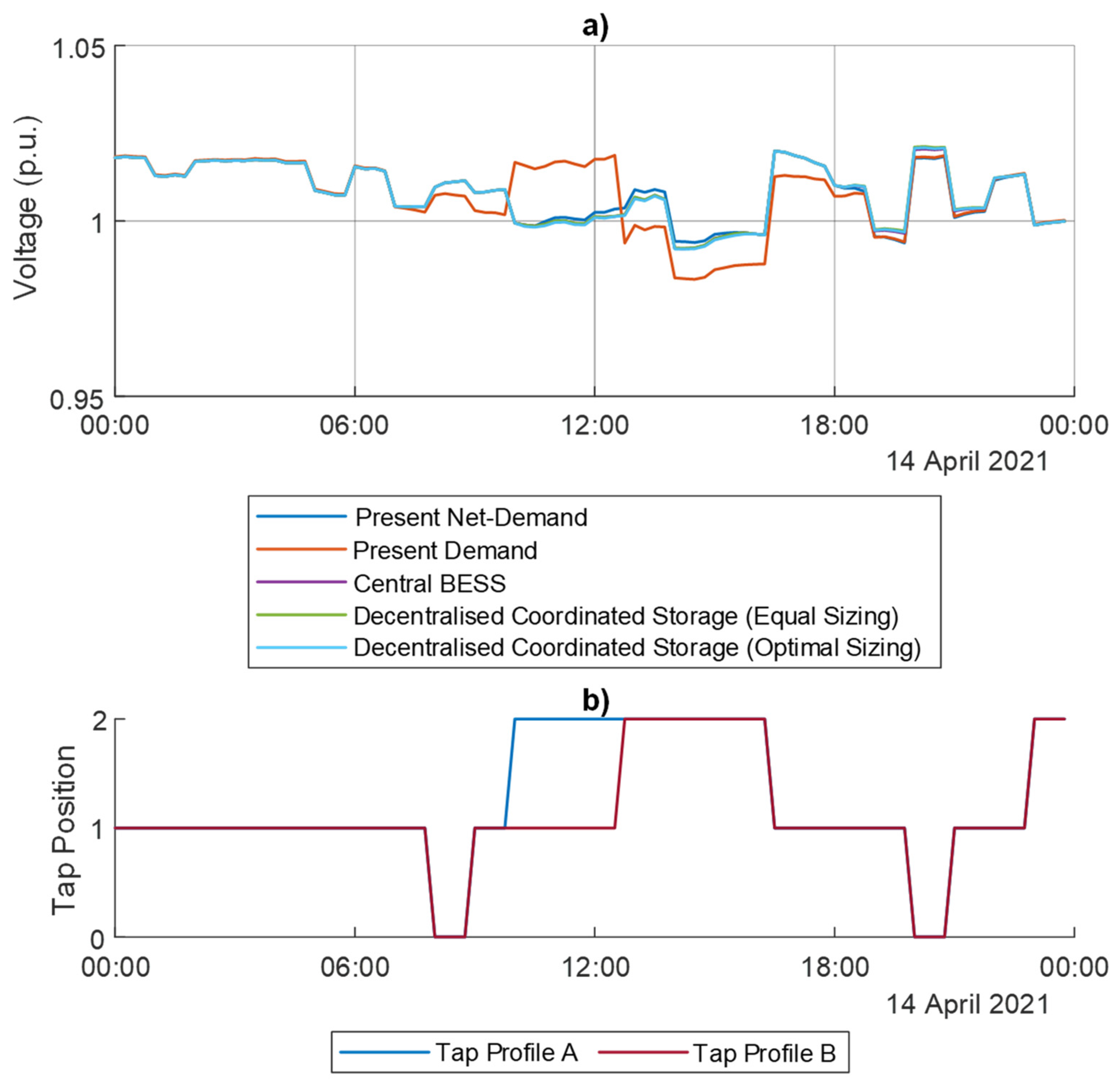
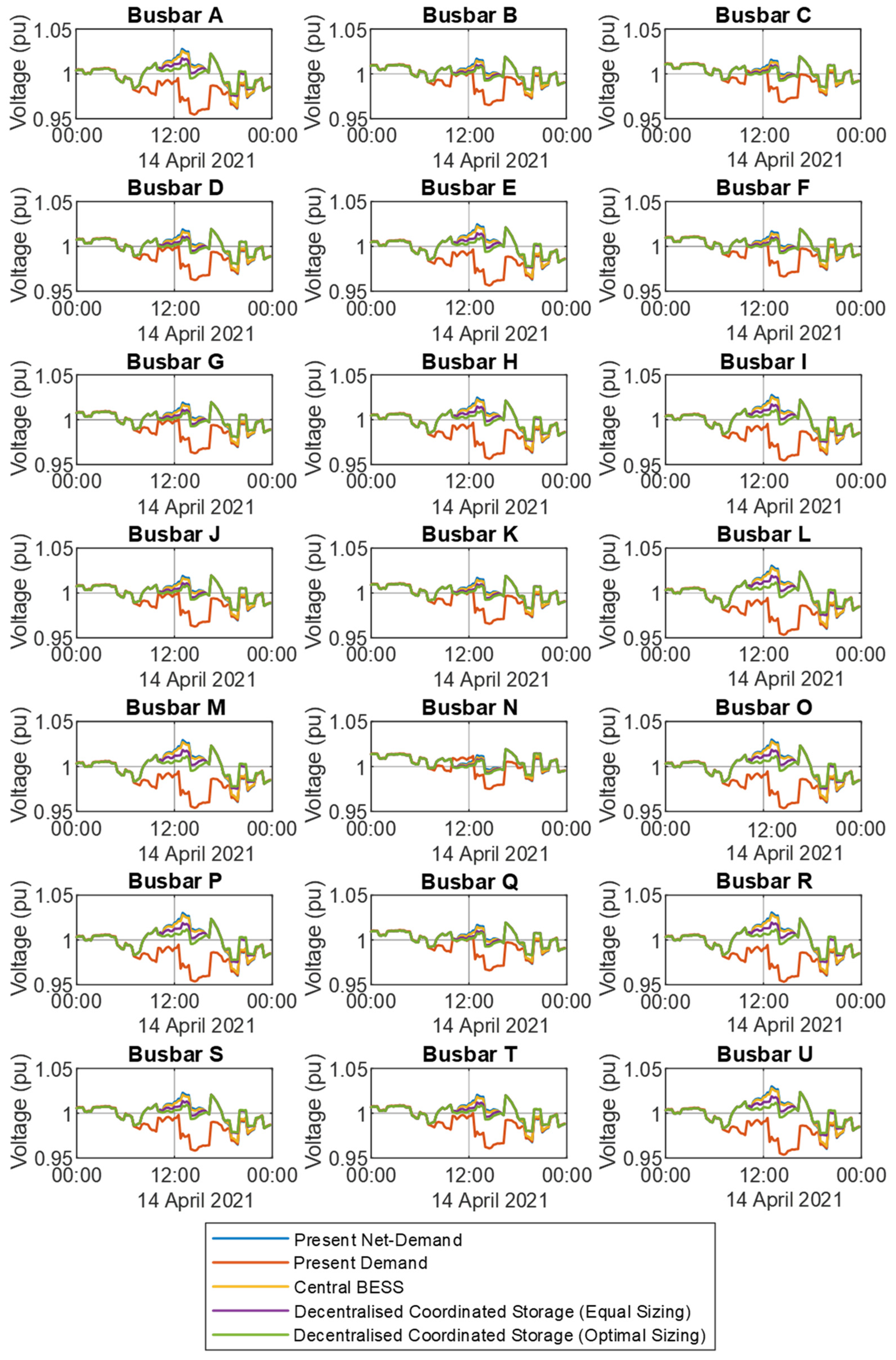

| Substation | BESS (MWh) |
|---|---|
| A | 1.800 |
| B | 0.030 |
| C | 0 |
| D | 0 |
| E | 0.040 |
| F | 0.005 |
| G | 0 |
| H | 0 |
| I | 0.100 |
| J | 0.060 |
| K | 0.100 |
| L | 0.002 |
| M | 1.400 |
| N | 0 |
| O | 0 |
| P | 0.110 |
| Q | 0.100 |
| R | 1.500 |
| S | 0.010 |
| T | 0.010 |
| U | 0.040 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Micallef, A.; Spiteri Staines, C.; Cassar, A. Utility-Scale Storage Integration in the Maltese Medium-Voltage Distribution Network. Energies 2022, 15, 2724. https://doi.org/10.3390/en15082724
Micallef A, Spiteri Staines C, Cassar A. Utility-Scale Storage Integration in the Maltese Medium-Voltage Distribution Network. Energies. 2022; 15(8):2724. https://doi.org/10.3390/en15082724
Chicago/Turabian StyleMicallef, Alexander, Cyril Spiteri Staines, and Alan Cassar. 2022. "Utility-Scale Storage Integration in the Maltese Medium-Voltage Distribution Network" Energies 15, no. 8: 2724. https://doi.org/10.3390/en15082724
APA StyleMicallef, A., Spiteri Staines, C., & Cassar, A. (2022). Utility-Scale Storage Integration in the Maltese Medium-Voltage Distribution Network. Energies, 15(8), 2724. https://doi.org/10.3390/en15082724









