An Accurate Switching Transient Analytical Model for GaN HEMT under the Influence of Nonlinear Parameters

Abstract

The Gallium Nitride high electron mobility transistor (GaN HEMT) has been considered as a potential power semiconductor device for high switching speed and high power density application since its commercialization. Compared with the traditional Si transistors, GaN HEMT has faster switching speed and lower on-off loss. As a result, it is more sensitive to the nonlinear parameters due to the fast switching speed. The subsequent voltage and current overshooting will affect the efficiency and safety of the GaN HEMT and power electronic systems. In this paper, an accurate switching transient analytical model for GaN HEMT is proposed, which considers the effects of parasitic inductances, nonlinear junction capacitances and nonlinear transconductance. The model characteristic of turn-ON process and turn-OFF process is illustrated in detail, and the equivalent circuits are derived for each switching transition. The accuracy of the proposed model can be verified by comparing the predicted switching waveform and switching loss with that of the experimental results based on the double pulse test (DPT) circuit. Compared with the conventional model, the proposed model is more accurate and matches better with the experimental results than the conventional model. Finally, this model can be used for analyzing the influences of gate resistance, nonlinear junction capacitances, and parasitic inductances on switching transient waveform and refining calculation switching loss.

1. Introduction

GALLIUM NITRIDE (GaN) is a typical representative of the third generation wide band gap semiconductor materials and has a broad application prospect. In recent years, Gallium Nitride high electron mobility transistor (GaN HEMT) has been successfully applied to high frequency and high power density converters [1]. GaN HEMT can not only attain small conduction resistance, but also push the switching frequency to several megahertz when comparing with the state-of-the-art Si MOSFETs. Nevertheless, high frequency switching transient still brings some extra problems, such as voltage and current overshooting, and even instability. As a result, it is more sensitive to the nonlinear parameters because of high dv/dt and di/dt. Meanwhile, the subsequent switching process ringing will affect the efficiency and reliability of the GaN HEMT devices and power electronic systems [2]. In order to fully utilize the GaN HEMT, it is necessary to analyze the parameters’ effects upon switching loss and the switching transient characteristic.

Generally, the switching transient of devices can be analyzed by experimental testing [3] or software simulation method [4]. However, these methods cannot give a definitive or analytical explanation of the influence mechanism of the nonlinear parameters in devices. Therefore, an accurate switching transient analytical model for estimating the switching loss and influence of nonlinear parameters is necessary.

The popular switching transient analytical model is the piecewise linear model [5]. However, the nonlinear parameters are not taken into account so that the calculated results do not agree with the experimental results very well, especially in high frequency applications, since the switching transient and switching loss are not well evaluated. In study [6], a second-order analytical model is proposed. More comprehensive analytical models of Si MOSFETs are presented in [7,8,9]. These models consider the parasitic inductances and the nonlinear junction capacitances properly. On this basis, the authors of [10] apply the analysis model to develop the SiC MOSFET model, whereas, in some of the derivation, the parameter setting is idealistic. The nonlinear parameters’ modeling results in [11] is too complex due to the numerical method or iterative calculations. In studies [12,13,14], the impact of nonlinear capacitance and nonlinear transconductance in SiC MOSFET is discussed, and a semi-physical semi-behavioral analytical model for switching transient of SiC MOSFET power module is proposed. However, these models are still not suitable for GaN HEMT devices, because GaN HEMT have no reverse recovery characteristics, and have smaller charge capacitance and parasitic inductance in contrast to Si MOSFET and SiC MOSFET [15].

In study [16], a switching loss model for GaN HEMT is proposed. The model considers the nonlinear junction capacitances as piecewise linear structure, so it still cannot precisely represent the nonlinear characteristics. In studies [17,18,19], the adopted interpolation method is used to fit nonlinear junction capacitances of GaN HEMT. However, this method has no specific mathematical expression and the results are too complex. In study [20], the package and PCB parasitic inductances, as well as the nonlinear capacitances are considered in the GaN HEMT model, but this model only includes the turn-ON process without switching loss calculation and parameter analysis. Some analytical models are proposed for cascode GaN HEMT [21,22]. These models cannot be directly applied to the GaN HEMT because of the different structure. Therefore, a more accurate switching transient analytical model for GaN HEMT is needed to explain the influence of nonlinear parameters and calculate the loss accurately. The main contributions of this paper are:

(1)

An accurate model for nonlinear junction capacitances of GaN HEMT is given and an extraction method for nonlinear transconductance is proposed. The proposed approximation method for capacitances and transconductance have better performance than conventional approaches.

(2)

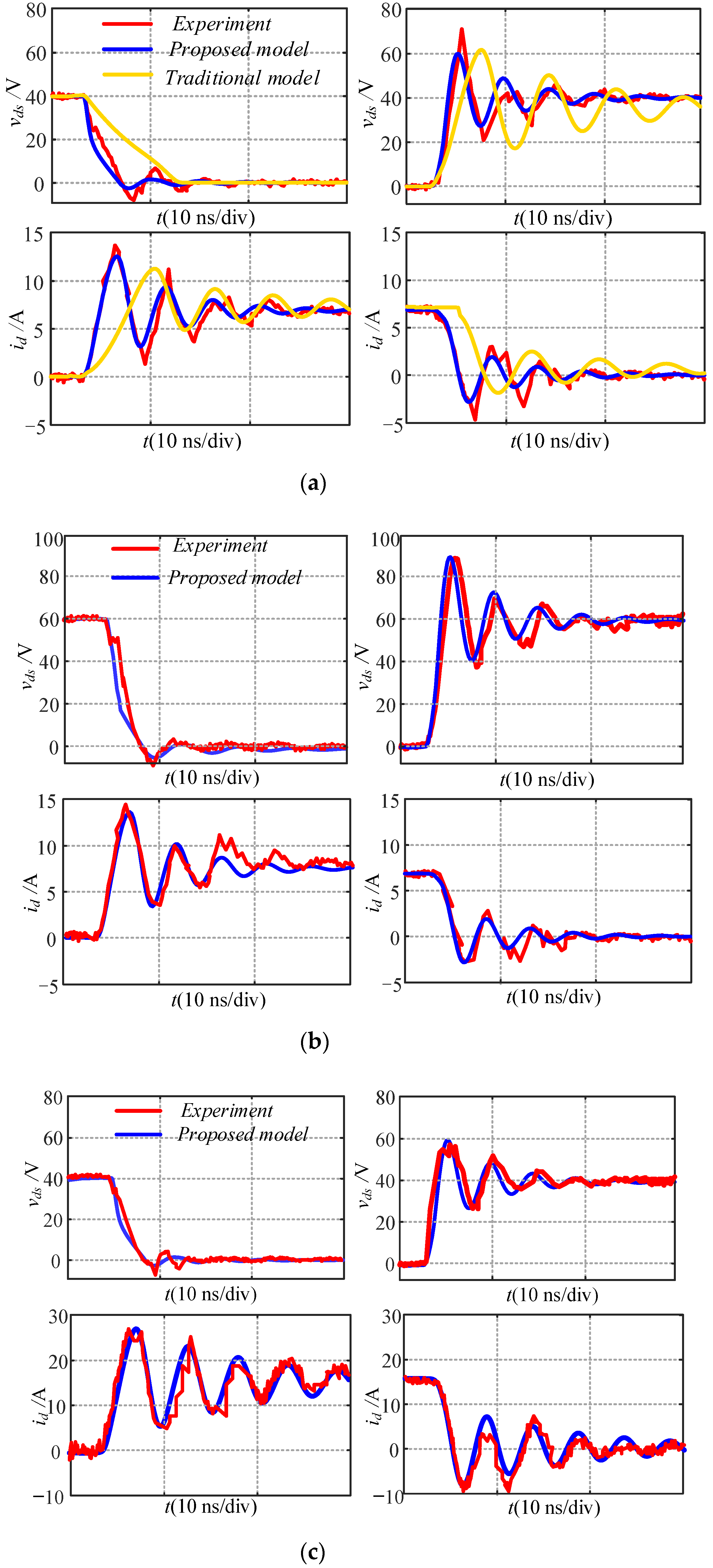
An accurately switching transient analytical model for GaN HEMT considering the influence of nonlinear parameters is proposed in this paper. The analytical derivation of turn-ON process and turn-OFF process is illustrated in detail, and the equivalent circuits are derived for each switching transition. The accuracy of the proposed model is verified by DPT circuit. Experiment results verify that the proposed model is more precise compared with the traditional model. The experimental results show that the maximum relative error of the switching loss can be kept within 10% by the proposed model.

(3)

The effects of gate resistance, gate source capacitance, gate drain capacitance, drain source capacitance, and parasitic inductances on switching characteristic and switching losses are systematically investigated based on the proposed model.

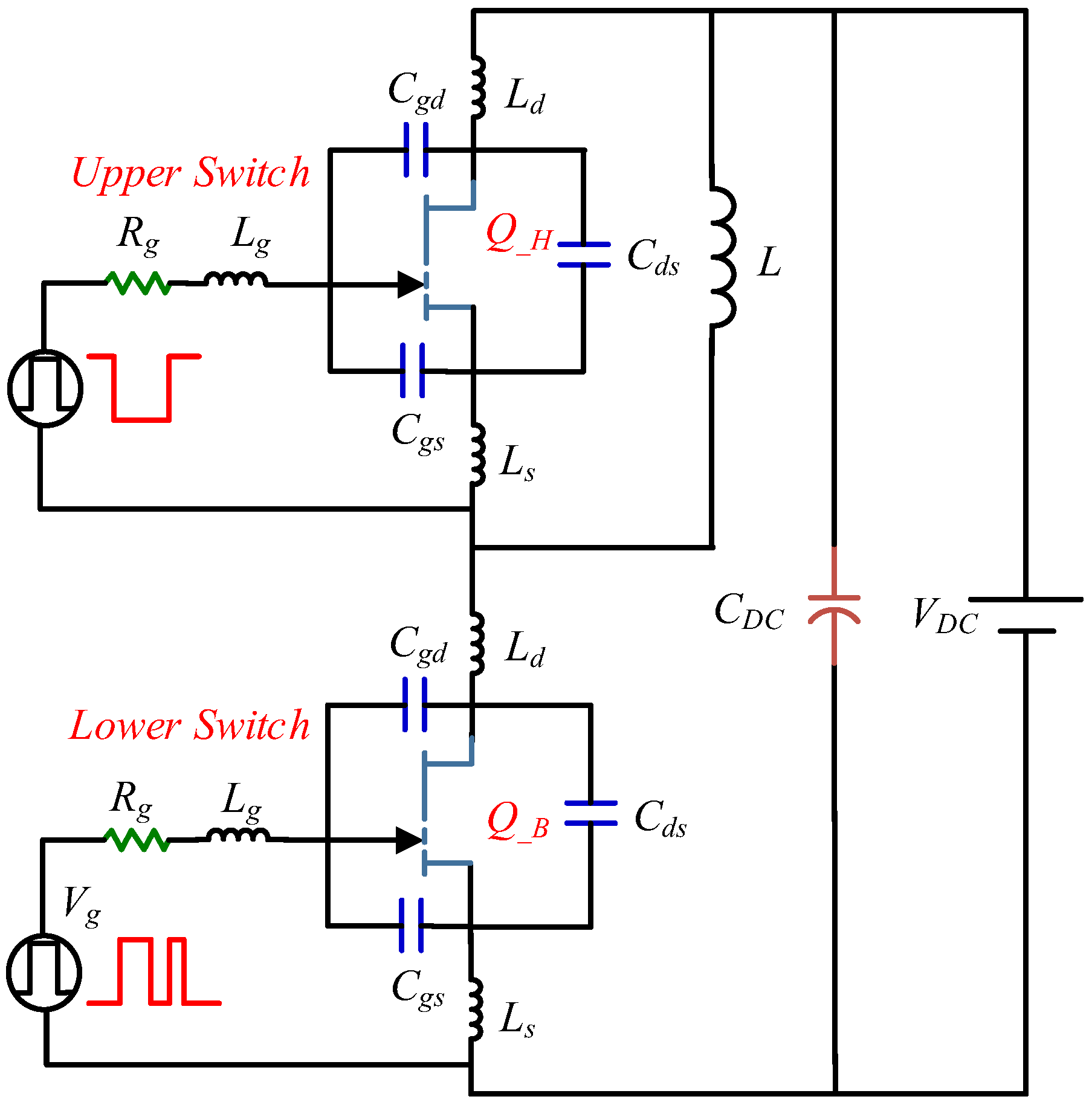
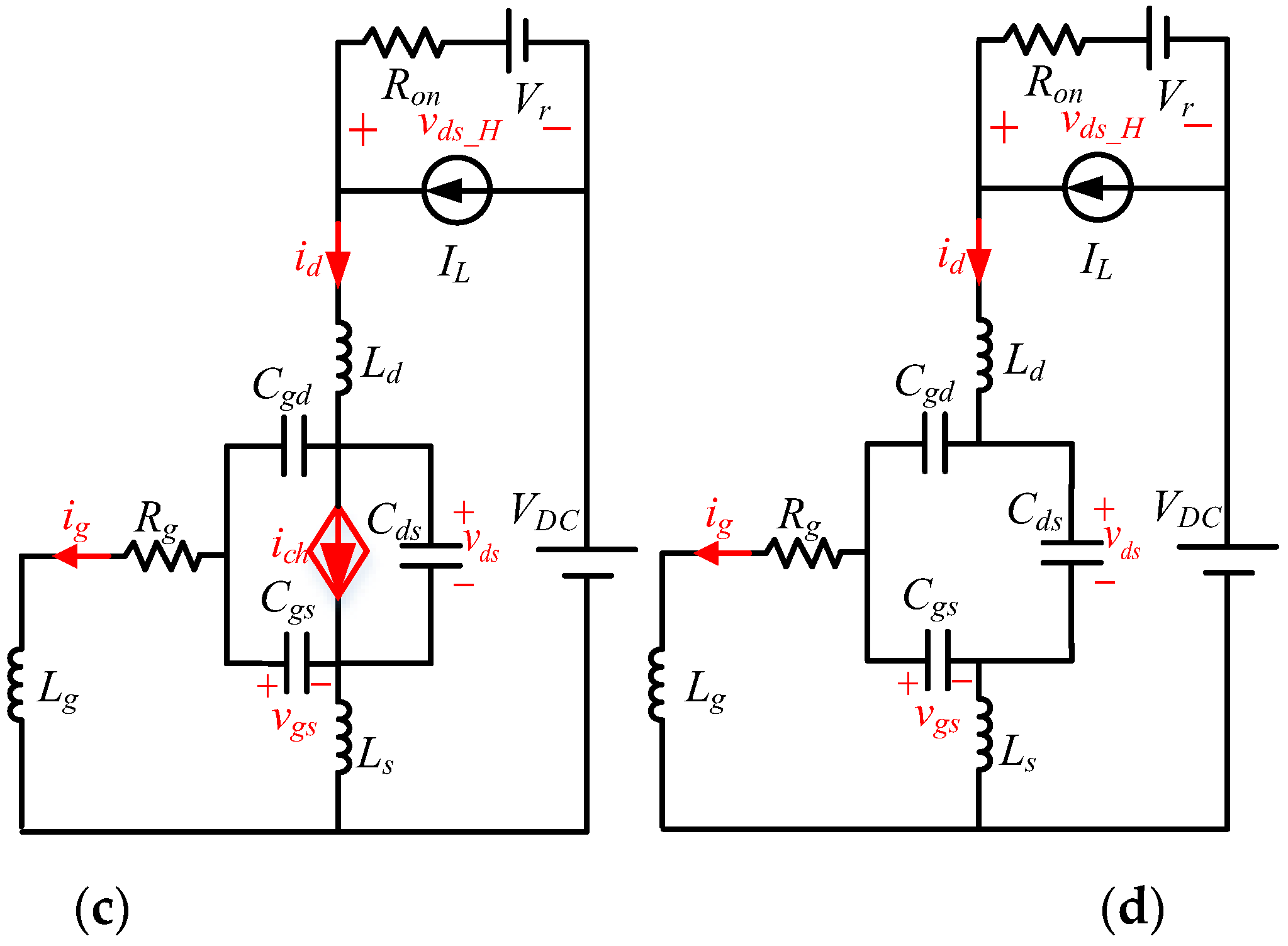
2. Novel Analytical Model of GaN HEMT Device

In order to test and evaluate the switching characteristics of GaN HEMT, a double pulse test (DPT) circuit with inductive load can be adopted as illustrated in Figure 1, where Q and Q_{_H} represent the lower switch and upper GaN HEMT device of the half bridge. In this paper, the GaN HEMT device of GS61004B produced by GaN systems company will be illustrated as an example. C_gs, C_gd, and C_ds represent the capacitors of gate source, gate drain, and drain source, respectively. To simplify the circuit analysis, the parasitic inductance and package stray inductance are accounted into L_d, L_s, L_g. L_loop lumps all of the parasitic inductances and package stray inductances along the power loop. The GaN HEMT device does not contain a p-n diode, but the way they conduct in the reverse direction is similar to diodes because this channel is formed by turning on the two-dimensional electron gas (2DEG) in the device.

In Figure 1, it is very important to determine the parasitic inductances and nonlinear parameters to obtain an accurate switching transient analytical model. Generally, the parasitic inductances can be acquired by Maxwell 3-D software and the nonlinear parameters can be obtained by the modeling method, such as the input capacitance C_iss = C_gs + C_gd, the output capacitance C_oss = C_ds + C_gd, and the reverse capacitance C_rss = C_gd. C_iss and C_rss can be fitted by simple piecewise linear equation due to their low degree of nonlinearity. However, C_oss is a parameter that changes dramatically with the variation of v_ds at low voltage level, which is with high degree of nonlinearity, and is more difficult to be accurately modeled by the above methods. A nonlinear function tanh(x) will be introduced to represent C_oss in this paper, as shown in Equation (1). This function can be used to approximate the C_oss during switching process.

$$\tanh (x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

(1)

Based on tanh(x), a nonlinear function shown in Equation (2) is proposed to fitting the nonlinear characteristic of the C_oss of GS61004B, which can model different changing rate of C_oss when v_ds began to change in low voltage.

$$C_{oss}=C_{o\mathit{max}}{(1+v_{ds}(1+k_1(1+\tanh (k_2\cdot v_{ds}+k_3))))}^{k_4}$$

(2)

where C_omax, k₁, k₂, k₃, and k₄ are the fitting parameters and are given in

Table 1. Fitting parameters.

Symbol	Value
Comax	311 pF
k1	−0.456
k2	−0.51
k3	9.5
k4	−0.256
k5	30
k6	0.75

. This method has more accuracy modeling results. The modeling results C_oss of GaN HEMT is verified in Figure 2a, and it can be concluded that the maximum error between the fitted data and extracted data from the datasheet is less than 3%. Furthermore, this model can also be applied to other different types of devices by adjusting the parameters.

Transconductance g_fs describes the dynamic behavioral feature of i_ch when v_gs changes. Using a single value of transconductance has a large opportunity to cause great errors. In this paper, the slope of the tangent line in the transfer characteristic curve is used to approximate the transconductance at the corresponding operation point. Thus, the equation of g_fs can be expressed as Equation (3).

$$\{\begin{array}{l}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{g}_{fs}=0\hspace{1em}\hspace{1em}\hspace{1em}{v}_{gs}<V_{th}\\ g_{fs}=\frac{d{i}_{ch}}{d{v}_{gs}}=k_5{(v_{gs}-V_{th})}^{k_6-1}\hspace{1em}\hspace{1em}\hspace{1em}{v}_{gs}\ge V_{th}\end{array}$$

(3)

where k₅ and k₆ are the fitting parameters which are given in Table 1 as well. V_th is the threshold voltage of gate to source for the device. Figure 2b shows the curve of i_ch versus v_gs. It is obvious that the modeling result makes an accurate estimation based on the proposed model.

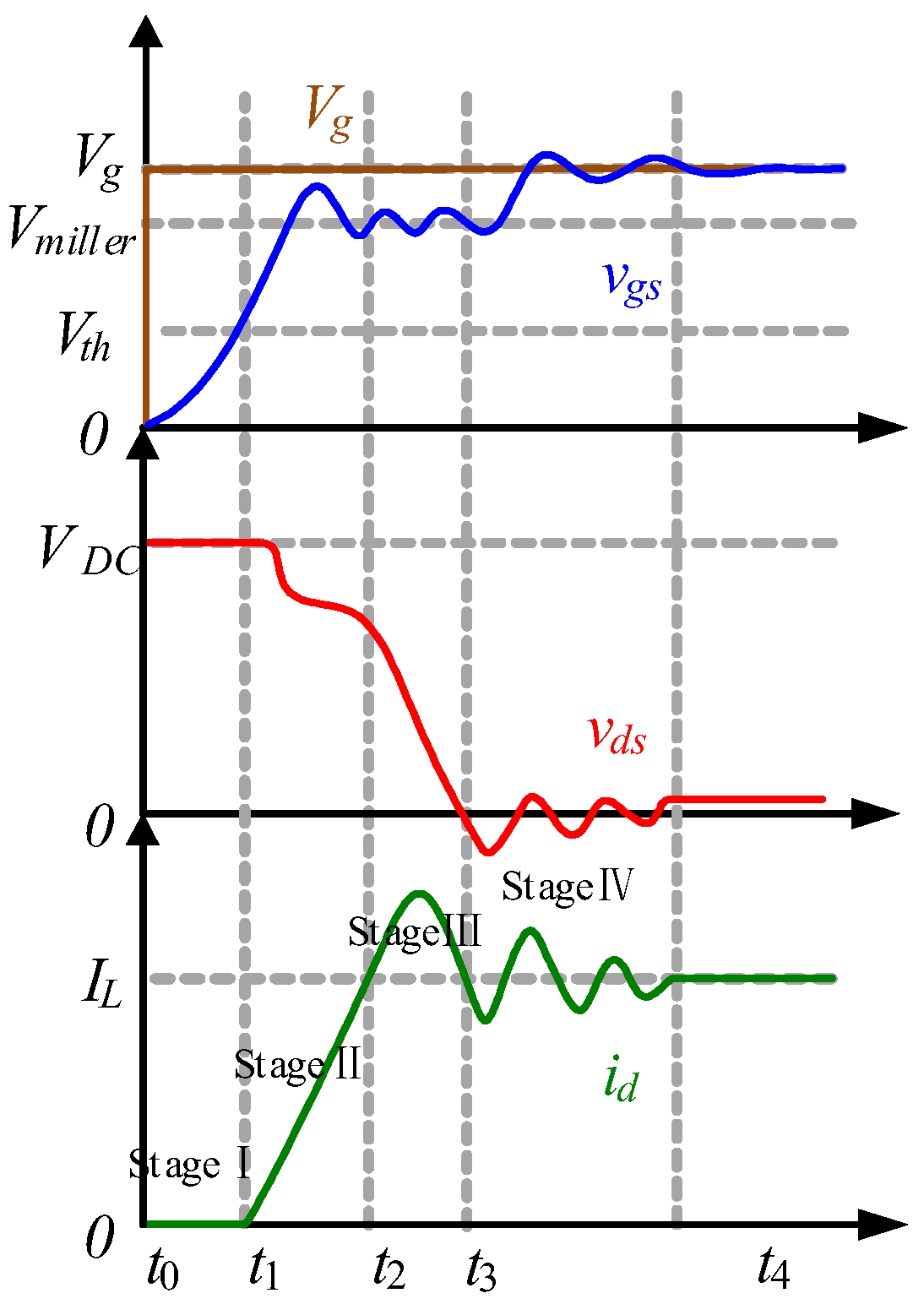
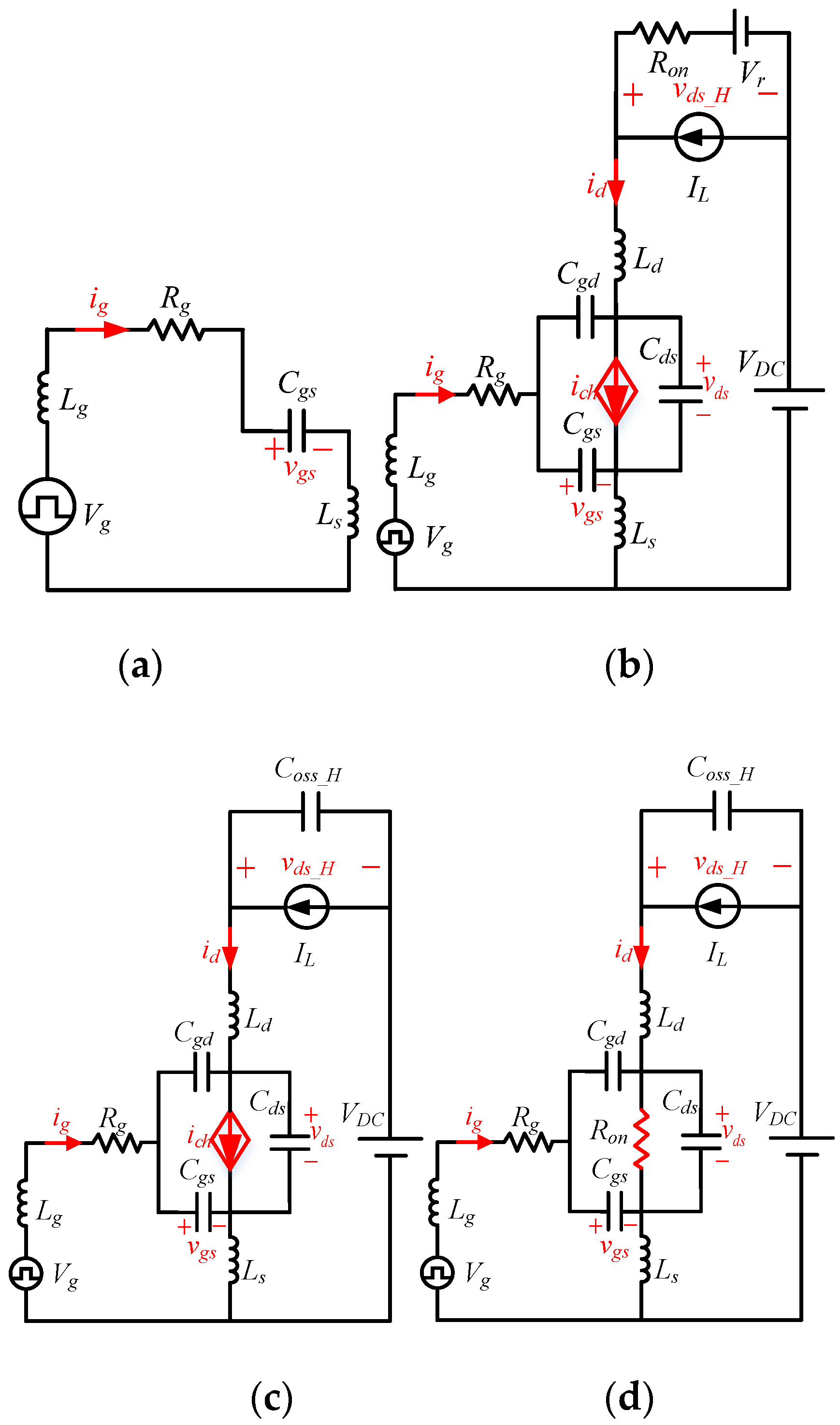
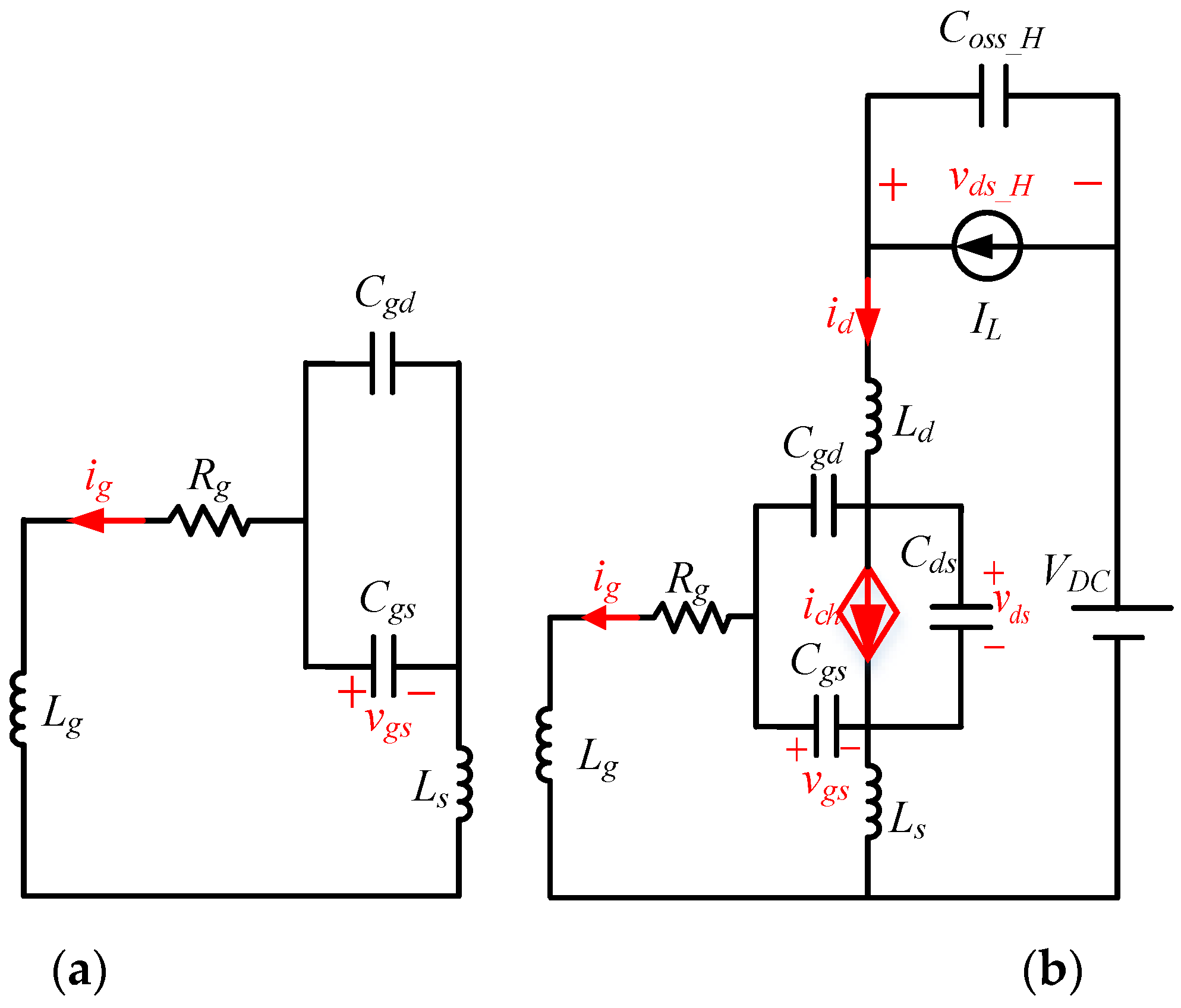
3. Transient Characteristic Analysis of Turn-On Process Based on the Proposed Model

A typical waveform during turn-ON process of the GaN HEMT half bridge is shown in Figure 3. There are four stages during the switching process and each stage has different features according to the change of the circuit structure. At each stage, the equations can be obtained from the corresponding equivalent circuit which is illustrated in Figure 4. By solving the equations, we can obtain five variables, namely, the gate current i_g, the gate source voltage v_gs, the drain current i_d, the drain source voltage v_ds, and the drain source voltage v_{ds_H}. The nonlinear junction capacitance and nonlinear transconductance modeling results proposed in Section 2 will be applied to the turn-ON process in the following analysis. Thus, the analytical model of each variable during turn-ON process can be derived. Furthermore, the switching loss during the turn-ON process can be obtained.

3.1. Stage I (t₀–t₁): Turn-On Delay Period

As shown in Figure 3, at time t₀, the gate drive voltage V_g is applied. In this stage, the gate current charges the capacitance C_gs which causes v_gs to rise. The equivalent circuit of this stage is shown in Figure 4a. According to the equivalent circuit, the following equations can be obtained:

$$V_g=(L_g+L_s)\frac{d{i}_g}{dt}+R_g{i}_g+v_{gs}$$

(4)

$$i_g=C_{gs}\frac{d{v}_{gs}}{dt}$$

(5)

This stage ends at time t₁ when v_gs reaches the threshold voltage V_th. During this stage, Q is still OFF, the drain source voltage v_ds, and the drain current i_d are constant, so there is no switching loss.

3.2. Stage II (t₁–t₂): Current Rise Period

As shown in Figure 3, at time t₁, v_gs reaches the threshold voltage V_th, and the channel current i_ch begins to rise which can be expressed by Equation (3). At the same time, the capacitances C_oss begins to discharge through the channel of Q. The drain current id is clamped to the sum of the channel current i_ch and the C_oss discharging current. However, Q_{_H} is still in reverse conduction condition, where R_on is the on-state resistance and V_r represents the reverse conducting voltage drop of Q_{_H}. There will be a voltage drop ΔV between v_ds and its initial voltage V_DC + V_r on the parasitic inductance of the power loop. As shown in the equivalent circuit of Figure 4b, the equations of this stage are as follows:

$$V_g=v_{gs}+R_g{i}_g+L_g\frac{d{i}_g}{dt}+L_s(\frac{d{i}_d}{dt}+\frac{d{i}_g}{dt})$$

(6)

$$i_g=C_{gs}\frac{d{v}_{gs}}{dt}+C_{gd}(\frac{d{v}_{gs}}{dt}-\frac{d{v}_{ds}}{dt})$$

(7)

$$i_d=g_{fs}(v_{gs}-V_{th})+C_{ds}\frac{d{v}_{ds}}{dt}-C_{gd}\frac{d(v_{gs}-v_{ds})}{dt}$$

(8)

$$V_{DC}=v_{ds}+v_{ds\_H}+(L_d+L_s)\frac{d{i}_d}{dt}+L_s\frac{d{i}_g}{dt}$$

(9)

$$v_{ds\_H}=R_{on}(I_L-i_d)-V_r$$

(10)

This stage ends when the drain current i_d reaches the load current I_L. Meanwhile, v_gs reaches Miller plateau voltage. It should be especially noted that the voltage drop ΔV is shown in the following equation:

$$\Delta V=(L_d+L_s)\frac{d{i}_d}{dt}$$

(11)

In case of L_d and L_s being larger, ΔV will drop faster, so i_d would change even slower than v_ds. The transient will skip the voltage drop stage III into ringing stage IV directly. While for small L_d and L_s of properly designed PCB and reasonable current rising speed, stage III will occur as expected.

During this stage, the energy loss can be expressed as:

$$E_{on}={\displaystyle {\int }_{t2}^{t1}{v}_{ds}\cdot i_{ch}dt}$$

(12)

The power loss in this stage can be determined by:

$$\begin{array}{ll}{P}_{on}& =f_s\cdot E_{on}\\ & =f_s\cdot {\displaystyle {\int }_{t2}^{t1}{v}_{ds}\cdot i_{ch}dt}\end{array}$$

(13)

where f_s is the switching frequency. However, only id can be measured experimentally, ich cannot. During the turn-ON process, a part of the energy stored in C_oss is dissipated through the channel, which is not included in the loss calculated by i_d. Thus, the relationship can be expressed as:

$$P_{on}=f_s\cdot {\displaystyle {\int }_{t2}^{t1}{v}_{ds}\cdot i_{d}dt}+P_{Coss}$$

(14)

where P_Coss represents the energy stored in the output capacitance when the applied voltage is V_DC + V_r and can be expressed as:

$$P_{Coss}=f_s\cdot {\displaystyle {\int }_0^{V_{DC}+V_r}{v}_{ds}\cdot C_{oss}(v_{ds})d{v}_{ds}}$$

(15)

C_oss(v_ds) can be determined by Equation (2), which is plotted in Figure 2a.

3.3. Stage III (t₂–t₃): Voltage Decline Period

As shown in Figure 3, at time t₂, the upper switch GaN HEMT device Q_{_H} stops conducting, and the channel current i_ch surpasses the load current I_L. This surpasses current charge of the output capacitance C_{oss_H} of Q_{_H}. The upper switch can be equivalent to the output capacitor C_{oss_H}, and v_{ds_H} is increased. Correspondingly, v_ds decreases and C_oss continues to discharge through the channel of Q. i_d may have a ringing because of the effect of parasitic LC elements on the device. The equivalent circuit of this stage is illustrated in Figure 4c. The circuit equations can be expressed as:

$$i_d=g_{fs}(v_{gs}-V_{th})+C_{ds}\frac{d{v}_{ds}}{dt}-C_{gd}\frac{d(v_{gs}-v_{ds})}{dt}$$

(16)

$$V_g=v_{gs}+R_g{i}_g+L_g\frac{d{i}_g}{dt}+L_s(\frac{d{i}_d}{dt}+\frac{d{i}_g}{dt})$$

(17)

$$i_g=C_{gs}\frac{d{v}_{gs}}{dt}+C_{gd}(\frac{d{v}_{gs}}{dt}-\frac{d{v}_{ds}}{dt})$$

(18)

$$V_{DC}=v_{ds}+v_{ds\_H}+(L_d+L_s)\frac{d{i}_d}{dt}+L_s\frac{d{i}_g}{dt}$$

(19)

$$i_d=I_L+C_{oss\_H}\frac{d{v}_{ds\_H}}{dt}$$

(20)

This period ends when v_ds decreases to zero. A current overshoot is caused by the rapid dv/dt action on the output capacitance:

$$\Delta i_d=C_{oss\_H}\frac{d{v}_{ds\_H}}{dt}-C_{oss}\frac{d{v}_{ds}}{dt}$$

(21)

In addition, the Miller plateau time on v_gs for GaN HEMT is less than Si MOSFET because of small transfer capacitance C_gd. This characteristic can help us to understand why GaN HEMT can turn-ON at a high speed. The turn-ON switching loss calculation method is the same as that of Equation (15).

3.4. Stage IV (t₃–t₄): Ringing Period

As shown in Figure 3, at time t₃, Q will work in the linear region and behave equivalent to a loop resistor, as illustrated in Figure 4d. Usually, the ringing is serious due to small damping resistance with large parasitic inductances. The key equations can be expressed as:

$$V_g=v_{gs}+R_g{i}_g+L_g\frac{d{i}_g}{dt}+L_s(\frac{d{i}_d}{dt}+\frac{d{i}_g}{dt})$$

(22)

$$i_g=C_{gs}\frac{d{v}_{gs}}{dt}+C_{gd}(\frac{d{v}_{gs}}{dt}-\frac{d{v}_{ds}}{dt})$$

(23)

$$V_{DC}=v_{ds}+v_{ds\_H}+(L_d+L_s)\frac{d{i}_d}{dt}+L_s\frac{d{i}_g}{dt}$$

(24)

$$i_d=\frac{v_{ds}}{R_{on}}+C_{ds}\frac{d{v}_{ds}}{dt}-C_{gd}\frac{d(v_{gs}-v_{ds})}{dt}$$

(25)

$$i_d=I_L+C_{oss\_H}\frac{d{v}_{ds\_H}}{dt}$$

(26)

where R_on represents the on-state resistance of Q. During this stage, the turn-ON switching loss can be expressed as:

$$P_{on}=f_s\cdot {\displaystyle {\int }_{t4}^{t3}{(i_d-I_L)}^2\cdot R_{on}dt}$$

(27)

This period ends when the ringing is fully damped.

4. Transient Characteristic Analysis of Turn-Off Process Based on the Proposed Model

There are still four stages and the typical waveforms during turn-OFF process. At each stage, the equations can be obtained from each equivalent circuit. Similarly, the nonlinear junction capacitance and nonlinear transconductance modeling results proposed in Section 2 are applied to the turn-OFF process and five state variables can be calculated according to the equations obtained from the equivalent circuit of each stage. Furthermore, the switching loss during the turn-OFF process can be obtained. The calculation of each stage will be discussed as follows.

4.1. Stage I (t₅–t₆): Turn-Off Delay Period

As shown in Figure 5, at time t₅, the gate drive voltage V_g declines to 0 V. In this stage, C_gs and C_gd are discharged, so v_gs begins to reduce. However, Q is still in the turn-ON state, I_L keeps flowing through the channel of Q. The equivalent circuit of this stage is shown in Figure 6a. The following equations can be obtained:

$$0=(L_g+L_s)\frac{d{i}_g}{dt}+R_g{i}_g+v_{gs}$$

(28)

$$i_g=(C_{gs}+C_{gd})\frac{d{v}_{gs}}{dt}$$

(29)

This period ends at time t₆ when v_gs reaches the Miller plateau voltage v_miller.

$$v_{miller}=V_{th}+\frac{I_L}{g_{fs}}$$

(30)

v_ds and i_d are constants, so there is no turn-OFF switching loss in this stage.

4.2. Stage II (t₆–t₇): Voltage Rise Period

As shown in Figure 5, at time t₆, the channel of Q starts to turn-OFF, so the channel current i_ch decreases and begins to charge the capacitances C_ds and C_gd, then v_ds is rapidly increased. At the same time, C_{oss_H} begins to discharge, resulting in the decline of v_{ds_H}. However, Q_{_H} is still not reverse conducting because i_d is limited by the power loop parasitic inductances. Therefore, the decrease rate of i_d is smaller than that of i_ch. The equivalent circuit is shown in Figure 6b, and the equations of this stage are as follows:

$$0=v_{gs}+R_g{i}_g+L_g\frac{d{i}_g}{dt}+L_s(\frac{d{i}_d}{dt}+\frac{d{i}_g}{dt})$$

(31)

$$i_g=C_{gs}\frac{d{v}_{gs}}{dt}+C_{gd}(\frac{d{v}_{gs}}{dt}-\frac{d{v}_{ds}}{dt})$$

(32)

$$i_d=g_{fs}(v_{gs}-V_{th})+C_{ds}\frac{d{v}_{ds}}{dt}-C_{gd}\frac{d(v_{gs}-v_{ds})}{dt}$$

(33)

$$V_{DC}=v_{ds}+v_{ds\_H}+(L_d+L_s)\frac{d{i}_d}{dt}$$

(34)

$$i_d=I_L+C_{oss\_H}\frac{d{v}_{ds\_H}}{dt}$$

(35)

This period ends when v_{ds_H} reaches −V_r. During this stage, the energy loss can be calculated as:

$$E_{off}={\displaystyle {\int }_{t7}^{t6}{v}_{ds}\cdot i_{ch}dt}$$

(36)

The power loss in this stage can be determined by:

$$\begin{array}{ll}{P}_{off}& =f_s\cdot E_{off}\\ & =f_s\cdot {\displaystyle {\int }_{t7}^{t6}{v}_{ds}\cdot i_{ch}dt}\end{array}$$

(37)

Usually, the energy stored in C_oss is quite large due to the high peak v_ds. The power loss is different from turn-ON process because i_d contains the charge current from C_oss. Thus, the relationship can be modified as:

$$P_{off}=f_s\cdot {\displaystyle {\int }_{t7}^{t6}{v}_{ds}\cdot i_{d}dt}-P_{Coss}$$

(38)

where P_Coss is the energy stored in C_oss when the applied voltage is v_Peak and can be calculated as:

$$P_{Coss}=f_s\cdot {\displaystyle {\int }_0^{v_{peak}}{v}_{ds}\cdot C_{oss}(v_{ds})d{v}_{ds}}$$

(39)

C_oss(v_ds) can be determined by Equation (2) and is plotted in Figure 2a.

4.3. Stage III (t₇–t₈): Current Decline Period

As shown in Figure 5, at time t₇, Q_{_H} starts to reverse conduct. During this stage, i_d and v_gs decreases, v_ds continues to increase, and C_ds and C_gd are charged. The equivalent circuit is shown in Figure 6c, and the circuit equations can be expressed as:

$$0=v_{gs}+R_g{i}_g+L_g\frac{d{i}_g}{dt}+L_s(\frac{d{i}_d}{dt}+\frac{d{i}_g}{dt})$$

(40)

$$i_g=C_{gs}\frac{d{v}_{gs}}{dt}+C_{gd}(\frac{d{v}_{gs}}{dt}-\frac{d{v}_{ds}}{dt})$$

(41)

$$i_d=g_{fs}(v_{gs}-V_{th})+C_{ds}\frac{d{v}_{ds}}{dt}-C_{gd}\frac{d(v_{gs}-v_{ds})}{dt}$$

(42)

$$V_{DC}=v_{ds}+v_{ds\_H}+(L_d+L_s)\frac{d{i}_d}{dt}+L_s\frac{d{i}_g}{dt}$$

(43)

$$v_{ds\_H}=R_{on}(I_L-i_d)-V_r$$

(44)

This stage ends when i_d drops to zero. The turn-OFF power loss calculation method is the same as Stage II.

4.4. Stage IV (t₈–t₉): Ringing Period

As shown in Figure 5, at time t₈, when v_gs drops below V_th, the channel of Q is totally shut down. Then v_gs continues to decrease until it reaches zero. During this stage, v_ds and i_d both have a ringing due to the oscillation between the parasitic inductances and C_oss. The equivalent circuit is shown in Figure 6d, and the circuit equations can be expressed as:

$$0=v_{gs}+R_g{i}_g+L_g\frac{d{i}_g}{dt}+L_s(\frac{d{i}_d}{dt}+\frac{d{i}_g}{dt})$$

(45)

$$i_g=C_{gs}\frac{d{v}_{gs}}{dt}+C_{gd}(\frac{d{v}_{gs}}{dt}-\frac{d{v}_{ds}}{dt})$$

(46)

$$i_d=C_{ds}\frac{d{v}_{ds}}{dt}-C_{gd}\frac{d(v_{gs}-v_{ds})}{dt}$$

(47)

$$V_{DC}+V_r=v_{ds}+(L_d+L_s)\frac{d{i}_d}{dt}$$

(48)

During this stage, the turn-OFF power loss calculation method can be expressed as:

$$P_{off}=f_s\cdot {\displaystyle {\int }_{t9}^{t8}{i}_d\cdot v_{ds}dt}$$

(49)

This period ends when the ringing is fully damped.

5. Experimental Verifications

In order to verify the accuracy of the proposed switching transient analytical model, a DPT experiment prototype was built, as shown in Figure 7. The double pulses will be applied to the gate of the bottom GaN HEMT by TMS320F28335. The device under test is the GS61004B 100 V enhanced GaN HEMT and the driver is Si8271. The oscilloscope is MDPO3054 by Tektronix Inc. The switching current is measured with 2000 MHz bandwidth current shunt SSDN-10 by T&M Research Products Inc. The parasitic inductance and package stray inductance can be acquired by Maxwell 3-D. The specifications and the main circuit parameters are shown in

Table 2. Specifications and main circuit parameters.

Parameters	Value
VDC	40 V
IL	7 A
Ron	0.57 Ω
Ls	5.6 nH
Ld	3.7 nH
Lg	2.8 nH
Rg	10 Ω
Vg	6 V

. The comparisons among the switching waveforms provided by the experiment, the proposed model, and the traditional mode in [16] are shown in Figure 8. The calculated results from the models for the variables v_ds and i_d with fitting value from Figure 2 will be used to evaluate the model accuracy. The loss calculation results are shown in Figure 9.

It can be concluded that the proposed model matches more accurately with the experimental results than the traditional model according to the slope and spike of i_d and v_ds from Figure 8. The oscillation frequency and amplitude of the waveforms from the experimental results deviate from the traditional model while the proposed model results agree with that accurately. The reason is that the traditional model treats the nonlinear parameters in the device as fixed values.

Subsequently, the energy loss of E_on and E_off is calculated by the proposed loss calculation method as shown in Figure 9. The results show that the energy loss increases when the load current changes from 5 A to 10 A. It is obvious that the loss calculation results of the proposed model in this paper are more precise compared with the traditional model. Experiment results verify the accuracy of the proposed loss calculation method with a maximum relative error of less than 10%. Finally, it can be concluded that the proposed switching transient analytical model is quite accurate and the loss analysis results based on the model is believable.

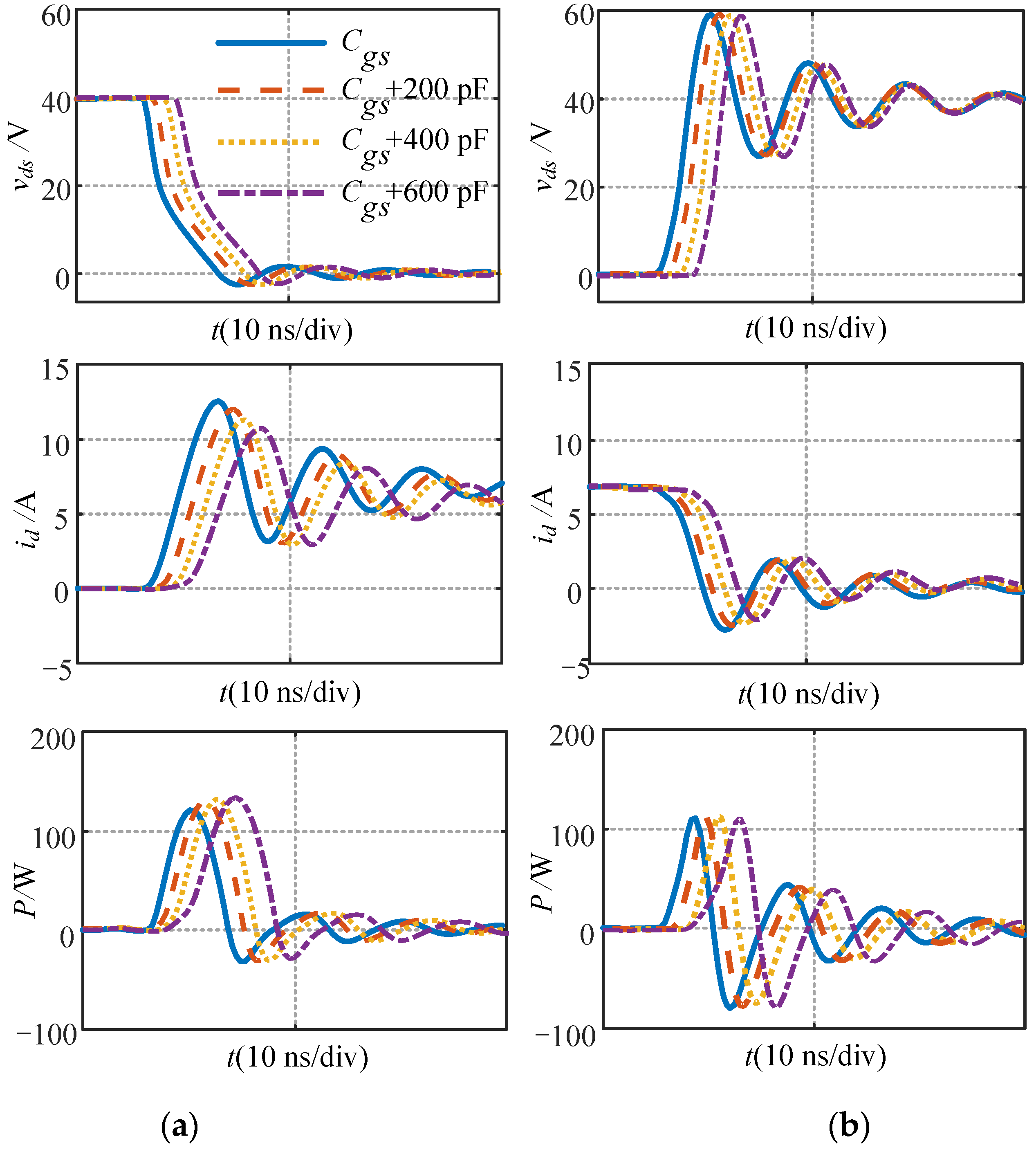
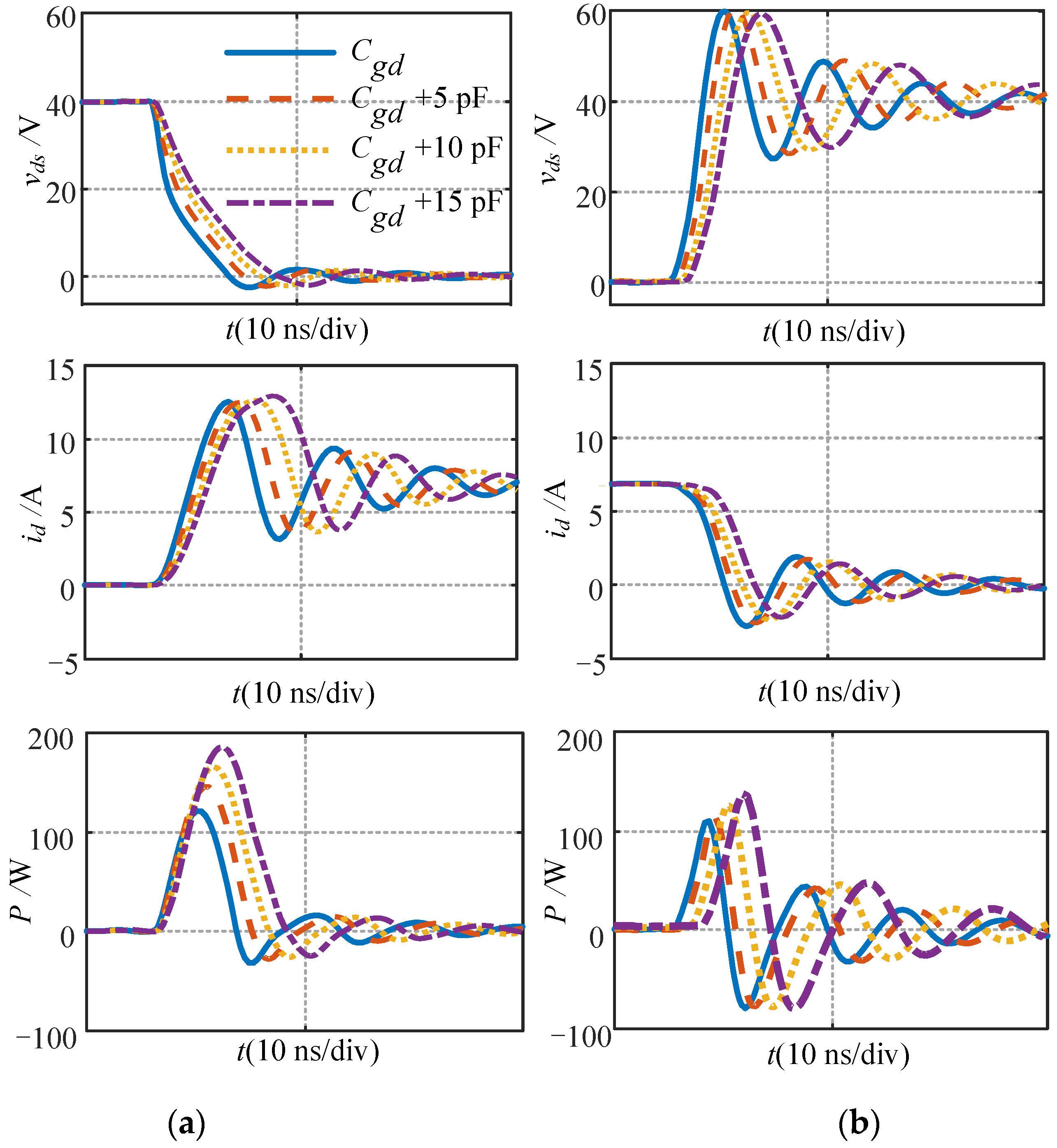
6. Effect of Parameter Variation on the Analytical Model

The effectiveness of the proposed switching transient analytical model is verified in the previous section. Moreover, it is important to evaluate how the gate resistance R_g, the nonlinear junction capacitances C_gs, C_gd, C_ds, and the parasitic inductance L_loop affect the switching transient and switching loss, thus the further improvement of packaging and application of the device can be inspired.

Figure 10 shows the effect of different driving resistors R_g on the switching transition behavior. The waveforms of v_ds and i_d are plotted. It can be seen that the oscillation of v_ds and i_d can be effectively suppressed by increasing the R_g. However, the larger R_g limits the gate charging current and reduces the charging speed, thus resulting the switching time increase of the device. In addition, Figure 10 also calculates the influence of different R_g on switching loss. With the increase of R_g, the turn-ON and turn-OFF switching loss is also increased. However, with the increase of R_g, the current overshoot for turn-ON transient and the voltage overshoot for turn-OFF transient decreased. Therefore, considering the impact of switching loss and overshoot in practical application, it is necessary to select an appropriate R_g value.

In order to simplify the analysis, L_loop lumps all of the parasitic inductances and package stray inductances along the power loop. As the package stray inductances are accounted into L_d and L_s, so L_loop is the sum of L_d and L_s. The effect of different L_loop on the switching transition behavior is shown in Figure 11. During the turn-ON process, the change rate of i_d and v_ds become slower with the increase of L_loop. Meanwhile, the current overshoot decreases but the voltage overshoot increases. In addition, the ringing period of i_d and v_ds becomes larger. These factors cause the turn-ON switching loss to become larger due to overlap area increases. During the turn-OFF process, the increase of L_loop has an obvious influence on i_d overshoot, which also leads to the increase of loss. It can be concluded that the total loss also increases, therefore, the value of L_loop should be minimized as much as possible on the PCB design and optimization process.

For the same type of GaN HEMT, the value of the nonlinear junction capacitances should be the same. However, due to different production processes or different production lines, the capacitance values may change. In order to explore the effect of the nonlinear junction capacitance on the switching transient, we make corresponding changes for each nonlinear junction capacitance value within a reasonable range.

The influence of C_gs is shown in Figure 12. Set the variation value of C_gs as 200 pF, 400 pF, 600 pF. It is observed that the increasing of C_gs caused the charge time to become longer, thus resulting in the turn-ON delay time notably increasing. Meanwhile, the current overshoot and the voltage overshoot during the turn-OFF process can be suppressed by increasing C_gs. In general, C_gs can effectively reduce the waveform oscillation, but will also lead to an increase in switching loss. Therefore, an extra capacitor paralleled with C_gs can be used to reduce the oscillation when the oscillation is too large. However, the value of the parallel capacitor should be selected properly, otherwise the loss will be too large.

The effect of C_gd is shown in Figure 13. As stated previously, the increase of C_gd has a large effect on the switching loss model. It can be concluded that the magnitude of C_gd mainly affects the turn-ON process, i.e., the change rate of i_d and v_ds decreases and the conducting time increases. Although the increase of C_gd is only 5 pF–15 pF, it has a great impact on the on-off time and switching loss due to the capacitor which affects the length of Miller platform time. Therefore, C_gd should be designed as small as possible in device production. Compared with the Si devices, GaN HEMT is able to achieve much faster switching speeds and lower switching losses due to its smaller C_gd.

The influence of C_ds is shown in Figure 14. As we know, C_oss is a nonlinear junction capacitance of v_ds. It can be concluded that the increase of C_ds mainly affects the change rate of i_d. Since C_oss increases with the increase of C_ds, according to Equation (17), the energy stored in C_oss will increase, which will result in an increase in the switching loss. In addition, the switching speed is increased and the ringing period becomes larger. For the convenience of overall consideration, the influencing parameter of switching characteristics and their specific impact analysis are listed in

Table 3. Analysis of The Influencing Parameter of Switching Characteristics.

Parameters	Turn-On Switching Speed	Turn-Off Switching Speed	Turn-On Current Overshoot	Turn-Off Voltage Overshoot	Turn-Off Current Overshoot	Turn-On Loss	Turn-Off Loss
Rg	Increase	Increase	Decrease	Decrease	Decrease	Increase	Increase
Lloop	Increase	Increase	Decrease	Invariant	Increase	Increase	Increase
Cgs	Increase	Increase	Decrease	Invariant	Decrease	Increase	Increase
Cgd	Increase	Increase	Increase	Invariant	Invariant	Increase	Increase
Cds	Invariant	Increase	Invariant	Invariant	Increase	Invariant	Increase

.

7. Conclusions

In this paper, an accurate switching transient analytical model for GaN HEMT under the influence of nonlinear parameters was proposed. The proposed model covers the process of turn-ON and turn-OFF, which is of great significance in understanding the dynamic characteristics during the switching process. In addition, this model can be applied to evaluate the influence of parameter changes on the switching characteristics of devices, and calculate the switching loss. Finally, the following conclusions can be drawn:

(1)

Switching speed. The switching process of the GaN HENT are essentially the charging process of its nonlinear junction capacitances. With the increases of C_gs, C_gd, C_ds, L_loop and R_g, the switching speed is slowed down. Since the channel current is gate-source voltage dependent in the saturation region, it is out of the question that C_gs can affect the current slew rate. As for the voltage slew rate, it is clarified that the charging of C_gd leads to the change in the drain source voltage. The loop parasitic inductances L_loop and gate resistance R_g decrease the change rate of i_d and v_ds with the increase of L_loop and R_g.

(2)

Current and voltage overshoot. The current and voltage overshoot in switching transient can be suppressed by increasing R_g. The current overshoot can be suppressed by increasing C_gs. The current and voltage overshoot can be worsened by increasing L_loop. The current overshoot can be worsened by increasing C_ds. C_gd cannot affect the current and voltage overshoot.

(3)

Switching loss. Both C_gs, C_gd, C_ds, L_loop and R_g increases switching loss by slowing down the switching speed and prolonging the switching process.

(4)

Design guidelines. It can be concluded that parameter changes of the GaN HEMT have a profound influence on the switching performance; hence, it calls for special attention to the selection of components and circuit design. The voltage change rate is most sensitive to C_gd, L_loop and R_g; for high-speed high-voltage applications, these values should not be large. The current change rate is most sensitive to C_gs, C_ds, L_loop, and R_g. Therefore, the PCB traces should be carefully routed to reduce the stray inductance in the circuit. The other parasitic elements should be minimized to achieve fast switching and low loss.