Hydraulic Tests of the PZ0 Gear Micropump and the Importance Rank of Its Design and Operating Parameters
Abstract
:1. Introduction
1.1. Gear Pumps in Microhydraulics
1.2. Knowledge Management in Terms of Expert Systems
1.3. Methodology
- (1)
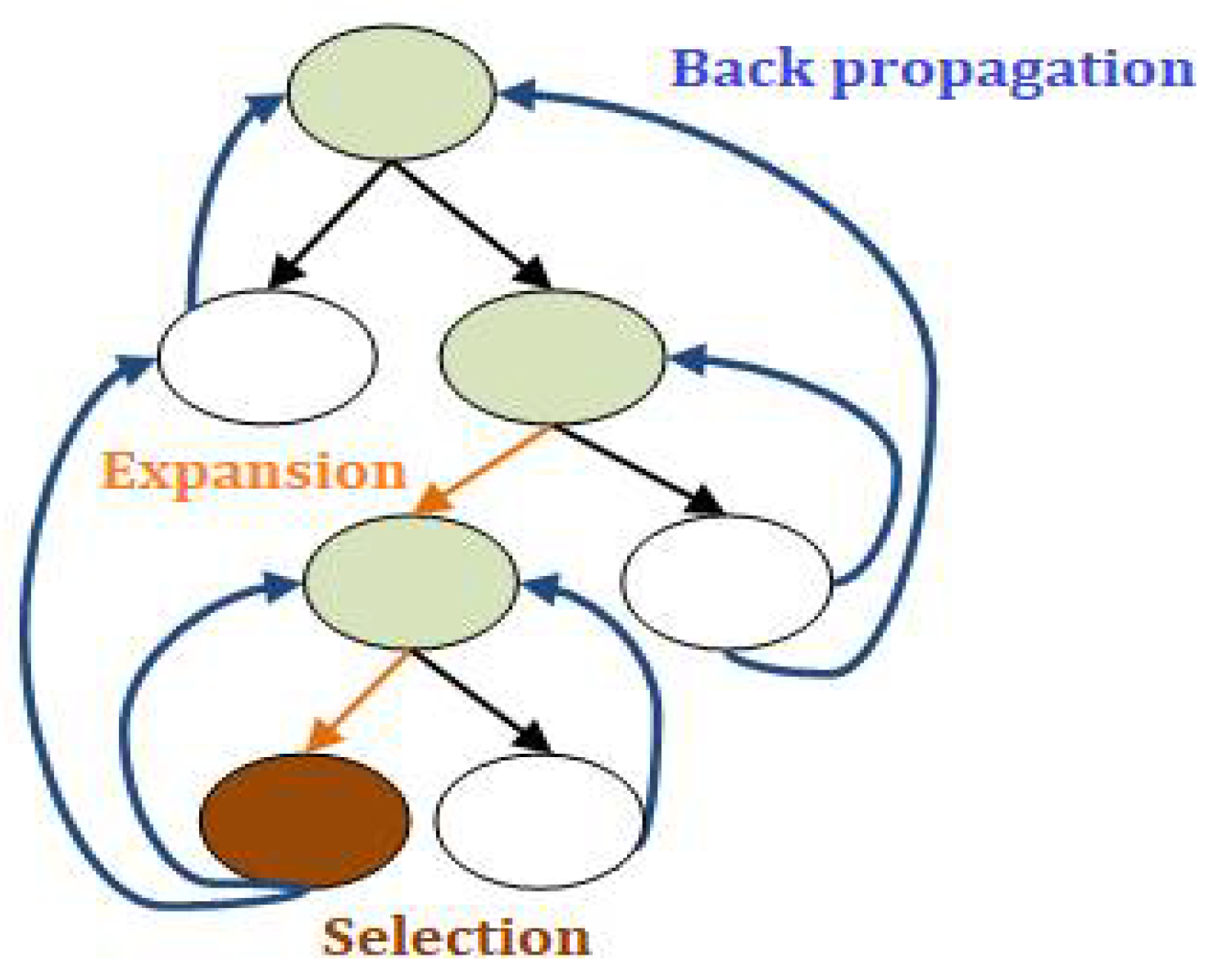
- An inductive decision tree generator (a modified DeTreex program was used)
- (2)
- domain-independent rule language tool (a modified PC Shell program was used).
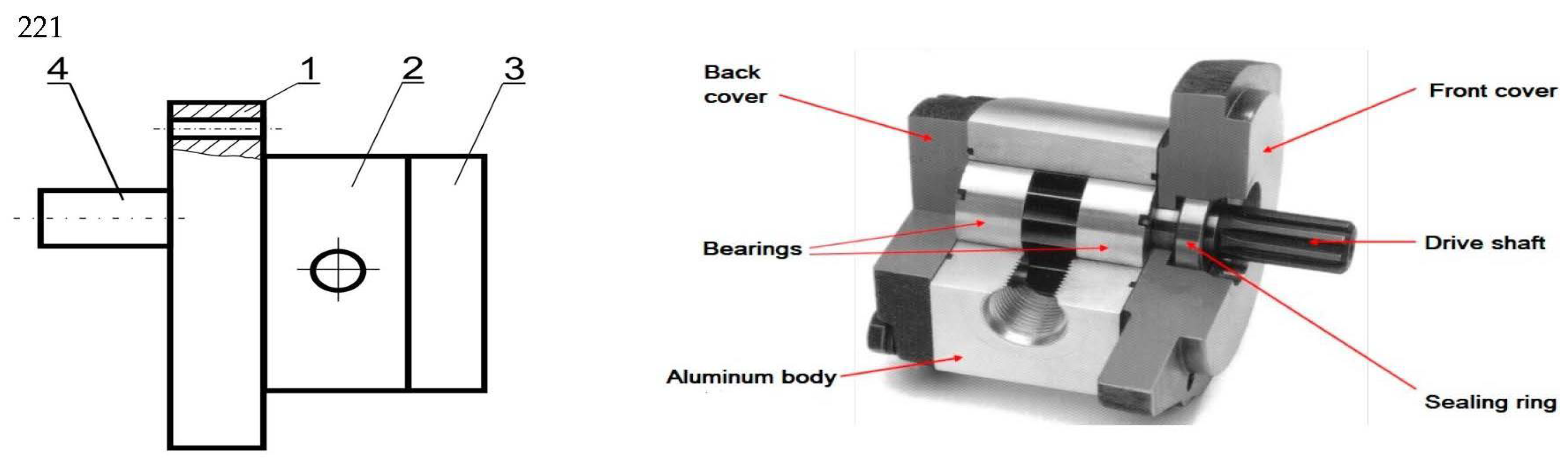
2. The Research Object and Test Stand
Test Stand
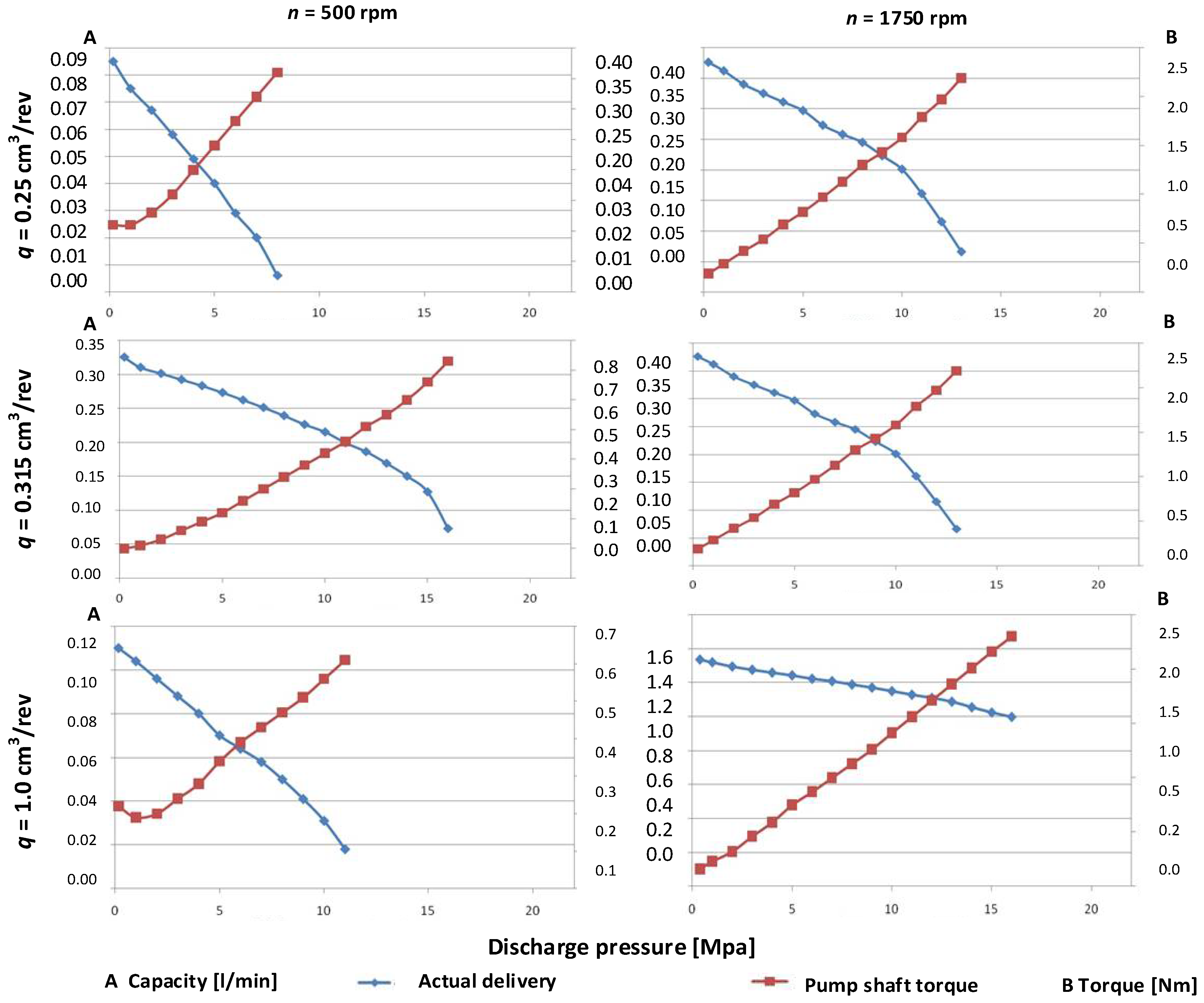
3. Hydraulic Tests of the Micropump
Selected Measurement Results for the Azolla ZS 22 Hydraulic Oil
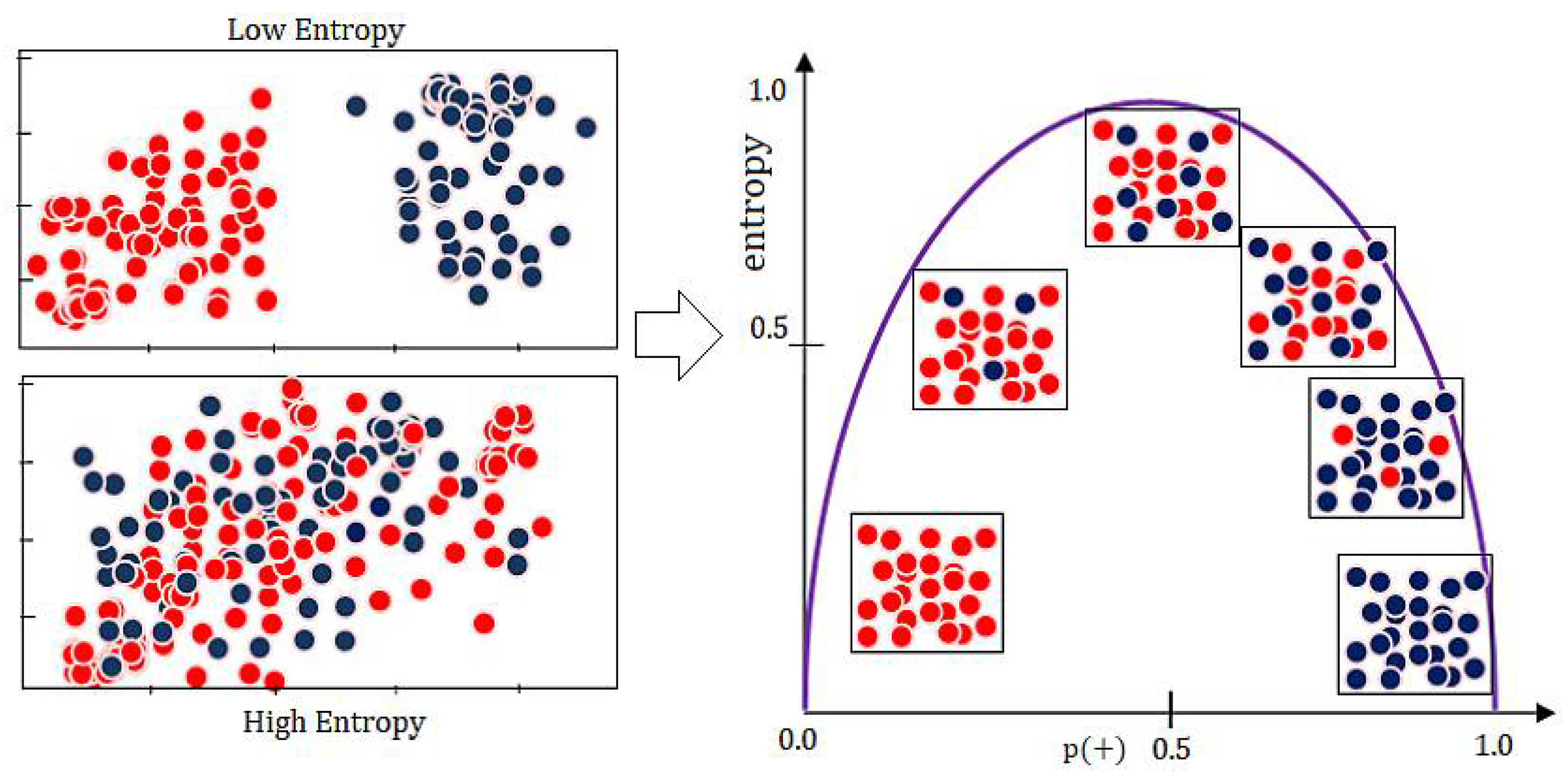
4. Tests of the Importance Rank of the Design and Operating Parameters from a Classification Perspective
4.1. Determination of Importance Rank for Design Parameters with the Use of the Rule-Based Knowledge Representation
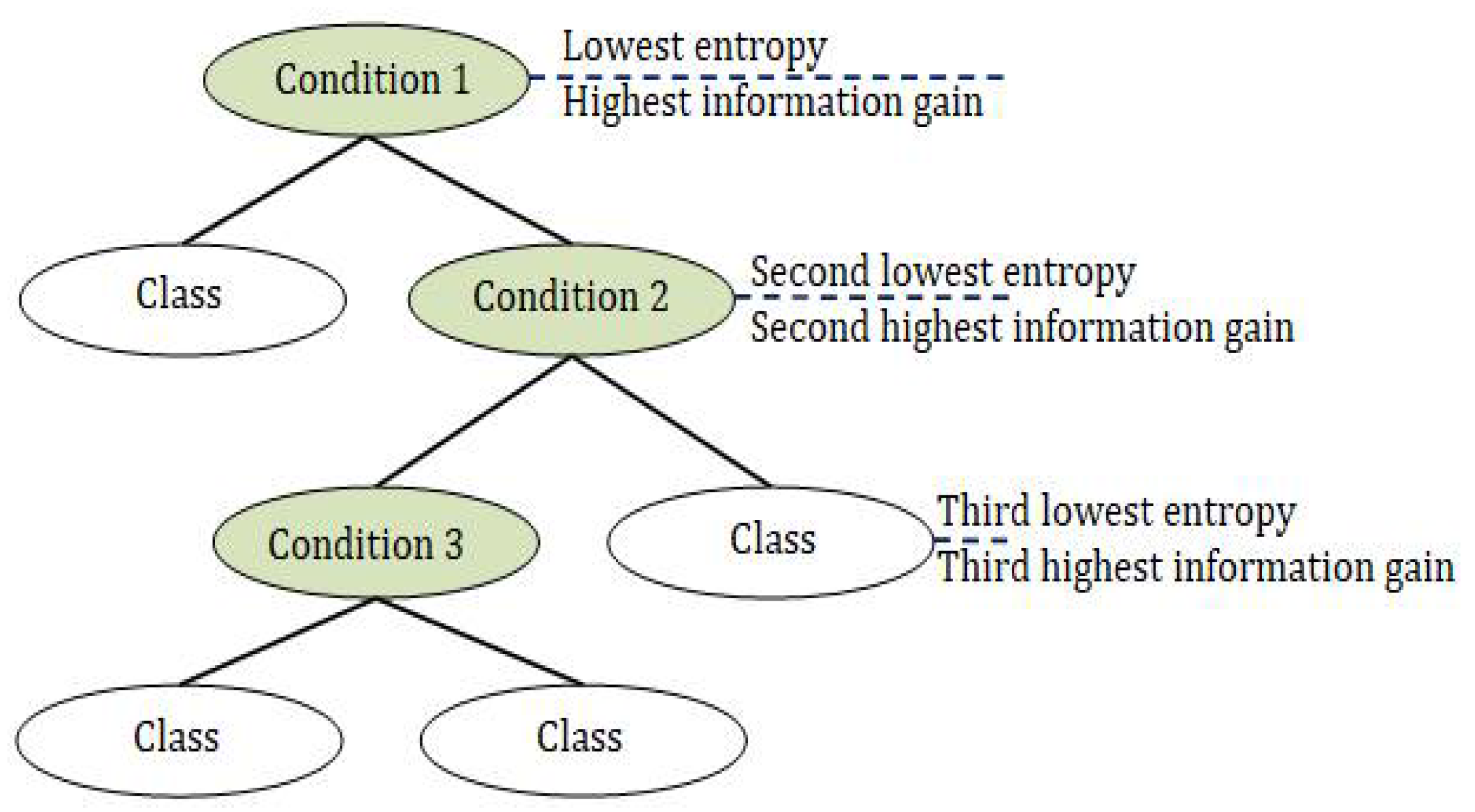
4.1.1. Application of Induction Trees
- -
- the set of input parameters:
- -
- the set of output parameters: .
- -
- Declarative in the form of rules and facts;
- -
- Triple: object, attribute, value;
- -
- Imperative in the form of an algorithmic program;
- -
- Knowledge in the form of texts;
- -
- Distributed knowledge in a neural network;
- -
- The possibility of dividing the knowledge base into a number of knowledge sources.
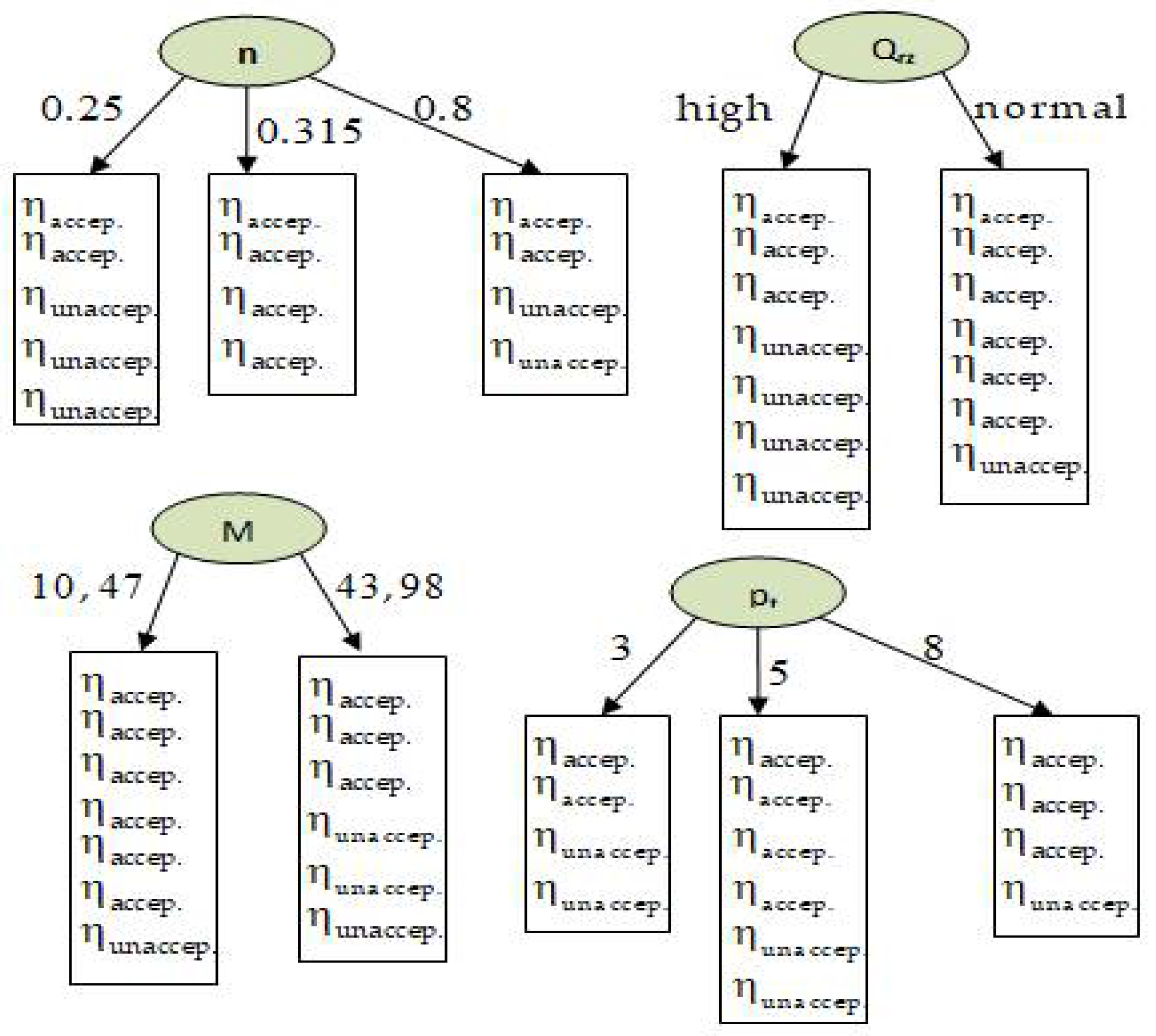
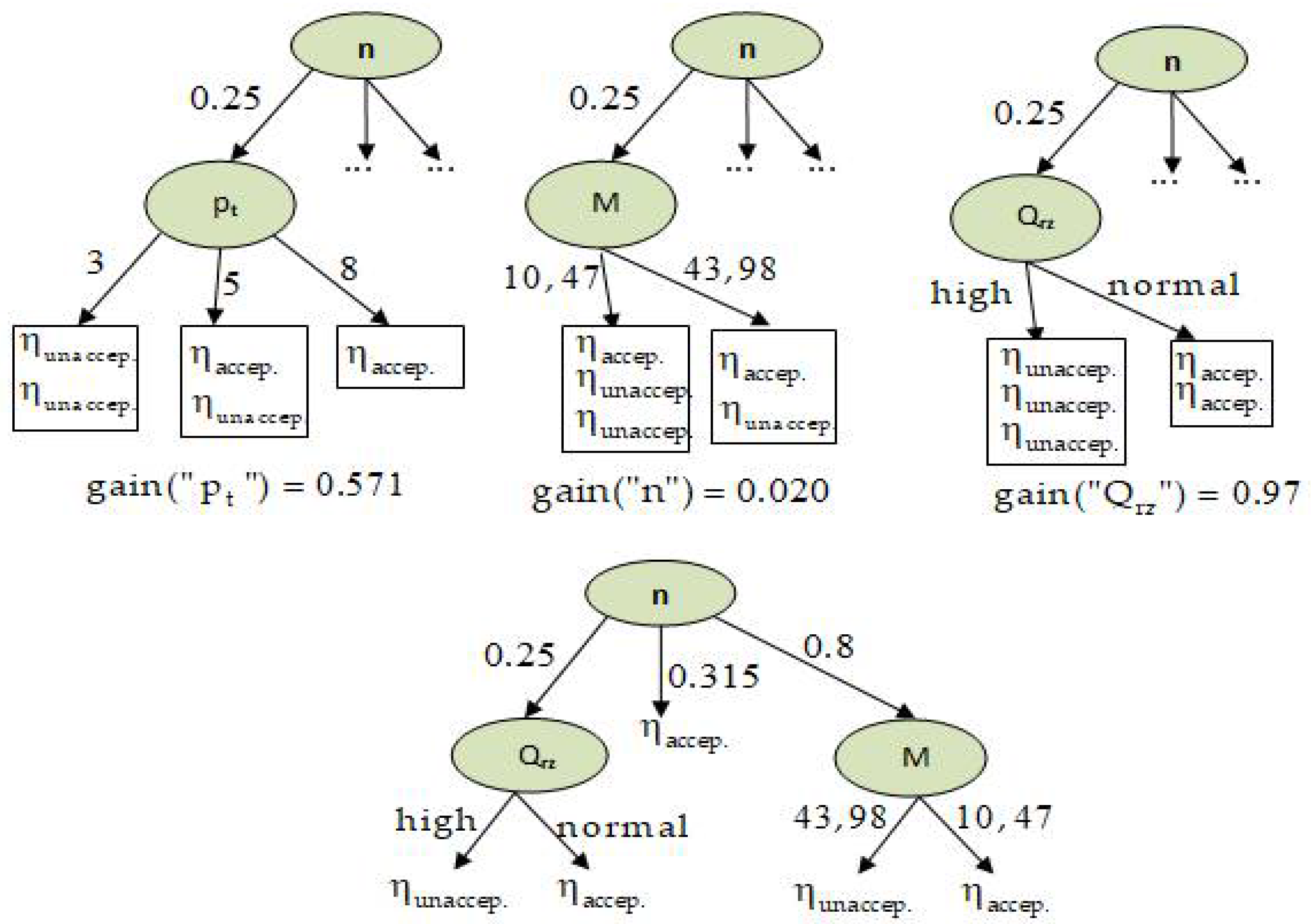
4.1.2. Calculation Example
- -
- the input attributes (in) are the following parameters: x1 = n, x2 = pt, x3 = Qrz, x4 = M, x5 = Nm, x6 = Nh.
- -
- the output parameter (out) is the total efficiency ηc.
- The input attributes (in) are the following parameters: x1= n, x2 = pt, x3 = Qrz, x4= M, x5 = Nm, x6 = Nh.
- The output parameter (out) is the total efficiency ηc.
- I.
- Microanalysis
- separately for each of the instantaneous specific deliveries—0.25 cm3/rev; 0.315 cm3/rev; 0.5 cm3/rev; 0.8 cm3/rev; and 1.0 cm3/rev.
- separately for two types of oil: Azolla ZS type 22 and HL 68
- the efficiency values were divided into 10 groups
- II.
- Microanalysis
- in combination for all of the instantaneous specific deliveries—0.25 cm3/rev; 0.315 cm3/rev; 0.5 cm3/rev; 0.8 cm3/rev; and 1.0 cm3/rev.
- separately for two types of oil: Azolla ZS type 22 and HL 68
- the efficiency values were divided into X groups
- III.
- Microanalysis
- in combination for all of the instantaneous specific deliveries—0.25 cm3/rev; 0.315 cm3/rev; 0.5 cm3/rev; 0.8 cm3/rev; and 1.0 cm3/rev.
- in combination for two types of oil: Azolla ZS type 22 and HL 68
- the efficiency values were divided into X groups
- q = 0.315, in the case when the actual delivery Qrz value is greater than 0.172 L/min;
- q = 0.5, in the case when the actual delivery Qrz value is smaller than or equal to 0.571 L/min;
- q = 0.8, in the case when the actual delivery Qrz value is greater than 0.378 L/min.
5. Discussion
6. Conclusions
- Successive groups of micro-hydraulic pumps with different unit capacities operating with different oils will be subjected to hydraulic tests. The aim will be to develop a comprehensive method for testing the importance of design and operational parameters for the entire range of micro-pumps.
- The authors will strive to build a “complete” and “automatic” information system for decision support, taking into account the heuristic method and techniques of searching the space of possible solutions. The expert system should have the ability to justify to the user the solution adopted. This is necessary not only after complete inference and presentation of the solution, problem or diagnosis, but also at each stage of inference, i.e., after each stage involving a partial solution. The system performs backward inference as an additional task, requiring expert opinion. It is important that the results are obtained from inference with the facts contained in the knowledge base. To preserve this principle, expert systems have a so-called non-contradiction module. This module allows the system to self-analyse and reconstruct a certain sequence of inference. A strict quantitative measurement of the systems ability to self-analyse is not made, as it would be a very difficult process, and is not always possible or necessary. However, it plays a very important role in the prototype design of pumps and micro-hydraulic devices.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, J.; Vacca, A.; Casoli, P. A novel approach for predicting the operation of external gear pumps under cavitating conditions. Simul. Model. Pract. Theory 2014, 45, 35–49. [Google Scholar] [CrossRef]
- Zardin, B.; Natali, E.; Borghi, M. Evaluation of the Hydro-Mechanical Efficiency of External Gear Pumps. Energies 2019, 12, 2468. [Google Scholar] [CrossRef] [Green Version]
- Schiffer, J.; Benigni, H.; Jaberg, H. Development of a novel miniature high-pressure fuel pump with a low specific speed. J. Automob. Eng. 2013, 227, 997–1006. [Google Scholar] [CrossRef]
- Frosina, E.; Senatore, A.; Rigosi, M. Study of a High-Pressure External Gear Pump with a Computational Fluid Dynamic Modelling Approach. Energies 2017, 10, 1113. [Google Scholar] [CrossRef] [Green Version]
- Śliwiński, P. The Basics of Design and Experimental Tests of the Commutation Unit of a Hydraulic Satellite Motor. Arch. Civ. Mech. Eng. 2016, 16, 634–644. [Google Scholar] [CrossRef]
- Patrosz, P. Influence of Properties of Hydraulic Fluid on Pressure Peaks in Axial Piston Pumps’ Chambers. Energies 2021, 14, 3764. [Google Scholar] [CrossRef]
- Załuski, P. Experimental research of an axial piston pump with displaced swash plate axis of rotation. In Advances in Hydraulic and Pneumatic Drives and Control; Springer: Berlin, Germany, 2020; pp. 135–145. [Google Scholar]
- Jasiński, R. Volumetric and torque efficiency of pumps during start-up in low ambient temperatures. In Advances in Hydraulic and Pneumatic Drives and Control; Stryczek, J., Warzyńska, U., Eds.; Springer: New York, NY, USA, 2020; pp. 28–39. [Google Scholar]
- Casoli, P.; Vacca, A.; Berta, G.L. Potentials of a Numerical Tool for the Simulation of Flow in External Gear Machines. In Proceedings of the Tenth Scandinavian International Conference on Fluid Power, Tampere, Finland, 21–23 May 2007. [Google Scholar]
- Ivantysyn, J.; Ivantysynova, M. Hydrostatic Pumps and Motors, Principles, Designs, Performance. In Modelling, Analysis, Control and Testing; Akademia Books International: New Delhi, India, 2002. [Google Scholar]
- Borghi, M.; Zardin, B.; Specchia, E. External Gear Pump Volumetric Efficiency: Numerical and Experimental Analysis; SAE Technical Paper: Chicago, IL, USA, 2009. [Google Scholar] [CrossRef]
- Abel, F. Johannes Kepler and His Importance to Modern Science; Inter Nations Bonn: Bad Godesberg, Germany, 1971. [Google Scholar]
- Eckle, F.J.; Bickert, P.; Lachenmann, R.; Wortmann, B. Pumping speed of diaphragm pumps for various gases. Vacuum 1996, 47, 799–801. [Google Scholar] [CrossRef]
- Rundo, M.; Nervegna, N. Geometry Assessment of Variable Displacement Vane Pumps. ASME J. Dyn. Syst. Meas. Control 2007, 129, 446–455. [Google Scholar] [CrossRef]
- Yan, D.; Kovacevic, A.; Tang, Q.; Rane, S.; Zhang, W. Numerical modelling of twin-screw pumps based on computational fluid dynamics. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 4617–4634. [Google Scholar] [CrossRef] [Green Version]
- Scott, C. Considerations for a canned motor pump. World Pumps 2004, 459, 22–25. [Google Scholar] [CrossRef]
- Muzzioli, G.; Montorsi, L.; Polito, A.; Lucchi, A.; Sassi, A.; Milani, M. About the Influence of Eco-Friendly Fluids on the Performance of an External Gear Pump. Energies 2021, 14, 799. [Google Scholar] [CrossRef]
- Pareja-Corcho, J.; Moreno, A.; Simoes, B.; Pedrera-Busselo, A.; San-Jose, E.; Ruiz-Salguero, O.; Posada, J. A Virtual Prototype for Fast Design and Visualization of Gerotor Pumps. Appl. Sci. 2021, 11, 1190. [Google Scholar] [CrossRef]
- Deptuła, A.; Osiński, P.; Partyka, M.A. Analysis of Dimensional Tolerances on Hydraulic and Acoustic Properties of a New Type of Prototypal Gear Pumps. Appl. Sci. 2020, 10, 8535. [Google Scholar] [CrossRef]
- Osiński, P.; Chruścielski, G. Strength calculations of an element compensating circumferential backlash in the external gear pump. J. Theor. Appl. Mech. 2016, 54, 251–262. [Google Scholar] [CrossRef] [Green Version]
- Osiński, P. High-Pressure and Low-Pulse Gear Pumps with External Meshing; Publishing House of Wrocław University of Technology: Wrocław, Poland, 2013. [Google Scholar]
- Amman, R. Zahnradpumpen mit Evolventenverzahnung. Ph.D. Thesis, Technischen Hochschule München, Munich, Germany, 1926. [Google Scholar]
- Judin, E.M. Gear Pumps; PWT: Warsaw, Poland, 1958. [Google Scholar]
- Goliński, J. Vibration Isolation of Machines and Devices; WNT: Warsaw, Poland, 1979. [Google Scholar]
- Lätzel, M.; Schwuchow, D. An innovative external gear pump for low noise applications. In Proceedings of the 8th International Fluid Power Conference, Dresden, Germany, 26–28 March 2012. [Google Scholar]
- Osiński, P.; Kollek, W. Performance pulsation of externally meshed gear pumps. Hydraul. Pneum. 2000, 2, 24–26. [Google Scholar]
- Wittke, W. Beanspruchungsgerechte und Geräuschoptimierte Stirnradgetrieben: Toleranzvorgaben und Flankenkorrekturen. Ph.D. Thesis, RWTH-Aachen University, Aachen, Germany, 1994. [Google Scholar]
- Schwuchow, D. Design tools for modern external gear pumps. In Proceedings of the 3rd International Fluid Power Conterence, Aachen, Germany, 5–6 March 2002. [Google Scholar]
- Osiński, P.; Deptuła, A.; Partyka, M.A. Discrete optimization of a gear pump after tooth root undercutting by means of multi—Valued logic trees. Arch. Civ. Mech. Eng. 2013, 13, 422–431. [Google Scholar] [CrossRef]
- Deptuła, A.; Osiński, P. The Optimization of Three—Involute Tooth Outline with Taking into Consideration Multi—Valued Logic Trees. In Book: Proceedings of the 13th International Scientific Conference, Struga, North Macedonia, 26–28 September 2022; Springer International Publishing: New York, NY, USA, 2017; pp. 99–107. [Google Scholar]
- Fiebig, W. Schwingungs-und Geräuschverhalten der Verdrängerpumpen und Hydraulischen Systeme; Band 19; Universität Stuttgart: Stuttgart, Germany, 2000. [Google Scholar]
- Kollek, W. Optimerung das Wirkungsgrades von Zahnradpumpen und—Motoren. Konstruktion 1985, 35, 147–151. [Google Scholar]
- Osiński, P.; Kollek, W. Geräuschuntersuchungen der zahnradpumpen mit Hilfe der energetischen Methode. In Proceedings of the IV Polnisch-Deutsches Seminar: Innovationen und Fortschritte in der Hydraulik und Pneumatik, Sopot, Poland, 20–21 September 2001. [Google Scholar]
- Dindorf, R.; Wołkow, J. Micro fluidic systems, microhydraulics. In Proceedings of the IX Conference Cylinder 1999 Testing, Design, Manufacture and Operation of Hydraulic Systems, Zakopane, Poland, 23–25 September 1999. [Google Scholar]
- Dindorf, R.; Wołkow, J. Microhydraulics. Hydraul. Pneum. 1999, 6, 13–16. [Google Scholar]
- Kudźma, Z.; Łomotowski, G.; Osiński, P.; Rutański, J.; Stosiak, M.; Wilczyński, J. Investigations of hydraulic and vibroacoustic properties of fabricated prototypes. In Fundamentals of Design, Modelling and Operation of Microhydraulic Components and Systems; Publishing House of Wrocław University of Technolog: Wrocław, Poland, 2012. [Google Scholar]
- Kollek, W.; Wilczyński, A.; Osiński, P.; Rutański, J.; Maga, K. Hydraulic Testing of PZ0 Pinion Micropump; Ser. SPR no S- 07/2011; Reports of the Mechanical Engineering Department of Wrocław University of Technology: Wrocław, Poland, 2011. [Google Scholar]
- Kollek, W.; Osiński, P.; Stosiak, M.; Wilczyński, A.; Cichoń, P. Problems relating to high-pressure gear micropumps. Arch. Civ. Mech. Eng. 2014, 14, 88–95. [Google Scholar] [CrossRef]
- Fayyad, U.M.; Piatetsky-Shapiro, G.; Smyth, P.; Uthurusamy, R. From data mining to knowledge discovery. Al Mag. 1996, 17, 37–54. [Google Scholar]
- Han, J.; Kamber, M. Data Mining: Concepts and Techniques; Morgan Kaufmann: San Francisco, CA, USA, 2000. [Google Scholar]
- Alexandropoulos, S.; Kotsiantis, S.; Vrahatis, M. Data preprocessing in predictive data mining. In The Knowledge Engineering Review; Cambridge University Press: Cambridge, UK, 2019; Volume 34. [Google Scholar]
- Ahmad, W.; Ayub, N.; Ali, T.; Irfan, M.; Awais, M.; Shiraz, M.; Glowacz, A. Towards Short Term Electricity Load Forecasting Using Improved Support Vector Machine and Extreme Learning Machine. Energies 2020, 13, 2907. [Google Scholar] [CrossRef]
- Kuk, E.; Stopa, J.; Kuk, M.; Janiga, D.; Wojnarowski, P. Petroleum Reservoir Control Optimization with the Use of the Auto-Adaptive Decision Trees. Energies 2021, 14, 5702. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Vapnik, V.N. Statistical Learning Theory; John Wiley and Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Bingzhen, S.; Xiangtang, C.; Liye, Z.; Weimin, M. Three-way decision making approach to conflict analysis and resolution using probabilistic rough set over two universes. Inf. Sci. 2020, 507, 809–822. [Google Scholar]
- Xiancheng, J.; Yan, R.; Hesheng, T.; Jiawei, X. DSmT-based three-layer method using multi-classifier to detect faults in hydraulic systems. Mech. Syst. Signal Processing 2021, 153, 107513. [Google Scholar]
- Deptuła, A. Application of parametric trees with logical minimization in the analysis of automatic transmissions. J. Mech. Mechatron. Eng. IJMME-IJENS 2021, 21, 11–21. [Google Scholar]
- Kollek, W.; Osiński, P.; Wilczyński, A.; Brzeziński, T. Design Documentation of a Gear Micropump; Report S-09/2011; Wrocław University of Technology: Wrocław, Poland, 2011. [Google Scholar]
- Kollek, W.; Osiński, P.; Wilczyński, A. Construction of a Test Rig for Measuring Microhydraulic Systems; Report S-08/2011; Wrocław University of Technology: Wrocław, Poland, 2011. [Google Scholar]
- Kruthika, K.R.; Maheshappa, H.D. Multistage classifier-based approach for Alzheimer’s disease prediction and retrieval. Inform. Med. Unlocked 2019, 14, 34–42. [Google Scholar] [CrossRef]
- Chen, Y.; Kang, X.; Shi, Y.Q.; Wang, Z.J. A multi-purpose image forensic method using densely connected convolutional neural works. J. Real-Time Image Proc. 2019, 16, 725–740. [Google Scholar] [CrossRef]
- Costabal, F.S.; Perdikaris, P.; Kuhl, E.; Hurtado, D.E. Multi-fidelity classification using Gaussian processes: Accelerating the prediction of large-scale computational models. Comput. Methods Appl. Mech. Eng. 2019, 357, 112602. [Google Scholar] [CrossRef] [Green Version]
- Quinlan, J.R. Induction of Decision Trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef] [Green Version]
- Quinlan, J.R. C4.5 Program for Machine Learning; Morgan Kaufmann: San Mateo, CA, USA, 1993. [Google Scholar]
- Feretzakis, G.; Kalles, D.; Verykios, V.S. Using Minimum Local Distortion to Hide Decision Tree Rules. Entropy 2019, 21, 334. [Google Scholar] [CrossRef] [Green Version]












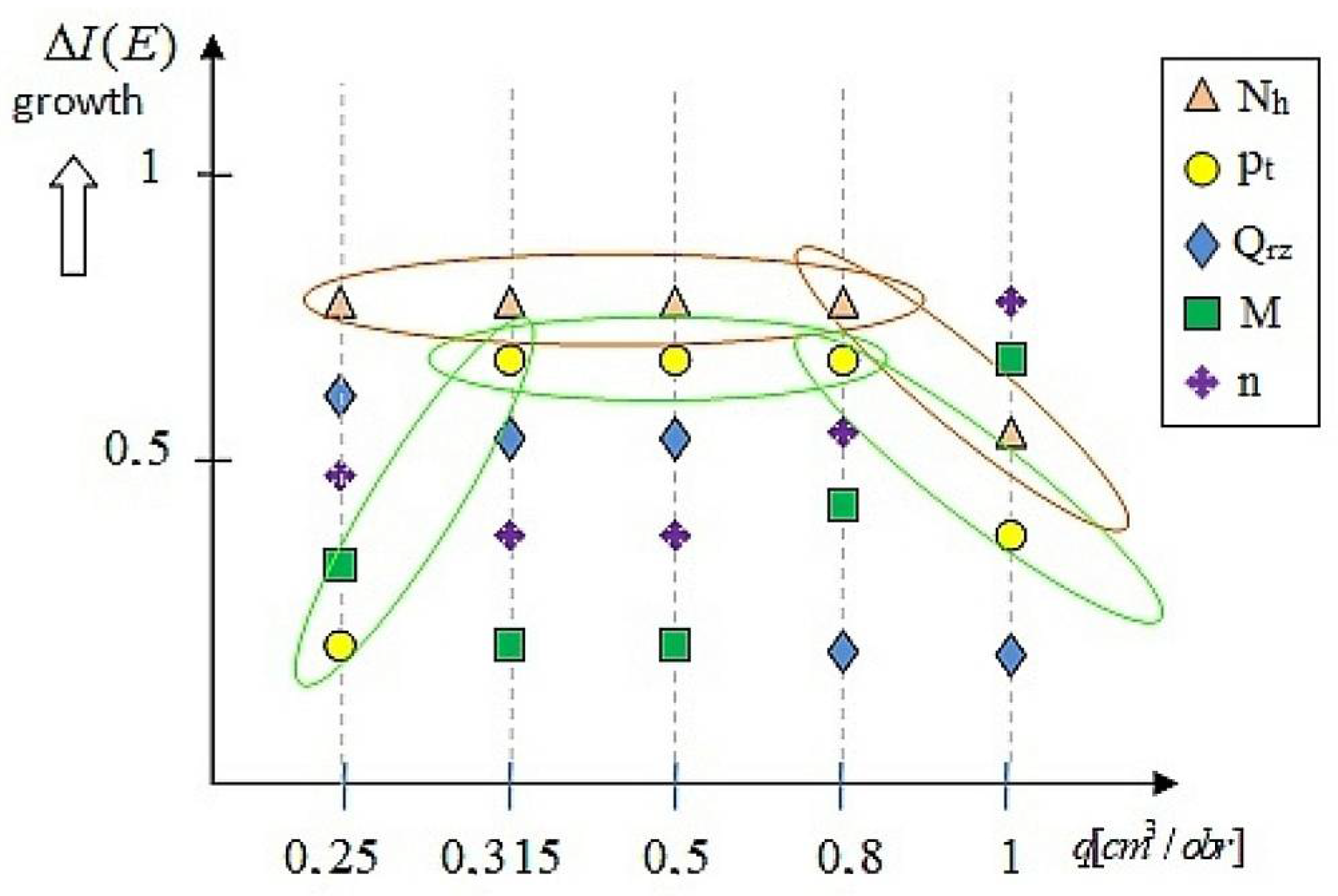
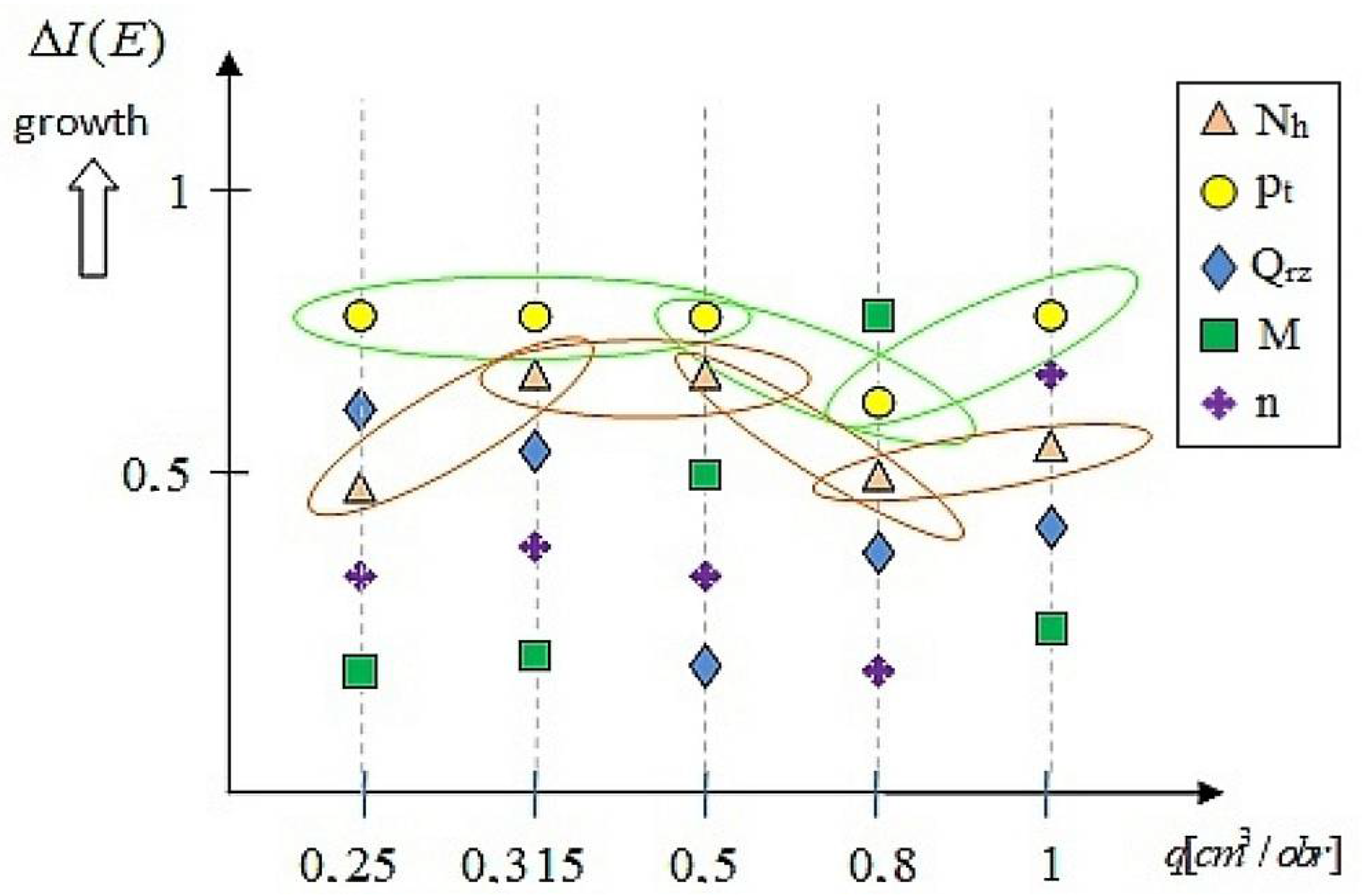



| Parameters | Symbol and Unit | Specific Delivery [cm3/rev] | |||||
|---|---|---|---|---|---|---|---|
| 0.25 | 0.315 | 0.5 | 0.8 | 1.0 | |||
| Number of teeth | z | [-] | 14 | 14 | 14 | 14 | 14 |
| Module | m0 | [mm] | 1 | 1 | 1 | 1 | 1 |
| Pressure angle | α0 | [0] | 20 | 20 | 20 | 20 | 20 |
| Addendum height coefficient | y | [-] | 1 | 1 | 1 | 1 | 1 |
| Addendum modification coefficient | x | [-] | 0.61 | 0.61 | 0.61 | 0.61 | 0.61 |
| Toothed wheel width | b | [mm] | 2.32 | 2.92 | 4.64 | 7.42 | 9.28 |
| Axis-to-axis distance | a | [-] | 15 | 15 | 15 | 15 | 15 |
| Generating-circle pressure angle | αt | [0] | 28.71 | 28.71 | 28.71 | 28.71 | 28.71 |
| n [rpm] | pt [MPa] | Qrz [L/min] | M [Nm] | Nm [W] | Nh [W] | ηv [%] | ηhm [%] | ηc [%] |
|---|---|---|---|---|---|---|---|---|
| 500 | ≈0 | 0.085 | 0.11 | 5.76 | 0.24 | 100.00 | 4.18 | 4.18 |
| 3 | 0.058 | 0.16 | 8.38 | 2.90 | 68.24 | 50.73 | 34.62 | |
| 6 | 0.029 | 0.28 | 14.66 | 2.90 | 34.12 | 57.98 | 19.78 | |
| 8 | 0.006 | 0.36 | 18.85 | 0.80 | 7.06 | 60.13 | 4.24 | |
| 12 | * | * | * | * | * | * | * | |
| 16 | * | * | * | * | * | * | * | |
| 750 | ≈0 | 0.133 | 0.10 | 7.85 | 0.38 | 100.00 | 4.80 | 4.80 |
| 3 | 0.104 | 0.16 | 12.57 | 5.20 | 78.20 | 52.92 | 41.38 | |
| 6 | 0.075 | 0.27 | 21.21 | 7.50 | 56.39 | 62.72 | 35.37 | |
| 9 | 0.042 | 0.39 | 30.63 | 6.30 | 31.58 | 65.13 | 20.57 | |
| 11 | 0.017 | 0.48 | 37.70 | 3.12 | 12.78 | 64.68 | 8.27 | |
| 16 | * | * | * | * | * | * | * | |
| 1000 | ≈0 | 0.182 | 0.10 | 10.47 | 0.52 | 100.00 | 4.92 | 4.92 |
| 3 | 0.151 | 0.15 | 15.71 | 7.55 | 82.97 | 57.93 | 48.06 | |
| 6 | 0.121 | 0.26 | 27.23 | 12.10 | 66.48 | 66.85 | 44.44 | |
| 9 | 0.089 | 0.38 | 39.79 | 13.35 | 48.90 | 68.60 | 33.55 | |
| 13 | 0.027 | 0.56 | 58.64 | 5.85 | 14.84 | 67.24 | 9.98 | |
| 16 | * | * | * | * | * | * | * | |
| 1250 | ≈0 | 0.229 | 0.10 | 13.09 | 0.73 | 100.00 | 5.54 | 5.54 |
| 3 | 0.193 | 0.15 | 19.63 | 9.65 | 84.28 | 58.31 | 49.15 | |
| 6 | 0.162 | 0.27 | 35.34 | 16.20 | 70.74 | 64.79 | 45.84 | |
| 9 | 0.126 | 0.37 | 48.43 | 18.90 | 55.02 | 70.92 | 39.02 | |
| 12 | 0.081 | 0.51 | 66.76 | 16.20 | 35.37 | 68.61 | 24.27 | |
| 14 | 0.022 | 0.60 | 78.54 | 5.13 | 9.61 | 68.03 | 6.54 | |
| 1500 | ≈0 | 0.278 | 0.11 | 17.28 | 0.88 | 100.00 | 5.09 | 5.09 |
| 3 | 0.249 | 0.16 | 25.13 | 12.45 | 89.57 | 55.31 | 49.54 | |
| 6 | 0.218 | 0.27 | 42.41 | 21.80 | 78.42 | 65.55 | 51.40 | |
| 9 | 0.177 | 0.39 | 61.26 | 26.55 | 63.67 | 68.07 | 43.34 | |
| 12 | 0.132 | 0.52 | 81.68 | 26.40 | 47.48 | 68.07 | 32.32 | |
| 16 | 0.016 | 0.75 | 117.81 | 4.27 | 5.76 | 62.93 | 3.62 | |
| 1750 | ≈0 | 0.325 | 0.10 | 18.33 | 1.14 | 100.00 | 6.21 | 6.21 |
| 3 | 0.292 | 0.16 | 29.32 | 14.60 | 89.85 | 55.42 | 49.79 | |
| 6 | 0.262 | 0.26 | 47.65 | 26.20 | 80.62 | 68.21 | 54.99 | |
| 9 | 0.226 | 0.38 | 69.64 | 33.90 | 69.54 | 70.00 | 48.68 | |
| 12 | 0.186 | 0.51 | 93.46 | 37.20 | 57.23 | 69.55 | 39.80 | |
| 16 | 0.073 | 0.73 | 133.78 | 19.47 | 22.46 | 64.78 | 14.55 |
| n | pt | Qrz | M | Nm | Nh | ηv | ηhm | ηc |
|---|---|---|---|---|---|---|---|---|
| [rpm] | [MPa] | [L/min] | [Nm] | [W] | [W] | [%] | [%] | [%] |
| 500 | ≈0 | 0.110 | 0.22 | 11.52 | 0.31 | 100.00 | 2.71 | 2.71 |
| 5 | 0.070 | 0.34 | 17.80 | 5.83 | 63.64 | 51.49 | 32.77 | |
| 10 | 0.031 | 0.56 | 29.32 | 5.17 | 28.18 | 62.53 | 17.62 | |
| 11 | 0.018 | 0.61 | 31.94 | 3.30 | 16.36 | 63.14 | 10.33 | |
| 20 | * | * | * | * | * | * | * | |
| 22 | * | * | * | * | * | * | * | |
| 750 | ≈0 | 0.170 | 0.18 | 14.14 | 0.51 | 100.00 | 3.61 | 3.61 |
| 5 | 0.134 | 0.33 | 25.92 | 11.17 | 78.82 | 54.66 | 43.08 | |
| 10 | 0.099 | 0.54 | 42.41 | 16.50 | 58.24 | 66.81 | 38.90 | |
| 15 | 0.036 | 0.80 | 62.83 | 9.00 | 21.18 | 67.64 | 14.32 | |
| 16 | 0.005 | 0.88 | 69.12 | 1.33 | 2.94 | 65.59 | 1.93 | |
| 22 | * | * | * | * | * | * | * | |
| 1000 | ≈0 | 0.229 | 0.17 | 17.80 | 0.69 | 100.00 | 3.86 | 3.86 |
| 5 | 0.196 | 0.32 | 33.51 | 16.33 | 85.59 | 56.95 | 48.74 | |
| 10 | 0.141 | 0.53 | 55.50 | 23.50 | 61.57 | 68.77 | 42.34 | |
| 15 | 0.074 | 0.78 | 81.68 | 18.50 | 32.31 | 70.09 | 22.65 | |
| 17 | 0.025 | 0.91 | 95.29 | 7.08 | 10.92 | 68.09 | 7.43 | |
| 22 | * | * | * | * | * | * | * | |
| 1250 | ≈0 | 0.290 | 0.16 | 20.94 | 1.06 | 100.00 | 5.08 | 5.08 |
| 5 | 0.242 | 0.30 | 39.27 | 20.17 | 83.45 | 61.54 | 51.35 | |
| 10 | 0.192 | 0.52 | 68.07 | 32.00 | 66.21 | 71.01 | 47.01 | |
| 15 | 0.126 | 0.76 | 99.48 | 31.50 | 43.45 | 72.88 | 31.66 | |
| 19 | 0.032 | 1.02 | 133.52 | 10.13 | 11.03 | 68.78 | 7.59 | |
| 22 | * | * | * | * | * | * | * | |
| 1500 | ≈0 | 0.349 | 0.16 | 25.13 | 1.28 | 100.00 | 5.09 | 5.09 |
| 5 | 0.299 | 0.30 | 47.12 | 24.92 | 85.67 | 61.72 | 52.87 | |
| 10 | 0.250 | 0.52 | 81.68 | 41.67 | 71.63 | 71.21 | 51.01 | |
| 15 | 0.189 | 0.75 | 117.81 | 47.25 | 54.15 | 74.06 | 40.11 | |
| 20 | 0.022 | 1.08 | 169.65 | 7.33 | 6.30 | 68.57 | 4.32 | |
| 22 | * | * | * | * | * | * | * | |
| 1750 | ≈0 | 0.410 | 0.17 | 31.15 | 1.50 | 100.00 | 4.83 | 4.83 |
| 5 | 0.360 | 0.28 | 51.31 | 30.00 | 87.80 | 66.59 | 58.47 | |
| 10 | 0.306 | 0.51 | 93.46 | 51.00 | 74.63 | 73.11 | 54.57 | |
| 13 | 0.245 | 0.74 | 135.61 | 61.25 | 59.76 | 75.58 | 45.17 | |
| 20 | 0.130 | 1.05 | 192.42 | 43.33 | 31.71 | 71.02 | 22.52 | |
| 21 | 0.079 | 1.14 | 208.92 | 27.65 | 19.27 | 68.69 | 13.23 |
| n | pt | Qrz | M | Nm | Nh | ηv | ηhm | ηc |
|---|---|---|---|---|---|---|---|---|
| [rpm] | [MPa] | [L/min] | [Nm] | [W] | [W] | [%] | [%] | [%] |
| 500 | ≈0 | 0.376 | 0.19 | 9.95 | 1.38 | 100.00 | 13.86 | 13.86 |
| 5 | 0.297 | 0.82 | 42.94 | 24.75 | 78.99 | 72.98 | 57.65 | |
| 10 | 0.201 | 1.58 | 82.73 | 33.50 | 53.46 | 75.75 | 40.49 | |
| 13 | 0.066 | 2.19 | 114.67 | 14.30 | 17.55 | 71.05 | 12.47 | |
| 20 | * | * | * | * | * | * | * | |
| 22 | * | * | * | * | * | * | * | |
| 750 | ≈0 | 0.565 | 0.18 | 14.14 | 2.45 | 100.00 | 17.32 | 17.32 |
| 5 | 0.487 | 0.81 | 63.62 | 40.58 | 86.19 | 74.01 | 63.79 | |
| 10 | 0.391 | 1.53 | 120.17 | 65.17 | 69.20 | 78.36 | 54.23 | |
| 15 | 0.176 | 2.43 | 190.85 | 44.00 | 31.15 | 74.01 | 23.05 | |
| 20 | * | * | * | * | * | * | * | |
| 22 | * | * | * | * | * | * | * | |
| 1000 | ≈0 | 0.760 | 0.18 | 18.85 | 3.67 | 100.00 | 19.49 | 19.49 |
| 5 | 0.679 | 0.78 | 81.68 | 56.58 | 89.34 | 77.54 | 69.27 | |
| 10 | 0.593 | 1.47 | 153.94 | 98.83 | 78.03 | 82.28 | 64.20 | |
| 15 | 0.436 | 2.25 | 235.62 | 109.00 | 57.37 | 80.64 | 46.26 | |
| 18 | 0.123 | 2.64 | 276.46 | 36.90 | 16.18 | 82.47 | 13.35 | |
| 22 | * | * | * | * | * | * | * | |
| 1250 | ≈0 | 0.951 | 0.17 | 22.25 | 5.39 | 100.00 | 24.22 | 24.22 |
| 5 | 0.869 | 0.73 | 95.56 | 72.42 | 91.38 | 82.93 | 75.78 | |
| 10 | 0.780 | 1.46 | 191.11 | 130.00 | 82.02 | 82.93 | 68.02 | |
| 15 | 0.653 | 2.25 | 294.52 | 163.25 | 68.66 | 80.72 | 55.43 | |
| 19 | 0.352 | 3.02 | 395.32 | 111.47 | 37.01 | 76.18 | 28.20 | |
| 22 | * | * | * | * | * | * | * | |
| 1500 | ≈0 | 1.146 | 0.17 | 26.70 | 7.26 | 100.00 | 27.18 | 27.18 |
| 5 | 1.066 | 0.73 | 114.67 | 88.83 | 93.02 | 83.28 | 77.47 | |
| 10 | 0.972 | 1.43 | 224.62 | 162.00 | 84.82 | 85.03 | 72.12 | |
| 15 | 0.844 | 2.16 | 339.29 | 211.00 | 73.65 | 84.44 | 62.19 | |
| 20 | 0.602 | 3.20 | 502.65 | 200.67 | 52.53 | 76.00 | 39.92 | |
| 22 | 0.395 | 3.39 | 532.50 | 144.83 | 34.47 | 78.91 | 27.20 | |
| 1750 | ≈0 | 1.335 | 0.16 | 29.32 | 8.46 | 100.00 | 28.84 | 28.84 |
| 5 | 1.242 | 0.75 | 137.44 | 103.50 | 93.03 | 80.94 | 75.30 | |
| 10 | 1.149 | 1.41 | 258.40 | 191.50 | 86.07 | 86.11 | 74.11 | |
| 15 | 1.023 | 2.16 | 395.84 | 255.75 | 76.63 | 84.31 | 64.61 | |
| 16 | 0.997 | 2.30 | 421.50 | 265.87 | 74.68 | 84.46 | 63.08 | |
| 21 | ** | ** | ** | ** | ** | ** | ** |
| we | we | we | we | wy |
|---|---|---|---|---|
| n | pt | Qrz | M | ηc |
| 0.25 | 3 | high | 10.47 | unacceptable |
| 0.25 | 3 | high | 43.98 | unacceptable |
| 0.315 | 3 | high | 10.47 | acceptable |
| 0.8 | 5 | high | 10.47 | acceptable |
| 0.8 | 8 | normal | 10.47 | acceptable |
| 0.8 | 8 | normal | 43.98 | unacceptable |
| 0.315 | 8 | normal | 43.98 | acceptable |
| 0.25 | 5 | high | 10.47 | unacceptable |
| 0.25 | 8 | normal | 10.47 | acceptable |
| 0.8 | 5 | normal | 10.47 | acceptable |
| 0.25 | 5 | normal | 43.98 | acceptable |
| 0.315 | 5 | high | 43.98 | acceptable |
| 0.315 | 3 | normal | 10.47 | acceptable |
| 0.8 | 5 | high | 43.98 | unacceptable |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Osiński, P.; Deptuła, A.; Partyka, M.A. Hydraulic Tests of the PZ0 Gear Micropump and the Importance Rank of Its Design and Operating Parameters. Energies 2022, 15, 3068. https://doi.org/10.3390/en15093068
Osiński P, Deptuła A, Partyka MA. Hydraulic Tests of the PZ0 Gear Micropump and the Importance Rank of Its Design and Operating Parameters. Energies. 2022; 15(9):3068. https://doi.org/10.3390/en15093068
Chicago/Turabian StyleOsiński, Piotr, Adam Deptuła, and Marian A. Partyka. 2022. "Hydraulic Tests of the PZ0 Gear Micropump and the Importance Rank of Its Design and Operating Parameters" Energies 15, no. 9: 3068. https://doi.org/10.3390/en15093068
APA StyleOsiński, P., Deptuła, A., & Partyka, M. A. (2022). Hydraulic Tests of the PZ0 Gear Micropump and the Importance Rank of Its Design and Operating Parameters. Energies, 15(9), 3068. https://doi.org/10.3390/en15093068








