Thermal Characterization and Thermal Effect Assessment of Biofouling around a Dynamic Submarine Electrical Cable
Abstract
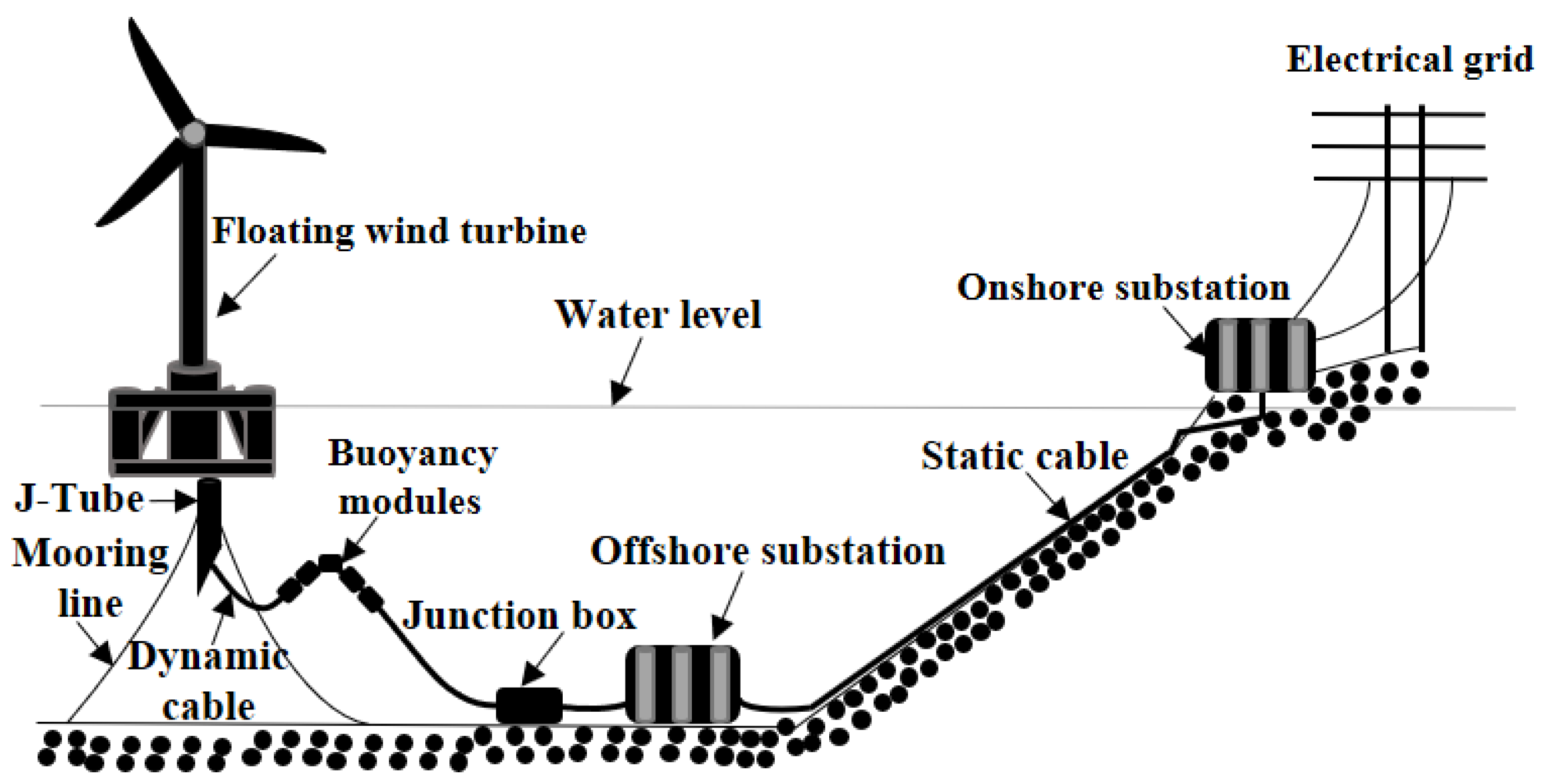
:1. Introduction
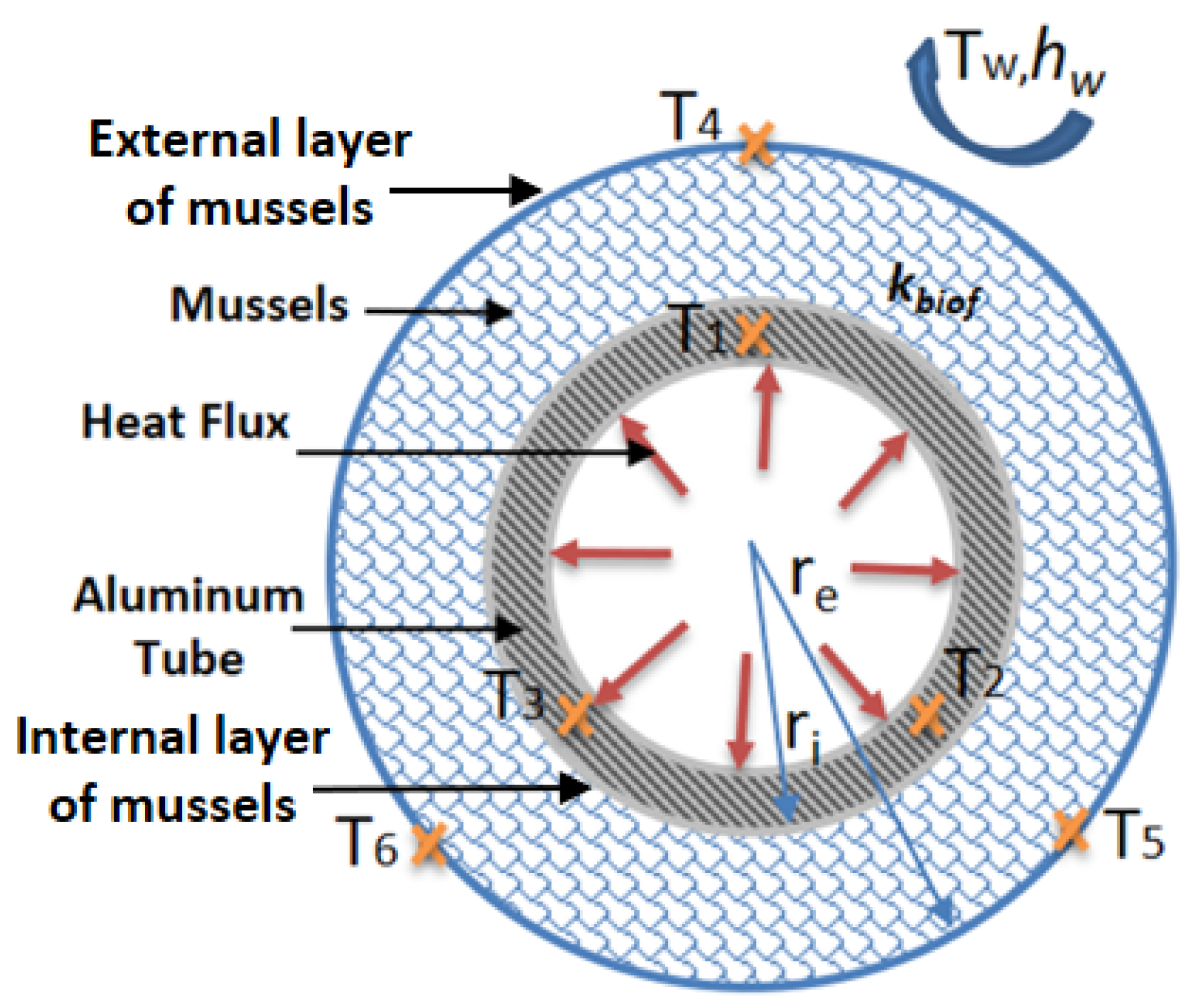
2. Thermal Characterization of Mussels
2.1. Experimental Setup and Mussel’s Samples
2.2. Thermal Characterization for a Uniform Colonization of Mussels around the Tube
2.2.1. Measurement Method
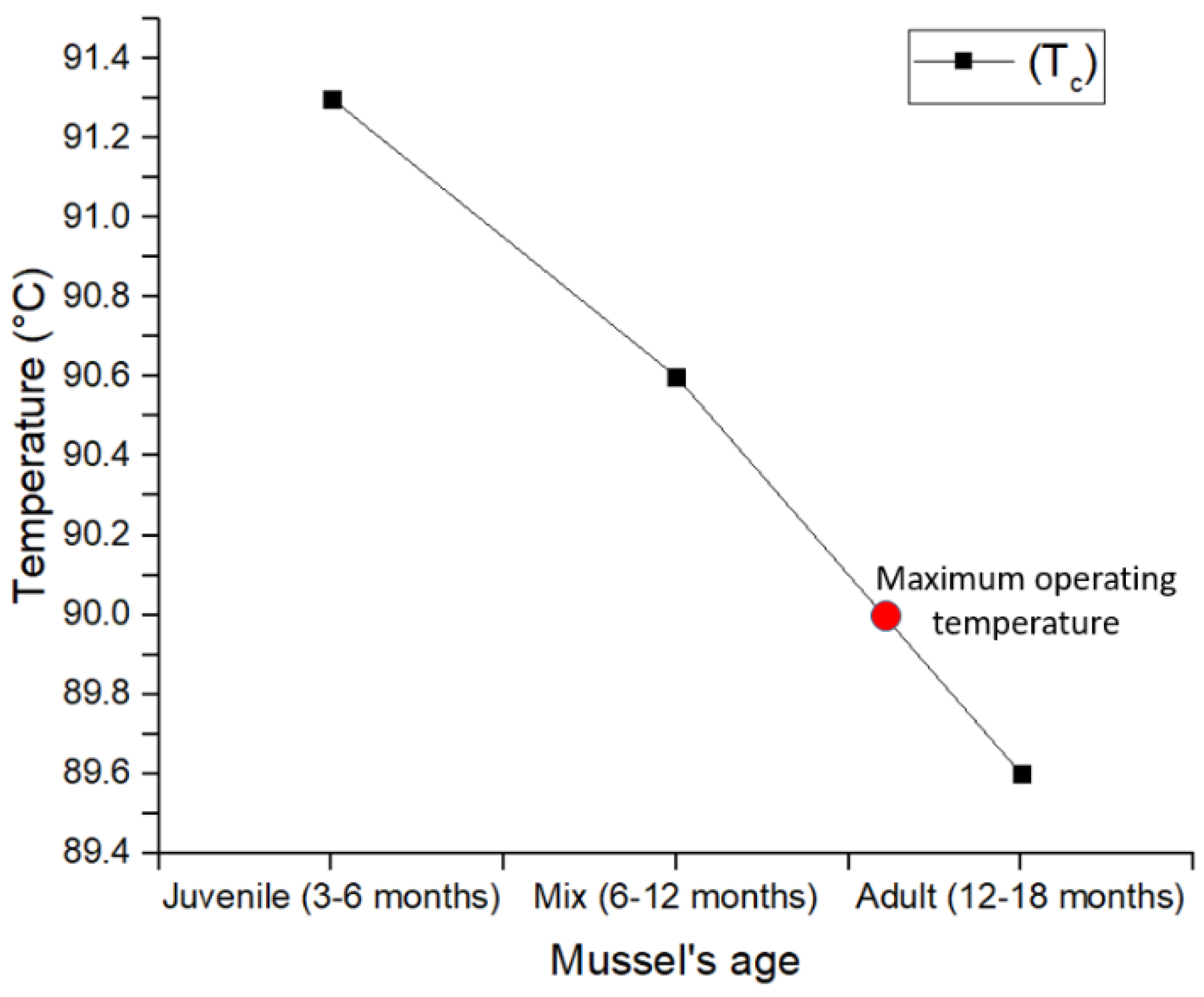
2.2.2. Effective Thermal Conductivity Measurement Results
2.2.3. Heat Transfer Coefficient of the Water around the Mussels Measurement Results
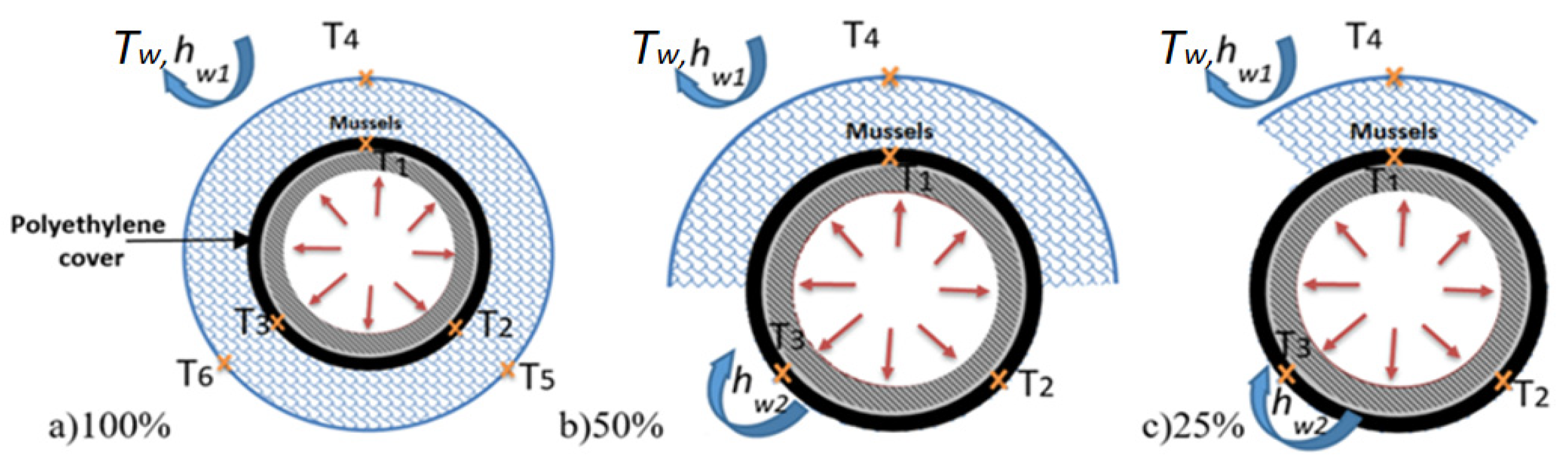
2.3. Thermal Characterization of a Non-Uniform Colonization of Biofouling around the Tube
3. Thermal Effect of Mussels on the DSEC Copper Wire
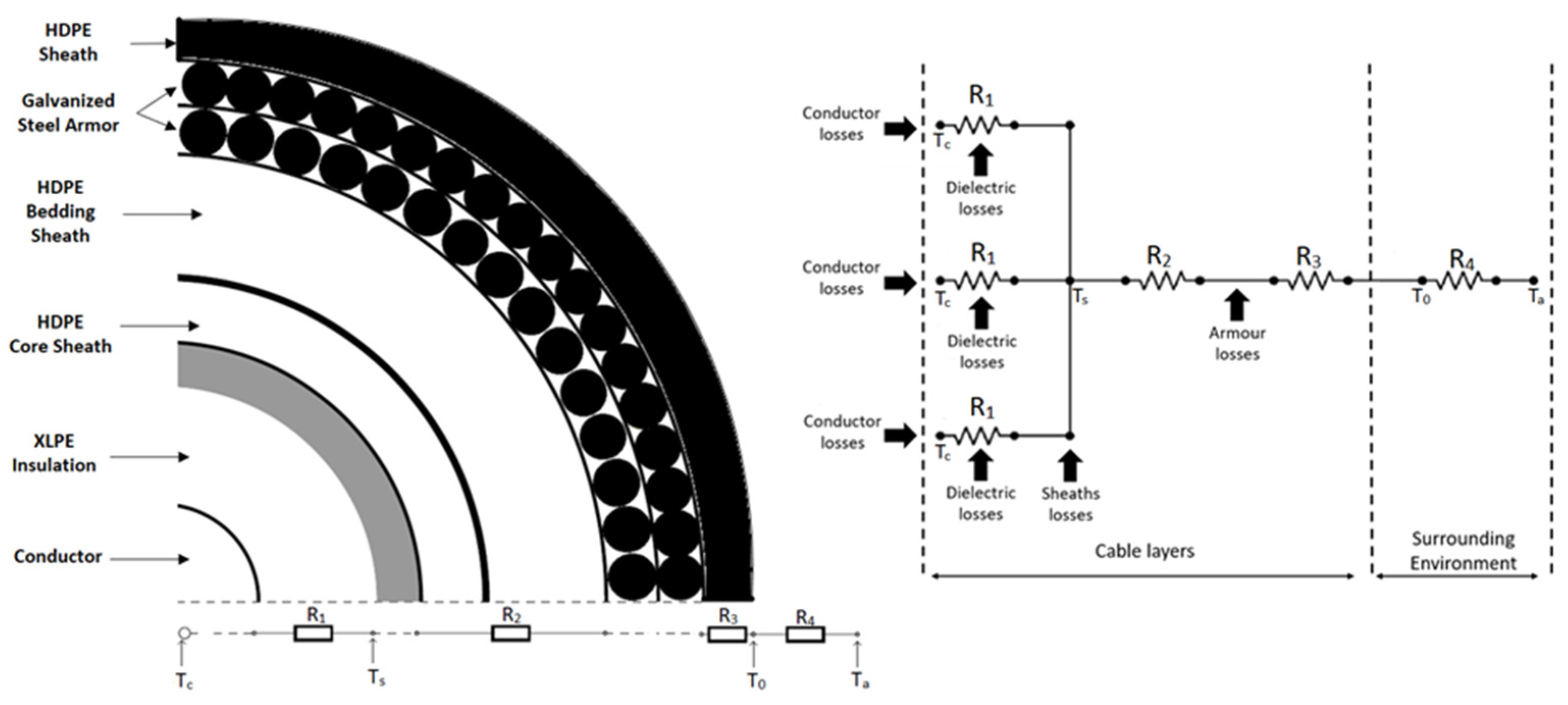
3.1. Analytical Model Based on IEC Standard
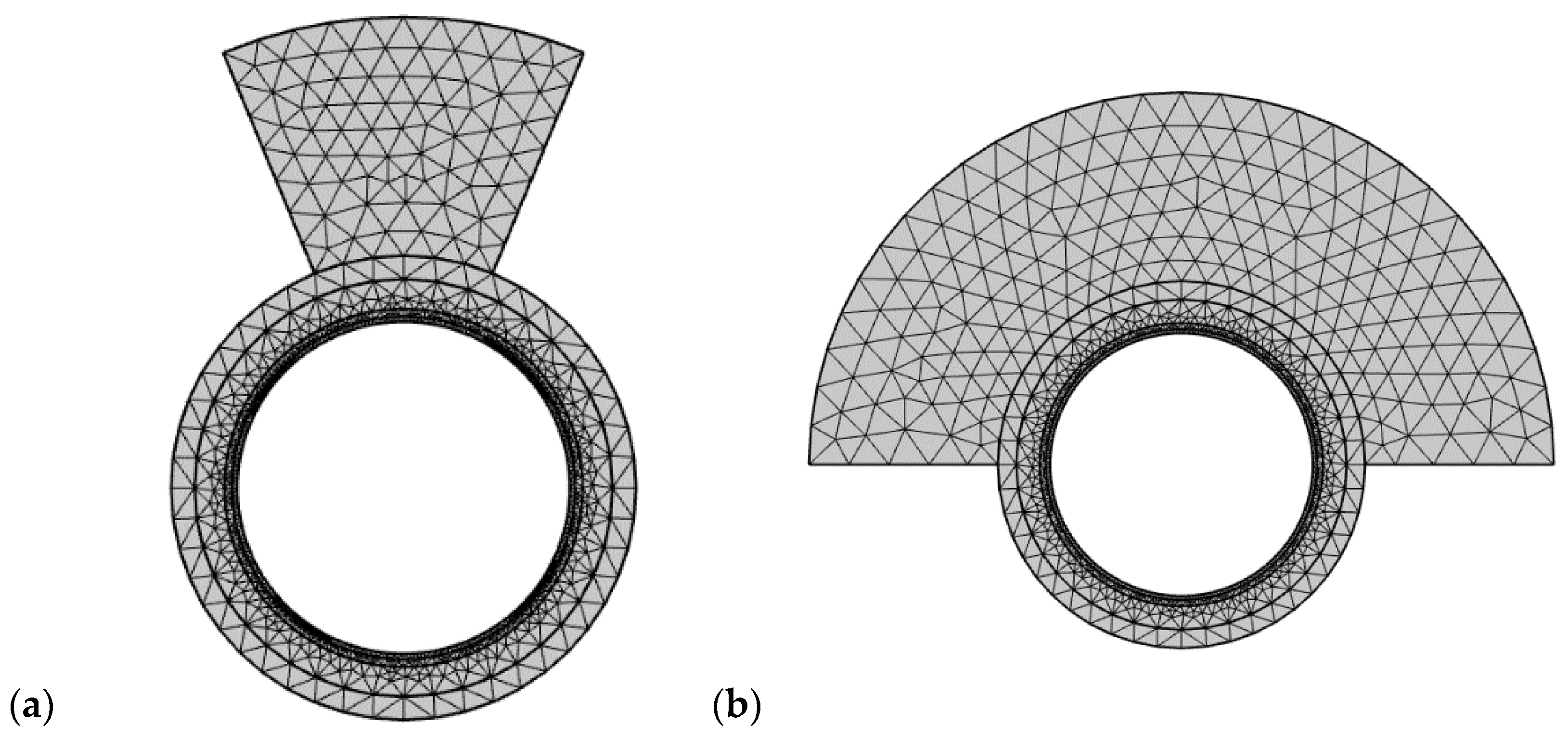
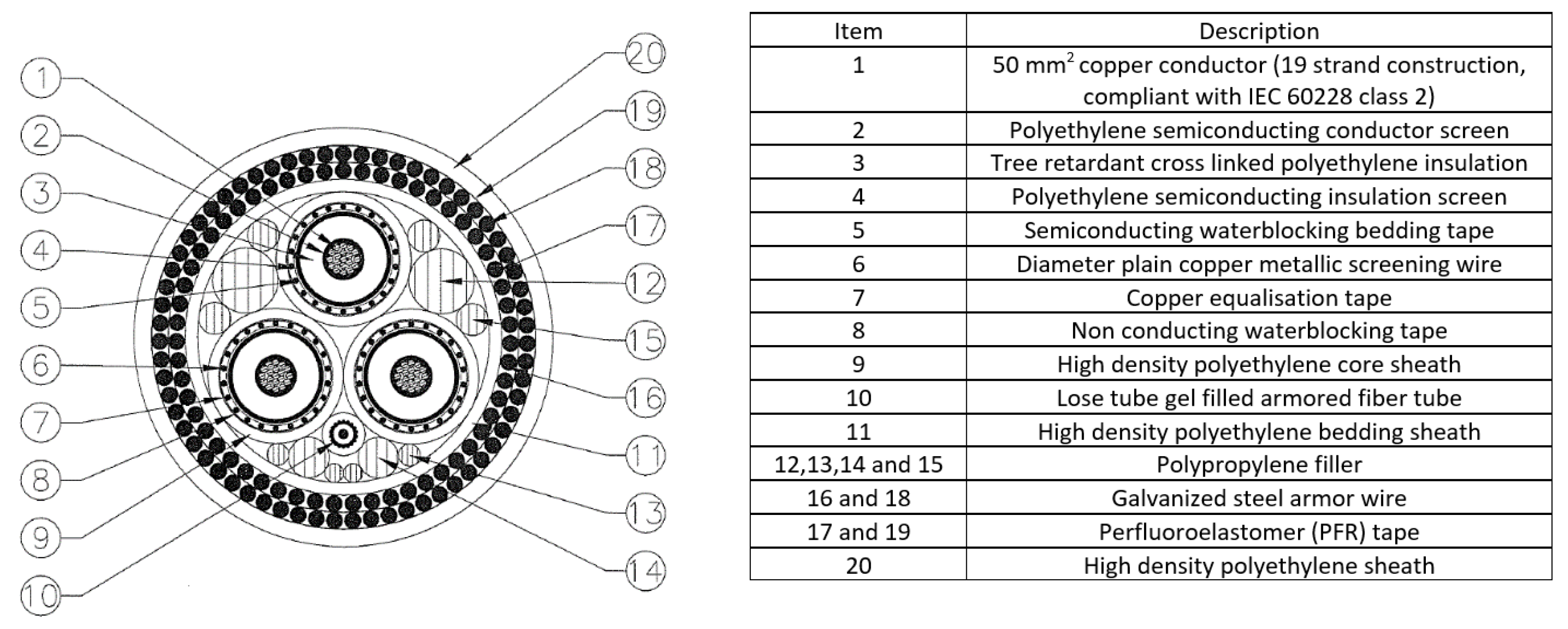
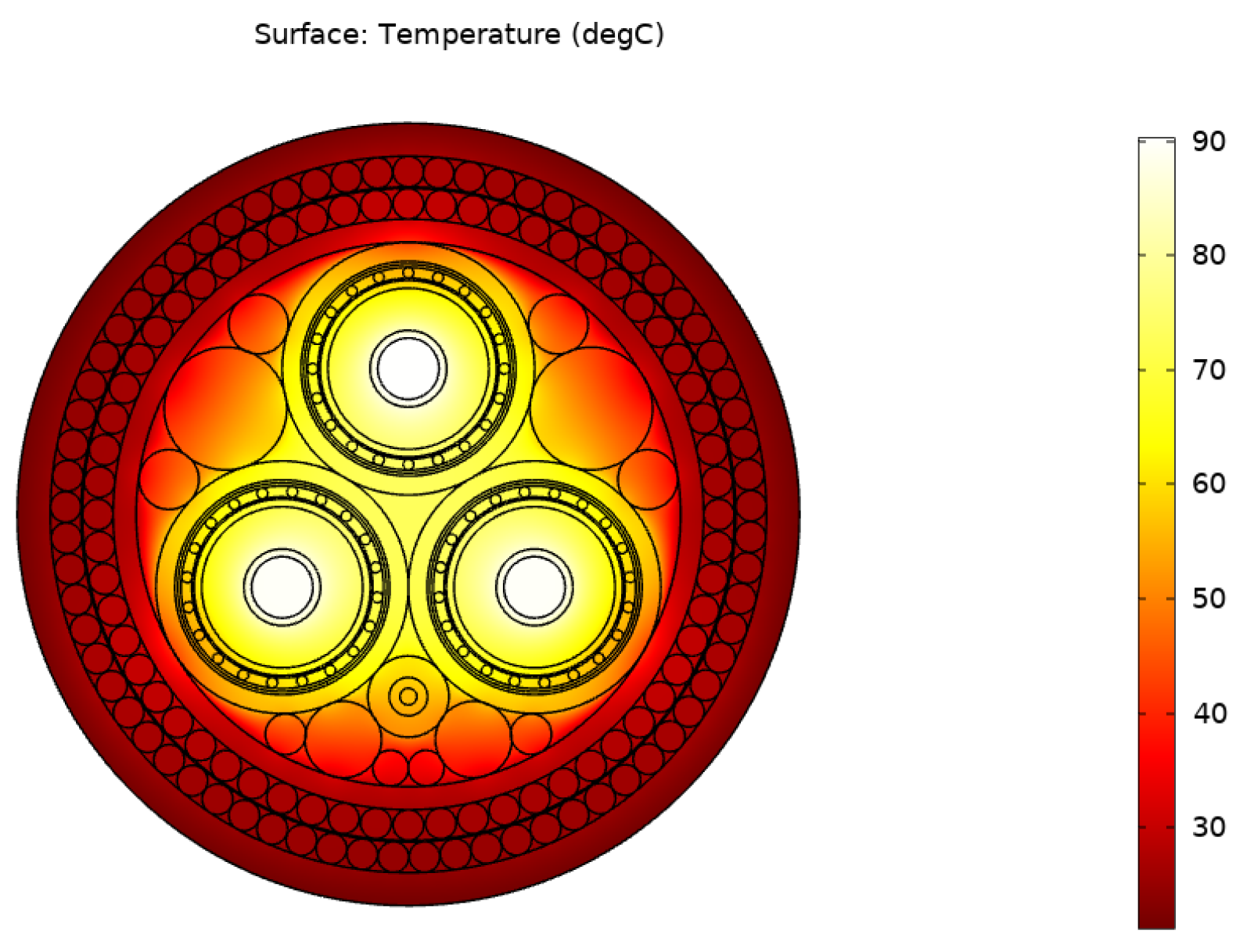
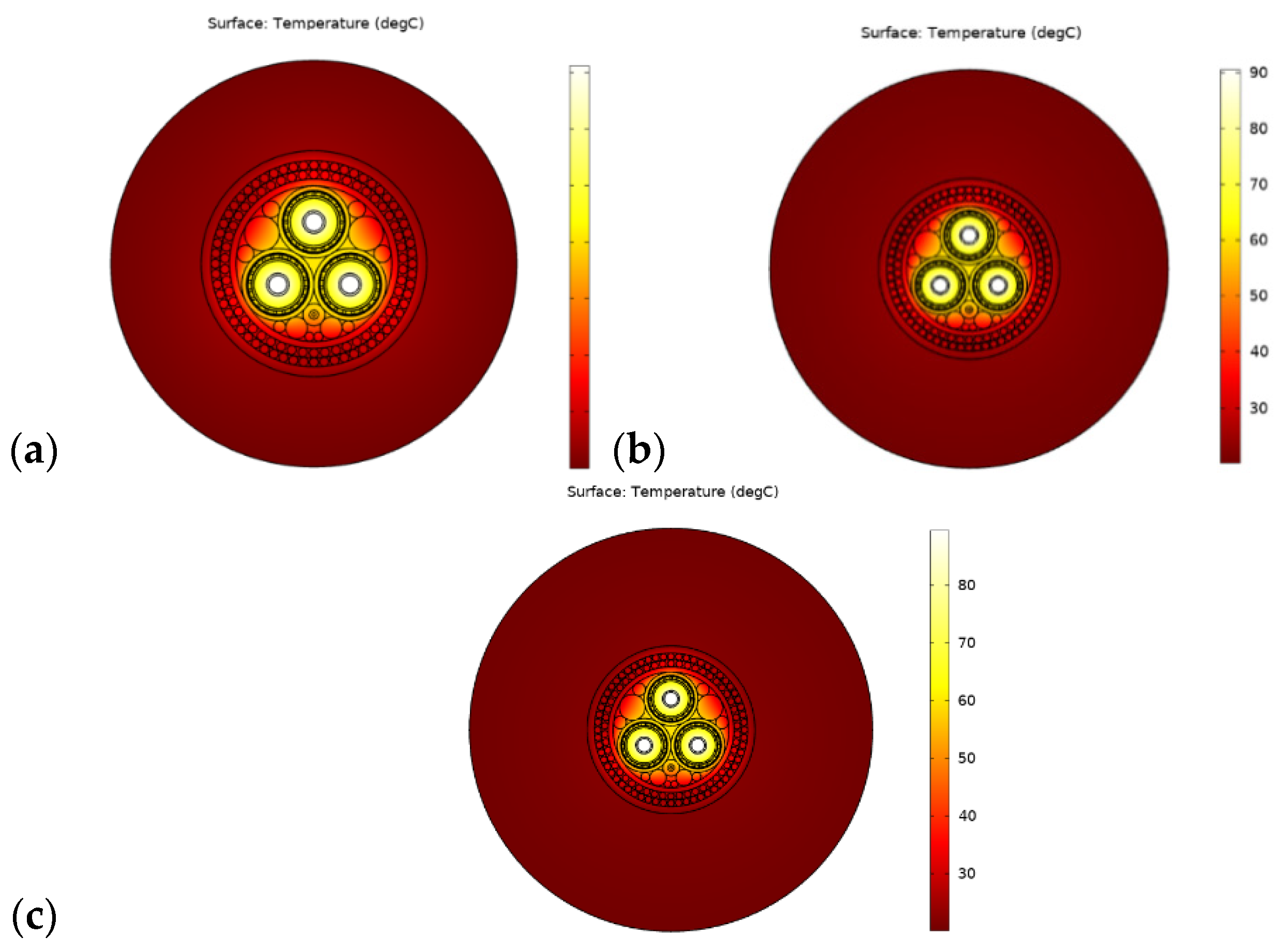
3.2. Numerical Simulation of Temperature Field in a 2D DSEC
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wind Systems. Available online: https://www.windsystemsmag.com/the-advantages-of-floating-wind-turbines/ (accessed on 10 March 2022).
- American Geosciences Institute. Available online: https://www.americangeosciences.org/critical-issues/faq/what-are-advantages-and-disadvantages-offshore-wind-farms/ (accessed on 5 May 2020).
- Benifla, V.; Adam, F. Development of a Genetic Algorithm Code for the Design of Cylindrical Buoyancy Bodies for Floating Offshore Wind Turbine Substructures. Energies 2022, 15, 1181. [Google Scholar] [CrossRef]
- Marini, M.; Baccoli, R.; Mastino, C.; Di Bella, A.; Bernardini, C.; Masullo, M. Assessment of the Noise Generated by Wind Turbines at Low Frequencies. Energy Resour. Technol. 2017, 139, 051215. [Google Scholar] [CrossRef]
- Yang, H.-S.; Alkhabbaz, A.; Edirisinghe, D.S.; Tongphong, W.; Lee, Y.-H. FOWT Stability Study According to Number of Columns Considering Amount of Materials Used. Energies 2022, 15, 1653. [Google Scholar] [CrossRef]
- Weerheim, R. Development of Dynamic Power Cables for Commercial Floating Wind Farms. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 12 November 2018. [Google Scholar]
- Cruciani, M. L’éolien Offshore Flottant dans sa Dimension Industrielle et Technologie; French; Etudes de l’Ifri: Paris, France, 2019. [Google Scholar]
- Sievers, M. Biofouling leads to reduced shell growth and flesh weight in the cultured mussel Mytilus galloprovincialis. Biofouling 2012, 29, 97–107. [Google Scholar] [CrossRef]
- Valdez, B.; Ramirez, J.; Eliezer, A.; Schorr, M.; Ramos, R.; Salinas, R. Corrosion assessment of infrastructure assets in coastal seas. Mar. Eng. Tech. 2016, 15, 124–134. [Google Scholar] [CrossRef] [Green Version]
- Schoefs, F.; Tran, T.-B. Reliability Updating of Offshore Structures Subjected to Marine Growth. Energies 2022, 15, 414. [Google Scholar] [CrossRef]
- Marty, A.; Berhault, C.; Damblans, G.; Facq, J.V.; Gaurier, B.; Germain, G.; Soulard, T.; Schoefs, F. Experimental study of marine growth effect on the hydrodynamical behaviour of a submarine cable. Appl. Oce. Res. 2021, 114, 102810. [Google Scholar] [CrossRef]
- Marty, A.; Schoefs, F.; Soulard, T.; Berhault, C.; Facq, J.-V.; Gaurier, B.; Germain, G. Effect of Roughness of Mussels on Cylinder Forces from a Realistic Shape Modelling. Mar. Sci. Eng. 2021, 9, 598. [Google Scholar] [CrossRef]
- IEC 60287-1 2014; The International Electroctechnical Comission. Electric Cables—Calculation of the Current Rating—Current Rating Equations (100% Load Factor) and Calculation of Losses. IEC: Geneva, Switzerland, 2014.
- Fitridge, I. Ruinous resident: The hydroid Ectopleura crocea negatively affects suspended culture of the mussel Mytilus galloprovincialis. Biofouling 2013, 29, 119–131. [Google Scholar] [CrossRef] [PubMed]
- Incropera, F.P.; Dewitt, B.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; John Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Moffat, R. Describing the uncertainties in experimental results. Exp. Therm and Fluid Sc. 1988, 1, 3–17. [Google Scholar] [CrossRef] [Green Version]
- Maxwell, J.C. A Treatise on Electricity and Magnetism, 3rd ed.; Oxford University Press: Oxford, UK, 1982. [Google Scholar]
- IEC 60287-2 2015; The International Electroctechnical Comission. Electric Cables—Calculation of the Current Rating, Thermal Resistance—Calculation of Thermal Resistance. IEC: Geneva, Switzerland, 2015.







| Mussels Type | T1 | T2 | T3 | T4 | T5 | T6 | Tw | ri | re | Q |
|---|---|---|---|---|---|---|---|---|---|---|
| °C | °C | °C | °C | °C | °C | °C | mm | mm | W | |
| Juvenile | 35.7 | 32.82 | 31.39 | 23.56 | 23.1 | 23.13 | 23 | 35 | 75 | 228.03 |
| Mix (juvenile and adult) | 27.28 | 26.72 | 26.6 | 23.47 | 22.32 | 22.31 | 22.3 | 35 | 95 | 127.75 |
| Adult | 28.77 | 27.9 | 28.28 | 23.62 | 23.52 | 23.52 | 23.36 | 35 | 105 | 211.63 |
| Mussels Type | kbiof | Absolute Uncertainty | Relative Uncertainty |
|---|---|---|---|
| W·m−1·K−1 | W·m−1·K−1 | % | |
| Juvenile | 4.4 | ±0.4 | 9 |
| Mix (juvenile and adult) | 8.0 | ±0.52 | 6.5 |
| Adult | 12.8 | ±0.97 | 7.6 |
| Mussels Type | hw | Absolute Uncertainty | Relative Uncertainty | ΔTm,w | Absolute Uncertainty | Relative Uncertainty |
|---|---|---|---|---|---|---|
| W·m−2·K−1 | W·m−2·K−1 | % | °C | °C | % | |
| Juvenile | 3395 | ±1123 | 33 | 0.23 | ±0.07 | 30 |
| Mix (juvenile & adult) | 873 | ±164 | 19 | 0.4 | ±0.07 | 17.5 |
| Adult | 2682 | ±1003 | 37 | 0.2 | ±0.07 | 35 |
| hw (Experimental) | hw (Churchill & Chu) | hw Discrepancy (Experimental and Churchill & Chu) | hw (Morgan) | hw Discrepancy (Experimental and Morgan) |
|---|---|---|---|---|
| W·m−2·K−1 | W·m−2·K−1 | % | W·m−2·K−1 | % |
| 220 | 309 | 29 | 234 | 6 |
| Mussels Type | Rconductive(biof) | Rconvective | Roverall | Rwithout(biof) | Effective Conductive Resistance Contribution | External Convective Resistance Contribution |
|---|---|---|---|---|---|---|
| K·W−1 | K·W−1 | K·W−1 | K·W−1 | % | % | |
| Juvenile | 0.045 | 0.001 | 0.046 | 0.03 | 97.8 | 2.2 |
| Mix (juvenile and adult) | 0.033 | 0.003 | 0.036 | 91.7 | 8.3 | |
| Adult | 0.022 | 0.0009 | 0.023 | 95.7 | 4.3 |
| Juvenile Mussels Colonization | T1 | T2 | T3 | T4 | T5 | T6 | Tw | ri | re | Q |
|---|---|---|---|---|---|---|---|---|---|---|
| % | °C | °C | °C | °C | °C | °C | °C | mm | mm | W |
| 25 | 28.12 | 26.44 | 24.8 | 22.55 | - | - | 22.3 | 38.9 | 78.9 | 66.33 |
| 50 | 30.82 | 28.5 | 26 | 22.92 | - | - | 22.45 | 38.9 | 78.9 | 85.43 |
| 100 | 29.48 | 28.46 | 28.95 | 23.03 | 22.6 | 22.4 | 22.12 | 38.9 | 78.9 | 40.74 |
| Juvenile Mussels Colonization | kbiof | Sensitivity for kbiof | hw1 | Sensitivity for hw1 | hw2 | Sensitivity for hw2 |
|---|---|---|---|---|---|---|
| % | W·m−1·K−1 | °C | W·m−2·K−1 | °C | W·m−2·K−1 | °C |
| 25 | 1.4 | 1 | 1510 | 0.1 | 1960 | 0.9 |
| 50 | 1.9 | 1 | 310 | 0.1 | 3910 | 0.88 |
| 100 | 1.6 | 5 | 910 | 0.1 | - | - |
| Symbol | Material | Value |
|---|---|---|
| R1 | Thermal resistance between one conductor and the sheath per unit length (K·m·W−1) | 0.587 |
| R2 | Thermal resistance of the bedding between the sheath and the armor per unit length (K·m·W−1) | 0.095 |
| R3 | Thermal resistance of the cable’s external serving per unit length (K·m·W−1) | 0.035 |
| R4 | Thermal resistance between the cable surface and the surrounding medium per unit length (K·m·W−1) | 0.011 |
| λ1 | Ratio of losses in the metal sheath to total losses in all conductors in that cable | 0.05 |
| λ2 | Ratio of losses in the armoring to total losses in all conductors in that cable. | 0.112 |
| RAC | Alternating current resistance per unit conductor length at maximum operating temperature (Ω·Km−1) | 0.5 |
| Wd | The dielectric loss per unit length of the insulation that surrounds the conductor (W·m−1) | 0.074 |
| Mussels Type | ΔT (Measurement) | ΔT (COMSOL) |
|---|---|---|
| K | K | |
| Juvenile | 10 | 3.3 |
| Mix (juvenile & adult) | 4.2 | 2.4 |
| Adult | 4.8 | 1.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maksassi, Z.; Garnier, B.; Moctar, A.O.E.; Schoefs, F.; Schaeffer, E. Thermal Characterization and Thermal Effect Assessment of Biofouling around a Dynamic Submarine Electrical Cable. Energies 2022, 15, 3087. https://doi.org/10.3390/en15093087
Maksassi Z, Garnier B, Moctar AOE, Schoefs F, Schaeffer E. Thermal Characterization and Thermal Effect Assessment of Biofouling around a Dynamic Submarine Electrical Cable. Energies. 2022; 15(9):3087. https://doi.org/10.3390/en15093087
Chicago/Turabian StyleMaksassi, Ziad, Bertrand Garnier, Ahmed Ould El Moctar, Franck Schoefs, and Emmanuel Schaeffer. 2022. "Thermal Characterization and Thermal Effect Assessment of Biofouling around a Dynamic Submarine Electrical Cable" Energies 15, no. 9: 3087. https://doi.org/10.3390/en15093087
APA StyleMaksassi, Z., Garnier, B., Moctar, A. O. E., Schoefs, F., & Schaeffer, E. (2022). Thermal Characterization and Thermal Effect Assessment of Biofouling around a Dynamic Submarine Electrical Cable. Energies, 15(9), 3087. https://doi.org/10.3390/en15093087








