Consensus-Based Distributed Secondary Frequency Control Method for AC Microgrid Using ADRC Technique
Abstract
:1. Introduction
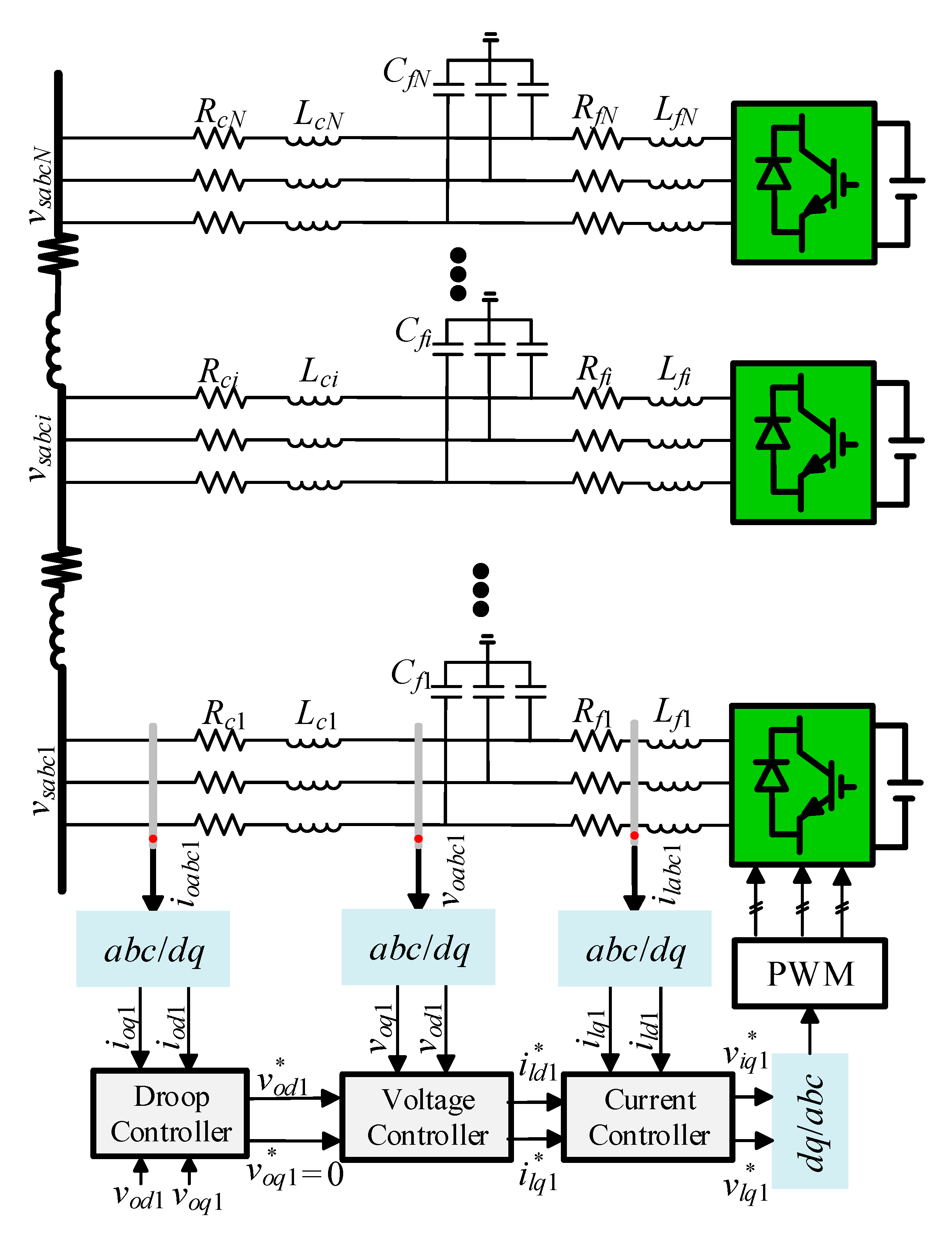
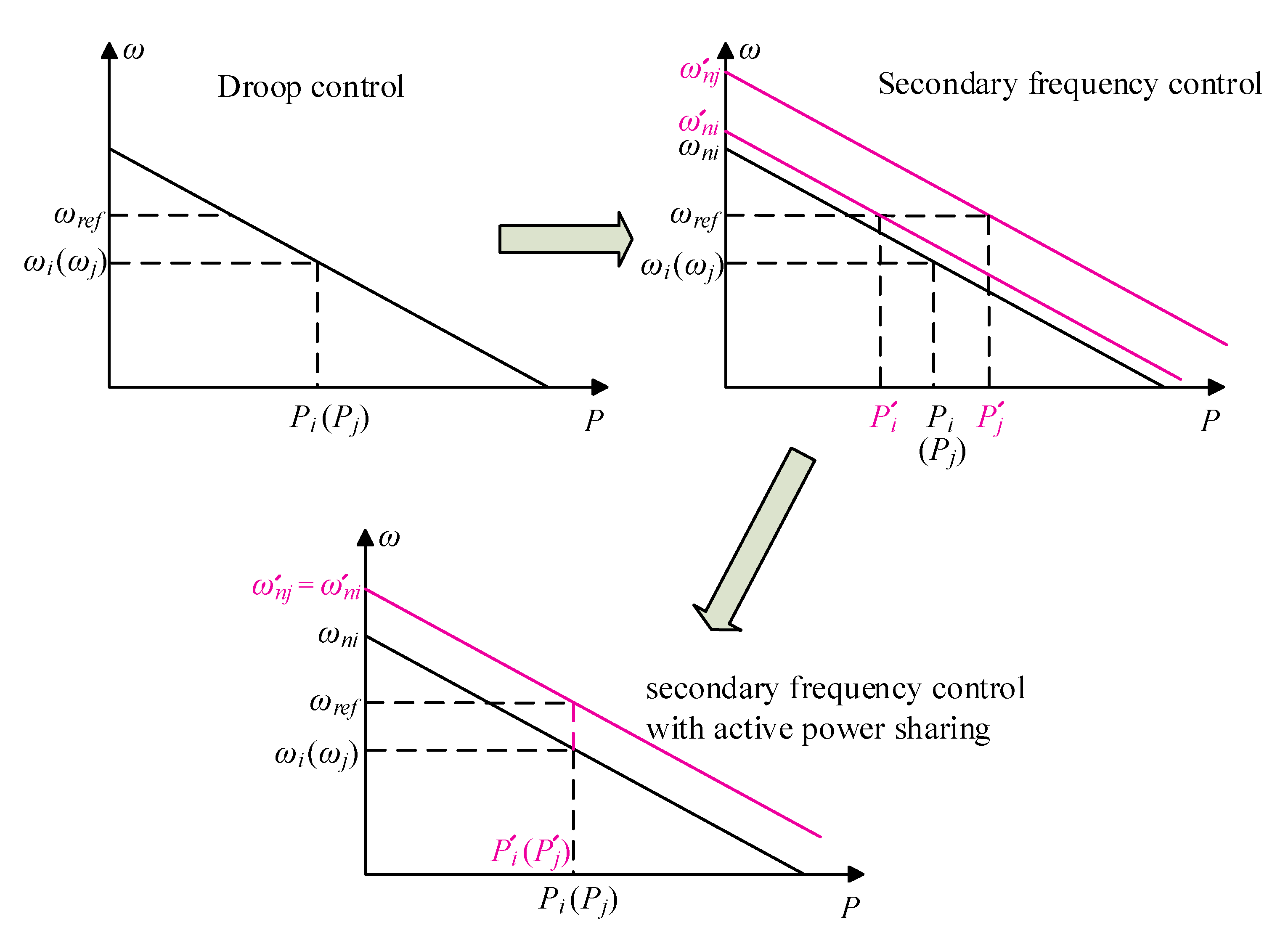
2. Droop Control and Frequency Control System Modelling
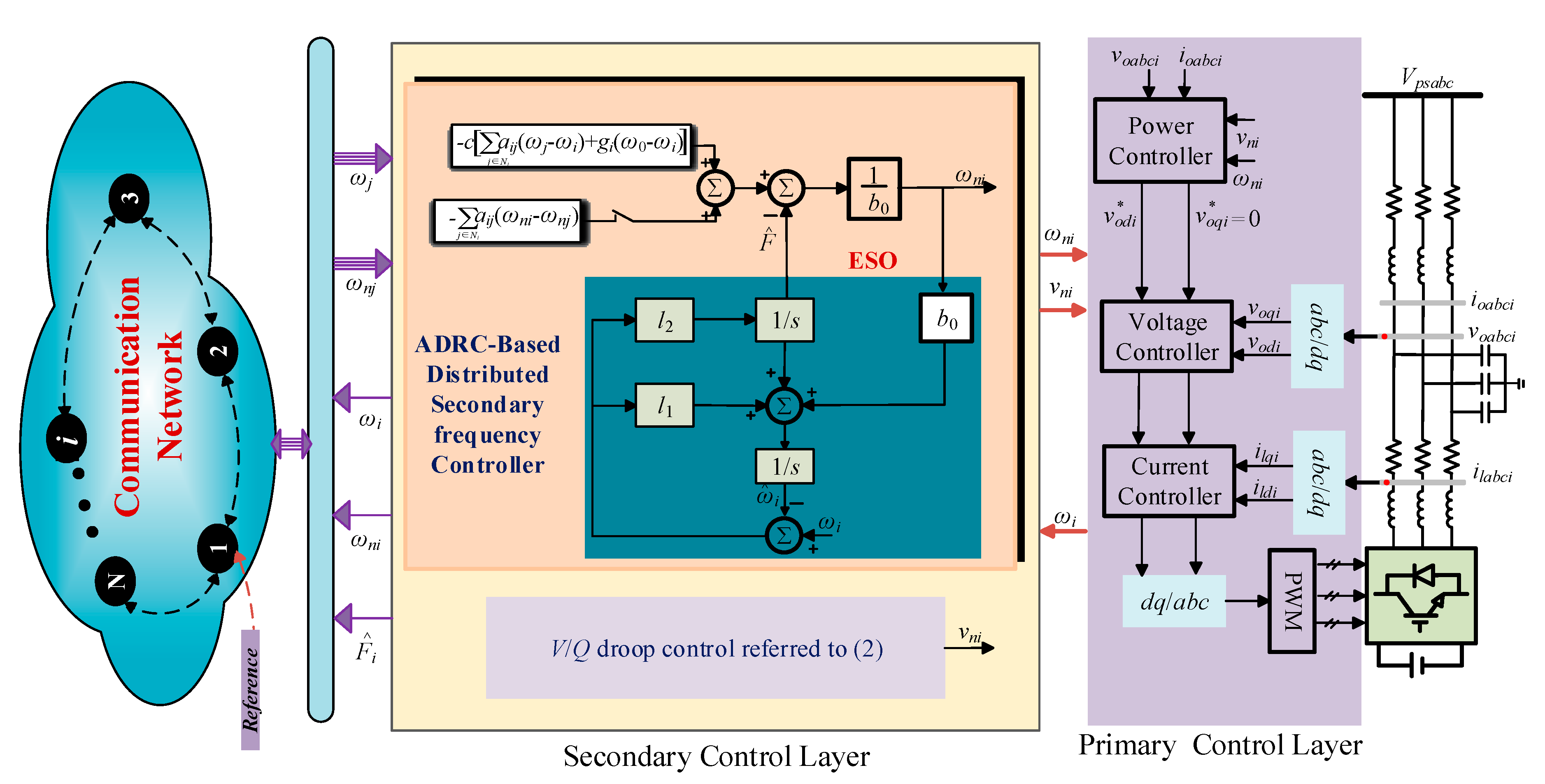
3. Proposed Distributed Secondary Frequency Control
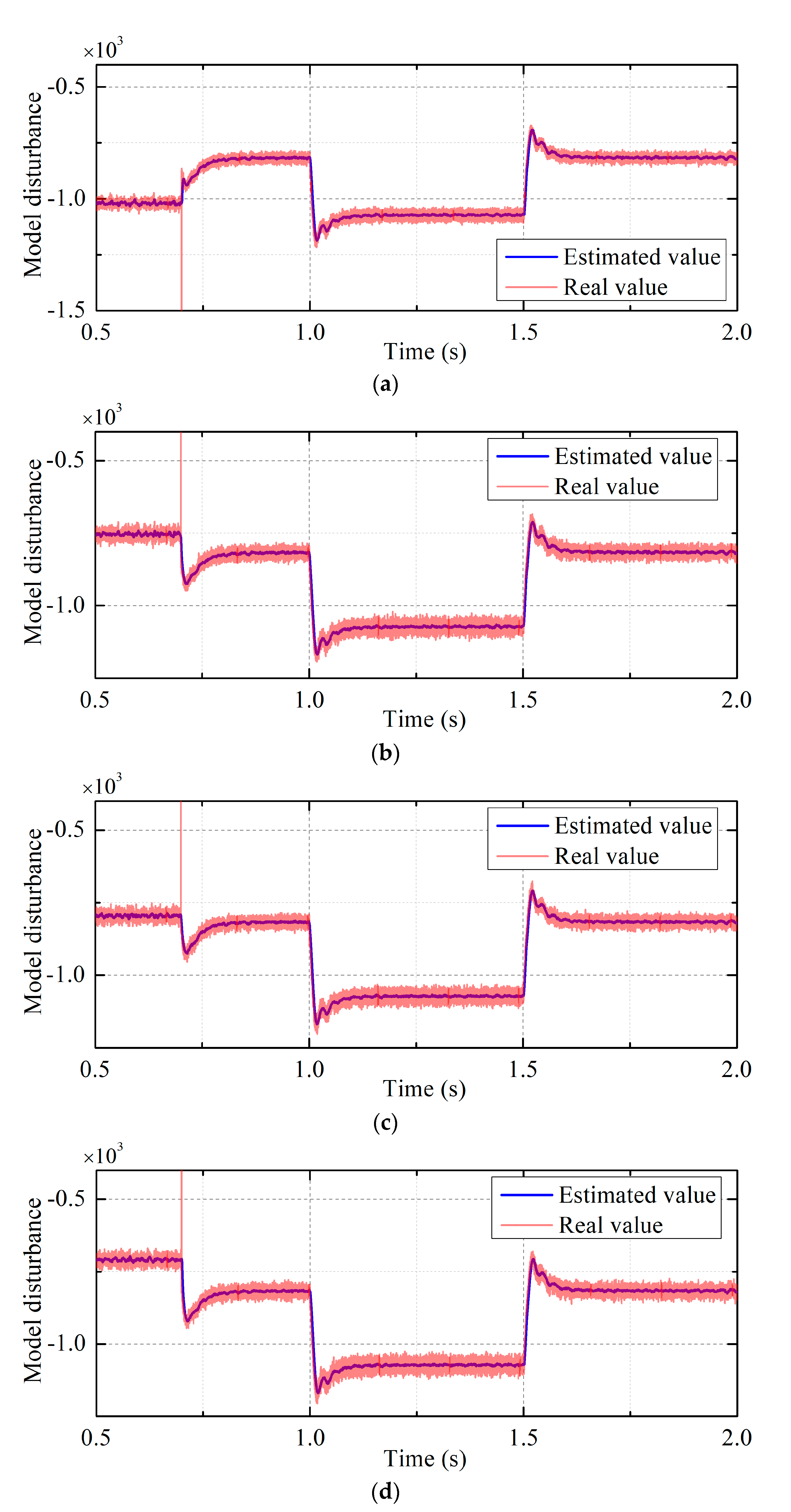
3.1. Linear Extended State Observer
3.2. Proposed Consensus-Based Distributed Secondary Frequency Controller Design
3.3. Stability Analysis and Controller Parameter Selection
3.3.1. Stability Analysis of Proposed Control Law without Active Power Sharing
3.3.2. Stability Analysis of Proposed Control Law with Active Power Sharing
4. Results
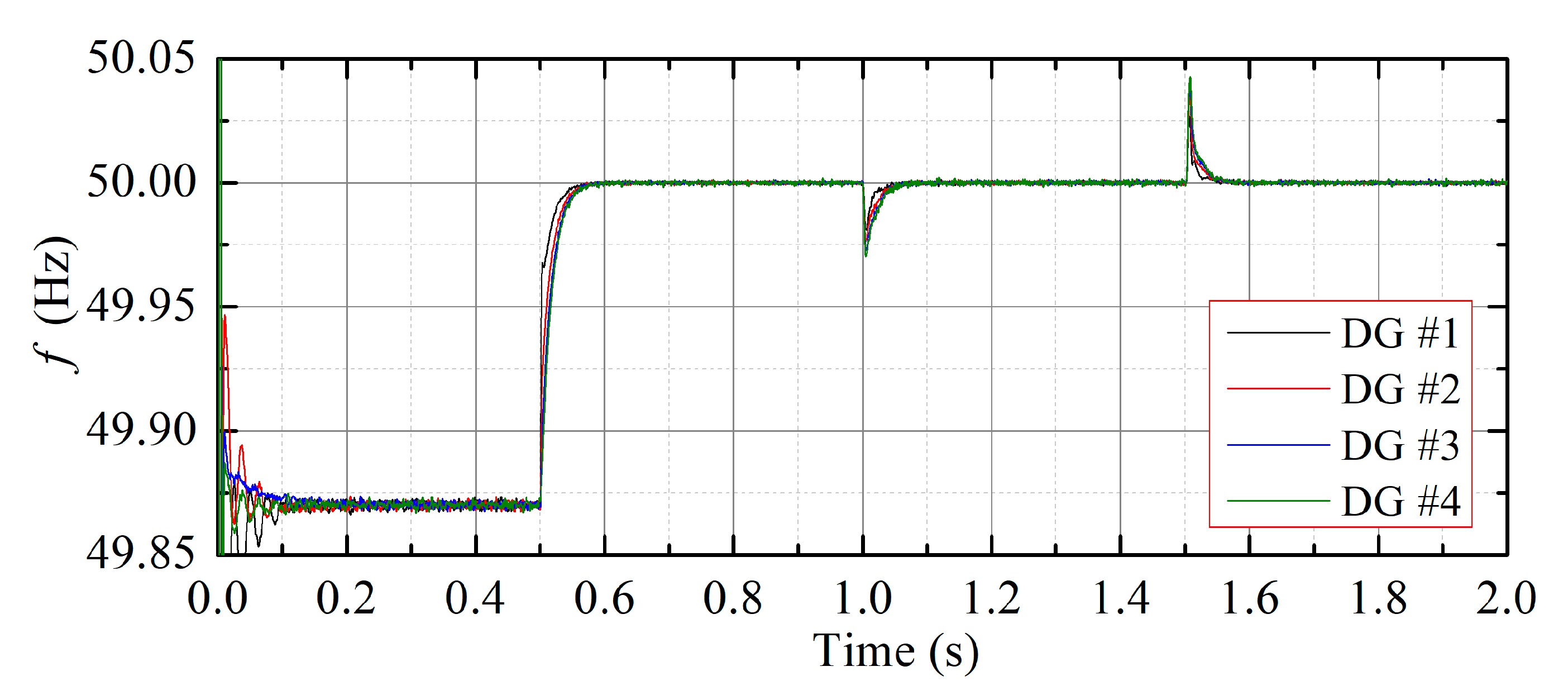
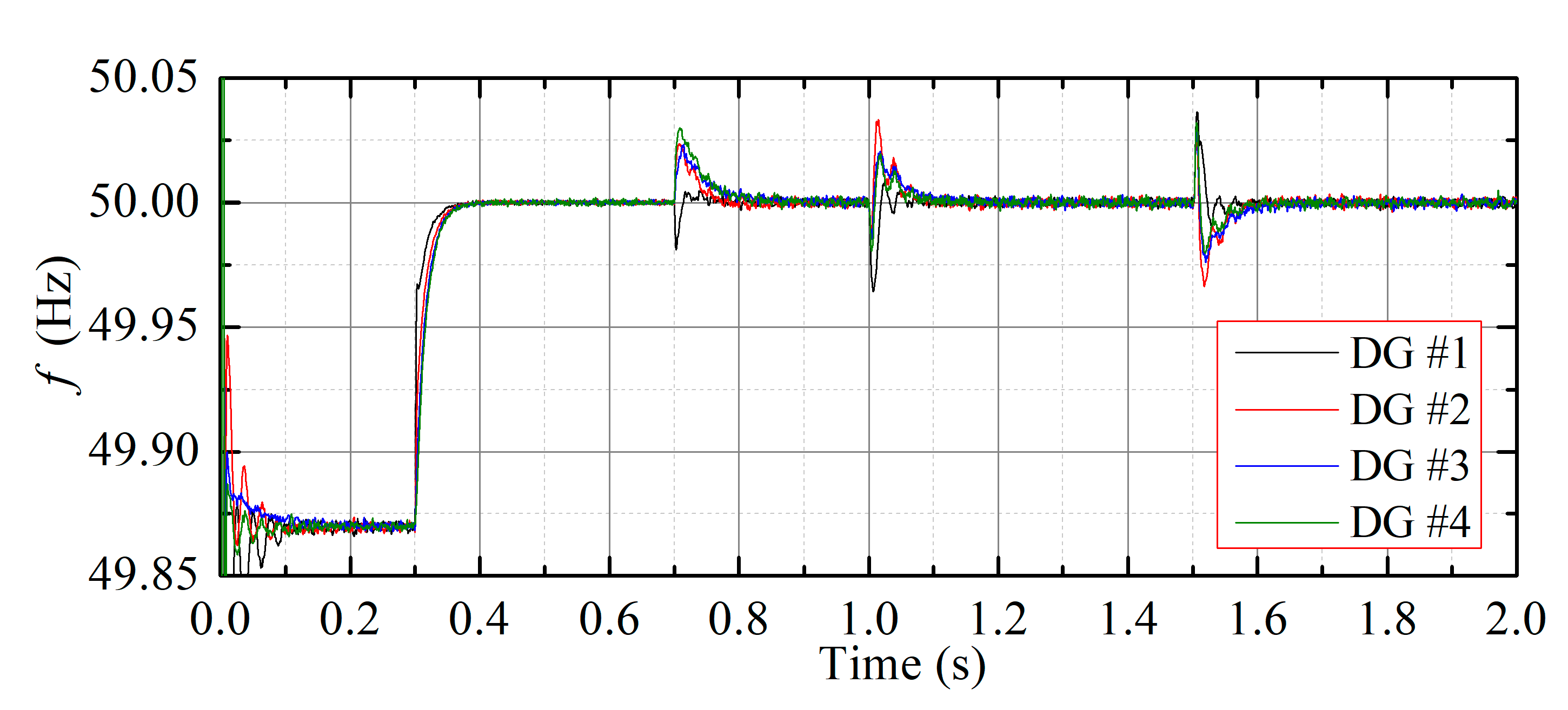
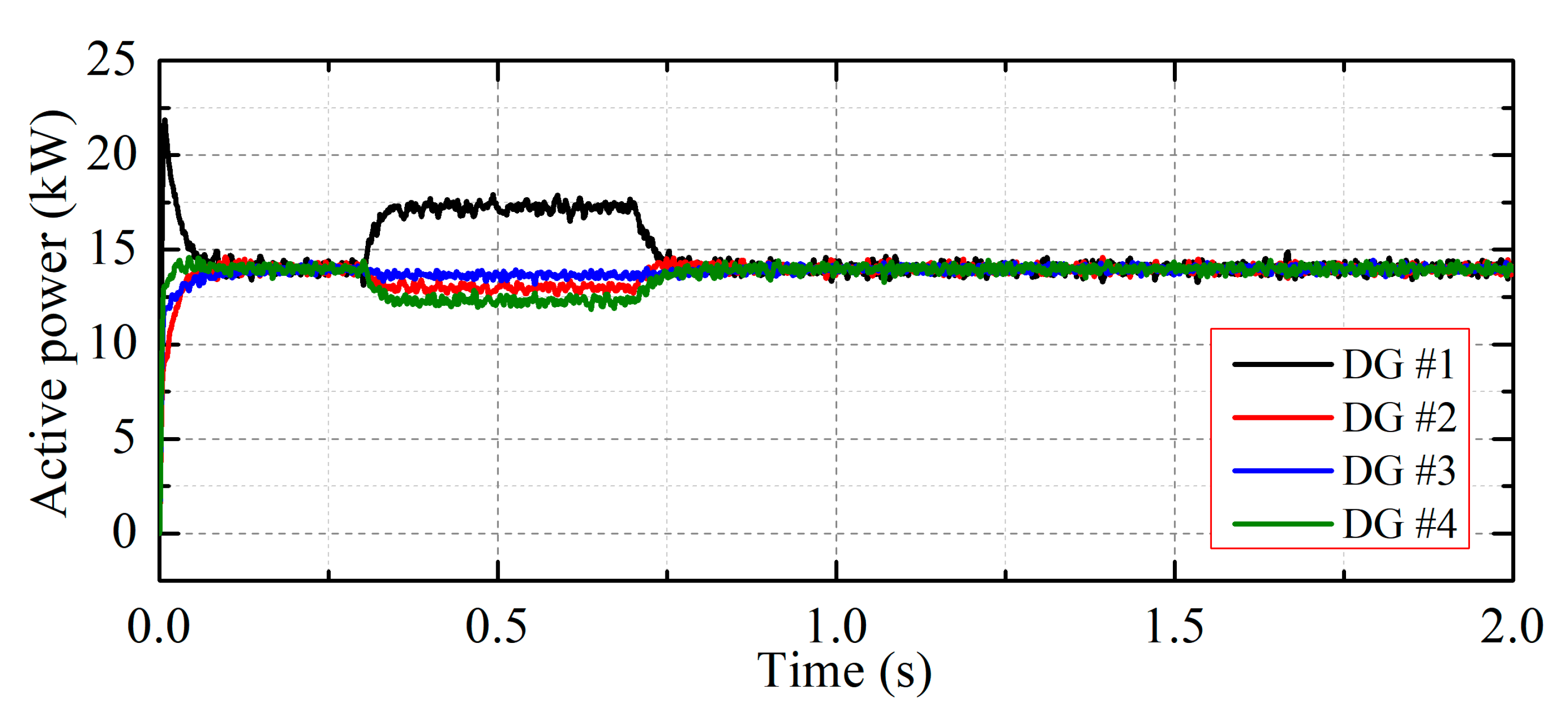
4.1. Case Study 1: Frequency Restoration without Active Power Sharing Control
4.2. Case Study 2: Frequency Restoration with Active Power Sharing Control
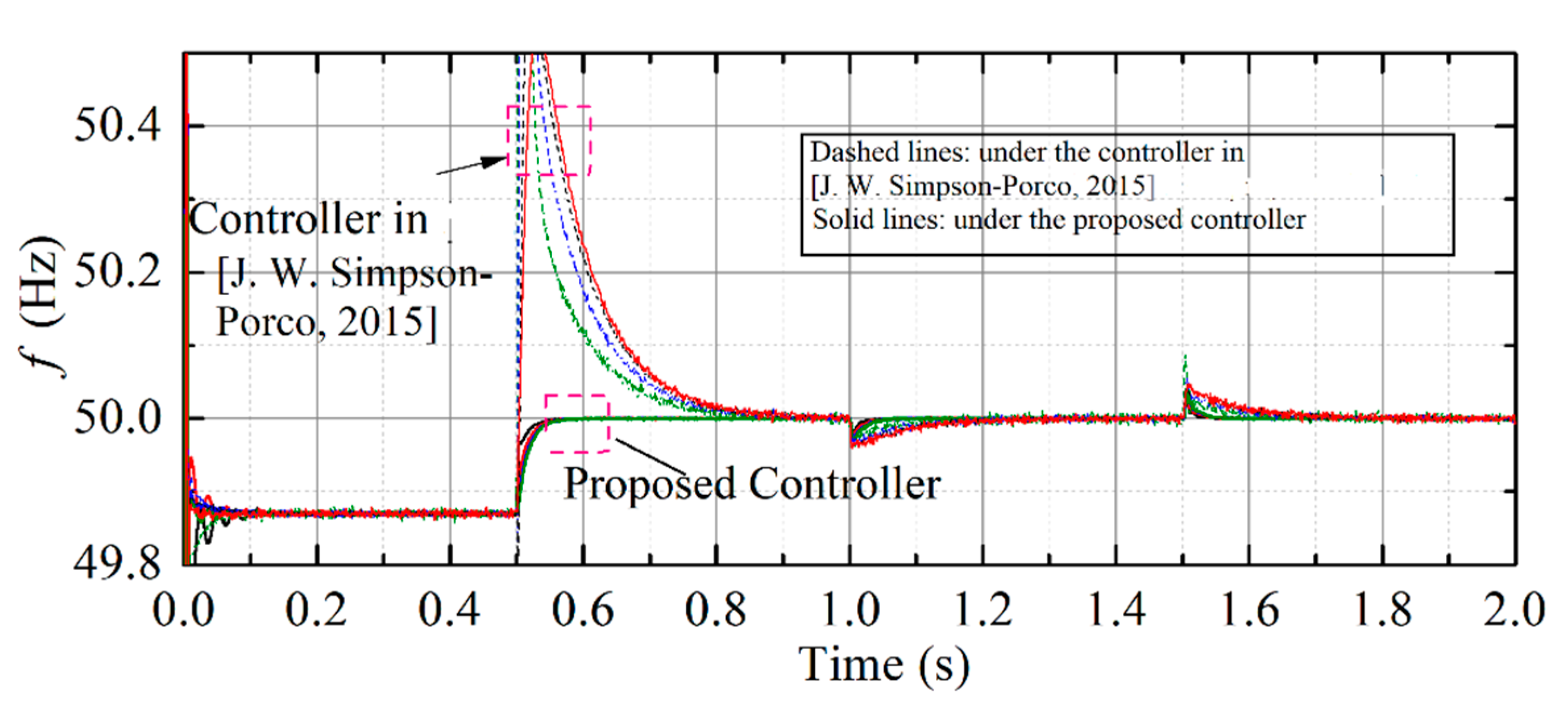
4.3. Case Study 3: Dynamic Performance Comparsion with Convention Integrator-Based Distributed Secondary Frequency Controller
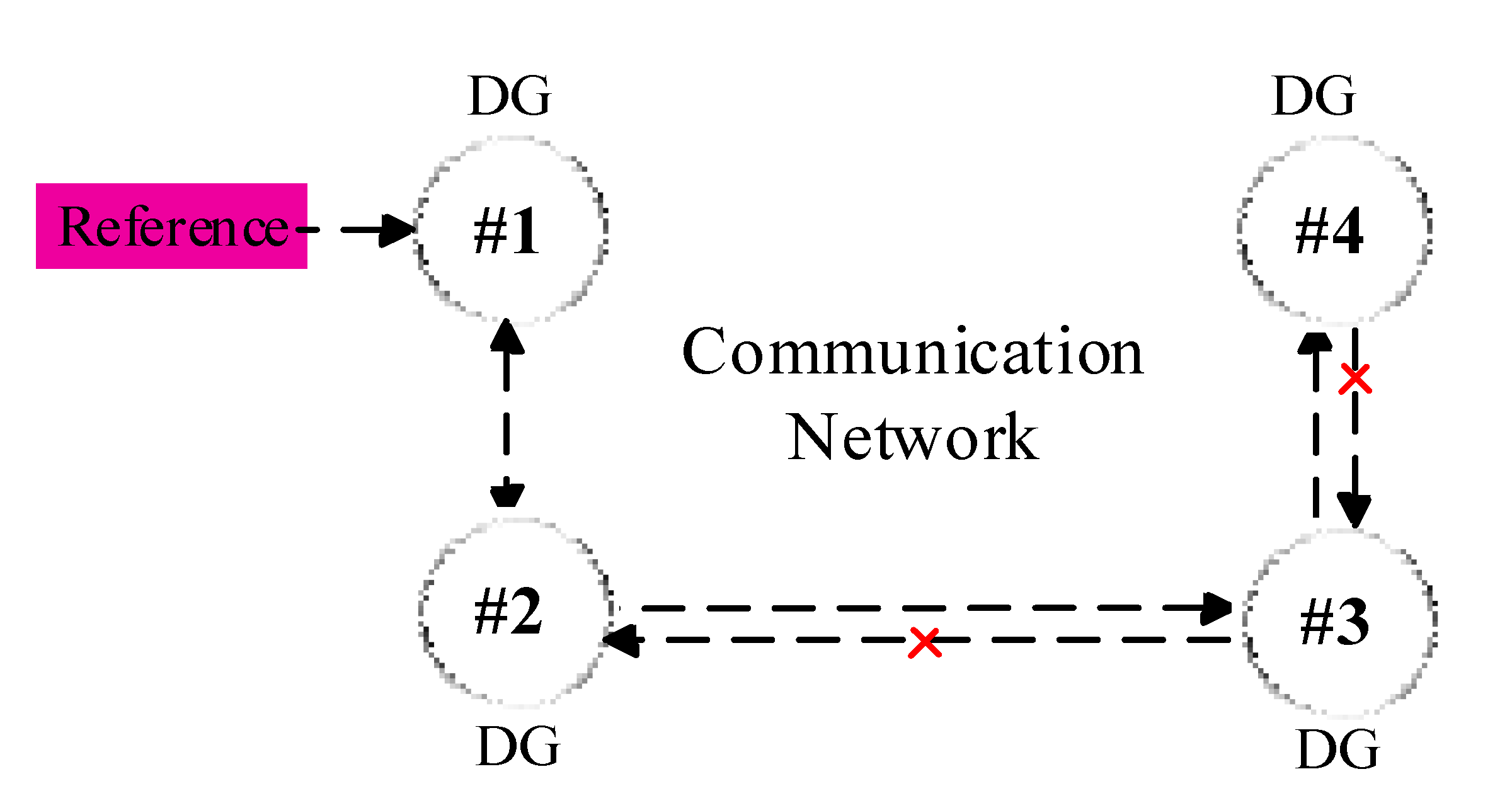
4.4. Case Study 4: Comunication Failure Roustness Test
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| ωc | Bandwidth of low-pass filter |
| Fi | Lumped model disturbance |
| ωni(ui) | Secondary frequency control input |
| ωi | Angular speed |
| zi | Agumented system state vector |
| Estimated system state vector | |
| l | Observer gain vector |
| ω0 | Bandwidth of extended state observer |
| c | Frequency coupling gain |
| P0, Q0 | Rated active and reactive power. |
| Pi, Qi | filtered active and reactive power. |
| mPi | Droop coefficients of DG #i. |
| N | Number of DG unit |
| Y | Global system output vector |
| U | Global system control vector |
| F | Global model disturbance vector |
| E | Global tracking error vector |
| L | Laplace Matrix |
| G | Pinned Matrix |
| gi | Pinned gain |
| i | Global estimated disturbance vector |
| β1, β2 | Observer gain |
References
- Rahbar, K.; Chai, C.C.; Zhang, R. Energy cooperation optimization in microgrids with renewable energy integration. IEEE Trans. Smart Grid 2018, 9, 1482–1493. [Google Scholar] [CrossRef]
- Mai, T.; Hand, M.; Baldwin, S.; Wiser, R.; Brinkman, G.; Denholm, P.; Arent, D.; Porro, G.; Sandor, D.; Hostick, D.; et al. Renewable electricity futures for the united states. IEEE Trans. Sustain. Energy 2014, 5, 372–378. [Google Scholar] [CrossRef]
- Du, E.; Zhang, N.; Hodge, B.; Wang, Q.; Kang, C.; Kroposki, B.; Xia, Q. The role of concentrating solar power toward high renewable energy penetrated power systems. IEEE Trans. Power Syst. 2018, 33, 6630–6641. [Google Scholar] [CrossRef]
- Bollen, M.H.J.; Sannino, A. Voltage control with inverter-based distributed generation. IEEE Trans. Power Deliv. 2005, 20, 519–520. [Google Scholar]
- Cui, Q.; Bai, X.; Dong, W. Collaborative planning of distributed wind power generation and distribution network with large-scale heat pumps. CSEE J. Power Energy Syst. 2019, 5, 335–347. [Google Scholar]
- Che, L.; Shahidehpour, M.; Alabdulwahab, A.; Al-Turki, Y. Hierarchical coordination of a community microgrid with AC and DC microgrids. IEEE Trans. Smart Grid 2015, 6, 3042–3051. [Google Scholar] [CrossRef]
- Wan, Q.; Bian, Y.; Chen, Y. Research on a Micro-Grid Frequency Modulation Strategy Based on Optimal Utilization of Air Conditioners. Energies 2016, 9, 1085. [Google Scholar] [CrossRef] [Green Version]
- Zhou, S.; Gu, Y.; Song, W.; Wang, C.; Bai, F.; Cai, Y. Research on control strategy of grid-connected inverter in microgrid System. In Proceedings of the 2019 IEEE 3rd Conference on Energy Internet and Energy System Integration, Changsha, China, 8–10 November 2019; pp. 392–396. [Google Scholar]
- Patarroyo-Montenegro, J.F.; Andrade, F.; Guerrero, J.M.; Vasquez, J.C. A linear quadratic regulator with Optimal Reference tracking for three-phase inverter-based islanded microgrids. IEEE Trans. Power Electron. 2021, 36, 7112–7122. [Google Scholar] [CrossRef]
- Andrade, A.I.; Blasco-Gimenez, R.; Peña, R.S. Constant power control of grid connected inverters during unbalanced faults. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–7. [Google Scholar]
- Meng, X.; Liu, J.; Liu, Z. A generalized droop control for grid-supporting inverter based on comparison between traditional droop control and virtual synchronous generator control. IEEE Trans. Power Electron. 2019, 34, 5416–5438. [Google Scholar] [CrossRef]
- Bassey, O.; Butler-Purry, K.L. Black Start Restoration of Islanded Droop-Controlled Microgrids. Energies 2020, 13, 5996. [Google Scholar] [CrossRef]
- Meng, L.; Savaghebi, M.; Andrade, F.; Vasquez, J.C.; Guerrero, J.M.; Graells, M. Microgrid central controller development and hierarchical control implementation in the intelligent microgrid lab of Aalborg University. In Proceedings of the 2015 IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, USA, 15–19 March 2015; pp. 2585–2592. [Google Scholar]
- Shafiee, Q.; Guerrero, J.M.; Vasquez, J.C. Distributed secondary control for islanded microgrids—A novel approach. IEEE Trans. Power Electron. 2014, 29, 1018–1031. [Google Scholar] [CrossRef] [Green Version]
- Bidram, A.; Davoudi, A.; Lewis, F.L.; Guerrero, J.M. Distributed cooperative secondary control of microgrids using feedback linearization. IEEE Trans. Power Syst. 2013, 28, 3462–3470. [Google Scholar] [CrossRef] [Green Version]
- Simpson-Porco, J.W.; Shafiee, S.Q.; Dörfler, F.; Vasquez, J.C.; Guerrero, J.M.; Bullo, F. Secondary frequency and voltage control of islanded microgrids via distributed averaging. IEEE Trans. Ind. Electron. 2015, 62, 7025–7038. [Google Scholar] [CrossRef]
- Dehkordi, N.M.; Sadati, N.; Hamzeh, M. Distributed robust finite-time secondary voltage and frequency control of islanded microgrids. IEEE Trans. Power Syst. 2017, 32, 3648–3659. [Google Scholar] [CrossRef]
- Zuo, S.; Davoudi, A.; Song, Y.; Lewis, F.L. Distributed finite-time voltage and frequency restoration in islanded AC microgrids. IEEE Trans. Ind. Electron. 2016, 63, 5988–5997. [Google Scholar] [CrossRef]
- Chen, G.; Lewis, F.L.; Feng, E.N.; Song, Y. Distributed optimal active power control of multiple generation systems. IEEE Trans. Ind. Electron. 2015, 62, 7079–7090. [Google Scholar] [CrossRef]
- Yang, Z.; Xiang, J.; Li, Y. Distributed consensus based supply–demand balance algorithm for economic dispatch problem in a smart grid with switching graph. IEEE Trans. Ind. Electron. 2017, 64, 1600–1610. [Google Scholar] [CrossRef]
- Binetti, G.; Davoudi, A.; Lewis, F.L.; Naso, D.; Turchiano, B. Distributed consensus-based economic dispatch with transmission losses. IEEE Trans. Power Syst. 2014, 29, 1711–1720. [Google Scholar] [CrossRef]
- Liu, W.; Wen, Z.; Shen, Y.; Zhang, Z. Reinforcement learning-based distributed secondary optimal control for multi-microgrids. In Proceedings of the 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017; pp. 1–4. [Google Scholar]
- Smith, E.; Robinson, D.A.; Agalgaonkar, A. Cooperative secondary voltage control of static converters in a microgrid using model-free reinforcement learning. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE ‘19 ECCE Europe), Genova, Italy, 3–5 September 2019; pp. 1–10. [Google Scholar]
- Liu, Z.; Luo, Y.; Zhuo, R.; Jin, X. Distributed reinforcement learning to coordinate current sharing and voltage restoration for islanded DC microgrid. J. Mod. Power Syst. Clean Energy 2018, 6, 364–374. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Wang, X.; Liu, P.X. Impact of communication delays on secondary frequency control in an islanded microgrid. IEEE Trans. Ind. Electron. 2015, 62, 2021–2031. [Google Scholar] [CrossRef]
- Lai, J.; Zhou, H.; Lu, X.; Yu, X.; Hu, W. Droop-based distributed cooperative control for microgrids with time-varying delays. IEEE Trans. Smart Grid 2016, 7, 1775–1789. [Google Scholar] [CrossRef]
- Wu, X.; Shen, C.; Iravani, R. A distributed, cooperative frequency and voltage control for microgrids. IEEE Trans. Smart Grid 2018, 9, 2764–2776. [Google Scholar] [CrossRef]
- Ullah, S.; Khan, L.; Jamil, M.; Jafar, M.; Mumtaz, S.; Ahmad, S. A finite-time robust distributed cooperative secondary control protocol for droop-based islanded AC microgrids. Energies 2021, 14, 2936. [Google Scholar] [CrossRef]
- Guo, F.; Wen, C.; Mao, J.; Song, Y. Distributed secondary voltage and frequency restoration control of droop-controlled inverter-based microgrids. IEEE Trans. Ind. Electron. 2015, 62, 4355–4364. [Google Scholar] [CrossRef]
- Cady, S.T.; Domínguez-García, A.D.; Hadjicostis, C.N. A distributed generation control architecture for islanded AC microgrids. IEEE Trans. Control Syst. Technol. 2015, 23, 1717–1735. [Google Scholar] [CrossRef]
- Islam, S.; Liu, P.X.; Saddik, A. Distributed robust adaptive finite-time voltage control for microgrids with uncertainty. In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Banff, AB, Canada, 5–8 October 2017; pp. 2200–2202. [Google Scholar]
- Pilloni, A.; Pisano, A.; Usai, E. Robust finite-time frequency and voltage restoration of inverter-based microgrids via sliding-mode cooperative control. IEEE Trans. Ind. Electron. 2018, 65, 907–917. [Google Scholar] [CrossRef]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Gao, Z.; Huang, Y.; Han, J. An alternative paradigm for control system design. In Proceedings of the 40th IEEE Conference on Decision and Control (Cat. No.01CH37228), Orlando, FL, USA, 4–7 December 2001; Volume 5, pp. 4578–4585. [Google Scholar]
- Gaol, Q. On stability analysis of active disturbance rejection control for nonlinear time-varying plants with unknown dynamics. In Proceedings of the 2007 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007. [Google Scholar]
- Brabandere, K.; Bolsens, B.; Keybus, J.; Woyte, A.; Driesen, J.; Belmans, R. A voltage and frequency droop control method for parallel inverters. IEEE Trans. Power Electron. 2007, 22, 1107–1115. [Google Scholar] [CrossRef]
- Mahmood, H.; Michaelson, D.; Jiang, J. Reactive power sharing in islanded microgrids using adaptive voltage droop control. IEEE Trans. Smart Grid. 2015, 6, 3052–3060. [Google Scholar] [CrossRef]
- Xue, W.; Bai, W.; Yang, S.; Song, K.; Huang, Y.; Xie, H. ADRC with adaptive extended state observer and its application to air–fuel ratio control in gasoline engines. IEEE Trans. Ind. Electron. 2015, 62, 5847–5857. [Google Scholar] [CrossRef]
- Wu, D.; Chen, K. Design and analysis of precision active disturbance rejection control for noncircular turning process. IEEE Trans. Ind. Electron. 2009, 56, 2746–2753. [Google Scholar]






| DG Parameters | DG #1 | DG #2 | DG #3 | DG #4 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Droop control | mP | 1 × 10−5 | 1 × 10−5 | 1 × 10−5 | 1 × 10−5 | |||||||||
| nQ | 3 × 10−2 | 3 × 10−3 | 3 × 10−3 | 3 × 10−3 | ||||||||||
| Voltage control | KPvi | 0.12 | 0.12 | 0.12 | 0.12 | |||||||||
| KIvi | 180 | 180 | 180 | 180 | ||||||||||
| Current control | KPci | 15 | 15 | 15 | 15 | |||||||||
| KIci | 20,000 | 20,000 | 20,000 | 20,000 | ||||||||||
| LC filter | Lfi | 1.35 mH | 1.35 mH | 1.35 mH | 1.35 mH | |||||||||
| Cfi | 50 μF | 50 μF | 50 μF | 50 μF | ||||||||||
| Rfi | 0.2 Ω | 0.2 Ω | 0.2 Ω | 0.2 Ω | ||||||||||
| Connector impedance Zci | Rci | 0.014 Ω | 0.014 Ω | 0.014 Ω | 0.014 Ω | |||||||||
| Lci | 0.234 mH | 0.834 mH | 0.834 mH | 0.634 mH | ||||||||||
| Line | Zline1 | Zline2 | Zline3 | |||||||||||
| Rline | 0.14 Ω | 0.14 Ω | 0.24 Ω | |||||||||||
| Lline | 0.21 mH | 0.86 mH | 0.16 mH | |||||||||||
| Load | Zload1 | Zload2 | Zload3 | Zload4 | ||||||||||
| Rload | 10 Ω | 10 Ω | 10 Ω | 10 Ω | ||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Zhang, M.; Deng, Y. Consensus-Based Distributed Secondary Frequency Control Method for AC Microgrid Using ADRC Technique. Energies 2022, 15, 3184. https://doi.org/10.3390/en15093184
Li W, Zhang M, Deng Y. Consensus-Based Distributed Secondary Frequency Control Method for AC Microgrid Using ADRC Technique. Energies. 2022; 15(9):3184. https://doi.org/10.3390/en15093184
Chicago/Turabian StyleLi, Wenguo, Mingmin Zhang, and Yaqi Deng. 2022. "Consensus-Based Distributed Secondary Frequency Control Method for AC Microgrid Using ADRC Technique" Energies 15, no. 9: 3184. https://doi.org/10.3390/en15093184
APA StyleLi, W., Zhang, M., & Deng, Y. (2022). Consensus-Based Distributed Secondary Frequency Control Method for AC Microgrid Using ADRC Technique. Energies, 15(9), 3184. https://doi.org/10.3390/en15093184





