Horizontal Vibration Characteristics of a Tapered Pile in Arbitrarily Layered Soil
Abstract
:1. Introduction
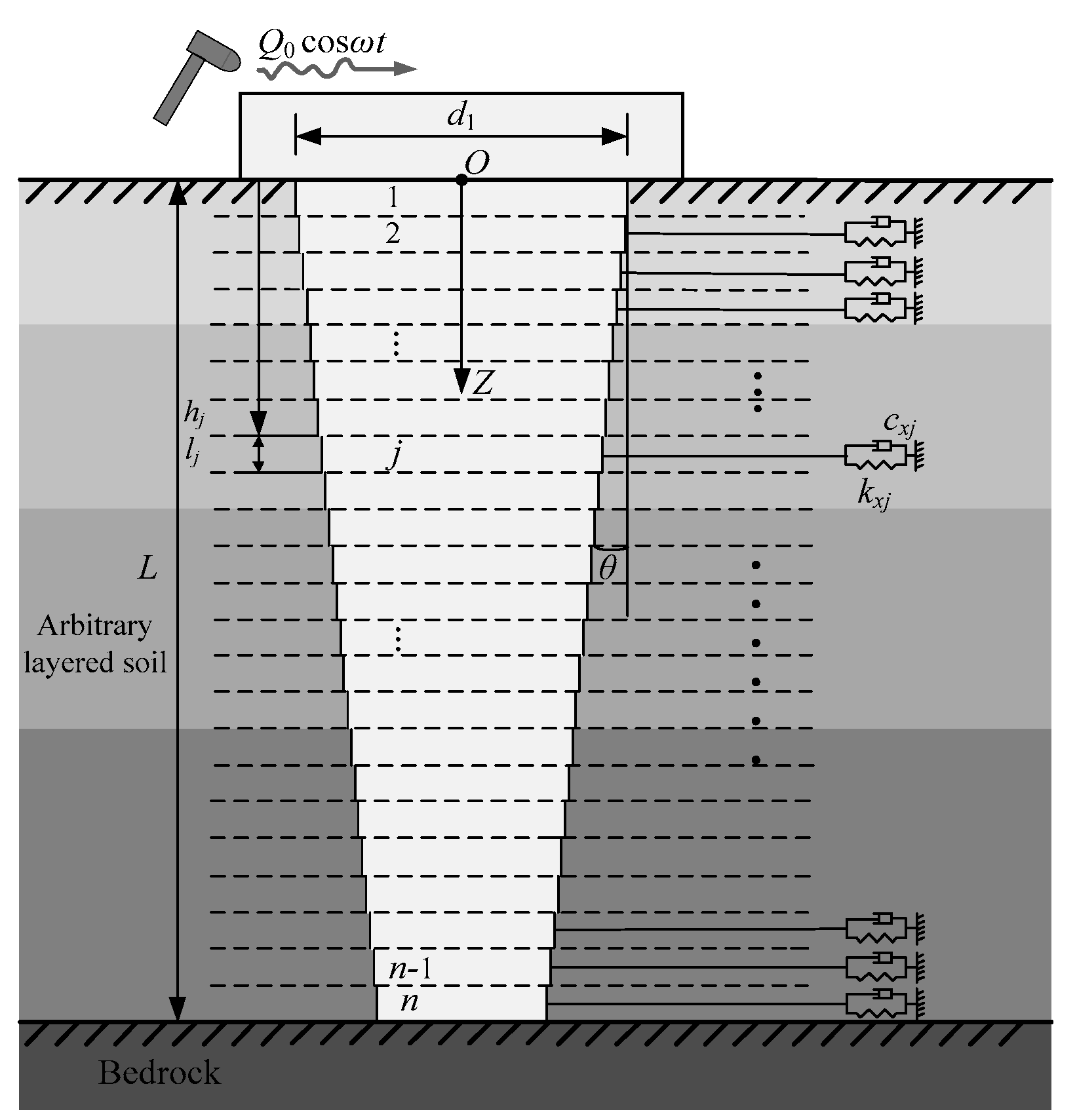
2. Computational Model and Assumptions
- (1)
- The TP is a viscoelastic frustum, and its diameter reduces linearly along the length direction.
- (2)
- To obtain the analytical solution for the established model, only the vertical load caused by the pile cap acting on the TP head is considered, and the interaction between the pile cap and its lower soil layer is not considered.
- (3)
- The pile-surrounding soil is arbitrarily layered soil, and each soil layer is homogeneous and isotropic, which can be regarded as a linear viscoelastic medium.
- (4)
- During horizontal vibration, the TP–soil system will undergo small deformations and strains.
- (5)
- The soil and pile are in completely continuous contact, and the pile cap effect is not considered.
- (6)
- During horizontal vibrations, the pile top does not rotate, and the pile bottom does not move because it is fixed by the bedrock.
3. Governing Equations and Their Solutions
4. Rationality Analysis of the Present Solutions
5. Parametric Study
5.1. Influence of Shear Modulus of Soil
5.2. Influence of Upper Soil Thickness
5.3. Influence of Weak Pile Segment Length
5.4. Influence of the Weak Pile Segment Position
6. Conclusions
- (1)
- In practical engineering, the ability of the TP–soil system to resist horizontal vibrations can be improved by strengthening the upper soil. There is a critical-influence thickness for the influence of upper soil thickness on the horizontal vibration characteristics of TP. If the reinforcement depth exceeds the critical-influence thickness, increasing the reinforcement depth will not further enhance the ability of the TP–soil system to resist horizontal vibration.
- (2)
- The effect of the weak pile segment length on the horizontal vibration characteristics of the TP in the low-frequency range is less than that in the high-frequency range. Compared with the damping factor of dynamic impedance of the TP, the stiffness is more affected by the weak pile segment length.
- (3)
- A closer position of the weak pile segment to the pile head can lead to greater absolute values for the three kinds of dynamic impedances of the pile head. When the depth of weak pile segment increases, the absolute values of the three kinds of dynamic impedance of the pile head decrease, and its reduction rate decreases with the increase in depth.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- El Naggar, M.H.; Wei, J.Q. Response of tapered piles subjected to lateral loading. Can. Geotech. J. 1999, 36, 52–71. [Google Scholar] [CrossRef]
- El Naggar, M.H.; Wei, J.Q. Axial capacity of tapered piles established from model tests. Can. Geotech. J. 1999, 36, 1185–1194. [Google Scholar] [CrossRef]
- Ghazavi, M.; Ahmadi, H.A. Long-term capacity of driven non-uniform piles in cohesive soil–field load tests. In Proceedings of the 8th International Conference on the Application of Stress Wave Theory to Piles, Lisbon, Portugal, 9 July–9 December 2008; pp. 132–139. [Google Scholar]
- Zil’berberg, S.D.; Sherstnev, A.D. Construction of compaction tapered pile foundations. Soil Mech. Found. Eng. 1990, 27, 96–101. [Google Scholar] [CrossRef]
- Wang, L.X.; Wu, W.B.; Zhang, Y.P.; Li, L.C.; Liu, H.; El Naggar, M.H. Nonlinear analysis of single pile settlement based on stress bubble fictitious soil pile model. Int. J. Numer. Anal. Meth. 2022. [Google Scholar] [CrossRef]
- El Naggar, M.H.; Mohammed, S. Evaluation of axial performance of tapered piles from centrifuge tests. Can. Geotech. J. 2000, 37, 1295–1308. [Google Scholar] [CrossRef]
- Li, L.C.; Liu, H.; Wu, W.B.; Wen, M.J.; El Naggar, M.H.; Yang, Y.Z. Investigation on the behavior of hybrid pile foundation and its surrounding soil during cyclic lateral loading. Ocean Eng. 2021, 240, 110006. [Google Scholar] [CrossRef]
- Li, L.C.; Zheng, M.Y.; Liu, X.; Wu, W.B.; Liu, H.; El Naggar, M.H.; Jiang, G.S. Numerical analysis of the cyclic loading behavior of monopile and hybrid pile foundation. Comput. Geotech. 2022, 144, 104635. [Google Scholar] [CrossRef]
- Saha, S.; Ghosh, D. Vertical vibration of tapered piles. J. Geotech. Eng. 1986, 112, 290–302. [Google Scholar] [CrossRef]
- Xie, J.; Vaziri, H.H. Vertical vibration of nonuniform piles. J. Eng. Mech. 1991, 117, 1105–1118. [Google Scholar] [CrossRef]
- Ghazavi, M. Response of tapered piles to axial harmonic loading. Can. Geotech. J. 2008, 45, 1622–1628. [Google Scholar] [CrossRef]
- Wu, W.B.; Jiang, G.S.; Dou, B.; Leo, C.J. Vertical dynamic impedance of tapered pile considering compacting effect. Math. Probl. Eng. 2013, 2013, 304856. [Google Scholar] [CrossRef] [Green Version]
- El Naggar, M.H. Vertical and torsional soil reactions for radially inhomogeneous soil layer. Struct. Eng. Mech. 2000, 10, 299–312. [Google Scholar] [CrossRef]
- Wu, W.B.; Yang, Z.J.; Liu, X.; Zhang, Y.P.; Liu, H.; El Naggar, M.H.; Xu, M.J.; Mei, G.X. Horizontal dynamic response of pile in unsaturated soil considering its construction disturbance effect. Ocean Eng. 2022, 245, 110483. [Google Scholar] [CrossRef]
- Zhang, Y.P.; Jiang, G.S.; Wu, W.B.; El Naggar, M.H.; Liu, H.; Wen, M.J.; Wang, K.H. Analytical solution for distributed torsional low strain integrity test for pipe pile. Int. J. Numer. Anal. Meth. 2022, 46, 47–67. [Google Scholar] [CrossRef]
- Zhang, Y.P.; Liu, H.; Wu, W.B.; Wang, S.; Wu, T.; Wen, M.J.; Jiang, G.S.; Mei, G.X. Interaction model for torsional dynamic response of thin-wall pipe piles embedded in both vertically and radially inhomogeneous soil. Int. J. Geomech. 2021, 21, 04021185. [Google Scholar] [CrossRef]
- Wu, W.B.; Liu, H.; Yang, X.Y.; Jiang, G.S.; El Naggar, M.H.; Mei, G.X.; Liang, R.Z. New method to calculate apparent phase velocity of open-ended pipe pile. Can. Geotech. J. 2020, 57, 127–138. [Google Scholar] [CrossRef]
- Huang, Y.M.; Wang, P.G.; Zhao, M.; Zhang, C.; Du, X.L. Dynamic responses of an end-bearing pile subjected to horizontal earthquakes considering water-pile-soil interactions. Ocean Eng. 2021, 238, 109726. [Google Scholar] [CrossRef]
- Huang, K.; Sun, Y.W.; Zhou, D.Q.; Li, Y.J.; Jiang, M.; Huang, X.Q. Influence of water-rich tunnel by shield tunneling on existing bridge pile foundation in layered soils. J. Cent. South Univ. 2021, 28, 2574–2588. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, D.; Zhang, Y.Q.; Cai, W. Vertical impedance of a tapered pile in inhomogeneous saturated soil described by fractional viscoelastic model. Appl. Math. Model 2019, 75, 88–100. [Google Scholar] [CrossRef]
- Bryden, C.; Arjomandi, K.; Valsangkar, A. Dynamic axial stiffness and damping parameters of tapered piles. Int. J. Geomech. 2018, 18, 06018014. [Google Scholar] [CrossRef]
- Bryden, C.; Arjomandi, K.; Valsangkar, A. Dynamic axial response of tapered piles including material damping. Pract. Period. Struct. 2020, 25, 04020001. [Google Scholar] [CrossRef]
- Wu, W.B.; Jiang, G.S.; Lü, S.H.; Huang, S.G.; Xie, B.H. Torsional dynamic impedance of a tapered pile considering its construction disturbance effect. Mar. Georesour. Geotec. 2016, 34, 321–330. [Google Scholar] [CrossRef]
- Guan, W.J.; Wu, W.B.; Jiang, G.S.; Leo, C.J.; Deng, G.D. Torsional dynamic response of tapered pile considering compaction effect and stress diffusion effect. J. Cent. South Univ. 2020, 27, 3839–3851. [Google Scholar] [CrossRef]
- Ghazavi, M. Analysis of kinematic seismic response of tapered piles. Geotech. Geol. Eng. 2007, 25, 37–44. [Google Scholar] [CrossRef]
- Lee, J.K.; Park, S.H.; Kim, Y. Transverse free vibration of axially loaded tapered friction piles in heterogeneous soil. Soil Dyn. Earthq. Eng. 2019, 117, 116–121. [Google Scholar] [CrossRef]
- Gupta, B.K.; Basu, D. Applicability of Timoshenko, Euler–Bernoulli and rigid beam theories in analysis of laterally loaded monopiles and piles. Géotechnique 2018, 68, 772–785. [Google Scholar] [CrossRef]
- Gupta, B.K.; Basu, D. Timoshenko beam theory–based dynamic analysis of laterally loaded piles in multilayered viscoelastic soil. J. Eng. Mech. 2018, 144, 04018091. [Google Scholar] [CrossRef]
- Ding, X.M.; Luan, L.B.; Zheng, C.J.; Zhou, W. Influence of the second-order effect of axial load on lateral dynamic response of a pipe pile in saturated soil layer. Soil Dyn. Earthq. Eng. 2017, 103, 86–94. [Google Scholar] [CrossRef]
- Zheng, C.J.; Luan, L.B.; Qin, H.Y.; Zhou, H. Horizontal dynamic response of a combined loaded large-diameter pipe pile simulated by the Timoshenko bean theory. Int. J. Struct. Stab. Dyn. 2019, 20, 2071003. [Google Scholar] [CrossRef]
- Gazetas, G.; Dobyr, R. Horizontal response of piles in layered soils. J. Geotech. Eng. 1984, 110, 20–40. [Google Scholar] [CrossRef]
- Hu, A.F.; Xie, K.H.; Ying, H.W.; Qian, L. Analytical theory of lateral vibration of single pile in visco-elastic subgrade considering shear deformation. Chin. J. Rock. Mech. Eng. 2004, 23, 1515–1520. (In Chinese) [Google Scholar]
















Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Jiang, G.; Liu, H.; Wu, W.; Mei, G.; Yang, Z. Horizontal Vibration Characteristics of a Tapered Pile in Arbitrarily Layered Soil. Energies 2022, 15, 3193. https://doi.org/10.3390/en15093193
Yang X, Jiang G, Liu H, Wu W, Mei G, Yang Z. Horizontal Vibration Characteristics of a Tapered Pile in Arbitrarily Layered Soil. Energies. 2022; 15(9):3193. https://doi.org/10.3390/en15093193
Chicago/Turabian StyleYang, Xiaoyan, Guosheng Jiang, Hao Liu, Wenbing Wu, Guoxiong Mei, and Zijian Yang. 2022. "Horizontal Vibration Characteristics of a Tapered Pile in Arbitrarily Layered Soil" Energies 15, no. 9: 3193. https://doi.org/10.3390/en15093193
APA StyleYang, X., Jiang, G., Liu, H., Wu, W., Mei, G., & Yang, Z. (2022). Horizontal Vibration Characteristics of a Tapered Pile in Arbitrarily Layered Soil. Energies, 15(9), 3193. https://doi.org/10.3390/en15093193





