Performance Analysis of Tubular Moving Magnet Linear Oscillating Actuator for Linear Compressors

Abstract

To overcome energy crises, attention is being paid to saving energy from household appliances. Traditional compressors are in need of being replaced by efficient linear compressors. This paper presents a new tubular moving magnet linear oscillating actuator (TMM-LOA) for compressor application. The proposed topology utilizes outer mover topology with separators between the mover and stator modules. The number of stator and mover modules can be increased or decreased based on the requirement. The addition of a separator avoids the flux cancellation and makes the proposed topology fault-tolerant. The design variables are optimized by using a parametric sweep, and the performance in terms of thrust force is observed. Both the static and transient analyses were performed to analyze the machine performance at various currents and stroke. Both mechanical and electrical resonance phenomena are discussed. The efficiency of the proposed TMM-LOA is calculated for one, two and three modules. Finally, the proposed topology is compared with other topologies proposed in the literature to show the superiority of the proposed design.

1. Introduction

The linear oscillating actuator (LOA) which performs linear oscillatory motion between two extreme points is an electro-mechanical system that allows a mover (piston) to reciprocate on the same axis without the use of gears, screws, or a crankshaft [1,2]. The absence of mechanical interfaces helps achieve high efficiency and a long lifespan. Because of its reciprocating movement qualities, the linear oscillating motor is used in the linear compressors of a household refrigerator, electric hammers, electric shavers, electric toothbrushes, artificial hearts, and linear pumps [3,4].

Due to the high cost and scarcity of energy, much attention is being paid to energy conservation. Energy must be saved in household appliances, particularly refrigerators, which consume 20–40% of household electricity. The compressor in a refrigerator consumes a significant amount of energy which can be saved by using a high-efficiency compressor. In a traditional compressor, a rotary motor, usually an induction motor, is utilized but suffers from low efficiency and substantial mechanical losses due to mechanical friction in the crank-driven mechanism. The efficiency of a rotary motor system is often poor, with added mechanical friction. Compressor efficiency is low due to friction, the number of parts and the influence of the tangential and radial components of the thrust force [5]. LOAs are employed in a broad range of applications due to their numerous advantages, including high efficiency, ease of fabrication, and controllability [4]. Because it has no crank mechanism, the linear compressor motor is commonly used to efficiently reduce the excessive energy waste and save the volume caused by the crank mechanism in the rotary motor system. Permanent magnet linear motors (PMLMs) were proposed to drive the linear compressors directly with the primary goal of improving the thrust force density, power, and efficiency [6]. The theory was validated by LG, which developed a linear oscillating motor so it had better efficiency and low noise for refrigerators and air conditioners [7].

Because of the growing need for permanent magnets (PMs) and electronic circuits for controlling motors, the number of alternative topologies of LOA for diverse purposes is rapidly expanding. There are three types of configurations, LOA with moving coils (MCs), moving iron (MI), and moving magnets (MMs) [8]. The MM arrangement is the best based on low inertia, high thrust force density, rapid reaction, and low losses [9]. On the other hand, tubular linear actuators (TLAs) offer the advantages of high air-gap flux density and high efficiency over flat linear actuators due to the lack of end windings and high PM use [10,11]. An MM-LOA was presented in [12], with four cores on which coils are wound and there are three moving PMs. The presented topology has the freedom of other combinations, keeping one PM less than the number of cores. Using finite element analysis (FEA), the static forces and magnetic spring effect were analyzed. The transient force and losses of the same topology were presented in [13]. However, the high volume of PM makes it costlier for commercial usage. Another single-phase MM-LOA topology was presented in [14], in which the authors successfully minimized the detent force and reduced the axial length, thereby increasing the thrust force (TF).

In [15], a thermodynamic model was used to analyze leakages, piston dynamics, an electrical motor model, and valve dynamics while performing the theoretical analysis of an MM-LOA for the linear compressor. In [16], an axially magnetized MM-LOA was presented in which a flux bridge was used to provide an additional path to the flux, increasing the mass of the mover. An oil-free MM-LOA was manufactured in [17], in which helical springs are used for interconnecting the mover and stator. The helical springs also helped in calculating the mechanical resonance frequency. Another single-phase MM-LOA topology using different PM shapes in the Halbach arrangement was presented in [18], with high thrust and lower detent forces. However, the Halbach arrangement of PMs increases the cost of LOA and decreases the mover strength.

This paper presents an outer mover tubular moving magnet LOA (TMM-LOA) with a separator between the C-cores to avoid flux cancellation. Similarly, a separator is also added in the mover between the two opposite polarity magnets. The addition of a separator in both the mover and stator adds the fault-tolerant capability to the proposed topology. The parametric sweep is used to find the optimum design parameters of the proposed TMM-LOA. FEA simulations are performed to find the stroke and thrust force of the proposed topology under the DC and AC currents.

2. Design and Operating Principle

Figure 1 illustrates the cross-sectional view of the proposed TMM-LOA design that includes three stator C-cores and a mover. A 3D view and an exploded view of the proposed model are shown in Figure 2. A separator separates the stator C-cores. Both the ends of the C-cores are enlarged to make it easier for preventing magnetic flux lines to bounce back through the core’s sharp edges. A single-phase concentrated winding is enclosed in the same direction in each C-core. Like the stator, the mover also has three modules separated by a separator. Each module is composed of a core and two PMs at both ends of the core with opposite polarity. The PMs are axially magnetized, pointing to the center of the core. The aim of using a core material between the magnets is to provide a low reluctance path to the flux generated at the stator after excitation. The separator is made up of aluminum, and the core of the stators and mover is constructed of low-carbon steel to improve the passage of flux. The separator avoids flux cancellation and adds the fault-tolerant capability to the topology.

The operating principle of the proposed TMM-LOA is explained via flux linkage. When the stator coil is energized from the AC supply, flux is generated at the stator core, which passes through one stator leg, and enters the mover core through the air gap. The mover adjusts itself to provide a low reluctance path and help the flux bounce back and enter the stator’s next leg to complete the flux linking path. Furthermore, each stator leg has a pole-shoe connected to it; this arrangement also gives the flux a low reluctance path. When the current direction is into the coil, the mover adjusts itself towards the positive z axis and towards the negative z axis if the current direction reverses, as shown in Figure 3a,b. The force that tends to adjust the mover position in the changing current direction is called the electromagnetic force, while the distance between the positive z axis and negative z axis is called a stroke. The mover will reciprocate between the positive and negative extremes until the AC supply is removed.

3. FEA of Proposed TMM-LOA

COMSOL Multiphysics v. 5.8 was used to perform the 2D-FEA of the proposed TMM-LOA. The detail of the design parameters is given in

Table 1. Parameter details of proposed TMM-LOA.

Parameter Description	Stmbol	Value
Mover length	$M_L$	130 mm
Mover module length	$M_{MDL}$	40 mm
PM length	$P{M}_L$	14 mm
Mover core length	$M_{CL}$	12 mm
Radius	R	40 mm
Center core radius	$C_{CR}$	16 mm
Coil radius	$C_R$	18 mm
Mover radius	$M_R$	5 mm
Stator length	$S_L$	120 mm
Stator Module length	$S_{MDL}$	40 mm
Coil length	$C_L$	30 mm
Air gap	–	1 mm

and illustrated in Figure 4. Initially, a 2D axisymmetric model of the proposed topology was built-in an r–z plane shown in Figure 5, using the dimensions given in Table 1. The overall geometry of TMM-LOA is divided into sub-regions. $R_o$ represents the external environment, and the air is assigned to it. Sub-regions $R_1$–$R_6$ represents the PMs and the remanent flux density of 1.4 T is assigned to it. The core part is represented by $R_7$–$R_{18}$ to which low carbon steel is assigned. $R_{19}$–$R_{21}$ represents the coil region to which copper is assigned. The aluminum separator is represented by $R_{22}$–$R_{25}$.

The performance of the proposed topology is analyzed under both static and transient conditions. Under static conditions, the coil is fed from a DC source with a different amplitude of currents of both polarities. The coil is simply fed from a single-phase AC source under transient conditions.

4. Optimization

COMSOL in-built parametric sweep optimization was adopted to optimize the geometric parameters of the proposed TMM-LOA. Leading geometric variables such as the outer diameter and stack length are kept constant. The values of parameters given in Table 1 are taken as the base values and optimized in a defined range to prevent the saturation of the core part. The response in terms of thrust force was observed based on the variation in the variables. As all the stator and mover modules share the same geometric structure, a single mover and stator module are optimized, and its replicas are taken. The coil radial length is optimized along the core radial length and the response in terms of thrust force under different magnitudes of DC supply of both polarity, as shown in Figure 6. At +3 A DC supply, a maximum of 285 N force was obtained at 22 mm coil radial length, while at +6 A, 433 N force was achieved at 18 mm.

Then, the stator pole length was optimized alongside the coil length across the z axis. The stator pole length varied from 3 mm to 10 mm, while the coil length across the z axis varied from 20 mm to 34 mm, and the performance of the proposed TMM-LOA is observed. The analysis in Figure 7 reveals that the proposed design achieves the highest thrust force value of 237.81 N and 446.65 N when excited from +3 A and +6 A DC supply, respectively, at a stator pole length of 5 mm. Finally, the PM length is optimized alongside the mover core length, and the results obtained are shown in Figure 8. The length of PM varies from 10 mm to 20 mm, while the mover core length varies from 0 to 20 mm. At a PM length of 13.76 mm, the proposed topology achieves a maximum of 240.37 N and 453.76 N at +3 A and +6 A from DC supply, respectively. After the optimization of a single module, its replicas are taken, and different conclusions are made, which are discussed in detail in the following section.

5. Results and Discussion

5.1. Static Analysis

The proposed TMM-LOA is simulated by supplying a current of different magnitudes and polarities such as +6 A, +3 A, −3 A and −6 A from the DC source. Figure 9 shows the magnetic flux lines distribution and directions across all the parts of the topology. Figure 9a shows the flux distribution when the TMM-LOA is at an extreme positive position, while Figure 9b shows the flux distribution when the TMM-LOA is at an extreme negative position. The arrows indicate that the flux is uniformly distributed throughout the stator and mover core. The magnetic flux density in the air gap is determined in front of each stator pole numbered from 1 to 6 as shown in Figure 10. Figure 10b shows that when the mover in an extreme positive position, the magnetic flux density in the air gap will be maximum in front of even poles and minimum in front of odd poles and vice versa. The thrust force is analyzed for the defined discrete values of current from −10 A to +10 A, taking one module, two modules, and all three modules shown in Figure 11. The blue line shows a single module performance when fed from the varying DC supply. It can be observed that the single module has a force per ampere slope (called motor constant) of 75.5 N/A. After +7 A current, the relationship between the force and current is not linear, showing a slight saturation of iron parts. When a second module to both the stator and mover is added, the performance of the topology becomes double, and 150 N/A motor constant is achieved, represented by green color in Figure 11. Finally, the third module is added, and the response of the complete topology is observed shown by the purple color in Figure 11. A motor constant of 212.33 N/A is achieved. When all three modules are taken, the relation of the force and current is not linear beyond +6A. Thus, the rated current of the proposed TMM-LOA is 6 A, and it is used for further analysis.

Then, under static conditions, the performance of the proposed TMM-LOA is observed at the discrete points in the intended stroke (from −6 mm to +6 mm). The blue lines with different markers in Figure 12 show a single module trust force versus different stroke lengths at distinct values (−3 A, −6 A, +3 A, +6 A) of DC. Similarly, green lines show the two modules, and purple lines show the three-module response. When the current is positive, the mover experiences a force in the positive direction and reaches a stroke value of +6 mm. When the current direction is reversed, the mover experiences an opposing force and reaches a stroke value of −6 mm. As such, the mover performs an oscillatory motion between the limits of the intended stroke.

5.2. Transient Analysis

Once the static force at different magnitudes and polarities of the current is analyzed, the proposed topology is fed from the AC source to analyze the time-dependent thrust force performance. The thrust force is observed at the mean position of the mover at different peak-to-peak values of the AC supply. The positive value of force shows that the mover is forced towards a positive extreme while the negative value of force is the other way around. Figure 13a shows the time-dependent thrust force of a single module at three different peak-to-peak values of currents from the AC supply. Figure 13b shows the time-dependent force of two modules, while Figure 13c shows the time-dependent force of three modules. It can be observed from Figure 13 that the thrust force increases with the increase in the peak-to-peak value of current equally on both sides. The analysis demonstrates that the mover experiences a sinusoidal force upon applying a sinusoidal source. Furthermore, the proposed topology has a flexible structure and has the freedom of increasing the number of stator and mover modules based on the requirement.

6. Resonance

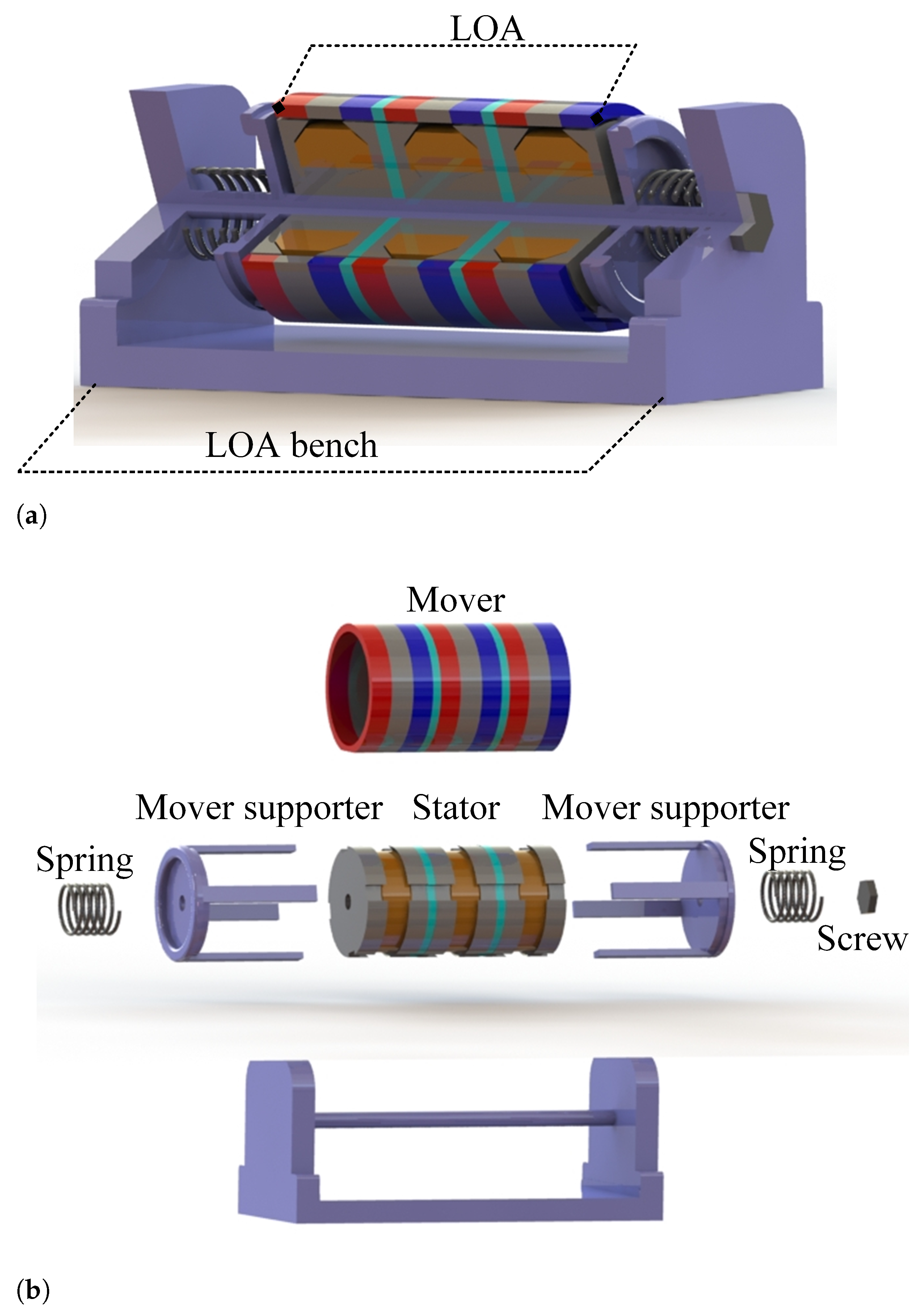
Resonance is an important features when analyzing an oscillating device. Compared with rotating oscillating actuators, LOAs can provide a stable frequency, faster response and less power consumption, i.e., a minimum input current is required for the viable operation of the LOA at resonance [19]. As a small amount of current flows in the resonance condition, consequently, the mover experiences a small thrust force, and the stroke-to-current ratio attains a maximum value. In addition, the impedance to the LOA operation has minimal effect on the resonant frequency. The resonance frequency value can be improved by decreasing the mass of the mover. In LOAs, both types of resonance: electrical and mechanical, are taken under consideration. The full assembly of the proposed TMM-LOA is shown in Figure 14a. The exploded view of the full assembly is provided in Figure 14b. Two supporters are used with resonant mechanical springs for the mover to oscillate in the intended stroke. The stator is fixed on the supporting rod.

6.1. Mechanical Resonance

The mechanical resonance is achieved by operating LOA at the mechanical resonance frequency, which is dependent on the mover mass, and spring stiffness is given in Equation (1). In conventional LOAs, the mechanical springs suffer from friction, aging and material degradation. To address these problems, the authors in [20] used magnetic springs to replace the mechanical springs and considered the best replacement for high-frequency long-stroke oscillations.

$$f_r=\frac{\omega }{2\pi }=\frac{1}{2\pi }\sqrt{\frac{k}{m}}$$

(1)

where $f_r$ is the operating resonance frequency, k is the spring stiffness, and m is the mass of the mover. The mover mass of the proposed topology is calculated using the relation given in Equation (2).

$$m=\rho \pi L_m(r_o^2-r_i^2)$$

(2)

In (2), m is the calculated value of mover mass, $\rho$ is the density of the core material and Neodymium PM, $L_m$ is the length of the tubular-shaped mover, $r_o$ is the outer radius of the mover, and $r_i$ is the inner radius of the mover. The value of spring stiffness is selected to meet the requirement of the resonance frequency. The spring stores and releases energy when the system requires. The LOA performs oscillations in the optimum stroke range, utilizing a small thrust force at resonance, and LOA operation also protects the actuator from high reactive current during resonance [2]. Furthermore, by varying the input voltage amplitude and frequency, the stroke length and the oscillations per unit time can be controlled. The equivalent mechanical system of the proposed TMM-LOA is given in Figure 15 which shows the different forces acting on the various components. The forces can be expressed by Equation (3).

$$f_{magnetic}=f_{inertial}+f_{damper}+f_{spring}$$

(3)

where $f_{magnetic}$, $f_{inertial}$, $f_{damper}$, and $f_{spring}$ is the magnetic force, inertial force, damping force, and spring force, respectively. The Equation (3) can be further extended to Equation (4).

$$\alpha i\left(t\right)=ma\left(t\right)+b\vartheta \left(t\right)+Kx\left(t\right)$$

(4)

where

$$\left\{\begin{array}{c}{f}_{magnatic}=\alpha i\left(t\right)\hfill \\ f_{inertial}=ma\left(t\right)\hfill \\ f_{damper}=b\vartheta \left(t\right)\hfill \\ f_{spring}=Kx\left(t\right)\hfill \end{array}\right.$$

(5)

In Equation (5), the constants $\alpha$, m, b, and K are the motor constant, mass, damper coefficient, and spring constant, respectively, while time-dependent coefficients such as $i\left(t\right)$ is current, $a\left(t\right)$ is acceleration, $\vartheta \left(t\right)$ is velocity and $x\left(t\right)$ is the intended stroke of the proposed TMM-LOA.

6.2. Electrical Resonance

Another unique feature of LOA is the generation of electrical resonance during its operation. The mechanical resonance circuit of the LOA can be replaced by its equivalent electrical resonance circuit, as shown in Figure 16. As the mechanical system of the proposed TMM-LOA is analogous to an electrical system, the mass is therefore replaced by the inductor, a capacitor replaces the spring, the damper is replaced by a resistor, and the magnetic force is replaced by an AC source. $\alpha \nu$ is the back emf induced, and its magnitude and motor constant give an identical value [1], for that it is represented by $\alpha$.

The purpose of a series capacitor is to cancel out the inductive reactance ($X_L$) with capacitive reactance ($X_C$), develop a voltage drop across the resistor and create electrical resonance. When the electrical resonance is achieved, the impedance of the circuit decreases and the entire TMM-LOA will act as a resistive load. This will decrease the copper losses and hence input power losses. The value of the capacitor required to achieve the electrical resonance can be found using Equation (6).

$$C=\frac{1}{4{\pi }^2{f}^{2}L}$$

(6)

C is the value of the capacitor to be calculated, $f_r$ represents the operating frequency, and L is the inductance of the coil. In Figure 17, the resonant frequency of the proposed TMM-LOA is depicted using Equation (1) for various values of the spring constant, with mover masses of 353 g for one module, 706 g for two modules, and 1050 g for all three modules. Furthermore, Figure 17 also shows the value of required capacitance which is the function of the operating frequency calculated by using Equation (6) to achieve electrical resonance. Using the Kirchhoff Law, the equation of electrical circuit can be expressed as

$$V_s=v_R+v_L+v_C+v_{bemf}$$

(7)

In (7), $V_s$ is the supplied voltage, $v_R$ and $v_L$ is the voltage drop across the resistor and the inductor, and $v_C$ is the voltage across the capacitor, while $v_{bemf}$ is the back emf. Equation (7) can also be expressed as

$$V_{s\left(t\right)}=Ri\left(t\right)+L\frac{di\left(t\right)}{dt}+\frac{1}{C}\int i\left(t\right)d\left(t\right)+v_{bemf}$$

(8)

where R and L is the resistance and inductance of the coil, $i\left(t\right)$ is the current from the AC supply.

6.3. Simulation Results of Resonance Analysis

When the TMM-LOA is operating under resonance conditions, the difference between the applied voltage and back emf becomes very small, and hence the voltage drop across the coil becomes minimal. Because of this small voltage difference, a small amount of current flows result in high efficiency. The voltage difference relation given in Equation (9) can be extracted from Equations (4) and (8).

$$|V_{diff}|=\frac{\vartheta }{\alpha }\sqrt{b^2{R}^2+m^2{\omega }^2{\sigma }_m^2{Z}_e+L^2{\omega }^2{\sigma }_e^2{Z}_m}$$

(9)

where:

$$\left\{\begin{array}{c}{\zeta }_e=\frac{{\omega }_{ne}}{\omega }\hfill \\ {\zeta }_m=\frac{{\omega }_{nm}}{\omega }\hfill \\ {\sigma }_m=1-{\zeta }_m^2\hfill \\ {\sigma }_e=1-{\zeta }_e^2\hfill \\ Z_e=b^2+m^2{\omega }^2{\sigma }_m^2/2\hfill \\ Z_m=R^2+L^2{\omega }^2{\sigma }_e^2/2\hfill \end{array}\right.$$

(10)

Figure 18 presents the difference between the applied voltage and back emf at different operating frequency values, using single, two and three modules at their respective motor constant values. Since the proposed TMM-LOA is designed to operate at a 50 Hz operating frequency, the voltage difference is minimal at this operating frequency value.

The thrust force is also minimal since a small current flows through the TMM-LOA coil. The relation of the input current with other parameters of TMM-LOA is given in Equation (11). This relation of input current gives a minimum value at the resonance frequency.

$$\left|I\right|=\frac{\left|V\right|{\omega }^2}{{\mathrm{Y}}^2+{\Psi }^2}\sqrt{b^2+{\zeta }_m^2}$$

(11)

where

$$\mathrm{Y}=mL{\omega }^2(1-{\Gamma }_e^2)(1-{\Gamma }_m^2)-{\omega }^2(bR+{\alpha }^2)$$

$$\Psi =-mR{\omega }^3(1-{\Gamma }_m^2)-bL{\omega }^3(1-{\Gamma }_e^2)$$

$${\zeta }_m=\omega m(1-{\Gamma }_m^2)$$

The response of TMM-LOA in terms of input current taking one, two, and all three modules at different values of operating frequency in Figure 19 by dotted lines. As the thrust force is the product of input current and motor constant, the response of TMM-LOA in terms of thrust force at different operating frequencies is therefore shown in Figure 19 by solid lines for the single, two, and three modules.

The stroke-to-current ratio can be found using Equation (12). The stroke-to-current ratio is a function of input frequency and provides a maximum value at the resonance frequency. Figure 20 presents the stroke to the current ratio of proposed TMM-LOA with one, two and three modules, which shows that it has a maximum value at the resonance frequency.

$$\frac{x}{I}={\displaystyle \frac{\alpha }{\left(\omega \sqrt{b^2+{\zeta }_m^2}\right)}}$$

(12)

The efficiency of the proposed TMM-LOA is calculated at various frequency values. The product of the supply voltage and the current flowing through the coil of TMM-LOA is used to compute the input power. While calculating the output power of the proposed TMM-LOA, the mover velocity and thrust force are multiplied. Figure 21 shows the response of the input power and output power for one single, two, and three modules. As can be observed, the difference between the input and output power is minimum at the resonance frequency. The efficiency of the proposed TMM-LOA, using one, two, and three modules, is calculated and is shown in Figure 22. As it was observed from Figure 21 that the difference between input and output was very small, so the proposed TMM-LOA provides maximum efficiency at the resonance frequency. Furthermore, a slight reduction in the efficiency of the proposed TMM-LOA can be seen by increasing the number of modules due to the increase in copper losses.

7. Comparison with Regular LOAs

The proposed TMM-LOA is compared in terms of standard LOA performance indices such as LOA type, stroke, volume, motor constant, thrust force density, and thrust force per PM mass. For fair comparison, all the topologies taken are of moving magnet (MM) type. The proposed TMM-LOA has got the highest motor constant, thrust force density and thrust force per PM mass among all other topologies compared listed in

Table 2. Comparison of proposed TMM-LOA with different LOA topologies.

Parameter	[1]	[2]	[16]	[21]	[22]	TMM-LOA
Moving Type	MM	MM	MM	MM	MM	MM
Stroke (mm)	$8.8$	12	14	14	10	12
Volume (${\mathrm{mm}}^3$)	$1.95\times {10}^6$	$6.78\times {10}^5$	$9.15\times {10}^5$	$2.72\times {10}^5$	$7.7\times {10}^5$	$6.53\times {10}^5$
Motor Constant (N/A)	38	200	34.6	56.6	48	212.34
TFD 1 (${\mathrm{N}/\mathrm{m}}^3$)	$1.95\times {10}^4$	$2.94\times {10}^5$	$3.78\times {10}^4$	$2.08\times {10}^5$	$6.2\times {10}^4$	$3.25\times {10}^5$
TF per PM mass	146.957	263.744	163.246	254.799	147.761	308.244

¹ Thrust force density.

.

8. Conclusions

This paper presents an outer mover TMM-LOA with a separator between the mover and stator modules for compressor applications. The proposed topology has the freedom of adding or removing stator and mover modules based on user requirements. As both the stator and mover modules share the same geometric structure, a single module was optimized and extended to the whole topology. Different performance analyses under static and transient conditions were performed using FEA. Resonance, which is an important parameter in actuation phenomena, was analyzed. A detailed comparison was carried out with conventional topologies in terms of stroke length, mover mass, and thrust force per PM volume. From the comparison analysis, it was concluded that the proposed design has a superior performance compared to others.