Effect of the Azimuth Axis Tilt Error on the Tracking Performance of a Solar Dish Concentrator System
Abstract
:1. Introduction
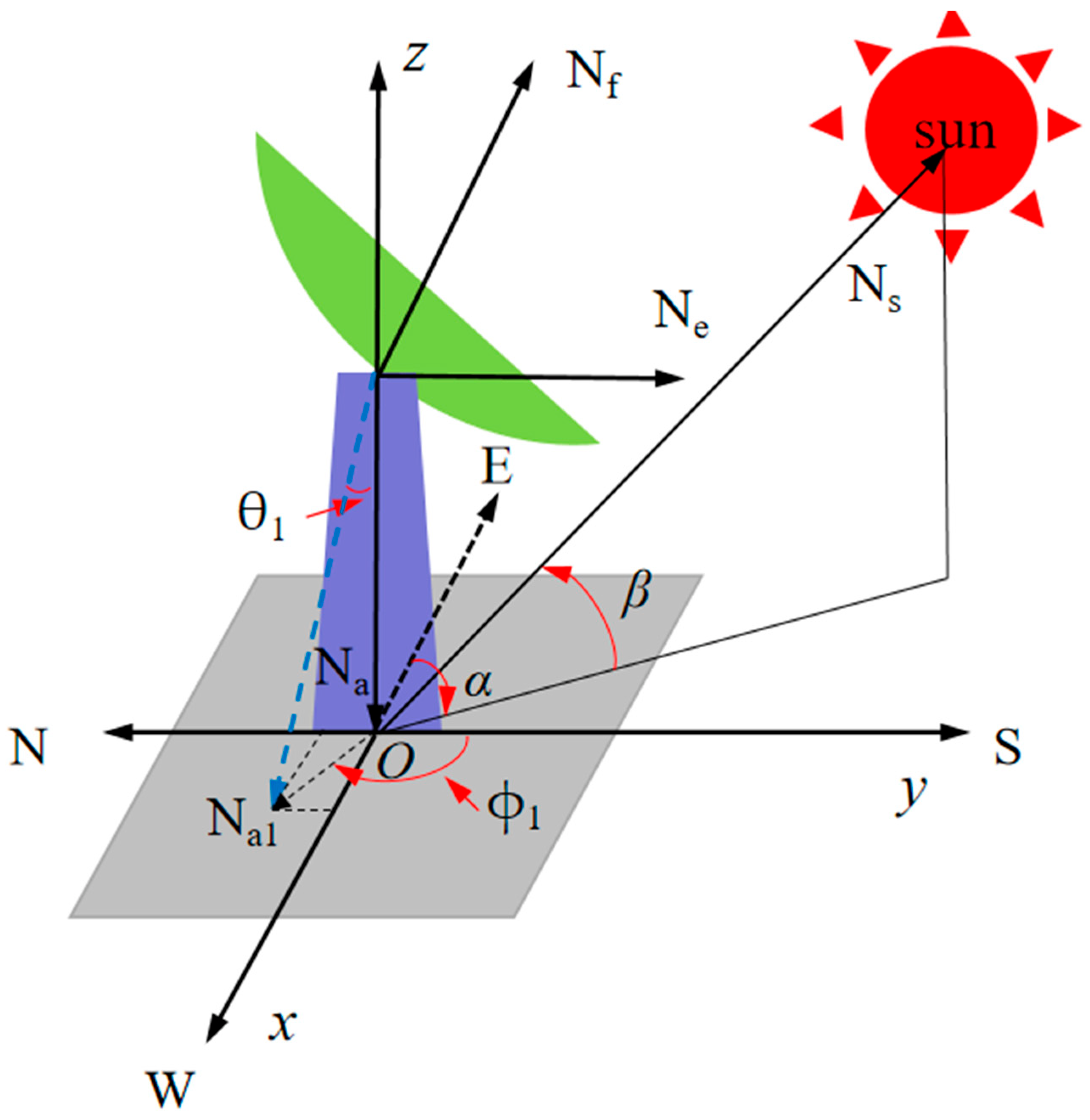
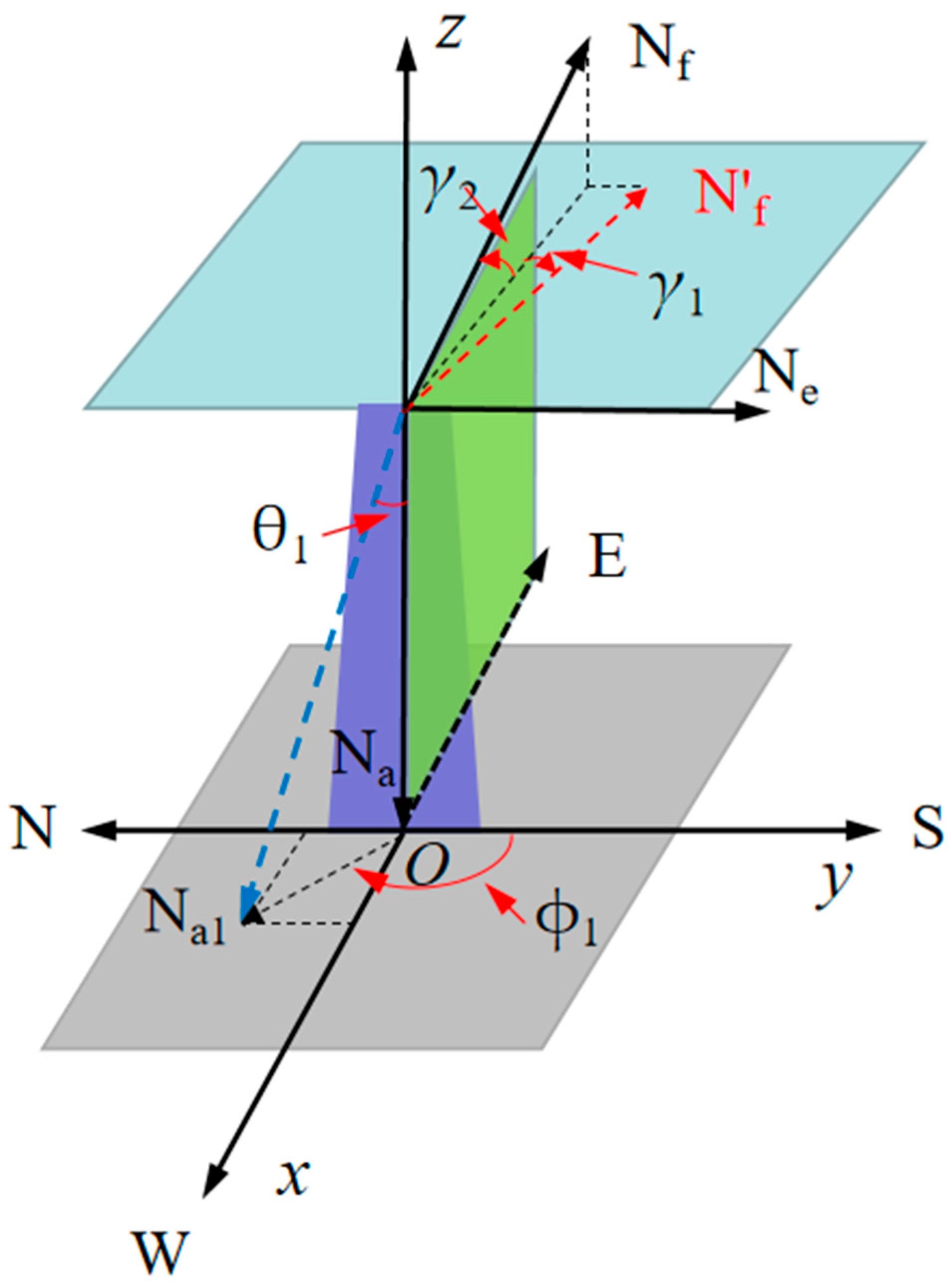
2. Tracking Error Model of Azimuth Axis Tilt Influence
2.1. Azimuth Axis Tilt Error
2.2. Tracking Error Model of the SDC System
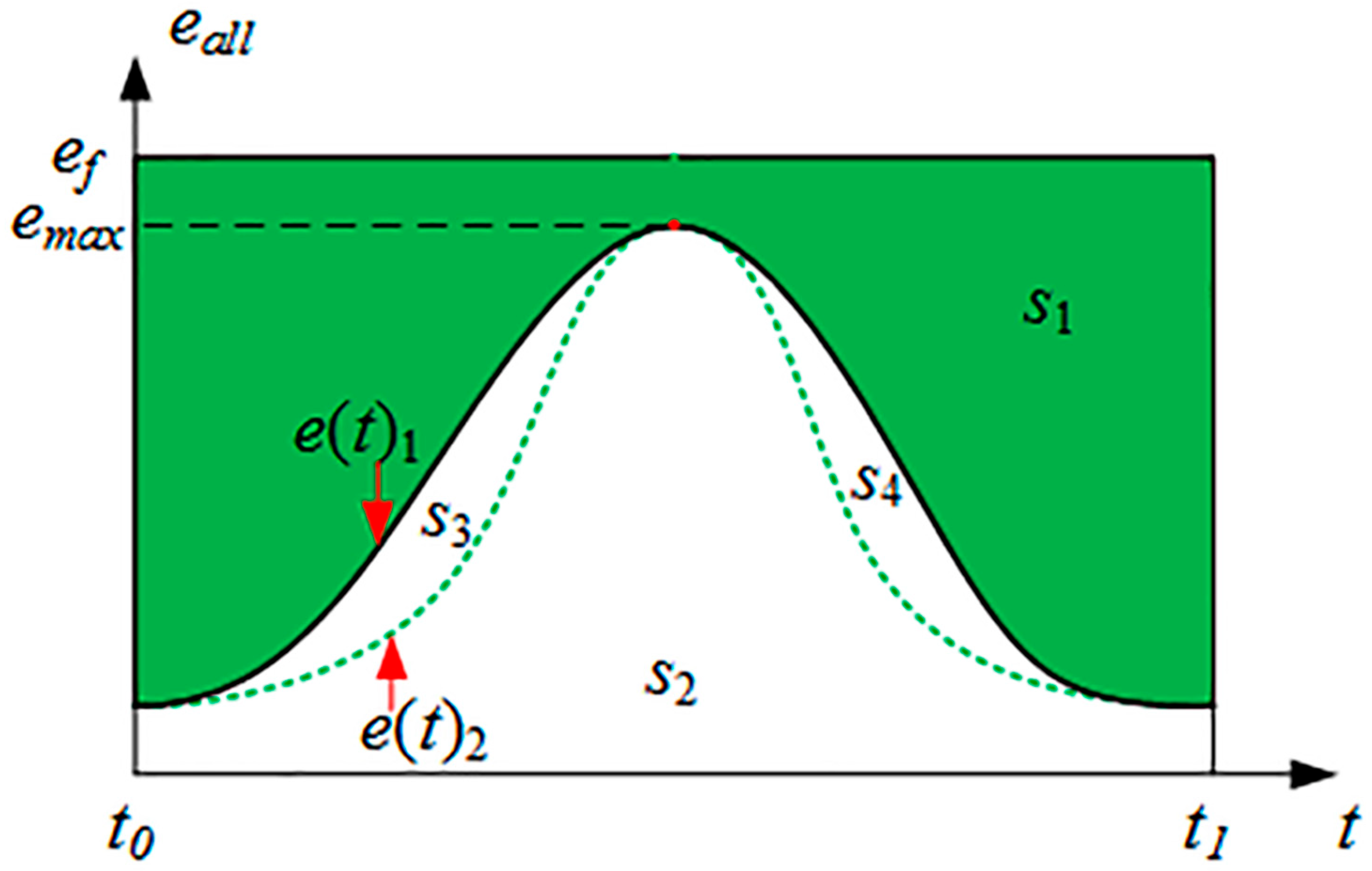
3. Evaluation Index
4. Results and Discussion
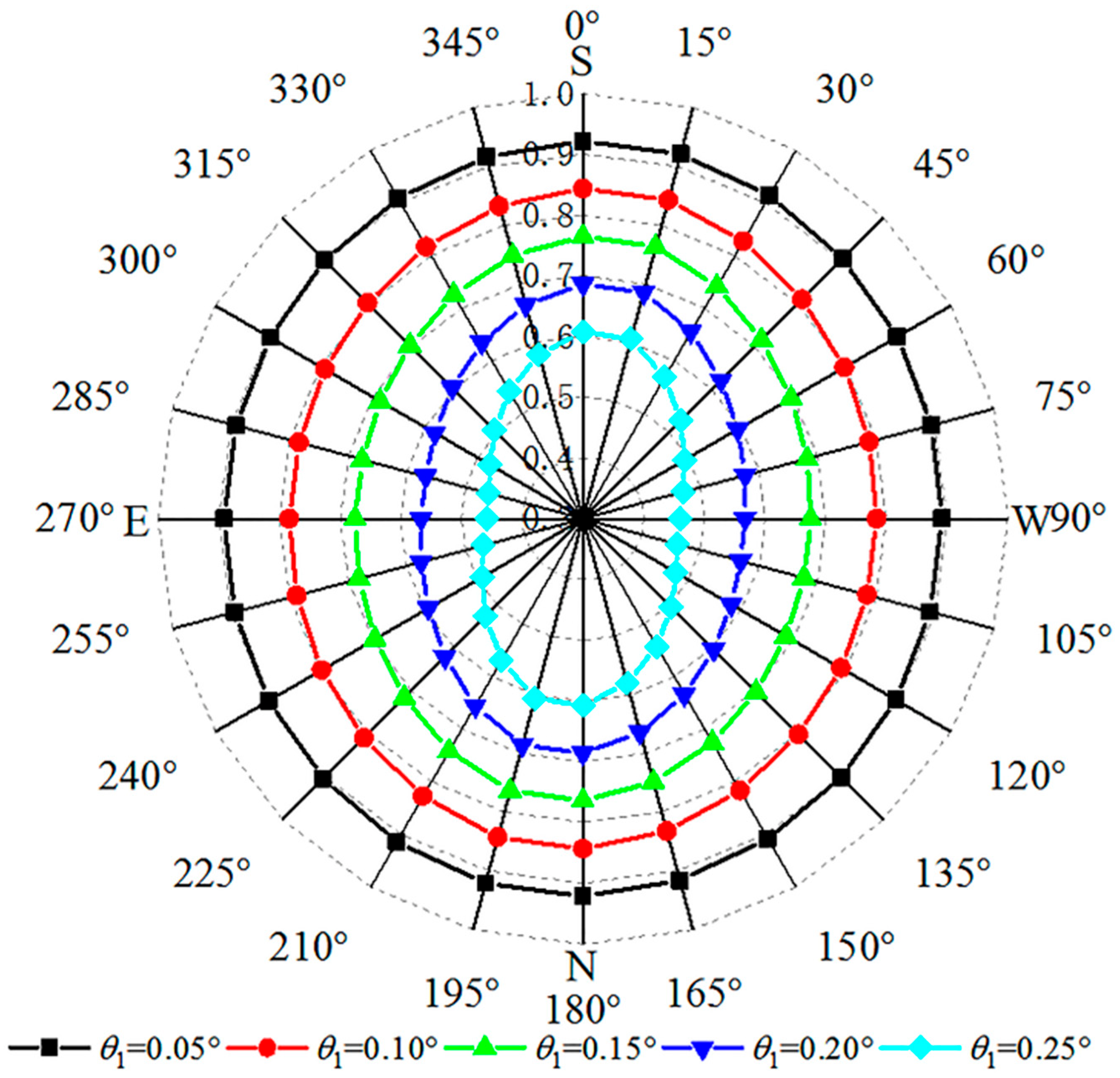
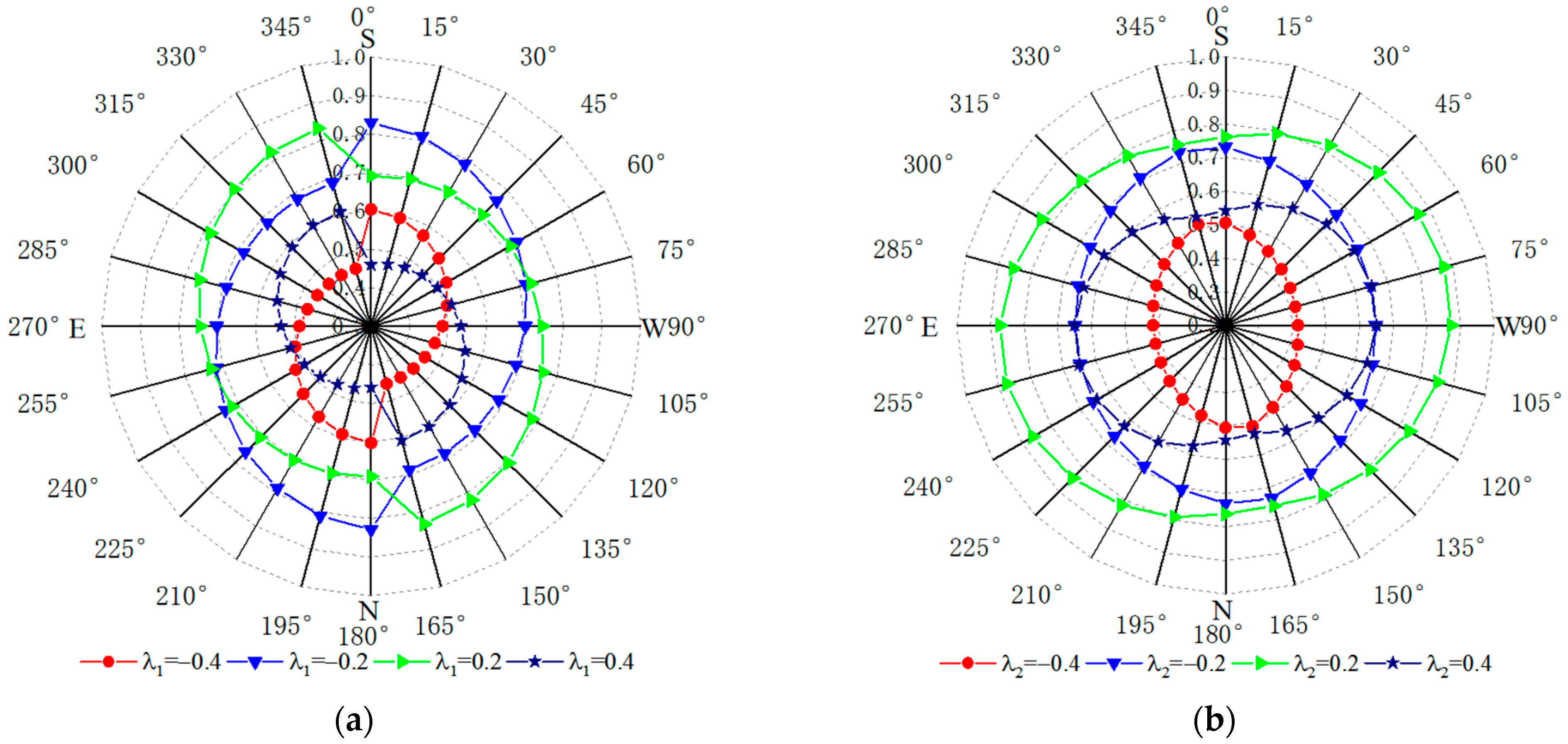
4.1. Influence of Azimuth Radial Angle and Tangential Angle on Tracking Performance of an SDC System
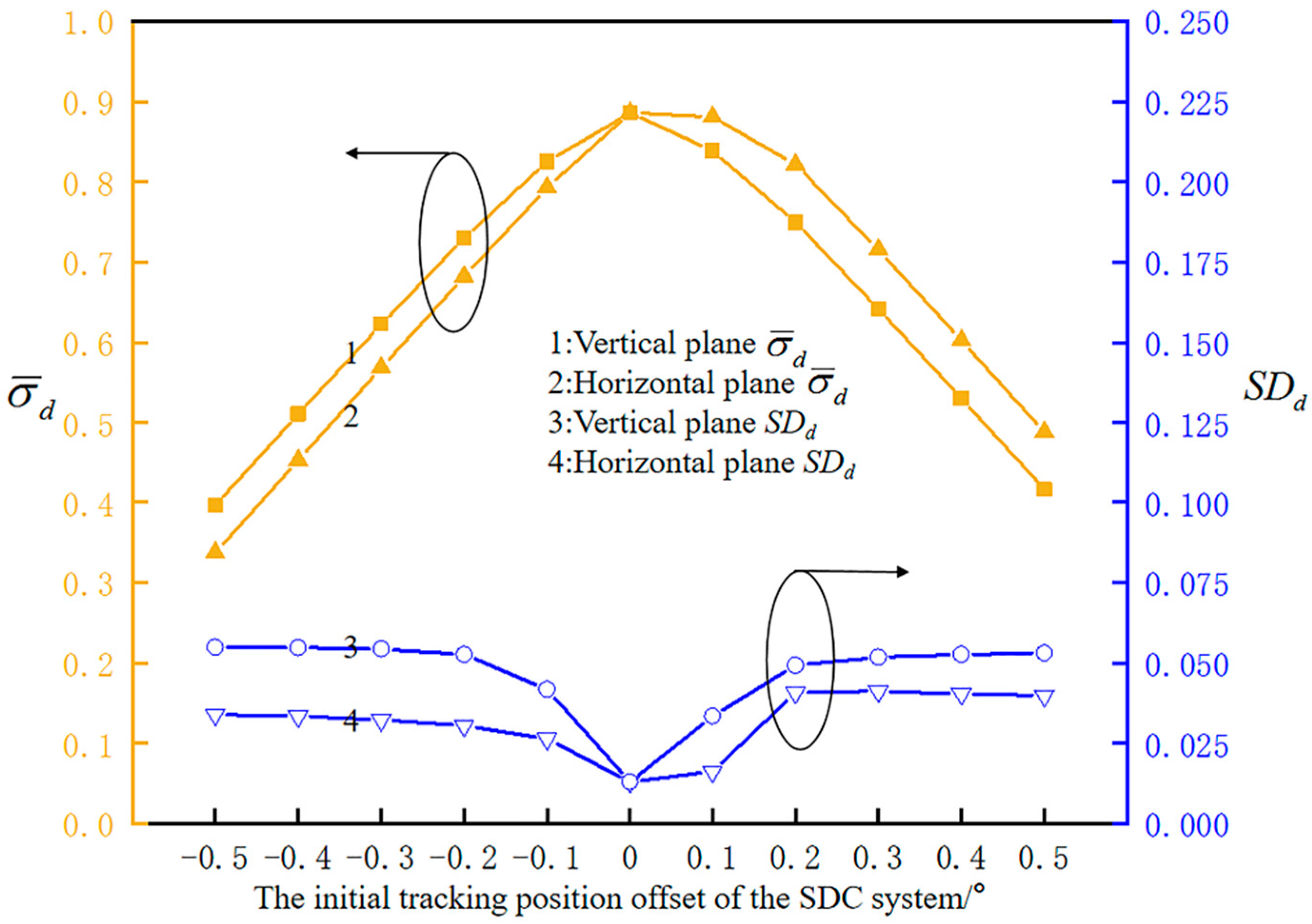
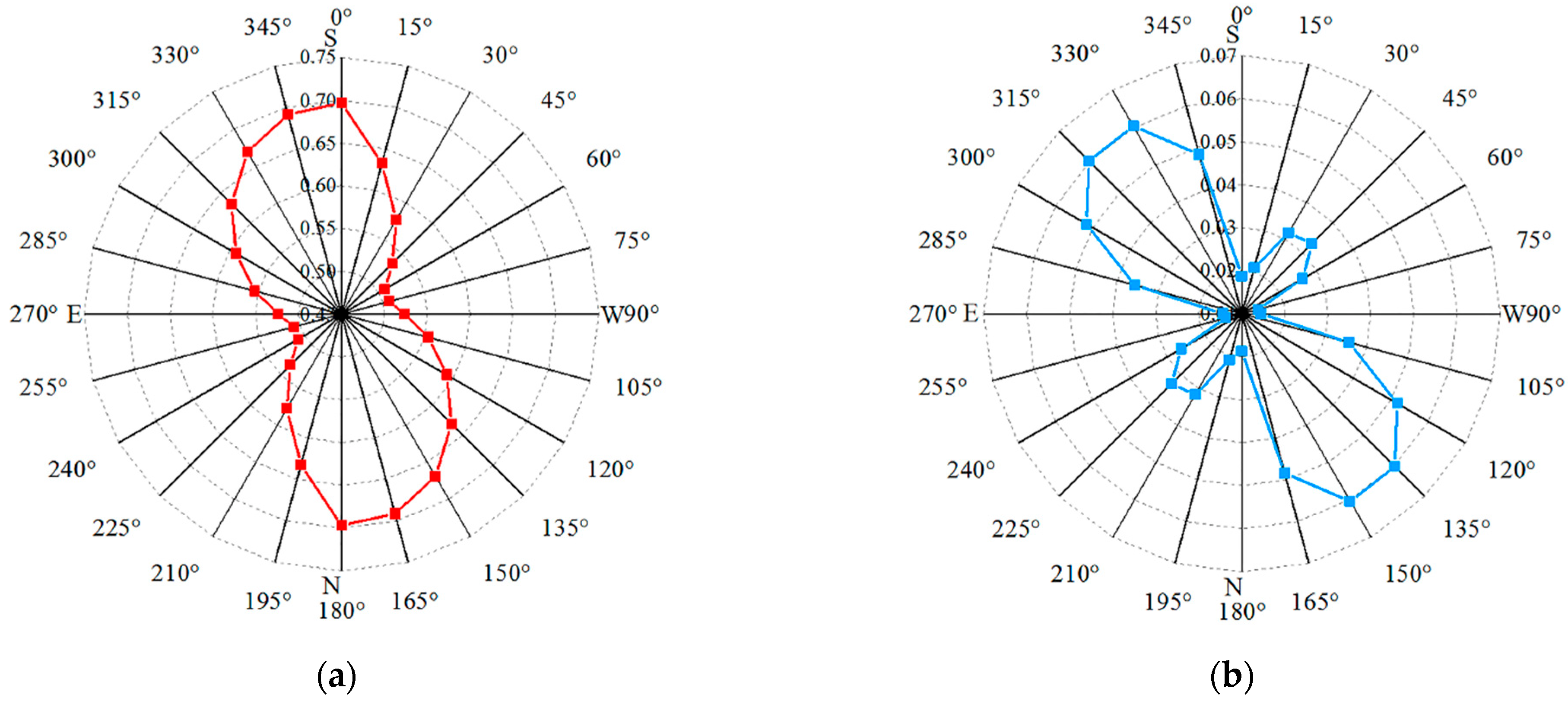
4.2. Influence of Initial Tracking Position of an SDC System under Azimuth Axis Tilt Error
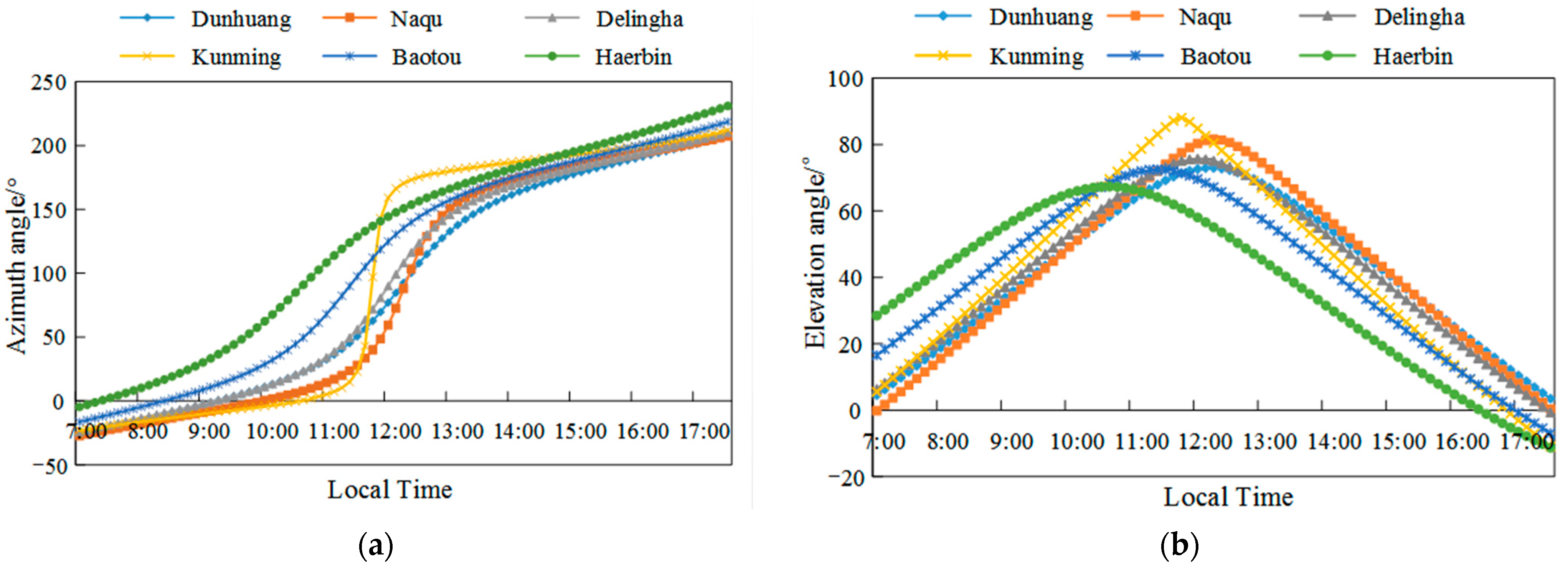
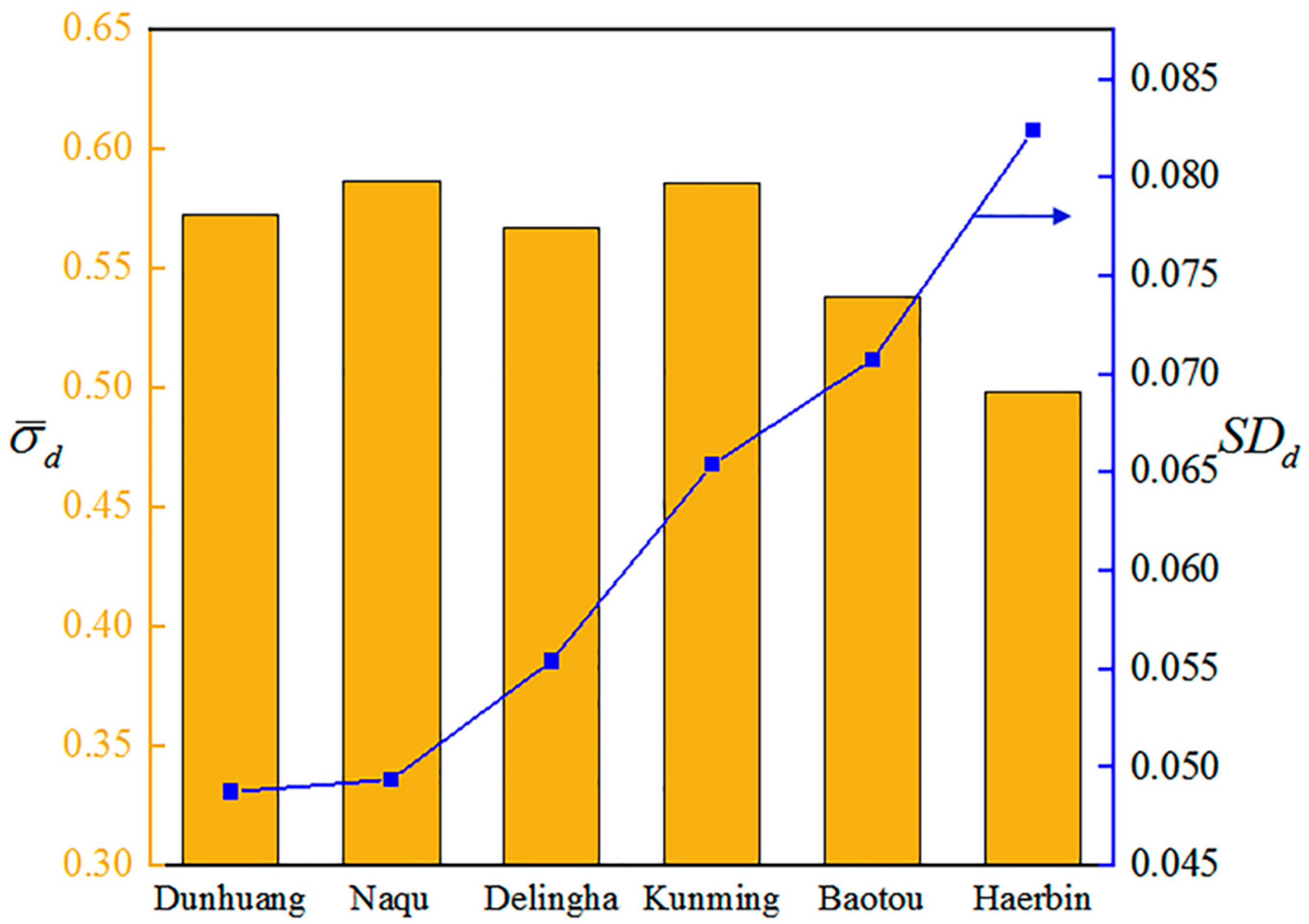
4.3. Tracking Performance of an SDC System Running in Different Regions under Azimuth Axis Tilt Error
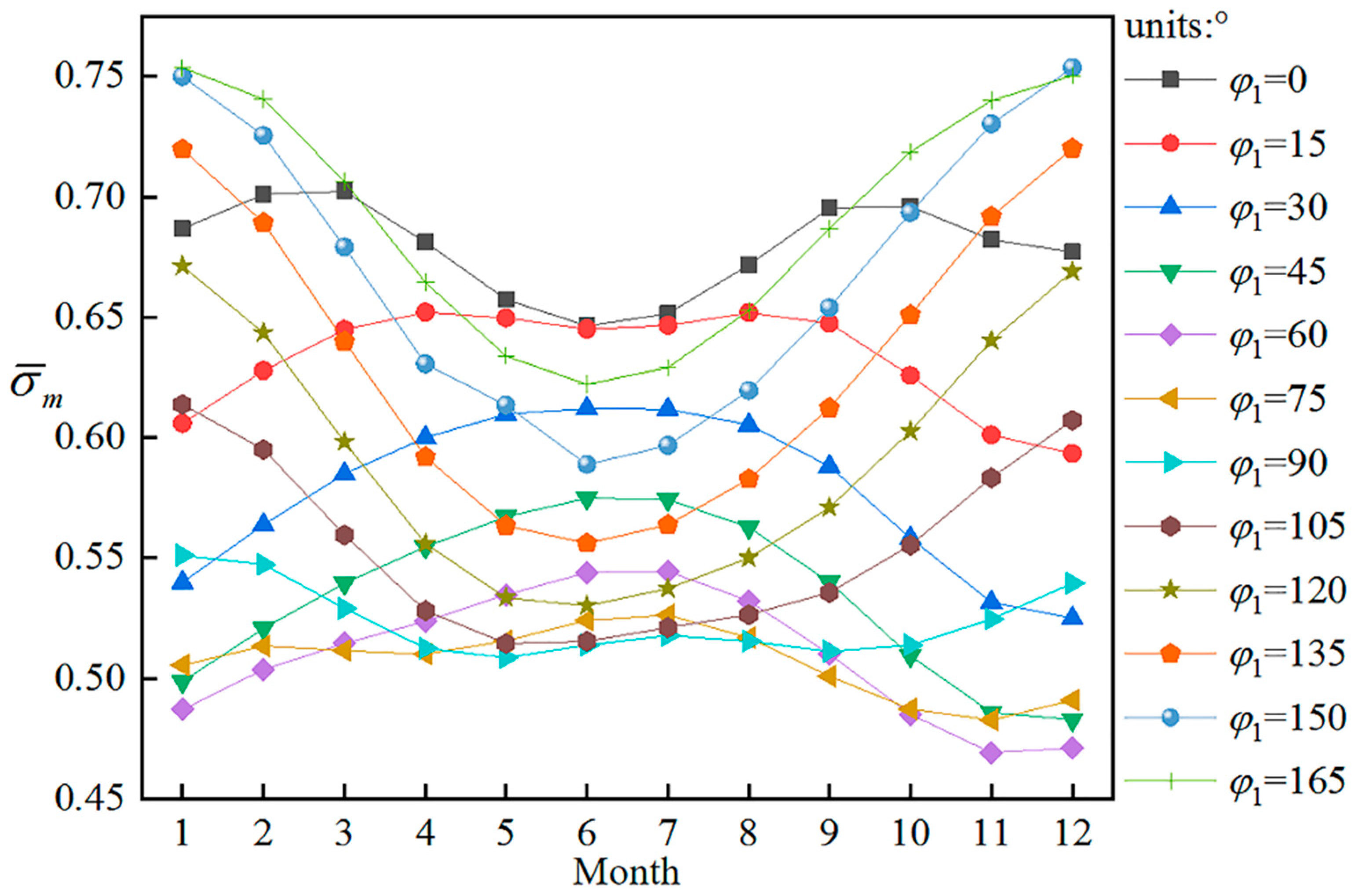
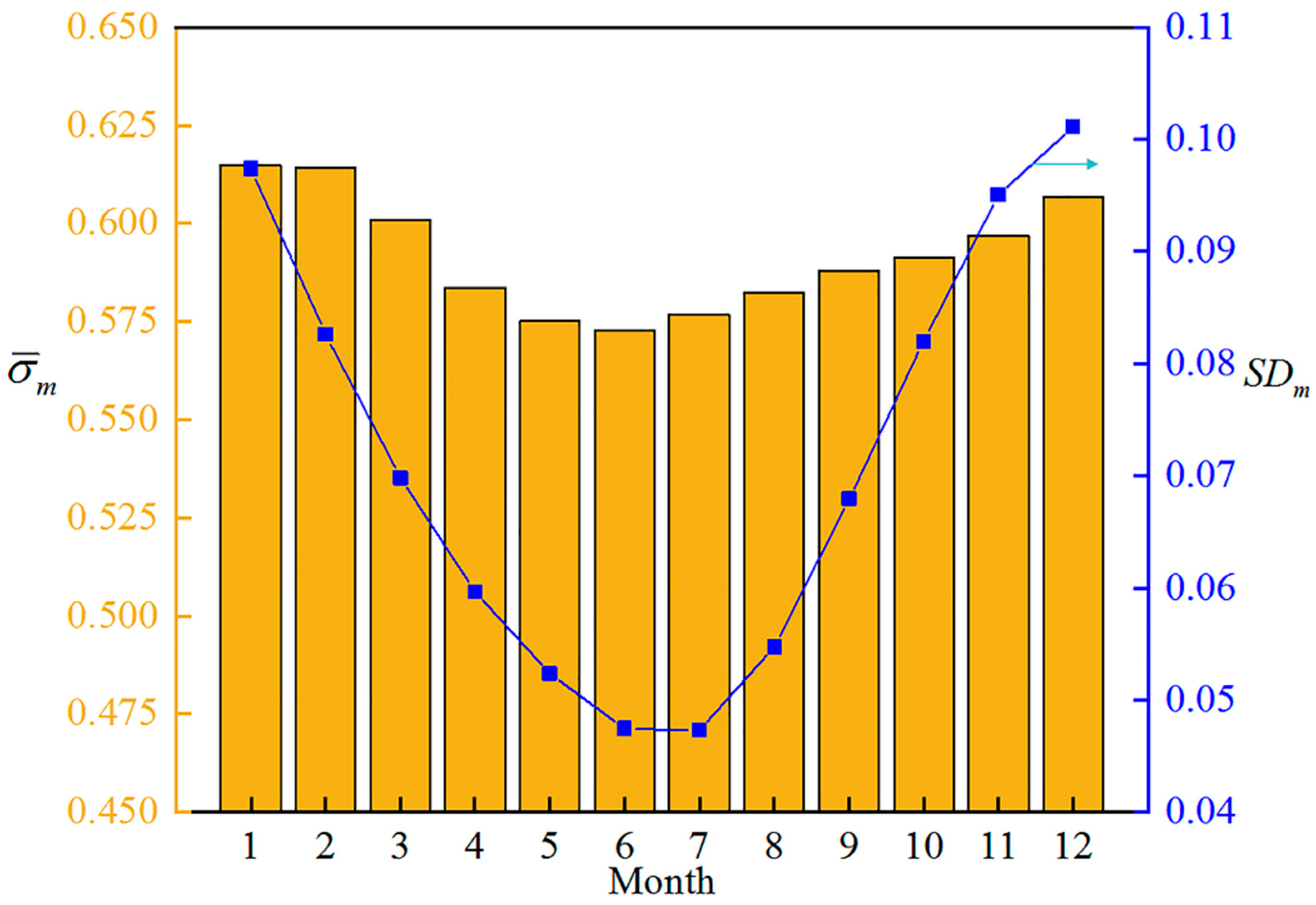
4.4. Tracking Performance of an SDC System in a Whole Year Operation Cycle under Azimuth Axis Tilt Error
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Na | Azimuth axis initial unit vector |
| Ne | Elevation axis initial unit vector |
| Nf | Focal axis initial unit vector |
| Ns | Sun’s ray direction vector |
| eall | Tracking error of an SDC system (mrad) |
| Greek symbols | |
| θ1 | Radial angle of azimuth axis (degree) |
| ϕ1 | Tangential angle of azimuth axis (degree) |
| γ1, γ2 | Offset angles of initial tracking position (degree) |
| α | sun’s azimuth angle (degree) |
| β | sun’s elevation angle (degree) |
| σ | Effective tracking factor of SDC system |
| Abbreviations | |
| DATD | Double-axis tracking device |
| ETF | Effective tracking factor |
| SDC | Solar dish concentrator |
| SD | Standard deviation |
| SDSP | Solar dish Stirling thermal power |
| SPA | Solar position algorithm |
References
- Gauché, P.; Rudman, J.; Mabaso, M.; Landman, W.A.; von Backström, T.W.; Brent, A.C. System value and progress of CSP. Sol. Energy 2017, 152, 106–139. [Google Scholar]
- Merchán, R.P.; Santos, M.J.; Medina, A.; Hernández, A.C. High temperature central tower plants for concentrated solar power: 2021 overview. Renew. Sustain. Energy Rev. 2021, 155, 111828. [Google Scholar] [CrossRef]
- Singh, U.R.; Kumar, A. Review on solar Stirling engine: Development and performance. Therm. Sci. Eng. Prog. 2018, 8, 244–256. [Google Scholar]
- Bataineh, K.M. Optimization analysis of solar-powered average temperature Stirling heat engine. J. Energy South. Afr. 2015, 26, 55–66. [Google Scholar]
- Sandia. News Releases: Stirling Energy Systems Set New World Record for Solar-to-Grid Conversion Efficiency. 2008. Available online: https://share.sandia.gov/news/resources/releases/2008/solargrid.html (accessed on 13 February 2008).
- Zayed, M.E.; Zhao, J.; Elsheikh, A.H.; Li, W.; Sadek, S.; Aboelmaaref, M.M. A comprehensive review on Dish/Stirling concentrated solar power systems: Design, optical and geometrical analyses, thermal performance assessment, and applications. J. Clean. Prod. 2021, 283, 124664. [Google Scholar] [CrossRef]
- Yan, J.; Peng, Y.D.; Cheng, Z.R.; Liu, F.M.; Tang, X.H. Design and implementation of a 38 kW dish-Stirling concentrated solar power system [C]//IOP conference series: Earth and environmental science. IOP Publ. 2017, 93, 012052. [Google Scholar]
- Coventry, J.; Andraka, C. Dish systems for CSP. Sol. Energy 2017, 152, 140–170. [Google Scholar] [CrossRef]
- Yan, J.; Cheng, Z.; Peng, Y. Effects of geometrical parameters of a dish concentrator on the optical performance of a cavity receiver in a solar dish-Stirling system. Int. J. Energy Res. 2018, 42, 2152–2168. [Google Scholar]
- Castellanos, L.S.; Caballero, G.E.; Cobas, V.R.; Lora, E.E.; Reyes, A.M. Mathematical modeling of the geometrical sizing and thermal performance of a Dish/Stirling system for power generation. Renew. Energy 2017, 107, 23–35. [Google Scholar]
- Li, X.L.; Xia, X.L.; Li, Z.H.; Chen, X. Effects of double windows on optical and thermal performance of solar receivers under concentrated irradiation. Sol. Energy 2019, 184, 331–344. [Google Scholar]
- Yang, B.; Liu, S.; Zhang, R.; Yu, X. Influence of reflector installation errors on optical-thermal performance of parabolic trough collectors based on a MCRT-FVM coupled model. Renew. Energy 2022, 185, 1006–1017. [Google Scholar] [CrossRef]
- Yan, J.; Cheng, Z.; Peng, Y. Effect of tracking error of double-axis tracking device on the optical performance of solar dish concentrator. Int. J. Photoenergy 2018, 2018, 9046127. [Google Scholar] [CrossRef] [Green Version]
- Badescu, V. Different tracking error distributions and their effects on the long-term performances of parabolic dish solar power systems. Int. J. Sol. Energy 1994, 14, 203–216. [Google Scholar] [CrossRef]
- Badescu, V. Theoretical derivation of heliostat tracking errors distribution. Sol. Energy 2008, 82, 1192–1197. [Google Scholar] [CrossRef]
- Guo, M.; Wang, Z.; Zhang, J.; Sun, F.; Zhang, X. Accurate altitude–azimuth tracking angle formulas for a heliostat with mirror–pivot offset and other fixed geometrical errors. Sol. Energy 2011, 85, 1091–1100. [Google Scholar] [CrossRef]
- Guo, M.; Wang, Z.; Zhang, J.; Sun, F.; Zhang, X. Determination of the angular parameters in the general altitude–azimuth tracking angle formulas for a heliostat with a mirror-pivot offset based on experimental tracking data. Sol. Energy 2012, 86, 941–950. [Google Scholar] [CrossRef]
- Ukita, N.; Ezawa, H.; Ikenoue, B.; Saito, M. Thermal and wind effects on the azimuth axis tilt of the ASTE 10-m antenna. Publ. Natl. Astron. Obs. Japan 2007, 10, 25–33. [Google Scholar]
- Huang, B.; Li, Z.H.; Tian, X.Z.; Yang, L.; Zhang, P.J.; Chen, B. Modeling and correction of pointing error of space-borne optical imager. Optik 2021, 247, 167998. [Google Scholar] [CrossRef]
- Geng-Jun, M.; Bin-Bin, X.; Na, W.A.; Zhao-Jun, W. Correction method of antenna pointing error caused by the main reflector deformation. Chin. Astron. Astrophys. 2021, 45, 236–251. [Google Scholar] [CrossRef]
- Wang, H.; Huang, J.; Song, M.; Hu, Y.; Wang, Y.; Lu, Z. Simulation and experimental study on the optical performance of a fixed-focus fresnel lens solar concentrator using polar-axis tracking. Energies 2018, 11, 887. [Google Scholar] [CrossRef] [Green Version]
- Pavlovic, S.; Daabo, A.M.; Bellos, E.; Stefanovic, V.; Mahmoud, S.; alDadah, R.K. Experimental and numerical investigation on the optical and thermal performance of solar parabolic dish and corrugated spiral cavity receiver. J. Clean Prod. 2017, 150, 75–92. [Google Scholar] [CrossRef] [Green Version]
- Yan, J.; Peng, Y.D.; Wang, H. Assessing the impact of non-ideal optical factors on optimized solar dish collector system with mirror rearrangement. Int. J. Energy Res. 2020, 44, 8799–8822. [Google Scholar] [CrossRef]
- Sun, F.; Guo, M.; Wang, Z.; Liang, W.; Xu, Z.; Yang, Y.; Yu, Q. Study on the heliostat tracking correction strategies based on an error-correction model. Sol. Energy 2015, 111, 252–263. [Google Scholar] [CrossRef]
- Flores-Hernández, D.A.; Luviano-Juárez, A.; Lozada-Castillo, N.; Gutiérrez-Frías, O.; Domínguez, C.; Antón, I. Optimal strategy for the improvement of the overall performance of dual-axis solar tracking systems. Energies 2021, 14, 7795. [Google Scholar] [CrossRef]
- Huang, L.; Ma, W.; Huang, J. Modeling and calibration of pointing errors with alt-az telescope. New Astronom. 2016, 47, 105–110. [Google Scholar] [CrossRef]
- Funda, J.; Paul, R.P. A computational analysis of screw transformations in robotics. IEEE Trans. Robot. Autom. 1990, 6, 348–356. [Google Scholar] [CrossRef]
- Reda, I.; Andreas, A. Solar position algorithm for solar radiation applications. Sol. Energy 2004, 76, 577–589. [Google Scholar] [CrossRef]
- Liu, Y.; Yan, J.; Peng, Y.; Tian, Y. Effect of the shafting nonorthogonal error on the tracking performance of solar dish concentrator system. Int. J. Energy Res. 2021, 45, 18182–18193. [Google Scholar] [CrossRef]
- García-Ferrero, J.; Heras, I.; Santos, M.J.; Merchán, R.P.; Medina, A.; González, A.; Calvo Hernández, A. Thermodynamic and Cost Analysis of a Solar Dish Power Plant in Spain Hybridized with a Micro-Gas Turbine. Energies 2020, 13, 5178. [Google Scholar] [CrossRef]


| Researchers | Research Objects | Main Contribution |
|---|---|---|
| Wang et al. [21] | Fresnel lens solar concentrator | Uses polar-axis tracking |
| Pavlovic et al. [22] | Solar parabolic dish and cavity receiver | Proposes a low-cost solar collector |
| Yan et al. [23] | An optimized solar dish collector | The non-ideal optical factors considered are relatively comprehensive |
| Sun et al. [24] | Heliostat | Proposes a tracking error correction model to improve the tracking accuracy |
| Flores-Hernández et al. [25] | Dual-axis tracking systems | Proposes a novel methodology for optimizing the overall performance |
| Huang et al. [26] | Large telescopes | Establishes a new model of a telescope pointing error |
| Regions | ||||||
|---|---|---|---|---|---|---|
| Dunhuang | Naqu | Delingha | Kunming | Baotou | Haerbin | |
| Latitude | 40.13° N | 31.29° N | 37.22° N | 25° N | 40.32° N | 45.42° N |
| Longitude | 94.67° E | 92.04° E | 97.23° E | 102.39° E | 109.53° E | 125.15° E |
| 0.57234 | 0.5868 | 0.56715 | 0.58612 | 0.53792 | 0.49776 | |
| SDd | 0.04874 | 0.04935 | 0.05539 | 0.06537 | 0.07072 | 0.08238 |
| Azimuth Axis Tangential Angle ϕ1/° | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | |
| Date (month/day) | 06/21 | 12/12 | 12/10 | 12/05 | 11/27 | 11/01 | 05/01 | 06/01 | 06/01 | 06/19 | 06/16 | 06/19 |
| σmin | 0.646 | 0.592 | 0.524 | 0.480 | 0.467 | 0.481 | 0.507 | 0.513 | 0.529 | 0.555 | 0.588 | 0.621 |
| Date (month/day) | 02/05 | 08/01 | 07/01 | 07/01 | 07/01 | 07/01 | 02/01 | 01/01 | 01/01 | 01/01 | 01/01 | 01/01 |
| σmax | 0.705 | 0.654 | 0.613 | 0.577 | 0.545 | 0.528 | 0.553 | 0.616 | 0.678 | 0.728 | 0.761 | 0.757 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Peng, Y.; Yan, J. Effect of the Azimuth Axis Tilt Error on the Tracking Performance of a Solar Dish Concentrator System. Energies 2022, 15, 3261. https://doi.org/10.3390/en15093261
Liu Y, Peng Y, Yan J. Effect of the Azimuth Axis Tilt Error on the Tracking Performance of a Solar Dish Concentrator System. Energies. 2022; 15(9):3261. https://doi.org/10.3390/en15093261
Chicago/Turabian StyleLiu, Yongxiang, Youduo Peng, and Jian Yan. 2022. "Effect of the Azimuth Axis Tilt Error on the Tracking Performance of a Solar Dish Concentrator System" Energies 15, no. 9: 3261. https://doi.org/10.3390/en15093261
APA StyleLiu, Y., Peng, Y., & Yan, J. (2022). Effect of the Azimuth Axis Tilt Error on the Tracking Performance of a Solar Dish Concentrator System. Energies, 15(9), 3261. https://doi.org/10.3390/en15093261






