Variation Characteristic Analysis of Water Content at the Flow Channel of Proton Exchange Membrane Fuel Cell
Abstract
:1. Introduction
2. WCR Model
2.1. Condensation Rate
2.2. Channel and GDL/CL Diffusion Transmission
2.3. Boundary Conditions
3. Simulation
3.1. Schedule Diagram of the Simulation
3.2. Geometric Model and Mesh
3.3. Boundary Conditions and Model Parameters
4. Experimental Setup
5. Results and Discussion
5.1. Contours of Water Content Molar Concentrations
5.1.1. Cathode Channels
5.1.2. Anode Channels
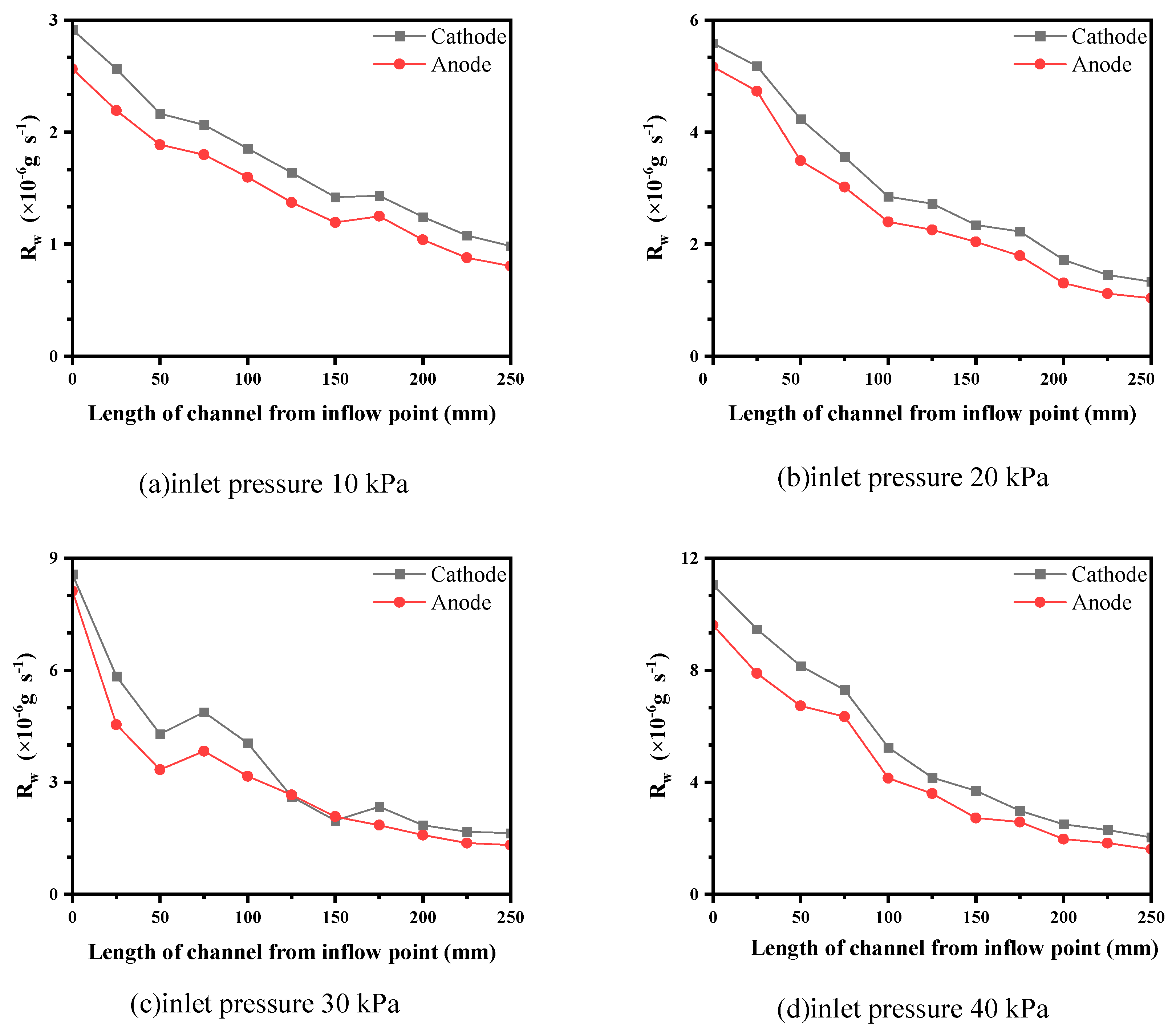
5.2. Condensation Rate Curves
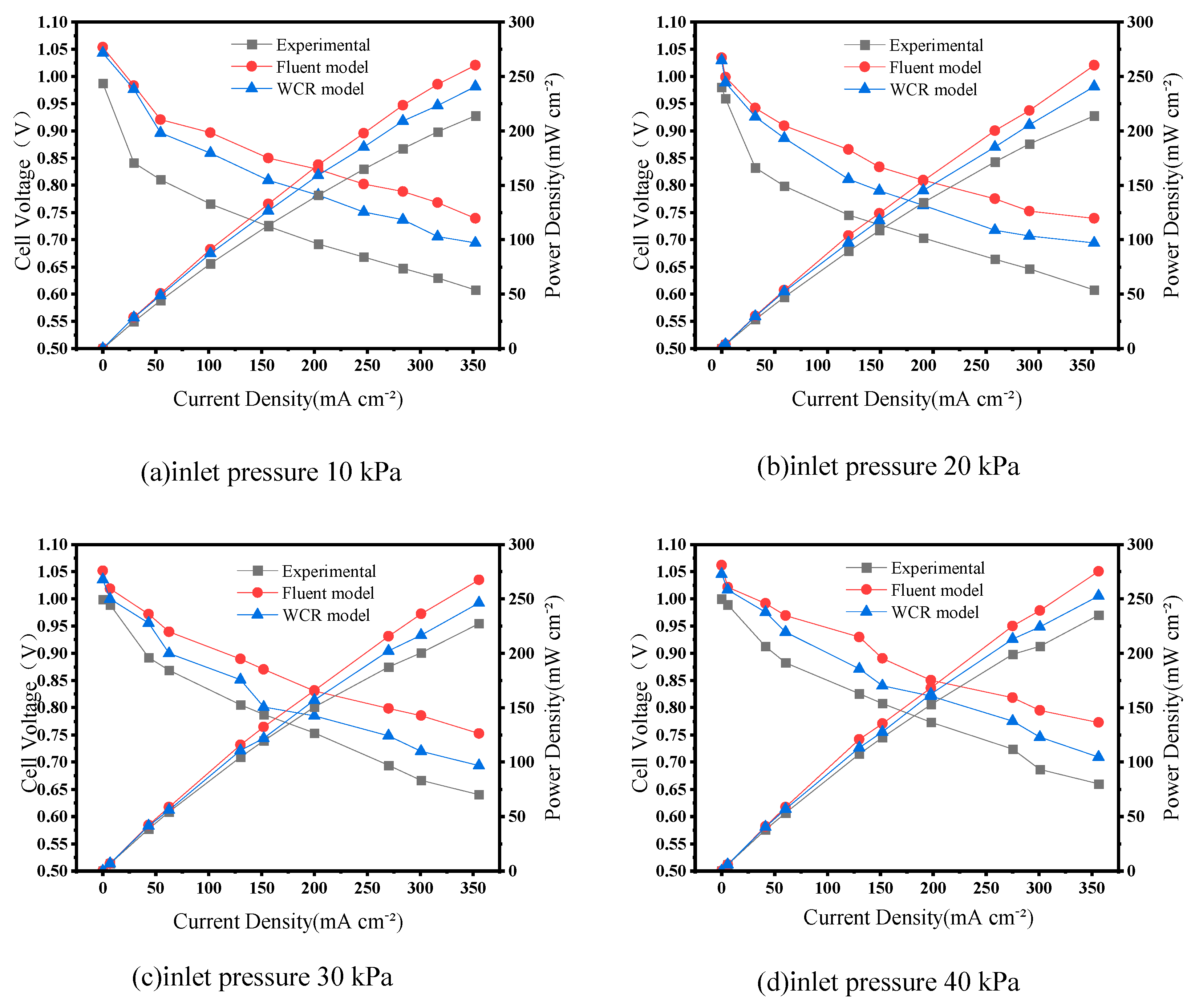
5.3. Polarization Curves
5.3.1. Intake Pressure 10 kPa
5.3.2. Intake Pressure 20 kPa
5.3.3. Intake Pressure 30 kPa
5.3.4. Intake Pressure 40 kPa
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Symbols
| Water condensation rate (g·s−1) | |
| Water evaporation rate (g·s−1) | |
| Inlet water flow rate (g·s−1) | |
| Volumetric water condensation rate in a local position (g·s−1·m−3) | |
| Volumetric water evaporation rate in a local position (g·s−1·m−3) | |
| P | Fluid pressure in the flow channel (kPa) |
| Psat | Saturated vapor pressure (kPa) |
| pwv | Local pressure at a point in the flow channel (kPa) |
| psat | Saturated vapor pressure at a point in the flow channel (kPa) |
| Inlet pressure of hydrogen (kPa) | |
| Saturation pressure of hydrogen (kPa) | |
| Inlet pressure for oxygen (kPa) | |
| Saturation pressure for oxygen (kPa) | |
| pc | Capillary pressure (kPa) |
| Pressure drop in the anode (kPa) | |
| Pressure drop in the cathode (kPa) | |
| xw | Mass fraction of water |
| xsat | The maximum mass fraction of water vapor in dry gas |
| The fraction of water vapor in dry gas | |
| yw | Mole fraction of water vapor |
| Molar mass of water (g·mol−1) | |
| Molar mass of gas (g·mol−1) | |
| D | Diffusion coefficient of water vapor through the gas (m2·s−1) |
| Universal gas constant (8.314 J·mol−1·K−1) | |
| T | Working temperature (K) |
| Afg | Phase-change surface area per unit volume (m−1) |
| I | Total current (A) |
| Current density in the catalyst (A·cm−2) | |
| Cd | Depth of flow channels (m) |
| Cw | Width of flow channels (m) |
| L | Length of flow channels (m) |
| n | Number of flow channels |
| A | Cross-sectional area of a channel (m2) |
| Ain | Cross sectional area of inlet pipe (m2) |
| Dh | Hydraulic diameter of a channel (m) |
| hpc | Condensation parameter |
| cr | Rate constant (s−1) |
| s | Liquid water saturation |
| cp | Heat capacity (J·g−1·K−1) |
| Thermal conductivity of humid gas (W·m−1·K−1) | |
| vd | Kinematic viscosity of dry gas (m2·s−1) |
| vh | Kinematic viscosity of humid gas (m2·s−1) |
| q | Switching function |
| K | Permeability of the gas diffusion layer or the catalyst layer (m2) |
| Velocity vector (m·s−1) | |
| Sm | Momentum source term |
| Vl | Liquid phase rate (m·s−1) |
| Effective electric conductivity of the GDL (S·cm−1) |
Greek Letters
| μeff | Average viscosity (kg·m−1·s−1) |
| Evaporation coefficient (g·m−2·s−1) | |
| Heat transfer coefficient (W·m2·K−1) | |
| ρ | Density of humid air (g·m−3) |
| ρl | Density of liquid water (g·m−3) |
| Hydrogen excess coefficient | |
| λO2 | Oxygen excess coefficient |
| ξ | Local loss coefficient |
| μl | Viscosity (kg·m−1·s−1) |
| ε | Porosity |
| Potential (V) |
Abbreviations
| PEMFC | Proton exchange membrane fuel cell |
| WCR | Water condensation rate |
| GDL | Gas diffusion layers |
| CL | Catalyst layer |
Superscripts and Subscripts
| H2O | Water |
| H2 | Hydrogen |
| O2 | Oxygen |
| cond | Condensation |
| evap | Evaporation |
| in | Inlet |
| sat | Saturation |
| an | Anode |
| cat | Cathode |
| g | Gas |
| l | Liquid |
References
- Ren, P.; Pei, P.; Chen, D.; Li, Y.; Wu, Z.; Zhang, L.; Li, Z.; Wang, M.; Wang, H.; Wang, B.; et al. Novel analytic method of membrane electrode assembly parameters for fuel cell consistency evaluation by micro-current excitation. Appl. Energy 2021, 306, 118068. [Google Scholar] [CrossRef]
- Liu, Q.; Lan, F.; Chen, J.; Zeng, C.; Wang, J. A review of proton exchange membrane fuel cell water management: Membrane electrode assembly. J. Power Sources 2021, 517, 230723. [Google Scholar] [CrossRef]
- Li, Y.; Pei, P.; Wu, Z.; Ren, P.; Jia, X.; Chen, D.; Huang, S. Approaches to avoid flooding in association with pressure drop in proton exchange membrane fuel cells. Appl. Energy 2018, 224, 42–51. [Google Scholar] [CrossRef]
- Fathy, A.; Rezk, H.; Nassef, A.M. Robust hydrogen-consumption-minimization strategy based salp swarm algorithm for energy management of fuel cell/supercapacitor/batteries in highly fluctuated load condition. Renew. Energy 2019, 139, 147–160. [Google Scholar] [CrossRef]
- Liu, Y.; Bai, S.; Wei, P.; Pei, P.; Yao, S.; Sun, H. Numerical and experimental investigation of the asymmetric humidification and dynamic temperature in proton exchange membrane fuel cell. Fuel Cells 2020, 20, 48–59. [Google Scholar] [CrossRef]
- Ren, P.; Pei, P.; Chen, D.; Li, Y.; Wang, H.; Fu, X.; Zhang, L.; Wang, M.; Song, X. Micro-current excitation for efficient diagnosis of membrane electrode assemblies in fuel cell stacks: Error analysis and method optimization. Energy Convers. Manag. 2022, 258, 115489. [Google Scholar] [CrossRef]
- Ren, P.; Pei, P.; Li, Y.; Wu, Z.; Chen, D.; Huang, S. Degradation mechanisms of proton exchange membrane fuel cell under typical automotive operating conditions. Prog. Energy Combust. Sci. 2020, 80, 100859. [Google Scholar] [CrossRef]
- Wu, F.; Maier, J.; Yu, Y. Guidelines and trends for next-generation rechargeable lithium and lithium-ion batteries. Chem. Soc. Rev. 2020, 49, 1569–1614. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Sun, C. Cost-effective iron-based aqueous redox flow batteries for large-scale energy storage application: A review. J. Power Sources 2021, 493, 229445. [Google Scholar] [CrossRef]
- Jayakumar, A.; Sethu, S.P.; Ramos, M.V.; Robertson, J.; Al-Jumaily, A. A technical review on gas diffusion, mechanism and medium of PEM fuel cell. Ionics 2015, 21, 1–18. [Google Scholar] [CrossRef]
- Jiao, K.; Li, X. Water transport in polymer electrolyte membrane fuel cells. Prog. Energy Combust. Sci. 2011, 37, 221–291. [Google Scholar] [CrossRef]
- Sun, C.; Negro, E.; Nale, A.; Pagot, G.; Vezzù, K.; Zawodzinski, T.A.; Meda, L.; Gambaro, C.; Di Noto, V. An efficient barrier toward vanadium crossover in redox flow batteries: The bilayer [Nafion/(WO3)x] hybrid inorganic-organic membrane. Electrochim. Acta 2021, 378, 138133. [Google Scholar] [CrossRef]
- Tardy, E.; Courtois, F.; Chandesris, M.; Poirot-Crouvezier, J.-P.; Morin, A.; Bultel, Y. Investigation of liquid water heterogeneities in large area PEM fuel cells using a pseudo-3D multiphysics model. Int. J. Heat Mass Transf. 2019, 145, 118720. [Google Scholar] [CrossRef]
- Afshari, E.; Ziaei-Rad, M.; Shariati, Z. A study on using metal foam as coolant fluid distributor in the polymer electrolyte membrane fuel cell. Int. J. Hydrogen Energy 2016, 41, 1902–1912. [Google Scholar] [CrossRef]
- Kim, J.; Luo, G.; Wang, C.-Y. Modeling liquid water re-distributions in bi-porous layer flow-fields of proton exchange membrane fuel cells. J. Power Sources 2018, 400, 284–295. [Google Scholar] [CrossRef]
- Abdollahzadeh, M.; Ribeirinha, P.; Boaventura, M.; Mendes, A. Three-dimensional modeling of PEMFC with contaminated anode fuel. Energy 2018, 152, 939–959. [Google Scholar] [CrossRef]
- Passalacqua, E.; Squadrito, G.; Lufrano, F.; Patti, A.; Giorgi, L. Effects of the diffusion layer characteristics on the performance of polymer electrolyte fuel cell electrodes. J. Appl. Electrochem. 2001, 31, 449–454. [Google Scholar] [CrossRef]
- Malhotra, S.; Ghosh, S. Effects of channel diameter on flow pattern and pressure drop for air–water flow in serpentine gas channels of PEM fuel cell-An Ex situ experiment. Exp. Therm. Fluid Sci. 2019, 100, 233–250. [Google Scholar] [CrossRef]
- Noguer, N.; Candusso, D.; Kouta, R.; Harel, F.; Charon, W.; Coquery, G. A PEMFC multi-physical model to evaluate the consequences of parameter uncertainty on the fuel cell performance. Int. J. Hydrogen Energy 2015, 40, 3968–3980. [Google Scholar] [CrossRef]
- Chen, H.; Liu, B.; Zhang, T.; Pei, P. Influencing sensitivities of critical operating parameters on PEMFC output performance and gas distribution quality under different electrical load conditions. Appl. Energy 2019, 255, 113849. [Google Scholar] [CrossRef]
- Li, Y.; Pei, P.; Wu, Z.; Xu, H.; Chen, D.; Huang, S. Novel approach to determine cathode two-phase-flow pressure drop of proton exchange membrane fuel cell and its application on water management. Appl. Energy 2017, 190, 713–724. [Google Scholar] [CrossRef]
- Shen, J.; Zeng, L.; Liu, Z.; Liu, W. Performance investigation of PEMFC with rectangle blockages in Gas Channel based on field synergy principle. Heat Mass Transf. 2018, 55, 811–822. [Google Scholar] [CrossRef]
- Zhang, G.; Jiao, K. Three-dimensional multi-phase simulation of PEMFC at high current density utilizing Eulerian-Eulerian model and two-fluid model. Energy Convers. Manag. 2018, 176, 409–421. [Google Scholar] [CrossRef]
- Han, C.; Chen, Z. Numerical simulation for the effect of vaporization intensity in membrane on the performance of PEM fuel cell. Numer. Heat Transf. Part A Appl. 2018, 73, 177–194. [Google Scholar] [CrossRef]
- Lei, H.; Huang, H.; Li, C.; Pan, M.; Guo, X.; Chen, Y.; Liu, M.; Wang, T. Numerical simulation of water droplet transport characteristics in cathode channel of proton exchange membrane fuel cell with tapered slope structures. Int. J. Hydrogen Energy 2020, 45, 29331–29344. [Google Scholar] [CrossRef]
- Falagüerra, T.; Muñoz, P.; Correa, G. Analysis of the cathode side of a PEMFC varying design parameters to optimize current distribution and power density. J. Electroanal. Chem. 2021, 880, 114820. [Google Scholar] [CrossRef]
- Lim, I.S.; Park, J.Y.; Kang, D.G.; Choi, S.H.; Kang, B.; Kim, M.S. Numerical study for in-plane gradient effects of cathode gas diffusion layer on PEMFC under low humidity condition. Int. J. Hydrogen Energy 2020, 45, 19745–19760. [Google Scholar] [CrossRef]
- Bao, Y.; Gan, Y. Roughness effects of gas diffusion layers on droplet dynamics in PEMFC flow channels. Int. J. Hydrogen Energy 2020, 45, 17869–17881. [Google Scholar] [CrossRef]
- Xie, X.; Yin, B.; Xu, S.; Jia, H.; Dong, F.; Chen, X. Effects of microstructure shape parameters on water removal in a PEMFC lotus-like flow channel. Int. J. Hydrogen Energy 2020, 47, 3473–3483. [Google Scholar] [CrossRef]
- Sun, Y.; Bao, C.; Jiang, Z.; Zhang, X.; Gao, T. A two-dimensional numerical study of liquid water breakthrough in gas diffusion layer based on phase field method. J. Power Sources 2020, 448, 227352. [Google Scholar] [CrossRef]
- Hu, Z.; Xu, L.; Li, J.; Hu, J.; Xu, X.; Du, X.; Sun, W.; Ouyang, M. A cell interaction phenomenon in a multi-cell stack under one cell suffering fuel starvation. Energy Convers. Manag. 2018, 174, 465–474. [Google Scholar] [CrossRef]
- Bodner, M.; Schenk, A.; Salaberger, D.; Rami, M.; Hochenauer, C.; Hacker, V. Air starvation induced degradation in polymer electrolyte fuel cells. Fuel Cells 2017, 17, 18–26. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Zhao, X.; Zhang, T.; Pei, P. The reactant starvation of the proton exchange membrane fuel cells for vehicular applications: A review. Energy Convers. Manag. 2019, 182, 282–298. [Google Scholar] [CrossRef]
- Hu, J.; Xu, L.; Li, J.; Fang, C.; Cheng, S.; Ouyang, M.; Hong, P. Model-based estimation of liquid saturation in cathode gas diffusion layer and current density difference under proton exchange membrane fuel cell flooding. Int. J. Hydrogen Energy 2015, 40, 14187–14201. [Google Scholar] [CrossRef]
- Xia, L.; Zhang, C.; Hu, M.; Jiang, S.; Chin, C.S.; Gao, Z.; Liao, Q. Investigation of parameter effects on the performance of high-temperature PEM fuel cell. Int. J. Hydrogen Energy 2018, 43, 23441–23449. [Google Scholar] [CrossRef]
- Zhang, G.; Fan, L.; Sun, J.; Jiao, K. A 3D model of PEMFC considering detailed multiphase flow and anisotropic transport properties. Int. J. Heat Mass Transf. 2017, 115, 714–724. [Google Scholar] [CrossRef]
- Min, C.; He, J.; Wang, K.; Xie, L.; Yang, X. A comprehensive analysis of secondary flow effects on the performance of PEMFCs with modified serpentine flow fields. Energy Convers. Manag. 2019, 180, 1217–1224. [Google Scholar] [CrossRef]
- Houreh, N.B.; Shokouhmand, H.; Afshari, E. Effect of inserting obstacles in flow field on a membrane humidifier performance for PEMFC application: A CFD model. Int. J. Hydrogen Energy 2019, 44, 30420–30439. [Google Scholar] [CrossRef]
- Afra, M.; Nazari, M.; Kayhani, M.H.; Sharifpur, M.; Meyer, J. 3D experimental visualization of water flooding in proton exchange membrane fuel cells. Energy 2019, 175, 967–977. [Google Scholar] [CrossRef]
- Mammar, K.; Saadaoui, F.; Laribi, S. Design of a PEM fuel cell model for flooding and drying diagnosis using fuzzy logic clustering. Renew. Energy Focus 2019, 30, 123–130. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, P.; Chen, H.; Pei, P. A review of automotive proton exchange membrane fuel cell degradation under start-stop operating condition. Appl. Energy 2018, 223, 249–262. [Google Scholar] [CrossRef]
- Chen, B.; Wang, J.; Yang, T.; Cai, Y.; Zhang, C.; Chan, S.H.; Yu, Y.; Tu, Z. Carbon corrosion and performance degradation mechanism in a proton exchange membrane fuel cell with dead-ended anode and cathode. Energy 2016, 106, 54–62. [Google Scholar] [CrossRef]
- Wang, B.; Wu, K.; Xi, F.; Xuan, J.; Xie, X.; Wang, X.; Jiao, K. Numerical analysis of operating conditions effects on PEMFC with anode recirculation. Energy 2019, 173, 844–856. [Google Scholar] [CrossRef]
- Yang, Z.; Du, Q.; Jia, Z.; Yang, C.; Jiao, K. Effects of operating conditions on water and heat management by a transient multi-dimensional PEMFC system model. Energy 2019, 183, 462–476. [Google Scholar] [CrossRef]
- Xu, Y.; Qiu, D.; Yi, P.; Lan, S.; Peng, L. An integrated model of the water transport in nonuniform compressed gas diffusion layers for PEMFC. Int. J. Hydrogen Energy 2019, 44, 13777–13785. [Google Scholar] [CrossRef]
- Ijaodola, O.; Hassan, Z.E.-; Ogungbemi, E.; Khatib, F.; Wilberforce, T.; Thompson, J.; Olabi, A. Energy efficiency improvements by investigating the water flooding management on proton exchange membrane fuel cell (PEMFC). Energy 2019, 179, 246–267. [Google Scholar] [CrossRef]
- Barbir, F. PEM Fuel Cells: Theory and Practice; Elsevier Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Wu, H.; Li, X.; Berg, P. On the modeling of water transport in polymer electrolyte membrane fuel cells. Electrochim. Acta 2009, 54, 6913–6927. [Google Scholar] [CrossRef]
- Meng, H. A two-phase non-isothermal mixed-domain PEM fuel cell model and its application to two-dimensional simulations. J. Power Sources 2007, 168, 218–228. [Google Scholar] [CrossRef]
- Lu, J.B.; Wei, G.H.; Zhu, F.J.; Yan, X.H.; Zhang, J.L. Pressure effect on the PEMFC performance. Fuel Cells 2019, 19, 211–220. [Google Scholar] [CrossRef]
- Bosnjakovic, F.; Perry, L.B. Technical Thermodynamics; Holt, Rinehart & Winston: New York, NY, USA, 1965. [Google Scholar]
- Pei, P.; Ouyang, M.; Feng, W.; Lu, L.; Huang, H.; Zhang, J. Hydrogen pressure drop characteristics in a fuel cell stack. Int. J. Hydrogen Energy. 2006, 31, 371–377. [Google Scholar] [CrossRef]
- Ye, Q.; Van Nguyen, T. Three-dimensional simulation of liquid water distribution in a PEMFC with experimentally measured capillary functions. J. Electrochem. Soc. 2007, 154, B1242–B1251. [Google Scholar] [CrossRef]
- Han, J.; Yu, S.; Yi, S. Adaptive control for robust air flow management in an automotive fuel cell system. Appl. Energy 2017, 190, 73–83. [Google Scholar] [CrossRef]
- Sahraoui, M.; Kharrat, C.; Halouani, K. Two-dimensional modeling of electrochemical and transport phenomena in the porous structures of a PEMFC. Int. J. Hydrogen Energy 2009, 34, 3091–3103. [Google Scholar] [CrossRef]
- Falcão, D.S.; Rangel, C.M.; Pinho, C.; Pinto, A.M.F.R. Water transport through a Proton-Exchange Membrane (PEM) fuel cell operating near ambient conditions: Experimental and modeling studies. Energy Fuels 2008, 23, 397–402. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, L.; Pei, P.; Yao, S.; Wang, F. Asymptotic analysis for the inlet relative humidity effects on the performance of proton exchange membrane fuel cell. Appl. Energy 2018, 213, 573–584. [Google Scholar] [CrossRef]
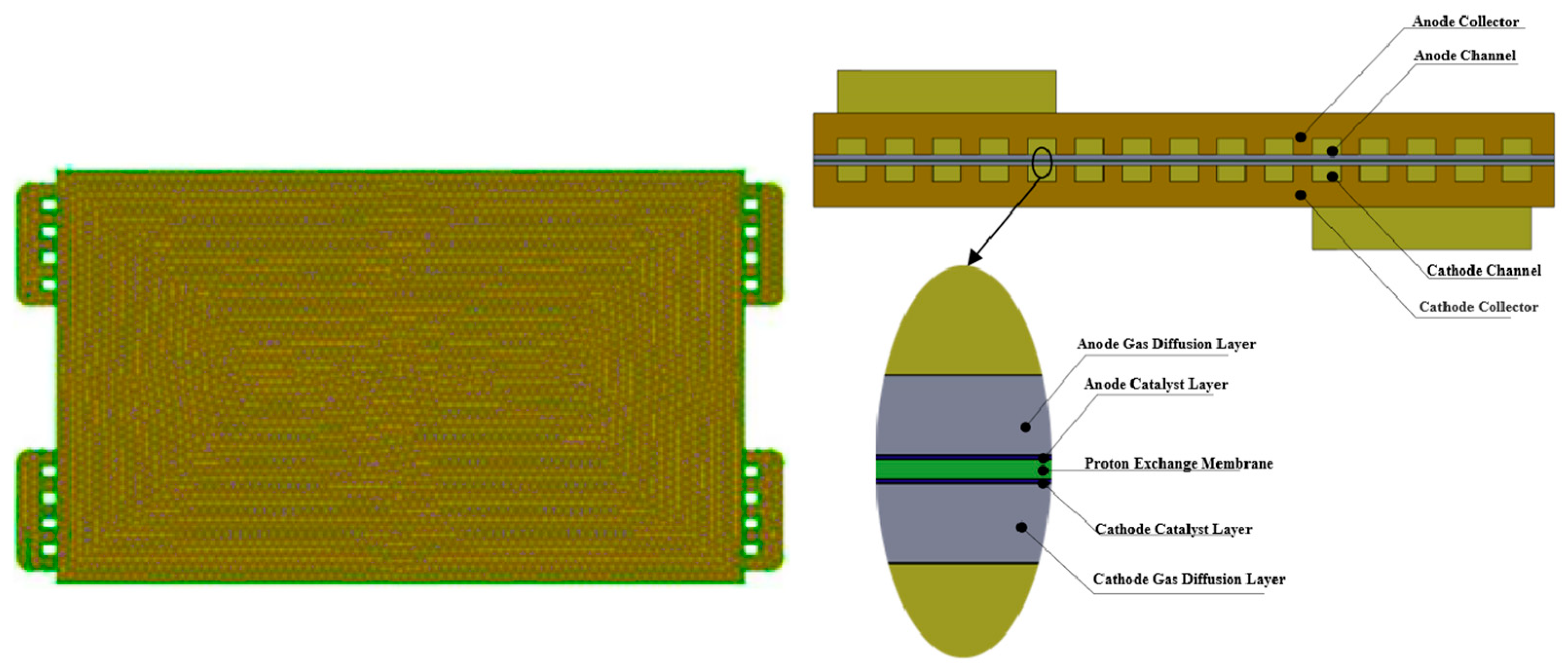
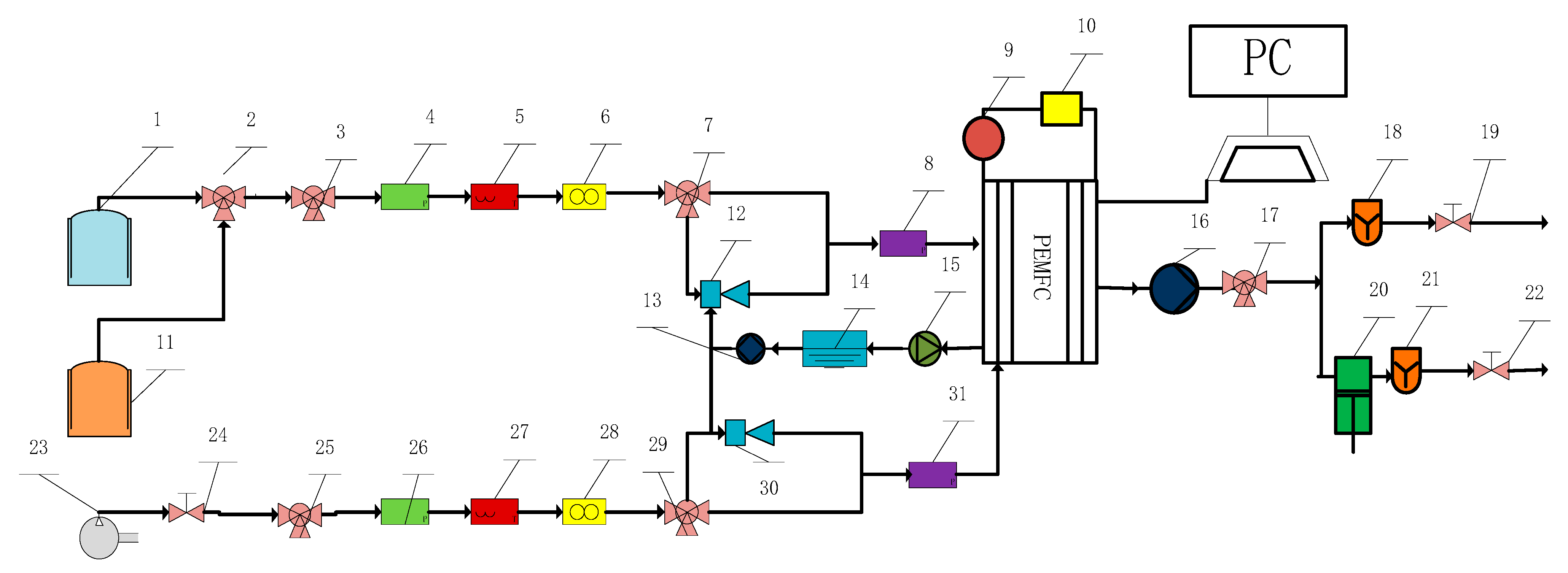
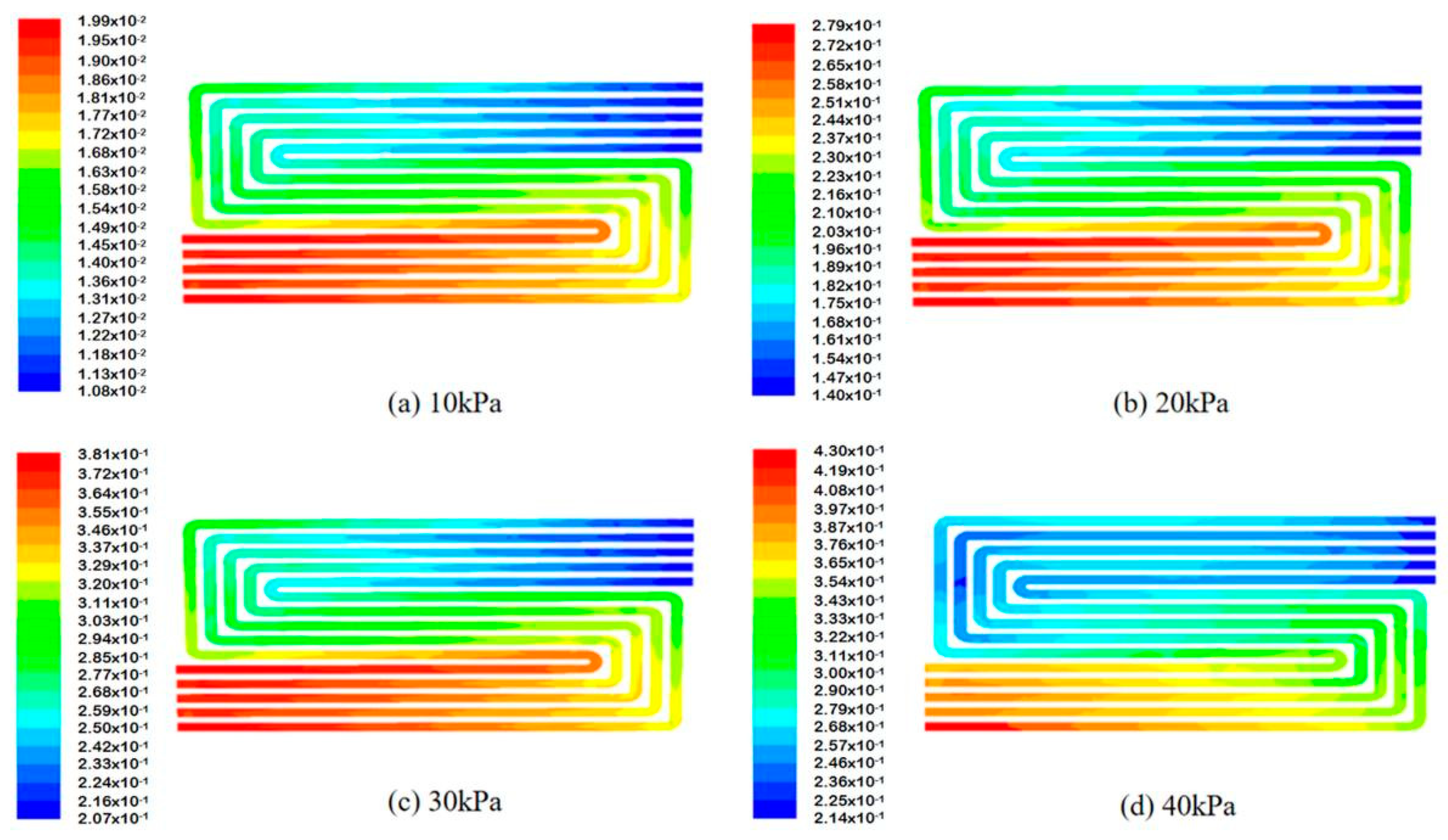
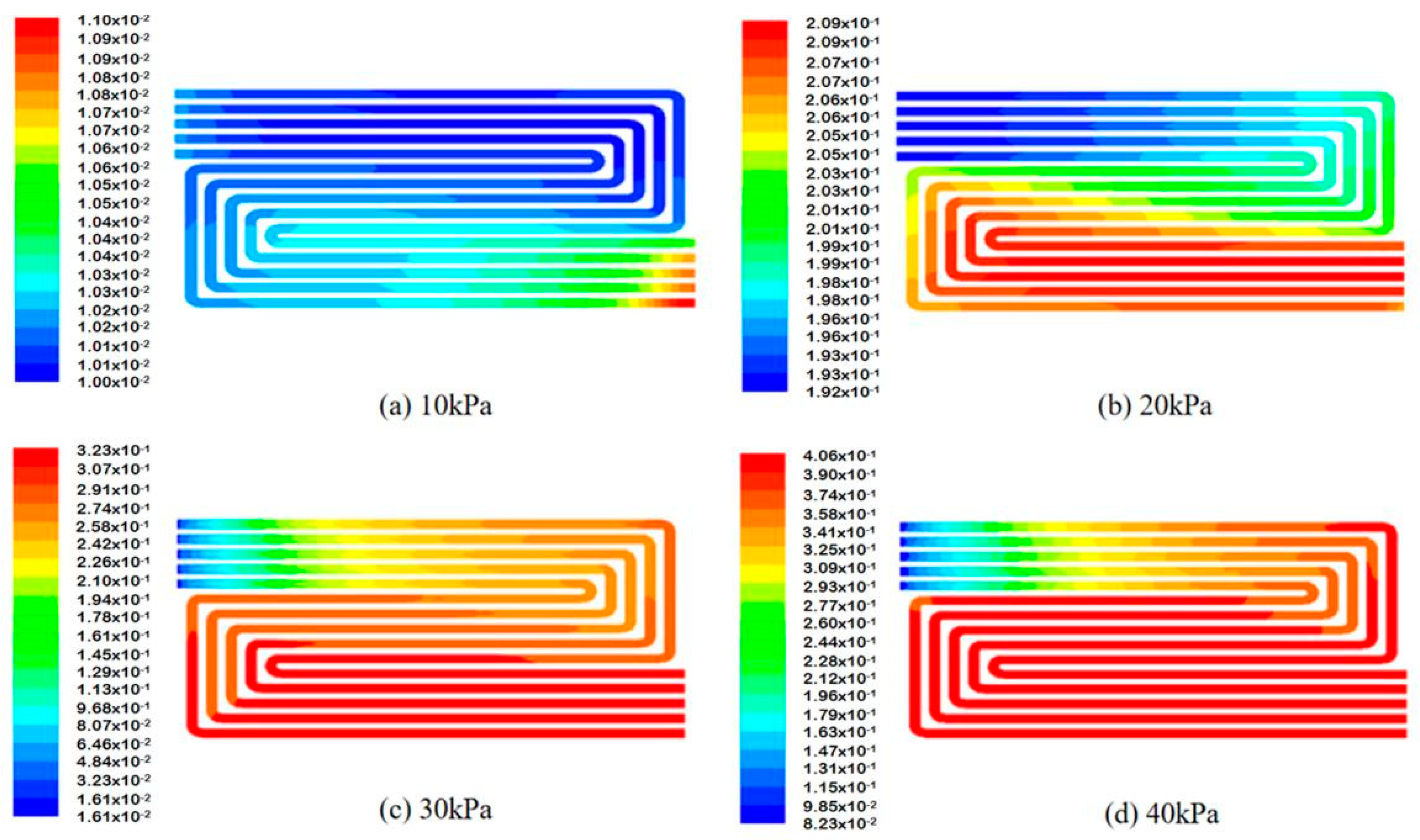
| Structure | Value | Units |
|---|---|---|
| Active area | ||
| Channel length | ||
| Channel width | ||
| Channel depth of the anode | ||
| Channel depth of the cathode | ||
| Channel number | 5.00 | -- |
| Thickness of proton exchange membrane | ||
| Thickness of gas diffusion layer | ||
| Thickness of catalytic layer |
| Name | Region | Type |
|---|---|---|
| collector-a | SOLID | 1 interface/other wall |
| collector-c | SOLID | 1 interface/other wall |
| diff-a FLUID | FLUID | 1 interface/other wall |
| diff-c FLUID | FLUID | 1 interface/other wall |
| cata-a FLUID | FLUID | 1 interface/other wall |
| cata-c FLUID | FLUID | 1 interface/other wall |
| mem FLUID | FLUID | 1 interface/other wall |
| ch-a FLUID | FLUID | 1 mass-flow inlets/1 pressure-outlet |
| ch-c FLUID | FLUID | 1 mass-flow inlets/1 pressure-outlet |
| Parameter | Value | Units |
|---|---|---|
| Thermal conductivity of the catalyst layer | 1.5 | W·(m·K)−1 |
| Thermal conductivity of the current collector | 20 | W·(m·K)−1 |
| Electrical conductivity of the gas diffusion layer | 2500 | S·m−1 |
| Electrical conductivity of the catalyst layer | 2500 | S·m−1 |
| Electrical conductivity of the current collector | 20,000 | S·m−1 |
| Porosity of the gas diffusion layer | 0.5 | -- |
| Porosity of the catalyst layer | 0.28 | -- |
| Membrane equivalent weight | 1100 | kg·kmol−1 |
| Hydrogen reference exchange current density | 4000 | A·m−2 |
| Anode reference concentration | 1 | kmol·m−3 |
| Anode transfer coefficient | 0.5 | -- |
| Oxygen reference exchange current density | 5.75 | A·m−2 |
| Cathode reference concentration | 1 | kmol·m−3 |
| Cathode transfer coefficient | 0.5 | -- |
| Open circuit voltage | 0.95 | V |
| Leakage current | 0 | A |
| Electrochemical equivalent of hydrogen | 1.05 × 10−8 | kg·(A·s)−1 |
| Electrochemical equivalent of oxygen | 8.29 × 10−8 | kg·(A·s)−1 |
| Reference diffusivity of hydrogen | 9.15 × 10−5 | m2·s−1 |
| Reference diffusivity of oxygen | 2.2 × 10−5 | m2·s−1 |
| Reference diffusivity of water | 2.56 × 10−5 | m2·s−1 |
| Anode catalyst layer surface/volume ratio | 2 × 106 | m−1 |
| Cathode catalyst layer surface/volume ratio | 1 × 107 | m−1 |
| Operating temperature | 75 | °C |
| Operating pressure | 10, 20, 30, 40 | kPa |
| Anode inlet gas flow rate | 7 | L·min−1 |
| Cathode inlet gas flow rate | 15 | L·min−1 |
| Anode relative humidity | 100 | % |
| Cathode relative humidity | 100 | % |
| Parameter | Fuel Cell |
|---|---|
| Area of membrane (cm2) | 168 |
| Flow field | Multi-serpentines |
| Membrane | NafionTM117 |
| GDL | Toray 200 um |
| Cat. loading | 0.1/0.4 mg·cm−2 |
| Material of bipolar plate | Metal |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Liu, Y.; Pei, P.; Liu, X.; Wang, L.; Wan, Y. Variation Characteristic Analysis of Water Content at the Flow Channel of Proton Exchange Membrane Fuel Cell. Energies 2022, 15, 3280. https://doi.org/10.3390/en15093280
Zhang L, Liu Y, Pei P, Liu X, Wang L, Wan Y. Variation Characteristic Analysis of Water Content at the Flow Channel of Proton Exchange Membrane Fuel Cell. Energies. 2022; 15(9):3280. https://doi.org/10.3390/en15093280
Chicago/Turabian StyleZhang, Lu, Yongfeng Liu, Pucheng Pei, Xintong Liu, Long Wang, and Yuan Wan. 2022. "Variation Characteristic Analysis of Water Content at the Flow Channel of Proton Exchange Membrane Fuel Cell" Energies 15, no. 9: 3280. https://doi.org/10.3390/en15093280
APA StyleZhang, L., Liu, Y., Pei, P., Liu, X., Wang, L., & Wan, Y. (2022). Variation Characteristic Analysis of Water Content at the Flow Channel of Proton Exchange Membrane Fuel Cell. Energies, 15(9), 3280. https://doi.org/10.3390/en15093280







