Study on the Dynamic Ice Load of Offshore Wind Turbines with Installed Ice-Breaking Cones in Cold Regions
Abstract
:1. Introduction
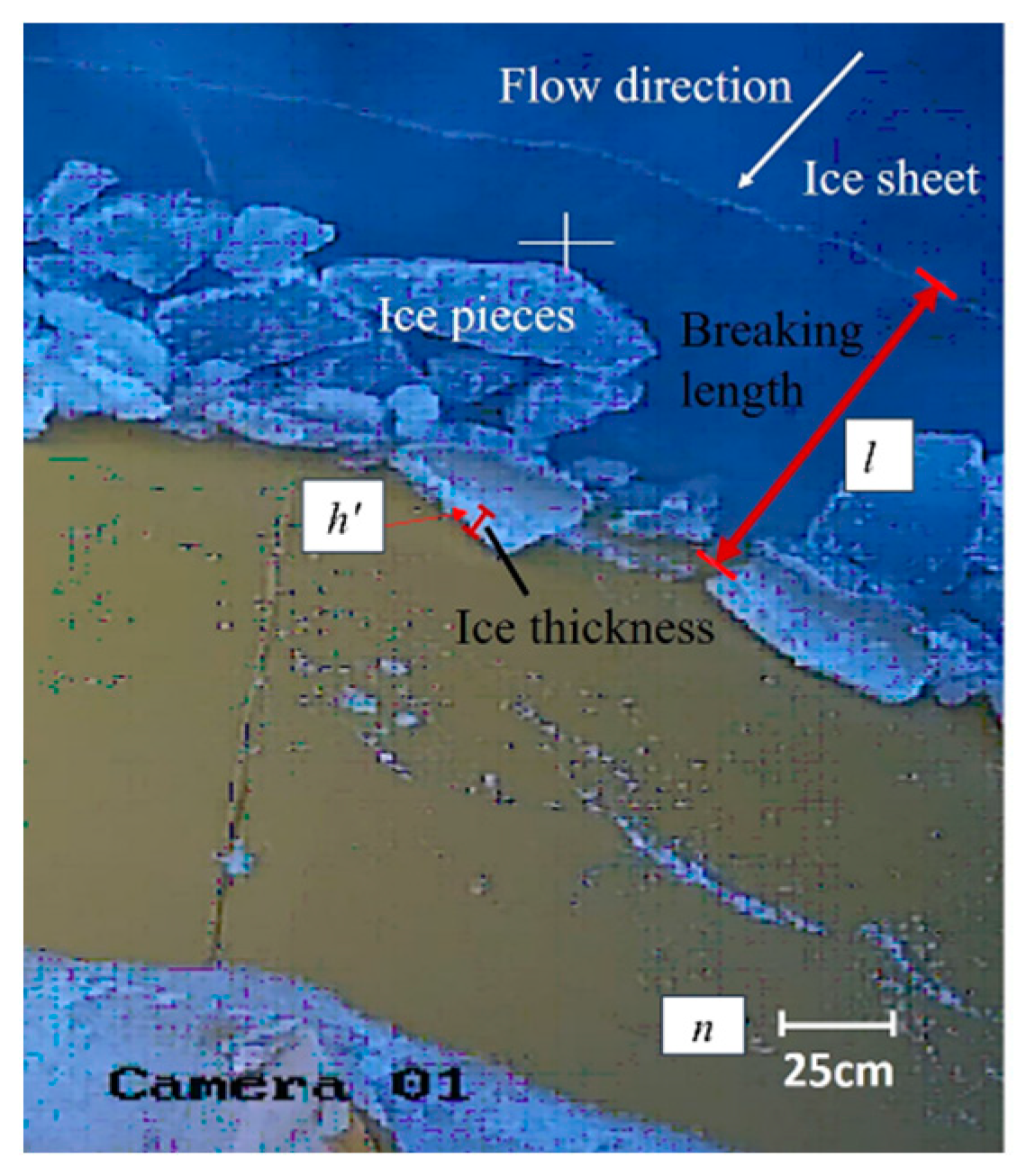
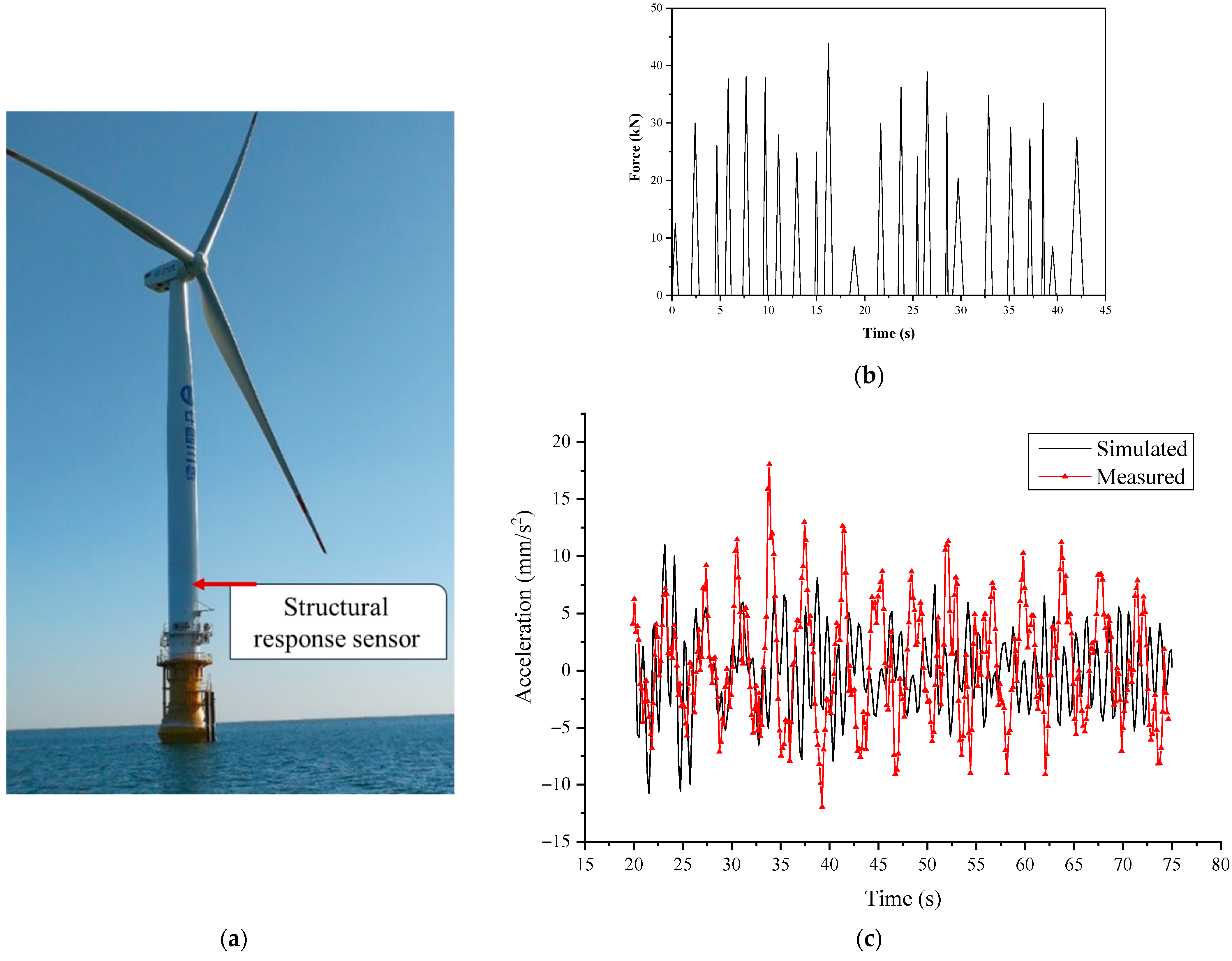
2. Field Monitoring of an OWT in Ice Regions
3. Results
3.1. Deterministic Ice Force Function
3.2. Sea Ice Breaking Characteristics of Conical Structure
4. Discussion
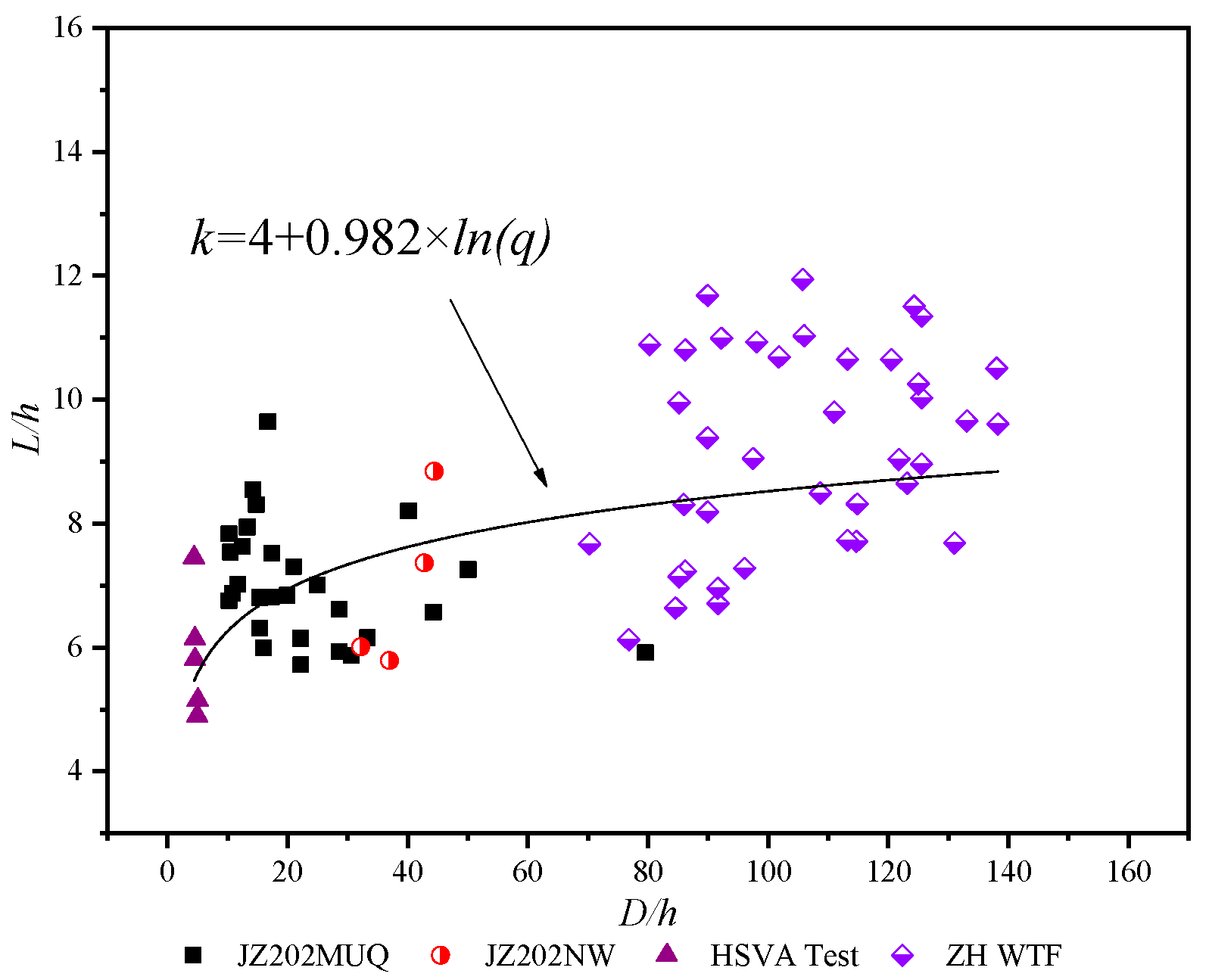
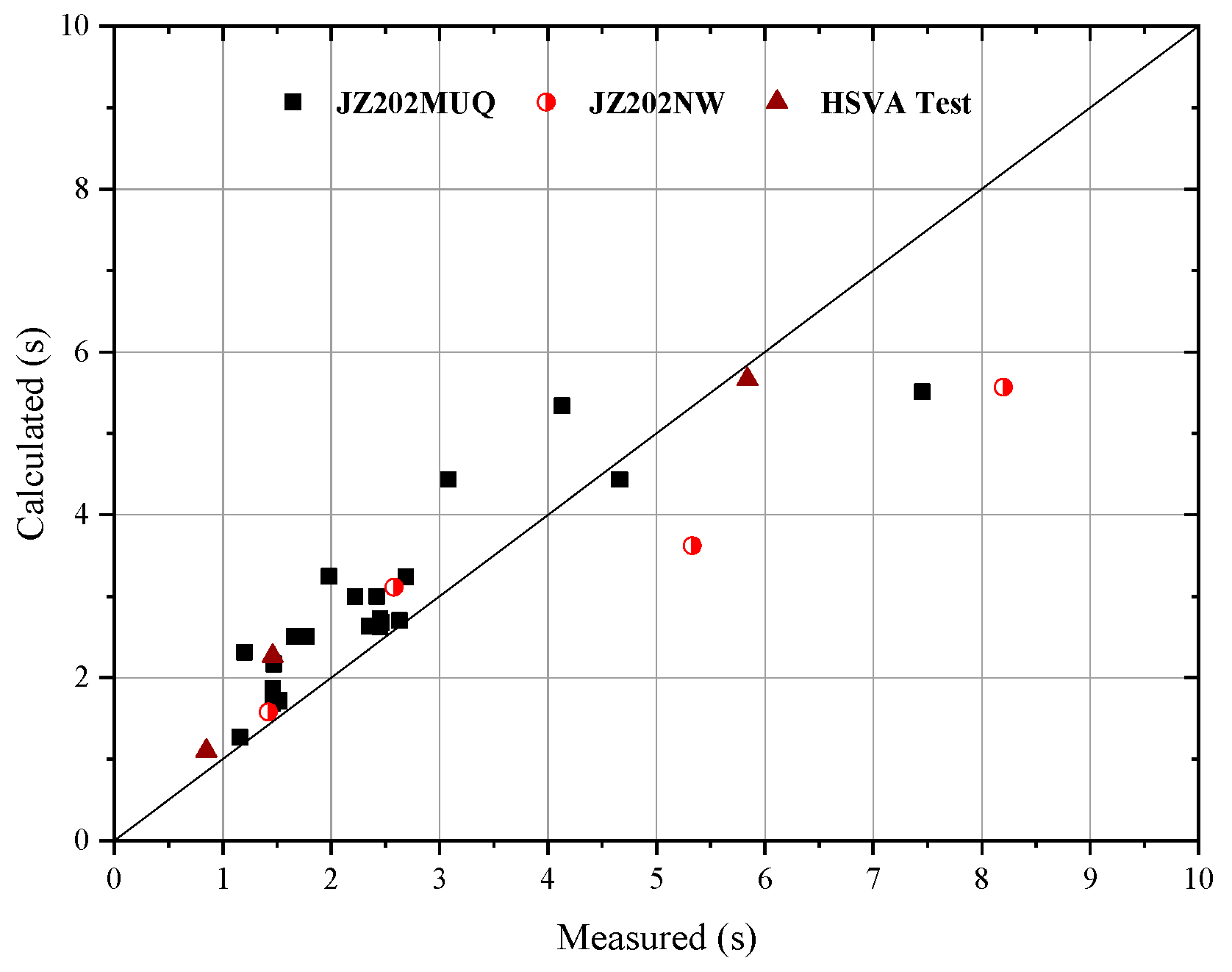
4.1. Average Period of Ice Force
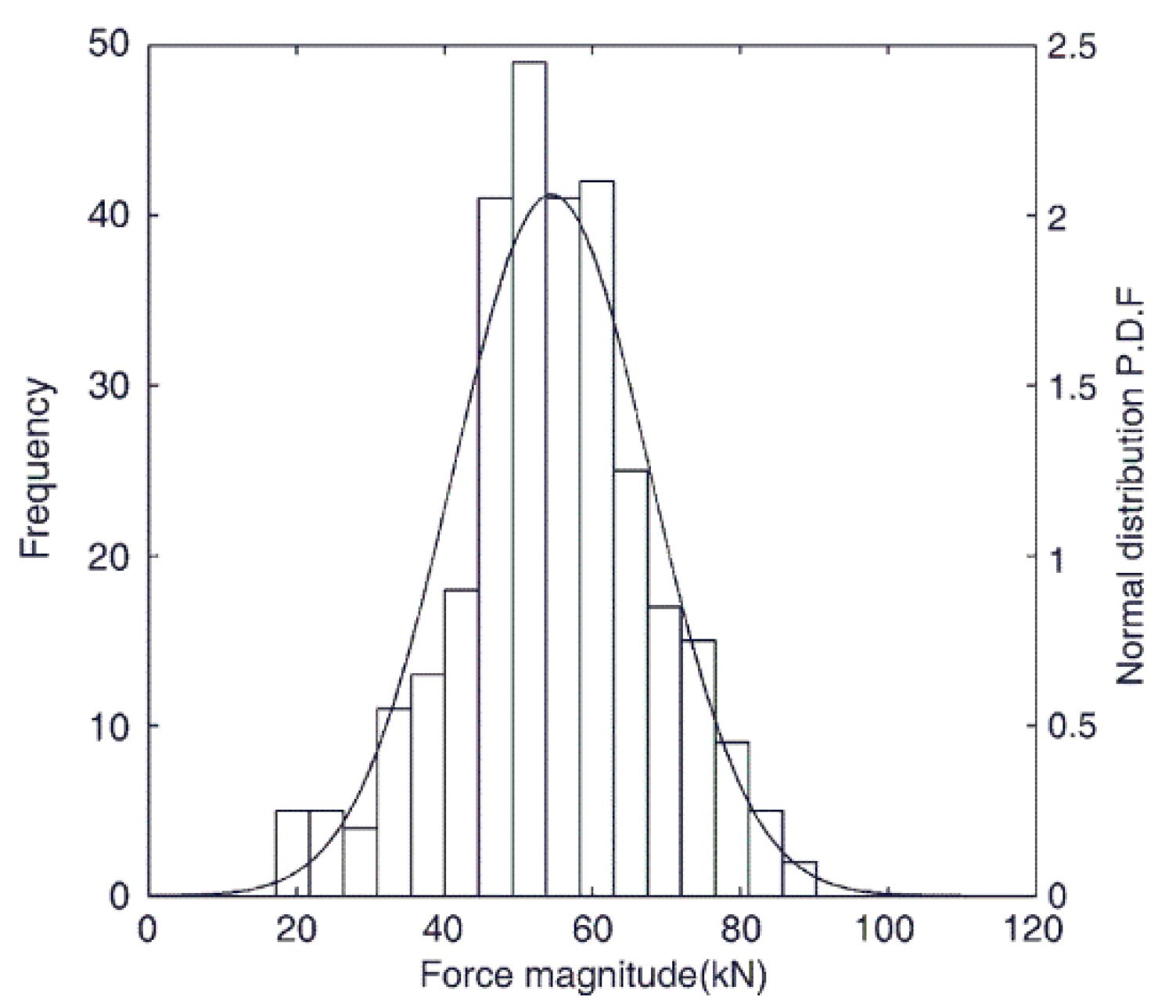
4.2. Ice Force Amplitude
4.3. Dynamic Ice Load Analysis of Conical OWT
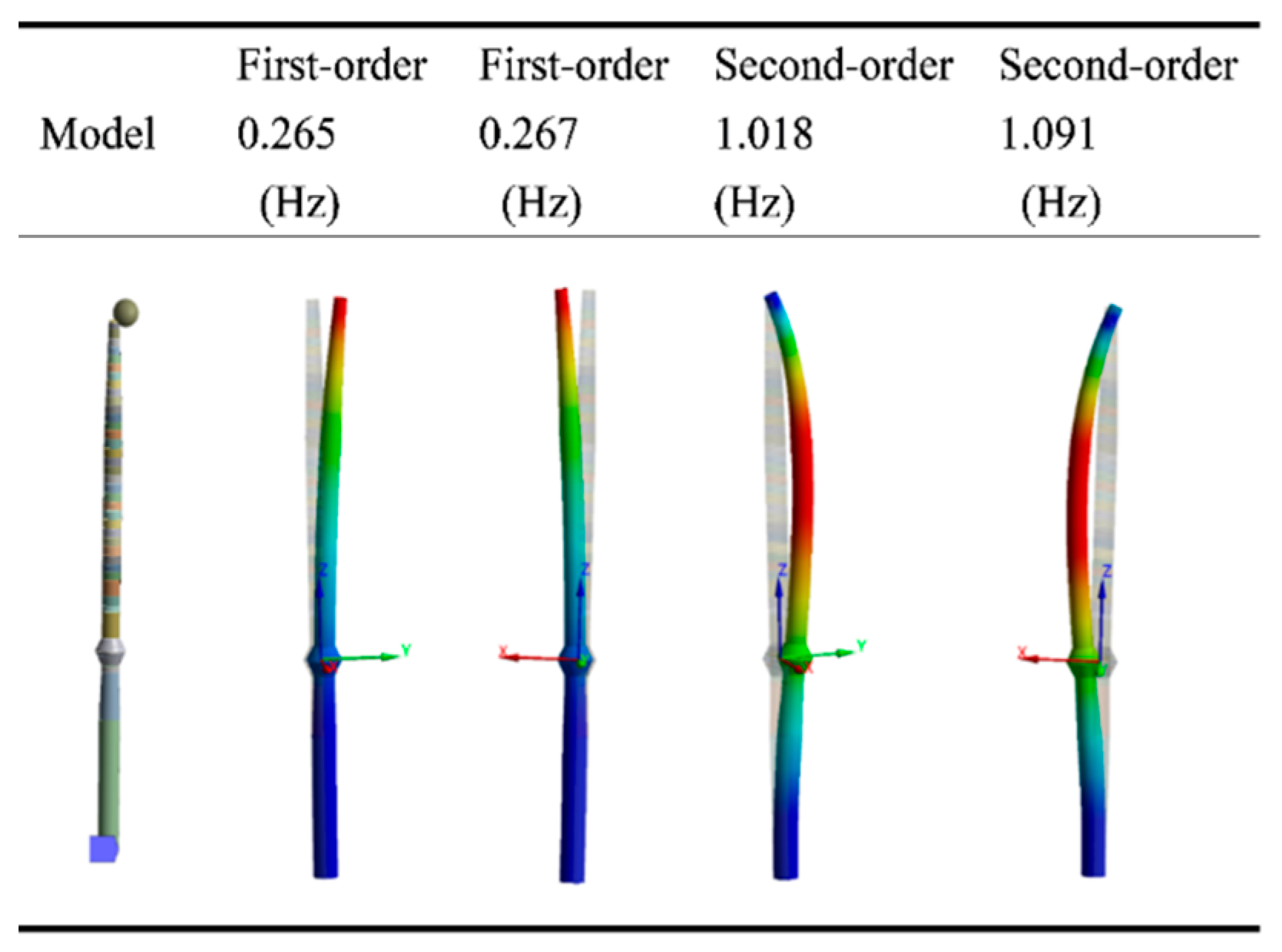
4.3.1. Characteristics of the OWT
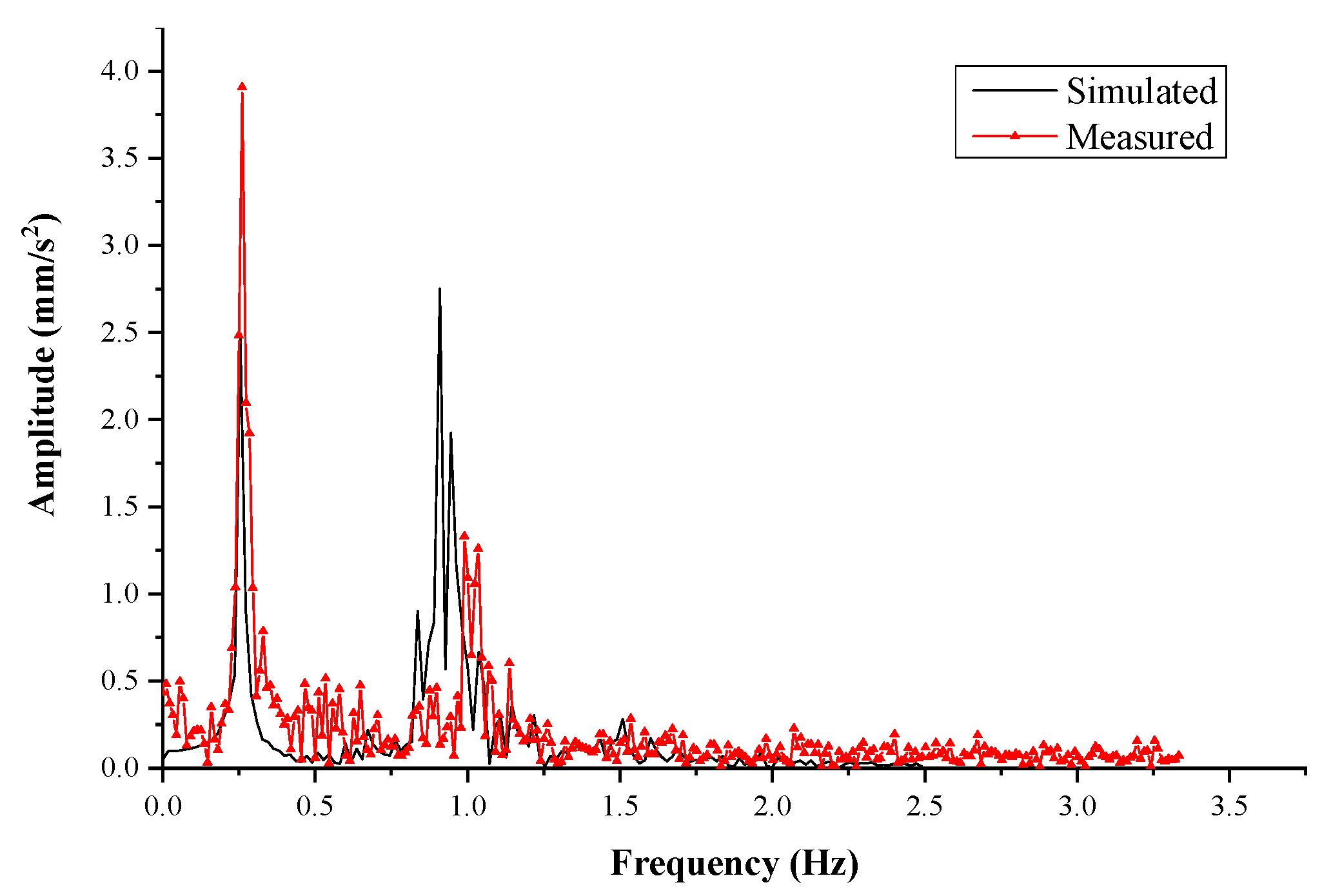
4.3.2. Verification of the Random Ice Load Model of the OWT
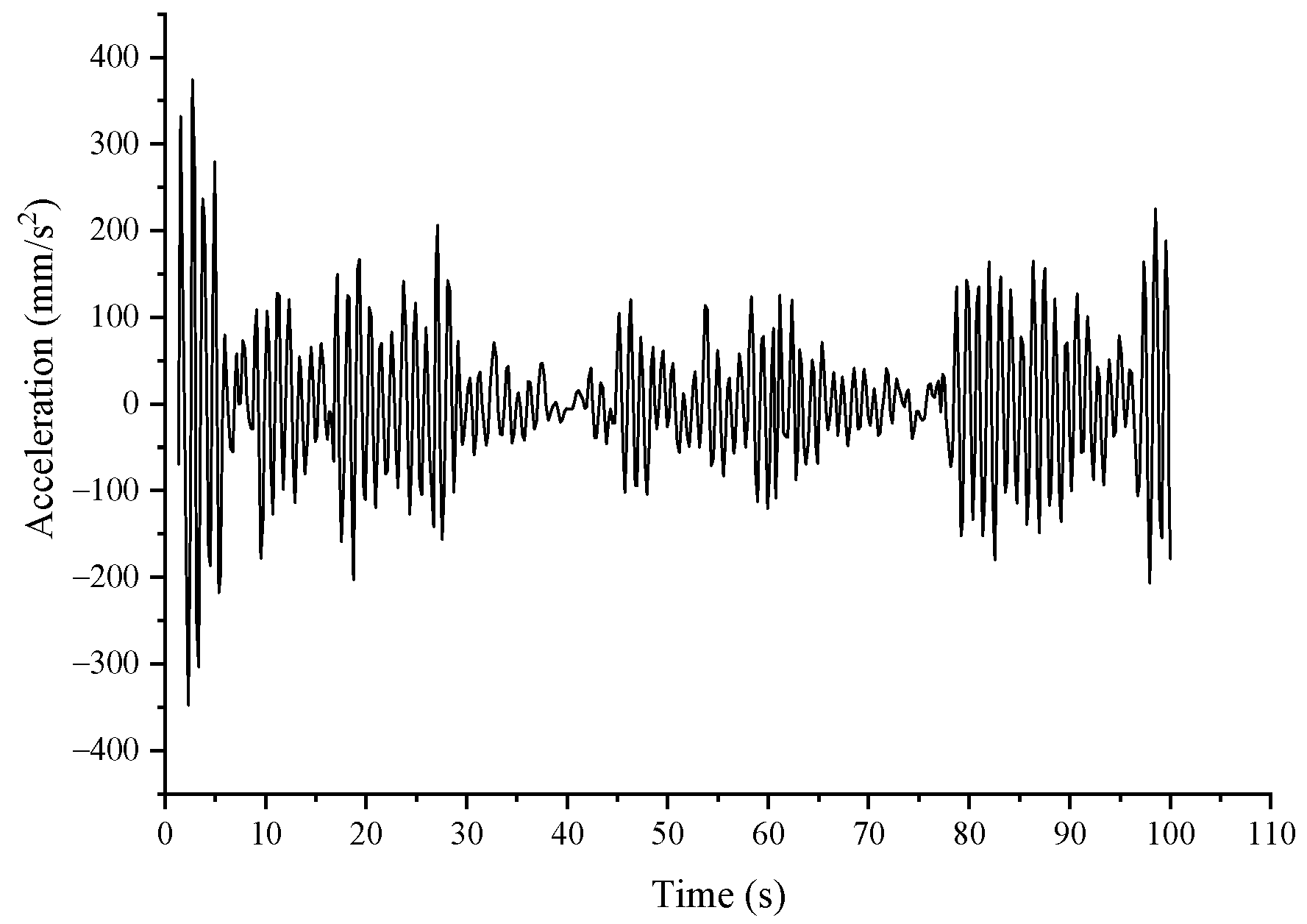
4.3.3. Ice-Induced Vibration of the OWT
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Guojun, W.; Dayong, Z.; Chunjuan, L. Vibration analysis of offshore wind turbine foundation in ice zone. Ship Ocean Eng. 2016, 45, 109–113. [Google Scholar] [CrossRef]
- Chunjuan, L. Study on the Design of Simple Offshore Wind Turbine Foundation; Dalian University of Technology: Dalian, China, 2017. [Google Scholar]
- Ye, K.; Li, C.; Yang, Y.; Zhang, W.; Xu, Z. Research on influence of ice-induced vibration on offshore wind turbines. J. Renew. Sustain. Energy. 2019, 11, 1–19. [Google Scholar] [CrossRef]
- Hendrikse, H.; Seidel, M.; Metrikine, A.; Løset, S. Initial results of a study into the estimation of the development of frequency lock-in for offshore structures subjected to ice loading. In Proceedings of the 24th International Conference on Port and Ocean Engineering under Arctic Conditions, Busan, Korea, 11–16 June 2017. [Google Scholar]
- Seidel, M.; Hendrikse, H. Analytical assessment of sea ice-induced frequency lock-in for offshore wind turbine monopoles. Mar. Struct. 2018, 60, 87–100. [Google Scholar] [CrossRef] [Green Version]
- Q/HSn 3000-2002; Regulations for Offshore Ice Condition & Application in China Sea. CNOOC: Beijing, China, 2002.
- Yue, Q.; Xu, N.; Cui, H.; Ma, C.J. Effect of adding cone to mitigate ice-induced vibration. Ocean Eng. 2011, 29, 18–24. [Google Scholar] [CrossRef]
- Lavoie, N.Y. Ice effects on structures in the Northumberland Strait crossing. In Ice Pressures against Structures, NRC Technical Memo No. 92; (NRC No. 985); Department of Fisheries and Oceans, Department of Transport: Ottawa, ON, Canada, 1966. [Google Scholar]
- Croasdale, K.R.; Cammaert, A.B.; Metge, M. A method for the calculation of sheet ice loads on sloping structures. In Proceedings of the 12th International Symposium on Ice, Trondheim, Norway, 23–26 August 1994. [Google Scholar]
- Ralston, T.D. Ice force design considerations for conical offshore structures. In Proceedings of the 4th International Conference on Port and Ocean Engineering under Arctic Conditions, St. John’s, NL, Canada, 26–30 September 1977. [Google Scholar]
- Kato, K. Experimental studies of ice forces on conical structures. In Proceedings of the 8th IAHR Ice symposium, Iowa City, IA, USA, 18–22 August 1986. [Google Scholar]
- Hirayama, K.; Obara, I. Ice forces on inclined structures. In Proceedings of the 5th International Offshore Mechanics and Arctic Engineering, Tokyo, Japan, 13–18 April 1986. [Google Scholar]
- Yonghai, Y.; Qianjin, Y. Prediction methods of sheet ice load on conical structures. Acta Oceanol. Sin. 2000, 22, 74–85. (In Chinese) [Google Scholar] [CrossRef]
- Sodhi, D.S.; Morris, C.E.; Cox, G.F.N. Dynamic analysis of failure modes on ice sheets encountering sloping structures. In Proceedings of the 6th International Conference on Offshore Mechanics and Arctic Engineering, Houston, TX, USA, 1 March 1987. [Google Scholar]
- Frederking, R. Dynamic ice forces on an inclined structure. In Physics and Mechanics of Ice; Springer: Berlin/Heidelberg, Germany, 1980; pp. 104–116. [Google Scholar]
- Qianjin, Y.; Xiangjun, B. Ice-induced jacket structure vibrations in Bohai Sea. J. Cold Reg. Eng. 2000, 14, 81–92. [Google Scholar] [CrossRef]
- Xu, N. Research on Ice Force of Conical Offshore Structures; Dalian University of Technology: Dalian, China, 2011. [Google Scholar]
- Qianjin, Y.; Xianjun, B.; Xiao, Y.; Zhongmin, S. Ice-induced vibration and ice force function of conical structure. China Civ. Eng. J. 2003, 36, 16–19. [Google Scholar] [CrossRef]
- Yan, Q.; Qianjin, Y.; Xiangjun, B.; Tuomo, K. A random ice force model for narrow conical structures. Cold Reg. Sci. Technol. 2006, 45, 148–157. [Google Scholar] [CrossRef]
- Qianjing, Y.; Yan, Q.; Xiangjun, B. Ice force spectrum on narrow conical structures. Cold Reg. Eng. 2007, 49, 161–169. [Google Scholar] [CrossRef]
- Shunying, J.; Qianjin, Y. Monte-Carlo simulation of fatigue ice-load for offshore platform with ice-broken cone in the Liaodong Gulf. Acta Oceanol. Sin. 2003, 25, 114–119. [Google Scholar] [CrossRef]
- Feng, L.; Qianjin, Y. Failure of ice sheet under simultaneously longitudinal and transverse load on slope structures. J. Hydraul. Eng. 2000, 31, 44–48. [Google Scholar] [CrossRef]
- ISO 19906; Petroleum and Natural Gas Industries-Arctic Offshore Structures. International Standard Organization (ISO): Geneva, Switzerland, 2010.
- Xiao, Y. Research on Ice Force of Conical Structures in Bohai; Dalian University of Technology: Dalian, China, 2001. [Google Scholar]
- DNV-Os-J101; Design of Offshore Wind Turbine Structures. Det Norske Veritas: Bærum, Norway, 2014; pp. 129–130.













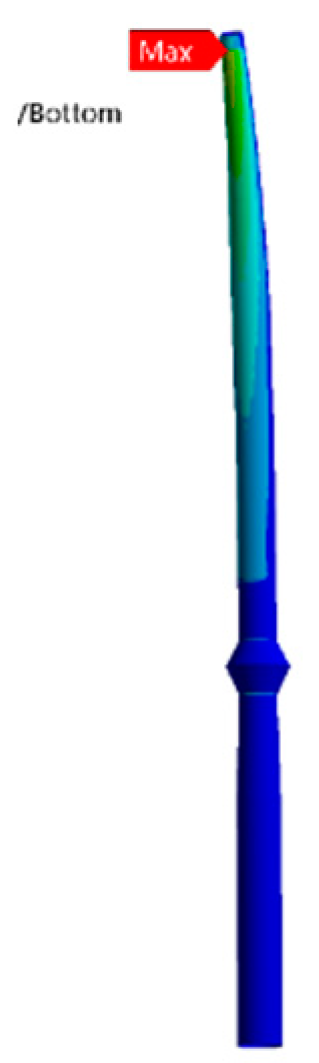

| OWT | Parameters |
|---|---|
| Top mass | 218 t |
| Tower length | 79 m |
| Tower thickness | 0.014~0.039 m |
| Waterline Diameter | 5.5 m |
| Foundation Thickness | 0.065~0.07 m |
| Ice-breaking cone diameter | 9.2 m |
| Water depth | 19 m |
| h | L | k | h | L | k |
|---|---|---|---|---|---|
| cm | cm | - | cm | cm | - |
| 5.41 | 62.26 | 11.51 | 8.49 | 93.69 | 11.03 |
| 5.87 | 40.11 | 6.83 | 8.51 | 101.64 | 11.94 |
| 6.51 | 62.55 | 9.61 | 8.84 | 94.51 | 10.69 |
| 6.52 | 68.53 | 10.51 | 9.18 | 100.39 | 10.94 |
| 6.76 | 65.31 | 9.66 | 9.23 | 83.54 | 9.05 |
| 6.87 | 52.81 | 7.69 | 9.37 | 68.25 | 7.28 |
| 7.14 | 88.96 | 12.47 | 9.76 | 107.33 | 10.99 |
| 7.17 | 81.37 | 11.35 | 9.82 | 65.91 | 6.71 |
| 7.17 | 64.26 | 8.96 | 9.82 | 68.31 | 6.96 |
| 7.17 | 71.91 | 10.03 | 10.01 | 93.95 | 9.39 |
| 7.20 | 73.84 | 10.26 | 10.01 | 116.97 | 11.69 |
| 7.24 | 83.33 | 11.50 | 10.01 | 82.01 | 8.20 |
| 7.31 | 63.26 | 8.66 | 10.44 | 75.53 | 7.24 |
| 7.39 | 66.78 | 9.04 | 10.44 | 112.82 | 10.81 |
| 7.47 | 79.56 | 10.66 | 10.47 | 87.00 | 8.31 |
| 7.84 | 65.24 | 8.32 | 10.57 | 75.52 | 7.14 |
| 7.84 | 60.53 | 7.72 | 10.57 | 105.21 | 9.95 |
| 7.95 | 84.71 | 10.66 | 10.64 | 70.65 | 6.64 |
| 7.95 | 61.46 | 7.73 | 11.21 | 122.11 | 10.89 |
| 7.95 | 50.55 | 6.36 | 11.72 | 71.82 | 6.13 |
| 8.11 | 79.50 | 9.80 | 12.80 | 98.24 | 7.68 |
| 8.28 | 70.35 | 8.49 | 14.90 | 123.67 | 8.30 |
| FF (Hz) | WS (N·m−1) | MCD (m) | k | |
|---|---|---|---|---|
| JZ20-2 MUQ | 0.87 | 4.5 × 107 | 4 | 7.16 |
| JZ20-2 NW | 1 | 2.54 × 107 | 6 | 6.28 |
| HSVA-Test | - | - | 0.61 | 5.29 |
| ZH-WTF | 0.2–0.3 | 2.66 × 107 | 9.2 | 9.19 |
| astd (mm·s−2) | amax (mm·s−2) | Tave (s) | Tstd (s) | |
|---|---|---|---|---|
| Simulated | 3.61 | 10.98 | 1.52 | 0.35 |
| Measured | 4.91 | 11.30 | 1.88 | 0.36 |
| Error (%) | 26.6 | 2.8 | 19.1 | 2.8 |
| First Peak Frequency (Hz) | Second Peak Frequency (Hz) | Third Peak Frequency (Hz) | |
|---|---|---|---|
| Simulated | 0.251 | 0.907 | 0.951 |
| Measured | 0.262 | 0.988 | 1.042 |
| Error (%) | 4.2 | 8.2 | 8.8 |
| IC | Thickness (m) | Velocity (m·s−1) | Period (s) |
|---|---|---|---|
| RIC | 0.32 | 0.63 | 3.77 |
| UIC | 0.32 | 0.75 | 3.17 |
| IC | Hub | ToF | ||
|---|---|---|---|---|
| MD (mm) | MA (mm·s−2) | MD (mm) | MA (mm·s−2) | |
| RIC | 253 | 319 | 32 | 374 |
| UIC | 237 | 323 | 27 | 313 |
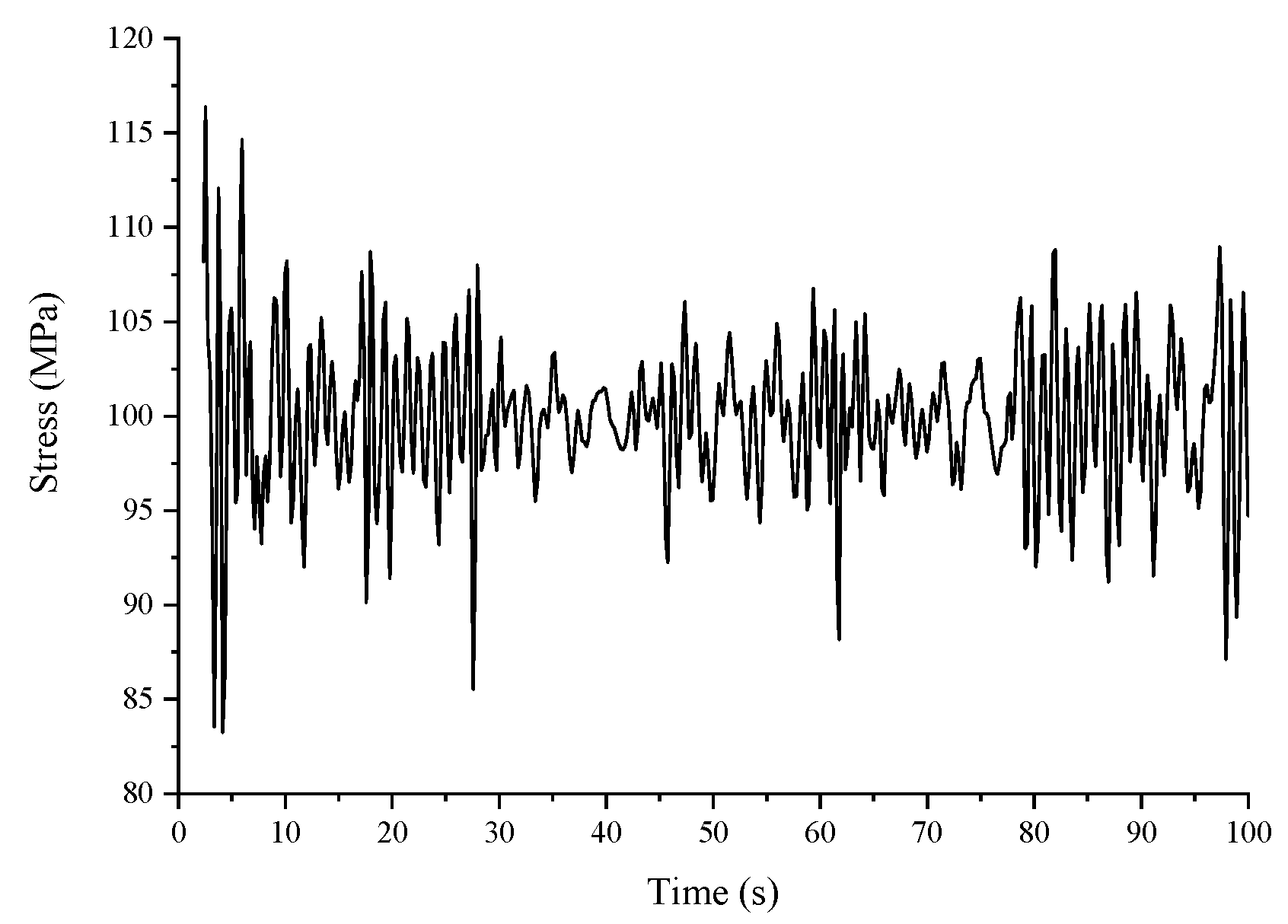
| IC | Sa (MPa) | Sm (MPa) | Su (MPa) | S−1 (MPa) | FL (MPa) |
|---|---|---|---|---|---|
| RIC | 37.7 | 97.5 | 600 | 44.8 | 37.3 |
| UIC | 35.6 | 97.5 | 600 | 42.5 | 37.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Zhang, D.; Yue, Q.; Yu, S. Study on the Dynamic Ice Load of Offshore Wind Turbines with Installed Ice-Breaking Cones in Cold Regions. Energies 2022, 15, 3357. https://doi.org/10.3390/en15093357
Wang G, Zhang D, Yue Q, Yu S. Study on the Dynamic Ice Load of Offshore Wind Turbines with Installed Ice-Breaking Cones in Cold Regions. Energies. 2022; 15(9):3357. https://doi.org/10.3390/en15093357
Chicago/Turabian StyleWang, Guojun, Dayong Zhang, Qianjin Yue, and Songsong Yu. 2022. "Study on the Dynamic Ice Load of Offshore Wind Turbines with Installed Ice-Breaking Cones in Cold Regions" Energies 15, no. 9: 3357. https://doi.org/10.3390/en15093357





