Anti-Wind Experiments and Damage Prediction of Transmission Tower under Typhoon Conditions in Coastal Areas
Abstract
:1. Introduction
2. Simulation Model
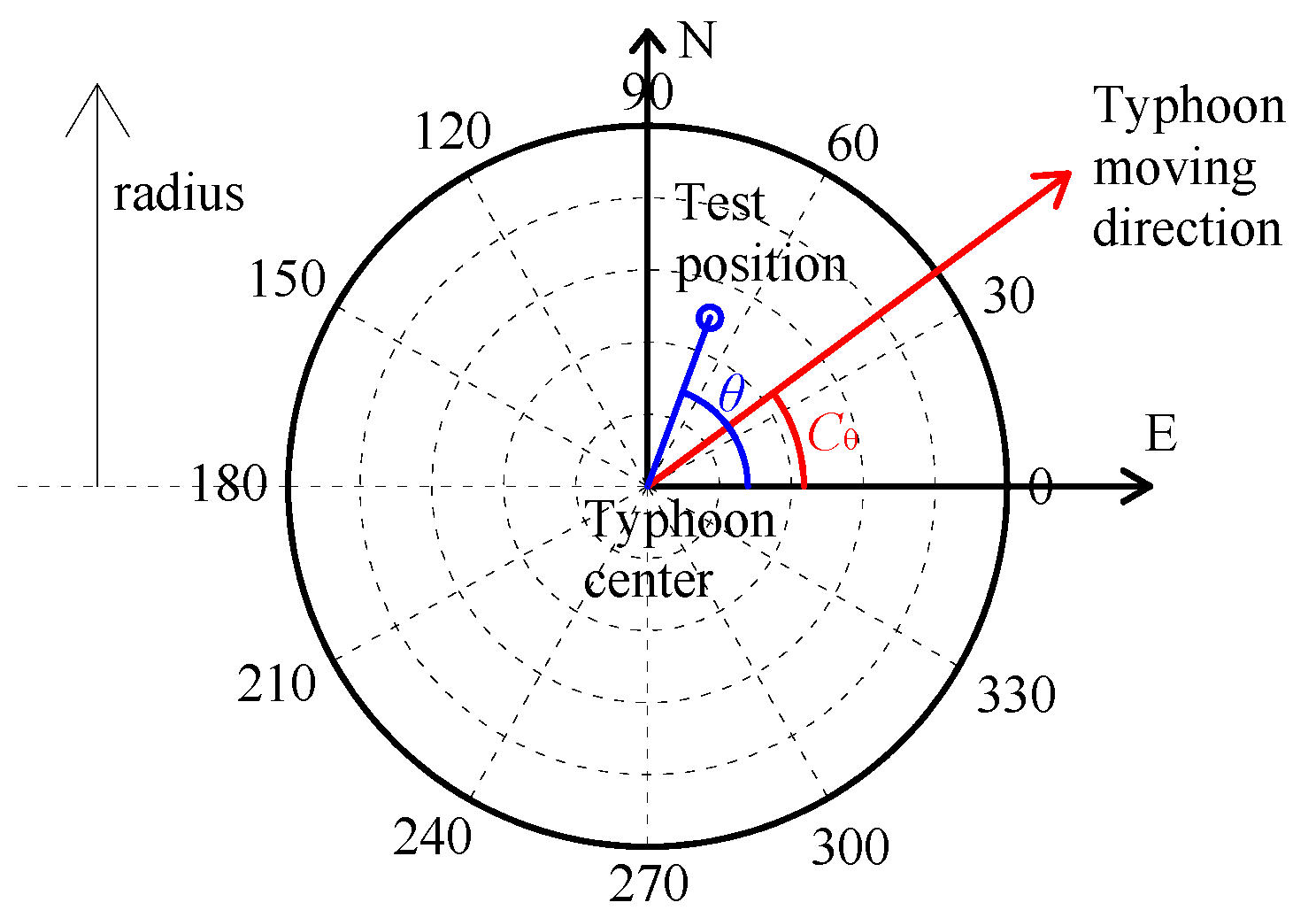
2.1. Real-Time Wind Field Mathematical Model
2.2. Tower-Line Coupled Calculation Model
3. Simulation Results and Analysis
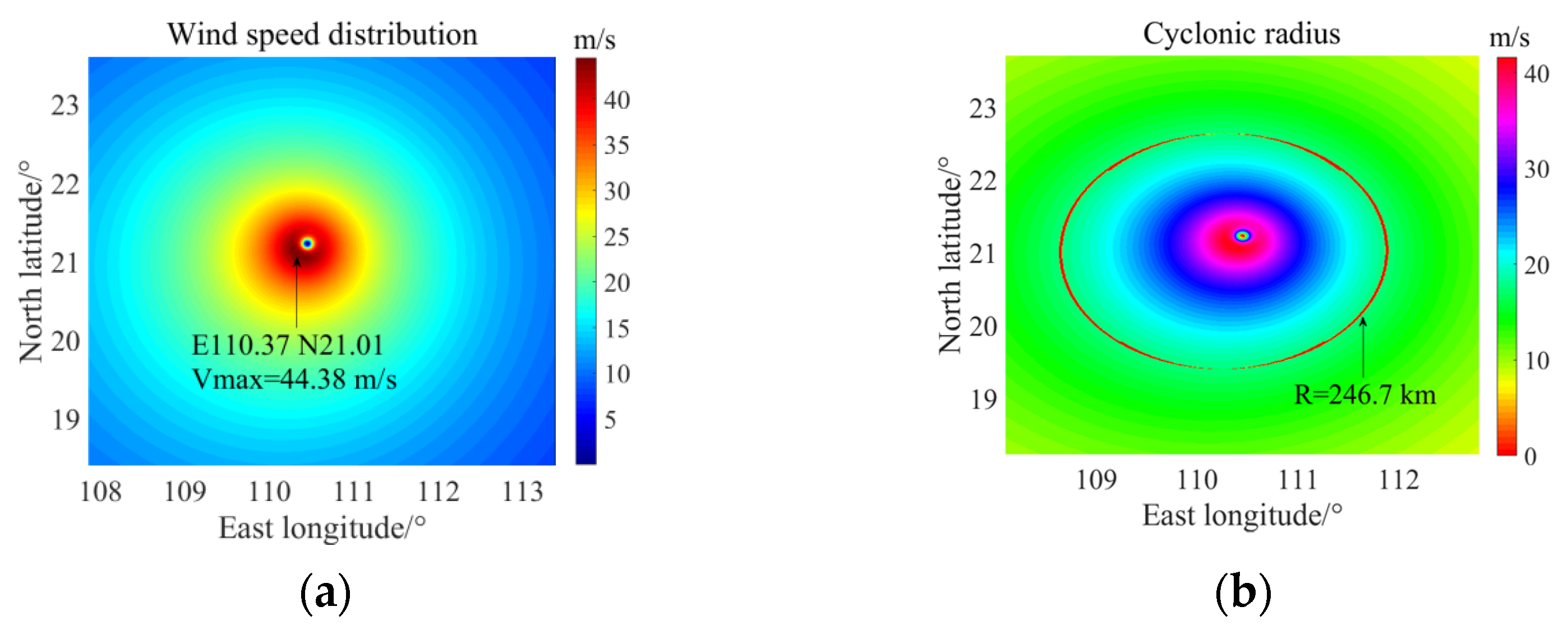
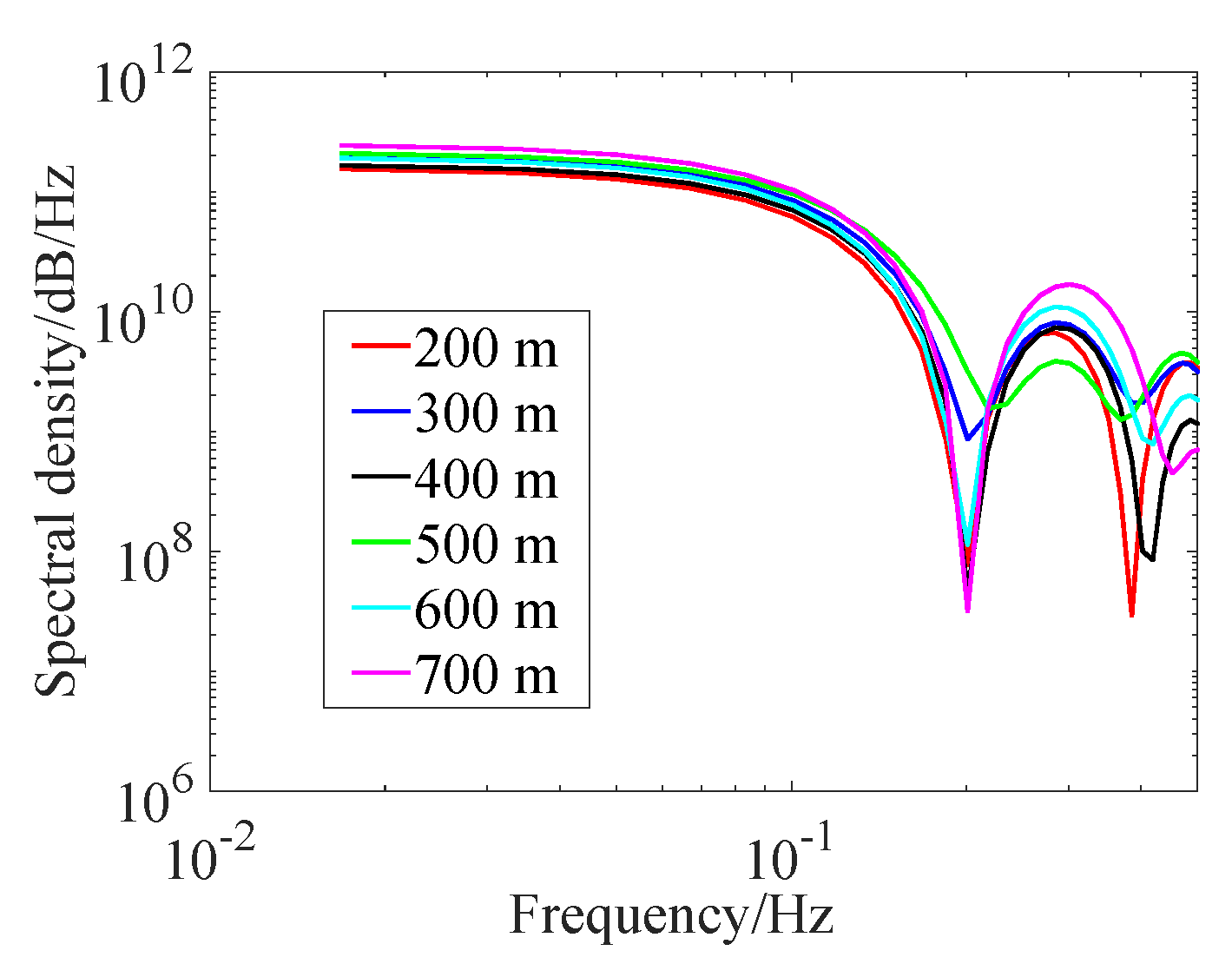
3.1. Real-Time Wind Field Distribution
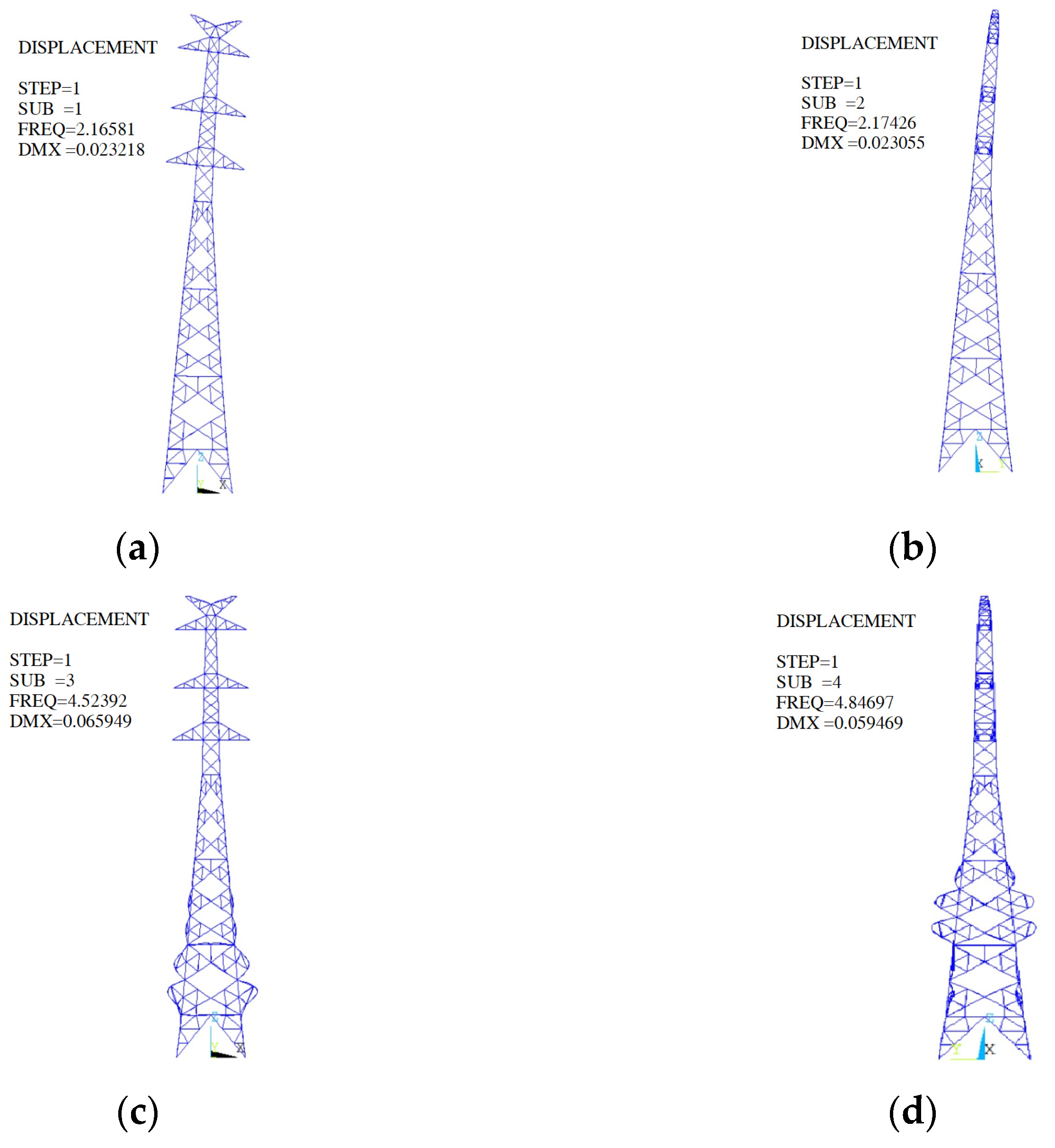
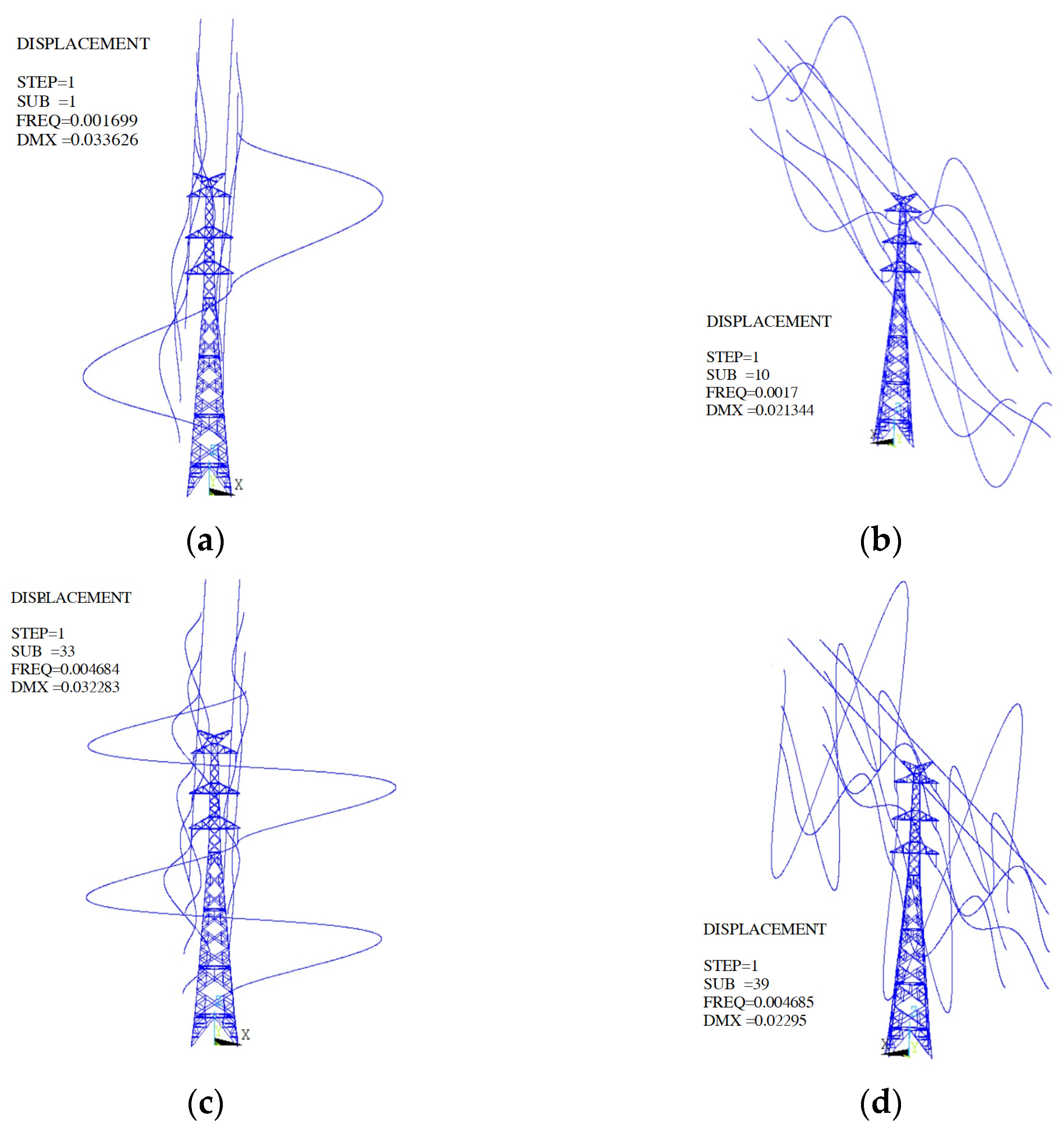
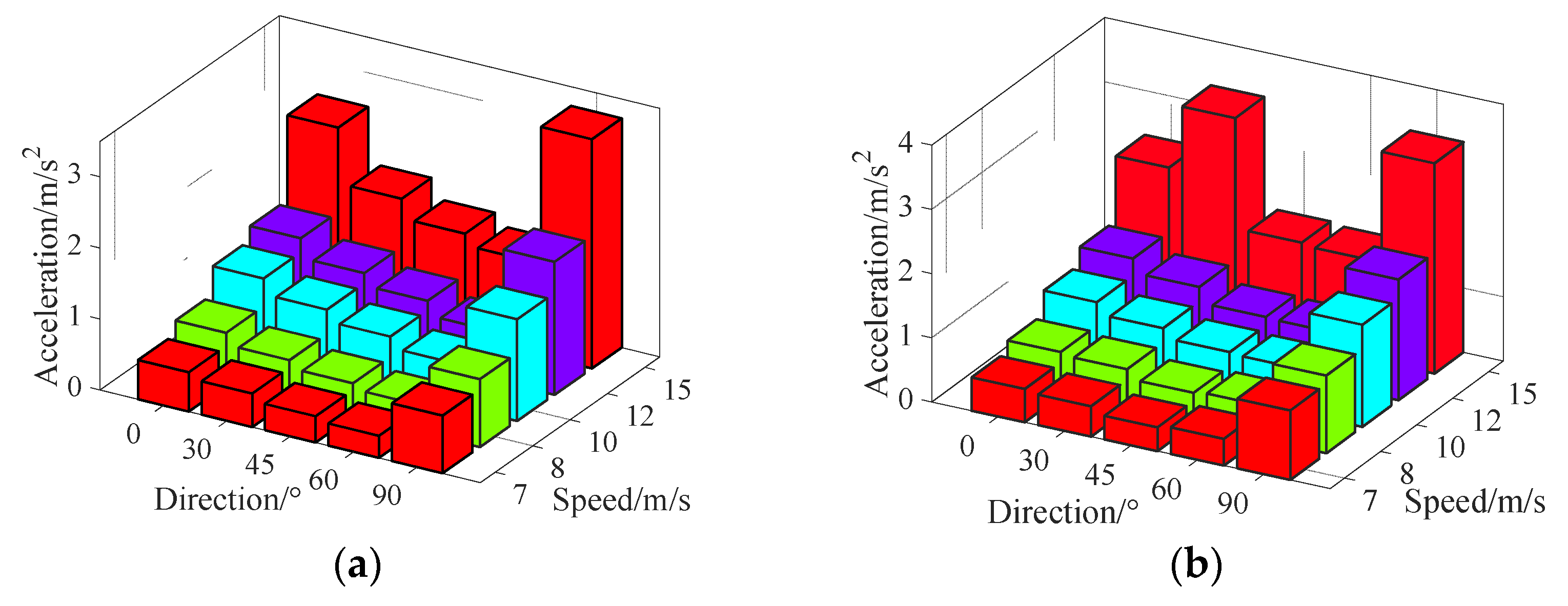
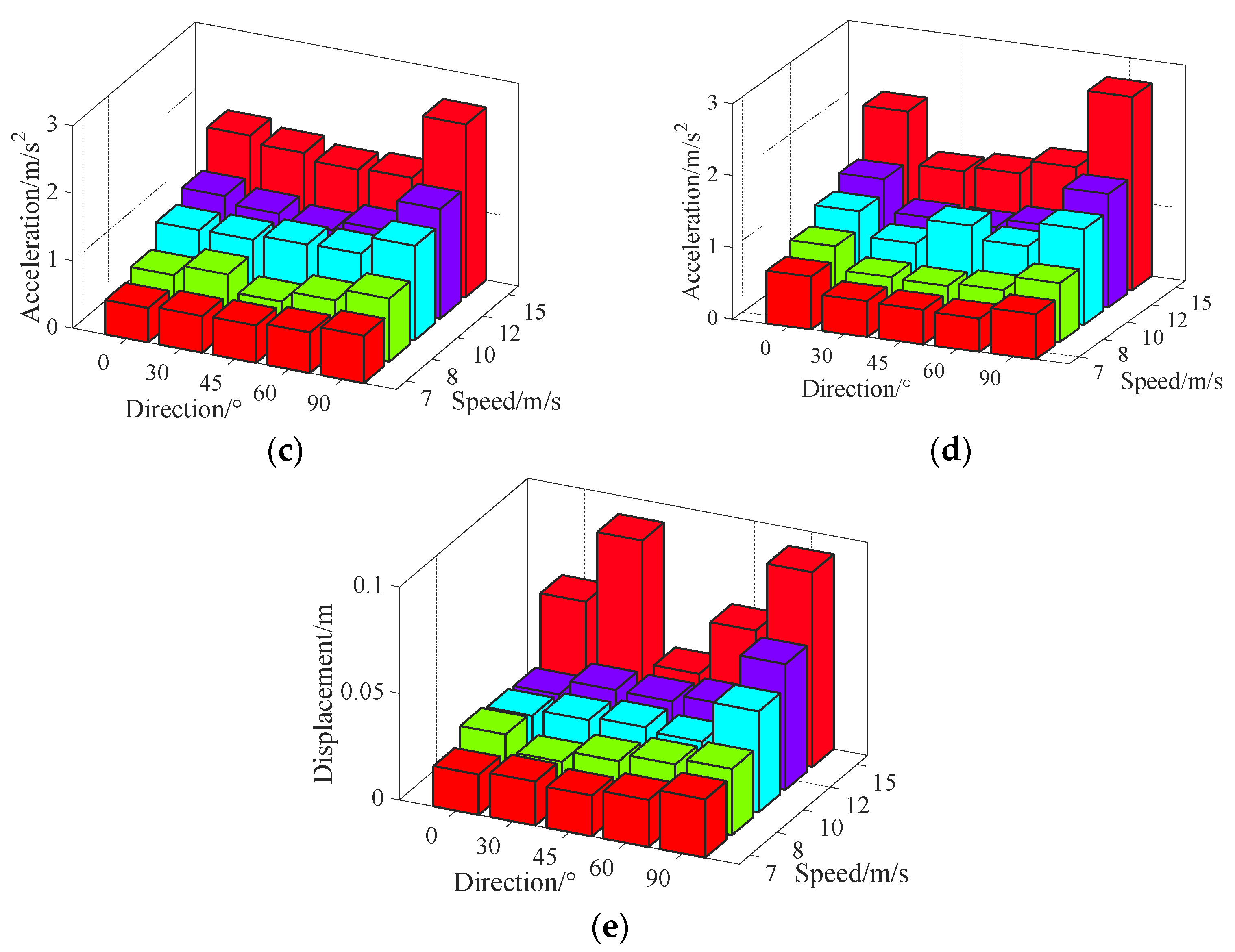
3.2. Mechanical Vibration
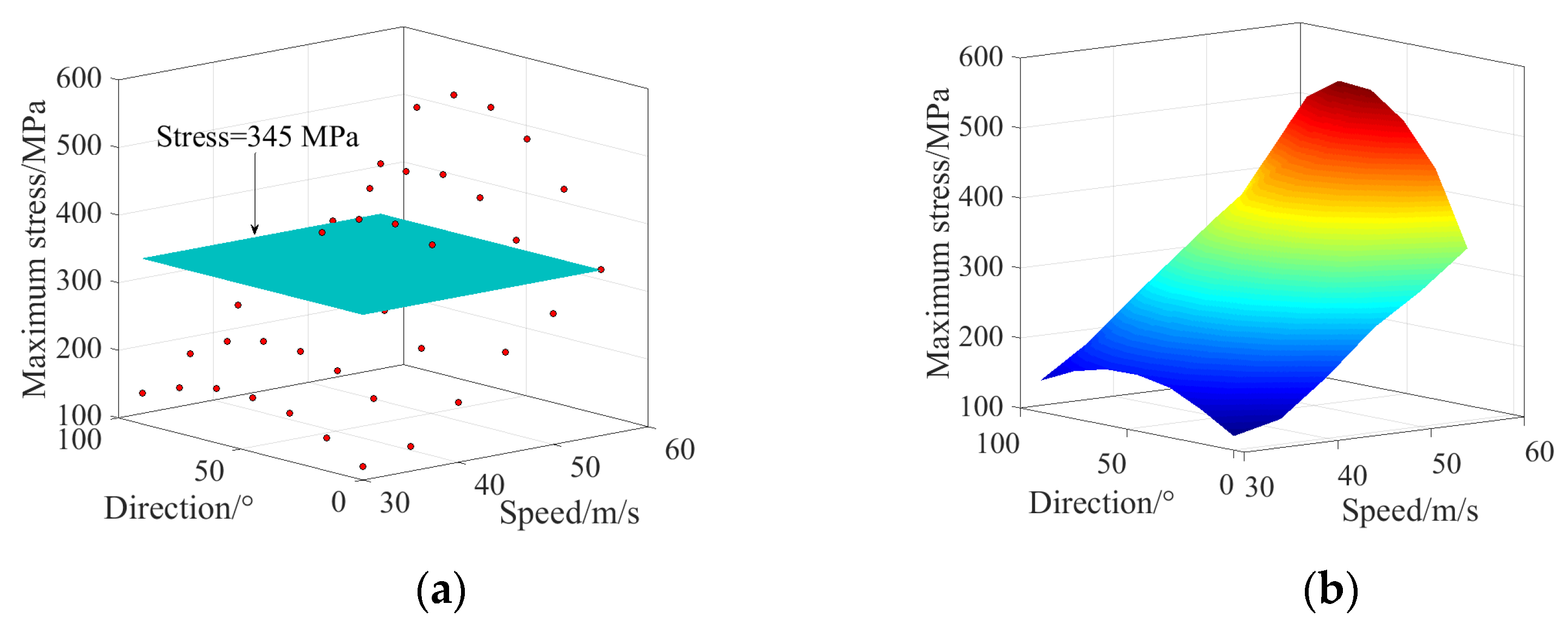
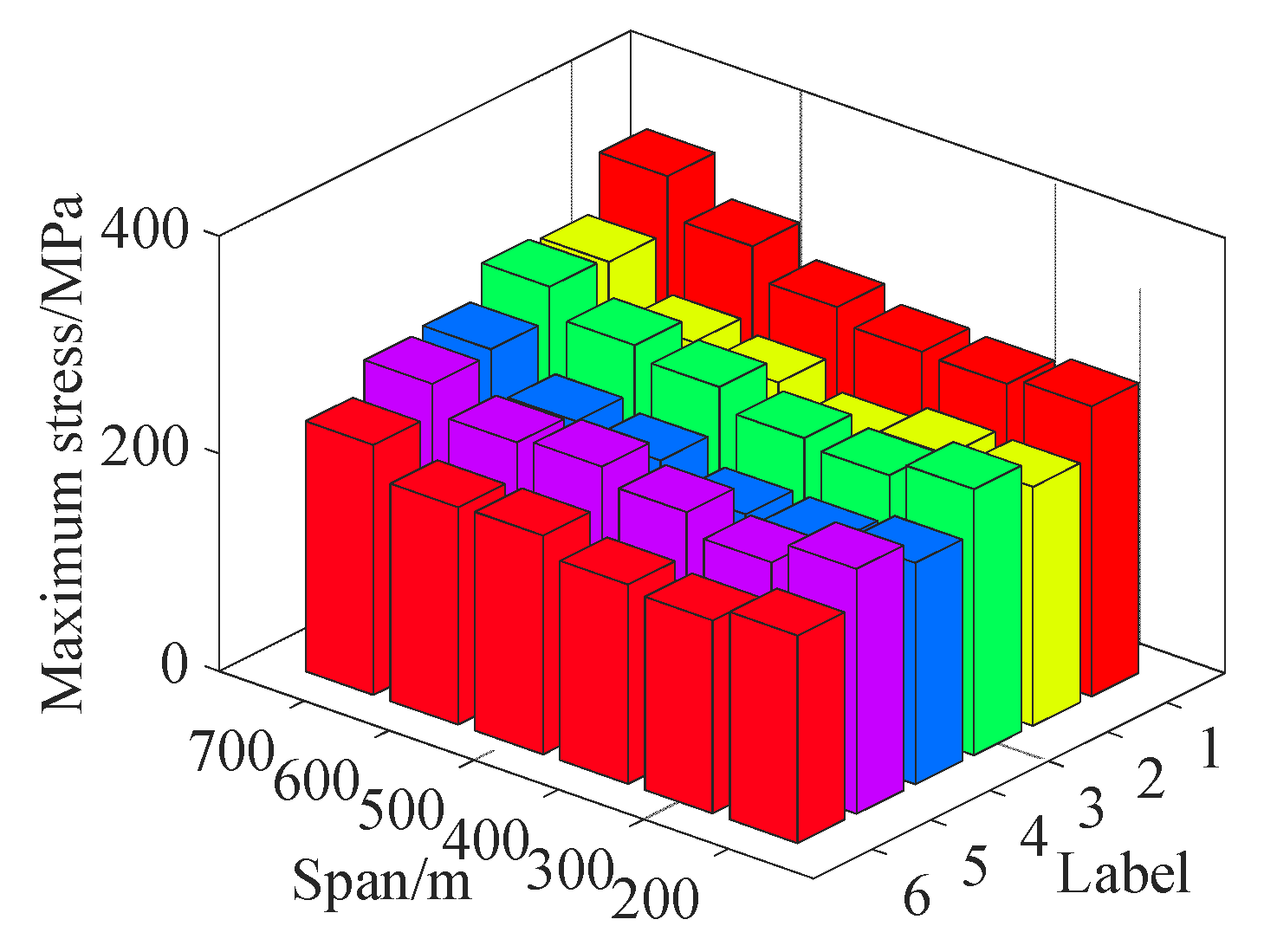
3.3. Damage Prediction
4. Anti-Wind Experiments
4.1. Scale Model and Similarity Criterion
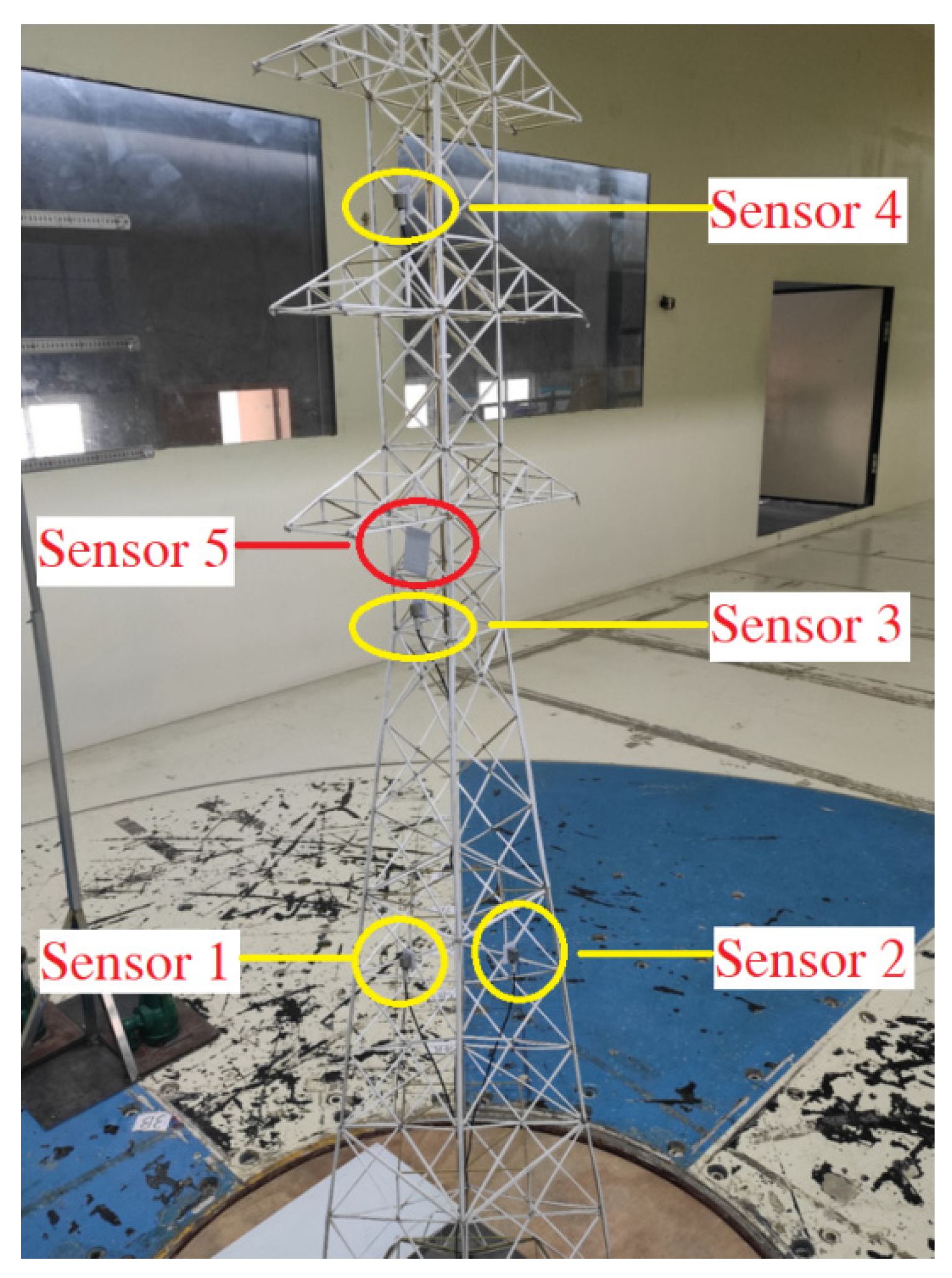
4.2. Anti-Wind Experimental Method and Device
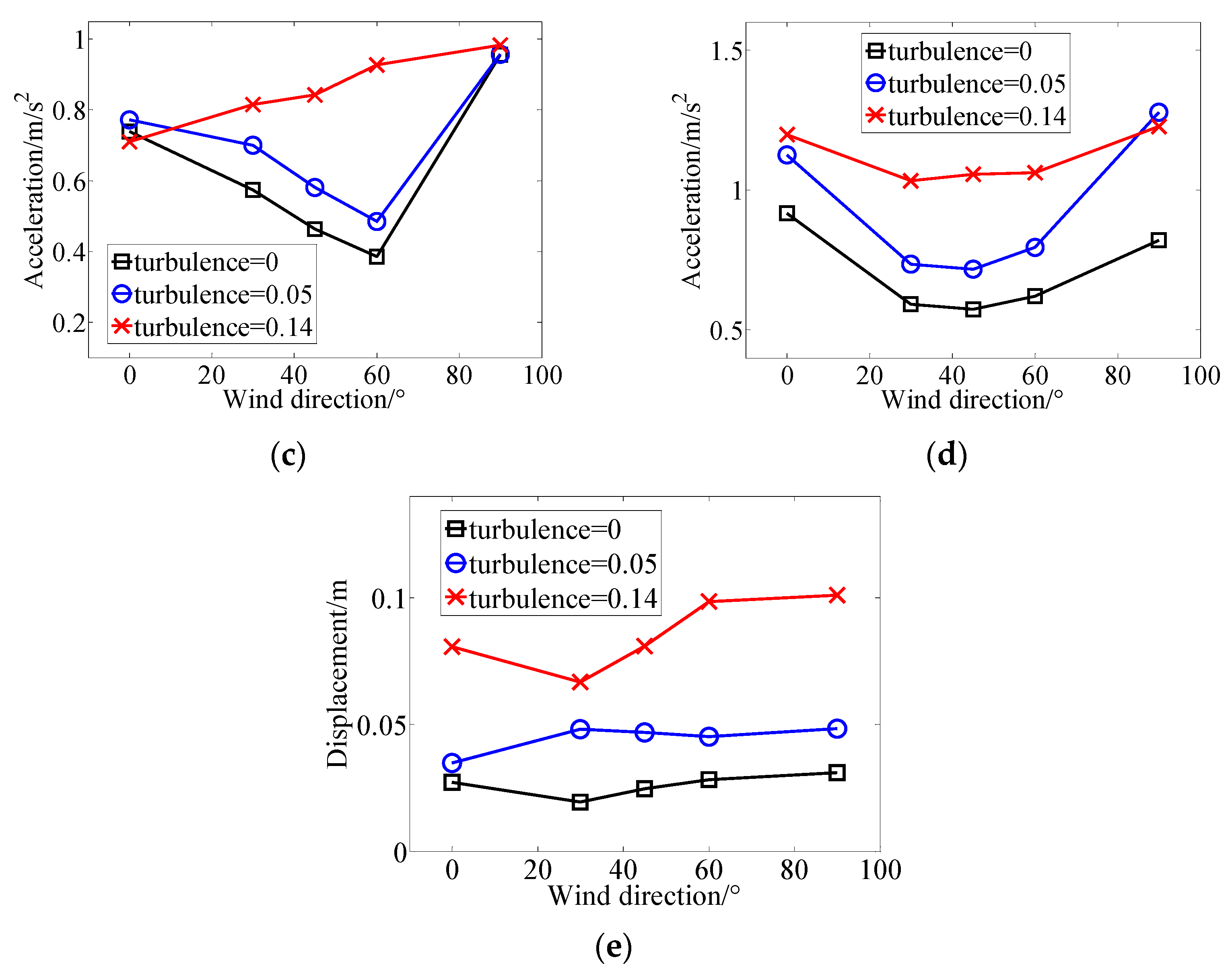
4.3. Experimental Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Zhang, Z.; An, L.; Pang, S. The study of wind resistance performance in coastal region tower based on transmission line system model. Electr. Power Sci. Eng. 2016, 32, 642–650. [Google Scholar]
- Hou, H.; Yu, J.; Huang, Y. Risk assessment of transmission line trip caused by wind age yaw under typhoon. High Volt. Eng. 2019, 45, 3907–3915. [Google Scholar]
- Soisuvarn, S.; Oudomying, S. Characterization of the Tropical Cyclones Wind Radii in the North Western Pacific Basin Using the ASCAT Winds Data Products. In Proceedings of the 2018 Progress in Electromagnetics Research Symposium (PIERS-Toyama), Toyama, Japan, 1–4 August 2018; pp. 1428–1433. [Google Scholar]
- Fenerci, A.; Øiseth, O.; Rønnquist, A. Long-term monitoring of wind field characteristics and dynamic response of a long-span suspension bridge in complex terrain. Eng. Struct. 2017, 147, 269–284. [Google Scholar] [CrossRef]
- Chen, X.; Zhong, L.; Li, M. Review on the research status of power system risk identification under typhoon disaster. Proceed Comput. Sci. 2019, 155, 780–784. [Google Scholar] [CrossRef]
- Zheng, Y.; Chun, X.; Wei, P. Analytical Study on Wind-Induced Vibration and its Control of Transmission Towers in Mountainous Area. Appl. Mech. Mater. 2012, 78, 1473–1478. [Google Scholar]
- Batts, M.E.; Cordes, M.R.; Russell, L.R. Hurricane wind speeds in the United States. J. Struct. Div. 1980, 106, 25–30. [Google Scholar] [CrossRef]
- Shapiro, J.L. The Asymmetric Boundary layer Flow Under a Translating Hurricane. J. Atmos. Sci. 1984, 40, 85–92. [Google Scholar] [CrossRef] [Green Version]
- Cardone, V.J.; Greenwood, C.V.; Greenwood, J.A. Unified Program for the Specification of Hurricane Boundary Layer Winds Over Surfaces of Specified Roughness. Ocean Weather 1992, 64, 285–290. [Google Scholar]
- Holland, G.J. An analytic model of the wind and pressure profiles in Hurricanes. Mon. Weather 1980, 108, 1212–1218. [Google Scholar] [CrossRef]
- Meng, Y.; Matsui, M.; Hibi, K. An analytical model for simulation of the wind field in a typhoon boundary layer. J. Wind Eng. Ind. Aerodyn. 1995, 56, 291–310. [Google Scholar] [CrossRef]
- Xie, R.; Wu, T.; Wang, Y. Adaptability research on typhoon wind-field model. J. Hefei Univ. Nat. Sci. 2014, 24, 84–88. [Google Scholar]
- Zhang, L.; Niu, H.; Qi, Q. Comparisons of several typhoon field models. Shanxi Archit. 2015, 41, 27–28. [Google Scholar]
- Battista, R.C.; Rodrigues, R.S.; Pfeil, M.S. Dynamic behavior and stability of transmission line towers under wind forces. J. Wind. Eng. Ind. Aerodyn. 2003, 91, 145–150. [Google Scholar] [CrossRef]
- Wu, X.; Peng, K.; Geng, L. Real-time online monitoring and evaluation of wind-induced vibration response of transmission tower in typhoon environment. Chin. J. Appl. Mech. 2018, 35, 328–332. [Google Scholar]
- Zhu, H.; Yang, Z. Numerical study on scale of high speed train model for wind tunnel testing. In Proceedings of the 2011 International Conference on Electrical and Control Engineering, Yichang, China, 16–18 September 2011; pp. 725–728. [Google Scholar]
- Guo, Y.; Sun, B.; Ye, Y. Wind tunnel test on aeroelastic model of long span transmission line system. J. Zhejiang Univ. 2007, 41, 1482–1486. [Google Scholar]
- Tian, L.; Wang, W.; Zeng, Y. Design study of an aero-elastic model of long span transmission tower-line system wind tunnel. Ind. Archit. 2017, 47, 74–78. [Google Scholar]
- Li, X.; Pan, Z.; She, J. A method for adjusting typhoon parameters. Adv. Mar. Sci. 1995, 2, 11–15. [Google Scholar]
- Wei, J. Analysis of Typhoon Characteristics and Wind-Induced Vibration Measurement of Super Tall Building; Harbin Institute of Technology: Harbin, China, 2019. [Google Scholar]
- Li, L. Study on Typhoon Fluctuating Wind Speed Spectrum Based on Near-Earth Observation; Harbin Institute of Technology: Harbin, China, 2008. [Google Scholar]


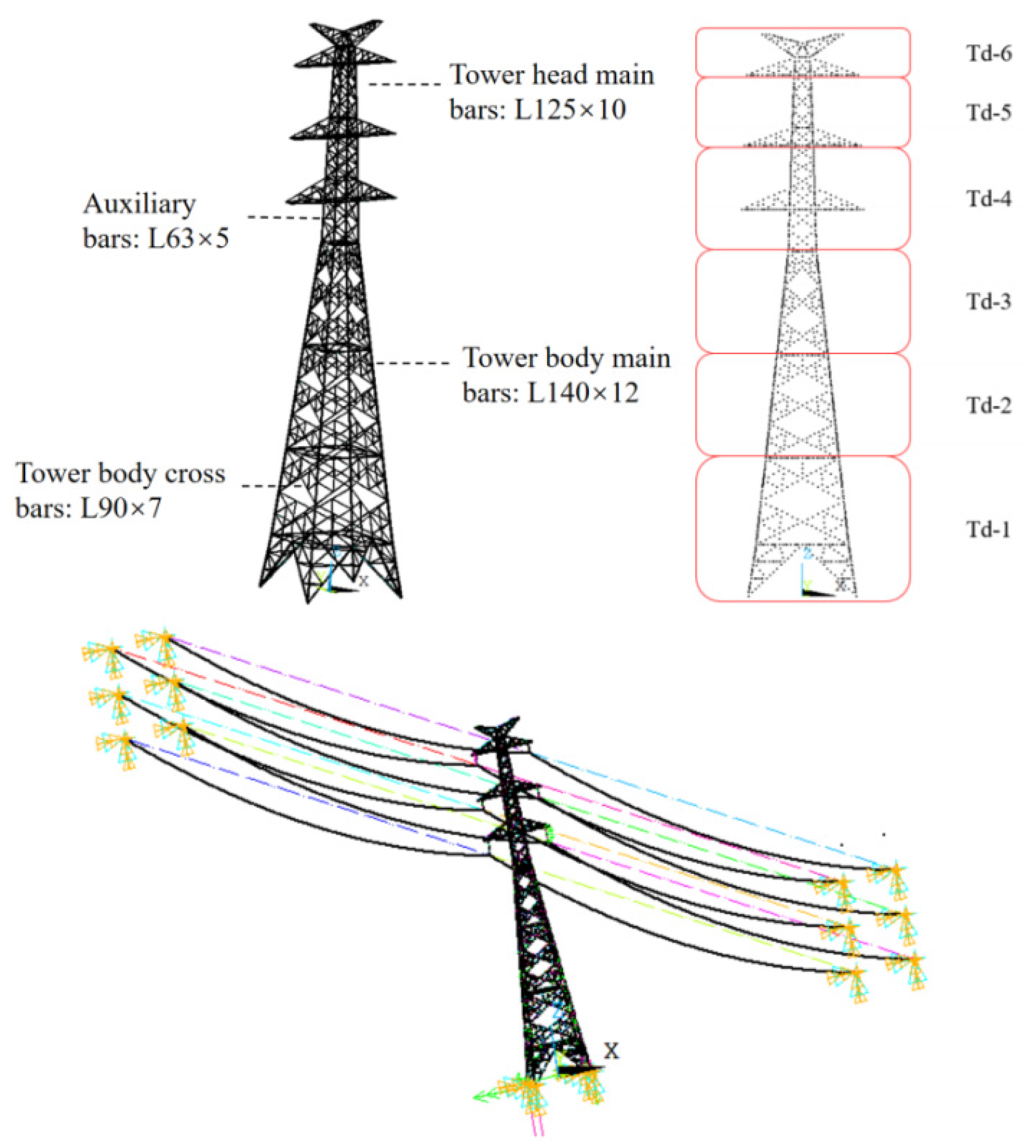





| Items | Value/Type | Items | Value/Type |
|---|---|---|---|
| Voltage level | 220 kV | Tower full height | 48.9 m |
| Tower | SZ631-33 | Cross-arm height | 33 m |
| Tower main bar | Q345 | Root width | 8.9 m |
| Tower auxiliary bar | Q235 | Tower simulation element | Beam188 |
| Line conductor | LGJ-300/25 | Line simulation element | Link180 |
| Grounding line | GJ-50 | Span between towers | 300 m |
| Tower pattern | Straight | Calculation type | Transient analysis |
| Line pattern | Suspended loop line |
| Items | Value | Items | Value | Items | Value |
|---|---|---|---|---|---|
| Time | 6:00, 4 October 2015 | Maximum wind speed | 46.8 m/s | Longitude | E110.45 |
| Pressure | 94.2 kPa | Cyclonic radius | 224.1 km | Latitude | N21.22 |
| Steady Wind | Transient Wind | |||
|---|---|---|---|---|
| Speed | Direction Angle | Speed m/s | Direction Angle | Turbulence |
| 7 m/s | 0° | 8 m/s | 0° | 0.05 |
| 8 m/s | 30° | 30° | 0.14 | |
| 10 m/s | 45° | 45° | / | |
| 12 m/s | 60° | 60° | / | |
| 15 m/s | 90° | 90° | / | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, R.; Xiang, C.; Jia, Z. Anti-Wind Experiments and Damage Prediction of Transmission Tower under Typhoon Conditions in Coastal Areas. Energies 2022, 15, 3372. https://doi.org/10.3390/en15093372
Guan R, Xiang C, Jia Z. Anti-Wind Experiments and Damage Prediction of Transmission Tower under Typhoon Conditions in Coastal Areas. Energies. 2022; 15(9):3372. https://doi.org/10.3390/en15093372
Chicago/Turabian StyleGuan, Ruiyang, Chuyuan Xiang, and Zhidong Jia. 2022. "Anti-Wind Experiments and Damage Prediction of Transmission Tower under Typhoon Conditions in Coastal Areas" Energies 15, no. 9: 3372. https://doi.org/10.3390/en15093372
APA StyleGuan, R., Xiang, C., & Jia, Z. (2022). Anti-Wind Experiments and Damage Prediction of Transmission Tower under Typhoon Conditions in Coastal Areas. Energies, 15(9), 3372. https://doi.org/10.3390/en15093372






