Prediction and Mitigation of Wind Farm Blockage Losses Considering Mesoscale Atmospheric Response
Abstract
1. Introduction
2. Theory
2.1. Farm-Scale Momentum Balance
2.2. Wind Extractability
2.3. Power and Thrust Coefficients
3. Methodology
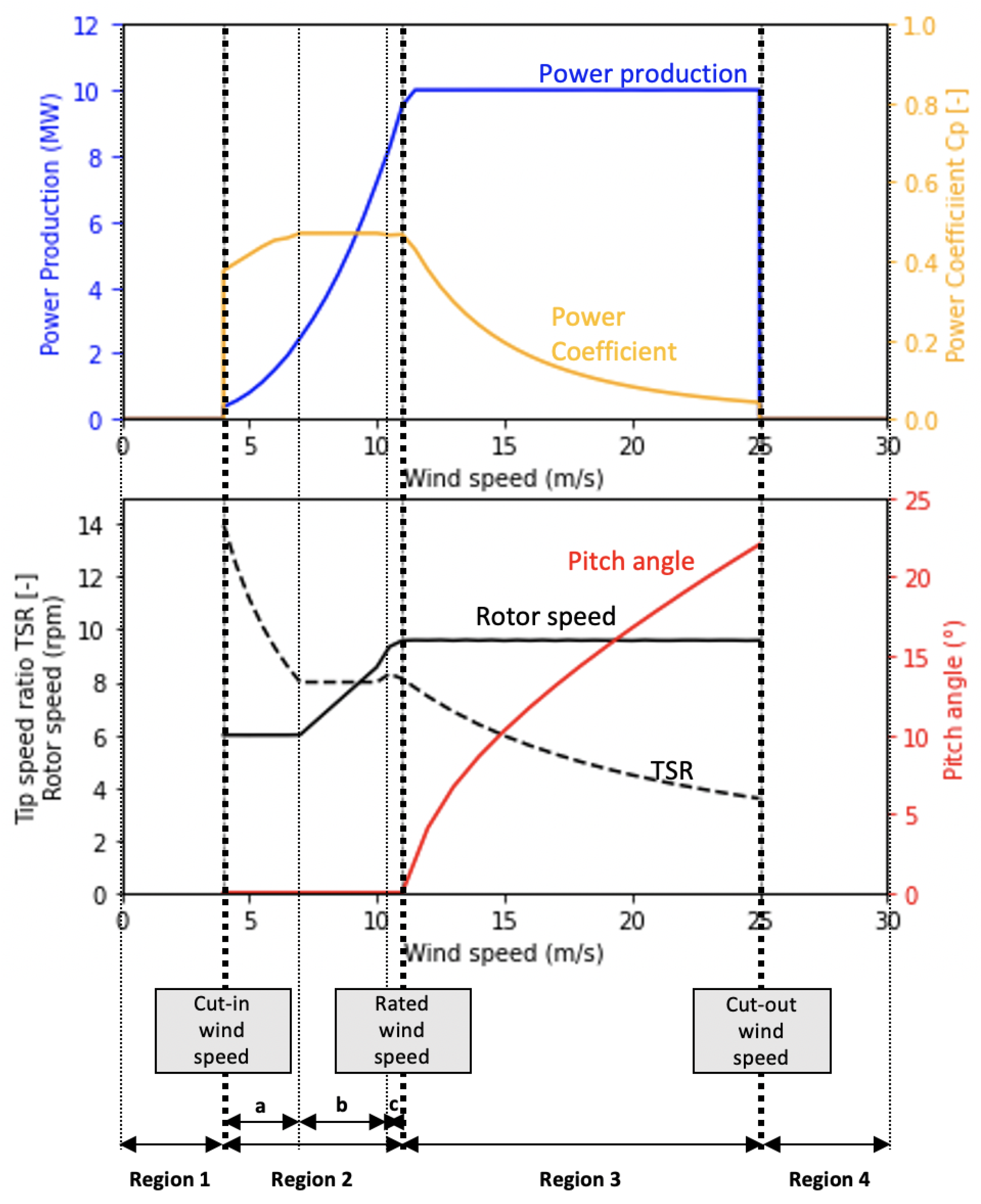
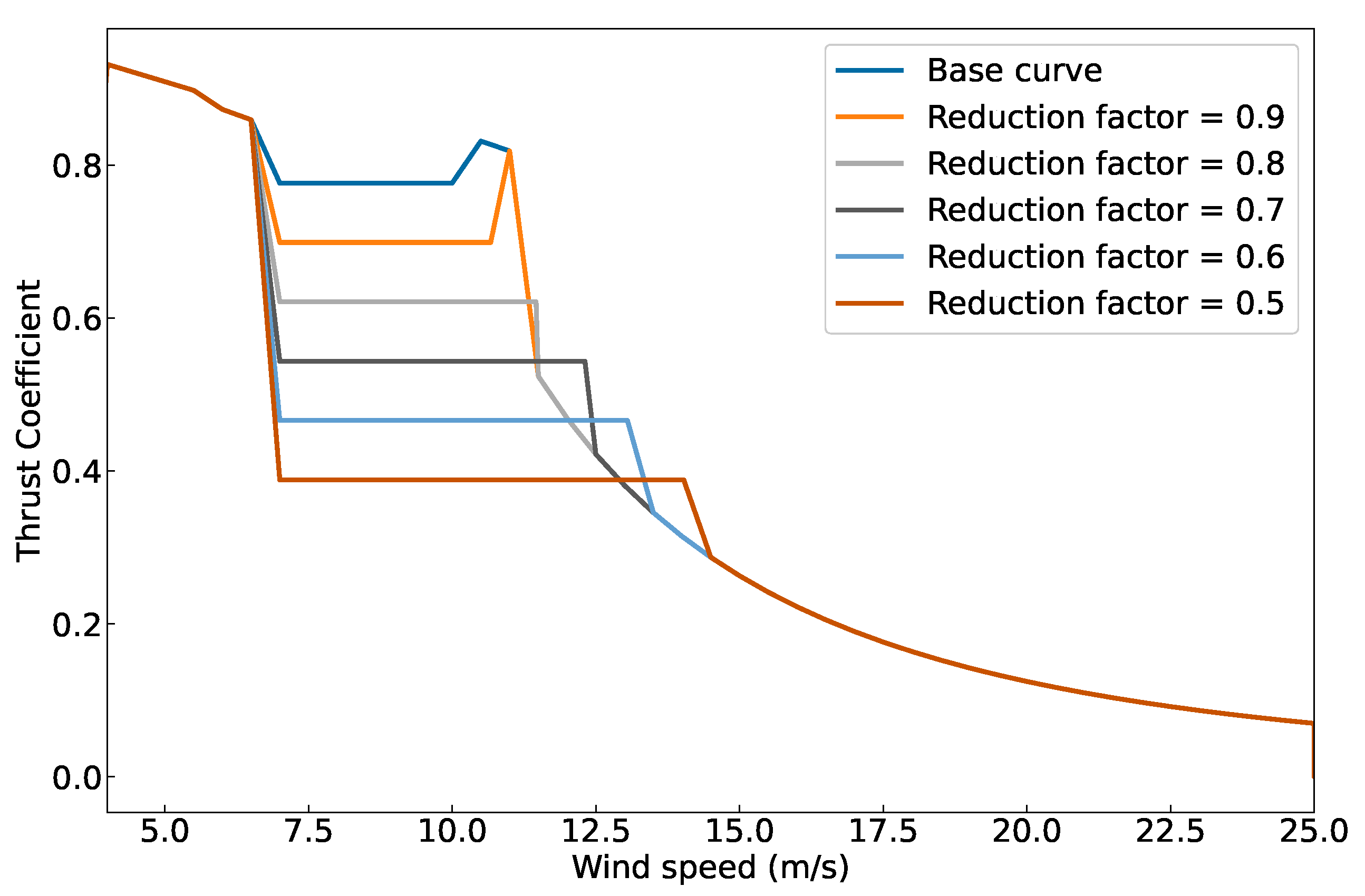
3.1. Load Control Strategy
3.2. Wind Turbine
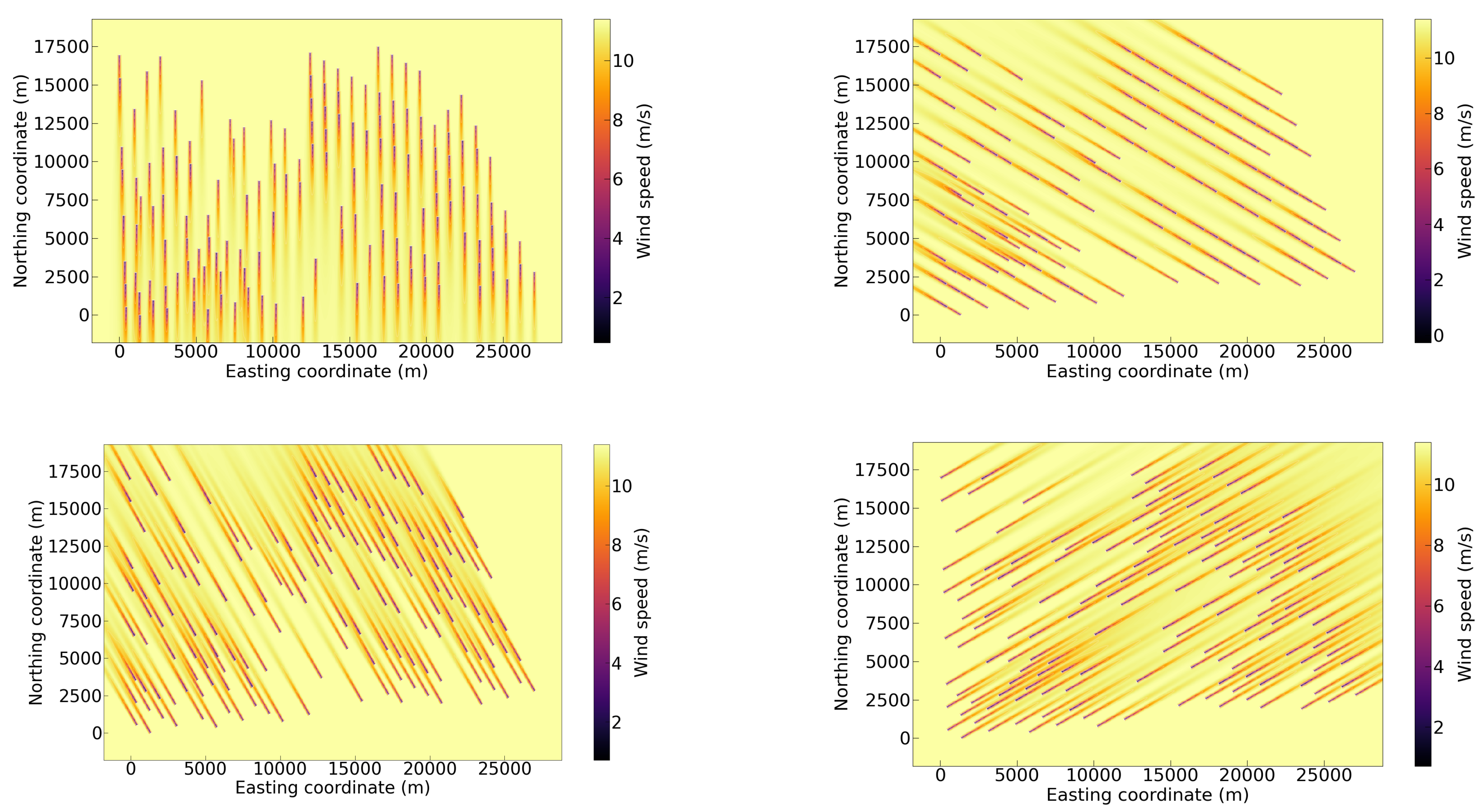
3.3. Wind Farm
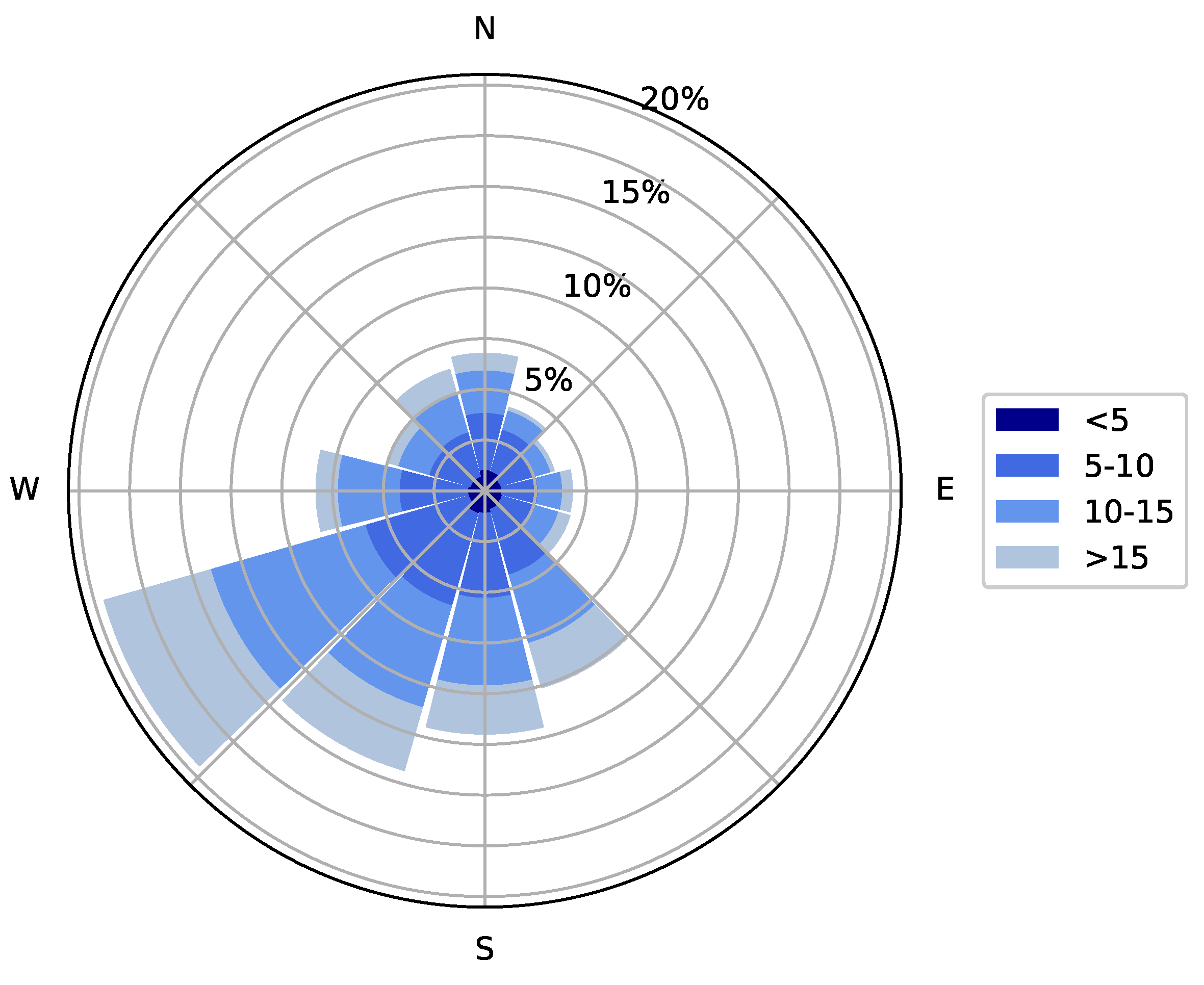
3.4. Wind Rose
3.5. FLORIS
3.6. AEP Calculation
4. Results
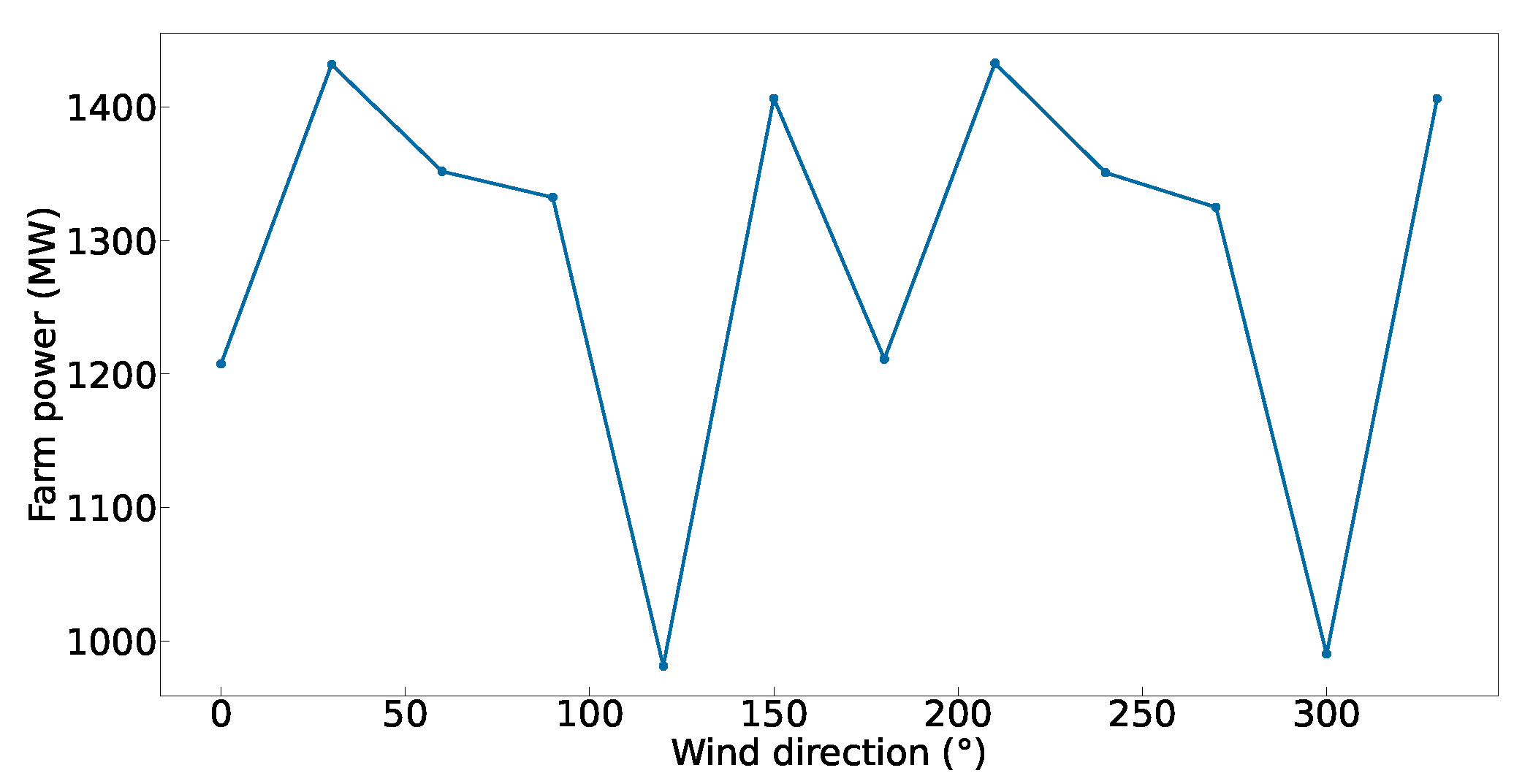
4.1. Case 0
4.2. Case A
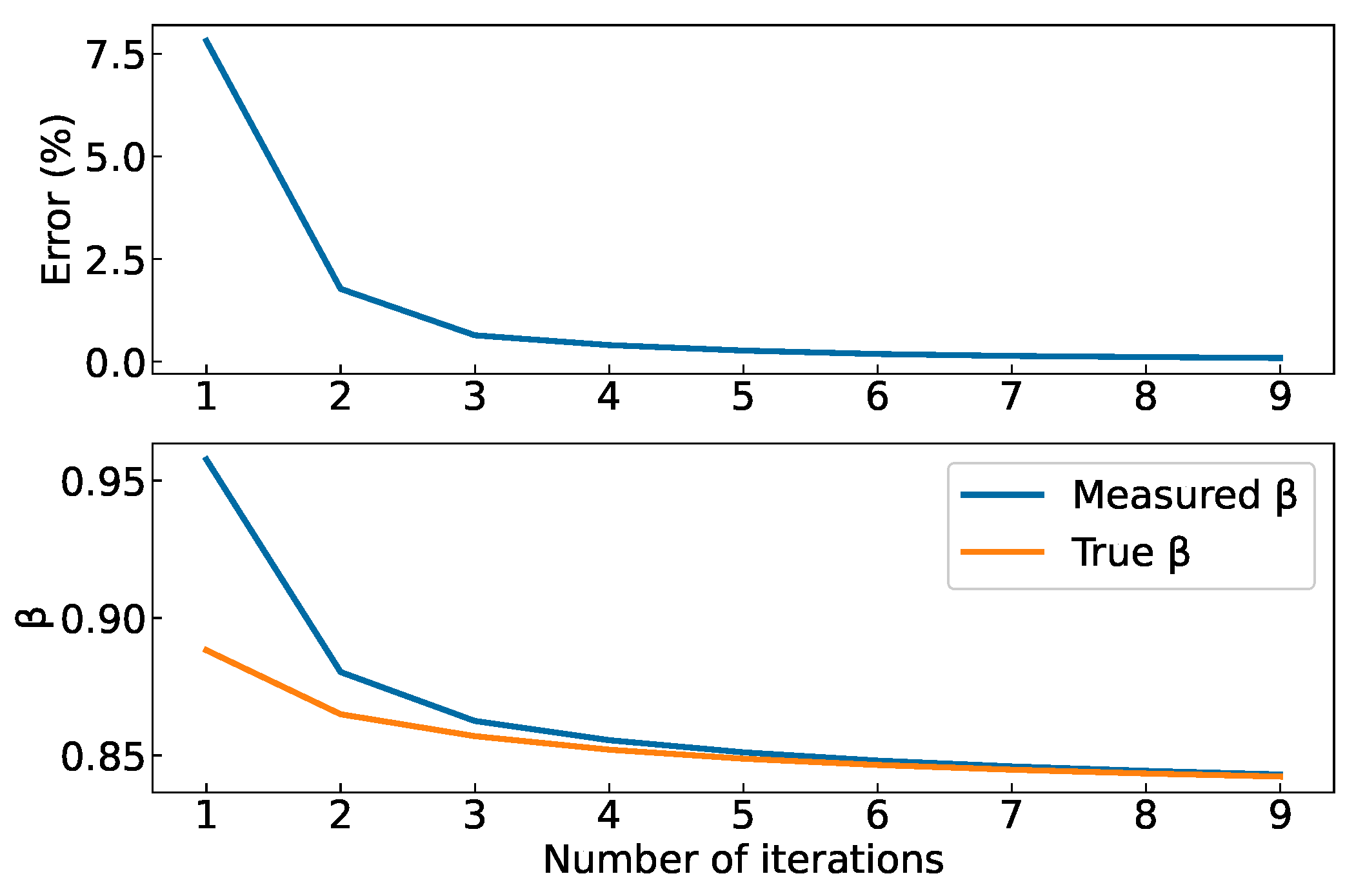
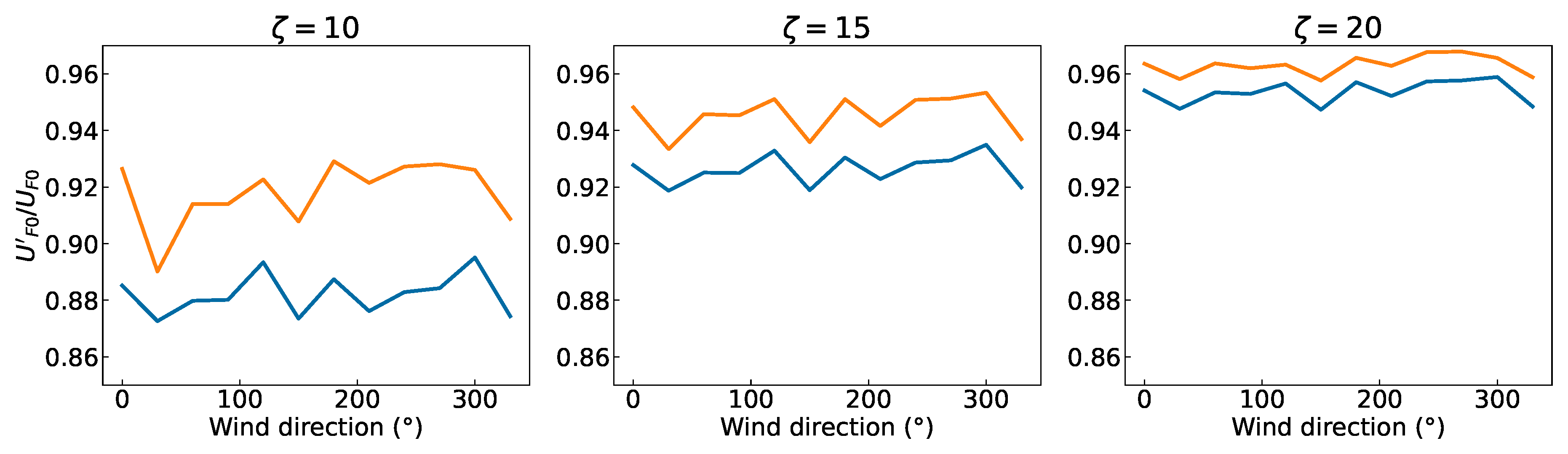
4.2.1. Correcting Farm-Upstream Wind Speed
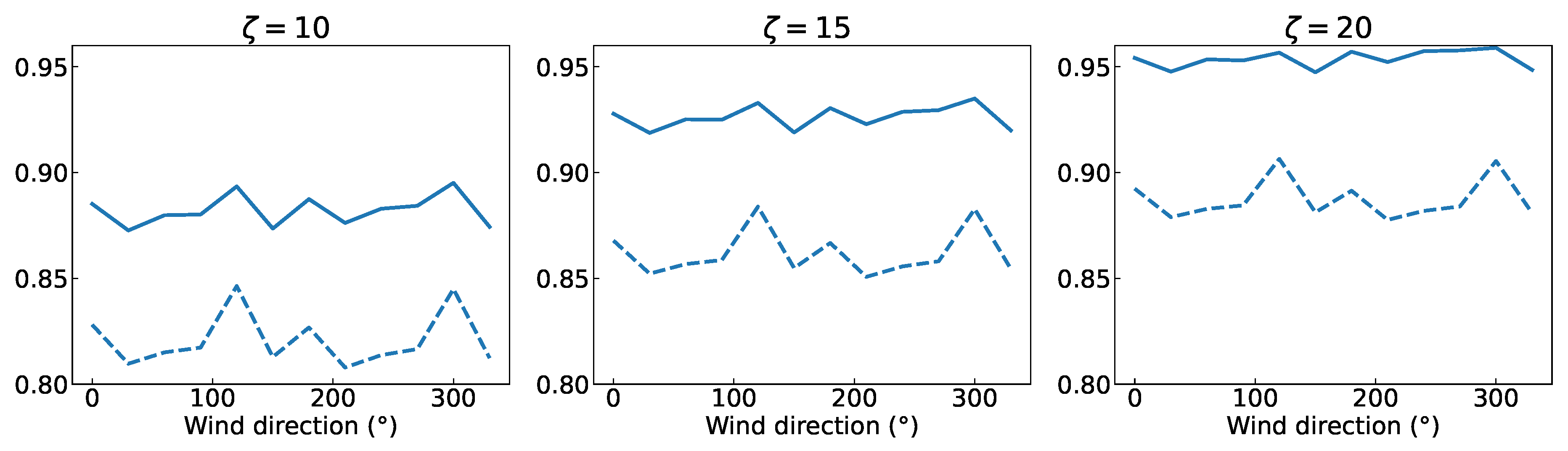
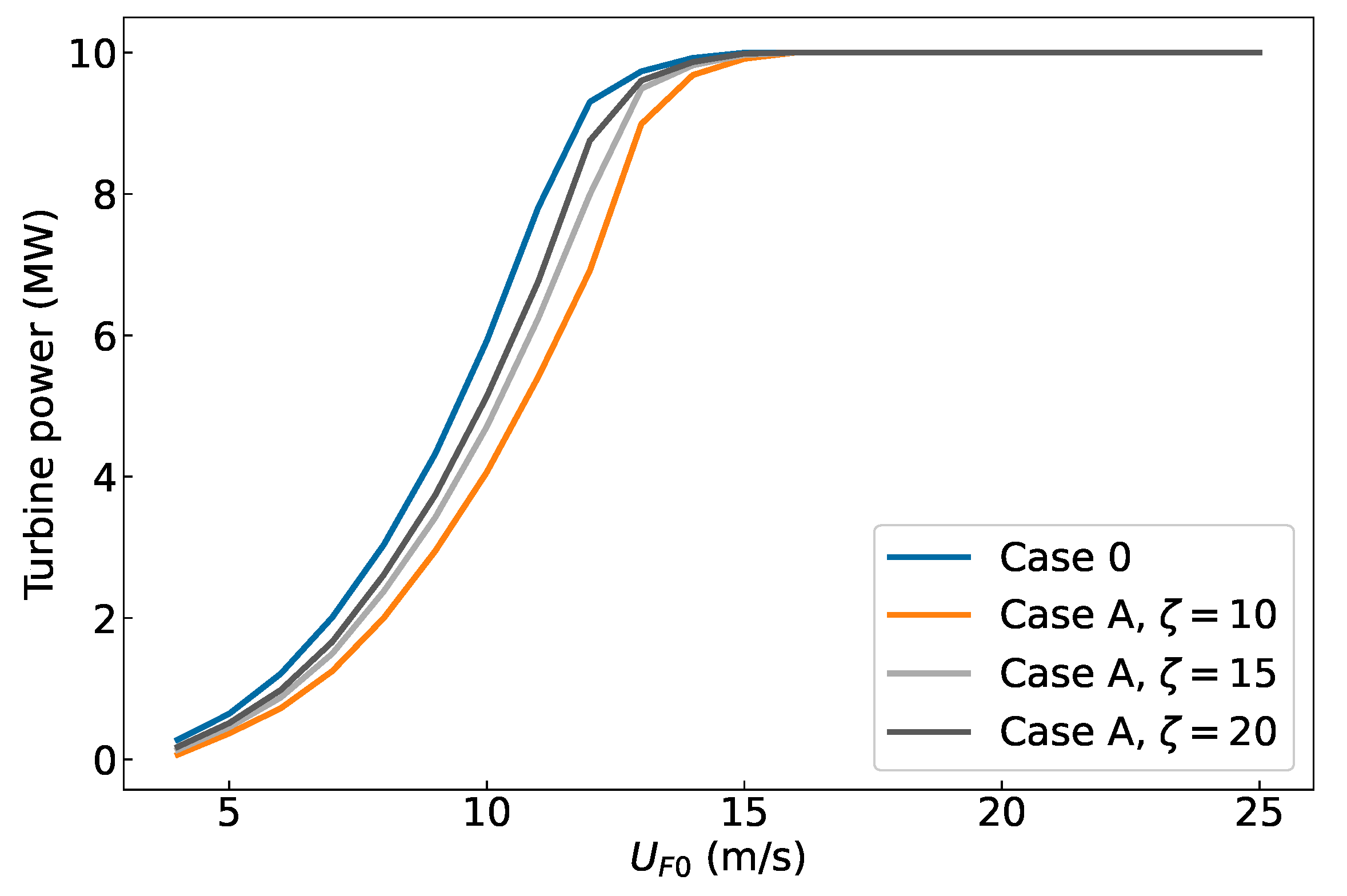
4.2.2. Results
4.3. Case B
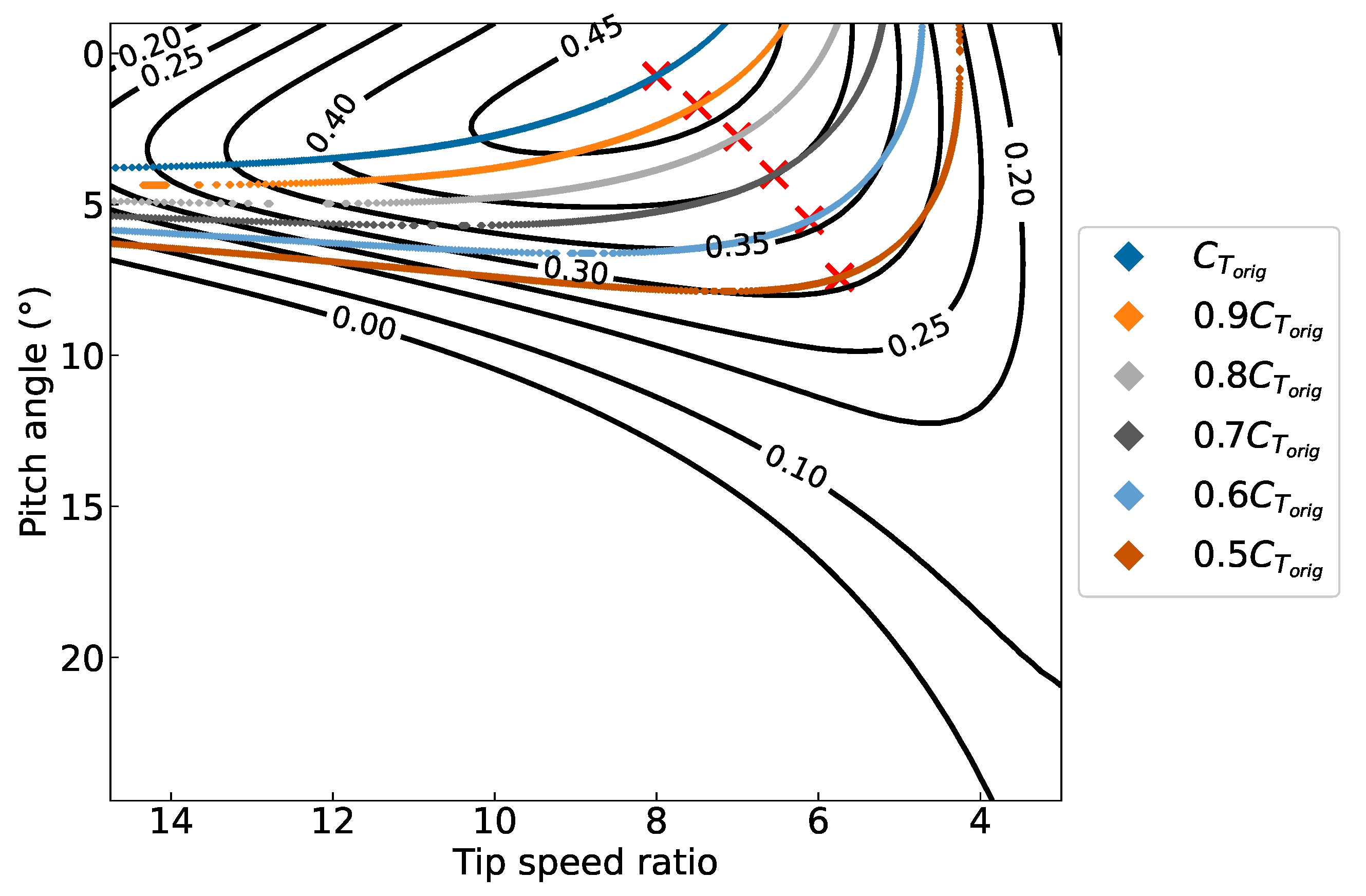
4.3.1. Re-Optimising Turbine Operating Conditions
4.3.2. Results
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ABL | Atmospheric boundary layer |
| AEP | Annual energy production |
| CV | Control volume |
| NDFM | Non-dimensional farm momentum |
| NWP | Numerical weather prediction |
| TSR | Tip-speed ratio |
References
- Department for Business, Energy and Industrial Strategy (BEIS). Energy Trends UK, October to December 2020 and 2021; Department for Business, Energy and Industrial Strategy (BEIS) of the Government of the UK: London, UK, 2022.
- Howland, M.F.; Lele, S.K.; Dabiri, J.O. Wind farm power optimization through wake steering. Proc. Natl. Acad. Sci. USA 2019, 116, 14495–14500. [Google Scholar] [CrossRef] [PubMed]
- Munters, W.; Meyers, J. Towards practical dynamic induction control of wind farms: Analysis of optimally controlled wind-farm boundary layers and sinusoidal induction control of first-row turbines. Wind Energy Sci. 2018, 3, 409–425. [Google Scholar] [CrossRef]
- Frederik, J.A.; Weber, R.; Cacciola, S.; Campagnolo, F.; Croce, A.; Bottasso, C.; van Wingerden, J.-W. Periodic dynamic induction control of wind farms: Proving the potential in simulations and wind tunnel experiments. Wind Energy Sci. 2020, 5, 245–257. [Google Scholar] [CrossRef]
- Zhang, M.; Arendshorst, M.G.; Stevens, R.J.A.M. Large eddy simulations of the effect of vertical staggering in large wind farms. Wind Energy 2019, 22, 189–204. [Google Scholar] [CrossRef]
- Chatterjee, T.; Peet, Y. Exploring the benefits of vertically staggered wind farms: Understanding the power generation mechanisms of turbines operating at different scales. Wind Energy 2019, 22, 283–301. [Google Scholar] [CrossRef]
- Meyers, J.; Bottasso, C.; Dykes, K.; Fleming, P.; Gebraad, P.; Giebel, G.; Göçmen, T.; van Wingerden, J.-W. Wind farm flow control: Prospects and challenges. Wind Energy Sci. 2022, 7, 2271–2306. [Google Scholar] [CrossRef]
- Bleeg, J.; Purcell, M.; Ruisi, R.; Traiger, E. Wind farm blockage and the consequences of neglecting its impact on energy production. Energies 2018, 11, 1609. [Google Scholar] [CrossRef]
- Nishino, T.; Dunstan, T.D. Two-scale momentum theory for time-dependent modelling of large wind farms. J. Fluid Mech. 2020, 894, A2. [Google Scholar] [CrossRef]
- Branlard, E.; Meyer Forsting, A.R. Assessing the blockage effect of wind turbines and wind farms using an analytical vortex model. Wind Energy 2020, 23, 2068–2086. [Google Scholar] [CrossRef]
- Segalini, A. An analytical model of wind-farm blockage. J. Renew. Sustain. Energy 2021, 13, 033307. [Google Scholar] [CrossRef]
- Patel, K.; Dunstan, T.D.; Nishino, T. Time-dependent upper limits to the performance of large wind farms due to mesoscale atmospheric response. Energies 2021, 14, 6437. [Google Scholar] [CrossRef]
- Kirby, A.; Nishino, T.; Dunstan, T.D. Two-scale interaction of wake and blockage effects in large wind farms. J. Fluid Mech. 2022, 953, A39. [Google Scholar] [CrossRef]
- Lanzilao, L.; Meyers, J. Set-point optimization in wind farms to mitigate effects of flow blockage induced by atmospheric gravity waves. Wind Energy Sci. 2021, 6, 247–271. [Google Scholar] [CrossRef]
- Allaerts, D.; Meyers, J. Sensitivity and feedback of wind-farm-induced gravity waves. J. Fluid Mech. 2019, 862, 990–1028. [Google Scholar] [CrossRef] [PubMed]
- HAWC2. DTU 10-MW Reference Wind Turbine. Available online: https://www.hawc2.dk/Download/HAWC2-Model/DTU-10-MW-Reference-Wind-Turbine (accessed on 25 March 2022).
- GitHub. Cp-Ct-Cq Table for Control. Available online: https://github.com/Seager1989/DTU10MW_FAST_LIN/blob/main/Cp_Ct_Cq.DTU10MW.txt (accessed on 25 March 2022).
- Marine Scotland. Seagreen Offshore Wind Farm. Available online: https://marine.gov.scot/sites/default/files/owf_dslp.pdf (accessed on 26 March 2022).
- NREL. FLORIS: FLOw Redirection and Induction in Steady State. Available online: https://www.nrel.gov/wind/floris.html (accessed on 26 March 2022).
- Niayifar, A.; Porté-Agel, F. Analytical modeling of wind farms: A new approach for power prediction. Energies 2016, 9, 741. [Google Scholar] [CrossRef]
- Crespo, A.; Hernandez, J. Turbulence characteristics in wind-turbine wakes. J. Wind Eng. Ind. Aerodyn. 1996, 61, 71–85. [Google Scholar] [CrossRef]






| Parameters | Values |
|---|---|
| Rated power | 10 MW |
| Rated wind speed (for Cases 0 and A) | 11.4 m/s |
| Cut-in wind speed | 4.0 m/s |
| Cut-out wind speed | 25.0 m/s |
| Rotor diameter | 178.3 m |
| Hub height | 119.0 m |
| Models/Parameters | Values/References |
|---|---|
| Wake model | Niayifar & Porté-Agel [20] |
| Wake growth rate () | 0.38I + 0.004 |
| Turbulence intensity model | Crespo & Hernandez [21] |
| Superposition method | Sum of squares freestream superposition |
| Number of grid points for | 3 × 3 (for each rotor) |
| Number of grid points for | 250 × 160 |
| Air density | 1.225 kg/m |
| Median Number of Iterations | Max. Number of Iterations | |
|---|---|---|
| 10 | 3 | 9 |
| 15 | 3 | 5 |
| 20 | 2 | 5 |
| AEP [GWh] | Reduction from Case 0 [%] | |
|---|---|---|
| 10 | 6243 | 15.4 |
| 15 | 6685 | 9.4 |
| 20 | 6957 | 5.7 |
| AEP [GWh] | Reduction from Case 0 [%] | Improvement from Case A [%] | |
|---|---|---|---|
| 10 | 6367 | 13.7 | 2.0 |
| 15 | 6759 | 8.4 | 1.1 |
| 20 | 7000 | 5.1 | 0.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Legris, L.; Pahus, M.L.; Nishino, T.; Perez-Campos, E. Prediction and Mitigation of Wind Farm Blockage Losses Considering Mesoscale Atmospheric Response. Energies 2023, 16, 386. https://doi.org/10.3390/en16010386
Legris L, Pahus ML, Nishino T, Perez-Campos E. Prediction and Mitigation of Wind Farm Blockage Losses Considering Mesoscale Atmospheric Response. Energies. 2023; 16(1):386. https://doi.org/10.3390/en16010386
Chicago/Turabian StyleLegris, Leila, Morten Lindholt Pahus, Takafumi Nishino, and Edgar Perez-Campos. 2023. "Prediction and Mitigation of Wind Farm Blockage Losses Considering Mesoscale Atmospheric Response" Energies 16, no. 1: 386. https://doi.org/10.3390/en16010386
APA StyleLegris, L., Pahus, M. L., Nishino, T., & Perez-Campos, E. (2023). Prediction and Mitigation of Wind Farm Blockage Losses Considering Mesoscale Atmospheric Response. Energies, 16(1), 386. https://doi.org/10.3390/en16010386







