Modern Bitumen Oil Mixture Models in Ashalchinsky Field with Low-Viscosity Solvent at Various Temperatures and Solvent Concentrations
Abstract
1. Introduction
2. Materials and Methods
2.1. Rheological Properties of Bituminous Oil
- (1)
- Nonlinear viscous liquids (shear stress is a nonlinear function of the shear rate);
- (2)
- Fluid with non-stationary rheological characteristics (the functional dependence between the shear stress and the shear rate depends on the time or history of the process);
- (3)
- Viscoelastic liquids (exhibit elastic recovery of shape after stress relief).
2.2. Analysis of Foreign Experience in Calculating the Viscosity of Oil Mixtures
2.3. Experimental Apparatus and Procedure
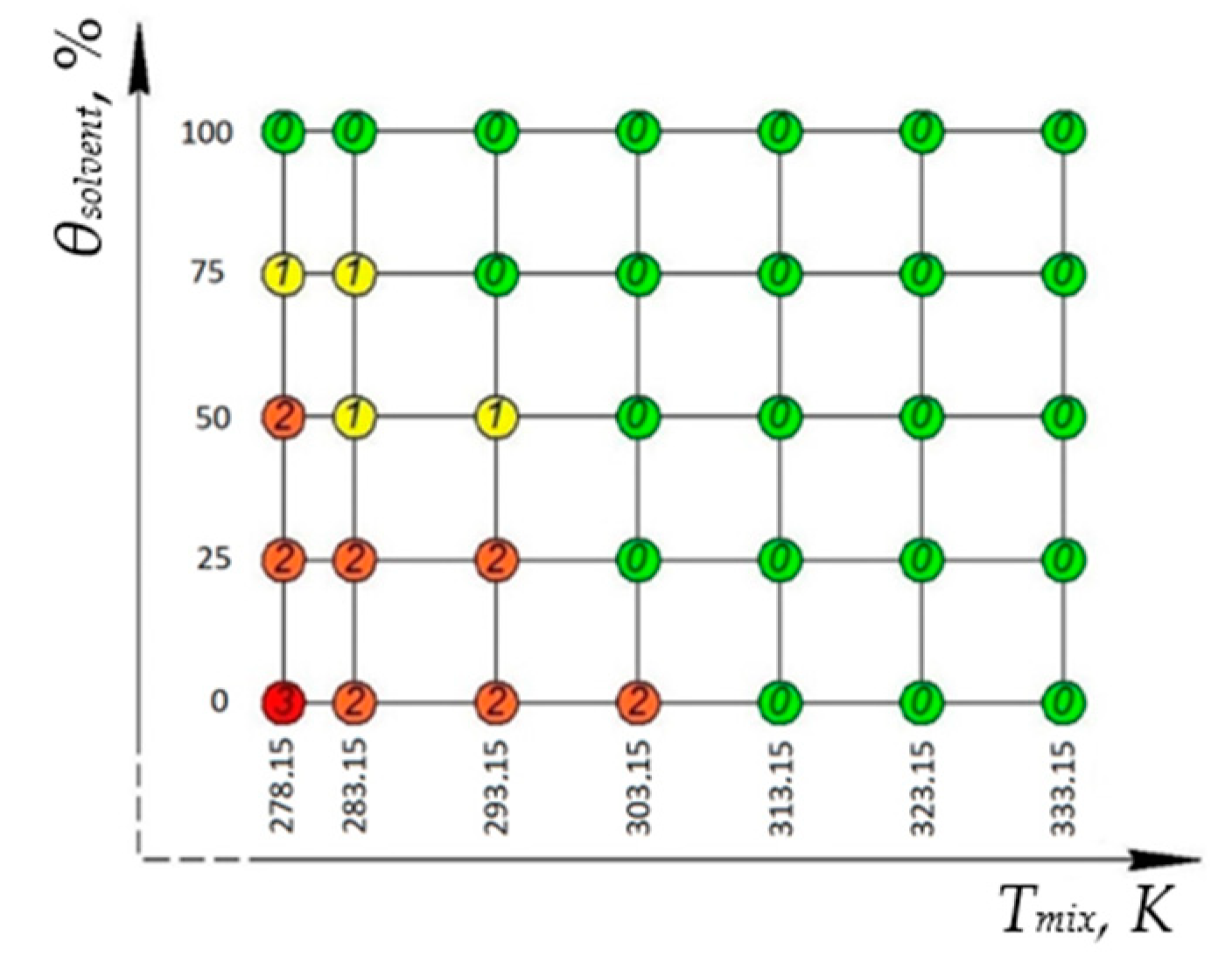
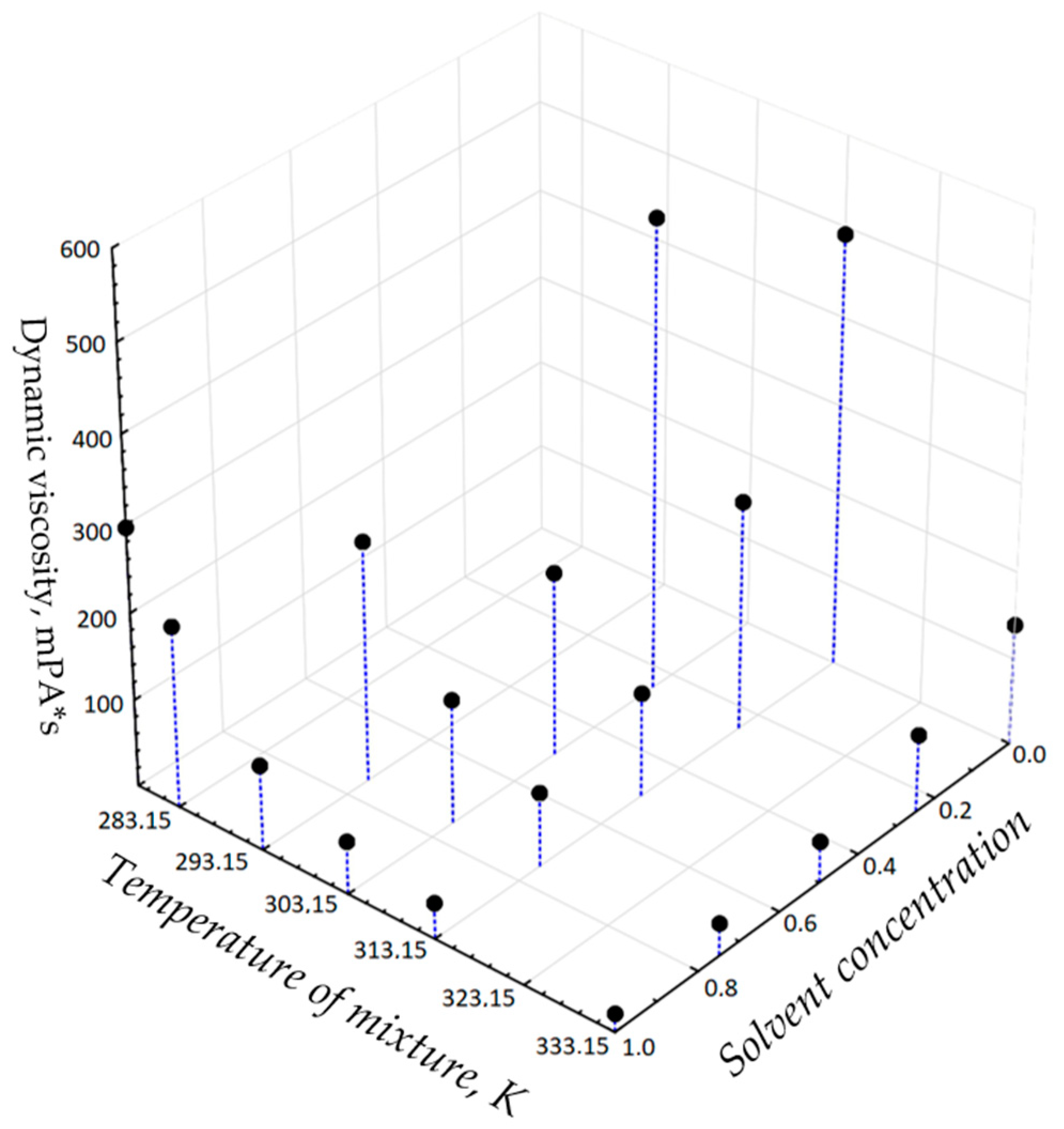
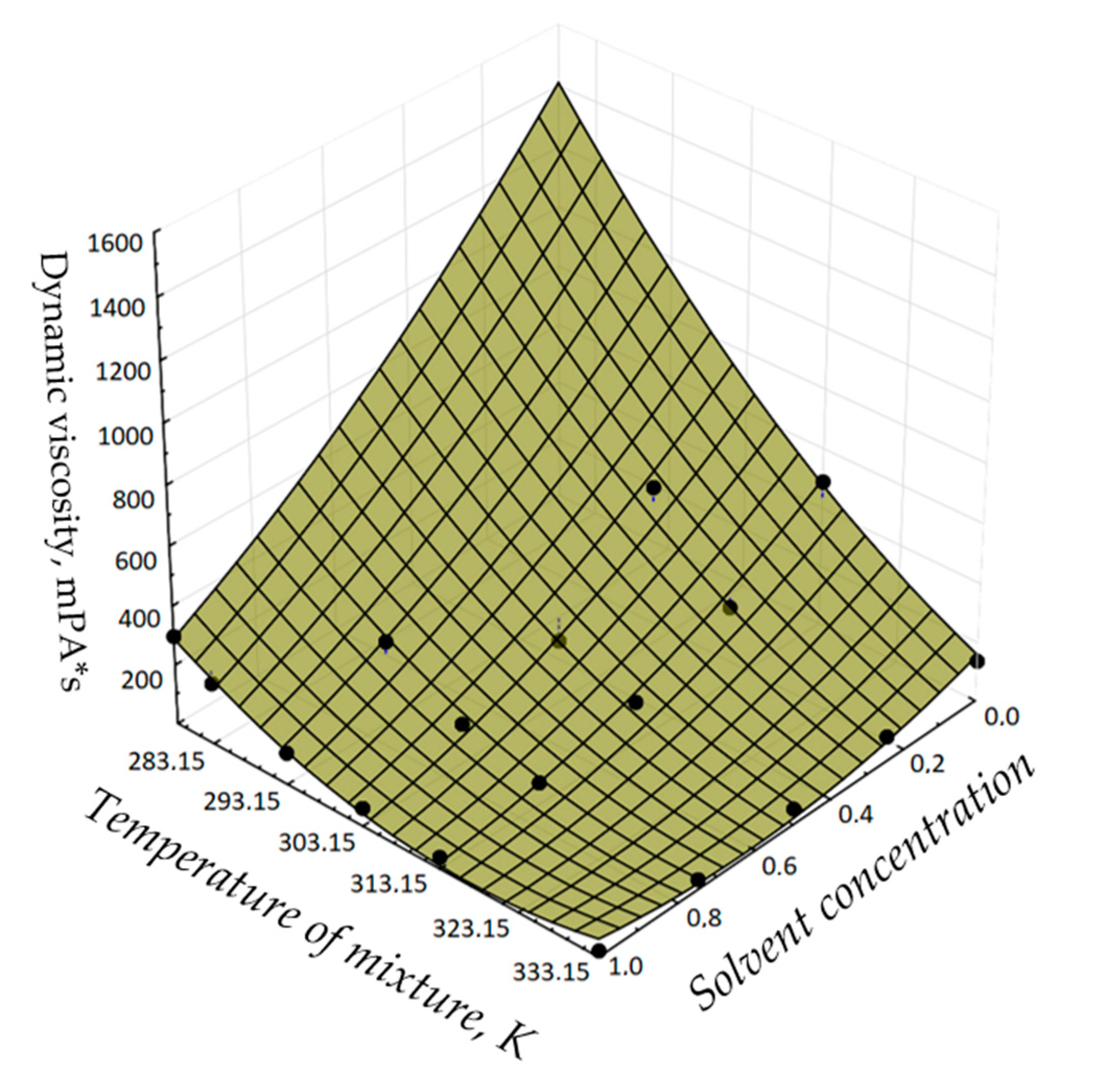
3. Results
- 0—Newton model;
- 1—Ostwald de Waele model or power-law;
- 2—Ellis fluid model;
- 3—Carreau model.
4. Conclusions
- A detailed analysis of rheological models of non-Newtonian fluids is performed. Due to a number of assumptions in existing rheological models (a limited number of rheological models, variability in model coefficients, etc.), it is proposed to supplement the standard list of rheological models with the Carreau model and the Ellis fluid model.
- Complex experimental studies on rheological models of bituminous oil and a solvent (which is a low-viscosity carbon oil) mixture are carried out on the example of the Ashalchinsky field. On the basis of the conducted studies, a two-dimensional field of rheological models of the oil mixture is built, which allows for determining the rheological model of the pumped oil mixture depending on the concentration of the solvent and the temperature of the mixture, as at the design stage, and during the operational phase of the facility. This approach can be used successfully in other fields to improve the efficiency of oil transportation.
- Formulas for predicting the rheological properties of the oil mixture on the basis of statistical processing of the results of experimental studies are theoretically substantiated. It is proven that the viscosity of binary oil mixtures in the Newtonian fluid field should be determined by a modified Arrhenius equation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| τ | shear stress (Pa) |
| μ | coefficient of dynamic viscosity (Pa∙s) |
| V | velocity (m/s) |
| shear rate (s−1) | |
| Ρ | density (kg/m3) |
| T | temperature (K) |
| Ν | kinematic viscosity coefficient (m2/s) |
References
- Longley, H. Conflicting Interests: Development Politics and the Environmental Regulation of the Alberta Oil Sands Industry, 1970–1980. Environ. Hist. 2021, 27, 97–125. [Google Scholar] [CrossRef]
- Hart, A. A review of technologies for transporting heavy crude oil and bitumen via pipelines. J. Pet. Explor. Prod. Technol. 2013, 4, 327–336. [Google Scholar] [CrossRef]
- Bekibayev, T.T.; Zhapbasbayev, U.K.; Ramazanova, I.G. Optimization of oil-mixture “hot” pumping in main oil pipelines. J. Physics Conf. Ser. 2017, 894, 012127. [Google Scholar] [CrossRef]
- Yaseen, M.; Rawat, S.K.; Kumar, M. Cattaneo–Christov heat flux model in Darcy–Forchheimer radiative flow of MoS2–SiO2/kerosene oil between two parallel rotating disks. J. Therm. Anal. Calorim. 2022, 147, 10865–10887. [Google Scholar] [CrossRef]
- Bekibayev, T.; Zhapbasbayev, U.; Ramazanova, G. Optimal regimes of heavy oil transportation through a heated pipeline. J. Process Control 2022, 115, 27–35. [Google Scholar] [CrossRef]
- Muñoz, J.A.D.; Ancheyta, J.; Castañeda, L.C. Required Viscosity Values To Ensure Proper Transportation of Crude Oil by Pipeline. Energy Fuels 2016, 30, 8850–8854. [Google Scholar] [CrossRef]
- Litvinenko, V.S.; Tsvetkov, P.S.; Dvoynikov, M.V.; Buslaev, G.V. Barriers to implementation of hydrogen initiatives in the context of global energy sustainable development. J. Min. Inst. 2020, 244, 428–438. [Google Scholar] [CrossRef]
- Jameel, M.F.; Sharife, W.A. Transportation of Heavy Crude Oil: A Review. Int. Res. J. Eng. Technol. (IRJET) 2020, 7, 5817–5823. [Google Scholar]
- dos Santos, R.G.; Brinceño, M.I.; Loh, W. Laminar pipeline flow of heavy oil–in–water emulsions produced by continuous in-line emulsification. J. Pet. Sci. Eng. 2017, 156, 827–834. [Google Scholar] [CrossRef]
- Lyu, Y.; Huang, Q.; Li, R.; Zhang, F.; Liu, L.; Zhang, H.; Zhang, Y.; Cui, Y.; Wang, Q. Effect of temperature on wall sticking of heavy oil in low-temperature transportation. J. Pet. Sci. Eng. 2021, 206, 108944. [Google Scholar] [CrossRef]
- Nikolaev, A.K.; Zaripova, N. Substantiation of analytical dependences for hydraulic calculation of high-viscosity oil transportation. J. Min. Inst. 2021, 252, 885–895. [Google Scholar] [CrossRef]
- Coelho, N.M.D.A.; Taqueda, M.E.S.; Souza, N.M.O.; de Paiva, J.L.; Santos, A.R.; Lia, L.R.B.; de Moraes, M.S.; Júnior, D.D.M. Energy savings on heavy oil transportation through core annular flow pattern: An experimental approach. Int. J. Multiph. Flow 2019, 122, 103127. [Google Scholar] [CrossRef]
- Yaseen, M.; Rawat, S.K.; Shafiq, A.; Kumar, M.; Nonlaopon, K. Analysis of Heat Transfer of Mono and Hybrid Nanofluid Flow between Two Parallel Plates in a Darcy Porous Medium with Thermal Radiation and Heat Generation/Absorption. Symmetry 2022, 14, 1943. [Google Scholar] [CrossRef]
- Shishlyannikov, D.; Zverev, V.; Ivanchenko, A.; Zvonarev, I. Increasing the Time between Failures of Electric Submersible Pumps for Oil Production with High Content of Mechanical Impurities. Appl. Sci. 2021, 12, 64. [Google Scholar] [CrossRef]
- Boda, M.A.; Bhasagi, P.N.; Sawade, A.S.; Andodgi, R.A. Analysis of Kinematic Viscosity for Liquids by Varying Temperature. Int. J. Innov. Res. Sci. Eng. Technol. 2015, 4, 1951–1954. [Google Scholar] [CrossRef]
- Isaev, A.A.; Aliev, M.M.O.; Drozdov, A.N.; Gorbyleva, Y.A.; Nurgalieva, K.S. Improving the Efficiency of Curved Wells’ Operation by Means of Progressive Cavity Pumps. Energies 2022, 15, 4259. [Google Scholar] [CrossRef]
- Abdollahpour, P.; Moradi, S.S.T.; Leusheva, E.; Morenov, V. A Numerical Study on the Application of Stress Cage Technology. Energies 2022, 15, 5439. [Google Scholar] [CrossRef]
- Han, S.-P.; Jiang, W.-X.; Zhang, J.-J. Approaches to predict viscosities of crude oil blends. J. Central South Univ. Technol. 2007, 14, 466–470. [Google Scholar] [CrossRef]
- Eleyedath, A.; Swamy, A.K. Prediction of density and viscosity of bitumen. Pet. Sci. Technol. 2018, 36, 1779–1786. [Google Scholar] [CrossRef]
- Yaseen, M.; Rawat, S.K.; Kumar, M. Falkner–Skan Problem for a Stretching or Shrinking Wedge With Nanoparticle Aggregation. J. Heat Transf. 2022, 144, 102051. [Google Scholar] [CrossRef]
- Frauenfeld, T.W.J.; Kissel, G.A.; Zhou, W.S. PVT and viscosity measurements for lloydminster-aberfeldy and cold lake blended oil systems. In Proceedings of the SPE International Thermal Operations and Heavy Oil Symposium and International Horizontal Well Technology Conference, Calgary, AB, Canada, 4–7 November 2002. [Google Scholar]
- Mehrotra, A.K. Viscosity of cold lake bitumen and its fractions. Can. J. Chem. Eng. 1990, 68, 348. [Google Scholar] [CrossRef]
- Aginey, R.V.; Firstov, A.A. Improving the method for assessment of bending stresses in the wall of an underground pipeline. J. Min. Inst. 2022, 257, 744–754. [Google Scholar] [CrossRef]
- Miadonye, A.; Dan-Ali, F.; Onwude, R.; Osirim, O.O. Study of the influence of asphaltenes on modeling of viscosity of Nigerian crude mixtures. WIT Trans. Model. Simul. 2011, 51, 133–144. [Google Scholar] [CrossRef]
- MacDonald, B.A.; Miadonye, A. Improvement on the Viscosity Models for the Effects of Temperature and Pressure on the Viscosity of Heavy Crude Oils. J. Chem. Eng. Data 2017, 62, 924–930. [Google Scholar] [CrossRef]
- Raupov, I.; Burkhanov, R.; Lutfullin, A.; Maksyutin, A.; Lebedev, A.; Safiullina, E. Experience in the Application of Hydrocarbon Optical Studies in Oil Field Development. Energies 2022, 15, 3626. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, H.; Hu, M.; Xiao, Q.; Li, J.; Cai, C. A Simple Correlation for the Viscosity of Heavy Oils From Liaohe Basin, NE China. J. Can. Pet. Technol. 2007, 46, 8–11. [Google Scholar] [CrossRef]
- Shu, W.R. A Viscosity correlation for mixtures of heavy oil, bitumen, and petroleum fractions. Soc. Pet. Eng. J. Repr. Ser. 2008, 61, 277–282. [Google Scholar] [CrossRef]
- Dzhemilev, E.; Shammazov, I.; Sidorkin, D.; Mastobaev, B.; Gumerov, A.; Arctic, S.C. Developing technology and device for the main pipelines repair with cutting out their defective sections. Oil Ind. 2022, 10, 78–82. [Google Scholar] [CrossRef]
- Litvinenko, V.S. Digital Economy as a Factor in the Technological Development of the Mineral Sector. Nat. Resour. Res. 2020, 29, 1521–1541. [Google Scholar] [CrossRef]
- Severa, L.; Havlíček, M.; Kumbár, V. Temperature dependent kinematic viscosity of different types of engine oils. Acta Univ. Agric. Silvic. Mendel. Brun. 2014, 57, 95–102. [Google Scholar] [CrossRef]
- Yui, S. Producing Quality Synthetic Crude Oil from Canadian Oil Sands Bitumen. J. Jpn. Pet. Inst. 2008, 51, 1–13. [Google Scholar] [CrossRef]
- Al-Maamari, R.; Vakili-Nezhaada, G.; Vatani, M. Experimental and Modeling Investigations of the Viscosity of Crude Oil Binary Blends: New Models Based on the Genetic Algorithm Method. J. Eng. Res. [TJER] 2015, 12, 81–91. [Google Scholar] [CrossRef]
- Rahmes, M.H.; Nelson, W.L. Viscosity Blending Relationships of Heavy Petroleum Oils. Anal. Chem. 1948, 20, 912–915. [Google Scholar] [CrossRef]
- Leusheva, E.; Morenov, V. Effect of Temperature Conditions in Arctic Offshore Oil Fields on the Rheological Properties of Various Based Drilling Muds. Energies 2022, 15, 5750. [Google Scholar] [CrossRef]
- Utting, N. Long-term column leaching study of centrifuged oil sands fine tailings. Environ. Earth Sci. 2021, 80, 462. [Google Scholar] [CrossRef]
- Jagoda, K.; Lin, X.; Wojcik, P. Enabling Chinese FDI in Canadian oil sands: Process and structure. Transnatl. Corp. Rev. 2018, 10, 268–279. [Google Scholar] [CrossRef]
- Maksarov, V.V.; Keksin, A.I.; Filipenko, I.A. Influence of magnetic-abrasive processing on roughness of flat products made of AMts grade aluminum alloy. Tsvetnye Met. 2022, 7, 82–87. [Google Scholar] [CrossRef]
- Wang, K.; Vredenburg, H.; Wang, J.; Xiong, Y.; Feng, L. Energy Return on Investment of Canadian Oil Sands Extraction from 2009 to 2015. Energies 2017, 10, 614. [Google Scholar] [CrossRef]
- Hounjet, L.J.; Xin, Q.; McDonald, R. Bitumen processing reduces diluent content of pipeline-transportable products and can mitigate impacts of spills into various water types. Fuel 2023, 331, 125826. [Google Scholar] [CrossRef]
- Xing, R.; Chiappori, D.V.; Arbuckle, E.J.; Binsted, M.T.; Davies, E.G.R. Canadian Oil Sands Extraction and Upgrading: A Synthesis of the Data on Energy Consumption, CO2 Emissions, and Supply Costs. Energies 2021, 14, 6374. [Google Scholar] [CrossRef]
- Lin, R.; Zhang, J.; Li, X.; Wang, X.; Yang, Y.; Xu, D.; Zhang, J. Rules of paraffin deposit and comparative study on hot washing technology. J. China Univ. Pet. (Ed. Nat. Sci.) 2022, 46, 155–162. [Google Scholar] [CrossRef]
- Sultanbekov, R.R.; Schipachev, A.M. Manifestation of incompatibility of marine residual fuels: A method for determining compatibility, studying composition of fuels and sediment. J. Min. Inst. 2022, 257, 843–852. [Google Scholar] [CrossRef]
- Mardashov, D.V.; Bondarenko, V.; Raupov, I.R. Technique for calculating technological parameters of non-Newtonian liquids injection into oil well during workover. J. Min. Inst. 2022, 254, 1–14. [Google Scholar] [CrossRef]
- Xu, B. Influencing factors governing paraffin wax deposition of heavy oil and research on wellbore paraffin remover. Pet. Sci. Technol. 2018, 36, 1635–1641. [Google Scholar] [CrossRef]
- Haj-Shafiei, S.; Mehrotra, A.K. Achieving cold flow conditions for ‘waxy’ mixtures with minimum solid deposition. Fuel 2019, 235, 1092–1099. [Google Scholar] [CrossRef]
- Quan, Q.; Gong, J.; Wang, W.; Wang, P. The Influence of Operating Temperatures on Wax Deposition During Cold Flow and Hot Flow of Crude Oil. Pet. Sci. Technol. 2015, 33, 272–277. [Google Scholar] [CrossRef]
- Zhang, L.; Du, C.; Wang, H.; Zhao, J. Three-dimensional numerical simulation of heat transfer and flow of waxy crude oil in inclined pipe. Case Stud. Therm. Eng. 2022, 37, 102237. [Google Scholar] [CrossRef]
- Dmitrieva, D.; Cherepovitsyna, A.; Stroykov, G.; Solovyova, V. Strategic Sustainability of Offshore Arctic Oil and Gas Projects: Definition, Principles, and Conceptual Framework. J. Mar. Sci. Eng. 2021, 10, 23. [Google Scholar] [CrossRef]
- Melissianos, V.E. Onshore Buried Steel Fuel Pipelines at Fault Crossings: A Review of Critical Analysis and Design Aspects. J. Pipeline Syst. Eng. Prac. 2022, 13, 03122002. [Google Scholar] [CrossRef]
- Tikariha, L.; Sanyal, A.; Kumar, L. Numerical study of gelation and flow restart in a waxy crude oil riser. J. Pet. Sci. Eng. 2022, 217, 110871. [Google Scholar] [CrossRef]
- Kelbaliyev, G.I.; Salavatov, T.S.; Rasulov, S.R.; Mamedova, E.V. Rheology of Structured Non-Newtonian Oils in the Gas-Lift Recovery Method. J. Eng. Phys. 2021, 94, 143–150. [Google Scholar] [CrossRef]
- Palyanitsina, A.; Safiullina, E.; Byazrov, R.; Podoprigora, D.; Alekseenko, A. Environmentally Safe Technology to Increase Efficiency of High-Viscosity Oil Production for the Objects with Advanced Water Cut. Energies 2022, 15, 753. [Google Scholar] [CrossRef]
- Ghoneim, N.I.; Megahed, A.M. Numerical Analysis of the Mixed Flow of a Non-Newtonian Fluid over a Stretching Sheet with Thermal Radiation. Fluid Dyn. Mater. Process 2023, 19, 407–419. [Google Scholar] [CrossRef]
- Yang, C.; Wang, Z.; Yang, Z.; Hollebone, B.; Brown, C.E.; Landriault, M.; Fieldhouse, B. Chemical Fingerprints of Alberta Oil Sands and Related Petroleum Products. Environ. Forensics 2011, 12, 173–188. [Google Scholar] [CrossRef]

| Name of Pipeline System | Type of Transported Product | Volume of Transported Product, mln. Barrels per Day |
|---|---|---|
| Enbridge | Light | 1.08 |
| Heavy | 1.25 | |
| Trans Canada | Mixture of light and heavy oil (25%/75%) | 0.59 |
| Kinder Morgan Trans Mountain | Mixture of light and heavy oil (80%/20%) | 0.30 |
| Kinder Morgan Express | Mixture of light and heavy oil (35%/65%) | 0.28 |
| Model Name | Model Equation |
|---|---|
| Newton’s | |
| Shwedov–Bingham | |
| Ostwald–de Waele’s | |
| Herschel–Bulkley | |
| Prandtl’ | |
| Powell–Eyring | |
| Rabinovich’s | |
| Siscoe’s | |
| De Haven’s | |
| Reiner–Filippov | |
| Kross’s | |
| Meyer’s | |
| Casson’s | |
| Schulman’s | |
| Reimer ‘s |
| Model Name | Equation | Note |
|---|---|---|
| Newton’s Shwedov–Bingham | Newtonian fluid model, model complexity n = 1 | |
| Model complexity n = 2 | ||
| Ostwald–de Waele’s | Power model, model complexity n = 2 | |
| Herschel–Bulkley | Model complexity n = 3 |
| Temperature, K | Density, kg/m3 |
|---|---|
| 288.15 | 1012 |
| 295.15 | 1001 |
| 313.15 | 997 |
| 343.15 | 978 |
| Temperature, K | Dynamic Viscosity Coefficient, mPa·s |
|---|---|
| 284.05 | 1,850,000 |
| 293.35 | 350,167 |
| 303.05 | 81,006 |
| 312.65 | 22,788 |
| 322.15 | 8625 |
| 331.75 | 3477 |
| 341.25 | 1568 |
| 350.75 | 777.6 |
| 360.25 | 420.7 |
| Model Name (Year of Appearance) | Model Equation |
|---|---|
| Arrhenius (1887) | . |
| Bingham (1914) | =. |
| Koval (1963) | |
| Parkash (2003) | =, |
| Refutas (1989) | =, |
| Maxwell (1950) | =, |
| Wallace and Henry (1987) | =, |
| Chevron (2005) | = |
| Cragoe (1933) | =, |
| Latour/Miadonye (2000) | =, a=ln(ln(+1)), n= |
| Shan-Peng №1 (2007) | |
| Shan-Peng №2 (2007) | |
| Al-Besharah (1989) | . |
| Parameter | Value |
|---|---|
| Modes of operation | Direct deformation control, shear rate control, shear stress control |
| Torque range | 5 nN·m–250 mN·m (viscosimetry–shear speed and stress monitoring) |
| Torque range | 0.5 nN·m–250 mN·m (oscillation–shear deformation and stress control) |
| Moment resolution | 0.05 nN·m |
| Position resolution | <10 nrad |
| Model Name | Equation | Model Parameters |
|---|---|---|
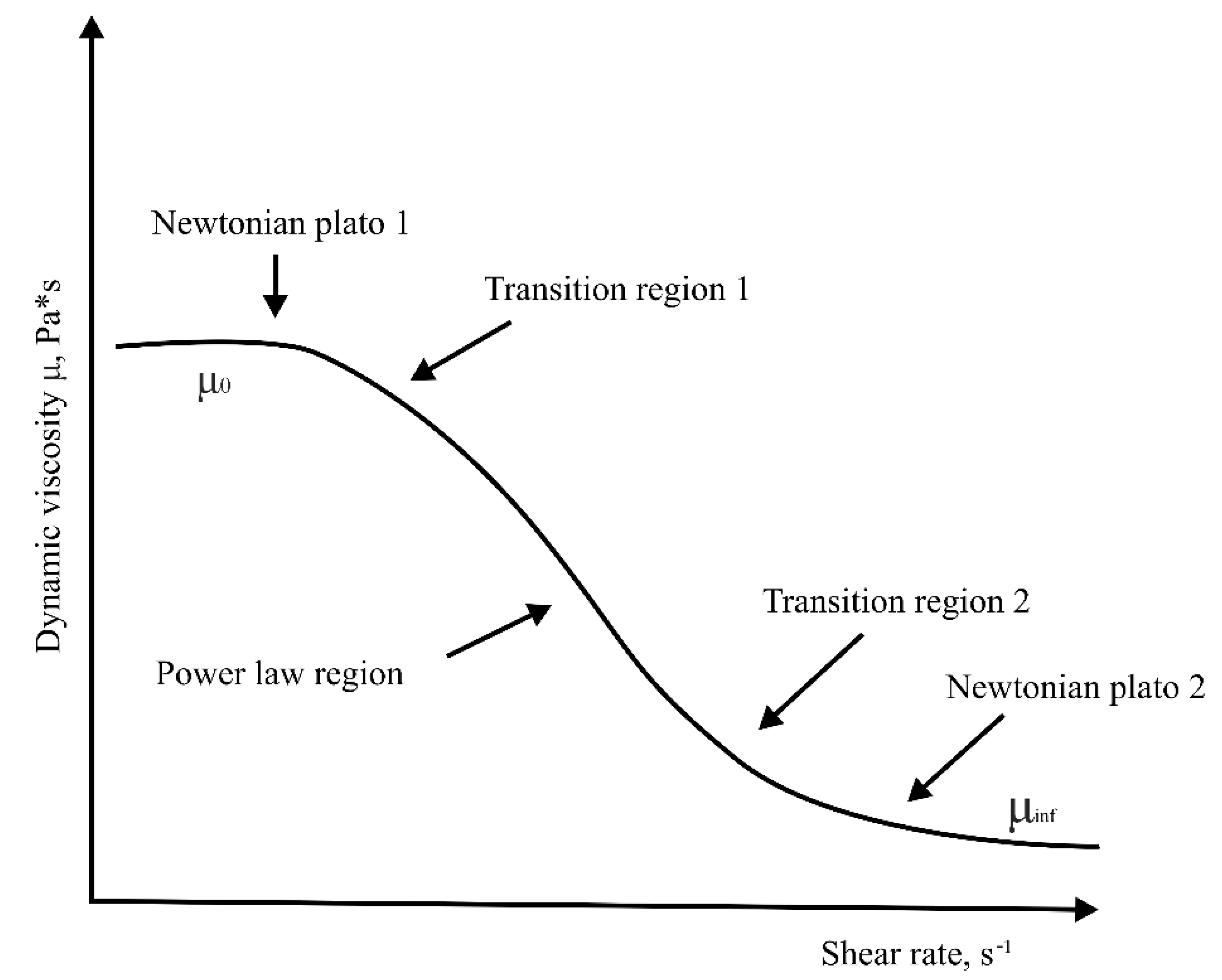
| Ostwald de Waele model or power-law | τ—shear stress; —shear rate; K—consistency index; n—flow index; μ—Newtonian viscosity; , —dynamic viscosity coefficient for →0 and for →∞, respectively; —shear stress at ; —key parameter associated with flow index ; b—relaxation time; c—index. | |
| Ellis fluid model | ||
| Carreau model |
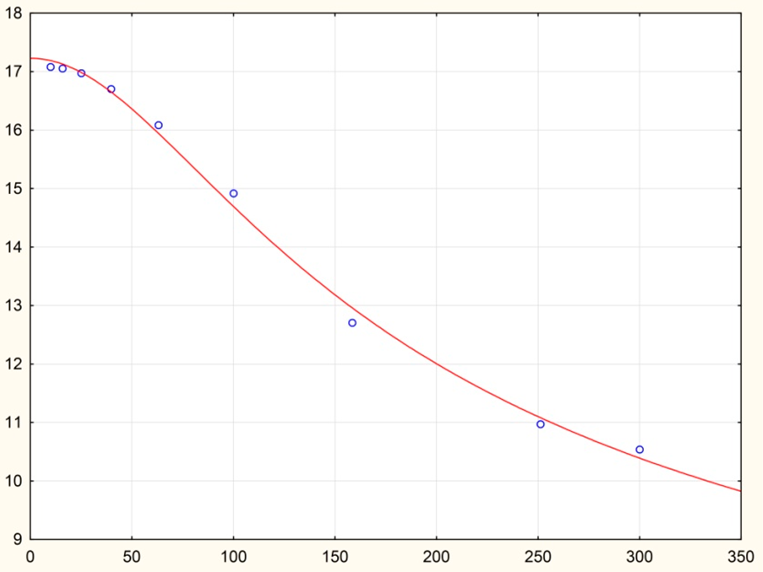
| θsolvent, % | Tmix, K | Shear Rate Boundaries, 1/s | Rheological Model | Model Parameters | Figure (Table 3) |
|---|---|---|---|---|---|
| 75 | 283.15 | 1–300 | Ostwald de Waele model or power-law | K = 0.638 | 1 |
| n = 0.995 | |||||
| 75 | 278.15 | 1–300 | Ostwald de Waele model or power-law | K = 1.006 | 2 |
| n = 0.991 | |||||
| 50 | 293.15 | 1–300 | Ostwald de Waele model or power-law | K = 0.436 | 3 |
| n = 0.990 | |||||
| 50 | 283.15 | 1–300 | Ostwald de Waele model or power-law | K = 1.0154 | 4 |
| n = 0.991 | |||||
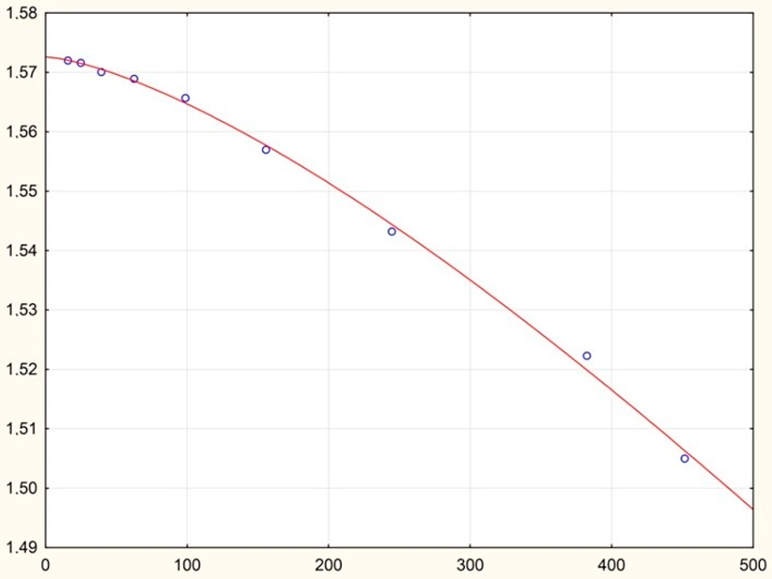
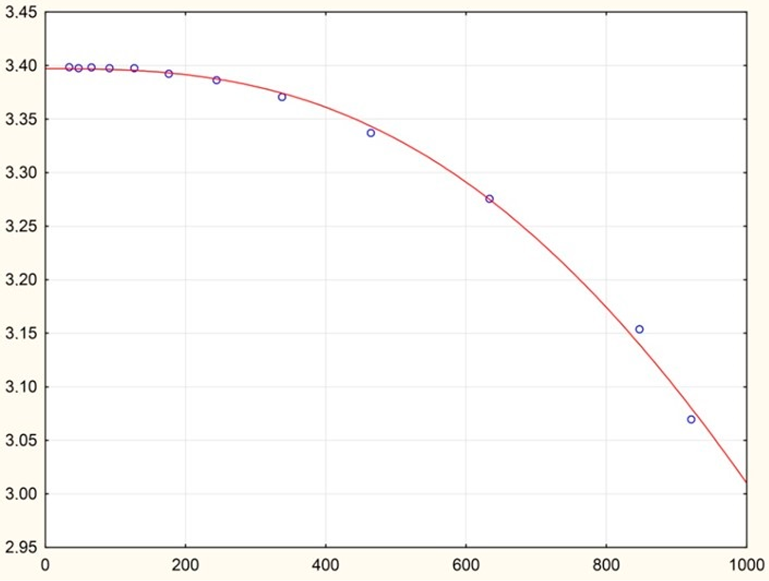
| 50 | 278.15 | 10–300 | Ellis fluid model | = 1.573 | 5 |
| = 3984.220 | |||||
| α = 2.435 | |||||
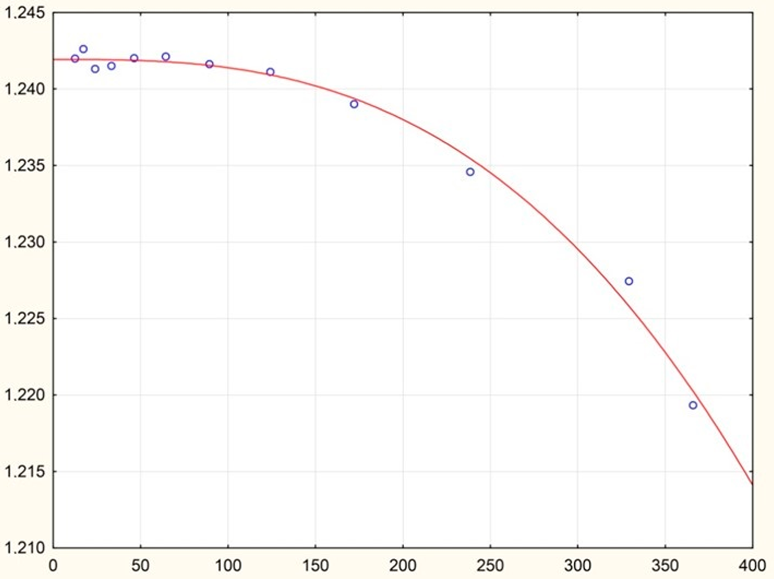
| 25 | 293.15 | 10–300 | Ellis fluid model | = 1.242 | 6 |
| = 1503.811 | |||||
| α = 3.851 | |||||
| 25 | 283.15 | 10–300 | Ellis fluid model | = 3.397 | 7 |
| = 2131.171 | |||||
| α = 3.711 | |||||
| 25 | 278.15 | 10–300 | Ellis fluid model | = 5.911 | 8 |
| = 2706.125 | |||||
| α = 3.464 | |||||
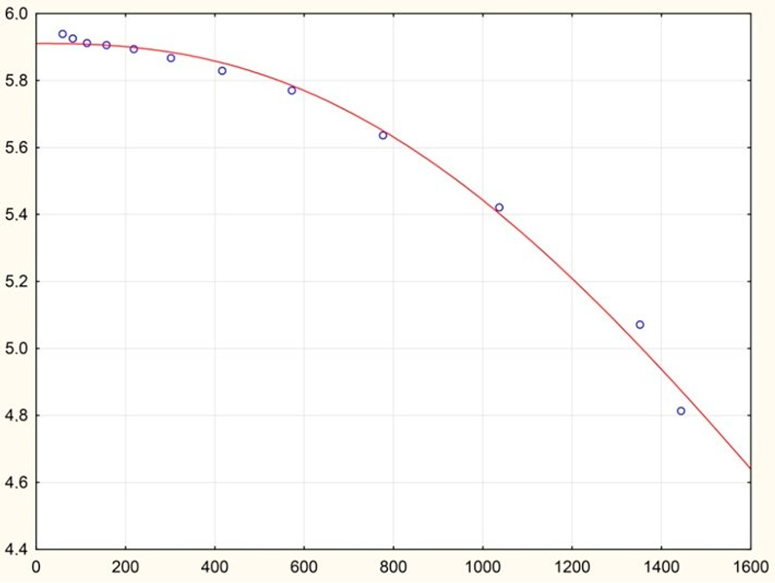
| 0 | 303.15 | 10–300 | Ellis fluid model | = 1.070 | 9 |
| = 1411.198 | |||||
| α = 3.991 | |||||
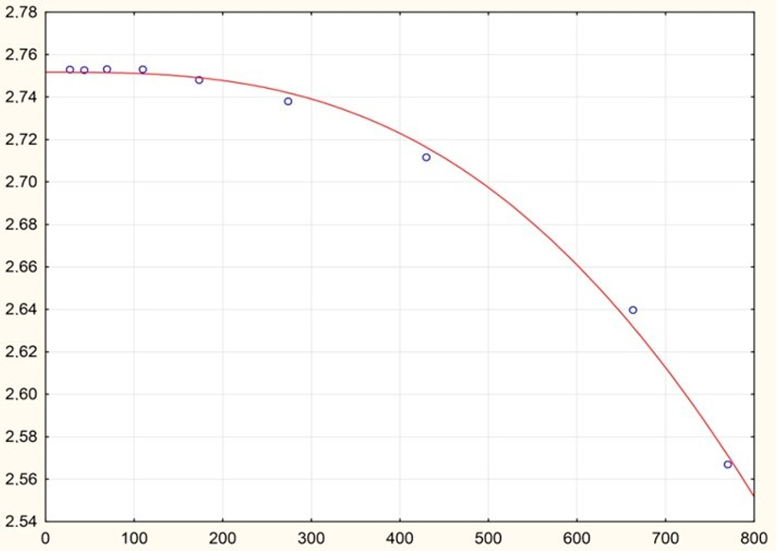
| 0 | 293.15 | 10–300 | Ellis fluid model | = 2.752 | 10 |
| = 1930.464 | |||||
| α = 3.890 | |||||
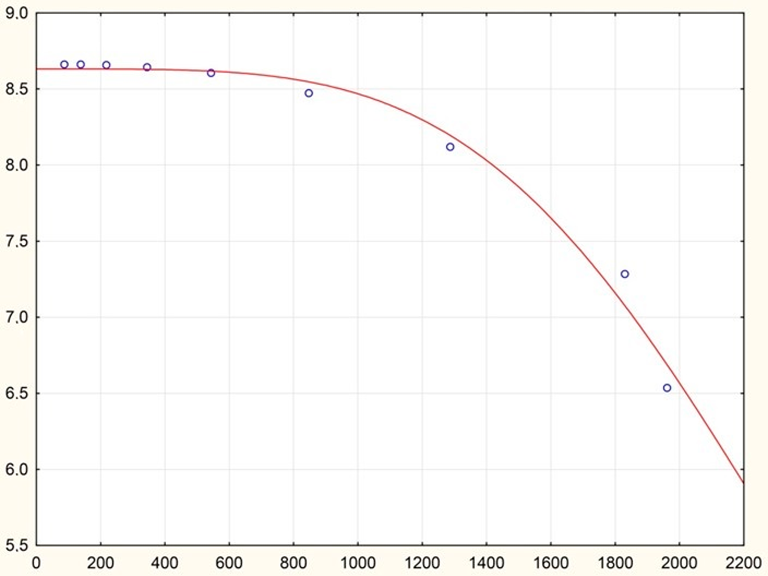
| 0 | 283.15 | 10–300 | Ellis fluid model | = 8.632 | 11 |
| = 2665.803 | |||||
| α = 5.027 | |||||
| 0 | 278.15 | 10–300 | Carreau model | = 3.309 | 12 |
| = 17.228 | |||||
| = 0.01 | |||||
| c = 0.405 |
| 1 | 2 |
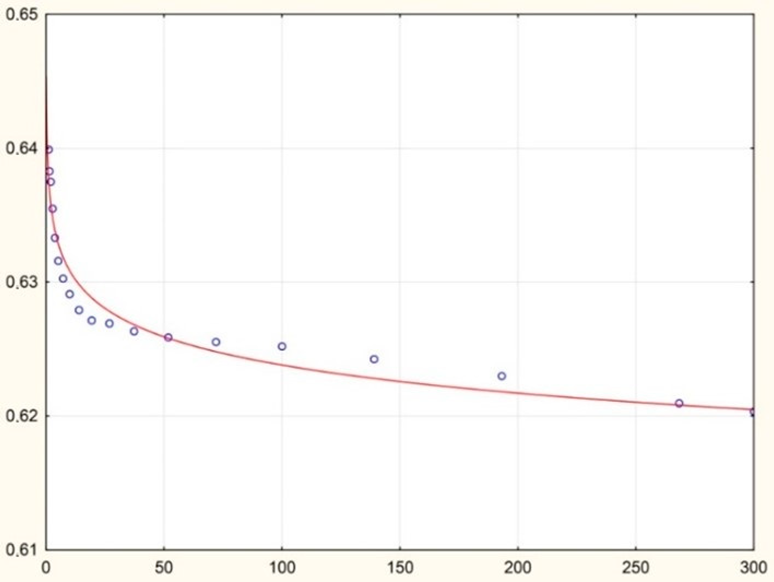 |  |
| 3 | 4 |
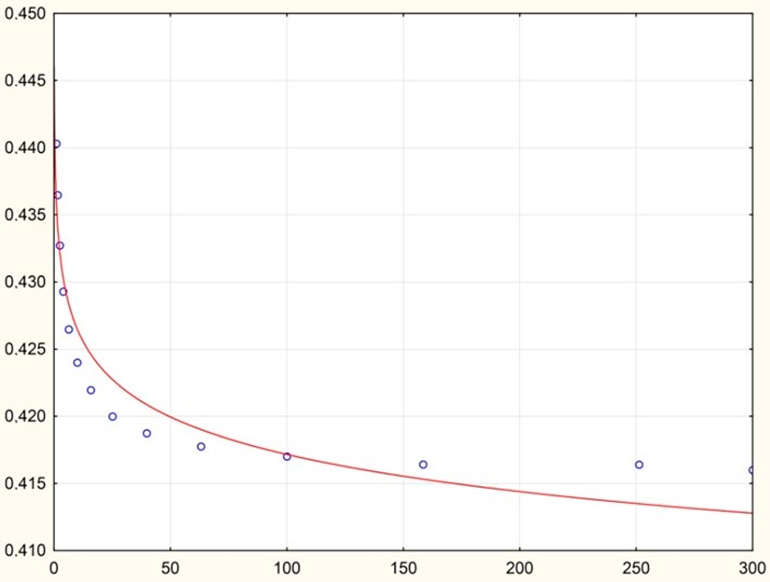 |  |
| 5 * | 6 * |
 |  |
| 7 * | 8 * |
 |  |
| 9 * | 10 * |
 |  |
| 11 * | 12 |
 |  |
| Solvent Concentration, Unit Fractions | Oil Mixture Temperature, K | Experimental Values of Dynamic Viscosity Coefficient of Petroleum Mixture, mPa·s | Dynamic Viscosity Coefficient Values According to Equation (18), mPa·s | The Difference between the Experimental Values of the Dynamic Viscosity Coefficient and the Values Obtained by Equation (18), mPa·s | Relative Error, % |
|---|---|---|---|---|---|
| 0.5 | 293.15 | 274.9000 | 274.2237 | 0.67626 | 0.246 |
| 0.75 | 303.15 | 142.2000 | 143.4942 | −1.29425 | 0.910 |
| 0.75 | 313.15 | 85.0000 | 83.9168 | 1.08316 | 1.274 |
| 0.75 | 333.15 | 37.8000 | 40.0621 | −2.26212 | 5.984 |
| 0.5 | 303.15 | 211.0000 | 213.8619 | −2.86186 | 1.356 |
| 0.5 | 313.15 | 119.7000 | 114.8989 | 4.80109 | 4.011 |
| 0.5 | 333.15 | 47.6000 | 46.2953 | 1.30473 | 2.741 |
| 0.25 | 303.15 | 535.3000 | 534.7329 | 0.56708 | 0.106 |
| 0.25 | 313.15 | 262.9000 | 263.9292 | −1.02923 | 0.391 |
| 0.25 | 333.15 | 89.4000 | 89.7520 | −0.35201 | 0.394 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zakirova, G.; Pshenin, V.; Tashbulatov, R.; Rozanova, L. Modern Bitumen Oil Mixture Models in Ashalchinsky Field with Low-Viscosity Solvent at Various Temperatures and Solvent Concentrations. Energies 2023, 16, 395. https://doi.org/10.3390/en16010395
Zakirova G, Pshenin V, Tashbulatov R, Rozanova L. Modern Bitumen Oil Mixture Models in Ashalchinsky Field with Low-Viscosity Solvent at Various Temperatures and Solvent Concentrations. Energies. 2023; 16(1):395. https://doi.org/10.3390/en16010395
Chicago/Turabian StyleZakirova, Gulnur, Vladimir Pshenin, Radmir Tashbulatov, and Lyubov Rozanova. 2023. "Modern Bitumen Oil Mixture Models in Ashalchinsky Field with Low-Viscosity Solvent at Various Temperatures and Solvent Concentrations" Energies 16, no. 1: 395. https://doi.org/10.3390/en16010395
APA StyleZakirova, G., Pshenin, V., Tashbulatov, R., & Rozanova, L. (2023). Modern Bitumen Oil Mixture Models in Ashalchinsky Field with Low-Viscosity Solvent at Various Temperatures and Solvent Concentrations. Energies, 16(1), 395. https://doi.org/10.3390/en16010395





