Design of Selective TPV Thermal Emitters Based on Bayesian Optimization Nesting Simulated Annealing
Abstract
:1. Introduction
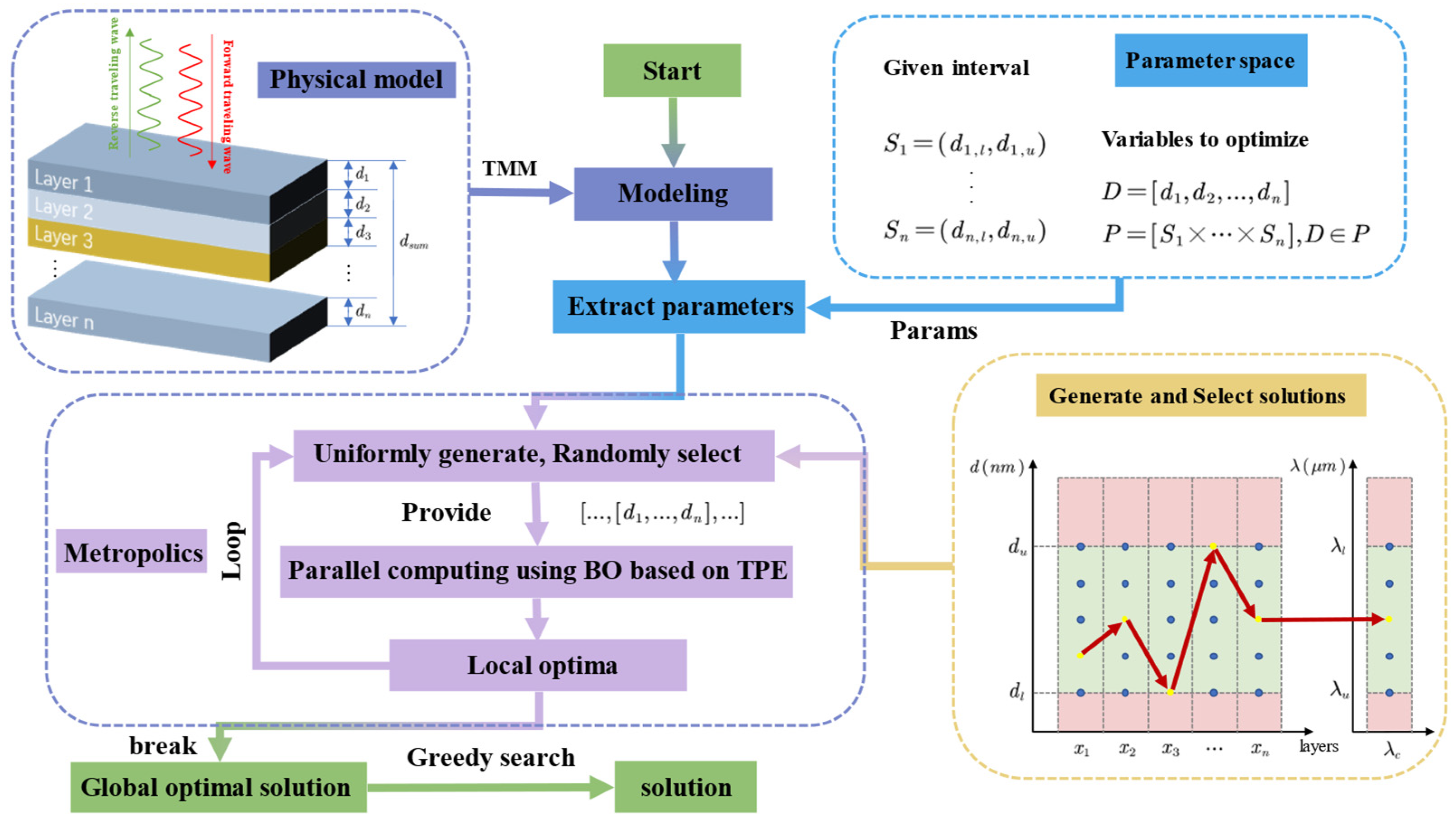
2. Mathematical Models and Optimization Algorithms
2.1. PEF Evaluator
2.2. BOnSA Algorithm
3. Results
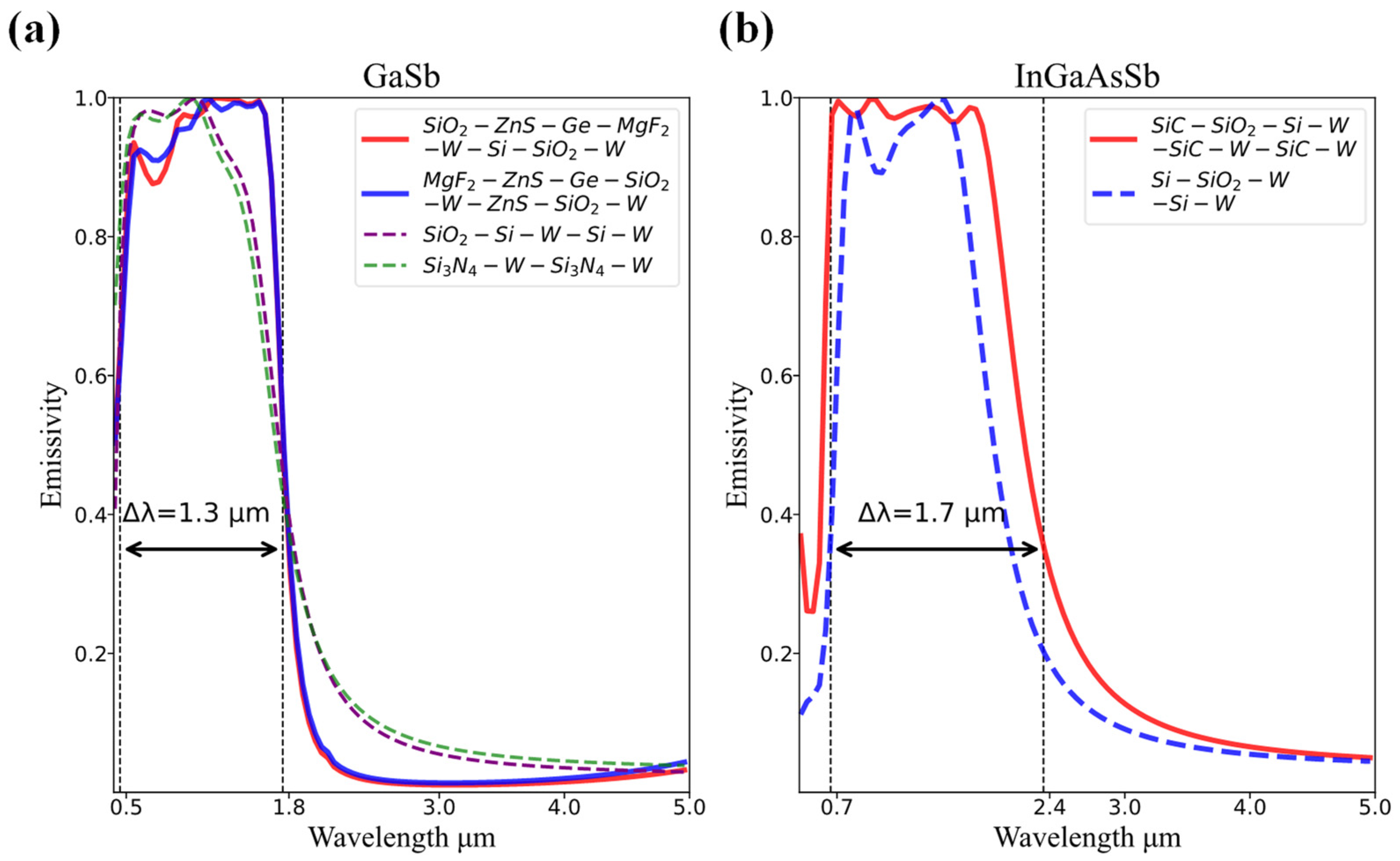
3.1. Determination of the Material Structure
3.2. Performance of BOnSA
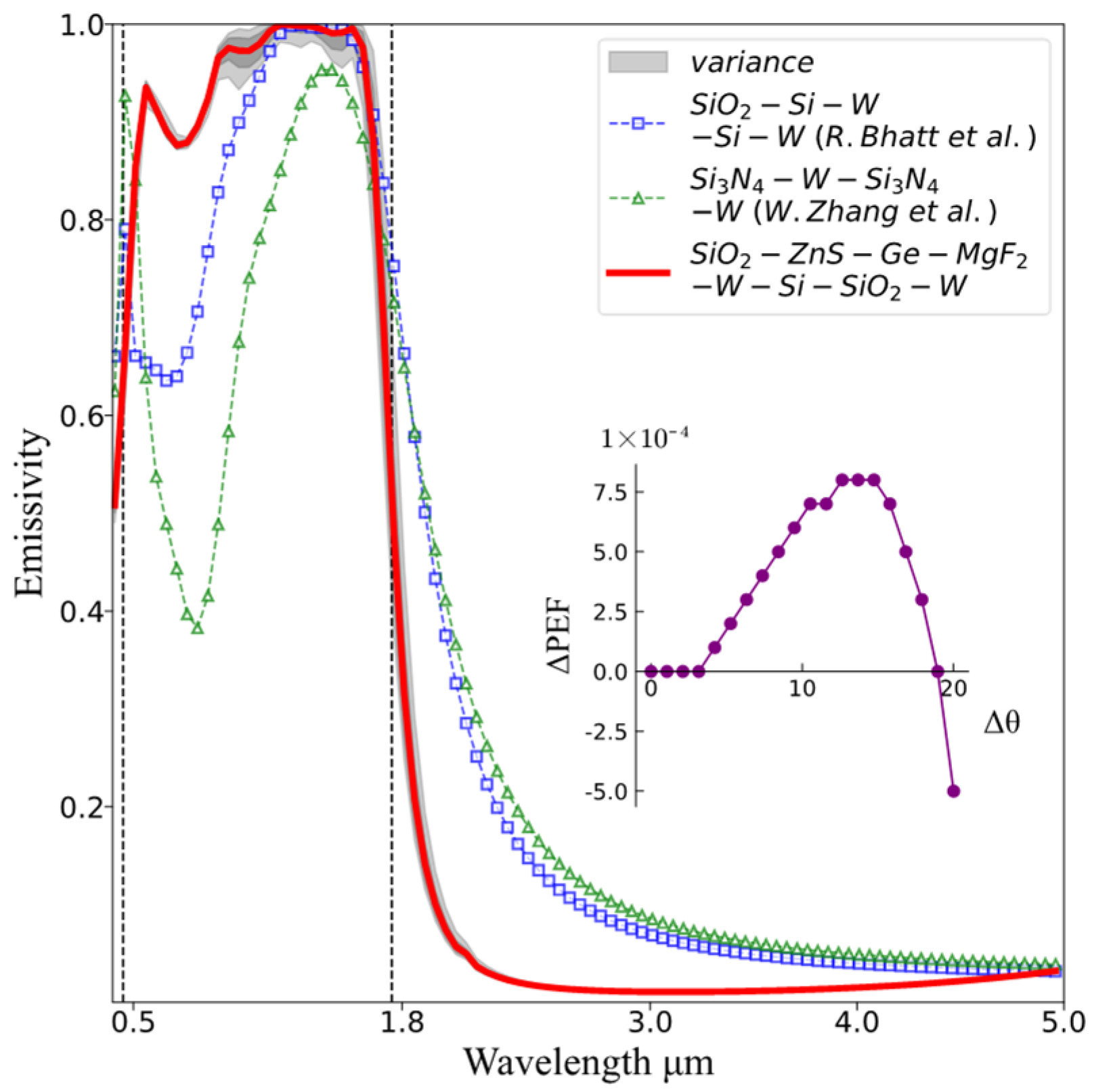
3.2.1. The Emission Spectrum of Different Optimal Structures
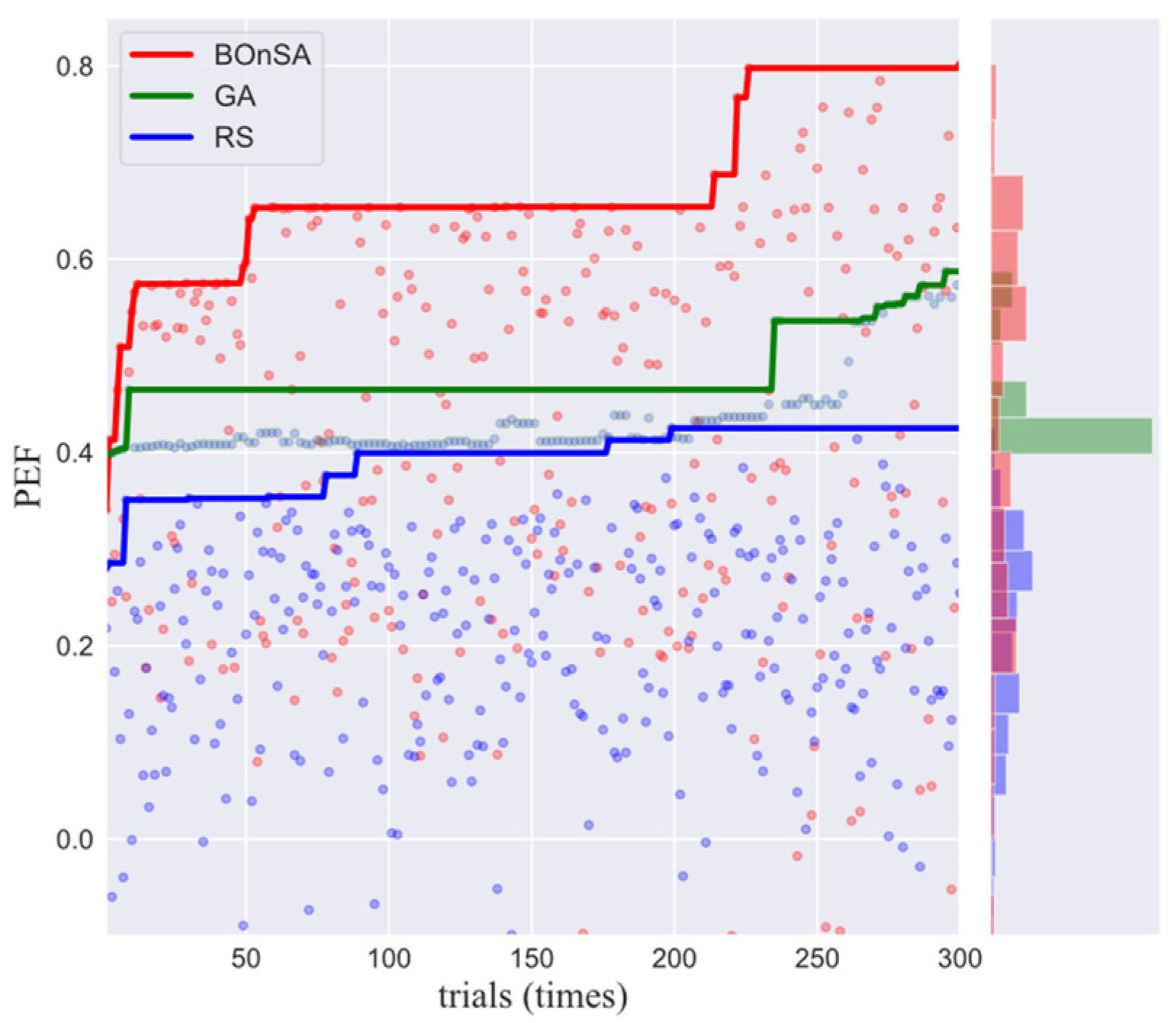
3.2.2. The Optimization Trajectories of BOnSA and Other Algorithms
3.2.3. Sensitivity Analysis
4. Discussion
4.1. Main Novelties
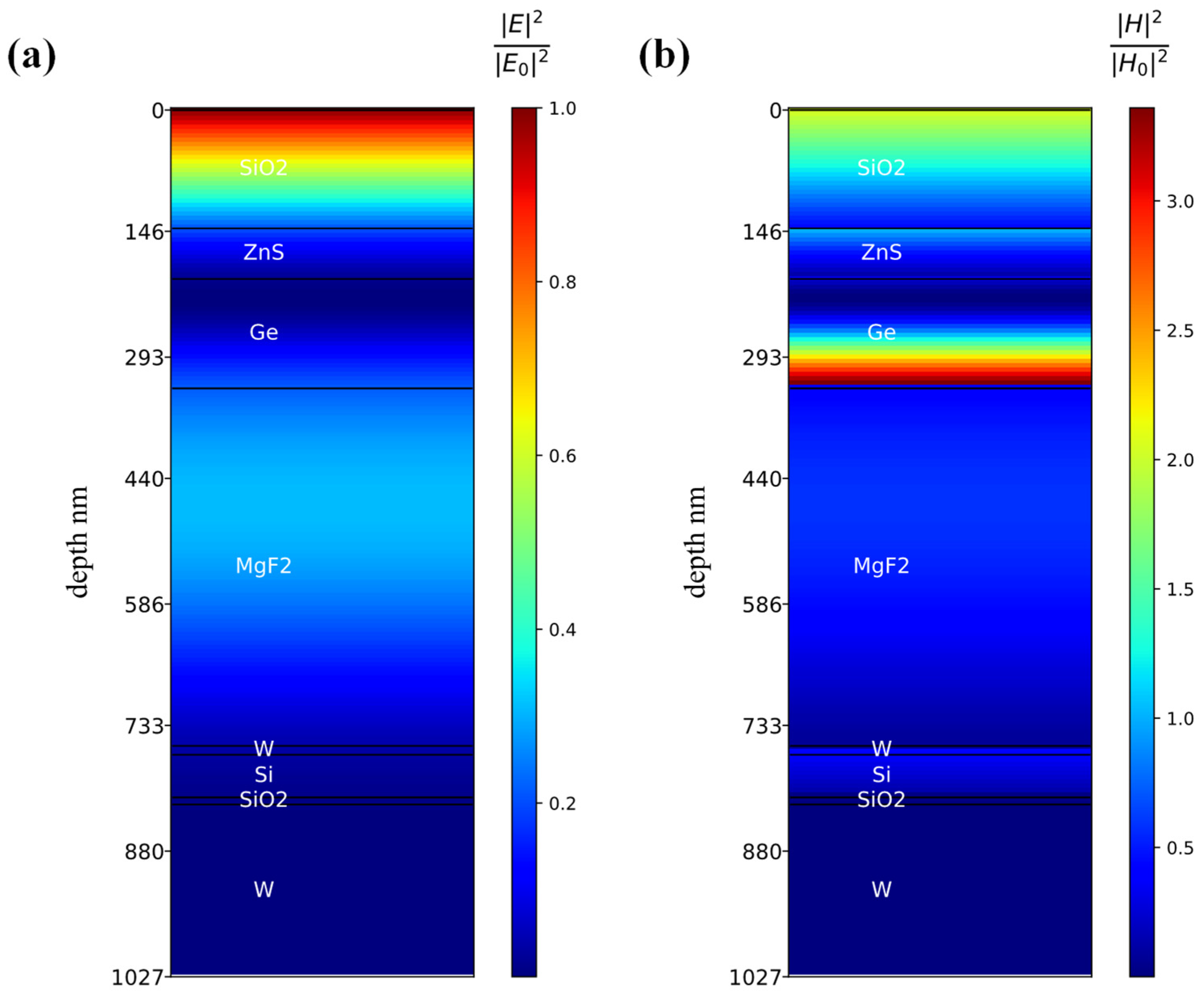
4.2. Mechanism Explanation
4.3. Calculation of Conversion Efficiency
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
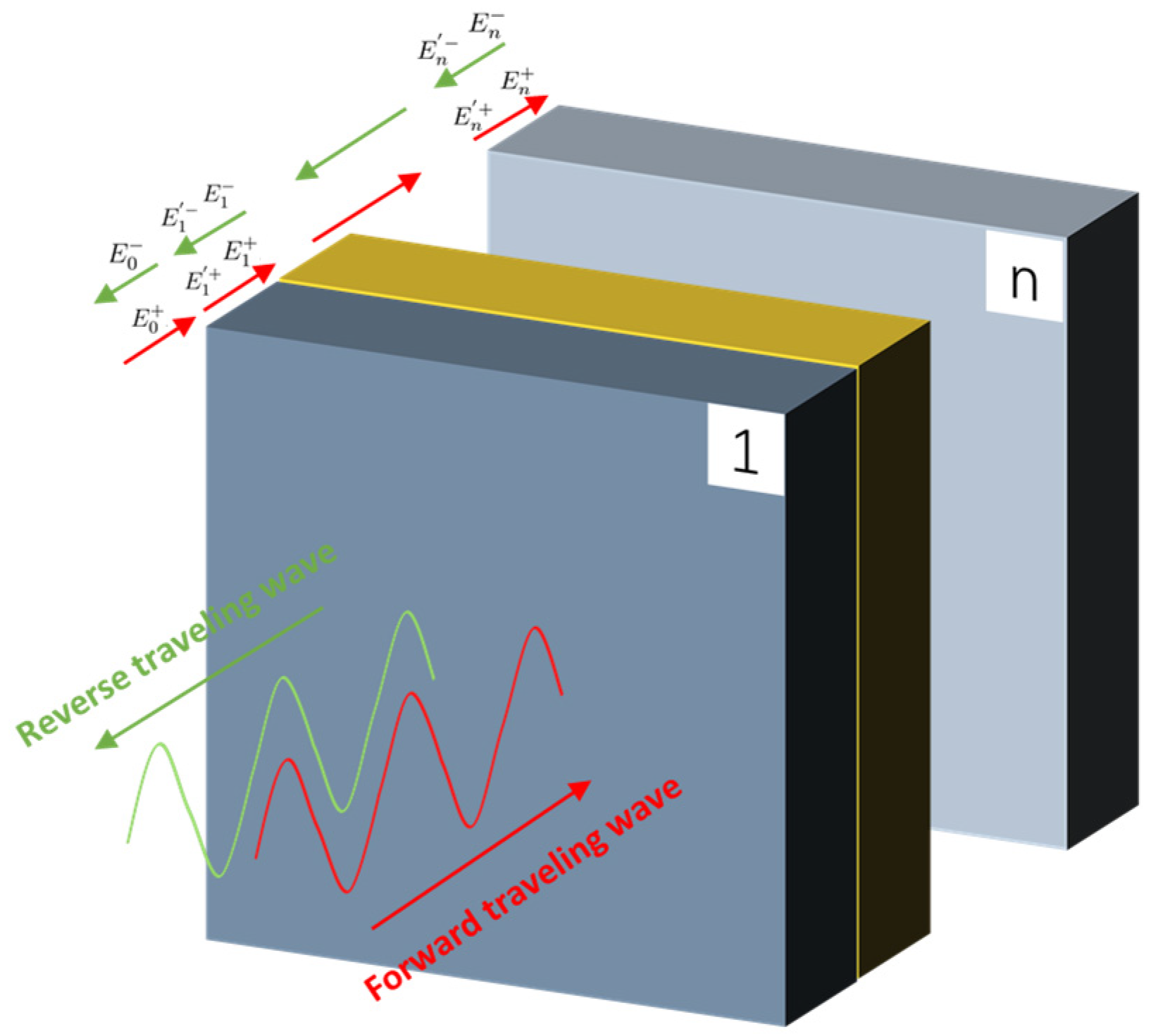
Appendix B
| Type | Title | Notation | Value |
|---|---|---|---|
| Physical | Center wavelength | Range from 1.0 to 1.2 μm | |
| Band gap wavelength of PV cell | μm (GaSb cell) | ||
| Lower bounds of emissivity | 0.4 μm | ||
| Upper bounds of emissivity | 5 μm | ||
| Bandwidth | 1.3 μm | ||
| Thickness of each layer | \ | Range from 5 to 305 nm | |
| Algorithmic | Total epoch of SA | \ | 400 |
| Epoch implementation Rate | 0.4 | ||
| Acceptance probability constant | 0.4 | ||
| Searching field ratio of BO | 0.1 |
References
- Wang, Q.; Zuo, W.; Cheng, M.; Deng, F.; Buja, G. Decoupled power control with indepth analysis of single-phase electric springs. IEEE Access 2020, 8, 21866–21874. [Google Scholar] [CrossRef]
- Mlangeni, S.; Ezugwu, A.E.; Chiroma, H. Deep Learning Model for Forecasting Institutional Building Energy Consumption. In Proceedings of the Conference on Information Communications Technology and Society (ICTAS), Durban, South Africa, 11–12 March 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–8. [Google Scholar]
- Zhang, S. The Conquest of the Energy Kingdom. In Man-Made Sun; Springer: Berlin/Heidelberg, Germany, 2021; pp. 1–28. [Google Scholar]
- Reza, S.E.; Nitol, T.A.; Abd-Al-Fattah, I. Present scenario of renewable energy in Bangladesh and a proposed hybrid system to minimize power crisis in remote areas. Int. J. Renew. Energy Res. 2012, 2, 280–288. [Google Scholar]
- Laird, F.N.; Stefes, C. The diverging paths of German and United States policies for renewable energy: Sources of difference. Energy Policy 2009, 37, 2619–2629. [Google Scholar] [CrossRef]
- Bahadori, A.; Nwaoha, C. A review on solar energy utilisation in Australia. Renew. Sustain. Energy Rev. 2013, 18, 1–5. [Google Scholar] [CrossRef]
- Kannan, N.; Vakeesan, D. Solar energy for future world—A review. Renew. Sustain. Energy Rev. 2016, 62, 1092–1105. [Google Scholar] [CrossRef]
- Davies, P.; Luque, A. Solar thermophotovoltaics: Brief review and a new look. Sol. Energy Mater. Sol. Cells 1994, 33, 11–22. [Google Scholar] [CrossRef]
- Shockley, W.; Queisser, H.J. Detailed balance limit of efficiency of p-n junction solar cells. J. Appl. Phys. 1961, 32, 510–519. [Google Scholar] [CrossRef]
- Baranov, D.G.; Xiao, Y.; Nechepurenko, I.A.; Krasnok, A.; Alù, A.; Kats, M.A. Nanophotonic engineering of far-field thermal emitters. Nat. Mater. 2019, 18, 920–930. [Google Scholar] [CrossRef] [Green Version]
- Datas, A.; Algora, C. Detailed balance analysis of solar thermophotovoltaic systems made up of single junction photovoltaic cells and broadband thermal emitters. Sol. Energy Mater. Sol. Cells 2010, 94, 2137–2147. [Google Scholar] [CrossRef] [Green Version]
- Cuevas, J.C.; García-Vidal, F.J. Radiative heat transfer. ACS Photonics 2018, 5, 3896–3915. [Google Scholar] [CrossRef]
- Colodrero, S.; Mihi, A.; Häggman, L.; Ocana, M.; Boschloo, G.; Hagfeldt, A.; Miguez, H. Porous one-dimensional photonic crystals improve the power-conversion efficiency of dye-sensitized solar cells. Adv. Mater. 2009, 21, 764–770. [Google Scholar] [CrossRef]
- Zhou, Z.; Sakr, E.; Sun, Y.; Bermel, P. Solar thermophotovoltaics: Reshaping the solar spectrum. Nanophotonics 2016, 5, 1–21. [Google Scholar] [CrossRef]
- Ferguson, L.; Fraas, L. Theoretical study of GaSb PV cells efficiency as a function of temperature. Sol. Energy Mater. Sol. Cells 1995, 39, 11–18. [Google Scholar] [CrossRef]
- Torsello, G.; Lomascolo, M.; Licciulli, A.; Diso, D.; Tundo, S.; Mazzer, M. The origin of highly efficient selective emission in rare-earth oxides for thermophotovoltaic applications. Nat. Mater. 2004, 3, 632–637. [Google Scholar] [CrossRef] [PubMed]
- Bitnar, B.; Durisch, W.; Mayor, J.-C.; Sigg, H.; Tschudi, H. Characterisation of rare earth selective emitters for thermophotovoltaic applications. Sol. Energy Mater. Sol. Cells 2002, 73, 221–234. [Google Scholar] [CrossRef]
- Lin, S.-Y.; Moreno, J.; Fleming, J. Three-dimensional photonic-crystal emitter for thermal photovoltaic power generation. Appl. Phys. Lett. 2003, 83, 380–382. [Google Scholar] [CrossRef] [Green Version]
- Laroche, M.; Carminati, R.; Greffet, J.-J. Coherent thermal antenna using a photonic crystal slab. Phys. Rev. Lett. 2006, 96, 123903. [Google Scholar] [CrossRef]
- Liu, X.; Tyler, T.; Starr, T.; Starr, A.F.; Jokerst, N.M.; Padilla, W.J. Taming the blackbody with infrared metamaterials as selective thermal emitters. Phys. Rev. Lett. 2011, 107, 045901. [Google Scholar] [CrossRef] [Green Version]
- Veselago, V.G. Electrodynamics of substances with simultaneously negative and. Usp. Fiz. Nauk 1967, 92, 517. [Google Scholar] [CrossRef]
- Zhang, S.; Fan, W.; Panoiu, N.; Malloy, K.; Osgood, R.; Brueck, S. Experimental demonstration of near-infrared negative-index metamaterials. Phys. Rev. Lett. 2005, 95, 137404. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhang, S. Research advances in thermal metamaterials. Opto-Electron. Eng. 2017, 44, 49–63. [Google Scholar]
- Kadic, M.; Bückmann, T.; Schittny, R.; Wegener, M. Metamaterials beyond electromagnetism. Rep. Prog. Phys. 2013, 76, 126501. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Sivan, V.P.; Mitchell, A.; Rosengarten, G.; Phelan, P.; Wang, L. Highly efficient selective metamaterial absorber for high-temperature solar thermal energy harvesting. Sol. Energy Mater. Sol. Cells 2015, 137, 235–242. [Google Scholar] [CrossRef]
- Jia, Y.; Wang, X.; Yin, H.; Yao, H.; Wang, J.; Fan, C. Highly tunable thermal emitter with vanadium dioxide metamaterials for radiative cooling. Appl. Opt. 2021, 60, 5699–5706. [Google Scholar] [CrossRef]
- Dyachenko, P.N.; Molesky, S.; Petrov, A.Y.; Störmer, M.; Krekeler, T.; Lang, S.; Ritter, M.; Jacob, Z.; Eich, M. Controlling thermal emission with refractory epsilon-near-zero metamaterials via topological transitions. Nat. Commun. 2016, 7, 11809. [Google Scholar] [CrossRef] [Green Version]
- Behera, S.; Joseph, J. Plasmonic metamaterial based unified broadband absorber/near infrared emitter for thermophotovoltaic system based on hexagonally packed tungsten doughnuts. J. Appl. Phys. 2017, 122, 193104. [Google Scholar] [CrossRef]
- Woolf, D.; Hensley, J.; Cederberg, J.; Bethke, D.; Grine, A.; Shaner, E. Heterogeneous metasurface for high temperature selective emission. Appl. Phys. Lett. 2014, 105, 081110. [Google Scholar] [CrossRef]
- Kudyshev, Z.A.; Kildishev, A.V.; Shalaev, V.M.; Boltasseva, A. Machine-learning-assisted metasurface design for high-efficiency thermal emitter optimization. Appl. Phys. Rev. 2020, 7, 021407. [Google Scholar] [CrossRef]
- Wilson, B.A.; Kudyshev, Z.A.; Kildishev, A.V.; Kais, S.; Shalaev, V.M.; Boltasseva, A. Metasurface design optimization via D-Wave based sampling. In Proceedings of the 2021 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 9–14 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–2. [Google Scholar]
- Maremi, F.T.; Lee, N.; Choi, G.; Kim, T.; Cho, H.H. Design of multilayer ring emitter based on metamaterial for thermophotovoltaic applications. Energies 2018, 11, 2299. [Google Scholar] [CrossRef] [Green Version]
- Hou, G.; Wang, Q.; Zhu, Y.; Lu, Z.; Xu, J.; Chen, K. Tunable Narrowband Silicon-Based Thermal Emitter with Excellent High-Temperature Stability Fabricated by Lithography-Free Methods. Nanomaterials 2021, 11, 1814. [Google Scholar] [CrossRef]
- Kildishev, A.V.; Boltasseva, A.; Shalaev, V.M. Planar photonics with metasurfaces. Science 2013, 339, 1232009. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sakurai, A.; Matsuno, Y. Design and fabrication of a wavelength-selective near-infrared metasurface emitter for a thermophotovoltaic system. Micromachines 2019, 10, 157. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Guler, U.; Kinsey, N.; Naik, G.V.; Boltasseva, A.; Guan, J.; Shalaev, V.M.; Kildishev, A.V. Refractory plasmonics with titanium nitride: Broadband metamaterial absorber. Adv. Mater. 2014, 26, 7959–7965. [Google Scholar] [CrossRef] [PubMed]
- Sakr, E.; Zhou, Z.; Bermel, P. High efficiency rare-earth emitter for thermophotovoltaic applications. Appl. Phys. Lett. 2014, 105, 111107. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Liu, J.; Ma, W.-Z.; Yu, G.-X.; Chen, J.-Q.; Cai, H.-Y.; Yang, C.-F. Numerical study of multilayer planar film structures for ideal absorption in the entire solar spectrum. Appl. Sci. 2020, 10, 3276. [Google Scholar] [CrossRef]
- Shuai, Y.; Tan, H.; Liang, Y. Polariton-enhanced emittance of metallic–dielectric multilayer structures for selective thermal emitters. J. Quant. Spectrosc. Radiat. Transf. 2014, 135, 50–57. [Google Scholar] [CrossRef]
- Wu, J.; Wu, F.; Zhao, T.; Antezza, M.; Wu, X. Dual-band nonreciprocal thermal radiation by coupling optical Tamm states in magnetophotonic multilayers. Int. J. Therm. Sci. 2022, 175, 107457. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, B.; Zhao, C. Selective thermophotovoltaic emitter with aperiodic multilayer structures designed by machine learning. ACS Appl. Energy Mater. 2021, 4, 2004–2013. [Google Scholar] [CrossRef]
- Sakurai, A.; Yada, K.; Simomura, T.; Ju, S.; Kashiwagi, M.; Okada, H.; Nagao, T.; Tsuda, K.; Shiomi, J. Ultranarrow-band wavelength-selective thermal emission with aperiodic multilayered metamaterials designed by Bayesian optimization. ACS Cent. Sci. 2019, 5, 319–326. [Google Scholar] [CrossRef]
- Babiker, S.G.; Shuai, Y.; Sid-Ahmed, M.O.; Xie, M. One-dimensional multilayer microstructure emitter for thermophotovoltaic applications. Int. J. Energy Inf. Commun. 2014, 5, 9–20. [Google Scholar] [CrossRef]
- Langlais, M.; Bru, H.; Ben-Abdallah, P. High temperature layered absorber for thermo-solar systems. J. Quant. Spectrosc. Radiat. Transf. 2014, 149, 8–15. [Google Scholar] [CrossRef]
- Liang, H.; Lai, J.; Zhou, Z. Ultra-narrowband infrared thermal emitter based on Fabry–Perot-like vacuum resonance cavity. J. Opt. A Pure Appl. Opt. 2009, 11, 105001. [Google Scholar] [CrossRef]
- Cai, H.; Sun, Y.; Wang, X.; Zhan, S. Design of an ultra-broadband near-perfect bilayer grating metamaterial absorber based on genetic algorithm. Opt. Express 2020, 28, 15347–15359. [Google Scholar] [CrossRef] [PubMed]
- Silva-Oelker, G.; Jerez-Hanckes, C.; Fay, P. High-temperature tungsten-hafnia optimized selective thermal emitters for thermophotovoltaic applications. J. Quant. Spectrosc. Radiat. Transf. 2019, 231, 61–68. [Google Scholar] [CrossRef]
- Akhtar, S.; Khan, M.N.; Kurnia, J.C.; Shamim, T. Investigation of energy conversion and flame stability in a curved micro-combustor for thermo-photovoltaic (TPV) applications. Appl. Energy 2017, 192, 134–145. [Google Scholar] [CrossRef]
- Simovski, C.; Maslovski, S.; Nefedov, I.; Tretyakov, S. Optimization of radiative heat transfer in hyperbolic metamaterials for thermophotovoltaic applications. Opt. Express 2013, 21, 14988–15013. [Google Scholar] [CrossRef]
- Hatakeyama-Sato, K.; Kashikawa, T.; Kimura, K.; Oyaizu, K. Tackling the challenge of a huge materials science search space with quantum-Inspired annealing. Adv. Intell. Syst. 2021, 3, 2000209. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.-Y.; Zhang, H.; Xiong, L.-D.; Lei, H.; Deng, S.-H. Hyperparameter optimization for machine learning models based on Bayesian optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; De Freitas, N. Taking the human out of the loop: A review of Bayesian optimization. Proc. IEEE 2015, 104, 148–175. [Google Scholar] [CrossRef] [Green Version]
- Akhtar, S.; Kurnia, J.C.; Shamim, T. A three-dimensional computational model of H2–air premixed combustion in non-circular micro-channels for a thermo-photovoltaic (TPV) application. Appl. Energy 2015, 152, 47–57. [Google Scholar] [CrossRef]
- Katsidis, C.C.; Siapkas, D.I. General transfer-matrix method for optical multilayer systems with coherent, partially coherent, and incoherent interference. Appl. Opt. 2002, 41, 3978–3987. [Google Scholar] [CrossRef] [PubMed]
- Pigeat, P.; Rouxel, D.; Weber, B. Calculation of thermal emissivity for thin films by a direct method. Phys. Rev. B 1998, 57, 9293. [Google Scholar] [CrossRef]
- Koulamas, C.; Antony, S.; Jaen, R. A survey of simulated annealing applications to operations research problems. Omega 1994, 22, 41–56. [Google Scholar] [CrossRef]
- Eglese, R.W. Simulated annealing: A tool for operational research. Eur. J. Oper. Res. 1990, 46, 271–281. [Google Scholar] [CrossRef]
- Schulz, E.; Speekenbrink, M.; Krause, A. A tutorial on Gaussian process regression: Modelling, exploring, and exploiting functions. J. Math. Psychol. 2018, 85, 1–16. [Google Scholar] [CrossRef]
- Quinonero-Candela, J.; Rasmussen, C.E. A unifying view of sparse approximate Gaussian process regression. J. Mach. Learn. Res. 2005, 6, 1939–1959. [Google Scholar]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. In Proceedings of the 24th International Conference on Neural Information Processing Systems (NIPS’11), Granada, Spain, 12–15 December 2011; Curran Associates Inc.: Red Hook, NY, USA, 2011; pp. 2546–2554. [Google Scholar]
- Beichl, I.; Sullivan, F. The metropolis algorithm. Comput. Sci. Eng. 2000, 2, 65–69. [Google Scholar] [CrossRef] [Green Version]
- Haario, H.; Saksman, E.; Tamminen, J. An adaptive Metropolis algorithm. Bernoulli 2001, 7, 223–242. [Google Scholar] [CrossRef] [Green Version]
- Otaka, M.; Takahashi, S.; Utaka, K.; Horita, M.; Yazaki, T. Fundamental evaluation of semiconductor waveguide-type in-line wavelength selective filter with Fabry-Perot etalon resonator. In Proceedings of the 2001 International Conference on Indium Phosphide and Related Materials, 13th IPRM (Cat. No. 01CH37198), Nara, Japan, 14–18 May 2001; IEEE: Piscataway, NJ, USA, 2001; pp. 170–173. [Google Scholar]
- Gamel, M.M.A.; Jern, K.P.; Rashid, W.E.; Yau, L.K.; Jamaludin, M.Z. The effect of illumination intensity on the performance of germanium based-thermophotovoltaic cell. In Proceedings of the 2019 IEEE Regional Symposium on Micro and Nanoelectronics (RSM), Putrajaya, Malaysia, 21–23 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 129–132. [Google Scholar]
- Dhass, A.D.; Kumar, R.S.; Lakshmi, P.; Natarajan, E.; Arivarasan, A. An investigation on performance analysis of different PV materials. Mater. Today Proc. 2020, 22, 330–334. [Google Scholar] [CrossRef]
- Zulkefle, A.A.; Zainon, M.; Zakaria, Z.; Sopian, K.; Amin, N. Numerical modeling of silicon/germanium (Si/Ge) superlattice solar cells. In Proceedings of the 7th WSEAS International Conference on. Renewable Energy Sources (RES ‘13), Kuala Lumpur, Malaysia, 2–4 April 2013; p. 233. [Google Scholar]
- Han, J.; Lu, L.; Yang, H. Numerical evaluation of the mixed convective heat transfer in a double-pane window integrated with see-through a-Si PV cells with low-e coatings. Appl. Energy 2010, 87, 3431–3437. [Google Scholar] [CrossRef]
- Khorrami, Y.; Fathi, D. Broadband thermophotovoltaic emitter using magnetic polaritons based on optimized one-and two-dimensional multilayer structures. JOSA B 2019, 36, 662–666. [Google Scholar] [CrossRef]
- Tong, J.K.; Hsu, W.-C.; Huang, Y.; Boriskina, S.V.; Chen, G. Thin-film ‘thermal well’emitters and absorbers for high-efficiency thermophotovoltaics. Sci. Rep. 2015, 5, 10661. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bhatt, R.; Kravchenko, I.; Gupta, M. High-efficiency solar thermophotovoltaic system using a nanostructure-based selective emitter. Sol. Energy 2020, 197, 538–545. [Google Scholar] [CrossRef]
- Wang, H.; Alshehri, H.; Su, H.; Wang, L. Design, fabrication and optical characterizations of large-area lithography-free ultrathin multilayer selective solar coatings with excellent thermal stability in air. Sol. Energy Mater. Sol. Cells 2018, 174, 445–452. [Google Scholar] [CrossRef]
- Liu, G.; Xuan, Y.; Han, Y.; Li, Q. Investigation of one-dimensional si/sio2 hotonic crystals for thermophotovoltaic filter. Sci. China Ser. E Technol. Sci. 2008, 51, 2031–2039. [Google Scholar] [CrossRef]
- Zhang, W.B.; Zhao, C.Y.; Wang, B.X. Enhancing near-field heat transfer between composite structures through strongly coupled surface modes. Phys. Rev. B 2019, 100, 075425. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.B.; Wang, B.X.; Zhao, C.Y. Active control and enhancement of near-field heat transfer between dissimilar materials by strong coupling effects. Int. J. Heat Mass Tran. 2022, 188, 122588. [Google Scholar] [CrossRef]
- Mohammed, Z.H. The Fresnel Coefficient of Thin Film Multilayer Using Transfer Matrix Method TMM; IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; p. 032026. [Google Scholar]
- Carrera-Escobedo, V.H.; Rosu, H.C. Electromagnetic transmittance in alternating material-metamaterial layered structures. Rev. Mex. Física 2017, 63, 402–410. [Google Scholar]
- Tran, A.M.; Houshmand, B.; Itoh, T. Analysis of electromagnetic coupling through a thick aperture in multilayer planar circuits using the extended spectral domain approach and finite difference time-domain method. IEEE Trans. Antennas Propag. 1995, 43, 921–926. [Google Scholar] [CrossRef]
- Moharam, M.; Pommet, D.A.; Grann, E.B.; Gaylord, T. Stable implementation of the rigorous coupled-wave analysis for surface-relief gratings: Enhanced transmittance matrix approach. JOSA A 1995, 12, 1077–1086. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ueno, T.; Rhone, T.D.; Hou, Z.; Mizoguchi, T.; Tsuda, K. COMBO: An efficient Bayesian optimization library for materials science. Mater. Discov. 2016, 4, 18–21. [Google Scholar] [CrossRef]
- Martinez-Cantin, R. BayesOpt: A Bayesian optimization library for nonlinear optimization, experimental design and bandits. J. Mach. Learn. Res. 2014, 15, 3735–3739. [Google Scholar]
- Bergstra, J.; Yamins, D.; Cox, D. Making a Science of Model Search: Hyperparameter Optimization in Hundreds of Dimensions for Vision Architectures. PMLR: Proceedings of Machine Learning Research. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, Atlanta, GA, USA, 16–21 June 2013; Sanjoy, D., David, M., Eds.; Volume 28, pp. 115–123. [Google Scholar]



| Method | Functionality | Structure | Materials | Refs. |
|---|---|---|---|---|
| Metasurface | High temperature selective emission | An array of crosses above a backplane | Pt, Al2O3, EBR | [29] |
| High efficiency thermal emitter optimization | Topology optimized designs | TiN, Si3N4 | [30] | |
| Rapidly generated globally optimized meta structure | Topology optimized designs | TiN, SiN | [31] | |
| Light modulation and control | A representative nanoantenna array | Gold | [34] | |
| Wavelength-selective near-infrared metasurface emitter | A periodic metallic disk pattern on a dielectric film | W, SiO2 | [35] | |
| Multilayer | Tunable narrowband Silicon-based thermal emitter | SiN/SiNO photonic crystal and a metallic W film on Si substrate | SiNyOz, SiNx, Si, W | [33] |
| High efficiency rare-earth emitter for TPV system | ErAG emitter with chirped-mirror (Q-matched Fabry–Perot modes) | ErAG, other filters | [37] | |
| Polariton-enhanced emittance for selective thermal emitter | Metallic–dielectric multilayer structure | W, SiO2 | [39] | |
| Achieve dual-band nonreciprocal thermal radiation | A 1-D PC (AC)n, a 1-D PC (CA)m and a metal layer | InAs, SiO2, Al | [40] | |
| Selective TPV emitter with aperiodic multilayer structure | Aperiodic multilayer structure | W, Si, SiO2 | [41] |
| Classification | Substructures | Material Combination | Optimization Algorithm | Refs. |
|---|---|---|---|---|
| Aperiodic | None | Simulation and optimization | BO | [41] |
| Anti-reflective coating, FP substructure | Manual arrangement | Enumeration and simulation | [38] | |
| Anti-reflective coating, FP substructure | Manual arrangement | particle-swarm optimization (PSO) | [71] | |
| Periodic | None | Simulation and optimization | BO | [42] |
| Anti-reflective coating, excitation medium | Manual arrangement | GA | [46] | |
| None | Enumeration | Enumeration and simulation | [72] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Zhang, Z.; Xie, P.; Miao, Z. Design of Selective TPV Thermal Emitters Based on Bayesian Optimization Nesting Simulated Annealing. Energies 2023, 16, 416. https://doi.org/10.3390/en16010416
Liu Z, Zhang Z, Xie P, Miao Z. Design of Selective TPV Thermal Emitters Based on Bayesian Optimization Nesting Simulated Annealing. Energies. 2023; 16(1):416. https://doi.org/10.3390/en16010416
Chicago/Turabian StyleLiu, Zejia, Zigui Zhang, Peifeng Xie, and Zibo Miao. 2023. "Design of Selective TPV Thermal Emitters Based on Bayesian Optimization Nesting Simulated Annealing" Energies 16, no. 1: 416. https://doi.org/10.3390/en16010416
APA StyleLiu, Z., Zhang, Z., Xie, P., & Miao, Z. (2023). Design of Selective TPV Thermal Emitters Based on Bayesian Optimization Nesting Simulated Annealing. Energies, 16(1), 416. https://doi.org/10.3390/en16010416






