Accurate Peer-to-Peer Hierarchical Control Method for Hybrid DC Microgrid Clusters

Abstract

Hybrid DC microgrid clusters contain various types of converters such as BOOST, BUCK, and bidirectional DC/DC converters, making the control strategy complex and difficult to achieve plug-and-play. The common master–slave hierarchical control strategy makes it difficult to achieve accurate and stable system control. This paper proposes an accurate peer-to-peer hierarchical control method for the hybrid DC microgrid cluster, and the working principle of this hierarchical control method is analyzed in detail. The microgrid cluster consists of three sub-microgrids, where sub-microgrid A consists of three BUCK converters, sub-microgrid B consists of three BOOST converters, and sub-microgrid C consists of two bidirectional DC/DC converters. According to all possible operations of various sub-microgrids in the microgrid cluster, the top-, mid-, and bottom-level controls are designed to solve the coordination control problem among different types of sub-microgrids. In this paper, a hybrid microgrid cluster simulation model is built in the PLECS simulation environment, and an experimental hardware platform is designed. The simulation and experiment results verified the accuracy of the proposed control strategy and its fast plug-and-play regulation ability for the system.

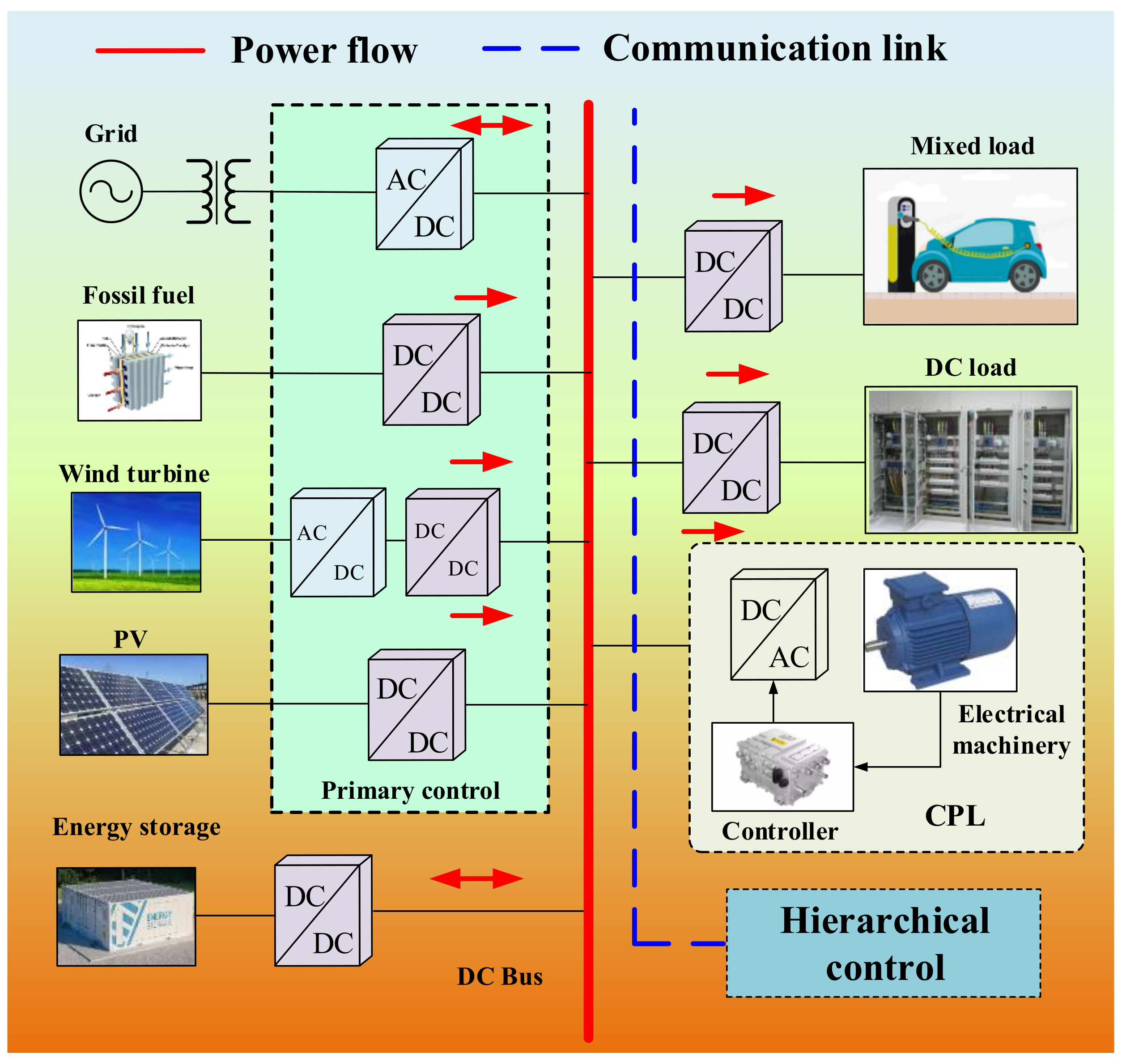
1. Introduction

Microgrids are small-scale generation and distribution grids that integrate distributed power sources of different types, attributions, and output characteristics to supply loads together or inject power into the grid [1,2,3]. The previous research on microgrids mainly focused on AC microgrids [4,5,6]. With the rapid development of power electronics technology in recent years, DC microgrids have received more and more attention from researchers. Figure 1 shows a typical DC microgrid structure. In general, DC microgrids tend to integrate various distributed power sources and energy storage devices [7,8,9]. It mainly includes photovoltaic arrays, wind power generation devices, energy storage devices, etc. [10,11,12].

However, external disturbances often affect DC microgrids due to the integration of multiple distributed power sources [13,14]. Microgrids can be divided into multiple sub-microgrids according to geographical locations or different types to reduce the impact of external disturbances on them. The sub-microgrids are independent and serve as a backup to each other [15,16].

Multiple DC sub-microgrids are connected to the DC bus through parallel networking, and a switch is installed between each sub-microgrid and the DC bus to control the connection and removal of the sub-microgrid. The energy interconnection between sub-microgrids is performed through the DC bus. Each sub-microgrid consists of several converters connected in parallel in a similar geographic location. The power from the converters, excluding the power consumed by the local load and the power lost in the line resistance, is injected into the DC bus [17]. In addition, by adding energy storage devices and using bidirectional DC/DC converters to realize the bidirectional energy transmission between the energy storage devices and the DC bus, the power is stored when the power output energy is sufficient and released when the power output energy is low. This ensures the balance of energy supply and energy consumption in the DC microgrid cluster and maximizes the use of the power generated by the distributed power supply [18].

Although the sub-microgrids are independent, all sub-microgrids share a common control objective, i.e., the bus voltage is consistent with the voltage reference [19,20]. The steady-state value of the DC bus voltage cannot be changed when the sub-microgrid is removed and connected to the microgrid cluster system. Moreover, the sub-microgrid needs to be accurately distributed with current according to a set ratio, which is also a very important control objective for DC microgrid clusters [13,21,22].

To realize these control objectives for controlling DC microgrid cluster systems, scholars have proposed various hierarchical control methods for the microgrid cluster systems. The secondary control has been of wide concern by scholars. A distributed two-layer secondary controller based on fixed time has been proposed in [13]. This method improves the dynamic performance of the DC microgrid cluster system in fixed time based on the online measurement of adjacent sub-microgrids. Some scholars propose a coordinated power control strategy for DC microgrid clusters dominated by isolated bidirectional DC/DC converters [23]. This method can ensure the normal operation of the system when a sub-microgrid faults. To expand the operating range of the modular-based energy router and improve the multi-directional energy exchange of the DC microgrid cluster, a DC voltage regulation strategy and control method are proposed for a modular-based energy router in [15]. However, this method is mainly applicable for the scenarios including modular-based energy routers and may not be available for a common DC microgrid cluster.

In addition, some scholars deal with the tertiary control scheme, which can be applied to the power flow control of microgrid systems. Some scholars have proposed a distributed adaptive energy management system based on a cooperative power switching regulator [24]. However, whether this method is effective for DC microgrid cluster system needs to be further verified. A pinning control strategy is proposed in [25] that can be applied to DC microgrid cluster systems to adjust the power flow between each sub-microgrid.

Moreover, the authors in [26] concluded that the coordinated control among multiple sub-microgrids can be carried out with the idea of peer-to-peer control, but no specific microgrid cluster control strategy was proposed. The work presented in [27] proposed a hierarchical control strategy with three layers for the microgrid cluster system. Based on the traditional master-–lave control, the droop control and distributed communication network coordination control strategies are combined to achieve stable operation and regulation of the microgrid system. The hierarchical control architecture of the microgrid cluster proposed in [28] can be divided into three layers, where the bottom and middle layer controls are mainly responsible for the power distribution among the converters within a sub-microgrid, and the top layer control achieves coordinated control among sub-microgrids by adjusting the voltage reference value of each sub-microgrid. In [14], a decentralized peer-to-peer control of the microgrid cluster was proposed in the study of hybrid AC–DC microgrid clusters, and coordinated control between DC and AC sub-microgrids was achieved without communication busses. A commonly used control architecture was proposed before [29], and the control strategy consists of a droop-based primary controller for the bottom control and a secondary control, which compensates for the voltage deviations caused by the primary controller. This control scheme can be applied to parallel scenarios of BUCK and BOOST converters. However, the control architecture does not have plug-and-play functionality.

To sum up, the comparison of various hierarchical control methods for DC microgrids are summarized in

Table 1. Comparison of various hierarchical control methods for DC microgrids.

Control Methods	Characteristics	Merits	Demerits
Secondary control	Fixed time control [13]	Improving the dynamic performance	Rely on the online measurement
	Coordinated power control [23]	Normal operating under sub-microgrids fault	Mainly applicable to bidirectional DC/DC converters
	Modular energy tracker control [15]	Improving multidirectional energy exchange	May not be available for a common DC microgrid cluster
Tertiary control	Energy management system control [24]	Improving the voltage accuracy	Lacking operation of internal microgrids
	Power flow control [25]	Good robustness	Complex microgrid cluster is not considered
Master-slave control	Alternating direction method of multipliers [27]	Removing the coupling within the cluster and individual microgrid	Rely on the communication networks
	Cooperative distributed control [28]	Adjust voltage set point and mitigate load mismatches	Lack of flexibility, prone to single points of fault
Peer-to-peer control	Autonomous operation control [14]	Suitable for hybrid microgrids	Rely on interlinking converters
	Restraining limit cycle oscillations control [29]	Suppress oscillations caused by constant power loads	No plug-and-play functionality

. In the work presented before [30,31,32], a master–slave hierarchical control method and a peer-to-peer hierarchical control method were designed to control BOOST-type DC microgrid clusters to achieve the set control objectives. However, this cluster is a simple case where the input voltage sources have lower voltages than the DC bus voltage. When the DC microgrid cluster needs to integrate voltage sources with some voltages higher than the bus voltage and some lower than the bus voltage, both BOOST converters and BUCK converters are required for the microgrid cluster. The control strategy of a hybrid DC microgrid cluster is more complex because it contains multiple types of converters. Some distributed power sources can provide unstable power and are affected by other uncontrollable factors, such as photovoltaic arrays, wind power generation, etc. In this case, there is a need for energy storage devices in the microgrid cluster to store energy when the output power of distributed power sources is large and output energy when the output power of distributed voltage sources is zero or the output power is small, to ensure the stability of the DC bus voltage and ensure that all loads connected to the DC bus can obtain enough power. The energy storage device requires a bidirectional DC/DC converter as the interface converter to connect to the DC bus, resulting in a bidirectional energy flow between the energy storage device and the DC bus.

To realize the integration of distributed power sources of different voltage levels, this paper investigates a hybrid DC microgrid cluster containing different types of converters. In order to solve the problems of current distribution among sub-microgrids, current distribution among converters within sub-microgrids, and energy storage device operation mode switching, a peer-to-peer hierarchical control method is proposed for hybrid microgrid clusters. The main contributions of this paper are summarized as follows:

• For the specific structure and possible operating states of the hybrid microgrid cluster, an in-depth analysis of the control objectives that should be achieved under various scenarios is presented;
• The paper proposes a peer-to-peer hierarchical control method to achieve the desired control objectives of the hybrid microgrid cluster. Multiple operation scenarios of DC microgrid clusters are analyzed, and the top, mid, and bottom layers of control are designed;
• Simulation models and experimental platforms are built, and the simulation and experimental results verify the accuracy of the proposed control strategy and the fast plug-and-play regulation of the system.

The remainder of the paper is structured as follows. The structure and control objectives of the hybrid DC microgrid cluster are performed in Section 2. In Section 3, the operating modes of the bidirectional DC/DC converter are analyzed. The peer-to-peer hierarchical control method is illustrated in Section 4. In Section 5, the simulations and experiments are performed, and the results are discussed. Finally, the overall study is concluded in Section 6.

2. Structure and Control Objectives of the Hybrid DC Microgrid Cluster

The circuit structure of the hybrid microgrid cluster is shown in Figure 2. For the convenience of control, the converters in the microgrid cluster are grouped by type in this paper. The hybrid microgrid cluster contains 8 converters, of which 3 are BUCK converters, 3 are BOOST converters, and the remaining 2 are bidirectional DC/DC converters. The input voltage of the three BUCK converters is higher than the voltage of the DC bus, which together form the sub-microgrid #A. The three BUCK converters are numbered #1, #2, and #3. The input voltage of the three BOOST converters is lower than the voltage of the bus, which together form the sub-microgrid #B. The three BOOST converters are numbered #4, #5, and #6. The input voltage source of the two bidirectional DC/DC converters is the energy storage device. The input voltage source of the two bidirectional DC/DC converters is the energy storage device, whose voltage is lower than that of the DC bus, forming the sub-microgrid #C together. The two bidirectional DC/DC converters are numbered #7 and #8.

There is a line resistance between all converters and the DC bus. The line resistance is composed of the converter line resistance and the sub-microgrid line resistance. The line resistances of the eight converters are r₁~r₈ in turn, and the line resistances of the three sub-microgrids are r_A, r_B and r_C, respectively. Whether or not each converter is connected to the DC bus is decided by the converter switch and the sub-microgrid switch. The line switches of the eight converters are S₁~S_8, respectively, and the line switches of the three sub-microgrids are S_A, S_B, and S_C, respectively.

As shown in Figure 2, the voltage and current values required for control are indicated in red, where i₁~i₈ is the output current of the eight converters; in turn, u₁~u₆ is the output voltage of the first six converters; in turn, i_7a is the current flowing through the inductance L_7A in converter #7. i_7b is the current flowing through the inductance L_7B in converter #7, and i_8a is the current flowing through the inductance L_8A in converter #8. i_8b is the current flowing through the inductance L_8B in converter #8. i_sumA, i_sumB, and i_sumC are the output current of sub-microgrid A, sub-microgrid B, and sub-microgrid C, respectively. i_sum is the total load current, V_bus is the DC bus voltage, i_ch1 is the charging current of energy storage device #1, and i_ch2 is the charging current of energy storage device #2.

The control objectives of the DC microgrid cluster when the energy storage device releases power and all converters are in the connection state are as follows:

• The DC bus voltage must be controlled at the reference voltage value; otherwise, the DC microgrid cluster load will not obtain the rated power from the DC bus;
• The ratio of the output current of the three sub-microgrids to the total load current must be the same as the reference value of the sub-microgrid current distribution ratio;
• The output currents of the converters in the connection state inside sub-microgrid A and sub-microgrid B are equal;
• The output current ratio of the two bidirectional DC/DC converters needs to conform to the set ratio since the input power source in sub-micro-grid C is an energy storage device. In addition, the state of charge of the energy storage device may differ if two DC/DC converters output the same current. After a long time, the energy stored in one of the energy storage devices may be depleted while the other one still has a lot of stored energy.

The output current ratio of the two bidirectional DC/DC converters is related to the state of charge of the energy storage devices and the coordination rules among the energy storage devices, which are not deeply investigated here and are assumed to be the distribution ratio of m:n. The control objective of the hybrid microgrid cluster, in this case, is shown in Equation (1):

$$\left\{\begin{array}{c}{V}_{bus}=V_{ref}\\ \frac{i_{sumA}}{i_{sum}}={\chi }_{A\_ref} , i_1=i_2=i_3=\frac{i_{sumA}}{3}\\ \frac{i_{sumB}}{i_{sum}}={\chi }_{B\_ref} , i_4=i_5=i_6=\frac{i_{sumB}}{3}\\ \frac{i_{sumC}}{i_{sum}}={\chi }_{C\_ref}, i_7=\frac{m}{m+n}{i}_{sumC}, i_8=\frac{n}{m+n}{i}_{sumC} \end{array}\right.$$

(1)

where χ_{A_ref}, χ_{B_ref}, and χ_{C_ref} are the reference values of the current distribution ratio of the three sub-microgrids, respectively.

When a converter is removed from the DC microgrid cluster, the ratio of the output current to the total load current of the three microgrids must still be the same as the current distribution ratio reference value. In the case of converter #1 being removed, the control objective, in this case, is shown in Equation (2):

$$\left\{\begin{array}{c}{V}_{bus}=V_{ref}\\ \frac{i_{sumA}}{i_{sum}}={\chi }_{A\_ref}, i_1=0, i_2=i_3=\frac{i_{sumA}}{2}\\ \frac{i_{sumB}}{i_{sum}}={\chi }_{B\_ref}, i_4=i_5=i_6=\frac{i_{sumB}}{3}\\ \frac{i_{sumC}}{i_{sum}}={\chi }_{C\_ref}, i_7=\frac{m}{m+n}{i}_{sumC}, i_8=\frac{n}{m+n}{i}_{sumC}\end{array}\right.$$

(2)

When a sub-microgrid is removed from the DC microgrid cluster, the ratio of the currents of the remaining unremoved sub-microgrids needs to be kept constant. Considering that sub-microgrid A is excised, the ratio of i_sumB and i_sumC remains χ_{B_ref}:χ_{C_ref}, so the control objective, in this case, is shown in Equation (3):

$$\left\{\begin{array}{c}{V}_{bus}=V_{ref}\\ i_{sumA}=i_1=i_2=i_3=0\\ \frac{i_{sumB}}{i_{sum}}=\frac{{\chi }_{B\_ref}}{{\chi }_{B\_ref}+{\chi }_{C\_ref}}, i_4=i_5=i_6=\frac{i_{sumB}}{3}\\ \frac{i_{sumC}}{i_{sum}}=\frac{{\chi }_{C\_ref}}{{\chi }_{B\_ref}+{\chi }_{C\_ref}}, i_7=\frac{m}{m+n}{i}_{sumC}, i_8=\frac{n}{m+n}{i}_{sumC}\end{array}\right.$$

(3)

Energy storage devices mainly play an important role not only to output energy when the input power of the input voltage source is insufficient but also to store energy when the input power of the input voltage source is sufficient. The simple charging methods of energy storage devices are constant-current charging and constant-voltage charging.

The charging voltage remains constant in the process of constant-voltage charging; although the charging speed is fast, its charging current cannot be adjusted, and it is not easy for the bidirectional DC/DC converter in the DC microgrid cluster to control the voltage at both ends of the energy storage device. The charging current remains constant in the process of constant-current charging, and the charging current can be arbitrarily selected, which is beneficial to extend the life of the energy storage device, and it is easier to control the charging current of the energy storage device through the bidirectional DC/DC converter in the DC microgrid cluster.

Taking this into account, the energy storage devices of the microgrid cluster need to be charged by the improved constant-current charging method. The improved constant-current charging method divides the state of charge (SOC) of the energy storage device into several intervals, and each interval takes a specific charging current. When the SOC of the energy storage device is small, a larger current is used for charging, and when the SOC is large, a smaller current is used for charging until the energy storage device is fully charged and removed from the microgrid cluster.

After determining the charging mode of the energy storage device, the control objective of the DC microgrid cluster during the charging of the energy storage device is also determined. As the energy storage equipment charging needs to obtain energy from the DC bus, the output current of sub-microgrid A and sub-microgrid B needs to be increased in order to keep the DC bus voltage stable. The increase in the output current of the two sub-microgrids must be proportional, and the ratio of the output current of the two sub-microgrids cannot be changed; otherwise, the system will be out of control. The control objectives at this point can be expressed as follows:

$$\left\{\begin{array}{c}{V}_{bus}=V_{ref}\\ \frac{i_{sumA}}{i_{sum}-i_{sumC}}=\frac{{\chi }_{A\_ref}}{{\chi }_{A\_ref}+{\chi }_{B\_ref}} , i_1=i_2=i_3=\frac{i_{sumA}}{3}\\ \frac{i_{sumB}}{i_{sum}-i_{sumC}}=\frac{{\chi }_{B\_ref}}{{\chi }_{A\_ref}+{\chi }_{B\_ref}} , i_4=i_5=i_6=\frac{i_{sumB}}{3}\\ i_{ch1}=i_{ch1\_ref} , i_{ch2}=i_{ch2\_ref}\end{array}\right.$$

(4)

where i_{ch1_ref} is the charging current reference value of energy storage device #1, and i_{ch2_ref} is the charging current reference value of energy storage device #2. The charging current reference value of the energy storage device is determined by the state of charge of the energy storage device and the coordination rules among the energy storage devices, etc.

In the charging state of the energy storage device, if a converter in the sub-microgrid is removed, the output current ratio between sub-microgrid A and B should remain χ_{A_ref}:χ_{B_ref}. Taking the example that converter #1 in sub-microgrid A and converter #4 in sub-microgrid B are removed, the control objective, in this case, can be expressed as follows:

$$\left\{\begin{array}{c}{V}_{bus}=V_{ref}\\ \frac{i_{sumA}}{i_{sum}-i_{sumC}}=\frac{{\chi }_{A\_ref}}{{\chi }_{A\_ref}+{\chi }_{B\_ref}} , i_1=0, i_2=i_3=\frac{i_{sumA}}{2}\\ \frac{i_{sumB}}{i_{sum}-i_{sumC}}=\frac{{\chi }_{B\_ref}}{{\chi }_{A\_ref}+{\chi }_{B\_ref}} , i_4=0, i_5=i_6=\frac{i_{sumB}}{2}\\ i_{ch1}=i_{ch1\_ref} , i_{ch2}=i_{ch2\_ref}\end{array}\right.$$

(5)

In the charging state of the energy storage device, when a sub-microgrid is removed, then the remaining sub-microgrids provide the load current and the charging current. Taking the example of sub-microgrid A being removed, the control objective, in this case, can be expressed as follows:

$$\left\{\begin{array}{c}{V}_{bus}=V_{ref}\\ i_{sumA}=i_1=i_2=i_3=0\\ i_{sumB}=i_{sum}-i_{sumC}, i_4=i_5=i_6=\frac{i_{sumB}}{3}\\ i_{ch1}=i_{ch1\_ref} , i_{ch2}=i_{ch2\_ref}\end{array}\right.$$

(6)

3. Operating Modes of the Bidirectional DC/DC Converter

The converter #7 is used as an example to illustrate the operation mode of the bidirectional DC/DC converter in the microgrid cluster. The circuit structure of the converter #7 is shown in Figure 3. A bidirectional DC/DC converter consists of two capacitors, two inductors, four switching tubes, and four diodes. The bidirectional DC/DC converter is in BOOST operation mode when the energy storage device is discharged. On the other hand, the bidirectional DC/DC converter is in BUCK operation mode when the energy storage device is charged.

The equivalent circuit diagram of converter #7 in the BOOST operation mode is shown in Figure 4. In this operation mode, energy storage device #1 is discharged, VT_7A and VT_7B are turned off, and VD_7C and VD_7D are cut off due to the reverse voltage. VT_7C and VT_7D are controlled by PWM_7C and PWM_7D signals to turn on and turn off, respectively.

When PWM_7C is high level, VT_7C switches on, VD_7A bears reverse voltage and cutoff, L_7A stores electrical energy, and C_7B discharges to inject current into the DC bus. When PWM_7C is low level, VT_7C switches off, VD_7A switches on, L_7A discharges electrical energy, the energy storage device and L_7A are connected in series to charge C_7B and inject current into DC bus. Similarly, when PWM_7D is high level, VT_7D switches on, VD_7B bears reverse voltage and cutoff, L_7B stores electrical energy, and C_7B discharges to inject current into the DC bus. When PWM_7D is low level, VT_7D switches off, VD_7B switches on, L_7B discharges electrical energy, the energy storage device and L_7B are connected in series to charge C_7B and inject current into the DC bus.

In summary, L_7A, VT_7C, VD_7A, and C_7B form a BOOST circuit, and L_7B, VT_7D, VD_7B, and C_7B form a BOOST circuit. Therefore, converter #7 in BOOST operation mode can be seen as two BOOST converters connected in parallel. When the energy storage device is discharged, the output current of the converter is the object to be controlled. The commonly controlled quantity in the BOOST circuit is the inductor current. So, the output current control needs to be achieved indirectly by controlling the current in L_7A and L_7B.

The equivalent circuit of the converter #7 in the BUCK operation mode is shown in Figure 5. The bidirectional DC/DC converter in this operation mode obtains power from the DC bus, reduces the voltage, and then charges the power to the energy storage device. VT_7C and VT_7D are switched off in this operation mode, and VD_7A and VD_7B are cut off due to reverse voltage. VT_7A and VT_7B are controlled by PWM_7A and PWM_7B signals to turn on and off, respectively.

When PWM_7A is high level, VT_7A switches on, and VD_7C cuts off due to reverse voltage; at this time, L_7A and C_7A store electrical energy, and energy storage device #1 charges. When PWM_7A is low level, VT_7A switches off, and VD_7C switches on. At this time, L_7A and C_7A release electrical energy, and energy storage device #1 charges. Similarly, when PWM_7B is high level, VT_7B switches on, and VD_7D cuts off due to reverse voltage, at which time L_7B and C_7A store electrical energy, and energy storage device #1 charges. When PWM_7B is low level, VT_7B switches off, and VD_7D switches on, at which time L_7B and C_7A discharge electrical energy, and energy storage device #1 charges.

In summary, VT_7A, L_7A, VD_7C, and C_7A form a BUCK circuit; VT_7B, L_7B, VD_7D, and C_7A form a BUCK circuit. Therefore, converter #7 in BUCK operation mode can be seen as two BUCK converters connected in parallel. When the energy storage device is charged, the charging current of the energy storage device is the object to be controlled. The capacitor voltage is equal at the beginning of a switching cycle and at the end of that switching cycle. So, it can be assumed that the average value of the capacitor current is 0, and the charging current is equal to the sum of the currents flowing through L_7A and L_7B. Therefore, the charging current can be managed by controlling the current flowing in L_7A and L_7B.

4. Peer-to-Peer Hierarchical Control Method

The peer-to-peer hierarchical control method has a better control effect than the master–slave hierarchical control method. Therefore, an accurate peer-to-peer hierarchical control method is proposed in this paper for hybrid DC microgrid groups.

The output current relationship between each sub-microgrid in the two energy storage device charge and discharge cases is completely different, and there is no unified expression for the output current relationship between the two cases. The switching states of the diodes and switching tubes in the bidirectional DC/DC converter are different in the two cases of energy storage device charge and discharge. Therefore, when designing the peer-to-peer hierarchical control method for hybrid DC microgrid clusters, the two cases of charging and discharging of energy storage devices need to be studied separately.

4.1. Top-Level Control of Peer-to-Peer Hierarchical Control Method

The main objective of the top-level control is to determine the output current reference value of converters within each sub-microgrid based on the connection status of converters, total load current, output current of each sub-microgrid, and current distribution ratio reference value. The variables S₁, S₂, S₃, S₄, S₅, S₆, S₇, and S₈ indicate whether the converters #1~#8 are in the connection state, respectively. When the variable is equal to 1, it means that the corresponding converter has been connected to the DC microgrid cluster, and when the variable is equal to 0, it means that the converter has been removed from the microgrid cluster. S_α, S_β, and S_γ indicate whether the sub-microgrid A, sub-microgrid B, and sub-microgrid C are connected to the microgrid cluster, respectively. The logical expressions for calculating S_α, S_β, and S_γ are as follows:

$$\left\{\begin{array}{c}{S}_{\alpha }=S_A(1-{\overline{S}}_1{\overline{S}}_2{\overline{S}}_3)\\ S_{\beta }=S_B(1-{\overline{S}}_4{\overline{S}}_5{\overline{S}}_6)\\ S_{\gamma }=S_C(1-{\overline{S}}_7{\overline{S}}_8)\end{array}\right.$$

(7)

where S_A, S_B, and S_C are the line switches opening states of the sub-microgrid A, B, and C, respectively. Setting up n_A and n_B denotes the number of converters connected to sub-microgrid A and B, respectively. n_A and n_B can be expressed as:

$$\left\{\begin{array}{c}{n}_A=S_1+S_2+S_3\\ n_B=S_4+S_5+S_6\end{array}\right.$$

(8)

When all sub-microgrids are in the connection state (S_α = S_β = S_γ = 1), the expected values of output currents of each converter are expressed as:

$$\left\{\begin{array}{c}{i}_1=\frac{{\chi }_{A\_ref}{i}_{sum}{S}_1}{n_A}, i_2=\frac{{\chi }_{A\_ref}{i}_{sum}{S}_2}{n_A}, i_3=\frac{{\chi }_{A\_ref}{i}_{sum}{S}_3}{n_A}\\ i_4=\frac{{\chi }_{B\_ref}{i}_{sum}{S}_4}{n_B}, i_5=\frac{{\chi }_{B\_ref}{i}_{sum}{S}_5}{n_B}, i_6=\frac{{\chi }_{B\_ref}{i}_{sum}{S}_6}{n_B}\\ i_7=\frac{m{\chi }_{C\_ref}{i}_{sum}{S}_7}{m{S}_7+n{S}_8}, i_8=\frac{n{\chi }_{C\_ref}{i}_{sum}{S}_8}{m{S}_7+n{S}_8}\end{array}\right.$$

(9)

Similarly, each possible scenario should be discussed in turn. When sub-microgrid A is in the removed state, and the rest of the sub-microgrids are in the connection state, S_α = 0 and S_β = S_γ = 1. When sub-microgrid B is in the removed state, and the rest of the sub-microgrids are in the connection state, S_β = 0 and S_α = S_γ = 1. When sub-microgrid C is in the removed state, and the rest of the sub-microgrids are in the connection state, S_γ = 0 and S_α = S_β = 1. When only sub-microgrid A in the microgrid cluster is in the connection state, and the rest of the sub-microgrids are in the removed state, S_α = 1, S_β = S_γ = 0. When only sub-microgrid B in the microgrid cluster is in the connection state, and the rest of the sub-microgrids are in the removed state, S_β = 1, S_α = S_γ = 0. When only sub-microgrid C in the microgrid cluster is in the connection state, and the rest of the sub-microgrids are in the removed state, S_γ = 1, S_α = S_β = 0.

By combining all the above cases, the expected value of the output current of each converter of sub-microgrid A can be expressed as:

$$\left\{\begin{array}{c}{i}_1=\frac{S_{\alpha }{\chi }_{A\_ref}{i}_{sum}{S}_1}{(S_{\alpha }{\chi }_{A\_ref}+S_{\beta }{\chi }_{B\_ref}+S_{\gamma }{\chi }_{C\_ref})n_A}\\ i_2=\frac{S_{\alpha }{\chi }_{A\_ref}{i}_{sum}{S}_2}{(S_{\alpha }{\chi }_{A\_ref}+S_{\beta }{\chi }_{B\_ref}+S_{\gamma }{\chi }_{C\_ref})n_A}\\ i_3=\frac{S_{\alpha }{\chi }_{A\_ref}{i}_{sum}{S}_3}{(S_{\alpha }{\chi }_{A\_ref}+S_{\beta }{\chi }_{B\_ref}+S_{\gamma }{\chi }_{C\_ref})n_A}\end{array}\right.$$

(10)

The expected value of the output current of each converter of sub-microgrid B can be expressed as follows:

$$\left\{\begin{array}{c}{i}_4=\frac{S_{\beta }{\chi }_{B\_ref}{i}_{sum}{S}_4}{(S_{\alpha }{\chi }_{A\_ref}+S_{\beta }{\chi }_{B\_ref}+S_{\gamma }{\chi }_{C\_ref})n_B}\\ i_5=\frac{S_{\beta }{\chi }_{B\_ref}{i}_{sum}{S}_5}{(S_{\alpha }{\chi }_{A\_ref}+S_{\beta }{\chi }_{B\_ref}+S_{\gamma }{\chi }_{C\_ref})n_B}\\ i_6=\frac{S_{\beta }{\chi }_{B\_ref}{i}_{sum}{S}_6}{(S_{\alpha }{\chi }_{A\_ref}+S_{\beta }{\chi }_{B\_ref}+S_{\gamma }{\chi }_{C\_ref})n_B}\end{array}\right.$$

(11)

The expected value of the output current of each converter of sub-microgrid C can be expressed as:

$$\left\{\begin{array}{c}{i}_4=\frac{S_{\beta }{\chi }_{B\_ref}{i}_{sum}{S}_4}{(S_{\alpha }{\chi }_{A\_ref}+S_{\beta }{\chi }_{B\_ref}+S_{\gamma }{\chi }_{C\_ref})n_B}\\ i_5=\frac{S_{\beta }{\chi }_{B\_ref}{i}_{sum}{S}_5}{(S_{\alpha }{\chi }_{A\_ref}+S_{\beta }{\chi }_{B\_ref}+S_{\gamma }{\chi }_{C\_ref})n_B}\\ i_6=\frac{S_{\beta }{\chi }_{B\_ref}{i}_{sum}{S}_6}{(S_{\alpha }{\chi }_{A\_ref}+S_{\beta }{\chi }_{B\_ref}+S_{\gamma }{\chi }_{C\_ref})n_B}\end{array}\right.$$

(12)

The current reference value must be consistent with the expected value of the output current to achieve the control objective. So, according to Equations (10)–(12), the current reference value can be expressed as:

$$\left\{\begin{array}{c}{i}_{ref\_A}=\frac{S_{\alpha }{\chi }_{A\_ref}{i}_{sum}}{(S_{\alpha }{\chi }_{A\_ref}+S_{\beta }{\chi }_{B\_ref}+S_{\gamma }{\chi }_{C\_ref})n_A}\\ i_{ref\_B}=\frac{S_{\beta }{\chi }_{B\_ref}{i}_{sum}}{(S_{\alpha }{\chi }_{A\_ref}+S_{\beta }{\chi }_{B\_ref}+S_{\gamma }{\chi }_{C\_ref})n_B}\\ i_{ref7}=\frac{m{S}_{\gamma }{\chi }_{C\_ref}{i}_{sum}{S}_7}{(S_{\alpha }{\chi }_{A\_ref}+S_{\beta }{\chi }_{B\_ref}+S_{\gamma }{\chi }_{C\_ref})(m{S}_7+n{S}_8)}\\ i_{ref8}=\frac{n{S}_{\gamma }{\chi }_{C\_ref}{i}_{sum}{S}_8}{(S_{\alpha }{\chi }_{A\_ref}+S_{\beta }{\chi }_{B\_ref}+S_{\gamma }{\chi }_{C\_ref})(m{S}_7+n{S}_8)}\end{array}\right.$$

(13)

where i_{ref_A} is the output current reference value of the three converters of sub-microgrid A, i_{ref_B} is the output current reference value of the three converters of sub-microgrid B, i_ref7 is the output current reference value of converter #7, and i_ref8 is the output current reference value of converter #8.

When the energy storage device is charging, sub-microgrid C is presented as a load on the DC bus, so the top-level control only needs to calculate the current reference values within sub-microgrid A and B.

Combining various possible operating conditions, when the energy storage device is charging, the expected value of the output current of converters #1 to #6 can be expressed as:

$$\left\{\begin{array}{c}\begin{array}{c}{i}_1=\frac{{\chi }_{A\_ref}{S}_{\alpha }(i_{sum}-i_{sumC})S_1}{({\chi }_{A\_ref}{S}_{\alpha }+{\chi }_{B\_ref}{S}_{\beta })n_A},i_2=\frac{{\chi }_{A\_ref}{S}_{\alpha }(i_{sum}-i_{sumC})S_2}{({\chi }_{A\_ref}{S}_{\alpha }+{\chi }_{B\_ref}{S}_{\beta })n_A}\hfill \\ i_3=\frac{{\chi }_{A\_ref}{S}_{\alpha }(i_{sum}-i_{sumC})S_3}{({\chi }_{A\_ref}{S}_{\alpha }+{\chi }_{B\_ref}{S}_{\beta })n_A},i_4=\frac{{\chi }_{B\_ref}{S}_{\beta }(i_{sum}-i_{sumC})S_4}{({\chi }_{A\_ref}{S}_{\alpha }+{\chi }_{B\_ref}{S}_{\beta })n_B}\hfill \end{array}\\ i_5=\frac{{\chi }_{B\_ref}{S}_{\beta }(i_{sum}-i_{sumC})S_5}{({\chi }_{A\_ref}{S}_{\alpha }+{\chi }_{B\_ref}{S}_{\beta })n_B},i_6=\frac{{\chi }_{B\_ref}{S}_{\beta }(i_{sum}-i_{sumC})S_6}{({\chi }_{A\_ref}{S}_{\alpha }+{\chi }_{B\_ref}{S}_{\beta })n_B}\end{array}\right.$$

(14)

To obtain a uniform expression for the current reference value, the variable λ is used to characterize the state of the energy storage device. λ is equal to 1 when the energy storage device is discharged, and λ is equal to 0 when the energy storage device is charged. i_ref7 and i_ref8 will not be used for control when λ = 0. Therefore, the current reference value can be expressed as:

$$\left\{\begin{array}{c}{i}_{ref\_A}=\frac{\lambda S_{\alpha }{\chi }_{A\_ref}{i}_{sum}}{(S_{\alpha }{\chi }_{A\_ref}+S_{\beta }{\chi }_{B\_ref}+S_{\gamma }{\chi }_{C\_ref})n_A}+\frac{(1-\lambda ){\chi }_{A\_ref}{S}_{\alpha }(i_{sum}-i_{sumC})}{({\chi }_{A\_ref}{S}_{\alpha }+{\chi }_{B\_ref}{S}_{\beta })n_A}\\ i_{ref\_B}=\frac{\lambda S_{\beta }{\chi }_{B\_ref}{i}_{sum}}{(S_{\alpha }{\chi }_{A\_ref}+S_{\beta }{\chi }_{B\_ref}+S_{\gamma }{\chi }_{C\_ref})n_B}+\frac{(1-\lambda ){\chi }_{B\_ref}{S}_{\beta }(i_{sum}-i_{sumC})}{({\chi }_{A\_ref}{S}_{\alpha }+{\chi }_{B\_ref}{S}_{\beta })n_B}\\ i_{ref7}=\frac{\lambda m{S}_{\gamma }{\chi }_{C\_ref}{i}_{sum}{S}_7}{(S_{\alpha }{\chi }_{A\_ref}+S_{\beta }{\chi }_{B\_ref}+S_{\gamma }{\chi }_{C\_ref})(m{S}_7+n{S}_8)}\\ i_{ref8}=\frac{\lambda n{S}_{\gamma }{\chi }_{C\_ref}{i}_{sum}{S}_8}{(S_{\alpha }{\chi }_{A\_ref}+S_{\beta }{\chi }_{B\_ref}+S_{\gamma }{\chi }_{C\_ref})(m{S}_7+n{S}_8)}\end{array}\right.$$

(15)

In order to prevent the calculation of the current reference value with a denominator being 0 and causing an error to be declared, it is necessary to superimpose a very small positive number ε (ε → 0) on the denominator part of all equations in Equation (15) that does not affect the result, which can be expressed as:

$$\left\{\begin{array}{c}{i}_{ref\_A}=\frac{\lambda S_{\alpha }{\chi }_{A\_ref}{i}_{sum}}{(S_{\alpha }{\chi }_{A\_ref}+S_{\beta }{\chi }_{B\_ref}+S_{\gamma }{\chi }_{C\_ref})n_A+\epsilon }+\frac{(1-\lambda ){\chi }_{A\_ref}{S}_{\alpha }(i_{sum}-i_{sumC})}{({\chi }_{A\_ref}{S}_{\alpha }+{\chi }_{B\_ref}{S}_{\beta })n_A+\epsilon }\\ i_{ref\_B}=\frac{\lambda S_{\beta }{\chi }_{B\_ref}{i}_{sum}}{(S_{\alpha }{\chi }_{A\_ref}+S_{\beta }{\chi }_{B\_ref}+S_{\gamma }{\chi }_{C\_ref})n_B+\epsilon }+\frac{(1-\lambda ){\chi }_{B\_ref}{S}_{\beta }(i_{sum}-i_{sumC})}{({\chi }_{A\_ref}{S}_{\alpha }+{\chi }_{B\_ref}{S}_{\beta })n_B+\epsilon }\\ i_{ref7}=\frac{\lambda m{S}_{\gamma }{\chi }_{C\_ref}{i}_{sum}{S}_7}{(S_{\alpha }{\chi }_{A\_ref}+S_{\beta }{\chi }_{B\_ref}+S_{\gamma }{\chi }_{C\_ref})(m{S}_7+n{S}_8)+\epsilon }\\ i_{ref8}=\frac{\lambda n{S}_{\gamma }{\chi }_{C\_ref}{i}_{sum}{S}_8}{(S_{\alpha }{\chi }_{A\_ref}+S_{\beta }{\chi }_{B\_ref}+S_{\gamma }{\chi }_{C\_ref})(m{S}_7+n{S}_8)+\epsilon }\end{array}\right.$$

(16)

Equations (7), (8), and (16) are the operations included in the top-level control of the peer-to-peer hierarchical control method.

4.2. Mid-Level and Bottom-Level Control of Peer-to-Peer Hierarchical Control Method

The mid-level and bottom-level control objectives of both sub-microgrid A and B are to make the output current of the converters in the group follow the current reference value obtained from the top-level control, while ensuring that the DC bus voltage is equal to the voltage reference value. The control block diagram of sub-microgrid A is shown in Figure 6, and that of sub-microgrid B is shown in Figure 7. The basic component unit of sub-microgrid A is the BUCK converter, and the basic component unit of sub-microgrid B is the BOOST converter. The principles of mid-level and bottom-level control are the same for sub-microgrids A and B.

The mid-level control consists of bus voltage compensation control and droop coefficient correction control, and the bottom-level control consists of droop control and voltage closed-loop control. As shown in Figure 6, PWM₁, PWM₂, and PWM₃ are used to control the turn-on and turn-off of VT₁ in converter #1, VT₂ in converter #2, and VT₃ in converter #3, respectively. As shown in Figure 7, PWM₄, PWM₅, and PWM₆ are used to control the turn-on and turn-off of VT₄ in converter #4, VT₅ in converter #5, and VT₆ in converter #6, respectively. The droop coefficient reference value K_ref is a constant.

The control principles of sub-microgrid A and sub-microgrid B are to change the voltage inner loop reference value by continuously adjusting the droop coefficient, which in turn changes the PWM signal duty cycle of the switching tubes, thus realizing the tracking control of the current reference value. At the same time, the DC bus voltage is accurately managed by compensating control.

The control block diagram of sub-microgrid C during the energy storage device is discharged as shown in Figure 8. When the energy storage device is discharged, both converters #7 and #8 are in BOOST operation mode; i₇ and i₈ are the state quantities to be controlled. VT_7A and VT_7B in converter #7 are continuously off, and PWM_7C and PWM_7D are used to control the turn-on and turn-off of VT_7C and VT_7D. VT_8A and VT_8B in converter #8 are continuously off, and PWM_8C and PWM_8D are used to control the turn-on and turn-off of VT_7C and VT_7D.

The output current directions of energy storage devices #1 and #2 are opposite to the positive directions of i_ch1 and i_ch2, labeled in Figure 2, so −i_ch1 and −i_ch2 are used to indicate the output current of energy storage devices #1 and #2, respectively.

The control block diagram of the two DC/DC converters in the sub-microgrid C is similar when the energy storage device is discharged. The controller inputs the difference between the current reference value and the output current value into the PI controller and then obtains the output current compensation amount of the energy storage device. The output current of the energy storage device is superimposed on the output current compensation amount and divided by 2 to obtain the current reference value of the two inductors in the converter, and, finally, the inductor current closed-loop control is performed. By assuming the relationship between the output current of the converter and the current reference value, the regulation process can be obtained as follows:

$$\left\{\begin{array}{c}\left\{\begin{array}{c}{i}_{ref7}>i_7\Rightarrow i_{7a\_ref}\uparrow ,i_{7b\_ref}\uparrow \Rightarrow d_{7C}\uparrow ,d_{7D}\uparrow \Rightarrow i_{7a}\uparrow ,i_{7b}\uparrow \Rightarrow i_7\uparrow \Rightarrow i_{ref7}=i_7\\ i_{ref7}<i_7\Rightarrow i_{7a\_ref}\downarrow ,i_{7b\_ref}\downarrow \Rightarrow d_{7C}\downarrow ,d_{7D}\downarrow \Rightarrow i_{7a}\downarrow ,i_{7b}\downarrow \Rightarrow i_7\downarrow \Rightarrow i_{ref7}=i_7\end{array}\right.\\ \left\{\begin{array}{c}{i}_{ref8}>i_8\Rightarrow i_{8a\_ref}\uparrow ,i_{8b\_ref}\uparrow \Rightarrow d_{8C}\uparrow ,d_{8D}\uparrow \Rightarrow i_{8a}\uparrow ,i_{8b}\uparrow \Rightarrow i_8\uparrow \Rightarrow i_{ref8}=i_8\\ i_{ref8}<i_8\Rightarrow i_{8a\_ref}\downarrow ,i_{8b\_ref}\downarrow \Rightarrow d_{8C}\downarrow ,d_{8D}\downarrow \Rightarrow i_{8a}\downarrow ,i_{8b}\downarrow \Rightarrow i_8\downarrow \Rightarrow i_{ref8}=i_8\end{array}\right.\end{array}\right.$$

(17)

As seen from Equation (17), the controller will adjust the output current of the converter to be exactly consistent with the current reference value regardless of the magnitude relationship between the output current of the converter and the current reference value.

The control block diagram of sub-microgrid C while the energy storage device is charging is shown in Figure 9.

When the energy storage device is charging, converters #7 and #8 are in BUCK operation mode, and the charging currents i_ch1 and i_ch2 of the energy storage device are the state quantities to be controlled. VT_7C and VT_7D in converter #7 are continuously off, and PWM_7A and PWM_7B are used to control the turn-on and turn-off of VT_7A and VT_7B. VT_8C and VT_8D in converter #8 are continuously off, and PWM_8A and PWM_8B are used to control the turn-on and turn-off of VT_7A and VT_7B.

The actual direction of current flowing In L_7A, L_7B, L_8A, and L_8B is opposite to the positive direction of i_7a, i_7b, i_7c, and i_7d, labeled in Figure 2, so they are denoted by −i_7a, −i_7b, −i_7c, and −i_7d to indicate the magnitude (absolute value) of the currents flowing in L_7A, L_7B, L_8A, and L_8B.

The control block diagram of the two converters in sub-microgrid C is also similar when the energy storage device is charged. The controller inputs the difference between the charging current reference value of the energy storage device and the charging current into the PI controller to obtain the charging current correction value. The charging current is superimposed on the charging current correction value and then divided by 2 to obtain the current reference values of the two inductors in the converter, and, finally, the inductor current closed-loop control is performed. The regulation process can be obtained by assuming the relationship between the charging current of the energy storage device and the charging current reference value as follows:

$$\left\{\begin{array}{c}\left\{\begin{array}{c}{i}_{ch1\_ref}>i_{ch1}\Rightarrow i_{7a\_ref}\uparrow ,i_{7b\_ref}\uparrow \Rightarrow d_{7A}\uparrow ,d_{7B}\uparrow \Rightarrow -i_{7a}\uparrow ,-i_{7b}\uparrow \Rightarrow i_{ch1}\uparrow \Rightarrow i_{ch1\_ref}=i_{ch1}\\ i_{ch1\_ref}<i_{ch1}\Rightarrow i_{7a\_ref}\downarrow ,i_{7b\_ref}\downarrow \Rightarrow d_{7A}\downarrow ,d_{7B}\downarrow \Rightarrow -i_{7a}\downarrow ,-i_{7b}\downarrow \Rightarrow i_{ch1}\downarrow \Rightarrow i_{ch1\_ref}=i_{ch1}\end{array}\right.\\ \left\{\begin{array}{c}{i}_{ch2\_ref}>i_{ch2}\Rightarrow i_{8a\_ref}\uparrow ,i_{8b\_ref}\uparrow \Rightarrow d_{8A}\uparrow ,d_{8B}\uparrow \Rightarrow -i_{8a}\uparrow ,-i_{8b}\uparrow \Rightarrow i_{ch2}\uparrow \Rightarrow i_{ch2\_ref}=i_{ch2}\\ i_{ch2\_ref}<i_{ch2}\Rightarrow i_{8a\_ref}\downarrow ,i_{8b\_ref}\downarrow \Rightarrow d_{8A}\downarrow ,d_{8B}\downarrow \Rightarrow -i_{8a}\downarrow ,-i_{8b}\downarrow \Rightarrow i_{ch2}\downarrow \Rightarrow i_{ch2\_ref}=i_{ch2}\end{array}\right.\end{array}\right.$$

(18)

As can be seen from Equation (18), the controller will regulate the charging current of the energy storage device until it is completely consistent with the reference value of the charging current, regardless of the magnitude relationship between the charging current of the energy storage device and the reference value of the charging current.

A flow chart of peer-to-peer hierarchical control is shown in Figure 10. This diagram gives details of the information transfer relationship between the top, mid, and bottom levels of the peer-to-peer hierarchical control.

5. Results and Discussion

5.1. Simulation Results and Discussion

To test and verify whether the peer-to-peer hierarchical control method proposed in this paper can effectively control the hybrid DC microgrid cluster, a microgrid cluster model, as shown in Figure 2, is built in the PLECS simulation model. The simulations of converter-by-converter removal, converter-by-converter connection, bidirectional DC/DC converter current distribution ratio variation, energy storage devices working mode switching, and the converter input voltage fluctuation are performed in this simulation model. Considering the steady-state and dynamic performance of the system, the PI controller parameters are designed. In addition, the system performance is corrected according to the time domain and frequency domain performance indicators. For example, the system overshoot is specified to be less than 30%, and the amplitude margin should be greater than 5 dB, etc. The circuit and control parameters of the hybrid microgrid cluster are shown in

Table 2. Circuit parameters and control parameters for the DC hybrid microgrid cluster.

Parameters	Symbols and Values	Parameters	Symbols and Values
Group A converters input voltage	Vdc1 = Vdc2 = Vdc3 = 90V	Sub-microgrid A line resistance	rA = 0.2 Ω
Group B converters input voltage	Vdc4 = Vdc5 = Vdc6 = 48V	Sub-microgrid B line resistance	rB = 0.4 Ω
Energy storage device voltage	Vdc7 = Vdc8 = 48V	Sub-microgrid C line resistance	rC = 0.8 Ω
Reference value of droop coefficient	Kref = 30	Control program run frequency	f0 = 20 kHz
Frequency of PWM	fs = 20 kHz	PWM carrier amplitude	Vm = 1
Kp1 of sub-microgrid A	0.1	Ki1 of sub-microgrid A	500
Kp2 of sub-microgrid A	1	Ki2 of sub-microgrid A	100
Kp3 of sub-microgrid A	0.1	Ki3 of sub-microgrid A	10
Kp1 of sub-microgrid B	0.3	Ki1 of sub-microgrid B	3000
Kp2 of sub-microgrid B	1	Ki2 of sub-microgrid B	100
Kp3 of sub-microgrid B	0.01	Ki3 of sub-microgrid B	0.1
Kp1 of sub-microgrid C	0.1	Ki1 of sub-microgrid C	1.5
Kp2 of sub-microgrid C	0.1	Ki2 of sub-microgrid C	1.5
Kp3 of sub-microgrid C	2	Ki3 of sub-microgrid C	200
Kp4 of sub-microgrid C	1	Ki4 of sub-microgrid C	100
Kp5 of sub-microgrid C	2	Ki5 of sub-microgrid C	200

.

5.1.1. Simulation Results of Converter’s Removal from Hybrid DC Microgrid Clusters

To verify the effect of the converter’s removal on the hybrid DC microgrid cluster, simulations are performed for the following conditions. During 0~1s, all the converters are in the connection state. Converter #3 is removed at 1 s, and converter #4 is removed at 1.3 s, converter #5 is removed at 1.6 s, and converter #6 is removed at 1.9 s. During the whole simulation, χ_{A_ref} = 16.7%, χ_{B_ref} = 33.3%, χ_{C_ref} = 50%, m:n = 2:3, and S₁ and S₂ are in the closed state. The DC bus voltage reference value V_ref = 60 V. The obtained simulation waveforms are shown in Figure 11.

As shown in Figure 11a, the removal of converters #3, #4, and #5 do not change the total output current in the steady state of the sub-microgrid. The steady output current of sub-microgrid A is always 2 A, the steady output current of sub-microgrid B is always 4A, and the steady output current of sub-microgrid C is always 6 A. The proportion of each sub-microgrid to the total load current is the same as the proportional reference value. Converter #6 is removed at 1.9 s, which means that the whole sub-microgrid #B is completely removed from the microgrid group, and the current can only be supplied by sub-microgrids A and C. The output current of sub-microgrid A is 3 A, and the output current of sub-microgrid B is 9 A at 2.3 s. The ratio of the output currents of the two sub-microgrids is 1:3, which is consistent with χ_{A_ref}: χ_{B_ref,} and the control objective is achieved.

As shown in Figure 11b,c, the output currents between the converters in the connection state are equal regardless of how many are in the connection state in sub-microgrid A and B. As shown in Figure 11d, the output currents of converters #7 and #8 are following the 2:3 ratio throughout, which is consistent with the set current distribution ratio m:n.

The above simulation results show that the hybrid microgrid cluster with peer-to-peer hierarchical control can maintain the output current of the sub-microgrid at the steady state when a single converter is removed, and the ratio of the output currents of the remaining sub-microgrids can be maintained when the whole sub-microgrid is removed. The output currents of the remaining converters in the sub-microgrid are still equal after the converters are removed.

5.1.2. Simulation Results of Converter Connected to Hybrid DC Microgrid Clusters

To verify the effect of converters connected to the hybrid DC microgrid cluster, simulations are performed for the following conditions. Converters #4, #5, #6, #7, and #8 are connected during 0 to 1 s. Converter #1 is connected at 1 s, converter #2 is connected at 1.7 s, and converter #3 is connected at 2.4 s. During the whole simulation, χ_{A_ref} = 50%, χ_{B_ref} = 33.3%, χ_{C_ref} = 16.7%, m:n = 2:3, and S₁ and S₂ are in the closed state. The DC bus voltage reference value V_ref = 60 V. The obtained simulation waveform is shown in Figure 12.

As shown in Figure 12a, before converter #1 is connected, the output current of sub-microgrid B is 8 A, and that of sub-microgrid C is 4 A. The ratio of the output currents of the two sub-microgrids is 2:1, which is equal to χ_{B_ref}: χ_{C_ref}. After converter #1 is connected, the output current of sub-microgrid A rises sharply and then gradually stabilizes at 6 A. Meanwhile, the output currents of sub-microgrid B and C stabilize at 4 A and 2 A, respectively. After converters #2 and #3 were connected, the output currents of sub-microgrid A both declined, and the output currents of sub-microgrid B and C both rise. After the regulation of time duration 0.2 s, the output currents of sub-microgrids both stabilized gradually and were equal to the output currents before the converter was connected.

As shown in Figure 12b, the output currents of converters in sub-microgrid A are equal regardless of the number of connected converters (except 0), and the total current of all converters is 6 A. The output currents of all converters fluctuate periodically because of the perturbation introduced by the converter connection. As shown in Figure 12c,d, the converters within sub-microgrid B and C output currents according to the control requirements.

The above simulation results show that the hybrid microgrid cluster with peer-to-peer hierarchical control can still operate stably when converters are connected, and the newly connected converters can work in coordination with the rest of the converters and output current according to the control requirements. This indicates that the peer-to-peer hierarchical control method has strong plug-and-play performance, and the microgrid cluster with the peer-to-peer hierarchical control method can increase the number of converters and the number of sub-microgrids according to its demand.

5.1.3. Simulation Results of Bidirectional DC/DC Converter Current Distribution Ratio Variation

To verify whether the microgrid cluster can be quickly adjusted when the current distribution ratio of two bidirectional DC/DC converters changes, simulations are performed for the following conditions. The current distribution ratio is set as m:n = 2:3 during 0~1 s, m:n = 1:2 during 1~1.5 s, m:n = 1:1 during 1.5~2 s, and m:n = 3:2 during 2~2.5 s. During the whole simulation, χ_{A_ref} = 16.7%, χ_{B_ref} = 33.3%, χ_{C_ref} = 50%, and S₁ and S₂ are in the closed state. The DC bus voltage reference value V_ref = 60 V. The obtained simulation waveform is shown in Figure 13.

As shown in Figure 13a, the change in current distribution ratio of the two bidirectional DC/DC converters in sub-microgrid C causes fluctuations in the output currents of the three sub-microgrids for a short period of time. The output current of sub-microgrid C fluctuates the most, reaching the maximum value of 6.5 A at 1.008 s and the minimum value of 5.3 A at 1.508 s. The current fluctuation of sub-microgrid A and sub-microgrid B is in the opposite direction to that of sub-microgrid C; the main purpose is to reduce the impact of the current fluctuation of sub-microgrid C on the total load current. As shown in Figure 13b–d, the converter currents inside sub-microgrid A and sub-microgrid B are still equally divided. When the system reaches stability, the ratio of the output currents of converter #7 to converter #8 is exactly the same as the set current distribution ratio.

5.1.4. Simulation Results of Energy Storage Devices Working Mode Switching

To verify the effect of energy storage device operating mode switching on the hybrid DC microgrid cluster, simulations were performed for the following conditions. During 0 to 0.8 s, the energy storage device is in the discharge state. During 0.8 to 1.5 s, the energy storage device is in the charge state, i_{ch1_ref} = 5 A, i_{ch2_ref} = 3 A. During 1.5–2.2 s, the energy storage device is in the charging state, i_{ch1_ref} = 3 A, i_{ch2_ref} = 2 A. During 2.2~2.6 s, the energy storage device gradually stops charging, i_{ch1_ref} = 0 A, i_{ch2_ref} = 0 A. During 2.6 to 3.3 s, the energy storage device is in the discharge state again. During the whole simulation, χ_{A_ref} = 50%, χ_{B_ref} = 33.3%, χ_{C_ref} = 16.7%, m:n = 2:3, and S₁ and S₂ are in the closed state, and all converters are connected. The DC bus voltage reference value V_ref = 60 V. The obtained simulation waveform is shown in Figure 14 and Figure 15.

As shown in Figure 14a, the output current of sub-microgrid C is always negative when the energy storage device is charging, and the bidirectional DC/DC converter continuously obtains power from the DC bus to charge the energy storage device. The larger the charging current reference value of the two energy storage devices, the larger the current flowing into sub-microgrid C, and the larger the output current of sub-microgrid A and B is required. After the process of discharging, charging, and discharging, the system reaches stability at 3 s, the currents of sub-microgrid A, B, and C are 6 A, 4 A, and 2 A, respectively, which account for 50%, 33.3%, and 16.7% of the total load current, respectively. When the energy storage device is charged and the system reaches the steady state, the ratio of the currents of sub-microgrid A and sub-microgrid B is always 3:2, which is the same as χ_{A_ref}: χ_{B_ref}.

Figure 14b,c illustrate that the output currents between the converters within sub-microgrid A and B are always equal, and the converters within the sub-microgrid have high accuracy in current distribution. Figure 14d illustrates that when the energy storage device is charged, i7 and i8 are determined by the reference value of the charging current of the energy storage device and are no longer influenced by the current distribution ratio.

As shown in Figure 15a, at the moment of 1.4 s, the charging current of #1 energy storage device is 5 A, and the charging current of #2 energy storage device is 3 A. At the moment of 2.1 s, the charging current of #1 energy storage device is 3 A, and the charging current of #2 energy storage device is 2A. At the moment of 2.5 s, the charging current of both energy storage devices is 0 A. As shown in Figure 15b, when the working mode of energy storage equipment is switched, the bus voltage fluctuates within 3 V and can be kept stable after 0.2 s. When the system reaches stability, the DC bus voltage is stable at 60 V, which is consistent with the voltage reference value. It can be concluded that when the energy storage devices are in charging state, the charging current of the energy storage device is exactly the same as the set charging current reference value, and the control target has been achieved. After the change of the charging current reference value, the system is stabilized again after 0.2 s of regulation, and the energy storage device can be charged stably with the new charging current, which shows that the proposed control method is fast in tracking the change of the charging current reference value, and the bus voltage remains stable throughout the whole process.

5.1.5. Simulation Results of the Converter Input Voltage Fluctuation

To verify the effect of input voltage fluctuation on the DC bus voltage, simulations were performed for the following conditions. At 1.0 s, the input voltage of #1 converter increases 5 V. At 1.3 s, the input voltage of #3 converter dips 5 V. At 1.6 s, the input voltage of #4 converter increases 5 V. At 1.9 s, the input voltage of #6 converter dips 5 V. During the whole simulation, χ_{A_ref} = 50%, χ_{B_ref} = 33.3%, χ_{C_ref} = 16.7%, m:n = 2:3, and S₁ and S₂ are in the closed state, and all converters are connected. The DC bus voltage reference value V_ref = 60 V. The obtained simulation waveform is shown in Figure 16.

As shown in Figure 16, when the input voltage of the converter in each sub-microgrid changes due to the fluctuation of the wind and PV power supply, the DC bus voltage will fluctuate, but the maximum value does not exceed 3 V. After about 0.1 s of adjustment, the bus voltage can reach the reference value again. It can be concluded that the DC bus voltage can basically be kept stable when the converter input voltage changes.

5.2. Experiment Results and Discussion

To verify the effectiveness of the peer-to-peer hierarchical control method proposed in this paper from actual operation scenarios, a DC microgrid cluster experimental platform consisting of three sub-microgrids is built, as shown in Figure 17. It mainly includes the main circuit and sampling circuit of DC microgrid cluster, drive power supply and auxiliary circuit, low-pass filter, DSP controller, upper computer, etc. The technical specifications of the DC hybrid microgrid cluster are listed in

Table 3. Technical specifications of the DC hybrid microgrid cluster.

Technical Specifications	Converter #1~#3	Converter #4~#6	Converter #7~#8
Power rating	150 W	180 W	160 W
Efficiency	93.43%	94.36%	95.21%
Switches	FQA28N50	FQA28N50	FQA28N50
Inductors	2 mH	0.5 mH	1 mH
Capacitors	1880 μF	1410 μF	480 μF
Switching losses	2.4 W	2.6 W	2.3 W
Conduction losses	0.96 W	1.02 W	0.89 W
Gate drives	IR2110	IR2110	IR2110
Duty cycles of the PWM signals (%)	0.8	0.8	0.8
Line resistance power rating	0.12 W	0.13 W	0.12 W
Load rating	1200 W	1200 W	1200 W

. In this experiment, the removal and connect experiments of converters and sub-microgrids are performed.

5.2.1. Experiment Results of Converter’s Removal and Connection to Hybrid DC Microgrid Clusters

The microgrid is performed with the proposed peer-to-peer hierarchical control method for the converter removal and connection experiments. The experimental procedure is as follows: firstly, all converters are connected to the microgrid cluster, and after a period of time, converter #2 is removed, and after another period of time, converter #2 is connected. In order to derive the response of the DC microgrid cluster under the same distribution ratio of the converter’s removal and connection, the reference values of the distribution ratio of the three sub-microgrids are χ_{A_ref} = 33.3%, χ_{B_ref} = 33.3%, and χ_{C_ref} = 33.4%. Then, the DC bus voltage and sub-microgrid’s output current waveforms when converter #2 is removed and connected are obtained, as shown in Figure 18.

As shown in Figure 18, it can be seen that the output current of sub-microgrid A drops to 1 A after converter #2 is removed and then gradually rises, and the output currents of the three sub-microgrids are equal again after 1 s of regulation time. After converter #2 is connected, the output current of sub-microgrid A rises to 5 A and then gradually decreases, and the output currents of the three sub-microgrids are equal after 2.5 s regulation time.

It is worth noting that the higher the output current of sub-microgrid A, the longer the regulation time required for the system after converter #2 is removed or connected. Removing a converter will reduce the output current of the sub-microgrid where the converter is located for a short time, and converter connection will increase the output current of the sub-microgrid where the converter is located for a short time, but neither will affect the output current of each sub-microgrid when the system reaches the steady state. The impact of converter removal and connection to the DC bus voltage is also relatively small, causing a voltage fluctuation of no more than 4 V.

5.2.2. Experiment Results of Sub-Microgrid’s Removal and Connection to Hybrid DC Microgrid Clusters

The microgrid is performed with the proposed peer-to-peer hierarchical control method for the sub-microgrid removal and connection experiments. The experimental procedure is as follows: firstly, all sub-microgrids have been connected to the microgrid cluster, and after a period of time, sub-microgrid B is removed, and after another period of time, sub-microgrid B is re-connected. In order to derive the response of the DC microgrid cluster under different distribution ratios of the sub-microgrid’s removal and connection, the reference values of distribution ratios for the three sub-microgrids are χ_{A_ref} = 22.2%, χ_{B_ref} = 33.3%, and χ_{C_ref} = 44.5%. Then, the DC bus voltage and sub-microgrid’s output current waveforms when the sub-microgrid B is removed and connected are obtained, as shown in Figure 19.

As shown in Figure 15, it can be seen that the DC bus voltage dropped slightly within 0.2 s after the removal of sub-microgrid B. The DC bus voltage raised slightly within 0.6 s after the connection of sub-microgrid B. However, the bus voltage was stabilized at 60 V again under the regulation of the controller, and the change of bus voltage did not exceed 6 V during the whole process.

The above experiment results indicate that after a sub-microgrid is removed, the remaining sub-microgrids can still work normally, the bus voltage is still maintained at the voltage reference value, and the ratio of the output current of the remaining sub-microgrid remains unchanged. After the sub-microgrid is reconnected, after a period of regulation, the later connected sub-microgrid can work together with the original sub-microgrids in a coordinated manner.

It is worth noting that 60 V is the commonly used DC low-voltage civil voltage level. The charging voltage rating of various commonly used DC loads, such as batteries, is usually a multiple of 12 V, such as 48 V, 60 V, 72 V, etc. Therefore, choosing 60 V as the DC bus reference voltage is an appropriate solution. Furthermore, the voltage ripple of the experimental results is mainly caused by the electromagnetic interference and limitations of experimental conditions, and the quality of the waveforms can be further improved in practical applications by selecting electronic components with better performance and improving the manufacturing process.

6. Conclusions

This paper focuses on a hybrid DC microgrid cluster consisting of three sub-microgrids, where sub-microgrid A consists of three BUCK converters, sub-microgrid B consists of three BOOST converters, and sub-microgrid C consists of two bidirectional DC/DC converters. According to the specific structure and possible operating states of the hybrid microgrid cluster, the control objectives that the hybrid microgrid cluster should achieve in various cases are analyzed. The input voltage source of the bidirectional DC/DC converter is the energy storage device, which has different operation modes, current flow direction, input–output relationship, and on-state sequence of switching tubes in the two states of charging and discharging. Hence, the BUCK and BOOST operation modes of the bidirectional DC/DC converter are studied in detail.

To achieve the desired control objectives for the hybrid microgrid cluster, a peer-to-peer hierarchical control method is proposed in this paper. The most critical part of the peer-to-peer hierarchical control method is the design of the top-level control, because the top-level control is to provide current reference values for the three sub-microgrids, and, once the current reference values are selected incorrectly, the whole system will be paralyzed as the sub-microgrids cannot collaborate with each other. Therefore, the output current reference values of each converter for all possible cases are listed in this study, and then variables are introduced to generalize the reference current expressions for all scenarios gradually. In addition, the mid-level and bottom-level controls of sub-microgrids A and B are designed, and the control of sub-microgrid C is designed for both charging and discharging of energy storage devices, and the detailed principles of this control are analyzed in detail.

To verify whether the peer-to-peer hierarchical control method proposed in this paper can effectively control the hybrid microgrid cluster, a hybrid microgrid cluster model is built in the PLECS simulation environment, and simulations of converter removal and converter connection are performed. In addition, experimental validation is performed on the experimental platform. The simulation and experimental results fully demonstrate that the proposed peer-to-peer hierarchical control method can effectively realize the accurate control of the microgrid cluster, and the system can be quickly adjusted in a short time to achieve the effect of plug-and-play.