Comparison of Corrected and Uncorrected Enthalpy Methods for Solving Conduction-Driven Solid/Liquid Phase Change Problems
Abstract
:1. Introduction
- How does the optimum approach perform compared to non-iterative methods in terms of accuracy and speed?
- How do the mesh, the time step and an artificial melting temperature range affect the accuracy of the methods?
- How do the mesh, the time step and an artificial melting temperature range influence the calculation speed?
- Does using a smoothed temperature/enthalpy curve for isothermal phase changes give some advantages for solvers relying on an apparent heat capacity?
- Does the use of higher-order methods for the time discretization give any benefit?
- Which methods are appropriate when implementing the solid/liquid phase change in solvers with an automated time step control—like the ODE solvers in MATLAB? Moreover, how do they perform compared to the other solvers studied?
- Does linearizing the diffusion term of the energy equation instead of the transient term (i.e., the optimum approach) give any benefits?
2. Problem Statement
2.1. Physical Problem and Governing Equations
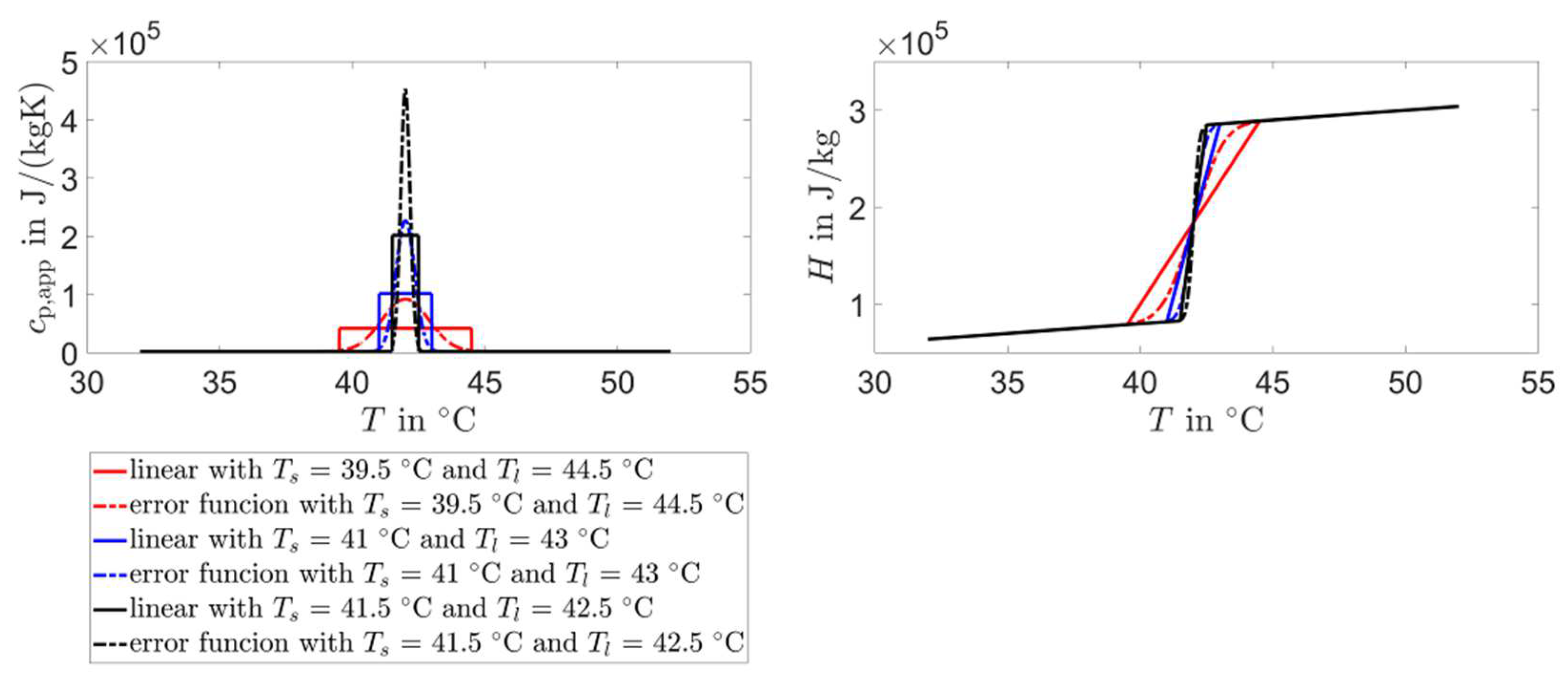
2.2. Implementation of the Temperature/Enthalpy Relation
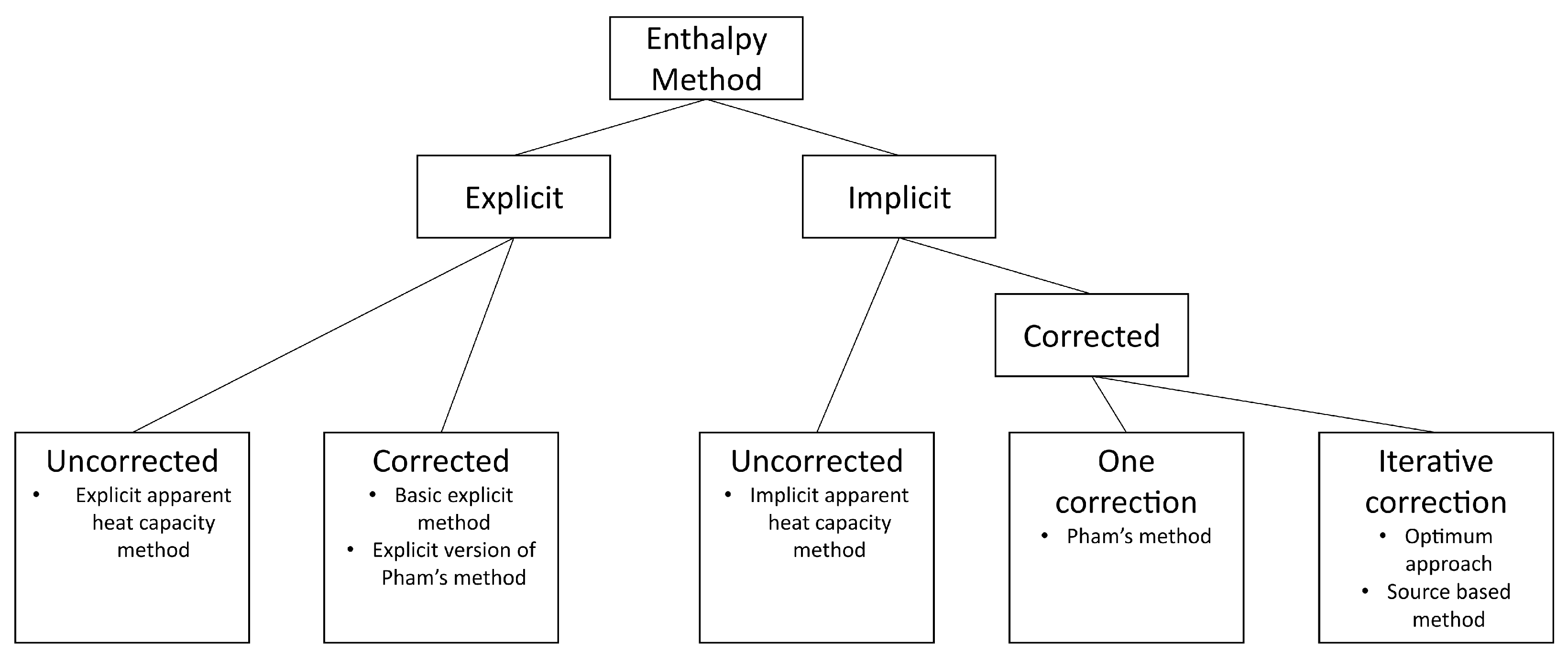
2.3. Numerical Methods
- Correcting the temperature/enthalpy relation
- ○
- Uncorrected solvers
- ○
- Corrected solvers, the correction is performed once
- ○
- Iterative solvers, the correction is performed iteratively until a convergence criterion is reached
- Slope of the temperature/enthalpy relation during phase change
- ○
- Linear function
- ○
- Error function
- Time stepping
- ○
- Fixed-step explicit
- ○
- Fixed-step implicit
- ○
- Fixed-step Crank–Nicolson
- ○
- Variable step solver (ode15s solver)
2.3.1. Basic Explicit Method (Corrected)
- Solve Equation (7)
- Update and as well as and , if the material properties or the boundary conditions change
- Go to the next time step
2.3.2. Apparent Heat Capacity Methods (Uncorrected)
- Determine and build
- Calculate with Equation (9) (explicit solvers) or Equation (10) (implicit solvers)
- Go to the next time step
2.3.3. Apparent Heat Capacity Methods (Corrected)
- Determine and build
- Calculate a preliminary with Equation (9) (explicit solvers) or Equation (10) (implicit solvers)
- Calculate with Equation (11)
- Update with Equation (6) or a look-up table.
- Go to the next time step
2.3.4. Optimum Approach (Iteratively Corrected)
- Determine and build
- Calculate with Equation (10)
- Calculate with Equation (12)
- Update with the Equation (6) or the look-up table.
- Calculate the residual ()
- Update and
- Depending on the obtained residual value, go to step 1 or the next time step
2.3.5. Linearized Diffusion Term (Iteratively Corrected)
- Determine and build ;
- Calculate with Equation (16);
- Calculate with Equation (17);
- Update with Equation (4);
- Calculate the residual ;
- Update and ;
- Depending on the obtained residual value, go to step 1 or the next time step.
2.3.6. The ODE Solvers
- T/H-lin-ODE:Equation (1) is implemented semi-discretized, and is updated with Equation (6)
- cp-app-lin-ODE:Equation (8) is implemented semi-discretized, and is determined by Equation (2)
- cp-app-erf-ODE:Equation (8) is implemented semi-discretized, and is determined by Equation (3)
- cp-app-1xcorr-lin-ODE:Equation (8) is implemented semi-discretized, is determined by Equation (2) and the correction is performed with Equations (6) and (11).
- cp-app-1xcorr-erf-ODE:Equation (8) is implemented semi-discretized, is determined by Equation (3) and the correction is performed with Equation (11) and a look-up table.
2.4. Parameter Variation
2.5. Error Calculation
3. Validation and Benchmark Solution
4. Results
4.1. General Results
4.2. Influence of the Varied Parameters
4.3. Implicit vs. Explicit Approaches
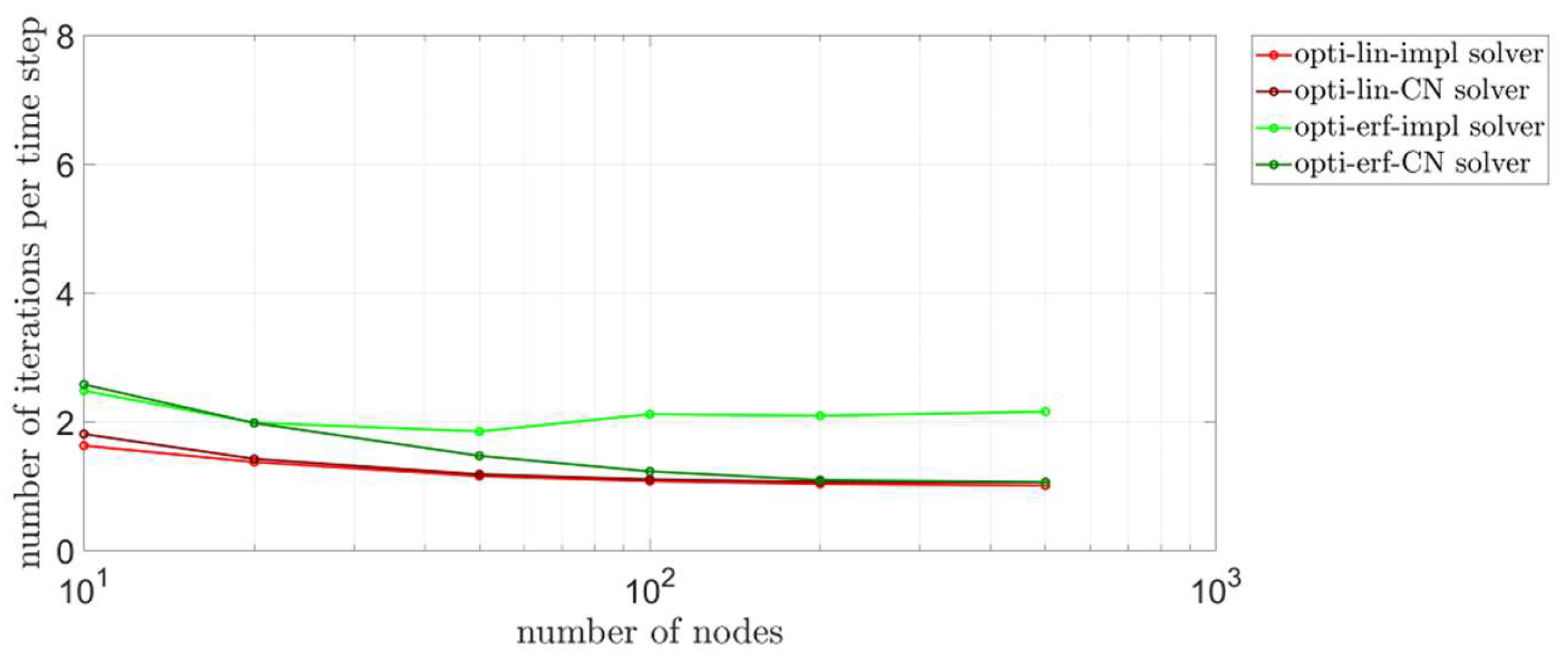
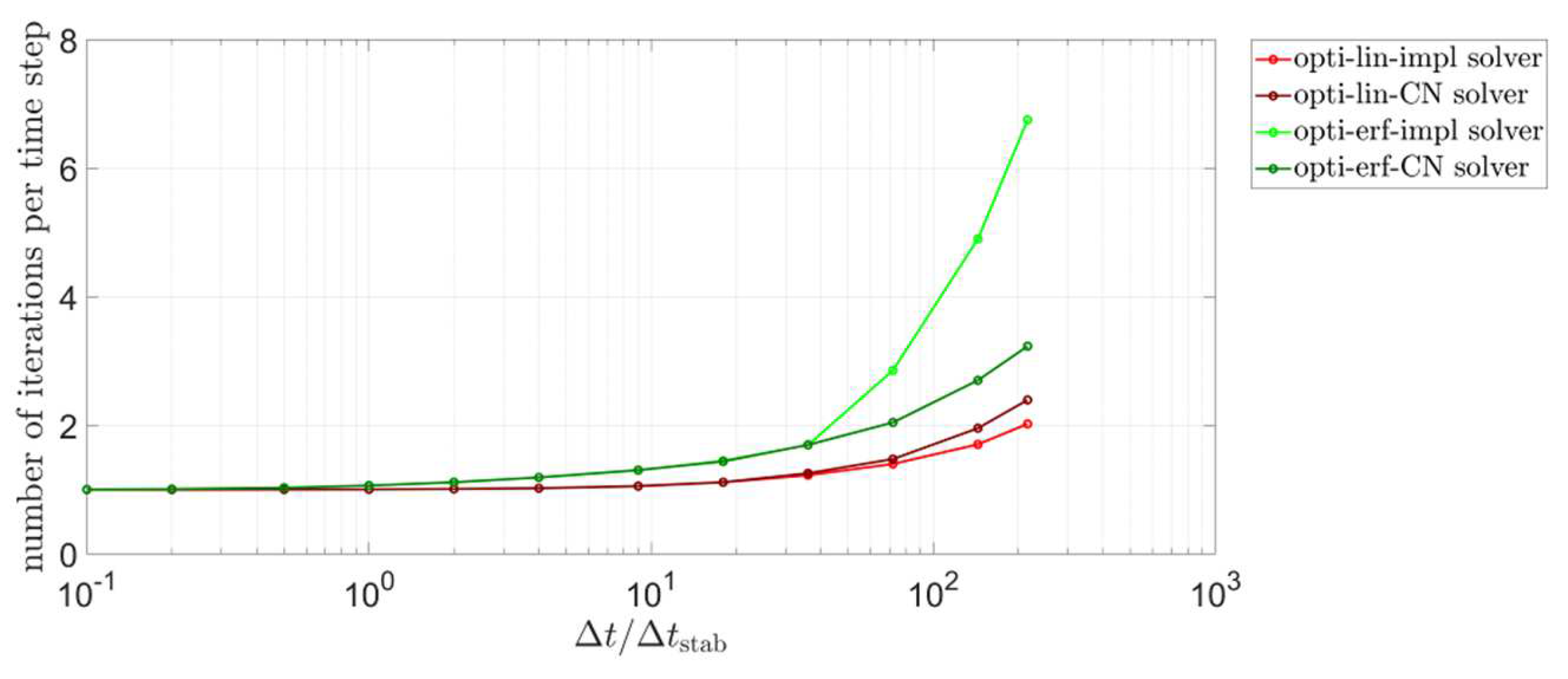
4.4. Iterations of the Optimum Approach Solvers
5. Discussion
- How does the optimum approach perform compared to non-iterative methods in terms of accuracy and speed?
- The optimum approach led to the fastest simulations of the tested methods while still maintaining high accuracy. The basic explicit method (with the T/H-lin-expl solver) and, for certain parameter values, the apparent heat capacity method with one correction (cp-app-1xcorr solvers without the ODE solvers) also gave accurate results within an acceptable simulation time.
- How do the mesh, the time step, and an artificial melting temperature range affect the accuracy of the methods?
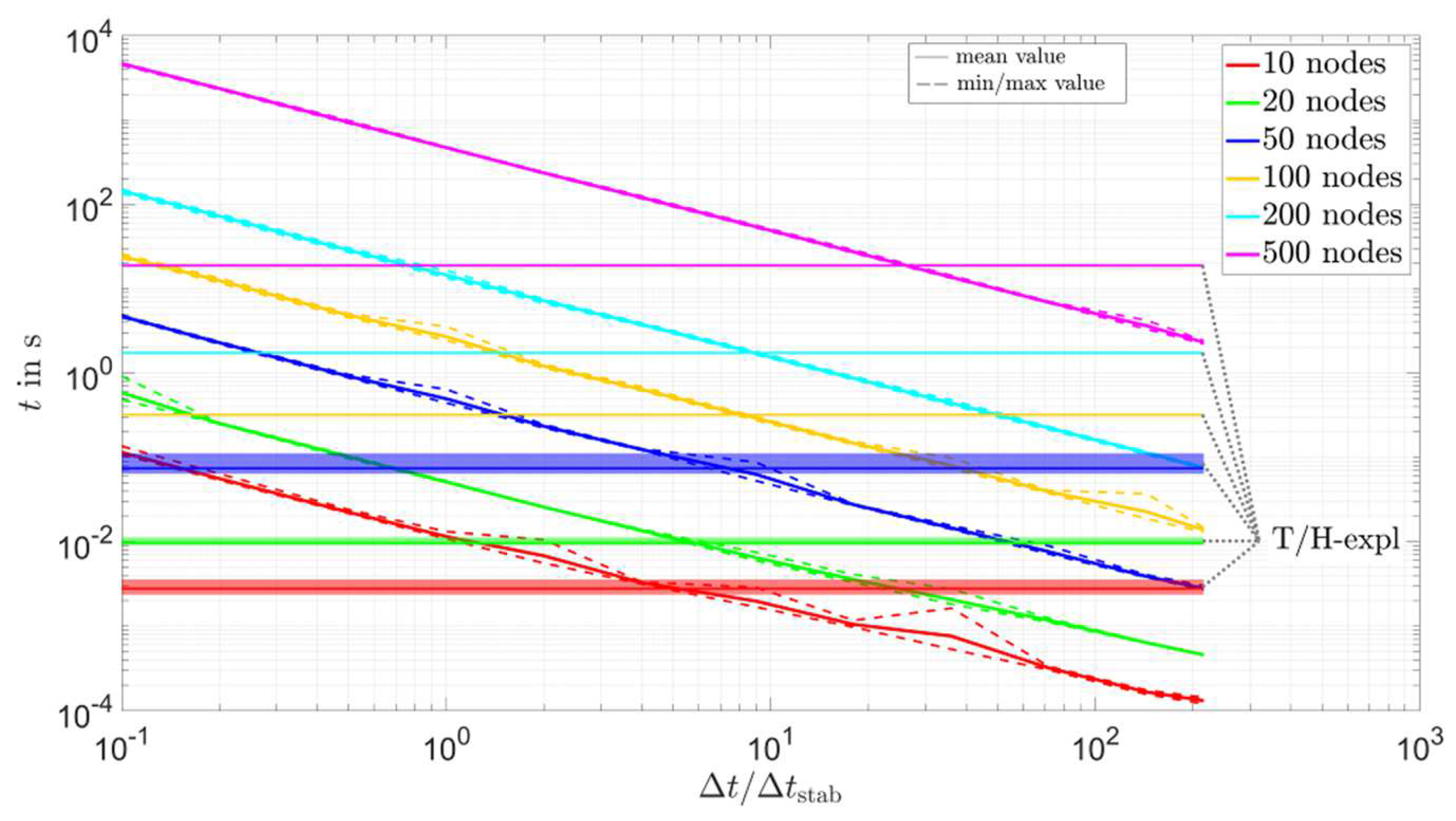
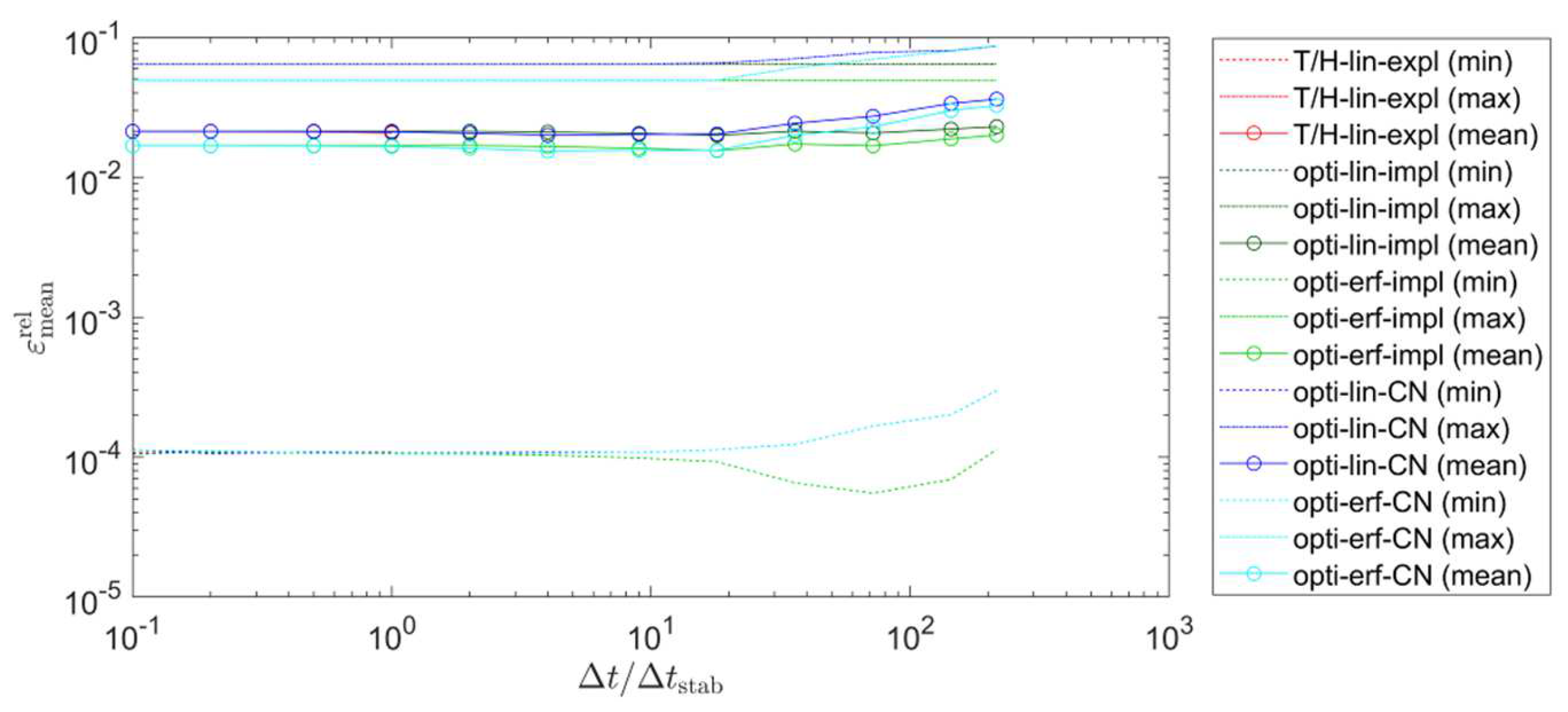
- For the most accurate solvers (optimum approach and T/H-lin-expl), the mesh and using an artificial melting temperature range had a large effect on the accuracy. For example, by increasing the number of nodes from 10 to 500, the minimum value of was reduced by about two orders of magnitude. If no artificial melting temperature range was implemented, the minimum of was about 10−4; while, for a melting temperature range of 1 K, the minimum of increased to about 10−2. On the contrary, the influence of was much smaller. Up to a value of 10, there was a negligible influence on . For the largest time steps tested (), the minimum of was only distinctive below 10−3.
- How do the mesh, the time step and an artificial melting temperature range influence the calculation speed?
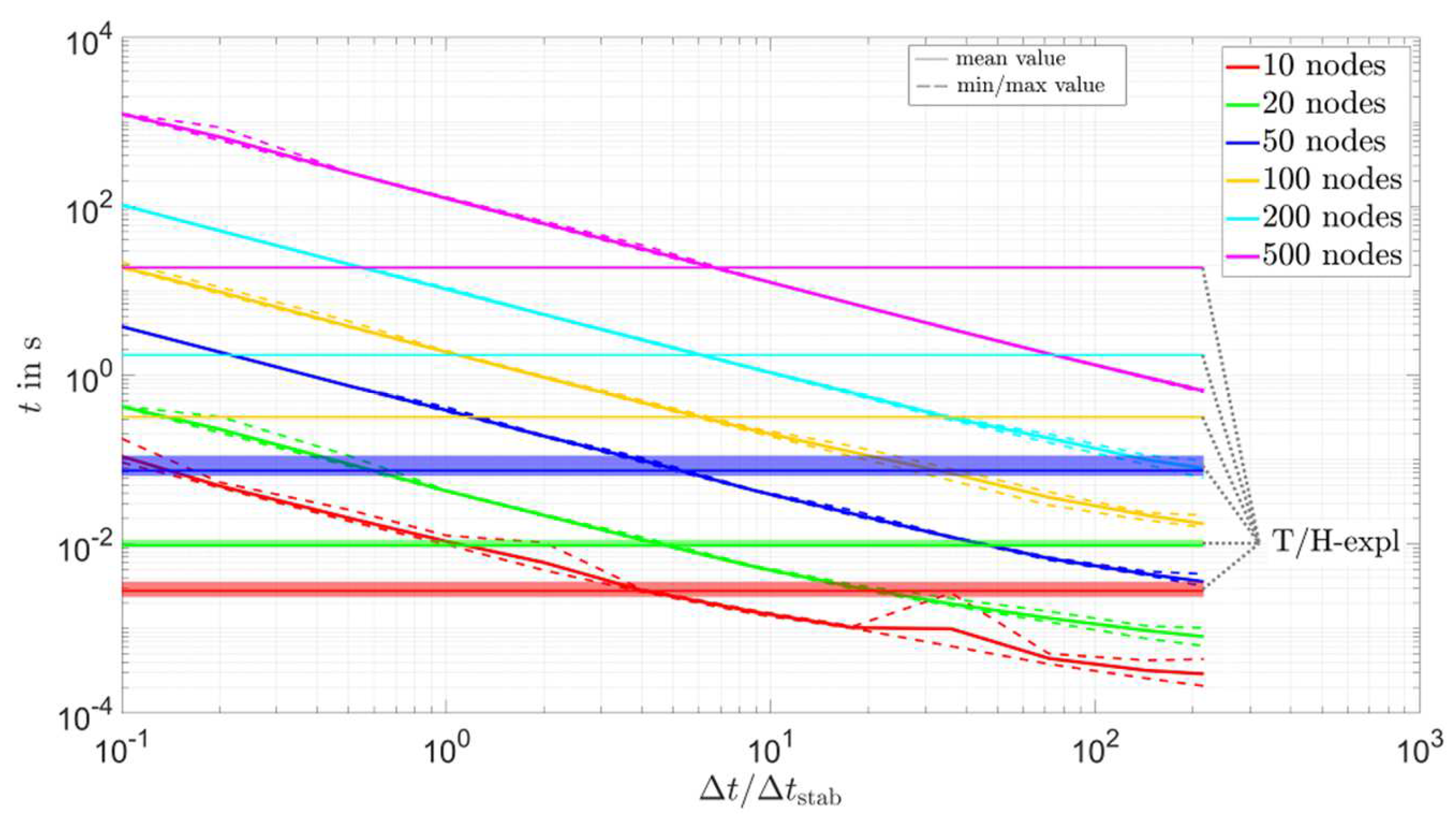
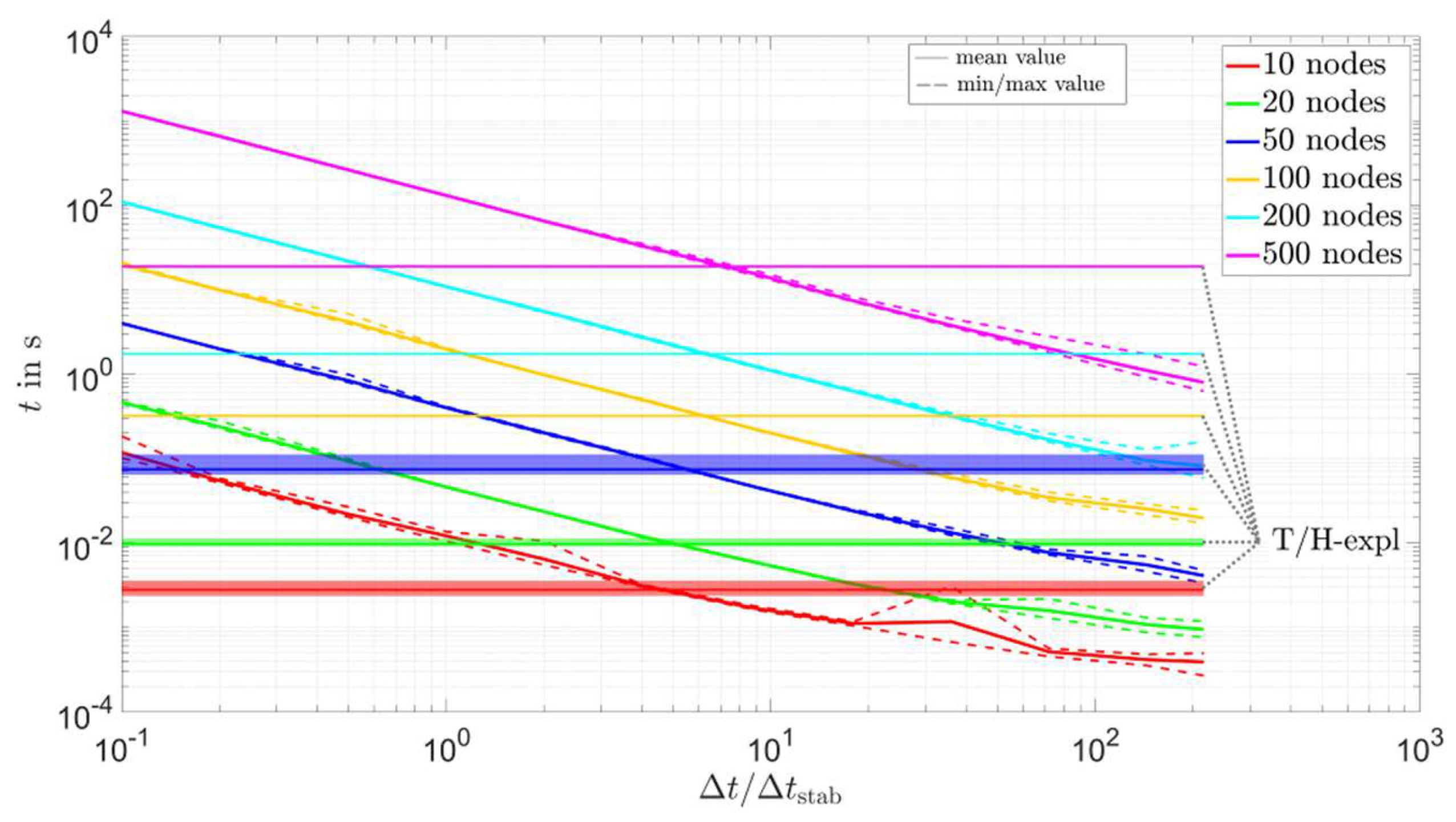
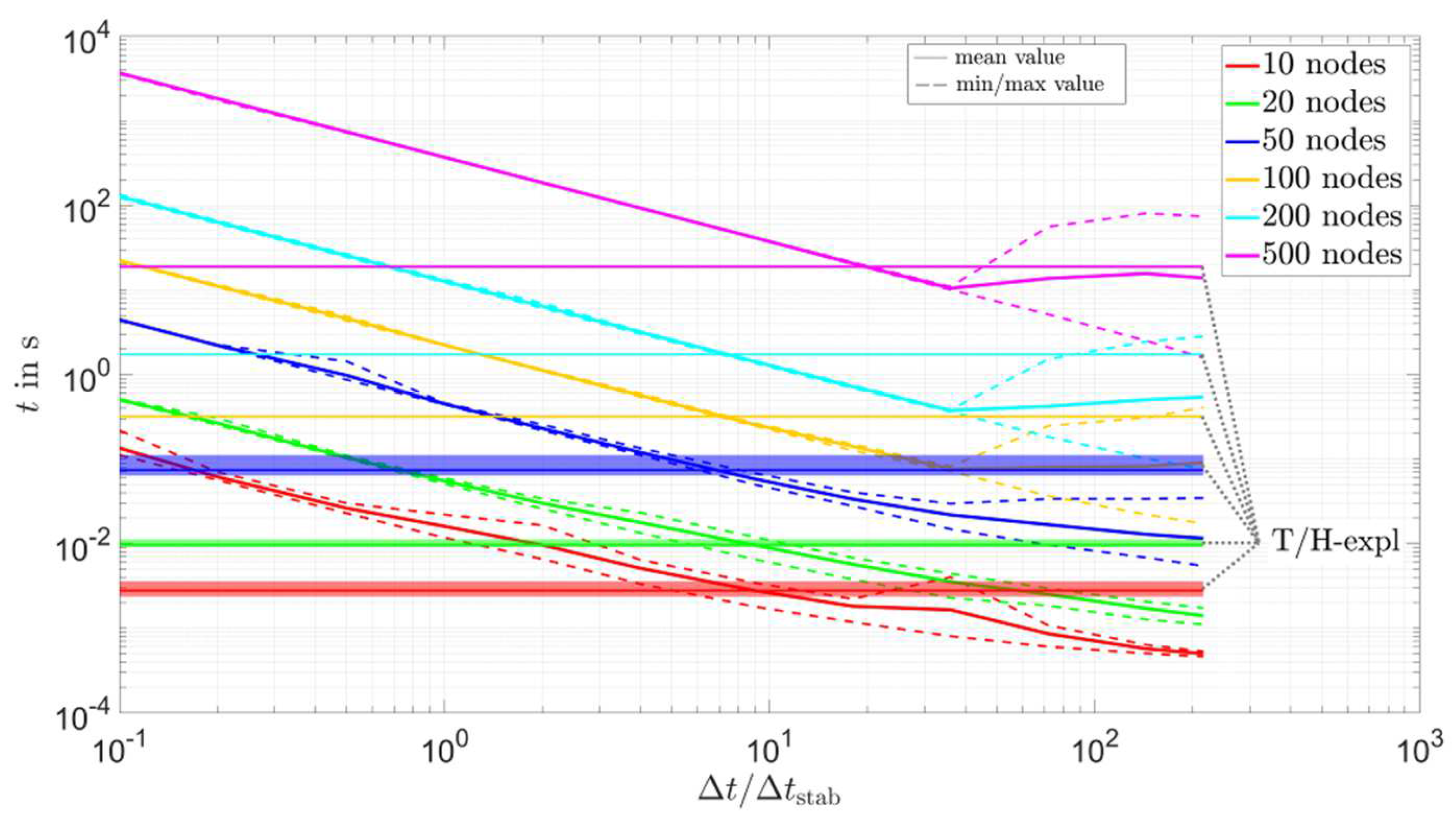
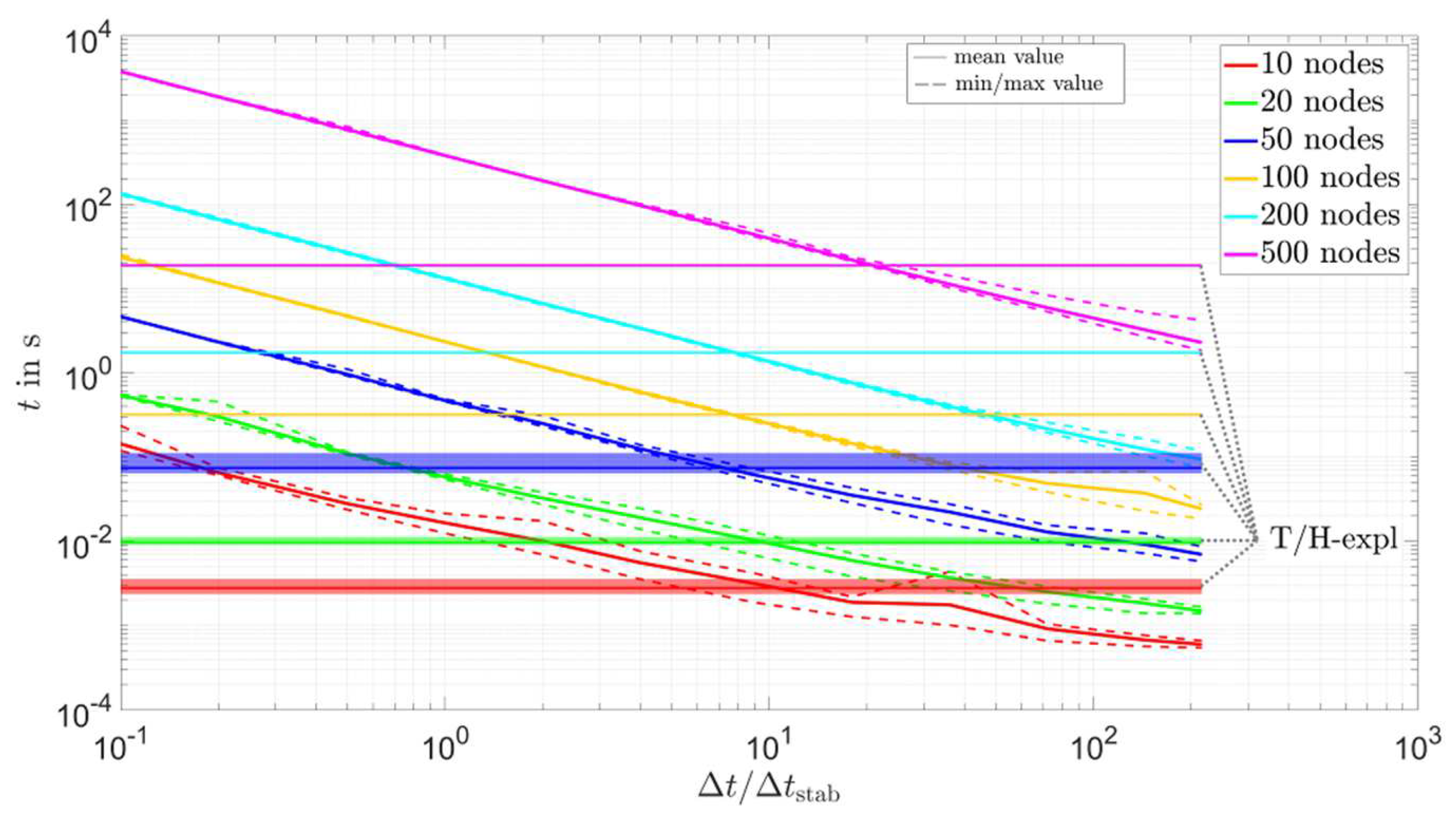
- For the implicit solvers with acceptable accuracy (optimum approach and cp-app-1xcorr-impl solvers), the number of nodes in the mesh had the largest influence on the simulation time. As shown in the results, changing the number of nodes from 10 to 500 increased the simulation time by about four orders of magnitude. The second most important parameter was the time step size; increasing from 0.1 to 216 reduced the simulation time by about three orders of magnitude. Here, it should be noted that changing the number of nodes also changed the absolute size of the time step. In comparison to the two said parameters, the influence of on the simulation time was small.
- Does using a smoothed temperature/enthalpy curve for isothermal phase changes give some advantages for solvers relying on an apparent heat capacity?
- The optimum approach solvers needed fewer iterations if the function is linear, compared to the error function case; in addition, the temperature update is faster and easier to derive and program when a linear function is used. For the remaining solvers, relying on a , the implementation of an error function can increase the accuracy to some extent, but these methods are still, by far, not preferred over the optimum approach.
- Does the use of higher-order methods for the time stepping give any benefit?
- Using the MATLAB ODE solvers did not give any benefits, so it should only be an option when their use is mandatory due to the given simulation framework. Applying the Crank–Nicolson method instead of the implicit Euler method for the optimum approach solvers did not give significantly more accurate results for the same simulation time, and, in some cases, the implicit Euler method gave even more accurate results for the same simulation time. This underlines the fact that the accuracy is driven by a correct updating of the temperature/enthalpy relation and not by order of the discretization scheme of the transient term.
- Which methods are appropriate when implementing the solid/liquid phase change in solvers with an automated time step control—like the ODE solvers in MATLAB? Moreover, how do they perform compared to the other solvers studied?
- The best results for the MATLAB ODE solvers were achieved with a method (T/H-lin-ODE) developed from the basic explicit method, which uses the temperature field of the old-time step to calculate the new enthalpy field. This enthalpy field is then used to update the temperature field for the next time step. In terms of accuracy, this solver achieved results comparable to the optimum approach solvers. With the cp-app-ODE solvers, acceptable results were also achieved when the tolerance was set tight enough—the absolute value depends on the solver and the mesh—and the artificial melting temperature range width was chosen carefully. As a reference (based on the conditions applied in this work), values between 0.1 to 1 K can be used, which are not so large as to give errors due to the artificial melting temperature range itself and not so small as to over-jump the phase change region. Regarding the simulation time, a large discrepancy to the best solvers studied can be seen for all ODE solvers. For a given accuracy, the ODE solvers were up to two orders of magnitude slower.
- Does linearizing the diffusion term instead of the transient term (i.e., the optimum approach) give any benefits?
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Property | Value | Units |
| coefficient matrix | ||
| heat capacity | ||
| complementary error function | ||
| enthalpy | ||
| time step count variable | ||
| length | m | |
| melting enthalpy | ||
| number of time steps or nodes | ||
| ODE | ordinary differential equation | |
| heat flux | ||
| boundary condition vector | ||
| time | s | |
| temperature | K | |
| time step size | s | |
| temperature range | K | |
| coordinate | ||
| phase front position | ||
| heat transfer coefficient | ||
| error | ||
| thermal conductivity | ||
| density | ||
| subscripts | ||
| ambient | ||
| apparent | ||
| time step count variable | ||
| Initial | ||
| node count variable | ||
| old iteration step | ||
| new iteration step | ||
| liquid | ||
| melting | ||
| Mean | ||
| New time step | ||
| old time step | ||
| solid | ||
| stability | ||
| time step | ||
| test case | ||
| validation case | ||
| x-direction | ||
| superscripts | ||
| reference | ||
| relative | ||
| simulation | ||
| temperature | ||
| preliminary |
Appendix A



References
- Dutil, Y.; Rousse, D.R.; Salah, N.B.; Lassue, S.; Zalewski, L. A review on phase-change materials: Mathematical modeling and simulations. Renew. Sustain. Energy Rev. 2011, 15, 112–130. [Google Scholar] [CrossRef]
- Mackwood, A.P.; Crafer, R.C. Thermal modelling of laser welding and related processes: A literature review. Opt. Laser Technol. 2005, 37, 99–115. [Google Scholar] [CrossRef]
- Thomas, B.G.; Zhang, L. Mathematical modeling of fluid flow in continuous casting. ISIJ Int. 2001, 41, 1181–1193. [Google Scholar] [CrossRef]
- Pham, Q.T. Modelling heat and mass transfer in frozen foods: A review. Int. J. Refrig. 2006, 29, 876–888. [Google Scholar] [CrossRef]
- Voller, V.R. An overview of numerical methods for solving phase change problems. In Advances in Numerical Heat Transfer; Minkowycz, W.J., Sparrow, E.M., Eds.; Taylor & Francis: New York, NY, USA, 1997; pp. 341–380. [Google Scholar]
- Furzeland, R.M. A comparative study of numerical methods for moving boundary problems. IMA J. Appl. Math 1980, 26, 411–429. [Google Scholar] [CrossRef]
- Voller, V.R.; Swaminathan, C.R.; Thomas, B.G. Fixed grid techniques for phase change problems: A review. Int. J. Numer. Methods Eng. 1990, 30, 875–898. [Google Scholar] [CrossRef]
- Hu, H.; Argyropoulos, S.A. Mathematical modelling of solidification and melting: A review. Modell. Simul. Mater. Sci. Eng. 1996, 4, 371–396. [Google Scholar] [CrossRef] [Green Version]
- Basu, B.; Date, A.W. Numerical modelling of melting and solidification problems—A review. Sadhana 1988, 13, 169–213. [Google Scholar] [CrossRef]
- Bertrand, O.; Binet, B.; Combeau, H.; Couturier, S.; Delannoy, Y.; Gobin, D.; Lacroix, M.; Le Quéré, P.; Médale, M.; Mencinger, J.; et al. Melting driven by natural convection a comparison exercise: First results. Int. J. Therm. Sci. 1999, 38, 5–26. [Google Scholar] [CrossRef]
- Gobin, D.; Le Quéré, P. Melting from an isothermal vertical wall. Synthesis of a numerical comparison exercise. Comput. Assist. Mech. Eng. Sci. 1999, 7, 289–306. [Google Scholar]
- Pointner, H.; de Gracia, A.; Vogel, J.; Tay, N.; Liu, M.; Johnson, M.; Cabeza, L.F. Computational efficiency in numerical modeling of high temperature latent heat storage: Comparison of selected software tools based on experimental data. Appl. Energy 2016, 161, 337–348. [Google Scholar] [CrossRef]
- Tamma, K.K.; Namburu, R.R. Recent advances, trends and new perspectives via enthalpy-based finite element formulations for applications to solidification problems. Int. J. Numer. Methods Eng. 1990, 30, 803–820. [Google Scholar] [CrossRef]
- Mauder, T.; Charvat, P.; Stetina, J.; Klimes, L. Assessment of basic approaches to numerical modeling of phase change problems—Accuracy, efficiency, and parallel decomposition. J. Heat Transf. 2017, 139, 084502. [Google Scholar] [CrossRef]
- König-Haagen, A.; Franquet, E.; Faden, M.; Brüggemann, D. Influence of the convective energy formulation for melting problems with enthalpy methods. Int. J. Therm. Sci. 2020, 158, 106477. [Google Scholar] [CrossRef]
- König-Haagen, A.; Franquet, E.; Faden, M.; Brüggemann, D. A study on the numerical performances of diffuse interface methods for simulation of melting and their practical consequences. Energies 2021, 14, 354. [Google Scholar] [CrossRef]
- Swaminathan, C.R.; Voller, V.R. On the enthalpy method. Int. J. Numer. Methods Heat Fluid Flow 1993, 3, 233–244. [Google Scholar] [CrossRef]
- Voller, V.R.; Swaminathan, C.R. General source-based method for solidification phase change. Numer. Heat Transf. Part B 1991, 19, 175–189. [Google Scholar] [CrossRef]
- Swaminathan, C.R.; Voller, V.R. A general enthalpy method for modeling solidification processes. Metall. Trans. B 1992, 23, 651–664. [Google Scholar] [CrossRef]
- Pham, Q.T. A fast, unconditionally stable finite-difference scheme for heat conduction with phase change. Int. J. Heat Mass Transf. 1985, 28, 2079–2084. [Google Scholar] [CrossRef]
- Comini, G.; Giudice, S.D.; Saro, O. A conservative algorithm for multidimensional conduction phase change. Int. J. Numer. Methods Eng. 1990, 30, 697–709. [Google Scholar] [CrossRef]
- Pham, Q.T. Comparison of general-purpose finite-element methods for the Stefan problem. Numer. Heat Transf. Part B 1995, 27, 417–435. [Google Scholar] [CrossRef]
- Al-Saadi, S.N.; Zhai, Z. Systematic evaluation of mathematical methods and numerical schemes for modeling PCM-enhanced building enclosure. Energy Build. 2015, 92, 374–388. [Google Scholar] [CrossRef]
- Kuznik, F.; Johannes, K.; Franquet, E.; Zalewski, L.; Gibout, S.; Tittelein, P.; Dumas, J.-P.; David, D.; Bédécarrats, J.-P.; Lassue, S. Impact of the enthalpy function on the simulation of a building with phase change material wall. Energy Build. 2016, 126, 220–229. [Google Scholar] [CrossRef]
- Dal Magro, F.; Jimenez-Arreola, M.; Romagnoli, A. Improving energy recovery efficiency by retrofitting a PCM-based technology to an ORC system operating under thermal power fluctuations. Appl. Energy 2017, 208, 972–985. [Google Scholar] [CrossRef]
- Griesbach, M.; König-Haagen, A.; Brüggemann, D. Numerical analysis of a combined heat pump ice energy storage system without solar Benefit—Analytical validation and comparison with long term experimental data over one year. Appl. Therm. Eng. 2022, 213, 118696. [Google Scholar] [CrossRef]
- Faden, M.; König-Haagen, A.; Höhlein, S.; Brüggemann, D. An implicit algorithm for melting and settling of phase change material inside macrocapsules. Int. J. Heat Mass Transf. 2018, 117, 757–767. [Google Scholar] [CrossRef]
- Kozak, Y.; Ziskind, G. Novel enthalpy method for modeling of PCM melting accompanied by sinking of the solid phase. Int. J. Heat Mass Transf. 2017, 112, 568–586. [Google Scholar] [CrossRef]
- Hummel, D.; Beer, S.; Hornung, A. A conjugate heat transfer model for unconstrained melting of macroencapsulated phase change materials subjected to external convection. Int. J. Heat Mass Transf. 2020, 149, 119205. [Google Scholar] [CrossRef]
- Kasibhatla, R.R.; Brüggemann, D. Coupled conjugate heat transfer model for melting of PCM in cylindrical capsules. Appl. Therm. Eng. 2021, 184, 116301. [Google Scholar] [CrossRef]
- Stefan, J. Uber einige probleme der theorie der warmeletung. Sitzungsber. Akad. Wiss. Wien Math.-Naturwiss. 1889, 98, 473–484. [Google Scholar]
- Lamé, G.; Clapeyron, B.P. Mémoire sur la solidification par refroidissement d’un globe liquide. Ann. Chim. Phys. 1831, 47, 250–256. [Google Scholar]
- Tarzia, D. An explicit solution for a two-phase unidimensional Stefan problem with a convective boundary condition at the fixed face. MAT-Ser. A 2004, 8, 21–27. [Google Scholar]
- Ma, Z.W.; Zhang, P. Modeling the heat transfer characteristics of flow melting of phase change material slurries in the circular tubes. Int. J. Heat Mass Transf. 2013, 64, 874–881. [Google Scholar] [CrossRef]
- Schiesser, W.E.; Griffiths, G.W. A Compendium of Partial Differential Equation Models: Method of Lines Analysis with Matlab; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]


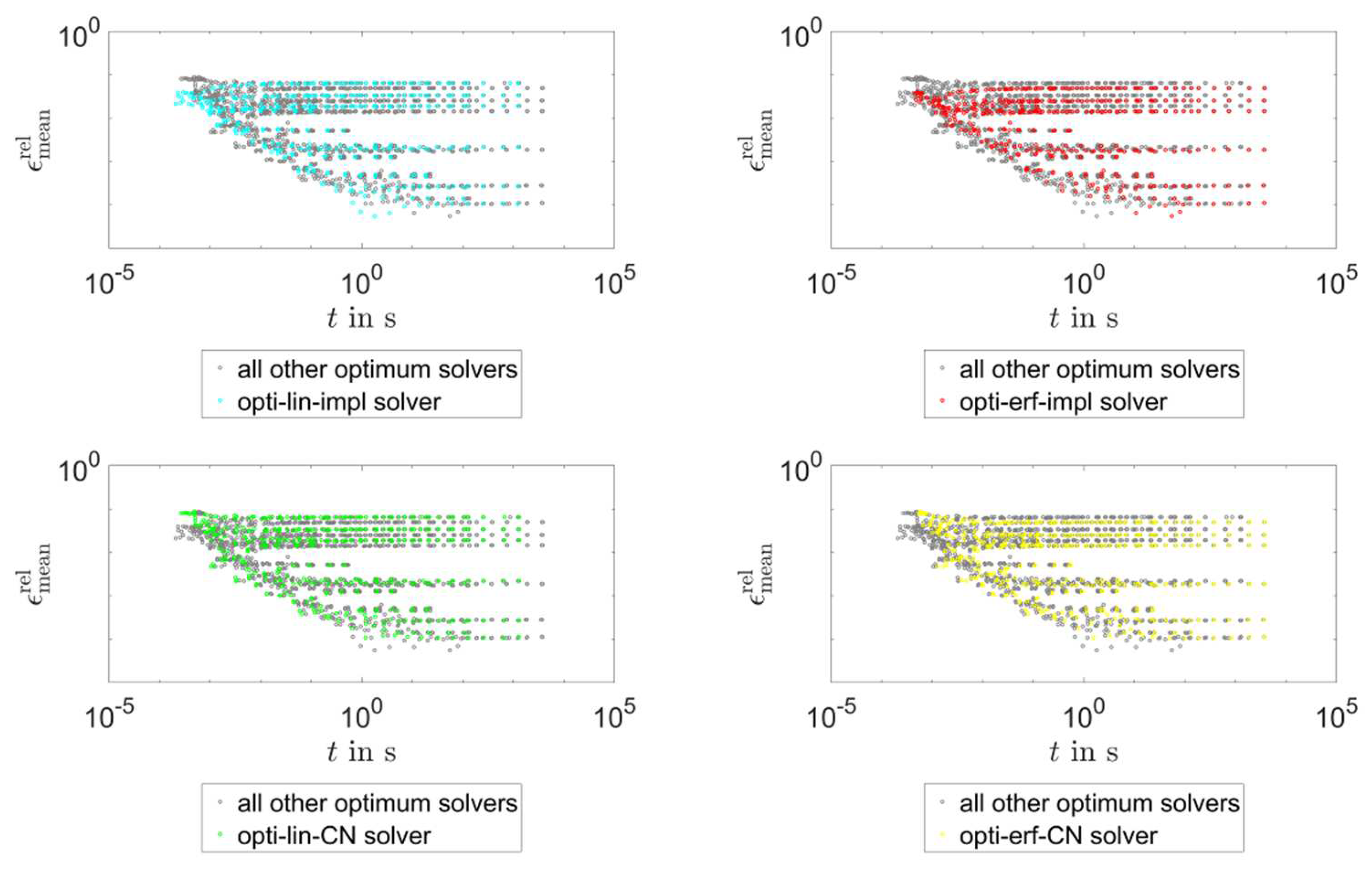
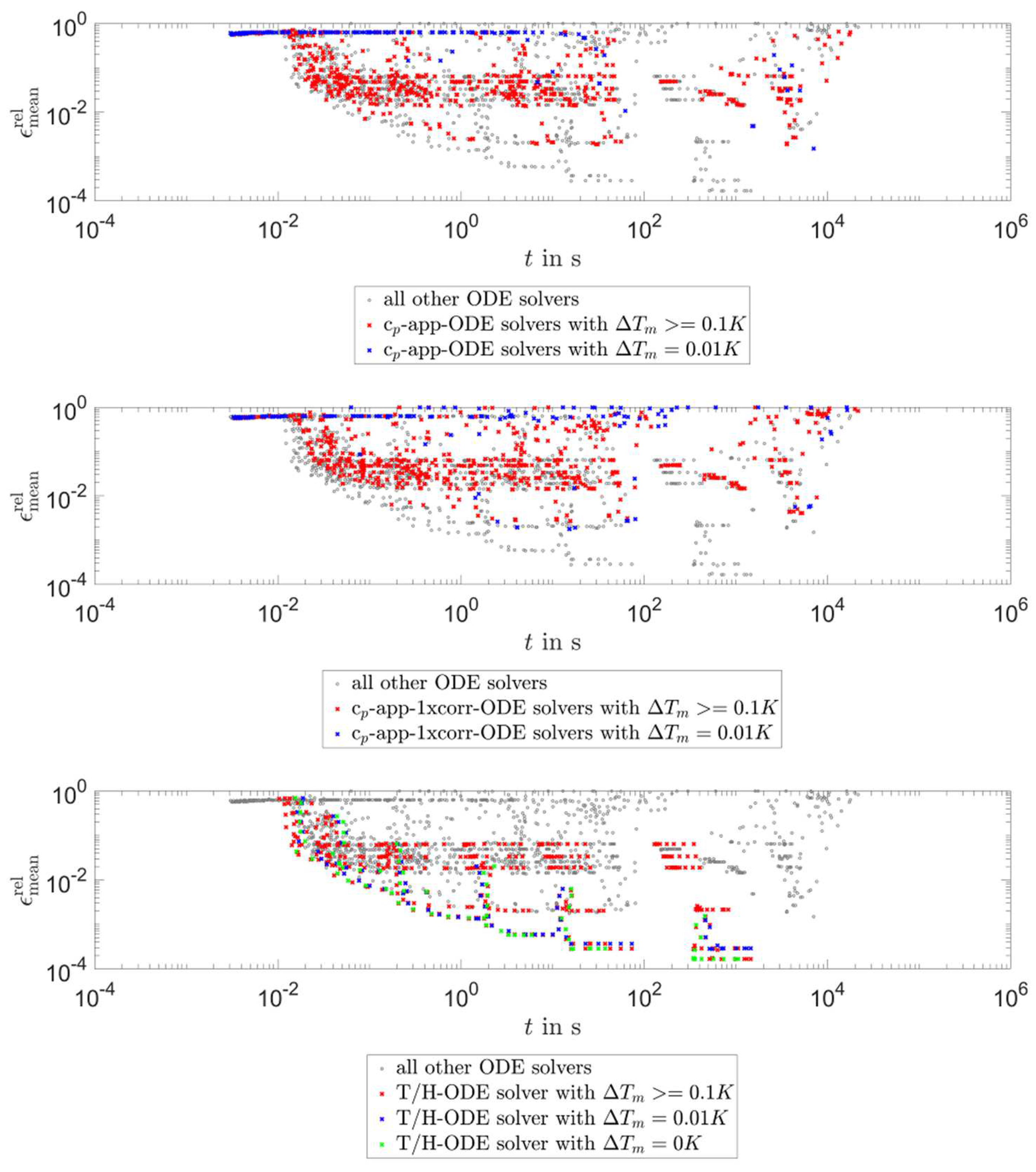



| Property | Value | Units |
|---|---|---|
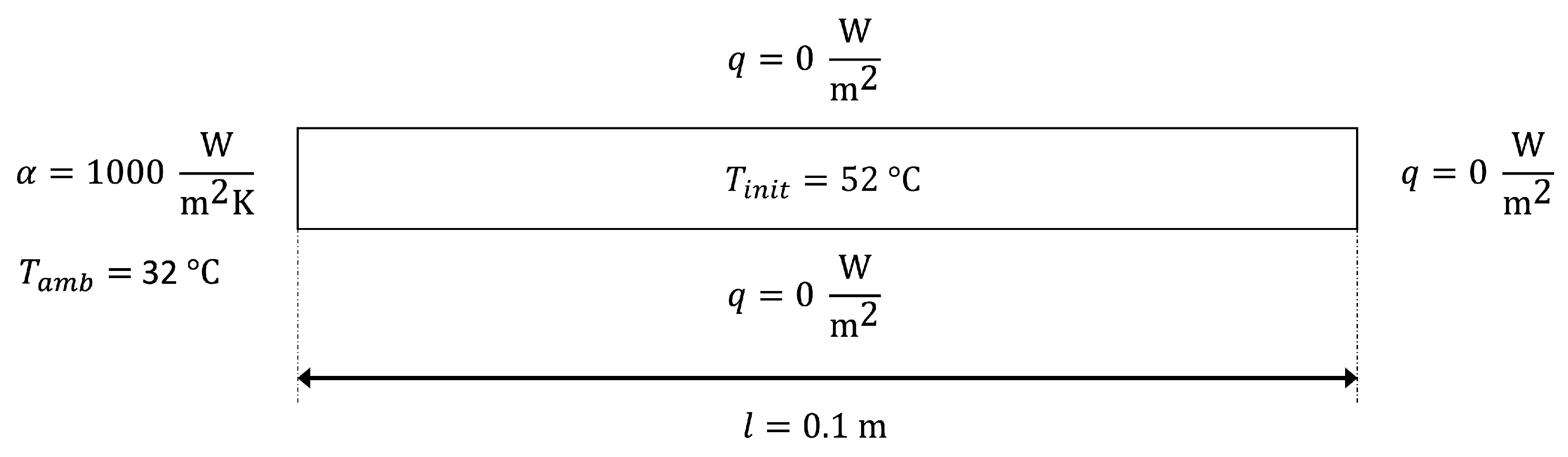
| 52 | °C | |
| 32 | °C | |
| 1000 | ||
| 42 | °C | |
| 2000 | ||
| 200,000 | ||
| 1000 | ||
| 1 | ||
| 0.1 | ||
| 1 |
| Identifier | Correcting Approach | Slope of the T/H Relation | Time Stepping |
|---|---|---|---|
| T/H-lin-expl | corrected * | linear | fixed-step explicit |
| T/H-lin-ODE | corrected * | linear | variable step ode15s |
| cp-app-lin-expl | uncorrected | linear | fixed-step explicit |
| cp-app-lin-impl | uncorrected | linear | fixed-step implicit |
| cp-app-erf-expl | uncorrected | error function | fixed-step explicit |
| cp-app-erf-impl | uncorrected | error function | fixed-step implicit |
| cp-app-lin-ODE | uncorrected | linear | variable step ode15s |
| cp-app-erf-ODE | uncorrected | error function | variable step ode15s |
| cp-app-1xcorr-lin-expl | one correction | linear | fixed-step explicit |
| cp-app-1xcorr-lin-impl | one correction | linear | fixed-step implicit |
| cp-app-1xcorr-erf-expl | one correction | error function | fixed-step explicit |
| cp-app-1xcorr-erf-impl | one correction | error function | fixed-step implicit |
| cp-app-1xcorr-lin-ODE | one correction | linear | variable step ode15s |
| cp-app-1xcorr-erf-ODE | one correction | error function | variable step ode15s |
| opti-lin-impl | Iterative correction | linear | fixed-step implicit |
| opti-erf-impl | Iterative correction | error function | fixed-step implicit |
| opti-lin-CN | Iterative correction | linear | fixed-step Crank–Nicolson |
| opti-erf-CN | Iterative correction | error function | fixed-step Crank–Nicolson |
| lin-diff-lin-impl | Iterative correction | linear | fixed-step implicit |
| Solvers | Variation | Variation [K] | Rel. Tolerance [-] | Mesh [Number of Nodes] |
|---|---|---|---|---|
| opti-lin-impl opti-erf-impl opti-lin-CN opti-erf-CN lin-diff-lin-impl | 0.1, 0.2, 0.5, 1, 2, 4, 9, 18, 36, 72, 144, 216 | 0, 0.01, 0.1, 1, 2, 5 | - | 10, 20, 50, 100, 200, 500 |
| cp-app-lin-impl cp-app-erf-impl cp-app-1xcorr-lin-impl cp-app-1xcorr-erf-impl | 0.1, 0.2, 0.5, 1, 2, 4, 9, 18, 36, 72, 144, 216 | 0.01, 0.1, 1, 2, 5 | - | 10, 20, 50, 100, 200, 500 |
| T/H-lin-expl | 0.1, 0.2, 0.5, 1 | 0, 0.01, 0.1, 1, 2, 5 | - | 10, 20, 50, 100, 200, 500 |
| cp-app-lin-expl cp-app-erf-expl cp-app-1xcorr-lin-expl cp-app-1xcorr-erf-expl | 0.1, 0.2, 0.5, 1 | 0.01, 0.1, 1, 2, 5 | - | 10, 20, 50, 100, 200, 500 |
| T/H-lin-ODE | - | 0, 0.01, 0.1, 1, 2, 5 | 1 × 10−9, 1 × 10−8, 1 × 10−7, 1 × 10−6, 1 × 10−5, 1 × 10−4, 2 × 10−4, 5 × 10−4, 1 × 10−3, 2 × 10−3, 5 × 10−3, 1 × 10−2 | 10, 20, 50, 100, 200, 500 |
| cp-app-lin-ODE cp-app-erf-ODE cp-app-1xcorr-lin-ODE cp-app-1xcorr-erf-ODE | - | 0.01, 0.1, 1, 2, 5 | 1 × 10−9, 1 × 10−8, 1 × 10−7, 1 × 10−6, 1 × 10−5, 1 × 10−4, 2 × 10−4, 5 × 10−4, 1 × 10−3, 2 × 10−3, 5 × 10−3, 1 × 10−2 | 10, 20, 50, 100, 200, 500 |
| Solver | Figures | |
|---|---|---|
| opti-lin-impl | ≈3–7 | Figure A3 in the Appendix A |
| opti-lin-CN | ≈3–8 | Figure A4 in the Appendix A |
| opti-erf-impl | ≈3.5–20 | Figure A5 in the Appendix A |
| opti-erf-CN | ≈4–20 | Figure A6 in the Appendix A |
| cp-app-1xcorr-lin-impl | ≈2.5–15 | Figure A7 in the Appendix A |
| cp-app-1xcorr-erf-impl | ≈3.5–25 | Figure A8 in the Appendix A |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
König-Haagen, A.; Diarce, G. Comparison of Corrected and Uncorrected Enthalpy Methods for Solving Conduction-Driven Solid/Liquid Phase Change Problems. Energies 2023, 16, 449. https://doi.org/10.3390/en16010449
König-Haagen A, Diarce G. Comparison of Corrected and Uncorrected Enthalpy Methods for Solving Conduction-Driven Solid/Liquid Phase Change Problems. Energies. 2023; 16(1):449. https://doi.org/10.3390/en16010449
Chicago/Turabian StyleKönig-Haagen, Andreas, and Gonzalo Diarce. 2023. "Comparison of Corrected and Uncorrected Enthalpy Methods for Solving Conduction-Driven Solid/Liquid Phase Change Problems" Energies 16, no. 1: 449. https://doi.org/10.3390/en16010449
APA StyleKönig-Haagen, A., & Diarce, G. (2023). Comparison of Corrected and Uncorrected Enthalpy Methods for Solving Conduction-Driven Solid/Liquid Phase Change Problems. Energies, 16(1), 449. https://doi.org/10.3390/en16010449






