Analysis of Interturn Faults on Transformer Based on Electromagnetic-Mechanical Coupling
Abstract
:1. Introduction
2. Finite Element Model of the Faulty Transformer
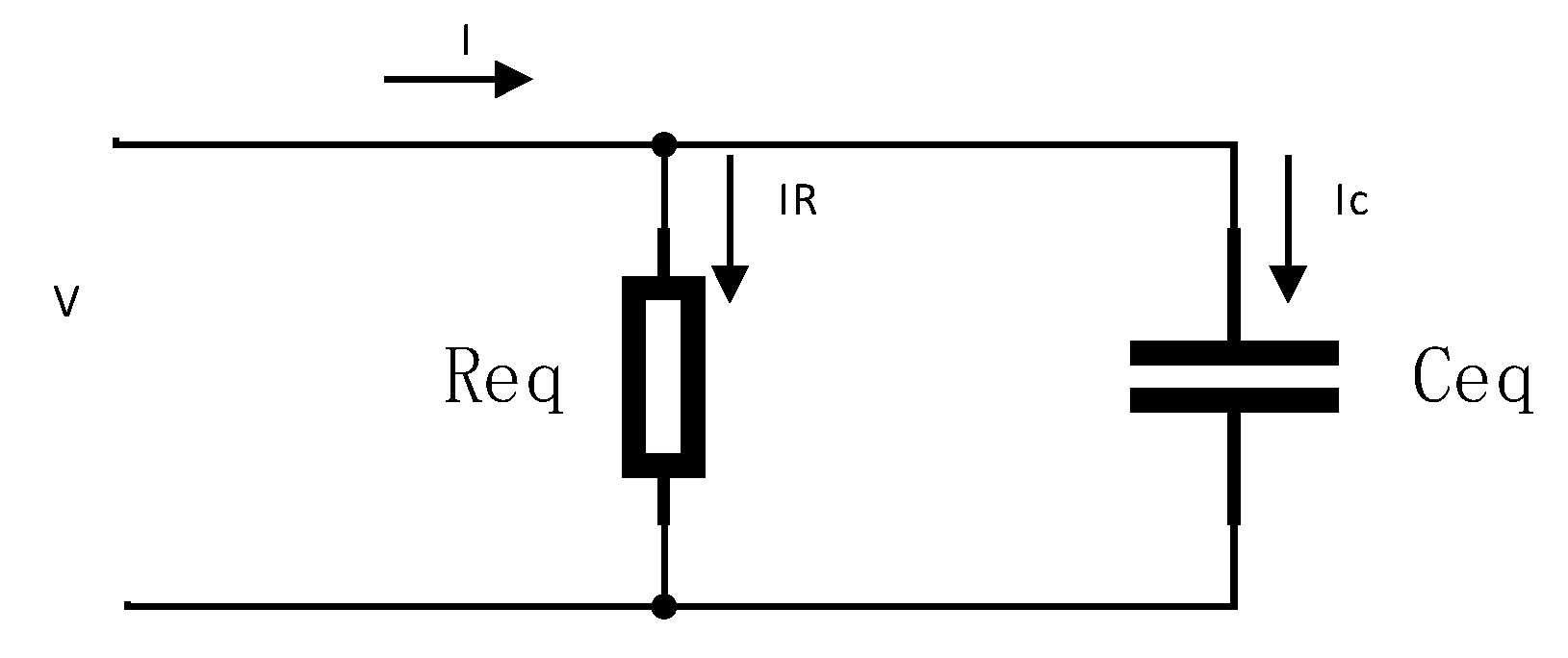
2.1. Electromagnetic Field Theory
2.2. Structural Mechanics Theory
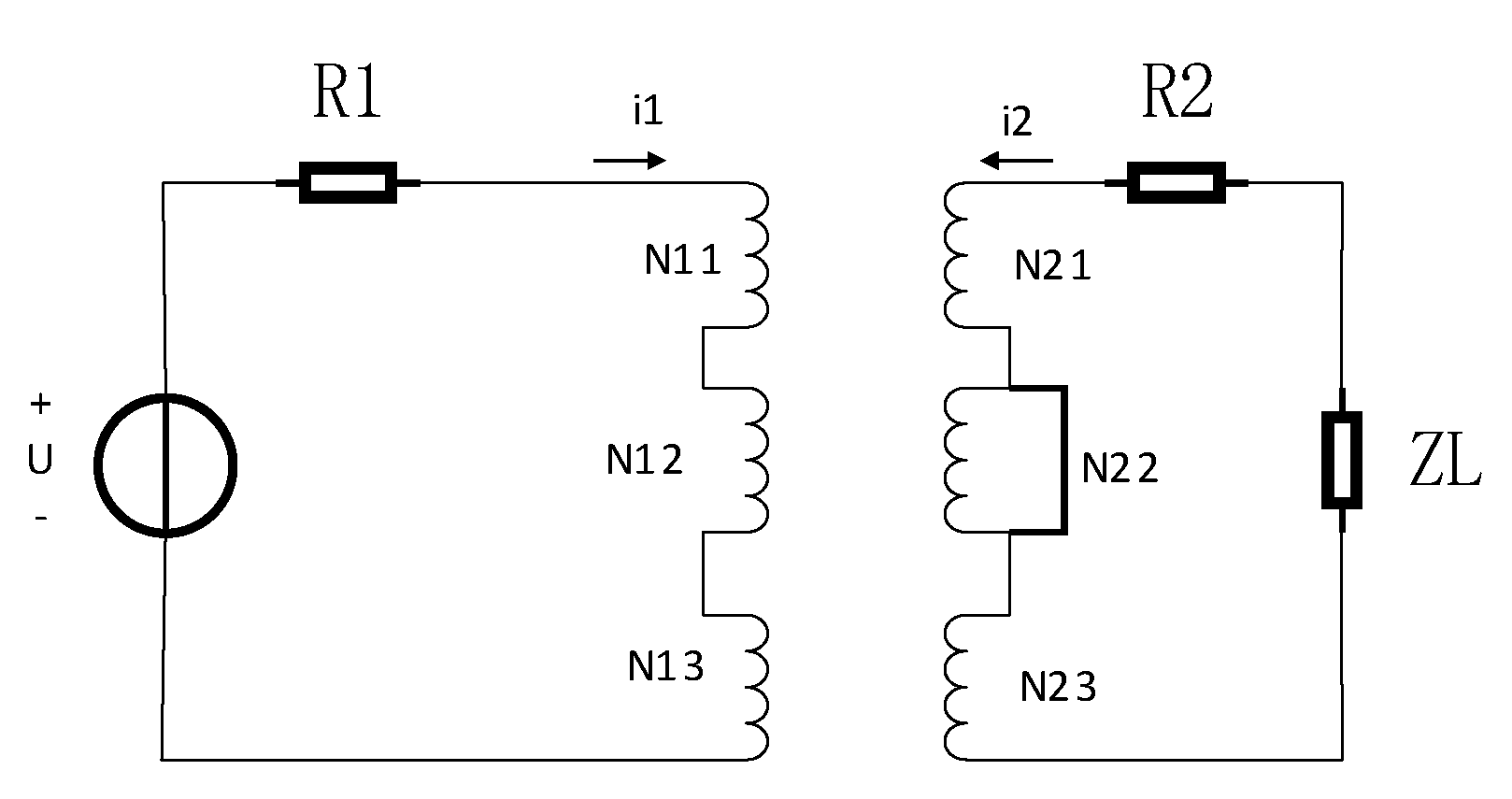
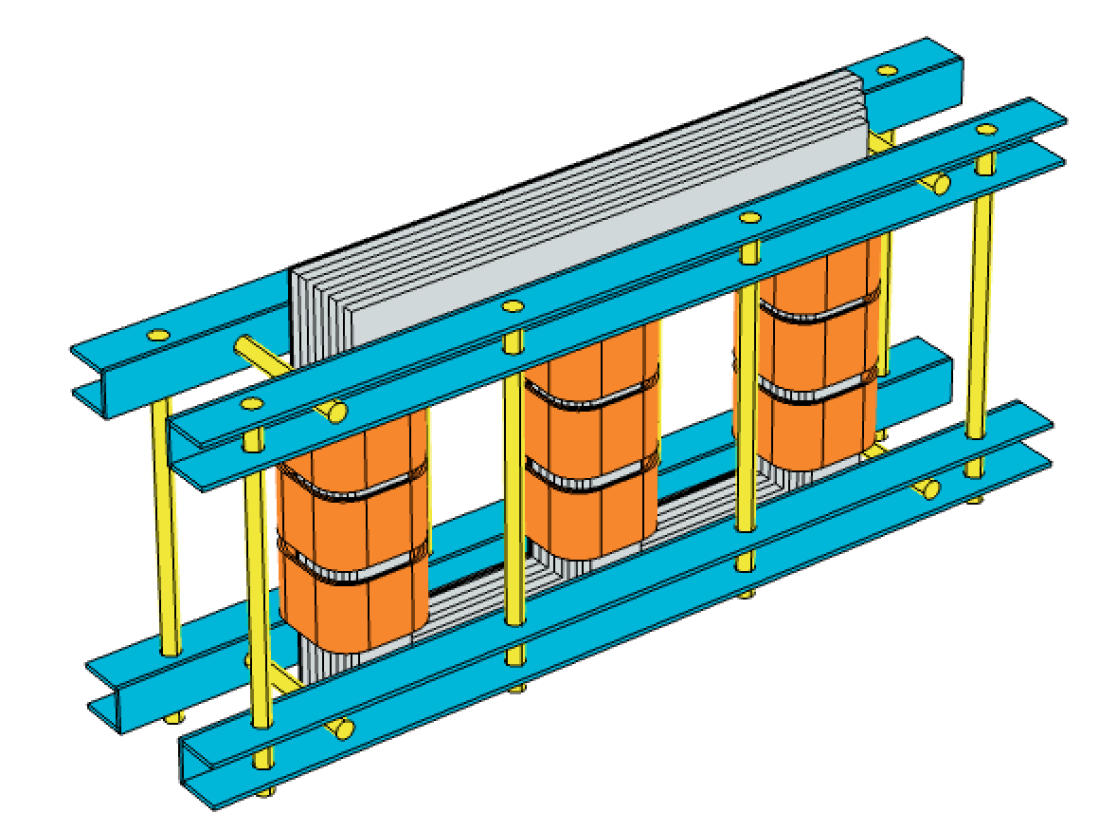
2.3. 3–D Model and Parameters of Power Transformer
3. Analysis of Interturn Faults on Transformers Based on Electromagnetic Characteristics
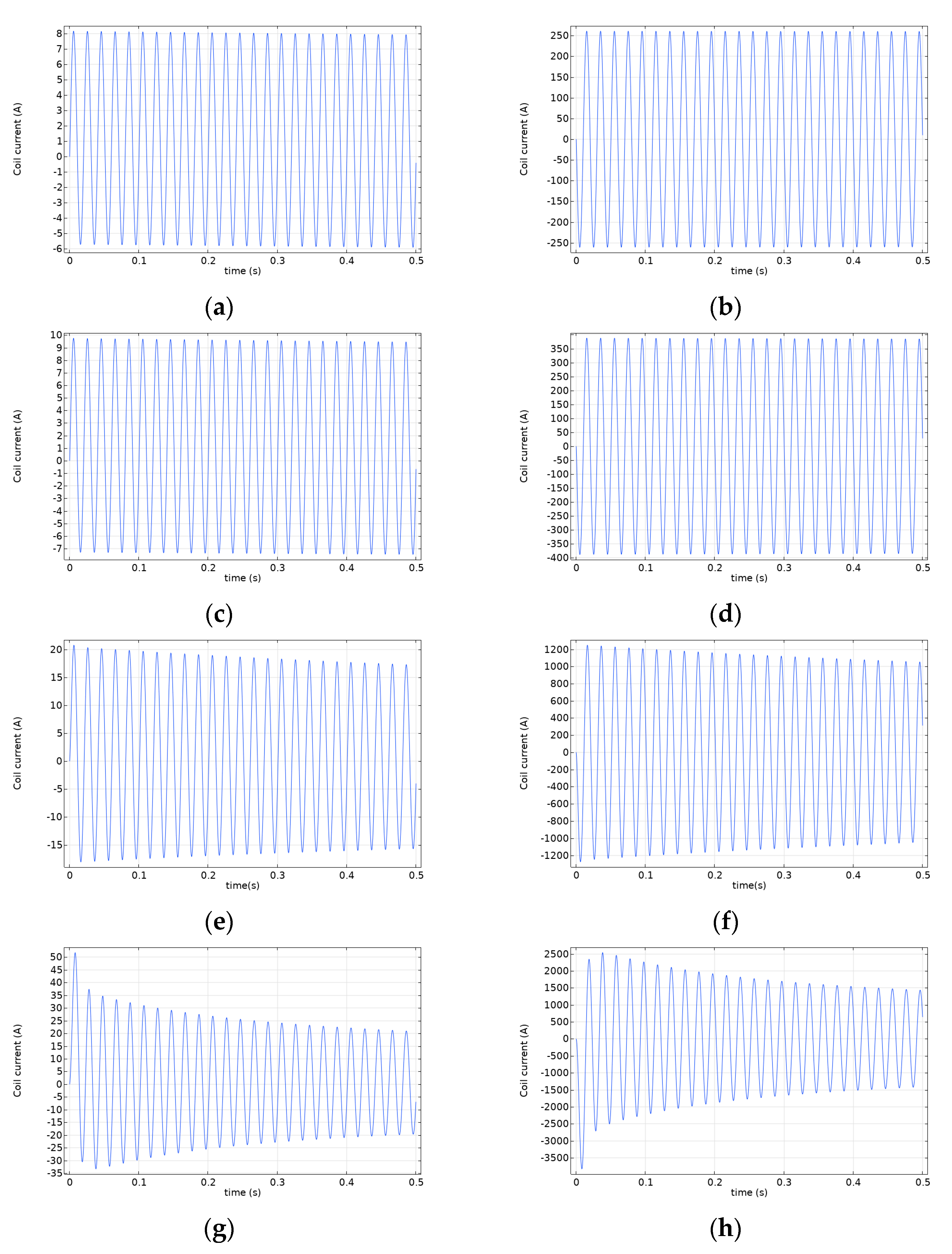
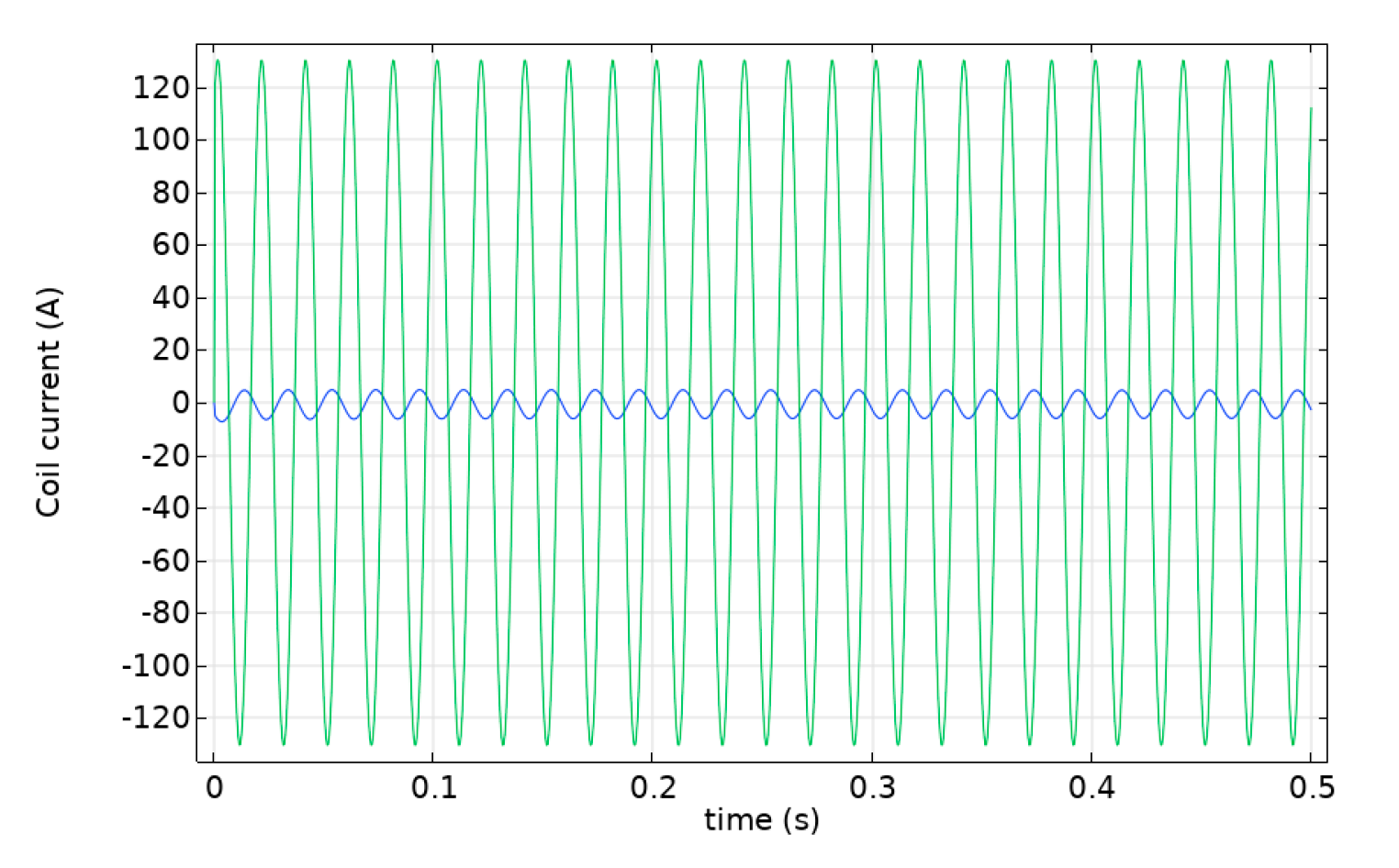
3.1. Winding Interturn Fault Current Analysis
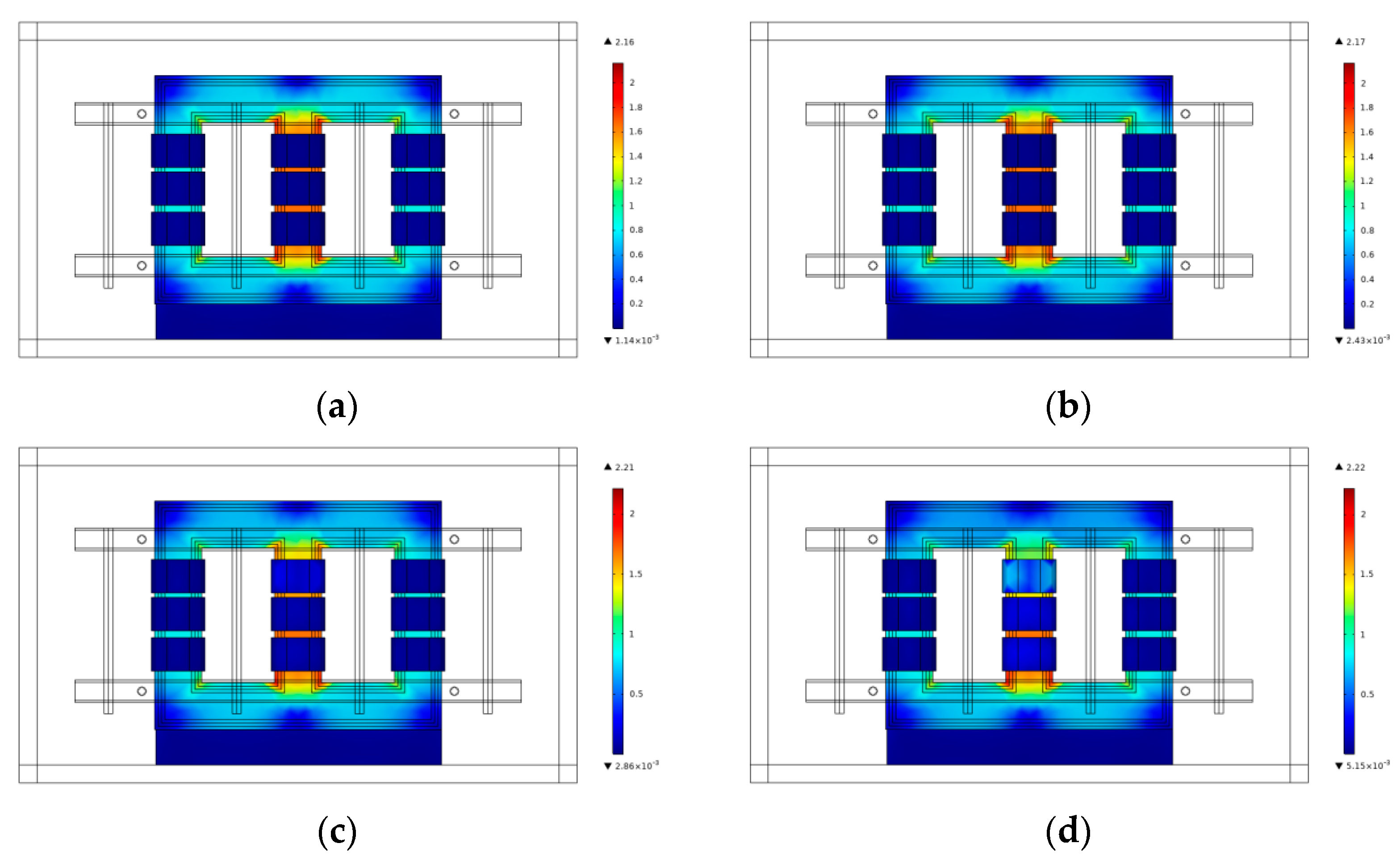
3.2. Magnetic Field Analysis
4. Analysis of Interturn Faults on Transformers Based on Mechanical Characteristics
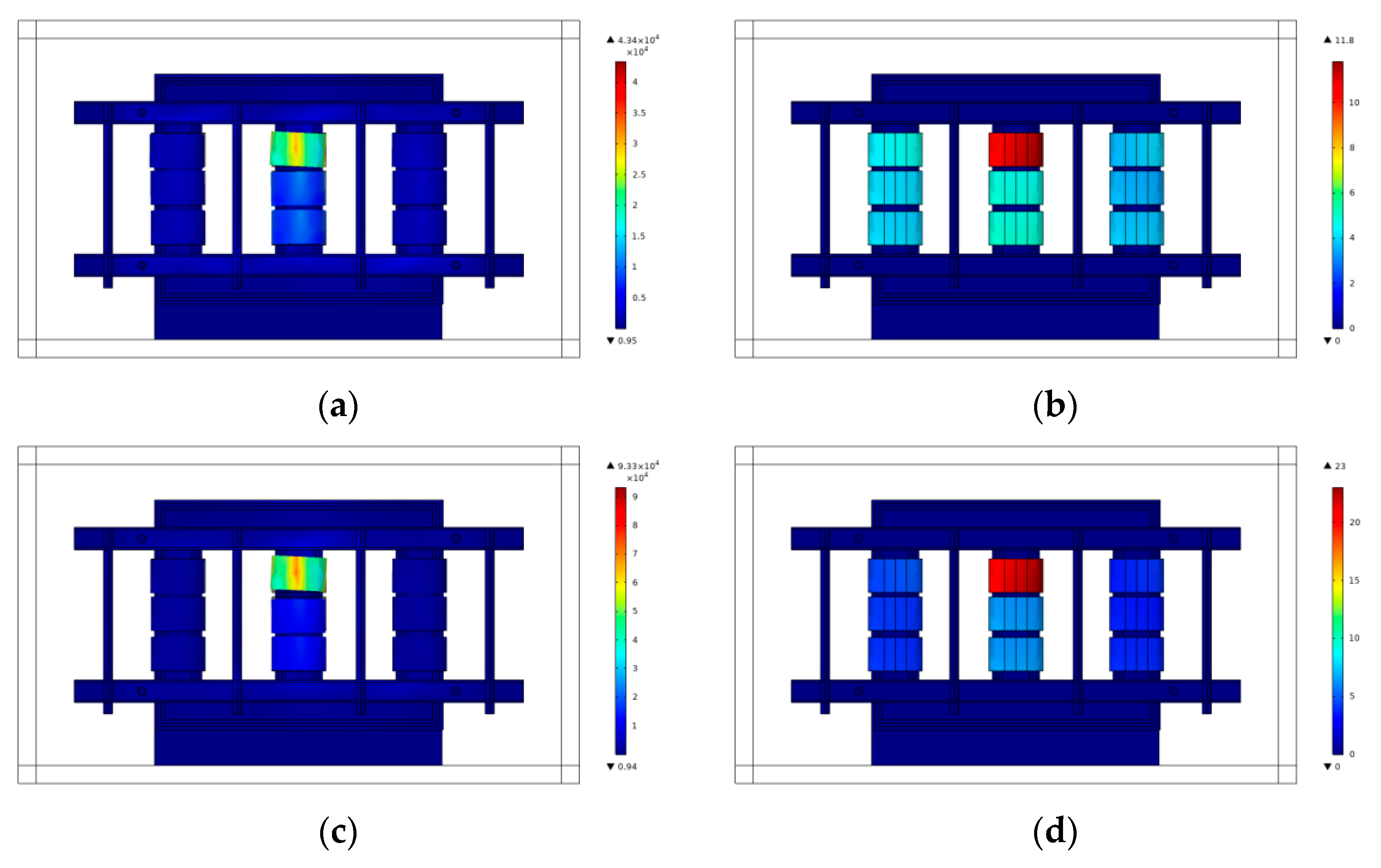
4.1. Analysis of Transformer Interturn Fault Force
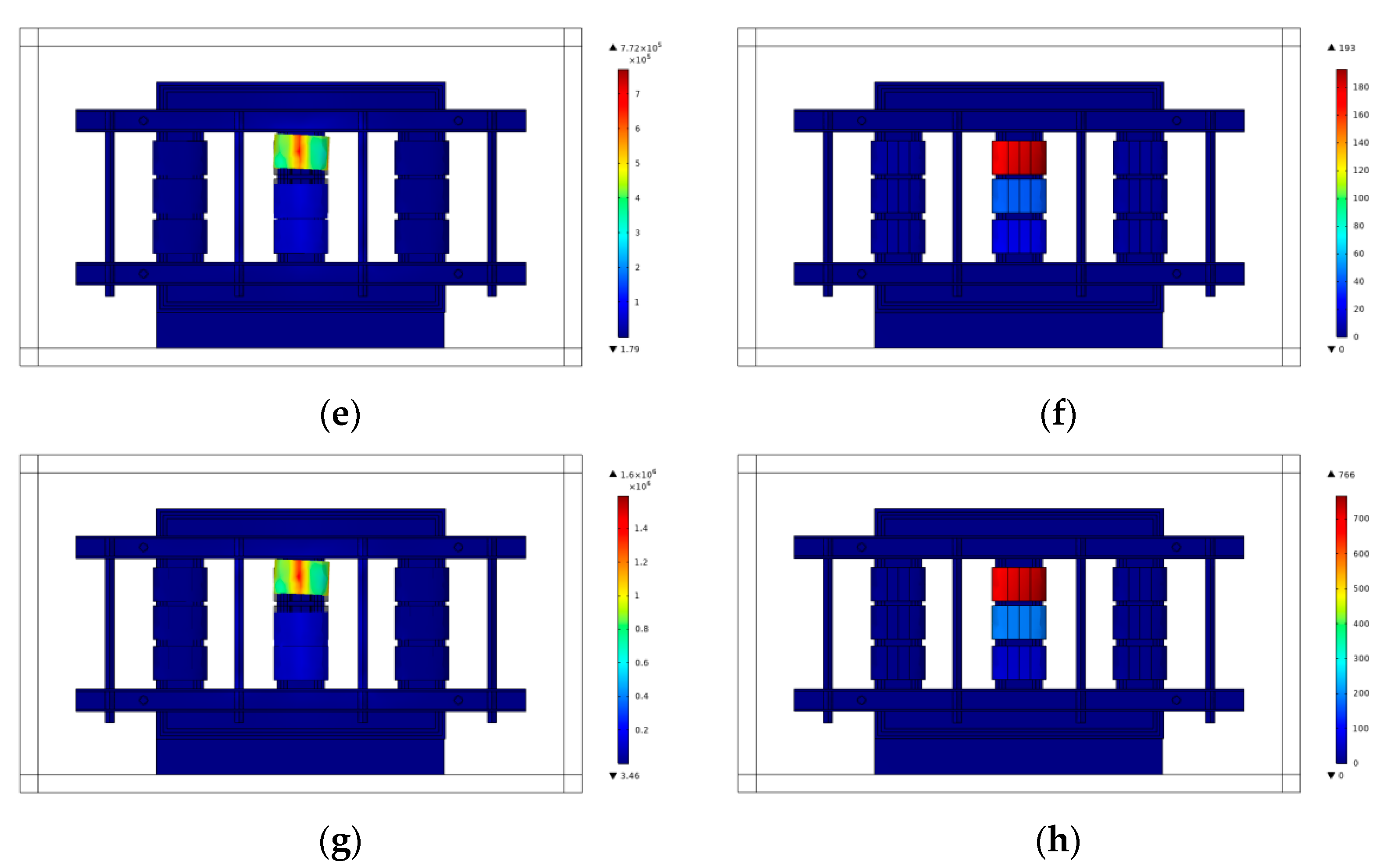
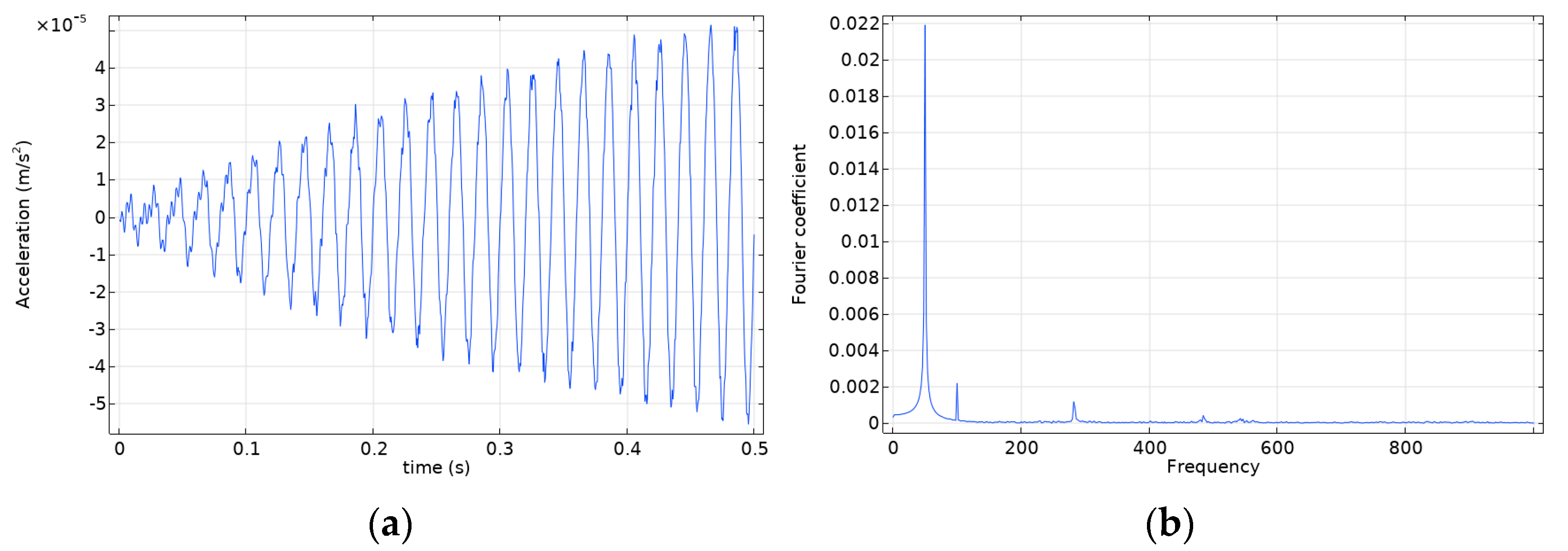
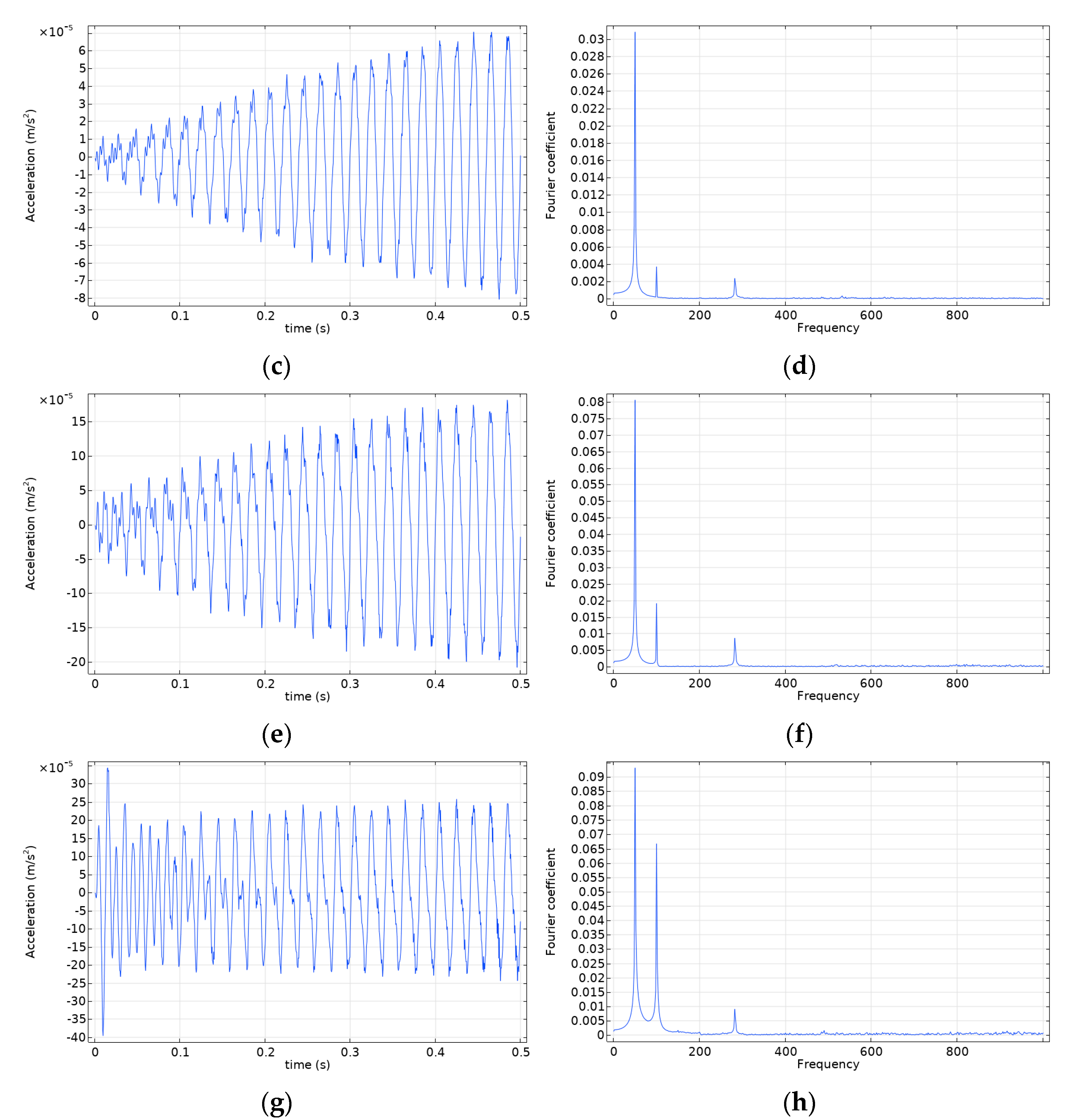
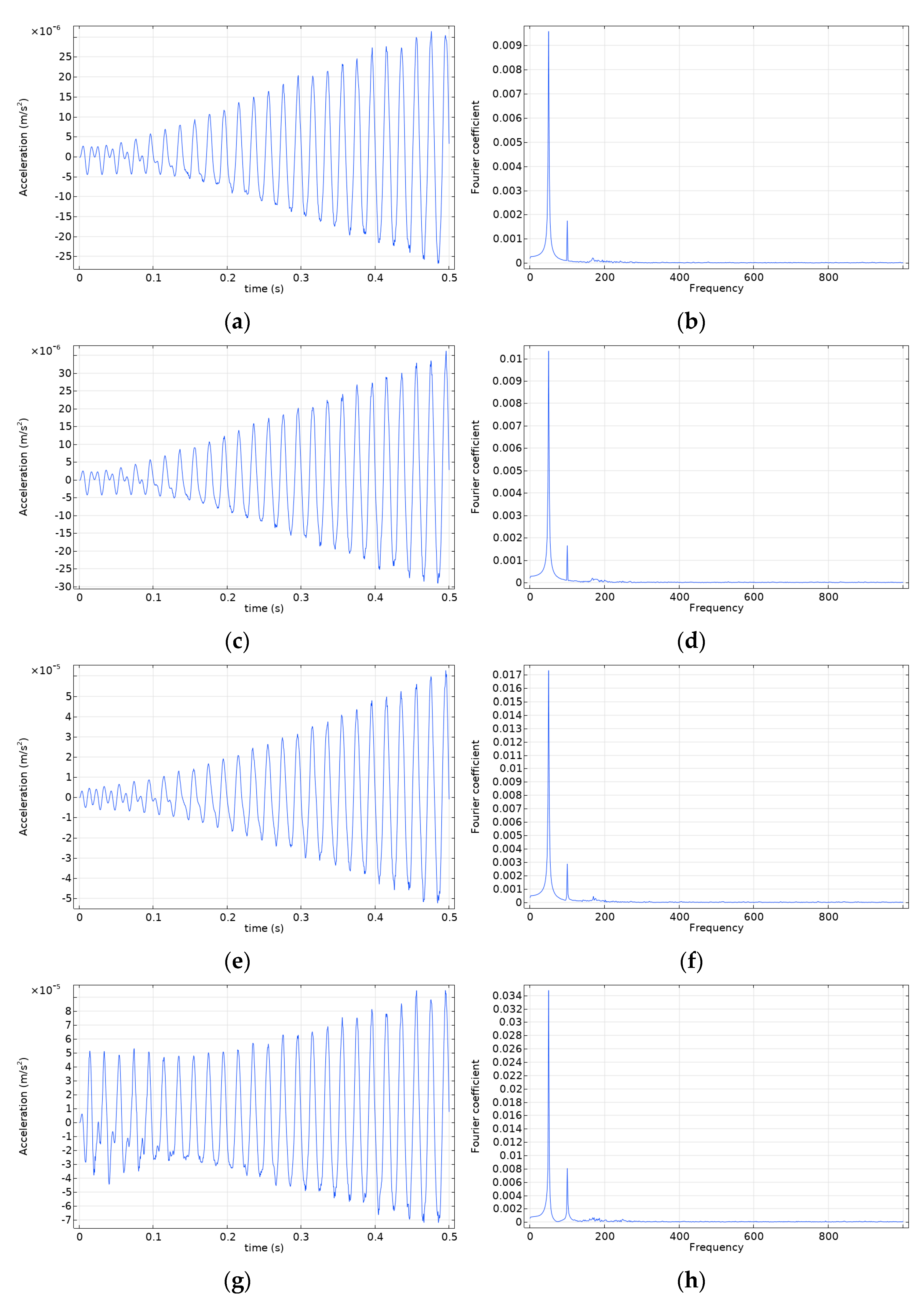
4.2. Analysis of the Vibration Situation under the Transformer Inter–Turn Fault
5. Conclusions
- In this model, the transformer interturn fault current becomes rapidly larger as the interturn insulation material ages. The magnetic flux density of the core is locally saturated where the fault is. As a result, the short–circuit winding’s local leakage magnetic field expands. When the interturn insulation material is completely damaged, the transformer experiences an interturn short circuit. The winding short–circuit current is tens of times the normal current. The leakage field from the short–circuit fault makes the core vibrate more by locally filling up the magnetic field of the core.
- When the transformer develops from interturn discharge to interturn short circuit, the strain on the short–circuit winding increases dramatically, resulting in a larger deformation of the short–circuit winding. Finally, the short–circuit winding causes damage. The mechanical characteristics of the winding will be reduced after the deformation occurs, leading to a decrease in short circuit resistance.
- In the time domain, the amplitude of the waveform at the core and case points increases as the inter–turn insulation material ages. The interharmonic Fourier coefficients also increase in the frequency domain. Therefore, in transformer fault detection, the vibration characteristics of the shell points in the time and frequency domains can be combined to analyze and detect transformer faults.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Baravati, P.R.; Moazzami, M.; Hosseini, S.M.H.; Mirzaei, H.R.; Fani, B. Achieving the exact equivalent circuit of a large-scale transformer winding using an improved detailed model for partial discharge study. Int. J. Electr. Power Energy Syst. 2022, 134, 107451. [Google Scholar] [CrossRef]
- Am, A.; Mv, A.; Ah, B.; Mf, A. HTS transformers leakage flux and short circuit force mitigation through optimal design of auxiliary windings. Cryogenics 2020, 110, 103148. [Google Scholar]
- Moradnouri, A.; Vakilian, M.; Hekmati, A.; Fardmanesh, M. Multi-segment Winding Application for Axial Short Circuit Force Reduction Under Tap Changer Operation in HTS Transformers. J. Supercond. Nov. Magn. 2019, 32, 3171–3182. [Google Scholar] [CrossRef]
- Moradnouri, A.; Vakilian, M.; Hekmati, A.; Fardmanesh, M. Inductance Calculation of HTS Transformers with Multi-segment Windings Considering Insulation Constraints. J. Supercond. Nov. Magn. 2021, 34, 1–11. [Google Scholar] [CrossRef]
- Mikhak-Beyranvand, M.; Faiz, J.; Rezaei-Zare, A.; Rezaeealam, B. Electromagnetic and thermal behavior of a single-phase transformer during Ferroresonance considering hysteresis model of core. Int. J. Electr. Power Energy Syst. 2020, 121, 106078. [Google Scholar] [CrossRef]
- Behjat, V.; Vahedi, A. Analysis of internal winding short circuit faults in power transformers using transient finite element method coupling with external circuit equations. Int. J. Numer. Model. Electron. Netw. Devices Fields 2013, 26, 425–442. [Google Scholar] [CrossRef]
- Yang, C.; Ding, Y.; Qiu, H.; Xiong, B. Analysis of Turn-to-Turn Fault on Split-Winding Transformer Using Coupled Field-Circuit Approach. Processes 2021, 9, 1314. [Google Scholar] [CrossRef]
- Asadi, N.; Kelk, H.M. Modeling, Analysis, and Detection of Internal Winding Faults in Power Transformers. IEEE Trans. Power Deliv. 2015, 30, 2419–2426. [Google Scholar] [CrossRef]
- Soleimani, M.; Faiz, J.; Nasab, P.S.; Moallem, M. Temperature Measuring-Based Decision-Making Prognostic Approach in Electric Power Transformers Winding Failures. IEEE Trans. Instrum. Meas. 2020, 69, 6995–7003. [Google Scholar] [CrossRef]
- Wang, H.; Butler, K.L. Modeling transformers with internal incipient faults. IEEE Power Eng. Rev. 2007, 22, 64. [Google Scholar] [CrossRef]
- Etumi, A.A.A.; Anayi, F.J. The Application of Correlation Technique in Detecting Internal and External Faults in Three-Phase Transformer and Saturation of Current Transformer. IEEE Trans. Power Deliv. 2016, 31, 2131–2139. [Google Scholar] [CrossRef]
- Oliveira, L.M.R.; Cardoso, A.J.M. A Permeance-Based Transformer Model and Its Application to Winding Interturn Arcing Fault Studies. IEEE Trans. Power Deliv. 2010, 25, 1589–1598. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Ge, W.; Xie, Y.; Li, Y. Comprehensive Analysis of Winding Electromagnetic Force and Deformation During No-Load Closing and Short-Circuiting of Power Transformers. IEEE Access 2021, 9, 73335–73345. [Google Scholar] [CrossRef]
- Duan, X.; Zhao, T.; Liu, J.; Zhang, L.; Zou, L. Analysis of Winding Vibration Characteristics of Power Transformers Based on the Finite-Element Method. Energies 2018, 11, 2404. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Yang, B.; Xu, W.; Wang, S.; Wang, G.; Huangfu, Y.; Zhang, J. Dynamic Deformation Analysis of Power Transformer Windings in Short-Circuit Fault by FEM. IEEE Trans. Appl. Supercond. 2014, 24, 1–4. [Google Scholar] [CrossRef]
- Jia, X.; Lin, M.; Su, S.; Wang, Q.; Yang, J. Numerical study on temperature rise and mechanical properties of winding in oil-immersed transformer. Energy 2022, 239, 121788. [Google Scholar] [CrossRef]
- Behjat, V.; Vahedi, A. An experimental approach for investigating low-level interturn winding faults in power transformers. Electr. Eng. 2013, 95, 135–145. [Google Scholar] [CrossRef]
- Nia, M.S.S.; Shamsi, P.; Ferdowsi, M. Investigation of Various Transformer Topologies for HF Isolation Applications. IEEE Trans. Plasma Sci. 2020, 48, 512–521. [Google Scholar]
- Li, M.; Wang, Z.; Zhang, J.; Ni, Z.; Tan, R. Temperature Rise Test and Thermal-Fluid Coupling Simulation of an Oil-Immersed Autotransformer Under DC Bias. IEEE Access 2021, 9, 32835–32844. [Google Scholar] [CrossRef]
- Liu, X.; Yang, Y.; Huang, Y.; Jadoon, A. Vibration characteristic investigation on distribution transformer influenced by DC magnetic bias based on motion transmission model. Int. J. Electr. Power Energy Syst. 2018, 98, 389–398. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, H.; Wang, S.; Li, H.; Yuan, D. Cumulative Deformation Analysis for Transformer Winding Under Short-Circuit Fault Using Magnetic–Structural Coupling Model. IEEE Trans. Appl. Supercond. 2016, 26, 0606605. [Google Scholar] [CrossRef]
- Zhang, F.; Ji, S.; Shi, Y.; Ren, F.; Zhan, C.; Zhu, L. Comprehensive vibration generation model of transformer winding under load current. IET Gener. Transm. Distrib. 2019, 13, 1563–1571. [Google Scholar] [CrossRef]
- Jingzhu, H.; Dichen, L.; Qingfen, L.; Yang, Y.; Shanshan, L. Electromagnetic vibration noise analysis of transformer windings and core. IET Electr. Power Appl. 2016, 10, 251–257. [Google Scholar] [CrossRef]
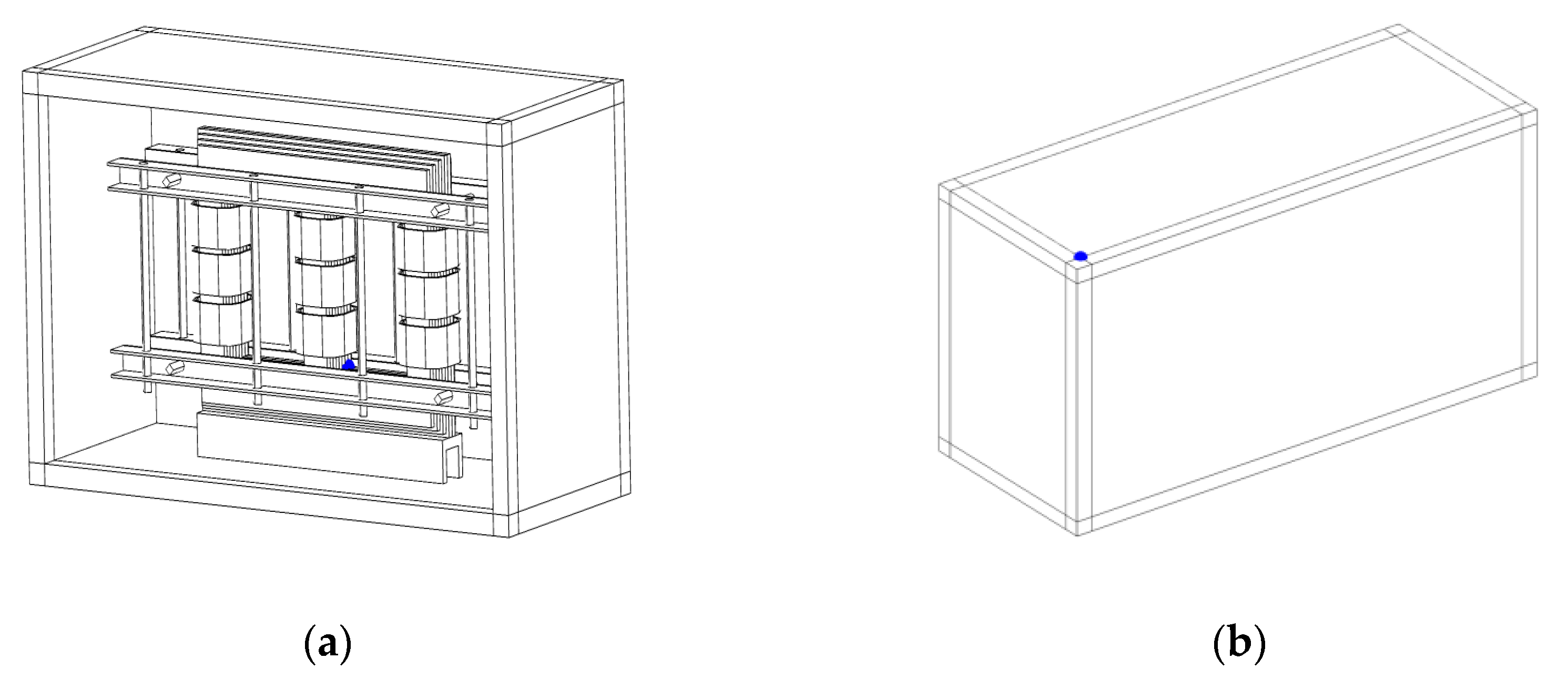
| Main Technical Indicators | Parameter |
|---|---|
| Phase number | three–phase |
| Rated frequency | 50 Hz |
| Rated capacity/kVA | 100 |
| Rated voltage/kV | 10/0.4 |
| Linkage group number | Yyn0 |
| short–circuit impedance (%) | 4.0 |
| Main Technical Indicators | Parameter |
|---|---|
| Number of turns of high voltage winding | 500 |
| Number of turns of low voltage winding | 20 |
| Diameter of high voltage winding/cm | 22–23 |
| Diameter of low voltage winding/cm | 23–24 |
| Height of high voltage winding/cm | 50 |
| Height of low voltage winding/cm | 50 |
| Shell size(W×H×D)/cm | 250 × 150 × 100 |
| Height of the upper and lower yoke of the core/cm | 102.4 |
| Core thickness/cm | 20 |
| Core length/cm | 128.48 |
| Core column radius of core/cm | 21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, N.; Li, J.; Shao, L.; Liu, H.; Ren, L.; Zhu, L. Analysis of Interturn Faults on Transformer Based on Electromagnetic-Mechanical Coupling. Energies 2023, 16, 512. https://doi.org/10.3390/en16010512
Zhu N, Li J, Shao L, Liu H, Ren L, Zhu L. Analysis of Interturn Faults on Transformer Based on Electromagnetic-Mechanical Coupling. Energies. 2023; 16(1):512. https://doi.org/10.3390/en16010512
Chicago/Turabian StyleZhu, Nan, Ji Li, Lei Shao, Hongli Liu, Lei Ren, and Lihua Zhu. 2023. "Analysis of Interturn Faults on Transformer Based on Electromagnetic-Mechanical Coupling" Energies 16, no. 1: 512. https://doi.org/10.3390/en16010512
APA StyleZhu, N., Li, J., Shao, L., Liu, H., Ren, L., & Zhu, L. (2023). Analysis of Interturn Faults on Transformer Based on Electromagnetic-Mechanical Coupling. Energies, 16(1), 512. https://doi.org/10.3390/en16010512






