An Experimental Approach for Secondary Consensus Control Tuning for Inverter-Based Islanded Microgrids
Abstract
:1. Introduction
2. Background and Methodology
2.1. Problem Formulation
2.1.1. Microgrid Description
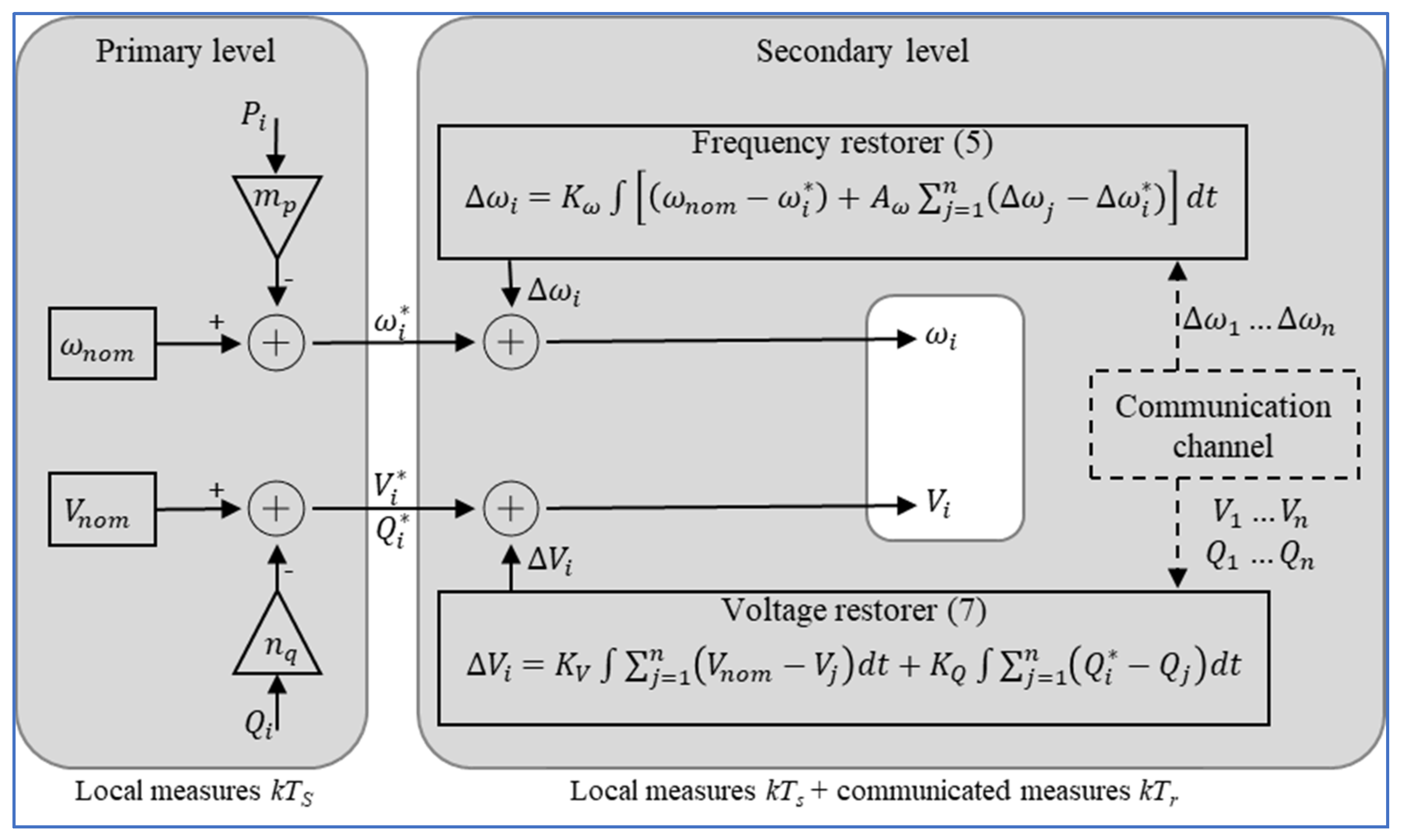
2.1.2. Controller and Tuning Methodology Description
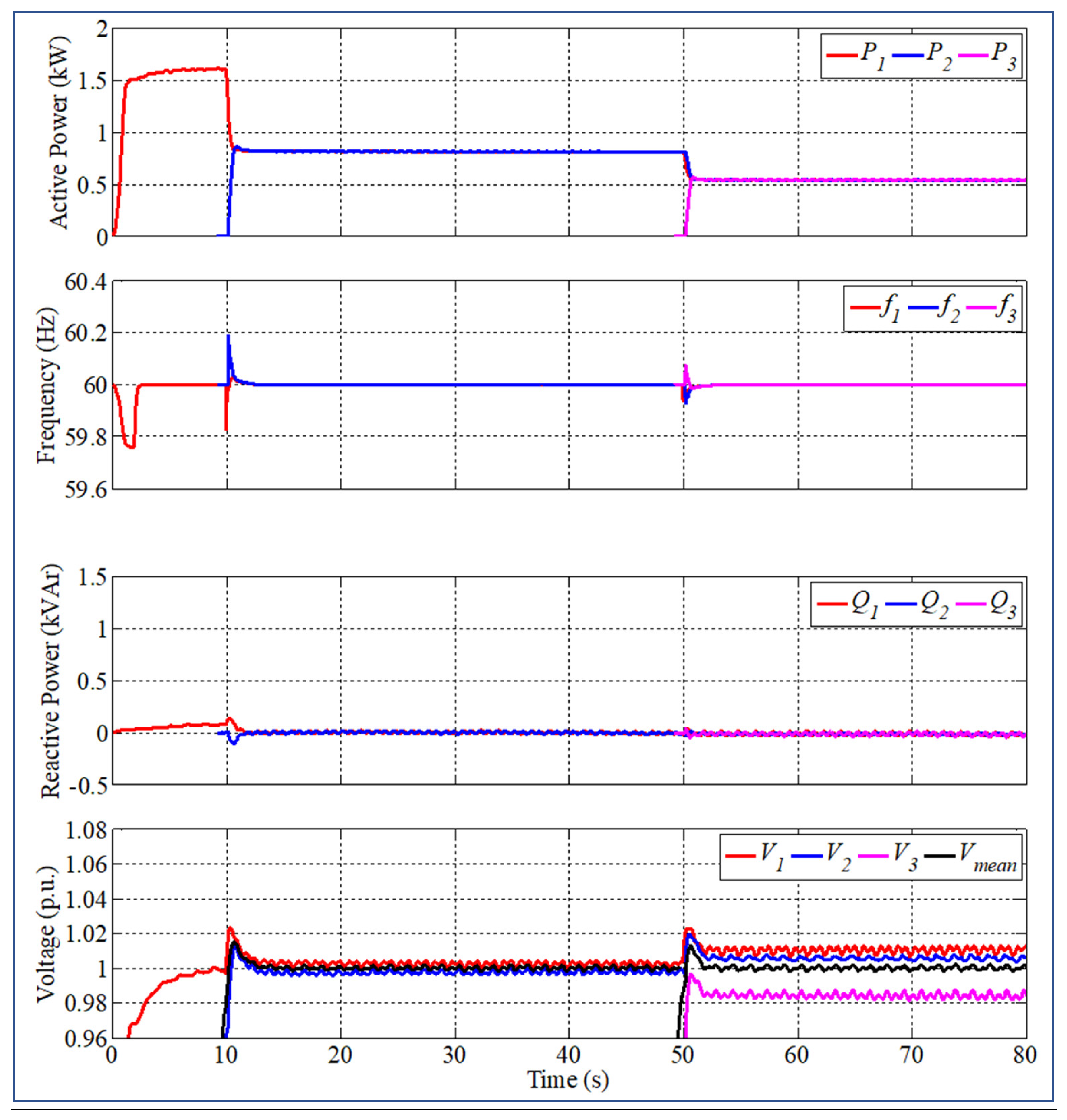
2.1.3. Merit Responses
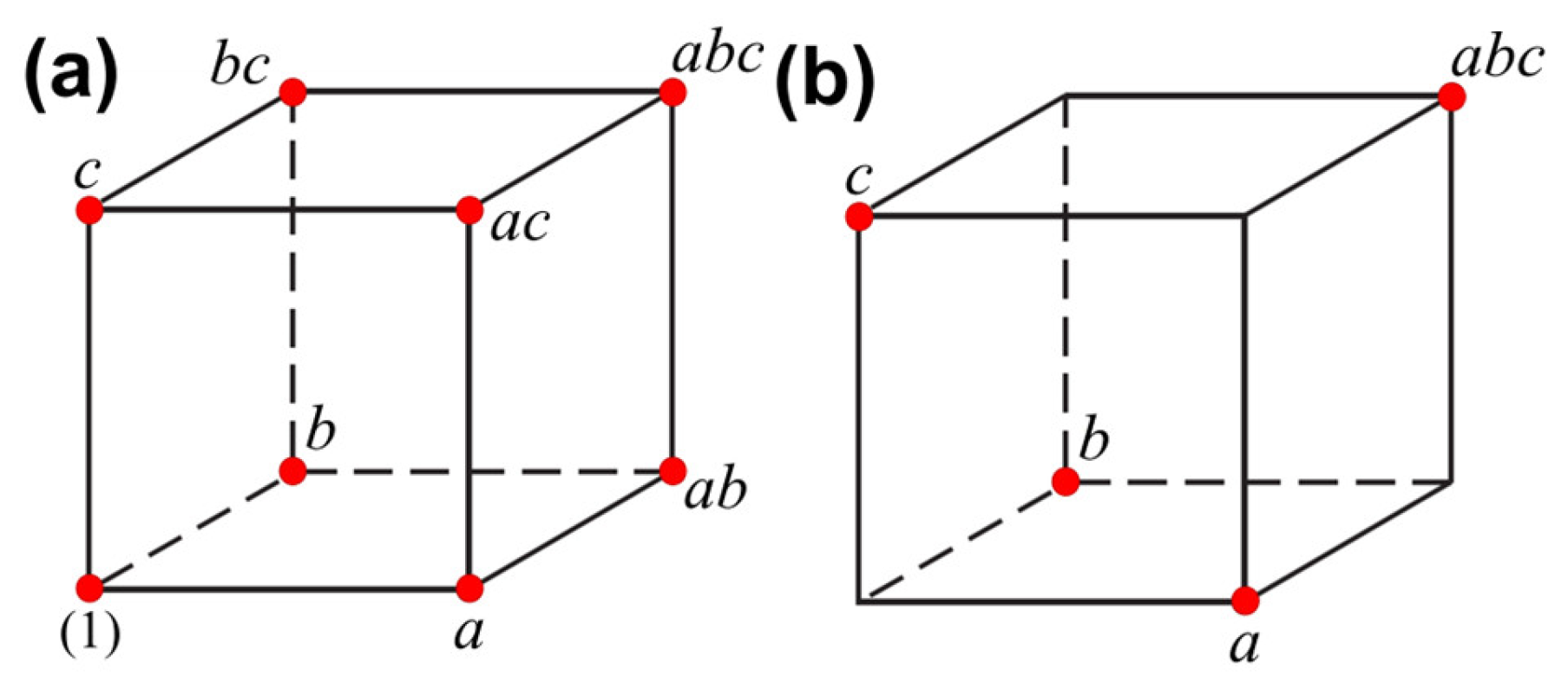
2.2. Design of Experiments for Parameters Tuning
3. Experimental Results and Discussion
3.1. Planning before Experiments
3.2. Designs and Results
3.2.1. Strategies for Choosing Parameters in a Factorial Design
3.2.2. Optimization Design
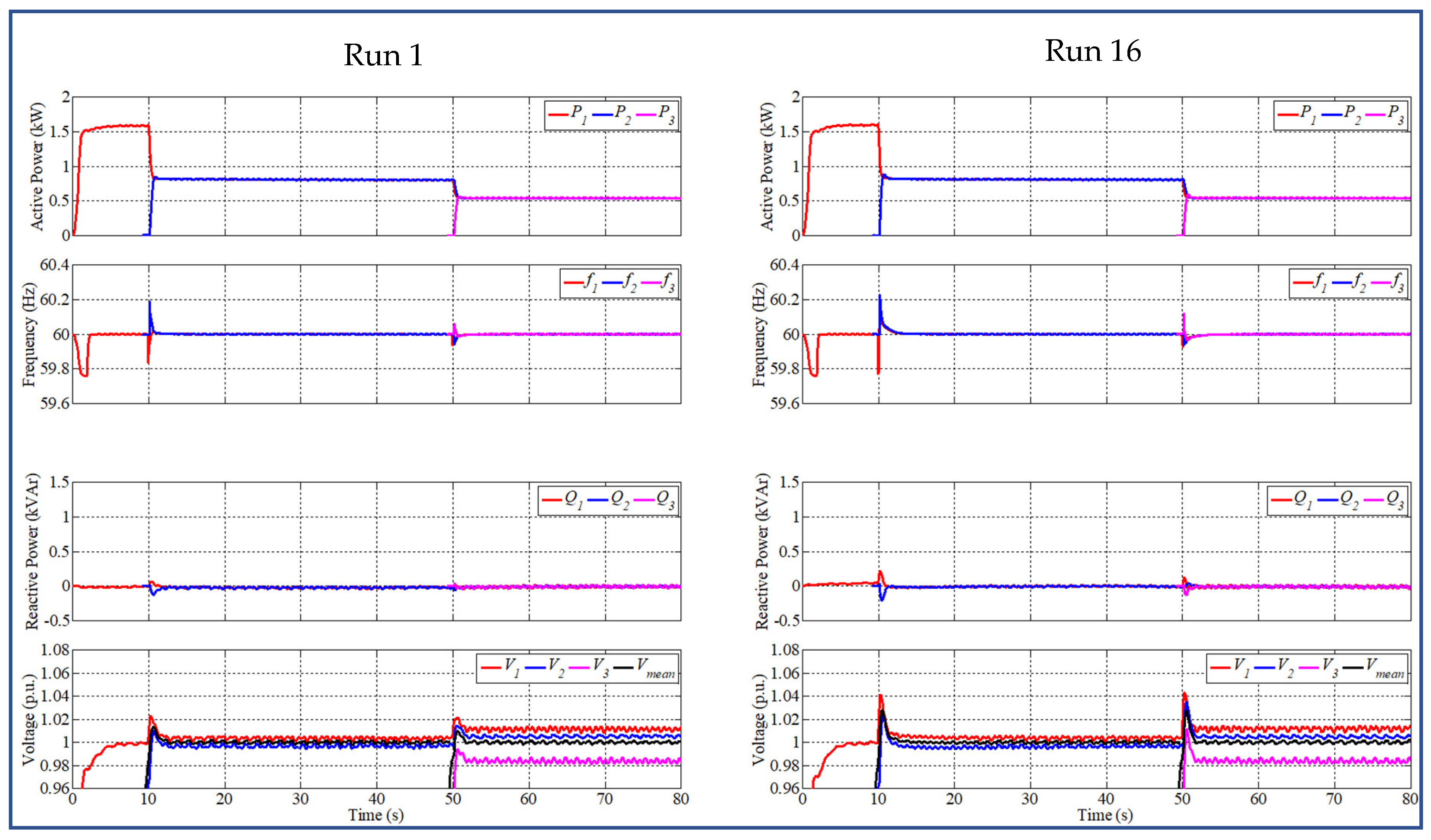
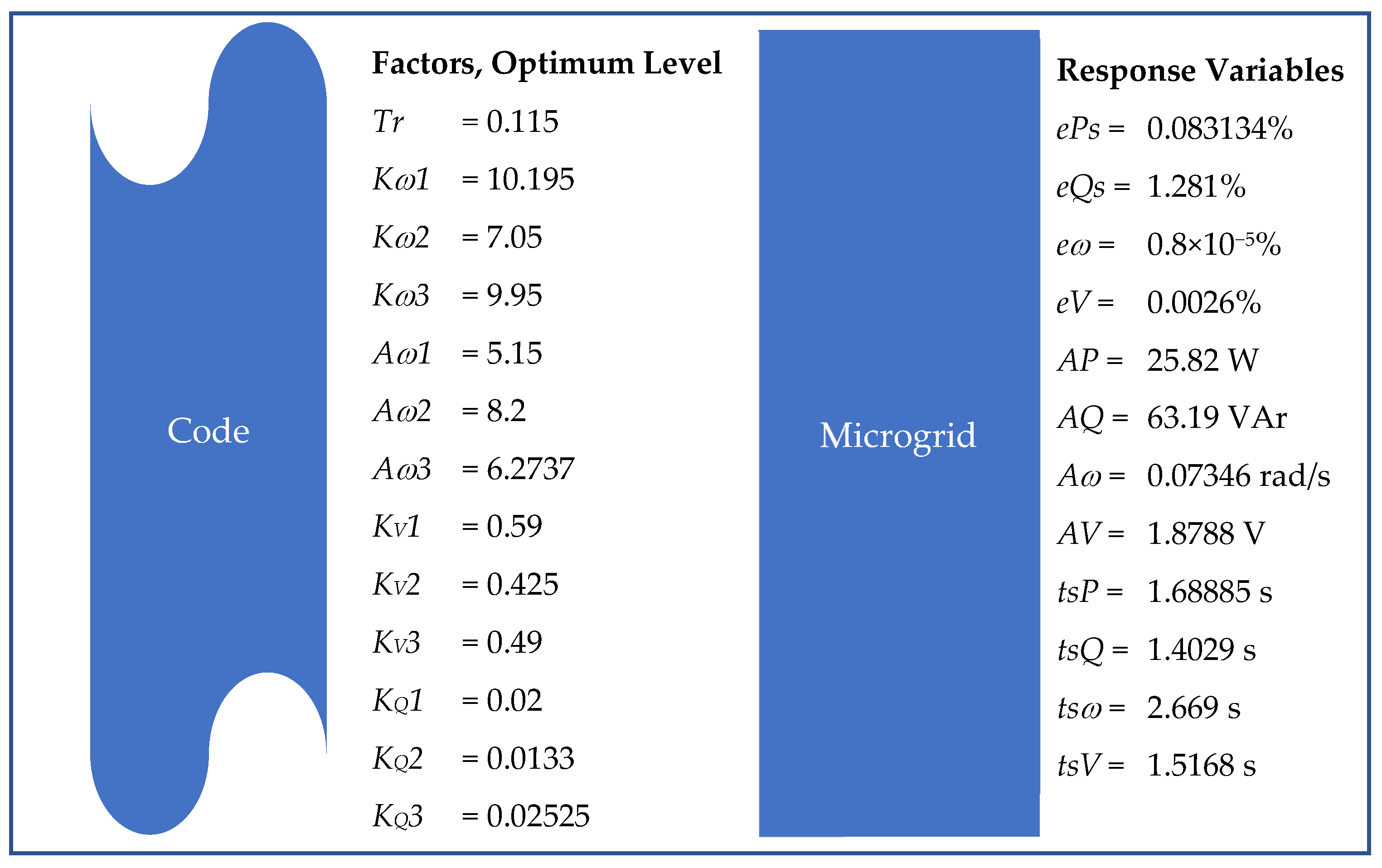
3.2.3. Verification
4. Conclusions and Recommendations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- U.S. Department of Energy (DOE). Combined Heat and Power Technology. 2016. Available online: https://www.energy.gov (accessed on 13 December 2022).
- Kroposki, B.; Lasseter, R.; Ise, T.; Morozumi, S.; Papathanassiou, S.; Hatziargyriou, N. Making Microgrids Work. IEEE Power Energy Mag. 2008, 6, 40–53. [Google Scholar] [CrossRef]
- Neukirchner, L.; Görbe, P.; Magyar, A. Voltage Unbalance Reduction in the Domestic Distribution Area Using Asymmetric Inverters. J. Clean. Prod. 2017, 142, 1710–1720. [Google Scholar] [CrossRef]
- Shahgholian, G. A Brief Review on Microgrids: Operation, Applications, Modeling, and Control. Int. Trans. Electr. Energy Syst. 2021, 31, e12885. [Google Scholar] [CrossRef]
- Tayab, U.B.; Bin Roslan, M.A.; Hwai, L.J.; Kashif, M. A Review of Droop Control Techniques for Microgrid. Renew. Sustain. Energy Rev. 2017, 76, 717–727. [Google Scholar] [CrossRef]
- Zhang, Y.; Mohammadpour Shotorbani, A.; Wang, L.; Mohammadi-Ivatloo, B. Enhanced PI Control and Adaptive Gain Tuning Schemes for Distributed Secondary Control of an Islanded Microgrid. IET Renew. Power Gener. 2021, 15, 854–864. [Google Scholar] [CrossRef]
- Rey, J.M.; Castilla, M.; Miret, J.; Velasco, M.; Martí, P.; Mojica-Nava, E. Negative-Sequence Voltage Elimination for Distributed Generators in Grid-Feeding Operation Mode. IET Power Electron. 2020, 13, 1764–1774. [Google Scholar] [CrossRef]
- Phurailatpam, C.; Rajpurohit, B.S.; Wang, L. Planning and Optimization of Autonomous DC Microgrids for Rural and Urban Applications in India. Renew. Sustain. Energy Rev. 2018, 82, 194–204. [Google Scholar] [CrossRef]
- Wolsink, M. Distributed Energy Systems as Common Goods: Socio-Political Acceptance of Renewables in Intelligent Microgrids. Renew. Sustain. Energy Rev. 2020, 127, 109841. [Google Scholar] [CrossRef]
- de Doile, G.N.D.; Rotella Junior, P.; Rocha, L.C.S.; Janda, K.; Aquila, G.; Peruchi, R.S.; Balestrassi, P.P. Feasibility of Hybrid Wind and Photovoltaic Distributed Generation and Battery Energy Storage Systems under Techno-Economic Regulation. Renew. Energy 2022, 195, 1310–1323. [Google Scholar] [CrossRef]
- Sharma, B.; Shrestha, A.; Terriche, Y.; Lashab, A.; Guerrero, J.M. Sharing Sequence Components of Reactive Power in a Three-Phase Four-Wire Islanded Microgrid. Electr. Power Syst. Res. 2022, 213, 108675. [Google Scholar] [CrossRef]
- Kaviri, S.M.; Hajebrahimi, H.; Poorali, B.; Pahlevani, M.; Jain, P.K.; Bakhshai, A. A Supervisory Control System for Nanogrids Operating in the Stand-Alone Mode. IEEE Trans. Power Electron. 2021, 36, 2914–2931. [Google Scholar] [CrossRef]
- Lv, Z.; Wu, Z.; Dou, X.; Zhou, M.; Hu, W. Distributed Economic Dispatch Scheme for Droop-Based Autonomous DC Microgrid. Energies 2020, 13, 404. [Google Scholar] [CrossRef] [Green Version]
- Rosero, C.X.; Velasco, M.; Martí, P.; Camacho, A.; Miret, J.; Castilla, M. Active Power Sharing and Frequency Regulation in Droop-Free Control for Islanded Microgrids under Electrical and Communication Failures. IEEE Trans. Ind. Electron. 2020, 67, 6461–6472. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; De Vicuña, L.G.; Castilla, M. Hierarchical Control of Droop-Controlled AC and DC Microgrids—A General Approach toward Standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Miret, J.; De Vicuña, J.L.G.; Guzmán, R.; Camacho, A.; Ghahderijani, M.M. A Flexible Experimental Laboratory for Distributed Generation Networks Based on Power Inverters. Energies 2017, 10, 1589. [Google Scholar] [CrossRef] [Green Version]
- Lu, L.Y.; Chu, C.C. Consensus-Based Droop Control Synthesis for Multiple DICs in Isolated Micro-Grids. IEEE Trans. Power Syst. 2015, 30, 2243–2256. [Google Scholar] [CrossRef]
- Miret, J.; Balestrassi, P.P.; Camacho, A.; Guzmán, R.; Castilla, M. Optimal Tuning of the Control Parameters of an Inverter-based Microgrid Using the Methodology of Design of Experiments. IET Power Electron. 2020, 13, 3651–3660. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments, 8th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013; ISBN 9781118146927. [Google Scholar]
- Amorim, L.F.; de Paiva, A.P.; Balestrassi, P.P.; Ferreira, J.R. Multi-Objective Optimization Algorithm for Analysis of Hardened Steel Turning Manufacturing Process. Appl. Math. Model. 2022, 106, 822–843. [Google Scholar] [CrossRef]
- Saeid Atabaki, M.; Mohammadi, M.; Aryanpur, V. An Integrated Simulation-Optimization Modelling Approach for Sustainability Assessment of Electricity Generation System. Sustain. Energy Technol. Assess. 2022, 52, 102010. [Google Scholar] [CrossRef]
- Xiang, Y.; Liu, J.; Liu, Y. Robust Energy Management of Microgrid with Uncertain Renewable Generation and Load. IEEE Trans. Smart Grid 2016, 7, 1034–1043. [Google Scholar] [CrossRef]
- Wang, L.; Xu, W.; Zou, K.; Lv, X.; Gao, F.; Yin, W. Integrated Scheduling for Intelligent Regional Grid Based on Differential Evolution. In Proceedings of the 2014 IEEE Innovative Smart Grid Technologies—Asia (ISGT ASIA), Kuala Lumpur, Malaysia, 20–23 May 2014; pp. 312–317. [Google Scholar] [CrossRef]
- Mauro, C.A.; Smith, D.E. Factor Screening in Simulation: Evaluation of Two Strategies Based on Random Balance Sampling. Manag. Sci. 1984, 30, 209–221. [Google Scholar] [CrossRef]



| Nominal voltage (line to neutral) | Vnom | 110 V rms |
| Nominal frequency | fnom | 60 Hz |
| Nominal rated power (base power) | Sb | 2.5 kVA |
| Line impedance Z1 | LZ1 | 4 mH |
| RZ1 | 0.5 Ω | |
| Line impedance Z2 | LZ2 | 1 mH |
| RZ2 | 0.5 Ω | |
| Line impedance Z3 | LZ3 | 0.6 mH |
| RZ3 | 1.13 Ω | |
| Line impedance Z4 | LZ4 | 0.8 mH |
| RZ4 | 0 Ω |
| Symbol (Unit) | Response | Equation | |
|---|---|---|---|
| ePs | Active power sharing error | (9) | |
| eQs | Reactive power sharing error | (10) | |
| eω | Frequency deviation from nominal value | (11) | |
| eV | Mean voltage deviation from the nominal value | (12) | |
| AP (W) | Active power overshoot | AP = Max (Pi − Pi_steady-state) | (13) |
| AQ (Var) | Reactive power overshoot | AQ = Max (Qi − Qi_steady-state) | (14) |
| Aω (rad/s) | Frequency overshoot | Aω = Max (ωi − ωi_steady-state) | (15) |
| AV (V) | Voltage overshoot | AV = Max (Vi − Vi_steady-state) | (16) |
| tsP (s) | Maximum step active-power change settling time | ||
| tsQ (s) | Maximum step reactive-power change settling time | ||
| tsω (s) | Maximum step frequency change settling time | ||
| tsV (s) | Maximum step-voltage change settling time |
| Run | Tr | Kω1 | Kω2 | Kω3 | Aω1 | Aω2 | Aω3 | KV1 | KV2 | KV3 | KQ1 | KQ2 | KQ3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.115 | 5.15 | 5.15 | 5.15 | 15.05 | 15.05 | 15.05 | 0.2575 | 0.2575 | 0.2575 | 0.01288 | 0.01288 | 0.03763 |
| 2 | 0.325 | 5.15 | 5.15 | 5.15 | 5.15 | 5.15 | 5.15 | 0.2575 | 0.7525 | 0.7525 | 0.03763 | 0.03763 | 0.03763 |
| 3 | 0.115 | 15.05 | 5.15 | 5.15 | 5.15 | 5.15 | 15.05 | 0.7525 | 0.7525 | 0.7525 | 0.01288 | 0.01288 | 0.01288 |
| 4 | 0.325 | 15.05 | 5.15 | 5.15 | 15.05 | 15.05 | 5.15 | 0.7525 | 0.2575 | 0.2575 | 0.03763 | 0.03763 | 0.01288 |
| 5 | 0.115 | 5.15 | 15.05 | 5.15 | 5.15 | 15.05 | 5.15 | 0.7525 | 0.7525 | 0.2575 | 0.03763 | 0.01288 | 0.01288 |
| 6 | 0.325 | 5.15 | 15.05 | 5.15 | 15.05 | 5.15 | 15.05 | 0.7525 | 0.2575 | 0.7525 | 0.01288 | 0.03763 | 0.01288 |
| 7 | 0.115 | 15.05 | 15.05 | 5.15 | 15.05 | 5.15 | 5.15 | 0.2575 | 0.2575 | 0.7525 | 0.03763 | 0.01288 | 0.03763 |
| 8 | 0.325 | 15.05 | 15.05 | 5.15 | 5.15 | 15.05 | 15.05 | 0.2575 | 0.7525 | 0.2575 | 0.01288 | 0.03763 | 0.03763 |
| 9 | 0.115 | 5.15 | 5.15 | 15.05 | 15.05 | 5.15 | 5.15 | 0.7525 | 0.7525 | 0.2575 | 0.01288 | 0.03763 | 0.03763 |
| 10 | 0.325 | 5.15 | 5.15 | 15.05 | 5.15 | 15.05 | 15.05 | 0.7525 | 0.2575 | 0.7525 | 0.03763 | 0.01288 | 0.03763 |
| 11 | 0.115 | 15.05 | 5.15 | 15.05 | 5.15 | 15.05 | 5.15 | 0.2575 | 0.2575 | 0.7525 | 0.01288 | 0.03763 | 0.01288 |
| 12 | 0.325 | 15.05 | 5.15 | 15.05 | 15.05 | 5.15 | 15.05 | 0.2575 | 0.7525 | 0.2575 | 0.03763 | 0.01288 | 0.01288 |
| 13 | 0.115 | 5.15 | 15.05 | 15.05 | 5.15 | 5.15 | 15.05 | 0.2575 | 0.2575 | 0.2575 | 0.03763 | 0.03763 | 0.01288 |
| 14 | 0.325 | 5.15 | 15.05 | 15.05 | 15.05 | 15.05 | 5.15 | 0.2575 | 0.7525 | 0.7525 | 0.01288 | 0.01288 | 0.01288 |
| 15 | 0.115 | 15.05 | 15.05 | 15.05 | 15.05 | 15.05 | 15.05 | 0.7525 | 0.7525 | 0.7525 | 0.03763 | 0.03763 | 0.03763 |
| 16 | 0.325 | 15.05 | 15.05 | 15.05 | 5.15 | 5.15 | 5.15 | 0.7525 | 0.2575 | 0.2575 | 0.01288 | 0.01288 | 0.03763 |
| Run | eω | eps | eV | eQs | tsω | tsp | tsV | tsQ | Aω | AP | AV | AQ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [%] | [%] | [%] | [%] | [s] | [s] | [s] | [s] | [rad/s] | [W] | [V] | [Var] | |
| 1 | 3.31 × 10−5 | 6.76 × 10−2 | 3.57 × 10−3 | 1.1017 | 4.160 | 0.490 | 5.330 | 0.690 | 0.120 | 0.000 | 1.338 | 71.900 |
| 2 | 3.63 × 10−5 | 6.80 × 10−2 | 1.60 × 10−2 | 7.7735 | 2.990 | 3.230 | 5.380 | 0.880 | 0.100 | 63.200 | 5.445 | 125.600 |
| 3 | 1.43 × 10−5 | 7.30 × 10−2 | 3.60 × 10−4 | 0.9244 | 0.880 | 0.490 | 1.320 | 1.300 | 0.120 | 27.000 | 1.960 | 38.100 |
| 4 | 5.55 × 10−5 | 5.98 × 10−2 | 7.57 × 10−3 | 0.2218 | 7.630 | 2.200 | 3.330 | 2.350 | 0.090 | 135.300 | 10.423 | 510.900 |
| 5 | 1.09 × 10−5 | 7.80 × 10−2 | 4.96 × 10−3 | 1.3999 | 2.690 | 0.540 | 1.370 | 0.340 | 0.090 | 0.000 | 1.400 | 71.600 |
| 6 | 4.04 × 10−5 | 6.15 × 10−2 | 1.57 × 10−3 | 1.6614 | 7.830 | 2.990 | 2.500 | 2.840 | 0.120 | 117.800 | 11.045 | 573.100 |
| 7 | 3.10 × 10−5 | 6.01 × 10−2 | 7.36 × 10−3 | 3.5684 | 2.200 | 0.590 | 1.370 | 0.790 | 0.090 | 0.000 | 0.964 | 88.900 |
| 8 | 2.19 × 10−5 | 6.39 × 10−2 | 1.32 × 10−2 | 1.6936 | 8.510 | 2.450 | 3.820 | 2.150 | 0.120 | 148.600 | 11.978 | 472.600 |
| 9 | 6.17 × 10−5 | 7.69 × 10−2 | 1.71 × 10−3 | 0.4699 | 1.570 | 1.130 | 1.520 | 1.860 | 0.110 | 83.500 | 7.311 | 193.500 |
| 10 | 4.15 × 10−5 | 5.08 × 10−2 | 9.53 × 10−4 | 6.977 | 9.680 | 0.880 | 1.960 | 2.200 | 0.120 | 21.800 | 2.707 | 102.300 |
| 11 | 4.60 × 10−6 | 8.14 × 10−2 | 4.81 × 10−3 | 1.5135 | 1.910 | 0.590 | 1.420 | 0.830 | 0.110 | 0.000 | 1.260 | 98.100 |
| 12 | 6.36 × 10−5 | 6.08 × 10−2 | 7.01 × 10−4 | 1.3926 | 8.680 | 1.670 | 1.960 | 3.570 | 0.120 | 37.800 | 3.422 | 96.700 |
| 13 | 1.90 × 10−5 | 9.17 × 10−2 | 3.37 × 10−3 | 9.7943 | 0.780 | 0.590 | 2.940 | 0.000 | 0.120 | 0.000 | 1.602 | 77.400 |
| 14 | 6.44 × 10−5 | 4.20 × 10−2 | 3.27 × 10−3 | 29.34 | 7.970 | 1.710 | 2.450 | 2.990 | 0.110 | 122.600 | 11.511 | 560.300 |
| 15 | 1.49 × 10−5 | 7.36 × 10−2 | 3.09 × 10−3 | 1.2465 | 4.550 | 0.980 | 1.320 | 0.000 | 0.110 | 82.400 | 7.156 | 206.100 |
| 16 | 2.99 × 10−5 | 7.07 × 10−2 | 1.21 × 10−3 | 2.2712 | 3.570 | 1.760 | 2.150 | 3.620 | 0.110 | 181.900 | 14.001 | 537.000 |
| Composite Desirability Interval | ||||
|---|---|---|---|---|
| Factor | Lower | Upper | Setting | Observation |
| Tr | 0.115 | 0.325 | 0.115 | The lower the better |
| Kω1 | 9.65 | 15.05 | To the next DOE | |
| Kω2 | 5.15 | 13.45 | 7.05 | Not significant (with desirability peak) |
| Kω3 | 5.15 | 15.05 | 9.95 | Not significant (with desirability peak) |
| Aω1 | 5.15 | 9.85 | To the next DOE | |
| Aω2 | 8.2 | 15.05 | To the next DOE | |
| Aω3 | 5.15 | 9.6 | To the next DOE | |
| KV1 | 0.59 | 0.7525 | To the next DOE | |
| KV2 | 0.2575 | 0.7525 | 0.425 | Not significant (with desirability peak) |
| KV3 | 0.49 | 0.7525 | To the next DOE | |
| KQ1 | 0.02 | 0.0376 | To the next DOE | |
| KQ2 | 0.0129 | 0.019 | To the next DOE | |
| KQ3 | 0.0129 | 0.0376 | 0.02525 | Not significant (with desirability peak) |
| Run | Kω1 | Aω1 | Aω2 | Aω3 | KV1 | KV3 | KQ1 | KQ2 |
|---|---|---|---|---|---|---|---|---|
| 1 | 9.65 | 5.15 | 8.2 | 5.15 | 0.59 | 0.49 | 0.02 | 0.0129 |
| 2 | 15.05 | 5.15 | 8.2 | 5.15 | 0.59 | 0.7525 | 0.0376 | 0.019 |
| 3 | 9.65 | 9.85 | 8.2 | 5.15 | 0.7525 | 0.49 | 0.0376 | 0.019 |
| 4 | 15.05 | 9.85 | 8.2 | 5.15 | 0.7525 | 0.7525 | 0.02 | 0.0129 |
| 5 | 9.65 | 5.15 | 15.05 | 5.15 | 0.7525 | 0.7525 | 0.0376 | 0.0129 |
| 6 | 15.05 | 5.15 | 15.05 | 5.15 | 0.7525 | 0.49 | 0.02 | 0.019 |
| 7 | 9.65 | 9.85 | 15.05 | 5.15 | 0.59 | 0.7525 | 0.02 | 0.019 |
| 8 | 15.05 | 9.85 | 15.05 | 5.15 | 0.59 | 0.49 | 0.0376 | 0.0129 |
| 9 | 9.65 | 5.15 | 8.2 | 9.6 | 0.7525 | 0.7525 | 0.02 | 0.019 |
| 10 | 15.05 | 5.15 | 8.2 | 9.6 | 0.7525 | 0.49 | 0.0376 | 0.0129 |
| 11 | 9.65 | 9.85 | 8.2 | 9.6 | 0.59 | 0.7525 | 0.0376 | 0.0129 |
| 12 | 15.05 | 9.85 | 8.2 | 9.6 | 0.59 | 0.49 | 0.02 | 0.019 |
| 13 | 9.65 | 5.15 | 15.05 | 9.6 | 0.59 | 0.49 | 0.0376 | 0.019 |
| 14 | 15.05 | 5.15 | 15.05 | 9.6 | 0.59 | 0.7525 | 0.02 | 0.0129 |
| 15 | 9.65 | 9.85 | 15.05 | 9.6 | 0.7525 | 0.49 | 0.02 | 0.0129 |
| 16 | 15.05 | 9.85 | 15.05 | 9.6 | 0.7525 | 0.7525 | 0.0376 | 0.019 |
| Run | eω | eps | eV | eQs | tsω | tsp | tsV | tsQ | Aω | AP | AV | AQ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [%] | [%] | [%] | [%] | [s] | [s] | [s] | [s] | [rad/s] | [W] | [V] | [Var] | |
| 1 | 1.27 × 10−5 | 8.40 × 10−2 | 2.31 × 10−3 | 0.658 | 2.592 | 1.663 | 1.418 | 1.490 | 0.065 | 22.855 | 1.591 | 52.920 |
| 2 | 1.25 × 10−5 | 8.80 × 10−2 | 2.60 × 10−3 | 4.8982 | 2.690 | 1.809 | 1.614 | 1.540 | 0.110 | 37.469 | 4.172 | 101.629 |
| 3 | 4.91 × 10−5 | 8.42 × 10−2 | 1.50 × 10−3 | 0.7462 | 3.276 | 1.858 | 1.760 | 1.590 | 0.109 | 50.210 | 4.774 | 136.320 |
| 4 | 4.45 × 10−5 | 9.68 × 10−2 | 4.10 × 10−3 | 1.3867 | 3.423 | 1.760 | 1.418 | 1.250 | 0.081 | 25.749 | 2.125 | 75.430 |
| 5 | 1.07 × 10−5 | 8.87 × 10−2 | 4.80 × 10−3 | 4.3778 | 2.934 | 1.809 | 1.614 | 1.880 | 0.109 | 45.352 | 4.957 | 133.294 |
| 6 | 2.03 × 10−5 | 8.35 × 10−2 | 5.00 × 10−3 | 4.7221 | 2.934 | 1.858 | 1.760 | 1.330 | 0.108 | 53.748 | 4.925 | 147.597 |
| 7 | 5.94 × 10−5 | 9.02 × 10−2 | 3.90 × 10−3 | 1.5435 | 2.445 | 1.760 | 1.614 | 1.880 | 0.107 | 27.007 | 3.585 | 62.612 |
| 8 | 2.80 × 10−5 | 6.06 × 10−2 | 6.10 × 10−3 | 9.6712 | 3.619 | 1.907 | 1.809 | 0.900 | 0.107 | 40.996 | 3.574 | 87.401 |
| 9 | 5.38 × 10−6 | 8.68 × 10−2 | 3.60 × 10−3 | 2.2609 | 3.032 | 1.760 | 1.565 | 1.440 | 0.118 | 41.647 | 4.813 | 140.314 |
| 10 | 3.11 × 10−6 | 8.87 × 10−2 | 2.60 × 10−3 | 8.3153 | 0.978 | 1.809 | 1.760 | 0.900 | 0.117 | 50.611 | 4.355 | 157.833 |
| 11 | 2.32 × 10−5 | 8.72 × 10−2 | 3.60 × 10−3 | 0.6566 | 4.010 | 1.760 | 1.712 | 1.640 | 0.118 | 42.914 | 3.895 | 103.365 |
| 12 | 9.41 × 10−6 | 8.82 × 10−2 | 4.60 × 10−3 | 8.3333 | 3.276 | 1.712 | 1.565 | 0.660 | 0.074 | 26.292 | 1.843 | 52.678 |
| 13 | 9.83 × 10−6 | 8.56 × 10−2 | 3.90 × 10−3 | 0.6013 | 3.423 | 1.809 | 1.858 | 1.390 | 0.120 | 39.684 | 3.924 | 106.555 |
| 14 | 9.25 × 10−6 | 8.09 × 10−2 | 6.10 × 10−3 | 1.6742 | 3.472 | 1.809 | 1.712 | 2.130 | 0.118 | 39.587 | 3.980 | 105.772 |
| 15 | 2.70 × 10−5 | 8.26 × 10−2 | 2.00 × 10−3 | 0.4831 | 4.499 | 1.858 | 1.809 | 1.640 | 0.118 | 59.258 | 4.792 | 157.127 |
| 16 | 3.25 × 10−5 | 9.29 × 10−2 | 3.80 × 10−3 | 1.0001 | 4.743 | 1.760 | 1.516 | 1.690 | 0.117 | 48.729 | 4.813 | 130.817 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Doile, G.N.D.; Balestrassi, P.P.; Castilla, M.; Zambroni de Souza, A.C.; Miret, J. An Experimental Approach for Secondary Consensus Control Tuning for Inverter-Based Islanded Microgrids. Energies 2023, 16, 517. https://doi.org/10.3390/en16010517
de Doile GND, Balestrassi PP, Castilla M, Zambroni de Souza AC, Miret J. An Experimental Approach for Secondary Consensus Control Tuning for Inverter-Based Islanded Microgrids. Energies. 2023; 16(1):517. https://doi.org/10.3390/en16010517
Chicago/Turabian Stylede Doile, Gabriel Nasser Doyle, Pedro Paulo Balestrassi, Miguel Castilla, Antonio Carlos Zambroni de Souza, and Jaume Miret. 2023. "An Experimental Approach for Secondary Consensus Control Tuning for Inverter-Based Islanded Microgrids" Energies 16, no. 1: 517. https://doi.org/10.3390/en16010517
APA Stylede Doile, G. N. D., Balestrassi, P. P., Castilla, M., Zambroni de Souza, A. C., & Miret, J. (2023). An Experimental Approach for Secondary Consensus Control Tuning for Inverter-Based Islanded Microgrids. Energies, 16(1), 517. https://doi.org/10.3390/en16010517











