PHE (Plate Heat Exchanger) for Condensing Duties: Recent Advances and Future Prospects
Abstract
:1. Introduction
2. Heat Transfer in Two-Phase Condensing Flows Inside PHE Channels
2.1. Overall Analysis of Published Studies
2.2. Recent Developments in PHE Condensers for Waste Heat Recovery, Heat Pumps and ORC Cycle
2.3. Studies of Refrigerants with Low Global Warming Potential
2.4. Local Process Parameters
2.5. Condensation of Steam and Other Process Vapours
2.6. The Accuracy of Heat Transfer Correlations for PHE
2.7. The Thermal Modelling and Design of PHE Condensers
3. Pressure Drop in Two-Phase Condensing Flows Inside PHE Channels
3.1. Correlations with Averaged Process Parameters
3.2. Pressure Drop Prediction with Local Process Parameters
4. The Structure of Two-Phase Condensing Flows Inside PHE Channels
5. The Conclusions and Future Prospects
- Further development of theoretical analysis and fundamental knowledge on heat transfer and hydrodynamics in condensing two-phase flows inside criss-cross flow channels, formed by plates with inclined corrugations of different geometries.
- The experimental studies of heat transfer and pressure losses during different vapour condensation in PHE channels, with an emphasis on local process parameters at small zones of channels and their distribution on channels field accounting for plates corrugation geometry.
- Experimental and theoretical studies of two-phase flow maldistribution inside PHE channels and between different channels in a system of channels at PHE with different numbers of plates.
- A deeper understanding of condensing two-phase flow structures, the change between different flow regimes and their effect on heat transfer intensity and pressure losses based on the methods of flow visualisation and CFD modelling.
- Reliable methods of PHE modelling and design for condensing duties, based on one-dimensional mathematical models accounting for the distribution of local process parameters along the channel length and the effects of flow distribution zones and port areas at commercially produced plates.
- Developing the methods for optimisation of PHE and their plate constructions for specified conditions of the vapour condensation process.
- Further development of methods and software for PHE condensers design and selection as part of heat exchanger networks in complex heat recuperation systems.
- Improving constructions of PHE for condensation of different vapours, based on newly acquired knowledge of process phenomena with the increased potential of energy saving and a reduced footprint on the environment.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chong, C.T.; Fan, Y.V.; Lee, C.T.; Klemeš, J.J. Post COVID-19 energy sustainability and carbon emissions neutrality. Energy 2022, 241, 122801. [Google Scholar] [CrossRef] [PubMed]
- Klemeš, J.J.; Arsenyeva, O.; Kapustenko, P.; Tovazhnyanskyy, L. Compact Heat Exchangers for Energy Transfer Intensification: Low Grade Heat and Fouling Mitigation; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Arsenyeva, O.P.; Tovazhnyanskyy, L.L.; Kapustenko, P.O.; Khavin, G.L.; Yuzbashyan, A.P.; Arsenyev, P.Y. Two types of welded plate heat exchangers for efficient heat recovery in industry. Appl. Therm. Eng. 2016, 105, 763–773. [Google Scholar] [CrossRef]
- Vakili-Farahani, F.; Amalfi, R.L.; Thome, J.R. Two-phase heat transfer and pressure drop within plate heat exchangers. Encyclopedia of Two-Phase Heat Transfer and Flow II: Special Topics and Applications. 2016, pp. 145–215. Available online: https://www.worldscientific.com/ (accessed on 15 November 2022).
- Eldeeb, R.; Aute, V.; Radermacher, R. A survey of correlations for heat transfer and pressure drop for evaporation and condensation in plate heat exchangers. Int. J. Refrig. 2016, 65, 12–26. [Google Scholar] [CrossRef]
- Tao, X.; Ferreira, C.A.I. Heat transfer and frictional pressure drop during condensation in plate heat exchangers: Assessment of correlations and a new method. Int. J. Heat Mass Transf. 2019, 135, 996–1012. [Google Scholar] [CrossRef]
- Zhang, J.; Baldasso, E.; Mancini, R.; Elmegaard, B.; Haglind, F. Evaluation of Heat Transfer Correlations for Flow Condensation in Plate Heat Exchangers and Their Impact on The Design of Organic Rankine Cycle Systems. In Proceedings of the 5th International Seminar on ORC Power Systems, Athens, Greece, 9–11 September 2019; National Technical University of Athens: Athens, Greece, 2019; p. 147. [Google Scholar]
- Zhang, J.; Kærn, M.R.; Ommen, T.; Elmegaard, B.; Haglind, F. Condensation heat transfer and pressure drop characteristics of R134a, R1234ze (E), R245fa and R1233zd (E) in a plate heat exchanger. Int. J. Heat Mass Transf. 2019, 128, 136–149. [Google Scholar] [CrossRef]
- Zhang, J.; Elmegaard, B.; Haglind, F. Condensation heat transfer and pressure drop correlations in plate heat exchangers for heat pump and organic Rankine cycle systems. Appl. Therm. Eng. 2021, 183, 116231. [Google Scholar] [CrossRef]
- Shah, M.M. Heat transfer during condensation in corrugated plate heat exchangers. Int. J. Refrig. 2021, 127, 180–193. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, S.K.; Sharma, D. A Comprehensive Review on Thermal Performance Enhancement of Plate Heat Exchanger. Int. J. Thermophys. 2022, 43, 1–68. [Google Scholar] [CrossRef]
- Würfel, R.; Ostrowski, N. Experimental investigations of heat transfer and pressure drop during the condensation process within plate heat exchangers of the herringbone-type. Int. J. Therm. Sci. 2004, 43, 59–68. [Google Scholar] [CrossRef]
- Amalfi, R.L.; Cataldo, F.; Thome, J.R. An optimization optimisation algorithm to design compact plate heat exchangers for waste heat recovery applications in high power datacenter racks. In Proceedings of the 18th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), Las Vegas, NV, USA, 29–31 May 2019; pp. 159–166. [Google Scholar]
- Zhang, J.; Elmegaard, B.; Haglind, F. Condensation heat transfer and pressure drop characteristics of zeotropic mixtures of R134a/R245fa in plate heat exchangers. Int. J. Heat Mass Transf. 2021, 164, 120577. [Google Scholar] [CrossRef]
- Blondel, Q.; Tauveron, N.; Lhermet, G.; Caney, N. Zeotropic Mixtures Study in Plate Heat Exchangers and ORC Systems. Appl. Therm. Eng. 2022, 219, 119418. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, J.; Haglind, F. Experimental analysis of hydrofluoroolefin zeotropic mixture R1234ze(E)/R1233zd(E) condensation in a plate heat exchanger. Int. Commun. Heat Mass Transf. 2022, 135, 106073. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, J.; Haglind, F. Experimental analysis of condensation of zeotropic mixtures from 70 °C to 90 °C in a plate heat exchanger. Int. J. Refrig. 2022, 137, 166–177. [Google Scholar] [CrossRef]
- Jung, J.H.; Ko, Y.M.; Kang, Y.T. Condensation heat transfer characteristics and energy conversion performance analysis for low GWP refrigerants in plate heat exchangers. Int. J. Heat Mass Transf. 2021, 166, 120727. [Google Scholar] [CrossRef]
- Ko, Y.M.; Jung, J.H.; Sohn, S.; Song, C.H.; Kang, Y.T. Condensation heat transfer performance and integrated correlations of low GWP refrigerants in plate heat exchangers. Int. J. Heat Mass Transf. 2021, 177, 121519. [Google Scholar] [CrossRef]
- Kwon, O.J.; Jung, J.H.; Kang, Y.T. Development of experimental Nusselt number and friction factor correlations for condensation of R-1233zd (E) in plate heat exchangers. Int. J. Heat Mass Transf. 2020, 15, 120008. [Google Scholar] [CrossRef]
- Cattelan, G.; Diani, A.; Azzolin, M. Condensation heat transfer of R1234ze (E) and R134a inside a brazed plate heat exchanger: Experimental data and model assessment. Int. J. Refrig. 2022, 143, 57–67. [Google Scholar] [CrossRef]
- Miyata, K.; Yanagihara, S.; Watanabe, N.; Mori, H.; Hamamoto, Y.; Umezawa, S.; Sugita, K. Effect of chevron angle on condensation heat transfer of refrigerants at high pressures in plate heat exchangers. Trans. Jpn. Soc. Refrig. Air Cond. Eng. 2018, 35, 383–388. [Google Scholar]
- Miyata, K.; Yamasaki, Y.; Kurose, K.; Hamamoto, Y.; Mori, H.; Umezawa, S. Cooling and condensation heat transfer and pressure drop of a refrigerant at high pressures in a chevron-type plate heat exchanger with high chevron angle. Mech. Eng. J. 2020, 7, 20-00107. [Google Scholar] [CrossRef]
- Tao, X.; Kirkenier, J.; Ferreira, C.I. Condensation of NH3 within a plate heat exchanger of small diameter channel. In Proceedings of the International Conference on Micro/Nanoscale Heat Transfer, Dalian, China, 8–10 July 2019; Volume 58905, p. V001T04A002. [Google Scholar]
- Tao, X.; Dahlgren, E.; Leichsenring, M.; Ferreira, C.A.I. NH3 condensation in a plate heat exchanger: Experimental investigation on flow patterns, heat transfer and frictional pressure drop. Int. J. Heat Mass Transf. 2020, 151, 119374. [Google Scholar] [CrossRef]
- Wang, R.; Kabelac, S. Condensation quasi-local heat transfer and frictional pressure drop of R1234ze (E) and R134a in a micro-structured plate heat exchanger. Appl. Therm. Eng. 2021, 197, 117404. [Google Scholar] [CrossRef]
- Wang, R.; Sun, T.; Polzin, A.E.; Kabelac, S. Experimental investigation of the two-phase local heat transfer coefficients for condensation of R134a in a micro-structured plate heat exchanger. Heat Mass Transf. 2022, 58, 1–18. [Google Scholar] [CrossRef]
- Longo, G.A.; Mancin, S.; Righetti, G.; Zilio, C. Local heat transfer coefficients of R32 and R410a condensation inside a brazed plate heat exchanger (BPHE). Int. J. Heat Mass Transf. 2022, 194, 123041. [Google Scholar] [CrossRef]
- Thonon, B.; Bontemps, A. Condensation of pure and mixture of hydrocarbons in a compact heat exchanger: Experiments and modelling. Heat Transf. Eng. 2002, 23, 3–17. [Google Scholar] [CrossRef] [Green Version]
- Müller, A.; Kabelac, S. The experimental determination of heat transfer and pressure drop during condensation in a plate heat exchanger with corrugated plates. Heat Transf. XIII Simul. Exp. Heat Mass Transf. 2014, 83, 337–349. [Google Scholar]
- Zhou, W.; Hu, S.; Ma, X.; Zhou, F. Condensation heat transfer correlation for water-ethanol vapor mixture flowing through a plate heat exchanger. Heat Mass Transf. 2018, 54, 3025–3033. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Zhao, Z.N. Analysis of performance of steam condensation heat transfer and pressure drop in plate condensers. Heat Transf. Eng. 1993, 14, 32–41. [Google Scholar] [CrossRef]
- Wang, L.; Sunden, B.; Manglik, R.M. Plate Heat Exchangers. Design, Applications and Performance; WIT Press: Southhampton, UK, 2007. [Google Scholar]
- Tovazhnyansky, L.L.; Kapustenko, P.O.; Nagorna, O.G.; Perevertaylenko, O.Y. The simulation of multicomponent mixtures condensation in plate condensers. Heat Transf. Eng. 2004, 25, 16–22. [Google Scholar] [CrossRef]
- Longo, G.A.; Righetti, G.; Zilio, C. A new computational procedure for refrigerant condensation inside herringbone-type Brazed Plate Heat Exchangers. Int. J. Heat Mass Transf. 2015, 82, 530–536. [Google Scholar] [CrossRef]
- Martin, H. A theoretical approach to predict the performance of chevron-type plate heat exchangers. Chem. Eng. Process. Process Intensif. 1996, 35, 301–310. [Google Scholar] [CrossRef]
- Dović, D.; Palm, B.; Švaić, S. Generalized correlations for predicting heat transfer and pressure drop in plate heat exchanger channels of arbitrary geometry. Int. J. Heat Mass Transf. 2009, 52, 4553–4563. [Google Scholar] [CrossRef]
- Arsenyeva, O.P.; Tovazhnyanskyy, L.L.; Kapustenko, P.O.; Demirskiy, O.V. Heat transfer and friction factor in criss-cross flow channels of plate-and-frame heat exchangers. Theor. Found. Chem. Eng. 2012, 46, 634–641. [Google Scholar] [CrossRef]
- Arsenyeva, O.; Kapustenko, P.; Tovazhnyanskyy, L.; Khavin, G. The influence of plate corrugations geometry on plate heat exchanger performance in specified process conditions. Energy 2013, 57, 201–207. [Google Scholar] [CrossRef] [Green Version]
- Kapustenko, P.O.; Klemeš, J.J.; Arsenyeva, O.P.; Kusakov, S.K.; Tovazhnyanskyy, L.L. The influence of plate corrugations geometry scale factor on performance of plate heat exchanger as condenser of vapour from its mixture with noncondensing gas. Energy 2020, 201, 117661. [Google Scholar] [CrossRef]
- Arman, B.; Rabas, T. Condensation Analysis for Plate and Frame Heat Exchangers; HTD-Vol 314; Argonne National Lab.(ANL): Argonne, IL, USA, 1995; Volume 12, pp. 97–104. [Google Scholar]
- Tovazhnyanski, L.L.; Kapustenko, P.A. Intensification of heat and mass transfer in channels of plate condensers. Chem. Eng. Commun. 1984, 31, 351–366. [Google Scholar] [CrossRef]
- Wang, L.; Christensen, R.; Sunden, B. An experimental investigation of steam condensation in plate heat exchangers. Int. J. Heat Exch. 2000, 1, 125–150. [Google Scholar]
- Arsenyeva, O.; Tovazhnyansky, L.; Kapustenko, P.; Perevertaylenko, O.; Khavin, G. Investigation of the new corrugation pattern for low pressure plate condensers. Appl. Therm. Eng. 2011, 31, 2146–2152. [Google Scholar] [CrossRef]
- Gullapalli, V.S. Estimation of Thermal and Hydraulic Characteristics of Compact Brazed Plate Heat Exchangers. Ph.D. Thesis, Lund University, Lund, Sweden, 2013. [Google Scholar]
- Lockhart, R.W.; Martinelli, R.C. Proposed correlation of data for isothermal two-phase, two-component flow in pipes. Chem. Eng. Prog. 1949, 45, 39–48. [Google Scholar]
- Wang, B.; Arsenyeva, O.; Zeng, M.; Klemeš, J.J.; Varbanov, P.S. An advanced Grid Diagram for heat exchanger network retrofit with detailed plate heat exchanger design. Energy 2022, 248, 123485. [Google Scholar] [CrossRef]
- Hu, S.; Ma, X. Experimental study of pressure drop during water–ethanol condensation in a vertical plate heat exchanger. Heat Mass Transf. 2022, 58, 1289–1302. [Google Scholar] [CrossRef]
- Wang, L.K.; Sunden, B.; Yang, Q.S. Pressure drop analysis of steam condensation in a plate heat exchanger. Heat Transf. Eng. 1999, 20, 71–77. [Google Scholar]
- Kapustenko, P.; Klemeš, J.J.; Arsenyeva, O.; Tovazhnyanskyy, L.; Zorenko, V. Pressure drop in two phase flow of condensing air-steam mixture inside PHE channels formed by plates with corrugations of different geometries. Energy 2021, 228, 120583. [Google Scholar] [CrossRef]
- Boyko, L.D.; Kruzhilin, G.N. Heat transfer and hydraulic resistance during condensation of steam in a horizontal tube and in a bundle of tubes. Int. J. Heat Mass Transf. 1967, 10, 361–373. [Google Scholar] [CrossRef]
- Tao, X.; Nuijten, M.P.; Ferreira, C.A.I. Two-phase vertical downward flow in plate heat exchangers: Flow patterns and condensation mechanisms. Int. J. Refrig. 2018, 85, 489–510. [Google Scholar] [CrossRef] [Green Version]
- Grabenstein, V.; Polzin, A.-E.; Kabelac, S. Experimental investigation of the flow pattern, pressure drop and void fraction of two-phase flow in the corrugated gap of a plate heat exchanger. Int. J. Multiph. Flow 2017, 91, 155–169. [Google Scholar] [CrossRef]
- Grabenstein, V.; Kabelac, S. Experimental and theoretical analysis of the local condensation heat transfer in a plate heat exchanger. J. Phys. Conf. Ser. 2012, 395, 012169. [Google Scholar] [CrossRef] [Green Version]
- Buscher, S. Visualization and modelling of flow pattern transitions in a cross-corrugated plate heat exchanger channel with uniform two-phase distribution. Int. J. Heat Mass Transf. 2019, 144, 118643. [Google Scholar] [CrossRef]
- Lee, D.; Yun, S.; Choi, J.; Kim, Y. Flow patterns and heat transfer characteristics of R-1234ze (E) for downward condensation in a plate heat exchanger. Int. J. Heat Mass Transf. 2021, 175, 121373. [Google Scholar] [CrossRef]
- Zhu, X.; Haglind, F. Computational fluid dynamics modeling of liquid–gas flow patterns and hydraulics in the cross-corrugated channel of a plate heat exchanger. Int. J. Multiph. Flow 2020, 122, 103163. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, T.; Zhang, H. A numerical study on condensation heat transfer and pressure drop characteristics of low pressure vapor in a plate heat exchanger. Therm. Sci. 2021, 25, 665–677. [Google Scholar] [CrossRef]
- AlfaLaval. AlfaCond Condensers. Available online: https://www.alfalaval.com/microsites/gphe/types/alfacond/ (accessed on 10 November 2022).

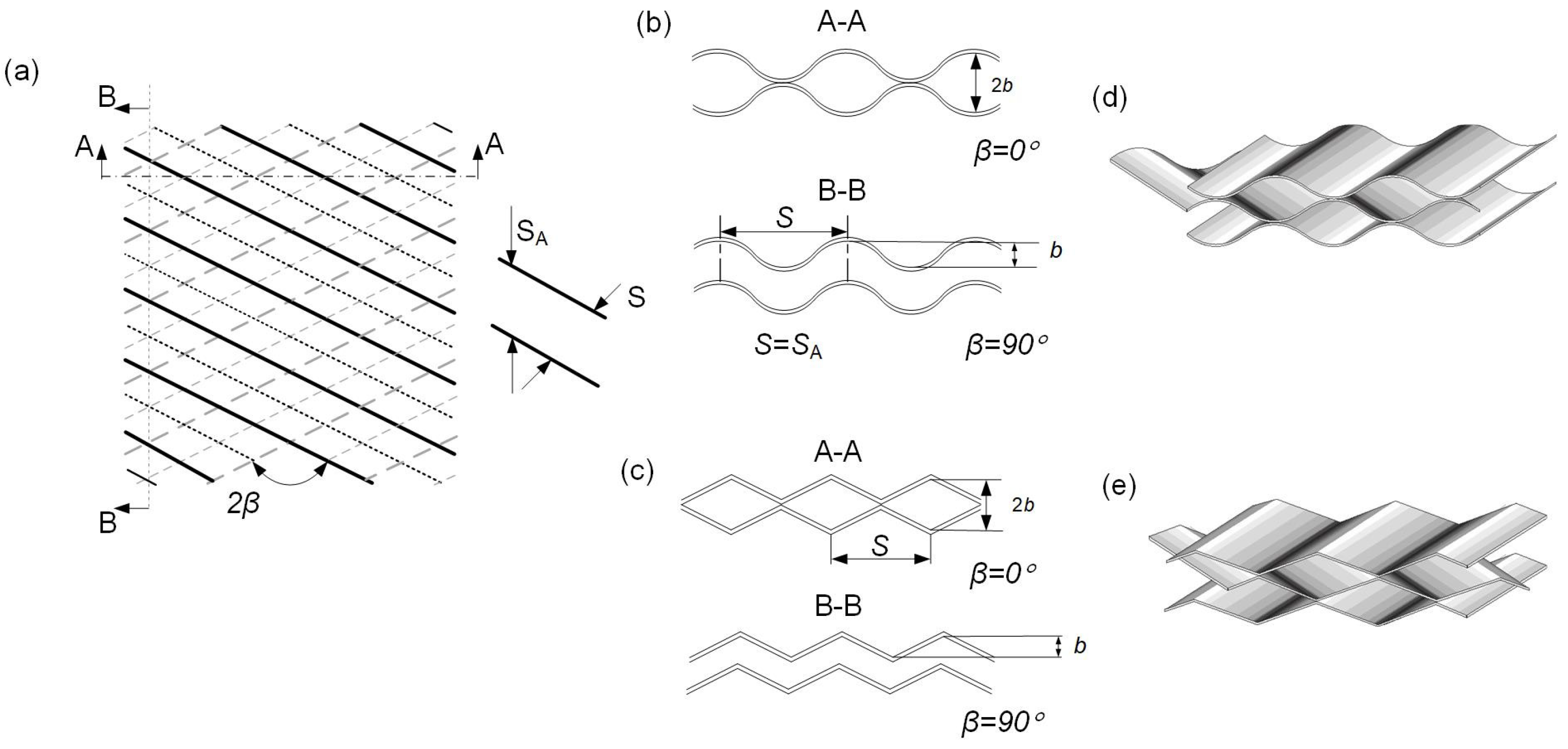
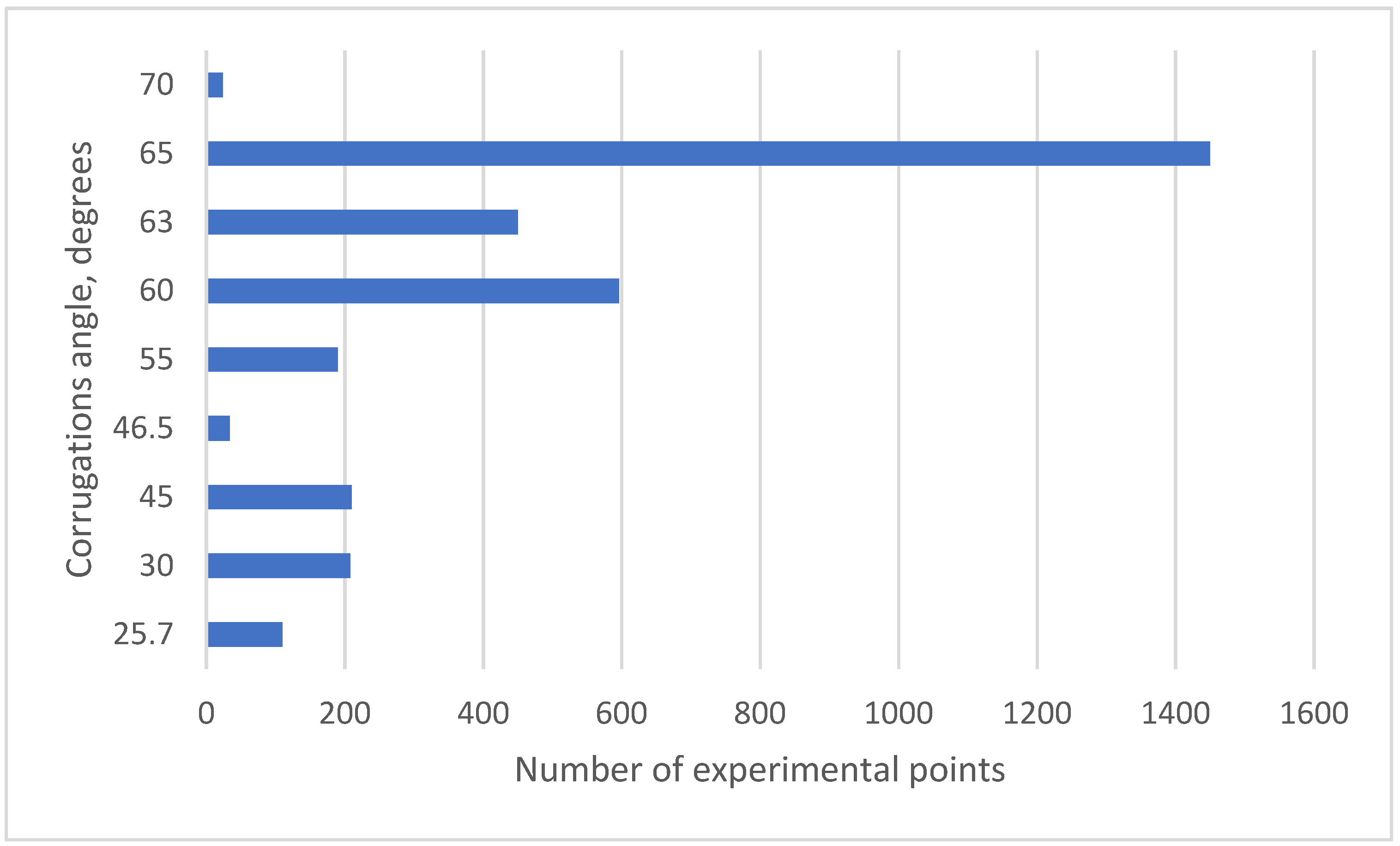
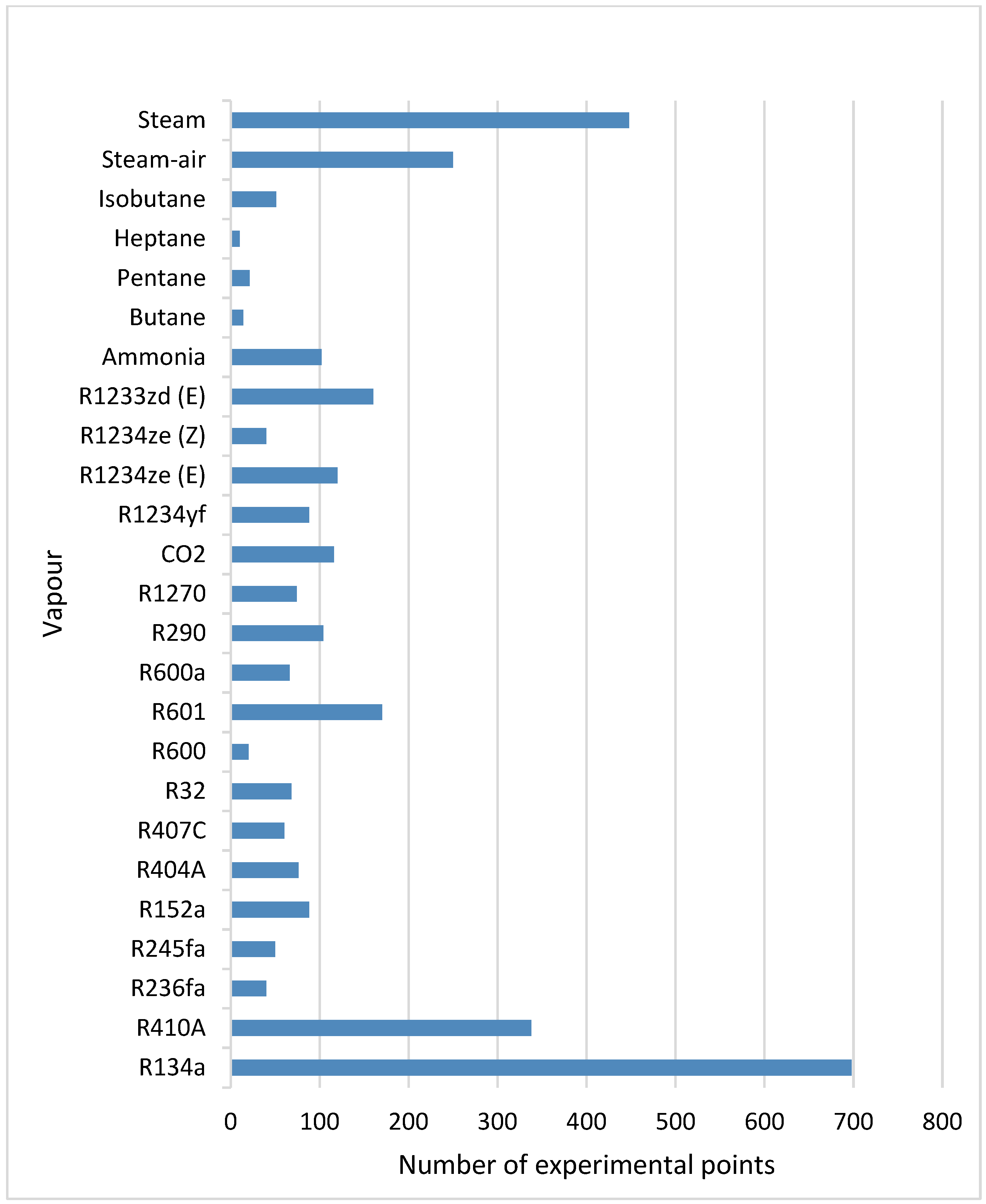
| Predicting Equations | Number of Data Points | MAE, % | % of Points with Error < 50% |
|---|---|---|---|
| Equations (1) and (5) | 2376 | 25.5 | 93 |
| Equations (3) and (5) | 984 | 22.9 | 93 |
| Equations (1) and (6) | 237 | 6.4 | 100− |
| Equations (1) and (7) | 283 | 8.9 | 100− |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kapustenko, P.; Klemeš, J.J.; Arsenyeva, O.; Tovazhnyanskyy, L. PHE (Plate Heat Exchanger) for Condensing Duties: Recent Advances and Future Prospects. Energies 2023, 16, 524. https://doi.org/10.3390/en16010524
Kapustenko P, Klemeš JJ, Arsenyeva O, Tovazhnyanskyy L. PHE (Plate Heat Exchanger) for Condensing Duties: Recent Advances and Future Prospects. Energies. 2023; 16(1):524. https://doi.org/10.3390/en16010524
Chicago/Turabian StyleKapustenko, Petro, Jiří Jaromír Klemeš, Olga Arsenyeva, and Leonid Tovazhnyanskyy. 2023. "PHE (Plate Heat Exchanger) for Condensing Duties: Recent Advances and Future Prospects" Energies 16, no. 1: 524. https://doi.org/10.3390/en16010524
APA StyleKapustenko, P., Klemeš, J. J., Arsenyeva, O., & Tovazhnyanskyy, L. (2023). PHE (Plate Heat Exchanger) for Condensing Duties: Recent Advances and Future Prospects. Energies, 16(1), 524. https://doi.org/10.3390/en16010524







